The analysis in [4], [5] and [6] depends significantly on the fact that the finite anti-plane shear problem is governed by a second-order quasi-linear partial differential equation and can therefore be successfully treated using the hodograph transformation. In this paper, we first show that the qualitative features of the results in [4] and [5] for the Mode III crack problem can be obtained by a direct local asymptotic analysis that does not use the hodograph transformation. The advantage of the procedure used here lies in its applicability to the Mode I problem of the plane strain, which is our main objective.
Section 2 begins with the formulation of the Mode III crack problem, addressed in [4]. We obtain the asymptotic representation near the crack tip of a number of solutions of the equilibrium displacement equation valid in overlapping domains. In this section we present a brief overview of the equilibrium theory of finitely deformed, homogeneous and isotropic elastic solids.
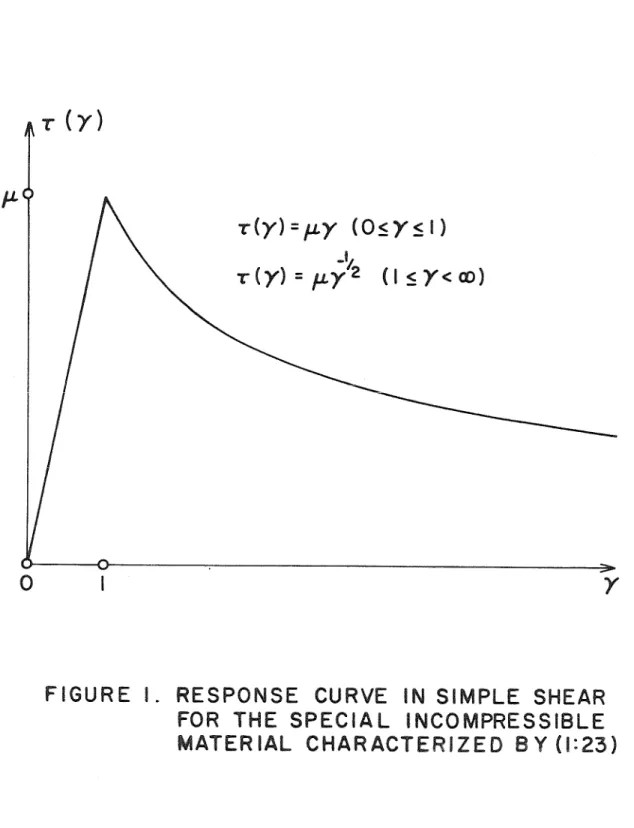
4], by substituting (l .14) into the constitutive law for incompressible materials (l allows the reduction of the field equations to. As a result of the inequality (1 .15), the displacement equation of equilibrium (1 .17) is shown to be elliptic at a solution u and at a point (x1,x2) if and only if.
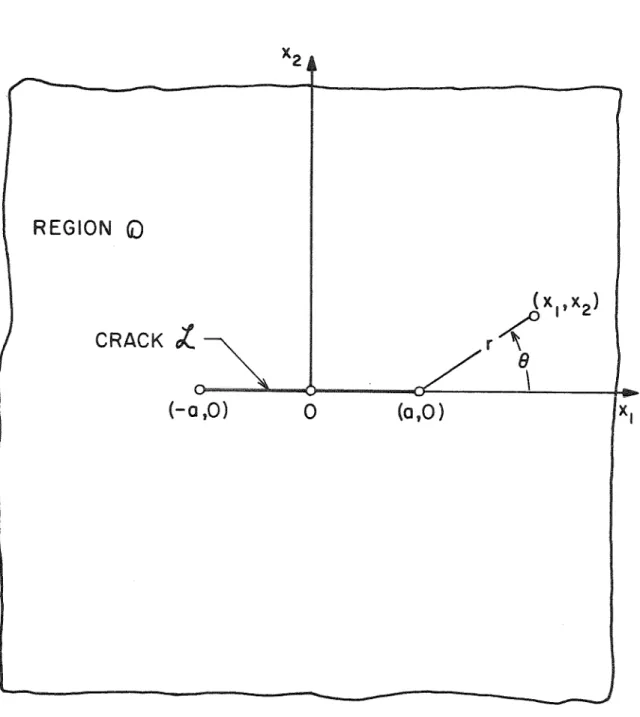
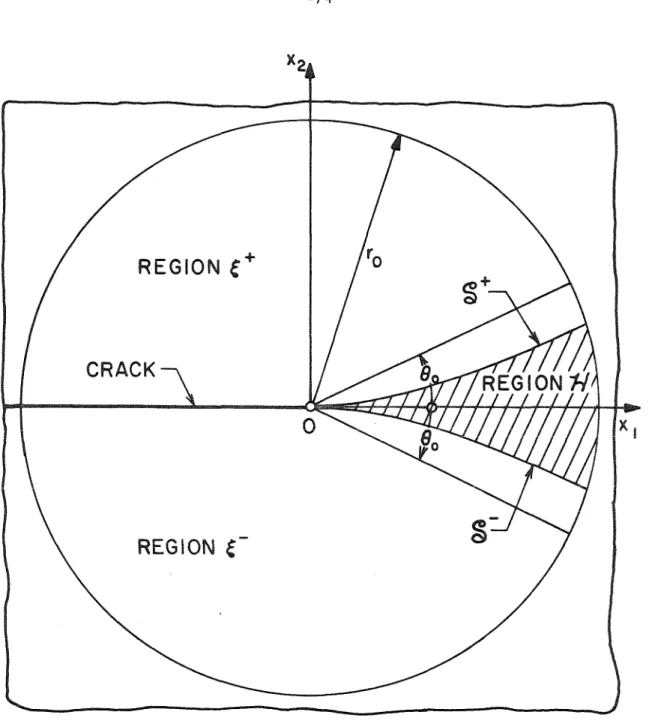
Further, we assume that the crack boundary in the deformed body remains tensile. In the small-scale problem, ~ is assumed to be small compared to unity and the finite slit is replaced by a semi-infinite one. Constraints (2.7) on m guarantee that the displacement remains bounded 1 The symbol of asymptotic equality is used in the following sense;.
In this way it can be seen that the general solution of (2.12) can be written in the form We first investigate the solutions of the differential equation (2.2b) which, in the region fl, have the asymptotic form (2.6), where v(6) is a. Asymptotic solutions for the next order of the equi- 1 ibrium displacement equation (2.2a), (2.2b) were found at s+ and 'JI in an attempt to eliminate some of the I-V cases in the figure.
Our aim, in this paper, is to reproduce the solution in [4] in the vicinity of the crack tip· and therefore we assume that case II holds, so that. To conclude, we summarize the asymptotic representation for the solution of the cracking problem in the vicinity of the right crack tip.
We also insist that the solution is bounded near the crack tip and that the limits Ya,B(x1.0±) exist and are continuous for -a< x. Instead, we consider the asymptotic nature of the solution near the crack tip.1. We follow the example of anti-plane shear in the previous section and assume that the local deformation field is represented by .
Here we assume that the deformations are "worst" in the x2-direction. where q is a continuously differentiable function for -8 < e < e and. 1We treat the case m1=m2<0 in a similar way to the case of positive equal exponents discussed in Appendix B. We find that the homogeneous solution is unbounded at e = 0 and is neglected, and a smooth particular solution gives.
1Deformation is normalized so that the crack tip does not move relative to the x1 axis. After a painstaking analysis, we prove that no smooth solution v2 exists at (0,TI] that is compatible with (B.28) and can be linked to the hyperbolic solution at 'JI over 8+. Physically in the vicinity from the crack plane we expect the leading order to represent homogeneous deformation and (3.35) a state of uniaxial stress parallel to the y2 direction.
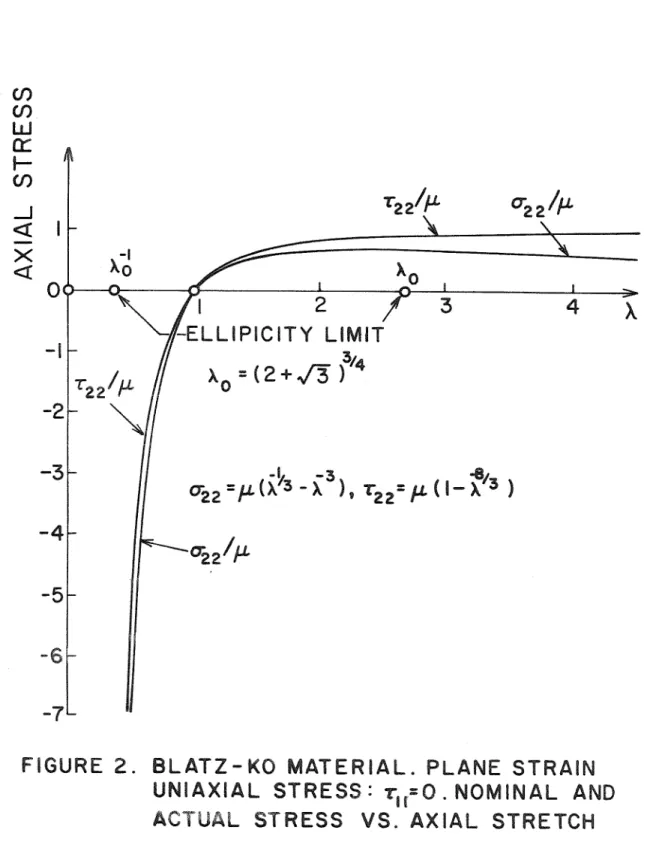
This further limits the range of the stretch relation so that elliptic solutions of interest obey. 1rt it can be shown that functions Va producing a vanishing determinant are not consistent with either the boundary conditions on the crack surface or the matching over g+. Equation (3.37) satisfies the differential equations (3.3) in the appropriate order if. 3.38), where L is the differential operator. 3.43).
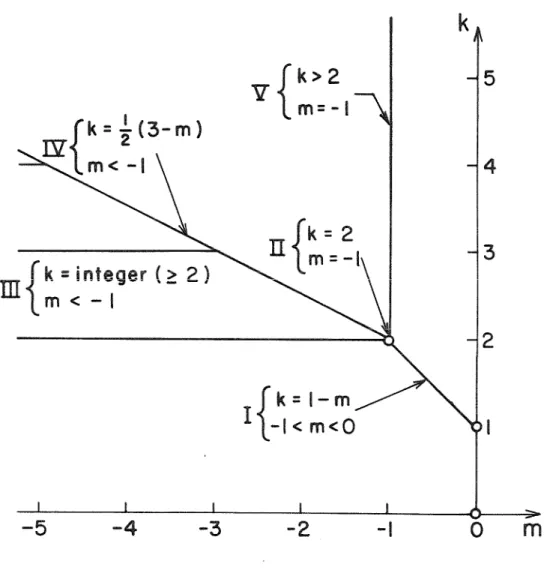
We now generate the first order asymptotic solution with the appropriate smoothness for the small-scale nonlinear crack problem. We confirm (3.49) by first assuming the existence of an equilibrium solution in the vicinity of the crack tip that has the general form. The relationships between the exponents k and m which 1The result (3.49) can ensure that no concentrated forces act at the crack tip.
HIGHER ORDER CONSIDERATIONS AND RESULTS
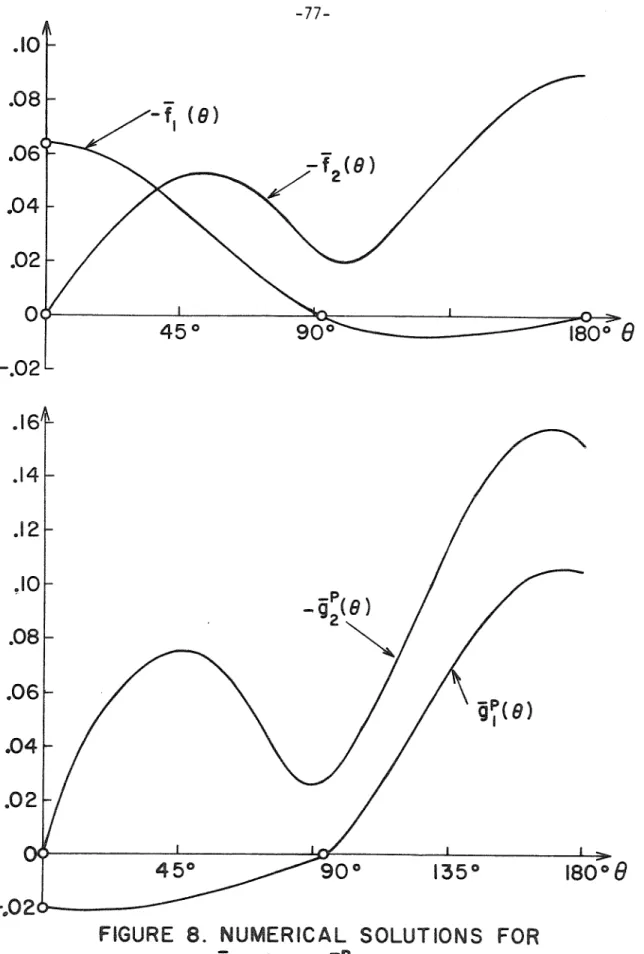
Recall that the calmness of the complete solution of the problem requires continuous coordinates and Piola traction at 8+. Consequently, in order for a solution to the inhomogeneous problem to exist, the eigenfunction (4.27) must be orthogonal on the right-hand side in (4.15). 1 This expression, with (4.22), facilitates a numerical investigation of the existence of a solution to the boundary value problem.
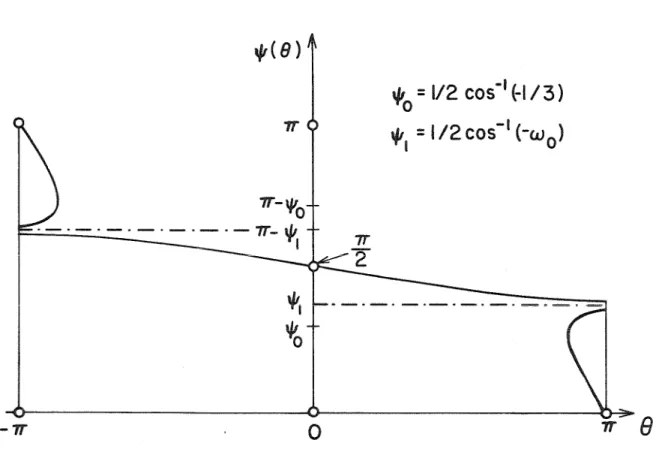
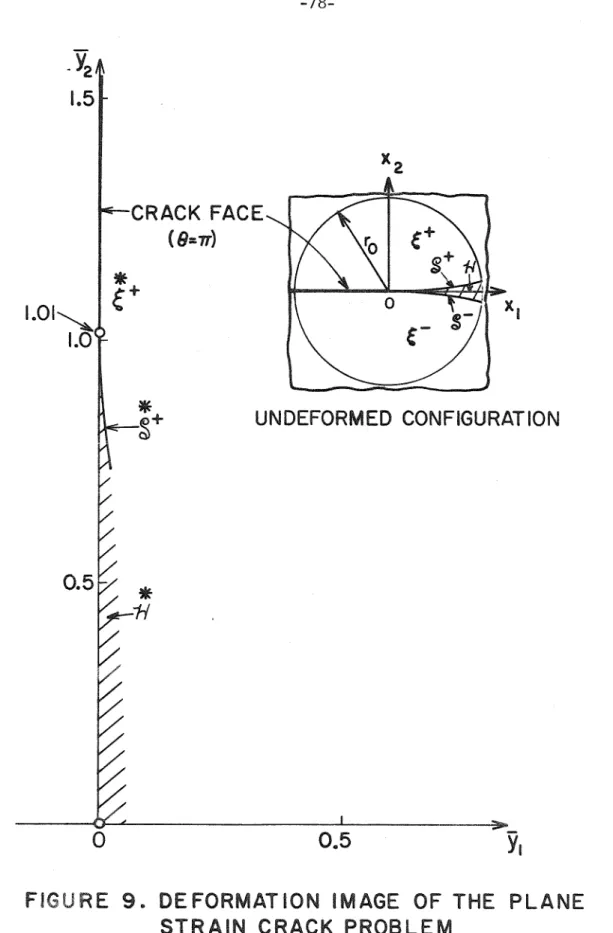
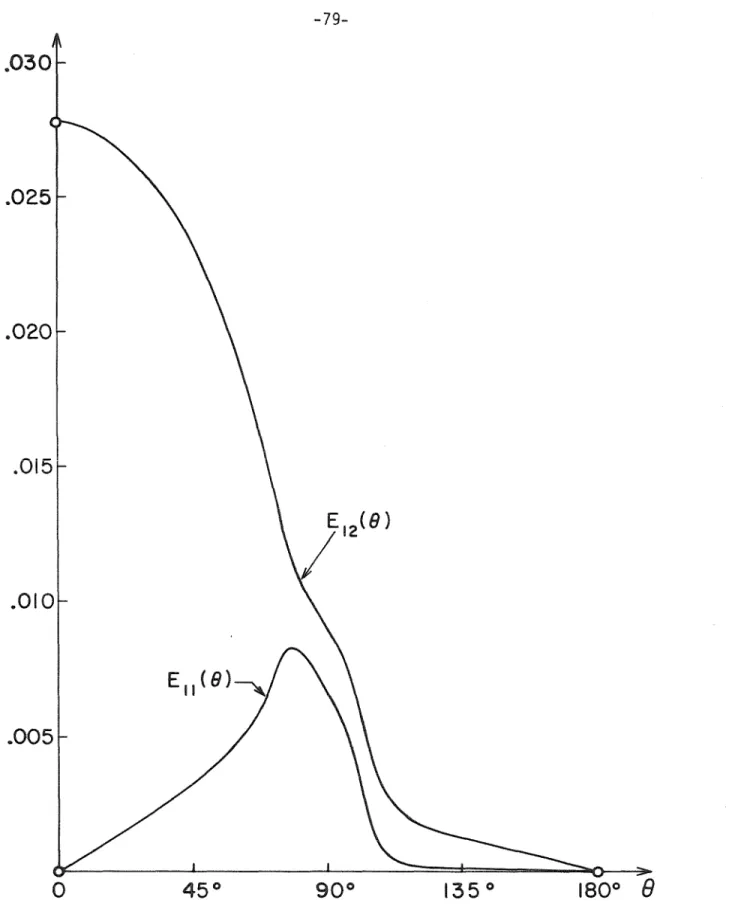
The results represent a local one-to-one map of the neighborhood of the crack tip. It can be seen from the figure that in the vicinity of r = 0 the traction-free surfaces (e =±TI) open up to nearly flat surfaces oriented in the direction of the applied load at infinity. In the hyperbolic region 'JI, the leadin9 terms in the coordinates do not contribute directly to the stresses T11 and T12.
The stresses (4.46) indicate that the material in the vicinity of the crack tip is subjected to deformation approximating uniaxial stress parallel to y. 8] P.J. Blatz and W.L.Ko, "Application of finite elastic theory to the deformation of rubbery materials11, Transactions of the Society of. 10] J.K.Knowles, "On finite anti-plane shear for incompressible elastic materials11, Journal of the Australian Mathematical Society, 19.
In this Appendix, solutions are found for the anti-plane shear crack problem involving two elastostatic shocks asymptotically tangent to rays emanating from the crack tips. In what follows, we consider o~e:;:;1T and refer to (A.4) for the displacement in the lower half-plane. The shock condition (A.17) can be made to hold simply by an appropriate choice of the ratio v1;v2.
As a result, there is a system of solutions to the crack problem in which the displacement field near the crack tip is shaped. In this study, the applied shear at infinity y was assumed to be small compared to one, and the solutions of the corresponding equilibrium displacement equation near the crack tip were chosen to facilitate agreement with the linear elastic solution valid otherwise. where. The symmetry (3.7) associated with this problem means B.4) Inequality (B.2) guarantees singular strain gradients and bounded displacements at r = 0.
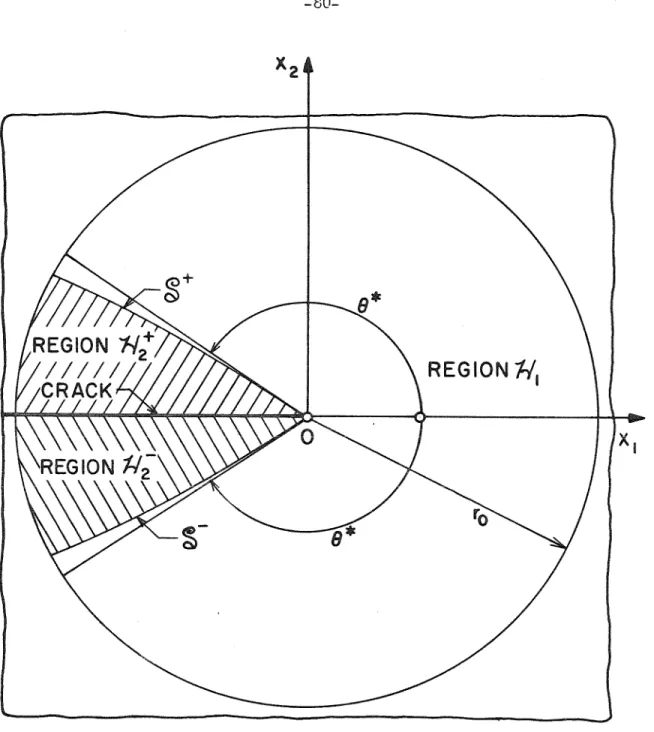
Now assume that the first condition in (B.14) holds and consider in particular the crack plane e =TI. LOCAL GEOMETRY NEAR THE TIP TIP FOR THE ANTI-FLATSLIDE PROBLEM TREATED IN APPENDIX A.