This dissertation presents a qualitative case study of three teachers teaching mathematics at the middle stage. Thus, focus group interviews, semi-structured one-to-one interviews and document analysis were used for data collection to explore teachers' experiences of teaching mathematics at the secondary stage.
Introduction
Furthermore, teachers teaching mathematics at the intermediate stage should be guided by skills experiences. The study aims to explore teachers' experiences in teaching mathematics at the intermediate stage.
Project tittle
Focus of the study
Location of the study
The study conducted by Brijlall and Maharaj (2013) examines teacher experiences of the implications of the Curriculum and Assessment Policy Statement (CAPS) (Context). Further, the study conducted by Moyo, Sibanda and Beushausen (2012) asserts that teachers can be guided by professional reasoning (reason from the profession), social reasoning (reason from society) and personal reasoning (reason from the individual). teaching subjects.
Objectives of the study
What is the financial condition of the majority of teachers who teach mathematics in the intermediate phase. What is the physical condition of the majority of teachers who teach mathematics in the intermediate phase.
Questions of the study
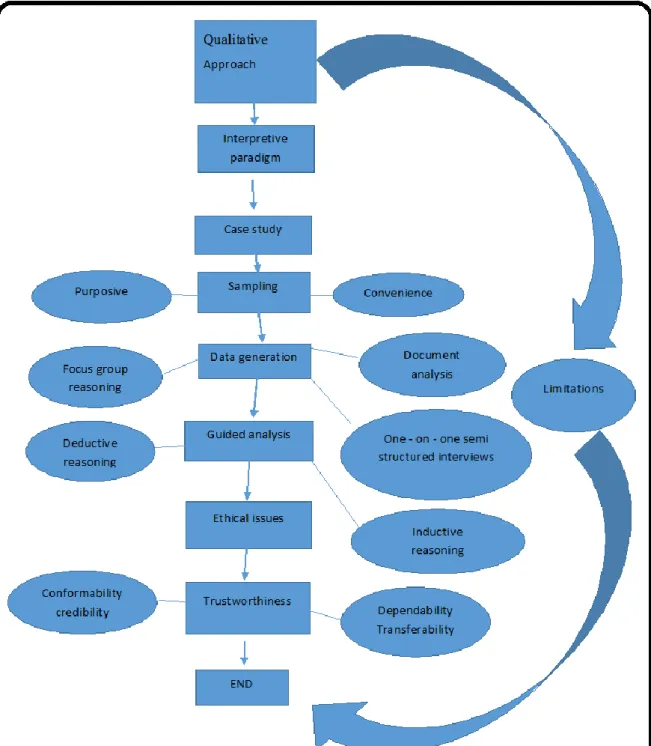
Research design and Methodology
Paradigm
I would subjectively explore their experiences based on their knowledge, skills and attitudes in teaching Mathematics in the Intermediate Phase. Findings from this study will enable me to draw conclusions in relation to teachers' experiences teaching Mathematics in the Intermediate Phase, because the success of my study will depend on my participants (teachers teaching Mathematics in the Intermediate Phase).
Research approach
Research style: case study
Data generation
Focus group
In response to this, I organized a meeting at my school for teachers who teach intermediate mathematics at my school, where I informed them about my study and its purpose. I also told the participants that they should not treat me as their supervisor at work, but as a researcher, and that the discussions were not intended to be judgmental.
One-on-one semi- structured interviews
However, Du Plessis (2013) defines focus groups as a form of group interview that relies on interaction within a group discussing a topic presented by the researcher and giving a collective rather than an individual perspective. Therefore, to overcome these challenges, I was punctual to save time, consider confidentiality during and after the interview, and use my professional knowledge and experience during the interview.
Document analysis
Sampling
Data analysis
Trustworthiness
Data collected in connection with the survey of teachers' experiences of teaching mathematics at the middle stage were obtained through face-to-face interviews and focus group discussions, which were recorded via mobile phone or tape recorder. The questions asked were based on the teaching of mathematics at the secondary stage in order to obtain relevant answers regarding the teachers' experience.
Anticipated problems/limitations
I have ensured that the data generated is credible and believable to the reader by providing the evidence and data analysis. Furthermore, transferability is defined by Brenner (2009) as the extent to which generalization can be made from the data and context of the study to the broader population and settings.
Ethics
This further suggests that teachers teaching mathematics at the intermediate stage should be guided by the experience of knowledge to use professionally. This suggests that teachers teaching mathematics at the intermediate stage should be guided by skills experience in order to equip students with mathematical skills.
Summary of chapter
Chapter one
Chapter two
Chapter three
Chapter four
Chapter five
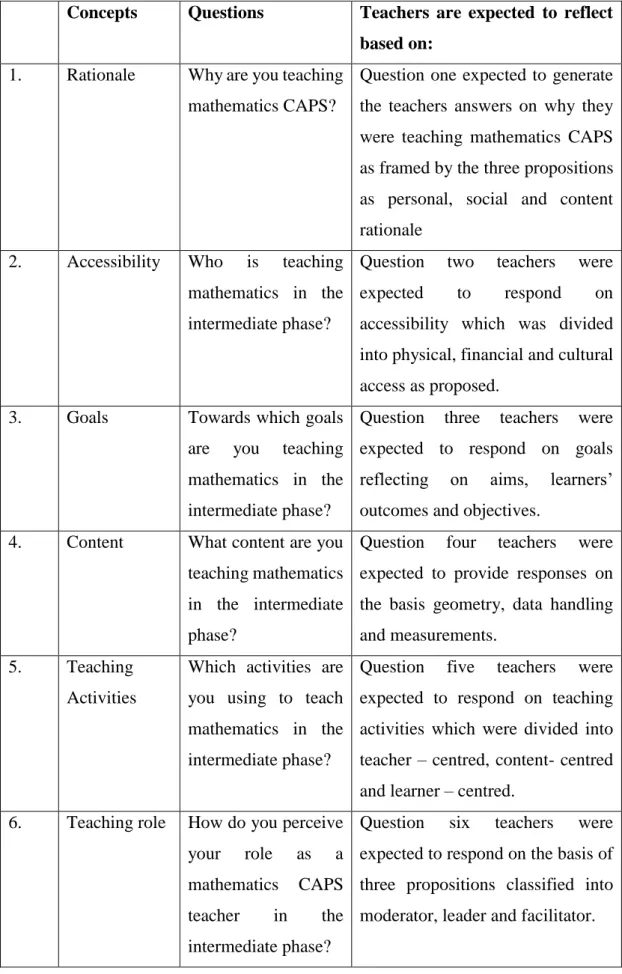
Why are they teaching mathematics? (Rational)
This may suggest that teachers teaching mathematics at the intermediate stage should be guided by experience of skills in order to increase social reasoning in their teaching. This may suggest that teachers teaching mathematics at the intermediate stage need to be guided by the experience of tenure to achieve the intended goals of the curriculum.
The teaching goals (To which goals are they teaching)
In other words, CAPS aims for teachers to cover content over a period of time, drawing heavily on their content knowledge and experience. This further suggests that teachers teaching mathematics at the middle stage should be guided and guided by knowledge and experience with attitude in order to achieve the curriculum objectives in teaching mathematics.
How are they teaching? (Teachers role)
Moreover, teachers who teach intermediate mathematics can play a great role in the teaching and learning process. Thus, this suggests that teachers teaching intermediate mathematics should be guided by knowledge experience during the activity moderation process.
What content are they teaching?
In addition to the above, learners must find the median, mean and mode from the numbers in the table. This therefore suggests that teachers who teach Mathematics in the Intermediate Phase should be driven more by knowledge experience than attitude and skill experience when teaching content from the CAPS document.
When are they teaching? (Time)
This suggests that teachers who teach mathematics in the intermediate phase should be driven by knowledge experience regarding the student's accessibility to teaching and learning processes. I kept them in focus for the exploration of the teachers' experiences of teaching mathematics in the intermediate phase.
How do you assess? (Assessment)
With what are they teaching? (Resources)
Thus, this suggests that teachers teaching mathematics in the middle stage should use their skills experience to get ideas for using all available software, hardware and ideological resources in the school. This suggests that teachers teaching middle-phase mathematics should be driven by knowledge experience when using hardware resources to teach any mathematics content.
With whom are you teaching (accessibility?)
This suggests that teachers teaching mathematics at the intermediate stage should use their experiences of skills to help students access finance. This suggests that teachers teaching mathematics at the intermediate stage may be motivated by knowledge experiences to approach students for teaching and learning.
Location (where are they teaching?)
In addition, teachers who teach mathematics at the intermediate stage must design activities that will lead to the achievement of the curriculum objectives. This suggests that teachers teaching mathematics at the intermediate stage should use experience of skills to use different strategies for teaching mathematics.
How are you teaching? (Activities)
This suggests that teachers teaching intermediate mathematics should be guided by skills experience when teaching and designing their activities. The previous chapter, the literature reviews, indicated the studies that have been conducted on teachers' experiences with teaching mathematics in the intermediate phase.
Research paradigm
As a result, I chose an interpretive approach because I wanted to share the rigor of the natural sciences and the concerns of the social sciences, and to describe and explain the human experience for the teachers who teach intermediate mathematics. Furthermore, one of the limitations of the interpretive paradigm is that the findings do not generalize to a broader population.
Methodological approach (qualitative approach)
I used this paradigm because it gave me the richest and most in-depth exploration of the phenomenon(s). In addition, Weiss (2018) and Creswell and Clark (2017) identified the weakness of the qualitative approach such that it produces findings that are not arrived at through statistical procedures or other quantification methods.
Research style (case study)
The case study was therefore the most suitable for this study because the findings are not generalizable as the population sample was too small, but the teachers can refer to the findings for their own context.
Data generation method
One on one semi- structured interviews
Teachers to question six were expected to respond based on three statements, divided into moderator, leader and facilitator. For question nine, teachers were expected to respond based on three statements about the environment (location), namely face-to-face, online and blended learning.
Focus group interview
So I overcame these challenges with accuracy to save time, consider the sense of confidentiality during and after the interview.
Document analysis
Sampling
In addition to the above, they were deliberately selected because they are the only three educators who teach Mathematics in the Intermediate Phase. Furthermore, the participants were deliberately selected because they have five years and more experience in teaching Mathematics in the Intermediate Phase.
Data Analysis
Thus, three participants were selected for their defining characteristics, specifically teaching intermediate mathematics at our school. The research is about experiences of teachers who teach mathematics in the intermediate phase. In addition, inductive reasoning was used to analyze the data generated through one-on-one semi-structured interviews, focus group interviews and document analyzes to draw conclusions.
Ethical issues
Trustworthiness
Furthermore, Mathematics teachers are influenced by the content of teaching Mathematics in the Intermediate Phase. Furthermore, the first research question is (what are the teachers' experiences with teaching Mathematics in the Intermediate Phase.
Limitation & possible problems
Conclusion
Therefore, in the next chapter, we will focus on the data analysis of the data generated by the described research method. In addition, the main focus of the next chapter is to discuss the research findings through the discussions that follow the data analysis described at the beginning of this chapter.
Findings and discussions
Rationale
Resources
Accessibility
Teaching goals
Content
Teaching activities
Teacher’s role
Location
Time
Assessment
Introduction
This chapter addresses the aforementioned research questions and objectives, summarizes the research findings, and provides conclusions based on the research findings, data analysis, and discussions presented in the previous chapter (Chapter Four). In addition, the conclusions provide a clear picture of teachers' experiences, whether they were driven by knowledge, skills, or attitudinal experiences.
Summary of chapters
In addition, the second chapter offered literature in relation to teachers' experiences in teaching mathematics at the secondary stage. Data obtained from teachers' experiences of teaching mathematics at the middle stage were explored in order for teachers to change their teaching practices.
Summary of findings and conclusions
Rationale
Furthermore, the findings revealed that there was a strong need for teachers to understand the conditions for teaching mathematics at the intermediate stage. Furthermore, these findings addressed the second research question, which is: Why are teachers' experiences teaching intermediate mathematics in a particular way?
Resources
Furthermore, teachers were driven by knowledge experience when teaching mathematics because they referred to the written policy document, which mostly outlines the hardware resources as relevant resources for teaching mathematics. This indicates that mathematics teachers should be driven by both attitude and knowledge experience when it comes to resource utilization when teaching mathematics in the intermediate phase.
Goals
For example, the goal of teaching measurements is to enable students to distinguish centimeters from millimeters. In line with the findings, the study found that the majority of teachers understood the purpose of mathematics education.
Assessment
This indicates that the majority of the teachers were driven by knowledge experience because the Mathematics policy document clearly states that formal assessment involves (summative) School Based Assessment and end of year Examination and is marked by the teacher and formally recorded for promotion purposes. In relation to the findings, the data generated revealed that the majority of the Mathematics teachers used summative assessment to assess their learners.
Content
In line with the above, Motshekga (2009) is outspoken about the Mathematics content that should be taught in the Intermediate Phase, as it articulates that space and shapes (geometry), data handling and measurements should be taught in the Intermediate Phase because "each content area contributes to the learning of specific skill" (DBE, 2011, p. 9). In accordance with the findings of the generated data, it revealed that the Mathematics teachers did data handling, measurements and geometry in the Intermediate Phase learned
Teachers role
Thus, this suggests that teachers teaching intermediate mathematics should be guided by skills experience so that they can improvise resources that facilitate students' access to mathematics lessons. In line with the above, Motshekga (2009) speaks louder about the environment in which students should be taught mathematics as it strongly articulates that the barriers and different curriculum strategies used need to be specifically addressed in the classroom.
Location
The first research question is thus the teachers' experiences of teaching mathematics in the intermediate phase. And the first research objective (to explore teachers' experiences of teaching mathematics in the intermediate phase) is addressed.
Time
As a result, the second research question is: why are teachers' experiences of teaching intermediate mathematics in a certain way? And the second research objective (to understand the reasons for teachers' experiences of teaching mathematics at the intermediate stage) is addressed.
Teachers’ activity
Consequently, the first research question (What are teachers' experiences of teaching mathematics at the secondary level. What learning activities do you use when teaching mathematics at the secondary level.
Suggestions for further research
Recommendations
- Recommendation 1
- Recommendations 2
- Recommendations 3
- Recommendations 4
- Recommendations 5
- Recommendations 6
- Recommendations 7
In accordance with this, it is recommended that the professional unqualified teachers should be teaching Mathematics. Consequently, it is recommended that the objectives of Mathematics teaching be unpacked, and policy document copies distributed to teachers for reference purposes.
Study limitations
Conclusion
The Impact of the Curriculum Change on Science Teaching and Learning: A Case Study in Low Resource Schools in Vhembe District. What is the time allocation for each aspect (content) of middle stage mathematics.
Annexures
Document analysis schedule
Interview schedule
Focus group discussion
A letter from the editor
Turnitin Report
Gate keepers letter
Clearance Letter
