PERBANDINGAN METODE ANALISIS HOMOTOPI DAN METODE
ITERASI VARIASIONAL PADA PENYELESAIAN MASALAH
GELOMBANG INTERNAL DI ATMOSFER
ZULFIQAR BUSRAH
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa tesis berjudul Perbandingan Metode Analisis Homotopi dan Metode Iterasi Variasional pada Penyelesaian Masalah Gelombang Internal di Atmosfer adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
RINGKASAN
ZULFIQAR BUSRAH. Perbandingan Metode Analisis Homotopi dan Metode Iterasi Variasional pada Penyelesaian Masalah Gelombang Internal di Atmosfer. Dibimbing oleh JAHARUDDIN dan TONI BAKHTIAR.
Gelombang internal merupakan fenomena alam yang keberadaannya tidak dapat dilihat secara langsung. Selain terdapat di lautan, gelombang internal juga terdapat pada lapisan atmosfer. Gelombang internal di atmosfer dapat direpresentasikan dalam suatu model matematika. Representasi matematis gelombang internal di atmosfer diturunkan dari persamaan dasar fluida ideal yang memiliki sifat takkental dan taktermampatkan. Penurunan persamaan dasar fluida didasarkan pada hukum kekekalan massa dan hukum kekekalan momentum. Selain itu, diasumsikan pula bahwa ketinggian gelombang relatif jauh lebih kecil jika dibandingkan dengan panjang gelombang. Asumsi ini dikenal sebagai asumsi fluida dangkal.
Pada dasarnya perambatan gelombang internal di atmosfer yang direpresentasikan dengan persamaan dasar fluida berupa sistem persamaan diferensial parsial (PDP) taklinear. Penyelesaian analitik dari sistem PDP taklinear umumnya sulit diselesaikan, sehingga diperlukan suatu metode pendekatan analitik tertentu. Pendekatan analitik yang dapat diterapkan dalam memperoleh penyelesaian hampiran adalah metode analisis homotopi (HAM) dan metode iterasi variasional (VIM). Pada penelitian ini persamaan dasar fluida yang menggambarkan perambatan gelombang internal di atmosfer diselesaikan dengan HAM dan VIM.
Dalam penentuan penyelesaian hampiran persamaan dasar fluida, berdasarkan HAM, persamaan deformasi orde nol dikonstruksi berdasarkan bentuk dari persamaan dasar fluida. Persamaan deformasi orde nol terdiri atas operator linear, operator taklinear, pendekatan awal dan parameter bantu. Kemudian bentuk dari persamaan deformasi orde tinggi ditentukan berdasarkan pendekatan awal pada persaman deformasi orde nol. Penyelesaian persamaan dasar fluida dengan HAM diperoleh dalam bentuk deret. Suku-suku yang digunakan pada penyelesaian deret diperoleh dari persamaan deformasi orde nol dan persamaan deformasi orde tinggi. Daerah kekonvergenan penyelesaian hampiran HAM dapat dikontrol melalui pemilihan parameter bantu.
Keunggulan VIM dalam menyelesaikan masalah taklinear yaitu dalam penyelesaiannya tidak perlu dilakukan linearisasi, transformasi dan perturbasi. Selain itu penyelesaian hampiran VIM cepat konvergen ke penyelesaian eksak. Dalam penentuan penyelesaian hampiran persamaan dasar fluida, berdasarkan VIM, fungsi koreksi dikonstruksi berdasarkan bentuk persamaan dasar, kemudian nilai optimal pengali Lagrange ditentukan melalui teori variasional. Fungsi koreksi dan pengali Lagrange yang diperoleh menghasilkan suatu rumus iterasi.
Hasil yang diperoleh menunjukkan bahwa penyelesaian hampiran HAM mendekati dengan baik penyelesaian numeriknya. Demikian pula dengan penyelesaian dari VIM memberikan hasil dengan galat mutlak yang sangat kecil terhadap penyelesaian numerik persamaan dasar fluida. Pada kasus ini, VIM lebih mudah digunakan daripada HAM. Secara umum, kedua metode ini sangat efisien dalam menyelesaikan sistem PDP taklinear.
SUMMARY
ZULFIQAR BUSRAH. Comparison of the Homotopy Analysis and Variational Iteration Methods in Solving Internal Waves Problem in the Atmosphere. Supervised by JAHARUDDIN and TONI BAKHTIAR.
Internal waves are natural phenomena whose existence can’t be seen directly. In addition to being at a layer of the ocean, internal waves can be found at the layers of atmosphere. Internal waves in the atmosphere can be represented by a mathematical model. The mathematical representation of internal waves in the atmosphere is obtained from the basic equation of ideal fluid which is inviscid and incompressible. Fundamental equations of fluid are governed by the laws of conservation of mass and momentum. Furthermore, it is also assumed that the wave height is relatively much smaller than the wavelength. This is known as the assumption of shallow fluid.
Basically a mathematical model of internal waves in the atmosphere is a system of nonlinear partial differential equations (PDE). Generally, the solution of nonlinear PDE system cannot be obtained analytically, so we need an approaching method. The approaches that can be applied to obtain approximation solutions are Homotopy Analysis Method (HAM) and Variational Iteration Method (VIM). In this study, the basic equations of fluid that describe the propagation of internal waves in the atmosphere are solved by HAM and VIM.
In determining the approximation solutions of the basic equations of fluid, based on HAM, zero-order deformation equations are constructed based on the form of the basic equations of fluid. Zero-order deformation equations consist of linear operator, nonlinear operator, the initial approximations and auxiliary parameters. Then, the high-order deformation equations are determined based on the initial approximations at zero-order deformation equations. Solutions of the basic equations of fluid by HAM are obtained in the form of series. The terms of the series are obtained by zero-order deformation and the high-order deformation equations. Convergence region of approximation solutions of HAM can be controlled via the auxiliary parameters.
VIM has many advantages, especially in solving nonlinear problems which their iteration formulas can be determined directly without linearization, transformation and perturbation. In addition, the approximation solutions of VIM converge quickly to the exact solution. In determining the approximation solutions of the basic equations of fluid, based on VIM, correction function is constructed based on the form of the basic equations, then the optimal value of the Lagrange multipliers are determined via the variational theory. Correction function and Lagrange multipliers thus provide iteration formulas.
In determining the deviation of HAM and VIM, both methods are compared with numerical solutions. Numerical solutions are calculated by using package of symbolic computational program. In this package, standard numerical methods are used in solving the problem with finite differences method.
VIM is easier than HAM. Moreover, both methods are efficient in approximating the numerical solutions.
© Hak Cipta Milik IPB, Tahun 2014
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
Sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Matematika Terapan
PERBANDINGAN METODE ANALISIS HOMOTOPI DAN METODE
ITERASI VARIASIONAL PADA PENYELESAIAN MASALAH
GELOMBANG INTERNAL DI ATMOSFER
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2014
Judul Tesis : Perbandingan Metode Analisis Homotopi dan Metode Iterasi Variasional pada Penyelesaian Masalah Gelombang Internal di Atmosfer
Nama : Zulfiqar Busrah NIM : G551120081
Disetujui oleh Komisi Pembimbing
Dr Jaharuddin, MS Ketua
Dr Toni Bakhtiar, MSc Anggota
Diketahui oleh
Ketua Program Studi Matematika Terapan
Dr Jaharuddin, MS
Dekan Sekolah Pascasarjana
Dr Ir Dahrul Syah, MScAgr
Tanggal Ujian: 18 September 2014
PRAKATA
Puji syukur penulis panjatkan ke hadirat Allah subhana wa ta’ala atas segala limpahan rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak Januari 2014 ialah gelombang internal, dengan judul Perbandingan Metode Analisis Homotopi dan Metode Iterasi Variasional pada Penyelesaian Gelombang Internal di Atmosfer.
Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada Program Studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis menyadari bahwa bantuan-bantuan dan arahan-arahan dari kedua pembimbing sangat membantu dalam menyelesaikan karya tulis ini. Terima kasih penulis ucapkan kepada Dr Jaharuddin, MS selaku pembimbing I, dan Dr Toni Bakhtiar, MSc selaku pembimbing II.
Pada kesempatan ini penulis juga menyampaikan terima kasih kepada : 1. Prof Dr Ir Herry Suhardiyanto, MSc selaku Rektor Institut Pertanian Bogor. 2. Dr Ir Dahrul Syah, MScAgr selaku Dekan Sekolah Pascasarjana Institut
Pertanian Bogor.
3. Dr Jaharuddin, MS selaku Ketua Program Studi Matematika Terapan. 4. Dr Ir Endar H Nugrahani, MS selaku penguji luar komisi pembimbing.
5. Ayahanda dan Ibunda tercinta, Bustang, SPd dan Husrah, AMaPd yang telah membesarkan dan mendidik penulis dengan penuh kasih sayang demi keberhasilan penulis selama menjalani proses pendidikan, juga kepada saudara-saudara penulis Zhulfitrani Busrah, SP dan Zhulmuqzith Busrah serta keluarga besar penulis atas doa dan dukungannya.
6. Seluruh dosen dan staf pegawai tata usaha Departemen Matematika IPB. 7. Seluruh mahasiswa Departemen Matematika khususnya teman-teman
angkatan tahun 2012 pada Program Studi Matematika Terapan Sekolah Pascasarjana IPB.
8. Rekan-rekan Wisma Celebes Bara III, Ahmad Firman Ashari, Muhammad Mu’min F, Muhammad Fitrah Irawan, Seniarwan, Munawir Syarif yang telah menjadi keluarga baru di Bogor.
9. Rekan-rekan Forum Mahasiswa Pascasarjana Sulawesi Selatan.
10.Sahabat-sahabat yang tidak dapat disebutkan satu persatu yang telah banyak membantu penulis dalam penyelesaian tesis ini.
Semoga segala bantuan, bimbingan dan motivasi yang telah diberikan kepada penulis senantiasa mendapat balasan dari Allah subhana wa ta’ala.
Akhirnya, semoga penulisan karya ilmiah ini dapat bermanfaat bagi semua pihak yang membutuhkan.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
1 PENDAHULUAN 1
Latar Belakang ... 1
Tujuan Penelitian ... 2
2 TINJAUAN PUSTAKA 2 Persamaan Dasar Fluida ... 2
Asumsi Fluida Dangkal ... 3
Metode Analisis Homotopi ... 6
Metode Iterasi Variasional ... 8
3 METODE 9 4 HASIL DAN PEMBAHASAN 10 Analisis Metode ... 10
Aplikasi Metode... 15
Hasil ... 19
5 SIMPULAN DAN SARAN 27 Simpulan ... 27
Saran ... 28
DAFTAR PUSTAKA 28
LAMPIRAN 30
DAFTAR TABEL
1 Galat mutlak antara penyelesaian numerik dengan penyelesaian hampiran HAM pada saat dan 20 2 Galat mutlak antara penyelesaian numerik dengan penyelesaian
hampiran HAM pada dan 21
3 Galat mutlak antara penyelesaian numerik dengan penyelesaian hampiran VIM pada saat dan 24 4 Galat mutlak antara penyelesaian numerik dengan penyelesaian
hampiran VIM pada dan 24
DAFTAR GAMBAR
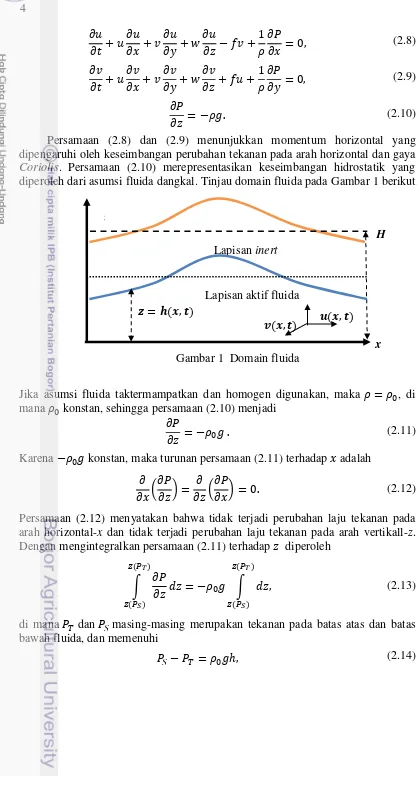
1 Domain fluida 4
2 Perbandingan antara penyelesaian numerik dengan penyelesaian hampiran HAM pada saat dan untuk 21 3 Perbandingan antara penyelesaian numerik dengan penyelesaian
hampiran HAM pada saat dan untuk 22 4 Perbandingan antara penyelesaian numerik dengan penyelesaian
hampiran HAM pada saat dan untuk 22 5 Perbandingan antara penyelesaian numerik dengan penyelesaian
hampiran HAM pada dan 23
6 Perbandingan antara penyelesaian numerik dengan penyelesaian hampiran VIM pada saat dan untuk 25 7 Perbandingan antara penyelesaian numerik dengan penyelesaian
hampiran VIM pada saat dan untuk 25 8 Perbandingan antara penyelesaian numerik dengan penyelesaian
hampiran VIM pada saat dan untuk 25 9 Perbandingan antara penyelesaian numerik, penyelesaian hampiran
HAM dan VIM pada saat dan 26 10 Perbandingan antara penyelesaian numerik, penyelesaian hampiran
HAM dan VIM pada dan 26
11 Grafik penyelesaian numerik 2D pada dan
27
DAFTAR LAMPIRAN
1 Penurunan persamaan (2.1) dan (2.2) 30
2 Penurunan persamaan (2.3), (2.4) dan (2.5) 31
3 Penurunan persamaan (4.17) 33
4 Penurunan persamaan (4.31) 38
1
PENDAHULUAN
Latar Belakang
Gelombang internal merupakan fenomena alam yang keberadaannya tidak dapat dilihat secara langsung. Selain terdapat di laut dalam, gelombang internal juga terdapat pada lapisan atmosfer. Gelombang ini terus merambat dan berinteraksi dengan aliran lain, namun sulit untuk diamati. Keberadaan gelombang tersebut dapat dikenali melalui perubahan rapat massa fluida yang disebabkan oleh perubahan temperatur udara (Cassady 2010). Berdasarkan variabel temperatur, lapisan atmosfer secara vertikal dibedakan atas empat lapisan utama, yaitu troposfer, stratosfer, mesosfer, dan thermosfer. Penelitian mengenai gelombang internal di atmosfer, sebelumnya telah diterapkan pada model peramalan kecepatan dan arah angin menggunakan pendekatan deret Fourier (Rottman et al. 2007).
Gelombang internal di atmosfer dapat dimodelkan dalam persamaan matematika dengan menggunakan asumsi fluida dangkal (Warner 2011). Asumsi fluida dangkal telah diterapkan pada pemodelan iklim, gelombang Kelvin (Clancy dan Lynch 2011), gelombang Rossby (Duba dan McKenzie 2012) dan gelombang tsunami (Blaise dan St-Cyr 2012). Pada dasarnya representasi matematis dari gelombang internal di atmosfer berupa suatu sistem persamaan diferensial parsial (PDP) taklinear (Warner 2011). Dalam berbagai kasus, sistem PDP taklinear sangat sulit diselesaikan secara analitik. Dengan demikian dibutuhkan suatu metode pendekatan analitik yang dapat memberikan penyelesaian hampiran.
Pendekatan analitik yang dapat digunakan dalam menyelesaikan PDP taklinear yaitu Homotopy Analysis Method (HAM) yang pertama kali diperkenalkan oleh Liao pada tahun 1992. Keunggulan HAM terletak pada pemilihan nilai awal dan parameter bantu sehingga dapat memperluas daerah kekonvergenan (Liao 2004). HAM sebelumnya telah diterapkan dalam berbagai penyelesaian masalah taklinear di antaranya pada persamaan Klein-Gordon (Alomari et al. 2008), model El Nino Southern Oscillation (Jiaqi et al. 2010), persamaan Huxley (Hemida dan Mohamed 2010), persamaan Zakharov-Kuznetsov (Usman et al. 2013) dan model pertumbuhan satu spesies pada lingkungan yang tercemar (Jaharuddin 2014).
2
dari kedua metode tersebut akan dibandingkan terhadap penyelesaian numerik melalui perhitungan galat dan visualisasi grafik penyelesaian.
Tujuan Penelitian
Tujuan yang akan dicapai pada penelitian ini adalah sebagai berikut 1. Menggunakan HAM dalam menentukan penyelesaian hampiran model
matematika gelombang internal di atmosfer.
2. Menggunakan VIM dalam menentukan penyelesaian hampiran model matematika gelombang internal di atmosfer.
3. Membandingkan penyelesaian hampiran HAM dan VIM terhadap penyelesaian numerik masalah gelombang internal di atmosfer.
2
TINJAUAN PUSTAKA
Persamaan Dasar Fluida
Pada bagian ini, atmosfer dianggap sebagai fluida ideal yang memiliki sifat takkental (inviscid) dan taktermampatkan (incompressible). Persamaan dasar fluida ideal diturunkan berdasarkan hukum kekekalan massa dan hukum kekekalan momentum. Hukum kekekalan massa menghasilkan persamaan kontinuitas yang didasarkan pada kesetimbangan massa sedangkan hukum kekekalan momentum menghasilkan persamaan momentum yang didasarkan pada hukum Newton II. Hukum kekekalan massa menyatakan bahwa laju perubahan massa merupakan selisih antara massa yang masuk dengan massa yang keluar dalam suatu sistem (Anderson 1995).
Misalkan patikel-partikel fluida diasumsikan bergerak dalam arah tiga dimensi memunyai rapat massa , dengan merupakan koordinat gerak partikel fluida dalam arah horizontal, sebagai koordinat gerak partikel fluida dalam arah vertikal dan merupakan waktu. Misalkan pula kecepatan gerak partikel fluida dinotasikan dengan dalam arah horizontal- , dalam arah horizontal- , dan w pada arah vertikal- . Berdasarkan hukum kekekalan massa, jika digunakan asumsi fluida taktermampatkan (incompressible) berarti fluida yang mengalir tidak mengalami perubahan kerapatan massa terhadap perubahan waktu selama terjadi aliran, maka diperoleh persamaan kontinuitas berikut
3 Selanjutnya hukum kekekalan momentum menyatakan bahwa, laju perubahan momentum dalam suatu sistem merupakan selisih antara momentum masuk dengan yang keluar ditambah dengan gaya-gaya yang bekerja pada sistem tersebut. Gaya yang terjadi pada sistem tersebut yaitu adanya gaya gravitasi dan perubahan tekanan fluida baik arah horizontal maupun vertikal. Sedangkan gaya gesek diabaikan karena diasumsikan fluida bersifat takkental (inviscid). Berdasarkan hukum kekekalan momentum diperoleh persamaan momentum atau persamaan Euler berikut Penurunan persamaan (2.3), (2.4) dan (2.5) dapat dilihat pada Lampiran 2
Asumsi Fluida Dangkal
Pada bagian ini persamaan momentum disederhanakan dengan menggunakan asumsi fluida dangkal. Asumsi fluida dangkal menyatakan bahwa panjang gelombang relatif jauh lebih panjang bila dibandingkan dengan ketinggian lapisan fluida (Warner 2011). Hal ini menunjukkan bahwa percepatan aliran arah vertikal sangat kecil daripada percepatan gravitasi. Demikian pula dengan kecepatan arah vertikal yang jauh lebih kecil dibandingkan dengan kecepatan arah horizontal, sehingga
(2.6)
Dalam hal ini
merupakan operator turunan total dalam bentuk
(2.7)
Selanjutnya, atmosfer juga diasumsikan sebagai fluida yang memiliki sifat autobarotropik, hal ini berarti bahwa fluida memunyai rapat massa yang konstan dan homogen. Selain perubahan tekanan, gaya lain yang memengaruhi momentum pada arah horizontal adalah gaya yang dihasilkan oleh rotasi bumi. Fenomena perputaran bumi pada porosnya menghasilkan angin dan mengakibatkan adanya gaya Coriolis dengan parameter . Adanya keseimbangan antara gaya Coriolis dengan perubahan tekanan dan gaya gravitasi menghasilkan arus geostropik.
4
Persamaan (2.8) dan (2.9) menunjukkan momentum horizontal yang dipengaruhi oleh keseimbangan perubahan tekanan pada arah horizontal dan gaya Coriolis. Persamaan (2.10) merepresentasikan keseimbangan hidrostatik yang diperoleh dari asumsi fluida dangkal. Tinjau domain fluida pada Gambar 1 berikut.
Jika asumsi fluida taktermampatkan dan homogen digunakan, maka , di mana konstan, sehingga persamaan (2.10) menjadi
(2.11)
Karena konstan, maka turunan persamaan (2.11) terhadap adalah
(2.12)
Persamaan (2.12) menyatakan bahwa tidak terjadi perubahan laju tekanan pada arah horizontal-x dan tidak terjadi perubahan laju tekanan pada arah vertikall-z. Dengan mengintegralkan persamaan (2.11) terhadap diperoleh
5 dengan sebagai ketinggian fluida. Jika atau , maka
(2.15)
Jika persamaan (2.15) diturunkan terhadap , maka diperoleh
(2.16)
Hal ini menunjukkan bahwa perubahan tekanan batas bawah pada arah horizontal sebanding dengan perubahan ketinggian fluida terhadap arah horizontal-x. Demikian pula untuk arah horizontal-y yaitu
Pendekatan lain yang dipertimbangkan adalah dengan memisalkan
Kemudian dengan mengintegralkan persamaan (2.1) terhadap ketinggian , maka diperoleh
6
Dengan demikian diperoleh persamaan dasar yang terdiri dari tiga variabel takbebas dan sebagai berikut
Sebagai penyederhanaan, diasumsikan bahwa kecepatan partikel fluida hanya bergantung pada arah horizontal-x dan perubahan tekanan dalam arah horizontal-y bernilai konstan. Sehingga persamaan satu dimensi dari persamaan (2.24), (2.25) dan (2.26) dapat ditulis dalam bentuk berikut
di mana merupakan ketinggian fluida yang dipengaruhi oleh tekanan pada arah horizontal-y sedangkan merupakan suatu konstanta yang merepresentasikan kecepatan arus geostropik. Persamaan (2.27) – (2.30) merupakan persamaan dasar fluida yang akan digunakan untuk menggambarkan perambatan gelombang internal di atmosfer, dan akan diselesaikan dengan menggunakan pendekatan HAM dan VIM.
Metode Analisis Homotopi
Metode analisis homotopi adalah suatu metode pendekatan analitik untuk menyelesaikan suatu masalah taklinear. Pada bagian ini akan diberikan secara ringkas konsep dasar dari metode homotopi dalam penyelesaian masalah taklinear (Liao 2004). Misalkan diberikan persamaan diferensial sebagai berikut
(2.31)
di mana merupakan suatu operator turunan, merupakan fungsi yang tidak diketahui serta dan sebagai variabel bebas. Kemudian didefinisikan suatu operator linear yang memenuhi
7 Selanjutnya jika kedua ruas pada persamaan (2.36) diturunkan terhadap hingga kali dan mengevaluasinya pada kemudian dibagi oleh , maka diperoleh bentuk persamaan orde ke- berikut
8
Dengan pada saat , maka berdasarkan persamaan (2.37) diperoleh
(2.43) Dengan demikian persamaan (2.43) merupakan penyelesaian masalah taklinear yang diberikan pada persamaan (2.31), di mana diperoleh dari penyelesaian persamaan (2.39) sedangkan merupakan pendekatan awal yang didefinisikan. Hasil ini menunjukkan adanya hubungan antara penyelesaian eksak dengan pendekatan awal dan .
Metode Iterasi Variasional
Pada bagian ini, diberikan konsep dasar VIM dalam menentukan penyelesaian hampiran dari suatu masalah taklinear (He 1997; He 1999). Misalkan diberikan suatu persamaan diferensial berikut
(2.44)
di mana merupakan operator linear, sebagai suatu operator taklinear, merupakan fungsi yang didefinisikan dan merupakan fungsi yang akan dicari dari persamaan diferensial yang diberikan. Berdasarkan metode iterasi variasional, dikonstruksi suatu fungsi koreksi yang dinyatakan dalam bentuk berikut
(2.45)
di mana merupakan pengali Lagrange. Nilai optimal pada faktor koreksi dapat diidentifikasi melalui teori kalkulus variasional. Suku kedua pada persamaan (2.45) disebut sebagai koreksi sedangkan indeks untuk menyatakan hampiran orde-k. Selanjutnya merupakan variasi terbatas dan . Dalam menentukan pengali Lagrange dapat diidentifikasi dengan
(2.46)
Fungsi koreksi mencapai kondisi stasioner, jika memenuhi
(2.47)
Selanjutnya dengan fungsi koreksi dan nilai pengali Lagrange, maka diperoleh suatu rumus iterasi. Iterasi dapat terus dilakukan untuk memperluas daerah kekonvergenan. Secara umum, penyelesaian pendekatan VIM dapat dinyatakan sebagai berikut
(2.48)
9
3
METODE
Pada penelitian ini, difokuskan pada penentuan penyelesaian hampiran persamaan dasar fluida yang menggambarkan perambatan gelombang internal di atmosfer yang direpresentasikan oleh persamaan (2.27) – (2.30) dengan menggunakan HAM dan VIM. Implementasi di komputer akan menggunakan bantuan program komputasi simbolik berbasis fungsional. Berikut langkah-langkah yang akan dilakukan.
1. Metode numerik
Penyelesaian numerik dilakukan dengan menggunakan bantuan program komputasional simbolik berbasis fungsional. Pada program ini, tersedia package yang dapat digunakan untuk menyelesaiakn sistem persamaan diferensial parsial taklinear. Metode yang digunakan berupa metode beda hingga melalui skema implisit terpusat (centered implicit scheme). Dengan ini didefinisikan parameter, syarat awal, dan syarat batas. Selanjutnya penyelesaian yang diperoleh, ditampilkan dalam grafik pada variabel bebas tertentu.
2. Metode analisis homotopi. a. Analisis metode.
Pada bagian analisis metode, dilakukan perluasan konsep dasar metode analisis homotopi. Perluasan tersebut berupa penyesuaian jumlah fungsi dan variabel bebas yang digunakan.
b. Aplikasi metode.
1. Mendefinisikan operator linear dan taklinear berdasarkan persamaan dasar.
2. Menetapkan pendekatan awal berdasarkan syarat awal pada penyelesaian numerik.
3. Mendefinisikan fungsi homotopi, fungsi bantu dan parameter bantu. 4. Menentukan penyelesaian deformasi orde tinggi
5. Menyusun algoritma untuk kebutuhan penyusunan program komputasi metode homotopi.
6. Mengevaluasi penyelesaian hampiran. 3. Metode iterasi variasional.
a. Analisis metode.
Pada bagian analisis metode, dilakukan perluasan konsep dasar metode iterasi variasional. Perluasan tersebut berupa penyesuaian jumlah fungsi dan variabel bebas yang digunakan.
b. Aplikasi metode.
1. Mendefinisikan operator taklinear dan operator linear berdasarkan persamaan dasar.
2. Mengonstruksi fungsi koreksi.
3. Menentukan nilai optimal pengali Lagrange. 4. Menentukan rumus iterasi.
5. Menyusun algoritma untuk kebutuhan penyusunan program komputasi metode iterasi variasional.
10
4. Membandingkan hasil penyelesaian persamaan dasar fluida antara penyelesaian hampiran HAM dan VIM dengan penyelesaian numerik pada nilai awal dan parameter yang sama, melalui perhitungan galat mutlak dan visualisasi grafik penyelesaian.
4
HASIL DAN PEMBAHASAN
Analisis Metode
Metode Analisis Homotopi
Pada penelitian ini, masalah gelombang internal di atmosfer direpresentasikan dengan sistem PDP taklinear yang terdiri atas tiga fungsi yang tidak diketahui yaitu , dan . Pada bagian ini akan dibahas perluasan dari konsep dasar HAM sebagai penyelesaian persamaan (2.27) - (2.30). Berikut didefinisikan operator turunan taklinear yang dinyatakan dalam bentuk berikut
(4.1)
dengan , dan masing-masing merupakan operator turunan taklinear, dan adalah peubah bebas, sedangkan dan merupakan fungsi yang tidak diketahui. Selanjutnya didefinisikan , dan sebagai operator linear yang memenuhi
a
a
a
(4.2)
Misalkan pula , dan masing-masing sebagai pendekatan awal dari penyelesaian persamaan dan , fungsi real
dan , serta parameter bantu dan Didefinisikan fungsi dan dengan suatu parameter sebagai berikut
11
12 persamaan (4.1) melalui penyelesaian persamaan deformasi orde nol. Misalkan,
(4.11)
berdasarkan persaman (4.3) dan (4.11), maka diperoleh deformasi orde nol berikut masing-masing memetakan pendekatan awal ke penyelesaian eksak yaitu dari,
13
Kemudian persamaan (4.12) diturunkan terhadap parameter sebanyak kali kemudian dibagi dengan maka diperoleh persamaan deformasi orde- berikut
14
Berdasarkan persamaan (4.14) dan (4.16) pada saat diperoleh
(4.22)
Persamaan (4.22) merupakan penyelesaian masalah taklinear yang diberikan pada persamaan (4.1), di mana dan untuk diperoleh dari penyelesaian persamaan (4.18) sedangkan , dan masing-masing sebagai pendekatan awal yang didefinisikan. Metode Iterasi Variasional
Pada bagian ini akan dibahas perluasan dari konsep dasar VIM dalam menentukan penyelesaian hampiran persamaan (2.27) – (2.30). Berdasarkan persamaan (2.44) didefinisikan fungsi berikut
(4.23)
Selanjutnya berdasarkan persamaan (2.45) dikonstruksi suatu fungsi koreksi berikut
(4.24)
15
Iterasi dapat terus dilakukan untuk memperluas daerah kekonvergenan. Secara umum, penyelesaian hampiran VIM dapat ditulis dengan
(4.26)
Persamaan (4.26) merupakan penyelesaian dari persamaan (4.23).
Aplikasi Metode
Tinjau persamaan fluida satu dimensi pada persamaan (2.27) - (2.29) dalam bentuk berikut
Persamaan (4.27) merupakan representasi matematis untuk menggambarkan perambatan gelombang internal di atmosfer. Karena bentuknya yang taklinear, maka model ini sulit diselesaikan secara analitik. Oleh karena itu, dalam penyelesaian persamaan (4.27) dapat ditentukan melalui metode numerik (NUM). Dalam penerapan metode numerik ditetapkan syarat awal dan syarat batas untuk memperoleh penyelesaiannya. Syarat awal yang digunakan, dipilih dalam bentuk berikut
(4.28)
16
program komputasi simbolik. Penyelesaian numerik yang dihasilkan akan dibandingkan dengan penyelesaian hampiran yang dihasilkan dengan HAM dan VIM.
Adapun parameter yang digunakan untuk kebutuhan evaluasi di antaranya parameter Coriolis yang bergantung pada kecepatan sudut rotasi bumi dan . Parameter lain adalah ketinggian yang diakibatkan oleh perubahan tekanan horizontal arah yang dirumuskan dengan di mana sebagai kecepatan arus geostropik yang bernilai konstan. Selanjutnya terdapat pula konstanta percepatan gravitasi
Aplikasi Metode Analisis Homotopi
Pada bagian ini, HAM akan diimplementasikan untuk menentukan penyelesaian hampiran sistem PDP taklinear pada persamaan (4.27). Berdasarkan persamaan (4.27) dan perluasan konsep HAM pada analisis metode yang telah diuraikan, didefinisikan operator linear sebagai berikut
Berdasarkan operator linear persamaan (4.29) dan deformasi orde- pada persamaan (4.18) diperoleh
17
Penurunan persamaan (4.31) dapat dilihat pada Lampiran 4.
Berdasarkan operator taklinear , dan diperoleh bentuk umum
Penurunan persamaan (4.32) dapat dilihat pada Lampiran 5
Penerapan HAM pada penyelesaian persamaan (4.27), melibatkan proses perhitungan yang rekursif. Berikut langkah-langkah penggunaan HAM dalam menentukan penyelesaian hampiran persamaan (4.27) .
1. Penyelesaian awal dipilih berdasarkan persamaan (4.28) sebagai syarat awal yang digunakan pada penentuan penyelesaian numerik.
2. Nilai dari , dan , untuk ditentukan berdasarkan persamaan (4.32).
3. Untuk , nilai dari dan ditentukan berdasarkan persamaan (4.31). Secara umum, nilai dan dapat ditentukan berdasarkan persamaan (4.21) dan (4.32) yang disubstitusikan pada persamaan (4.31) di mana parameter bantu dan dapat dipilih sembarang, sebagai penyederhanaan dapat dipilih . Langkah (2) dan (3) diulangi untuk .
18
5. Evaluasi penyelesaian hampiran untuk nilai dan yang kontinu melalui penyelesaian deret yang diperoleh pada langkah 4. Penentuan orde hampiran HAM bergantung pada kemampuan program komputasi yang digunakan.
Aplikasi Metode Iterasi Variasional
Pada bagian ini, VIM digunakan untuk menentukan penyelesaian hampiran pada penyelesaian persamaan (4.27) , dengan pendekatan awal yang diberikan pada persamaan (4.28). Berdasarkan persamaan (4.27) dan (4.24) dapat dikonstruksi fungsi koreksi sebagai berikut
(4.33)
di mana dan merupakan pengali Lagrange. Persamaan (4.33) dapat ditulis kembali dengan menetapkan variasi terhadap variabel bebas dan
dalam bentuk berikut
(4.34)
dengan dan maka pengali lagrange dapat ditentukan dari persamaan berikut
19 Persamaan (4.35) memberikan kondisi stasioner berikut
(4.36)
sehingga diperoleh nilai optimal dari pengali Langrange dan berikut
(4.37)
Substitusi pengali Lagrange persamaan (4.37) pada fungsi koreksi persamaan (4.33), maka diperoleh rumus iterasi sebagai berikut
(4.38)
Penerapan VIM pada penyelesaian persamaan (4.27), melibatkan proses perhitungan yang berulang. Berikut langkah-langkah penggunaan VIM dalam menentukan penyelesaian hampiran persamaan (4.27) .
1. Penyelesaian awal dipilih berdasarkan persamaan (4.28) sebagai syarat awal yang digunakan pada penentuan penyelesaian numerik dan HAM.
2. Untuk , nilai dari dan ditentukan berdasarkan penyelesaian awal persamaan (4.28) yang disubstitusi pada persamaan (4.38). Secara umum, untuk nilai dan dapat ditentukan berdasarkan persamaan (4.38).
3. Penyelesaian hampiran VIM diperoleh berdasarkan persamaan (4.26) berupa fungsi yang bergantung pada dan .
4. Penyelesaian hampiran VIM dievaluasi pada nilai dan tertentu berdasarkan fungsi yang diperoleh pada langkah (3).
Hasil
20
penyelesaian hampiran dari HAM. Penyelesaian hampiran yang diperoleh dibandingkan dengan penyelesaian numeriknya melalui perhitungan galat mutlak dan visualisai grafik penyelesaian.
Berdasarkan pendekatan awal pada persamaan (4.28) dan parameter-parameter yang diberikan, diperoleh penyelesaian deformasi orde tinggi berikut
Dengan menggunakan bantuan program komputasi simbolik, penyelesaian deformasi orde yang lebih tinggi di atas dapat dilanjutkan hingga Berdasarkan penyelesaian deformasi orde tinggi, diperoleh penyelesaian HAM yang dapat dinyatakan dalam bentuk berikut
Selanjutnya dengan memilih parameter bantu diperoleh galat mutlak antara penyelesaian numerik dengan hampiran HAM yang dievaluasi pada saat dan .
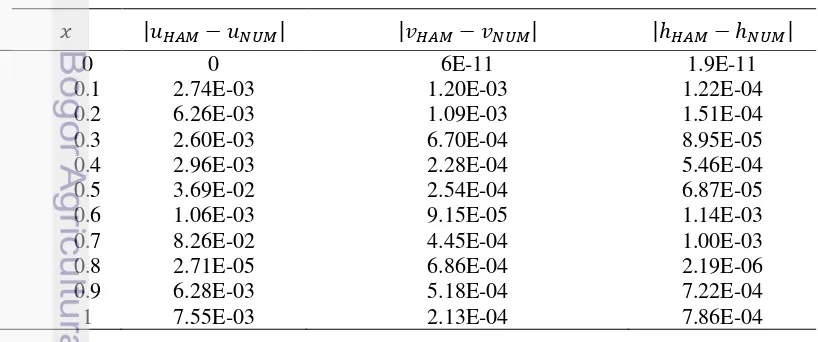
21 Berikut diberikan pula perbandingan antara penyelesaian numerik dengan penyelesaian hampiran HAM yang dievaluasi pada dan melalui perhitungan galat mutlak.
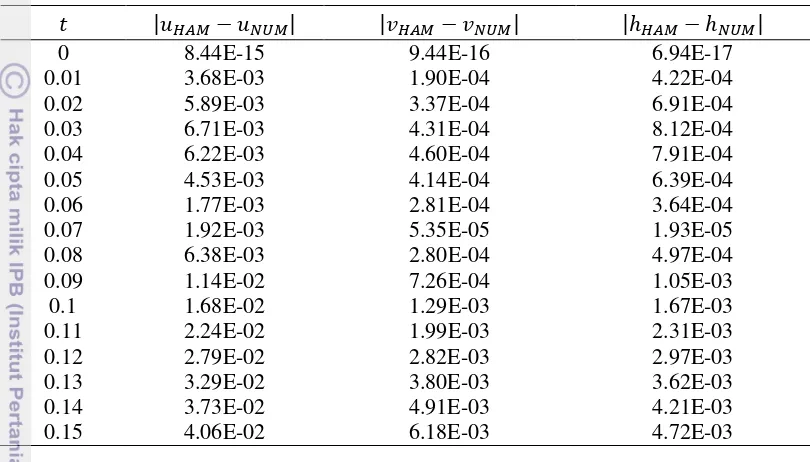
Tabel 2 Galat mutlak antara penyelesaian numerik dengan penyelesaian hampiran HAM pada dan
0 8.44E-15 9.44E-16 6.94E-17
0.01 3.68E-03 1.90E-04 4.22E-04 0.02 5.89E-03 3.37E-04 6.91E-04 0.03 6.71E-03 4.31E-04 8.12E-04 0.04 6.22E-03 4.60E-04 7.91E-04 0.05 4.53E-03 4.14E-04 6.39E-04 0.06 1.77E-03 2.81E-04 3.64E-04 0.07 1.92E-03 5.35E-05 1.93E-05 0.08 6.38E-03 2.80E-04 4.97E-04 0.09 1.14E-02 7.26E-04 1.05E-03
0.1 1.68E-02 1.29E-03 1.67E-03
0.11 2.24E-02 1.99E-03 2.31E-03
0.12 2.79E-02 2.82E-03 2.97E-03
0.13 3.29E-02 3.80E-03 3.62E-03
0.14 3.73E-02 4.91E-03 4.21E-03
0.15 4.06E-02 6.18E-03 4.72E-03
Berdasarkan Tabel 1 dan Tabel 2, diperoleh bahwa pada metode analisis homotopi, penyelesaian hampiran memiliki galat mutlak yang kecil terhadap penyelesaian numerik yang dievaluasi pada nilai veriabel bebas tertentu.
Penyelesaian hampiran pada kasus ini juga dapat ditinjau melalui visualisasi grafik penyelesaian. Berikut perbandingan antara grafik penyelesaian hampiran HAM dengan penyelesaian metode numerik yang dievaluasi pada saat dan .
22
Gambar 2, Gambar 3 dan Gambar 4 menunjukkan perbandingan antara penyelesaian numerik dengan penyelesaian hampiran HAM memiliki galat mutlak yang sangat kecil.
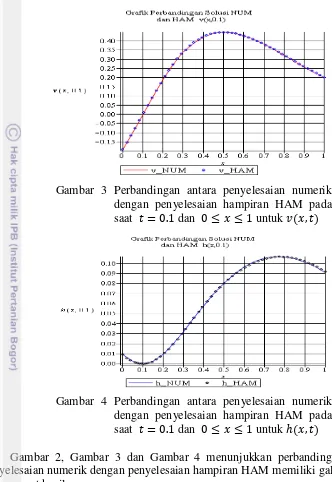
Berikut visualisasi grafik perbandingan antara penyelesaian hampiran HAM dengan penyelesaian metode numerik yang dievaluasi pada dan .
Gambar 3 Perbandingan antara penyelesaian numerik dengan penyelesaian hampiran HAM pada saat dan untuk
23
Gambar 5 menunjukkan perbandingan antara penyelesaian numerik dengan penyelesaian hampiran HAM memiliki galat mutlak yang sangat kecil.
Pada aplikasi VIM, diperoleh penyelesaian hampiran berupa fungsi yang bergantung pada nilai dan . Sebagai kebutuhan simulasi, penyelesaian awal dan parameter-parameter yang digunakan disesuaikan dengan metode numerik dan HAM. Berdasarkan pemilihan nilai awal persamaan (4.28) dan rumus iterasi (4.38) diperoleh
Dengan menggunakan bantuan program komputasi simbolik, iterasi dapat dilanjutkan hingga . Berikut diberikan galat mutlak antara penyelesaian hampiran VIM dengan penyelesaian dengan metode numerik yang dievaluasi pada dan pada daerah .
24
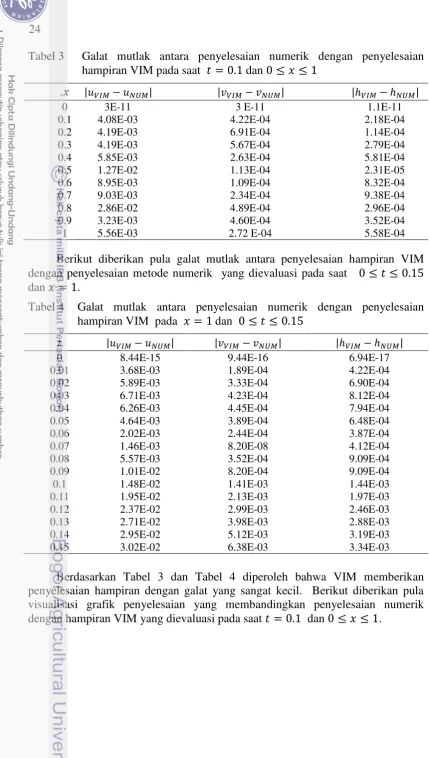
Tabel 3 Galat mutlak antara penyelesaian numerik dengan penyelesaian hampiran VIM pada saat dan
Berikut diberikan pula galat mutlak antara penyelesaian hampiran VIM dengan penyelesaian metode numerik yang dievaluasi pada saat dan .
25
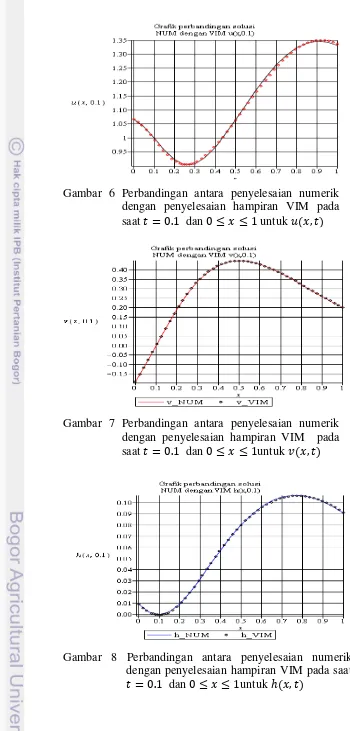
Gambar 6 Perbandingan antara penyelesaian numerik dengan penyelesaian hampiran VIM pada saat dan untuk
Gambar 7 Perbandingan antara penyelesaian numerik dengan penyelesaian hampiran VIM pada saat dan untuk
26
Gambar 6, Gambar 7 dan Gambar 8, menunjukkan bahwa perbandinagn antara penyelesaian numerik dengan penyelesaian hampiran VIM memiliki galat mutlak yang kecil.
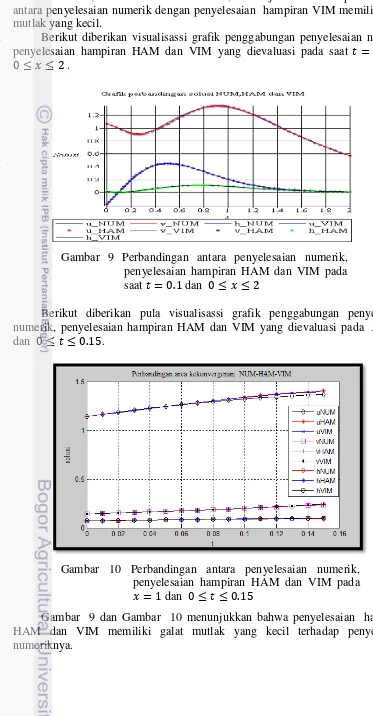
Berikut diberikan visualisassi grafik penggabungan penyelesaian numerik, penyelesaian hampiran HAM dan VIM yang dievaluasi pada saat dan .
Berikut diberikan pula visualisassi grafik penggabungan penyelesaian numerik, penyelesaian hampiran HAM dan VIM yang dievaluasi pada dan .
Gambar 9 dan Gambar 10 menunjukkan bahwa penyelesaian hampiran HAM dan VIM memiliki galat mutlak yang kecil terhadap penyelesaian numeriknya.
Gambar 9 Perbandingan antara penyelesaian numerik, penyelesaian hampiran HAM dan VIM pada saat dan
27 Selanjutnya Gambar 11 menunujukkan grafik 2D dari penyelesaian numerik yang dievaluasi pada dan .
a. b. c.
Gambar 11a menunjukkan bahwa kecepatan arah horizontal-x berubah terhadap waktu. Semakin bertambah waktu, berakibat pada semakin tingginya kecepatan maksimal fluida. Selain itu, kecepatan maksimal dari waktu ke waktu mengalami perubahan posisi. Gambar 11b menunjukkan bahwa perubahan kecepatan maksimal fluida arah horizontal-y relatif tidak berubah terhadap perubahan waktu. Kecepatan maksimal dari waktu ke waktu hanya mengalami perubahan posisi dalam arah horizontal-x.
Selanjutnya grafik penyelesaian pada Gambar 11c menunjukkan perubahan ketinggian maksimal atau titik puncak fluida terhadap perubahan waktu. Semakin bertambah waktu, berakibat pada semakin berkurangnya ketinggian maksimal fluida. Selain itu, ketinggian maksimal fluida dari waktu ke waktu juga mengalami perubahan posisi.
5
SIMPULAN DAN SARAN
Simpulan
Masalah gelombang internal di atmosfer dapat digambarkan melalui persamaan dasar fluida. Representasi matematis dari persamaan dasar fluida berupa sistem persamaan diferensial parsial taklinear yang sulit diselesaikan secara analitik. HAM dan VIM dapat diterapkan dalam menentukan penyelesaian hampiran pada masalah tersebut. Penggunaan HAM dan VIM pada penyelesaian persamaan dasar fluida efisien dan sederhana, karena hanya melibatkan perhitungan yang sederhana dengan memanfaatkan integral biasa.
28
Penggunaan HAM dalam menyelesaikan persamaan dasar fluida diperlukan suatu operator linear dan taklinear. Berdasarkan bentuk operator linear dan taklinear, diperoleh persamaan deformasi orde tinggi. Penyelesaian hampiran HAM ditentukan melalui penyelesaian deret. Suku-suku pada deret dihasilkan dari penyelesaian deformasi orde nol dan deformasi orde tinggi. Kekonvergenan penyelesaian hampiran terhadap penyelesaian numerik dapat dikontrol melalui pemilihan parameter bantu. Penerapan VIM dalam menyelesaikan persamaan dasar fluida dilakukan dengan mengonstruksi fungsi koreksi dan menentukan nilai pengali Lagrange yang optimal. Berdasarkan fungsi koreksi dan pengali Lagrange, diperoleh rumus iterasi yang dapat memberikan penyelesaian hampiran.
Penyelesaian persamaan dasar fluida yang menggambarkan perambatan gelombang internal di atmosfer menunjukkan bahwa kecepatan maksimal fluida dalam arah horizontal-x mengalami perubahan nilai dan perubahan posisi terhadap perubahan waktu. Selanjutnya, kecepatan maksimal fluida dalam arah horizontal-y relatif tidak berubah dan hanya megalami perubahan posisi terhadap perubahan waktu. Sedangkan titik puncak fluida mengalami penurunan dan perubahan posisi terhadap perubahan waktu.
Saran
Pada penelitian ini hanya difokuskan pada penentuan penyelesaian hampiran sistem PDP taklinear satu dimensi. Dengan ini disarankan perlunya dilakukan penentuan penyelesaian untuk dua dimensi. Selanjutnya untuk kebutuhan validasi model, perlu dilakukan pengembangan simulasi numerik dengan melibatkan data-data meteorologi yang tepat. Penerapan HAM dan VIM pada penyelesaian masalah taklinear efisien. Dengan ini disarankan pula untuk dapat menerapkan HAM dan VIM dalam berbagai model matematis dari fenomena alam lainnya.
DAFTAR PUSTAKA
Alomari AK, Noorani MS, Roslinda MN. 2008. Approximate analytical solutions of the Klein-Gordon equation by means of the homotopy analysis method. JQMA. 4(1):45-57.
Anderson JD, 1995. Computational Fluid Dynamics The Basics with Aplication . New York (US). McGraw-Hill, Inc.
Blaise S, St-Cyr A. 2012. A dynamic hp-Adaptive discontinuous Galerkin method for shallow-water flows on the sphere with application to a global tsunami simulation. Mont Wea Rev. 140:978-996.
Clancy C, Lynch P. 2011. Laplace transform integration of the shallow-water equations: Eulerian formulation and Kelvin wave. Quart J Roy Meteor Soc. 137 (656):792-799.
29 Duba CT, McKenzie JF. 2012. Propagation properties of Rosby waves for latitudinal β-plane variations off and zonal variations of the shallow water speed. Ann. Geophys. 30:849-855.
Duangpithak S, Torvattanabun M. 2012. Variational iteration method for solving nonlinear reaction-diffusion-convection poblems. AMS. 6(17): 843 – 849.
Jafar H, Yazdan A, Vah d J, Gan DD. 2008. Appl cat on of He’s Var at onal
Iteration Method for solving seventh order Sawada-Kotera Equations. Applied Mathematical Science. 2(10):471-477. Huxley equation by homotopy analysis method. JAFA. 5(4): 334-350.
Jaharuddin. 2014. A single species population model in polluted environment solved by homotopy analysis method. AMS. 8(20):951-961.
Jiaqi M, Wantao L, Hai W. 2009. A class of homotopic solving method for ENSO model. Acta Mathematica Scientis. 29B(1):101-110.
Liao SJ. 1992. The proposed homotopy analysis technique for the solution of nonlinear problem. Ph.D thesis, Sanghai Jiao Tong University.
Liao SJ. 2004. Beyond Perturbation: Introduction to The Homotopy Analysis Method. New York (US) . A CRC Press Company.
Matinfar M, Fereidoon A, Aliasghartoyeh A, Ghanbari M. 2009. Variational iteration method for solving nonlinear WBK equations. IJNS. 8(4):419-423. Miansari MO, Miansari ME, Barari A, Ganji DD. 2009. Applcat on of He’s
variational iteration method to nonlinear Helmholtz and fifth-order KdV equations. JAMSI. 5(1):5-20.
Rottman JW, Brottman D, Eckermann SD. 2007. A forecast model for atmospheric internal waves produced by a mountain. 16th Australian Fluid Mechanics Confrence Crown Plaza, Goal Coast. Australia.
Safari M, Ganji DD, Moeslemi M. 2009. Application of He's variational iteration method and Adomian's decomposition method to the fractional KdV Burgers Kuramoto equation. Comp. Math. App. 58(2009):2091-2097.
Swheilam NH. and Khader MM. 2007. Variational iteration method for one dimensional nonlinear thermoelasticity. Chaos, Solitons and Fractals. 32(2007): 145-149.
Usman M, Zubair T, Rashid I, Rashid I, Yildirim A, Mohyud-din ST. 2013. Modified Homotopy Analysis Method for Zakharov-Kuznetsov. Walailak. 10(5): 467-478.
30 dan arah vertikal-z. Selisih antara massa yang masuk dengan yang keluar adalah
dan
masing-masing untuk arah horizontal , arah horizontal-y dan arah vertikal-z. Laju perubahan massa fluida adalah
Persamaan (L1.5) dapat dinyatakan dalam bentuk lain dengan menggunakan operator turunan total suatu fungsi terhadap , yaitu
(L1.6)
31
Substitusi persamaan (L1.5) ke persamaan (L1.7), dengan demikian diperoleh
Dengan menggunakan asumsi fluida taktermampatkan, yaitu fluida tidak mengalami perubahan rapat massa selama waktu aliran diperoleh
Berdasarkan persamaan (L1.8) dan (L1.9), maka diperoleh
Lampiran 2 Penurunan persamaan (2.3), (2.4) dan (2.5)
Momentum yang masuk adalah dan masing-masing pada arah horizontal- , arah horizontal- dan arah vertikal- , sedangkan momentum yang keluar adalah , dan masing-masing pada arah horizontal- , arah horizontal- dan arah vertikal- .
32
33
(L2.10)
(L2.11)
(L2.12)
Dengan menggunakan asumsi fluida taktermampatkan, jika persamaan (L1.10) dan (L1.11) disubstitusi pada persamaan (L2.10), (L2.11) dan (L2.12), maka diperoleh
(L2.13)
(L2.14)
(L2.15)
Lampiran 3 Penurunan persamaan (4.17) Berikut persamaan deformsi orde nol
(L3.1)
(L3.2)
(L3.3)
atau
(L3.4)
(L3.5)
34
Turunkan persamaan deformasi orde nol terhadap sebanyak kali. Turunan pertama
Turunan pertama persamaan (L3.4) terhadap adalah
Turunan pertama persamaan (L3.5) terhadap adalah
Turunan pertama persamaan (L3.6) terhadap adalah
Turunan kedua persamaan (L3.4) terhadap adalah
Turunan kedua persamaan (L3.5) terhadap adalah
35 Turunan kedua persamaan (L3.6) terhadap adalah
Turunan ketiga persamaan (L3.4) terhadap adalah
Turunan ketiga persamaan (L3.5) terhadap adalah
Turunan ketiga persamaan (L3.6) terhadap adalah
36
Turunan ke-
37
maka persamaan (L3.19), (L3.20) dan (L3.21) menjadi
38
Lampiran 4 Penurunan persamaan (4.31)
Dengan menggunakan turunan deformasi orde nol pada persamaan (L3.22), (L3.23) dan (L3.24) dan operator linear pada persamaan (4.29) yang dapat diuraikan menjadi
(L4.1)
(L4.2)
(L4.3)
diperoleh
(L4.4)
(L4.5)
(L4.6) jika kedua ruas pada persamaan (L4.4), (L4.5), dan (L4.6) diintegralkan terhadap
, maka diperoleh
(L4.7)
(L4.8)
(L4.9)
Lampiran 5 Penurunan persamaan (4.32)
43 Berdasarkan persamaan (L5.1) dan (L5.4), maka diperoleh bentuk umum dari
, yaitu
(L5.7)
Berdasarkan persamaan (L5.2) dan (L5.5), maka diperoleh bentuk umum dari , yaitu
(L5.8)
Berdasarkan persamaan (L5.3) dan (L5.6) maka diperoleh bentuk umum dari , yaitu
44