PEMODELAN
GEOGRAPHICALLY WEIGHTED RIDGE
REGRESSION
DAN
GEOGRAPHICALLY WEIGHTED LASSO
PADA DATA SPASIAL DENGAN MULTIKOLINIERITAS
TIYAS YULITA
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
Dengan ini saya menyatakan bahwa tesis berjudul Pemodelan
Geographically Weighted Ridge Regression dan Geographically Weighted Lasso
pada Data Spasial dengan Multikolinieritas adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Januari 2016
Tiyas Yulita
TIYAS YULITA. Pemodelan Geographically Weighted Ridge Regression dan
Geographically Weighted Lasso pada Data Spasial dengan Multikolinieritas.
Dibimbing oleh ASEP SAEFUDDIN dan AJI HAMIM WIGENA.
Data spasial berorientasi secara geografis dan memiliki sistem koordinat tertentu sebagai dasar referensinya sehingga dapat disajikan dalam sebuah peta. Permasalahan yang sering ditemukan pada data spasial adalah ragam yang tidak selalu homogen pada setiap lokasi pengamatan atau heterogenitas spasial. Jika data spasial dengan masalah heterogenitas spasial dianalisis dengan Metode Kuadrat Terkecil (MKT) atau dimodelkan dengan regresi linier maka dugaan parameter yang diperoleh akan memiliki ragam yang besar.
Geographically Weighted Regression (GWR) dapat digunakan untuk mengeksplorasi keragaman spasial dengan membentuk model regresi yang berbeda pada setiap lokasi pengamatan. Metode ini cukup efektif dalam melakukan pendugaan parameter pada data dengan heterogenitas spasial. Permasalahan lain mungkin dapat muncul seperti adanya hubungan antarpeubah penjelasnya yang disebut dengan multikolinieritas. Pada data spasial, masalah multikolinieritas juga dapat menyebabkan model spasial yang diperoleh tidak stabil sehingga kesalahan interpretasi dapat terjadi, maka diperlukan metode yang mampu menangani masalah multikolinieritas seperti Geographically Weighted Ridge Regression (GWRR) dan Geographically Weighted Lasso (GWL). Sukmantoro (2014) menggunakan GWRR untuk memodelkan nilai tanah di Perumahan Pondok Indah Jakarta Selatan tahun 2011 yang menghasilkan dugaan parameter dengan GWRR memiliki akurasi dan presisi pendugaan yang lebih baik dari GWR. Munikah et al. (2014) menggunakan GWL untuk mengatasi masalah heterogenitas spasial dan multikolinieritas pada data spasial dengan studi kasus kerawanan pangan di Kabupaten Tanah Laut dengan hasil GWL memiliki performa yang lebih baik dari GWR.
Pada penelitian ini performa dari kedua model pendugaan dalam mengatasi multikolinieritas akan dievaluasi dengan menggunakan data Produk Domestik Regional Bruto (PDRB) dari 113 kabupaten/kota di Pulau Jawa tahun 2010. Sebelum menggunakan GWL dan GWRR pada data, dilakukan pemodelan dengan menggunakan GWR terlebih dahulu untuk mengetahui adanya multikolinieritas lokal antara peubah penjelasnya. Nilai VIF yang diperoleh pada model GWR dari data menunjukkan bahwa terdapat multikolinieritas lokal pada peubah-peubah penjelasnya. Ini dapat disebabkan oleh adanya penambahan matriks pembobot dalam proses pendugaan. Fungsi yang digunakan untuk membentuk matriks pembobot pada setiap model adalah dengan fungsi fixed exponential kernel.
mampu mengatasi multikolinieritas lokal yang kuat dengan menghasilkan dugaan yang lebih baik dari model GWR maupun GWRR, namun performa yang dihasilkan oleh model GWRR tidak lebih baik dari hasil yang diberikan oleh model GWR.
TIYAS YULITA. Geographically Weighted Ridge Regression and Geographically Weighted Lasso Models in Spatial Data with Multicollinearity. Supervised by ASEP SAEFUDDIN and AJI HAMIM WIGENA
Spatial data is geographically oriented and it has a specific coordinate system as reference and it can be presented in a map. The problem of spatial data is variance in over observation location which is not always homogen (spatial heterogeneity). If the spatial data with spatial heterogeneity problem is analyzed by Ordinary Least Squares Method (OLS), it will has large variance. Geographically Weighted Regression (GWR) can be used to explore the spatial heterogeneity by forming the different regression models for each observation location. This method is quite effective in parameter estimation on the data with spatial heterogeneity. Another problem is any relationship between explanatory variables which called as multicollinearity. On the spatial data, multicollinearity problem can obtain spatial models which is not stable so it will occur misinterpretations models.
To solve the spatial heterogeneity and local multicollinearity problem, Geographically Weighted Ridge Regression (GWRR) and Geographically Weighted Lasso (GWL) will be used. Sukmantoro (2014) use GWRR to form models of land value in Pondok Indah, South Jakarta in 2011 and the result is accuracy and precision of GWRR has better estimation than GWR. Munikah et al. (2014) use GWL to resolve the problem of spatial heterogeneity and local multicollinearity on spatial data with study case of food insecurity in Tanah Laut, and the result is GWL has better performance than GWR.
Performance of the prediction model to overcome spatial heterogeneity and local multicollinearity will be evaluated by using data Gross Regional Domestic Product (GRDP) of 113 districts / cities in Java on 2010. Before we use GWL and GWRR on data, checking multicollinearity between explanatory variables before is needed. VIF value which obtained in GWR models indicate that there are local multicollinearity between explanatory variables. It can be caused by the addition of weighted matrix in the estimation process. Fixed exponential kernel function is used to form the weighted matrix on each model over location observation.
© Hak Cipta Milik IPB, Tahun 2016
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB.
PEMODELAN
GEOGRAPHICALLY WEIGHTED RIDGE
REGRESSION
DAN
GEOGRAPHICALLY WEIGHTED LASSO
PADA DATA SPASIAL DENGAN MULTIKOLINIERITAS
TIYAS YULITA
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Statistika
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
Puji dan syukur penulis ucapkan kehadirat Allah Subhanahuwata’ala atas segala karunia-Nya sehingga penulis dapat menyelesaikan tesis ini. Shalawat serta salam semoga senantiasa tercurah kepada junjungan kita Nabi Muhammad SAW beserta keluarga, para sahabat, serta para penerus perjuangan Beliau hingga akhir zaman. Penelitian ini berjudul “Pemodelan Geographically Weighted Ridge Regression dan Geographically Weighted Lasso pada Data Spasial dengan Multikolinieritas”. Penulisan karya ilmiah ini tidak lepas dari bantuan, bimbingan, dan petunjuk dari berbagai pihak. Oleh karena itu, penulis menyampaikan penghargaan dan ucapan terima kasih khususnya kepada:
1. Prof Dr Asep Saefuddin, MSc selaku pembimbing I dan Dr Ir Aji Hamim Wigena, MSc selaku pembimbing II yang dengan kesabaran telah banyak memberi bimbingan, arahan, serta saran kepada penulis selama penyusunan tesis ini.
2. Dr Ir Indahwati, MSi selaku penguji luar komisi yang telah memberikan masukan dan arahan yang sangat membangun dalam penyusunan tesis ini. 3. Seluruh staf pengajar Sekolah Pascasarjana Statistika IPB yang telah banyak
memberikan ilmu dan arahan selama perkuliahan sampai dengan penyusunan tesis ini.
4. Teman-teman statistika angkatan 2013 atas kebersamaan dan bantuannya kepada penulis selama kuliah.
5. Kedua orang tua serta seluruh keluarga atas doa, dukungan moril, dan kasih sayang yang diberikan kepada penulis.
6. Direktorat Jenderal Pendidikan Tinggi sebagai sponsor pemberi beasiswa BPPDN yang mendukung kelanjutan studi S2 penulis.
7. Seluruh pihak yang namanya tidak dapat disebutkan satu per satu.
Atas segala bantuan yang diberikan, penulis hanya bisa berdoa dengan harapan semoga semua kebaikan yang penuh keikhlasan tersebut dicatat sebagai amal ibadah dan mendapatkan balasan berupa pahala disisi Allah Subhanahuwata’ala Aamiin Ya Rabbal‘Alamin. Semoga karya ilmiah ini bermanfaat serta dapat menambah wawasan bagi para pembaca.
Bogor, Januari 2016
DAFTAR TABEL xi
DAFTAR GAMBAR xi
DAFTAR LAMPIRAN xi
PENDAHULUAN
Latar Belakang 1
Tujuan Penelitian 2
TINJAUAN PUSTAKA
Uji Heterogenitas Spasial 3
Multikolinieritas 4
Geographically Weighted Regression (GWR) 5
Fungsi Pembobot Spasial 6
Korelasi Pearson Terboboti Geografis 6 Pengujian Goodness of Fit 7
Regresi Ridge 7
Geographically Weighted Ridge Regression (GWRR) 8
Locally Compensated Ridge Geographically Weighted
Regression (LCR-GWR) 9
Least Absolute Shrinkage and Selection Operator (LASSO) 10
Geographically Weighted Lasso (GWL) 11
METODE PENELITIAN
Data 12
Metode Analisis 13
HASIL DAN PEMBAHASAN
Eksplorasi Data 15
Pemodelan Regresi Linier 17
Pengujian Pengaruh Heterogenitas Spasial 18 Pemodelan Geographically Weighted Regression (GWR) 18 Pemodelan Geographically Weighted Ridge Regression (GWRR) 21
Pemodelan LCR-GWR 22
Pemodelan Geographically Weighted Lasso (GWL) 23 Kekonsitenan Metode Terhadap Multikolinieritas 24 SIMPULAN DAN SARAN
Simpulan 28
Saran 28
DAFTAR PUSTAKA 29
1 Peubah penjelas gugus data pertama 12
2 Peubah penjelas gugus data kedua 12
3 Statistik deskriptif peubah respon dan penjelas 16 4 Koefisien korelasi antara peubah respon dan penjelas 16 5 Hasil pengujian parsial dari dugaan parameter dengan MKT 17
6 Hasil analisis ragam dengan MKT 17
7 Matriks pembobot pada model GWR 19
8 Ringkasan pendugaan parameter pada model GWR 19 9 Ringkasan nilai VIF untuk gugus data pertama pada seluruh
lokasi 20
10 Ringkasan hasil pendugaan parameter pada model GWRR 21 11 Nilai multikolinieritas untuk gugus data kedua pada model dengan
MKT 24
12 Ringkasan nilai VIF untuk gugus data kedua pada seluruh lokasi 24 13 Perbandingan model GWR, GWRR, LCR-GWR dan GWL
untuk gugus data pertama 26
14 Perbandingan model GWR, GWRR, LCR-GWR, dan GWL
untuk gugus data kedua 27
DAFTAR GAMBAR
1 Peta PDRB pada setiap kabupaten/kota di Pulau Jawa tahun 2010 15
2 Scatterplot hubungan antar peubah penjelas 17
3 Peta dugaan nilai PDRB pada model GWR 20
4 Peta dugaan nilai PDRB pada model GWRR 22
5 Peta dugaan nilai PDRB pada model LCR-GWR 22
6 Peta dugaan nilai PDRB pada model GWL 23
7 Peta dugaan nilai PDRB pada model GWR(a), GWRR(b),
LCR-GWR (c), dan GWL(d) 25
DAFTAR LAMPIRAN
1 Plot nilai sisaan (residual) terhadap dugaan nilai PDRB 31 2 Tabel hasil dugaan parameter pada model GWRR dan nilai dugaan
PDRB untuk setiap lokasi pengamatan 31
5 Tabel korelasi Pearson terboboti geografis antara peubah respon
dan peubah-peubah penjelasnya (X1, X2, X3, dan X4) 41 6 Tabel korelasi Pearson terboboti geografis antara peubah respon
dan peubah-peubah penjelasnya (X5, X6, X7, dan X8) 44 7 Syntax Pemodelan GWR, GWRR, LCR-GWR, dan GWL dengan
PENDAHULUAN
Latar Belakang
Metode statistika seringkali digunakan sebagai alat untuk mengetahui hubungan antarpeubah dengan cara membentuk suatu model yang sesuai dalam menggambarkan karakteristik data. Seperti pada model regresi linier yang mampu menggambarkan hubungan antara peubah penjelas dengan peubah responnya. Melihat hubungan antarpeubah pada data spasial dapat dilakukan dengan metode statistika spasial.Data spasial merupakan data yang berorientasi secara geografis dan memiliki sistem koordinat tertentu sebagai dasar referensinya, sehingga dapat disajikan dalam sebuah peta.
Permasalahan yang sering ditemukan pada data spasial adalah ragam yang tidak selalu homogen pada setiap lokasi pengamatan atau disebut dengan heterogenitas spasial. Heterogenitas spasial dapat disebabkan oleh beberapa hal seperti perbedaan kondisi geografis, sosial-budaya, hingga kebijakan ekonomi yang berbeda-beda pada setiap lokasi. Hal ini akan menjadi masalah jika data spasial tetap dianalisis dengan menggunakan Metode Kuadrat Terkecil (MKT) dalam pendugaan parameternya, karena dapat menyebabkan ragam dugaan menjadi besar. Untuk mengatasi permasalahan ini, diperlukan metode yang mampu mengatasi heterogenitas ragam pada data spasial untuk membentuk model yang lebih efisien.
Geographically Weighted Regression (GWR) adalah metode statistika spasial yang merupakan pergeseran dari model global menjadi model lokal. Model GWRbertujuan untuk mengeksplorasi keragaman spasial dengan membentuk model regresi yang berbeda pada setiap lokasi pengamatan. Metode ini cukup efektif dalam melakukan pendugaan parameter pada data dengan heterogenitas spasial (Fotheringham et al.2002). Masalah lain yang mungkin muncul pada pemodelan dengan peubah penjelas lebih dari satu adalah multikolinieritas. Multikolinieritas disebabkan oleh adanya hubungan linier yang hampir sempurna (near dependence) pada kolom-kolom matriks X dan apabila terjadi hubungan linier yang sempurna akan menyebabkan |���| = 0, sehingga kondisi ini disebut dengan multikolinieritas sempurna (exact multicollinearity) (Draper &Smith 1998). Kondisi tersebut dapat menyebabkan hasil dugaan parameter memiliki ragam yang besar sehingga pengujian signifikansi peubah menjadi tidak stabil. Seperti pada pemodelan dengan regresi linier berganda, masalah multikolinieritas juga dapat ditemui pada regresi spasial yang disebut dengan mutikolinieritas lokal.
Pada regresi spasial, multikolinieritas dapat diatasi dengan menggunakan konsep dari metode regresi ridge dan lasso ke dalam GWR. Geographically Weighted Lasso(GWL) merupakan metode GWR yang menggunakan konsep lasso dalam pendugaan parameter untuk mengatasi masalah multikolinieritas, sehingga diharapkanhasil dugaan parameter yang diperoleh lebih stabil. Metode GWL mampu mengatasi masalah heterogenitas spasial dan multikolinieritas pada data spasial dengan studi kasus kerawanan pangan di Kabupaten Tanah Laut dengan hasil GWL memiliki performa yang lebih baik dari GWR (Munikah et al.
2014). Metode lain yang dapat digunakan untuk mengatasi multikolinieritas pada data spasial adalah Geographically Weighted Ridge Regression (GWRR), metode ini menggunakan konsep regresi ridge dalam proses pendugaan parameternya. GWRR pernah digunakan untuk memodelkan nilai tanah di Perumahan Pondok Indah Jakarta Selatan tahun 2011 yang menghasilkan dugaan parameter dengan GWRR memiliki akurasi dan presisi pendugaan yang lebih baik dari GWR (Sukmantoro 2014).
Fatulloh (2013) menggunakan GWR dalam memodelkan Produk Domestik Regional Bruto (PDRB) pada 113 kabupaten/kota diPulau Jawa tahun 2010 yang mempunyai efek spasial berupa heterogenitas spasial. PDRB merupakan jumlah nilai tambah yang timbul dari seluruh sektor perekonomian di suatu wilayah tertentu, atau merupakan jumlah nilai barang dan jasa akhir yang dihasilkan oleh seluruh unit ekonomi. PDRB dapat dijadikan sebagai ukuran atau gambaran menyeluruh tentang kondisi perekonomian suatu daerah karena merupakan suatu indikator ekonomi. Pertumbuhan ekonomi Indonesia pada tahun 2010 sebesar 6,4% per tahun, dan Pulau Jawa memberikan kontribusi PDRB sebesar 58,7% terhadap Produk Domestik Bruto (PDB) nasional. Selain dilihat dari sumber pendukung perekonomian secara fisik, pertumbuhan ekonomi dari suatu wilayah tidak lepas dari kualitas SDM dari wilayah tersebut. Pada penelitian ini akan digunakan peubah-peubah yang meliputi faktor penyusun PDRB serta faktor dari kualitas SDM berupa IPM untuk menduga nilai PDRB. Pada penelitian sebelumnya (Fatulloh 2013) tidak menggunakan peubah yang mengandung multikolinieritas dalam menduga nilai PDRB, sehingga pada penelitian ini digunakan peubah penjelas yang mengandung multikolinieritas yang kemudian diatasi dengan menggunakan model GWRR dan GWL.
Tujuan Penelitian Tujuan dari penelitian ini adalah:
1. Membangun model GWRR dan GWL dari data PDRB113 kabupaten/kota di Pulau Jawa tahun 2010.
TINJAUAN PUSTAKA
Data spasial merupakan data yang memiliki referensi berupa ruang kebumian (georeference) dengan data atribut sebagai pelengkap untuk setiap unit spasialnya. Data atribut merupakan informasi non-spasial yang berfungsi sebagai penjelas objek bagi suatu data spasial. Salah satu cara dasar dalam penyajian data spasial adalah dengan menggunakan titik (point) berupa informasi koordinat dari suatu wilayah pengamatan. Pada penelitian ini, data PDRB diperoleh dari 113 kabupaten/kota yang terdapat di Pulau Jawa sehingga sangat dimungkinkan jika data spasial maupun data atribut memiliki keragaman yang tidak homogen. GWR dipilih karena dinilai mampu mengatasi keragaman spasial dengan membentuk model yang berbeda untuk setiap unit spasialnya. Penggunaan beberapa peubah penjelas pada penelitian ini juga memungkinkan terjadinya masalah multikolinieritas yang kemudian diatasi dengan menggunakan model GWRR dan GWL. Beberapa referensi yang terkait dan mendukung tercapainya tujuan dalam penelitian ini diberikan sebagai berikut.
Uji Heterogenitas Spasial
Perbedaan kondisi sosial-budaya maupun geografis dari beberapa wilayah dapat menyebabkan adanya heterogenitas spasial pada model. Anselin (1988) menggunakan Uji Breusch-Pagan untuk menguji adanya heterogenitas spasial dalam model dengan hipotesis seperti berikut:
� ∶ ��2 = �2 (tidak terdapat heterogenitas spasial)
� ∶ minimal ada satu ��2 ≠ �2 (terdapat heterogenitas spasial) ; � = , , … , �
Statistik Uji Breusch-Pagan (BP)
� = �� � − �� ~ �2
�+ (1)
dengan elemen vektor �
� = �� 2
�2−
dengan :
�� = sisaan untuk pengamatan ke-i dengan matriks berukuran � ×
� = vektor berukuran � ×
� = banyaknya wilayah pengamatan
�2 = ragam sisaan � �
=matriks berukuran � × � + yang berisi vektor dari X dengan pengamatan yang telah dibakukan.
pengambilan keputusan pada uji BP tolak � jika BP > χ,2p+ dimana χ,2p+ merupakan titik kritis uji �2 dengan taraf nyata .
Multikolinieritas
Draper dan Smith (1998) menyatakan bahwa multikolinieritas disebabkan oleh adanya hubungan linier yang hampir sempurna (near dependence) pada kolom-kolom matriks X dan apabila terjadi hubungan linier yang sempurna akan menyebabkan | � | = sehingga kondisi ini disebut dengan multikolinieritas sempurna (exact multicollinearity).
Jika X merupakan matriks berukuran � × � + dan tiap vektor
, , , … , � pada matriks X tidak memiliki hubungan liner, maka rank (X) = p + 1. Karena X adalah matriks dengan rank penuh (full rank) maka � adalah matriks persegi yang berukuran (p+1) × (p+1) dengan rank ( � ) = rank (X) = p + 1. Jika � merupakan matriks persegi dengan rank penuh, maka
� merupakan matriks non-singular, sehingga | � |bersifat unik. Maka dari itu penyelesaian untuk persamaan berikut juga bersifat unik.
�̂ = � − � (2)
Namun jika terdapat hubungan linier antar vektor , , , … , �pada matriks X, maka � bukan merupakan matriks dengan rank penuh sehingga � − tidak bersifat unik, yang menyebabkan penyelesaian untuk persamaan (2) tidak diperoleh secara unik. Multikolinieritas yang ada pada peubah penjelas dalam model regresi linear dapat menyebabkan pendugaan parameter dari model regresi yang dihasilkan memiliki ragam yang besar.Mengidentifikasi adanya multikolinieritas pada peubah penjelas dapat dilakukan dengan melihat hasil pengujian parsial dan serentak pada koefisien model regresi. Jika hasil pengujian parsial menunjukkan peubah-peubah penjelas tidak berpengaruh signifikan sedangkan pada pengujian secara serentak menunjukkan hasil yang sebaliknya atau signifikan maka dicurigai terdapat masalah multikolinieritas pada peubah penjelasnya.
Indikator lain dari adanya multikolinieritas dapat dilihat dari nilai VIF (Variance Inflation Factor) yang merupakan invers dari nilai toleransi − �2 . Nilai toleransi yang mengindikasikan adanya mutikolinearitas bernilai kurang dari 0,20 atau 0,10 dan atau nilai VIF-nya lebih besar dari 5 atau 10. Nilai VIF yang lebih besar dari 10 sangat mempengaruhi dugaan kuadrat terkecil dari koefisien regresi (Friday & Emenonye 2012). Pada pemodelan GWR, nilai VIF dihitung untuk masing-masing peubah penjelasnya pada setiap lokasi pengamatan dengan matriks pembobot sebagai area deteksi kolinieritas pada model GWR. Nilai VIF dinyatakan sebagai berikut :
dengan �2 �, � adalah koefisien determinasi antara dengan peubah penjelas lainnya utuk setiap lokasi �, � (Wheeler 2007).
Geographically Weighted Regression (GWR)
Fotheringham et al. (2002) mengatasi data yang memiliki masalah keheterogenan spasial melalui pendugaan titik yang efektif dengan menggunakan GWR. Dalam prinsipnya GWR mengadopsi konsep yang ada pada model regresi linier menjadi model regresi terboboti. Model GWR menerapkan hubungan regresi spasial non-stasioner untuk kasus keheterogenan spasial dengan menghasilkan koefisien model regresi pada masing-masing lokasi. Jika koefisien parameter yang dihasilkan pada setiap lokasi bernilai konstan disebut model regresi global. Model regresi global dinotasikan sebagai berikut:
�� = + ∑�= � + �; � = , , … , � (4)
dengan( , … , � adalah koefisien parameter lokasi dan sisaan diasumsikan �~� , �2 . Sedangkan notasi untuk model GWR adalah:
�� = �, � + ∑�= �, � � + � ; � = , , … , � (5)
dimana �� adalah peubah respon pada lokasi ke-i, � merupakan peubah penjelas ke-k pada lokasi ( �, � , adalah koefisien parameter lokal untuk masing-masing lokasi ( �, � dan sisaan diasumsikan �~� , �2 . Ini mengakibatkan setiap lokasi memiliki koefisien parameter yang berbeda-beda sehingga menghasilkan keragaman yang memberi informasi mengenai hubungan regresi antara peubah penjelas dan respon secara lokal.
Leung et al. (2000) menerangkan bahwa pendugaan koefisien parameter lokal dari model GWR dilakukan dengan metode Weighted Least Square (WLS) dari persamaan (5) diturunkan terhadap �� �, � , dugaan parameter untuk setiap lokasi ̂ �, � adalah sebagai berikut:
� �, � = [ �� �, � ]− �� �, � (6)
dengan :
=
2 2 22
� 2�
⋮ ⋱ ⋮
� �2 ��
) = � �2
⋮ ��
)
� �, � =
�, �
2 �, �
⋮ ⋮
…⋱ � ⋮�, �
Fungsi Pembobot Spasial
Untuk membentuk matriks pembobot diperlukan fungsi pembobot yang dipengaruhi oleh ukuran ketetanggaan (neighborhood size) yang seringkali disebut dengan bandwidth atau lebar jendela dan disesuaikan dengan kedekatan titik lokasi pengamatan ke-i. Pada model GWR, koordinat dari data spasial digunakan untuk menghitung jarak antar titik lokasi dari suatu pengamatan yang kemudian menghasilkan bobot antar pengamatan. Matriks pembobot pada GWR dihitung dari suatu fungsi kernel yang menjadikan lokasi pengamatan yang lebih dekat dengan titik lokasi pengamatan ke- � memiliki bobot yang lebih besar daripada lokasi pengamatan yang letaknya lebih jauh. Fungsi fixed exponential kernel digunakan untuk membentuk matriks pembobot karena merupakan fungsi
kernel yang paling sederhana. Fungsi kernel tersebut memiliki nilai bandwidth
yang sama untuk setiap pengamatan dengan bentuk fungsi sebagai berikut:
�, � = � − ℎ (7)
dengan ℎ pada fungsi kernel merupakan bandwidth pada lokasi pengamatan ke- i. Pada fungsi kernel di atas, � adalah jarak antara titik di lokasi ke-i dan lokasi
ke-j yang diperoleh dari jarak euclidean seperti berikut ini:
� = √ � − 2+ �− 2 (8)
Sebelum melakukan pemodelan dengan GWR, hal lain yang harus diperhatikan adalah menduga nilai bandwidth. Pendugaannya dilakukan dengan metode Cross Validation leave-one-out pada seluruh lokasi. Bentuk matematis dari CV adalah sebagai berikut:
� ℎ = ∑ [���= � − �̂≠� ℎ ]2 (9)
dengan �̂≠� ℎ adalah nilai dugaan untuk �� dengan menghilangkan pengamatan titik lokasi ke- i pada proses prediksi dan bandwidth optimum (h) akan diperoleh dengan proses iterasi sampai diperoleh CV yang minimum (Fotheringham et al.
2002).
Korelasi Pearson Terboboti Geografis
Korelasi Pearson tanpa diberikan pembobot dalam perhitungannya menghasilkan koefisien korelasi yang bersifat global. Maka Kalogitou (2013) memberikan korelasi secara lokal dengan pemberian bobot secara geografis untuk mengetahui kondisi korelasi peubah-peubahnya pada setiap lokasi pengamatan. Koefisien korelasi terboboti geografis untuk dua peubah diberikan sebagai berikut:
�, = ∑ = ( − ̅ − ̅ √∑= ( − ̅ √∑= − ̅
(10)
Pengujian Goodness of Fit
Untuk mengetahui apakah model GWR yang diperoleh lebih baik dari Metode Kuadrat Terkecil (MKT) dalam menjelaskan keragaman maka dilakukan pengujian kebaikan model dengan mengukur perbedaan jumlah kuadrat galat (JKG) dari MKT dan GWR. Hipotesis nol menyatakan bahwa kemampuan model GWR dan MKT dalam mendeskripsikan data tidak berbeda. Statistik uji yang digunakan adalah sebagai berikut:
� = �� �/
���/ �−�− (11)
dengan � = � �− ���� = �[ − − − � � − � ] = �� dan� = − − − � � − � adalah matriks semidefinit positif, karena
� untuk setiap . � � = � − , dimana = � − �dan
− bersifat idempoten. ���� = �[ − � � − � ] .
� = (
�[ �� ]− �� �[ �� ]− ��
⋮
�
�[ �� � ]− �� � )
Tolak � jika � > � , � − � − , dengan = � dan 2 = �2 ( Leung et al. 2000).
Regresi Ridge
Hoerl & Kennard (2000) memperkenalkan regresi ridge untuk mengendalikan ketidakstabilan penduga kuadrat terkecil. Regresi ridge mengatasi masalah multikolinieritas dengan cara meminimumkan jumlah kuadrat galat yang menambahkan kendala pada kuadrat terkecil sehingga koefisien menyusut mendekati nol (Hastie et al. 2009). Secara spesifik, penduga koefisien pada regresi ridge diperoleh dengan cara meminimumkan persamaan berikut:
̂� = �rg �i� {∑ (�� − − ∑ �
�
=
)
2 �
�=
+ ∑ 2
�
=
}
dengan kendala ∑�= 2 �, dimana � merupakan besaran yang mengendalikan besarnya penyusutan dengan nilai � . Pendugaan koefisien dalam bentuk matriks diperoleh dengan cara meminimumkan jumlah kuadrat galat untuk model seperti berikut ini:
= +
∑ �2 = ��� �=
��� = − �
� � − ��
dengan syarat pembatas ∑�= 2 �, dugaan parameter regresi ridge diperoleh dengan menurunkan jumlah kuadrat galat terhadap ̂, maka diperoleh
�̂� = � + − � (12)
dengan �erup�k�� matriks identitas berukuran � × �, dan adalah tetapan bias yang bernilai positif. Menurut Montgomery & Peck (1992), pemilihan nilai yang optimal dapat diperoleh dengan menggunakan validasi silang terampat atau
Generalized Cross Validation (GCV). Penduga koefisien yang optimal diperoleh dari pemilihan nilai yang menghasilkan nilai GCV paling minimum. Nilai GCV dirumuskan sebagai berikut:
� � = ∑�= ,�
{�−[ + � �]} (13)
dengan,
�,�2 = sisaan kuadrat ke-i untuk nilai c tertentu � = matriks hat
Regresi ridge menghasilkan penduga yang berbias tetapi cenderung stabil dibandingkan dengan hasil dugaan menggunakan MKT.
Geographically Weighted Ridge Regression (GWRR)
Menurut Wheeler (2007), GWRR merupakan salah satu metode yang dapat mengatasi masalah multikolinieritas pada data spasial. GWRR adalah metode perkembangan dari metode regresi ridge, yang membedakan antara metode regresi ridgedan GWRR adalah pada penggunaan pembobot sebagai informasi tambahan.
̂�= �rg �i� {∑ (��− �, � − ∑� � �, �
= 2
�
�= + ∑�= 2 �, � } (14)
Pendugaan koefisien pada GWRR dengan lokasi pengamatan �, � dilakukan dengan menambahkan unsur pembobot � �, � yang dapat ditulis sebagai berikut:
� �, � = � �, � � + � (15)
∑ � �, � �2 = ��� �, � � �
�=
���
�, � � = � �, � − �� � − ��
dengan syarat pembatas ∑�= ̂2 �, maka
���
�, � = �� �, � − � � �� �, � + � � �� �, � ��
+ ∑ ̂
�
=
Dugaan parameter GWRR diperoleh dengan menurunkan jumlah kuadrat galat terhadap �̂ �, � seperti berikut ini:
���
�, � �
�̂ �, � = ��
�, � − � � �� �, � + � � �� �, � � + (∑�= ̂
�̂ �, � =
�̂ �, � = �� �, � + − �� �, � (16)
dengan adalah matriks identitas berukuran � × �, tetapan bias yang bernilai positif, dan � �, � merupakan matriks pembobot spasial berdimensi � × �.
Locally Compensated Ridge Geographically Weighted Regression (LCR-GWR) Model GWRR pada persamaan (16) menggunakan satu koefisien bias untuk seluruh lokasi pengamatan. Gollini et al. (2015) memperkenalkan model LCR-GWR yang menggunakan satu koefisien bias untuk suatu lokasi tertentu, jika terdapat N lokasi pengamatan maka terdapat n koefisien bias ridge yang berbeda. Metode tersebut menghasilkan koefisien bias ridge secara lokal. Model regresi pada LCR-GWR adalah sebagai berikut:
�̂ �, � = �� �, � + �, � −
��
�, � (17)
dengan �, � merupakan nilai locally-compensated (LC) dari pada lokasi �, � .
Nilai parameter regresi ridge diperoleh dengan menghubungkan nilai
eigen dan conditional number κ dari perkalian matriks � . Jika diperoleh nilai eigen dari matriks � adalah � , �2, … , �� maka nilai eigen dari matriks
� + adalah � + , �
2+ , … , ��+ . Conditional number κ dari matriks persegi didefinisikan sebagai� /��, dengan � merupakan nilai eigen
terbesar dan ��adalah nilai eigen terkecil. Dengan menggunakan aturan tersebut, maka koefisien bias ridge yang diperoleh dari nilai eigen dan conditional number
antara nilai eigen dengan conditional number κ dari matriks �� �, � , dengan harapan mampu menghasilkan model yang lebih akurat dengan adanya masalah multikolinieritas pada peubah penjelasnya.
Least Absolute Shrinkage and Selection Operator (LASSO)
Metode lasso diperkenalkan pertama kali oleh Tibshirani pada tahun 1996. Penduga koefisien parameter lasso tidak dapat diperoleh dalam bentuk tertutup seperti pada MKT atau regresi ridge, tetapi dengan menggunakan pemrograman kuadratik (Hastie et al. 2009). Lasso didefinisikan sebagai berikut:
( ̂ = �rg �i� {∑ (�� − − ∑�= � 2
+ ∑�= | |
�
�= } (18)
dengan syarat ∑�= | ̂ | .Tibshirani (1996) menyatakan bahwa konstrain
∑�= | ̂ | sama halnya dengan menambahkan penalti ∑�= | | pada jumlah kuadrat galat (JKG), sehingga terdapat hubungan langsung antara parameter dan yang mengendalikan jumlah penyusutan dari koefisien regresi. Nilai mutlak konstrain dari koefisien regresi meyebabkan persamaan yang dihasilkan bersifat non-linier sehingga memerlukan pemrograman kuadratik untuk menyelesaikannya. Diketahui bahwa t merupakan suatu besaran yang mengendalikan besarnya penyusutan pada pendugaan koefisien lasso dengan t≥ 0.
Jika merupakan penduga parameter koefisien lasso terkecil dan t0 = ∑�= | ̂ |, maka nilai t<t0 akan menyebabkan solusi MKT menyusut ke arah nol, dan memungkinkan beberapa koefisien tepat nol. Jika nilai t yang dipilih lebih besar atau sama dengan t0, maka penduga lasso memberikan hasil yang sama dengan penduga koefisen MKT.
Pedugaan koefisien lasso diperoleh dengan menentukan batas yang dibakukan yaitu s = t /∑�= | ̂ | dengan t = ∑�= | ̂ | dan ̂ adalah penduga parameter untuk model penuh atau ditulis sebagai | |/ | |. Efron et al. (2004) telah menyelesaikan masalah lasso dengan cara yang menarik yaitu dengan modifikasi algoritma LARS (Least Angle Regression). Adapun algoritma LARS secara umum sebagai berikut:
1. Memulai dengan semua koefisien dari bernilai nol, dan menjadikan sisaan
� =
2. Memilih peubah penjelas yang memiliki koefisien korelasi tertinggi dengan sisaan � .
3. Menduga koefisien untuk � yang memiliki korelasi tertinggi dengan sisaan �.
4. Menghitung sisaan � = − ̂ dengan peubah penjelas yang masuk ke dalam model.
5. Menghitung korelasi parsial antara peubah penjelas yang tersisa dengan sisaan terbaru.
Pada tahap penyelesaian lasso dengan algoritma LARS, parameter penyusutan (s) harus diduga terlebih dahulu sebelum solusi akhir lasso. Parameter tersebut digunakan sebagai batasan lassountuk menduga parameter lasso yang berpengaruh signifikan terhadap peubah respon dandidefinisikan sebagai berikut:
= ∑�= |̂ |
∑�= | ̂ | (19)
dengan s menyatakan parameter penyusutan (shrinkage) yang memiliki nilai 0 sampai 1.
Geographically Weighted Lasso (GWL)
Konsep dari lasso yang diterapkan dalam suatu pemodelan GWR yang kemudian lebih dikenal dengan GWL merupakan suatu metode spasial yang digunakan untuk mengatasi heterogenitas pada metode MKT serta masalah adanya multikolinieritas lokal. Dengan menggunakan GWL diharapkan dugaan koefisien parameter yang diperoleh lebih stabil sehingga hasil prediksi yang didapatkan lebih akurat. Solusi pada GWL adalah dengan menyelesaikan formulasi lasso terkendala berikut:
̂ = �rg �i� {∑ (��=� �− �, � − ∑�= � �, � 2+ ∑�= | �, � |} (20)
Dengan batasan kendala yang mensyaratkan ∑�= | �, � | � yang bersifat mutlak, maka solusi GWL juga menggunakan algoritma LARS dengan tambahan matriks pembobot pada matriks peubahnya. Pendugaan parameter akhir lasso dilakukan secara serentak sehingga solusi akhir lasso tergantung pada bandwidth
kernel yang telah diduga sebelumnya (Wheeler 2009). Langkah-langkah yang dilakukan dalam pendugaan parameter GWL sebagai berikut:
1. Menduga bandwith kernel yang optimum dengan metode Cross Validation
(CV).
2. Menghitung matriks pembobot W berukuran � × �. 3. Untuk setiap lokasi � = , , … , �.
a) � � = � (� �
b) � = � dan = � /2 � menggunakan akar kuadrat dari pembobot kernel � � di setiap lokasi ke-i.
c) Panggil algoritma lars �, pada software R, kemudian simpan solusi lasso, kemudian temukan solusi lasso yang meminimumkan sisaan untuk ��.
4. Dugaan parameter akhir lasso sesuai dengan CV berdasarkan fraksi dari nilai penyusutan �.
Pada langkah – langkah pendugaan parameter pada model GWL, nilai parameter penyusutan (s) harus diduga terlebih dahulu sebelum solusi akhir lasso. Dugaan parameter penyusutan (s) pada model GWL dilakukan dengan metode
METODE PENELITIAN
Data
Metode GWRR dan GWL digunakan pada data yang meliputi 113 kabupaten/kota di Pulau Jawa. Data yang digunakan dalam penelitian ini adalah data sekunder yang berasal dari Badan Pusat Statistik (BPS), yaitu data Potensi Desa (PODES), Produk Domestik Regional Bruto (PDRB) kabupaten/kota, dan jumlah penduduk tingkat kabupaten/kota pada tahun 2010. Peubah respon yang digunakan adalah data PDRB pada setiap kabupaten/kota di Pulau Jawa. Peubah penjelas dikelompokkan menjadi dua gugus data.Gugus data pertama merupakan data yang dianggap relevan untuk menduga nilai PDRB yang meliputi informasi mengenai sumber daya manusia pada suatu kabupaten/kota, fasilitas pendidikan, maupun fasilitas perekonomian yang disediakan oleh pemerintah daerah. Gugus data pertama terdiri dari 8 peubah penjelas dengan rincian sebagai berikut :
Tabel 1 Peubah penjelas gugus data pertama
Peubah Keterangan Satuan
X1 Persentase penduduk miskin persen
X2 Persentase RT (rumah tangga) menggunakan listrik persen
X3 Jumlah fasilitas pendidikan unit
X4 Indeks Pembangunan Manusia (IPM) -
X5 Rata-rata lama sekolah tahun
X6 Persentase desa mayoritas menggunakan gas persen
X7 Jumlah pertokoan dan pasar permanen unit
X8 Jumlah hotel dan penginapan unit
Peubah penjelas untuk gugus data kedua meliputi 11 peubah yang dianggap relevan dalam mengevaluasi pengaruh adanya masalah multikolinieritas terhadap model dugaan dengan rincian sebagai berikut :
Tabel 2 Peubah penjelas gugus data kedua
Peubah Keterangan Satuan
X1 Persentase penduduk miskin persen
X2 Persentase RT (rumah tangga) menggunakan listrik persen
X3 Jumlah fasilitas pendidikan unit
X4 Indeks Pembangunan Manusia (IPM) -
X5 Rata-rata lama sekolah tahun
X6 Persentase desa mayoritas menggunakan gas persen
X7 Jumlah pertokoan dan pasar permanen unit
X8 Jumlah hotel dan penginapan unit
X9 Angka Harapan Hidup tahun
X10 Pengeluaran perkapita ribu rupiah
Metode Analisis
Adapun tahapan-tahapan yang dilakukan untuk mencapai tujuan dalam penelitian ini juga dibagi menjadi dua bagian karena penggunaan peubah dengan tujuan berbeda. Tahapan yang dilakukan pada gugus data pertama untuk menduga nilai PDRB pada 113 kabupaten/kota di Pulau Jawa tahun 2010 adalah sebagai berikut :
1. Melakukan eksplorasi data dari peubah penjelas bagian pertama dan peubah respon untuk mengetahui gambaran umum data.
2. Melakukan pemodelan regresi linier dengan metode kuadrat terkecil (MKT). 3. Melakukan pengujian dengan uji Breusch-Pagan untuk mengetahui adanya
keheterogenan spasial pada data.
4. Melakukan pemodelan GWR dengan tahapan sebagai berikut :
a) Menduga nilai bandwidth (h) dengan fungsi fixed exponential kernel
yang meminimumkan nilai Cross Validation pada persamaan (9).
b) Membentuk matriks pembobot � �, � untuk setiap lokasi pengamatan dengan menggunakan bandwidth (h) yang diperoleh sebelumnya.
c) Menduga nilai koefisien dugaan parameter regresi untuk setiap lokasi berdasarkan matriks pembobot sehingga diperoleh model lokal.
5. Mendeteksi multikolinieritas lokal dengan VIF seperti pada persamaan (3) dan mencari nilai koefisien korelasi terboboti geografis dengan menggunakan persamaan (10).
6. Melakukan pemodelan GWRR dengan tahapan sebagai berikut :
a) Menduga nilai koefisien bias dan bandwidth (h) dengan fungsi fixed exponential kernel secara simultan sampai diperoleh nilai bandwidth (h) yang optimal dengan menggunakan Cross Validation.
b) Membentuk matriks pembobot � �, � untuk setiap lokasi pengamatan dengan menggunakan bandwidth (h) yang diperoleh sebelumnya.
c) Menduga nilai koefisien dugaan parameter regresi untuk setiap lokasi berdasarkan matriks pembobot dan koefisien bias yang diperoleh sebelumnya seperti pada persamaan (16).
d) Memodelkan data dengan LCR-GWR yang menggunakan koefisien bias
ridge lokal berbeda untuk setiap lokasi pengamatan seperti pada persamaan (17).
7. Melakukan pemodelan GWL pada data menggunakan algoritma LARS dengan modifikasi penambahan matriks pembobot pada peubah-peubahnya.
8. Memetakan hasil dugaan dari model GWR, GWRR dan GWL untuk dapat membandingkan hasil dugaan secara visual.
9. Membandingkan nilai RMSE dan �2 yang diperoleh pada model GWR, GWL dan GWRR untuk mengetahui metode yang terbaik dalam menduga nilai PDRB.
�� � = √�∑ [���= �− �̂�]2 (21)
�2 = − � / (22)
Untuk mengetahui kekonsistenan metode dalam mengatasi multikolinieritas dapat diketahui dengan melakukan pemodelan pada gugus data kedua. Tahapan yang dilakukan adalah sebagai berikut :
1. Melakukan pemodelan GWR dengan tahapan sebagai berikut :
a) Menduga nilai bandwidth (h) dengan fungsi fixed exponential kernel
yang meminimumkan nilai Cross Validation pada persamaan (9).
b) Membentuk matriks pembobot � �, � untuk setiap lokasi pengamatan dengan menggunakan bandwidth (h) yang diperoleh sebelumnya.
c) Menduga nilai koefisien dugaan parameter regresi untuk setiap lokasi berdasarkan matriks pembobot sehingga diperoleh model lokal.
2. Mendeteksi multikolinieritas lokal dengan VIF seperti pada persamaan (3). 3. Melakukan pemodelan GWRR dengan tahapan sebagai berikut :
a) Menduga nilai koefisien bias dan bandwidth (h) dengan fungsi fixed exponential kernel secara simultan sampai diperoleh nilai bandwidth (h) yang optimal dengan menggunakan Cross Validation.
b) Membentuk matriks pembobot � �, � untuk setiap lokasi pengamatan dengan menggunakan bandwidth (h) yang diperoleh sebelumnya.
c) Menduga nilai koefisien dugaan parameter regresi untuk setiap lokasi berdasarkan matriks pembobot dan koefisien bias yang diperoleh sebelumnya seperti pada persamaan (16).
d) Memodelkan data dengan LCR-GWR yang menggunakan koefisien bias
ridge lokal berbeda untuk setiap lokasi pengamatan seperti pada persamaan (17).
4. Melakukan pemodelan GWL pada data menggunakan algoritma LARS dengan modifikasi penambahan matriks pembobot pada peubah-peubahnya.
5. Membandingkan nilai RMSE dan �2 yang diperoleh pada model GWR, GWL dan GWRR untuk mengetahui metode yang terbaik dalam menduga nilai PDRB ketika antarpeubah penjelasnya terdapat multikolinieritas yang tinggi.
�� � = √�∑ [���= � − �̂�]2 (23)
�2 = − � / (24)
dengan (Jumlah Kuadrat Total) = ∑��= ��− �̅ 2dan � (Jumlah Kuadrat Galat) = ∑��= ��− �̂� 2 (Fotheringham et al. 2002).
HASIL DAN PEMBAHASAN
Eksplorasi Data
Eksplorasi data spasial diperlukan untuk mengetahui informasi awal mengenai data. Data yang digunakan dalam penelitian ini adalah data PDRB pada 113 kabupaten/kota di pulau Jawa pada tahun 2010. Berikut ini adalah pemetaan data PDRB (dalam milyar rupiah) di seluruh lokasi pengamatan.
Gambar 1 Peta PDRB pada setiap kabupaten/kota di Pulau Jawa tahun 2010
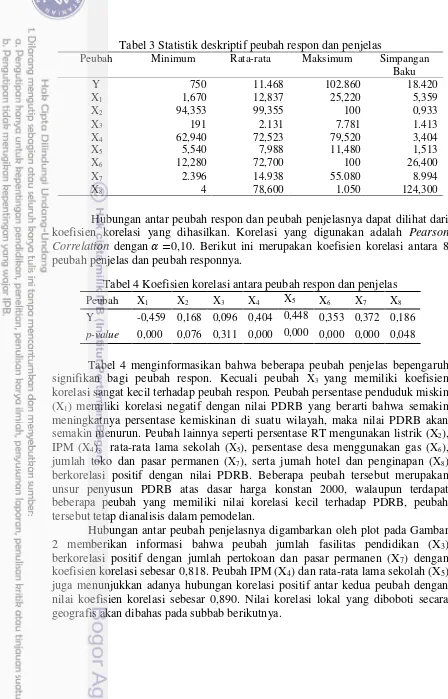
Tabel 3 Statistik deskriptif peubah respon dan penjelas
Peubah Minimum Rata-rata Maksimum Simpangan
Baku
Y 750 11.468 102.860 18.420
X1 1,670 12,837 25,220 5,359
X2 94,353 99,355 100 0,933
X3 191 2.131 7.781 1.413
X4
X5
62,940 5,540
72,523 7,988
79,520 11,480
3,404 1,513
X6 12,280 72,700 100 26,400
X7 2.396 14.938 55.080 8.994
X8 4 78,600 1.050 124,300
Hubungan antar peubah respon dan peubah penjelasnya dapat dilihat dari koefisien korelasi yang dihasilkan. Korelasi yang digunakan adalah Pearson Correlation dengan =0,10. Berikut ini merupakan koefisien korelasi antara 8 peubah penjelas dan peubah responnya.
Tabel 4 Koefisien korelasi antara peubah respon dan penjelas
Peubah X1 X2 X3 X4 X5 X6 X7 X8
Y -0,459 0,168 0,096 0,404 0,448 0,353 0,372 0,186
p-value 0,000 0,076 0,311 0,000 0,000 0,000 0,000 0,048
Tabel 4 menginformasikan bahwa beberapa peubah penjelas bepengaruh signifikan bagi peubah respon. Kecuali peubah X3 yang memiliki koefisien
korelasi sangat kecil terhadap peubah respon. Peubah persentase penduduk miskin (X1) memiliki korelasi negatif dengan nilai PDRB yang berarti bahwa semakin
meningkatnya persentase kemiskinan di suatu wilayah, maka nilai PDRB akan semakin menurun. Peubah lainnya seperti persentase RT mengunakan listrik (X2),
IPM (X4), rata-rata lama sekolah (X5), persentase desa menggunakan gas (X6),
jumlah toko dan pasar permanen (X7), serta jumah hotel dan penginapan (X8)
berkorelasi positif dengan nilai PDRB. Beberapa peubah tersebut merupakan unsur penyusun PDRB atas dasar harga konstan 2000, walaupun terdapat beberapa peubah yang memiliki nilai korelasi kecil terhadap PDRB, peubah tersebut tetap dianalisis dalam pemodelan.
Gambar 2 Scatterplot hubungan antarpeubah penjelas
Pemodelan Regresi Linier
Pemodelan regresi linier ini bertujuan untuk melakukan analisis awal pada data PDRB. Pendugaan parameter pada regesi linier menggunakan MKT. Pada Tabel 5 tercantum ringkasan hasil pendugaan parameter beserta pengujian parsial pada setiap dugaan parameter.
Tabel 5 Hasil pengujian parsial dari dugaan parameter dengan MKT
Peubah Koefisien p-value VIF
Intersep -68,7 0,706
X1 -0,635 0,090 2,162
X2 -0,015 0,994 1,799
X3 -0,003 0,133 4,754
X4 0,7629 0,419 5,620
X5 3,151 0,221 8,202
X6 -0,046 0,565 2,443
X7
X8
0,001 -0,018
0,000 0,162
3,883 1,428
Tabel 6 Hasil analisis ragam dengan MKT
Sumber db JK KT F p-value �2
Regresi 8 16746,3 2093,3 10,24 0,000 44,1%
Galat 104 21266,9 204,5
Total 112 38013,2
peubah X4 dan X5 menghasilkan nilai VIF>5. Pengujian parameter secara serempak memberikan p-value sebesar 0,000, sehingga dinyatakan bahwa seluruh peubah penjelasnya memberikan pengaruh yang nyata terhadap nilai PDRB, namun nilai �2yang dihasilkan hanya sebesar 44,1%. Hal ini bertentangan dengan hasil pengujian secara parsial, ini bisa disebabkan karena besarnya nilai standard error akibat dari ragam yang tidak homogen sehingga berdampak pada kesalahan interpretasi hasil pengujian. Adanya heterogenitas ragam dapat dilihat dari plot antara sisaan terhadap nilai dugaan PDRB yang membentuk pola tertentu atau tidak menyebar acak di sekitar nol seperti pada Lampiran 1.
Pengujian Pengaruh Heterogenitas Spasial
Pada Gambar 1, nilai PDRB berbeda-beda pada setiap lokasi dan sangat beragam, sehingga dimungkinkan untuk melakukan analisis secara spasial. Untuk mengetahui adanya keragaman spasial antar lokasi pengamatan dapat diketahui dengan melakukan uji Breusch-Pagan dengan hipotesis sebagai berikut :
� ∶ ��2 = ∀� = , , … , � ( tidak terdapat heterogenitas spasial)
� ∶ Paling sedikit ada satu ��2 ≠ (terdapat heterogenitas spasial)
Hipotesis� ditolak jika hasil uji Breusch-Pagan lebih besar dari nilai
��+2 dengan � merupakan banyaknya peubah penjelas. Pengujian yang dilakukan menghasilkan nilai Chi-square sebesar 14,266 lebih besar dari �2; , =13,361 dengan p-value 0,075, sehingga dapat disimpulkan bahwa terdapat pengaruh heterogenitas spasial di setiap lokasi pengamatan pada taraf nyata = 0,10. Apabila analisis dengan mengunakan MKT tetap diterapkan pada data maka hasil pendugaan yang diperoleh akan memiliki ragam dugaan parameter yang besar.
Pemodelan Geographically Weighted Regression (GWR)
Pengujian dengan Uji Breusch-Pagan menunjukkan adanya keragaman data PDRB secara spasial yaitu ragam yang tidak homogen antarlokasipengamatan, sehingga diperlukan pemodelan yang dapat mengatasi keragaman spasial dengan membentuk model regresi pada setiap lokasi pengamatan. Untuk memperoleh model pada setiap lokasi diperlukan bandwidth
yang diperoleh dengan metode Cross Validation (CV) seperti pada persamaan (9) yang selanjutnya digunakan untuk memperoleh matriks pembobot pada proses pendugaan parameternya. Fungsi pembobot yang digunakan untuk membentuk matriks pembobot pada penelitian ini adalah fungsi fixed exponential kernel
karena merupakan fungsi kernel yang paling sederhana, dengan menggunakan jarak euclidean berdasarkan informasi derajat lintang dan bujur dari lokasi pengamatan.
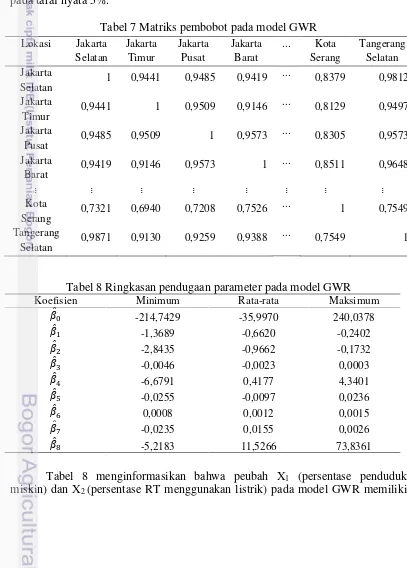
lokasi pengamatan masih memberikan pengaruh pada nilai PDRB lokasi pengamatan tersebut. Setelah diperoleh nilai bandwidth, langkah selanjutnya adalah membentuk matrik pembobot. Matrik pembobot � yang diperoleh untuk seluruh lokasi dapat dilihat Pada Tabel 7, jika suatu lokasi semakin jauh dari titik lokasi pengamatan maka nilai pembobotnya semakin menurun sehingga pengaruhnya semakin kecil. Matriks pembobot yang digunakan untuk pendugaan parameter di lokasi pengamatan �, � adalah matriks diagonal � � � dengan unsur diagonalnya merupakan elemen baris dari matrik pembobot � untuk lokasi pengamatan �, � . Pengujian kebaikan model GWR dilakukan dengan menggunakan persamaaan (11) diperoleh nilai F-hitung sebesar 1,996. Nilai
� , (42,07;104) = 1,501 maka tolak � yang berarti bahwa model GWR mampu mendeskripsikan data dengan lebih baik jika dibandingkan dengan model MKT pada taraf nyata 5%.
Tabel 7 Matriks pembobot pada model GWR
Lokasi Jakarta
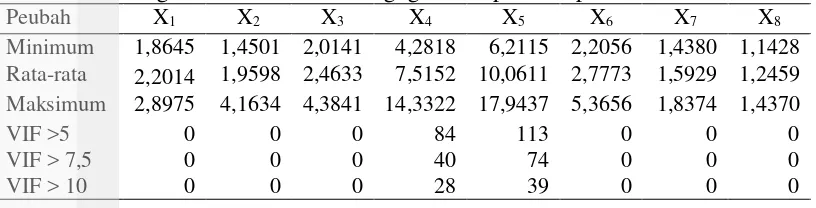
Tabel 8 Ringkasan pendugaan parameter pada model GWR
Koefisien Minimum Rata-rata Maksimum
̂ -214,7429 -35,9970 240,0378
koefisien dugaan parameter yang bernilai negatif pada setiap lokasi pengamatan. Peubah X6 (persentase desa mayoritas menggunakan gas) memiliki tanda koefisien dugaan parameter yang bernilai positif terhadap nilai PDRB. Peubah X3 (jumlah fasilitas pendidikan), dan X5 (rata-rata lama sekolah) memiliki rata-rata koefisien dugaan parameter yang bernilai negatif.
Gambar 3 Peta dugaan nilai PDRB pada model GWR.
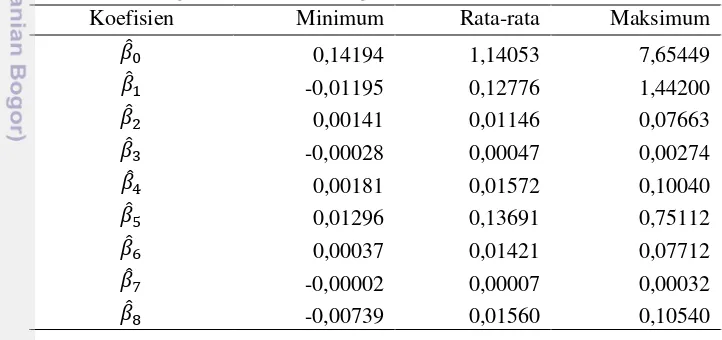
Peta hasil dugaan nilai PDRB pada model GWR (Gambar 3), menunjukkan bahwa terdapat 63 kabupaten/kota dengan PDRB sangat tinggi, 17 kabupaten/kota dengan PDRB sedang, 33 kabupaten/kota dengan PDRB rendah. Pada model GWR, nilai RMSE yang diperoleh adalah 11,4767 dengan R2 bernilai 60,84%. Selanjutnya untuk mengetahui adanya multikolinieritas lokal pada model GWR dapat dilihat dari nilai VIF lokal. Nilai VIF pada Tabel 9 menunjukkan bahwa terdapat multikolinieritas lokal pada peubah penjelas dilihat dari beberapa nilai VIF yang lebih besar dari 10. Sebagai contoh, VIF untuk peubah X5 di lokasi Jakarta Selatan bernilai 13,1419 artinya nilai standard error bagi koefisien dugaan parameter pada peubah X5 akan meningkat sebesar 3,6251 (√13,1419) kali dibandingkan dengan standard error koefisien peubah X5 jika tanpa berkorelasi dengan peubah lain.
Tabel 9 Ringkasan nilai VIF untuk gugus data pertama pada seluruh lokasi
Peubah X1 X2 X3 X4 X5 X6 X7 X8
Minimum 1,8645 1,4501 2,0141 4,2818 6,2115 2,2056 1,4380 1,1428
Rata-rata 2,2014 1,9598 2,4633 7,5152 10,0611 2,7773 1,5929 1,2459
Maksimum 2,8975 4,1634 4,3841 14,3322 17,9437 5,3656 1,8374 1,4370
VIF >5 0 0 0 84 113 0 0 0
VIF > 7,5 0 0 0 40 74 0 0 0
VIF > 10 0 0 0 28 39 0 0 0
Pada Tabel 4 dapat dilihat bahwa peubah X3 memiliki p-value yang tidak signifikan pada taraf nyata 10%, dengan koefisien korelasi bernilai 0,096 yang artinya hampir tidak ada hubungan antara jumlah fasilitas pendidikan terhadap nilai PDRB. Namun peubah X3 tetap dianalisis pada tahap selanjutnya karena berdasarkan nilai korelasi Pearson yang diboboti secara geografis seperti pada persamaan (10) diperoleh beberapa wilayah yang memiliki nilai korelasi signifikan antara peubah X3 dengan PDRB. Nilai koefisien korelasi terboboti geografis antara peubah respon dengan peubah-peubah penjelasnya diberikan secara lengkap pada Lampiran 5 dan 6.
Pemodelan Geographically Weighted Ridge Regression (GWRR)
Konsep metode regresi ridge yang diterapkan pada GWR mampu mengatasi multikolinieritas pada data spasial. Pemodelan dengan metode GWRR dilakukan untuk menangani masalah multikolinieritas pada GWR dengan menambahkan koefisien bias ( tertentu pada matriks dugaan parameternya (Wheeler 2007). Hasil dugaan parameter pada model GWRR bersifat bias namun memiliki ragam yang lebih kecil daripada GWR. Pada GWRR, nilai diperoleh secara simultan dengan metode iterasi untuk setiap bandwidth (h), sehingga nilai dan h yang terpilih untuk pendugaan adalah yang meminimumkan nilai CV. Kemudian parameter tersebut digunakan untuk menduga koefisien pada GWRR. Nilai yang diperoleh untuk memodelkan GWRR adalah 1,8435 untuk seluruh lokasi pengamatan dengan dugaan bandwidth bernilai 0,09.
Tabel 10 Ringkasan hasil pendugaan parameter pada model GWRR
Koefisien Minimum Rata-rata Maksimum
̂ 0,14194 1,14053 7,65449
̂ -0,01195 0,12776 1,44200
̂2 0,00141 0,01146 0,07663
̂ -0,00028 0,00047 0,00274
̂ 0,00181 0,01572 0,10040
̂ 0,01296 0,13691 0,75112
̂ 0,00037 0,01421 0,07712
̂ -0,00002 0,00007 0,00032
̂ -0,00739 0,01560 0,10540
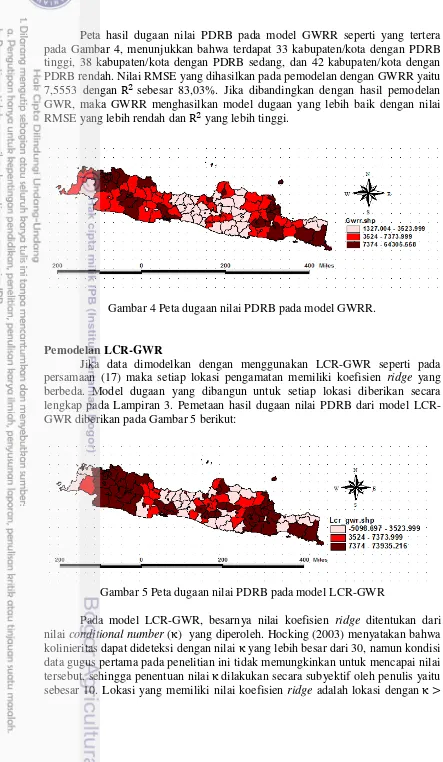
Peta hasil dugaan nilai PDRB pada model GWRR seperti yang tertera pada Gambar 4, menunjukkan bahwa terdapat 33 kabupaten/kota dengan PDRB tinggi, 38 kabupaten/kota dengan PDRB sedang, dan 42 kabupaten/kota dengan PDRB rendah. Nilai RMSE yang dihasilkan pada pemodelan dengan GWRR yaitu 7,5553 dengan R2 sebesar 83,03%. Jika dibandingkan dengan hasil pemodelan GWR, maka GWRR menghasilkan model dugaan yang lebih baik dengan nilai RMSE yang lebih rendah dan R2 yang lebih tinggi.
Gambar 4 Peta dugaan nilai PDRB pada model GWRR.
Pemodelan LCR-GWR
Jika data dimodelkan dengan menggunakan LCR-GWR seperti pada persamaan (17) maka setiap lokasi pengamatan memiliki koefisien ridge yang berbeda. Model dugaan yang dibangun untuk setiap lokasi diberikan secara lengkap pada Lampiran 3. Pemetaan hasil dugaan nilai PDRB dari model LCR-GWR diberikan pada Gambar 5 berikut:
Gambar 5 Peta dugaan nilai PDRB pada model LCR-GWR
10. Nilai R2 yang dihasilkan oleh pemodelan dengan menggunakan LCR-GWR sebesar 61,31%, dengan RMSE sebesar 11,4081.
Pemodelan Geographically Weighted Lasso (GWL)
Konsep dari lasso yang diterapkan dalam pemodelan GWR yang kemudian lebih dikenal dengan Geographically Weighted Lasso (GWL) merupakan suatu metode spasial yang digunakan untuk mengatasi heterogenitas pada metode MKT sekaligus kolinearitas lokal (Wheeler 2009). GWL menghasilkan dugaan koefisien parameter yang efisien sehingga hasil prediksi yang diperoleh lebih akurat. Seperti pada pemodelan dengan menggunakan lasso, koefisien regresi pada GWL juga akan disusutkan ke nol melalui koefisien
shrinkage yang diberikan. Dengan demikian, koefisien yang bernilai nol tersebut sudah pasti tidak berpengaruh pada model. Nilai bandwidth yang diperoleh dari proses iterasi menggunakan CV pada GWL bernilai 0,09. Koefisien penyusutandiperoleh dengan metode CV, nilai bandwidth dan koefisien penyusutan yang dihasilkan kemudian digunakan untuk menduga parameter GWL. Hasil model dugaan GWL dan koefisien penyusutan untuk seluruh lokasi pengamatan diberikan pada Lampiran 4.
Gambar 6 Peta dugaan nilai PDRB pada model GWL
Kekonsistenan Metode Terhadap Multikolinieritas
Untuk memperoleh metode yang konsisten dalam mengatasi masalah multikolinieritas dapat dilihat dari hasil analisis model dengan menggunakan sebelas peubah. Penambahan 3 peubah bertujuan untuk meningkatkan multikolinieritas pada peubah-peubah penjelasnya dilihat dari nilai VIF yang dihasilkan.Tabel 11 merupakan nilai VIF yang dihasilkan pada model MKT. Pada tabel dapat dilihat bahwa peubah X2, X4, X5, X7, X9, dan X11 memiliki nilai VIF > 5, bahkan nilai VIF peubah X4, X5, dan X9 lebih besar dari 10.
Tabel 11 Nilai multikolinieritas untuk gugus data kedua pada model dengan MKT Peubah VIF
X1 2,487
X2 2,403
X3 5,593
X4 55,520
X5 10,408
X6 3,714
X7 4,511
X8 1,466
X9 14,272
X10 3,698
X11 9,963
Tabel 12 Ringkasan nilai VIF untuk gugus data kedua pada seluruh lokasi Peubah Minimum Rata-rata Maksimum VIF>5 VIF>7,5 VIF>10
X1 2,163 2,411 2,966 0 0 0
X2 1,905 2,308 3,985 0 0 0
X3 2,208 2,718 4,455 0 0 0
X4 25,810 95,159 256,448 113 113 113
X5 6,514 16,516 39,099 113 88 65
X6 3,332 3,824 5,171 0 0 0
X7 1,508 1,620 1,796 0 0 0
X8 1,154 1,260 1,400 0 0 0
X9 8,214 22,137 60,038 113 113 82
X10 2,775 5,105 10,026 41 22 1
X11 6,990 13,026 22,293 113 102 60
melebihi 5. Nilai RMSE yang diperoleh dengan pemodelan GWR adalah 6,5258 dengan R2 sebesar 87,34%.
(a)
(b)
(c)
(d)
Pemodelan GWRR dan GWL pada gugus data kedua dilakukan untuk mengetahui kekonsistenan metode dalam mengatasi multikolinieritas. Nilai RMSE bagi model GWRR adalah 7,1845 dengan R2 sebesar 84,65%. Sedangkan nilai RMSE bagi model GWL adalah 2,9346 dengan R2 sebesar 97,43%. Untuk mempermudah dalam membandingkan hasil dugaan, berikut ini diberikan peta pada Gambar 7 mengenai hasil dugaan nilai PDRB pada 113 Kabupaten/Kota dari model GWR, GWRR, dan GWL.
Hasil dugaan nilai PDRB untuk 113 kabupaten/kota di Pulau Jawa berbeda pada setiap model. Pada model GWR Gambar 7(a) dapat dilihat bahwa nilai dugaan terbesar adalah 81.690,573 milyar rupiah, Cianjur dengan PDRB berada di kategori tinggi, masuk ke kategori sedang jika dimodelkan dengan GWR. Kabupaten/kota dengan nilai PDRB rendah seperti Grobogan, Ngawi, Sragen hasil dugaannya masuk ke dalam kategori sedang. Terdapat beberapa wilayah dengan pendugaan yang kurang sesuai jika dimodelkan dengan GWR. Ini bisa disebabkan karena ragam dugaan pada model GWR masih tinggi dikarenakan masalah multikolinieritas antara peubah penjelas yang belum diatasi. Hasil dugaan PDRB tertinggi yang diperoleh dengan model GWRR pada Gambar 7(b) senilai 66.021,291 milyar rupiah. Pada model GWRR, hasil dugaan PDRB wilayah Kab. Sukabumi dan Cianjur masuk ke kategori sedang dengan nilai PDRB yang tinggi. Begitupun hasil pendugaan wilayah Boyolali dan Kab. Magelang termasuk ke dalam wilayah dengan PDRB rendah, sedangkan nilai PDRB yang sebenarnya termasuk ke dalam kategori sedang.
Dari peta dugaan nilai PDRB dengan menggunakan model LCR-GWR pada Gambar 7(c) dapat dilihat bahwa nilai dugaan PDRB tertinggi yaitu sebesar 73.694,756 milyar rupiah. Pada pemodelan dengan LCR-GWR, nilai conditional number (κ) yang digunakan untuk memperoleh koefisien ridge yaitu � > 30, karena pada gugus data kedua nilai multikolinieritas antara peubah-peubah penjelasnya sangat tinggi. Hasil dugaan model GWL pada Gambar 7(d) memberikan nilai dugaan PDRB tertinggi sebesar 87.633,285 milyar rupiah yang merupakan nilai dugaan bagi PDRB di Kota Surabaya. Pada model GWL masih ditemukan beberapa hasil pendugaan yang belum tepat seperti pada wilayah Kab. Sukabumi, Tulungagung, dan Kota Depok. Jika dilihat dari rentang nilai dugaan yang dihasilkan, model GWL menghasilkan dugaan yang mendekati nilai PDRB sebenarnya. Perbandingan dari performa model GWR, GWRR, LCR-GWR, dan GWL untuk gugus data pertama diberikan pada Tabel 13.
Tabel 13 Perbandingan model GWR, GWRR, LCR-GWR, dan GWL gugus data pertama
Model GWR GWRR LCR-GWR GWL
Bandwidth 2,1158 0,09 2,0181 0,09
RMSE 11,4767 7,5553 11,4081 2,3379
R2 60,84% 83,03% 61,31% 98,37%
hasil yang tidak lebih baik dari GWRR, namun sedikit lebih baik dari GWR. Pemodelan dengan LCR-GWR diharapkan mampu mengatasi masalah multikolinieritas pada data karena setiap lokasi pengamatan memiliki nilai koefisien ridge yang berbeda, namun hasil dari pemodelan pada data tidak mendukung hal tersebut dikarenakan parameter yang digunakan dalam pemodelan sangat banyak sehingga tidak efektif.
Tabel 14 Perbandingan model GWR, GWRR, LCR-GWR, dan GWL gugus data kedua
Model GWR GWRR LCR-GWR GWL
Bandwidth 0,4245 0,09 2,2195 0,09
RMSE 6,5258 7,1845 11,0351 2,9346
R2 87,34% 84,65% 63,80% 97,43%
SIMPULAN DAN SARAN
Simpulan
Berdasarkan tujuan dan hasil dari penelitian yang telah dilakukan, diperoleh kesimpulan bahwa metode pada model GWRR dan GWL untuk gugus data pertama mampu mengatasi masalah akibat adanya heterogenitas spasial sekaligus multikolinieritas lokal pada data PDRB dari 113 kabupaten/kota di Pulau Jawa tahun 2010 dengan membentuk model regresi yang lebih stabil dilihat dari RMSE dan R2 yang dihasilkan. Penggunaan parameter yang sangat banyak seperti pada LCR-GWR dinilai tidak efektif dalam memodelkan data PDRB dari 113 kabupaten/kota di Pulau Jawa. Berdasarkan RMSE yang diperoleh dari keempat model pada gugus data pertama maupun kedua, GWL memiliki keakuratan dugaan dan tingkat kestabilan yang lebih baik dari GWR, GWRR, maupun LCR-GWR. GWL dinilai lebih konsisten dalam menangani masalah multikolinieritas lokal walaupun antarpeubah penjelas memiliki tingkat multikolinieritas yang tinggi.
Saran
D
AFTAR PUSTAKA
Anselin L. 1988. Spatial Econometrics: Methods and Models. Dordrecht(NL): Kluwer Academic.
[BPS] Badan Pusat Statistik. 2014. Tinjauan Regional Berdasarkan PDRB Kabupaten/Kota 2010-2013 Pulau Jawa-Bali. Jakarta (ID): BPS.
Draper NR, Smith H. 1998. Applied Regression Analysis. Ed ke-3. New York (US): John Wiley & Sons..
Efron B, Hastie T, Johnstone I, Tibshirani R. 2004. Least Angle Regression. The Annals of Statistics 32(2): 407-451.
Fatulloh. 2013. Penerapan Regresi Terboboti Geografis untuk Data Produk Domestik Regional Bruto (Studi Kasus: 113 Kabupaten/Kota di Pulau Jawa Tahun 2010) [Skripsi]. Bogor (ID) : IPB Pr.
Friday OR, Emenonye C. 2012. The Detention and Correction of Multicollinearity Effects in a Multiple Regression Diagnostics. Elixir Statistics 49:10108-10112.
Fotheringham AS, Brunsdon C, Charlton M. 2002. Geographically Weighted Regression the Analysis of Spatially Varying Relationships. England (GB): John Wiley and Sons.
Gollini I, Lu B, Charlton M, Brunsdon C, Harris P. 2015. GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. Journal of Statistical Software 63(17): 1-50
Hastie T, Tibshirani R, Friendman J. 2009. The Elements od Statistical Learning Data Mining, Inference, and Prediction. New York (US): Springer.
Hocking RR. 2003. Methods and Applications of Linear Models. Ed ke-2. New York (US): John Wiley & Sons.
Hoerl AE, Kennard RW. 2000. Ridge Regression: Biased Estimation for Nonortogonal Problems. Technometrics 12: 80-86.
Kalogirou S. 2013. Testing Geographically Weighted Multicollinearity Diagnostics. GISRUK 2013; 2013 April 3-5; Liverpool. UK. Tersedia pada: http://gisc.gr/docs/sk_papers/2_7_Kalogirou_2013.pdf
Leung Y, Mei CL, Zhang WX. 2000. Statistical Test for Spatial Nonstationarity Based on The Geographically Weighted Regression Model. Environment and Planning A 32 : 9-32
Montgomery DC, Peck EA. 1992. Introduction to Linier Regression Analysis. Ed ke-2. New York (US): John Wiley & Sons.
Munikah T, Pramoedyo H, Fitriani R. 2014. Pemodelan Geographically Weighted Regression dengan Pembobot Fixed Gaussian Kernel pada Data Spasial (Studi Kasus KetahananPangan di Kabupaten Tanah Laut Kalimantan Selatan). Natural B, Vol. 2, No.3.
Ramadhan AZ. 2013. Perbandingan Metode Geographically Weighted Lasso
(GWL)- Lokal dan Metode Geographically Weighted Lasso (GWL)- Global Dalam Mengatasi Kasus Multikolinieritas Lokal Pada Metode
Geographically Weighted Regression (GWR) [Skripsi]. Malang (ID): Brawijaya Univ Pr.
TibshiraniR. 1996. Regression Shrinkage and Selection Via The Lasso. Journal of the Royal Statistical Society B 58(1): 267-288.
Wheeler D, Tiefelsdorf M. 2005. Multicollinearity and Correlation Among Local Regression Coefficients in Geographically Weighted Regression. J Geograph Syst (2005) 7: 161-187.
Wheeler DC. 2007. Diagnostic Tools and a Remedial Method for Collinearity in Geographically Weighted Regression. Environment and Planning A 39: 2464-2481.