REGRESI 2
(R.1)
KAJIAN MODEL GEOGRAPHICALLY WEIGHTED POISSON REGRESSION UNTUK MASALAH DATA SPASIAL DISKRIT
Dani Robini, Budi Nurani R., Nurul Gusriani Jurusan Matematika FMIPA Universitas Padjadjaran
Jl. Raya Bandung-Sumedang Km 21 Jatinangor Email : [email protected]
Abstrak
Dalam makalah ini dikaji metode Geographically Weighted Poisson Regression (GWPR) yang merupakan metode non parametrik untuk mendapatkan parameter model regresi dengan memperhitungkan faktor spasial. Metode ini digunakan jika variabel tak bebas adalah variabel acak diskrit berdistribusi Poisson dan melibatkan variabel lokasi yang memperhatikan faktor spasial berupa koordinat lokasi. Penentuan parameter pada GWPR dilakukan dengan menggunakan metode maksimum likelihood dengan melibatkan matriks pembobot untuk faktor lokasi.
Kata Kunci : distribusi Poisson, data spasial, GWPR, maksimum likelihood
1. LATAR BELAKANG MASALAH
Analisis regresi dipergunakan untuk mengetahui bagaimana variasi dari beberapa variabel bebas mempengaruhi variabel tak bebas dalam suatu fenomena yang kompleks.
Jika dilihat dari klasifikasi data menurut jenisnya, adakalanya informasi yang didapat di lapangan berupa data diskrit. Metode statistik yang telah dikembangkan untuk analisis data dengan memperhitungkan faktor spasial dan cocok untuk data diskrit yaitu Geographically Weighted Poisson Regression (GWPR). Dengan GWPR dapat diperoleh parameter regresi dari variabel tak bebas yang berdistribusi Poisson dengan memperhitungkan faktor spasial.
2 KAJIAN REGRESI POISSON 2.1 Model Regresi Poisson
Definisi 1 Distribusi Poisson adalah distribusi peluang variabel acak Poisson Y yang menyatakan banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah tertentu dinyatakan dengan t, diberikan oleh :
( ) = ( ; ) = ( )
! = 0,1,2, …. (1)
menyatakan rata–rata banyaknya sukses yang terjadi per satuan waktu atau daerah dan
= 2,71828 …. (Walpole & Myers, 1972).
Regresi Poisson merupakan suatu bentuk analisis regresi nonlinear yang digunakan untuk memodelkan data yang berbentuk diskrit, yaitu banyaknya kejadian yang terjadi pada suatu periode waktu dan/atau wilayah tertentu. Regresi Poisson mengasumsikan bahwa variabel tak bebas Y berdistribusi Poisson seperti pada persamaan (1).
Jenis regresi ini mempunyai asumsi equi-dispersion, yaitu kondisi dengan nilai rata- rata dan varians dari variabel respon bernilai sama. Model regresi Poisson dapat ditulis sebagai berikut : (Myers, 1990)
log( ) = + = 1,2, … (2)
= ( ) = exp ( + ) (3)
Keterangan :
= rata – rata dari model regresi Poisson pada observasi ke - i = koefisien intercept
= koefisien regresi Poisson ( k = 1,2,. . ., p)
= nilai observasi variabel bebas ke-k pada pengamatan ke-i
Jika ditulis dengan notasi matriks maka menjadi sebagai berikut :
= exp ( ) (4)
Dengan
= [1 … ] dan = [ … ]
2.2 Menaksir Parameter pada Model Regresi Poisson
Untuk melakukan estimasi parameter pada model regresi Poisson dapat digunakan metode Maximum Likelihood Estimation (MLE). Taksiran maksimum likelihood untuk parameter k dinyatakan dengan yang merupakan penyelesaian dari turunan pertama dari fungsi likelihoodnya, dengan langkah-langkah sebagai berikut (Hogg & McKean, 2005) : 1. Membentuk fungsi kepadatan peluang gabungan yang berasal dari distribusi Poisson
seperti pada persamaan (1).
2. Membuat fungsi likelihood
( ) = [− ( , )] [ ( , )]
! (5)
3. Membentuk fungsi logaritma natural untuk persamaan (5), yaitu ln ( ) = ( [− ( , )] [ ( , )]
! ) (6)
4. Menaksir parameter dengan memaksimumkan fungsi ln likelihood
Estimasi parameter diperoleh dengan mendifferensialkan persamaan (6) terhadap : ( )
= − + (7)
5. Memaksimumkan bentuk differensial tersebut sehingga diperoleh : ( )
= − + = 0 (8)
Karena fungsi pada persamaan (8) berbentuk implisit, maka untuk mendapatkan solusinya digunakan suatu prosedur iterasi numerik yaitu metode Newton-Raphson . Secara umum persamaan untuk iterasi Newton – Raphson adalah :
( ) = ( )− ( ) ( ) . ( ) ( ) (9)
dengan :
( ) ( ) = ( )
(10))
dan fungsi Hessian :
( ) ( ) = ( ) (11)
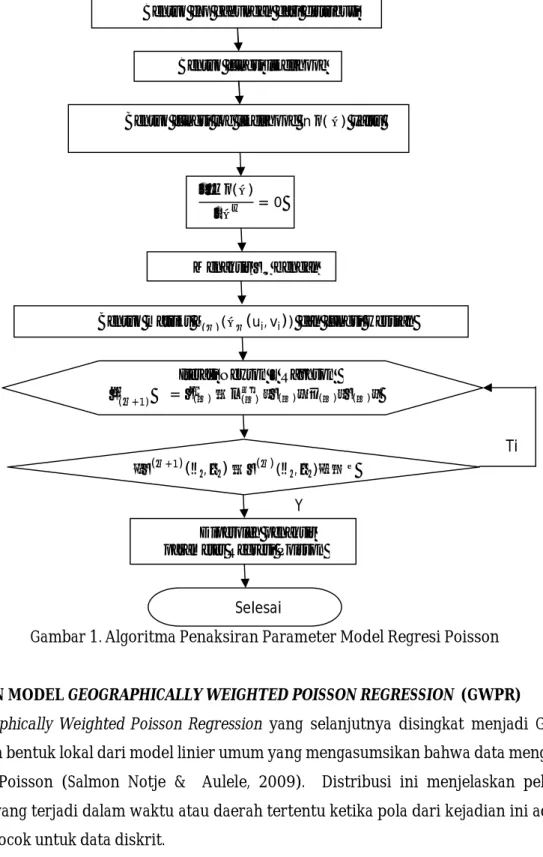
Prosedur di atas dapat dibentuk seperti pada Gambar 1.
Gambar 1. Algoritma Penaksiran Parameter Model Regresi Poisson
3. KAJIAN MODEL GEOGRAPHICALLY WEIGHTED POISSON REGRESSION (GWPR)
Geographically Weighted Poisson Regression yang selanjutnya disingkat menjadi GWPR merupakan bentuk lokal dari model linier umum yang mengasumsikan bahwa data mengikuti distribusi Poisson (Salmon Notje & Aulele, 2009). Distribusi ini menjelaskan peluang peristiwa yang terjadi dalam waktu atau daerah tertentu ketika pola dari kejadian ini adalah acak, dan cocok untuk data diskrit.
Model GWPR dapat ditulis sebagai berikut :
= exp( ( , ) + ( , ) + ) = 1,2, … , (12)
( +1)( , )− ( )( , ) ≤
Iterasi Newton – Raphson
( +1) = ( )− ( ) ( ) . ( ) ( ) Bentuk fungsi likelihood
( )
Bentuk fungsi log likelihood ln ( ) yaitu
( )
( )
= 0
Menaksir dengan
Bentuk matriks ( )( (ui, vi)) dan fungsi Hessian
( (u , v))
Selesai
Bentuk fkp gabungan dari distribusi
Diperoleh penaksir parameter Regresi Poisson
Ti
Y
Suku pada bagian kanan pada (12) ditulis dalam notasi matriks menjadi sebagai berikut :
= exp( ) (13)
dengan :
: nilai observasi variabel tak bebas ke-i
( , ) : titik koordinat (longitude, latitude) lokasi ke-i ( , ) : koefisien regresi
: nilai observasi variabel bebas ke-k pada pengamatan ke-i : error pada pengamatan ke-i
3.1 Menentukan Nilai dari dan Setiap Lokasi yang Diamati
Misalkan dan adalah data koordinat lintang–bujur (longitude–latitude). Data ini terlebih dahulu harus dikonversikan menjadi bentuk koordinat bawah permukaan kartesius.
Untuk mengubah data koordinat lintang-bujur menjadi data koordinat dalam kartesius digunakan software bantu yaitu MapInfo Professional 7.5 SCP.
3.2 Bandwidth Optimum.
Bandwidth merupakan parameter yang berperan penting dalam menentukan kemulusan sebuah kurva. Secara teoritis bandwidth merupakan lingkaran dengan jari - jari R yang ditarik dari titik pusat lokasi, yang digunakan sebagai dasar menentukan bobot pada setiap pengamatan terhadap model regresi di lokasi tersebut. (Hardle, 1991)
Beberapa bandwidth yang disarankan oleh para peneliti , yaitu 1. Hasen(2004) menyarankan penggunaan bandwidth sebagai berikut :
ℎ = 4 (14)
dengan
= 2 ( ) ( ) (15)
( ) = ∫ ( ) (16)
( ) = fungsi kernel
2. Weiβbach dan Gefeller (2004) menyarankan bandwidth sebagai berikut :
ℎ = 8 ∫ ( ) )
3(∫ ( ) )
(17)
Bandwidth optimal untuk GWPR adalah bandwidth dengan nilai AIC terkecil (Marthin Carlton, 2009).
3.3 Matriks Pembobot dengan Fungsi Kernel
Untuk menghitung matriks pembobot pada makalah ini digunakan fungsi Kernel Gaussian yang dimodifikasi, yaitu
( , ) = exp −
ℎ , = 1,2, … , (18)
dengan
( , ) : entri untuk matriks pembobot antara lokasi ke – i dan ke-j : jarak Euclidian lokasi ke – i dan ke – j
ℎ : bandwidth optimum
3.4 Penaksiran Parameter Model GWPR
Untuk menaksir parameter dari model GWPR digunakan metode Maximum Likelihood Estimation (MLE). Langkah awal dari metode tersebut adalah dengan membentuk fungsi likelihood. Karena variabel tak bebas berdistribusi Poisson ( ~ ( ( , ))) maka fungsi likelihood bisa didapat seperti pada persamaan (5).
Menurut Septika (2010), faktor letak geografis merupakan faktor pembobot pada model GWPR. Faktor ini memiliki nilai yang berbeda untuk setiap daerah yang menunjukkan sifat lokal pada model GWPR. Oleh karena itu pembobot diberikan pada bentuk log- likelihood-nya untuk model lokal GWPR, maka diperoleh :
∗( ( , )) = − + − ( !) ( , ) (19)
Estimasi parameter ( , ), diperoleh dengan mendiferensialkan persamaan (19) terhadap ( , ) maka diperoleh :
∗( ( , )
( , ) = − + ( , ) (20)
Nilai estimasi diperoleh dengan memaksimumkan bentuk diferensial tersebut sehingga diperoleh
∗( ( , ))
( , ) = − + ( , ) = 0 (21)
Karena fungsi pada persamaan (21) berbentuk implisit, maka digunakan suatu prosedur iterasi numerik seperti pada penyelesaian untuk regresi Poisson.
3.5 Pengujian Kecocokan Model GWPR (Goodness of Fit)
Untuk menguji kelayakan model regresi Poisson, terlebih dahulu ditentukan dua buah fungsi likelihood yang berhubungan dengan model regresi yang diperoleh.
Fungsi-fungsi likelihood yang dimaksud adalah
L ( ) yaitu nilai likelihood untuk model lengkap dengan melibatkan variabel bebas dan
L ( ) yaitu nilai likelihood untuk model sederhana tanpa melibatkan variabel bebas.
Salah satu metode yang digunakan untuk menentukan statistik uji dalam pengujian kecocokan model regresi Poisson adalah dengan menggunakan metode Maximum Likelihood Ratio Test (MLRT) dengan hipotesis:
∶ = = ⋯ = = 0
: paling tidak ada satu ≠ 0, = 1,2, … ,
Prinsip utama dari metode MLRT adalah membandingkan nilai observasi dari variabel tak bebas dengan nilai prediksi yang diperoleh dari model (Hosmer & Lemeshow ,1989).
Statistik uji untuk kelayakan model regresi Poisson sebagai berikut :
= −2 ln( ( ̂ )
(Ω)) (22)
dengan
( ̂) = ̂
! (23)
dan
Ω =
Ω Ω
! (24)
sehingga
= −2 − ̂ + Ω + ln ̂
Ω (25)
Hasil selisih dari nilai D untuk model tanpa variabel prediktor dengan nilai D untuk model dengan variabel prediktor digunakan untuk menguji signifikasi parameter dan dilambangkan dengan statistik G yaitu,
= − (26)
dengan
= nilai D untuk model tanpa variabel bebas = nilai D untuk model dengan variabel bebas Keputusan :
Tolak H0 jika ≥ , .
3.6 Pengujian Parameter Model GWPR secara Parsial
Jika hasil dari pengujian kecocokan model GWPR memberikan kesimpulan tolak yang berarti bahwa parameter model GWPR berpengaruh terhadap model. Hal ini tidak menjamin semua parameter mempunyai pengaruh yang signifikan pada model. Untuk itu perlu dilakukan pengujian terhadap parameter model regresi Poisson secara individu, dengan menggunakan hipotesis sebagai berikut :
H0 : βk = 0 (pengaruh variabel ke-k tidak signifikan) H1 : βk ≠ 0 (pengaruh variabel ke-k signifikan)
Statistik uji yang digunakan sebagai berikut.
= (27) Nilai didapat dari akar pangkat dua elemen diagonal dari invers matriks C yang mempunyai elemen sebagai berikut (Myers, 1990).
= − ( ) (28)
dan
= − ( )
( )
≠ , = 1, … , (29)
daerah penolakannya adalah H0 akan ditolak jika |thit| > tα/2;v dengan α adalah tingkat signifikansi dan v adalah derajat bebas.
4. KESIMPULAN
Model GWPR adalah suatu model regresi yang merepresentasikan pengaruh variabel bebas terhadap variabel tak bebas berdistribusi Poisson dengan melibatkan data spasial.
Distribusi dari variabel tak bebas untuk model GWPR adalah distribusi Poisson.
Parameter model GWPR dapat ditaksir dengan metode Maximum Likelihood Estimation (MLE), yang selanjutnya dapat diuji kesesuaiannya dengan metode Maximum Likelihood Ratio Test (MLRT).
Untuk mendapatkan model yang mampu menggambarkan pengaruh variabel secara individu terhadap variasi variabel bebas dengan model GWPR dapat digunakan uji statistic Wald.
5 . DAFTAR PUSTAKA
Aulele, S. N. 2009 Model Geographically Weighted Poisson Studi Kasus : Jumlah Kematian Bayi di Jawa Timur dan Jawa Tengah Tahun 2007, Institut Teknologi Sepuluh Nopember, Surabaya
Fotheringham AS., & Charlton M (2009), Geographically weighted regression, a Strategic Research Cluster grant (07/SRC/I1168), 8
Hardle,W. (1991), Smoothing Techniques with Implementation in S, New York: Springer- Verlag.
Hansen, B. E. 2004. Nonparametric Estimation of Smooth Conditional Distributions, University of Wisconsin.
Hosmer D. W. & Lemeshow S. 1989, Applied Logistic Regression, New York, John Wiley and Sons
Hogg & McKean, 2005. Introduction to Mathematical Statistics, sixth edition, Upper Saddle River, New Jersey Pearson Education.
Myers, R. H. 1990. Classical and Modern Regression with Applications, second edition. Boston:
PWS-KENT Publishing Company.
Septika, T. 2010. Pemodelan Angka Kematian Bayi dengan Pendekatan Geographically Weighted Poisson Regression di Provinsi Timur. Program Sarjana, Institut Teknologi Sepuluh Nopember, Surabaya
Walpole R. E. & Myers R. H (1972), Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuwan, Bandung, ITB Bandung
Wei bach dan Gefeller. 2004, Double-Smoothing in Kernel Hazard Rate Estimation, Institut für Wirtschafts- und Sozialstatistik, Fachbereich Statistik, Universität Dortmund, 44221 Dortmund, Germany