PERSEMBAHAN
MOTTO
SANWACANA
Alhamdulillahi robbil ‘alamin, puji dan syukur penulis panjatkan kepada Alloh
SWT atas izin dan ridho-Nya dalam menyelesaikan tesis ini. Shalawat beriring salam atas Nabi Agung Muhammad SAW, tuntunan dan tauladan utama bagi seluruh umat manusia. Tesis ini disusun sebagai salah satu syarat untuk memperoleh gelar magister sains pada program studi Magister Matematika, Jurusan Matematika FMIPA Universitas Lampung.
Penulis ingin mengucapkan terima kasih yang tak berkesudahan kepada
Dr.Asmiati, S.Si.,M.Si., selaku Dosen Pembimbing I yang telah membimbing dan mengarahkan penelitian tesis ini. Demikian juga Dr. Muslim Ansori, S.Si.,M.Si., selaku Dosen Pembimbing II yang telah membantu dan memberikan pengarahan dalam proses penyusunan tesis ini. Terakhir, Drs. Suharsono, M.S.,M.Sc.,Ph.D., selaku Pembimbing Akademik dan Dosen Penguji, atas kesediaannya menguji, memberikan saran dan kritik yang membangun dalam proses penyelesaian tesis ini.
Lampung serta Dosen, staf, dan karyawan Jurusan Matematika FMIPA UNILA yang telah memberikan ilmu pengetahuan dan bantuan kepada penulis.
Kepada kedua orang tuaku tercinta , Ibu Muntinah dan Bapak Suroyo yang telah
memberikan dukungan secara moril dan materi, mengirimkan do‟a, nasihat dan
semangat yang sangat membantu selama penyusunan tesis. Serta Adikku Dwi
Indah Yanti, serta keponakan kecilku Restu Ayu Ramadhani atas Do‟a dan
keceriaannya.
Terima kasih dan salam hangat kepada keluarga besar Sekolah Tinggi Manajemen Informatika dan Komputer (STMIK) Pringsewu dan keluarga besar SMA Bina Mulya Gadingrejo Pringsewu atas dukungannya.
Terima kasih dan salam sayang kepada keluarga besar “Magister Matematika
2013”, atas kebersamaan dan kecerianya selama ini, semoga terjalin sampai
kapanpun. Terima kasih juga untuk semua pihak yang telah membantu penulis dalam menyelesaikan tesis ini, yang tidak dapat penulis sebutkan satu persatu.
Semoga amal baik Bapak, Ibu dan saudara mendapatkan balasan dari Alloh SWT. Akhir kata semoga tulisan ini dapat memberikan manfaat khususnya bagi penulis dan bagi pembaca umumnya. Semoga Alloh SWT senantiasa memberikan umur
dan ilmu untuk kita semua. Amin Ya Rabbal „Alamin.
DAFTAR ISI BAB II KONSEP DASAR GRAF DAN GRAF POHON
2.1 Konsep Dasar Graf ... 2.2 Graf Pohon ...
6 9 BAB III BILANGAN KROMATIK LOKASI GRAF
DAFTAR GAMBAR
Halaman
Gambar 1. Graf kembang api ... 3
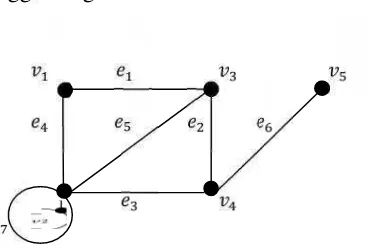
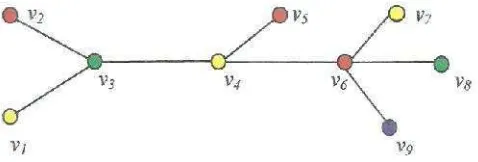
Gambar 2. Contoh graf G dengan 5 titik dan 7 sisi ... 6
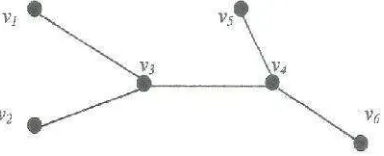
Gambar 3. Contoh pohon G dengan enam titik ... 9
Gambar 4. Contoh hutan (forest) ... 10
Gambar 5. Contoh graf bintang K1,6 ... 10
Gambar 6. Contoh graf bintang ganda S3,2 ... 10
Gambar 7. Contoh graf ulat C(3, 3, 3)... 11
Gambar 8. Contoh graf almagasi bintang tak seragam ... 11
Gambar 9. Contoh graf almagamasi bintang S3,4 ... 11
Gambar 10. Contoh graf pohon pisang B3,4 ... 12
Gambar 11. Contoh graf kembang api F3,4 ... 12
Gambar 12. Pewarnaan lokasi minimum graf G ... 17
Gambar 13. Pewarnaan lokasi minimum graf lintasan ... 18
Gambar 14. Pewarnaan lokasi minimum pada ... 19
Gambar 15. Pohon T berorde n dengan ... 19
Gambar 19. Pewarnaan lokasi minimum ... 31
Gambar 20. Pewarnaan lokasi minimum ... 33
Gambar 21. Pewarnaan lokasi minimum ... 36
Gambar 22. Pewarnaan lokasi minimum ... 39
Gambar 23. Pewarnaan lokasi minimum ... 41
I. PENDAHULUAN
1.1 Latar Belakang Masalah
Pada tahun 1736, Leonardo Euler memperkenalkan konsep teori graf dalam permasalahan Jembatan Konigsberg. Teori pewarnaan lokasi merupakan salah satu teori graf yang memiliki kontribusi besar bagi perkembangan ilmu pengetahuan. Konsep bilangan kromatik pertama kali dikaji oleh Chartrand dkk. pada tahun 2002, dengan mengembangkan dua konsep graf, yaitu pewarnaan titik dan dimensi partisi graf.
2 Pada tahun 2002, Chartrand dkk. telah menentukan pewarnaan lokasi pada graf terhubung G. Jika u dan v adalah dua titik yang berbeda di G sedemikian sehingga d(u,w)=d(v,w) untuk setiap ( ) { , }, maka ( ) ( ). Secara khusus, jika u dan v titik – titik yang tidak bertetangga di G sedemikian sehingga ( ) ( ),maka ( ) ( ).Kemudian telah ditentukan bilangan kromatik lokasi pada beberapa kelas graf, diantaranya pada graf lintasan untuk 3 diperolah ( ) = 3; pada graf siklus diperoleh dua hasil yaitu untuk n ganjil diperoleh ( ) = 3, dan untukngenap diperoleh ( ) = 4; pada graf
bintang ganda , , 1 dan 2, diperoleh , = + 1.
Dilanjutkan pada tahun 2003, Chartrand dkk. telah menunjukan graf berorde n dengan bilangan kromatik lokasinya (n–1) dan juga graf–graf yang mempunyai bilangan kromatik lokasi dengan batas atasnya (n – 2). Selain itu, Chartrand dkk.(2003). menunjukan bahwa terdapat pohon berorde 5 yang mempunyai bilangan kromatik lokasik jika dan hanya jika (3,4, , 2, ).
Selanjutnya pada tahun 2011 dan 2012, Asmiati dkk. telah berhasil menentukan bilangan kromatik lokasi pada beberapa graf pohon, diantaranya graf kembang api , untuk 2diperoleh ( , ) = 4sedangkan untuk k ≥ 5 diperoleh
, = 1, untuk 2 1 dan ( , ) = untuk lainnya; pada
graf almagamasi bintang seragam, , adalah almagamasi dari k buah graf bintang K1,m bila = , untuk setiap i diperoleh jika ( ) = ( +
1) + 1
1 untuk 0, 2, dan 3 maka ( , ) = untuk
Selanjutnya, Asmiati (2014) telah telah mendapatkan bilangan kromatik lokasi graf almagamansi bintang tak homogen.
Permasalahan penentuan bilangan kromatik lokasi pada suatu graf, masih terbuka karena belum adanya teorema yang digunakan untuk menentukan bilangan kromatik lokasi pada sembarang graf. Oleh karena itu, pada penelitian ini akan dikaji tentang bilangan kromatik lokasi dengan mensubdivisi graf kembang api
, . Penelitian ini merupakan penelitian lanjutan dari hasil – hasil penelitian Asmiati dkk. (2012).
1.2 Perumusan Masalah
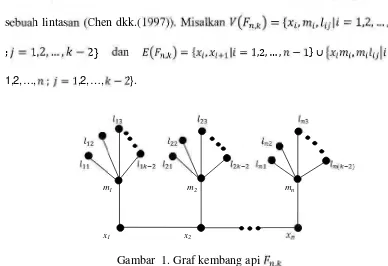
Graf kembang api seragam, , adalah graf yang diperoleh darinbuah buah graf bintang dengan cara menghubungkan sebuah daun dari setiap melalui sebuah lintasan (Chen dkk.(1997)). Misalkan , = { , , | = 1,2, ,
; = 1,2, , 2} dan , = { , | = 1,2, , 1} , =
1,2,…, ; = 1,2,…, − 2}.
( )
m1 m2 mn
x1 x2 xn
4 Graf kembang api ∗, diperoleh dengan mensubdivisi graf kembang api , sebanyak satu titik pada masing – masing sisi untuk setiap ∈[1, ]. Selanjutnya graf kembang api ,∗ diperoleh dengan mensubdivisi graf ∗, sebanyak ≥ 2titik genap pada masing–masing sisi dan untuk setiap
∈[1, ]. Akibatnya dan menjadi sebuah lintasan untuk setiap ∈[1, ]. Misalkan lintasan = { , , ,…, , } untuk setiap ∈ [1, ] dan ≥ 2 genap, lintasan = { , , ,…, , } untuk setiap
∈[1, ] dan ≥ 2genap. Adapun permasalahan akan dibatasi pada penentuan bilangan kromatik lokasi pada graf kembang api ,∗dengan n, k bilangan asli dan ≥ 2titik genap.
1.3 Tujuan Penelitian
Tujuan dari penelitian tugas akhir ini adalah menentukan bilangan kromatik lokasi dari graf kembang api ∗, dan ,∗dengan , bilangan asli dan ≥ 2titik genap.
1.4 Manfaat Penelitian
Manfaat yang didapat dari penelitian ini adalah sebagai berikut :
1. Mengembangkan wawasan tentang teori graf terutama tentang bilangan kromatik lokasi pada graf pohon.
6
II. KONSEP DASAR GRAF DAN GRAF POHON
2.1 Konsep Dasar Graf
Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989).
Graf G adalah himpunan terurut (V(G), E(G)), dengan V(G) menyatakan himpunan titik dari G dengan ( )✧ , dan ( )menyatakan himpuanan sisi yaitu pasangan tak terurut dari ( ). Banyaknya himpunan titik ( ) disebut orde dari graf G. Misalkan v dan w adalah titik pada graf G, jika v dan w dihubungkan oleh sisi e, maka v dan w dikatakan bertetangga (adjacent), sedangkan titik v dan w dikatakan menempel (incident) dengan sisi e, demikian juga sisi e dikatakan menempel dengan titik v dan w. Himpunan tetangga (Neigborhood) dari suatu titikv, dinotasikan dengan N(v) adalah himpunan titik-titik yang bertetangga denganv.
Pada Gambar 2. Graf (V, E) dengan ( ) ✁ , , , , ✂ dan ( ) ✁ , , , , , , ✂. Titik bertetangga dengan titik , , dan sedangkan dan menempel dengan . Sebaliknya, sisi menempel pada titik dan titik . ( ) ✁ , ✂ .
Derajat suatu titikvpada grafGadalah banyaknya sisi yang menempel pada titik v, dinotasikan dengan d(v). Daun (pendant vertex) adalah titik yang berderajat 1. Pada Gambar 2. ( ) 2, ( ) ✄, ( ) 3, ( ) 3 dan adalah daun karena berderajat satu.
Loop adalah sisi yang memiliki titik awal dan titik akhir yang sama. Sisi paralel adalah sisi yang memiliki dua titik ujung yang sama. Graf yang tidak mempunyai sisi ganda atau loop disebut graf sederhana. Graf pada Gambar 2. bukan merupakan graf sederhana karena pada graf tersebut terdapat loop, yaitu pada titik .
Pada graf terhubung G, jarak diantara dua titik x dan y adalah panjang lintasan terpendek diantara kedua titik tersebut, dinotasikan dengan d(x, y). Istilah lain yang sering muncul pada pembahasan graf adalah jalan (walk), lintasan (path) dan sirkuit (circuit). Jalan (walk) adalah barisan berhingga dari titik dan sisi dimulai dan diakhiri sedemikian sehingga setiap sisi menempel dengan titik sebelum dan sesudahnya. Contoh jalan berdasarkan Gambar 2. adalah ☎ ☎
8
Lintasan (path) adalah jalan yang melewati titik yang berbeda-beda. Graf G dikatakan graf terhubung jika terdapat lintasan yang menghubungkan setiap dua titik yang berbeda. Pada Gambar 2., Contoh lintasan adalah ✆ ✆ ✆ ✆
✆ ✆ ✆ ✆ .
Sirkuit (circuit) adalah lintasan tertutup (closed path), yaitu lintasan yang memiliki titik awal dan titik akhir yang sama. Sirkuit dibedakan menjadi dua macam, yaitu sirkuit genap dan sirkuit ganjil. Sirkuit genap adalah sirkuit dengan banyaknya titik genap, dan sirkuit ganjil adalah sirkuit dengan banyaknya titik ganjil. Contoh sirkuit berdasarkan gambar pada Gambar 2. adalah ✆ ✆ ✆
✆ ✆ ✆ .
Berikut ini adalah lemma yang menyatakan kaitan antara jumlah derajat semua titik pada suatu graf G dengan banyak sisinya.
Lemma 2.1 (Narsing Deo dkk. 1989) Misalkan G(V,E) adalah graf terhubung dengan✝ ✝✞ , maka :
( )✞2
Sebagai contoh pada graf Gambar 2 adalah ( ) + ( ) + ( ) + ( ) + ( )=2 +✟+ 3 + 3 + 1= 14 = dua kali jumlah sisi .
Bukti : MisalkanVgenapdanVganjil masing – masing adalah himpunan himpunan simpul yang berderajat genap dan berderajat ganjil pada G(V,E). Maka persamaan dapat ditulis sebagi berikut :
( )✠ + ( )
Karena untuk setiap ✡ , maka suku pertama dari ruas kanan persamaan harus bernilai genap. Ruas kiri persamaan juga harus bernilai genap. Ninai genap pada ruas kiri hanya benar bila suku kedua dari ruas kanan juga harus genap. Karena ( )untuk setiap ✡ , maka banyaknya titik di dalam harus genap agar jumlah seluruh derajatnya bernilai genap. Jadi banyaknya titik yang berderajat ganjil selalu genap.
2.2 Graf Pohon
Graf pohon (tree) adalah suatu graf terhubung yang tidak memuat siklus. Suatu graf yang setiap titiknya mempunyai derajat satu disebut daun (pendant vertex).
Gambar 3. Contoh pohonGdengan enam titik
10
Gambar 4. Contoh hutan (forest)
Selanjutnya, akan diberikan definisi beberapa kelas graf pohon.Suatu graf bintangK1,n (star) adalah suatu graf terhubung yang mempunyai satu titik berderajatnyang disebut pusat dan titik lainnya berderajat satu (Chartrand dkk., 1998).
Gambar 5. Contoh graf bintangK1,6
Graf pohon disebut graf bintang ganda (double star) jika graf pohon tersebut mempunyai tepat dua titikxdanyberderajat lebih dari satu. Jikaxdany berturut-turut berderajata+1 danb+1, dinotasikan dengan Sa,b,(Chartrand dkk., 1998)
Gambar 6. Contoh graf bintang gandaS3,2
Gambar 7. Contoh graf ulatC(3, 3, 3)
Misalkan ☛
, untuk setiap ☞ [1, ] dan 1 . Graf almagamasi bintang tak seragam, ,( , , , ), untuk 2 adalah graf pohon yang diperoleh dengan menyatukan sebuah daun dari setiap graf . Titik penyatuan tersebut dikatakan sebagai titik pusat dari ,( , , , ), dinotasikan dengan x. Titik – titik yang berjarak 1 dari titik pusat disebut dengan titik antara, dinotasikan dengan untuk [1, ]. Titk daun ke-j dari titik dinotasikan dengan untuk 1, 1 (Carlson., 2006).
Gambar 8. Contoh graf almagasi bintang tak seragam ,( , , , )
12
Graf pohon pisang, , adalah graf yang diperoleh dari n buah graf bintang dengan cara menghubungkan sebuah daun dari setiap ke suatu titik baru (Chen dkk.(1997)).
Gambar 10. Contoh graf pohon pisang ,
Graf kembang api seragam, , adalah graf yang diperoleh darinbuah buah graf bintang dengan cara menghubungkan sebuah daun dari setiap melalui sebuah lintasan (Chen dkk.(1997)).
Gambar 11.Contoh graf kembang api ,
Selanjutnya diberikan beberapa teorema mengenai graf pohon sebagai berikut :
Teorema 2.2 (Harsfield, N. dan G. Ringel, 1994) Jika adalah pohon dengan titik (vertex ) dan sisi (edge), maka ✌ + 1.
tidak lintasan akan menjadi lebih panjang atau terbentuk siklus di . selanjutnya kita buang titik , akibatnya sisi terhubung titik terbuang. Sehingga pohon terbentuk dengan ( ✎1) dan ( ✎1) sisi dengan asumsi ✎1✏ ( ✎1) + 1) diperoleh ✎1✏ atau ✏ + 1.
Teorema 2.3 (Harsfield, N. dan G. Ringel, 1994) Graf adalah pohon jika dan hanya jika ada terdapat tepat satu lintasan di antara kedua titik tersebut.
Bukti:
(1) Akan ditunjukkan graf adalah pohon maka ada terdapat tepat satu lintasan di antara kedua titik.
Kita asumsikan adalah pohon. Misal dan titik-titik di . Maka pohon dihubungkan lintasan ke . Anggaplah dua lintasan dari ke ,
✏ ✥ dan ✏ ✥ .Jika berbeda dengan
, selanjutnya sampai ditemukan suatu titik yang ada dalam yang juga dalam . Maka kita mempunyai siklus . Jika = , maka kita lihat pada . Untuk beberapa , , karena ada dua lintasan sebagai asumsi. Selanjutnya dari sampai ditemukan suatu titik yang ada dalam yang juga dalam dan selanjutnya ambil kembali ke , dan kita mendapatkan siklus lagi. Tetapi adalah pohon, sehingga tidak ada siklus. Jadi asumsi bahwa ada dua lintasan salah.
14
Kita asumsikan adalah graf dengan tepat satu lintasan di antara dua titik . Pertama perhatikan terhubung. Anggaplah bahwa memuat siklus
III. BILANGAN KROMATIK LOKASI GRAF
Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.(2002). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan titik pada graf adalah ✒ ( ) {1,2,3, , } dengan syarat untuk setiap titik bertetangga harus memiliki warna yang berbeda. Minimum banyaknya warna yang digunakan untuk pewarnaan titik pada graf G disebut bilangan kromatik, yang dinotasikan dengan ( ).
Berikut ini diberikan definisi bilangan kromatik lokasi graf yang diambil dari Chartrand dkk.(2002). Misalkan c suatu pewarnaan titik pada graf G dengan ( ) ( ) untuk udanv yang bertetangga diG. Misalkan himpunan titik–
titik yang diberi warna i , yang selanjutnya disebut kelas warna, maka = { , , , } adalah himpunan yang terdiri dari kelas – kelas warna dari V(G). Kode warna ( ) dari v adalah k-pasang terurut( ( , ), ( , ),..., ( , ))dengan ( , )= min{ ( , )| }untuk1 . Jika setiapG mempunyai kode warna yang berbeda, maka c disebut pewarnaan lokasi G. Banyaknya warna minimum yang digunakan untuk pewarnaan lokasi disebut bilangan kromatik lokasi dari G, dan dinotasikan dengan ( ). Karena setiap
16
Berikut ini Chartrand dkk.(2002) telah memberikan teorema dasar dari bilangan kromatik lokasi suatu graf.
Teorema 3.1 (Chartrand dkk, 2002) Misalkan c adalah pewarnaan lokasi pada graf terhubung G. Jika u dan v adalah dua titik yang berbeda di G sedemikian sehingga d(u,w)=d(v,w) untuk setiap ✓ ( )✔✕ , ✖, maka ( ) ( ). Secara khusus, jika u dan v titik – titik yang tidak bertetangga di G sedemikian sehingga ( ) ( ), maka ( ) ( ).
Bukti : misalkan c adalah suatu pewarnaan lokasi pada graf terhubung G dan misalkan ✗✘ ✕ , ,✙, ✖ adalah partisi dari titik – titik G ke dalam kelas warna . Untuk suatu titik , ✓ ( ), andaikan ( )✘ ( ) sedemikian sehingga titik udan v berada dalam kelas warna yang sama, misalkan dari✗. Akibatnya ( , ) ✘ ( , )✘✚. Karena ( , ) ✘ ( , ) untuk setiap
✓ ( )✔✕ , ✖, maka ( , )✘ , untuk setiap , ✛ . Akibatnya, ( )✘ ( ) sehingga c bukan pewarnaan lokasi. Jadi ( )
( ).
Akibat dari teorema tersebut, dapat ditentukan batas bawah trivial bilangan kromatik lokasi graf.
Bukti :Misalkanvadalah satu titik yang bertetangga dengankdaun , ,✢, di G. Berdasarkan teorema 3.1 , setiap pewarnaan lokasi diGmempunyai warna yang berbeda untuk setiap , ✣✤,✦,✢, . Karenav bertetangga dengan semua maka v harus mempunyai warna yang berbeda dengan semua daun . Akibatnya, ( ) +✤.
Selanjutnya, akan diberikan contoh menentukan bilangan kromatik lokasi pada suatu grafGseperti Gambar 12 berikut ini :
Gambar 12. Pewarnaan lokasi minimum pada grafG
Diberikan graf G seperti terlihat pada Gambar 12. akan ditentukan terlebih dahulu batas bawah bilangan kromatik lokasi dari grafG. Karena terdapat titik yang memiliki 3 daun, maka berdasarkan Akibat 3.1, ( ) ★. (3.1.1)
Selanjutnya, akan ditentukan batas atas bilangan kromatik lokasi graf G. Titik –
18
Karena kode warna semua titik di ( ) berbeda, maka pewarnaan tersebut
merupakan pewarnaan lokasi, dengan ( ) ✭. (3.1.2)
Berdasarkan persamaan (3.1.1) dan (3.1.2) diperoleh ( )✮ ✭.
Teorema 3.2 (Chartrand dkk, 2002) Misalkan k adalah derajat maksimum di graf G, maka ( ) ✯+ .
Berikut ini akan diberikan bilangan kromatik lokasi beberapa kelas graf sederhana.
Teorema 3.3 (Chartrand dkk, 2002) Bilangan kromatik lokasi graf lintasan ( ✰) adalah 3.
Gambar 13. Pewarnaan lokasi minimum pada graf lintasan
Teorema 3.4 (Chartrand dkk, 2002) Untuk bilangan bulat a dan b dengan
Bukti : Berdasarkan Akibat 3.1, diperoleh batas bawah yaitu , +✲. Selanjutnya, akan ditentukan batas atasnya yaitu , +✲. Misalkan c adalah pewarnaan titik menggunakan (b+1) warna sebagaimana terlihat pada Gambar 14. Perhatikan bahwa kode warna dari setiap titik , berbeda, akibatnyac adalah pewarnaan lokasi. Jadi , +✲.
Gambar 14. Pewarnaan lokasi minimum pada ,
Chartrand dkk. (2003) telah mendapatkan bentuk graf pohon berorde 5 yang memiliki bilangan kromatik lokasi dari 3 sampai n, kecuali n-1, sebagaimana torema berikut ini.
Teorema 3.5 (Chartrand dkk, 2002) Terdapat Pohon berorde 5 yang mempunyai bilangan kromatik k jika dan hanya jika (3,4, , 2, ).
20
Selanjutnya akan diberikan beberapa definisi tentang titik dominan danclearpath yang diambil dari Asmiati dkk. (2012). Misalkan c adalah k-pewarnaan lokasi pada graf G(V,E)dan misalkanΠ✳✴ , ,✵, ✶ adalah partisi dariV(G) yang diinduksi olehc. Titik vV
Gdikatakan suatu titik dominan jika
( , )✳✷,jika v . Suatu lintasan yang menghubungkan dua titik dominan di graf G disebutclear path, jika semua titik internalnya bukan merupakan titik dominan.
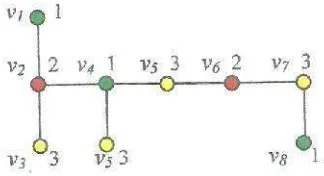
Gambar 16. GrafGdengan 3 titik dominan
Titik dominan pada Gambar 16. adalah v2, v4,dan v7.Clear path pada Gambar 16. adalah lintasan yang menghubungkan v4 dan v7 dimana tidak terdapat titik dominan dalam titik internalnya. Karena graf G pada Gambar 16. mempunyai bilangan kromatik lokasi tiga, maka panjangclear pathdari grafGganjil.
Lemma 3.1 (Asmiati dkk, 2013) Diberikan graf G dengan ( )✳ maka terdapat paling banyak k titik dominan di G dan masing-masing titik dominan memiliki warna yang berbeda.
maka kelas partisiΠmemuatkkelas warna, katakan , ,✹, dan setiapxG memiliki kode warna yang berbeda. Oleh karena itu, G paling banyak memuat sebanyak k titik dominan dan masing – masing titik dominan pada G memiliki kode warna yang berbeda.
Lemma 3.2 (Asmiati dkk, 2013) Misalkan graf G dengan ( )✺✻ , maka panjang dari setiap clear path di G adalah ganjil.
Bukti : Misalkan G adalah graf terhubung dan P adalah clear path yang menghubungkan 2 titik dominan x dan y di G. Asumsikan c(x) = 1 dan c(y)=2. Karena P adalahclear path maka warna dari titik titik didalamnya harus 1 dan 2 berturut-turut. Misalkan x dan y akan membentuk barisan alternating. Karena banyaknya titik dalamclear pathP harus genap, maka panjang P ganjil.
Lemma 3.3 (Asmiati dkk, 2013) Misalkan G adalah graf terhubung dengan ( )✺✻ Jika memuat 3 titik dominan maka terdapat 3 titik dominan dalam suatu lintasan.
22
ganjil. Sekarang, pertimbangkan lintasan L2 yang menghubungkan y ke u kemudian ke z. Maka, L2 merupakan clear path. Oleh karena itu, panjangnya adalah ganjil. Kedua fakta tersebut menyatakan panjang dari lintasan yang menghubungkan x ke u ditambahpanjang lintasan yang menghubungkan u ke z panjangnya adalah genap, kontradiksi.
Selanjutnya Asmiati dkk. (2012) telah mendapatkan bilangan kromatik lokasi graf kembang api , untuk ✼dan ✽, sebagimana teorema berikut ini.
Teorema 3.6(Asmiati dkk, 2012) Misalkan , graf kembang api, maka: i. ( , )✾ ✿❀ ✼
Pertama akan ditentukan batas bawah dari , untukn ≥ 2. Berdasarkan Akibat
3.1, χ ( , ) ≥ 3untukn ≥ 2. Selanjutnya akan ditunjukan bahwaχ ( , ) ≥ 4.
Untuk suatu kontradiksi, andaikan terdapat pewarnaan-3 lokasi untuk , ; n ≥
2, jika ketiga warna itu adalah 1,2,3 maka { ( ), ( ), ( )} =
{ ( ), ( ), ( )} = {1,2,3} sangat jelas, c(m ) ≠ c(m ), jika tidak, kode
warna titik akan sama dengan kode warna dari atau , suatu kontradiksi.
Untuk semua titikl , definisikan:
c l =
dari semua titik , berbeda, makacadalah pewarnaan lokasi.
Jadi χ ( , ) ≤ 4. (3.1.4)
Berdasarkan persamaan (3.1.3) dan (3.14), diperolehχ ( , ) = 4; ≥ 2
Akan ditunjukan bahwa untuk ≥ 5,χ ( , ) = k dan χ ( , ) = − 1
24
Kasus 1.Untuk ≥ 5 dan 2 ≤ ≤ − 1
Pertama akan ditentukan batas bawah dari , , untuk ≥ 5dan 2 ≤ ≤ − 1.
Karena setiap titik bertetangga dengan ( − 2) daun, maka berdasarkan Akibat
3.1,χ ( , ) ≥ − 1. (3.1.5)
Akan ditunjukan bahwa χ ( , ) ≤ k − 1 untuk k ≥ 5 dan n ≤ k − 1. Definisikan suatu pewarnaan-( − 1) pada , sebagai berikut. Beri warna
( ) = , untuk ∈[1, ] dan semua daun: = 1,2,…, − 2 dengan
{1,2,…,k − 1}\ {i} untuk sembarang i. Selanjutnya definisikan ( ), untuk
∈[1, ] secara berturut – turut dengan warna 3, 4, 5, . . . , n,2,3. Catatan: jika
= 2, maka ( ) = 2 dan ( ) = 3. Akibatnya, pewarnaan c akan membangun suatu partisi ∏ = { , ,…, } pada , , dengan adalah
himpunan dari semua titik yang berwarnai.
Jika = , = untuk suatui, j, h, maka terdapat tepat satu himpunan di
Π yang mempunyai jarak 1 di u dan terdapat sedikitnya dua himpunan di Π
yang mempunyai jarak 1 div. Jadi ( ) ≠ ( ).
Berdasarkan persamaan (3.1.5) dan (3.1.6), diperoleh χ , = k − 1 untuk k≥ 5 dann ≤ k − 1.
Sebagai ilustrasi, diberikan pewarnaan lokasi dari , yang dapat dilihat pada
Gambar 17.
3 3 2 2
2 4 1 4 1 4 1 3
1 2 3 4
3 4 2 3
Gambar 17. Pewarnaan lokasi minimum dari ,
Kasus 2,Untuk k≥ 5 dan n≥k
Akan ditentukan batas bawah untuk k≥ 5 dan ≥ . Berdasarkan Akibat 3.1 , diperoleh ( , ) ≥ − 1. Tetapi akan ditunjukan bahwa k− 1 warna tidaklah
26 (k− 1) lokasi c pada , untukk≥ 5 dan ≥ . Karena n≥ k, maka terdapat dua i, j, ≠ sedemikian sehingga { ( )| = 1,2,…, − 2} = { | =
1,2,…, − 2}. Akibatnya kode warna dan akan sama, suatu kontradiksi.
Akan ditentukan batas atas dari , untuk k ≥ 5, n≥ k. Untuk menunjukan
Gambar 18. Pewarnaan lokasi minimum dari ,
bilangan kromatik lokasinya. Perluasan graf kembang api yang peneliti lakukan adalah dengan memberikan subdivisi pada sisi untuk setiap ∈[1, ].
Kasus 1. Graf kembang api yang disubdivisi satu titik pada untuk setiap
∈[1, ] , dinotasikan dengan ∗, . Langkah – langkah untuk menentukan
bilangan kromatik lokasi graf kembang api ∗, adalah sebagai berikut :
1) Penentuan batas bawah dari ( ∗, ). Berdasarkan Akibat 3.1, dapat ditentukan batas awal dari bilangan kromatik lokasi .
2) Penentuan batas atas dari ( ∗, ). Pada graf kembang api ∗, dapat dilakukan counting untuk menentukan batas atasnya. Pewarnaan lokasinya sama dengan graf kembang api , , tetapi disubdivisi satu titik pada
untuk setiap ∈[1, ].
Kasus 2. Graf kembang api ,∗ diperoleh dengan mensubdivisi graf ∗, sebanyak ≥ 2 titik genap pada masing–masing sisi dan untuk setiap
∈[1, ]. Akibatnya dan menjadi sebuah lintasan untuk setiap
∈[1, ]; untuk setiap ∈[1, ] dan s ≥ 2 genap. Misalkan lintasan
= { , , ,…, , } dan lintasan = { , , ,…, , } untuk
setiap ∈[1, ]; untuk setiap ∈[1, ] dan s ≥ 2 genap. Langkah – langkah untuk menentukan bilangan kromatik lokasi graf kembang api ,∗ adalah sebagai berikut :
1) Penentuan batas bawah dari ( ,∗). Berdasarkan Akibat 3.1, dapat ditentukan batas awal dari bilangan kromatik lokasi .
28
sama dengan graf kembang api ∗, , tetapi disubdivisi sebanyak ≥ 2 titik genap pada masing – masing sisi dan untuk setiap ∈[1, ]. Untuk ( ) = ( ) untukrganjil dan ( ) = ( ) untukrgenap, untuk
( ) = ( ) untuk r ganjil dan ( ) = ( ) untuk r genap setiap
V. KESIMPULAN DAN SARAN
4.1 Kesimpulan
Pada penentuan bilangan kromatik lokasi graf kembang api ❆ , Asmiati.dkk (2012), memperoleh ❆
❇ ❈❉❊❋● ❊k ❍ ■; sedangkan untuk k ≥ 5,
❆
❇ ❏❑❉❊❋●❊k■▲ ▲ ❏❑ dan k untuk n yang lainnya. Pada penelitian tesis ini, peneliti melanjutkan penelitian Asmiati.dkk(2012) dengan mensubdivisi graf kembang api ❆ . Apabila salah satu sisi yang bukan sisi daun pada graf kembang api ❆ disubdivisi satu titik pada untuk setiap
▼
[1, ],dinotasikan dengan , , diperoleh :
i. χ ( , ) = 4 ; n 2
ii. Untuk k≥ 5
χ ( , ) =
k 1 ; 1 n k 1
k ; lainnya
Selanjutnya graf kembang apai ∗, disubdivisi sebanyak ≥ 2 titik genap pada
masing – masing sisi dan untuk setiap ∈[1, ], dinotasikan dengan
,
∗. Akibatnya dan menjadi sebuah lintasan untuk setiap ∈[1, ];
◆6 i. χ ( ,∗) = 4 ; n ≥ 2
ii. Untuk k≥ 5
χ ( ,∗) = k − 1 ; 1 ≤ n ≤ k − 1 k ; lainnya
Sehingga terlihat perluasan yang dapat dilakukan pada graf kembang api , sedemikian sehingga mempertahankan bilangan kromatik lokasinya.
4.2 Saran
DAFTAR PUSTAKA
Asmiati, The Locating-Chromatic Number of Non-Homogeneous Almagamation of Starts, Far East Journal of Mathematical Science (FJMS), 93(1), 89-96, 2014.
Asmiati, Baskoro, E.T, Characteristic pf graphs Containing Cycle with Locating-cromatic Number Three,AIP Conf.Proc.,1450, 351-357, 2012.
Asmiati, Assiyatun, H, Baskoro, E.T, Suprijanto, D, Simanjuntak, R, Uttunggadewa, S, Locating-Chromatic Number of Firecracker Graph, Far East Journal of Mathematical Sciences,63(1),11-23, 2012.
Asmiati, Assiatun, H, Baskoro, E.T, Locating-Chromatic Number of Almagamation of Starts,ITB J.Sci.,43A, 1-8, 2011.
Baskoro, E.T, and Purwasih, I.A, The locating-chromatic number of corona product of graph,Southeast Asian Journal of Science,1:1 , 89-101, 2011. Carslon, K., (2006): Generalized books and Cm-snakes are prime graphs, Ars
Combinatorics,80,215-221.
Chartrand, G, Erwin, D, Henning, M.A, Slater, P.J, dan Zhang, P.2002. The locating-chromatic number of a graph, Bull.inst. combin. Apll., 36, 89-101.
Chartrand, G, Erwin, D, Henning, M.A, Slater, P.J, dan Zhang, P.2003. graf of order n with locating-chromatic numbern-1,Discrate Math.,269,65-79. Chartrand, G.Zhang, P,Chromatic Graph Teory.2009.CRC Press.
Chen,W., Lii, H., and Yeh, Y., (1997): Operation of Interlaced Tree and Graceful Tree,Shoutheast Asian Bull. Math.,21, 337-348.