BILANGAN KROMATIK LOKASI GRAF ,
(Skripsi)
Oleh
Agustina Ambar Wulan
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
ABSTRAK
BILANGAN KROMATIK LOKASI GRAF ,
Oleh
Agustina Ambar Wulan
Bilangan kromatik lokasi diperkenalkan pada tahun 2000 oleh Chartrand dkk. sebagai perkembangan dari dua konsep dalam graf yaitu pewarnaan titik pada graf dan dimensi partisi graf. Misalkan c suatu pewarnaan sejati di dengan ( ) ( ) untuk dan yang bertetangga di . Misalkan adalah kelas warna dari ( ). Kode warna, ( ) dari adalah k-pasang terurut dengan ( , ) = min ( , ) untuk 1≤ . Banyaknya warna
minimum yang digunakan pada pewarnaan lokasi disebut bilangan kromatik lokasi dari , dinotasikan dengan ( ). Graf , diperoleh dari graf , dan setiap titik nya dihubungkan oleh suatu lintasan. Bilangan kromatik lokasi dari graf nS4,k sudah ditentukan yakni :χL(nS4,2) = 4 untuk 1 2
dan 5 untuk n lainnya; misalkan 3 χL(nS4,k) = + 1; 1 dan
+ 2untuk lainnya.
RIWAYAT HIDUP
Penulis dilahirkan di Bandar Lampung pada tanggal 17 Agustus 1992. Penulis
merupakan anak keempat dari pasangan Bapak Iawar dan Ibu Rohayani, adik dari Hendra Widjaya, Budi Permana, dan Lina Sudarwati.
Penulis menyelesaikan pendidikan dari Taman Kanak-kanak Negeri Pembina Pahoman, Bandar Lampung pada tahun 1998. Pendidikan sekolah dasar di SD Negeri 2 Pahoman, Bandar Lampung pada tahun 2004. Pendidikan sekolah
menengah pertama di SMP Negeri 16 Bandar Lampung pada tahun 2007. Pendidikan sekolah menengah atas di SMA Negeri 4, Bandar Lampung pada tahun 2010.
Pada tahun 2010, Penulis melanjutkan pendidikan di perguruan tinggi dan terdaftar sebagai mahasiswa Jurusan Matematika Fakultas Matematika dan Ilmu
Pengetahuan Alam Universitas Lampung melalui jalur SNMPTN. Pada periode tahun 2010/2011 penulis terdaftar sebagai anggota GEMATIKA (Generasi Muda
HIMATIKA) Himpunan Mahasiswa Matematika FMIPA Unila. Penulis pernah menjadi anggota biro Kesekretariatan Organisasi Himpunan Mahasiswa Matematika FMIPA Unila pada periode tahun 2011/2012 - 2012/2013. Penulis
Pendapatan Kota Bandar Lampung serta Kuliah Kerja Nyata (KKN) selama 40
PERSEMBAHAN
Dengan penuh rasa syukur kepada Allah SWT atas nikmat yang luar biasa
yang selalu diberikan kepadaku sehingga aku dapat menyelesaikan hasil
karyaku ini
Kupersembahkan hasil karyaku ini untuk Ayah, Ibuku tersayang, abangku
Hendra Widjaya, Budi Permana, Mbaku Lina, sebagai salah satu wujud
cintaku.
Terima kasih untuk setiap doa,semangat, dan kasih sayang yang selalu
menemani disetiap hariku.
Sahabat-sahabat terbaikku, terima kasih untuk semua kisah yang telah kita
MOTO
Sungguh bersama kesukaran dan keringanan, karna itu bila kau telah selesai
(mengerjakan yang lain) dan kepada Tuhan , berharaplah .
(Q.S Al Insyirah : 6-8)
Kesuksesan berbanding lurus pada tindakan yang dilakukan
.
Selalu berusaha menjadi seseorang yang berguna untuk orang di sekitar kita .
SANWACANA
Alhamdulillahi robbil ‘alamin, puji dan syukur penulis kepada Allah SWT atas izin
serta ridho-Nya dalam menyelesaikan skripsi ini. Shalawat serta salam kepada junjungan nabi Muhammad SAW yang telah menjadi suri tauladan yang baik bagi
kita.
Pada proses penyusunan skripsi ini, penulis memperoleh banyak bimbingan, kritik,
dan saran yang membangun sehingga skripsi ini mampu penulis selesaikan. Untuk itu penulis ingin mengucapkan terima kasih kepada :
1. Ibu Dr. Asmiati, S,Si., M.Si., selaku dosen pembimbing I yang senantiasa
membimbing, memberikan arahan, saran, dan dukungan kepada penulis dalam menyelesaikan skripsi ini.
2. Ibu Fitriani, S,Si., M.Si., selaku dosen pembimbing II yang telah banyak
membantu dan memberikan pembelajaran serta bimbingan kepada penulis.
3. Bapak Amanto, S.Si., M.Si., selaku dosen penguji yang telah memberikan kritik
dan saran pada penelitian ini.
4. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D., selaku dosen pembimbing akademik dan selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.
6. Seluruh dosen, staff, dan karyawan Jurusan Matematika FMIPA Universitas
Lampung.
7. Untuk kedua orang tuaku yang luar biasa, abang tercinta Kahen, serta mbaku Lina
yang tak pernah lelah untuk memberikan doa, kasih sayang, perhatian serta dukungan kepada penulis.
8. Untuk Abu Dzar Algi Fahri atas semangat, nasehat, kesabaran, kebersamaan serta
waktu luang yang sangat bermanfaat selama ini.
9. Sahabat-sahabat penulis, Engine, Indri, Dian, Dinda, Tri, karim, Miftah, Ridho,
Sofyan, Andi, Puput, Senja, Dede, Fany, Rofa serta Nisa yang selalu ada menemani dan memberikan semangat melalui keceriaan serta kebersamaan . 10. Untuk Staff pengajar Soesilo 43 serta anak murid tercinta, para calon Brigadir dan
AKPOL yang memberikan keceriaan.
11. Untuk teman-teman Matematika 2010 dan keluarga besar HIMATIKA 12. Seluruh pihak yang telah membantu dalam penyusunan skripsi ini yang tidak
dapat disebutkan satu persatu.
Akhir kata, penulis menyadari skripsi ini jauh dari kesempurnaan akan tetapi semoga
dapat berguna dan bermanfaat bagi kita semua.
Bandar Lampung, Februari 2015
Penulis,
DAFTAR GAMBAR
Halaman
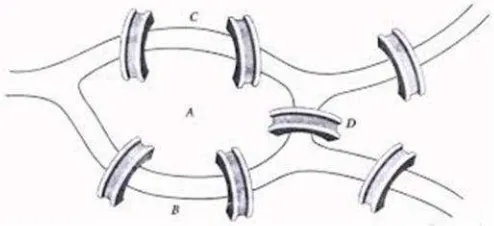
Gambar 1. Permasalahan JembatanKonigsberg………...2
Gambar 2 GrafS4,k………....4
Gambar 3 Contoh graf dengan 5 titik dan 5 sisi………6
Gambar 4 Contoh graf dengan 5 titik dan 8 sisi………7
Gambar 5 Contoh graf lengkap K4……….8
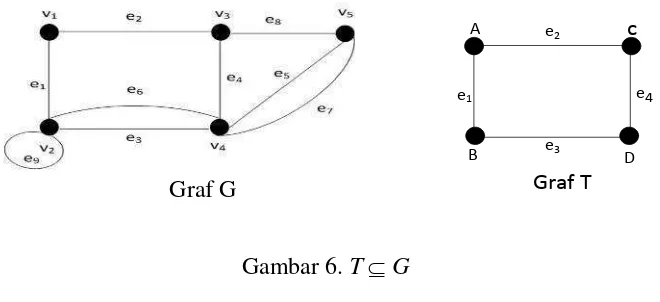
Gambar 6 TG………...8
Gambar 7 Contoh graf dengan 6 titik dan 7 sisi ………9
Gambar 8 T adalahcontoh pohon dan H adalah contoh hutan ……….10
Gambar 9 GrafS4,k……….11
Gambar 10 Graf 3S4,5………...11
Gambar 11 Graf bintangK1,6………12
Gambar 12 Graf bintang gandaS3,2...12
Gambar 14 Contoh graf pohon pisang………...13
Gambar 15 Pewarnaan lokasi minimum dari graf G……….15
Gambar 16 Pewarnaan lokasi minimum pada graf lintasan Pn………..17
Gambar 17 Pewarnaan lokasi minimum padaSa,b……….17
Gambar 18 Pohon T berordendenganχ (T)= k………..……..18
Gambar 19 Pewarnaan lokasi minimum graf bintangK1,n……….18
Gambar 20 Konstruksi grafnS4,k………21
Gambar 21 Konstruksi batas bawahχ (S4,2)...……….…22
Gambar 22 Pewarnaan lokasi minimum grafS4,2……….………….23
Gambar 23 Konstruksi batas bawahχ (2nS4,2)………...…...24
Gambar 24 Pewarnaan lokasi minimum graf 2S4,2………….……….……...25
Gambar 25 Pewarnaan lokasi minimum grafnS4,k, untukn≥3……….……….26
Gambar 26 Pewarnaan lokasi minimum grafnS4,k, untukn ……...29
1
I. PENDAHULUAN
1.1 Latar Belakang
Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus
mengalami kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini mengalami perkembangan yang berguna untuk kemajuan teknologi. Para peneliti terus melakukan penelitian untuk selalu menemukan
penemuan-penemuan baru yang dapat memberikan sumbangan ilmu pengetahuannya sebagai penunjang berkembangnya ilmu-ilmu lain.
Teori graf merupakan salah satu dari contoh ilmu matematika yang semakin lama semakin berkembang. Berawal dari permasalahan jembatan
Konigsberg (Konigsberg problem) memiliki tujuh jembatan yang menghubungkan empat daerah. Penduduk kota tersebut ingin melewati
ketujuh jembatan tersebut tepat satu kali dan kembali lagi ke tempat awal keberangkatan. Dari permasalahan tersebut, seorang matematikawan Swiss, Leonard Euler pada tahun 1736 menemukan jawaban, yaitu memodelkan
2
(edge). Representasi tersebut mempermudah menganalisis dan menentukan solusi dari permasalahan tersebut yang sangat membutuhkan dana besar dan waktu lama untuk membuktikannya secara langsung.
Gambar 1. Permasalahan JembatanKonigsberg
Salah satu ilmu dalam teori graf adalah bilangan kromatik lokasi. Konsep bilangan kromatik lokasi diperkenalkan pada tahun 2000 oleh Chartrand,
Erwin, Henning, Slater, Zhang sebagai perkembangan dari dua konsep dalam graf yaitu pewarnaan titik dan dimensi partisi graf. Kajian penentuan
bilangan kromatik lokasi graf dilakukan dengan membatasi kelas-kelas graf tertentu atau dengan membatasi bilangan kromatik lokasi tertentu.
Sejauh penelusuran literatur, penelitian yang terkait dengan penentuan bilangan kromatik lokasi dari graf pohon masih terbatas pada lintasan, graf
bintang, dan graf bintang ganda. Pada penelitian sebelumnya, telah berhasil ditentukan bilangan kromatik lokasi untuk kelas graf pohon, khususnya kelas graf pohon yang merupakan amalgamasi darinbuah graf bintang yang
tidak harus isomorfik dan dilanjutkan dengan menentukan sifat kemonotonannya (Asmiati dkk., 2011). Penelitian lainnya yang telah
3
kembang api (firecracker graphs) yakni kelas dari graf pohon yang
dikontruksi darinbuah graf bintang dengan menghubungkan satu daun dari setiap graf bintang menjadi sebuah lintasanPn(Asmiati. 2012).
Chartrand dkk. (2002) mendefinisikan bilangan kromatik lokasi sebagai
berikut. Misalkanc suatu pewarnaan sejati di Gdengan ( ) ( )untuk
dan yang bertetangga di G. Misalkan adalah himpunan titik-titik
yang diberi warna , yang selanjutnya disebut kelas warna, maka = { , , . . } adalah himpunan yang terdiri dari kelas-kelas warna dari
( ). Kode warna, ( ) dari adalah k-pasang terurut
( ( , ), ( , ), . , ( , ))dengan ( , ) = min ( , )
untuk 1≤ . Jika setiap titik di Gmempunyai kode warna yang berbeda, makac disebut pewarnaan lokasi dariG. Banyaknya warna minimum yang
digunakan pada pewarnaan lokasi disebut bilangan kromatik lokasi dari G,
dan dinotasikan dengan ( ).
Chartrand dkk.(2002) telah mendapatkan bilangan kromatik lokasi untuk
beberapa graf antara lain ( ) = 3 untuk 3, untuk 3 berlaku ( ), adalah 3 jikan ganjil dan 4 jikan genap, untuk graf bintang ganda
( , ), 1 dan 2, bilangan kromatik lokasinya adalah + 1.
Misalkan graf terhubung berorde 3, maka ( ) = jika dan hanya
4
Selanjutnya, Chartrand dkk. (2003) telah menunjukkan kelas-kelas graf
yang berorde n dengan bilangan kromatik lokasinya ( 1) dan juga
graf-graf yang mempunyai bilangan kromatik loksai dengan batas atasnya ( 2). Chartrand dkk. (2003) juga menunjukkan bahwa terdapat pohon
berorde 5 dengan bilangan kromatik lokasi n jika dan hanya jika {3,4, . . , 2, }.
1.2 Perumusan Masalah
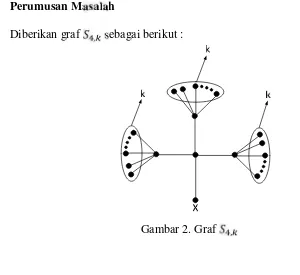
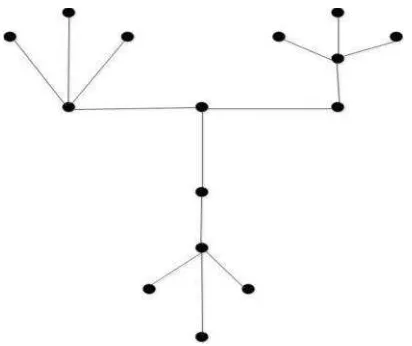
Diberikan graf , sebagai berikut :
Gambar 2. Graf ,
Graf , diperoleh dari graf , dan setiap titik nya dihubungkan oleh
suatu lintasan. Pada penelitian ini akan ditentukan bilangan kromatik lokasi
grafnS4,kuntukn,ksebarang bilangan asli.
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah mendapatkan bilangan kromatik lokasi dari
5
1.4 Manfaat Penelitian
Adapun manfaat dari penelitian ini adalah :
1. Memberikan pemahaman mengenai bilangan kromatik lokasi dari suatu
graf
6
II. LANDASAN TEORI
Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan
kromatik lokasi sebagai landasan teori pada penelitian ini.
2.1 Konsep Dasar Graf
Pada sub bab ini akan diberikan beberapa definisi dan teorema tentang graf yang diambil dari Deo (1989).
Suatu graf G adalah pasangan himpunan terurut ( ( ), ( ) ) dengan ( )
menyatakan himpunan titik (vertex) tak kosong dan ( ) menyatakan himpunan
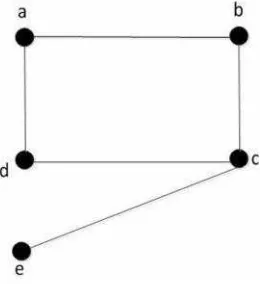
sisi (edge)yakni pasangan tak terurut dari ( ). Pada Gambar 3, terlihat ( )=
{ , , , , }dan ( ) = { , , , , }.
7
Graf digunakan untuk mempresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Representasi visual dari graf adalah dengan menyatakan objek-objek sebagai bulatan atau titik, sedangkan hubungan antara objek
dinyatakan dengan sisi. Banyak sekali struktur yang bisa direpresentasikan dengan graf, dan banyak masalah yang bisa diselesaikan dengan bantuan graf. Sebagai
contoh representasi dari graf adalah perjalanan bus untuk menemukan rute paling ekonomis dari sebuah terminal ke halte-halte yang harus dilewati tepat satu kali tanpa ada yang terlewati dua kali dan harus kembali ke terminal asal, merupakan
upaya untuk mengefisienkan biaya dan waktu pada sistem transportasi. Sistem transportasi perjalanan bus dapat dimodelkan dalam graf dengan halte sebagai
titik dan jalur yang menghubungkan halte-halte tersebut sebagai sisi.
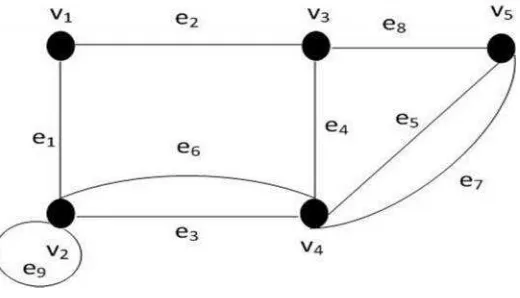
Gambar 4. Contoh graf dengan 5 titik dan 8 sisi
Loop adalah sisi yang memiliki titik awal dan titik akhir yang sama. Sisi paralel
adalah sisi yang memiliki dua titik ujung yang sama. Pada Gambar 4, terdapat loop pada titik v2 yaitu e8, sedangkan e3, e6, e5dan e7 disebut sisi paralel. Graf
8
(simple graph). Graf pada Gambar 4. bukan graf sederhana (simple graf) karena terdapatloop(e9) dan sisi ganda (e5dane7).
Suatu graf G dikatakan graf lengkap jika untuk setiap pasangan titik terdapat sisi
yang menghubungkannya.
Gambar 5. Contoh Graf Lengkap K4
Misalkan adalah graf dengan himpunan titik ( ) dan sisi ( ), maka graf
dikatakan subgraf dinotasikan denganTG jika dan hanya jika ( )himpunan
bagian dari ( )dan ( )himpunan bagian dari ( ). Graf dikatakan subgraf
sejati jika dan hanya jika subgraf dari dan . Contoh subgraf dapat
dilihat pada gambar berikut:
Dua titik pada graf dikatakan bertetangga (adjacent) bila keduanya terhubung
9
dilihat bahwa sisi menempel (incident) dengan titik dan dan titik
menempel pada sisi dan . Titik bertetangga (adjacent) dengan titik
karena terdapat sisi-sisi yang menghubungkan dan . Demikian pula dengan
titik bertetangga dengan titik , dan titik bertetangga dengan titik .
Derajat (degree) dari suatu titik v ( ),dinotasikan dengan ( ) dari graf
adalah banyaknya sisi yang menempel pada titik . Jika setiap titik pada graf
mempunyai derajat yang sama, maka disebut graf reguler. Daun (pendant
vertex) adalah titik yang berderajat satu. Pada Gambar 4. d( ) = 2, ( ) = 5,
( ) = 3, ( ) = 5dan ( ) = 3. Graf tersebut tidak memiliki daun
karena setiap titiknya memiliki derajat lebih dari satu.
Jalan (walk) adalah barisan berhingga dari titik dan sisi dimulai dan diakhiri dengan titik sedemikian sehingga setiap sisi menempel dengan titik sebelum dan
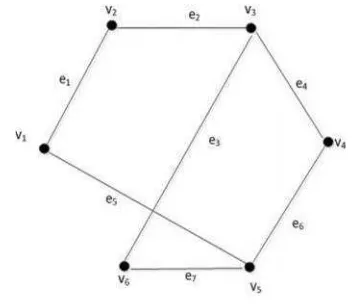
sesudahnya. Contoh walk dari graf pada gambar 7 adalah v1e1v2e2v3e4v4e6v5
e7v6e3.
Gambar 7. Contoh Graf dengan 6 titik dan 7 sisi
10
atau siklus. Graf G pada Gambar 7. v1v2v3v4v5v6 adalah salah satu lintasan
tertutup. Siklus yang banyak titiknya genap disebut sirkuit genap, sedangkan jika banyak titiknya ganjil, maka disebut siklus ganjil. Graf G dikatakan terhubung
jika terdapat lintasan yang menghubungkan setiap dua titik yang berbeda
2.2. Kelas Graf Pohon
Pohon (tree) adalah graf terhubung yang tidak memuat siklus. Suatu Graf
adalah pohon jika dan hanya jika terdapat tepat satu lintasan untuk setiap
pasangan titik di Graf (Deo,1989).
Berikut ini akan diberikan beberapa kelas graf pohon yang berkaitan dengan penelitian ini.
Misalkan adalah graf terhubung, disebut pohon jika dan hanya jika tidak
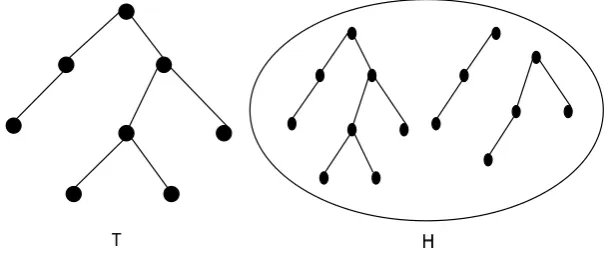
memuat sirkuit. Gabungan dari pohon disebut hutan (forest) (Deo, 1989).
Gambar 8. T adalah contoh pohon dan H adalah contoh hutan
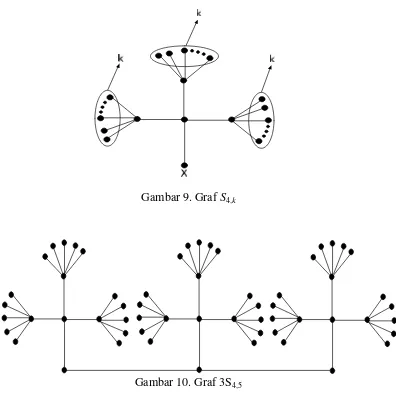
Graf , adalah graf yang diperoleh dari graf , dan setiap titik nya
11
Gambar 9. GrafS4,k
Gambar 10. Graf 3S4,5
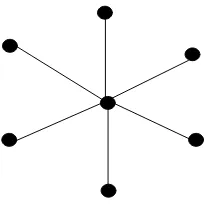
Graf bintang K1,n (star) adalah suatu graf terhubung yang mempunyai satu
titik berderajatnyang disebut pusat dan titik lainya berderajat satu (Chartrand
12
Gambar 11. Graf bintangK1,6
Suatu graf pohon disebut graf bintang ganda (double star) jika graf pohon
tersebut mempunyai tepat dua titik x dan y berderajat lebih dari satu. Jika x dan y berturut-turut berderajat a + 1 dan b + 1, dinotasikan dengan Sa,b
(Chartrand dkk., 1998).
Gambar 12. Graf bintang gandaS3,2
Graf ulat (caterpillar graf) adalah graf pohon yang memiliki sifat apabila
dihapus semua daunnya akan menghasilkan lintasan (Chartrand dkk., 1998).
Gambar 13. Contoh graf ulat
Graf pohon pisang , adalah graf yang diperoleh dari n buah kegraf bintang
dengan cara menghubungkan sebuah daun dari setiap graf bintang , suatu titik
13
Gambar 14. Contoh Graf Pohon Pisang
2.3 Bilangan Kromatik Lokasi
Bilangan kromatik lokasi diperkenalkan oleh Chartrand dkk. (2002). Bilangan kromatik lokasi didefinisikan sebagai berikut. Misalkan c suatu pewarnaan sejati
di dengan ( ) ( ) untuk dan yang bertetangga di . Misalkan
adalah himpunan titik-titik yang diberi warna , yang selanjutnya disebut kelas
warna, maka = { , , . . } adalah himpunan yang terdiri dari kelas-kelas
warna dari ( ). Kode warna, ( ) dari adalah k-pasang terurut
( ( , ), ( , ), . , ( , )) dengan ( , ) = min ( , )
untuk 1≤ . Jika setiap titik di mempunyai kode warna yang berbeda, maka
c disebut pewarnaan lokasi dari . Banyaknya warna minimum yang digunakan
pada pewarnaan lokasi disebut bilangan kromatik lokasi dari , dan dinotasikan
14
Berikut ini diberikan teorema dasar tentang bilangan kromatik lokasi yang telah
dibuktikan oleh Chartrand dkk. (2002). Lingkungan dari , dinotasikan dengan
N(u) adalah himpunan titik-titik yang bertetangga dengan .
Teorema 2.1. Misalkan c adalah pewarnaan lokasi pada graf . Jika u dan v adalah dua titik yang berbeda di sedemikian sehingga d(u,w) = d (v,w) untuk
semua w ϵ V(G) – {u,v}, maka c(u) ≠ c(v). Secara khusus, jika u danv titik-titik
yang tidak bertetangga di sedemikian sehinggaN(u) =N(v), makac(u)≠c(v).
Bukti: Misalkan c adalah suatu pewarnaan lokasi pada graf terhubung dan misalkan П = { C1 ,C2 , .... , Ck} adalah partisi dari titik-titik kedalam kelas
Akibat 2.1. Jika adalah graf terhubung dengan suatu titik yang bertetangga dengankdaun, maka ( )≥ k+1.
Bukti: Misalkan v adalah suatu titik yang bertetangga dengan k daun, yaitu x1,
x2, .... ,xk di . Berdasarkan Teorema 2.1, setiap pewarnaan lokasi dari
15
dengan semua xi, maka v harus mempunyai warna yang berbeda dengan semua
daunxi. Akibatnya,χL(G)≥ k+1. ■
Berikut ini diberikan graf dan akan ditentukan bilangan kromatik lokasi dari graf tersebut.
G
Gambar 15. Pewarnaan lokasi minimum dari graf
Diberikan graf seperti yang terlihat pada Gambar 15. Akan ditentukan terlebih
dahulu batas bawah bilangan kromatik lokasi dari graf .Karena terdapat titik v3
yang mempunyai 3 daun, maka berdasarkan Akibat 2.1,χL( )≥ 4. (2.1)
Misalkan c adalah pewarnaan titik menggunakan empat warna. Pada graf
diberikan kelas warna sedemikian sehingga diperoleh = { , , , } dengan
= { , }, = { , , }, = { , }dan = { , }. Oleh karena
itu, didapatkan kode warna sebagai berikut :
( ) = (0,1,2,3); ( ) = (1,0,1,2); ( ) = (0,1,1,1); ( ) =
(1,0,2,2); ( ) = (1,2,0,2); ( ) = (1,2,2,0); ( ) =
16
Karena kode warna dari semua titik di berbeda, maka c adalah pewarnaan
lokasi. Jadi,χL( )≤ 4 (2.2)
Berdasarkan (2.1) dan (2.2), maka adalah pewarnaan lokasi dari dan
χL( ) = 4.
Selanjutnya akan didiskusikan bilangan kromatik lokasi dari beberapa kelas graf pohon.
Teorema 2.2.Bilangan kromatik lokasi graf lintasanPn(n≥ 3)adalah 3.
Bukti: Perhatikan bahwa χL (P1) = 1 dan χL (P2) = 2. Berdasarkan Akibat 2.1,
diperoleh χL (Pn) 2. Misalkan c adalah 2-pewarnaan lokasi pada Pn, n 3
akibatnya akan terdapat dua titik yang memiliki kode warna yang sama,
kontradiksi. MakaχL(Pn) 3;n 3.
Selanjutnya konstruksi batas atas pada Pn; n 3 sebagai berikut. Misalkan c
adalah 3-pewarnaan titik, c(v1)= 1; c(vi)= 2 untukigenap; dan c(vi)= 3 untuki 3
ganjil. Diperoleh kode warna ( ) = (0,1,2); ( ) = ( 1,0,1)untuk i
genap; ( ) = ( 1,1,0)untuk i 3 ganjil. Karena semua titik mempunyai
kode warna berbeda, maka c adalah pewarnaan lokasi. Akibatnya, χL (Pn) 3;
17
Gambar 16. Pewarnaan lokasi minimum pada graf lintasan Pn
Teorema 2.3.Untuk bilangan bulatadanbdengan 1≤ a≤ b danb≥ 2 χL(Sa,b) =b+1
Bukti : Berdasarkan Akibat 2.1, diperoleh batas bawah yaitu χL (Sa,b) ≥ b+1.
Selanjutnya, akan ditentukan batas atasnya, yaitu χL (Sa,b) ≤ b+1. Misalkan c
adalah pewarnaan titik menggunakan (b+1) warna sebagaimana terlihat pada
Gambar 17. Perhatikan bahwa kode warna dari setiap titik Sa,bberbeda, akibatnya
cadalah pewarnaan lokasi. Jadi χL(Sa,b)≤b+1. ■
Gambar 17. Pewarnaan lokasi minimum padaSa,b.
Chartrand dkk. (2003) telah mendapatkan bentuk graf pohon berorden≥5 yang memiliki bilangan kromatik lokasi dari 3 sampai n, kecuali n-1, sebagaimana
18
Teorema 2.4.Terdapat pohon dengan berorde n ≥5 yang mempunyai bilangan kromatikkjika dan hanya jikak (3,4,..,n-2,n).
Pewarnaan pada Teorema 2.4 dapat diberikan sebagai berikut:
v
2v
3v
4v
5Gambar 19. Pewarnaan lokasi minimum graf bintangK1,n
Karena terdapat daun sebanyak n,maka berdasarkan Akibat 2.1, χL( ) ≥ n+1.
Misalkanc adalah pewarnaan pada grafK1,n, dengan c(v1)= 1; c(vi)= i;i≥2. Kode
19
komponen warna lainnya. Sedangkan kode warna titik ; 2, akan bernilai 1 untuk komponen warna ke-1, 0 untuk warna ke-i,dan 2 untuk lainnya. Karena
kode warna dari semua titik adalah berbeda, makacmerupakan pewarnaan lokasi.
III. METODE PENELITIAN
3.1 Waktu dan Tempat Penelitian
Adapun waktu dan tempat penelitian yaitu pada semester ganjil tahun 2014 –
2015 bertempat di Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Lampung.
3.2 Metode Penelitian
Metode yang dilakukan untuk menentukan bilangan kromatik lokasi dari
graf , yaitu sebagai berikut :
1. Menentukan batas bawah dari✄ ✁
Berdasarkan Akibat 2.1. dapat ditentukan batas bawah trivial dari bilangan
kromatik lokasi . Hal ini dapat dilakukan karena terdapat titik pada
yang mempunyai daun, akibatnya,✄ ( ✂ ✧ ☎✆✁
2. Menentukan batas atas dari✄ ✁
Batas atas dari ✄ diperoleh dengan cara mengkonstruksi graf
✁Himpunan titik-titik pada graf dikelompokkan berdasarkan diameternya ke dalam kelas-kelas warna. Minimum banyaknya kelas-kelas
V. SIMPULAN DAN SARAN
Pada bagian ini akan diberikan simpulan dan saran dari hasil yang sudah diperoleh untuk penelitian ini.
5.1. Simpulan
Adapun simpulan dalam penelitian ini secara umum adalah sebagai berikut :
1. χL(nS4,2) =
4 ; 1 2 5 ; lainnya
Misalkan 3.
2. χL(nS4,k) =
+ 1; 1
+ 2; lainnya
5.2. Saran
Penelitian ini dapat dilanjutkan dengan menentukan bilangan kromatik lokasi
DAFTAR PUSTAKA
Asmiati, Baskoro, E.T, Characteristic of graph Containing Cycle with Locating-chromatic Number Three,AIP Conf. Proc.,1450, 351-357, 2012.
Asmiati, Assiyatun, H, Baskoro, E.T, Suprijanto, D, Simanjutak, R, Uttunggadewa, S, The Locating-Chromatic Number of Firecracker Graphs. Far East Journal of Mathematical Science. 63(1), 11-23, 2012.
Asmiati, Assiyatun, H, Baskoro, E.T, Locating-Chromatic Number of Amalgamation of Stars.Bulletin Mathematics,4(2), 1-8, 2011.
Chartrand, G, Erwin, D, dan Zhang, P. 2003. Graph of Order n with Locating-chromatic Numbern-1, Discrete Mathematics,269, 65-79.
Chartrand, G, Erwin, D, dan Zhang, P. 2003. The Locating- Chromatic Number of a Graph,Aequationes Math,89-100.
DAFTAR ISI
Halaman
DAFTAR ISI………..i
DAFTAR GAMBAR……….ii
BAB IPENDAHULUAN 1.1 Latar Belakang……….1
1.2 Perumusan Masalah……….…4
1.3 Tujuan Penelitian……….4
1.4 Manfaat Penelitian………...………5
BAB II TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf………...6
2.2 Kelas Pohon ……….………..10
2.3 Bilangan Kromatik Lokasi………...13
3.2 Metode Penelitian………..20
BAB IV HASIL DAN PEMBAHASAN
4.1 Bilangan Kromatik Lokasi Graf nS4,2...21
4.2 Bilangan Kromatik Lokasi Graf nS4,k untuk k ≥ 3…………...27
BAB V SIMPULAN DAN SARAN
DAFTAR PUSTAKA