SCRAMBLING INDEX DARI GRAF TERDIRI ATAS
DUA
CYCLE
GANJIL YANG DIHUBUNGKAN
OLEH BEBERAPA LINTASAN
SKRIPSI
SUNDARI ATIKAH 110803048
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SCRAMBLING INDEX DARI GRAF TERDIRI ATAS DUA CYCLE
GANJIL YANG DIHUBUNGKAN OLEH BEBERAPA LINTASAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
SUNDARI ATIKAH 110803048
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Scrambling Index dari Graf Terdiri Atas Dua Cycle Ganjil yang Dihubungkan oleh Beberapa Lintasan
Kategori : Skripsi
Nama : Sundari Atikah
Nomor Induk Mahasiswa : 110803048
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, Juli 2015
Komisi Pembimbing :
Pembimbing 2, Pembimbing 1,
Dr. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc
NIP.19630405 198811 2 001 NIP.19640109 198803 1 004
Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
SCRAMBLING INDEX DARI GRAF TERDIRI ATAS DUA CYCLE
GANJIL YANG DIHUBUNGKAN OLEH BEBERAPA LINTASAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2015
PENGHARGAAN
Puji syukur penulis ucapkan kehadirat Allah SWT, sang pencipta langit dan bumi serta segala isinya yang telah melimpahkan rahmat, hidayah serta kasih sayang-Nya sehingga penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Scrambling Index dari Graf Terdiri Atas Dua Cycle Ganjil Saling Lepas yang Di-hubungkan oleh Beberapa Lintasan. Tak lupa pula shalawat dan salam penulis ucapkan kepada Rasulullah Muhammad SAW, keluarga dan para sahabatnya.
Terima kasih sebesar-besarnya penulis sampaikan kepada:
1. Ibunda Darlina Ruspida, Ayahanda Supeno serta Ananda Faisal Shabri yang senantiasa memberikan do’a dan dukungan dalam menyelesaikan skripsi ini. 2. Bapak Prof. Dr. Saib Suwilo, M.Sc selaku pembimbing 1 dan Ibu Dr.
Mar-diningsih, M.Si selaku pembimbing 2 yang telah meluangkan waktu, tenaga dan pikiran selama penyusunan skripsi ini.
3. Bapak Dr. Suwarno Ariswoyo, M.Si dan Bapak Prof. Dr. Tulus, M.Si selaku dosen penguji yang telah memberikan masukan dan saran selama penyusunan skripsi ini.
4. Seluruh Dosen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
5. Seluruh staff administrasi Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
6. Rekan-rekan kuliah Matematika stambuk 2011 khusunya Aisyah, Ica, Nisa, Tari, Uni Tari, Ratih, Indah yang telah banyak membantu dan memberikan dukungan demi penyelesaian skripsi ini.
SCRAMBLING INDEX DARI GRAF TERDIRI ATAS DUA CYCLE
GANJIL YANG DIHUBUNGKAN OLEH BEBERAPA LINTASAN
ABSTRAK
Scrambling index dari suatu graf primitif G adalah bilangan bulat posi-tif terkecil k sehingga untuk setiap pasangan titik u dan v yang berbeda terdapat sebuah titik w dengan sifat ada jalan yang menghubungkan titik
u dan w dan jalan yang menghubungkan titik v dan w dengan panjang
k. Pada tugas akhir ini akan didiskusikan mengenai scrambling index dari graf primitifGterdiri atas duacycleganjil saling lepas dengan panjang tiap
cycleadalahsyang dihubungkan oleh beberapa lintasan dengan panjangℓ. Untuk tiap graf primitifG, akan diperoleh bentuk umum scrambling index yang bergantung padas danℓ.
SCRAMBLING INDEX OF GRAPH CONSISTING OF TWO DISJOINT ODD CYCLES CONNECTED BY SOME PATHS
ABSTRACT
The scrambling index of a primitive graphGis the smallest positive integer
ksuch that for each pair of verticesudanv there is a vertexwthat we can get towfromuandvinGby walks of lenghtk. We discuss the scrambling index of primitive graph G consisting of two disjoint odd cycles each of lengthsconnected by some paths of lengthℓ. For such primitive graphs G
we present formulae for scrambling index that depend onsand ℓ.
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR vii
DAFTAR LAMPIRAN viii
BAB 1. PENDAHULUAN
1.1 Latar Belakang 1
1.2 Perumusan Masalah 4
1.3 Tujuan Penelitian 4
1.4 Manfaat Penelitian 4
BAB 2. TINJAUAN PUSTAKA
2.1 Definisi Graf 5
2.2 Istilah-istilah dalam Graf 5
2.3 Matriks Ketetanggaan 6
2.4 Graf Terhubung 8
2.5 Primitivitas Graf 9
2.6 Scrambling Index 11
BAB 3. METODOLOGI PENELITIAN 15
BAB 4. HASIL DAN PEMBAHASAN
4.1 Scrambling Index dari Graf Barbel 17 4.2 Scrambling Index dari Graf Barbel Dua Lintasan 23 4.3 Scrambling Index dari Graf Prisma 28
BAB 5. KESIMPULAN DAN SARAN
5.1 Kesimpulan 30
5.2 Saran 30
DAFTAR PUSTAKA 31
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
1.1 G0
n,r, r≡1(mod 2), 1≤r≤n−1 dan 1≤m ≤n−r 2 1.2 Gm
n,r, r≡1(mod 2) dan 3≤r ≤n 2 1.3 Graf Primitif terdiri atas Dua Cycle Terhubung tanpa Lintasan 3
2.1 Contoh Graf 5
2.2 Graf Terhubung dan Tidak Terhubung 8 2.3 Graf Primitif dan Tidak Primitif 9 2.4 Graf Terdiri dari Sebuah Cycle dengan panjang 5 11
4.1 Graf Barbel 17
4.2 Graf Barbel Dua Lintasan 24
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lamp
SCRAMBLING INDEX DARI GRAF TERDIRI ATAS DUA CYCLE
GANJIL YANG DIHUBUNGKAN OLEH BEBERAPA LINTASAN
ABSTRAK
Scrambling index dari suatu graf primitif G adalah bilangan bulat posi-tif terkecil k sehingga untuk setiap pasangan titik u dan v yang berbeda terdapat sebuah titik w dengan sifat ada jalan yang menghubungkan titik
u dan w dan jalan yang menghubungkan titik v dan w dengan panjang
k. Pada tugas akhir ini akan didiskusikan mengenai scrambling index dari graf primitifGterdiri atas duacycleganjil saling lepas dengan panjang tiap
cycleadalahsyang dihubungkan oleh beberapa lintasan dengan panjangℓ. Untuk tiap graf primitifG, akan diperoleh bentuk umum scrambling index yang bergantung padas danℓ.
SCRAMBLING INDEX OF GRAPH CONSISTING OF TWO DISJOINT ODD CYCLES CONNECTED BY SOME PATHS
ABSTRACT
The scrambling index of a primitive graphGis the smallest positive integer
ksuch that for each pair of verticesudanv there is a vertexwthat we can get towfromuandvinGby walks of lenghtk. We discuss the scrambling index of primitive graph G consisting of two disjoint odd cycles each of lengthsconnected by some paths of lengthℓ. For such primitive graphs G
we present formulae for scrambling index that depend onsand ℓ.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Graf merupakan bagian dari matematika diskrit yang digunakan untuk merepre-sentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Rep-resentasi visual dari graf adalah dengan menyatakan objek sebagai titik (vertex) dan hubungan antara objek-objek tersebut dinyatakan dengan sisi (edge). Den-gan kata lain, suatu graf G(E(G), V(G)) terdiri atas suatu himpunan tak kosong daan berhingga V(G) yang anggotanya disebut titik (vertex) dan suatu himpunan berhingga E(G) yang anggotanya saling berbeda yang disebut sisi(edge), dimana sisi tersebut merupakan pasangan tak berurut dari titik-titik pada V(G).
Andaikan Gadalah sebuah graf. Sebuah jalan yang menghubungkanu danv diGadalah sebuah barisan titiku=v0, v1, v2, ..., vt=v ∈V(G) dan sebuah barisan
sisi (u = v0, v1), ...,(vt−1, vt = v) ∈ E(G). Sebuah lintasan yang menghubungkan
titik u dan v adalah sebuah jalan dengan tiap titik yang berbeda kecuali u = v. Lintasan yang berawal dan berakhir pada titik yang sama disebut cycle.
Sebuah graf G dikatakan terhubung jika untuk tiap pasangan titik u dan v yang berbeda di G terdapat jalan yang menghubungkan kedua titik tersebut. Graf primitif merupakan graf terhubung dimana terdapat bilangan bulat positif k, sehingga untuk setiap pasangan titik u dan v diG, terdapat jalan dengan panjang k yang menghubungkan kedua titik tersebut. Sebuah grafGdikatakan primitif jika dan hanya jika graf G memuat paling sedikit satu cycle dengan panjang ganjil.
2
dan Kirkland 2009a, 2009b).
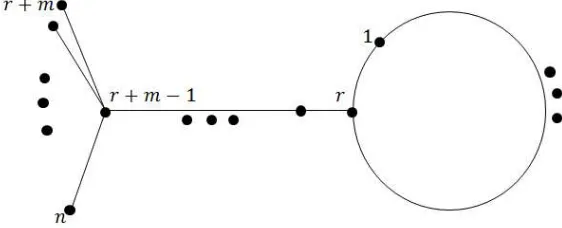
Chen dan Liu (2010) membahas mengenai scrambling index dari graf primitif yang terdiri atasn titik dengan sebuahcycledengan panjangr seperti ditunjukkan oleh Gambar 1.1 dan Gambar 1.2.
Gambar 1.1. G0
n,r, r≡1(mod 2) dan 3≤r≤n
Gambar 1.2. Gm
n,r, r≡1(mod 2),1≤r≤n−1 dan 1≤m ≤n−r
Andaikan n dan r adalah bilangan bulat positif dengan r ≡ 1(mod 2) dan 3 ≤ r ≤ n. Andaikan G0
n,r adalah graf primitif seperti yang ditunjukkan oleh
Gambar 1.1, maka k(G0
n,r) =
(r−1) 2 .
Andaikan n, r dan m adalah bilangan bulat positif dengan r ≡ 1(mod 2), 1≤r≤n−1 dan 1≤m ≤n−r. Andaikan Gm
n,r adalah graf primitif seperti yang
ditunjukkan oleh Gambar 1.2, maka k(Gm
n,r) = m+
(r−1) 2 .
3
dengan n merupakan jumlah titik pada graf tersebut. Andaikan G adalah graf primitif dengan n≥3 titik tanpa loop. Scrambling indexk(G) = 1 jika dan hanya jika G memenuhi dua kondisi berikut:
1. Tiap titik diG berada di sebuah segitiga.
2. Untuk tiap dua titikvi danvj yang berada di segitiga yang berbeda, terdapat
Wvivj dengan panjang 2.
Andaikan Sn adalah graf primitif tanpa loop dengan n ≥ 3 titik dengan
k(Sn) = 1. Nilai minimum dariSnadalah (3n−3)/2 jikanganjil dan nilai minimum
dari Sn adalah (3n−2)/2 jikan genap.
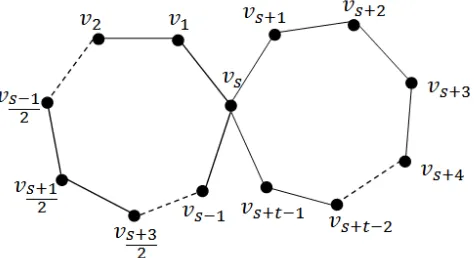
Gambar 1.3. Graf Primitif terdiri atas DuaCycleTerhubung tanpa Lintasan
Izzati (2014) membahas mengenai scrambling Index dari graf primitif terdiri atas dua cycle terhubung tanpa lintasan. Graf primitif terdiri atas dua cycle ter-hubung tanpa lintasan dinotasikan dengan Ct
s, yaitu cycle Cs dan cycle Ct seperti
ditunjukkan oleh Gambar 1.3.
Karena Ct
s merupakan graf primitif, maka Cst harus memuat paling sedikit
satucycleganjil. Scrambling index dariCt
sdengan keduacycleadalah ganjil
didefin-isikan k(Ct
s) = max{(s− 1)/2,(t− 1)/2}. Sedangkan scrambling index dari Cst
dengan salah satu cycle adalah genap didefinisikank(Ct
4
1.2 Perumusan Masalah
Istilah scrambling index pertama kali diperkenalkan pada tahun 2009. Selanjut-nya penelitian mengenai scrambling index terus berkembang. Salah satuSelanjut-nya, Izzati (2014) membahas mengenai scrambling index dari graf primitif terdiri atas dua cycle terhubung tanpa lintasan. Namun demikian, penelitian mengenai scrambling index dari graf terdiri atas dua cycle yang dihubungkan oleh beberapa lintasan belum dibahas dalam literatur. Secara khusus rumusan masalah dari penelitian ini adalah sebagai berikut:
Andaikan G adalah sebuah graf terdiri atas dua cycle ganjil C1 yaitu cycle v1 ↔ v2 ↔ ... ↔ vs ↔ v1 dan C2 yaitu cycle vs+1 ↔ vs+2 ↔ ... ↔ v2s ↔ vs+1 yang saling lepas dengan panjang tiapcycleadalahs. Andaikan terdapat beberapa lintasan dengan panjang tiap lintasan adalah ℓ yang menghubungkan C1 dan C2. Fungsi f(s, ℓ) manakah yang memenuhi k(G)≤f(s, ℓ)?
1.3 Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah menentukan bentuk umum scrambling index dari graf terdiri atas dua cycle ganjil saling lepas dengan panjang tiapcycle adalah s yang dihubungkan oleh beberapa lintasan dengan panjang tiap lintasan adalah ℓ.
1.4 Manfaat Penelitian
BAB 2
GRAF PRIMITIF
Pada bagian ini akan dijelaskan mengenai definisi graf, istilah-istilah dalam graf, matriks ketetanggaan, graf terhubung, primitivitas graf, dan scrambling index.
2.1 Definisi Graf
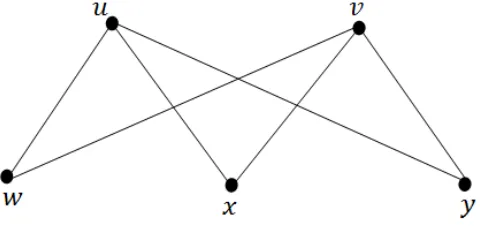
Sebuah graf G terdiri atas suatu himpunanan tak kosong dan berhingga V(G) yang anggotanya disebut titik (vertex) dan sebuah himpunan berhinggaE(G) yang anggotanya disebut sisi (edge) dimana sisi tersebut merupakan pasangan tak beru-rut dari titik-titik pada V(G). Sebuah sisi{v, w} adalah sisi yang menghubungkan titik v dan titik w, yang biasanya disingkat menjadi vw. Sebagai contoh, Gambar 2.1 merepresentasikan graf G dengan himpunan titik V(G) = {u, v, w, x, y} dan himpunan sisi E(G) yang terdiri dari sisi uw, ux, vx, vy, uy dan vw.
Gambar 2.1. Contoh Graf
2.2 Istilah-istilah dalam Graf
Andaikan terdapat sebuah graf G, berikut akan dijelaskan beberapa istilah dan notasi dalam graf yang digunakan dalam penjelasan selanjutnya.
6
... ↔ vm dimana v0 merupakan titik awal dan vm merupakan titik akhir.
Sebuah jalan yang menghubungkanvi danvj dinotasikan denganWvivj. Pada Gambar 2.1, w↔v ↔y↔v ↔x adalah sebuah jalan Wwx.
b. Panjang. Panjang dari sebuah jalan Wvivj adalah banyaknya sisi di jalan Wvivj dan dinotasikan dengan ℓ(Wvivj). Pada Gambar 2.1, w ↔ u ↔y ↔v adalah sebuah jalan Wwv dengan panjang 3, atau dapat dinotasikan dengan
ℓ(Wwv) = 4.
c. Lintasan. Lintasan merupakan sebuah jalan dengan titik yang berbeda ke-cuali jika titik awal juga merupakan titik akhir (v0 = vm). Lintasan yang
menghubungkan vi dan vj dinotasikan dengan Pvivj. Pada Gambar 2.1, u ↔ x ↔ v ↔ y adalah sebuah lintasan Puy dengan panjang 3 atau dapat
dino-tasikan dengan ℓ(Puy) = 3.
d. Cycle. Cycle merupakan sebuah lintasan yang berawal dan berakhir pada titik yang sama. Pada Gambar 2.1, lintasan u ↔ y ↔ v ↔ w ↔ u adalah sebuah cycle dengan panjang 4. Sebuah cycle dengan panjang ganjil disebut cycle ganjil dan sebuah cycle dengan panjang genap disebut cycle genap.
e. Distance. Panjang dari jalan terpendek yang menghubungkan u dan v di G disebut distance dinotasikan dengan d(u, v). Pada Gambar 2.1, diperoleh d(w, y) = 2.
2.3 Matriks Ketetanggaan
Matriks ketetanggaan (adjacency matrix) dari sebuah grafGatasntitikv1, v2, ..., vn
adalah sebuah matriks bujur angkar A = (aij) dengan ordo n yang setiap entrinya
didefinisikan sebagai:
aij =
1,bila {vi, vj} ∈E(G)
0,bila {vi, vj}∈/E(G).
Oleh definisi tersebut, diperoleh bahwa aij = aji. Hal ini berakibat
7
pada Gambar 2.1 dapat direpresentasikan menjadi matriks ketetanggaanA sebagai berikut:
Sebuah matriks A dikatakan matriks non negatif jika semua entri (aij) ≥ 0.
Sedangkan sebuah matriks A dikatakan matriks positif jika semua entri (aij) ≥ 1.
Perhatikan contoh berikut:
MatriksX merupakan matriks tak negatif karena semua entri (xij)≥0. Sedangkan
matriks Y merupakan matriks positif karena semua entri (yij)≥1.
Teorema 2.1 (Bona, 2006) Andaikan G adalah sebuah graf dan A= (aij) adalah
sebuah matriks ketetanggaan dari G. Misalkan ak
ij adalah entri (i, j) dari matriks
Ak. Maka ak
ij menyatakan banyaknya jalan dengan panjang k yang menghubungkan
titik i dengan titik j.
Bukti. Kita buktikan dengan menggunakan induksi atas k. Bila k = 1 entri
a(1)ij = aij dari A yang menyatakan banyaknya jalan dengan panjang satu yang
menghubungkan titik i dengan titik j. Asumsikan bahwa entri a(ijk) dari Ak
meny-atakan banyaknya jalan dengan panjangkyang menghubungkan titikidengan titik j. Karena Ak+1 =AkA, maka
8
penjumlahana(iℓk+1) adalah banyaknya jalan dengan panjangk+ 1 yang menghubu-ngkan titik i dengan titik j.
2.4 Graf Terhubung
Sebuah graf G dikatakan terhubung (connected graph) jika untuk setiap titik u dan v diG dihubungkan oleh sebuah jalan denganu dan v merupakan titik ujung. Sebaliknya, graf tidak terhubung (disconnected graph) merupakan graf terdapat sembarang titik yang tidak terhubung ke titik lainnya di G. Dengan kata lain, tidak terdapat yang jalan menghubungkan titik tersebut ke titik yang lain di G.
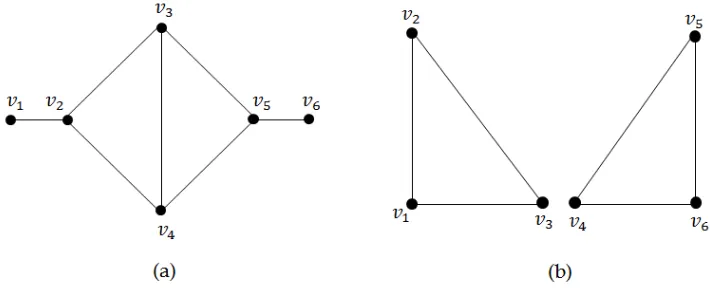
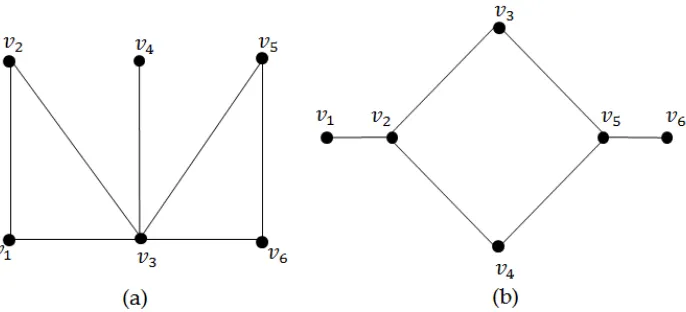
Gambar 2.2. (a) Graf Terhubung dan (b) Graf tidak Terhubung
Graf pada Gambar 2.2(a) merupakan graf terhubung, karena untuk tiap titik terdapat jalan yang menghubungkan antara satu titik ke titik lainnya. Sedangkan graf pada Gambar 2.2(b) merupakan graf tidak terhubung, karena tidak terdapat jalan yang menghubungkan satu titik dengan titik lainnya seperti v3 kev4,v2 kev3 dan lainnya.
Teorema 2.2 (Bona, 2006) Andaikan G adalah sebuah graf atas n titik dengan
matriks ketetanggaan A. Graf G adalah terhubung jika dan hanya jika matriks A+A2+...+An−1 mempunyai entri yang semuanya positif.
Bukti. Andaikan G adalah sebuah graf terhubung dengan n titik dan misalkan
9
titik j. Sebuah lintasan diG tidak terdapat titik berulang kecuali i=j, bila i6=j terdapat lintasan dengan panjang kurang dari n yang menghubungkani denganj. Hal ini berarti untuk setiap pasangan titik i dan j yang berbeda, terdapat sebuah bilangan bulat positif k dengan 1 ≤ k ≤ n −1 sehingga entri ak
ij > 0. Sehingga
semua entri di luar entri diagonal dari matriks B adalah positif. Bila i=j, maka terdaoat sebuahcycledengan panjang 2 yang memuat titiki, sehingga entria(2)ij >0 untuk semua i = 1,2, ..., n. Jadi entri diagonal dari matriks B adalah positif. Sekarang dapat disimpulkan bahwa semua entri dari matriksB =A+A2+...+An−1
adalah positif.
Sekarang andaikan setiap entri dari matriksA+A2+...+An−1 adalah positif. Akibatnya untuk setiap pasangan titik i dan j terdapat sebuah bilangan positif k dengan 1≤k ≤n−1 sehinggaak
ij >0. Hal ini berarti untuk setiap pasangan titik
i dan j di G terdapat sebuah jalan dengan panjang k yang menghubungkan i dan j. Sehingga oleh definisiG adalah sebuah graf terhubung.
2.5 Primitivitas Graf
Graf primitif merupakan graf terhubung dimana terdapat bilangan bulat positif k sehingga untuk setiap pasangan titik u dan v terdapat sebuah jalan Wuv dengan
panjangk. Sebuah grafGdikatakan primitif jikaGmerupakan graf terhubung dan terdapat paling sedikit satu cycleganjil (Liu et al., 1990).
10
Graf pada Gambar 2.3(a) merupakan graf primitif, karena terdapat cycle dengan panjang ganjil. Sedangkan graf pada Gambar 2.3(b) bukan merupakan graf primitif, karena tidak terdapat cycle dengan panjang ganjil.
Sebuah grafGdapat direpresentasikan menjadi sebuah matriks ketetanggaan A. Sebuah matriks persegi non negatif A dikatakan primitif jika terdapat bilangan bulat k sedemikian hingga semua entri di Ak bernilai positif (Brualdi dan Ryser,
1991).
Graf pada Gambar 2.3(a) dapat direpresentasikan menjadi matriks persegi non negatif A sebagai berikut:
A=
Untuk memperlihatkan bahwa matriks A merupakan matriks primitif, maka akan diperlihatkan terdapat bilangan bulat positif terkecil k sehingga semua entri di Ak bernilai positif. Dengan kata lain, matriks Ak merupakan matriks positif.
Perhatikan matriks A4 berikut :
A4 =
Diperoleh bahwa setiap entri di matriks A4 bernilai positif. Karena terdapat bilan-gan bulat positif k sehingga matriks Ak merupakan matriks positif, maka matriks
11
2.6 Scrambling Index
Scrambling index dari graf primitif G dinotasikan dengan k(G) adalah bilangan bulat positif terkecil k sehingga untuk setiap pasangan titik yang berbedau danv, terdapat sebuah titik w sehingga terdapat jalan dari titik u dan titik v ke titik w dengan panjang k atau dengan kata lain terdapat Wuw dan Wvw dengan panjang k
(Alkebek dan Kirkland 2009a, 2009b).
Untuk setiap u, v ∈V(G) dan u6=v, scrambling index lokal dari titik u dan v di G didefinisikan sebagai berikut:
ku,v(G) = min
w∈V(G){k: terdapat Wuw dan Wvw dengan panjang k}.
Jika scrambling index lokal dari titik u dan v di G adalah ku,v(G), maka
untuk setiap k′
≥ ku,v(G), terdapat titik w′ sehingga terdapat Wuw′ dan Wvw′ dengan panjang k′. Sehingga scrambling index dari graf G didefinisikan sebagai
berikut:
k(G) = max
u,v∈V(G){ku,v(G)}.
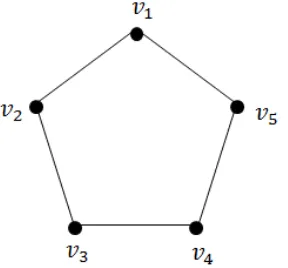
Contoh 2.1AndaikanGadalah graf yang terdiri dari sebuahcycledengan panjang
5 seperti pada Gambar 2.4.
Gambar 2.4. Graf yang Terdiri Atas Sebuah Cycle dengan Panjang 5
12
kv1,v2(G) = min{kv1,v2(v1), kv1,v2(v2), kv1,v2(v3), kv1,v2(v4), kv1,v2(v5)} = min{4,4,3,2,3}= 2
kv1,v3(G) = min{kv1,v3(v1), kv1,v3(v2), kv1,v3(v3), kv1,v3(v4), kv1,v3(v5)} = min{2,1,2,3,3}= 1
kv1,v4(G) = min{kv1,v4(v1), kv1,v4(v2), kv1,v4(v3), kv1,v4(v4), kv1,v4(v5)} = min{2,3,3,2,1}= 1
kv1,v5(G) = min{kv1,v5(v1), kv1,v5(v2), kv1,v5(v3), kv1,v5(v4), kv1,v5(v5)} = min{4,3,2,3,4}= 2
kv2,v3(G) = min{kv2,v3(v1), kv2,v3(v2), kv2,v3(v3), kv2,v3(v4), kv2,v3(v5)} = min{3,4,4,3,2}= 2
kv2,v4(G) = min{kv2,v4(v1), kv2,v4(v2), kv2,v4(v3), kv2,v4(v4), kv2,v4(v5)} = min{3,2,1,2,3}= 1
kv2,v5(G) = min{kv2,v5(v1), kv2,v5(v2), kv2,v5(v3), kv2,v5(v4), kv2,v5(v5)} = min{1,2,3,3,2}= 1
kv3,v4(G) = min{kv3,v4(v1), kv3,v4(v2), kv3,v4(v3), kv3,v4(v4), kv3,v4(v5)} = min{2,3,4,4,3}= 2
kv3,v5(G) = min{kv3,v5(v1), kv3,v5(v2), kv3,v5(v3), kv3,v5(v4), kv3,v5(v5)} = min{3,3,2,1,2}= 1
kv3,v5(G) = min{kv4,v5(v1), kv4,v5(v2), kv4,v5(v3), kv4,v5(v4), kv4,v5(v5)} = min{3,2,3,4,4}= 2
Setelah memperoleh scrambling index lokal untuk tiap dua titik yang berbeda di graf G, selanjutnya adalah menentukan scrambling index untuk graf G.
k(G) = max
vi,vj∈V(G){kvi,vj(G)}= max{2,1,1,2,2,1,1,2,1,2}= 2.
Scrambling index dari matriks primitifAadalah bilangan bulat positif terke-cil k sehingga untuk setiap dua baris di Ak terdapat sedikitnya satu entri positif
13
Untuk k = 1, pada baris pertama dan kedua di Mk = M tidak terdapat
bilangan positif pada kolom yang sama. Sehingga, perlu dicari bilangan bulat positif k >1, sehingga untuk setiap dua baris di Mk terdapat sedikitnya satu entri
positif pada posisi kolom yang sama. Perhatikan matriks M2 berikut:
M2 =
• Pada baris pertama dan baris kedua, terdapat entri positif pada kolom yang sama yaitu kolom keempat.
• Pada baris pertama dan baris ketiga, terdapat entri positif pada kolom yang sama yaitu kolom pertama dan ketiga.
• Pada baris pertama dan baris keempat, terdapat entri positif pada kolom yang sama yaitu kolom pertama dan keempat.
• Pada baris pertama dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom ketiga.
• Pada baris kedua dan baris ketiga, terdapat entri positif pada kolom yang sama yaitu kolom kelima.
14
• Pada baris kedua dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom kedua dan kelima.
• Pada baris ketiga dan baris keempat, terdapat entri positif pada kolom yang sama yaitu kolom pertama.
• Pada baris ketiga dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom ketiga dan kelima.
• Pada baris keempat dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom kedua.
Oleh karena 2 merupakan bilangan bulat positif terkecil sehingga setiap dua baris diM2 terdapat elemen positif pada posisi kolom yang sama, maka scrambling index dari matriks M adalah 2.
Proposisi 2.3 Andaikan G adalah sebuah graf dan k′
adalah bilangan bulat genap
positif. Jika untuk tiap pasangan titik yang berbeda u dan v di G, terdapat sebuah jalan dengan panjang genap Wuv≤k′, maka k(G)≤k′/2.
Bukti. Andaikan u dan v adalah dua titik yang berbeda di G dan andaikan Wuv
adalah jalan dengan panjang genap u = v0 ↔ v1 ↔ v2 ↔ ... ↔ v2m−1 ↔ v2m =v
untuk beberapa bilangan bulat positifmdengan panjangℓ(Wuv)≤k′. AndaikanC2 adalahcycle v2m ↔v2m−1 ↔v2m dengan panjang 2. Maka jalanWuv′ yang berawal
di u, bergerak ke v sepanjang jalan Wuv dan bergerak k′ −ℓ(Wuv) kali disekitar
C2 adalah sebuah sebuah Wuv dengan panjang k′. Karena k′ adalah genap, maka
terdapat sebuah titikwsehingga terdapat sebuah jalanWuw dengan panjang k
′ 2 dan terdapat sebuah jalan Wvw dengan panjang k
′
2. Sehinggak(G)≤
k′
BAB 3
METODE PENELITIAN
Pada bab ini, akan dijelakan langkah-langkah untuk memperoleh scrambling index dari graf terdiri atas duacycleganjil saling lepas dengan panjang tiapcycle adalah s yang dihubungkan oleh beberapa lintasan dengan panjang tiap lintasan adalahℓ. Adapun langkah-langkahnya sebagai berikut:
1. Menentukan bentuk umum scrambling index dari graf terdiri atas dua cycle ganjil saling lepas yang dihubungkan oleh satu lintasan.
AndaikanG1 adalah sebuah graf terdiri atas duacycleganjil saling lepas den-gan panjang tiapcycle adalahs yang dihubungkan oleh satu lintasan dengan panjang lintasan adalah ℓ. Untuk mencari bentuk umum scrambling index dari graf G1 dapat dilakukan dengan langkah-langkah sebagai berikut:
a. Menentukan nilai scrambling index.
Sebuah graf G1 dapat direpresentasikan menjadi sebuah matriks kete-tanggaan simetris A berukuran n×n. Untuk menentukan nilai scram-bling index dari grafG1 dapat dilakukan dengan menggunakan program yang dibuat di M AT LAB.
b. Menentukan bentuk umum scrambling index.
Setelah memperoleh nilai-nilai scrambling index untuk grafG1yang telah didapat dari program yang dibuat diM AT LAB, kita dapat menentukan persamaan untuk nilai scrambling index yang bergantung padas dan ℓ.
c. Membuktikan bentuk umum scrambling index.
16
sehingga memenuhi k(G)≤f(s, ℓ).
2. Menentukan bentuk umum scrambling index dari graf terdiri atas dua cycle ganjil saling lepas yang dihubungkan oleh dua lintasan.
AndaikanG2 adalah sebuah graf terdiri atas duacycleganjil saling lepas den-gan panjangs engan panjang tiap cycleadalahs yang dihubungkan oleh dua lintasan dengan panjang tiap lintasan adalahℓ. Untuk mencari bentuk umum scrambling index dari graf G2 dapat dilakukan seperti pada langkah-langkah (1). Tetapi pada langkah (b) yaitu menentukan batas atas dari graf G2, juga menggunakan batas atas pada G1.
3. Menentukan bentuk umum scrambling index dari graf terdiri atas dua cycle ganjil saling lepas yang dihubungkan oleh s lintasan.
BAB 4
HASIL DAN PEMBAHASAN
4.1 Scrambling Index dari Graf Barbel
Andaikan terdapat dua cycle ganjil C1 yaitu cycle v1 ↔ v2 ↔ ... ↔ vs ↔ v1 dan C2 yaitu cycle vs+1 ↔ vs+2 ↔ ... ↔ v2s ↔ vs+1 yang saling lepas dengan panjang tiap cycle adalah s. Andaikan lintasan P adalah sebuah lintasan dengan panjang ℓ dengan titik awal berada di C1 dan titik akhirnya berada di C2. Sebuah graf G terdiri atas dua cycle ganjil saling lepas C1 dan C2 yang dihubungkan oleh sebuah lintasan P disebut graf (s, ℓ)-barbel. Andaikan vs adalah titik di P yang
berada diC1 danvs+ℓ adalah titik diP yang berada diC2 seperti yang ditunjukkan pada Gambar 4.1.
Untuk tiap titik vi di C1, diasumsikan Pvivs adalah lintasan terpendek yang menghubungkan titikvidanvsdan diasumsikanPv′ivs adalah lintasan yang menghubu-ngkan titik vi dan vs dengan panjang s−d(vi, vs). Sedangkan untuk tiap titik vj
di C2, diasumsikan Pvjvs+ℓ adalah lintasan terpendek yang menghubungkan titik vj dan vs+ℓ dan diasumsikanPv′jvs+ℓ adalah lintasan yang menghubungkan titikvj dan vs+ℓ dengan panjang s−d(vj, vs+ℓ).
18
Lemma 4.1 Andaikan s adalah bilangan bulat positif ganjil dan G adalah graf
(s, ℓ)-barbel. Jika ℓ adalah bilangan bulat positif ganjil, maka k(G) = s+ℓ 2 .
Bukti. Dengan memperhatikan titik vs−1
2 dan v 3s−1
2 +ℓ, terdapat beberapa jalan yang menghubungkan kedua titik tersebut. Diantaranya adalah:
a. JalanWvs−1 2
v3s−1 2 +ℓ
yang terdiri dari lintasan Pvs−1 2
vs, lintasanP dan lintasan Pvs+ℓv3s−1
yang terdiri dari lintasan P′
vs−1 2
vs, lintasanP dan lintasan Pvs+ℓv3s−1
yang terdiri dari lintasan Pvs−1 2
19
d. JalanWvs−1 2
v3s−1 2 +ℓ
yang terdiri dari lintasan P′
vs−1 2
vs, lintasanP dan lintasan P′
Keempat jalan tersebut merupakan lintasanPvs−1 2
v3s−1 2 +ℓ
dan dapat dipastikan bahwa keempat jalan tersebut merupakan jalan terpendek dibandingkan jalan yang lainnya karena jalan tersebut tidak terdapat pengulangan sisi yang memungkinkan panjang ℓ(Wvs−1 sedangkan jalan (b) dan (c) merupakan jalan Wvs−1
2
v3s−1 2 +ℓ
dengan panjang genap.
Untuk mencari scrambling index lokal dari titik vs−1 2 dan v
3s−1
2 +ℓ, diperlukan sebuah jalan yang menghubungkan kedua titik tersebut dengan panjang genap. Andaikan panjang jalan ℓ(Wvs−1
2
v3s−1 2 +ℓ
) adalah 2k, untuk suatu bilangan bulat positif k. Maka akan terdapat suatu titik vw di G sehingga panjang dari jalan
Wvs−1
2 = k. Oleh karena itu, diperlukan jalan ℓ(Wvs−1
2
v3s−1 2 +ℓ
) dengan panjang genap. Dengan memilih jalan (b) atau (c), diper-oleh jalan ℓ(Wvs−1
2
v3s−1 2 +ℓ
) dengan panjang genap yaitus+ℓ.
Karena ℓ(Wvs−1 2
v3s−1 2 +ℓ
) adalah genap, maka terdapat suatu titik vw di G
se-hingga terdapat jalan Wvs−1 2
vw dan jalan Wv3s−1 2 +ℓ
vw dengan panjang (s + ℓ)/2. Karena jalan (b) dan jalan (c) merupakan jalan terpendek dengan panjang genap, sehingga menurut definisi scrambling index lokal, yaitu:
ku,v(G) = min
20
Maka dapat diperoleh kvs−1 2
,v3s−1 2 +ℓ
(G) = (s+ℓ)/2. Oleh definisi scrambling index dimana k(G) merupakan nilai maksimum dari nilai scrambling index lokal untuk tiap dua titik yang berbeda di G, maka dapat diperolehk(G)≥ s+ℓ
2 .
Selanjutnya akan diperlihatkan bahwa untuk tiap dua titik yang berbeda vi dan vj di G, terdapat jalan Wvivj dengan panjang genap dimana ℓ(Wvivj) ≤ s +ℓ. Jika d(vi, vj) genap, maka lintasan tersebut dapat diperpanjang menjadi
jalan dengan panjang tepat s+ℓ. Sekarang diasumsikan d(vi, vj) ganjil. Terdapat
4 kasus, yaitu:
1. Kedua titikvi, vj dicycle C1 atauvi, vj dicycle C2. Andaikanvi danvj diC1, maka lintasan terpendek dengan panjang genap yang meghubungkan kedua titik tersebut adalah s−d(vi, vj)≤s−1< s+ℓ. Hal ini juga berlaku untuk
vi dan vj diC2.
2. Titik vi dicycle C1 dan vj di cycle C2. Andaikan Pv′ivj adalah lintasan yang menghubungkan vi dan vj dengan panjang genap, terdiri dari lintasanPv′ivs, lintasan P, dan lintasanPvs+ℓ,vj dengan panjangℓ(P
Dengan memperhatikan lintasanP′
vivj danP Oleh karenas+ℓadalah genap, maka terdapat tiga kasus yaituℓ(P′
vivj) = s+ℓ
21
Dengan memperhatikan jalanW′
vivj danW
cycle C1. Andaikan Wvivj adalah jalan terpendek yang menghubungkan vi dan vj dengan panjang genap terdiri dari lintasan Pv′ivs dan lintasan Pvsvj. Sehingga diperoleh ℓ(Wvivj) = s−d(vi, vj) +ℓ≤s+ℓ.
Untuk setiap pasangan titik vi dan vj yang berbeda di G, telah dibuktikan
bahwa terdapat jalan Wvivj dengan panjang ℓ(Wvivj) ≤ s+ℓ. Oleh proposisi 2.3,
diperoleh k(G)≤ s+ℓ
2 . Jadi, dapat disimpulkan bahwak(G) = s+ℓ
2 .
Lemma 4.2 Andaikan s adalah bilangan bulat positif ganjil dan G adalah graf
(s, ℓ)-barbel. Jika ℓ adalah bilangan bulat positif genap, maka k(G) = s+ℓ−1
2 .
Bukti. Pembuktian pada bagian ini mengggunakan cara yang sama seperti pada
Lemma 4.1. Dengan memperhatikan titik vs−1
2 dan v
seperti pada Lemma 4.1. Oleh karena ℓ merupakan bilan-gan bulat positif genap, maka jalan (a) dan (d) merupakan jalan denbilan-gan panjang genap. Sedangkan jalan (b) dan (c) merupakan jalan dengan panjang ganjil. Den-gan memilih jalan terpendek Wvs−1
2
v3s−1 2 +ℓ
yaitu jalan (a), maka diperoleh:
ℓ(Wvs−1
) adalah genap, maka terdapat sebuah titik vw sehingga
ter-dapat sebuah jalan Wvs−1 2
vw dan jalan Wv3s−1 2 +ℓ
vw dengan panjang (s+ℓ−1)/2. Dengan cara yang sama seperti pada Lemma 4.1 dapat diperoleh:
22
Sehingga, oleh definisi scrambling index diperoleh k(G)≥ s+ℓ−1
2 .
Selanjutnya akan memperlihatkan bahwa untuk tiap dua titik yang berbeda vi dan vj di G, terdapat jalan Wvivj dengan panjang genap dimana ℓ(Wvivj) ≤ s+ℓ−1. Jika d(vi, vj) genap, maka lintasan tersebut dapat diperpanjang menjadi
jalan dengan panjang tepat s +ℓ −1. Sekarang kita asumsikan d(vi, vj) ganjil.
Terdapat 4 kasus, yaitu :
1. Kedua titik vi, vj di C1 atau vi, vj di C2. Andaikan vi, vj di C1, maka lin-tasan terpendek dengan panjang genap yang meghubungkan dua titik tersebut adalah s−d(vi, vj)≤s−1< s+ℓ−1.
vivj adalah lintasan yang menghubungkan vi dan vj dengan pan-jang genap, terdiri dari lintasanPvivs, lintasanP, dan lintasanP
′
vs+pvj dengan panjang ℓ(P′′
vivj) = d(vi, vs) +ℓ+s−d(vs+ℓ, vj).
Dengan memperhatikan lintasanP′
vivj danP
vivj) adalah genap, maka terdapat empat kasus yaitu ℓ(P
′ lintasan Pvsvj. Selain itu, andaikan jalan W
′′
vivj adalah jalan dengan pan-jang genap yang menghubungkan titik vi dan vj, terdiri dari lintasanPvivs+ℓ,
Dengan memperhatikan jalanW′
vivjdanW
′′
vivj, dapat diperolehℓ(W
′
23
ℓ(W′′
vivj) = d(vi, vs) + s+ d(vs, vi) + d(vi, vj) + d(vi, vj) +d(vj, vs+ℓ) +s + d(vs+ℓ, vj) = 2s+ 2ℓ. Oleh karenas+ℓganjil makas+ℓ−1 adalah genap,
se-hingga terdapat empat kasus yaituℓ(W′
vivj) = s+ℓ−1 danℓ(W
vivj adalah lintasan terpendek dengan panjang genap terdiri dari lintasan P′
vivs dan lintasan Pvsvj. Sehingga diperoleh ℓ(P
′
vivj) = s −d(vi, vj) +ℓ ≤ s−1 +ℓ.
Untuk setiap pasangan titik vi dan vj yang berbeda di G, telah
dibuk-tikan bahwa terdapat jalan Wvivj yang menghubungkan vi dan vj dengan panjang ℓ(Wvivj) ≤ s+ℓ−1. Oleh proposisi 2.3, diperoleh k(G) ≤
s+ℓ−1
2 . Jadi dapat disimpulkan bahwa k(G) = s+ℓ−1
2 .
4.2 Scrambling Index dari Graf Barbel Dua Lintasan
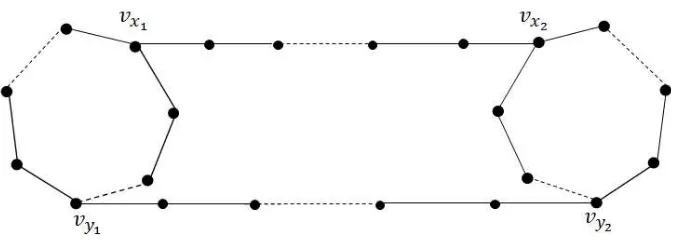
Andaikan terdapat dua cycle ganjil C1 yaitu cycle v1 ↔ v2 ↔ ... ↔ vs ↔ v1 dan C2 yaitu cycle vs+1 ↔ vs+2 ↔ ... ↔ v2s ↔ vs+1 yang saling lepas dengan panjang tiap cycle adalah s. Andaikan vx1, vy1 ∈ C1 dan vx2, vy2 ∈ C2 sehingga d(vx1, vy1) = d(vx2, vy2) dengan 1≤ d(vx1, vy1)≤
s−1
2 . Andaikan lintasanP1 adalah sebuah lintasan yang menghubungkanvx1 denganvx2 dan lintasanP2adalah sebuah lintasan yang menghubungkanvy1 denganvy2 dengan panjang tiap lintasan adalahℓ. Sebuah grafGterdiri dari duacycleganjil saling lepasC1danC2yang dihubungkan oleh dua lintasanP1danP2seperti ditunjukkan pada Gambar 4.2 disebut graf (s, ℓ)-barbel dua lintasan.
Asumsikan Pvx1vy1 adalah lintasan terpendek yang menghubungkan titik vx1 dan vy1 sedangkan P
′
vx1vy1 adalah lintasan yang menghubungkan titik vi dan vs dengan panjang s−d(vx1, vy1). Selain itu, asumsikan Pvx2vy2 adalah lintasan ter-pendek yang menghubungkan titik vx2 dan vy2 dan P
′
24
Gambar 4.2. Graf (s, ℓ)-Barbel Dua Lintasan
Lemma 4.3Andaikansadalah bilangan bulat positif ganjil danGadalah graf(s, ℓ)
-barbel dua lintasan. Jika ℓ adalah bilangan bulat positif ganjil, maka k(G) = s+ℓ 2 .
Bukti. Andaikanvadanvbadalah dua titik tengah di lintasanP1dimanad(va, vb) =
1 dan d(va, vx1) = d(vb, vx2) =
ℓ−1
2 . Dengan memperhatikan titik va dan vb, diper-oleh jalan terpendek yang menghubungkan va dan vb adalah 1. Untuk mencari
scrambling index lokal dari dua titik tersebut, perlu ditemukan sebuah jalan den-gan panjang genap yang menghubungkan kedua titik tersebut. Untuk memperoleh jalan dengan panjang genap, maka jalan yang menghubungkan kedua titik terse-but harus melewati satu cycle dengan panjang ganjil. Sehingga terdapat dua jalan Wvavb terpendek sebagai berikut:
a. Jalan Wvavb dengan panjang genap yang melewati C1. Terdiri dari lintasan Pvavx1,cycle C1, dan lintasan Pvx1vb. Sehingga diperoleh:
ℓ(Wvavb) = d(va, vx1) +s+d(vx1, va) +d(vva, vb)
= ℓ−1 2 +s+
ℓ−1 2 + 1 =s+ℓ.
b. Jalan Wvavb dengan panjang genap yang melewati C2. Terdiri dari lintasan Pvavx2,cycle C2, dan lintasan Pvx2vb. Sehingga diperoleh:
ℓ(Wvavb) =d(va, vb) +d(vb, vx2) +s+d(vx2, vb)
= 1 + ℓ−1 2 +s+
25
Dengan memilih jalan (a) maupun (b) dengan panjang genap, maka diperoleh suatu titikvw sehingga terdapat sebuah jalanWvavw dan jalanWvbvw dengan panjang
s+ℓ
2 . Dengan cara yang sama seperti pada Lemma 4.1, maka diperolehk(G)≥ s+ℓ
2 .
Selanjutnya akan diperlihatkan bahwa untuk tiap dua titik yang berbeda di G, terdapat jalan Wvivj dengan panjang genap dimana ℓ(Wvivj) ≤ s+ℓ. Untuk tiap dua titik vi dan vj di G, jika d(vi, vj) genap, maka lintasan tersebut dapat
diperpanjang menjadi jalan dengan panjang tepat s +ℓ. Sekarang diasumsikan d(vi, vj) ganjil. Terdapat 5 kasus, yaitu :
Untuk kasus pertama, kedua, ketiga dan keempat telah dibuktikan pada Lemma 4.1. Sekarang akan dibuktikan kasus kelima yaitu untuk titik vi berada
di lintasan P1 dan titik vj berada di lintasan P2. Asumsikan lintasanPv′ivj adalah lintasan yang terdiri dari lintasanPvivx1, lintasanP
′
Dengan memperhatikan lintasan P′
vivj dan P
vivj adalah genap, maka terdapat empat kemungkinan yaitu ℓ(P′
Untuk setiap pasangan titik vi dan vj yang berbeda di G, telah
26
ℓ(Wvivj) ≤ s+ℓ. Oleh proposisi 2.3, diperoleh k(G) ≤ s+ℓ
2 . Jadi dapat disim-pulkan bahwa k(G) = s+ℓ
2 .
Lemma 4.4 Andaikan s adalah bilangan bulat positif ganjil dan G adalah graf
(s, ℓ)-barbel dua lintasan. Jika ℓ adalah bilangan bulat positif genap, maka k(G) = s+ℓ−1
2 .
Bukti. Andaikan vb adalah titik tengah di lintasan P1 dengan dan d(vb, vx1) =
ℓ
2. Andaikan terdapat sebuah titik va dimana d(va, vb) = 1 dan d(va, vx1)< d(vb, vx1). Dengan kata lain, d(vx1, va) =d(vx1, vb)−d(va, vb). Dengan memperhatikan titikva dan vb, diperoleh jalan terpendek yang menghubungkan titikva dan titik vb adalah
1. Dengan menggunakan cara yang sama pada Lemma 4.3, maka diperoleh :
a. Jalan Wvavb dengan panjang genap yang melewati C1. Terdiri dari lintasan Pvavx1,cycle C1, dan lintasan Pvx1vb. Sehingga diperoleh:
ℓ(Wvavb) = d(va, vx1) +s+d(vx1, va) +d(vva, vb)
= ℓ
2 −1 +s+ ℓ
2 −1 + 1 =s+ℓ−1.
b. Jalan Wvavb dengan panjang genap yang melewati C2. Terdiri dari lintasan Pvavx2,cycle C2, dan lintasan Pvx2vb. Sehingga diperoleh:
ℓ(Wvavb) =d(va, vb) +d(vb, vx2) +s+d(vx2, vb)
= 1 + ℓ
2 +s+ ℓ 2 =s+ℓ+ 1.
Karena ℓ merupakan bilangan bulat, maka jalan (a) maupun (b) merupakan jalan Wvavb dengan panjang genap. Dengan memilih jalan (a) yaitu jalanWvavbterpendek dengan panjang genap, maka diperoleh suatu titik vw sehingga terdapat sebuah
jalanWvavw dan jalanWvbvw dengan panjang
s+ℓ−1
2 . Dengan cara yang sama seperti pada Lemma 4.1, maka diperoleh k(G)≥ s+ℓ−1
27
Selanjutnya akan diperlihatkan bahwa untuk tiap dua titik yang berbeda di G, terdapat jalanWvivj dengan panjang genap dimana ℓ(Wvivj)≤s+ℓ−1. Untuk tiap dua titik vi dan vj di G, jika d(vi, vj) genap, maka lintasan tersebut dapat
diperpanjang menjadi jalan dengan panjang tepat s+ℓ−1. Sekarang diasumsikan d(vi, vj) ganjil. Terdapat 5 kasus, yaitu :
Untuk kasus pertama, kedua, ketiga dan keempat telah dibuktikan pada Lemma 4.2. Sekarang akan dibuktikan kasus kelima yaitu untuk titik vi berada di lintasan
P1 dan titik vj berada di lintasan P2. Asumsikan lintasan Pv′ivj adalah lintasan yang terdiri dari lintasan Pvivx1, lintasan P
Dengan memperhatikan lintasan P′
vivj dan P
vivj adalah genap, maka terdapat tiga kemungkinan yaitu ℓ(P′
Untuk setiap pasangan titik vi dan vj yang berbeda di G, telah
dibuk-tikan bahwa terdapat jalan Wvivj yang menghubungkan vi dan vj dengan panjang ℓ(Wvivj)≤s+ℓ−1. Oleh proposisi 2.3, diperolehk(G)≤
s+ℓ−1
2 . Jadi dapat dis-impulkan bahwak(G) = s+ℓ−1
28
4.3 Scrambling Index dari Graf Prisma
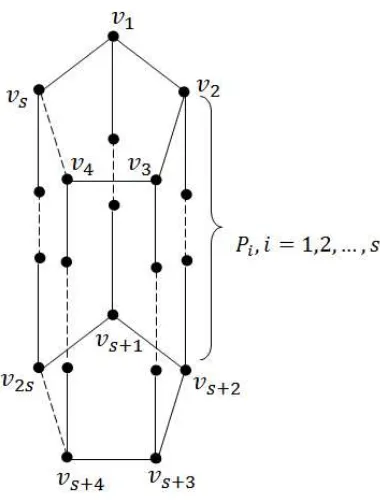
Andaikan terdapat dua cycle ganjil C1 yaitu cycle v1 ↔ v2 ↔ ... ↔ vs ↔ v1 dan C2 yaitu cycle vs+1 ↔ vs+2 ↔ ... ↔ v2s ↔ vs+1 yang saling lepas dengan panjang tiap cycle adalahs. Andaikan terdapat sebuah lintasan Pi dengan panjang ℓ yang
menghubungkan vi dan vs+i untuk tiapi= 1,2, ..s. Sebuah grafG terdiri atas dua
cycle ganjil saling lepas C1 dan C2 yang dihubungkan oleh lintasan P1, P2, ..., Ps
seperti pada Gambar 4.3 disebut graf (s, ℓ)-prisma.
Gambar 4.3. Graf (s, ℓ)-Prisma
Teorema 4.5 Andaikan s adalah bilangan bulat positif ganjil. Jika G adalah graf
(s, ℓ)-prisma, maka k(G) =ls+ℓ−1 2
m .
Bukti. Batas bawah dari grafGdapat diperoleh dengan mencari scrambling index
lokal dari dua titik diGdimana kedua titiknya berada di Pi dengani= 1,2,3, ..., s
seperti pada pembahasan di sub bab 4.2. Sehingga diperoleh k(G) ≥ s+ℓ
2 untuk ℓ adalah ganjil dan k(G)≥ s+ℓ−1
2 untuk ℓ adalah genap.
Selanjutnya akan diperlihatkan bahwa untuk tiap dua titik yang berbeda va
29
untuk ℓ adalah ganjil dan ℓ(Wvavb) ≤ s+ℓ −1 untuk ℓ adalah genap. Sekarang diasumsikan d(va, vb) ganjil. Terdapat 5 kasus, yaitu :
1. Kedua titikva dan vb berada diC1 atau C2.
2. Titik va berada di C1 dan titik vb berada diC2.
3. Kedua titikva dan vb berada diPi untuki= 1,2, ..., s.
4. Titik va berada di C1 atau C2 dan titik vb berada di Pi untuk i= 1,2, ..., s.
5. Titik va berada di Pi dan titik vb berada di Pj untuk 1≤i, j ≤s.
Untuk kasus pertama, kedua, ketiga dan keempat telah dibuktikan pada sub bab 4.1 bahwa terdapat jalanWvavb dengan panjang genap dimanaℓ(Wvavb)≤s+ℓ untuk ℓ adalah ganjil dan ℓ(Wvavb) ≤ s+ ℓ− 1 untuk ℓ adalah genap. Sedan-gkan untuk kasus kelima telah dibuktikan pada sub bab 4.2 bahwa terdapat jalan Wvavb dengan panjang genap dimana ℓ(Wvavb) ≤ s+ℓ untuk ℓ adalah ganjil dan ℓ(Wvavb)≤ s+ℓ−1 untuk ℓ adalah genap. Sehingga oleh proposisi 2.3 diperoleh k(G) ≤ s+ℓ
2 untuk ℓ adalah ganjil dan k(G) ≤
s+ℓ−1
2 untuk ℓ adalah genap. Jadi dapat disimpulkan bahwa k(G) =ls+ℓ−1
2 m
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Penelitian ini membahas mengenai scrambling index dari garf primitif terdiri atas dua cycleganjil saling lepas dengan panjang tiap cycle adalahsyang dihubungkan oleh beberapa lintasan dengan panjang tiap lintasan adalahℓ. Hasil yang diperoleh adalah sebagai berikut :
1. Jika G adalah graf (s, ℓ)-barbel, maka scrambling index dari graf Gadalah
k(G) = ls+ℓ−1 2
m
, s≥3.
2. JikaGadalah graf (s, ℓ)-barbel dua lintasan, maka scrambling index dari graf G adalah
k(G) = ls+ℓ−1 2
m
, s≥3.
3. Jika G adalah graf (s, ℓ)-prisma, maka scrambling index dari graf G adalah
k(G) = ls+ℓ−1 2
m
, s≥3.
Dari hasil yang diperoleh, dapat disimpulkan bahwa untuk 3 jenis graf yang berbeda yaitu graf (s, ℓ)-barbel, (s, ℓ)-barbel dua lintasan dan (s, ℓ)-prisma
memi-liki nilai scrambling index yang sama yaitu ls+ℓ−1 2
m
dengans ≥3.
5.2 Saran
DAFTAR PUSTAKA
Akelbek, M and Kirkland, S. 2009. Coefficients of Ergodicity and The Scrambling Index. Linear Algebra and its Applications, Volume 430, Issue 4, 1111-1130.
Bona, Miklos. 2006. A Walk Through Combinatorics Second Edition. World Scientific, Singapore.
Brualdi, R. A and Ryser, H.J. 1991. Combinatorial Matrix Theory. Cambridge University Press,Cambridge.
Chen, S and Liu, B. 2010. The Scrambling Index of Symmetric Primitive Ma-trices. Linear Algebra and its Applications, Volume 433, Issue 6, 1110-1126.
Izzati, N. 2014. Scrambling Index dari Graf primitif terdiri atas Dua Lingkaran. [Skripsi]. Medan: Universitas Sumatera Utara.
Liu, Bolian., McKay, B.D., Wormald, N.C, Min, Z.K. 1990. The Exponent Set of Symetric Primitive (0,1) Matrices with Zero Trace. Linear Algebra and its Applications, Volume 133, 121-131
Lampiran 1. Program Mencari Nilai Scrambling Index dari Graf Barbel dengan Menggunakan MATLAB
1 function [hasil]=barbel(cycle,lintasan) 2 order=2*cycle+lintasan-1;
3 matriks=zeros(order); 4 for i=1:cycle-1
5 matriks(i,i+1)=1;
6 end
7 matriks(cycle,1)=1;
8 for i=cycle:cycle+lintasan-1
9 matriks(i,i+1)=1;
10 end
11 for i=cycle+lintasan:order-1
12 matriks(i,i+1)=1;
13 end
14 matriks(cycle+lintasan,order)=1;
15 matriks_lengkap=matriks+transpose(matriks);
16 [baris,kolom]=size(matriks_lengkap); 17 vektor1=zeros(1,kolom);
18 for i=1:kolom
19 vektor1(i)=i;
20 end
21 nchoose2=nchoosek(baris,2);
22 comb=nchoosek(set,2); 23 vektor2=zeros(1,nchoose2); 24 B=eye(baris);
25 k=0;
26 while sum(vektor2) < nchoose2
27 B=B*matriks_lengkap;
28 for j=1:nchoose2
29 for k=1:kolom
30 if B(comb(j,1),k) * B(comb(j,2),k)>0
31 vektor2(j)=1;
32 break;
33 end
34 end
35 end
36 k=k+1;
37 end
Lampiran 2. Nilai Scrambling Index yang Diperoleh dengan Program
a. Graf Barbel
PanjangCycle Panjang Lintasan Scrambling Index
3 4 3
5 3 4
5 4 4
7 5 6
7 6 6
9 7 8
9 8 8
11 9 10
11 10 10
b. Graf Barbel Dua Lintasan
PanjangCycle Panjang Lintasan Scrambling Index
3 2 2
3 3 3
5 3 4
7 3 5
7 8 7
9 10 9
9 15 12
13 4 8
15 10 12
c. Graf Prisma
PanjangCycle Panjang Lintasan Scrambling Index
3 3 3
5 2 3
7 4 5
11 3 7
15 6 10
17 10 13
19 11 15
21 6 13