GRAF PRIMITIF
Pada bagian ini akan dijelaskan mengenai definisi graf, istilah-istilah dalam graf, matriks ketetanggaan, graf terhubung, primitivitas graf, dan scrambling index.
2.1 Definisi Graf
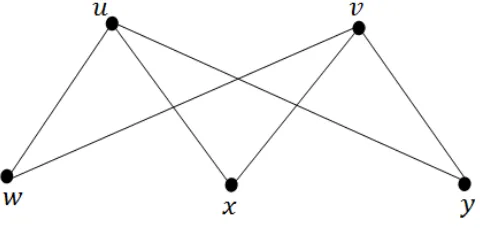
Sebuah graf G terdiri atas suatu himpunanan tak kosong dan berhingga V(G) yang anggotanya disebut titik (vertex) dan sebuah himpunan berhinggaE(G) yang anggotanya disebut sisi (edge) dimana sisi tersebut merupakan pasangan tak beru-rut dari titik-titik pada V(G). Sebuah sisi{v, w} adalah sisi yang menghubungkan titik v dan titik w, yang biasanya disingkat menjadi vw. Sebagai contoh, Gambar 2.1 merepresentasikan graf G dengan himpunan titik V(G) = {u, v, w, x, y} dan himpunan sisi E(G) yang terdiri dari sisi uw, ux, vx, vy, uy dan vw.
Gambar 2.1. Contoh Graf
2.2 Istilah-istilah dalam Graf
Andaikan terdapat sebuah graf G, berikut akan dijelaskan beberapa istilah dan notasi dalam graf yang digunakan dalam penjelasan selanjutnya.
... ↔ vm dimana v0 merupakan titik awal dan vm merupakan titik akhir. Sebuah jalan yang menghubungkanvi danvj dinotasikan denganWvivj. Pada Gambar 2.1, w↔v ↔y↔v ↔x adalah sebuah jalan Wwx.
b. Panjang. Panjang dari sebuah jalan Wvivj adalah banyaknya sisi di jalan Wvivj dan dinotasikan dengan ℓ(Wvivj). Pada Gambar 2.1, w ↔ u ↔y ↔v adalah sebuah jalan Wwv dengan panjang 3, atau dapat dinotasikan dengan ℓ(Wwv) = 4.
c. Lintasan. Lintasan merupakan sebuah jalan dengan titik yang berbeda ke-cuali jika titik awal juga merupakan titik akhir (v0 = vm). Lintasan yang menghubungkan vi dan vj dinotasikan dengan Pvivj. Pada Gambar 2.1, u ↔ x ↔ v ↔ y adalah sebuah lintasan Puy dengan panjang 3 atau dapat dino-tasikan dengan ℓ(Puy) = 3.
d. Cycle. Cycle merupakan sebuah lintasan yang berawal dan berakhir pada titik yang sama. Pada Gambar 2.1, lintasan u ↔ y ↔ v ↔ w ↔ u adalah sebuah cycle dengan panjang 4. Sebuah cycle dengan panjang ganjil disebut cycle ganjil dan sebuah cycle dengan panjang genap disebut cycle genap.
e. Distance. Panjang dari jalan terpendek yang menghubungkan u dan v di G disebut distance dinotasikan dengan d(u, v). Pada Gambar 2.1, diperoleh d(w, y) = 2.
2.3 Matriks Ketetanggaan
Matriks ketetanggaan (adjacency matrix) dari sebuah grafGatasntitikv1, v2, ..., vn adalah sebuah matriks bujur angkar A = (aij) dengan ordo n yang setiap entrinya didefinisikan sebagai:
aij =
1,bila {vi, vj} ∈E(G)
0,bila {vi, vj}∈/E(G).
pada Gambar 2.1 dapat direpresentasikan menjadi matriks ketetanggaanA sebagai
Sebuah matriks A dikatakan matriks non negatif jika semua entri (aij) ≥ 0. Sedangkan sebuah matriks A dikatakan matriks positif jika semua entri (aij) ≥ 1. Perhatikan contoh berikut:
MatriksX merupakan matriks tak negatif karena semua entri (xij)≥0. Sedangkan matriks Y merupakan matriks positif karena semua entri (yij)≥1.
Teorema 2.1 (Bona, 2006) Andaikan G adalah sebuah graf dan A= (aij) adalah sebuah matriks ketetanggaan dari G. Misalkan ak
ij adalah entri (i, j) dari matriks Ak. Maka ak
ij menyatakan banyaknya jalan dengan panjang k yang menghubungkan titik i dengan titik j.
Bukti. Kita buktikan dengan menggunakan induksi atas k. Bila k = 1 entri a(1)ij = aij dari A yang menyatakan banyaknya jalan dengan panjang satu yang menghubungkan titik i dengan titik j. Asumsikan bahwa entri a(k)ij dari Ak meny-atakan banyaknya jalan dengan panjangkyang menghubungkan titikidengan titik j. Karena Ak+1 =AkA, maka
penjumlahana(k+1)iℓ adalah banyaknya jalan dengan panjangk+ 1 yang menghubu-ngkan titik i dengan titik j.
2.4 Graf Terhubung
Sebuah graf G dikatakan terhubung (connected graph) jika untuk setiap titik u dan v diG dihubungkan oleh sebuah jalan denganu dan v merupakan titik ujung. Sebaliknya, graf tidak terhubung (disconnected graph) merupakan graf terdapat sembarang titik yang tidak terhubung ke titik lainnya di G. Dengan kata lain, tidak terdapat yang jalan menghubungkan titik tersebut ke titik yang lain di G.
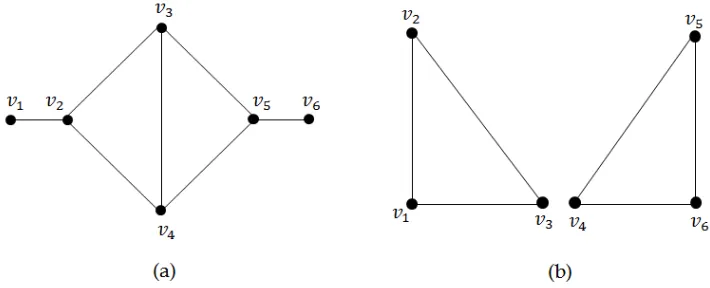
Gambar 2.2. (a) Graf Terhubung dan (b) Graf tidak Terhubung
Graf pada Gambar 2.2(a) merupakan graf terhubung, karena untuk tiap titik terdapat jalan yang menghubungkan antara satu titik ke titik lainnya. Sedangkan graf pada Gambar 2.2(b) merupakan graf tidak terhubung, karena tidak terdapat jalan yang menghubungkan satu titik dengan titik lainnya seperti v3 kev4,v2 kev3 dan lainnya.
Teorema 2.2 (Bona, 2006) Andaikan G adalah sebuah graf atas n titik dengan matriks ketetanggaan A. Graf G adalah terhubung jika dan hanya jika matriks A+A2+...+An−1 mempunyai entri yang semuanya positif.
titik j. Sebuah lintasan diG tidak terdapat titik berulang kecuali i=j, bila i6=j terdapat lintasan dengan panjang kurang dari n yang menghubungkani denganj. Hal ini berarti untuk setiap pasangan titik i dan j yang berbeda, terdapat sebuah bilangan bulat positif k dengan 1 ≤ k ≤ n −1 sehingga entri ak
ij > 0. Sehingga semua entri di luar entri diagonal dari matriks B adalah positif. Bila i=j, maka terdaoat sebuahcycledengan panjang 2 yang memuat titiki, sehingga entria(2)ij >0 untuk semua i = 1,2, ..., n. Jadi entri diagonal dari matriks B adalah positif. Sekarang dapat disimpulkan bahwa semua entri dari matriksB =A+A2+...+An−1
adalah positif.
Sekarang andaikan setiap entri dari matriksA+A2+...+An−1 adalah positif. Akibatnya untuk setiap pasangan titik i dan j terdapat sebuah bilangan positif k dengan 1≤k ≤n−1 sehinggaak
ij >0. Hal ini berarti untuk setiap pasangan titik i dan j di G terdapat sebuah jalan dengan panjang k yang menghubungkan i dan j. Sehingga oleh definisiG adalah sebuah graf terhubung.
2.5 Primitivitas Graf
Graf primitif merupakan graf terhubung dimana terdapat bilangan bulat positif k sehingga untuk setiap pasangan titik u dan v terdapat sebuah jalan Wuv dengan panjangk. Sebuah grafGdikatakan primitif jikaGmerupakan graf terhubung dan terdapat paling sedikit satu cycleganjil (Liu et al., 1990).
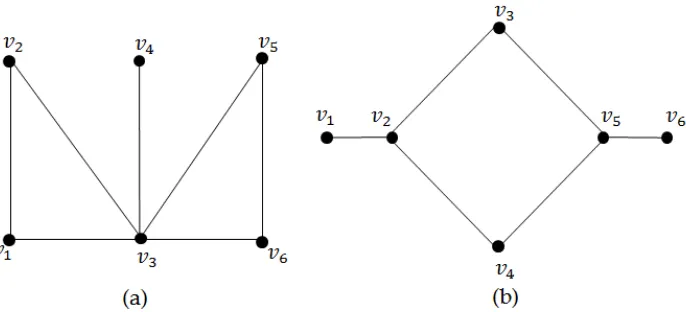
Graf pada Gambar 2.3(a) merupakan graf primitif, karena terdapat cycle dengan panjang ganjil. Sedangkan graf pada Gambar 2.3(b) bukan merupakan graf primitif, karena tidak terdapat cycle dengan panjang ganjil.
Sebuah grafGdapat direpresentasikan menjadi sebuah matriks ketetanggaan A. Sebuah matriks persegi non negatif A dikatakan primitif jika terdapat bilangan bulat k sedemikian hingga semua entri di Ak bernilai positif (Brualdi dan Ryser, 1991).
Graf pada Gambar 2.3(a) dapat direpresentasikan menjadi matriks persegi non negatif A sebagai berikut:
A=
Untuk memperlihatkan bahwa matriks A merupakan matriks primitif, maka akan diperlihatkan terdapat bilangan bulat positif terkecil k sehingga semua entri di Ak bernilai positif. Dengan kata lain, matriks Ak merupakan matriks positif. Perhatikan matriks A4 berikut :
A4 =
2.6 Scrambling Index
Scrambling index dari graf primitif G dinotasikan dengan k(G) adalah bilangan bulat positif terkecil k sehingga untuk setiap pasangan titik yang berbedau danv, terdapat sebuah titik w sehingga terdapat jalan dari titik u dan titik v ke titik w dengan panjang k atau dengan kata lain terdapat Wuw dan Wvw dengan panjang k (Alkebek dan Kirkland 2009a, 2009b).
Untuk setiap u, v ∈V(G) dan u6=v, scrambling index lokal dari titik u dan v di G didefinisikan sebagai berikut:
ku,v(G) = min
w∈V(G){k: terdapat Wuw dan Wvw dengan panjang k}.
Jika scrambling index lokal dari titik u dan v di G adalah ku,v(G), maka untuk setiap k′
≥ ku,v(G), terdapat titik w′
sehingga terdapat Wuw′ dan Wvw′
dengan panjang k′. Sehingga scrambling index dari graf G didefinisikan sebagai
berikut:
k(G) = max
u,v∈V(G){ku,v(G)}.
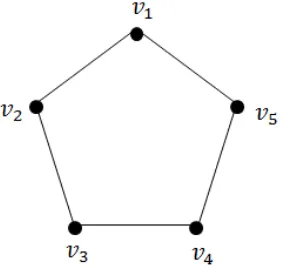
Contoh 2.1AndaikanGadalah graf yang terdiri dari sebuahcycledengan panjang 5 seperti pada Gambar 2.4.
Gambar 2.4. Graf yang Terdiri Atas Sebuah Cycle dengan Panjang 5
kv1,v2(G) = min{kv1,v2(v1), kv1,v2(v2), kv1,v2(v3), kv1,v2(v4), kv1,v2(v5)}
= min{4,4,3,2,3}= 2
kv1,v3(G) = min{kv1,v3(v1), kv1,v3(v2), kv1,v3(v3), kv1,v3(v4), kv1,v3(v5)}
= min{2,1,2,3,3}= 1
kv1,v4(G) = min{kv1,v4(v1), kv1,v4(v2), kv1,v4(v3), kv1,v4(v4), kv1,v4(v5)}
= min{2,3,3,2,1}= 1
kv1,v5(G) = min{kv1,v5(v1), kv1,v5(v2), kv1,v5(v3), kv1,v5(v4), kv1,v5(v5)}
= min{4,3,2,3,4}= 2
kv2,v3(G) = min{kv2,v3(v1), kv2,v3(v2), kv2,v3(v3), kv2,v3(v4), kv2,v3(v5)}
= min{3,4,4,3,2}= 2
kv2,v4(G) = min{kv2,v4(v1), kv2,v4(v2), kv2,v4(v3), kv2,v4(v4), kv2,v4(v5)}
= min{3,2,1,2,3}= 1
kv2,v5(G) = min{kv2,v5(v1), kv2,v5(v2), kv2,v5(v3), kv2,v5(v4), kv2,v5(v5)}
= min{1,2,3,3,2}= 1
kv3,v4(G) = min{kv3,v4(v1), kv3,v4(v2), kv3,v4(v3), kv3,v4(v4), kv3,v4(v5)}
= min{2,3,4,4,3}= 2
kv3,v5(G) = min{kv3,v5(v1), kv3,v5(v2), kv3,v5(v3), kv3,v5(v4), kv3,v5(v5)}
= min{3,3,2,1,2}= 1
kv3,v5(G) = min{kv4,v5(v1), kv4,v5(v2), kv4,v5(v3), kv4,v5(v4), kv4,v5(v5)}
= min{3,2,3,4,4}= 2
Setelah memperoleh scrambling index lokal untuk tiap dua titik yang berbeda di graf G, selanjutnya adalah menentukan scrambling index untuk graf G.
k(G) = max
vi,vj∈V(G){kvi,vj(G)}= max{2,1,1,2,2,1,1,2,1,2}= 2.
M =
Untuk k = 1, pada baris pertama dan kedua di Mk = M tidak terdapat bilangan positif pada kolom yang sama. Sehingga, perlu dicari bilangan bulat positif k >1, sehingga untuk setiap dua baris di Mk terdapat sedikitnya satu entri positif pada posisi kolom yang sama. Perhatikan matriks M2 berikut:
M2 =
• Pada baris pertama dan baris kedua, terdapat entri positif pada kolom yang sama yaitu kolom keempat.
• Pada baris pertama dan baris ketiga, terdapat entri positif pada kolom yang sama yaitu kolom pertama dan ketiga.
• Pada baris pertama dan baris keempat, terdapat entri positif pada kolom yang sama yaitu kolom pertama dan keempat.
• Pada baris pertama dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom ketiga.
• Pada baris kedua dan baris ketiga, terdapat entri positif pada kolom yang sama yaitu kolom kelima.
• Pada baris kedua dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom kedua dan kelima.
• Pada baris ketiga dan baris keempat, terdapat entri positif pada kolom yang sama yaitu kolom pertama.
• Pada baris ketiga dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom ketiga dan kelima.
• Pada baris keempat dan baris kelima, terdapat entri positif pada kolom yang sama yaitu kolom kedua.
Oleh karena 2 merupakan bilangan bulat positif terkecil sehingga setiap dua baris diM2 terdapat elemen positif pada posisi kolom yang sama, maka scrambling index dari matriks M adalah 2.
Proposisi 2.3 Andaikan G adalah sebuah graf dan k′
adalah bilangan bulat genap
positif. Jika untuk tiap pasangan titik yang berbeda u dan v di G, terdapat sebuah jalan dengan panjang genap Wuv≤k′, maka k(G)≤k′/2.
Bukti. Andaikan u dan v adalah dua titik yang berbeda di G dan andaikan Wuv adalah jalan dengan panjang genap u = v0 ↔ v1 ↔ v2 ↔ ... ↔ v2m−1 ↔ v2m =v untuk beberapa bilangan bulat positifmdengan panjangℓ(Wuv)≤k′
. AndaikanC2 adalahcycle v2m ↔v2m−1 ↔v2m dengan panjang 2. Maka jalanWuv′ yang berawal di u, bergerak ke v sepanjang jalan Wuv dan bergerak k′
−ℓ(Wuv) kali disekitar C2 adalah sebuah sebuah Wuv dengan panjang k′. Karena k′ adalah genap, maka terdapat sebuah titikwsehingga terdapat sebuah jalanWuw dengan panjang k′
2 dan terdapat sebuah jalan Wvw dengan panjang k′
2. Sehinggak(G)≤ k′