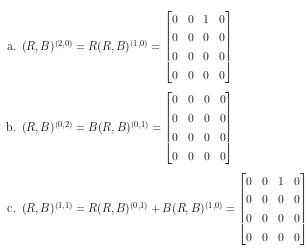EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG BERSINGGUNGAN
SKRIPSI
TAUFIK ZUHRI 050803037
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG BERSINGGUNGAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
TAUFIK ZUHRI 050803037
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2011
i
PERSETUJUAN
Judul : EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG BERSINGGUNGAN
Kategori : SKRIPSI
Nama : TAUFIK ZUHRI Nomor Induk Mahasiswa : 050803037
Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, Mei 2011
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Pangeran Sianipar, M.S. Dr. Saib Suwilo, M.Sc. NIP. 19470208 197403 1 001 NIP. 19640109 198803 1 004
Diketahui oleh
Departemen Matematika FMIPA USU Ketua,
ii
PERNYATAAN
EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG SALING BERSINGGUNGAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Mei 2011
TAUFIK ZUHRI 050803037
iii
PENGHARGAAN
Dengan puji dan syukur kepada Allah SWT, karena berkat dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul” EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG SALING BERSINGGUNGAN”ini dengan baik.
Dalam menyelesaikan skripsi ini penulis banyak sekali menerima bantuan dan masukan dari berbagai pihak. Pada kesempatan ini penulis mengucapkan terima kasih sebesar-besarnya kepada:
1. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I, Drs. Pangeran Sianipar, M.S selaku dosen pembimbing II, Dra. Mardiningsih, M.Si dan Drs. Ujian Sinulingga, M.Si yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini. 2. Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu
Pengetahuan Alam, Universitas Sumatera Utara.
3. Bapak Prof. Dr. Tulus, M.Si. dan Dra. Mardiningsih, M.Si., selaku Ketua dan Sekretraris Departemen Matematika di FMIPA USU Medan.
4. Seluruh Staf Pengajar Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.
5. Ayahanda Gusron Ainuddin Hasibuan dan Ibunda Meriati Lubis tercinta, abanganda Ardinal Sakti serta adik-adikku Faisal Hamdi, Kholyda Hafni, Zulfadli, dan Indra Gusti yang selalu memberikan dukungan moril dan ma-teriel maupun doa yang tiada hentinya kepada penulis.
Tidak lupa kiranya penulis juga mengucapkan terima kasih kepada Astri Syafrianti, Firdaus Safran, Kiki Winarti, Fitri, bang Deni Ramadani, bang Ramidin, bang Darto Siregar, M. Haikal Lubis, Novi Yuanda Lubis, Ibnu Haris Lubis (Loebsy Community), Aghni Syahmarani yang telah menjadi sahabat dekat penulis selama menimbah ilmu di USU. Kepada guru-guru dan kawan-kawan sewaktu duduk di bangku SD, SMP, dan SMA, juga tidak lupa kiranya penulis mengucapkan terima kasih atas didikan dan persahabatan selama ini.
Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta saran dan kritik yang membangun dari pembaca sekalian.
iv
ABSTRAK
Andaikan D(2) adalah suatu digraph dwi-warna yang primitif atas n = 2m−2, m ≥ 3 verteks dengan dua buah cycle yang saling bersinggungan di satu verteks dengan panjang cycle masing-masing adalah m dan m − 1. Tulisan ini akan memperlihatkan pola eksponen verteks dari digraph dwi-warna D(2), sehingga
expD(2)(vk) = 12(n2−2) +⌊k2⌋.
v
VERTEX EXPONENT OF TWO-COLORED DIGRAPHS WITH TWO CYCLES WHOSE HAVE A COMMON VERTEX
ABSTRACT
Let D(2) be a primitive two-colored digraph on n= 2m−2, m ≥3 vertices whose two cycles which has a common vertex and the lenght of each cycle is m and m−1. This paper will give the formula of vertex exponent of 2-digraph D(2) such
vi
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR vii
BAB
1. PENDAHULUAN 1
1.1. Latar Belakang Penelitian 1
1.2. Perumusan Masalah 2
1.3. Tinjauan Pustaka 2
1.4. Tujuan Penelitian 6
1.5. Manfaat Penelitian 6
1.6. Metodologi Penelitian 6
2. LANDASAN TEORI 8
2.1. Digraph 8
2.2. Digraph Dwi-Warna 18
3. EKSPONEN VERTEKS 2-DIGRAPH DENGAN DUA CYCLE
YANG BERSINGGUNGAN 33
4. KESIMPULAN DAN RISET LANJUTAN 36
4.1. Kesimpulan 36
4.2. Riset Lanjutan 37
DAFTAR PUSTAKA 38
vii
DAFTAR GAMBAR
Gambar Halaman
2.1 Digraph dengan 6 verteks dan 8 arc 9
2.2 Digraph dengan 5 verteks dan 7 arc 10 2.3 (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat 11
2.4 Digraph primitif 11
2.5 Digraph dengan 4 verteks dan 5 arc 16
2.6 Sebuah 2-Digraph yang terdiri dari 5 verteks dan 7 arc 19
2.7 (a) 2-Digraph terhubung kuat (b) 2-Digraph tidak terhubung
kuat 21
2.8 Sebuah 2-Digraph yang terdiri dari 4 verteks dan 5 arc 23
iv
ABSTRAK
Andaikan D(2) adalah suatu digraph dwi-warna yang primitif atas n = 2m−2, m ≥ 3 verteks dengan dua buah cycle yang saling bersinggungan di satu verteks dengan panjang cycle masing-masing adalah m dan m − 1. Tulisan ini akan memperlihatkan pola eksponen verteks dari digraph dwi-warna D(2), sehingga
expD(2)(vk) = 12(n2−2) +⌊k2⌋.
v
VERTEX EXPONENT OF TWO-COLORED DIGRAPHS WITH TWO CYCLES WHOSE HAVE A COMMON VERTEX
ABSTRACT
Let D(2) be a primitive two-colored digraph on n= 2m−2, m ≥3 vertices whose two cycles which has a common vertex and the lenght of each cycle is m and m−1. This paper will give the formula of vertex exponent of 2-digraph D(2) such
EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG BERSINGGUNGAN
SKRIPSI
TAUFIK ZUHRI 050803037
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2011
EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG BERSINGGUNGAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
TAUFIK ZUHRI 050803037
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
i
PERSETUJUAN
Judul : EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG BERSINGGUNGAN
Kategori : SKRIPSI
Nama : TAUFIK ZUHRI Nomor Induk Mahasiswa : 050803037
Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, Mei 2011
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Pangeran Sianipar, M.S. Dr. Saib Suwilo, M.Sc. NIP. 19470208 197403 1 001 NIP. 19640109 198803 1 004
Diketahui oleh
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si NIP. 19620901 198803 1 002
ii
PERNYATAAN
EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG SALING BERSINGGUNGAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Mei 2011
iii
PENGHARGAAN
Dengan puji dan syukur kepada Allah SWT, karena berkat dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul” EKSPONEN VERTEKS DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG SALING BERSINGGUNGAN”ini dengan baik.
Dalam menyelesaikan skripsi ini penulis banyak sekali menerima bantuan dan masukan dari berbagai pihak. Pada kesempatan ini penulis mengucapkan terima kasih sebesar-besarnya kepada:
1. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I, Drs. Pangeran Sianipar, M.S selaku dosen pembimbing II, Dra. Mardiningsih, M.Si dan Drs. Ujian Sinulingga, M.Si yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini. 2. Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu
Pengetahuan Alam, Universitas Sumatera Utara.
3. Bapak Prof. Dr. Tulus, M.Si. dan Dra. Mardiningsih, M.Si., selaku Ketua dan Sekretraris Departemen Matematika di FMIPA USU Medan.
4. Seluruh Staf Pengajar Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.
5. Ayahanda Gusron Ainuddin Hasibuan dan Ibunda Meriati Lubis tercinta, abanganda Ardinal Sakti serta adik-adikku Faisal Hamdi, Kholyda Hafni, Zulfadli, dan Indra Gusti yang selalu memberikan dukungan moril dan ma-teriel maupun doa yang tiada hentinya kepada penulis.
Tidak lupa kiranya penulis juga mengucapkan terima kasih kepada Astri Syafrianti, Firdaus Safran, Kiki Winarti, Fitri, bang Deni Ramadani, bang Ramidin, bang Darto Siregar, M. Haikal Lubis, Novi Yuanda Lubis, Ibnu Haris Lubis (Loebsy Community), Aghni Syahmarani yang telah menjadi sahabat dekat penulis selama menimbah ilmu di USU. Kepada guru-guru dan kawan-kawan sewaktu duduk di bangku SD, SMP, dan SMA, juga tidak lupa kiranya penulis mengucapkan terima kasih atas didikan dan persahabatan selama ini.
Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta saran dan kritik yang membangun dari pembaca sekalian.
Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini berguna bagi yang membutuhkan.
Medan, Mei 2011 Penulis,
iv
ABSTRAK
Andaikan D(2) adalah suatu digraph dwi-warna yang primitif atas n = 2m−2, m ≥ 3 verteks dengan dua buah cycle yang saling bersinggungan di satu verteks dengan panjang cycle masing-masing adalah m dan m − 1. Tulisan ini akan memperlihatkan pola eksponen verteks dari digraph dwi-warna D(2), sehingga
v
VERTEX EXPONENT OF TWO-COLORED DIGRAPHS WITH TWO CYCLES WHOSE HAVE A COMMON VERTEX
ABSTRACT
Let D(2) be a primitive two-colored digraph on n= 2m−2, m ≥3 vertices whose two cycles which has a common vertex and the lenght of each cycle is m and m−1. This paper will give the formula of vertex exponent of 2-digraph D(2) such
thatexpD(2)(vk) = 12(n2−2) +⌊k2⌋.
vi
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR vii
BAB
1. PENDAHULUAN 1
1.1. Latar Belakang Penelitian 1
1.2. Perumusan Masalah 2
1.3. Tinjauan Pustaka 2
1.4. Tujuan Penelitian 6
1.5. Manfaat Penelitian 6
1.6. Metodologi Penelitian 6
2. LANDASAN TEORI 8
2.1. Digraph 8
2.2. Digraph Dwi-Warna 18
3. EKSPONEN VERTEKS 2-DIGRAPH DENGAN DUA CYCLE
YANG BERSINGGUNGAN 33
4. KESIMPULAN DAN RISET LANJUTAN 36
4.1. Kesimpulan 36
4.2. Riset Lanjutan 37
vii
DAFTAR GAMBAR
Gambar Halaman
2.1 Digraph dengan 6 verteks dan 8 arc 9
2.2 Digraph dengan 5 verteks dan 7 arc 10 2.3 (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat 11
2.4 Digraph primitif 11
2.5 Digraph dengan 4 verteks dan 5 arc 16
2.6 Sebuah 2-Digraph yang terdiri dari 5 verteks dan 7 arc 19
2.7 (a) 2-Digraph terhubung kuat (b) 2-Digraph tidak terhubung
kuat 21
2.8 Sebuah 2-Digraph yang terdiri dari 4 verteks dan 5 arc 23
2.9 Sebuah 2-Digraph dengan 3 verteks dan 4 arc 27 2.10 Sebuah 2-Digraph dengan dua cycle 32
BAB 2
LANDASAN TEORI
Pada bab ini akan diberikan beberapa konsep dasar seperti definisi dan beberapa teorema sebagai landasan dalam penelitian ini. Konsep dasar ini berkaitan dengan masalah yang dibahas dalam tulisan ini seperti digraph, keterhubungan suatu digraph, eksponen digraph, 2-digraph, dan eksponen dari 2-digraph.
2.1 Digraph
Secara sederhanagraphadalah kumpulan titik atau lingkaran kecil yang dihubung-kan oleh garis tak berarah. Jika garis penghubung diberi arah, maka graph demikian dinamakan digraph (directed graph).
2.1.1 Definisi.
Suatu digraphD adalah suatu objek Matematika yang terdiri dari dua himpunan yaitu :
1. Himpunan berhingga tak kosongV ={v0, v1,· · · , vn}. Unsur dariV disebut
verteks dari Digraph D.
2. HimpunanAyang merupakan himpunan bagian dari pasangan tak berurutan
V ×V dengan verteks-verteksnya tidak harus berbeda, dan unsur-unsurnya disebutarc dari digraph D.
Suatu α(u, v) adalah arc yang dibentuk dari verteks u ke verteks v. Suatu arc (u, v) dapat juga dinotasikan dengan u→v.
him-9
Suatu digraph dapat direpresentasikan secara grafis dengan cara setiap verteks direpresentasikan sebagai sebuah titik dan setiap arc (u, v) direpresentasikan garis berarah dari titiku kev.
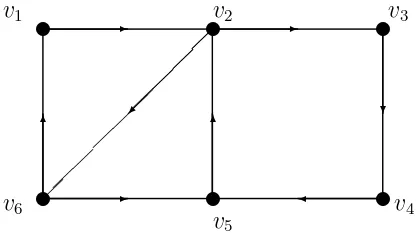
Contoh 2.2Representasi grafis dari digraph pada Contoh 2.1
✈ ✈ ✈
✈ ✈ ✈
v6
v5
v4
v1 v2 v3
✲ ✲
✛ ✲
✻ ✠ ✻ ❄
Gambar 2.1 : Digraph dengan 6 verteks dan 8 arc
Andaikan D adalah suatu digraph dan misalkan u dan v adalah verteks di digraphD. Suatu walk dengan panjangmdariukevdidefinisikan sebagai barisan arc dan dituliskan sebagai
v0 →v1 →v2 → · · · →vm−1 →vm
dengan m > 0, v0 = u, dan vm = v. Suatu walk dikatakan terbuka jika u 6=
v dan dikatakan tertutup jika sebaliknya. Suatu path adalah suatu walk tanpa perulangan verteks kecuali mungkin verteks awal dan verteks akhir. Suatu path yang memilikiv0 =vm disebutcycle.
Digraph pada Gambar 2.1 di atas memiliki walk, path, dan cycle sebagai berikut :
a. Barisan arc v1 →v2 →v3 →v4 →v5 →v2 →v6 adalah suatu walk terbuka
tetapi bukan path karena ada verteks yang berulang.
b. Barisan arc v1 → v2 → v3 → v4 → v5 → v6 disebut path karena tidak ada
verteks yang berulang.
c. Barisan arc v2 →v3 →v4→v5 disebut cycle.
10
2.1.2 Matriks Adjacency Digraph.
Keterhubungan sebuah digraph D dengan n verteks dapat dinyatakan ke dalam bentuk matriks ordon×nyang entri dari matriks tersebut adalah bilangan 1 atau 0. Matriks yang demikian disebut sebagai matriks adjacency.
Untuk setiap digraph D dengan m verteks dapat dituliskan suatu (0,1)-matriks A(D)=[aij] sebagai berikut
ai,j =
1, jika terdapat arc dari vi ke vj
0, jika sebaliknya.
untuki, j = 1,2,· · · , m
Berikut ini diberikan contoh matriks adjacency dari sebuah digraph yang direpresentasikan secara grafis.
Contoh 2.3Representasi dari sebuah digraph
✈ ✈
✈
✈ ✈
v5 v4
v1 v2
v3
✲ ✲
❅ ❅
❅ ❅❅ ❅
❅❅❘
✻ ✻
✒ ✠
Gambar 2.2 : Digraph dengan 5 verteks dan 7 arc
Dari representasi digraph diatas diperoleh matriks adjacency sebagai berikut
A(D) =
0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 1 0 0
11
2.1.3 Digraph Primitif.
Suatu digraphD dikatakan terhubung kuat (strongly connected) jika untuk setiap pasangan verteksu dan vdi D terdapat walk dari uke vdan sebaliknya. Berikut contoh digraph terhubung kuat dan tidak terhubung kuat.
Contoh 2.4Representasi dari digraph yang terhubung kuat dan tidak terhubung kuat. t t t t t t v1 v6 v2 v5 v3 v4 ✒ ✲ ❅ ❅ ❅ ❅❅❘ ✠ ✛ ❅ ❅ ❅ ❅ ❅ ■ t t t t t t v1 v6 v2 v5 v3 v4 ✒ ✲ ❅ ❅ ❅ ❅❅❘ ✠ ✛ ❅ ❅ ❅ ❅❅❘
Gambar 2.3 : (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat
Pada Gambar 2.3, ditunjukkan bahwa (a) adalah suatu digraph terhubung kuat karena terdapat walk dari satu verteks ke verteks lainnya, dan (b) adalah suatu digraph tidak terhubung kuat karena tidak terdapat walk dari v6 ke v1.
Suatu digraph terhubung kuat dikatakan primitif jika terdapat bilangan bulat positifk sedemikian hingga untuk setiap pasangan verteks udan v di D terdapat walk dariukevdengan panjangk. Berikut ini diberikan representasi grafis digraph yang terhubung kuat dan primitif.
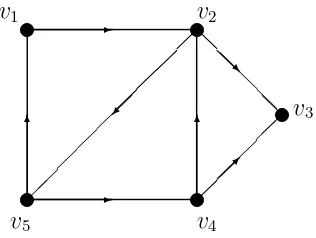
Contoh 2.5Digraph terhubung kuat di bawah ini adalah primitif.
t t t t v4 v1 v3 v2 ✲ ❄ ✛ ✻ ✚✚ ✚✚ ✚✚ ✚✚ ✚✚ ✚✚❃
Gambar 2.4 : Digraph primitif
Pada Gambar 2.4 di atas, D adalah digraph terhubung kuat dengan dua cycle yaitu : v1 → v2 →v3 →v4 →v1 dengan panjang 4 dan cycle v2 →v3 → v4 →v2
12
dengan panjang 3. Brualdi dan Ryser menjamin bahwa suatu digraph D adalah primitif jika dan hanya jika pembagi persekutuan terbesar dari panjang-panjang cycle diD adalah 1.
Lemma berikut ini akan menjamin bahwa setiap verteks di digraphD terletak pada suatu cycle bila digraphD terhubung kuat.
Lemma 2.1 Andaikan D adalah digraph terhubung kuat maka setiap verteks v di D terletak pada cycle.
Bukti: Ambil sebarang verteks v di D. Karena D terhubung kuat, maka ada suatu arc dari verteksv ke verteks u. Karena D terhubung kuat, maka terdapat path dari verteks u ke v yang berakibat akan diperoleh suatu path tertutup di
D yang dibentuk oleh arc dari verteks u ke v dan path dari verteks v keu di D. Oleh definisi, path tertutup adalah suatu cycle danvsebarang verteks diD, maka setiap verteksv diD terletak pada suatu cycle.
2.1.4 Eksponen Digraph.
Pada bahasan sebelumnya, telah dijelaskan bahwa suatu digraph terhubung kuat dikatakan primitif bila terdapat bilangan bulat positifk sedemikian hingga untuk setiap pasangan verteksudanv diDterdapat suatu walk dari verteksuke verteks vdan sebaliknya dengan panjang k. Bilangan bulat terkecil dari semuak tersebut dikatakan sebagai eksponen digraphD, dan dinotasikan exp(D). Berikut ini akan dijelaskan hubungan antara matriks adjecency dari sebuah digraph primitif dan eksponen dari digraph tersebut.
Pada tahun 2005, Zaini dan Suwilo menyatakan bahwa verteksvi kevj diAk
13
Bukti: AndaikanA adalah suatu matriks adjacency dari digraph D, maka setiap entri (i, j) dari A menyatakan arc dari vi ke vj di digraph D. Hal ini berakibat
untukk = 1, maka setiap entria1ij dari A1 menyatakan banyaknya walk dari vi ke
vj yang panjangnya satu.
Asumsikan setiap entri a(k)ij dan Ak menyatakan banyaknya walk dariv i dan
vj yang panjangnya k di D, untuk k ≥1. Berikut ini diperlihatkan a(k+1)ij adalah
banyaknya walk dari vi ke vj yang panjangnya k+ 1 di D, untukk ≥1.
Perhatikan setiap walk darivi kevj di D dengan panjang k+ 1 yang terdiri
dari walk dari vi ke vj dengan panjang k untuk l = 1,2, . . . , n dan dilanjutkan
dengan arc darivikevj. Sehinggaa (k)
il aljadalah menyatakan walk yang panjangnya
k+ 1 dari vi ke vj di D, untuk k = 1,2, . . . , n. Jika tidak terdapat walk yang
panjang k dari vi ke vj diD, maka a (k)
il = 0 sehingga a (k)
il alj = 0. Hal ini berarti
tidak terdapat walk dengan panjangk+1 darivikevjyang melaluivldiDsehingga
diperoleh banyaknya walk yang panjangnya k+ 1 dari vi ke vj diD adalah
a(k)i1 a1j+a(k)i2 a2j+· · ·+a(k)inanj = n X
i=1
a(k)il alj
karena
Ak+1 =AkA
maka
a(k)ij =
n X
i=1
a(k)il alj
Hal ini berakibata(k+1)ij adalah benar menyatakan banyaknya walk darivi ke
vj yang panjangnyak+ 1 diD. Jadi, elemen (i, j) dariAk adalah banyaknya walk
yang panjangnya k dari vi ke vj.
Berikut ini adalah matriks adjecency dari digraph yang diberikan pada Gam-bar 2.4 dan selanjutnya akan dicari eksponennya dengan menggunakan Proposisi 2.2 pada halaman sebelumnya.
14
Dari representasi grafis pada Gambar 2.4 diperoleh matriks adjacency sebagai
berikutA=
0 1 0 0 0 0 1 0 0 0 0 1 1 1 0 0
, dengan Proposisi 2.2 untuk mencari banyak walk dari
verteks vi ke vj dengan panjang k adalah entri dari matriks akij dari Ak dengan
demikian nilaik adalah eksponen dari digraph. Perhatikan matriks Ak.
a. Untuk k = 1 ; diperolehA =
0 1 0 0 0 0 1 0 0 0 0 1 1 1 0 0
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 1 dariv1 kev1.
b. Untuk k = 2 ; diperolehA =
0 0 1 0 0 0 0 1 1 1 0 0 0 1 1 0
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 2 dariv1 kev1.
c. Untuk k = 3 ; diperolehA =
0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 3 dariv1 kev1.
d. Untuk k = 4 ; diperolehA =
1 1 0 0 0 1 1 0 0 0 1 1 1 1 0 1
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 4 dariv1 kev3.
e. Untuk k = 5 ; diperolehA =
0 1 1 0 0 0 1 1 1 1 0 1 1 2 1 0
, maka bukan merupakan
15
f. Untuk k = 6 ; diperolehA =
0 0 1 1 1 1 0 1 1 2 1 0 0 1 2 1
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 6 dariv1 kev1.
g. Untuk k = 7 ; diperolehA =
1 1 0 1 1 2 1 0 0 1 2 1 1 1 1 2
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 7 dariv1 kev3.
h. Untuk k = 8 ; diperolehA =
1 2 1 0 0 1 2 1 1 1 1 2 2 3 1 1
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 8 dariv1 kev4.
i. Untuk k = 9 ; diperolehA =
0 1 2 1 1 1 1 2 2 3 1 1 1 3 3 1
, maka bukan merupakan
ekspo-nen digraph, karena tidak terdapat walk dengan panjang 9 dariv1 kev1.
i. Untuk k = 10 ; diperoleh A =
1 1 1 2 2 3 1 1 1 3 3 1 1 2 3 3
, karena terdapat walk dengan
panjang 10 dari tiap pasangan verteks di D, maka eksponen dari digraph pada Gambar 2.4 adalah 10.
2.1.5 Eksponen verteks digraph.
Misalkan D adalah sebuah digraph primitif dengan himpunan verteks V(D) = {v1, v2,· · · , vn}. Untuk suatu vk ∈ V(D) dan X ⊆ V(D), eksponen verteks
expD(vk) adalah bilangan bulat positif terkecil m sedemikian hingga terdapat
walk dengan panjang m dari vk ke setiap verteks di D, dan eksponen himpunan
16
vj di D terdapat sebuah walk dari paling sedikit satu verteks di X ke vj dengan
panjang p.
Misalkan D adalah digraph primitif dengan orde n. Jika verteks-verteks di
D adalah v1, v2,· · · , vn sedemikian hingga
expD(v1)≤expD(v2)≤ · · · ≤expD(vn)
maka expD(vk) adalah tipe pertama eksponen ke-k dari D yang digeneralisasikan.
Berikut ini diberikan contoh representasi grafis digraph yang akan dicari eksponen verteksnya dengan menggunakan Proposisi 2.2.
Contoh 2.6Digraph primitif dengan dua cycle
t
t t t
v1
v4
v3
v2
✲
❘
✒
✛ ✛
Gambar 2.5 : Digraph dengan 4 verteks dan 5 arc
Dari representasi grafis pada Gambar 2.5 di atas diperoleh matriks adjacency
sebagai berikut A =
0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0
, dengan Proposisi 2.2 dapat dicari eksponen
verteks dari masing-masing verteks di D, yaitu dengan melihat entri matriks ak ij
dari Ak, dimana entri pada baris ke-ipositif untuk suatu bilangan bulat k.
a. Untuk k = 1 ; diperoleh A =
0 1 1 0 0 0 1 0 0 0 0 1
17
b. Untuk k = 2 ; diperoleh A =
0 0 1 1 0 0 0 1 1 0 0 0 0 1 1 0
, tidak ada baris yang seluruh
entrinya bernilai positif.
c. Untuk k = 3 ; diperoleh A =
1 0 0 1 1 0 0 0 0 1 1 0 0 0 1 1
, tidak ada baris yang seluruh
entrinya bernilai positif.
d. Untuk k = 4 ; diperoleh A =
1 1 1 0 0 1 1 0 0 0 1 1 1 0 0 1
, tidak ada baris yang seluruh
entrinya bernilai positif.
e. Untuk k = 5 ; diperoleh A =
0 1 2 1 0 0 1 1 1 0 0 1 1 1 1 0
, tidak ada baris yang seluruh
entrinya bernilai positif.
f. Untuk k = 6 ; diperoleh A =
1 0 1 2 1 0 0 1 1 1 1 0 0 1 2 1
, tidak ada baris yang seluruh
entrinya bernilai positif.
g. Untukk= 7 ; diperoleh A=
2 1 1 1 1 1 1 0 0 1 2 1 1 0 1 2
, pada baris ke-1 seluruh entrinya
positif, maka exp(v1) = 7
h. Untukk = 8 ; diperolehA=
1 2 3 1 0 1 2 1 1 0 1 2 2 1 1 1
, pada baris ke-4 seluruh entrinya
positif, maka exp(v4) = 8
18
i. Untukk = 9 ; diperolehA=
1 1 3 3 1 0 1 2 2 1 1 1 1 2 3 1
, pada baris ke-3 seluruh entrinya
positif, maka exp(v3) = 9
j. Untukk = 10 ; diperolehA=
3 1 2 3 2 1 1 1 1 2 3 1 1 3 3 3
, pada baris ke-2 seluruh entrinya
positif, maka exp(v2) = 10
Karena ketiga verteks tersebut masing-masing telah memperoleh eksponen verteks, maka operasi selesai. Diperolehlah kesimpulan bahwa exp(v1) = 7, exp(v2) =
10, exp(v3) = 9, dan exp(v4) = 8.
2.2 Digraph Dwi-Warna
Suatu digraph dwi-warna D(2) (atau 2-digraph) adalah suatu digraph D yang
setiap arcnya diwarnai merah atau biru tetapi tidak keduanya.
2.2.1 Definisi.
Suatu digraph dwi-warnaD(2)adalah suatu objek yang terdiri dari himpunanV = {v0, v1,· · · , vn} yang unsur-unsurnya disebut verteks dari D(2), bersama dengan
himpunan R ⊆ V ×V yang unsur-unsurnya disebut arc merah dan himpunan
B ⊆ V ×V yang unsur-unsurnya disebut arc biru dari D(2). Suatu arc merah (u, v) dinotasikan dengan u −→r v dan suatu arc biru (u, v) dinotasikan dengan
u−→b v.
Suatu digraph dwi-warna dapat direpresentasikan secara grafis dengan cara sebagai berikut:
19
3. Setiap arc biru direpresentasikan sebagai garis atau kurva berarah putus-putus.
Suatu (h, k)-walk dalam digraph dwi-warna D(2) adalah sebuah walk yang
terdiri dariharc merah dan k arc biru. Untuk sebuah walk wdiD(2) notasi r(w)
menyatakan banyak arc merah danb(w) menyatakan banyak arc biru. Panjang su-atu walkwadalah banyak arc merah dan arc biru yang membentuk walk tersebut, dinotasikan ℓ(w) =r(w) +b(w). Vektorhr(w)b(w)i disebut komposisi dari w.
Suatu path adalah suatu walk dengan verteks berbeda kecuali mungkin verteks awal dan verteks akhir. Suatu cycle adalah suatu path tertutup. Berikut ini diberikan contoh representasi grafis 2-digraph.
Contoh 2.7 Himpunan verteks V = {1,2,3,4,5} bersama dengan himpunan arc merah R = {(1,2),(2,3),(2,5),(4,2),(4,3)} dan arc biru B = {(1,5),(5,4)} adalah suatu digraph dwi-warna dengan 5 verteks, 5 arc merah dan 2 arc biru. Rep-resentasi grafis dari digraph dwi-warna dari Contoh 2.2.1 adalah sebagai berikut:
t t
t t
t
v5 v4
[image:32.612.246.393.457.573.2]v3 v2 v1 ✲ ✒ ❅ ❅ ❅ ❅❅ ❅ ❅❅❘ ✻ ✲ ✻ ✠
Gambar 2.6 : Sebuah 2-Digraph yang terdiri dari 5 verteks dan 7 arc
Dari Contoh 2.7 di atas dapat ditemukan beberapa walk, path, dan cycle, yaitu:
a. Walk v1 r
− →v2
r
− →v5
b
− →v4
r
− →v2
r
−
→v3 dengan komposisi "
4 1
#
b. Path v1 r
− →v2
r
− →v5
b
− →v4
r
−
→v3 dengan komposisi "
3 1
#
20
c. Cycle v2 r
− →v5
b
− →v4
r
−
→v2 dengan komposisi "
2 1
#
2.2.2 Matriks Adjacency Digraph Dwi-Warna.
Pada digraph dwi-warna D(2) atas n verteks, untuk menentukan (0,1)-matriks
adalah sebagai berikut.
Matriksadjacency merah, R = [rij] pada D(2) adalah matriksn×n dengan
ri,j =
1, jika terdapat arc merah
0, jika sebaliknya
Matriksadjacency biruB = [bij] pada D(2) adalah matriksn×n dengan
bi,j =
1, jika terdapat arc biru
0, jika sebaliknya
Berikut ini akan diberikan sebuah digraph dwi-warna dan direpresentasikan ke dalam matriks adjacency-nya.
Contoh 2.8Dari Gambar 2.6 dapat kita peroleh matriks adjacency-nya yaitu:
R=
0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0
adalah matriks adjacency merah ;
B =
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0
adalah matriks adjacency biru.
21
dan B kali sebanyak k kali. Sebagai contoh, (R, B)(0,1) = B dan (R, B)(2,2) = R2B2+RBRB +RB2R+BRBR+BR2B +B2R2.
2.2.3 Digraph Dwi-Warna Primitif.
Suatu digraph dwi-warna D(2) dikatakan terhubung kuat strongly connectedjika untuk setiap pasangan verteksu danvdiD(2)terdapat walk dariukevdan seba-liknya, tanpa memperhitungkan komposisi yang ada. Berikut ini akan diberikan contoh digraph dwi-warna yang terhubung kuat dan yang tidak terhubung kuat.
[image:34.612.168.513.321.416.2]Contoh 2.9Representasi dari digraph dwi-warna yang terhubung kuat dan tidak terhubung kuat t t t t t t v1 v6 v2 v5 v3 v4 ✒ ✲ ❅ ❅ ❅ ❅❅❘ ✠ ❅ ❅ ❅ ❅ ❅ ■ ✛ t t t t t t v1 v6 v2 v5 v3 v4 ✒ ✲ ❅ ❅ ❅ ❅❅❘ ✠ ❅ ❅ ❅ ❅❅❘ ✛
Gambar 2.7 : (a) 2-Digraph terhubung kuat (b) 2-Digraph tidak terhubung kuat
Pada Gambar 2.7 ditunjukkan bahwa (a) adalah 2-digraph terhubung kuat karena terdapat walk dari satu verteks ke verteks lainnya. Sedangkan (b) adalah 2-digraph tidak terhubung kuat, karena tidak terdapat walk dariv6 kev1.
Sebuah digraph dwi-warna terhubung kuat D(2) dikatakan 2-primitif jika dan hanya jika terdapat bilangan bulat tak negatifh dan k sehingga untuk setiap pasangan dua verteksu dan v di D(2) terdapat (h, k)T-walk dari u ke v dan dari
v ke u. Andaikan D(2) adalah digraph dwi-warna terhubung kuat dan andaikan C={γ1, γ2, . . . , γt}merupakan himpunan semua cycle diD(2). Matriks cycleD(2)
adalah matriks berordo 2×t
M =
"
r(γ1) r(γ2) ... r(γt)
b(γ1) b(γ2) ... b(γt) #
dimana kolom ke-t dari M merupakan komposisi dari cycle γt dan 2 menyatakan
22
banyak warna yang di pakai. Suatu digraph dwi-warna D(2) dikatakan primitif jika dan hanya jika pembagi persekutuan terbesar dari minor-minor 2×2 dari M adalah 1 (Fornasini dan Valcher, 1997).
2.2.4 Eksponen Digraph Dwi-Warna.
Pada bagian digraph warna primitif, dijelaskan bahwa suatu digraph dwi-warna D(2) terhubung kuat dikatakan 2-primitif jika dan hanya jika terdapat bi-langan bulat tak negatifhdanksedemikian hingga untuk setiap pasangan verteks
u dan v di D(2) terdapat (h, k)-walk dari u ke v dan sebaliknya. Bilangan bulat positif terkecil dari semuah+k dikatakan sebagai 2-eksponen digraph dwi-warna
D(2).
Lemma 2.3 Andaikan D(2) adalah sebuah digraph dwi-warna atas n verteks dan misalkan R dan B masing-masing adalah matriks adjacency merah dan biru dari digraph dwi-warna D(2). Maka elemen (i, j) dari (R, B)(h,k) adalah banyaknya
(h, k)T-walk dari verteks v
i ke verteks vj.
Bukti. Akan dibuktikan dengan induksi pada (h+k) dan (h+k+ 1), jika h= 0 maka k = 1 atau jika h = 1 maka k = 0. jika h = 0 maka elemen (i, j) dari
(R, B)(0,1) = B adalah walk dengan komposisi "
0 1
#
di digraph dwi-warna D(2).
Dengan cara yang sama, jika k = 0 maka (R, B)(1,0) = R adalah walk dengan
elemen (i, j) menyatakan walk dengan komposisi
"
1 0
#
di digraph dwi-warna D(2).
Andaikan Lemma 2.3 benar untuk semua bilangan bulat tak negatif h′ dan
k′ dengan h′+k′ ≤ h+k akan diperlihatkan untukh+k+ 1 adalah benar dengan catatan sebagai berikut.
(R, B)(h+1,k) =R(R, B)(h,k)+B(R, B)(h+1,k−1)
23
diikuti oleh (h+ 1, k−1)-walk sedemikian hingga elemen (i, j) dari (R, B)(h+1,k) adalah jumlah (h+ 1, k)-walk dari vi ke vj. Jadi, elemen (i, j) dari (R, B)(h,k)
adalah jumlah (h, k)T-walk dari verteks v
i ke verteksvj.
Berikut ini diberikan representasi grafis 2-digraph yang selanjutnya akan di-cari eksponennya.
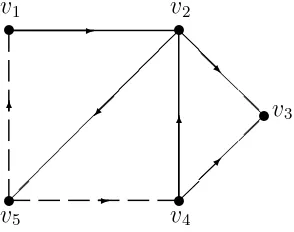
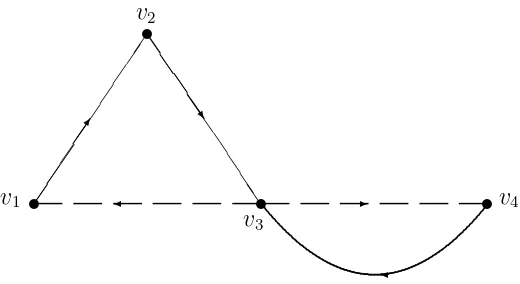
Contoh 2.10Digraph dwi-warna terhubung kuat di bawah ini adalah primitif.
[image:36.612.198.458.249.391.2]t t t t v1 v2 v3 v4 ✡✡ ✡✡ ✡✡ ✡✡✡ ✡✡ ✡✡✡ ✣ ❏ ❏ ❏ ❏ ❏ ❏ ❏ ❏❏ ❏ ❏ ❏ ❏❏❫ ✛ ✲ ✛
Gambar 2.8 : Sebuah 2-Digraph yang terdiri dari 4 verteks dan 5 arc
Dari representasi grafis 2-digraph di atas, dapat dibuat dua buah matriks adjacency sebagi berikut
1. Matriks R =
0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0
adalah matriks adjacency merah pada Gambar
2.8
2. MatriksB =
0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0
adalah matriks adjacency biru pada Gambar 2.8
Dari Lemma 2.3, entri (i, j) dari (R, B)(h,k) adalah banyaknya (h, k)-walk
24
1. Untuk h+k = 2, maka diperoleh ;
a. (R, B)(2,0)=R(R, B)(1,0)=
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
b. (R, B)(0,2)=B(R, B)(0,1)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
c. (R, B)(1,1)=R(R, B)(0,1)+B(R, B)(1,0)=
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
[image:37.612.141.446.95.346.2]Untukh+k = 2, maka bukan merupakan 2-eksponen dari 2-digraph pada Gambar 2.8 karena untuk setiap komposisi dari (R, B)(h,k) memuat (h, k
)-walk dengan panjang tidak sama dengan 2.
2. Untuk h+k = 3, maka diperoleh ;
a. (R, B)(3,0)=R(R, B)(2,0)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
b. (R, B)(0,3)=B(R, B)(0,2)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
c. (R, B)(1,2)=R(R, B)(0,2)+B(R, B)(1,1)=
0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0
25
[image:38.612.137.444.232.738.2]Untukh+k = 3, maka bukan merupakan 2-eksponen dari 2-digraph pada Gambar 2.8 karena untuk setiap komposisi dari (R, B)(h,k) memuat (h, k
)-walk dengan panjang tidak sama dengan 3.
Selanjutnya
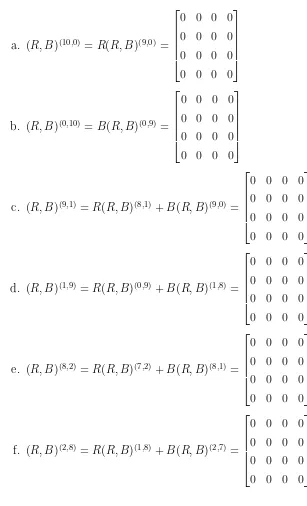
10. Untuk h+k = 10, maka diperoleh ;
a. (R, B)(10,0)=R(R, B)(9,0)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
b. (R, B)(0,10)=B(R, B)(0,9)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
c. (R, B)(9,1)=R(R, B)(8,1)+B(R, B)(9,0)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
d. (R, B)(1,9)=R(R, B)(0,9)+B(R, B)(1,8)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
e. (R, B)(8,2)=R(R, B)(7,2)+B(R, B)(8,1)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
f. (R, B)(2,8)=R(R, B)(1,8)+B(R, B)(2,7)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
26
g. (R, B)(6,4)=R(R, B)(5,4)+B(R, B)(6,3)=
3 1 1 3 3 3 4 3 1 2 6 1 3 3 4 3
Karena untuk setiap pasangan verteks u dan v di 2-digraph D(2) terdapat walk dengan panjang 10 dengan 6 arc merah dan 4 arc biru, maka eksponen dari 2-digraph D(2) adalah 10.
2.2.5 Eksponen Verteks Digraph Dwi-Warna Primitif.
MisalkanD(2)adalah sebuah digraph primitif dwi-warna dengan himpunan verteks
V(D(2)) = (v1, v2,· · · , vn). Untuk suatuvk ∈V(D(2)) danX ⊆V(D(2)),eksponen
verteks expD(2)(vk) adalah bilangan bulat positif terkecil m1 +m2 sedemikian
hingga terdapat (m1, m2)-walk dari vk ke setiap verteks di D(2), dan eksponen
himpunanexpD(2)(X) adalah bilangan bulat positif terkecilp1+p2sehingga untuk setiap verteks vj di D(2) terdapat sebuah (p1, p2)-walk dari paling sedikit satu
verteks diX ke vj.
MisalkanD(2)adalah digraph primitif dwi-warna dengan orden. Jika verteks-verteks diD(2) adalah (v1, v2,· · · , vn) sedemikian hingga
expD(2)(v1)≤expD(2)(v2)≤ · · · ≤expD(2)(vn)
maka expD(2)(vk) adalah tipe pertama eksponen ke-kdariDyang digeneralisasikan.
27
Contoh 2.11Diberikan 2-digraph di bawah ini
s v1
s v2
sv3
[image:40.612.239.392.119.213.2]✲ ✒ ❅ ❅ ❅ ❅ ❅ ❅❅ ❅ ❅ ❅❅❘ ✛
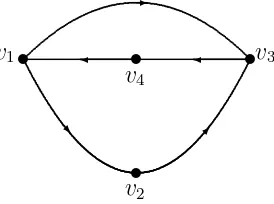
Gambar 2.9 : Sebuah 2-Digraph dengan 3 verteks dan 4 arc
Contoh 2.12Dari gambar 2.9 tersebut dapat kita peroleh matriks adjacency-nya yaitu: R=
0 1 1 0 0 1 0 0 0
adalah matriks adjacency merah;
B =
0 0 0 0 0 0 1 0 0
adalah matriks adjacency biru.
Selanjutnya dari Contoh 2.12 di atas dapat dicari eksponen verteks dari masing-masing verteks di D(2), yaitu dengan melihat penjumlahan h arc merah
dank arc biru pada matriks (R, B)(h,k) dimana entri pada baris ke-ipositif untuk
suatu bilangan bulat tak negatif terkecilh dan k.
a. untukh+k = 1
1. (R, B)(1,0) = R =
0 1 1 0 0 1 0 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
2. (R, B)(0,1) = B =
0 0 0 0 0 0 1 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
28
1. (R, B)(2,0) = R2 =
0 0 1 0 0 0 0 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
2. (R, B)(0,2) = B2 =
0 0 0 0 0 0 0 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
3. (R, B)(1,1) = RB + BR =
1 0 0 1 0 0 0 1 1
, tidak ada baris yang seluruh
entrinya bernilai positif.
c. untukh+k = 3
1. (R, B)(3,0) = R3 =
0 0 0 0 0 0 0 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
2. (R, B)(0,3) = B3 =
0 0 0 0 0 0 0 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
3. (R, B)(2,1)=R(R, B)(1,1)+B(R, B)(2,0)=
1 1 1 0 1 1 0 0 1
, pada baris ke-1,
seluruh entrinya bernilai positif. Maka expD(2)(v1) = 3 dengan
kompo-sisi walknya adalah
"
2 1
#
.
4. (R, B)(1,2) = R(R, B)(0,2)+B(R, B)(1,1) =
0 0 0 0 0 0 1 0 0
, tidak ada baris
yang seluruh entrinya bernilai positif.
d. untuk h+k = 4
29
2. (R, B)(0,4) = B4 =
0 0 0 0 0 0 0 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
3. (R, B)(3,1) = R(R, B)(2,1)+B(R, B)(3,0) =
0 1 2 0 0 1 0 0 0
, tidak ada baris
yang seluruh entrinya bernilai positif.
4. (R, B)(2,2)=R(R, B)(1,2)+B(R, B)(2,1)=
1 0 0 1 0 0 1 1 1
, pada baris ke-3,
seluruh entrinya bernilai positif. Maka expD(2)(v3) = 4 dengan
kompo-sisi walknya adalah
"
2 2
#
.
5. (R, B)(1,3) = R(R, B)(0,3)+B(R, B)(1,2) =
0 0 0 0 0 0 0 0 0
, tidak ada baris
yang seluruh entrinya bernilai positif.
d. untuk h+k = 5
1. (R, B)(5,0) = R5 =
0 0 0 0 0 0 0 0 0
, tidak ada baris yang seluruh entrinya
bernilai positif.
2. (R, B)(4,1) = R(R, B)(3,1)+B(R, B)(4,0) =
0 0 1 0 0 0 0 0 0
, tidak ada baris
yang seluruh entrinya bernilai positif.
3. (R, B)(3,2) = R(R, B)(2,2) +B(R, B)(3,1) =
2 1 1 1 1 1 0 1 2
, pada baris 1
dan 2, seluruh entrinya bernilai positif. Maka expD(2)(v1) = 5 dengan
komposisi walknya adalah
"
3 2
#
.
Dari operasi di atas diperoleh kesimpulan bahwa expD(2)(v1) = 5, expD(2)(v2) = 4, dan expD(2)(v3) = 3.
30
2.2.6 Batas Eksponen Verteks.
Pada bagian ini akan dijelaskan cara membentuk batas atas dan batas bawah eksponen verteks dari digraph dwi-warna primitif.
Proposisi 2.4 JikaD(2) adalah digraph dwi-warna primitif danvk adalah verteks
di D(2). Jika untuk beberapa bilangan bulat tak negatif s dan t dan beberapa path Pk,i dari vk ke vi, i= 1,2,· · · , n sistem persamaan
Mx+
"
r(Pk,i)
b(Pk,i) #
=
"
s t
#
memiliki solusi bilangan bulat tak negatif, sehingga γD(2)(vk)≤s+t.
Bukti : JikaM adalah sebuah matriks cycle 2×tdiD(2). Untuk setiap verteksv i,
i= 1,2,· · · , ndiD(2)diklaim bahwa terdapat (s, t)-walk dariv
k kevi. Karenax=
(x1, x2,· · ·, xt)t adalah vektor bilangan bulat tak negatif, walk yang berawal dari
vk, menuju vi melalui path pk,i dan mengelilingi cycleγj sebanyak xj kali untuk
j = 1,2,· · · , t adalah sebuah (s, t)-walk dari vk ke vi. Oleh definisi eksponen
verteks kita peroleh bahwa γD(2)(vk)≤s+t.
Proposisi 2.5 Andaikan D(2) adalah 2-digraph primitif atas n verteks, dan jika v adalah verteks di D(2) dengan eksponen γD(2). Untuk sembarang verteks vk,
k= 1,2,· · · , n di D(2) diperoleh bahwaγD(2)(vk)≤γD(2)(v) +d(vk, v).
Bukti : Andaikanpk,v adalah (r(pk,v), b(pk,v))-path dari vk kev dengan panjang
d(vk, v). Karena eksponen verteks v adalah γD(2)(v), terdapat (s, t)-walk dengan panjang γD(2)(v) = s+t dari v ke setiap verteksvj, j = 1,2,· · · , n. Ini menun-jukkan bahwa untuk setiap verteks vk di D(2) terdapat sebuah (s +r(pk,v), t +
b(pk,v))-walk dari verteks vk ke setiap verteks vj, j = 1,2,· · · , n, dikatakan
31
Lemma 2.6 Andaikan D(2) adalah sebuah 2-digraph primitif terdiri atas 2 cy-cle dengan matriks cycy-cle M =
"
r(γ1) r(γ2)
b(γ1) b(γ2) #
. Andaikan vk adalah sembarang
verteks di D(2) dan misalkan terdapat sebuah (s, t)-walk dari v
k ke setiap verteks
vi di D(2)dengan M = " s t # =M " u v #
untuk bilangan bulat tak negatif u dan v,
maka
"
u v
#
≥M−1
"
r(pki)
b(pki) #
untuk beberapa path pki dari vk ke vi.
Bukti : Andaikan pki adalah path dari vk ke vi. Karena setiap walk dapat
didekomposisikan ke dalam bentuk cycle dan path, diperoleh
"
s t
#
=Mx+
"
r(pki)
b(pki) #
untuk beberapa bilangan bulat tak negatif vektorx. KarenaD(2)adalah primitif, maka M adalah matriks yang dapat diinverskan. Mengingat bahwa
" s t # =M " u v # , diperoleh x= " u v #
−M−1
"
r(pki)
b(pki) # = " u v # − "
b(γ2)r(pki)−r(γ2)r(pki)
r(γ1)b(pki)−b(γ1)r(pki) #
≥0
Oleh karena itu Lemma memenuhi.
Akibat 2.7 Andaikan D(2) adalah digraph dwi-warna dengan dua cycle γ 1 dan
γ2. Andaikan vk di D(2) dan andaikan pk,i dan pk,j adalah path dari vk ke vi dan
path darivk ke vj dengan i6=j. Jika u0 =b(γ2)r(pk,i)−r(γ2)b(pk,i)≥0 danv0 =
r(γ1)b(pk,j)−b(γ1)r(pk,j)≥0, makaγD(2)(vk)≥(r(γ1)+b(γ1))u0+(r(γ2)+b(γ2))v0.
Bukti : Diasumsikan bahwa eksponen vk dapat diperoleh dengan sebuah (s, t
)-walk. Karena " s t # =M " u v #
untuk beberapa bilangan bulat tak negatif u dan
v. Oleh Lemma 3.3 diperoleh
" u v # ≥ "
b(γ2)r(pki)−r(γ2)r(pki)
r(γ1)b(pki)−b(γ1)r(pki) #
32
untuk sembarang path pk,i dari verteks vk ke verteks vi, i = 1,2,· · · , n. Oleh
karena itu " s t # =M " u v # ≥M " u0 v0 #
Ini menunjukkan bahwaγD(2)(vk)≥(r(γ1)+b(γ1))u0+(r(γ2)+b(γ2))v0 =ℓ(γ1)u0+
ℓ(γ2)v0.
2.2.7 Digraph Dwi-Warna Dengan Dua Cycle Bersinggungan. AndaikanD(2) adalah 2-digraph atasnverteksv
1, v2,· · · , vnyang terdiri dari dua
cycle yaitu γ1 : v1 → vn → vn−2 → · · · → v2 → v1 dengan ℓ(γ1) = n+ 2
2 dan γ2 : v1 → vn−1 → vn−3 → · · · → v3 → v1 dengan ℓ(γ2) =
n
2. Digraph dwi-warna D(2) dikatakan primitif jika dan hanya jika
M(D(2)) =
"
r(γ1) r(γ2)
b(γ1) b(γ2) #
=
"n
2 n−2
2
1 1
#
Deni Ramadani(2009) memberikan batas untuk eksponen digraph dwi-warnaD(2), yaitu 1
2(n
2+n)≤exp(D(2))≤ 1
2(2n
2+n−2). Pada penelitiannya Deni Ramadani
menyimpulkan bahwaD(2)memiliki eksponen tepat 1 2(2n
2+n−2) jika dan hanya
jikaD(2) memuat path merah dengan panjangn−1 dan path biru dengan panjang 2. Jika v1 adalah verteks persekutuan antara γ1 dan γ2, maka path biru yang
dimaksud adalah v3 →v1 →vn.
Berikut ini merupakan representasi grafis dari 2-digraph atas n verteks de-ngan expD(2) =
1 2(2n
2+n−2)
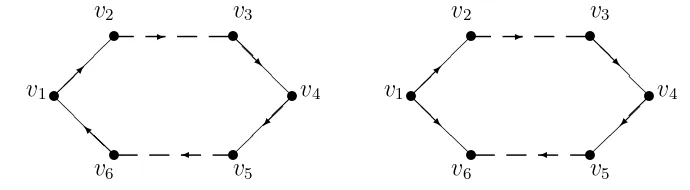
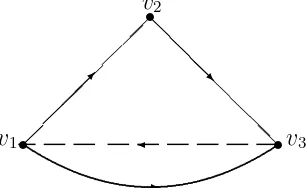
Contoh 2.13Digraph dwi-warna dengan dua cycle yang bersinggungan
r r r ❆❑ ❆❆❑ t v4 ✲
t v6 ✁
✁✁ ✁✁ ✁✁✁✕ t v2 ❆ ❆ ❆ ❆❆ ❆ ❆❆❯ t v1 ✁✁ ✁✁✁ ✁✁✁✕ ✁✁ ✁✁☛ ✁✁ ❆❆❑ ❆❆ ❆❆ t vn−1 ✲
t vn−3
❄
r r r
[image:45.612.203.425.617.732.2]BAB 3
EKSPONEN VERTEKS 2-DIGRAPH DENGAN DUA CYCLE YANG BERSINGGUNGAN
Pada bab ini akan diperlihatkan hasil utama dari penelitian ini. Adapun hasil utama dari tulisan ini yaitu pola eksponen verteks dari 2-digraph dengan dua cycle yang bersinggungan.
Andaikan D(2) adalah 2-digraph primitif atas n verteks v1, v2,· · · , vn yang
terdiri dari dua cycle yaitu γ1 : v1 → vn → vn−2 → · · · → v2 → v1 dengan
ℓ(γ1) =
n+ 2
2 dan γ2 : v1 → vn−1 → vn−3 → · · · → v3 → v1 dengan ℓ(γ2) = n 2. Karena D(2) primitif, maka matriks cycleD(2) mempunyai bentuk
M(D(2)) =
"
r(γ1) r(γ2)
b(γ1) b(γ2) #
=
"n
2 n−2
2
1 1
#
Teorema 3.1 AndaikanD(2) adalah 2-digraph primitif atasn verteks dengan
eks-ponen 1
2(2n
2 +n − 2). Jika v
k, k = 1,2,· · · , n adalah verteks di D(2) maka
γD(2)(vk) =
n2−2 2 +⌊
k 2⌋.
Bukti : Pembuktian dilakukan dengan cara memperlihatkan batas bawah terlebih dahulu, yaitu akan ditunjukkan dengan menggunakan Akibat 2.7. Oleh karena itu adalah perlu didefinisikan terlebih dahulu nilai u0 dan v0. Nilai u0 dan v0 dapat
diperoleh dari path tunggal yang menghubungkan vk dengan vn dan path yang
menghubungkan vk dengan v3. Pembuktian dibagi ke dalam dua kasus, yaitu
kasus saat k ganjil dan saat k genap.
a. Kasus 1Untuk kasuskganjil, akan diperlihatkan bahwaγD(2)(vk)≥ n
2
−3+k
2 .
Kasus ini dibagi menjadi dua subkasus, yaitu ketikak = 1 dank = 2m−1, m= 2,3,· · · ,n
2.
34
(i) Untukk = 1 akan diperlihatkan γD(2)(v1)≥ n 2
−2
2 . Mengingat terdapat
(n−2
2 ,0)-path dari v1 ke v3, diperoleh u0 =b(γ2)r(p1,3)−r(γ2)b(p1,3) =
(1)(n−2
2 )−( n−2
2 )(0) = n−2
2 , dan terdapat (0,1)-path dari v1 kevn,
dipe-rolehv0 =r(γ1)b(p1,n)−b(γ1)r(p1,n) = (n2)(1)−(1)(0) = n2. Oleh Akibat
2.7 diperoleh " s t # ≥ " n 2 n−2
2
1 1
# " n
−2 2 n 2 # =
" n2
−2n
2
n−1
#
Oleh karena ituγD(2)(v1)≥ n 2
−2
2 .
(ii) Untukk = 2m−1, m = 2,3,· · · ,n
2. Mengingat terdapat ( k−3
2 ,0)-path
dari vk ke v3, diperoleh u0 = b(γ2)r(pk,3)−r(γ2)b(pk,3) = (1)(k−23)−
(n−2
2 )(0) = k−3
2 , dan terdapat ( k−3
2 ,2)-path dari vk ke vn, diperoleh
v0 = 2n−2k+3. Oleh Akibat 2.7 diperoleh
" s t # ≥ " n 2 n−2
2
1 1
# " k
−3
2 2n+3−k
2 #
=
" n2
−2n+k−3
2
n
#
Oleh karena ituγD(2)(vk)≥ n 2
−3+k
2 .
b. Kasus 2Untukk = 2m,m = 1,2,· · · ,n2 akan diperlihatkan bahwaγD(2)(vk)≥
n2−2+k
2 . Mengingat terdapat ( k
2,1)-path darivk kevn, diperolehv0 =r(γ1)(pk,n)−
b(γ1)r(pk,n) = (n2)(1)−(1)(nk) = n−2k, dan terdapat (n−2+k2 ,0)-path darivk ke
v3, diperoleh u0 =b(γ2)r(pk,3)−r(γ1)b(pk,3) = (1)(n−2+k2 )−(n2)(0) = n−2+k2 .
Oleh Akibat 2.7 diperoleh
" s t # ≥ " n 2 n−2
2
1 1
# " n
−2+k
2 n−k
2 #
=
" n2
−2n+k
2
n−1
#
Oleh karena ituγD(2)(vk)≥ n
2
−2+k
2 .
Selanjutnya pembuktian dilakukan dengan memperlihatkanγD(2)(vk)≤ n
2
−2
2 +⌊
k 2⌋.
Hal ini dapat dilakukan dengan memperlihatkan bahwaγ (v ) = n2 2
35
dari γD(2)(v1). Untuk setiap i = 1,2,· · · , n, jika P1,k adalah path dari v1 ke vk.
Persamaan
Mx+
"
r(p1,k)
b(p1,k) #
=
" n2
−2n
2
n−1
#
memiliki solusi
x=
"
x1
x2 #
=
" n
−2
2 +
n−2
2 b(P1,k)−r(P1,k) n
2 − n
2b(P1,k) +r(P1,k) #
Ketikab(p1,k) = 0, terdapat path dari v1 kevk denganr(p1,k)≤0. Oleh karena itu
x1 ≥ 0. Ketika b(p1,k) = 1 maka semua path dari v1 ke vk memenuhir(p1,k)≥ 0.
Ini menunjukkan bahwa x2 ≥ 0. Oleh karena itu persamaan ini memiliki solusi
bilangan bulat tak negatif. Oleh Proposisi 2.5 terdapat n2−2n
2 , n−1
-walk dari
v1 ke vk, k= 1,2,· · · , n. Oleh karena ituγD(2)(v1)≤ n
2
−2
2 . Dengan menggunakan
batas bawah γD(2)(v1) disimpulkan bahwa γD(2)(v1) = n
2
−2
2
Karena untuk setiapk = 2m−1,m= 2,3,· · · ,n
2 terdapat sebuah n−2
2 , 1
-walk dengan panjang n
2 darivk kev1, maka oleh Proposisi 2.5 diperolehγD(2)(vk)≤ n2−3+k
2 .
Untuk setiap k = 2m, m = 1,2,· · · ,n2 terdapat sebuah (k
2, 0)-walk dengan
panjang k
2 dari vk kev1, maka oleh Proposisi 2.5 diperoleh γD(2)(vk)≤ n 2
−2n+k
2 .
BAB 4
KESIMPULAN DAN RISET LANJUTAN
Pada bab ini akan diberikan kesimpulan yang diperoleh dari hasil penelitian pada bab sebelumnya. Selanjutnya akan diberikan saran untuk penelitian lebih lanjut.
4.1 Kesimpulan
DiberikanD(2)adalah 2-digraph primitif atasnverteksv1, v2,· · ·, vndengann ≥4
dan n genap terdiri dari dua cycle, yaitu γ1 :v1 →vn−2 → · · · → v2 →v1 dengan
ℓ(γ1) =
n+ 2
2 dan γ2 : v1 → vn−1 → vn−3 → · · ·v3 → v1 dengan ℓ(γ2) = n 2 serta komposisi matriks cyclenya adalah
M =
"n
2 n−2
2
1 1
#
Pewarnaan dilakukan dengan memberi warna biru pada path v3→v1 →vn,
sedangkan arc lainnya diberi warna merah.
Dengan pewarnaan tersebut, diperoleh bahwa eksponen verteks dari digraph dwi-warna D(2) adalah
expD(2)(vk) =
n2−2 2 +⌊
37
4.2 Riset Lanjutan
Penelitian ini telah memberikan pola eksponen verteks dari suatu digraph dwi-warna dengan dua cycle bersinggungan yang eksponennya 1
2(2n
2+n−2).
Dibu-tuhkan penelitian lebih lanjut untuk menentukan pola eksponen verteks dari suatu digraph dwi-warna dengan dua cycle bersinggungan.
38
DAFTAR PUSTAKA
Brualdi, R. A dan Ryser, H. J. 1991. Combinatorial Matrix Theory. Cam-bridge: Cambridge University Press.
Fornasini, E. dan Valcher, M. E. (1997). Directed graphs, 2D State Models, and characteristic polinomials of irreducible matrix pairs. Linear Al-gebra Appl., 263, 275-310.
Gao, Y dan Shao, Y. 2009. Generelized exponent of primitive two-colored digraph. Linear Algebra Appl, 430, 1550-1565.
Horn, R. A dan Johnson, C. R. 1985.Matrix Analysis. Cambridge: Cambridge University Press.
Liu, B. 1993. Generalized Exponents of Primitive Simple Graphs. Linear Al-gebra Appl..9(1): hal. 37-43.
Ramadani, D. 2009. Eksponen Digraph Dwi-Warna dengan Dua Cycle yang Bersinggungan. Skripsi. Medan : Universitas Sumatera Utara.
Shader, B. L. dan Suwilo, S. 2003. Exponents of nonnegative matrix pairs.Linear Algebra Appl., 363, 275-293.
Shao, J. 1987. The exponent set of symmetric primitive matrices, Scientia sinica Ser. A XXX. 4: hal. 348-358.
Suwilo, S. 2008. 2-Eksponen of Two-Coloured Lollipop.Linear Algebra Appl.. 21(1): hal. 11 - 12
Suwilo, S.2009.Notes on Exponent of Asymmetric Two-Coloured Digraph. J.Combin.Math.Combin.Comput.71