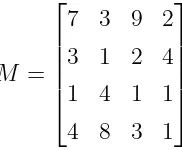GRAF PRIMITIF
Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkaitgraf, mat-riks adjency, terhubung, primitifitas, dan scrambling indexsebagai landasan teori yang menjadi acuan dalam penelitian ini. Akan dijelaskan pula beberapa termi-nologi serta notasi-notasi yang akan digunakan pada pembahasan berikutnya.
2.1 Definisi Graf
Secara umum graf mempresentasikan model matematika terhadap sejumlah ob-jek dalam bentuk simpul/titik (vertex) dan hubungan antara objek-objek tersebut dalam bentuk garis/sisi (edge). Sederhananya, graf dapat digambarkan sebagai kumpulan titik yang dihubungkan dengan garis. Secara matematika graf didefi-nisikan sebagai pasangan tak berurut yang terdiri dari dua himpunan berikut:
1. Himpunan berhingga tak kosong V ={v0, v1,· · · , vm}, dinotasikan dengan V(G). Elemen-elemen dari himpunan V ini disebut verteks atau titik dari graf G.
2. Himpunan sisi yang dinotasikan denganE(G), yaitu pasangan tak berurut dari elemen-elemenV(G) dalam bentukE ={(v0, v1); (v1, v2);·; (vm−1, vm)}. Elemen-elemen dari himpunan E ini disebut edge atau sisi dari graf G.
Sebuah grafG dengan himpunan titikV dan himpunan sisiE dinotasikan denganG(V, E). Banyaknya elemen diV disebutorderdariG, dinotasikan dengan
Suatu graf dengan size 0 dinamakan graf kosong (null graph) sedangkan graf dengan order 1 tanpa sebuah sisi sama sekali dinamakan graf trivial.
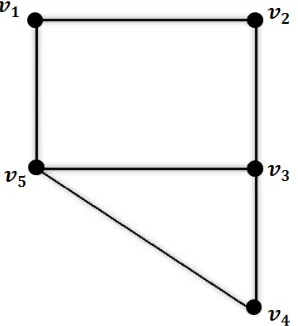
Contoh 2.1Berikut adalah grafG(V, E) dengan himpunan titikV ={v1, v2, v3, v4, v5} dan himpunan sisi E = {v1↔v2, v2↔v3, v3↔v4, v4↔v5, v3↔v5, v5↔v1}. Repre-sentasi graf tersebut diperlihatkan pada gambar berikut.
Gambar 2.1. Contoh representasi grafG(V, E)
Graf G(V, E) pada gambar 2.1 mempunyai 5 titik dan 6 sisi sehingga order dari G adalah|V|= 5 dan size dari Gadalah |E|= 6.
Apabila diketahui sisi e = (u, v) termuat dalam graf G, maka titik-titik u dan v disebut sebagai titik ujung dari sisi e. Titik u merupakan titik awal dan titik v merupakan titik akhir dalam graf G. Titik u dan v dikatakan bertemu dengan sisi edan sebaliknya sisi edikatakan bertemu dengan titik udanv. Dera-jat dari sebuah titiku, dinotasikan dengandeg(u) adalah banyaknya sisi-sisi yang bertemu dengan titik u.
AndaikanGadalah sebuah graf. Sebuah jalan (walk) yang menghubungkan titik u dan titik v di G dengan panjang m adalah sebuah barisan m sisi dengan bentuk
{u=v0, v1},{v1, v2}, ,{vm−1), vm =v}
Jalan yang menghubungkan titiku dan titikv dengan panjang m ini dinotasikan dengan u = v0 ↔ v1 ↔ v2 ↔ · · · ↔ vm = v yang selanjutnya disingkat dengan penulisan u↔m v.
Sebuah jalan yang menghubungkan u dan v dikatakan terbuka apabila u 6= v dan dikatakan tertutup apabila u = v. Sebuah jalan tanpa perulangan titik kecuali mungkin titik-titik ujungnya disebut dengan lintasan (path). Titik awal dan titik akhir dari suatu lintasan bisa saja merupakan titik yang sama, lin-tasan yang demikian disebut linlin-tasan tertutup (close path) dan merupakan sebuah lingkaran (cycle).
Suatu lingkaran-s (s-cycle) adalah lingkaran dengan panjang s dan dino-tasikan denganCs. Jarak (distance) dari titikumenuju titikv, dinotasikan dengan d(u, v) adalah panjang dari jalan terpendek yang menghubungkan titik u dan v. Adapun diameter dari suatu grafGmerupakan maksimum jarak yang dapat dite-mukan antara titik-titik pada grafG.
Dengan menggunakan graf pada gambar 2.1 akan dijelaskan beberapa ter-minologi tersebut di atas.
a. Barisan sisi v1↔v2↔v1↔v5↔v4 adalah sebuah jalan tetapi bukan lintasan karena ada perulangan titikv1. Karena titik awal dan titik akhirnya berbeda, jalan ini disebut jalan terbuka.
b. Barisan sisi v1↔v2↔v3↔v4↔v5 adalah sebuah lintasan terbuka.
d. Jarakd(v1, v5) adalah jarak dengan panjang ganjil dan jarakd(v1, v3) adalah jarak dengan panjang genap.
e. Jarak maksimum dari graf G adalah 2, yaitu antara d(v1, v3), d(v1, v4), d(v2, v4), ataupun d(v2, v5). Maka diameter graf G adalah 2.
2.2 Matriks Adjacency
Matriks adjacency (matriks ketetanggaan) adalah (0,1)-matriks, yaitu sebuah matriks yang hanya memuat elemen 0 atau 1. Matriks ini digunakan untuk menyatakan graf G atas n titik. Matriks adjacency dari sebuah graf G atas n titik v1, v2,· · · , vn adalah sebuah matriks bujursangkar A = [aij] dengan ordo n yang setiap elemennya didefinsikan dengan ketentuan berikut:
aij =
(
1, jika {vi, vj} ∈E(G) 0, jika {vi, vj}∈/ E(G)
Berdasarkan definisi dapat diketahui bahwa aij =aji untuk semua 1 ≤ i, j ≤ n. Hal ini berakibat matriks ketetanggaanA(G) dari grafGmerupakan sebuah mat-riks simetrik.
Contoh 2.2GrafG(V, E) pada gambar 2.1 dapat direpresentasikan dalam bentuk matriks adjacency A(G) = [aij] sebagai berikut:
A(G) =
0 1 0 1 0 1 0 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0
angka 1 pada baris pertama dari A(G) menyatakan derajat dari titikv1.
Teorema 2.1 Andaikan G adalah sebuah graf dan A = (aij) adalah sebuah mat-riks adjacency dari G. Misalkan ak
ij adalah elemen (i, j) dari matriks Ak. Maka ak
ij menyatakan banyaknya jalan dengan panjang k yang menghubungkan titik i dengan titik j.
Bukti. Pembuktian dilakukan dengan menggunakan induksi atas k. Asumsikan bahwa elemen ak
ij dari Ak menyatakan banyaknya jalan dengan panjang k yang menghubungkan titiki dengan titikj. Apabilak = 1, maka elemen a1
ij =aij dari A menyatakan banyaknya jalan dengan panjang 1 yang menghubungkan titik i dengan titik j. Karena Ak+1 =AkA, maka
ak+1ij = n
X
l=1 ak
il alj
untuk l = 1,2,· · · , n. Berdasarkan prinsip perkalian, ekspresi ak
il alj adalah banyaknya jalan dengan panjangk+ 1 yang melalui titikvl. Sehingga oleh prinsip penjumlahan, ak+1ij adalah banyaknya jalan dengan panjang k+ 1 yang menghu-bungkan titik i dengan titik j.
2.3 Matriks Tak Negatif
Matriks tak negatif A merupakan suatu matriks dengan aij ≥ 0, artinya setiap elemen-elemen aij dari matriksA memuat bilangan bulat tak negatif. Sebaliknya jika setiap elemen-elemen dari matriks A memuat bilangan bulat positif, yaitu aij > 0 maka matriks tersebut disebut matriks positif. Berikut diberikan dua buah matriks.
N =
1 3 0 7 3 2 1 5 4 0 2 0 3 2 0 0
M =
7 3 9 2 3 1 2 4 1 4 1 1 4 8 3 1
Matriks N adalah matriks tak negatif dan matriks M adalah matriks positif.
2.4 Graf Terhubung
Sebuah grafG dikatakan terhubung (connected graph) apabila untuk setiap pasa-ngan titik u dan v diGterdapat jalan yang menghubungkan u dan v, sebaliknya grafGdikatakan tidak terhubung apabila tidak terdapat jalan yang menghubung-kan titik u ke titik v.
Dua titik terhubung pada suatu graf bersifat refleksif, artinya apabila u dan v adalah dua titik yang terhubung maka terdapat jalan yang menghubung-kan u dengan v dan dengan bergerak mundur akan diperoleh sebuah jalan yang menghubungkan v dengan u. Maka dua titik terhubung pada suatu graf juga bersifat simetrik.
Gambar 2.2. Graf terhubung dan tidak terhubung
keter-hubungan dari suatu graf.
Teorema 2.2 Andaikan G adalah sebuah graf atas n titik dengan matriks kete-tanggaanA. GrafG adalah terhubung jika dan hanya jika matriksA+A2+· · ·+ An−1 mempunyai elemen yang semuanya bernilai positif.
Bukti. Andaikan G adalah sebuah graf terhubung dan misalkan B = A+A2 +
· · ·+An−1. Telah diketahui bahwa Gmempunyai n titik dan pada suatu lintasan tidak terdapat titik berulang kecuali u=v. Apabilau6=v, maka terdapat suatu lintasan dengan panjang kurang darin yang menghubungkanu dengan v.
Hal ini mengakibatkan untuk setiap pasangan titiku dan v yang berbeda, terdapat sebuah bilangan bulat positif k dengan 1≤k ≤n−1 sehingga elemen ak
ij > 0. Artinya, semua elemen di luar elemen diagonal dari matriks B adalah positif. Apabila u = v, maka terdapat sebuah lingkaran dengan panjang 2 yang memuat titik u sehingga elemen a2
uu > 0 untuk semua u = 1,2,· · · , n. Maka diagonal dari matriks B adalah positif sehingga dapat disimpulkan bahwa semua elemen dari matriks B =A+A2+· · ·+An−1 adalah positif.
Akibatnya, untuk setiap pasangan titiku danv terdapat sebuah bilangan positifkdengan 1≤k ≤n−1 sehinggaak
ij >0. Hal ini menyatakan bahwa untuk setiap pasangan titik udan v diG terdapat sebuah jalan dengan panjangk yang menghubungkan titik u dan v, artinya G adalah sebuah graf terhubung.
Berikut adalah proposisi yang menjelaskan beberapa sifat dari jalan yang menghubungkan titik u dan titik v yang dirujuk dari Harleni (2014).
Proposisi 2.1 Misalkan G adalah suatu graf yang memuat titik u dan v. Setiap jalan u ↔t v dapat dikembangkan menjadi sebuah jalan u t+2m↔ v, untuk sebarang
bilangan bulat positif m.
Bukti. Misalkan titik u dan v termuat dalam graf G dan misalkan W : u = v0 ↔ v1 ↔v2 ↔ · · · ↔vt−1 ↔vt =v merupakan jalan u
t
W′
yang dimulai dari titik u berpindah ke titik v sepanjang jalan W kemudian berpindah m kali mengelilingi lingkaran v ↔ vt−1 ↔ v merupakan sebuah jalan ut+2m↔ v.
Proposisi 2.2 Misalkan G adalah suatu graf yang memuat titik u,v dan w. Ter-dapat jalanu↔t wdan jalanv ↔t wdi Gjika dan hanya jika terdapat jalanu↔2t v di G.
Bukti. Andaikan terdapat jalan u ↔t w dan jalan v ↔t w di G. Maka dapat dinyatakan bahwa jalan yang dimulai dariuyang berpindah kewsepanjang jalan u↔t wkemudian berpindah kev sepanjang jalanv ↔t w, merupakan jalan u↔2t v. Asumsikan bahwa W : u =v0 ↔ v1 ↔ v2 ↔ · · · ↔v2t−1 ↔ v2t =v merupakan jalanu↔2t v di G. Jikaw=vt, maka terdapat u↔t w dan jalanv ↔t w di G.
Syahmarani dan Suwilo (2012) juga memberikan Lemma mengenai graf terhubung sebagai berikut.
Lemma 2.1 Andaikan G adalah graf terhubung maka setiap titik v di G ter-letak pada suatu lingkaran.
Bukti. Ambil sebarang titik v di G. Karena G terhubung, maka terdapat su-atu sisi yang menghubungkan titik v ke suatu titiku. Akibatnya, akan diperoleh suatu lintasan tertutup di G yang dibentuk oleh sisi dari titik u ke titik v dan lintasan dari titik v ke titik u di G. Oleh definisi, diketahui bahwa lintasan ter-tutup merupakan suatu lingkaran. Karena titik v adalah sebarang titik di G, maka setiap titik v diG terletak pada suatu lingkaran.
2.5 Primitifitas Graf
Graf G(V, E) yang ditunjukkan pada gambar 2.1 sebelumnya adalah salah satu contoh graf primitif. Berikut akan diperlihatkan graf primitif dan tidak pri-mitif.
Gambar 2.3. Graf primitif dan tidak primitif
Gambar 2.3 memperlihatkan bahwa (a) merupakan graf primitif karena graf tersebut memuat lingkaranv1 ↔v2 ↔v3 ↔v1 dengan panjang 3, sehingga syarat memuat paling sedikit sebuah lingkaran dengan panjang ganjil telah dipenuhi. Gambar (b) merupakan graf tidak primitif karena tidak memuat lingkaran ganjil sama sekali.
Primitifitas suatu graf juga dapat dilihat melalui representasi matriksnya. Sebuah matriks persegi non negatifAdikatakan primitif apabila terdapat bilangan bulat positif k sedemikian hingga Ak > 0. Berikut adalah representasi matriks dari graf primitif pada gambar 2.3 bagian (a).
A=
0 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0
A2 =
3 1 2 1 1 2 1 2 2 1 3 1 1 2 1 2
Karena terdapatk = 2 sedemikian hingga setiap elemen-elemen padaA2 memuat bilangan bulat positif, maka diketahui bahwa untuk matriksAdari graf tersebut, terdapat A2 >0. Sehingga terbukti bahwa graf tersebut adalah graf primitif.
2.6 Scrambling Index
Scrambling index dari graf primitif G, dinotasikan dengan k(G) adalah bilangan bulat positif terkecil k sehingga untuk setiap dua titik u dan v yang berbeda, terdapat sebuah titik w dengan sifat terdapat u ↔k w dan v ↔k w. Adapun un-tuk dua titik u dan v yang berbeda, scrambling index lokal dari u dan v adalah bilangan bulat positif ku,v(G) yang didefinisikan sebagai berikut:
ku,v(G) = min w∈V{k:u
k
↔w dan v ↔k w}
Dari definisi scrambling index k(G) dan scrambling index lokal ku,v(G) diperoleh hubungan k(G) ≥ ku,v(G). Karena G adalah graf terhubung, maka untuk setiap bilangan bulatl≥ku,v(G) dapat ditemukan sebuah titikw′
sehingga terdapat u ↔l w′
dan v ↔l w′
. Hal ini mengakibatkan nilai dari k(G) yang juga disebut dengan scrambling index global adalah maksimum dari nilai-nilai scrambling index lokal ku,v(G) yang didefinisikan sebagai berikut:
k(G) =max
u6=v {ku,v(G)}
Contoh 2.3 Dengan menggunakan graf G(V, E) pada gambar 2.1, nilai scram-bling index dari graf tersebut dapat ditentukan. Terlebih dahulu ditentukan nilai-nilai scrambling index lokal-nya sebagai berikut:
ku,v(G) = min
u,v,w,x,y{4,4,3,3,2}= 2 ku,w(G) = min
u,v,w,x,y{5,1,3,1,2}= 1 ku,x(G) = min
u,v,w,x,y{5,3,2,3,2}= 2 ku,y(G) = min
u,v,w,x,y{4,3,2,1,3}= 1 kv,w(G) = min
u,v,w,x,y{3,4,3,2,2}= 2 kv,x(G) = min
kv,y(G) = min
u,v,w,x,y{1,4,2,3,3}= 1 kw,x(G) = min
u,v,w,x,y{1,3,3,3,3}= 1 kw,y(G) = min
u,v,w,x,y{1,3,4,2,5}= 1 kx,y(G) = min
u,v,w,x,y{1,2,3,4,5}= 1
Maka scrambling index dari graf tersebut adalah maksimum dari semua scram-bling index lokal yang diperoleh, yaitu k(G) = max{2,1,2,1,2,2,1,1,1,1}= 2.
Karena graf dapat dinyatakan dalam bentuk matriksadjacency, nilai scram-bling index dapat pula ditentukan dari matriks primitif. Scramscram-bling index dari matriks primitifA, dinotasikan dengank(A) adalah bilangan bulat positif terkecil k sehingga untuk setiap dua baris padaAkterdapat sedikitnya satu elemen positif pada posisi kolom yang sama.
Dengan mempresentasikan graf G(V, E) pada gambar 2.1 dalam bentuk matriks adjacency A sebagai berikut, nilai scrambling index graf tersebut juga dapat diketahui. A=
0 1 0 1 0 1 0 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0
A2 =
2 0 2 0 1 0 2 0 2 1 2 0 3 1 1 0 2 1 3 1 1 1 1 1 2
sama telah dipenuhi. Sehingga diketahui nilai scrambling index dari graf tersebut adalah 2.
2.7 Scrambling Index dari Lingkaran Ganjil
Gao dan Shao (2013) dalam penelitiannya mengemukakan tentang scrambling index dari lingkaran ganjil. Scrambling index dari sebuah lingkaran atas n titik ganjil
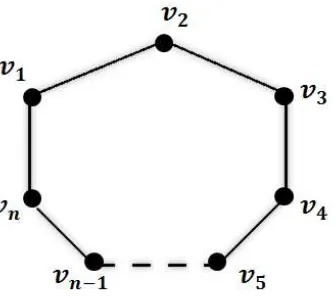
Cn :v1 ↔v2 ↔...↔vn−1 ↔vn↔v1 didefinisikan sebagai berikut:
Lemma 2.2 Andaikan Cn adalah sebuah lingkaran atas n titik ganjil, maka k(Cn) = (n−21)
Bukti. Jalan dengan panjang genap terpendek yang menghubungkan vn dengan vn−1 adalah jalan Wvn,vn−1 : vn ↔ v1 ↔ v2 ↔ ... ↔ vn−1 dengan panjang n−1.
Hal ini berakibat Kvn,vn−1(Cn) =
(n−1)
2 sehingga k(G)≥ (n−1)
2 .
Gambar 2.4. Lingkaran dengan panjang ganjil
Untuk dua titikvidanvj yang berbeda, telah diperlihatkan bahwa terdapat jalan yang menghubungkan vi dan vj dengan panjang genap t ≤ n−1. Hal ini berakibat untuk dua titik vi dan vj yang berbeda terdapat sebuah jalan yang menghubungkanvidanvj dengan panjang tepatn−1. Sehingga diperolehk(Cn)≤
(n−1)
2 . Maka terbukti k(Cn) = (n−1)