Akelbek, M and Kirkland, S. 2009a. Coefficients of Ergodicity and The Scrambling Index. Linear Algebra and its Applications. 430: 1111-1130.
Akelbek, M and Kirkland, S. 2009b. Primitive Digraphs with The Largest Scram-bling Index. Linear Algebra and its Applications. 430: 1099-1110.
Brualdi, R. A and Ryser, H.J. 1991. Combinatorial Matrix Theory. Cambridge University Press. Cambridge.
Fornasini, E and Valcher, M. E. 1997. Directed Graphs, 2D State Models, and Characteristic Polynomials of Irreducible Matrix Pairs.Linear Algebra. Appl. 263: 275-310.
Fornasini, E and Valcher, M. E. 1998. Primitivity Positive Matrix Pairs: Algebraic Characterization Graph Theoritic Description and 2D Systems Interpreta-tions. SIAM J. Matrix Anal. Appl. 19: 71-88.
Mulyono and Suwilo, S. 2014. The Scrambling Index of Two-Colored Wielandt Digraph. Universal Journal of Applied Mathematics. 2(6): 250-255.
Mulyono, Sumardi, H and Suwilo, S. 2015. The Scrambling Index of Primitive Two-colored Cycles whose Lengths Differ by 1.Far East J. Math. Sci. 96(1): 113-132.
METODOLOGI PENELITIAN
Berikut langkah - langkah dalam menentukan bentuk umum scrambling index dari digraf Hamilton dwiwarna atas n≡1 (mod 3) titik:
1. Mengecek primitifitas digraf Hamilton dwiwarna primitifD(2), yaitu
mem-bentuk matriks cycle M yang primitif dari D(2) atas n ≡ 1 (mod 3) titik,
terdiri dari dua cycle dengan panjang cycle satu adalahn−3 dan panjang cycle dua adalah n.
2. Mencari nilai scrambling index dariD(2) dengan (n−4)/3 busur biru
beru-rutan pada keduacycle menggunakan algoritma yang ditulis pada software MATLAB. Berikut algoritma untuk mencari scrambling index D(2) atas n≡1 (mod 3) titik.
a. Menginput matriks ketetanggaan merah R dan matriks ketetanggaan biru B dari D(2).
b. Menghitung (h, ℓ)-Hurwitz product, dinotasikan dengan (R, B)(h,ℓ).
Jika untuk setiap dua baris (R, B)(h,ℓ) terdapat sedikitnya satu entri
yang nilainya positif pada kolom yang sama, makak(D(2)) =h+ℓ.
3. Menentukan bentuk umum scrambling index dengan (n−4)/3 busur biru berurutan pada kedua cycle yang diperoleh pada (2), untukn ≥7.
4. Membuktikan bentuk umum yang diperoleh pada (3) dengan menentukan batas atas scrambling index yaitu k(D(2))≤h+ℓ dan batas bawah
scram-bling index yaitu k(D(2))≥ h+ℓ, dengan matriks cycle M yang diperoleh
pada (1). Bahwa batas atas diperoleh dari persamaan (2.2) dengan menen-tukan (h, ℓ) terlebih dahulu kemudian menunjukkan untuk setiap titik vw dimanaw= 1,2,3,· · · , ndiD(2), memiliki sebuah solusi bilangan bulat tak
negatifzuntuk beberapa lintasanPvwvtdarivw kevt, dengant = 1,2,· · · , n.
SCRAMBLING INDEX DIGRAF HAMILTON DWIWARNA
Bab ini akan memperlihatkan hasil yang diperoleh pada penelitian ini yaitu ben-tuk umum scrambling index dari digraf Hamilton dwiwarna primitif D(2) atas n
≡ 1 (mod 3) titik. Digraf Hamilton dwiwarna terdiri dari dua cycle. cycle satu yaituC1 :v1 →v2 → · · · →vn−3 →v1 dengan panjangn−3 dancycle dua yaitu C2 :v1 →v2 → · · · →vn−1 →vn→v1 dengan panjangn.
Akibat Teorema 2.2.3, diperoleh matriks cycle D(2) seperti ditunjukkan
Corollary berikut.
Corollary 4.1. Andaikan D(2) adalah sebuah digraf Hamilton dwiwarna primitif
terhubung kuat atas n ≡ 1 (mod 3) titik, n ≥ 7, terdiri dari dua cycle dengan panjang n−3 dan n. Matriks cycle D(2) adalah salah satu bentuk dari
M =
Bukti. Karena digraf Hamilton dwiwarnaD(2)terdiri dari dua warna dan
memi-liki duacyclemaka bentuk matrikscycledariD(2) adalah M =
r(C1) r(C2)
b(C1) b(C2)
.
Misalkan banyaknya busur merah pada cycle satu di D(2) adalah a, karena
pan-jang cycle satu adalahn−3 maka banyaknya busur biru pada cycle satu adalah
n−3−a. Misalkan juga banyaknya busur merah pada cycle dua di D(2) adalah
b, karena panjang cycle dua adalah n maka banyaknya busur biru pada cy-cle dua di D(2) adalah n −b. Sehingga Matriks cycle dari D(2) adalah M = KarenaD(2) adalah primitif, maka content dari matrikscycle adalah 1, sehingga
• Jika det(M) =n(a−b)+3b=−1, karenab≤nmaka nilaibyang memenuhi ketika (a−b) = −1, sehingga n(a−b) + 3b = −n+ 3b = −1, diperoleh
b= (n−1)/3 dana = (n−4)/3.
Dapat disimpulkan bahwa matriks cycle M salah satu bentuk berikut
M =
Perhatikan bahwa kedua matriks pada Corollary 4.1 hanya mempertukarkan elemen pada baris pertama dengan elemen pada baris kedua yaitu memper-tukarkan busur merah cycle satu menjadi busur biru cycle dua serta busur biru cycle satu menjadi busur merah cycle dua. Nilai scrambling index k(D(2))
meru-pakan penjumlahan busur merahhdan busur biruℓ. Sehingga dari kedua matriks tersebut memiliki nilai scrambling index yang sama, karena yang berbeda hanya banyaknya busur merahh dan busur biruℓ dari kedua matriks yang saling diper-tukarkan.
Dalam penelitian ini akan digunakan matrikscycledariD(2) adalah matriks
M =
adalah busur biru. Karena banyaknya busur biru pada cycle satu adalah (n − 4)/3 maka sebanyak (n−7)/3 busur biru terletak pada kedua cycle dan karena banyaknya busur biru padacycle dua adalah (n−1)/3 maka ada dua buah busur biru terletak pada C2 tetapi tidak terletak pada C1. Sehingga jumlah busur biru
D(2) adalah (n+ 2)/3. Selanjutnya, ketika busurv
n−3 →v1 adalah busur merah.
Karena banyaknya busur biru pada cycle satu adalah (n−4)/3 maka sebanyak (n−4)/3 busur biru terletak pada keduacycle dan karena banyaknya busur biru pada cycle dua adalah (n−1)/3 maka ada sebuah busur biru terletak pada C2
tetapi tidak terletak padaC1. Sehingga jumlah busur biruD(2) adalah (n−1)/3.
Ini menunjukkan bahwaD(2)primitif tersebut mempunyai paling banyak (n+2)/3
busur biru atau hanya (n−1)/3 busur biru. Penelitian kali ini, D(2) mempunyai (n −1)/3 busur biru yaitu sebanyak (n −4)/3 busur biru berada pada kedua cycle dan akan diletakkan secara berurutan dan sebuah busur biru terletak pada
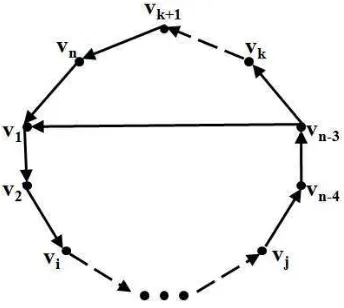
C2 tetapi tidak terletak pada C1. Representasi D(2) menggunakan grafis terlihat
seperti gambar 4.1.
Gambar 4.1 : Digraf Hamilton Dwiwarna Primitif.
Teorema 4.2. Andaikan D(2) adalah digraf Hamilton dwiwarna primitif terdiri
dari cycle Hamilton v1 → v2 → · · · → vn−1 → vn → v1 dan cycle v1 → v2 → · · · → vn−3 → v1 atas n ≡ 1 (mod 3) titik, n ≥ 7, dan memiliki (n −4)/3
busur biru berurutan pada kedua cycle. Jika d1 < d2, untuk 0 ≤ d1 ≤ 2 dan (2n+ 3d1−11)/3≤d2 ≤(2n−5)/3, maka
k(D(2)) = (2n2−8n+ 9 + (−n2+ 4n)d1+ (n2−4n+ 3)d2)/3.
Bukti. Langkah awal pembuktian ini akan memperlihatkan batas bawah scram-bling index yaitu k(D(2))≥ (2n2−8n+ 9 + (−n2+ 4n)d1+ (n2−4n+ 3)d2)/3.
Diasumsikan bahwa kvj,vk(vw) diperoleh dari (h, ℓ)-jalan dan andaikan terdapat
jalanvj
(h,ℓ)
−→vw dan jalanvk
(h,ℓ)
−→vw dengan vw ∈D(2), didefinisikan bahwa
e1 =b(C2)r(Pvjvw)−r(C2)b(Pvjvw) dan (4.1)
e2 =r(C1)b(Pvkvw)−b(C1)r(Pvkvw). (4.2)
Jika terdapat dua jalanvj →vw maka nilaie1yang memenuhi untuk menentukan batas bawah adalah nilaie1 yang terkecil. Jika terdapat dua jalanvk→vw maka nilai e2 yang memenuhi untuk menentukan batas bawah adalah nilai e2 yang
terkecil.
Terdapat empat kasus yang bergantung pada posisi titikvw.
Kasus 1 : Titikvw berada pada 1≤w≤i.
Terdapat dua buah lintasanPvjvw dari titik vj kevw yaitu l1 = (d(v1, vw) +d2,
0)-lintasan dan l2 = (d(v1, vw) +d2 + 2,1)-lintasan. Dengan menggunakan nilai e1 pada persamaan (4.1) dan lintasanl1 diperoleh,
e1 = ((n−1)/3)(d(v1, vw) +d2)−((2n+ 1)/3)(0)
dan dengan menggunakan nilaie1pada persamaan (4.1) dan lintasanl2diperoleh,
e1 = ((n−1)/3)(d(v1, vw) +d2 + 2)−((2n+ 1)/3)(1)
= (nd(v1, vw) +nd2−d(v1, w)−d2−3)/3 (4.4) Oleh karena itu, nilai e1 yang dipilih adalah nilai e1 pada persamaan (4.4).
Terdapat sebuah lintasan Pvkvw dari titik vk kevw yaitu (d(v1, vw) +d1,
1)-lintasan. Dengan menggunakan lintasan ini dan nilai e2 pada persamaan (4.2)
diperoleh,
e2 = ((2n−5)/3)(1)−((n−4)/3)(d(v1, vw) +d1)
= (2n−5−nd(v1, vw)−nd1 + 4d(v1, vw) + 4d1)/3. (4.5)
Oleh Lemma 2.4.2, dengan menggunakan nilaie1 pada persamaan (4.4) dan nilai e2 pada persamaan (4.5) disimpulkan bahwa
kvj,vk(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n2−8n+ 9 + (−n2+ 4n)d1+ (n2−4n+ 3)d2)/3 +d(v1, w)
untuk setiap vw pada 1≤w≤i.
Kasus 2 : Titikvw berada pada i+ 1 ≤w≤j.
Terdapat dua buah lintasan Pvjvw dari titik vj kevw yaitu l1 = (d(v1, vw) +d2−
d(vi, vw), d(vi, vw))-lintasan danl2 = (d(v1, vw) +d2+ 2−d(vi, vw),1 +d(vi, v w))-lintasan. Dengan menggunakan nilai e1 pada persamaan (4.1) dan lintasan l1
diperoleh,
e1 = ((n−1)/3)(d(v1, vw) +d2−d(vi, vw))−((2n+ 1)/3)(d(vi, vw)) = (nd(v1, vw) +nd2−3nd(vi, vw)−d(v1, vw)−d2)/3 (4.6) dan dengan menggunakan nilaie1pada persamaan (4.1) dan lintasanl2diperoleh,
e1 = ((n−1)/3)(d(v1, vw) +d2+ 2−d(vi, vw))−((2n+ 1)/3)(1 +d(vi, vw))) = (nd(v1, vw) +nd2−3nd(vi, vw)−d(v1, vw)−d2−3)/3. (4.7) Oleh karena itu, nilai e1 yang dipilih adalah nilai e1 pada persamaan (4.7).
Terdapat sebuah lintasan Pvkvw dari titik vk ke vw yaitu (d(v1, vw) +d1 −
d(vi, vw),1 +d(vi, vw))-lintasan. Dengan menggunakan lintasan ini dan nilai e2 pada persamaan (4.2) diperoleh,
e2 = ((2n−5)/3)(1 +d(vi, vw))−((n−4)/3)(d(v1, vw) +d1−d(vi, vw))
Oleh Lemma 2.4.2, dengan menggunakan nilaie1 pada persamaan (4.7) dan nilai e2 pada persamaan (4.8) disimpulkan bahwa
kvj,vk(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n2−8n+ 9 + (−n2+ 4n)d
1+ (n2−4n+ 3)d2)/3 +d(v1, vw)
untuk setiap vw pada i+ 1≤w≤j.
Kasus 3 : Titikvw berada pada j + 1≤w≤k.
Terdapat sebuah lintasan Pvjvw dari titik vj ke vw yaitu (d2 + 3−d(vw, v1),
0)-lintasan. Karena d(vw, v1) +d(v1, vw) = n, sehingga lintasan menjadi (d2 −n+ 3 +d(v1, vw),0)-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada persamaan (4.1) diperoleh,
e1 = ((n−1)/3)(d2−n+ 3 +d(v1, vw))−((2n+ 1)/3)(0)
= (nd(v1, vw)−n2+ 4n+nd2−d(v1, vw)−d2 −3)/3. (4.9)
Terdapat sebuah lintasan Pvkvw dari titik vk ke vw yaitu (d(v1, vw) +d1 −
((n−4)/3),(n−1)/3)-lintasan. Dengan menggunakan lintasan ini dan nilai e2
pada persamaan (4.2) diperoleh,
e2 = ((2n−5)/3)((n−1)/3)−((n−4)/3)(d(v1, vw) +d1−((n−4)/3))
= (n2 −5n+ 7−nd(v1, vw)−nd1+ 4d(v1, vw) + 4d1)/3. (4.10)
Oleh Lemma 2.4.2, dengan menggunakan nilaie1 pada persamaan (4.9) dan nilai e2 pada persamaan (4.10) disimpulkan bahwa
kvj,vk(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n2−8n+ 9 + (−n2+ 4n)d1+ (n2−4n+ 3)d2)/3 +d(v1, vw)
untuk setiap vw pada j+ 1 ≤w≤k.
Kasus 4 : Titikvw berada pada k+ 1 ≤w≤n.
Terdapat sebuah lintasan Pvjvw dari titik vj ke vw yaitu (d2 + 2−d(vw, v1),
1)-lintasan. Karena d(vw, v1) +d(v1, vw) = n, sehingga lintasan menjadi (d2+ 2−
n +d(v1, vw),1)-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada persamaan (4.1) diperoleh,
e1 = ((n−1)/3)(d2+ 2−n+d(v1, vw))−((2n+ 1)/3)(1)
Terdapat sebuah lintasan Pvkvw dari titik vk kevw yaitu (d1−d(vw, v1),
1)-lintasan. Karena d(vw, v1) +d(v1, vw) = n, sehingga lintasan menjadi (d1 −n+
d(v1, vw),1)-lintasan. Dengan menggunakan lintasan ini dan nilai e2 pada per-samaan (4.2) diperoleh,
Dengan mempertimbangkan vk → vw jalan. Karena lintasan Pvkvw adalah (d1 −
d(vw, v1),1)-lintasan dan solusi sistem
dan z2 = 0. Ini menunjukkan tidak terdapat vk
(p,q)
−→ vw. Bahwa jalan vk → vw terpendek yang memuat p busur merah dan q busur biru adalah sebuah jalan dengan (4n2 −17n+ 13 +d
Dari keempat kasus yang bergantung pada posisi titik vw diperoleh
kvj,vk(vw)≥(2n memiliki derajat masuk paling besar. Oleh karena itu
kvj,vk(D
dan karena k(D(2))≥max
Selanjutnya, pembuktian ini akan memperlihatkan batas atas scrambling index yaitu k(D(2)) ≤(2n2−8n+ 9 + (−n2+ 4n)d1+ (n2 −4n+ 3)d2)/3. Dari
pembuktian batas bawah diperoleh titikv1 memiliki nilai scrambling index terke-cil. Akan ditunjukkan bahwa untuk setiap titik vw, w = 1,2,3,· · · , n, terdapat
Berdasarkan persamaan (2.2), akan ditunjukkan sistem
Mz+
mempunyai sebuah solusi bilangan bulat tak negatif untuk beberapa lintasan
Pvwv1 dari titikvw kev1.
Solusi dari sistem (4.13) adalah vektor bilangan bulat berikut
z=M−1
Karena M memiliki det = 1, maka M memiliki invers yaitu
M−1 =
lintasan ini dan nilai z1 pada persamaan (4.14), diperoleh
Karenar(Pvwv1)≤(2n−5)/3 dand2 ≥(2n+ 3d1−11)/3 makaz1 ≥(2n
2−13n−
7)/9, untuk n = 7 diperoleh z1 ≥ 0. Dengan menggunakan lintasan ini dan nilai
z2 pada persamaan (4.15), diperoleh
z2 = (−2n2+ 19n−35 + (−3n+ 12)d1+ (3n−12)r(Pvwv1))/9.
Karena r(Pvwv1)≥d2 dan d1 < d2 makaz2 ≥(−2n
2+ 22n−47)/9, untuk n= 7
diperoleh z2 ≥1.
Jika titikvw berada padai+ 1≤w≤j, maka ada sebuah (d2+ 2, b(Pvwv1
))-lintasan dari titik vw ke v1 dengan 1 ≤ b(Pvwv1) ≤ (n −4)/3. Menggunakan
lintasan ini dan nilai z1 pada persamaan (4.14), diperoleh
z1 = ((2n+ 1)b(Pvwv1) + (−2n−1))/3.
Karenab(Pvwv1)≥1 makaz1 ≥0. Dengan menggunakan lintasan ini dan nilaiz2
pada persamaan (4.15), diperoleh
z2 = ((−n+ 4)d1+ (n−4)d2+ (4n−13) + (−2n+ 5)b(Pvwv1))/3.
Karenab(Pvwv1)≤(n−4)/3 dand1 < d2 makaz2 ≥(−2n
2+ 28n−71)/9, untuk n = 7 diperolehz2 ≥3.
Jika titik vw berada pada j + 1 ≤ w ≤ k, maka ada sebuah (r(Pvwv1),
1)-lintasan dari titikvw kev1 dengand1 ≤r(Pvwv1)≤d2+ 1. Menggunakan lintasan
ini dan nilai z1 pada persamaan (4.14), diperoleh
z1 = ((n−1)d2 + (−n+ 1)r(Pvwv1) + (2n−2))/3.
Karena r(Pvwv1) ≤ d2+ 1 maka z1 ≥ (n−1)/3), untuk n = 7 diperoleh z1 ≥ 2.
Dengan menggunakan lintasan ini dan nilaiz2 pada persamaan (4.15), diperoleh
z2 = ((−n+ 4)d1+ (n−4)r(Pvwv1))/3.
Karena r(Pvwv1)≥d1 maka z2 ≥0.
Jika titik vw berada pada k+ 1 ≤ w ≤ n, maka ada sebuah (r(Pvwv1),
0)-lintasan dari titik vw kev1 dengan 1≤r(Pvwv1)≤d1. Menggunakan lintasan ini
dan nilai z1 pada persamaan (4.14), diperoleh
z1 = ((n−1)d2+ (−n+ 1)r(Pvwv1)−3)/3.
Karena r(Pvwv1) ≤ d1 dan d1 < d2 maka z1 ≥ (n−4)/3, untuk n = 7 diperoleh z1 ≥ 1. Dengan menggunakan lintasan ini dan nilai z2 pada persamaan (4.15), diperoleh
Karena r(Pvwv1) ≥ 1 dan d1 ≤ 2 maka z2 ≥ (n−1)/3, untuk n = 7 diperoleh z2 ≥2.
Oleh karena itu, untuk setiap w = 1,2,3,· · · , n, terdapat sebuah lintasan
Pvwv1 dari vw ke v1 sedemikian hingga sistem (4.13) mempunyai solusi bilangan
bulat tak negatif. Oleh proposisi 2.4.1 untuk setiap titik vw, w = 1,2,3,· · · , n
Teorema 4.3. Andaikan D(2) adalah digraf Hamilton dwiwarna primitif terdiri
dari cycle Hamilton v1 → v2 → · · · → vn−1 → vn → v1 dan cycle v1 → v2 → · · · → vn−3 → v1 atas n ≡ 1 (mod 3) titik, n ≥ 7, dan memiliki (n −4)/3
busur biru berurutan pada kedua cycle. Jika d1 < d2, untuk 0 ≤ d1 ≤ 3 dan (d1+ 1)≤d2 ≤(2n+ 3d1−14)/3, maka
k(D(2)) = (2n3 −13n2+ 11n+ 27 + 9d2)/9.
Bukti. Langkah awal pembuktian ini akan memperlihatkan batas bawah scram-bling index yaituk(D(2))≥(2n3−13n2+ 11n+ 27 + 9d
2)/9. Diasumsikan bahwa kvj,vi(vw) diperoleh dari (h, ℓ)-jalan dan andaikan terdapat jalan vj
Jika terdapat dua jalanvj →vw maka nilaie1yang memenuhi untuk menentukan
batas bawah adalah nilai e1 yang terkecil. Jika terdapat dua jalanvi →vw maka nilai e2 yang memenuhi untuk menentukan batas bawah adalah nilai e2 yang terkecil.
Terdapat empat kasus yang bergantung pada posisi titikvw.
Kasus 1 : Titikvw berada pada 1≤w≤i.
Terdapat dua buah lintasanPvjvw dari titik vj kevw yaitu l1 = (d(v1, vw) +d2,
pada persamaan (4.16) dan lintasan l1 diperoleh,
e1 = ((n−1)/3)(d(v1, vw) +d2)−((2n+ 1)/3)(0)
= (nd(v1, vw) +nd2−d(v1, vw)−d2)/3 (4.18)
dan dengan menggunakan persamaan (4.16) dan lintasan l2 diperoleh,
e1 = ((n−1)/3)(d(v1, vw) +d2 + 2)−((2n+ 1)/3)(1)
= (nd(v1, vw) +nd2−d(v1, vw)−d2−3)/3. (4.19) Oleh karena itu, nilai e1 yang dipilih adalah nilai e1 pada persamaan (4.19).
Terdapat dua buah lintasanPvivw dari titikvikevwyaitul3 = (d2+d(v1, vw),
(n −4)/3)-lintasan dan l4 = (d2 + 2 + d(v1, vw),(n − 1)/3)-lintasan. Dengan
menggunakan nilai e2 pada persamaan (4.17) dan lintasan l3 diperoleh,
e2 = ((2n−5)/3)((n−4)/3)−((n−4)/3)(d2+d(v1, vw))
= (2n2−13n+ 20−3nd2−3nd(v1, vw) + 12d2+ 12d(v1, vw))/9 (4.20) dan dengan menggunakan nilai e2 pada persamaan (4.17) dan lintasan l4 diper-oleh,
e2 = ((2n−5)/3)((n−1)/3)−((n−4)/3)(d2+ 2 +d(v1, vw))
= (2n2−13n+ 29−3nd2−3nd(v1, vw) + 12d2+ 12d(v1, vw))/9. (4.21) Oleh karena itu, nilai e2 yang dipilih adalah nilai e2 pada persamaan (4.20).
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.19) dan nilai e2 pada persamaan (4.20) disimpulkan bahwa
kvj,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2+ 11n+ 27 + 9d2)/9 +d(v1, vw) untuk setiap vw pada 1≤w≤i.
Kasus 2 : Titikvw berada pada i+ 1 ≤w≤j.
Terdapat dua buah lintasanPvjvw dari titikvj kevwyaitul1 = ((2n−5)/3, d(v1, vw)
−d(v1, vi))-lintasan dan l2 = ((2n+ 1)/3, d(v1, vw)−d(v1, vi))-lintasan. Karena
d(v1, vi) + (n − 4)/3 + d2 = n − 3, sehingga kedua lintasan tersebut menja-di l1 = ((2n − 5)/3, d(v1, vw)−((2n −5 −3d2)/3))-lintasan dan l2 = ((2n + 1)/3, d(v1, vw)−((2n−5−3d2)/3) + 1)-lintasan. Dengan menggunakan nilaie1
pada persamaan (4.16) dan lintasan l1 diperoleh,
e1 = ((n−1)/3)((2n−5)/3)−((2n+ 1)/3)((3d(v1, vw)−2n+ 5 + 3d2)/3)
dan dengan menggunakan nilai e1 pada persamaan (4.16) dan lintasan l2 diper-oleh,
e1 = ((n−1)/3)((2n+ 1)/3)−((2n+ 1)/3)((3d(v1, vw)−2n+ 8 + 3d2)/3) = (6n2−15n−9−6nd2−6nd(v1, vw)−3d2−3d(v1, vw))/9. (4.23)
Oleh karena itu, nilai e1 yang dipilih adalah nilai e1 pada persamaan (4.23).
Terdapat sebuah lintasan Pvivw dari titik vi ke vw yaitu (0, d(v1, vw) −
d(v1, vi))-lintasan. Karena d(v1, vi) + (n−4)/3 +d2 = n−3, sehingga lintasan menjadi (0, d(v1, vw)−((2n−5−3d2)/3))-lintasan. Dengan menggunakan lintasan ini dan nilai e2 pada persamaan (4.17) diperoleh,
e2 = ((2n−5)3)((3d(v1, vw)−2n+ 5 + 3d2)/3)−((n−4)/3)(0)
= (−4n2+ 20n−25 + 6nd2+ 6nd(v1, vw)−15d2−15d(v1, vw))/9 (4.24)
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.23) dan nilai e2 pada persamaan (4.24) disimpulkan bahwa
kvj,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2+ 11n+ 27 + 9d2)/9 +d(v1, vw)
untuk setiap vw pada i+ 1≤w≤j.
Kasus 3 : Titikvw berada pada j + 1≤w≤k.
Terdapat sebuah lintasanPvjvw dari titikvj kevw yaitu (d(v1, vw)−(n−3−d2),
0)-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada persamaan (4.16) diperoleh,
e1 = ((n−1)/3)(d(v1, vw)−(n−3−d2))−((2n+ 1)/3)(0)
= (nd(v1, vw)−n2+ 4n+nd2−d(v1, vw)−d2−3)/3. (4.25)
Terdapat sebuah lintasan Pvivw dari titik vi ke vw yaitu (d(v1, vw)−(n −
3−d2),(n−4)/3)-lintasan. Dengan menggunakan lintasan ini dan nilaie2 pada persamaan (4.17) diperoleh,
e2 = ((2n−5)/3)((n−4)/3)−((n−4)/3)(d(v1, vw)−(n−3−d2))
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.25) dan nilai e2 pada persamaan (4.26) disimpulkan bahwa
kvj,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2+ 11n+ 27 + 9d2)/9 +d(v1, vw)
untuk setiap vw pada j+ 1 ≤w≤k.
kasus 4 : Titikvw berada pada k+ 1≤w≤n.
Terdapat sebuah lintasanPvjvw dari titikvj kevw yaitu (d(v1, vw)−1−(n−3−
d2),1)-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada persamaan (4.16) diperoleh,
e1 = ((n−1)/3)(d(v1, vw)−1−(n−3−d2))−((2n+ 1)/3)(1)
= (nd(v1, vw)−n2+n+nd2−d(v1, vw)−d2−3)/3. (4.27)
Terdapat sebuah lintasanPvivw dari titikvi kevw yaitu (d(v1, vw)−1−(n−
3−d2),(n−1)/3)-lintasan. Dengan menggunakan lintasan ini dan nilaie2 pada
persamaan (4.17) diperoleh,
e2 = ((2n−5)/3)((n−1)/3)−((n−4)/3)(d(v1, vw)−1−(n−3−d2)) = (5n2−25n+ 29−3nd(v1, vw)−3nd2+ 12d(v1, vw) + 12d2)/9 (4.28)
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.27) dan nilai e2 pada persamaan (4.28) disimpulkan bahwa
kvj,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2+ 11n+ 27 + 9d2)/9 +d(v1, vw)
untuk setiap vw pada k+ 1≤w≤n.
Dari keempat kasus yang bergantung pada posisi titik vw diperoleh
kvj,vi(vw)≥(2n
3−13n2+ 11n+ 27 + 9d2)/9 +d(v1, vw).
Berdasarkan definisi, kvj,vi(D
(2)) = min
vw∈V(D(2)){kvj,vi(vw)}. Nilai kvj,vi(vw) yang
minimum adalah ketika d(v1, vw) = 0 yakni ketika vw = v1, yaitu titik yang memiliki derajat masuk paling besar. Oleh karena itu
kvj,vi(D
dan karena k(D(2))≥max
Selanjutnya, pembuktian ini akan memperlihatkan batas atas scrambling index yaitu k(D(2)) ≤(2n3−13n2+ 11n+ 27 + 9d2)/9. Dari pembuktian batas
bawah diperoleh titik v1 memiliki nilai scrambling index terkecil. Akan ditun-jukkan bahwa untuk setiap titik vw, w = 1,2,3,· · · , n, terdapat jalan vw
Berdasarkan persamaan (2.2), akan ditunjukkan sistem
Mz+
mempunyai sebuah solusi bilangan bulat tak negatif untuk beberapa lintasan
Pvwv1 dari titikvw kev1.
Solusi dari sistem (4.29) adalah vektor bilangan bulat berikut
z=M−1
Karena M memiliki det = 1, maka M memiliki invers yaitu
M−1 =
lintasan ini dan nilai z1 pada persamaan (4.30), diperoleh
z1 = (2n2−7n−13 + (3n−3)d2+ (−3n+ 3)r(Pvwv1))/9.
Karenar(Pvwv1)≤(2n−5)/3 dand2 ≥(d1+ 1) makaz1 ≥(n−7)/3, untukn= 7
dipeoleh z1 ≥0. Dengan menggunakan lintasan ini dan nilai z2 pada persamaan (4.31), diperoleh
Karena r(Pvwv1)≥d2 maka z2 ≥0.
Jika titikvw berada padai+ 1≤w≤j, maka ada sebuah (d2+ 2, b(Pvwv1
))-lintasan dari titik vw ke v1 dengan 1 ≤ b(Pvwv1) ≤ (n −4)/3. Menggunakan
lintasan ini dan nilai z1 pada persamaan (4.30), diperoleh
z1 = ((2n+ 1)b(Pvwv1) + (−2n−1))/3.
Karenab(Pvwv1)≥1 makaz1 ≥0. Dengan menggunakan lintasan ini dan nilaiz2
pada persamaan (4.31), diperoleh
z2 = (2n2 −7n−4 + (−6n+ 15)b(Pvwv1))/9.
Karenab(Pvwv1)≤(n−4)/3 makaz2 ≥(2n−8)/3, untukn = 7 diperolehz2 ≥2.
Jika titik vw berada pada j + 1 ≤ w ≤ k, maka ada sebuah (r(Pvwv1),
1)-lintasan dari titikvw kev1 dengand1 ≤r(Pvwv1)≤d2+ 1. Menggunakan lintasan
ini dan nilai z1 pada persamaan (4.30), diperoleh
z1 = ((n−1)d2 + (−n+ 1)r(Pvwv1) + (2n−2))/3.
Karena r(Pvwv1) ≤ d2 + 1 maka z1 ≥ (n−1)/3, untuk n = 7 diperoleh z1 ≥ 2.
Dengan menggunakan lintasan ini dan nilaiz2 pada persamaan (4.31), diperoleh
z2 = (2n2−19n+ 35 + (−3n+ 12)d2+ (3n−12)r(Pvwv1))/9.
Karena r(Pvwv1) ≥ d1 dan d2 ≤ (2n+ 3d1 −14)/3 maka z2 ≥ (n−7)/3, untuk n = 7 makaz2 ≥0.
Jika titik vw berada pada k+ 1 ≤ w ≤ n, maka ada sebuah (r(Pvwv1),
0)-lintasan dari titik vw kev1 dengan 1≤r(Pvwv1)≤d1. Menggunakan lintasan ini
dan nilai z1 pada persamaan (4.30), diperoleh
z1 = ((n−1)d2+ (−n+ 1)r(Pvwv1)−3)/3.
Karenar(Pvwv1)≤d1 dand2 ≥d1+1 makaz1 ≥(n−4)/3, untukn = 7 diperoleh z1 ≥ 1. Dengan menggunakan lintasan ini dan nilai z2 pada persamaan (4.31), diperoleh
z2 = (2n2−13n+ 20 + (−3n+ 12)d2+ (3n−12)r(Pvwv1))/9.
Karena r(Pvwv1) ≥ 1 dan d2 ≤ (2n + 3d1 −14)/3 maka z2 ≥ (n −4)/3, untuk n = 7 makaz2 ≥1.
Oleh karena itu, untuk setiap w = 1,2,3,· · · , n, terdapat sebuah lintasan
bulat tak negatif. Oleh proposisi 2.4.1 untuk setiap titik vw, w = 1,2,3,· · · , n terdapat sebuah jalan vw
(h,ℓ)
−→v1 dengan
h ℓ
=
(4n3−24n2+ 9n+ 65 + 27d2)/27
(2n3−15n2+ 24n+ 16)/27
sehingga, k(D(2)) ≤ (2n3 −13n2 + 11n+ 27 + 9d2)/9. Karenanya, disimpulkan
bahwa k(D(2)) = (2n3 − 13n2 + 11n + 27 + 9d2)/9, untuk 0 ≤ d1 ≤ 3 dan
(d1+ 1)≤d2 ≤(2n+ 3d1−14)/3, ketika d1 < d2.
Teorema 4.4. Andaikan D(2) adalah digraf Hamilton dwiwarna primitif terdiri
dari cycle Hamilton v1 → v2 → · · · → vn−1 → vn → v1 dan cycle v1 → v2 → · · · → vn−3 →v1 atas n ≡ 1 (mod 3) titik, n ≥7, dan memiliki (n−4)/3 busur
biru berurutan pada kedua cycle. Jika d1 ≥d2, untuk 1≤d1 ≤3 dan 1≤d2 ≤3, maka
k(D(2)) = (2n3−13n2+ 20n+ (3n2−12n+ 9)d1 + (−3n2+ 12n)d2)/9.
Bukti. Langkah awal pembuktian ini akan memperlihatkan batas bawah scram-bling index yaitu
k(D(2))≥(2n3−13n2+ 20n+ (3n2−12n+ 9)d1+ (−3n2+ 12n)d2)/9.
Diasumsikan bahwakvk+1,vi(vw) diperoleh dari (h, ℓ)-jalan dan andaikan terdapat
jalanvk+1 (h,ℓ)
−→vw dan jalan vi
(h,ℓ)
−→vw denganvw ∈D(2), didefinisikan bahwa
e1 =b(C2)r(Pvk+1vw)−r(C2)b(Pvk+1vw) dan (4.32)
e2 =r(C1)b(Pvivw)−b(C1)r(Pvivw) (4.33)
Jika terdapat dua jalan vk+1 → vw maka nilai e1 yang memenuhi untuk menen-tukan batas bawah adalah nilaie1 yang terkecil. Jika terdapat dua jalanvi →vw maka nilai e2 yang memenuhi untuk menentukan batas bawah adalah nilai e2
yang terkecil.
Terdapat empat kasus yang bergantung pada posisi titikvw.
Kasus 1 : Titikvw berada pada 1≤w≤i.
Terdapat sebuah lintasan Pvk+1vw dari titik vk+1 ke vw yaitu (d(v1, vw) +d1,
0)-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada persamaan (4.32) diperoleh,
e1 = ((n−1)/3)(d(v1, vw) +d1)−((2n+ 1)/3)(0)
Terdapat dua buah lintasanPvivw dari titikvikevwyaitul1 = (d2+d(v1, vw),
(n −4)/3)-lintasan dan l2 = (d2 + 2 + d(v1, vw),(n − 1)/3)-lintasan. Dengan menggunakan nilai e2 pada persamaan (4.33) dan lintasan l1 diperoleh,
e2 = ((2n−5)/3)((n−4)/3)−((n−4)/3)(d2+d(v1, vw))
= (2n2−13n+ 20−3nd2−3nd(v1, vw) + 12d2+ 12d(v1, vw))/9 (4.35)
dan dengan menggunakan nilai e2 pada persamaan (4.33) dan lintasan l2
diper-oleh,
e2 = ((2n−5)/3)((n−1)/3)−((n−4)/3)(d2+ 2 +d(v1, vw))
= (2n2−13n+ 29−3nd2−3nd(v1, vw) + 12d2+ 12d(v1, vw))/9 (4.36)
Oleh karena itu, nilai e2 yang dipilih adalah nilai e2 pada persamaan (4.35).
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.34) dan nilai e2 pada persamaan (4.35) disimpulkan bahwa
kvk+1,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2 + 20n+ (3n2−12n+ 9)d1+ (−3n2+ 12n)d2)/9 +d(v1, vw)
untuk setiap vw pada 1≤w≤i.
Kasus 2 : Titikvw berada pada i+ 1 ≤w≤j.
Terdapat sebuah lintasanPvk+1vw dari titikvk+1kevwyaitu (d1+d(v1, vi), d(v1, vw)
−d(v1, vi))-lintasan. Karena d(v1, vi) + (n−4)/3 +d2 = n−3, sehingga kedua lintasan tersebut menjadi (d1+ (2n−5−3d2)/3, d(v1, vw)−((2n−5−3d2)/ 3))-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada persamaan (4.32) diperoleh,
e1 = ((n−1)/3)((3d1+ 2n−5−3d2)/3)−((2n+ 1)/3)((3d(v1, vw)−2n+ 5 + 3d2)/3)
= (6n2−15n+ 3nd1−9nd2−6nd(v1, vw)−3d1−3d(v1, vw))/9. (4.37)
Terdapat sebuah lintasan Pvivw dari titik vi ke vw yaitu (0, d(v1, vw) −
d(v1, vi))-lintasan. Karena d(v1, vi) + (n−4)/3 +d2 = n−3, sehingga lintasan menjadi (0, d(v1, vw)−((2n−5−3d2)/3))-lintasan. Dengan menggunakan lintasan ini dan nilai e2 pada persamaan (4.33) diperoleh,
e2 = ((2n−5)/3)((3d(v1, vw)−2n+ 5 + 3d2)/3)−((n−4)/3)(0) = (−4n2+ 20n−25 + 6nd
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.37) dan nilai e2 pada persamaan (4.38) disimpulkan bahwa
kvk+1,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2 + 20n+ (3n2−12n+ 9)d1+ (−3n2+ 12n)d2)/9 +d(v1, vw)
untuk setiap vw pada i+ 1≤w≤j.
Kasus 3 : Titikvw berada pada j + 1≤w≤k.
Terdapat sebuah lintasanPvk+1vw dari titikvk+1 kevw yaitu (d1+d(v1, vw)−((n−
4)/3),(n−4)/3)-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada persamaan (4.32) diperoleh,
e1 = ((n−1)/3)((3d1+ 3d(v1, vw)−n+ 4)/3)−((2n+ 1)/3)((n−4)/3) = (3nd(v1, vw)−3n2+ 12n+ 3nd1 −3d(v1, vw)−3d1)/9. (4.39)
Terdapat sebuah lintasan Pvivw dari titik vi ke vw yaitu (d(v1, vw)−(n −
3−d2),(n−4)/3)-lintasan. Dengan menggunakan lintasan ini dan nilaie2 pada
persamaan (4.33) diperoleh,
e2 = ((2n−5)/3)((n−4)/3)−((n−4)/3)(d(v1, vw)−(n−3−d2))
= (5n2−34n+ 56−3nd(v1, vw)−3nd2+ 12d(v1, vw) + 12d2)/9. (4.40)
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.39) dan nilai e2 pada persamaan (4.40) disimpulkan bahwa
kvk+1,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2 + 20n+ (3n2−12n+ 9)d1+ (−3n2+ 12n)d2)9 +d(v1, vw)
untuk setiap vw pada j+ 1 ≤w≤k.
Kasus 4 : Titikvw berada pada k+ 1 ≤w≤n.
Terdapat sebuah lintasan Pvk+1vw dari titik vk+1 ke vw yaitu (d1 −d(vw, v1),
0)-lintasan. Karena d(v1, vw) +d(vw, v1) = n, sehingga lintasan menjadi (d1 −n+
d(v1, vw),0)-lintasan. Dengan menggunakan lintasan ini dan nilai e1 pada per-samaan (4.32) diperoleh,
e1 = ((n−1)/3)(d1−n+d(v1, vw))−((2n+ 1)/3)(0)
Terdapat sebuah lintasanPvivw dari titikvi kevw yaitu (d(v1, vw)−1−(n−
3−d2),(n−1)/3)-lintasan. Dengan menggunakan lintasan ini dan nilaie2 pada persamaan (4.33) diperoleh,
e2 = ((2n−5)/3)((n−1)/3)−((n−4)/3)(d(v1, vw)−1−(n−3−d2)) = (5n2−25n+ 29−3nd(v1, vw)−3nd2+ 12d(v1, vw) + 12d2)/9. (4.42)
Oleh Lemma 2.4.2, dengan menggunakan nilai e1 pada persamaan (4.41) dan nilai e2 pada persamaan (4.42) disimpulkan bahwa
kvk+1,vi(vw)≥ℓ(C1)e1+ℓ(C2)e2 = (n−3)e1+ (n)e2
= (2n3−13n2 + 20n+ (3n2−12n+ 9)d1+ (−3n2+ 12n)d2)/9 +d(v1, vw)
untuk setiap vw pada k+ 1≤w≤n.
Dari keempat kasus yang bergantung pada posisi titik vw diperoleh
kvk+1,vi(vw)≥(2n memiliki derajat masuk paling besar. Oleh karena itu
kvk+1,vi(D
Selanjutnya, pembuktian ini akan memperlihatkan batas atas scrambling index yaituk(D(2))≤(2n3−13n2+ 20n+ (3n2−12n+ 9)d
1+ (−3n2+ 12n)d2)/9.
Dari pembuktian batas bawah diperoleh titik v1 memiliki nilai scrambling index
terkecil. Akan ditunjukkan bahwa untuk setiap vw, w = 1,2,3,· · · , n, terdapat
Berdasarkan persamaan (2.2), akan ditunjukkan sistem
mempunyai sebuah solusi bilangan bulat tak negatif untuk beberapa lintasan
Pvwv1 dari titikvw kev1.
Solusi dari sistem (4.43) adalah vektor bilangan bulat berikut
z=M−1
h−r(Pvwv1) ℓ−b(Pvwv1)
.
Karena M memiliki det = 1, maka M memiliki invers yaitu
M−1 =
(n−1)/3 (−2n−1)/3 (4−n)/3 (2n−5)/3
,
sehingga diperoleh
z1 = ((n−1)d1+ (−n+ 1)r(Pvwv1) + (2n+ 1)b(Pvwv1))/3 (4.44) z2 = ((2n2−13n+ 20) + (−3n+ 12)d2+ (3n−12)r(Pvwv1) + (−6n+ 15)b(Pvwv1))/9.
(4.45)
Jika titikvw berada pada 1≤w≤i, maka ada sebuah (r(Pvwv1),(n−4)/
3)-lintasan dari titik vw ke v1 dengan d2 ≤ r(Pvwv1) ≤ (2n−5)/3. Menggunakan
lintasan ini dan nilai z1 pada persamaan (4.44), diperoleh
z1 = (2n2−7n−4 + (3n−3)d1+ (−3n+ 3)r(Pvwv1))/9.
Karena r(Pvwv1) ≤ (2n−5)/3 dan d1 ≥ 1 maka z1 ≥ (n −4)/3, untuk n = 7
diperolehz1 ≥1. Dengan menggunakan lintasan ini dan nilaiz2 pada persamaan
(4.45), diperoleh
z2 = ((−n+ 4)d2+ (n−4)r(Pvwv1))/3.
Karena r(Pvwv1)≥d2 maka z2 ≥0.
Jika titikvw berada padai+ 1≤w≤j, maka ada sebuah (d2+ 2, b(Pvwv1
))-lintasan dari titik vw ke v1 dengan 1 ≤ b(Pvwv1) ≤ (n −4)/3. Menggunakan
lintasan ini dan nilai z1 pada persamaan (4.44), diperoleh
z1 = ((2n+ 1)b(Pvwv1) + (−2n+ 2) + (n−1)d1+ (−n+ 1)d2)/3.
Karena b(Pvwv1) ≥ 1 dan d1 ≥ d2 maka z1 ≥ 1. Dengan menggunakan lintasan
ini dan nilai z2 pada persamaan (4.45), diperoleh
z2 = (2n2 −7n−4 + (−6n+ 15)b(Pvwv1))/9.
Jika titik vw berada pada j + 1 ≤ w ≤ k, maka ada sebuah (r(Pvwv1),
1)-lintasan dari titikvw kev1 dengand1 ≤r(Pvwv1)≤d2+ 1. Menggunakan lintasan
ini dan nilai z1 pada persamaan (4.44), diperoleh
z1 = ((n−1)d1+ (−n+ 1)r(Pvwv1) + (2n+ 1))/3.
Karenar(Pvwv1)≤d2+1 dand1 ≥d2 makaz1 ≥(n+2)/3, untukn = 7 diperoleh z1 ≥ 3. Dengan menggunakan lintasan ini dan nilai z2 pada persamaan (4.45), diperoleh
z2 = (2n2−19n+ 35 + (−3n+ 12)d2+ (3n−12)r(Pvwv1))/9.
Karena r(Pvwv1) ≥ d1 dan d1 ≥ d2 maka z2 ≥ (2n
2−19n+ 35)/9, untuk n = 7
diperoleh z2 ≥0.
Jika titik vw berada pada k+ 1 ≤ w ≤ n, maka ada sebuah (r(Pvwv1),
0)-lintasan dari titik vw kev1 dengan 1≤r(Pvwv1)≤d1. Menggunakan lintasan ini
dan nilai z1 pada persamaan (4.44), diperoleh
z1 = ((n−1)d1+ (−n+ 1)r(Pvwv1))/3.
Karena r(Pvwv1)≤ d1 maka z1 ≥ 0. Dengan menggunakan lintasan ini dan nilai z2 pada persamaan (4.45), diperoleh
z2 = (2n2−13n+ 20 + (−3n+ 12)d2+ (3n−12)r(Pvwv1))/9.
Karena r(Pvwv1) ≥ 1 dan d2 ≤ 3 maka z2 ≥ (2n
2 −19n + 44)/9, untuk n = 7
diperoleh z2 ≥1.
Oleh karena itu, untuk setiap w = 1,2,3,· · · , n, terdapat sebuah lintasan
Pvwv1 dari vw ke v1 sedemikian hingga sistem (4.43) mempunyai solusi bilangan
bulat tak negatif. Oleh proposisi 2.2 untuk setiap titik vw, w = 1,2,3,· · · , n terdapat sebuah jalan vw
(h,ℓ)
−→v1 dengan
h ℓ
=
(4n3−24n2+ 27n+ 20 + (6n2 −21n+ 15)d1+ (−6n2+ 21n+ 12)d2)/27
(2n3−15n2+ 33n−20 + (3n2−15n+ 12)d1+ (−3n2+ 15n−12)d2)/27
sehingga, k(D(2))≤(2n3−13n2+ 20n+ (3n2−12n+ 9)d1+ (−3n2+ 12n)d2)/9.
Karenanya, disimpulkan bahwa
k(D(2)) = (2n3−13n2+ 20n+ (3n2−12n+ 9)d1 + (−3n2+ 12n)d2)/9,
Nilai scrambling index digraf Hamilton dwiwarna atasn≡1 (mod 3) titik,
n ≥ 7, dengan (n−4)/3 busur biru berurutan pada kedua lingkaran diperoleh dalam 3 bentuk umum seperti terlihat pada teorema 4.2, 4.3 dan 4.4. Bah-wa ketiga teorema tersebut dipengaruhi oleh banyak titik dan letak busur biru terhadap titik yang memiliki derajat masuk paling besar. Titik yang memiliki derajat masuk paling besar mempunyai nilai scrambling index terkecil. Sehing-ga nilai scrambling index pada setiap titik di D(2) akan bertambah - tambah
satu mengikuti siklus penamaan titik pada D(2) tersebut. Pada akhirnya nilai
KESIMPULAN DAN SARAN
Pada bab ini akan diberikan kesimpulan dari hasil penelitian ini serta saran untuk penelitian lebih lanjut.
5.1 Kesimpulan
Suatu digraf Hamilton dwiwarna D(2) yang terdiri dari dua cycle dengan C1 : v1 → v2 → · · · → vn−3 → v1 dengan panjang n−3 dan C2 : v1 → v2 → · · · → vn−1 →vn→ v1 dengan panjang n, atas n ≡1 (mod 3) titik, n ≥7. Digraf D(2) tersebut memiliki sebanyak (2n− 5)/3 busur merah dan (n−4)/3 busur biru padaC1 serta (2n+ 1)/3 busur merah dan (n−1)/3 busur biru padaC2. Dengan ketentukan banyaknya busur merah dan busur biru tiapcycle tersebut kemudian dibentuk formula umum scrambling index. Formula tersebut dipengaruhi oleh n
titik serta jarak busur vi → vj dan vk → vk+1 terhadap titik v1 yang masing
-masing didefinisikan sebagai d1 dan d2.
Ketiga bentuk umum scrambling index dari digrafD(2) sebagai berikut:
1. Jika d1 < d2, untuk 0 ≤ d1 ≤ 2 dan (2n+ 3d1 −11)/3 ≤ d2 ≤ (2n−5)/3 makak(D(2)) = (2n2 −8n+ 9 + (−n2+ 4n)d1+ (n2−4n+ 3)d2)/3.
2. Jikad1 < d2, untuk 0≤d1 ≤3 dan (d1+ 1)≤d2 ≤(2n+ 3d1−14)/3 maka
k(D(2)) = (2n3−13n2+ 11n+ 27 + 9d2)/9.
3. Jika d1 ≥ d2, untuk 1 ≤ d1 ≤ 3 dan 1 ≤ d2 ≤ 3 maka k(D(2)) = (2n3 −
13n2+ 20n+ (3n2−12n+ 9)d1+ (−3n2+ 12n)d2)/9.
5.2 Saran
Pada penelitian ini hanya membahas ketikaD(2) mempunyai (n−1)/3 busur biru,
DIGRAF DWIWARNA
Pada bab ini akan dibahas beberapa konsep dasar seperti definisi dan teore-ma yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan digraf dwiwarna, primitifitas, scrambling index, dan batas -batas scrambling index.
2.1 Digraf Dwiwarna
Sub-bab ini akan membahas definisi digraf dwiwarna dan beberapa istilah yang digunakan pada digraf dwiwarna, serta representasi digraf dwiwarna menggu-nakan grafis dan matriks.
2.1.1 Definisi Digraf Dwiwarna
Sebuah digraf D adalah sebuah objek terdiri atas sebuah himpunan berhingga dan tak kosong V ={v1, v2, v3,· · · , vr} yang unsur - unsurnya disebut titik dari
digraf D, bersama dengan sebuah himpunan B = {b1, b2, b3,· · · , bs} merupakan himpunan bagian dari himpunanV ×V yang unsur - unsurnya disebut busur dari digraf D. Sebuah digraf D dengan himpunan titik - titik V dan busur - busur
B dinotasikan dengan D{V, B}. Bila b1 = (v1, v2) subset V ×V adalah sebuah busur dari digraf D, maka titik v1 disebut sebagai titik asal dan titikv2 disebut sebagai titik terminal dari busurb1.
Fornasini dan Valcher (1997) memperkenalkan digraf dengan dua jenis busur yaitu setiap busur pada suatu digraf D diberi dua warna, namun tidak sekaligus kedua warna tersebut berada pada busur yang sama. Digraf tersebut disebut sebagai digraf dwiwarna (D(2)). Warna yang dipergunakan adalah warna merah
dan warna biru. Secara aplikasi digraf dwiwarna dapat direpresentasi ke dalam grafis dengan cara sebagai berikut :
• Setiap busur b = (vi, vj) direpresentasikan dengan menggunakan garis be-rarah dari titik vi ke titik vj. Busur berwarna merah dan berwarna biru masing - masing ditandai dengan garis berarah tak putus dan garis berarah putus - putus.
Terdapat beberapa istilah dalam digraf dwiwarna, diantaranya yaitu jalan, lintasan dan cycle. Untuk bilangan bulat tak negatif h dan ℓ, suatu (h, ℓ)-jalan pada digraf D(2) adalah suatu jalan dengan h busur merah dan ℓ busur biru.
Sebuah jalan dengan panjang k = h+ℓ yang menghubungkan titik vi dan vj, dinotasikan denganvi
k
→vj, merupakan sebuah barisan berhinggak busur dalam bentuk
{vi =v0, v1},{v1, v2},{v2, v3},· · · ,{vk−1, vk =vj},
juga dapat dinotasikan dalam bentuk
vi =v0 →v1 →v2 →v3 → · · · →vk−1 →vk =vj.
Untuk sebuah jalanWvivj diD
(2), dinotasikan bahwar(W
vivj) danb(Wvivj) masing
- masing merupakan banyaknya busur merah dan busur biru dari titik vi ke vj di W. Vektor (r(Wvivj), b(Wvivj))
T adalah komposisi pada jalan W
vivj. Jalan
tersebut disebut tertutup jika titik vi = vj dan jalan disebut terbuka jika titik
vi 6=vj.
Suatu jalan dari titikvike titikvjmemuat titik yang berbeda - beda disebut sebagai lintasan, dinotasikan dengan Pvivj. Vektor (r(Pvivj), b(Pvivj))
T adalah
komposisi pada lintasanPvivj, denganr(Pvivj) danb(Pvivj) adalah masing - masing
banyaknya busur merah dan busur biru diPvivj. Jika titikvi =vj diPvivj disebut
sebagai lintasan tertutup atau cycle. Jarak antara dua titik berbeda dari vi ke
vj padaPvivj, dinotasikan dengan d(vi, vj), didefinisikan sebagai panjang lintasan
(r(Pvivj) +b(Pvivj)) yang dilewati dari titik vi ke titik vj.
Suatu digrafD(2)dikatakan sebagai digraf Hamilton dwiwarna jika terdapat
cycleHamilton yaitu sebuahcycleyang memuat setiap titik pada digrafD(2)tepat
sekali kecuali kedua titik ujung pada barisan cycle tersebut.
Contoh 2.1.1. Himpunan V = {v1, v2, v3, v4, v5, v6, v7} bersama dengan
him-punan busur merah R = {(v1, v2),(v3, v4),(v4, v1),(v4, v5),(v6, v7),(v7, v1)} dan
Gambar 2.1 : Digraf Hamilton Dwiwarna dengan 7 titik dan 8 busur.
Dari gambar 2.1 dapat ditemukan contoh jalan, lintasan dan cycle antara lain sebagai berikut:
• Barisan v1 →r v2 →b v3 →r v4 →r v1 →r v2 adalah jalan terbuka dari v1 ke v2
dengan komposisi (4,1)T.
• Barisan v7 →r v1 →r v2 →b v3 →r v4 →r v1 →r v2 →b v3 →r v4 →r v5 →b v6 →r v7
adalah jalan tertutup dariv7 kev7 dengan komposisi (8,3)T.
• Barisan v6 →r v7 →r v1 →r v2 →b v3 →r v4 →r v5 adalah lintasan terbuka dari
v6 ke v5 dengan komposisi (5,1)T.
• Barisan v1 →r v2 →b v3 →r v4 →r v1 adalah lintasan tertutup atau cycle dari
v1 ke v1 dengan komposisi (3,1)T.
• Barisan v1 →r v2 →b v3 →r v4 →r v5 →b v6 →r v7 →r v1 adalah cycle Hamilton dengan komposisi (5,2)T, sehingga gambar 2.1 merupakan digraf Hamilton dwiwarna dengan panjang cycle Hamilton adalah 7.
2.1.2 Matriks Ketetanggaan Digraf Dwiwarna
Konsep ketetanggaan antara dua titik dan konsep insidensi antara titik dan busur pada digraf dwiwarna didefinisikan dengan mengandaikan b = (vi, vj) adalah sebuah busur diD(2)dengan titik asalv
titik vi, dinotasikan dengan od(vi), adalah banyaknya busur yang insiden dari titik vi yakni banyaknya busur dengan titik asal vi. Derajat dari sebuah titik vi adalah jumlahan dari derajat masuk dan derajat keluar dari titik tersebut.
Representasi digraf dwiwarna dengan matriks menggunakan konsep kete-tanggaan. AndaikanD(2)adalah sebuah digraf dwiwarna atasntitikv1, v2,· · ·, vn.
Matriks ketetanggaan dari sebuah digraf D(2) didefiniskan sebagai berikut:
1. Matriks ketetanggaan merah dariD(2) adalah sebuah matriks bujursangkar R= (rij) dengan ordo n yang setiap entri didefinisikan sebagai
rij =
2. Matriks ketetanggaan biru dari D(2) adalah sebuah matriks bujursangkar B = (bij) dengan ordo n yang setiap entri didefinisikan sebagai
bij =
Contoh 2.1.2. Berikut adalah representasi menggunakan matriks yang diperoleh dari gambar 2.1.
AndaikanRdanB adalah matriks tak negatif berordon×ndan andaikanh
dan ℓ adalah bilangan bulat tak negatif. Suatu (h, ℓ)-Hurwitz product dari R
dan B didefinisikan secara rekursif, yang dinotasikan dengan (R, B)(h,ℓ), adalah
jumlah keseluruhan matriks dari hasil perkalianRsebanyakhkali danBsebanyak
ℓ kali yaitu,
(R, B)(h,0) =Rh, (R, B)(0,ℓ)=Bℓ dan
Contoh 2.1.3.
(R, B)(1,0) =R, (R, B)(2,0) =R2, (R, B)(0,1) =B,
(R, B)(1,1) =R(R, B)(0,1)+B(R, B)(1,0) =RB+BR, maka
(R, B)(2,1) =R(R, B)(1,1)+B(R, B)(2,0) =R(RB+BR) +B(R2)
=R2B+RBR+BR2.
Lemma 2.1.4. Andaikan D(2) adalah digraf dwiwarna atasn titik dan andaikan
R dan B adalah matriks ketetanggaan merah dan matriks ketetanggaan biru dari
D(2). Maka (R, B)(h,ℓ) adalah banyaknya (h, ℓ)-jalan dari titik v
i ke vj.
Bukti. Pembuktian ini akan dilakukan dengan cara induksi. Pertama, dibuk-tikan bahwa untuk (h, ℓ) = (1,0) atau (h, ℓ) = (0,1), pernyataan (R, B)(h,ℓ)
benar merupakan banyaknya (h, ℓ)-jalan dari setiap titik vi ke vj. Perhatikan bahwa ketika (h, ℓ) = (1,0) diperoleh (R, B)(h,ℓ) = (R, B)(1,0) = R merupakan
jalan dengan dari titik vi ke vj dengan komposisi (1,0)T di D(2). Dan bahwa ketika (h, ℓ) = (0,1) diperoleh (R, B)(h,ℓ)= (R, B)(0,1) =B merupakan jalan dari
titik vi kevj dengan komposisi (0,1)T di D(2).
Kedua, asumsikan bahwa (R, B)(h,ℓ)adalah banyaknya (h, ℓ)-jalan dari titik vi ke vj. Akan diperlihatkan bahwa untuk semua bilangan bulat tak negatif
h+ℓ+ 1, pernyataan (R, B)(h+1,ℓ) benar merupakan banyaknya (h+ 1, ℓ)-jalan
dari setiap titik vi kevj dengan pembuktian mengikuti persamaan (2.1) yaitu
(R, B)(h,ℓ)=R(R, B)(h−1,ℓ)+B(R, B)(h,ℓ−1),
maka diperoleh
(R, B)(h+1,ℓ)=R(R, B)(h,ℓ)+B(R, B)(h+1,ℓ−1).
Berdasarkan asumsi maka R(R, B)(h,ℓ) merupakan jalan dari titik v
i ke vj yang dimulai dengan busur merah dan dilanjutkan oleh (h, ℓ)-jalan, danB(R, B)(h+1,ℓ−1)
merupakan jalan dari titik vi ke vj yang dimulai dengan busur biru dan dilan-jutkan oleh (h+ 1, ℓ−1)-jalan, sehingga (R, B)(h+1,ℓ)adalah banyaknya (h+ 1, ℓ
)-jalan dari titik vi ke vj. Karena langkah pertama dan kedua telah diperlihatkan maka terbukti bahwa (R, B)(h,ℓ)adalah banyaknya (h, ℓ)-jalan dari titikv
i kevj.
Suatu matriksS dikatakan sebagai matriks tak negatif jika setiap entri atau elemensij dari matriksSadalah bilangan bulat tak negatif, sedangkan jika setiap entri atau elemen sij dari matriks S adalah bilangan bulat positif maka matriks
Contoh 2.1.5. Perhatikan matriks tak negatif dan matriks positif berikut.
S =
3 0 5 0 10 0 7 1 4
, T =
13 10 25 2 10 9 23 4 17
.
matriks tak negatif matriks positif
2.2 Primitifitas
Pada sub-bab ini akan dijelaskan tentang digraf dwiwarna terhubung kuat dan digraf dwiwarna terhubung kuat yang primitif.
2.2.1 Digraf Dwiwarna Terhubung Kuat
Berikut akan didiskusikan konsep keterhubungan kuat pada sebuah digraf dwi-warna. Suatu digraf dwiwarna dikatakan terhubung kuat bila untuk dua titik
vi dan vj di D(2) terdapat sebuah jalan berarah dari vi ke vj dan terdapat se-buah jalan berarah dari vj ke vi, tanpa memperhatikan setiap warna busur yang dilalui. Sebaliknya, suatu digraf dwiwarna dikatakan tidak terhubung kuat bila untuk dua titik vi dan vj di D(2) terdapat sebuah jalan berarah dari vi ke vj, tetapi tidak terdapat jalan berarah dari vj kevi.
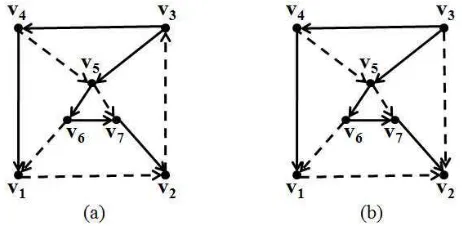
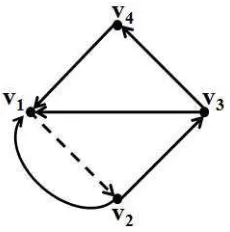
Contoh 2.2.1. Berikut diberikan contoh digraf dwiwarna terhubung kuat dan tidak terhubung kuat.
Gambar 2.2 : Digraf Dwiwarna Terhubung Kuat dan Tidak Terhubung Kuat.
Berikut diberikan sebuah sifat khusus dari digraf dwiwarna terhubung kuat yang berkaitan dengan keberadaan cycle.
Proposisi 2.2.2. AndaikanD(2) adalah sebuah digraf dwiwarna terhubung kuat.
Setiap titik di D(2) terletak pada sebuah cycle.
Bukti. Andaikan vi adalah sebarang titik di D(2). Karena D(2) merupakan se-buah digraf dwiwarna terhubung kuat maka terdapat titik vj di D(2) sehingga (vi, vj) adalah sebuah busur di D(2). Karena D(2) merupakan sebuah digraf dwi-warna terhubung kuat, terdapat lintasan sederhanaPvjvi darivj kevi. Kemudian,
busur (vi, vj) dilanjutkan dengan lintasan sederhanaPvjvi adalah sebuah lintasan
tertutup atau cycle yang memuat titik vi. Dengan perkataan lain bahwa setiap titik vi di D(2) terletak pada sebuah cycle.
2.2.2 Primitifitas Digraf Dwiwarna Terhubung Kuat
Andaikan D(2) adalah sebuah digraf dwiwarna terhubung kuat. Digraf D(2)
dikatakan primitif jika terdapat bilangan bulat tak negatif h dan ℓ sehingga un-tuk setiap pasangan titik vi dan vj di D(2) terdapat jalan vi
(h,ℓ)
−→ vj dan jalan
vj
(h,ℓ)
−→vi.
Andaikan C = {C1, C2,· · · , Cq} adalah himpunan semua cycle di D(2).
Definisi matriks cycle M dari D(2) adalah matriks yang banyak kolom
diper-oleh dari himpunan C dan banyak baris diperoleh dari banyak warna pada D(2),
sehingga
M =
r(C1) r(C2) · · · r(Cq)
b(C1) b(C2) · · · b(Cq)
.
Content dari matriksM2×qdidefinisikan menjadi 0 jika rank dari M kurang dari 2 dan pembagi persekutuan terbesar dari determinan submatriks 2×2.
Teorema 2.2.3. (Fornasini dan Valcher, 1998)Andaikan D(2) memiliki
pal-ing sedikit 1 busur setiap warna dan andaikan M merupakan matriks cycle di
Contoh 2.2.4. Berdasarkan gambar 2.1 terdapat dua cycle yaitu cycle satu adalah v1 →r v2 →b v3 →r v4 →r v1 dengan komposisi C1 = (3,1)T dan cycle dua yaitu v1 →r v2 →b v3 →r v4 →r v5 →b v6 →r v7 →r v1 dengan komposisi C2 = (5,2)T. Maka diperoleh matrikscycle dari digraf Hamilton dwiwarna tersebut, yaitu:
M =
3 5 1 2
karena det(M) = 1, maka D(2) tersebut terhubung kuat dan primitif.
2.3 Scrambling Index
Pada sub-bab ini akan didiskusikan mengenai definisi scrambling index lokal an-tara dua titik, scrambling index dari digraf dwiwarna primitif dan definisi scram-bling index dengan menggunakan matriks ketetanggaan dari digraf dwiwarna primitif.
Untuk dua titik berbedavidanvj diD(2), scrambling index lokal darividan
vj adalah bilangan bulat positifkvi,vj(D
(2)) yang didefinisikan sebagai berikut:
kvi,vj(D
(2)) = min
vw∈V(D(2)){kvi,vj(vw)}
= min
vw∈V(D(2)){min(h+ℓ) :vi (h,ℓ)
−→vw dan vj
(h,ℓ)
−→vw}
Scrambling index dari digraf dwiwarna primitif, yang dinotasikan dengan
k(D(2)), adalah bilangan bulat positif terkecil (h+ℓ) untuk semua bilangan bulat
tak negatif h busur merah dan ℓ busur biru sedemikian sehingga untuk setiap pasangan titik vi dan vj di D(2) terdapat sebuah titik vw di D(2) dengan sifat bahwa terdapat sebuah jalan vi
(h,ℓ)
−→vw dan sebuah jalanvj
(h,ℓ)
−→vw. Dari definisi
k(D(2)) dan k
vi,vj(D
(2)), diperoleh hubungan
k(D(2))≥max vi6=vj
{kvi,vj(D
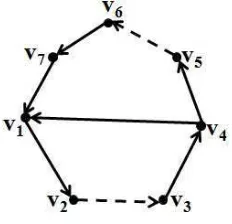
Contoh 2.3.1. Berikut scrambling index lokal dari digraf Hamilton dwiwarna primitif pada gambar 2.3.
Gambar 2.3 : Digraf Dwiwarna Primitif.
kv1,v2(D Hal ini menunjukkan k(D(2)) ≤ 3. Oleh karena itu, dapat disimpulkan bahwa k(D(2)) = 3.
Berdasarkan Lemma 2.1.4, scrambling index dari suatu digraf dwiwarna
D(2) dapat dicari dengan menggunakan matriks ketetanggaan R dan B di D(2).
Scrambling index dari matriks ketetanggaan R dan B adalah bilangan bulat positif terkecil (h, ℓ) sehingga (R, B)(h,ℓ) adalah sebuah scrambling matriks, yaitu
untuk setiap dua baris (R, B)(h,ℓ) terdapat sedikitnya satu entri yang nilainya
positif pada kolom yang sama, maka (h, ℓ) merupakan scrambling index dari digraf dwiwarna D(2).
Berikut scrambling index menggunakan matriks ketetanggaan di atas.
Scrambling index dariD(2) bukanlah (1,0), karena setidaknya ada dua
baris pada matriks (R, B)(1,0), yaitu baris pertama dan baris ketiga
tidak memiliki entri positif pada kolom yang sama.
b. (R, B)(0,1) =B =
Scrambling index dariD(2) bukanlah (0,1), karena setidaknya ada dua
baris pada matriks (R, B)(0,1), yaitu baris kedua dan baris keempat
tidak memiliki entri positif pada kolom yang sama.
2. Untukh+ℓ= 2, diperoleh
Scrambling index dariD(2) bukanlah (2,0), karena setidaknya ada dua
baris pada matriks (R, B)(2,0), yaitu baris pertama dan baris keempat
tidak memiliki entri positif pada kolom yang sama.
b. (R, B)(1,1) =RB+BR=
Scrambling index dariD(2) bukanlah (1,1), karena setidaknya ada dua
baris pada matriks (R, B)(1,1), yaitu baris pertama dan baris kedua
tidak memiliki entri positif pada kolom yang sama.
c. (R, B)(0,2) =B2 =
Scrambling index dariD(2) bukanlah (0,2), karena setidaknya ada dua
baris pada matriks (R, B)(0,2), yaitu baris kedua dan baris ketiga tidak
3. Untukh+ℓ= 3, diperoleh
Scrambling index dariD(2) bukanlah (3,0), karena setidaknya ada dua
baris pada matriks (R, B)(3,0), yaitu baris pertama dan baris keempat
tidak memiliki entri positif pada kolom yang sama.
b. (R, B)(1,2) =RB2+BRB+B2R=
Scrambling index dariD(2) bukanlah (1,2), karena setidaknya ada dua
baris pada matriks (R, B)(1,2), yaitu baris pertama dan baris kedua
tidak memiliki entri positif pada kolom yang sama.
c. (R, B)(0,3) =B3 =
Scrambling index dariD(2) bukanlah (0,3), karena setidaknya ada dua
baris pada matriks (R, B)(0,3), yaitu baris kedua dan baris ketiga tidak
memiliki entri positif pada kolom yang sama.
d. (R, B)(2,1) =R2B+RBR+BR2 =
Scrambling index dariD(2)adalah (2,1), karena untuk setiap dua baris
(R, B)(2,1) terdapat sedikitnya satu entri yang nilainya positif pada
kolom yang sama yaitu kolom satu.
2.4 Batas - Batas Scrambling Index
Pada sub-bab ini akan membahas mengenai batas - batas pada scrambling index yaitu batas atas dan batas bawah pada scrambling index digraf dwiwarna primitif.
Setiap jalan pada digraf dwiwarna dapat dikomposisi ke dalam sebuah lin-tasan dan beberapacycle. Ini menunjukkan untuk setiap jalanvi
(h,ℓ)
mengiku-ti hubungan berikut:
untuk beberapa lintasanPvivj darivi kevj dan beberapa vektor bulat tak negatif
z.
Batas atas scrambling index dari digraf dwiwarna primitif dinyatakan dalam proposisi berikut.
Proposisi 2.4.1. (Mulyono dan Suwilo, 2014) Andaikan D(2) adalah digraf
dwiwarna primitif terdiri dari dua cycle C1 dan C2. Andaikan vj adalah sebuah titik yang terletak pada kedua cycle. Jikahdanℓadalah bilangan bulat tak negatif, terdapat sebuah lintasan Pvivj dari vi ke vj sehingga sistem
Mz+
mempunyai sebuah solusi bilangan bulat tak negatif, maka ada jalan vi
(h,ℓ)
−→vj di
D(2).
Bukti. Asumsikan solusi dari sistem (2.2) adalah z = (z1, z2)T. Solusi tersebut dibagi menjadi empat kasus berikut:
1. Jika z1 > 0 dan z2 > 0, maka jalan dimulai dari titik vi bergerak ke ke titik vj sepanjang (r(Pvivj), b(Pvivj))-lintasan Pvivj, kemudian mengelilingi
C1 sebanyak z1 kali dan C2 sebanyak z2 kali, dan kembali ke titikvj adalah sebuah (h, ℓ)-jalan dari vi ke vj.
2. Jika z1 = 0 dan z2 > 0, maka jalan dimulai dari titik vi bergerak ke ke titik vj sepanjang (r(Pvivj), b(Pvivj))-lintasan Pvivj, kemudian mengelilingi
C2 sebanyak z2 kali, dan kembali ke titik vj adalah sebuah (h, ℓ)-jalan dari
vi ke vj.
3. Jika z1 > 0 dan z2 = 0, maka jalan dimulai dari titik vi bergerak ke ke titik vj sepanjang (r(Pvivj), b(Pvivj))-lintasan Pvivj, kemudian mengelilingi
C1 sebanyak z1 kali, dan kembali ke titik vj adalah sebuah (h, ℓ)-jalan dari
vi ke vj.
4. Jika z1 = z2 = 0, maka (r(Pvivj), b(Pvivj))-lintasan Pvivj adalah sebuah
Andaikan D(2) adalah digraf dwiwarna primitif terdiri dari dua cycle dan
andaikan vi dan vj adalah dua titik yang berbeda di D(2). Untuk beberapa titik
vw, andaikan bahwa kvi,vj(vw) diperoleh dari (h, ℓ)-jalan. Berikut Lemma untuk
menentukan batas bawah untuk kvi,vj(D
(2)) dan karenanya akan diperoleh batas
bawah scrambling index.
Lemma 2.4.2. (Mulyono, Sumardi dan Suwilo, 2015)AndaikanD(2)adalah
digraf dwiwarna primitif terdiri dari dua cycle dengan matriks cycle M dan andaikan det(M) = 1. Andaikan vi dan vj adalah dua titik berbeda di D(2).
Bukti. Karena det(M) = 1, terdapat bilangan bulate1 dan e2 sehingga
Karena setiap jalan dapat dikomposisi ke dalam lintasan dan beberapa cycle, maka
untuk beberapa lintasan Pvivw dari titik vi ke vw dan beberapa vektor bilangan
bulat tak negatif z. Bandingkan persamaan (2.3) dan (2.4), diperoleh
untuk beberapa lintasan Pvjvw dari titik vj ke vw dan beberapa vektor bilangan
bulat tak negatif z. Bandingkan persamaan (2.3) dan (2.5), diperoleh
PENDAHULUAN
1.1 Latar Belakang
Digraf merupakan salah satu pokok bahasan dalam ilmu matematika. Digraf dinotasikan dengan D. Digraf D terdiri atas himpunan titik - titik yang di-hubungkan oleh himpunan garis - garis berarah atau busur. Dalam aplikasinya, digraf dapat ditemukan pada proses jaring jaring makanan. Himpunan titik -titik tersebut diartikan sebagai kumpulan suatu objek yang dalam hal ini adalah kumpulan binatang dan himpunan busur - busur sebagai aktifitas memakan an-tara dua binatang berbeda. Siklus makan - memakan tersebut direpresentasikan menjadi digraf dalam ilmu matematika. Himpunan busur - busur dari digraf yang diberi dua warna, namun tidak sekaligus kedua warna tersebut berada pada satu busur disebut digraf dwiwarna, dinotasikan dengan D(2).
Andaikanh(W) dan ℓ(W) masing - masing adalah banyaknya busur merah dan busur biru pada jalanW. Suatu jalan dari titikvi ke titikvj dengan panjang (h+ℓ), dinotasikan dengan vi
(h,ℓ)
−→ vj, adalah sebuah barisan berhingga busur di D(2) yang diawali dengan titik v
0 =vi dan diakhiri titik v(h+ℓ) =vj. Sebuah
lintasanPvivj adalah suatu jalan dengan titik yang berbeda - beda dari titikvi ke
titikvj. Jika titik vi =vj maka disebut lintasan tertutup ataucycle. Digraf D(2) disebut sebagai digraf Hamilton dwiwarna jika ditemukan cycle yang memuat semua titik pada D(2).
Penelitian yang membahas tentang D(2) mulai banyak dilakukan dan
pa-rameter yang dikemukan adalah tentang eksponen. Dalam mencari nilai eksponen dari suatu D(2) terlebih dahulu digraf dwiwarna tersebut harus primitif. Sebuah D(2) terhubung kuat dikatakan primitif jika terdapat sebuah bilangan bulat tak
negatifhdanℓsedemikian sehingga untuk setiap pasangan titikvi danvj terdap-at sebuah jalanvi
(h,ℓ)
−→vj dan sebuah jalanvj
(h,ℓ)
−→vi. Bilangan bulat positif (h+ℓ) yang paling kecil disebut eksponen dari D(2), dinotasikan denganexp(D(2)).
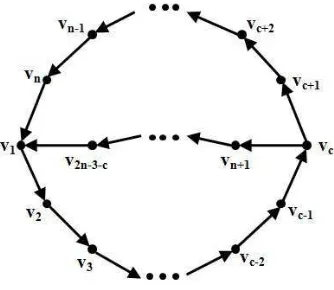
n dan panjang cycle dua adalah n−3. Akibatnya, titik vc berada pada interval 2≤c≤n−3.
Gambar 1.1 : Digraf PrimitifD.
Penelitian mengenai digraf dwiwarna berkembang menggunakan parameter baru bernama scrambling index. Pada tahun 2009 Akelbek dan Kirkland mem-perkenalkan parameter tersebut. Akelbek dan Kirkland (2009a) mengemukakan definisi scrambling index dari digraf primitif, dinotasikan dengan k(D), adalah bilangan bulat positif terkecil ℓ sehingga untuk setiap pasangan titik vi dan vj di D terdapat sebuah titik vw di D sedemikian sehingga terdapat sebuah jalan yang menghubungkan vi ke vw dan vj ke vw dengan panjang ℓ. Dalam artikel ini juga dijelaskan batas atas dari digraf primitif sehingga akan dicapai batas atas modulus terbesar kedua nilai eigen dari matriks primitif. Selanjutnya, Akel-bek dan Kirkland (2009b) mengklasifikasikan semua digraf primitif sehingga nilai scrambling index sama dengan batas atas.
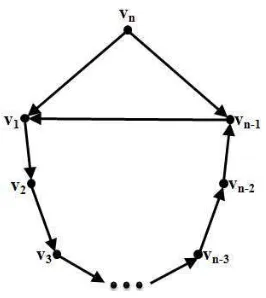
Tahun 2014, Mulyono dan Suwilo mendiskusikan nilai scrambling index dari digraf Wielandt dwiwarna. Digraf Wielandt tersebut dapat dilihat pada gambar 1.2. Scrambling index digraf Wielandt dwiwarna yang terdiri atascycleHamilton
v1 → v2 → · · · → vn−1 → vn → v1 dan busur vn−1 → v1 untuk n ≥ 4 berada
Gambar 1.2 : Digraf Wielandt Wn.
Mulyono dan Suwilo mengeneralisasikan definisi scrambling index dari di-graf primitif menjadi scrambling index dari didi-graf dwiwarna primitif. Definisi scrambling index dari digraf dwiwarna primitif, yang dinotasikan dengank(D(2)),
adalah bilangan bulat positif terkecil (h+ℓ) untuk semua bilangan bulat tak negatif hbusur merah danℓ busur biru sedemikian sehingga untuk setiap pasan-gan titik vi dan vj di D(2) terdapat sebuah titik vw di D(2) dengan sifat bahwa terdapat sebuah jalan vi
(h,ℓ)
−→ vw dan sebuah jalan vj
(h,ℓ)
−→ vw. Untuk dua titik berbeda vi dan vj, scrambling index lokal dari vi dan vj di (D(2)), dinotasikan dengan kvi,vj(D
(2)), adalah didefinisikan sebagai berikut :
kvi,vj(D
(2)) = min
vw∈V(D(2)){kvi,vj(vw)}
= min
vw∈V(D(2)){min(h+ℓ) :vi (h,ℓ)
−→vw dan vj
(h,ℓ)
−→vw}
Dari definisi, k(D(2)) dan k
vi,vj(D
(2)) diperoleh hubungan
k(D(2))≥ max
vi,vj∈V(D(2))
{kvi,vj(D
(2))}
1.2 Perumusan Masalah
Andaikan D(2) adalah digraf Hamilton dwiwarna primitif, terdiri atas dua cycle
yaitu v1 → v2 → · · · → vn−3 → v1 dengan panjang cycle satu adalah n−3 dan v1 → v2 → · · · → vn−1 → vn → v1 dengan panjang cycle dua adalah n, untuk
n ≡1 (mod3) titik,n≥7, dengan (n−4)/3 busur biru berurutan pada kedua cy-cle. Adapun masalah yang akan dibahas pada penelitian ini adalah menentukan bentuk umum scrambling index dari digraf Hamilton dwiwarna primitif seperti pada gambar 4.1.
1.3 Tujuan Penelitian
Penelitian ini bertujuan untuk menentukan matrikscycleagarD(2)primitif
kemu-dian menentukan bentuk umum scrambling index dari digraf Hamilton dwiwarna
D(2), dengan n ≡ 1 (mod 3) titik, n ≥ 7, terdiri atas dua cycle dengan panjang
cycle satu adalah n−3 dan panjangcycle dua adalah n dengan (n−4)/3 busur biru berurutan pada kedua cycle.
1.4 Manfaat Penelitian
ATAS n ≡ 1 (mod 3) TITIK
ABSTRAK
Sebuah digraf dwiwarna D(2) adalah sebuah digraf yang setiap busur berwarna
merah atau biru. Scrambling index dari D(2) merupakan bilangan bulat positif
terkecilh+ℓ untuk setiap bilangan bulat tak negatif hbusur merah dan ℓ busur biru sedemikian sehingga untuk setiap pasangan titik vi dan vj di D(2) terdapat sebuah titikvw diD(2) dengan sifat bahwa terdapat sebuah (h, ℓ)-jalan darivi ke
vw dan dari vj kevw. Tulisan ini mendiskusikan tentang rumus scrambling index dari digraf Hamilton dwiwarna primitif terdiri dua cycle dengan panjang cycle satu adalahn−3 dancycle dua adalahn, atasn ≡1 (mod3) titik, n≥7 dengan (n−4)/3 busur biru berurutan pada keduacycle.
Kata kunci: Digraf Dwiwarna, Primitif, Scrambling Index.
ABSTRACT
A two-colored digraph D(2) is a digraph whose arcs colored red or blue.
Scram-bling index of D(2) is smallest positive integerh+ℓ over all pairs of nonnegative
integers h red arcs and ℓ blue arcs such that for each pair of vertices vi and vj in D(2) there is a vertex v
w in D(2) with the property that there exist a (h, ℓ )-walk from vi to vw and from vj to vw. This paper discusses about formula for scrambling index of primitive two-colored Hamiltonian digraphs consists two cy-cles with length of cycle one is n−3 and length of cycle two isn, onn ≡1 (mod
3) vertices, n≥7 with (n−4)/3 consecutive blue arcs on both cycles.
Keywords: Two-Colored Digraphs, Primitive, Scrambling Index.
DWIWARNA ATAS
n
≡
1 (
mod
3)
TITIK
SKRIPSI
RATIH SURYANINGSIH 110803023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar Sarjana Sains
RATIH SURYANINGSIH 110803023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA