PENDAHULUAN
1.1 Latar Belakang Penelitian
Graf merupakan pokok bahasan matematika yang banyak mendapat perhatian karena aplikasinya sangat berguna untuk menyelesaikan persoalan kehidupan ma-nusia. Secara umum, graf mempresentasikan model matematika terhadap sejum-lah objek dalam bentuk simpul atau titik (vertex) dan hubungan antara objek-objek tersebut dalam bentuk garis atau sisi (edge).
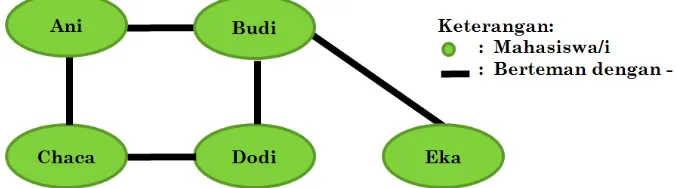
Pada persoalan komunikasi misalnya, graf dapat memodelkan hubungan sosial seseorang dengan seorang lainnya. Mahasiswa bernama Ani berteman dengan Budi dan Chaca tetapi tidak berteman dengan Dodi dan Eka, sedang-kan Dodi berteman dengan Budi dan Chaca tetapi tidak berteman dengan Ani dan Eka, dan Eka hanya berteman dengan Budi. Hubungan sosial yang demikian dapat direpresentasikan dalam graf tak berarah seperti pada gambar berikut:
Gambar 1.1. Representasi model hubungan sosial dengan graf tak berarah
dilakukan. Hal inilah yang menarik minat penulis untuk membahas scrambling index sebagai bagian dari pengembangan teori graf itu sendiri.
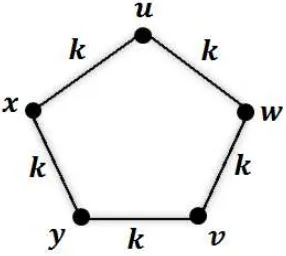
Istilah scrambling index pertama kali diperkenalkan oleh Akelbek dan Kir-kland pada tahun 2009. Apabila diketahui titik u, v, dan w serta sisi (u, w) dan (v, w) termuat dalam sebuah grafG, maka titik w merupakan common outneigh-bour (tetangga persekutuan luar) dari titik u dan v. Yang dinamakan scram-bling index adalah bilangan bulat positif terkecil k sedemikian hingga setiap pa-sangan titik-titik dalam graf G memiliki tetangga persekutuan luar yang mem-bentuk sisi-sisi dengan panjang k.
Gambar 1.2. Common outneighbour(tetangga persekutuan luar) dalam graf
Secara definisi, scrambling index dari sebuah graf primitif G, dinotasikan dengan k(G) adalah bilangan bulat positif terkecil k sehingga untuk setiap pa-sangan titik u dan v di G, terdapat sebuah titik w dengan sifat ada jalan yang menghubungkan titik u dan w dan jalan yang menghubungkan titik v dan w dengan panjang k.
Di tahun yang sama, Akelbek dan Kirkland (2009b) mengelompokkan semua graf primitif berarah sedemikian hingga nilai scrambling index sama dengan batas atasnya. Penelitian kemudian dilanjutkan Chen dan Liu (2010) yang mem-bahas hubungan antara scrambling index dan eksponen pada matrix primitif simetris. Mereka juga mengelompokkan semua matriks primitif simetris sede-mikian hingga nilai scrambling index mencapai maksimum.
Selanjutnya, Gao dan Shao (2013) juga telah membahas mengenai scram-bling index dari graf primitif berarah terdiri atas tepat dua lingkaran. Adapun penelitian ini secara khusus akan membahas mengenai scrambling index dari graf primitif tak berarah yang terdiri atas tepat dua lingkaran.
1.2 Masalah Penelitian
AndaikanCt
sadalah sebuah graf primitif terdiri atas dua lingkaran dengan panjang s dan t. Masalah yang akan diselesaikan pada penelitian ini adalah menentukan bagaimana bentuk umum scrambling index dariCt
s, dinotasikan dengank(Cst) un-tuk lingkarans dan t keduanya adalah ganjil dan untuk salah satu dari lingkaran s atau t adalah ganjil.
1.3 Batasan Masalah
Bentuk umum scrambling index yang dibahas dalam tulisan ini hanya dikhususkan pada satu objek graf, yaitu pada graf primitif yang terdiri atas tepat dua lingkaran, dinotasikan dengan k(Ct
s). Adapun bentuk umum yang ditentukan terbagi men-jadi dua kasus, yaitu bentuk umum scrambling index untuk kedua lingkaransdan t adalah ganjil dan untuk salah satu dari s atau t adalah ganjil.
1.4 Tinjauan Pustaka
u dan v di G, terdapat sebuah titikw dengan sifat ada jalan yang menghubung-kan titikudanwdan jalan yang menghubungkan titikvdanwdengan panjangk.
Dalam penelitiannya, Akelbek dan Kirkland (2009a) membahas mengenai scrambling index pada graf primitif berarah dan memberikan batas atas dari scrambling index pada graf primitif berarah terkait dengan order dan girthyang kemudian digunakan untuk menetapkan batas atas pada modulo terbesar kedua dari nilai eigen sebuah matriks primitif. Order adalah jumlah titik dan girth adalah panjang terpendek dari lingkaran pada graf primitif berarah.
Misalkan Dadalah sebuah graf primitif berarah denganntitik dansgirth, maka scrambling index k(D)≤K(n, s).
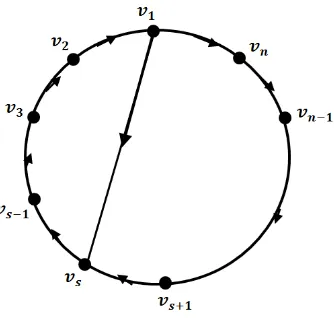
Gambar 1.3. Graf BerarahDs,n
JikaD=Ds,n dangcd(n, s) = 1 di manaDs,n merupakan graf berarah primitif sebagaimana diperlihatkan pada Gambar 1.3, makaK(n, s) = k(n, s) +n−sdan
k(n, s) =
( s−1
2 n, untuk s ganjil
n−1
2 s, untuk s genap
hanya jikaD =Ds,n dan gcd(n, s) = 1.
Misalkan Dadalah sebuah graf primitif berarah denganntitik dansgirth, dengan s genap dan s ≤ 3. Maka scrambling index k(D) = K(n, s) jika dan hanya jika gcd(n, s) = 1 dan D = Ds,n, atau D = Ds,n ∪ {n −r− ts+ 1 →
n − r − ts +ms} untuk sebarang m ∈ N dan sebarang t ∈ {1,2, ..., n−2r s − 1} sedemikian hingga n+h
2 −t−1≡0(modm).
Pada tahun berikutnya, Chen dan Liu (2010) membahas hubungan antara scrambling index dan eksponen pada matrix primitif simetris. Sebuah matriks persegi non negatifA dikatakan primitif apabila terdapat bilangan bulat positifk sedemikian hinggaAk>0. Scrambling index dari matriks primitifA, dinotasikan dengan k(A) adalah bilangan bulat positif terkecil k sehingga untuk setiap dua baris pada Ak terdapat sedikitnya satu elemen positif pada posisi kolom yang sama.
Eksponen dari matriks primitif A, dinotasikan dengan exp(A) adalah bi-langan bulat positif terkecil k sedemikian hingga Ak = dimana menotasikan 1-matriks, yaitu matriks yang semua elemennya memuat 1. Dalam penelitiannya dinyatakan bahwa untuk sebuah matriks primitif A berdasarkan definisi scram-bling index dan definisi eksponen, dapat diketahuik(A)≤exp(A).
Misalkan D adalah sebarang graf berarah primitif simetris dengan n ≥ 2 dan misalkan u dan v adalah pasangan titik di D. Maka
ku,v(D)≤ ⌈expD(u, v)
2 ⌉
dan
k(D) = ⌈exp(D)
2 ⌉
dimana⌈a⌉ menotasikan bilangan bulat positif terkecil yang tidak kurang daria. Misalkan D adalah sebarang graf berarah primitif simetris dengan n ≥ 2 dan misalkanu dan v adalah pasangan titik diD. Jikau k1
↔v dan u k2
↔v dengan k1−k2 ≡1(mod 2), maka
Selain itu, mereka juga mengelompokkan semua matriks primitif simetris sedemikian hingga nilai scrambling index mencapai maksimum. Diberikan Sn(r) adalah himpunan semua graf primitif dengan ntitik yang memiliki lingkaran sep-anjang r tetapi bukan lingkaran dengan panjang ganjil yang lebih kecil dari r.
Andaikan n dan m adalah bilangan bulat positif dengan n ≥ 2, r ≡
1(mod2) dan 1≤r≤n, dan misalkan
δr =
(
1, untuk r = 1
r−1
2 , untuk r≡1(mod2) dan r≥3
danGadalah graf primitif diSn(r), makak(G)≥δr. Misalkannadalah bilangan bulat positif dengan n ≥ 2 dan r adalah bilangan bulat positif ganjil dengan 1≤r≤n. AndaikanG adalah graf primitif di Sn(r) maka persamaan
k(G)≤n− r+ 1
2
dipenuhi jika dan hanya jika:
(i) n≥3 dan G isomorfis terhadapGn,rn−r, atau
(ii) n= 2 (r= 1)dan baikG isomorfis terhadapG21,1 atau Gisomorfis terhadap
G2′,1 ditentukan dari G 2,1
1 dengan menambahkan sebuah loop (titik yang
di-hubungkan dengan sebuah sisi ke dirinya sendiri) pada titik lainnya.
Gao dan Shao (2013) dalam penelitiannya mengemukakan tentang scram-bling index dari graf berarah primitif yang terdiri atas tepat dua lingkaran dan dalam penelitian ini secara khusus akan dibahas mengenai scrambling index dari graf primitif yang terdiri atas tepat dua lingkaran.
1.5 Tujuan Penelitian
yang ditentukan terbagi menjadi dua kasus, yaitu bentuk umum scrambling index dengan lingkaransdantkeduanya adalah ganjil dan bentuk umum scrambling in-dex dengan salah satu lingkarans atau t adalah ganjil.
1.6 Manfaat Penelitian