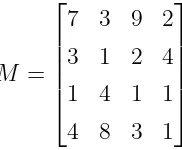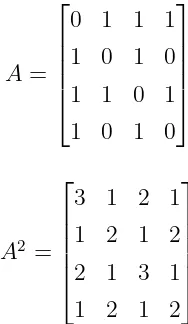SCRAMBLING INDEX DARI GRAF PRIMITIF
TERDIRI ATAS DUA LINGKARAN
SKRIPSI
NURUL IZZATI
100803026
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SCRAMBLING INDEX DARI GRAF PRIMITIF
TERDIRI ATAS DUA LINGKARAN
SKRIPSI
Diajukan untuk melengkapi tugas sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
NURUL IZZATI 100803026
DEPARTEMEN STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Scrambling Index dari Graf Primitif terdiri atas Dua Lingkaran
Kategori : Skripsi
Nama : Nurul Izzati
Nomor Induk Mahasiswa : 100803026
Program Studi : Sarjana (S1) Matematika Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, Juli 2014
Komisi Pembimbing :
Pembimbing 2, Pembimbing 1,
Dr. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc NIP.19630405 198811 2 001 NIP.19640109 198803 1 004
Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
SCRAMBLING INDEX DARI GRAF PRIMITIF TERDIRI ATAS DUA LINGKARAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2014
PENGHARGAAN
Tiada kata yang pantas diucapkan sebagai pembuka, selain ucapan syukur penulis kepada Allah SWT. Segala puji hanya bagiNya yang senantiasa memberikan kese-hatan dan nikmat kepada semua manusia, termasuk penulis, sehingga penyusunan skripsi dengan judul Scrambling Index dari Graf Primitif terdiri atas Dua Lingkaran ini dapat diselesaikan dengan baik. Shalawat serta salam juga disampaikan kepada Nabi Muhammad SAW, keluarganya, para sahabat, tabiin, dan setiap orang yang mengikuti mereka sampai hari akhir nanti.
Pada kesempatan ini penulis mengucapkan terima kasih kepada Bapak Prof. Dr. Saib Suwilo M.Sc dan Ibu Dr. Mardiningsih, M.Si selaku dosen pem-bimbing yang telah banyak membantu, meluangkan waktu, dan memberi dukun-gan, ilmu pengetahuan, motivasi, dan nasihat kepada penulis. Terima kasih juga kepada Bapak Dr. Suwarno Ariswoyo, M.Si dan Bapak Prof. Dr. Tulus, M.Si selaku dosen penguji yang telah memberikan banyak masukan, saran, dan dukun-gan yang baik dalam menyelesaikan skripsi ini.
Terima Kasih juga kepada Bapak Prof. Dr. Tulus, M.Si dan Ibu Dr. Mardiningsih, M.Si, selaku Ketua dan Sekretaris Departemen Matematika di FMIPA USU, Bapak Dr. Sutarman, M.Sc selaku Dekan FMIPA USU, Pembantu Dekan FMIPA USU, seluruh Staf Pengajar Departemen Matematika FMIPA USU, serta pegawai FMIPA USU atas ilmu pengetahuan, waktu, nasihat, dan motivasi yang diberikan selama masa perkuliahan. Mudah-mudahan Allah SWT senanti-asa memuliakan dan meninggikan derajat mereka.
Penulis juga mengucapkan terima kasih kepada Ibunda Inong Yasrida, Ayahanda Hidayat Bakhtiar, Kakanda Afdi Alfian, serta Adinda Rizky Ichwan, Nurul Agri, dan Saktira Surahiddin atas doa dan dukungan yang senantiasa diberikan sampai saat ini. Mudah-mudahan keberkahan dan keridhoanNya senan-tiasa melimpahi kita semua.
Penulis menyadari masih banyak kekurangan dari penyusunan skripsi ini. Oleh karena itu, saran dan kritik yang membangun tetap penulis nantikan demi perbaikan pada tulisan ini ataupun yang lain di masa yang akan datang. Harapan penulis, mudah-mudahan skripsi ini dapat bermanfaat sebagai tambahan penge-tahuan bagi pembaca dan semua pihak yang membutuhkan.
Medan, Juli 2014 Penulis
SCRAMBLING INDEX DARI GRAF PRIMITIF TERDIRI ATAS DUA LINGKARAN
ABSTRAK
Sebuah graf terhubungGdikatakan primitif apabila terdapat bilangan
bu-lat positifksehingga untuk setiap pasangan titikudanvdiGterdapat jalan yang menghubungkan titik u dan v dengan panjang k. Scrambling index
dari suatu graf primitifG, dinotasikan dengank(G), adalah bilangan bulat positif terkecilksehingga untuk setiap pasangan titikudanvyang berbeda
terdapat sebuah titik w dengan sifat ada jalan yang menghubungkan titik
u dan w dan jalan yang menghubungkan titik v dan w dengan panjang
k. Pada tulisan ini akan didiskusikan mengenai scrambling index dari
graf primitif G terdiri atas tepat dua lingkaran dengan panjang s dan t, dinotasikan dengan k(Ct
s). Apabila s dan t keduanya adalah ganjil, maka
k(Ct
s) = max
( (s−1)
2 , (t−1)
2 )
dan apabila salah satu dari s atau t adalah
ganjil, maka k(Ct s) =
(s+t−1)
2 .
SCRAMBLING INDEX OF PRIMITIVE GRAPHS CONSISTING OF EXACTLY TWO CYCLES
ABSTRACT
A connected graphs is called primitive if there is positive integerkthat for
each pair of verticesuand vthere is a walk that connecting vertexu andv
of lenghtk. Scrambling index of primitive graphG, denoted byk(G) is the
smallest positive integerksuch that for each pair of verticesu andv, there is a vertexwthat we can get to wfrom uand v inGby walks of lenght k.
In this paper, we discuss about scrambling index of primitive graphG con-sisting of exactly two cycles of lenghtsandt, denoted byk(Ct
s). Ifsandt,
both of them are cycle with odd vertices, then k(Ct
s) = max
( (s−1)
2 , (t−1)
2 )
and if one ofs ortis a cycle with odd vertices, thenk(Ct s) =
(s+t−1)
2 .
DAFTAR ISI
1.1 Latar Belakang Penelitian 1
1.2 Masalah Penelitian 3
1.3 Batasan Masalah 3
1.4 Tinjauan Pustaka 3
1.5 Tujuan Penelitian 6
1.6 Manfaat Penelitian 7
BAB 2 GRAF PRIMITIF
2.1 Definisi Graf 8
2.2 Matriks Adjacency 11
2.3 Matriks Tak Negatif 12
2.4 Graf Terhubung 13
2.5 Primitifitas Graf 15
2.6 Scrambling Index 17
2.7 Scrambling Index dari Lingkaran Ganjil 19
BAB 3 METODOLOGI PENELITIAN
3.1 Menentukan Nilai Scrambling Index 20
3.2 Menentukan Bentuk Umum Scrambling Index 20 3.3 Membuktikan Bentuk Umum Scrambling Index 21
BAB 4 SCRAMBLING INDEX Ct s
4.1 Scrambling index Ct
s untuk s dan t ganjil 23
4.2 Scrambling index Ct
s untuk s atau t ganjil 25
BAB 5 KESIMPULAN DAN SARAN
5.1 Kesimpulan 27
5.2 Saran 27
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
1.1 Representasi Hubungan Sosial dengan Graf tak Berarah 1 1.2 Common outneighbour (tetangga persekutuan luar) dalam graf 2
1.3 Graf Berarah Ds,n 4
2.1 Contoh representasi graf G(V, E) 9
2.2 Graf terhubung dan tidak terhubung 13
2.3 Graf primitif dan tidak primitif 16
2.4 Lingkaran dengan panjang ganjil 19
4.1 Graf primitif terdiri atas dua lingkaran 22
4.2 Graf Ct
s dengan s dan t keduanya ganjil 23
4.3 Graf Ct
SCRAMBLING INDEX DARI GRAF PRIMITIF TERDIRI ATAS DUA LINGKARAN
ABSTRAK
Sebuah graf terhubungGdikatakan primitif apabila terdapat bilangan
bu-lat positifksehingga untuk setiap pasangan titikudanvdiGterdapat jalan yang menghubungkan titik u dan v dengan panjang k. Scrambling index
dari suatu graf primitifG, dinotasikan dengank(G), adalah bilangan bulat positif terkecilksehingga untuk setiap pasangan titikudanvyang berbeda
terdapat sebuah titik w dengan sifat ada jalan yang menghubungkan titik
u dan w dan jalan yang menghubungkan titik v dan w dengan panjang
k. Pada tulisan ini akan didiskusikan mengenai scrambling index dari
graf primitif G terdiri atas tepat dua lingkaran dengan panjang s dan t, dinotasikan dengan k(Ct
s). Apabila s dan t keduanya adalah ganjil, maka
k(Ct
s) = max
( (s−1)
2 , (t−1)
2 )
dan apabila salah satu dari s atau t adalah
ganjil, maka k(Ct s) =
(s+t−1)
2 .
SCRAMBLING INDEX OF PRIMITIVE GRAPHS CONSISTING OF EXACTLY TWO CYCLES
ABSTRACT
A connected graphs is called primitive if there is positive integerkthat for
each pair of verticesuand vthere is a walk that connecting vertexu andv
of lenghtk. Scrambling index of primitive graphG, denoted byk(G) is the
smallest positive integerksuch that for each pair of verticesu andv, there is a vertexwthat we can get to wfrom uand v inGby walks of lenght k.
In this paper, we discuss about scrambling index of primitive graphG con-sisting of exactly two cycles of lenghtsandt, denoted byk(Ct
s). Ifsandt,
both of them are cycle with odd vertices, then k(Ct
s) = max
( (s−1)
2 , (t−1)
2 )
and if one ofs ortis a cycle with odd vertices, thenk(Ct s) =
(s+t−1)
2 .
BAB 1
PENDAHULUAN
1.1 Latar Belakang Penelitian
Graf merupakan pokok bahasan matematika yang banyak mendapat perhatian karena aplikasinya sangat berguna untuk menyelesaikan persoalan kehidupan ma-nusia. Secara umum, graf mempresentasikan model matematika terhadap sejum-lah objek dalam bentuk simpul atau titik (vertex) dan hubungan antara objek-objek tersebut dalam bentuk garis atau sisi (edge).
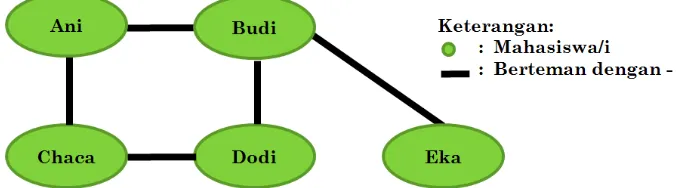
Pada persoalan komunikasi misalnya, graf dapat memodelkan hubungan sosial seseorang dengan seorang lainnya. Mahasiswa bernama Ani berteman dengan Budi dan Chaca tetapi tidak berteman dengan Dodi dan Eka, sedang-kan Dodi berteman dengan Budi dan Chaca tetapi tidak berteman dengan Ani dan Eka, dan Eka hanya berteman dengan Budi. Hubungan sosial yang demikian dapat direpresentasikan dalam graf tak berarah seperti pada gambar berikut:
Gambar 1.1. Representasi model hubungan sosial dengan graf tak berarah
2
dilakukan. Hal inilah yang menarik minat penulis untuk membahas scrambling index sebagai bagian dari pengembangan teori graf itu sendiri.
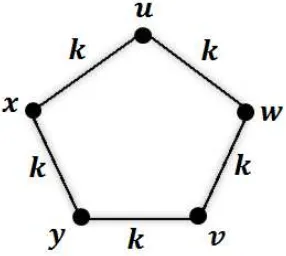
Istilah scrambling index pertama kali diperkenalkan oleh Akelbek dan Kir-kland pada tahun 2009. Apabila diketahui titik u, v, dan w serta sisi (u, w) dan (v, w) termuat dalam sebuah grafG, maka titik w merupakan common outneigh-bour (tetangga persekutuan luar) dari titik u dan v. Yang dinamakan scram-bling index adalah bilangan bulat positif terkecil k sedemikian hingga setiap pa-sangan titik-titik dalam graf G memiliki tetangga persekutuan luar yang mem-bentuk sisi-sisi dengan panjang k.
Gambar 1.2. Common outneighbour(tetangga persekutuan luar) dalam graf
Secara definisi, scrambling index dari sebuah graf primitif G, dinotasikan dengan k(G) adalah bilangan bulat positif terkecil k sehingga untuk setiap pa-sangan titik u dan v di G, terdapat sebuah titik w dengan sifat ada jalan yang menghubungkan titik u dan w dan jalan yang menghubungkan titik v dan w
dengan panjang k.
3
Di tahun yang sama, Akelbek dan Kirkland (2009b) mengelompokkan semua graf primitif berarah sedemikian hingga nilai scrambling index sama dengan batas atasnya. Penelitian kemudian dilanjutkan Chen dan Liu (2010) yang mem-bahas hubungan antara scrambling index dan eksponen pada matrix primitif simetris. Mereka juga mengelompokkan semua matriks primitif simetris sede-mikian hingga nilai scrambling index mencapai maksimum.
Selanjutnya, Gao dan Shao (2013) juga telah membahas mengenai scram-bling index dari graf primitif berarah terdiri atas tepat dua lingkaran. Adapun penelitian ini secara khusus akan membahas mengenai scrambling index dari graf primitif tak berarah yang terdiri atas tepat dua lingkaran.
1.2 Masalah Penelitian
AndaikanCt
sadalah sebuah graf primitif terdiri atas dua lingkaran dengan panjang s dan t. Masalah yang akan diselesaikan pada penelitian ini adalah menentukan bagaimana bentuk umum scrambling index dariCt
s, dinotasikan dengank(Cst)
un-tuk lingkarans dan t keduanya adalah ganjil dan untuk salah satu dari lingkaran
s atau t adalah ganjil.
1.3 Batasan Masalah
Bentuk umum scrambling index yang dibahas dalam tulisan ini hanya dikhususkan pada satu objek graf, yaitu pada graf primitif yang terdiri atas tepat dua lingkaran, dinotasikan dengan k(Ct
s). Adapun bentuk umum yang ditentukan terbagi
men-jadi dua kasus, yaitu bentuk umum scrambling index untuk kedua lingkaransdan
t adalah ganjil dan untuk salah satu dari s atau t adalah ganjil.
1.4 Tinjauan Pustaka
Pada tahun 2009, Akelbek dan Kirkland memperkenalkan istilah baru dalam graf primitif yang dinamakan scrambling index. Scrambling index, dinotasikan dengan
4
u dan v di G, terdapat sebuah titikw dengan sifat ada jalan yang menghubung-kan titikudanwdan jalan yang menghubungkan titikvdanwdengan panjangk.
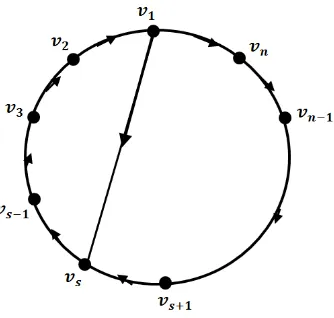
Dalam penelitiannya, Akelbek dan Kirkland (2009a) membahas mengenai scrambling index pada graf primitif berarah dan memberikan batas atas dari scrambling index pada graf primitif berarah terkait dengan order dan girthyang kemudian digunakan untuk menetapkan batas atas pada modulo terbesar kedua dari nilai eigen sebuah matriks primitif. Order adalah jumlah titik dan girth adalah panjang terpendek dari lingkaran pada graf primitif berarah.
Misalkan Dadalah sebuah graf primitif berarah denganntitik dansgirth, maka scrambling index k(D)≤K(n, s).
Gambar 1.3. Graf BerarahDs,n
JikaD=Ds,n dangcd(n, s) = 1 di manaDs,n merupakan graf berarah primitif sebagaimana diperlihatkan pada Gambar 1.3, makaK(n, s) = k(n, s) +n−sdan
k(n, s) = ( s−
1
2 n, untuk s ganjil
n−1
2 s, untuk s genap
5
hanya jikaD =Ds,n dan gcd(n, s) = 1.
Misalkan Dadalah sebuah graf primitif berarah denganntitik dansgirth, dengan s genap dan s ≤ 3. Maka scrambling index k(D) = K(n, s) jika dan hanya jika gcd(n, s) = 1 dan D = Ds,n, atau D = Ds,n ∪ {n −r− ts+ 1 →
n − r − ts +ms} untuk sebarang m ∈ N dan sebarang t ∈ {1,2, ..., n−2r s −
1} sedemikian hingga n+h
2 −t−1≡0(modm).
Pada tahun berikutnya, Chen dan Liu (2010) membahas hubungan antara scrambling index dan eksponen pada matrix primitif simetris. Sebuah matriks persegi non negatifA dikatakan primitif apabila terdapat bilangan bulat positifk
sedemikian hinggaAk>0. Scrambling index dari matriks primitifA, dinotasikan
dengan k(A) adalah bilangan bulat positif terkecil k sehingga untuk setiap dua baris pada Ak terdapat sedikitnya satu elemen positif pada posisi kolom yang
sama.
Eksponen dari matriks primitif A, dinotasikan dengan exp(A) adalah bi-langan bulat positif terkecil k sedemikian hingga Ak = dimana menotasikan
1-matriks, yaitu matriks yang semua elemennya memuat 1. Dalam penelitiannya dinyatakan bahwa untuk sebuah matriks primitif A berdasarkan definisi scram-bling index dan definisi eksponen, dapat diketahuik(A)≤exp(A).
Misalkan D adalah sebarang graf berarah primitif simetris dengan n ≥ 2 dan misalkan u dan v adalah pasangan titik di D. Maka
ku,v(D)≤ ⌈expD(u, v)
2 ⌉ dan
k(D) = ⌈exp(D)
2 ⌉
dimana⌈a⌉ menotasikan bilangan bulat positif terkecil yang tidak kurang daria. Misalkan D adalah sebarang graf berarah primitif simetris dengan n ≥ 2 dan misalkanu dan v adalah pasangan titik diD. Jikau↔k1 v dan u↔k2 v dengan
k1−k2 ≡1(mod 2), maka
6
Selain itu, mereka juga mengelompokkan semua matriks primitif simetris sedemikian hingga nilai scrambling index mencapai maksimum. Diberikan Sn(r) adalah himpunan semua graf primitif dengan ntitik yang memiliki lingkaran sep-anjang r tetapi bukan lingkaran dengan panjang ganjil yang lebih kecil dari r.
Andaikan n dan m adalah bilangan bulat positif dengan n ≥ 2, r ≡
1(mod2) dan 1≤r≤n, dan misalkan
δr = (
1, untuk r = 1
r−1
2 , untuk r≡1(mod2) dan r≥3
danGadalah graf primitif diSn(r), makak(G)≥δr. Misalkannadalah bilangan bulat positif dengan n ≥ 2 dan r adalah bilangan bulat positif ganjil dengan 1≤r≤n. AndaikanG adalah graf primitif di Sn(r) maka persamaan
k(G)≤n− r+ 1
2
dipenuhi jika dan hanya jika:
(i) n≥3 dan G isomorfis terhadapGn,rn−r, atau
(ii) n= 2 (r= 1)dan baikG isomorfis terhadapG21,1 atau Gisomorfis terhadap
G2′,1 ditentukan dari G 2,1
1 dengan menambahkan sebuah loop (titik yang
di-hubungkan dengan sebuah sisi ke dirinya sendiri) pada titik lainnya.
Gao dan Shao (2013) dalam penelitiannya mengemukakan tentang scram-bling index dari graf berarah primitif yang terdiri atas tepat dua lingkaran dan dalam penelitian ini secara khusus akan dibahas mengenai scrambling index dari graf primitif yang terdiri atas tepat dua lingkaran.
1.5 Tujuan Penelitian
pri-7
yang ditentukan terbagi menjadi dua kasus, yaitu bentuk umum scrambling index dengan lingkaransdantkeduanya adalah ganjil dan bentuk umum scrambling in-dex dengan salah satu lingkarans atau t adalah ganjil.
1.6 Manfaat Penelitian
BAB 2
GRAF PRIMITIF
Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkaitgraf, mat-riks adjency, terhubung, primitifitas, dan scrambling indexsebagai landasan teori yang menjadi acuan dalam penelitian ini. Akan dijelaskan pula beberapa termi-nologi serta notasi-notasi yang akan digunakan pada pembahasan berikutnya.
2.1 Definisi Graf
Secara umum graf mempresentasikan model matematika terhadap sejumlah ob-jek dalam bentuk simpul/titik (vertex) dan hubungan antara objek-objek tersebut dalam bentuk garis/sisi (edge). Sederhananya, graf dapat digambarkan sebagai kumpulan titik yang dihubungkan dengan garis. Secara matematika graf didefi-nisikan sebagai pasangan tak berurut yang terdiri dari dua himpunan berikut:
1. Himpunan berhingga tak kosong V ={v0, v1,· · · , vm}, dinotasikan dengan
V(G). Elemen-elemen dari himpunan V ini disebut verteks atau titik dari graf G.
2. Himpunan sisi yang dinotasikan denganE(G), yaitu pasangan tak berurut dari elemen-elemenV(G) dalam bentukE ={(v0, v1); (v1, v2);·; (vm−1, vm)}.
Elemen-elemen dari himpunan E ini disebut edge atau sisi dari graf G.
Sebuah grafG dengan himpunan titikV dan himpunan sisiE dinotasikan denganG(V, E). Banyaknya elemen diV disebutorderdariG, dinotasikan dengan
9
Suatu graf dengan size 0 dinamakan graf kosong (null graph) sedangkan graf dengan order 1 tanpa sebuah sisi sama sekali dinamakan graf trivial.
Contoh 2.1Berikut adalah grafG(V, E) dengan himpunan titikV ={v1, v2, v3, v4, v5}
dan himpunan sisi E = {v1↔v2, v2↔v3, v3↔v4, v4↔v5, v3↔v5, v5↔v1}.
Repre-sentasi graf tersebut diperlihatkan pada gambar berikut.
Gambar 2.1. Contoh representasi grafG(V, E)
Graf G(V, E) pada gambar 2.1 mempunyai 5 titik dan 6 sisi sehingga order dari
G adalah|V|= 5 dan size dari Gadalah |E|= 6.
Apabila diketahui sisi e = (u, v) termuat dalam graf G, maka titik-titik u
dan v disebut sebagai titik ujung dari sisi e. Titik u merupakan titik awal dan titik v merupakan titik akhir dalam graf G. Titik u dan v dikatakan bertemu dengan sisi edan sebaliknya sisi edikatakan bertemu dengan titik udanv. Dera-jat dari sebuah titiku, dinotasikan dengandeg(u) adalah banyaknya sisi-sisi yang bertemu dengan titik u.
10
AndaikanGadalah sebuah graf. Sebuah jalan (walk) yang menghubungkan titik u dan titik v di G dengan panjang m adalah sebuah barisan m sisi dengan bentuk
{u=v0, v1},{v1, v2}, ,{vm−1), vm =v}
Jalan yang menghubungkan titiku dan titikv dengan panjang m ini dinotasikan dengan u = v0 ↔ v1 ↔ v2 ↔ · · · ↔ vm = v yang selanjutnya disingkat dengan
penulisan u↔m v.
Sebuah jalan yang menghubungkan u dan v dikatakan terbuka apabila
u 6= v dan dikatakan tertutup apabila u = v. Sebuah jalan tanpa perulangan titik kecuali mungkin titik-titik ujungnya disebut dengan lintasan (path). Titik awal dan titik akhir dari suatu lintasan bisa saja merupakan titik yang sama, lin-tasan yang demikian disebut linlin-tasan tertutup (close path) dan merupakan sebuah lingkaran (cycle).
Suatu lingkaran-s (s-cycle) adalah lingkaran dengan panjang s dan dino-tasikan denganCs. Jarak (distance) dari titikumenuju titikv, dinotasikan dengan
d(u, v) adalah panjang dari jalan terpendek yang menghubungkan titik u dan v. Adapun diameter dari suatu grafGmerupakan maksimum jarak yang dapat dite-mukan antara titik-titik pada grafG.
Dengan menggunakan graf pada gambar 2.1 akan dijelaskan beberapa ter-minologi tersebut di atas.
a. Barisan sisi v1↔v2↔v1↔v5↔v4 adalah sebuah jalan tetapi bukan lintasan
karena ada perulangan titikv1. Karena titik awal dan titik akhirnya berbeda,
jalan ini disebut jalan terbuka.
b. Barisan sisi v1↔v2↔v3↔v4↔v5 adalah sebuah lintasan terbuka.
c. Barisan sisi v1↔v2↔v3↔v4↔v5↔v1 adalah sebuah lintasan tertutup dan
11
d. Jarakd(v1, v5) adalah jarak dengan panjang ganjil dan jarakd(v1, v3) adalah
jarak dengan panjang genap.
e. Jarak maksimum dari graf G adalah 2, yaitu antara d(v1, v3), d(v1, v4),
d(v2, v4), ataupun d(v2, v5). Maka diameter graf G adalah 2.
2.2 Matriks Adjacency
Matriks adjacency (matriks ketetanggaan) adalah (0,1)-matriks, yaitu sebuah matriks yang hanya memuat elemen 0 atau 1. Matriks ini digunakan untuk menyatakan graf G atas n titik. Matriks adjacency dari sebuah graf G atas n
titik v1, v2,· · · , vn adalah sebuah matriks bujursangkar A = [aij] dengan ordo n
yang setiap elemennya didefinsikan dengan ketentuan berikut:
aij = (
1, jika {vi, vj} ∈E(G) 0, jika {vi, vj}∈/ E(G)
Berdasarkan definisi dapat diketahui bahwa aij =aji untuk semua 1 ≤ i, j ≤ n. Hal ini berakibat matriks ketetanggaanA(G) dari grafGmerupakan sebuah mat-riks simetrik.
Contoh 2.2GrafG(V, E) pada gambar 2.1 dapat direpresentasikan dalam bentuk matriks adjacency A(G) = [aij] sebagai berikut: Elemen a12 = 1 menyatakan bahwa terdapat sisi yang menghubungkan titik v1
dengan titikv2, yakni sisi{1,2}dan elemena13= 0 menyatakan bahwa tidak
12
angka 1 pada baris pertama dari A(G) menyatakan derajat dari titikv1.
Teorema 2.1 Andaikan G adalah sebuah graf dan A = (aij) adalah sebuah mat-riks adjacency dari G. Misalkan ak
ij adalah elemen (i, j) dari matriks Ak. Maka ak
ij menyatakan banyaknya jalan dengan panjang k yang menghubungkan titik i
dengan titik j.
Bukti. Pembuktian dilakukan dengan menggunakan induksi atas k. Asumsikan bahwa elemen ak
ij dari Ak menyatakan banyaknya jalan dengan panjang k yang
menghubungkan titiki dengan titikj. Apabilak = 1, maka elemen a1
ij =aij dari A menyatakan banyaknya jalan dengan panjang 1 yang menghubungkan titik i
dengan titik j. Karena Ak+1 =AkA, maka
banyaknya jalan dengan panjangk+ 1 yang melalui titikvl. Sehingga oleh prinsip penjumlahan, akij+1 adalah banyaknya jalan dengan panjang k+ 1 yang
menghu-bungkan titik i dengan titik j.
2.3 Matriks Tak Negatif
Matriks tak negatif A merupakan suatu matriks dengan aij ≥ 0, artinya setiap elemen-elemen aij dari matriksA memuat bilangan bulat tak negatif. Sebaliknya jika setiap elemen-elemen dari matriks A memuat bilangan bulat positif, yaitu
13
M =
7 3 9 2 3 1 2 4 1 4 1 1 4 8 3 1
Matriks N adalah matriks tak negatif dan matriks M adalah matriks positif.
2.4 Graf Terhubung
Sebuah grafG dikatakan terhubung (connected graph) apabila untuk setiap pasa-ngan titik u dan v diGterdapat jalan yang menghubungkan u dan v, sebaliknya grafGdikatakan tidak terhubung apabila tidak terdapat jalan yang menghubung-kan titik u ke titik v.
Dua titik terhubung pada suatu graf bersifat refleksif, artinya apabila u
dan v adalah dua titik yang terhubung maka terdapat jalan yang menghubung-kan u dengan v dan dengan bergerak mundur akan diperoleh sebuah jalan yang menghubungkan v dengan u. Maka dua titik terhubung pada suatu graf juga bersifat simetrik.
Gambar 2.2. Graf terhubung dan tidak terhubung
Gambar 2.2 menunjukkan bahwa (a) adalah graf terhubung karena terdapat jalan yang menghubungkan satu titik ke titik lainnya, sedangkan (b) adalah graf tidak terhubung karena tidak terdapat jalan yang menghungkan titik v1, v2 dan v3 ke
keter-14
hubungan dari suatu graf.
Teorema 2.2 Andaikan G adalah sebuah graf atas n titik dengan matriks kete-tanggaanA. GrafG adalah terhubung jika dan hanya jika matriksA+A2+· · ·+
An−1 mempunyai elemen yang semuanya bernilai positif.
Bukti. Andaikan G adalah sebuah graf terhubung dan misalkan B = A+A2 +
· · ·+An−1. Telah diketahui bahwa Gmempunyai n titik dan pada suatu lintasan
tidak terdapat titik berulang kecuali u=v. Apabilau6=v, maka terdapat suatu lintasan dengan panjang kurang darin yang menghubungkanu dengan v.
Hal ini mengakibatkan untuk setiap pasangan titiku dan v yang berbeda, terdapat sebuah bilangan bulat positif k dengan 1≤k ≤n−1 sehingga elemen
ak
ij > 0. Artinya, semua elemen di luar elemen diagonal dari matriks B adalah
positif. Apabila u = v, maka terdapat sebuah lingkaran dengan panjang 2 yang memuat titik u sehingga elemen a2
uu > 0 untuk semua u = 1,2,· · · , n. Maka
diagonal dari matriks B adalah positif sehingga dapat disimpulkan bahwa semua elemen dari matriks B =A+A2+· · ·+An−1 adalah positif.
Akibatnya, untuk setiap pasangan titiku danv terdapat sebuah bilangan positifkdengan 1≤k ≤n−1 sehinggaak
ij >0. Hal ini menyatakan bahwa untuk
setiap pasangan titik udan v diG terdapat sebuah jalan dengan panjangk yang menghubungkan titik u dan v, artinya G adalah sebuah graf terhubung.
Berikut adalah proposisi yang menjelaskan beberapa sifat dari jalan yang menghubungkan titik u dan titik v yang dirujuk dari Harleni (2014).
Proposisi 2.1 Misalkan G adalah suatu graf yang memuat titik u dan v. Setiap jalan u ↔t v dapat dikembangkan menjadi sebuah jalan u t+2↔m v, untuk sebarang bilangan bulat positif m.
Bukti. Misalkan titik u dan v termuat dalam graf G dan misalkan W : u =
v0 ↔ v1 ↔v2 ↔ · · · ↔vt−1 ↔vt =v merupakan jalan u
t
15
W′
yang dimulai dari titik u berpindah ke titik v sepanjang jalan W kemudian berpindah m kali mengelilingi lingkaran v ↔ vt−1 ↔ v merupakan sebuah jalan
ut+2↔mv.
Proposisi 2.2 Misalkan G adalah suatu graf yang memuat titik u,v dan w. Ter-dapat jalanu↔t wdan jalanv ↔t wdi Gjika dan hanya jika terdapat jalanu↔2t v
di G.
Bukti. Andaikan terdapat jalan u ↔t w dan jalan v ↔t w di G. Maka dapat dinyatakan bahwa jalan yang dimulai dariuyang berpindah kewsepanjang jalan
u↔t wkemudian berpindah kev sepanjang jalanv ↔t w, merupakan jalan u↔2t v. Asumsikan bahwa W : u =v0 ↔ v1 ↔ v2 ↔ · · · ↔v2t−1 ↔ v2t =v merupakan
jalanu↔2t v di G. Jikaw=vt, maka terdapat u↔t w dan jalanv ↔t w di G.
Syahmarani dan Suwilo (2012) juga memberikan Lemma mengenai graf terhubung sebagai berikut.
Lemma 2.1 Andaikan G adalah graf terhubung maka setiap titik v di G ter-letak pada suatu lingkaran.
Bukti. Ambil sebarang titik v di G. Karena G terhubung, maka terdapat su-atu sisi yang menghubungkan titik v ke suatu titiku. Akibatnya, akan diperoleh suatu lintasan tertutup di G yang dibentuk oleh sisi dari titik u ke titik v dan lintasan dari titik v ke titik u di G. Oleh definisi, diketahui bahwa lintasan ter-tutup merupakan suatu lingkaran. Karena titik v adalah sebarang titik di G, maka setiap titik v diG terletak pada suatu lingkaran.
2.5 Primitifitas Graf
16
Graf G(V, E) yang ditunjukkan pada gambar 2.1 sebelumnya adalah salah satu contoh graf primitif. Berikut akan diperlihatkan graf primitif dan tidak pri-mitif.
Gambar 2.3. Graf primitif dan tidak primitif
Gambar 2.3 memperlihatkan bahwa (a) merupakan graf primitif karena graf tersebut memuat lingkaranv1 ↔v2 ↔v3 ↔v1 dengan panjang 3, sehingga syarat
memuat paling sedikit sebuah lingkaran dengan panjang ganjil telah dipenuhi. Gambar (b) merupakan graf tidak primitif karena tidak memuat lingkaran ganjil sama sekali.
Primitifitas suatu graf juga dapat dilihat melalui representasi matriksnya. Sebuah matriks persegi non negatifAdikatakan primitif apabila terdapat bilangan bulat positif k sedemikian hingga Ak > 0. Berikut adalah representasi matriks
dari graf primitif pada gambar 2.3 bagian (a).
17
Karena terdapatk = 2 sedemikian hingga setiap elemen-elemen padaA2 memuat
bilangan bulat positif, maka diketahui bahwa untuk matriksAdari graf tersebut, terdapat A2 >0. Sehingga terbukti bahwa graf tersebut adalah graf primitif.
2.6 Scrambling Index
Scrambling index dari graf primitif G, dinotasikan dengan k(G) adalah bilangan bulat positif terkecil k sehingga untuk setiap dua titik u dan v yang berbeda, terdapat sebuah titik w dengan sifat terdapat u ↔k w dan v ↔k w. Adapun un-tuk dua titik u dan v yang berbeda, scrambling index lokal dari u dan v adalah bilangan bulat positif ku,v(G) yang didefinisikan sebagai berikut:
ku,v(G) = min w∈V{k:u
k
↔w dan v ↔k w}
Dari definisi scrambling index k(G) dan scrambling index lokal ku,v(G) diperoleh hubungan k(G) ≥ ku,v(G). Karena G adalah graf terhubung, maka untuk setiap bilangan bulatl≥ku,v(G) dapat ditemukan sebuah titikw′
sehingga terdapat u ↔l w′
dan v ↔l w′
. Hal ini mengakibatkan nilai dari k(G) yang juga disebut dengan scrambling index global adalah maksimum dari nilai-nilai scrambling index lokal ku,v(G) yang didefinisikan sebagai berikut:
k(G) =max
u6=v {ku,v(G)}
Contoh 2.3 Dengan menggunakan graf G(V, E) pada gambar 2.1, nilai scram-bling index dari graf tersebut dapat ditentukan. Terlebih dahulu ditentukan nilai-nilai scrambling index lokal-nya sebagai berikut:
18
Maka scrambling index dari graf tersebut adalah maksimum dari semua scram-bling index lokal yang diperoleh, yaitu k(G) = max{2,1,2,1,2,2,1,1,1,1}= 2.
Karena graf dapat dinyatakan dalam bentuk matriksadjacency, nilai scram-bling index dapat pula ditentukan dari matriks primitif. Scramscram-bling index dari matriks primitifA, dinotasikan dengank(A) adalah bilangan bulat positif terkecil
k sehingga untuk setiap dua baris padaAkterdapat sedikitnya satu elemen positif
pada posisi kolom yang sama.
Dengan mempresentasikan graf G(V, E) pada gambar 2.1 dalam bentuk matriks adjacency A sebagai berikut, nilai scrambling index graf tersebut juga dapat diketahui.
Dapat dilihat bahwa pada matriks A2 terdapat sebuah kolom (kolom ke-5) yang
19
sama telah dipenuhi. Sehingga diketahui nilai scrambling index dari graf tersebut adalah 2.
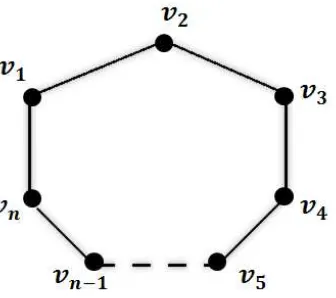
2.7 Scrambling Index dari Lingkaran Ganjil
Gao dan Shao (2013) dalam penelitiannya mengemukakan tentang scrambling index dari lingkaran ganjil. Scrambling index dari sebuah lingkaran atas n titik ganjil
Cn :v1 ↔v2 ↔...↔vn−1 ↔vn↔v1
didefinisikan sebagai berikut:
Lemma 2.2 Andaikan Cn adalah sebuah lingkaran atas n titik ganjil, maka
k(Cn) = (n−21)
Bukti. Jalan dengan panjang genap terpendek yang menghubungkan vn dengan
vn−1 adalah jalan Wvn,vn−1 : vn ↔ v1 ↔ v2 ↔ ... ↔ vn−1 dengan panjang n−1.
Hal ini berakibat Kvn,vn−1(Cn) =
(n−1)
2 sehingga k(G)≥ (n−1)
2 .
Gambar 2.4. Lingkaran dengan panjang ganjil
Untuk dua titikvidanvj yang berbeda, telah diperlihatkan bahwa terdapat jalan yang menghubungkan vi dan vj dengan panjang genap t ≤ n−1. Hal ini berakibat untuk dua titik vi dan vj yang berbeda terdapat sebuah jalan yang menghubungkanvidanvj dengan panjang tepatn−1. Sehingga diperolehk(Cn)≤
(n−1)
2 . Maka terbukti k(Cn) = (n−1)
BAB 3
METODE PENELITIAN
Adapun metodologi yang digunakan dalam penelitian ini adalah menggunakan metode kepustakaan, yaitu dengan mengumpulkan dan membaca informasi-informasi serta literatur yang berkaitan. Berikut akan dijelaskan langkah-langkah yang di-lakukan untuk menentukan bentuk umum scrambling index dari graf primitif ter-diri atas dua lingkaran.
3.1 Menentukan Nilai Scrambling Index
Dengan menggunakan algoritma program yang ditulis dalam M AT LAB akan diperoleh nilai-nilai scrambling index dari graf primitif terdiri atas dua lingkaran dengan panjang s dan t dengan s, t ≥ 3. Berikut adalah algoritma umum yang digunakan:
input(matriks A); k=1;
B=A;
while (B not scrambling) k=k+1;
B=B*A; end;
output(k);
3.2 Menentukan bentuk umum scrambling index
Setelah memperoleh nilai-nilai scrambling indexk(Ct
s) untuks, t ≥3 pada proses
sebelumnya, langkah selanjutnya adalah menentukan persamaan yang dapat diben-tuk berdasarkan nilai-nilaik(Ct
21
Karena graf primitif, maka persamaan yang perlu ditentukan terbagi men-jadi dua kasus, yaitu bentuk umum scrambling index untuk lingkaran s dan t
keduanya adalah ganjil dan bentuk umum scrambling index untuk salah satu dari lingkaran s atau t adalah ganjil.
3.3 Membuktikan bentuk umum scrambling index
Setelah ditemukan bentuk umum scrambling indexk(Ct
s) untuk lingkarans dant
keduanya adalah ganjil dan untuk salah satu dari lingkaransataut adalah ganjil. Langkah selanjutnya adalah membuktikan kedua persamaan tersebut.
Pembuktian dilakukan dengan menganalisa dan menentukan jalan terpen-dek dengan panjang genapk yang menghubungkan setiap pasangan titik berbeda pada graf primitif terdiri atas dua lingkaran sedemikian hingga untuk setiap pa-sangan titik vi dan vj yang berbeda pada graf tersebut, terdapat titik w dengan sifat terdapat vi ↔k w dan vj ↔k w. Sehingga akan didapatkan nilai scrambling index k(Ct
BAB 4
PEMBAHASAN: SCRAMBLING INDEX Cs t
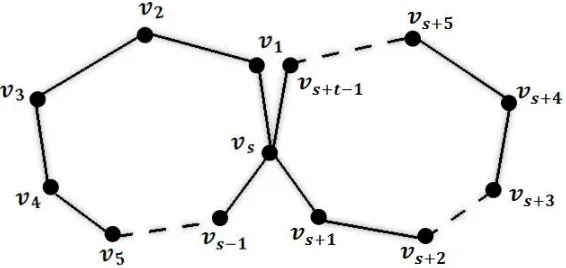
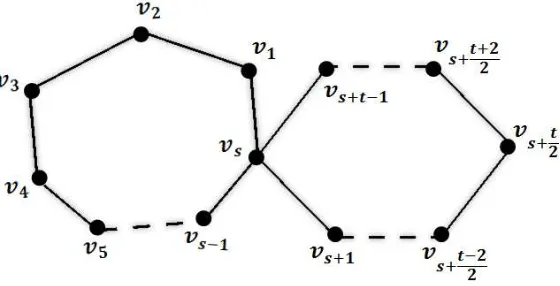
Andaikan Ct
s adalah graf primitif yang terdiri atas ”tepat dua lingkaran”, yakni
lingkaran
Cs :v1 ↔v2 ↔ · · · ↔vs−1 ↔vs ↔v1
dengan panjang s dan lingkaran
Ct:vs ↔vs+1 ↔ · · · ↔vs+t−1 ↔vs
dengan panjang t sebagaimana ditunjukkan pada gambar berikut:
Gambar 4.1. Graf primitif terdiri atas dua lingkaran
Karena Ct
s adalah graf primitif, maka graf tersebut harus memuat
se-dikitnya satu dari lingkaran s atau t adalah ganjil. Sehingga bentuk umum scrambling index yang perlu ditentukan terbagi menjadi dua kasus, yaitu un-tuk lingkarans dan t keduanya adalah ganjil dan untuk salah satu dari lingkaran
23
4.1 Scrambling index Ct
s untuk s dan t keduanya adalah ganjil
Teorema 4.1Andaikan Ct
s adalah sebuah graf primitif terdiri atas dua lingkaran
dengan panjang s dan t. Apabila s dan t adalah ganjil, maka
k(Ct
Bukti. Tanpa kehilangan keumuman pembuktian, andaikan s≤t. Dengan mem-perhatikan titik vs+t−1
2 dan titik vs+
t+1
2 , dapat diketahui jalan terpendek dengan
panjang genap yang menghubungkan kedua titik tersebut adalah jalan
vs+t+1
dengan panjang t−1. Sehingga kv
s+t−21, vs+
sdengansdant keduanya ganjil
Selanjutnya, untuk dua titik vi dan vj yang berbeda akan diperlihatkan terdapat jalan yang menghubungkan vi dan vj dengan panjang t−1. Apabila
24
Sekarang diasumsikan vi ∈ Cs dan vj ∈ Ct. Maka diketahui diameter dari Cs
tasan pvi,vj dapat diperpanjang menjadi jalan yang menghubungkan vi dan vj
dengan panjang t−1.
Selanjutnya diasumsikan bahwa jarak d(vi, vj) adalah ganjil dan diketahui
d(vi, vj) = d(vi, vs) +d(vs, vj). Apabila d(vi, vs) > d(vs, vj), maka jalan yang menghubungkan vi dan vj dengan panjang s −d(vi, vs) + d(vs, vj) adalah jalan dengan panjang genap kurang darit−1. Apabila d(vi, vs)< d(vs, vj), maka jalan yang menghubungkan vi dan vj dengan panjang t −d(vs, vj) +d(vi, vs) adalah jalan dengan panjang genap kurang dari t−1.
Untuk kedua kasus ganjil dan genap, lintasanpvi,vjdengan panjangd(vi, vj)
dapat diperpanjang menjadi jalan yang menghubungkan vi dan vj dengan pan-jang t−1. Akibatnya untuk titik-titik vi dan vj yang berbeda terdapat titik w
sehingga ada vi
Karena lingkaran s dan t keduanya adalah ganjil, jika diandaikan t < s
akan diperoleh jalan terpendek dengan panjang genap yang menghubungkan se-tiap pasangan titik vi dan vj yang berbeda pada graf Ct
s adalah jalan dengan
panjang s−1. Akibatnya untuk titik-titik vi dan vj yang berbeda terdapat titik
w sehingga adavi
s−1
25
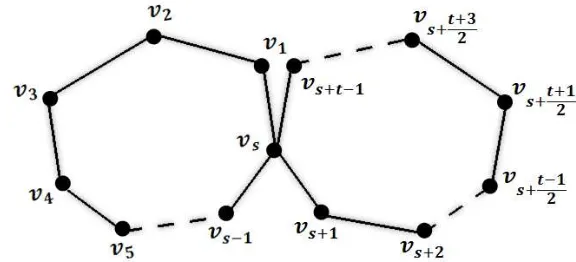
4.2 Scrambling index Ct
s untuk salah satu s atau t adalah ganjil
Teorema 4.2Andaikan Ct
s adalah sebuah graf primitif terdiri atas dua lingkaran
dengan panjang s dan t. Apabila salah satu dari s atau t adalah ganjil, maka
k(Ct
s) = s+2t−1.
Bukti. Andaikan lingkaran sadalah ganjil dan lingkaran tadalah genap. Dengan memperhatikan titik vs+t−2
2 dan titik vs+
t
2, berdasarkan Proposisi 2.2 diketahui
bahwa jalan terpendek dengan panjang genap yang menghubungkan kedua titik tersebut adalah jalanW, yaitu jalan yang bermula divs+t
2, bergerak kevs melalui
lintasan dengan panjang t
2, kemudian mengitari lingkaran Cs sekali dan kembali
ke vs, lalu dilanjutkan ke titikvs+t−2
2 melalui lintasan dengan panjang t−2
2 .
Maka diketahui bahwa jalan W mempunyai panjang s +t−1 sehingga
kv
sdengan salah satusataut adalah ganjil
Selanjutnya, untuk dua titikvidanvj yang berbeda akan diperlihatkan ter-dapat jalan yang menghubungkanvi dan vj dengan panjang genap tak lebih dari
s+t−1
2 . Apabilad(vi, vj) adalah genap, maka terdapat jalan yang menghubungkan
vidanvj dengan panjang genap kurang dari s+t−1
2 . Sekarang diasumsikand(vi, vj)
26
Apabilavi ∈Csdanvj ∈Ctmakad(vi, vj) = d(vi, vs)+d(vs, vj). Berdasar-kan Proposisi 2.2, hal ini mengakibatBerdasar-kan terdapat jalan W yang bermula di titik
vi menuju vs melalui lintasan dengan panjang d(vi, vs), kemudian mengitari Cs
sekali lalu lanjutkan ke titik vj melalui lintasan dengan panjang d(vs, vj) adalah sebuah jalan dengan panjang genaps+d(vi, vs) +d(vs, vj)≤s+t−1. Akibatnya,
k(Ct s)≤
s+t−1 2 .
Sehingga terbukti bahwa scrambling index dengan salah satu lingkaran s
atau t adalah ganjil yaitu
k(Cst) =
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Diberikan suatu graf primitif Ct
s terdiri atas tepat dua lingkaran, yakni lingkaran Cs :v1 ↔v2 ↔ · · · ↔vs−1 ↔vs ↔v1
dengan panjang s dan lingkaran
Ct:vs ↔vs+1 ↔ · · · ↔vs+t−1 ↔vs
dengan panjang t. Maka scrambling index dari graf primitif Ct
s, dinotasikan
dengan k(Ct
s) dapat ditentukan dengan menggunakan dua persamaan berikut:
1. Apabila sdan t pada graf primitif Cs
t keduanya adalah ganjil, maka
scram-bling index dari graf tersebut adalah
k(Ct
2. Apabila salah satu dari s atau t pada graf primitifCs
t adalah ganjil, maka
scrambling index dari graf tersebut adalah
k(Cst) =
s+t−1
2 ; s, t ≥3
5.2 Saran
Bentuk umum scrambling index yang dibahas dalam tulisan ini hanya terkhusus pada satu objek graf, yaitu pada graf primitif terdiri atas tepat dua lingkaran, dinotasikan k(Ct
s) untuk kedua lingkaran s dan t adalah ganjil dan salah satu
Daftar Pustaka
Akelbek, M and Kirkland, S. 2009a. Coefficients of Ergodicity and The Scram-bling Index. Linear Algebra and its Applications, Volume 430, Issue 4, 1111-1130.
Akelbek, M and Kirkland, S. 2009b. Primitive Digraphs with The Largest Scram-bling Index. Linear Algebra and its Applications, Volume 430, Issue 4, 1099-1110.
Brualdi, R. A and Ryser, H.J .1991. Combinatorial Matrix Theory. Cambridge University Press,Cambridge.
Chen, S and Liu, B. 2010. The Scrambling Index of Symmetric Primitive Ma-trices. Linear Algebra and its Applications, Volume 433, Issue 6, 1110-1126.
Gao, Y and Shao, Y. 2013. Scrambling Index of primitive Digraphs Consisting of Exactly Two Cycles. Ars Combinatoria.
Harleni, S. 2014. Batas Atas untuk Scrambling Index dari Graf Primitif. [Tesis]. Medan: Universitas Sumatera Utara, Program Pascasarjana.