BAB 1 PENDAHULUAN
1.1 Latar Belakang
Graf merupakan suatu representasi objek diskrit dan hubungan antara objek-objek tersebut. Representasi visual dari graf adalah dengan menyatakan objek-objek se-bagai titik (vertex) dan hubungan antara objek-objek tersebut dinyatakan dengan sisi (edge). Dengan kata lain, sebuah grafGadalah sebuah pasangan berurut yang dinotasikan G= (V, E) dimanaV adalah suatu himpunan tak kosong yang berisi elemen-elemen yang disebut titik (vertices) dan E adalah himpunan dari 2 subset pasangan tak berurut V yang disebut garis (edge).
Andaikan G adalah sebuah graf. Sebuah jalan dengan panjang p yang menghubungkan titik u dan v di G adalah sebuah barisan p buah sisi dalam bentuk
{u=u0, u1},{u1, u2},{u2, u3}, ...,{up−1, up =v}
dan dinotasikan dengan u −→p v. Sebuah lintasan yang menghubungkan titik u danv adalah sebuah jalan dengan tiap titik yang berbeda kecualiu=v. Lintasan yang berawal dan berakhir pada titik yang sama disebutcycle.
Sebuah graf G dikatakan terhubung jika untuk tiap pasangan titik u dan v yang berbeda diG terdapat jalan yang menghubungkan kedua titik tersebut. Se-buah graf terhubungG dikatakan primitif jika dan hanya jika graf Gmempunyai paling sedikit satucycledengan panjang ganjil. Graf primitif merupakan graf ter-hubung dimana terdapat bilangan bulat positifk, sehingga untuk setiap pasangan titiku dan v diG, terdapat jalan dengan panjang k yang menghubungkan kedua titik tersebut.
Scrambling index merupakan salah satu topik dalam teori graf. Pada tahun 2009, Alkebek dan Kirkland memperkenalkan scrambling index sebagai sebuah
1
2
parameter baru dari sebuah graf primitif. Scrambling index dari graf primitif G (k(G)) adalah bilangan bulat positif terkecil k sehingga untuk setiap pasangan titik u dan v di G, terdapat sebuah titik w sedemikian sehingga ada jalan dari titik u ke titik w dan jalan dari titik v ke titik w dengan panjang k. (Alkebek dan Kirkland 2009a, 2009b).
Lebih lanjut, penelitian kemudian dilanjutkan oleh Chen dan Liu (2010) membahas mengenai scrambling index dari matriks primitif simetris. Sebuah ma-triks persegi non-negatif Adikatakan primitif jika terdapat bilangan bulat positif k sedemikian hingga semua elemen di Ak > 0. Scrambling index dari matriks
primitif A, dinotasikan dengan k(A) bilangan bulat positif terkecil k sehingga untuk tiap dua baris di Ak terdapat sedikitnya satu elemen positif pada posisi
kolom yang sama.
Sumardi et al. (2014) membahas mengenai graf primitif dengan scrambling index 1. Suatu sisi yang menghubungkan suatu titik dengan titik yang sama disebut loop. Sebuah cycle dengan panjang 3 disebut segitiga yang dinotasikan dengan Sn dengan n merupakan jumlah titik pada graf tersebut. Andaikan G
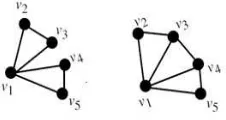
adalah graf primitif dengan n ≥ 3 titik tanpa loop. Scrambling index k(G) = 1 jika dan hanya jika G memenuhi dua kondisi berikut :
1. Tiap titik diG berada di sebuah segitiga
2. Untuk tiap dua titikvidanvjyang berada di segitiga yang berbeda, terdapat
Wvivj dengan panjang 2.
Gambar 1.1 Graf G dengan 5 titik yang mempunyai k(G) = 1
3
Andaikan Sn adalah graf primitif tanpa loop dengan n ≥ 3 titik dengan
k(Sn) = 1. Ukuran terkecil dari Sn adalah (3n−3)/2 jika n ganjil dan ukuran
terkecil dariSn adalah (3n−2)/2 jikan genap.
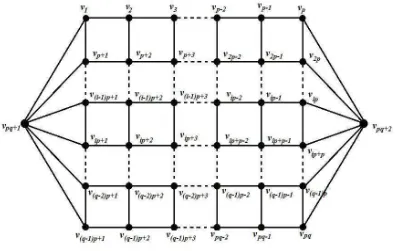
Penelitian ini akan membahas mengenai scrambling index dari suatu Graf Perahu G(p, q) seperti pada Gambar 1.2, yakni sebuah graf yang terdiri atas pq + 2 titik dan terdiri atas lintasan Pi : vpq+1 ↔ v(i−1)p+1 ↔ v(i−1)p+2 ↔ · · · ↔ v(i−1)p+p ↔ vpq+2 untuk i = 1,2, ..., q, dan lintasan Pj : vj ↔ vp+j ↔ v2p+j ↔
· · · ↔v(q−1)p+j untuk j = 1,2, ..., p.
Gambar 1.2 Graf Perahu G(p, q)
1.2 Perumusan Masalah
Penelitian mengenai scrambling index terus berkembang. Namun demikian, scram-bling index dari suatu graf perahu belum dibahas dalam literatur.
Andaikan G(p, q) adalah Graf Perahu dengan panjang p titik dan lebar q titik dengan p≥q, fungsi f(p, q) manakah yang memenuhi k(G(p, q))≤f(p, q)?
4
1.3 Tujuan Penelitian
Tujuan dari penelitian ini adalah menentukan bentuk umum scrambling index dari graf primitif yang berbentuk perahu yang terdiri atas pq + 2 titik dengan panjang p titik dan lebar q dimana p ≥ q titik berdasarkan fungsi f(p, q) yang memenuhi k(G(p, q))≤f(p, q).
1.4 Manfaat Penelitian
Hasil dari penelitian ini diharapkan dapat digunakan sebagai bahan informasi guna menambah wawasan dalam pembahasan yang berhubungan dengan scram-bling index serta dapat dijadikani bahan referensi bagi peneliti lain yang akan membahas tentang scrambling index dari graf primitif lainnya.