Model mangsa pemangsa dengan respon fungsional tak monoton

(1)

ABSTRAK

RIDWAN IDHAM. Model Mangsa Pemangsa dengan Respon Fungsional Tak Monoton. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan ALI KUSNANTO.

Penelitian ini mengkaji dinamika sistem mangsa pemangsa dengan respon fungsional tak monoton. Dalam model ini tingkat interaksi antara mangsadan pemangsa diasumsikan memenuhi fungsi kuadrat yang tidak monoton. Dengan asumsi ini selanjutnya dianalisis perilaku yang terjadi pada sistem dengan melihat pengaruh perubahan parameter model.

(2)

ABSTRACT

RIDWAN IDHAM. Predators Prey Model with Nonmonotonic Functional Response. Supervised by ENDAR HASAFAH NUGRAHANI and ALI KUSNANTO.

This study examines the dynamics of predator prey system with nonmonotonic functional response. In this model the level of interaction between prey and predator is assumed to satisfy a nonmonotonic quadratic function. With this assumption the behavior occurs in the system is analyzed by considering the effects of parameter changes.

(3)

I PENDAHULUAN 1.1 Latar Belakang

Pemodelan matematika memiliki cakupan yang luas, antara lain yaitu pemodelan ekonomi, pemodelan keuangan, dan pemodelan sosial.Dari sisi bentuk variabelnya pemodelan matematika dibagi menjadi pemodelan stokastik yang dimana peubahnya dalam bentuk acak, kemudian pemodelan deterministik yang peubahnya dapat diperkirakan serta pemodelan sistem dinamik. Sistem dinamik adalah suatu metode pemodelan yang diperkenalkan oleh JayForrester pada tahun 1950-an dan dikembangkan di Massa chusetts Institute of Technology Amerika. Sesuai dengan namanya, penggunaan metode ini erat berhubungan dengan pertanyaan-pertanyaan tentang tendensi-tendensi dinamik sistem-sistem yang kompleks, yaitu pola-pola tingkah laku yang dibangkitkan oleh sistem itu dengan bertambahnya waktu. Asumsi utama dalam paradigma dinamik sistem adalah bahwa tendensi-tendensi dinamik yang terjadi terus menerus pada setiap sistem yang kompleks bersumber dari struktur kausal yang membentuk sistem itu. Oleh karena itulah model-model dinamik sistem diklasifikasikan ke dalam model matematik kausal (theory-like).

Banyak kajian model yang dibahas dalam sistem dinamik antara lain model pertumbuhan yang meliputi didalamnya model logistik, model mangsa pemangsa Lotka-Volterra, dan model lainnya.

Pada dasarnya interaksi adalah suatu jenis tindakan atau aksi yang terjadi sewaktu dua atau lebih objek mempengaruhi atau memiliki efek satu sama lain. Ide efek dua arah ini penting dalam konsep interaksi, sebagai lawan dari hubungan satu arah pada sebab akibat. Kombinasi dari interaksi-interaksi sederhana dapat menuntun pada suatu fenomena baru yang mengejutkan. Dalam berbagai bidang ilmu, interaksi memiliki makna yang berbeda, sedangkan interaksi antara mangsa pemangsa adalah gejala alam yang alamiah dimana yang lebih kuat akan memiliki kemampuan bertahan lebih lama dibandingkan yang lemah yang lambat laun akan punah akibat tidak

mampunya bersaing dalam sebuah lingkungan.

Pemodelan mangsa pemangsa ini banyak memiliki manfaat di antaranya untuk melihat stabilitas jumlah populasi mangsa dan pemangsa yang ada dalam sebuah biota atau lingkungan. Model tersebut akan digunakan oleh peneliti untuk mengendalikan populasi mangsa agar tidak terjadi kepunahan.

Dalam tugas akhir ini akan dibahas salah satu model yang ada dalam sistem dinamik yaitu model mangsa pemangsa dengan respon fungsional tak monoton dimana respon fungsional adalah tingkat asupan konsumen sebagai fungsi dari kepadatan makanan yang berkaitan dengan tingkat reproduksi seorang konsumen sebagai fungsi kepadatan makanan.

1.2 Tujuan

a. Menganalisis model mangsa pemangsa dengan respon fungsional tak monoton dengan menentukan titik tetap serta kestabilan masing-masing titik tetap, bidang fase dan bidang solusinya dengan mensubstitusikan parameter-parameter yang telah ditentukan.

(4)

II LANDASAN TEORI

2.1 Sistem Persamaan Diferensial Linear

(SPDL)

Persamaan diferensial linear orde-1 dinyatakan sebagai berikut:

( ) ( )

x&+a t x=g t (2.1)

dengan ( )a t dan ( )g t adalah fungsi dari

waktu t. Bila ( )a t adalah suatu matriks

berukuran n n× dengan koefisien konstan dan ( )g t dinyatakan sebagai vektor konstan

b maka diperoleh bentuk SPDL sebagai berikut:

0

, (0)

dx

Ax b x x

dt = + = . (2.2)

(Farlow, 1990)

2.2 Titik Tetap

Diberikan sistem persamaan differensial sebagai berikut

1 2 ( , ,... )n

f x x x

= &

x _,

1 2

( , ,..., ) n n

x x x ∈ ℜ . (2.3)

Suatu titik x* yang memenuhi *

( ) 0

f x =

disebut titik kesetimbangan atau titik tetap dari sistem.

2.3 Nilai Eigen dan Vektor Eigen Misalkan A adalah matriks n n× , maka suatu vektor taknol x di dalam Rn

disebut vektor eigen dari A jika untuk suatu skalar

λ

berlaku

Ax=

λ

x (2.4)

vektorx disebut vektor eigen yang bersesuaian dengan nilai eigen

λ

.

Untuk mencari nilai eigen dari matriks A yang berukuran n n× maka persamaan (2.4) dapat dituliskan kembali sebagai berikut

(A−λI x) =0 (2.5)

denganI matriks identitas. Persamaan (2.5) mempunyai solusi taknol jika dan hanya jika

det(A−λI)= A−λI =0. (2.6)

Persamaan (2.7) disebut persamaan karakteristik dari matriks A.

[Tu, 1994]

2.4 Analisis Kestabilan Titik Tetap Diberikan sistem persamaan differensial sembarang

( )

x&= f x ,x∈ℜn. (2.7)

Analisis kestabilan titik tetap dilakukan melalui matriks Jacobi, yaitu matriks J.

Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigennya, yaitu λ_i dengan i=1, 2, 3, ...,n yang

diperoleh dari det

(

A−λI

)

=0

Secara umum kestabilan titik tetap mempunyai tiga perilaku sebagai berikut

1. Stabil, jika

a. Setiap nilai eigen real adalah negatif (λ_i <0untuk semua i)

b. Setiap komponen nilai eigen kompleks bagian realnya lebih kecilatau sama dengan nol (

( )

Re λ_i ≤0 untuk semua i).

2. Takstabil, jika

a. Setiap nilai eigen real adalah negatif (λ_i <0untuk semua i). b. Setiap komponen nilai eigen

kompleks bagian realnya lebih kecil atau sama dengan nol (Re

( )

λ_i ≤0

untuk semua i).

(5)

0 i j

λ λ < untuk i dan j sembarang). Titik tetap sadel ini bersifat takstabil.

[Tu, 1994] 2.5 Bidang Fase

Suatu persamaan diferensial ( )

x&= f x tidak semuanya dapat diselesaikan secara kuantitatif. Jika hal ini terjadi maka diperlukan solusi kualitatif. Salah satu solusi kualitatif adalah diagram fase. Diagram fase akan menggambarkan perubahan kecepatan

x&terhadap x

2.6 Bidang Solusi

Bidang solusi merupakan bidang yang menggambarkan solusi persamaan differensial terhadap parameter yang telah ditentukan.

2.7 Model Logistik

Model logistik adalah model yang diperkenalkan oleh Verhulst pada 1838. Model ini dapat dituliskan sebagai berikut :

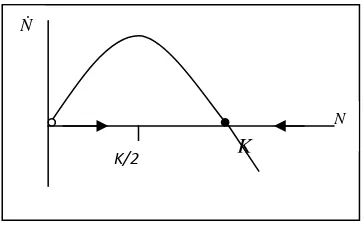
1 N N rN K ⎛ ⎞ = _⎜ − _⎟ ⎝ ⎠ & dimana:

Nadalah populasi pada waktu t Kadalah Konstanta

r_{adalah tingkat pertumbuhan}

Dari persamaan di atas dapat ditentukan titik tetapnya dengan menjadikan N& =0 sehingga diperoleh pada saat N =0atau

N=K, yang dapat dilihat pada gambar berikut.

Dalam gambar juga dapat dilihat aliran bahwa N* =0adalah titik tetap tak stabil dan N*=K adalah titik tetap stabil.

2.8 Model mangsa Pemangsa Lotka-Volterra

Persamaan Lotka-Volterra, juga dikenal sebagai persamaan predator-mangsa, yang merupakan sepasang persamaan diferensial orde pertama dan non-linear. Persamaan diferensial sering digunakan untuk menggambarkan dinamika sistem biologi dimana dua spesies berinteraksi, sebagai contoh predator dan mangsa yang lainnya. Mereka berkembang dalam waktu sesuai dengan sepasang persamaan:

( ) ( ) dx x y dt dy y x dt α β γ δ = − = − − dimana

x : banyaknya mangsa

y : banyaknya pemangsa

dx

dt : menggambarkan pertumbuhan

mangsa pada waktu t

dy

pemangsa pada waktu t t : waktu

α : laju kelahiran mangsa

γ : laju kematian pemangsa

N

N&

[image:5.595.329.511.83.198.2]

K/2 K

(6)

III PEMBAHASAN

3.1 Model Mangsa Pemangsa dengan

Respon Fungsional Tak Monoton

Sistem mangsa pemangsa yang telah dikenal banyak orang dan sering dikembangkan di antaranya sistem mangsa pemangsa Lotka-Volterra.

Dalam karya ilmiah ini akan dibahas model mangsa pemangsa dengan respon fungsional tak monoton yang dipelajari oleh Zhu, Campbell dan Wolkowicz (Xiao dan Zhu, 2006) dimana respon fungsional adalah tingkat asupan konsumen sebagai fungsi dari kepadatan makanan. Dalam penelitian ini digunakan kelas respon fungsional tak monoton.

2 2 1 1 (3.1) 1 x xy x rx

K x bx

x y y d

x bx ⎛ ⎞ = _⎜ − _⎟− + + ⎝ ⎠ ⎛ ⎞ = _⎜− + _⎟ + + ⎝ ⎠ & & di mana

: Banyaknya populasi mangsa pada waktu t

: Banyaknya populasi pemangsa pada waktu t

: Tingkat pertumbuhan maksimum (r > 0)

: Tingkat kematian pemangsa : Konstanta b R

: Carrying Capacity (K > 0)

Berikut ini akan ditentukan titik tetap dari persamaan (3.1) dengan menjadikan:

0 0 x y = = & &

diperoleh empat buah titik tetap berikut (perhitungan secara analitis di Lampiran 1 dan dengan Mathematica 7.0 di Lampiran 2)

2 2 2 2 2 2

3

2 2 2 2 2 2

1 2 2 2 3 2 2 3 4 1

( 1 2 1 2 4 2

(1 (0, 0) ( , 0)

1 2 4 ) (2 1 2 4 ))

1

( 1 2 1 2 1 4 ( 1 )

, 2

1 4 ( 1 ) ,

4 2

2 (

d b d bd d b d d K

d bd d b d K b T

T K

bd d bd

d T

d bd d b d dK r

bd d bd d T d − + − − − − + + + − − + + + − = = ⎛ − + − + − + ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ − + − ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ − + − + − + − = − − + − − − − + +

2 2 2 2 2 2

1 1 2bd 4d b d)K bd(2 1 2bd 4d b d dK r))

⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ + − − + + + − − + −

Sistem persamaan (3.1) mempunyai matriks Jacobi sebagai berikut :

3.2 Analisis Kestabilan Titik Tetap

Akan dilakukan penentuan kestabilan titik tetap pada masing-masing titik.

1. T1=(0, 0)kemudian kita subsititusikan

kedalam matriks Jacobi di atas akan diperoleh matriks Jacobi sebagai

berikut 0 0 r J d ⎡ ⎤ = ⎢ ₋ ⎥

⎣ ⎦ sehingga kita peroleh bahwa nilai λ =₁ r dan

2 d

λ = − sehingga kestabilan titik tetap tersebut adalah sadel.

2. T2 =( , 0)K kemudian kita subsititusikan kedalam matriks Jacobi

di atas akan diperoleh matriks Jacobi

sebagai berikut 2 2 1 0 1 K r bK K J K d bK K ⎡₋ ₋ ⎤ ⎢ ₊ ₊ ⎥ = ⎢ ⎥ ⎢ _{− +} ⎥ ⎢ ₊ ₊ ⎥ ⎣ ⎦ ,

sehingga kita peroleh λ = −1 rdan

2 2 1 K d bK K λ = − +

+ + maka kestabilan

titik tetap tersebut adalah stabil jika

2 2 2 2

( 2 ) 1

(1 ) 1 1

( 2 ) 1

(1 ) 1 1

rx x x b x y y x

r

K K bx x bx x bx x

J

x b x x

y d

bx x bx x bx x

(7)

2 1 K d bK K >

+ + dan sadel jika

2 1 K d bK K > + +

3.3 Simulasi Model pada r • r =1

Selanjutnya akan dilakukan simulasi terhadap model yang telah diberikan dengan cara mensubstitusikan parameter yang telah ditentukan yaitu r=1,

0

b= ,K=1.809, d =0.372

Dengan mensubstitusikan keempat nilai parameter tersebut akan diperoleh 4 buah titik tetap yaitu

1 2 3 4 (0, 0) (1.81, 0) (2.24, 1.44) (0.45, 0.9) T T T T = = = − =

Selanjutnya akan dibentuk matriks Jacobi dari persamaan yang telah disubstitusikan padanya parameter-parameter yang telah ditentukan, maka diperoleh matriks jacobi sebagai berikut :

Kemudian akan dilakukan analisis kestabilan titik tetap pada masing-masing titik sebagai berikut :

1. T1=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = ,

Menurut teori kestabilan titik tetap jika nilai eigen berbeda tanda maka titik tetap tersebut memiliki tipe Saddle Node

2. T2 =(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = ,

titik tetap ini memilik tipe titik tetap Saddle Node, karena nilai eigennya berbeda tanda.

3. T3 =(2.24, 1.44)− ,

λ

1 R ,

λ

2 R

− −

= =

,dan

τ

>0, maka menurut teori

nilai eigen bertanda sama dan tracenya positif, maka titik tetap tersebut memiliki tipe Node Stabil

4. T₄ =(0.45, 0.9), λ₁danλ₂ adalah anggota dari Bilangan Kompleks Konjugat, dan memiliki tanda yang sama maka menurut teori kestabilan titik tetap adalah tipe spiral tak stabil.

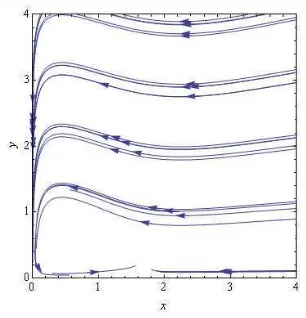
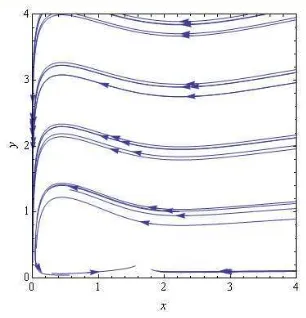
Bidang Fase

Dengan memasukkan parameter di atas kita akan mencari bidang fase dengan menggunakan software Mathematica, maka kita akan memperoleh bidang fase sebagai berikut.

Bidang Solusi

Untuk memperoleh bidang solusi program yang digunakan adalah Maple

2

2 2 2 2

2

2 2 2 2

2

1 1.0511 -

-(1 ) 1 1

2 1

- -0.372

(1 ) 1 1

x y y x

x

x x x

J

x x

y

x x x

[image:7.595.352.505.309.466.2]

⎡ ₋ ₊ + ⎤ ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ =_⎢ _⎥ ⎛ ₊ ⎞ ₊ ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

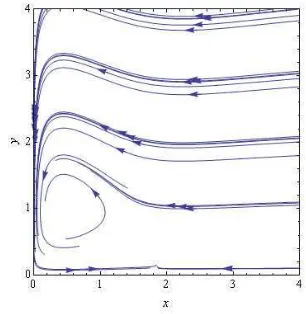
Gambar 2 Bidang Fase r = 1

[image:7.595.343.508.560.727.2]

(8)

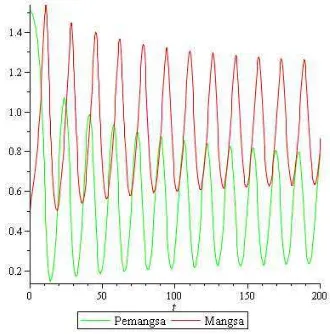
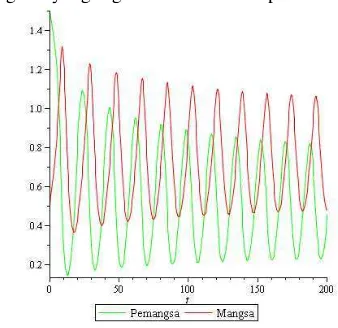
Pada bidang solusi terlihat bahwa mangsa (garis hitam) berosilasi pada titik 0.5 sedangkan pemangsa (garis redup) berosilasi pada titik 1.

• r_=0.8

Selanjutnya akan dilakukan simulasi terhadap model yang telah diberikan dengan cara mensubstitusikan parameter yang telah ditentukan yaitu

0.8

r= , b=0,K=1.809, dan d =0.372 Dengan mensubstitusikan keempat nilai parameter tersebut akan diperoleh 4 buah titik tetap yaitu

1 2 3 4 (0, 0) (1.81, 0) (2.24, 1.15) (0.45, 0.72) T T T T = = = − =

1. T1=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = , Menurut

teori kestabilan titik tetap jika nilai eigen berbeda tanda maka titik tetap tersebut memiliki tipe Saddle Node

2. T₃=(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = , titik

tetap ini memilik tipe titik tetap Saddle Node, karena nilai eigennya berbeda tanda.

3. T2 =(2.24, 1.15)− ,

λ

1 R ,

λ

2 R

− −

= = ,

dan kedua

τ

<0, maka menurut teori kestabilan titik tetap jika kedua nilai eigen dengan tanda sama dan tracenya negatif, maka titik tetap tersebut memiliki tipe Node Stabil.

4. T4 =(0.45, 0.72),λ1danλ2adalah

anggota dari Bilangan Kompleks Konjugat, dan memiliki tanda yang

sama maka menurut teori kestabilan titik tetap adalah tipe spiral tak stabil.

Bidang Fase

Dengan memasukkan parameter diatas kita akan mencari bidang fase dengan menggunakan software Mathematica, maka kita akan memperoleh bidang fase sebagai berikut.

Bidang Solusi

Untuk memperoleh bidang solusi program yang digunakan adalah Maple

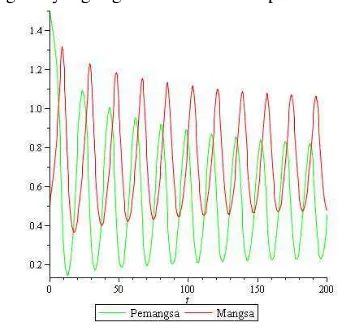
Pada bidang solusi terlihat bahwa mangsa (garis hitam) berosilasi pada titik 0.5 sedangkan pemangsa (garis redup) berosilasi pada titik 0.8.

2

2 2 2 2

2

2 2 2 2

2

0.8(1- 0.553 ) - 0.442 -

-(1 ) 1 1

2 1

- -0.372

(1 ) 1 1

x y y x

x x

x x x

J

x x

y

x x x

[image:8.595.354.502.214.368.2]

⎡ ₊ + ⎤ ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ = ⎢ ⎛ ₊ ⎞ ₊ ⎥ ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

Gambar 4 Bidang Fase r = 0.8

[image:8.595.340.509.460.624.2]

(9)

• r =0.4

0.4

r= , b=0,K=1.809, dan d =0.372

1 2 3 4 (0, 0) (1.81, 0) (2.24, 0.58) (0.45, 0.36) T T T T = = = − =

Selanjutnya akan dibentuk matriks Jacobi dari persamaan yang telah disubstitusikan padanya parameter-parameter yang telah ditentukan, maka diperoleh matriks Jacobi sebagai berikut :

Kemudian akan dilakukan analisis kestabilan titik tetap pada masing-masing titik. Hasil analisis tersebut adalah sebagai

berikut :

1. T₁=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = , Menurut

2. T2 =(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = , titik

3. T3=(2.24, 0.58)− ,

λ

1 R ,

λ

2 R

− −

= =

,dan kedua

τ

<0, maka menurut teori kestabilan titik tetap jika kedua nilai eigen bertanda sama dan tracenya negatif, maka titik tetap tersebut memiliki tipe Node stabil.

4. T4 =(0.45, 0.36),λ1danλ2adalah

sama maka menurut teori kestabilan titik tetap adalah tipe spiral tak stabil

Bidang Fase

Bidang Solusi

Dari simulasi analisis titik tetap di atas, diperoleh sebagai berikut

2

2 2 2 2

2

2 2 2 2

2

0.4(1- 0.553 ) - 0.221 -

-(1 ) 1 1

2 1

- -0.372

(1 ) 1 1

x y y x

x x

x x x

J

x x

y

x x x

[image:9.595.353.506.224.383.2]

⎡ ₊ + ⎤ ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ =_⎢ _⎥ ⎛ ₊ ⎞ ₊ ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

(10)

[image:10.595.122.299.120.235.2]

Tabel 1 Analisis terhadap perubahan r

T1 T2 T3 T4

r=1 Saddle

Node Saddle Node Node Stabil Spiral Tak Stabil

r=0.8 Saddle Node Saddle Node Node Stabil Spiral Tak Stabil

3.4 Simulasi Model pada d • d = 0.5

0

b= ,K=1.809, dan d =0.5

1 2 3 (0, 0) (1.81, 0) (1, 0.89) T T T = = =

Selanjutnya akan dibentuk matriks Jacobi dari persamaan yang telah disubstitusikan padanya parameter-parameter yang telah ditentukan, maka diperoleh matriks jacobi sebagai berikut:

1. T1=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = ,Menurut

2. T2 =(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = , titik

tetap ini memilik tipe titik tetapNode Stabil, karena nilai eigennya berbeda tanda

3. T4 =(1, 0.89),

λ

1 R ,

λ

2 0

−

= = , dan

0

Δ = maka titik tetap ini merupakan titik tetap terisolasi.

Bidang Fase

Bidang Solusi

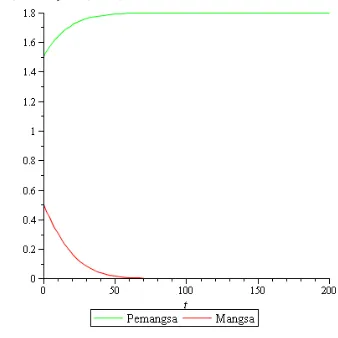
Pada bidang solusi terlihat bahwa mangsa (garis hitam) menuju kestabilan pada titik 1.8 sedangkan pemangsa (garis redup) meuju 0 dan cenderung punah.

Dari analisis kestabilan titik tetap diatas diperoleh tabel sebagai berikut

2

2 2 2 2

2

2 2 2 2

2

1-1.10511 -

-(1 ) 1 1

2 1

- -0.5

(1 ) 1 1

x y y x

x

x x x

J

x x

y

x x x

[image:10.595.343.506.242.412.2]

⎡ ⎤ + ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ = ⎢ _⎛ _⎞ ⎥ + + ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

Gambar 8 Bidang Fase d=0.5

[image:10.595.338.507.466.635.2]

(11)

[image:11.595.122.298.108.183.2]

Tabel 2 Analisis terhadap perubahan d

T1 T2 T3 T4

d=0.372 Saddle

Node

Saddle Node

Node Stabil

Spiral Tak Stabil

d=0.5 Saddle

Node

Node Stabil

Titik Tetap Terisolasi

(12)

IV KESIMPULAN

Dalam karya tulis ini dilakukan analisis

model mangsa pemangsa dengan respon fungsional tak monoton. Respon fungsional adalah tingkat asupan konsumen sebagai fungsi dari kepadatan makanan yang berkaitan dengan tingat reproduksi konsumen sebagai fungsi kepadatan makanan dan analisis ini kelas respon fungsional yang digunakan adalah respon fungsional tak monoton yang kemudian dilakukan substitusi terhadap masing-masing parameter untuk melihat pengaruh parameter tersebut.

Selanjutnya analisis terhadap parameter dikonsentrasikan pada perubahan parameter tingkat kelahiran mangsa dan tingkat

kematian pemangsa dengan mengasumsikan nilai parameter lainnya tetap. Berdasarkan simulasi yang telah dilakukan terhadap perubahan parameter tingkat kelahiran mangsa dapat disimpulkan bahwa semakin tinggi tingkat kelahiran mangsa maka akan terjadi perubahan pusat osilasi pada solusi. Sedangkan pada perubahan parameter tingkat kematian pemangsa dapat disimpulkan bahwa semakin tinggi tingkat kematian pemangsa maka akan merubah banyaknya titik tetap serta merubah kestabilan pada masing-masing titik tetap dan kestabilannya tetap. Apabila tingkat kematian pemangsa mencapai 0.5 menyebabkan pemangsa akan punah.

V DAFTAR PUSTAKA

Farlow SJ. 1994. An Introduction to Differential Equation and Their Applications. Mc Graw-Hill, New York.

Tu PNV. 1994. Dynamical System, An Introduction with Application in Economics and Biology. Springer-Verlag. Heidelberg, Germany

(13)

MODEL MANGSA PEMANGSA DENGAN

RESPON FUNGSIONAL TAK MONOTON

RIDWAN IDHAM

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(14)

MODEL MANGSA PEMANGSA DENGAN

RIDWAN IDHAM

INSTITUT PERTANIAN BOGOR

(15)

ABSTRAK

RIDWAN IDHAM. Model Mangsa Pemangsa dengan Respon Fungsional Tak Monoton. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan ALI KUSNANTO.

Penelitian ini mengkaji dinamika sistem mangsa pemangsa dengan respon fungsional tak monoton. Dalam model ini tingkat interaksi antara mangsadan pemangsa diasumsikan memenuhi fungsi kuadrat yang tidak monoton. Dengan asumsi ini selanjutnya dianalisis perilaku yang terjadi pada sistem dengan melihat pengaruh perubahan parameter model.

(16)

ABSTRACT

RIDWAN IDHAM. Predators Prey Model with Nonmonotonic Functional Response. Supervised by ENDAR HASAFAH NUGRAHANI and ALI KUSNANTO.

This study examines the dynamics of predator prey system with nonmonotonic functional response. In this model the level of interaction between prey and predator is assumed to satisfy a nonmonotonic quadratic function. With this assumption the behavior occurs in the system is analyzed by considering the effects of parameter changes.

(17)

MODEL MANGSA PEMANGSA DENGAN

RIDWAN IDHAM

G54052040

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

INSTITUT PERTANIAN BOGOR

(18)

Judul : Model Mangsa Pemangsa dengan Respon Fungsional Tak Monoton

Nama : Ridwan Idham

NIM : G54052040

Menyetujui

Pembimbing

I

Pembimbing

II

Dr. Ir. Endar Hasafah Nugrahani, MS

Drs. Ali Kusnanto, M.Si

NIP. 19631228 198903 2 001

NIP. 19650820 199003 1 001

Mengetahui

Ketua Departemen Matematika

Dr. Berlian Setiawaty, MS

NIP. 19650505 198903 2 004

(19)

KATA PENGANTAR

Alhamdulillahirobbil’alamin. Penulis mengucapkan syukur kehadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini tidak terlepas dari dukungan dan bantuan dari berbagai pihak. Pada kesempatan ini, penulis juga ingin mengucapkan terimakasih yang sebesar-besarnya kepada:

1. Bapak dan Ibu tersayang, terima kasih atas didikan, kasih sayang, nasehat, semangat, serta do’a yang tiada henti-hentinya. Do’a yang selalu menjadi penerang jalan penulis.

2. Dr. Ir. Endar Hasafah Nugrahani, MS. selaku dosen pembimbing I, Drs. Ali Kusnanto, M.Si. selaku pembimbing II. Terimakasih atas waktu, ilmu yang diberikan dan kesabarannya dalam membimbing penulis. Semua ilmu yang Bu Endar dan Pak Ali berikan sangat bermanfaat bagi penulis. Terima kasih.

3. Dr. Paian Sianturi selaku dosen penguji. Terimakasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis.

4. Adikku Wilda Idham tersayang terimakasih atas do’a, semangat dan dukungannya. 5. Semua dosen Departemen Matematika, terimakasih atas ilmu yang telah diberikan.

6. Pak Yono, Bu Ade, Bu Susi, Mas Bono, Mas Heri, Mas Deni dan seluruh staf pegawai Departemen Matematika, terimakasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di Departemen Matematika.

7. Sahabat – sahabatku seperjuangan : Suwarno, Septian, Carwidah dan teman-teman se-kosan yang telah memberikan dukungan

8. Teman-teman satu bimbingan yang sudah lulus terlebih dahulu terima kasih atas doa, bantuan, dukungan semangat, dan nasehatnya.

9. Kakak kelas angkatan 40 dan 41 yang tidak bisa penulis sebutkan satu per satu.

10. Teman-teman angkatan 42 Terimakasih atas doa, dukungan dan semangatnya, terimakasih atas kebersamaannya selama 3 tahun di Math’42.

11. Adik kelas angkatan 43, 44 dan 45 yang tidak bisa penulis sebutkan satu per satu.

Penulis menyadari tulisan ini masih memiliki kekurangan dan jauh dari kesempurnaan. Oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.

Semoga karya ilmiah ini bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan khususnya

Matematika.

Bogor, Maret 2011

(20)

RIWAYAT HIDUP

Penulis lahir di Jakarta pada tanggal 16 April 1987 sebagai anak pertama dari dua bersaudara, anak dari pasangan H. Salim dan Hj. Nurmaleni. Tahun 1999 penulis lulus dari SDN 01 Pulogadung Jakarta Timur. Tahun 2002 penulis lulus dari SLTPIT RAFAH Bogor. Tahun 2005 penulis lulus dari SMAIT RAFAH Bogor dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Beasiswa Utusan Daerah regional Jawa Barat, Tingkat Persiapan Bersama. Pada tahun 2006, penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

(21)

DAFTAR ISI

Halaman I. PENDAHULUAN

1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

II. LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Linear ... 2

2.2 Titik Tetap ... 2

2.3 Nilai Eigen dan Vektor Eigen ... 2

2.4 Analisis Kestabilan Titik Tetap ... 2

2.5 Bidang Fase ... 3

2.6 Bidang Solusi ... 3

2.7 Model Logistik ... 3

2.8 Model Lotka-Volterra ... 3

III. PEMBAHASAN 3.1 Model Mangsa Pemangsa dengan Respon Fungsional Tak Monoton ... 4

3.2 Analisis Kestabilan Titik Tetap ... 4

3.3 Simulasi Model pada r ... 5

3.4 Simulasi Model pada d ... 8

IV. KESIMPULAN ... 10

DAFTAR PUSTAKA ... 10

(22)

DAFTAR GAMBAR

Halaman 1. Plot antara dan N ... 3 2. Bidang Fase r=1 ... 5 3. Bidang Solusi r=1 ... 5 4. Bidang Fase r=0.8 ... 6 5. Bidang Solusi r=0.8 ... 6 6. Bidang Fase r=0.4 ... 7 7. Bidang Solusi r=0.4 ... 7 8. Bidang Fase d=0.5 ... 8 9. Bidang Solusi d=0.5 ... 8

DAFTAR TABEL

Halaman 1. Analisis terhadap perubahan r... 8 2. Analisis terhadap perubahan d ... 9

DAFTAR LAMPIRAN

(23)

I PENDAHULUAN 1.1 Latar Belakang

Pemodelan matematika memiliki cakupan yang luas, antara lain yaitu pemodelan ekonomi, pemodelan keuangan, dan pemodelan sosial.Dari sisi bentuk variabelnya pemodelan matematika dibagi menjadi pemodelan stokastik yang dimana peubahnya dalam bentuk acak, kemudian pemodelan deterministik yang peubahnya dapat diperkirakan serta pemodelan sistem dinamik. Sistem dinamik adalah suatu metode pemodelan yang diperkenalkan oleh JayForrester pada tahun 1950-an dan dikembangkan di Massa chusetts Institute of Technology Amerika. Sesuai dengan namanya, penggunaan metode ini erat berhubungan dengan pertanyaan-pertanyaan tentang tendensi-tendensi dinamik sistem-sistem yang kompleks, yaitu pola-pola tingkah laku yang dibangkitkan oleh sistem itu dengan bertambahnya waktu. Asumsi utama dalam paradigma dinamik sistem adalah bahwa tendensi-tendensi dinamik yang terjadi terus menerus pada setiap sistem yang kompleks bersumber dari struktur kausal yang membentuk sistem itu. Oleh karena itulah model-model dinamik sistem diklasifikasikan ke dalam model matematik kausal (theory-like).

Banyak kajian model yang dibahas dalam sistem dinamik antara lain model pertumbuhan yang meliputi didalamnya model logistik, model mangsa pemangsa Lotka-Volterra, dan model lainnya.

Pada dasarnya interaksi adalah suatu jenis tindakan atau aksi yang terjadi sewaktu dua atau lebih objek mempengaruhi atau memiliki efek satu sama lain. Ide efek dua arah ini penting dalam konsep interaksi, sebagai lawan dari hubungan satu arah pada sebab akibat. Kombinasi dari interaksi-interaksi sederhana dapat menuntun pada suatu fenomena baru yang mengejutkan. Dalam berbagai bidang ilmu, interaksi memiliki makna yang berbeda, sedangkan interaksi antara mangsa pemangsa adalah gejala alam yang alamiah dimana yang lebih kuat akan memiliki kemampuan bertahan lebih lama dibandingkan yang lemah yang lambat laun akan punah akibat tidak

mampunya bersaing dalam sebuah lingkungan.

Pemodelan mangsa pemangsa ini banyak memiliki manfaat di antaranya untuk melihat stabilitas jumlah populasi mangsa dan pemangsa yang ada dalam sebuah biota atau lingkungan. Model tersebut akan digunakan oleh peneliti untuk mengendalikan populasi mangsa agar tidak terjadi kepunahan.

Dalam tugas akhir ini akan dibahas salah satu model yang ada dalam sistem dinamik yaitu model mangsa pemangsa dengan respon fungsional tak monoton dimana respon fungsional adalah tingkat asupan konsumen sebagai fungsi dari kepadatan makanan yang berkaitan dengan tingkat reproduksi seorang konsumen sebagai fungsi kepadatan makanan.

1.2 Tujuan

a. Menganalisis model mangsa pemangsa dengan respon fungsional tak monoton dengan menentukan titik tetap serta kestabilan masing-masing titik tetap, bidang fase dan bidang solusinya dengan mensubstitusikan parameter-parameter yang telah ditentukan.

(24)

II LANDASAN TEORI

2.1 Sistem Persamaan Diferensial Linear

(SPDL)

Persamaan diferensial linear orde-1 dinyatakan sebagai berikut:

( ) ( )

x&+a t x=g t (2.1)

dengan ( )a t dan ( )g t adalah fungsi dari

waktu t. Bila ( )a t adalah suatu matriks

berukuran n n× dengan koefisien konstan dan ( )g t dinyatakan sebagai vektor konstan

b maka diperoleh bentuk SPDL sebagai berikut:

0

, (0)

dx

Ax b x x

dt = + = . (2.2)

(Farlow, 1990)

2.2 Titik Tetap

Diberikan sistem persamaan differensial sebagai berikut

1 2 ( , ,... )n

f x x x

= &

x _,

1 2

( , ,..., ) n n

x x x ∈ ℜ . (2.3)

Suatu titik x* yang memenuhi *

( ) 0

f x =

disebut titik kesetimbangan atau titik tetap dari sistem.

2.3 Nilai Eigen dan Vektor Eigen Misalkan A adalah matriks n n× , maka suatu vektor taknol x di dalam Rn

disebut vektor eigen dari A jika untuk suatu skalar

λ

berlaku

Ax=

λ

x (2.4)

vektorx disebut vektor eigen yang bersesuaian dengan nilai eigen

λ

.

Untuk mencari nilai eigen dari matriks A yang berukuran n n× maka persamaan (2.4) dapat dituliskan kembali sebagai berikut

(A−λI x) =0 (2.5)

denganI matriks identitas. Persamaan (2.5) mempunyai solusi taknol jika dan hanya jika

det(A−λI)= A−λI =0. (2.6)

Persamaan (2.7) disebut persamaan karakteristik dari matriks A.

[Tu, 1994]

2.4 Analisis Kestabilan Titik Tetap Diberikan sistem persamaan differensial sembarang

( )

x&= f x ,x∈ℜn. (2.7)

Analisis kestabilan titik tetap dilakukan melalui matriks Jacobi, yaitu matriks J.

Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigennya, yaitu λ_i dengan i=1, 2, 3, ...,n yang

diperoleh dari det

(

A−λI

)

=0

Secara umum kestabilan titik tetap mempunyai tiga perilaku sebagai berikut

1. Stabil, jika

a. Setiap nilai eigen real adalah negatif (λ_i <0untuk semua i)

b. Setiap komponen nilai eigen kompleks bagian realnya lebih kecilatau sama dengan nol (

( )

Re λ_i ≤0 untuk semua i).

2. Takstabil, jika

a. Setiap nilai eigen real adalah negatif (λ_i <0untuk semua i). b. Setiap komponen nilai eigen

kompleks bagian realnya lebih kecil atau sama dengan nol (Re

( )

λ_i ≤0

untuk semua i).

(25)

0 i j

λ λ < untuk i dan j sembarang). Titik tetap sadel ini bersifat takstabil.

[Tu, 1994] 2.5 Bidang Fase

Suatu persamaan diferensial ( )

x&= f x tidak semuanya dapat diselesaikan secara kuantitatif. Jika hal ini terjadi maka diperlukan solusi kualitatif. Salah satu solusi kualitatif adalah diagram fase. Diagram fase akan menggambarkan perubahan kecepatan

x&terhadap x

2.6 Bidang Solusi

Bidang solusi merupakan bidang yang menggambarkan solusi persamaan differensial terhadap parameter yang telah ditentukan.

2.7 Model Logistik

Model logistik adalah model yang diperkenalkan oleh Verhulst pada 1838. Model ini dapat dituliskan sebagai berikut :

1 N N rN K ⎛ ⎞ = _⎜ − _⎟ ⎝ ⎠ & dimana:

Nadalah populasi pada waktu t Kadalah Konstanta

r_{adalah tingkat pertumbuhan}

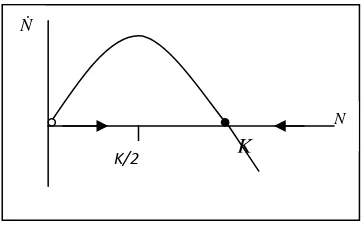
Dari persamaan di atas dapat ditentukan titik tetapnya dengan menjadikan N& =0 sehingga diperoleh pada saat N =0atau

N=K, yang dapat dilihat pada gambar berikut.

Dalam gambar juga dapat dilihat aliran bahwa N* =0adalah titik tetap tak stabil dan N*=K adalah titik tetap stabil.

2.8 Model mangsa Pemangsa Lotka-Volterra

Persamaan Lotka-Volterra, juga dikenal sebagai persamaan predator-mangsa, yang merupakan sepasang persamaan diferensial orde pertama dan non-linear. Persamaan diferensial sering digunakan untuk menggambarkan dinamika sistem biologi dimana dua spesies berinteraksi, sebagai contoh predator dan mangsa yang lainnya. Mereka berkembang dalam waktu sesuai dengan sepasang persamaan:

( ) ( ) dx x y dt dy y x dt α β γ δ = − = − − dimana

x : banyaknya mangsa

y : banyaknya pemangsa

dx

mangsa pada waktu t

dy

pemangsa pada waktu t t : waktu

α : laju kelahiran mangsa

γ : laju kematian pemangsa

N

N&

[image:25.595.329.511.83.198.2]

K/2 K

(26)

III PEMBAHASAN

3.1 Model Mangsa Pemangsa dengan

Respon Fungsional Tak Monoton

Sistem mangsa pemangsa yang telah dikenal banyak orang dan sering dikembangkan di antaranya sistem mangsa pemangsa Lotka-Volterra.

Dalam karya ilmiah ini akan dibahas model mangsa pemangsa dengan respon fungsional tak monoton yang dipelajari oleh Zhu, Campbell dan Wolkowicz (Xiao dan Zhu, 2006) dimana respon fungsional adalah tingkat asupan konsumen sebagai fungsi dari kepadatan makanan. Dalam penelitian ini digunakan kelas respon fungsional tak monoton.

2 2 1 1 (3.1) 1 x xy x rx

K x bx

x y y d

x bx ⎛ ⎞ = _⎜ − _⎟− + + ⎝ ⎠ ⎛ ⎞ = _⎜− + _⎟ + + ⎝ ⎠ & & di mana

: Banyaknya populasi mangsa pada waktu t

: Banyaknya populasi pemangsa pada waktu t

: Tingkat pertumbuhan maksimum (r > 0)

: Tingkat kematian pemangsa : Konstanta b R

: Carrying Capacity (K > 0)

Berikut ini akan ditentukan titik tetap dari persamaan (3.1) dengan menjadikan:

0 0 x y = = & &

diperoleh empat buah titik tetap berikut (perhitungan secara analitis di Lampiran 1 dan dengan Mathematica 7.0 di Lampiran 2)

2 2 2 2 2 2

3

2 2 2 2 2 2

1 2 2 2 3 2 2 3 4 1

( 1 2 1 2 4 2

(1 (0, 0) ( , 0)

1 2 4 ) (2 1 2 4 ))

1

( 1 2 1 2 1 4 ( 1 )

, 2

1 4 ( 1 ) ,

4 2

2 (

d bd d b d K b T

T K

bd d bd

d T

d bd d b d dK r

bd d bd d T d − + − − − − + + + − − + + + − = = ⎛ − + − + − + ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ − + − ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ − + − + − + − = − − + − − − − + +

2 2 2 2 2 2

1 1 2bd 4d b d)K bd(2 1 2bd 4d b d dK r))

⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ + − − + + + − − + −

Sistem persamaan (3.1) mempunyai matriks Jacobi sebagai berikut :

3.2 Analisis Kestabilan Titik Tetap

Akan dilakukan penentuan kestabilan titik tetap pada masing-masing titik.

1. T1=(0, 0)kemudian kita subsititusikan

kedalam matriks Jacobi di atas akan diperoleh matriks Jacobi sebagai

berikut 0 0 r J d ⎡ ⎤ = ⎢ ₋ ⎥

⎣ ⎦ sehingga kita peroleh bahwa nilai λ =₁ r dan

2 d

λ = − sehingga kestabilan titik tetap tersebut adalah sadel.

2. T2 =( , 0)K kemudian kita subsititusikan kedalam matriks Jacobi

di atas akan diperoleh matriks Jacobi

sebagai berikut 2 2 1 0 1 K r bK K J K d bK K ⎡₋ ₋ ⎤ ⎢ ₊ ₊ ⎥ = ⎢ ⎥ ⎢ _{− +} ⎥ ⎢ ₊ ₊ ⎥ ⎣ ⎦ ,

sehingga kita peroleh λ = −1 rdan

2 2 1 K d bK K λ = − +

+ + maka kestabilan

titik tetap tersebut adalah stabil jika

2 2 2 2

( 2 ) 1

(1 ) 1 1

( 2 ) 1

(1 ) 1 1

rx x x b x y y x

r

K K bx x bx x bx x

J

x b x x

y d

bx x bx x bx x

(27)

2 1 K d bK K >

+ + dan sadel jika

2 1 K d bK K > + +

3.3 Simulasi Model pada r • r =1

0

b= ,K=1.809, d =0.372

1 2 3 4 (0, 0) (1.81, 0) (2.24, 1.44) (0.45, 0.9) T T T T = = = − =

1. T1=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = ,

Menurut teori kestabilan titik tetap jika nilai eigen berbeda tanda maka titik tetap tersebut memiliki tipe Saddle Node

2. T2 =(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = ,

titik tetap ini memilik tipe titik tetap Saddle Node, karena nilai eigennya berbeda tanda.

3. T3 =(2.24, 1.44)− ,

λ

1 R ,

λ

2 R

− −

= =

,dan

τ

>0, maka menurut teori

nilai eigen bertanda sama dan tracenya positif, maka titik tetap tersebut memiliki tipe Node Stabil

4. T₄ =(0.45, 0.9), λ₁danλ₂ adalah anggota dari Bilangan Kompleks Konjugat, dan memiliki tanda yang sama maka menurut teori kestabilan titik tetap adalah tipe spiral tak stabil.

Bidang Fase

Dengan memasukkan parameter di atas kita akan mencari bidang fase dengan menggunakan software Mathematica, maka kita akan memperoleh bidang fase sebagai berikut.

Bidang Solusi

Untuk memperoleh bidang solusi program yang digunakan adalah Maple

2

2 2 2 2

2

2 2 2 2

2

1 1.0511 -

-(1 ) 1 1

2 1

- -0.372

(1 ) 1 1

x y y x

x

x x x

J

x x

y

x x x

[image:27.595.352.505.309.466.2]

⎡ ₋ ₊ + ⎤ ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ =_⎢ _⎥ ⎛ ₊ ⎞ ₊ ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

Gambar 2 Bidang Fase r = 1

[image:27.595.343.508.560.727.2]

(28)

Pada bidang solusi terlihat bahwa mangsa (garis hitam) berosilasi pada titik 0.5 sedangkan pemangsa (garis redup) berosilasi pada titik 1.

• r_=0.8

0.8

r= , b=0,K=1.809, dan d =0.372 Dengan mensubstitusikan keempat nilai parameter tersebut akan diperoleh 4 buah titik tetap yaitu

1 2 3 4 (0, 0) (1.81, 0) (2.24, 1.15) (0.45, 0.72) T T T T = = = − =

1. T1=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = , Menurut

2. T₃=(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = , titik

3. T2 =(2.24, 1.15)− ,

λ

1 R ,

λ

2 R

− −

= = ,

dan kedua

τ

<0, maka menurut teori kestabilan titik tetap jika kedua nilai eigen dengan tanda sama dan tracenya negatif, maka titik tetap tersebut memiliki tipe Node Stabil.

4. T4 =(0.45, 0.72),λ1danλ2adalah

sama maka menurut teori kestabilan titik tetap adalah tipe spiral tak stabil.

Bidang Fase

Bidang Solusi

2

2 2 2 2

2

2 2 2 2

2

0.8(1- 0.553 ) - 0.442 -

-(1 ) 1 1

2 1

- -0.372

(1 ) 1 1

x y y x

x x

x x x

J

x x

y

x x x

[image:28.595.354.502.214.368.2]

⎡ ₊ + ⎤ ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ = ⎢ ⎛ ₊ ⎞ ₊ ⎥ ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

[image:28.595.340.509.460.624.2]

(29)

• r =0.4

0.4

r= , b=0,K=1.809, dan d =0.372

1 2 3 4 (0, 0) (1.81, 0) (2.24, 0.58) (0.45, 0.36) T T T T = = = − =

Selanjutnya akan dibentuk matriks Jacobi dari persamaan yang telah disubstitusikan padanya parameter-parameter yang telah ditentukan, maka diperoleh matriks Jacobi sebagai berikut :

Kemudian akan dilakukan analisis kestabilan titik tetap pada masing-masing titik. Hasil analisis tersebut adalah sebagai

berikut :

1. T₁=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = , Menurut

2. T2 =(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = , titik

3. T3=(2.24, 0.58)− ,

λ

1 R ,

λ

2 R

− −

= =

,dan kedua

τ

<0, maka menurut teori kestabilan titik tetap jika kedua nilai eigen bertanda sama dan tracenya negatif, maka titik tetap tersebut memiliki tipe Node stabil.

4. T4 =(0.45, 0.36),λ1danλ2adalah

sama maka menurut teori kestabilan titik tetap adalah tipe spiral tak stabil

Bidang Fase

Bidang Solusi

Dari simulasi analisis titik tetap di atas, diperoleh sebagai berikut

2

2 2 2 2

2

2 2 2 2

2

0.4(1- 0.553 ) - 0.221 -

-(1 ) 1 1

2 1

- -0.372

(1 ) 1 1

x y y x

x x

x x x

J

x x

y

x x x

[image:29.595.353.506.224.383.2]

⎡ ₊ + ⎤ ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ =_⎢ _⎥ ⎛ ₊ ⎞ ₊ ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

(30)

[image:30.595.122.299.120.235.2]

Tabel 1 Analisis terhadap perubahan r

T1 T2 T3 T4

r=1 Saddle

Node Saddle Node Node Stabil Spiral Tak Stabil

3.4 Simulasi Model pada d • d = 0.5

0

b= ,K=1.809, dan d =0.5

1 2 3 (0, 0) (1.81, 0) (1, 0.89) T T T = = =

Selanjutnya akan dibentuk matriks Jacobi dari persamaan yang telah disubstitusikan padanya parameter-parameter yang telah ditentukan, maka diperoleh matriks jacobi sebagai berikut:

1. T1=(0, 0),

λ

1 R ,

λ

2 R

+ −

= = ,Menurut

2. T2 =(1.81, 0),

λ

1 R ,

λ

2 R

+ −

= = , titik

tetap ini memilik tipe titik tetapNode Stabil, karena nilai eigennya berbeda tanda

3. T4 =(1, 0.89),

λ

1 R ,

λ

2 0

−

= = , dan

0

Δ = maka titik tetap ini merupakan titik tetap terisolasi.

Bidang Fase

Bidang Solusi

Pada bidang solusi terlihat bahwa mangsa (garis hitam) menuju kestabilan pada titik 1.8 sedangkan pemangsa (garis redup) meuju 0 dan cenderung punah.

Dari analisis kestabilan titik tetap diatas diperoleh tabel sebagai berikut

2

2 2 2 2

2

2 2 2 2

2

1-1.10511 -

-(1 ) 1 1

2 1

- -0.5

(1 ) 1 1

x y y x

x

x x x

J

x x

y

x x x

[image:30.595.343.506.242.412.2]

⎡ ⎤ + ⎢ ₊ ₊ ₊ ⎥ ⎢ ⎥ = ⎢ _⎛ _⎞ ⎥ + + ⎢ ⎜ ₊ ₊ ⎟ ₊ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦

Gambar 8 Bidang Fase d=0.5

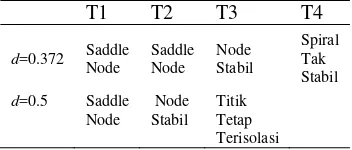
[image:30.595.338.507.466.635.2]

(31)

[image:31.595.122.298.108.183.2]

Tabel 2 Analisis terhadap perubahan d

T1 T2 T3 T4

d=0.372 Saddle

Node

Saddle Node

Node Stabil

Spiral Tak Stabil

d=0.5 Saddle

Node

Node Stabil

Titik Tetap Terisolasi

(32)

IV KESIMPULAN

Dalam karya tulis ini dilakukan analisis

model mangsa pemangsa dengan respon fungsional tak monoton. Respon fungsional adalah tingkat asupan konsumen sebagai fungsi dari kepadatan makanan yang berkaitan dengan tingat reproduksi konsumen sebagai fungsi kepadatan makanan dan analisis ini kelas respon fungsional yang digunakan adalah respon fungsional tak monoton yang kemudian dilakukan substitusi terhadap masing-masing parameter untuk melihat pengaruh parameter tersebut.

Selanjutnya analisis terhadap parameter dikonsentrasikan pada perubahan parameter tingkat kelahiran mangsa dan tingkat

kematian pemangsa dengan mengasumsikan nilai parameter lainnya tetap. Berdasarkan simulasi yang telah dilakukan terhadap perubahan parameter tingkat kelahiran mangsa dapat disimpulkan bahwa semakin tinggi tingkat kelahiran mangsa maka akan terjadi perubahan pusat osilasi pada solusi. Sedangkan pada perubahan parameter tingkat kematian pemangsa dapat disimpulkan bahwa semakin tinggi tingkat kematian pemangsa maka akan merubah banyaknya titik tetap serta merubah kestabilan pada masing-masing titik tetap dan kestabilannya tetap. Apabila tingkat kematian pemangsa mencapai 0.5 menyebabkan pemangsa akan punah.

V DAFTAR PUSTAKA

Farlow SJ. 1994. An Introduction to Differential Equation and Their Applications. Mc Graw-Hill, New York.

Tu PNV. 1994. Dynamical System, An Introduction with Application in Economics and Biology. Springer-Verlag. Heidelberg, Germany

(33)

(34)

LAMPIRAN 1. Penentuan Titik Tetap Persamaan (3.1)

Untuk menentukan titik tetap kita harus menentukan bahwa

(i)

(ii)

Dari (ii)

Diperoleh nilai

(iii) atau (iv)

Kemudian (iii) di substitusikan kedalam persamaan

Artinya

Maka diperoleh

Atau

Sehingga diperoleh titik tetap berikut , dan ,

(35)

Maka menjadi

Dilakukan perkalian silang maka diperoleh

Maka dengan menggunakan rumus abc diperoleh dua titik x yaitu

,

Atau dengan penjabaran diperoleh

Dan

Kemudian dilakukan substitusi ke dalam persamaan

Maka diperoleh dua pasang titik tetap yaitu

2 2 2 2 2 2 2 2 2 2 2 2

3 1

1

( 1 2 1 2 4 (1 1 2 4 ) (2 1 2 4 ))

2 d b d bd d b d d bd d b d K bd

y bd d b d dK r

d K − + − − − − + + + − − + + + − − + −

=

dan

2 2 2 2 2 2 2 2

3 2

2 2 2 2

1

( 1 2 1 2 4 (1 1 2 4 ) (2 1 2 4 ))

2d K d b d bd d b d d bd d b d K bd bd d b d d

(36)

Lampiran 2. Program Penentuan Titik Tetap dengan menggunakan Mathematica 7.0 1. Model Mangsa Pemangsa dengan Respon Fungsional

(37)

(38)

Lampiran 4. Simulasi Model pada r

1. Simulasi ketika , , . , .

1.1 Penentuan Titik Tetap

1.2 Konstruski Matriks Jacobi

1.3 Bidang Fase

1.4 Bidang Solusi

2. Simulasi ketika . , , . , .

(39)

2.3 Bidang Fase

2.4 Bidang Solusi

(40)

3.3 Bidang Fase

(41)

Lampiran 5. Simulasi Model pada d

1.3 Bidang Fase

(42)

(43)

LAMPIRAN 1. Penentuan Titik Tetap Persamaan (3.1)

Untuk menentukan titik tetap kita harus menentukan bahwa

(i)

(ii)

Dari (ii)

Diperoleh nilai

(iii) atau (iv)

Kemudian (iii) di substitusikan kedalam persamaan

Artinya

Maka diperoleh

Atau

Sehingga diperoleh titik tetap berikut , dan ,

(44)

Maka menjadi

Dilakukan perkalian silang maka diperoleh

Maka dengan menggunakan rumus abc diperoleh dua titik x yaitu

,

Atau dengan penjabaran diperoleh

Dan

Kemudian dilakukan substitusi ke dalam persamaan

Maka diperoleh dua pasang titik tetap yaitu

2 2 2 2 2 2 2 2 2 2 2 2

3 1

1

( 1 2 1 2 4 (1 1 2 4 ) (2 1 2 4 ))

2 d b d bd d b d d bd d b d K bd

y bd d b d dK r

d K − + − − − − + + + − − + + + − − + −

=

dan

2 2 2 2 2 2 2 2

3 2

2 2 2 2

1

( 1 2 1 2 4 (1 1 2 4 ) (2 1 2 4 ))

2d K d b d bd d b d d bd d b d K bd bd d b d d

(45)

Lampiran 2. Program Penentuan Titik Tetap dengan menggunakan Mathematica 7.0 1. Model Mangsa Pemangsa dengan Respon Fungsional

(46)

(47)

Lampiran 4. Simulasi Model pada r

1.3 Bidang Fase

1.4 Bidang Solusi

(48)

2.3 Bidang Fase

2.4 Bidang Solusi

(49)

3.3 Bidang Fase

(50)

Lampiran 5. Simulasi Model pada d

1.3 Bidang Fase