NELI YUSRI MARDIANA
G54102018
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
NELI YUSRI MARDIANA. Analysis of the Happiness Dynamical Models. Supervised by ANNIS DINIATI RAKSANAGARA and ALI KUSNANTO.
Happiness is a dynamical process, so it can be modeled as differential equation models. It was written by [Sprott, 2005] which explains the rate of change of happiness response as the rate of happiness.
Dynamical models are influenced by parameter, that reflect the internal influences. When the internal influences are small with positive values, the change of happiness and it’s response will be large, but this happiness will be lost quicker (will quicker reach the stability point). While when the internal influences are large with positive values, the change of happiness and it’s response will be small, but this happiness will be lost slower (will slower reach the stability point) or in other words, someone can maintains their happiness longer if the internal influences are large. When the internal influences are getting larger with negative values, the change of happiness and it’s response will quicker getting large.
NELI YUSRI MARDIANA. Analisis Dinamika Model Kebahagiaan. Dibimbing oleh ANNIS DINIATI RAKSANAGARA dan ALI KUSNANTO.
Kebahagiaan merupakan proses yang dinamis, sehingga dapat dimodelkan dalam model persamaan diferensial. Model yang digunakan adalah model yang ditulis oleh [Sprott, 2005] dengan menyatakan laju perubahan respon kebahagiaan sebagai tingkat kebahagiaan.
Dinamika model tersebut dipengaruhi oleh suatu parameter yang mencerminkan pengaruh internal. Ketika pengaruh internal ini kecil dengan nilai positif maka perubahan kebahagiaan dan responnya akan besar, namun kebahagiaan ini akan cepat hilang (cepat menuju keseimbangan). Sedangkan ketika pengaruh internal ini besar dengan nilai positif maka perubahan kebahagiaan dan responnya akan kecil, namun kebahagiaan ini akan lama hilang (lama menuju keseimbangan) atau dengan kata lain, seseorang dapat mempertahankan kebahagiaannya lebih lama jika pengaruh internal ini besar. Ketika pengaruh internal ini membesar dengan nilai negatif maka perubahan kebahagiaan dan responnya akan semakin cepat membesar.
Skripsi
Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
NELI YUSRI MARDIANA
G54102018
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Menyetujui :
Pembimbing I, Pembimbing II,
Dra. Annis Diniati Raksanagara, M.Si.
Drs. Ali Kusnanto, M.Si.
NIP 132133396 NIP 131913135
Mengetahui:
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Prof. Dr. Ir. Yonny Koesmaryono, MS.
NIP 131473999
Penulis dilahirkan di Payakumbuh pada tanggal 12 Maret 1984 sebagai anak pertama dari dua bersaudara dari pasangan Jhoneldi dan Yuniar.
Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1996 di SD Negeri 14 Guguk, melanjutkan ke SLTP Negeri 3 Guguk (lulus tahun 1999), kemudian melanjutkan ke SMU Negeri I Guguk (lulus tahun 2002) dan diterima sebagai mahasiswa di Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor melalui jalur USMI pada tahun yang sama.
P
uji syukur penulis panjatkan kepada Allah SWT yang selalu memberikan rahmat dan karunia-NYA sehingga penulis dapat menyelesaikan karya ilmiah yang berjudul ”Analisis Dinamika Model Kebahagiaan”. Shalawat serta salam semoga tercurah kepada Nabi Muhammad SAW, keluarga, para sahabat dan umatnya sampai akhir zaman.Keterbatasan dan ketidaksempurnaan membuat penulis membutuhkan bantuan, dukungan dan semangat dari semua pihak baik secara langsung maupun tidak langsung. Oleh karena itu penulis ingin mengucapkan teima kasih yang sebesar-besarnya kepada:
1. Dra. Annis DR, M.Si. selaku pembimbing pertama, Drs. Ali Kusnanto, M.Si. selaku pembimbing kedua, terima kasih atas kesabaran dan bimbingannya selama ini.
2. Ir. N. K. Kutha Ardhana, M.Sc. selaku penguji dan moderator seminar.
3.Bapak dan Ibuk yang selalu memberikan nasehat, bimbingan, bantuan, dukungan dan doa restunya dari penulis lahir dan selama menempuh pendidikan selama ini. Mama yang telah mengorbankan tenaga, waktu dan pikirannya serta Papa yang selalu mendoakan, adikku tercinta Ebi yang selalu memberikan semangat dan nasehat serta seluruh keluarga besar Caniago yang ada di Padang maupun di Jakarta yang selalu mendoakan dan memberikan dukungan selama ini. Keluarga PakOdang Al yang telah memberikan dukungan dan bantuannya.
4.Sahabat-sahabat yang selalu memberikan semangat, dukungan dan nasehat yang berharga bagi penulis. Azhari, Erra, Chicha yang selalu setia mendengar keluh kesah penulis selama ini. 5.Teman-teman kost-an Bagunde 34, Encah, Iffa, Yayu, Ririn, Pretty, Dini, Dina, Ita, Nuril, Tyas,
Acid dan Pipit yang selalu meminjamkan komputernya, terima kasih atas kebersamaannya. 6.Vina, Nci dan Ulfa yang telah bersedia menjadi pembahas.
7.Teman-teman angkatan 39, 40, 41 dan semua kakak kelas, terima kasih atas kebersamaannya selama penulis menempuh pendidikan di IPB selama ini. Arie, Desi, Ike yang selalu memberikan bantuan dan dukungannya.
8.Seluruh Dosen Departemen Matematika IPB yang telah memberikan ilmunya selama ini. Staf Departemen Matematika IPB (Bu Susi, Bu Ade, Mas Deny, Mas Bono, Mas Yono, dll), terima kasih atas nasehat dan bantuannya.
Dan semua pihak yang tidak bisa disebutkan satu per satu. Semoga karya ilmiah ini dapat bermanfaat bagi semua pihak.
Bogor, Juli 2007
Halaman
DAFTAR GAMBAR ... ix
DAFTAR LAMPIRAN ... x
I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan Penulisan ... 1
1.3 Sistematika Penulisan ... 1
II LANDASAN TEORI Sistem Persamaan Diferensial Linear ... 1
Sistem Persamaan Diferensial Mandiri ... 1
Nilai Eigen dan Vektor Eigen ... 2
Titik Tetap ... 2
Titik Tetap Stabil ... 2
Matrik Jacobi ... 2
Kestabilan Titik Tetap ... 3
Limit cycle ... 4
III PEMBAHASAN 3.1 Pengaruh Luar Diabaikan ... 5
3.1.1 Analisis Model I ... 5
Konstruksi Matriks Jacobi ... 5
Analisis Kestabilan ... 5
Contoh Kasus ... 6
Analisis ... 6
3.1.2 Analisis Model II ... 7
Konstruksi Matriks Jacobi ... 7
Analisis Kestabilan ... 7
Contoh Kasus ... 7
Analisis ... 8
3.2 Pengaruh Luar Dipertimbangkan ... 8
3.2.1 Analisis Model I ... 8
Konstruksi Matriks Jacobi ... 9
Analisis Kestabilan ... 9
Contoh Kasus ... 9
Analisis ... 10
3.2.2 Analisis Model II ... 11
Konstruksi Matriks Jacobi ... 11
Analisis Kestabilan ... 11
Contoh Kasus ... 12
IV SIMPULAN ... 14
DAFTAR PUSTAKA ... 14
Halaman
1. Titik Sadel (saddle point) ... 3
2. Simpul taksejati stabil ... 3
3. Simpul taksejati tak stabil ... 3
4. Spiral stabil ... 3
5. Spiral takstabil ... 3
6. Simpul sejati (star node) stabil ... 3
7. Simpul sejati (star node) takstabil ... 4
8. Degenerate node ... 4
9. Center ... 4
10. Titik Tetap tak terisolasi ... 4
11. Limit cycle stabil ... 4
12. Limit cycle takstabil ... 4
13. Limit cycle metastabil ... 4
14. Dinamika Kebahagiaan Model I Kasus I dengan
β
>
0
... 615. Respon Kebahagiaan Model I Kasus I dengan
β
>
0
... 616. Dinamika Kebahagiaan Model I Kasus I dengan
β
<
0
... 617. Respon Kebahagiaan Model I Kasus I dengan
β
<
0
... 618. Dinamika Kebahagiaan Model II Kasus I dengan
β
>
0
... 719. Respon Kebahagiaan Model II Kasus I dengan
β
>
0
... 820. Dinamika Kebahagiaan Model II Kasus I dengan
β
<
0
... 821. Respon Kebahagiaan Model II Kasus I dengan
β
<
0
... 822. Dinamika Kebahagiaan Model I Kasus II dengan
a
=
1
danβ
>
0
... 923. Respon Kebahagiaan Model I Kasus II dengan
a
=
1
danβ
>
0
... 924. Dinamika Kebahagiaan Model I Kasus II dengan
a
=
1
danβ
<
0
... 925. Respon Kebahagiaan Model I Kasus II dengan
a
=
1
danβ
<
0
... 926. Dinamika Kebahagiaan Model I Kasus II dengan
a
=
−
1
danβ
>
0
... 1027. Respon Kebahagiaan Model I Kasus II dengan
a
=
−
1
danβ
>
0
... 1028. Dinamika Kebahagiaan Model I Kasus II dengan
a
=
−
1
danβ
<
0
... 1029. Respon Kebahagiaan Model I Kasus II dengan
a
=
−
1
danβ
<
0
... 1030. Perubahan Kestabilan Sistem dalam sumbu a dan
β
... 1134. Respon Kebahagiaan Model II Kasus II dengan
−
2
<
β
<
0
... 1235. Dinamika Kebahagiaan Model II Kasus II dengan
0
<
β
<
2
... 1336. Respon Kebahagiaan Model II Kasus II dengan
0
<
β
<
2
... 1337. Dinamika Kebahagiaan Model II Kasus II dengan
β
>
2
... 1338. Respon Kebahagiaan Model II Kasus II dengan
β
>
2
... 13DAFTAR LAMPIRAN
Halaman 1. Penentuan Titik Tetap Kasus I untuk sistem persamaan (11) ... 162. Program untuk memperoleh grafik dinamika dan respon kebahagiaan pada kasus I untuk sistem persamaan (11) dengan menggunakan bantuan software Mathematica 5.2 ... 16
3. Penentuan Titik Tetap Kasus I untuk sistem persamaan (12) ... 17
4. Program untuk memperoleh grafik dinamika dan respon kebahagiaan pada kasus I untuk sistem persamaan (12) dengan menggunakan bantuan software Mathematica 5.2 ... 18
5. Penentuan Titik Tetap Kasus II untuk sistem persamaan (19) ... 19
6. Program untuk memperoleh grafik dinamika dan respon kebahagiaan pada kasus II untuk sistem persamaan (19) dengan menggunakan bantuan software Mathematica 5.2 ... 20
I PENDAHULUAN
1.1 Latar Belakang
Menurut sebagian orang, pencarian kebahagiaan merupakan tujuan utama dalam hidup dan banyak buku yang telah ditulis untuk masalah tersebut. Kebahagiaan merupakan perwujudan emosi diantaranya kegembiraan, kesenangan, keriangan, kesukaan, ketenangan, pemenuhan kebutuhan dan kepuasan hati (Orsucci, 2001) sehingga kebahagiaan merupakan proses yang dinamis. Kebahagiaan dibedakan berdasarkan suasana hati yang dapat dipengaruhi oleh pengaruh luar (lingkungan sekitar) (Goleman, 2003).
Penggunaan model matematika jarang diaplikasikan pada dinamika model kebahagiaan, namun beberapa model dinamika cinta telah dibuat, terilhami oleh model Strogatz (1994). Strogatz menyusun model dinamika cinta dalam bentuk sistem persamaan diferensial orde satu. Dengan ide yang hampir sama model kebahagiaan ini akan disusun dalam bentuk sistem persamaan diferensial orde satu juga.
Tugas akhir ini membahas perilaku dinamis model kebahagiaan dan respon kebahagiaan seseorang yang dimodelkan dalam bentuk sistem persamaan diferensial orde satu.
1.2 Tujuan Penulisan
Tujuan penulisan tugas akhir ini adalah menganalisis perilaku dinamis model kebahagiaan dan respon kebahagiaan seseorang.
1.3 Sistematika Penulisan
Bab I menjelaskan tentang pendahuluan yang berisikan latar belakang dan tujuan penulisan tugas akhir. Bab II mengenai landasan teori berisikan definisi-definisi yang menjadi dasar untuk membahas dan menganalisis model dinamika kebahagiaan. Sedangkan bab III menjelaskan tentang pemodelan yang telah dimodifikasi beserta pembahasannya yang dilengkapi oleh gambar-gambar dan akhirnya bab IV berisikan simpulan dari permasalahan.
II LANDASAN TEORI
Definisi (Sistem Persamaan Diferensial Linear) :
Jika suatu sistem persamaan diferensial (SPD) dinyatakan sebagai :
x
=
A
x b x
+
, (0)
=
x x
0,
∈ℜ
n (1) dengan A adalah matriks koefisiennxn
dan vektor konstanb
∈
ℜ
n, maka sistem tersebut dinamakan SPD linear orde satu dengan kondisi awalx
(
0
)
=
x
0. Sistem (1) disebut homogen jikab
=
0
dan nonhomogen jikab
≠
0
.[ Tu, 1994 ]
Definisi (Sistem Persamaan Diferensial Mandiri) :
SPD :
n
j
x
f
x
dt
dx
j j
j
,...,
2
,
1
),
(
=
=
=
(2)dengan
f
fungsi kontinu bernilai real darix
dan mempunyai turunan parsial kontinu disebut SPD mandiri (autonomous) jika tidak memuat waktu(
t
)
secara eksplisit di dalamnya.Definisi (Nilai Eigen dan Vektor Eigen) : Diberikan matriks koefisien konstan A berukuran
nxn
, dan SPD homogen berikut :x
=
A
x x
, (0)
=
x
0 (3) Suatu vektor tak nolx
dalam ruangℜ
n disebut vektor eigen dari A jika untuk suatu skalarλ
berlaku :
A
x
=
λ
x
. (4) Nilai skalarλ
dinamakan nilai eigen dari A. Untuk mencari nilaiλ
dari matriks A, maka persamaan (4) dapat ditulis kembali sebagai :
(
A
−
λ
I
)
x
=
0
(5) dengan I matriks diagonal satuan. Persamaan (5) mempunyai solusi tak nol jika dan hanya jika( )
det(
) |
| 0
p
λ
=
A
−
λ
I
= −
I
λ
I
=
. (6) Persamaan (6) disebut persamaan karakteristik dari matriks A.[ Kreyszig, 1998]
Definisi (Titik Tetap) : Diberikan SPD
x
f
(
x
)
dt
dx
=
=
nx
∈
ℜ
. (7) Titikx
* disebut titik tetap, jika0
)
(
x
*=
f
. Titik tetap disebut juga titik kritis atau titik kesetimbangan.[ Kreyszig, 1993]
Definisi (Titik Tetap Stabil) :
Misalkan
x
* adalah titik tetap sebuah SPD mandiri danx
(
t
)
adalah solusi SPD mandiri dengan nilai awaldengan
x
0≠
x
*. Titikx
* dikatakan titik tetap stabil jika untuk sembarang radius, terdapat sehingga jika posisi awal
x
0 memenuhi|
x
0−
x
*|
<
r
, maka solusix
(
t
)
memenuhiε
<
−
|
)
(
|
x
t
x
* untuk∀
t
>
0
. Selain kondisi ini, disebut titik tetap tak stabil.[ Verhulst, 1990 ]
Definisi (Matriks Jacobi) : Misalkan
)
,
(
)
,
(
y
x
g
y
y
x
f
x
=
=
andaikan
(
x
*,
y
*)
adalah titik tetap dari persamaan diatas, maka0
)
,
(
x
*y
*=
f
dang
(
x
*,
y
*)
=
0
. Misalkan,u
=
x
−
x
* danv
=
y
−
y
*, maka didapatkanx
u
=
=
f
(
x
*+
u
,
y
*+
v
)
)
,
,
(
)
,
(
* * 2 2uv
v
u
y
f
v
x
f
u
y
x
f
+
Ο
∂
∂
+
∂
∂
+
=
)
,
,
(
u
2v
2uv
y
f
v
x
f
u
+
Ο
∂
∂
+
∂
∂
=
y
v
=
)
,
(
x
*u
y
*v
g
+
+
=
* * 2 2
( , ) g g ( , , )
g x y u v u v uv
x y ∂ ∂ = + + + Ο ∂ ∂
)
,
,
(
u
2v
2uv
y
g
v
x
g
u
+
Ο
∂
∂
+
∂
∂
=
.Dalam bentuk matriks
⎜
⎜
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
x
g
x
f
v
u
(
u
2,
v
2,
uv
)
v
u
y
g
y
f
Ο
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎠
⎞
∂
∂
∂
∂
.Matriks * *
( , )
f f
x y
A x y
g g x y ∂ ∂ ⎡ ⎤ ⎢∂ ∂ ⎥ ⎢ ⎥ = ∂ ∂ ⎢ ⎥ ⎢∂ ∂ ⎥ ⎣ ⎦
disebut matriks Jacobi pada titik tetap
)
,
(
x
*y
*. Karena
Ο
(
u
2,
v
2,
uv
)
→
0
maka dapat diabaikan, sehingga didapatkan persamaan linear :
f f
u x y u
v g g v
x y ∂ ∂ ⎡ ⎤ ⎢∂ ∂ ⎥ ⎛ ⎞ ⎢ ⎥⎛ ⎞ = ⎜ ⎟ ⎢∂ ∂ ⎥⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎢∂ ∂ ⎥ ⎣ ⎦
. (8)
[ Strogatz, 1994 ]
0
)
0
(
x
x
=
0
>
Definisi (Kestabilan Titik Tetap) : Misalkan diberikan matriks A berukuran 2x2 sebagai berikut :
A
⎢
⎣
⎡
=
c
a
⎥
⎦
⎤
d
b
dengan persamaan karakteristik
det(
A
−
λ
I
)
=
0
, I adalah matriks identitas danλ
adalah nilai eigen, maka persamaan karakteristiknya menjadi :⎢
⎣
⎡ −
c
a
λ
det
⎥
=
0
⎦
⎤
−
λ
d
b
, sedemikian sehingga diperoleh persamaan
dengan dan
Dengan demikian diperoleh nilai eigen dari
A adalah
.
2
4
2 2
, 1
∆
−
±
=
τ
τ
λ
2 1,2
4
2
τ
τ
λ
=
±
− ∆
Berdasarkan nilai eigen yang diperoleh dari matriks A akan diperlihatkan kasus sebagai berikut:
1. Jika
∆
<
0
, nilai eigen mempunyai akar real yang berbeda tanda, maka titik tetap bersifat titik sadel (saddle point) dan tidak stabil. (lihat gambar 1).2. Jika
∆
>
0
dan memenuhi kondisi0
4
2−
∆
>
τ
, berarti nilai eigen mempunyai akar real dengan tanda yang sama.i. Jika
τ
>
0
maka titik tetap merupakan simpul taksejati (node) takstabil.ii. Jika
τ
<
0
maka titik tetap tersebut adalah simpul taksejati stabil. (lihat gambar 2 dan gambar 3).3. Jika
∆
>
0
, dan memenuhi kondisi0
4
2−
∆
<
τ
, berarti nilai eigennya merupakan complex conjugat (nilai eigennya berbentuka
+
bi
dana
−
bi
).
i. Jika
τ
>
0
maka titik tetapnya merupakan spiral takstabil. ii. Jikaτ
<
0
maka titik tetapnya merupakan spiral stabil . (lihat gambar 4 dan gambar 5).4. Jika
τ
2−
4
∆
=
0
,
τ
>
0
, dan ada 2 vektor eigen bebas linear, maka titik tetap bersifat simpul sejati (star node) takstabil. Jika
τ
<
0
maka titik tetap tersebut adalah simpul sejati stabil. (lihat gambar 6 dan gambar 7).
0
2−τλ
+
∆
=
λ
( )
trace
a
d
τ
=
A
= +
det( )
ad
bc
5. Jika
τ
2−
4
∆
=
0
,
τ
>
0
, dan ada 1 vektor eigen bebas linear, maka titik tetap tersebut degenerate node takstabil. Jika0
<
τ
maka titik tetap bersifat degenerate node stabil. (lihat gambar 8).6. Jika
τ
=
0
, nilai eigen merupakan imajiner murni, maka titik tetap bersifat center yang selalu stabil. (lihat gambar 9).7. Jika
∆
=
0
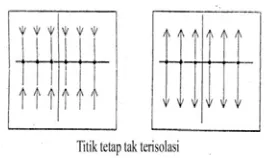
setidaknya ada satu nilai eigen yang sama dengan nol. Maka titik tetap merupakan titik tak terisolasi. Ada satu garis dimana semua titik pada garis tersebut adalah titik tetap seperti pada gambar 10.Gambar 10. Titik tetap tak terisolasi [ Strogatz, 1994 ]
Definisi (Limit cycle) :
Limit cycle adalah orbit tertutup yang terisolasi. Terisolasi artinya bahwa orbit di sekelilingnya tidak tertutup. Orbit tersebut menuju atau menjauhi limit cycle. Berdasarkan arah orbit di sekelilingnya, limit cycle tersebut terbagi menjadi 3, yaitu: 1. Limit cycle stabil
Gambar 11 Limit cycle stabil 2. Limit cycle takstabil
Gambar 12 Limit cycle takstabil 3. Limit cycle metastabil
III PEMBAHASAN
Dinamika model kebahagiaan yang digunakan adalah model yang ditulis oleh [Sprott, 2005]. Dengan mengasumsikan laju perubahan respon kebahagiaan yang menyatakan tingkat kebahagiaan dan laju perubahan kebahagiaan berbanding terbalik dengan parameter, maka model ini dapat dituliskan sebagai berikut :
)
(
t
F
R
H
dt
dH
H
dt
dR
+
−
−
=
=
β
(9) (Model I) dan)
(
)
1
(
R
2H
R
F
t
dt
dH
H
dt
dR
+
−
−
−
=
=
β
(10) (Model II) dengandR
dt
: Laju perubahan respon kebahagiaan yang menyatakan tingkat kebahagiaan pada waktut
.dt
dH
: Laju perubahan kebahagiaan pada waktu
t
.)
(
t
R
: Tingkat respon kebahagiaan pada waktu t.)
(
t
F
: Forcing function; sesuatu yang terjadi pada seseorang (pengaruh luar) pada waktut
.β
: Parameter yang berpengaruhterhadap kebahagiaan.
Dalam tulisan ini akan ditinjau dinamika kedua model terhadap perubahan perilaku parameter.
3.1.Pengaruh Luar Diabaikan
Dalam hal ini diasumsikan
F
(
t
)
=
0
. JikaF
(
t
)
=
0
disubstitusikan ke dalam persamaan (9)-(10) diperoleh:R
H
dt
dH
H
dt
dR
−
−
=
=
β
(11) danR
H
R
dt
dH
H
dt
dR
−
−
−
=
=
)
1
(
2β
. (12)
3.1.1 Analisis Model I
Titik tetap sistem persamaan (11) diperoleh dengan menentukan
=
0
dt
dR
dan0
=
dt
dH
, sehingga diperoleh satu titik tetap yaitu
T
1=
(
0
,
0
)
. [Lihat Lampiran 1].Konstruksi Matriks Jacobi
Dengan melakukan pelinearan pada sistem persamaan di atas, diperoleh matriks Jacobi :
. (13)
Analisis Kestabilan
Jika
T
1=
(
0
,
0
)
disubstitusikan pada matriks Jacobi (13), diperoleh :
⎥
⎦
⎤
⎢
⎣
⎡
−
=
β
1
1
0
1J
.Untuk memperoleh nilai eigen maka
0
)
det(
J
1−
λ
I
=
, yaitu :1
)
(
)
det(
J
1−
λ
I
=
λ
12−
−
β
λ
1+
(14) atau dapat dituliskan kembali.
0
1 1 1 21
−
τ
λ
+
∆
=
λ
(15) Dari persamaan (15) terlihat bahwatrace
J
1=
τ
1=
−
β
det
J
1=
∆
1=
1
dan diperoleh 2 1,2
4
2
2
β
β
λ
= − ±
−
. Berdasarkan teori kestabilan, jikaa.
β
>
2
, maka titik tetapT
1 merupakan simpul taksejati stabil.b.
β
<
−
2
, maka titik tetapT
1merupakan simpul taksejati takstabil.
0 1
1
-J
β
⎡
⎤
c.
0
<
β
<
2
, maka titik tetap1
T
merupakan spiral stabil. d.−
2
<
β
<
0
, maka titik tetap1
T
merupakan spiral takstabil. e.β
=
2
, maka titik tetapT
1merupakan simpul sejati stabil. f.
β
=
−
2
dan ada 2 vektor eigenbebas linear, maka titik tetap
T
1merupakan simpul sejati takstabil.
Dengan menggunakan bantuan software Mathematica 5.2 dan nilai awal (0.1, 0.1) diperoleh gambar dinamika dan respon kebahagiaan. [Lihat Lampiran 2].
Contoh Kasus
β
>
0
Gambar 14 Dinamika Kebahagiaan Model I Kasus I
Gambar 15 Respon Kebahagiaan Model I Kasus I
β
=
2
.
5
β
=
3
β
=
4
β
=
5
β
=
6
β
<
0
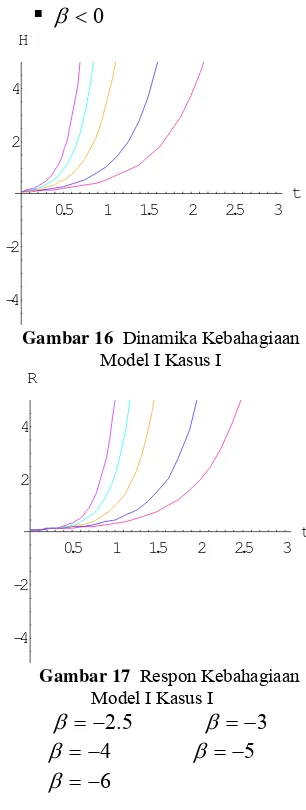
Gambar 16 Dinamika Kebahagiaan Model I Kasus I
Gambar 17 Respon Kebahagiaan Model I Kasus I
β
=
−
2
.
5
β
=
−
3
β
=
−
4
β
=
−
5
β
=
−
6
Analisis
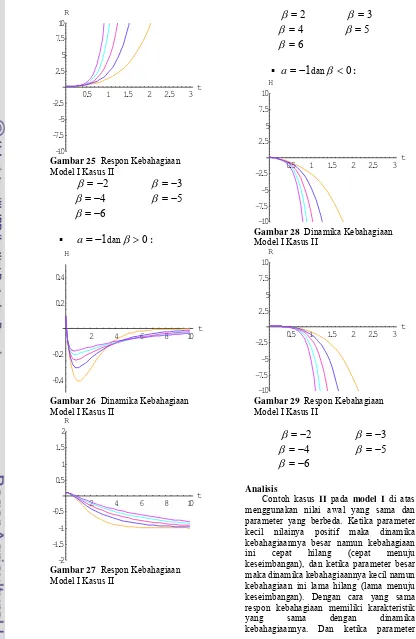
Contoh kasus I pada model I di atas menggunakan nilai awal yang sama dan parameter yang berbeda. Ketika parameter kecil nilainya positif maka dinamika kebahagiaannya besar namun kebahagiaan ini cepat hilang (cepat menuju keseimbangan), dan ketika parameter besar maka dinamika kebahagiaannya kecil namun kebahagiaan ini lama hilang (lama menuju keseimbangan). Dengan cara yang sama respon kebahagiaan memiliki karakteristik yang sama dengan dinamika kebahagiaannya. Dan ketika parameter membesar nilainya negatif maka dinamika dan respon kebahagiaan akan semakin cepat membesar.
10 20 30 40
t
-0.04 -0.02 0.02 0.04 H
10 20 30 40t
-0.1 -0.05 0.05 0.1 R
0.5 1 1.5 2 2.5 3 t
-4 -2 2 4 H
0.5 1 1.5 2 2.5 3 t
3.1.2 Analisis Model II
Titik tetap sistem persamaan (12) diperoleh dengan menentukan
=
0
dt
dR
dan0
=
dt
dH
, sehingga diperoleh satu titik tetap yaitu T2 =(0,0). [Lihat Lampiran 3]. Konstruksi Matriks Jacobi Dengan melakukan pelinearan pada sistem persamaan di atas, diperoleh matriks Jacobi :
2
0 1
2
1
-J
RH
R
β
β β
⎡
⎤
= ⎢
−
+
⎥
⎣
⎦
. (16)Analisis Kestabilan
Jika T2 =(0,0) disubstitusikan pada (16) maka diperoleh:
⎥
⎦
⎤
⎢
⎣
⎡
−
=
β
1
1
0
2J
.Untuk memperoleh nilai eigen maka
0
)
det(
J
2−
λ
I
=
, yaitu :1
)
(
)
det(
2 22
2
−
λ
I
=
λ
−
−
β
λ
+
J
(17)atau dapat dituliskan kembali
.
0
2 2 2 22
−
τ
λ
+
∆
=
λ
(18) Dari persamaan (18) terlihat bahwa traceJ
2=
τ
2=
−
β
det
J
2=
∆
2=
1
dan diperoleh 2 1,2
4
2
2
β
β
λ
= − ±
−
. Berdasarkan teori kestabilan, jikaa.
β
>
2
, maka titik tetapT
2merupakan simpul taksejati stabil.
b.
β
< −
2
, maka titik tetapT
2merupakan simpul taksejati takstabil.
c.
0
<
β
<
2
, maka titik tetap2
T
merupakan spiral stabil. d.−
2
<
β
<
0
, maka titik tetap2
T
merupakan spiral takstabil. e.β
=
2
, maka titik tetapT
2merupakan simpul sejati stabil. f.
β
=
−
2
dan ada 2 vektor eigenbebas linear, maka titik tetap
T
2merupakan simpul sejati takstabil.
Dengan menggunakan bantuan software Mathematica 5.2 dan nilai awal (0.1, 0.1) diperoleh gambar dinamika dan respon kebahagiaan. [Lihat Lampiran 4].
Contoh Kasus
β
>
0
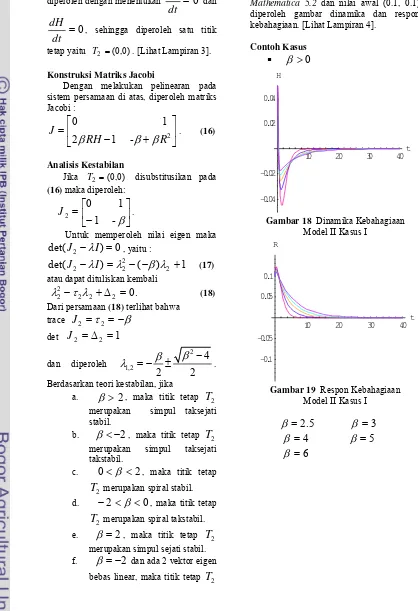
Gambar 18 Dinamika Kebahagiaan Model II Kasus I
Gambar 19 Respon Kebahagiaan Model II Kasus I
β
=
2
.
5
β
=
3
β
=
4
β
=
5
β
=
6
10 20 30 40t
-0.04 -0.02 0.02 0.04 H
10 20 30 40t
β
<
0
Gambar 20 Dinamika Kebahagiaan Model II Kasus I
Gambar 21 Respon Kebahagiaan Model II Kasus I
β
=
−
2
β
=
−
3
β
=
−
4
AnalisisContoh kasus I pada model II di atas menggunakan nilai awal yang sama dan parameter yang berbeda. Ketika parameter kecil nilainya positif maka dinamika kebahagiaannya besar namun kebahagiaan ini cepat hilang (cepat menuju keseimbangan), dan ketika parameter besar maka dinamika kebahagiaannya kecil namun kebahagiaan ini lama hilang (lama menuju keseimbangan). Dengan cara yang sama respon kebahagiaan memiliki karakteristik yang sama dengan dinamika kebahagiaannya. Dan ketika parameter membesar nilainya negatif maka dinamika dan respon kebahagiaan akan berosilasi. Amplitudo dan periode osilasi akan semakin besar jika nilai parameternya semakin menjauhi nol.
3.2 Pengaruh Luar Dipertimbangkan Dalam hal ini diasumsikan
F
(
t
)
≠
0
. Misalkan,F
(
t
)
=
a
dengana
adalah konstanta. Dengan mengasumsikanH
dt
dR
=
maka diperoleh sistem persamaan:a
R
H
dt
dH
H
dt
dR
+
−
−
=
=
β
(19) (Model I) dan.
)
1
(
R
2H
R
a
dt
dH
H
dt
dR
+
−
−
−
=
=
β
(20) (Model II)3.2.1 Analisis Model I Titik tetap sistem persamaan (19) diperoleh dengan menentukan
=
0
dt
dR
dan0
=
dt
dH
, sehingga diperoleh satu titik tetap yaitu
T
1=
(
a
,
0
)
.[Lihat Lampiran 5].
Konstruksi Matriks Jacobi
Dengan melakukan pelinearan pada sistem persamaan di atas, diperoleh matriks Jacobi :
0 1
1
-J
β
⎡
⎤
= ⎢
−
⎥
⎣
⎦
. (21) Analisis KestabilanJika
T
1=
(
a
,
0
)
disubstitusikan padamatriks Jacobi (21) :
⎥
⎦
⎤
⎢
⎣
⎡
−
=
β
1
1
0
1J
.Untuk memperoleh nilai eigen maka
0
)
det(
J
1−
λ
I
=
, yaitu :1
)
(
)
det(
J
1−
λ
I
=
λ
12−
−
β
λ
1+
(22) atau dituliskan kembali.
0
1 1 1 21
−
τ
λ
+
∆
=
λ
(23)Dari persamaan (23) terlihat bahwa
10 20 30 40t
-6 -4 -2 2 4 6 H
10 20 30 40t
trace
J
1=
τ
1=
−
β
detJ
1=
∆
1=
1
dan diperoleh
2 1,2
4
2
2
β
β
λ
= − ±
−
. Berdasarkan teori kestabilan, jikaa.
β
>
2
, maka titik tetapT
1merupakan simpul taksejati stabil.
b.
β
<
−
2
, maka titik tetapT
1merupakan simpul taksejati takstabil.
c.
0
<
β
<
2
, maka titik tetap1
T
merupakan spiral stabil. d.−
2
<
β
<
0
, maka titik tetap1
T
merupakan spiral tak stabil. e.β
=
2
, maka titik tetapT
1merupakan simpul sejati stabil. f.
β
=
−
2
dan ada 2 vektoreigen bebas linear, maka titik tetap
T
1 merupakan simpul sejati takstabil.Dengan menggunakan software Mathematica 5.2 dan nilai awal (0.1, 0.1) diperoleh gambar dinamika dan respon kebahagiaan. [Lihat lampiran 6].
Contoh Kasus
a
=
1
danβ
>
0
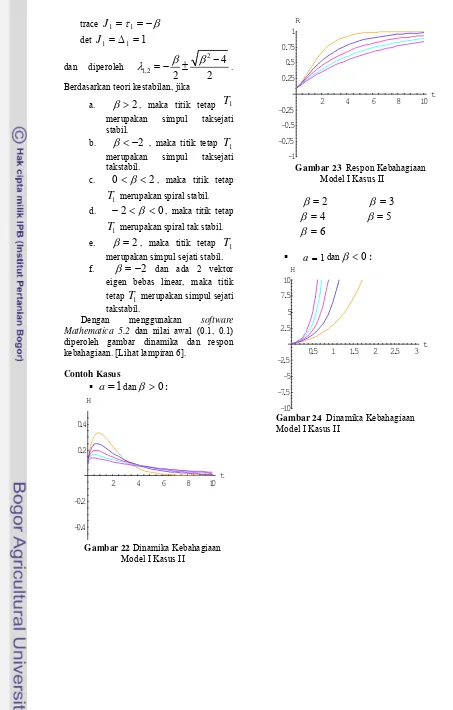
:Gambar 22 Dinamika Kebahagiaan Model I Kasus II
Gambar 23 Respon Kebahagiaan Model I Kasus II
β
=
2
β
=
3
β
=
4
β
=
5
β
=
6
a=1dan
β
<
0
:Gambar 24 Dinamika Kebahagiaan Model I Kasus II
2 4 6 8 10
t
-0.4 -0.2 0.2 0.4 H
2 4 6 8 10
t
-1 -0.75 -0.5 -0.25 0.25 0.5 0.75 1 R
0.5 1 1.5 2 2.5 3 t
Gambar 25 Respon Kebahagiaan Model I Kasus II
β
=
−
2
β
=
−
3
β
=
−
4
β
=
−
5
β
=
−
6
a
=
−
1
danβ
>
0
:Gambar 26 Dinamika Kebahagiaan Model I Kasus II
Gambar 27 Respon Kebahagiaan Model I Kasus II
β
=
2
β
=
3
β
=
4
β
=
5
β
=
6
a
=
−
1
danβ
<
0
:Gambar 28 Dinamika Kebahagiaan Model I Kasus II
Gambar 29 Respon Kebahagiaan Model I Kasus II
β
=
−
2
β
=
−
3
β
=
−
4
β
=
−
5
β
=
−
6
Analisis
Contoh kasus II pada model I di atas menggunakan nilai awal yang sama dan parameter yang berbeda. Ketika parameter kecil nilainya positif maka dinamika kebahagiaannya besar namun kebahagiaan ini cepat hilang (cepat menuju keseimbangan), dan ketika parameter besar maka dinamika kebahagiaannya kecil namun kebahagiaan ini lama hilang (lama menuju keseimbangan). Dengan cara yang sama respon kebahagiaan memiliki karakteristik yang sama dengan dinamika kebahagiaannya. Dan ketika parameter 0.5 1 1.5 2 2.5 3
t
-10 -7.5 -5 -2.5 2.5 5 7.5 10 R
2 4 6 8 10
t
-0.4 -0.2 0.2 0.4 H
2 4 6 8 10t
-2 -1.5 -1 -0.5 0.5 1 1.5 2 R
0.5 1 1.5 2 2.5 3t
-10 -7.5 -5 -2.5 2.5 5 7.5 10 H
0.5 1 1.5 2 2.5 3t
membesar nilainya negatif maka dinamika dan respon kebahagiaan akan semakin cepat membesar.
3.2.2 Analisis Model II
Titik tetap sistem persamaan (20)
diperoleh dengan menentukan
=
0
dt
dR
dan0
=
dt
dH
, sehingga diperoleh titik tetap yaitu
T
2=
(
a
,
0
)
. [Lihat Lampiran 7]. Konstruksi Matriks JacobiDengan melakukan pelinearan pada sistem persamaan di atas, diperoleh matriks Jacobi:
2
0 1
2
1
J
RH
R
β
β β
⎡
⎤
= ⎢
−
− +
⎥
⎣
⎦
. (24)Analisis Kestabilan
Jika
T
2=
(
a
,
0
)
disubstitusikan pada (24) maka diperoleh:
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
β
β
2 21
1
0
a
J
.Untuk memperoleh nilai eigen maka
0
)
det(
J
2−
λ
I
=
, yaitu :2 2
2 2 2
det(J −λI)=λ −(a β β λ− ) +1 (25) atau dapat dituliskan kembali
.
0
2 2 2 22
−
τ
λ
+
∆
=
λ
(26) Dari persamaan (26) terlihat bahwa traceJ
2=
τ
2=
a
2β
−
β
detJ
2=
∆
2=
1
dan diperoleh
2 2
2
1,2
( ( 1)) 4 ( 1) 2 2 a a β β λ = − ± − − .
Berdasarkan teori kestabilan, jika a.
β
(
a
2−
1
)
>
2
, maka titik tetap T2 merupakan simpul taksejati takstabil.
b.
β
(
a
2−
1
)
<
−
2
, maka titik tetap T2 merupakan simpul taksejati stabil.
c.
0
<
β
(
a
2−
1
)
<
2
, maka titik tetap T2 merupakan spiral takstabil.d.
−
2
<
β
(
a
2−
1
)
<
0
, maka titik tetap T2 merupakan spiral stabil.e.
β
(
a
2−
1
)
=
2
, maka titik tetap T2 merupakan simpul sejati takstabil.
f.
β
(
a
2−
1
)
=
−
2
dan ada 2 vektor eigen bebas linear, maka titik tetap T2 merupakan simpul sejati stabil.
Dengan menggunakan bantuan software Mathematica 5.2 dan nilai awal (0.1, 0.1) diperoleh gambar dinamika dan respon kebahagiaan. [Lihat lampiran 8].
Gambar 30 Perubahan Kestabilan sistem dalam sumbu a dan
β
-3 -2 -1 1 2 3 a
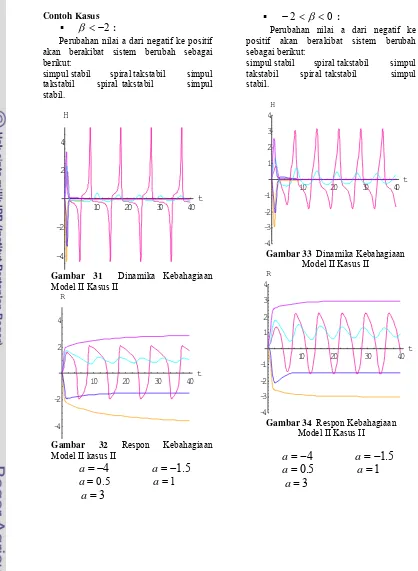
Contoh Kasus
β
<
−
2
:Perubahan nilai a dari negatif ke positif akan berakibat sistem berubah sebagai berikut:
simpul stabil spiral takstabil simpul takstabil spiral takstabil simpul stabil.
Gambar 31 Dinamika Kebahagiaan Model II Kasus II
Gambar 32 Respon Kebahagiaan Model II kasus II
a
=
−
4
a
=
−
1
.
5
a
=
0
.
5
a
=
1
a
=
3
−
2
<
β
<
0
:Perubahan nilai a dari negatif ke positif akan berakibat sistem berubah sebagai berikut:
simpul stabil spiral takstabil simpul takstabil spiral takstabil simpul stabil.
Gambar 33 Dinamika Kebahagiaan Model II Kasus II
Gambar 34 Respon Kebahagiaan Model II Kasus II
a
=
−
4
a
=
−
1
.
5
a
=
0
.
5
a
=
1
a
=
3
10 20 30 40
t
-4 -2 2 4 H
10 20 30 40
t
-4 -2 2 4 R
10 20 30 40
t
-4 -3 -2 -1 1 2 3 4 H
10 20 30 40t
0
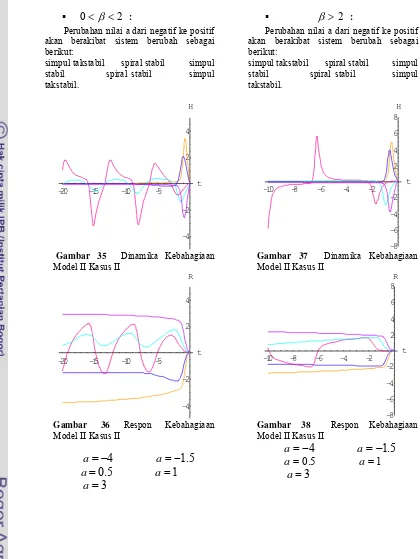
<
β
<
2
:Perubahan nilai a dari negatif ke positif akan berakibat sistem berubah sebagai berikut:
simpul takstabil spiral stabil simpul stabil spiral stabil simpul takstabil.
Gambar 35 Dinamika Kebahagiaan Model II Kasus II
Gambar 36 Respon Kebahagiaan Model II Kasus II
a
=
−
4
a
=
−
1
.
5
a
=
0
.
5
a
=
1
a
=
3
β
>
2
:Perubahan nilai a dari negatif ke positif akan berakibat sistem berubah sebagai berikut:
simpul takstabil spiral stabil simpul stabil spiral stabil simpul takstabil.
Gambar 37 Dinamika Kebahagiaan Model II Kasus II
Gambar 38 Respon Kebahagiaan Model II Kasus II
a
=
−
4
a
=
−
1
.
5
a
=
0
.
5
a
=
1
a
=
3
-20 -15 -10 -5
t
-4 -2 2 4 H
-20 -15 -10 -5
t
-4 -2 2 4 R
-10 -8 -6 -4 -2
t
-8 -6 -4 -2 2 4 6 8 H
-10 -8 -6 -4 -2 t
IV SIMPULAN
Dinamika kebahagiaan dimodelkan dalam bentuk sistem persamaan diferensial orde satu. Model ini menganalisis perilaku dinamis kebahagiaan dan respon kebahagiaan seseorang. Perilaku dinamis ini dipengaruhi oleh suatu parameter yang mencerminkan pengaruh internal dan juga dipengaruhi oleh pengaruh luar. Ketika pengaruh internal ini kecil dengan nilai positif maka perubahan kebahagiaan dan responnya akan besar, namun kebahagiaan ini akan cepat hilang (cepat menuju keseimbangan). Dan ketika pengaruh internal ini besar dengan nilai positif maka perubahan kebahagiaan dan responnya akan kecil, namun kebahagiaan ini akan lama hilang (lama menuju keseimbangan) atau dengan kata lain seseorang dapat mempertahankan kebahagiaannya lebih lama. Ketika pengaruh internal ini membesar dengan nilai negatif
maka perubahan kebahagiaan dan responnya akan semakin cepat membesar.
Dan pengaruh luar juga mempengaruhi perilaku dinamis ini. Jika pengaruh luar ada, ketika pengaruh luar kecil dengan nilai positif maka perubahan kebahagiaan dan responnya akan berosilasi, namun kebahagiaan akan lama hilang atau dengan kata lain seseorang dapat mempertahankan kebahagiaannya lebih lama dan ketika pengaruh luar besar dengan nilai positif maka perubahan kebahagiaan dan responnya akan kecil, namun kebahagiaan ini akan cepat hilang atau dengan kata lain seseorang akan kehilangan kebahagiaannya. Ketika pengaruh luar ini membesar dengan nilai negatif maka perubahan kebahagiaan dan responnya akan semakin cepat mengecil.
DAFTAR PUSTAKA
Goleman, D. 2003. Destructive emotions:A scientific dialogue with the Dalai Lama. Bantun, New York.
Kreyszig, M. 1993. Matematika Tehnik Lanjutan. Edisi ke-6, Buku I. Terjemahan Sumantri, B. Gramedia Pustaka Utama, Jakarta.
Orsucci, F. 2001. Happiness and deep ecology: On noise, harmony, and beauty in the mind. Nonlinear Dynamics, Psychology, and Life Sciences, 5, 65-76. Sprott, J. C. 2005. Dynamical Models of
Happiness. Nonlinear Dynamics,
Psychology, and Life Sciences, Vol. 9, No. 1.
Strogatz, S. H. 1994. Nonlinear Dynamics And Chaos with Application to Physic, Biology, Chemistry, and Engineering. Addison Wesley, Reading, Massachusetts Menlo Park, California. Tu, P. N. V. 1994. Dynamical System, An
Introduction with Application in Economics and Biology. Springer -Verlag. Heidelberg. Germany.
Lampiran 1
Penentuan Titik Tetap Kasus I untuk sistem persamaan (11). Diketahui :
.
R
H
dt
dH
H
dt
dR
−
−
=
=
β
(11)
Menentukan titik tetap
T
1 :Titik tetap
(
R
1,
H
1)
diperoleh dengan menentukan=
0
dt
dR
dan
=
0
,
dt
dH
dengan mensubstitusikan persamaan tersebut ke persamaan (11) didapatkan :
0
=
H
(27).
0
=
−
−
β
H
R
(28) Sehingga :0
1=
H
(29) dengan mensubstitusikan persamaan (29) ke persamaan (28) diperoleh :.
0
1=
R
(30) Dari persamaan (30) dan (29) diperoleh titik tetapT
1 sebagai berikut :).
0
,
0
(
1=
T
Lampiran 2
Program untuk memperoleh grafik dinamika dan respon kebahagiaan pada kasus I untuk sistem persamaan (11) dengan menggunakan bantuan software Mathematica 5.2.
model:={R'[t] H[t],H'[t] -β H[t]- R[t],R[0] 0.1,H[0] 0.1} β=2.5;
tMaksimum=40;
sol=NDSolve[model,{H,R},{t,0,tMaksimum}]
gambar1=Plot[H[x]/.sol[[1,1]],{x,0,tMaksimum},AxesLabel->{"t","H"},PlotStyle->{Hue[0.9]}, PlotRange→{-0.05,0.05}]
gambar2=Plot[R[x]/.sol[[1,2]],{x,0,tMaksimum},AxesLabel->{"t","R"},PlotStyle->{Hue[0.9]}, PlotRange→{-0.15,0.15}]
Program untuk memperoleh grafik dinamika dan respon kebahagiaan serta medan arah dan orbit kestabilan pada kasus I untuk sistem persamaan (11) dengan menggunakan bantuan software Mathematica 5.2.
Reset Parameter DynSys intreset;
plotreset;
Deklarasi Sistem setstate [{R, H}];
slopevec = {H, −βH −R}; setparm [{β}];
Cari Titik Tetap eqpoints = findpolyeq { {0, 0} }
classify [eqpoints[ [1] ] ] strictly stable
Integral
initvec = {-1, 0};
t0 = 0. 0;tMax = 40; h = 0.1;
nsteps
h tMax
= ;
firstsol = integrate [initvec, t0, h, nsteps];
Plotting time asprat = 1;
timeplot [firstsol, { 1 }]; timeplot [firstsol, {2}];
Plotting diagram fasa display = False;
fasa = phaseplot [firstsol, 1, 2];
Plotting medan arah display = False; eqpoints = findpolyeq; ptsize = 0. 03;
dotgraph = dots [eqpoints]; plrange = {{ -4, 4}, {-4, 4}}; graph5 = dirfield;
Plotting semua display = True;
show [ fasa, dotgraph, graph5];
Lampiran 3
Penentuan Titik Tetap Kasus I untuk sistem persamaan (12).
Diketahui :
.
)
1
(
R
2H
R
dt
dH
H
dt
dR
−
−
−
=
=
β
(12)
Menentukan titik tetap
T
2 :Titik tetap
(
R
2,
H
2)
diperoleh dengan menentukan=
0
dt
dR
dan
=
0
,
dt
dH
dengan mensubstitusikan persamaan tersebut ke persamaan (12) didapatkan :
0
=
.
0
)
1
(
−
2−
=
−
β
R
H
R
(32) Sehingga :0
2=
H
(33) dengan mensubstitusikan persamaan (33) ke persamaan (32) diperoleh :.
0
2=
R
(34) Dari persamaan (34) dan (33) diperoleh titik tetapT
2 sebagai berikut :).
0
,
0
(
2=
T
Lampiran 4
Program untuk memperoleh grafik dinamika dan respon kebahagiaan pada kasus I untuk sistem persamaan (12) dengan menggunakan bantuan software Mathematica 5.2.
Program untuk memperoleh grafik dinamika dan respon kebahagiaan serta medan arah dan orbit kestabilan pada kasus I untuk sistem persamaan (12) dengan menggunakan bantuan software Mathematica 5.2.
Reset Parameter DynSys intreset;
plotreset;
Deklarasi Sistem setstate [{R, H}];
slopevec = {H, −β(1−R2)H −R}; setparm [{β}];
parmval = {1};
Cari Titik Tetap eqpoints = findpolyeq { {0, 0} }
classify [eqpoints[ [1] ] ] strictly stable
model :=9R'@tD H@tD,
H'@tD −β I1−R@tD2MH@tD−R@tD, R@0D 0.1,
H@0D 0.1= β = −2;
tMaksimum=40;
sol=NDSolve@model,8H, R<,8t, 0, tMaksimum<D
gambar1=Plot@H@xD ê. sol@@1, 1DD,8x, 0, tMaksimum<, AxesLabel−>8"t", "H"<, PlotStyle−>[email protected]<, PlotRange→8−6, 6<D
Integral
initvec = {-1, 0};
t0 = 0. 0;tMax = 20; h = 0.1;
nsteps
h tMax
= ;
firstsol = integrate [initvec, t0, h, nsteps];
Plotting time asprat = 1;
timeplot [firstsol, { 2 }];
Plotting diagram fasa display = False;
fasa = phaseplot [firstsol, 2]; Plotting medan arah
display = False; eqpoints = findpolyeq; ptsize = 0. 03;
dotgraph = dots [eqpoints]; plrange = {{ -4, 4}, {-4, 4}}; graph5 = dirfield;
Plotting semua display = True;
show [ fasa, dotgraph, graph5];
Lampiran 5
Penentuan Titik Tetap Kasus II untuk sistem persamaan (19).
Diketahui :
.
a
R
H
dt
dH
H
dt
dR
+
−
−
=
=
β
(19)
Menentukan titik tetap T1 :
Titik tetap (R1,H1) diperoleh dengan menentukan
=
0
dt
dR
dan
=
0
,
dt
dH
dengan mensubstitusikan persamaan tersebut ke persamaan (19) didapatkan :
0
=
H
(35).
0
=
+
−
−
β
H
R
a
(36) Sehingga :0
1=
H (37) dengan mensubstitusikan persamaan (37) ke persamaan (36) diperoleh :
.
1a
).
0
,
(
1a
T
=
Lampiran 6
Program untuk memperoleh grafik respon kebahagiaan dan dinamika kebahagiaan pada kasus II untuk sistem persamaan (19) dengan menggunakan bantuan software Mathematica 5.2.
model:={R'[t] H[t],H'[t] -β H[t]- R[t]+a,R[0] 0.1,H[0] 0.1} a=1;
β=2;
tMaksimum=10;
sol=NDSolve[model,{H,R},{t,0,tMaksimum}]
gambar1=Plot[H[x]/.sol[[1,1]],{x,0,tMaksimum},AxesLabel->{"t","H"},PlotStyle->{Hue[0.1]}, PlotRange→{-0.5,0.5}]
gambar2=Plot[R[x]/.sol[[1,2]],{x,0,tMaksimum},AxesLabel->{"t","R"},PlotStyle->{Hue[0.1]}, PlotRange→{-1,1}]
Program untuk memperoleh grafik respon kebahagiaan dan dinamika kebahagiaan serta medan arah pada kasus II untuk sistem persamaan (19) dengan menggunakan bantuan software Mathematica 5.2.
Reset Parameter DynSys intreset;
plotreset;
Deklarasi Sistem setstate [{R, H}];
slopevec = {H, −βH−R+1}; setparm [{β}];
parmval = {1};
Cari Titik Tetap eqpoints = findpolyeq { {1, 0} }
classify [eqpoints[ [1] ] ] strictly stable
Integral
initvec = {1, 1};
t0 = 0. 0;tMax = 20; h = 0.1;
nsteps
h tMax
= ;
firstsol = integrate [initvec, t0, h, nsteps];
Plotting time asprat = 1;
timeplot [firstsol, { 1 }]; timeplot [firstsol, { 2 }];
Plotting diagram fasa display = False;
fasa = phaseplot [firstsol, 1, 2];
display = False; eqpoints = findpolyeq; ptsize = 0. 03;
dotgraph = dots [eqpoints]; plrange = {{ -4, 4}, {-4, 4}}; graph5 = dirfield;
Plotting semua display = True;
show [ fasa, dotgraph, graph5];
Lampiran 7
Penentuan Titik Tetap Kasus II untuk sistem persamaan (20).
Diketahui :
.
)
1
(
R
2H
R
a
dt
dH
H
dt
dR
+
−
−
−
=
=
β
(20)
Menentukan titik tetap T2 :
Titik tetap (R2,H2) diperoleh dengan menentukan
=
0
dt
dR
dan
=
0
,
dt
dH
dengan mensubstitusikan persamaan tersebut ke persamaan (20) didapatkan :
0
=
H
(39).
0
)
1
(
−
2−
+
=
−
β
R
H
R
a
(40) Sehingga :0
2=
H (41) dengan mensubstitusikan persamaan (41) ke persamaan (40) diperoleh :
.
2a
R
=
(42) Dari persamaan (42) dan (41) diperoleh titik tetap T2 sebagai berikut :).
0
,
(
2
a
Lampiran 8
Program untuk memeperoleh gambar perubahan kestabilan system dalam sumbu a dan
β
.<<Graphics`ImplicitPlot`
ImplicitPlot[y^2(x^2-1)^2 4,{x,-3,3},AxesLabel->{"x","y"}]
Program untuk memperoleh grafik respon kebahagiaan dan dinamika kebahagiaan pada kasus II untuk sistem persamaan (20) dengan menggunakan bantuan software Mathematica 5.2.
Program untuk memperoleh grafik respon kebahagiaan dan dinamika kebahagiaan serta medan arah pada kasus II untuk sistem persamaan (20) dengan menggunakan bantuan software Mathematica 5.2.
Reset Parameter DynSys intreset;
plotreset;
Deklarasi Sistem setstate [{R, H}];
slopevec = {H, −βH−R+1}; setparm [{β}];
parmval = { 1};
Cari Titik Tetap eqpoints = findpolyeq { {1, 0} }
classify [eqpoints[ [1] ] ] unstable
Integral
initvec = {1, 1};
t0 = 0. 0;tMax = 20; h = 0.1;
model :=9R'@tD H@tD,
H'@tD −β I1−R@tD2MH@tD− R@tD+a, R@0D 0.1,
H@0D 0.1= β = −3; a= −4;
tMaksimum=40;
sol=NDSolve@model,8H, R<,8t, 0, tMaksimum<D
gambar1=Plot@H@xD ê. sol@@1, 1DD,8x, 0, tMaksimum<, AxesLabel−>8"t", "H"<, PlotStyle−>[email protected]<, PlotRange→8−5, 5<D
gambar2=Plot@R@xD ê. sol@@1, 2DD,8x, 0, tMaksimum<,
nsteps
h tMax
= ;
firstsol = integrate [initvec, t0, h, nsteps];
Plotting time asprat = 1;
timeplot [firstsol, { 1 }]; timeplot [firstsol, { 2 }];
Plotting diagram fasa display = False;
fasa = phaseplot [firstsol, 1, 2]; Plotting medan arah
display = False; eqpoints = findpolyeq; ptsize = 0. 03;
dotgraph = dots [eqpoints]; plrange = {{ -3, 3}, {-3, 3}}; graph5 = dirfield;
Plotting semua display = True;
NELI YUSRI MARDIANA
G54102018
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
NELI YUSRI MARDIANA. Analysis of the Happiness Dynamical Models. Supervised by ANNIS DINIATI RAKSANAGARA andALI KUSNANTO.
Happiness is a dynamical process, so it can be modeled as differential equation models. It was written by [Sprott, 2005] which explains the rate of change of happiness response as the rate of happiness.
Dynamical models are influenced by parameter, that reflect the internal influences. When the internal influences are small with positive values, the change of happiness and it’s response will be large, but this happiness will be lost quicker (will quicker reach the stability point). While when the internal influences are large with positive values, the change of happiness and it’s response will be small, but this happiness will be lost slower (will slower reach the stability point) or in other words, someone can maintains their happiness longer if the internal influences are large. When the internal influences are getting larger with negative values, the change of happiness and it’s response will quicker getting large.
NELI YUSRI MARDIANA. Analisis Dinamika Model Kebahagiaan. Dibimbing oleh ANNIS DINIATI RAKSANAGARA danALI KUSNANTO.
Kebahagiaan merupakan proses yang dinamis, sehingga dapat dimodelkan dalam model persamaan diferensial. Model yang digunakan adalah model yang ditulis oleh [Sprott, 2005] dengan menyatakan laju perubahan respon kebahagiaan sebagai tingkat kebahagiaan.
Dinamika model tersebut dipengaruhi oleh suatu parameter yang mencerminkan pengaruh internal. Ketika pengaruh internal ini kecil dengan nilai positif maka perubahan kebahagiaan dan responnya akan besar, namun kebahagiaan ini akan cepat hilang (cepat menuju keseimbangan). Sedangkan ketika pengaruh internal ini besar dengan nilai positif maka perubahan kebahagiaan dan responnya akan kecil, namun kebahagiaan ini akan lama hilang (lama menuju keseimbangan) atau dengan kata lain, seseorang dapat mempertahankan kebahagiaannya lebih lama jika pengaruh internal ini besar. Ketika pengaruh internal ini membesar dengan nilai negatif maka perubahan kebahagiaan dan responnya akan semakin cepat membesar.
I PENDAHULUAN
1.1 Latar Belakang
Menurut sebagian orang, pencarian kebahagiaan merupakan tujuan utama dalam hidup dan banyak buku yang telah ditulis untuk masalah tersebut. Kebahagiaan merupakan perwujudan emosi diantaranya kegembiraan, kesenangan, keriangan, kesukaan, ketenangan, pemenuhan kebutuhan dan kepuasan hati (Orsucci, 2001) sehingga kebahagiaan merupakan proses yang dinamis. Kebahagiaan dibedakan berdasarkan suasana hati yang dapat dipengaruhi oleh pengaruh luar (lingkungan sekitar) (Goleman, 2003).
Penggunaan model matematika jarang diaplikasikan pada dinamika model kebahagiaan, namun beberapa model dinamika cinta telah dibuat, terilhami oleh model Strogatz (1994). Strogatz menyusun model dinamika cinta dalam bentuk sistem persamaan diferensial orde satu. Dengan ide yang hampir sama model kebahagiaan ini akan disusun dalam bentuk sistem persamaan diferensial orde satu juga.
Tugas akhir ini membahas perilaku dinamis model kebahagiaan dan respon kebahagiaan seseorang yang dimodelkan dalam bentuk sistem persamaan diferensial orde satu.
1.2 Tujuan Penulisan
Tujuan penulisan tugas akhir ini adalah menganalisis perilaku dinamis model kebahagiaan dan respon kebahagiaan seseorang.
1.3 Sistematika Penulisan
Bab I menjelaskan tentang pendahuluan yang berisikan latar belakang dan tujuan penulisan tugas akhir. Bab II mengenai landasan teori berisikan definisi-definisi yang menjadi dasar untuk membahas dan menganalisis model dinamika kebahagiaan. Sedangkan bab III menjelaskan tentang pemodelan yang telah dimodifikasi beserta pembahasannya yang dilengkapi oleh gambar-gambar dan akhirnya bab IV berisikan simpulan dari permasalahan.
II LANDASAN TEORI
Definisi (Sistem Persamaan Diferensial Linear) :
Jika suatu sistem persamaan diferensial (SPD) dinyatakan sebagai :
x
=
A
x b x
+
, (0)
=
x x
0,
∈ℜ
n (1) dengan A adalah matriks koefisiennxn
dan vektor konstanb
∈
ℜ
n, maka sistem tersebut dinamakan SPD linear orde satu dengan kondisi awalx
(
0
)
=
x
0. Sistem (1) disebut homogen jikab
=
0
dan nonhomogen jikab
≠
0
.[ Tu, 1994 ]
Definisi (Sistem Persamaan Diferensial Mandiri) :
SPD :
n
j
x
f
x
dt
dx
j j
j
,...,
2
,
1
),
(
=
=
=
(2)dengan
f
fungsi kontinu bernilai real darix
dan mempunyai turunan parsial kontinu disebut SPD mandiri (autonomous) jika tidak memuat waktu(
t
)
secara eksplisit di dalamnya.I PENDAHULUAN
1.1 Latar Belakang
Menurut sebagian orang, pencarian kebahagiaan merupakan tujuan utama dalam hidup dan banyak buku yang telah ditulis untuk masalah tersebut. Kebahagiaan merupakan perwujudan emosi diantaranya kegembiraan, kesenangan, keriangan, kesukaan, ketenangan, pemenuhan kebutuhan dan kepuasan hati (Orsucci, 2001) sehingga kebahagiaan merupakan proses yang dinamis. Kebahagiaan dibedakan berdasarkan suasana hati yang dapat dipengaruhi oleh pengaruh luar (lingkungan sekitar) (Goleman, 2003).
Penggunaan model matematika jarang diaplikasikan pada dinamika model kebahagiaan, namun beberapa model dinamika cinta telah dibuat, terilhami oleh model Strogatz (1994). Strogatz menyusun model dinamika cinta dalam bentuk sistem persamaan diferensial orde satu. Dengan ide yang hampir sama model kebahagiaan ini akan disusun dalam bentuk sistem persamaan diferensial orde satu juga.
Tugas akhir ini membahas perilaku dinamis model kebahagiaan dan respon kebahagiaan seseorang yang dimodelkan dalam bentuk sistem persamaan diferensial orde satu.
1.2 Tujuan Penulisan
Tujuan penulisan tugas akhir ini adalah menganalisis perilaku dinamis model kebahagiaan dan respon kebahagiaan seseorang.
1.3 Sistematika Penulisan
Bab I menjelaskan tentang pendahuluan yang berisikan latar belakang dan tujuan penulisan tugas akhir. Bab II mengenai landasan teori berisikan definisi-definisi yang menjadi dasar untuk membahas dan menganalisis model dinamika kebahagiaan. Sedangkan bab III menjelaskan tentang pemodelan yang telah dimodifikasi beserta pembahasannya yang dilengkapi oleh gambar-gambar dan akhirnya bab IV berisikan simpulan dari permasalahan.
II LANDASAN TEORI
Definisi (Sistem Persamaan Diferensial Linear) :
Jika suatu sistem persamaan diferensial (SPD) dinyatakan sebagai :
x
=
A
x b x
+
, (0)
=
x x
0,
∈ℜ
n (1) dengan A adalah matriks koefisiennxn
dan vektor konstanb
∈
ℜ
n, maka sistem tersebut dinamakan SPD linear orde satu dengan kondisi awalx
(
0
)
=
x
0. Sistem (1) disebut homogen jikab
=
0
dan nonhomogen jikab
≠
0
.[ Tu, 1994 ]
Definisi (Sistem Persamaan Diferensial Mandiri) :
SPD :
n
j
x
f
x
dt
dx
j j
j
,...,
2
,
1
),
(
=
=
=
(2)dengan
f
fungsi kontinu bernilai real darix
dan mempunyai turunan parsial kontinu disebut SPD mandiri (autonomous) jika tidak memuat waktu(
t
)
secara eksplisit di dalamnya.Definisi (Nilai Eigen dan Vektor Eigen) : Diberikan matriks koefisien konstan A berukuran
nxn
, dan SPD homogen berikut :x
=
A
x x
, (0)
=
x
0 (3) Suatu vektor tak nolx
dalam ruangℜ
n disebut vektor eigen dari A jika untuk suatu skalarλ
berlaku :
A
x
=
λ
x
. (4) Nilai skalarλ
dinamakan nilai eigen dari A. Untuk mencari nilaiλ
dari matriks A, maka persamaan (4) dapat ditulis kembali sebagai :
(
A
−
λ
I
)
x
=
0
(5) dengan I matriks diagonal satuan. Persamaan (5) mempunyai solusi tak nol jika dan hanya jika( )
det(
) |
| 0
p
λ
=
A
−
λ
I
= −
I
λ
I
=
. (6) Persamaan (6) disebut persamaan karakteristik dari matriks A.[ Kreyszig, 1998]
Definisi (Titik Tetap) : Diberikan SPD
x
f
(
x
)
dt
dx
=
=
nx
∈
ℜ
. (7) Titikx
* disebut titik tetap, jika0
)
(
x
*=
f
. Titik tetap disebut juga titik kritis atau titik kesetimbangan.[ Kreyszig, 1993]
Definisi (Titik Tetap Stabil) :
Misalkan
x
* adalah titik tetap sebuah SPD mandiri danx
(
t
)
adalah solusi SPD mandiri dengan nilai awaldengan
x
0≠
x
*. Titikx
* dikatakan titik tetap stabil jika untuk sembarang radius, terdapat sehingga jika posisi awal
x
0 memenuhi|
x
0−
x
*|
<
r
,