i
MENENTUKAN ALIRAN MAKSIMUM DENGAN
ALGORITMA FORD-FULKERSON DAN PREFLOW-PUSH
skripsi
disajikan sebagai salah satu syarat
untuk memperoleh gelar Sarjana Sains
Program Studi Matematika
oleh Rif’ah Ulya 4111409008
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS NEGERI SEMARANG
iii
PERNYATAAN
Saya menyatakan bahwa skripsi ini bebas plagiat, dan apabila di kemudian
hari terbukti terdapat plagiat dalam skripsi ini, maka saya bersedia menerima
sanksi sesuai ketentuan peraturan perundang-undangan.
Semarang, 01 Agustus 2013
Rif’ah Ulya
iv
PENGESAHAN
Skripsi yang berjudul
Menentukan Aliran Maksimum dengan Algoritma Ford-Fulkerson dan
Preflow-Push
disusun oleh Rif’ah Ulya 4111409008
telah dipertahankan di hadapan sidang Panitia Ujian Skripsi FMIPA UNNES pada
tanggal 01 Agustus 2013.
Panitia:
Ketua Sekretaris
Prof. Dr. Wiyanto, M.Si. Drs. Arief Agoestanto, M.Si.
196310121988031001 196807221993031005
Ketua Penguji
Dr. Rochmad, M.Si. 195711161987011001
Anggota Penguji/ Anggota Penguji/
Pembimbing Utama Pembimbing Pendamping
Dr. Mulyono, M.Si. Drs. Amin Suyitno, M.Pd.
v
PERSEMBAHAN
Untuk keluargaku tersayang,
Ayahanda H. Sidqon, sebagai sumber kekuatan hati di setiap
harapan dan cita-citaku,
Ibunda Hj. Nur Hikmah, sebagai sumber kehangatan yang
selalu mendukungku,
Kakekku H.M. Syarif, sebagai sumber kekuatan doa di setiap
langkahku,
Nenekku Suwaibah dan Hj. Tarwiyah, sebagai sumber nasehat
di setiap langkahku,
Kakakku Lulu’ Aina’ul Mardhiyyah, S.Pd, dengan semua kedewasaan yang selalu menginspirasiku, dan
Adikku Nurul Lathifah dan Fika Nur Aini yang mengisi
vi
MOTTO
“... niscaya Allah akan meninggikan orang-orang yang beriman di antaramu dan orang-orang yang diberi ilmu pengetahuan beberapa derajat. Dan Allah
vii
PRAKATA
Puji syukur ke hadirat Tuhan Yang Maha Esa, sehingga penulis dapat
menyelesaikan skripsi dengan judul “Menentukan Aliran Maksimum dengan
Algoritma Ford-Fulkerson dan Preflow-Push” sebagai salah satu syarat untuk mencapai gelar kesarjanaan pada Jurusan Matematika, Fakultas Matematika dan
Ilmu Pengetahuan Alam, Universitas Negeri Semarang.
Penulisan skripsi ini tidak lepas dari dukungan, bantuan, dan bimbingan
berbagai pihak. Dalam kesempatan ini penulis mengucapkan terima kasih dan
penghargaan sebesar-besarnya kepada:
1. Prof. Dr. Fathur Rokhman, M.Hum., Rektor Universitas Negeri Semarang.
2. Prof. Dr. Wiyanto, M.Si., Dekan FMIPA Universitas Negeri Semarang.
3. Drs. Arief Agoestanto, M.Si., Ketua Jurusan Matematika FMIPA Universitas
Negeri Semarang.
4. Dr. Rochmad, M.Si., Dosen Penguji Utama yang telah memberikan arahan
dan saran kepada penulis selama penyusunan skripsi ini.
5. Dr. Mulyono, M.Si., dan Drs. Amin Suyitno, M.Pd., selaku Dosen
Pembimbing Utama dan Dosen Pembimbing Pendamping yang telah sabar
memberikan bimbingan selama penyusunan skripsi ini.
6. Seluruh Dosen Pengajar Jurusan Matematika FMIPA Unnes serta staf TU
viii
7. Bapak H. Sidqon dan Ibu Hj. Nur Hikmah, kedua orang tuaku yang telah
dengan sabar dan ikhlas mencurahkan waktu untuk mendidik, memberi kasih
sayang, menasihati, dan membimbing penulis.
8. Mbak Lulu’, Dek Lathifah, dan Dek Fika, yang selalu mendukung dan membantu dalam penulisan skripsi ini.
9. Teman-temanku PP. Assabiila, Khoir, Imus, Zumi, Rina, Umi, Aini, Tami,
dkk., yang telah menemaniku selama empat tahun dalam suka maupun duka.
10. Teman seperjuanganku dalam menyelesaikan skripsi, Meely dan Mas Akbar.
11. Teman-temanku Prodi Matematika angkatan 2009, Meely, Firdha, Neni,
Zumi, Rista, Anggi, Sabrina, Indah, Julia, Noni, Tya, Bram, Putri, Arum,
Fresti, Tyas, Putut, Karisa, Devi, Fera, Rosita, Dian, Hanif, Maya, Bagus,
Ichsan, Chakim, Dinar, Aziz, St, Azizah dan Didik, yang telah memberikan
dukungannya hingga terselesaikannya skripsi ini.
12. Semua pihak yang telah membantu yang tidak dapat disebutkan satu persatu
sehingga skripsi ini dapat terselesaikan dengan baik.
Akhir kata penulis berharap semoga skripsi ini bermanfaat bagi para
pembaca dan dapat dipergunakan sebagai bahan referensi untuk
penelitian-penelitian lain di kemudian hari.
Semarang, Agustus 2013
ix
ABSTRAK
Ulya, Rif’ah. 2013. Menentukan Aliran Maksimum dengan Algoritma Ford-Fulkerson dan Preflow-Push. Skripsi, Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang. Pembimbing Utama Dr. Mulyono, M.Si dan Pembimbing Pendamping Drs. Amin Suyitno, M.Pd.
Kata Kunci: Algoritma Ford-Fulkerson, Algoritma Preflow-Push, dan Aliran Maksimum.
Pada sebuah jaringan dalam masalah aliran maksimum, selalu terdapat sebuah aliran yang nilainya sama dengan kapasitas pemutus minimum (minimal cut), yang dikenal dengan sebutan “Teorema Maximal Flow–Minimal Cut.” Dalam pencarian aliran maksimum, terdapat beberapa algoritma, algoritma yang digunakan dalam menyelesaikan masalah aliran maksimum secara umum menggunakan dua pendekatan dasar, yaitu pendekatan algoritma Aughmenting Path dan pendekatan algoritma Preflow-Push.
Permasalahan pada skripsi ini adalah bagaimana konsep aliran maksimum berdasarkan teorema Maximal Flow–Minimal Cut, bagaimana menentukan aliran maksimum dengan algoritma Ford-Fulkerson, dan bagaimana menentukan aliran maksimum dengan algoritma Preflow-Push dengan alat bantu software GIDEN. Metode penelitian yang digunakan adalah metode studi pustaka.
Pada skripsi ini dibahas tentang pembuktian teorema Maximal Flow– Minimal Cut, Algoritma Ford-Fulkerson dan Preflow-Push. Konsep aliran maksimum berdasarkan teorema Maximal Flow–Minimal Cut menjelaskan bahwa nilai aliran ∗ = ( , 1) dengan ( , 1) merupakan sebuah pemutus-( , ) minimum di , maka ∗ adalah aliran maksimum di yang nilainya sama dengan kapasitas pemutus-( , ) minimum di . Algoritma Ford-Fulkerson bekerja dengan mengkonstruksi aliran baru dengan nilai yang lebih besar dari aliran yang lama, dan menggunakan teknik pelabelan Routin, pencarian aliran baru akan berhenti ketika semua titik yang terlabel telah teramati dan titik tidak terlabel. Sedangkan algoritma Preflow-Push bekerja dengan operasi dasar push dan relabel, algoritma ini berhenti ketika tidak ada lagi titik yang aktif. Pada skripsi ini, Algoritma Ford-Fulkerson dihitung secara manual, sedangkan algoritma Preflow-Push menggunakan alat bantu yaitu software GIDEN. Dari contoh penggunaan aliran maksimum diperoleh aliran maksimum = pemutus-( , )
x
DAFTAR ISI
Halaman
PRAKATA ... vii
ABSTRAK ... ix
DAFTAR ISI ... x
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xv
BAB 1. PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Rumusan Masalah ... 3
1.3 Pembatasan Masalah ... 3
1.4 Tujuan Penelitian ... 4
1.5 Manfaat Penelitian ... 4
1.6 Sistematika Penulisan Skripsi ... 5
2. TINJAUAN PUSTAKA 2.1 Pengertian Graf ... 7
2.1.1 Incident dan Adjacent ... 8
2.1.2 Loop ... 9
2.2 Graf Bagian (Subgraf) ... 9
2.3 Jalan, Jejak, Lintasan, Sirkuit dan Siklus ... 10
2.4 Graf Terhubung dan Graf Berbobot ... 11
2.4.1 Graf Terhubung (Connected) ... 11
2.4.2 Graf Berbobot ... 12
2.5 Graf Berarah dan Derajat Titik pada Graf Berarah ... 12
2.5.1 Graf Berarah (Directed Graph) ... 12
2.5.2 Derajat Titik pada Graf Berarah ... 14
2.6 Jaringan (Network) ... 14
xi
2.8 Busur Maju dan Busur Balik ... 17
2.9 Inkremen dan Lintasan Peningkatan ... 18
2.10 Aliran Maksimum ... 19
2.11Preflow ... 20
2.12 Excess, Kapasitas Sisa, Jaringan Sisa, dan Titik Aktif ... 20
2.12.1 Excess ... 20
2.12.2 Kapasitas Sisa dan Jaringan Sisa ... 21
2.12.3 Titik Aktif ... 21
2.13 Pelabelan Jarak (Distance Label) ... 22
2.14 Aliran Jenuh dan Tak Jenuh ... 22
2.15Software GIDEN ... 23
3. METODE PENELITIAN 3.1 Menemukan Masalah ... 26
3.2 Merumuskan Masalah ... 26
3.3 Studi Pustaka ... 27
3.4 Analisis dan Pemecahan Masalah ... 27
3.5 Penarikan Kesimpulan ... 28
4. HASIL DAN PEMBAHASAN 4.1 Konsep Aliran pada Jaringan ... 29
4.2 Konsep Aliran Maksimum pada Jaringan ... 34
4.3 Algoritma Ford-Fulkerson ... 40
4.4 Algoritma Preflow-Push ... 42
4.5 Algoritma Preflow-Push dengan Software GIDEN ... 44
4.6 Contoh Penggunaan Aliran Maksimum ... 47
4.6.1 Penyelesaian dengan Algoritma Ford-Fulkerson ... 48
4.6.2 Penyelesaian dengan Algoritma Preflow-Push pada Software GIDEN ... 66
5 PENUTUP 5.1 Simpulan ... 68
5.2 Saran ... 70
xii
xiii
DAFTAR GAMBAR
Gambar Halaman
2.1 Graf dengan lima titik dan enam sisi ... 8
2.2 Graf graf bagian dari Graf ... 10
2.3 Graf ... 11
2.4 graf terhubung ... 11
2.5 graf berbobot ... 12
2.6 (a) Graf berarah terhubung lemah ... 13
(b) Graf berarah terhubung kuat ... 13
(b) Graf dasar ... 13
2.7 Jaringan dengan titik sumber dan titik tujuan ……… 14
2.8 Jaringan dengan dua titik antara 1 dan 2 ... 16
2.9 Jaringan dengan titik sumber dan titik tujuan ... 17
2.10 Lintasan peningkatan terhadap aliran ... 18
2.11 Software GIDEN ... 23
2.12 Tampilan menu utama pada software GIDEN ... 23
2.13 Tampilan untuk menggambar titik ... 24
2.14 Tampilan untuk menggambar garis ... 24
2.15 Tampilan graf yang sudah diberi nama pada titik dan bobot pada sisi ... 25
2.16 Tampilan menu dalam solvers ... 25
4.1 Jaringan dengan aliran bernilai 5 ... 30
4.2 Jaringan dengan aliran 1bernilai 6……….31
4.3 Jaringan dengan aliran bernilai 5 ... 33
4.4 Ilustrasi aliran pada busur maju dan busur balik ... 36
4.5 Jaringan dengan aliran bernilai 9 ... 39
4.6 Tampilan cara menggunakan algoritma Preflow-Push ... 45
4.7 Tampilan input data algoritma Preflow-Push ... 45
4.8 Tampilan untuk proses iterasi algoritma Preflow-Push ... 46
xiv
4.10 Kapasitas aliran air (liter per menit) ... 47
4.11 Jaringan dengan titik sumber dan titik tujuan ………48
4.12 Jaringan dengan 0= 0……….. 48
4.13 Pelabelan titik pada jaringan ………50
4.14 Jaringan dengan 1= 150 ... 51
4.15 Pelabelan titik pada jaringan ... 53
4.16 Jaringan dengan 2= 350 ... 54
4.17 Pelabelan titik pada jaringan ... 56
4.18 Jaringan dengan 3= 450 ... 57
4.19 Pelabelan titik pada jaringan ... 59
4.20 Jaringan dengan 4= 550 ... 60
4.21 Pelabelan titik pada jaringan ... 62
4.22 Jaringan dengan 5= 600 ... 63
4.23 Jaringan dengan aliran maksimum = pemutus-( , ) minimum ... 65
xv
DAFTAR LAMPIRAN
Lampiran Halaman
1. Pencarian himpunan pemutus-( , ) pada contoh penggunaan aliran
maksimum ... 73
1
BAB I
PENDAHULUAN
1.1
Latar Belakang
Teori graf merupakan topik yang banyak mendapat perhatian, karena
model-modelnya sangat berguna untuk aplikasi yang luas, seperti masalah dalam
jaringan komunikasi, transportasi, ilmu komputer, dan lain sebagainya. Secara
umum, graf merupakan suatu diagram yang memuat informasi tertentu jika
diinterpretasikan secara tepat. Dalam kehidupan sehari-hari, graf digunakan untuk
menggambarkan berbagai macam struktur yang ada. Tujuannya adalah sebagai
visualisasi objek-objek agar lebih mudah dimengerti. Beberapa contoh graf yang
sering dijumpai dalam kehidupan sehari-hari antara lain: struktur organisasi,
bagan alir pengambilan mata kuliah, peta, rangkaian listrik, dan lain-lain (Siang,
2004: 185).
Jaringan merupakan salah satu kajian dalam teori graf. Jaringan adalah
kumpulan titik dan sisi yang saling terhubung dengan arah tertentu. Di dalam
jaringan terdapat beberapa model yang bisa digunakan untuk membantu
memecahkan masalah-masalah, diantaranya adalah model rentang jaringan
minimum, model rute terpendek, dan model aliran maksimum.
Model aliran maksimum mempunyai tujuan untuk memaksimalkan jumlah
aliran yang melewati jaringan dalam sebuah sistem jaringan. Pada model masalah
pun. Sebaliknya, pada model masalah aliran maksimum, aliran tersebut tidak
membangkitkan biaya tetapi mempunyai batas kapasitas tertentu.
Pada sebuah jaringan dalam masalah aliran maksimum, selalu terdapat
sebuah aliran yang nilainya sama dengan kapasitas pemutus minimum (minimal
cut), yang dikenal dengan sebutan “Teorema Maximal Flow–Minimal Cut” (Budayasa, 2007: 235). Teorema Maximal Flow-Minimal Cut menjamin bahwa
aliran maksimum pada sebuah jaringan tidak akan melebihi kapasitas pemutus
minimum dalam jaringan tersebut. Dalam pencarian aliran maksimum, terdapat
beberapa algoritma, menurut Ahuja et al. (1993: 166-167), algoritma yang
digunakan dalam menyelesaikan masalah aliran maksimum secara umum
menggunakan dua pendekatan dasar, yaitu pendekatan algoritma Aughmenting
Path dan pendekatan algoritma Preflow-Push.
Algoritma yang menggunakan pendekatan Aughmenting Path diantaranya
adalah algoritma Ford-Fulkerson. Algoritma Ford-Fulkerson ditemukan oleh Ford
dan Fulkerson pada tahun 1956. Algoritma ini akan efektif bagi penggunanya
untuk melakukan suatu proses, tindakan atau pengambilan keputusan untuk tujuan
tertentu dengan mengetahui aliran maksimum yang terdapat dalam suatu jaringan.
Hal yang paling rapi dari algoritma Ford-Fulkerson adalah bahwa algoritma ini
selalu memberikan hasil yang benar dalam menyelesaikan sub-masalah dalam
mencari Augmenting Path dalam setiap iterasinya. Pada skripsi ini, algoritma
Preflow-Push digunakan hanya sebatas untuk mencocokkan hasil perhitungan
manual dari algoritma Ford-Fulkerson. Dalam hal ini, algoritma Preflow-Push
atas penulis tertarik untuk membahas skripsi dengan judul “Menentukan Aliran Maksimum dengan algoritma Ford-Fulkerson dan Preflow-Push.”
1.2
Rumusan Masalah
Dari latar belakang di atas, diperoleh rumusan masalah yang timbul dalam
penyusunan skripsi ini adalah sebagai berikut.
1. Bagaimana konsep aliran maksimum berdasarkan teorema Maximal
Flow-Minimal Cut?
2. Bagaimana menentukan aliran maksimum dengan algoritma
Ford-Fulkerson?
3. Bagaimana menentukan aliran maksimum dengan algoritma Preflow-Push
dengan bantuan software GIDEN?
1.3
Pembatasan Masalah
Dalam penyusunan skripsi ini, pembatasan permasalahan yang akan
dibahas adalah sebagai berikut.
1. Konsep aliran maksimum berdasarkan teorema Maximal Flow-Minimal
Cut meliputi definisi-definisi teorema, serta bukti-bukti yang terkait
dengan materi tersebut.
2. Algoritma Ford-Fulkerson dan Preflow-Push digunakan dalam skripsi ini
hanya untuk menentukan aliran maksimum, tidak membahas kompleksitas
kedua algoritma tersebut.
3. Algoritma Ford-Fulkerson akan dihitung secara manual dengan teknik
4. Algoritma Preflow-Push digunakan hanya sebatas untuk mencocokkan
hasil perhitungan manual dari algoritma Ford-Fulkerson. Dalam hal ini,
algoritma Preflow-Push akan dijalankan dengan alat bantu yaitu software
GIDEN.
5. Contoh penggunaan aliran maksimum yang digunakan adalah simulasi.
1.4
Tujuan Penelitian
Tujuan dari penelitian ini adalah sebagai berikut.
(1) Mengetahui konsep aliran maksimum berdasarkan teorema Maximal Flow-
Minimal Cut.
(2) Mengetahui cara menentukan aliran maksimum dengan algoritma
Ford-Fulkerson.
(3) Mengetahui cara menentukan aliran maksimum dengan menggunakan
algoritma Preflow-Push dengan alat bantu software GIDEN.
1.5
Manfaat Penelitian
Manfaat yang diharapkan dari penyusunan skripsi ini adalah sebagai
berikut.
1. Bagi peneliti
Dapat mengetahui tentang konsep teorema Maximal Flow-Minimal Cut,
mengetahui cara menentukan aliran maksimum dengan algoritma
Ford-Fulkersondan algoritma Preflow-Push.
2. Bagi mahasiswa
Membantu mahasiswa mempelajari konsep teorema Maximal Flow-Minimal
memotivasi mahasiswa untuk melanjutkan penelitian lebih mendalam
sehingga dapat menerapkannya dalam kehidupan nyata.
1.6
Sistematika Penulisan Skripsi
Dalam penulisan skripsi ini secara garis besar dibagi menjadi tiga bagian
pokok, yaitu bagian awal, bagian isi, dan bagian akhir.
1.6.1 Bagian Awal
Bagian awal skripsi memuat halaman sampul, halaman judul, pernyataan
keaslian tulisan, halaman pengesahan, motto, prakata, abstrak, daftar isi, dan
daftar gambar.
1.6.2 Bagian Isi
Bagian isi terdiri dari lima bab yaitu sebagai berikut.
(1) Bab I: Pendahuluan
Dikemukakan tentang latar belakang, rumusan masalah, pembatasan
masalah, tujuan, manfaat penelitian, dan sistematika penulisan.
(2) Bab II: Tinjauan Pustaka
Berisi uraian teoritis atau teori-teori yang mendasari pemecahan tentang
masalah-masalah yang berhubungan dengan judul skripsi.
(3) Bab III: Metode Penelitian
Berisi metode-metode yang digunakan dalam penelitian, meliputi studi
pustaka, analisis dan pemecahan masalah, dan penarikan kesimpulan.
(4) Bab IV: Hasil dan Pembahasan
(5) Bab V: Penutup
Berisi simpulan dan saran.
1.6.3 Bagian Akhir
Bagian akhir skripsi berisi tentang daftar pustaka dan lampiran-lampiran
7
BAB II
TINJAUAN PUSTAKA
2.1
Pengertian Graf
Definisi 2.1
Sebuah graf = ( , ) berisikan dua himpunan yaitu himpunan
berhingga tak kosong ( ) dari obyek-obyek yang disebut titik, dan himpunan
berhingga (mungkin kosong) ( ) yang elemen-elemennya disebut sisi,
sedemikian hingga setiap elemen dalam ( ) merupakan pasangan tak
berurutan dari titik-titik di ( ). Himpunan ( ) disebut himpunan titik-titik ,
dan himpunan ( ) disebut himpunan sisi-sisi (Budayasa, 2007: 1-2).
Cara mempresentasikan sebuah graf yang paling umum adalah dengan
diagram. Dalam diagram tersebut, titik-titik dinyatakan sebagai noktah dan tiap
sisi dinyatakan sebagai kurva sederhana yang menghubungkan tiap dua titik.
Misalnya, graf dengan = { 1, 2, 3, 4, 5} dan
= { 1, 2, 3, 4, 5, 6} dimana 1 = ( 1, 2), 2= ( 2, 3), 3 = ( 3, 5),
4= ( 1, 4), 5= ( 1, 4), 6= ( 5, 5), dapat dipresentasikan dalam bentuk
1
2
3 4
1
2
4 3
5
Gambar 2.1.Graf G dengan lima titik dan enam sisi. 6 5
Contoh 2.1:
2.1.1 Incident dan Adjacent Definisi 2.2
Jika sebuah titik merupakan titik ujung dari suatu sisi , maka dan
disebut saling berinsidensi atau titik terkait (incident) dengan sisi .
Sebagai contoh, pada Contoh 2.1 di atas, sisi 1, 4, dan 5 adalah sisi-sisi yang
terkait dengan titik 1. Dua sisi yang tidak paralel disebut bertetangga (adjacent),
bila kedua sisi tersebut terkait dengan titik yang sama. Sebagai contoh, 1 dan 2
dalam Contoh 2.1 merupakan dua sisi yang bertetangga. Selain itu, dua buah titik
disebut bertetangga jika kedua titik tersebut merupakan titik-titik ujung dari sisi
yang sama. Dalam Contoh 2.1 3 dan 5 adalah dua titik yang saling bertetangga,
sedangkan titik 2 dan 4 merupakan dua titik yang tidak saling bertetangga
2.1.2 Loop Definisi 2.3
Dalam sebuah graf, seperti terlihat pada Contoh 2.1, dimungkinkan adanya
suatu sisi yang dikaitkan dengan pasangan 5, 5 . Sisi yang dua titik ujungnya
sama disebut loop (gelang). Pada Contoh 2.1, sisi 6 merupakan sebuah loop.
Dalam sebuah graf dimungkinkan adanya lebih dari satu sisi yang dikaitkan
dengan sepasang titik. Pada contoh 2.1, sisi 4 dan sisi 5 dikaitkan dengan
pasangan titik 1, 4 . Pasangan sisi semacam ini disebut sisi-sisi paralel/sejajar
atau sisi rangkap. Sebuah graf yang tidak memiliki loop dan tidak memiliki sisi
rangkap disebut graf sederhana(Sutarno et al., 2003: 59).
2.2
Graf Bagian (Subgraf)
Definisi 2.4
graf dengan himpunan titik dan himpunan sisi . Sebuah graf
dengan himpunan titik dan himpunan sisi , disebut graf bagian
(subgraf) dari graf , dinotasikan ⊆ , jika ⊆ dan ⊆ .
Karena konsep graf bagian dapat dianalogikan dengan konsep himpunan bagian
dalam teori himpunan, maka sebuah graf bagian dapat dipandang sebagai bagian
dari graf yang lain.
Sifat-sifat dari graf bagian adalah sebagai berikut.
1. Setiap graf merupakan graf bagian dari dirinya sendiri.
2. Graf bagian dari suatu graf bagian merupakan graf bagian dari .
Sebuah sisi dari bersamaan dengan kedua titik ujungnya juga merupakan
graf bagian dari (Sutarno et al., 2003: 87).
Contoh 2.2:
G H
Gambar 2.2. Graf H graf bagian dari Graf G.
2.3
Jalan, Jejak, Lintasan, Sirkuit, dan Siklus
Definisi 2.4
Misalkan G adalah sebuah graf. Sebuah jalan (walk) di G adalah sebuah
barisan berhingga (tak kosong) = 0, 1, 1, 2, 2,…, , yang suku-sukunya
bergantian titik dan sisi, sedemikian hingga −1 dan adalah titik-titik akhir sisi
, untuk 1 (Budayasa, 2007: 6). Misalkan adalah sebuah jalan dari 0
ke , atau jalan 0, . Titik 0 dan berturut-turut disebut titik awal dan titik
akhir . Sedangkan titik-titik 1, 2,…, −1 disebut titik-titik internal dari ,
dan disebut panjang dari . Perhatikan bahwa panjang dari jalan adalah
banyaknya sisi dalam . Jika semua sisi 1, 2, 3…, dalam jalan berbeda,
maka disebut jejak (trail). Jika semua titik 0, 1, 2,…, dalam jalan juga
berbeda, maka disebut sebuah lintasan (path). Sebuah jalan disebut tertutup,
jika titik awal dan titik akhir dari identik (sama). Jejak tertutup disebut sirkuit.
Sirkuit yang titik awal dan titik internalnya berlainan disebut siklus. Siklus dengan
titik dinotasikan dengan (Sutarno et al., 2003: 65).
2 1
1
3
1 2
4 1
2
Contoh 2.3:
Jalan: a 6 f 7 b 2 c 3 d 3 c
Jalan tertutup : a 1 b 2 c 10 g 12 d 12 g 9 f 6 a Jejak : a 1 b 2 c 10 g 11 e 4 d 3 c
Jejak tertutup (sirkuit) : a 6 f 5 e 4 d 12 g 8 b 1 a Lintasan: a 1 b 2 c 10 g 9 f 5 e 4 d
Siklus : a 6 f 5 e 4 d 12 g 8 b 1 a.
2.4
Graf Terhubung dan Graf Berbobot
2.4.1 Graf Terhubung (Connected) Definisi 2.5
Sebuah graf G dikatakan terhubung (connected) jika untuk setiap dua titik
G yang berbeda terdapat sebuah lintasan yang menghubungkan kedua titik
tersebut (Budayasa, 2007: 8).
Contoh 2.4:
Gambar 2.4. G graf terhubung.
1 2 3 4 5 a b g c d e f 1 3 2 4 5 6 7 8 9 10 11 12
2.4.2 Graf Berbobot Definisi 2.6
Graf berbobot adalah graf yang setiap sisinya diberi sebuah harga (bobot).
Bobot pada tiap sisi dapat menyatakan jarak antara dua buah kota, waktu tempuh
antara dua buah kota, biaya perjalanan yang ditempuh, dan sebagainya (Sutarno et
al., 2003: 107).
Contoh 2.5:
2.5
Graf Berarah dan Derajat Titik pada Graf Berarah
2.5.1 Graf Berarah (Directed Graph) Definisi 2.7
Sebuah graf berarah = ( ,Γ ) adalah suatu pasangan berurutan
dari dua himpunan yaitu himpunan berhingga tak kosong yang
anggota-anggotanya disebut titik, dan Γ( ) yaitu himpunan berhingga (boleh kosong)
yang anggota-anggotanya disebut busur sedemikian hingga setiap busur
merupakan pasangan berurutan dari dua titik di . Jika 1 dan 2 adalah dua
titik pada graf berarah dan = ( 1, 2) sebuah busur , maka e disebut busur
keluar dari titik 1 dan e busur menuju 2 (Budayasa, 2007: 214). dikatakan
graf berarah sederhana jika semua busur dari berbeda dan tidak terdapat loop
(Setiawati, 1993).
B
A 12
15
10
8
14
9 11
Gambar 2.5. G graf berbobot.
C
1 2
3 4
1 2
3 4
1
3
2
4 Definisi 2.8
Misalkan sebuah graf berarah. Graf dasar dari graf adalah graf tak
berarah , sedemikian hingga = ( ) dan setiap busur ( , ) di
menjadi sisi( , ) pada (Budayasa, 2007: 215). Konsep jalan, jejak, lintasan,
sirkuit, dan siklus pada graf berarah serupa dengan konsep jalan, jejak, lintasan,
sirkuit, dan siklus pada graf tak berarah, hanya saja istilah sisi pada graf tak
berarah diganti dengan istilah busur pada graf berarah.
Ada dua macam keterhubungan pada graf berarah , yaitu terhubung
lemah dan terhubung kuat. Graf berarah dikatakan terhubung lemah jika graf
dasarnya terhubung, sedangkan dikatakan terhubung kuat jika untuk setiap dua
titik dan di D terdapat lintasan berarah dari ke dan sebaliknya
(Budayasa, 2007: 216).
Contoh 2.6:
D H G
Gambar 2.6 (a) Gambar 2.6 (b) Gambar 2.6 (c)
Pada Gambar 2.6 (a) adalah graf berarah terhubung lemah. Sebaliknya,
pada Gambar 2.6 (b) adalah graf berarah terhubung kuat. Pada Gambar 2.6 (c)
1
2
3
4
2
5
6
2.5.2 Derajat Titik pada Graf Berarah
Definisi 2.9
Misalkan sebuah graf berarah, dan ( ). Derajat keluar titik (out
degree ) dilambangkan ( ) adalah banyaknya busur pada graf berarah yang
keluar dati titik . Sedangkan derajat masuk titik (in degree ) dilambangkan
( ) adalah banyaknya busur yang menuju ke titik (Budayasa, 2007: 216).
2.6 Jaringan
(Network)
Definisi 2.10
Sebuah jaringan = ( ,Γ ) adalah sebuah graf berarah sederhana
terhubung lemah yang setiap busurnya dikaitkan dengan bilangan real non negatif.
Selanjutnya bilangan real non negatif yang dikaitkan pada busur ( , ), atau
disingkat ( , ), pada jaringan disebut kapasitas busur ( , ), dan
dilambangkan dengan ( , ) atau disingkat ( , ). Sebuah titik di jaringan
disebut titik sumber jika = 0 dan sebuah titik di jaringan disebut titik
tujuan jika = 0, sedangkan titik yang lain di jaringan N disebut titik-titik
antara (Budayasa, 2007: 227-228).
Contoh 2.7:
Definisi 2.11
Misalkan sebuah jaringan dengan titik sumber dan titik tujuan . Jika
adalah sebuah titik di , maka himpunan semua busur yang keluar dari titik
(meninggalkan titik ) dilambangkan dengan ( ) dan himpunan semua busur
yang menuju ke titik , dilambangkan ( ) (Budayasa, 2007: 229-230).
Perhatikan Gambar 2.7, terdapat dua busur di yang keluar dari titik ,
diperoleh = { , 1 , , 2 } dan = . Perhatikan titik 1,
diperoleh 1 = { 1, 2 , 1, } dan 1 = ( , 1) dan seterusnya.
2.7 Pemutus pada Jaringan
Definisi 2.12
Misalkan sebuah jaringan dengan titik sumber dan titik tujuan .
Misalkan adalah himpunan bagian tak kosong dari ( ) dan 1= − .
Jika dan 1, maka himpunan busur ( , 1) disebut sebuah
pemutus-( , ) dari jaringan . Disebut demikian, karena penghapusan semua busur
( , 1) dari , memutus semua lintasan berarah dari titik ke titik pada
jaringan . Misalkan adalah himpunan titik antara pada jaringan , dan ’
adalah sebuah himpunan bagian . Jika = { }∪ ′, maka ( , 1) sebuah
pemutus-( , ) pada . Jadi banyaknya pemutus-( , ) pada jaringan sama
dengan banyaknya himpunan bagian dari himpunan , yaitu 2 dengan =
1
2 3
4
5
6 2
[image:31.595.184.420.134.237.2]Contoh 2.8:
Gambar 2.8. Jaringan dengan dua titik antara 1 dan 2.
Pada Gambar 2.8 di atas, mempunyai dua titik antara 1 dan 2, sehingga
terdapat 22 = 4 pemutus-( , ) pada , yaitu:
, 1, 2, = , 1 , , 2
, 2 , 1, = , 1 , 2,
, 1 , 2, = , 2 , 1, 2 , 1,
, 1, 2 , = 1, , 2, .
Setiap pemutus-( , ) pada jaringan mempunyai kapasitas.
Pemutus-( , ) yang mempunyai kapasitas terkecil disebut pemutus-( , ) minimum.
Masing-masing kapasitas dari keempat pemutus tersebut adalah:
, 1, 2, = ( , ,1 + , 2 = 3 + 4 = 7
, 2 , 1, = , 1 + 2, = 3 + 6 = 9
, 1 , 2, = ( , 2 + 1, 2 + 1, = 4 + 2 + 5 = 11
, 1, 2 , = 1, + 2, = 5 + 6 = 11
Tampak bahwa , 1, 2, = { , 1 , , 2 } dengan kapasitas
2.8
Busur Maju dan Busur Balik
Definisi 2.13
Misalkan sebuah jaringan dan adalah graf dasar . Misalkan pada
graf terdapat lintasan = ( 1, 2, 3,…, , +1,…, ). Jika ( , +1) sebuah
busur pada , maka busur tersebut dinamakan busur maju terhadap , sebaliknya
jika ( +1, ) sebuah busur pada , maka busur tersebut dinamakan busur balik
terhadap . Jadi, suatu busur pada termasuk busur maju atau busur balik, sangat
tergantung pada lintasan pada graf dasarnya.
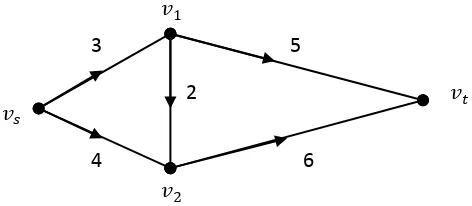
[image:32.595.168.438.349.471.2]Contoh 2.9:
Gambar 2.9. Jaringan dengan titik sumber dan titik tujuan .
Misalkan graf dasar dari jaringan pada Gambar 2.9, maka =
( , 2, 1, 3, 4, ) adalah sebuah lintasan ( , ) pada dan bukan lintasan
berarah pada . Sehingga, terhadap , busur-busur ( , 2), ( 1, 3), dan ( 4, )
merupakan busur-busur maju, sedangkan busur-busur ( 1, 2) dan ( 4, 3) adalah
busur-busur balik. Jika diperhatikan lintasan 1= , 1, 2, 4, pada , maka
semua busur yang berkorespondensi dengan sisi lintasan 1 merupakan busur
maju terhadap 1. Perhatikan bahwa busur ( 1, 2) pada merupakan busur balik
terhadap lintasan , tetapi busur tersebut merupakan busur maju terhadap lintasan
1.
_
1
2
3
4 8
3 4 5
2
3 3 4
2 4
2.9
Inkremen dan Lintasan Peningkatan
Definisi 2.14
Misalkan adalah sebuah aliran dari titik sumber ke titik tujuan pada
jaringan , dan misalkan adalah graf dasar , maka terdapat lintasan pada .
( ) adalah inkremen lintasan , didefinisikan sebagai berikut. ( ) =
min adalah busur yang bersesuaian dengan sisi .
Dengan adalah inkremen pada busur , didefinisikan sebagai berikut:
= − , jika busur maju , jika busur balik
Sebuah lintasan dengan > 0 disebut lintasan augmentasi.
Selanjutnya, lintasan augmentasi dari titik sumber ke titik tujuan dinamakan
sebuah lintasan peningkatan (Budayasa, 2007: 235-236).
Contoh 2.10:
Gambar 2.10. Lintasan peningkatan terhadap aliran .
Pada Gambar 2.10 di atas, dipunyai lintasan = ( , 2, 1, 3, 4, ).
Karena ( , 2), 1, 3 , ( 4, ) busur-busur maju dan 1, 2 , ( 4, 3)
busur-busur balik, maka:
( , 2) = ( , 2)− ( , 2) = 6−2 = 4,
1, 3 = 1, 3 − 1, 3 = 5−2 = 3,
1 3
8;4
3;1 4;1 5;2
2;1
3;2 3;1 4;3
4, = 4, − 4, = 3−1 = 2,
1, 2 = 1, 2 = 1, dan 4, 3 = 4, 3 = 1.
Sehingga = min 4,3,2,1,1 = 1. Karena > 0, maka =
( , 2, 1, 3, 4, ) adalah sebuah lintasan peningkatan.
2.10
Aliran Maksimum
Definisi 2.15
Sebuah aliran di jaringan dari titik sumber ke titik tujuan adalah
suatu fungsi yang memetakan setiap busur ( , ) di dengan sebuah bilangan
bulat non negatif yang memenuhi syarat-syarat sebagai berikut.
A flow in a network from the source s to sink t is a function f which assigns a non-negative integer to each of the arcs a in N such that
(1)(capacity constraint) ( ) ( ) for each arc ,
(2)the total flow into the sink t equals the total flow out of thr source s, and (3)(flow conservation) for any intermediate vertex x, the total flow into x
equals the total flow out of x (Clark & Holton, 1995: 262) .
Misalkan ( , ) adalah kapasitas busur ( , ). Aliran dalam jaringan pada
setiap busur ( , ) adalah bilangan bulat non negatif ( , ) sedemikian sehingga
(1) 0 , , ,∀ , �Γ , disebut kapasitas pembatas,
(2) ( , )� ( ) , = ( , )�( ) ( , ), disebut nilai aliran ,
(3) ( , )� ( ) , = ( , )�( ) , ,∀ � − , ,disebut
konservasi aliran.
Definisi 2.16
Jika terdapat sebuah aliran di yang nilainya sama dengan kapasitas
suatu pemutus-( , ), maka aliran tersebut adalah aliran maksimum dan
bernilai , dari titik sumber ke titik tujuan pada jaringan dikatakan aliran
maksimum jika,
, = min , 1 , 1 suatu pemutus− , pada jaringan (Budayasa, 2007: 234).
2.11
Preflow
Definisi 2.17
Given a transport network = ( , ) with vertices and edges, a pseudo-flow is an assignment of nonnegative real numbers to the edges of such that ( , ) ( , ) for ( , ) . A pseudo-flow is a preflow if , − ( , ) 0 for every ≠ , (Thulasiraman & Swamy, 1992: 411).
Definisi di atas mengatakan bahwa jaringan transportasi = ( , )
dengan titik dan busur, sebuah aliran-semu (pseudo-flow) merupakan
sebuah pengaitan bilangan real non negatif pada busur-busur di yang memenuhi
( , ) , dengan ( , ) . Sebuah aliran-semu dikatakan preflow jika
memenuhi , − ( , ) 0 untuk setiap ≠ , , dengan ,
adalah , ( ) , , dan , adalah , ( ) , , untuk setiap
( )−{ , }.
2.12
Excess
, Kapasitas Sisa, Jaringan Sisa, dan Titik Aktif
2.12.1 Excess Definisi 2.18
Dari definisi di atas, misalkan aliran pada jaringan = ( , ) dan
. Excess pada titik didefinisikan sebagai = , − , ,
∀ ≠ , .
2.12.2 Kapasitas Sisa dan Jaringan Sisa Definisi 2.19
Given a preflow f, let = ( , ) denote the residual network with respect to . Recall that each edge ( , ) induces an edge ( , ) , if ( , ) < ( , ), and edge ( , ) if , > 0. Edges of are all called residual edges. In the former case ( , ) is called a forward edge and in the latter case ( , ) is a backward edge. ( )
will denote the capacity of the residual edge e:
( ) = − ,
( ),
(Thulasiraman & Swamy, 1992: 411-412).
Dari definisi di atas, diberikan suatu preflow , maka jaringan =
( , ) merupakan jaringan sisa terhadap preflow . Setiap busur ( , )
membangun sebuah busur ( , ) jika ( , ) < ( , ), dan membangun
sebuah busur ( , ) jika , > 0. Busur-busur pada jaringan disebut
busur sisa. Pada kasus ini ( , ) dinamakan busur maju, dan sebaliknya
( , ) dinamakan busur balik. ( ) dikatakan kapasitas busur sisa dengan
nilai ( ) = − , jika busur maju ( ), jika busur balik.
Untuk selanjutnya dalam tulisan ini, kapasitas dari busur sisa disebut kapasitas
sisa busur .
2.12.3 Titik Aktif
Definisi 2.20
Dari definisi di atas, misalkan aliran pada jaringan = ( , ) dan
. Suatu titik dikatakan titik aktif jika > 0 dimana ≠ , .
2.13
Pelabelan Jarak
(Distance Label)
Definisi 2.21
A valid labeling of is an assignment of nonnegative integers to the vertices of such that = , = 0 and for every residual edge
( , ), + 1. It can be shown that if < , then ( ) is a lower bound on the distance from to in , and if ( ) , then
− is a lower bound on the distance from to in (Thulasiraman & Swamy, 1992: 412).
Definisi di atas mengatakan bahwa suatu pelabelan valid pada titik
(dilambangkan ( )) pada jaringan = ( , ), dengan titik dan busur,
adalah pemetaan bilangan bulat non negatif ke suatu titik di sedemikian
sehingga label pada titik sumber adalah = , label pada titik tujuan
adalah = 0, dan + 1 untuk setiap busur sisa ( , ). Dapat
ditunjukkan bahwa jika < , maka ( ) batas bawah pada jarak dari titik
ke titik tujuan pada jaringan sisa . Sebaliknya jika ( ) , maka −
batas bawah jarak dari titik ke titik sumber pada jaringan sisa .
2.14
Aliran Jenuh dan Tak Jenuh
Definisi 2.22
A push from to is a saturating push if , = 0 after the push, otherwise it is a nonsaturating push (Thulasiraman & Swamy, 1992: 412).
Dari definisi di atas, misalkan adalah aliran pada jaringan . Sebuah
selainnya. Artinya, dikatakan jenuh jika , = ( , ), dan tak jenuh jika
, < ( , ).
2.15
Software
GIDEN
Software GIDEN merupakan suatu software yang terorientasi untuk
menyelesaikan masalah-masalah optimasi jaringan. Software GIDEN digunakan
untuk memudahkan menemukan solusi yang tepat dalam menyelesaikan
masalah-masalah dalam jaringan yang melibatkan titik dan sisi dengan jumlah yang sangat
banyak. Masalah-masalah yang dapat diselesaikan dengan software GIDEN antara
lain: minimum spanning tree, shortest path, maximum flow, dan minimum-cost
flow. Langkah-langkah penggunaan software GIDEN adalah sebagai berikut.
Gambar 2.11. Software GIDEN.
[image:38.595.165.444.386.522.2]Klik file, kemudian pilih new, diperoleh gambar sebagai berikut.
Pilih new node untuk menggambar titik.
Gambar 2.13. Tampilan untuk menggambar titik.
Pilih new edge untuk menggambar sisi.
Gambar 2.14. Tampilan untuk menggambar garis.
Untuk memberi nama pada titik, klik node data, pilih add data field.
Misalkan beri nama “titik”, beri nilai awal “0”, kemudian ganti tipe data field
dengan text, kemudian klik OK. Sedangkan untuk memberi nilai pada sisi (bobot),
klik edge data, pilih add data field. Beri nama field “bobot”, beri nilai awal “0”, ganti tipe data field dengan integer, kemudian klik OK. Pilih edit value dan beri
nama pada masing-masing titik, kemudian beri nilai pada masing-masing sisi,
[image:39.595.156.463.336.488.2]Gambar 2.15. Tampilan graf yang sudah diberi nama pada titik dan bobot pada
sisi.
Klik solvers. Terlihat ada beberapa masalah yang dapat diselesaikan
dengan software GIDEN, diantaranya minimum spanning tree, shortest path,
[image:40.595.129.471.106.276.2]maximum flow, dan minimum cost flow.
Gambar 2.16. Tampilan menu dalam solvers.
Pilih menu dalam solvers sesuai dengan permasalahan yang diinginkan.
Dalam waktu yang singkat software ini akan menghasilkan solusi yang tepat
[image:40.595.124.499.426.606.2]26
BAB III
METODE PENELITIAN
Pada penelitian ini metode atau langkah-langkah yang digunakan adalah
sebagai berikut.
3.1
Menemukan Masalah
Dalam tahap ini dicari sumber pustaka dan dipilih bagian dari sumber
pustaka sebagai suatu masalah. Penulis mencari berbagai macam sumber pustaka
yang berhubungan dengan aliran maksimum serta algoritma-algoritma untuk
menyelesaikan masalah aliran maksimum, kemudian menyeleksi untuk ditetapkan
sebagai suatu masalah yang harus diselesaikan.
3.2 Merumuskan Masalah
Masalah yang ditemukan kemudian dirumuskan kedalam pertanyaan
yang harus diselesaikan yaitu:
(1) Bagaimana konsep aliran maksimum berdasarkan teorema Maximal
Flow-Minimal Cut?
(2) Bagaimana menentukan aliran maksimum dengan algoritma
Ford-Fulkerson?
(3) Bagaimana menentukan aliran maksimum dengan algoritma Preflow-Push
3.3
Studi Pustaka
Mengenai studi pustaka dilakukan untuk mengumpulkan informasi yang
diperlukan dalam penelitian ini terutama yang mengkaji jaringan, aliran
maksimum, algoritma Ford-Fulkerson, algoritma Preflow-Push, dan software
GIDEN. Mengumpulkan konsep pendukung yang diperlukan dalam
menyelesaikan masalah sehingga didapatkan suatu ide mengenai bahan dasar
pengembangan upaya pemecahan masalah. Studi pustaka diawali dengan
mengumpulkan sumber pustaka yang berupa buku-buku referensi yang mengkaji
teori graf dan software GIDEN. Selain itu sumber pustaka juga dapat diperoleh
secara online misalnya dengan cara mencarinya di situs www.google.com dengan
menggunakan kata kunci jaringan, aliran maksimum, algoritma Ford-Fulkerson,
algoritma Preflow-Push, dan software GIDEN.
3.4
Analisis dan Pemecahan Masalah
Dari berbagai sumber pustaka yang sudah menjadi bahan kajian, diperoleh
suatu pemecahan masalah di atas. Selanjutnya dilakukan langkah-langkah
pemecahan masalah sebagai berikut.
1. Mendeskripsikan konsep aliran pada jaringan.
2. Mendeskripsikan konsep aliran maksimum pada jaringan berdasarkan
teorema Maximal Flow-Minimal Cut.
3. Mendeskripsikan cara menentukan aliran maksimum dengan algoritma
Ford-Fulkerson yang didasari dengan pembuktian lemma dan teorema Maximal
4. Mendeskripsikan cara menentukan aliran maksimum dengan algoritma
Preflow-Push yang didasari operasi dasar push dan relabel.
5. Mendeskripsikan langkah-langkah menentukan aliran maksimum dengan
algoritma Preflow-Push menggunakan software GIDEN.
6. Menerapkan algoritma Ford-Fulkerson dan Preflow-Push dalam menentukan
aliran maksimum pada contoh simulasi tentang aliran air dalam suatu motel
dengan asumsi-asumsi tertentu.
7. Mencocokkan hasil perhitungan aliran maksimum dari algoritma
Ford-Fulkerson dan Preflow-Push dengan bantuan software GIDEN.
3.5
Penarikan Kesimpulan
Tahap ini merupakan tahap terakhir dalam metode penelitian. Penarikan
kesimpulan dari permasalahan diperoleh dari hasil langkah pemecahan masalah
29
BAB IV
HASIL DAN PEMBAHASAN
4.1 Konsep Aliran pada Jaringan
Sebuah aliran di jaringan = ( ,Γ ) dari titik sumber ke titik
tujuan adalah suatu fungsi yang memetakan setiap busur ( , ) di N dengan
sebuah bilangan bulat non negatif yang memenuhi syarat-syarat sebagai berikut.
(1) 0 , , ∀ , �Γ( )(disebut “kapasitas pembatas”).
Menyatakan bahwa nilai aliran pada setiap busur tidak pernah melebihi
kapasitas busur tersebut.
(2) ( , )� ( ) , = ( , )�( ) ( , )(disebut “nilai aliran f”).
Menyatakan bahwa total nilai aliran yang keluar dari titik sumber sama
dengan total nilai aliran yang sampai di titik tujuan. Nilai ini yang selanjutnya
disebut “nilai aliran ” dari s ke t pada jaringan .
(3) ( , )� ( ) , = ( , )�( ) , ,∀ � − , (disebut “konservasi
aliran”).
Menyatakan bahwa untuk setiap titik antara pada berlaku total aliran yang
meninggalkan titik x sama dengan total aliran yang menuju titik .
Jika nilai aliran dari titik sumber ke titik tujuan pada jaringan
,, jika = ...(4)
f(i,V) - f(V,i) = 0, jika ≠ , ...(5)
− , , jika = ...(6)
Keterangan persamaan di atas adalah sebagai berikut.
Persamaan (4): aliran yang keluar dari adalah , , aliran yang masuk ke titik
tujuan adalah ,.
Persamaan (5): aliran yang keluar dari titik antara (selain dan ) adalah nol.
Persamaan (6): aliran yang keluar dari titik adalah − , .
Contoh 4.1:
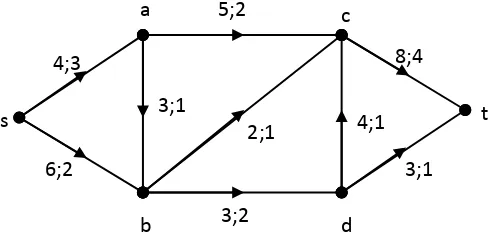
[image:45.595.168.417.411.527.2]Diberikan aliran dengan dari ke dengan nilai 5 pada graf di bawah ini.
Gambar 4.1. Jaringan dengan aliran bernilai 5.
Keterangan:
, = 4; , = 3 , = 3; , = 2
, = 6; , = 2 , = 4; , = 1
, = 3; , = 1 , = 8; , = 4
( , ) = 5; , = 2 , = 3; , = 1
, = 2; , = 1
s
a
b
c
d
t 8;4
3;1 4;1 5;2
2;1
3;2 3;1 4;3
Perhatikan Gambar 4.1 dengan aliran bernilai 5.
Jika = { , } dan 1= { , , , },
, 1 = , , , , , = { , , , , , } adalah pemutus-( , ) pada
dengan kapasitas , 1 = , + , + , = 6 + 3 + 5 = 14,
maka , 1 = , + , + , = 2 + 1 + 2 = 5.
Terlihat bahwa , 1 , 1 .
Contoh 4.2:
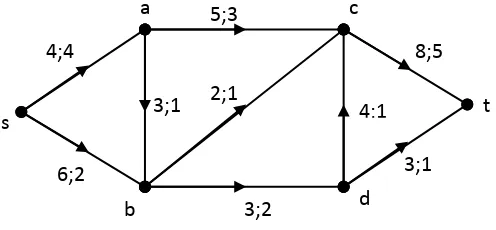
[image:46.595.155.403.335.450.2]Tingkatkan aliran f menjadi 1 dari s ke t dengan nilai 6, sehingga:
Gambar 4.2. Jaringan dengan aliran 1 bernilai 6.
Keterangan:
, = 4; , = 4 , = 3; , = 2
, = 6; , = 2 , = 4; , = 1
, = 3; , = 1 , = 8; , = 5
, = 5; , = 3 , = 3; , = 1
, = 2; , = 1
Perhatikan Gambar 4.1 dengan aliran 1 bernilai 6.
Jika = { , } dan 1= { , , , },
, 1 = , , , , , = { , , , , , } adalah pemutus-( , ) pada
maka , 1 = , + , + , = 2 + 1 + 3 = 6.
Terlihat bahwa , 1 , 1 .
Dari Contoh 4.1 dan 4.2 terlihat bahwa nilai aliran tidak melebihi kapasitas
pemutus-( , ), yaitu , 1 . Ternyata ini berlaku untuk sebarang aliran dan
sebarang pemutus di .
Teorema 4.1
Misalkan sebuah jaringan dengan titik sumber dan titik tujuan . Jika f adalah
sebuah aliran dari ke pada dengan nilai , dan ( , 1) sebuah
pemutus-( , ) pada , maka , = , 1 − ( 1, ) ( , 1) (Budayasa, 2007: 233).
Bukti:
Dari definisi aliran, untuk titik sumber diperoleh , − , = , ,
dan untuk setiap titik � − , diperoleh
, = ( , )� ( ) , = ( , )� ( ) , = ( , )
atau , − , = 0.
Sehingga untuk suatu pemutus- , , , 1 diperoleh
, − , = ( , − ( ,
= , − , + 0 = , ...(1)
sementara itu, , − , = , ∪ 1 − ∪ 1,
= , + , 1 − , + 1,
= , 1 − 1, ...(2)
karena nilai aliran pada setiap busur tidak negatif, maka 1, 0, sehingga
Selanjutnya, karena nilai aliran pada setiap busur N tidak melebihi kapasitas
busur, maka , 1 , 1 ...(4)
dari (1), (2), (3), (4) disimpulkan,
, = , 1 − 1, , 1 , 1
Dengan demikian bukti teorema lengkap.
Contoh 4.3:
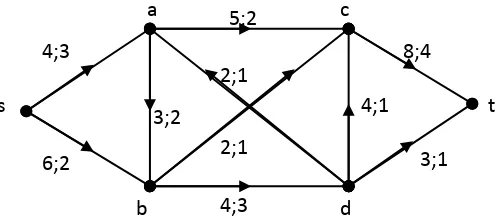
[image:48.595.163.414.307.415.2]Diberikan graf sebagai berikut
Gambar 4.3. Jaringan dengan aliran bernilai 5.
(a) Jika = { , } dan 1 = { , , , }, , 1 adalah pemutus ( , ) sehingga
, 1 = , + , + , = 2 + 2 + 2 = 6
1, = , = 1
, = , 1 − 1, = 6−1 = 5
dengan kapasitas , 1 = , + , + , = 6 + 3 + 5 = 14
terlihat bahwa , 1 − 1, , 1 , 1 . s
a
b
c
d
t 4;3
6;2
3;2
5;2 2;1
2;1 4;3
4;1 8;4
(b) Jika = { , , } dan 1 = { , , }, , 1 adalah pemutus ( , ) sehingga
, 1 = , + , + , = 2 + 1 + 3 = 6
1, = , = 1
, = , 1 − 1, = 6−1 = 5
dengan kapasitas , 1 = , + , + , = 5 + 2 + 4 = 11
terlihat bahwa , 1 − 1, , 1 , 1 .
Dari Contoh 4.3, menunjukkan bahwa aliran , dari ke akan sama
meskipun melalui pemutus-( , ) yang berbeda. Dalam hal ini, nilai aliran , dari
ke sama dengan 5 melalui dua pemutus- , , yaitu , , { , , , } dan
, , , { , , } . Terlihat bahwa , = , 1 − 1, , 1
, 1 .
4.2 Konsep Aliran Maksimum pada Jaringan
Definisi 4.1
Misalkan adalah sebuah aliran dari titik sumber ke titik tujuan pada
jaringan , dan misalkan adalah graf dasar , maka terdapat lintasan pada .
( ) adalah inkremen lintasan peningkatan , menurut Clark & Holton (1995:
268), didefinisikan sebagai berikut,
= min adalah busur yang bersesuaian dengan sisi
di mana adalah inkremen pada busur , didefinisikan sebagai berikut,
sebuah lintasan dengan = 0 dikatakan jenuh (f saturated), sedangkan
lintasan dengan > 0 dikatakan tak jenuh (f unsaturated) disebut lintasan
augmentasi. Selanjutnya, lintasan augmentasi dari titik sumber ke titik tujuan
dinamakan sebuah lintasan peningkatan.
Lemma 4.2
Misalkan sebuah aliran bernilai , dari titik sumber ke titik tujuan pada
jaringan . Jika terdapat lintasan dari titik ke titik dengan = > 0,
definisikan fungsi 1 pada himpunan Γ( ) sebagai berikut:
1 = + , jika busur maju terhadap ,
1 = − jika busur balik terhadap ,
1 = , jika busur yang lainnya. Maka 1 adalah aliran dari titik ke titik pada N dengan nilai , + (Budayasa, 2007: 236).
Bukti:
Berdasarkan definisi = > 0, dan = min{ }, maka ( ) positif.
Oleh sebab = − jika busur maju , dan = jika busur
balik terhadap , berakibat:
1 =
+ = ( )
− = 0
Jelas 0 1 ( ).
Karena positif, maka adalah lintasan augmentasi. Selanjutnya, lintasan
augmentasi dari titik sumber ke titik tujuan dinamakan sebuah lintasan
peningkatan dimana aliran pada busur yang melewati titik-titik pada lintasan
+
−
+ +
+
− −
−
konservasi aliran, maka aliran pada busur yang terkait dengan titik-titik antara
(titik selain dan ) perlu dicek.
Misalkan, dipunyai titik (titik antara) pada lintasan peningkatan , maka dua
busur yang terkait dengan titik diilustrasikan sebagai berikut.
Gambar 4.4. Ilustrasi aliran pada busur maju dan busur balik.
Dari ilustrasi di atas, aliran yang masuk ataupun keluar dari titik tidak berubah,
dengan demikian memenuhi sifat konservasi aliran sebagai berikut:
=
( )� ( ) ( )�( ) ,∀ � − , .
Akan ditunjukkan lintasan peningkatan yang alirannya ditingkatkan oleh .
Lintasan peningkatan ini dimulai dari titik sumber , misalkan busur 1 adalah
busur yang terkait dengan titik sumber pada lintasan peningkatan . Sehingga,
1 1 = 1 + , jika 1 busur maju terhadap ,
1 1 = 1 − , jika 1 busur balik terhadap ,
1 1 = 1 , jika busur 1 bukan busur yang terdapat pada lintasan .
Dari definisi aliran untuk titik sumber , pada persamaan (4) sebagai berikut
, − , = , , diperoleh 1 −0 = , artinya 1 = , .
Sehingga diperoleh nilai 1= ( ) 1 − ( ) 1
= 1 1 −0
= 1 + (syarat positif)
= , + .
x
x x
Teorema 4.3 (Teorema Maximal Flow-Minimal Cut)
Misalkan sebuah jaringan dengan titik sumber dan titik tujuan . Maka
terdapat sebuah aliran maksimum pada (Budayasa, 2007: 238-239).
Bukti:
Misalkan sebuah aliran dengan nilai dari ke pada jaringan .
Definisikan himpunan sebagai berikut:
sedemikian hingga = atau ada lintasan ( , ) pada graf dasar yang
inkremennya positif. Maka ada dua kemungkinan letak titik , yaitu � atau
� 1 = − .
Jika � , berdasarkan definisi , terdapat lintasan dari titik ke titik dengan
= > 0. Sehingga berdasarkan lemma 4.2, aliran dapat direvisi menjadi
aliran 1, sedemikian hingga 1 = + jika busur maju pada ,
1 = − jika busur balik pada , 1 = jika busur yang tidak terletak pada . Aliran 1 bernilai + > (karena > 0). Jadi 1 adalah
aliran dari ke di yang nilainya lebih besar dari nilai aliran . Dikatakan,
aliran 1 adalah revisi aliran . Selanjutnya menggunakan aliran 1 pada , cari
himpunan seperti sebelumnya. Jika titik tujuan menjadi anggota , maka
berdasarkan definisi , terdapat lintasan 1 dari ke dengan 1 = 1 > 0.
Berdasarkan lemma 4.2, bentuk aliran 2 dari 1 sedemikian hingga: 2 =
1 + 1 jika busur maju pada 1, 2 = 1 − 1 jika a busur balik pada
1, dan 2 = 1 untuk busur yang lainnya. Aliran 2 bernilai + + 1,
aliran 1 didasarkan atas lintasan peningkatan 1. Proses merevisi aliran seperti
itu dapat dilanjutkan sampai diperoleh suatu aliran, katakan aliran ∗, sedemikian
hingga terhadap aliran ∗ pada , himpunan tidak memuat titik , atau .
Ini berarti, tidak ada lagi lintasan pada graf dari ke yang inkremennya
positif. Selanjutnya, akan ditunjukkan ∗ adalah aliran maksimum pada . Untuk
itu cukup ditunjukkan bahwa nilai aliran ∗ sama dengan kapasitas sebuah
pemutus-( , ) pada .
Klaim 1. Jika � , � 1 = − , dan , �Γ( ), maka ∗ , = ( , ).
Andaikan ∗ , < ( , ). Karena , busur maju, maka , > 0.
Selanjutnya, karena � , maka ada lintasan ′ dari ke dengan ′ > 0 dan
karena , > 0, maka ada lintasan dari ke lewat yang inkremennya
positif. Berdasarkan definisi , maka � kontradiksi dengan .
Klaim 2. Jika � , � 1 = − , dan , �Γ( ), maka ∗ , = 0.
Andaikan ∗ , > 0. Karena , busur balik maka , = ∗ , > 0.
Seperti sebelumnya, karena � , maka ada lintasan ′ dari ke dengan ′ >
0 dan karena , > 0, maka pada graf dasar ada lintasan dari ke lewat
yang inkremennya positif. Berdasarkan definisi , maka � kontradiksi bahwa
titik terletak di dalam 1= − .
Berdasarkan klaim 1 dan klaim 2, secara berturut-turut diperoleh
∗ , 1 = ( ,
1) dan ∗ 1, = 0.
Berdasarkan teorema 4.1
Nilai aliran ∗= ∗ , 1 − ∗ 1,
Karena ( , 1) sebuah pemutus-( , ) pada dan nilai ∗= , 1 , maka ∗
adalah aliran maksimum di dan ( , 1) adalah sebuah pemutus-( , )
minimum pada jaringan .
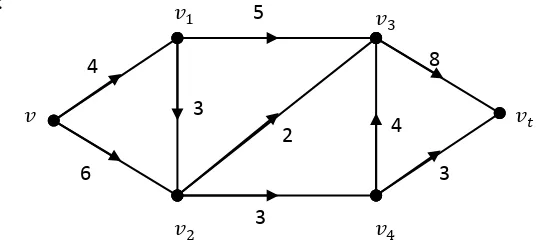
Contoh 4.4:
[image:54.595.177.428.237.354.2]Diberikan graf N sebagai berikut.
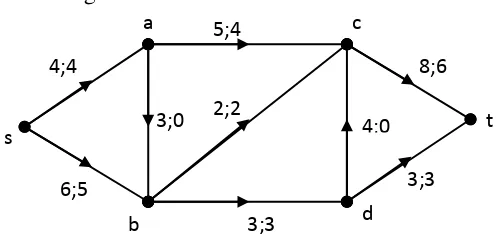
Gambar 4.5. Jaringan dengan aliran bernilai 9.
Graf adalah jaringan dengan aliran bernilai 9 dengan pemutus-( , )
minimum, yaitu , 1 = , , , , , = { , , , , , }
, 1 = , + , + ( , )
= 4 + 2 + 3 = 9
, 1 = , + , + ( , ) = 4 + 2 + 3 = 9.
Menurut teorema Maximal Flow-Minimal Cut aliran maksimum dari ke
dalam sama dengan kapasitas pemutus-( , ) minimum. Dari contoh 4.4,
diperoleh , 1 = , 1 atau = , 1 = 9, terlihat bahwa semua
busur dalam himpunan , 1 adalah jenuh karena , 1 = , 1 . 4;4
a
b
c
d
t s
6;5
3;0 5;4
2;2
3;3
4;0 8;6
4.3 Algoritma Ford-Fulkerson
Secara garis besar, prosedur algoritma Ford-Fulkerson sudah tersirat dalam
bukti teorema 4.3 dan prosedur untuk mengkonstruksi aliran baru yang nilainya
lebih besar dari nilai aliran lama sudah tersirat dalam lemma 4.2. Namun
prosedur untuk mendapatkan lintasan peningkatan tidak tersirat dalam lemma
maupun bukti teorema sebelumnya. Untuk mendapatkan lintasan yang
demikian, akan digunakan teknik pelabelan titik, yang pada prinsipnya melabel
titik-titik dengan teknik tertentu dimulai dari titik , kemudian dilanjutkan
melabel titik yang lain. Jika dengan teknik tersebut bisa melabel titik , maka
dengan teknik “prosedur balik” lintasan ditemukan. Tetapi sebaliknya, jika titik
tidak bisa dilabel, maka tidak ada lintasan seperti itu pada . Secara sistematis
algoritmanya adalah sebagai berikut.
Langkah 1: misalkan sebuah aliran dari ke pada . (Boleh dimulai dengan
aliran bernilai nol, yaitu , = 0,∀ ( , )�Γ(N). Dilanjutkan ke
Routin-Pelabelan.
Langkah 2: Routin-Pelabelan
2.1 Label = ( , +, = ~). Titik telah terlabel dan belum
teramati. Sebuah titik dikatakan telah teramati jika semua titik
yang dapat dilabel dari titik sudah terlabel.
2.2 Pilih sebarang titik yang terlabel tetapi belum teramati, misalkan
titik tersebut . Untuk ∀ ∃( , ) Γ(N), belum berlabel dan
, > 0, maka label = ( ,−, ) dengan =
teramati. Untuk ∀ ∃( , ) Γ(N), belum berlabel dan
, > ( , ), maka label = ( , +, ) dengan =
min , , − ( , ) . Sekarang titik terlabel tetapi
belum teramati, sedangkan titik telah terlabel dan teramati.
2.3 Ulangi langkah 2.2 sampai:
(1) titik terlabel, atau;
(2) semua titik terlabel telah teramati tetapi titik tak terlabel;
(3) jika titik terlabel, lanjut ke langkah 3;
(4) jika semua titik terlabel telah teramati tetapi titik tak
terlabel, maka BERHENTI. Aliran adalah aliran maksimum
pada jaringan .
Langkah 3: dengan prosedur “balik”, temukan lintasan peningkatan dengan
i(P) adalah label .
Langkah 4: tingkatkan nilai aliran sebesar label , berdasarkan lintasan
peningkatan dengan menggunakan “Routine-Peningkatan”: 4.1 Misal: = lanjutkan ke langkah 4.2.
4.2 Jika label = ( , +, ) tingkatkan nilai ( , ) dengan
= ( ). Jika label = ( ,−, ) turunkan nilai ( , )
dengan = ( ).
4.3 Jika = , hapus semua label. Pada tahap ini diperoleh aliran
baru dengan nilai = i(P) + nilai aliran lama. Ganti aliran dengan
aliran yang baru, dan kembali ke langkah 1 (Budayasa, 2007:
4.4 Algoritma
Preflow-Push
Algoritma Preflow-Push dapat mencari nilai aliran maksimum dengan
aliran-semu (pseudo-flow) f pada jaringan. Misalkan, jaringan = ( , ) dengan
titik dan busur, sebuah aliran-semu (pseudo-flow) f merupakan sebuah
pengaitan bilangan real non negatif pada busur-busur di yang memenuhi
, , ∀ , .
Sebuah aliran-semu (pseudo-flow) f dikatakan sebuah preflow, jika
memenuhi , − , 0 ∀ ≠ , , dengan , adalah
,
, ( ) , dan , adalah , ( ) , . Dengan = , − , merupakan excess pada titik . Jelas sebuah preflow f
adalah aliran jika = 0 untuk setiap ≠ , (Thulasiraman & Swamy, 1992:
411).
Misalkan = ( , ) dengan preflow f. Maka = ( , ) dikatakan
jaringan sisa terhadap preflow jika setiap busur ( , ) membangun sebuah
busur ( , ) jika ( , ) < ( , ), dan membangun sebuah busur ( , )
jika , > 0. Busur-busur pada jaringan sisa disebut busur sisa. Pada
kasus ini ( , ) dinamakan busur maju, dan sebaliknya ( , )
dinamakan busur balik. ( ) dikatakan kapasitas busur sisa jika,
= − , jika busur maju
, jika busur balik.
Suatu pelabelan valid pada = ( , ) adalah pemetaan bilangan bulat
+ 1 untuk setiap busur sisa ( , ). Sebuah titik disebut titik aktif
jika ≠ , , dan > 0 (Thulasiraman, 1992: 412).
Algoritma Preflow-Push dimulai dengan preflow f yang nilainya sama
dengan kapasitas busur untuk setiap busur yang meninggalkan titik sumber dan
bernilai nol untuk yang lainnya. Selanjutnya inisialisasi label dengan pelabelan
valid = , = 0, dan + 1 untuk setiap busur sisa ( , ).
Algoritma Preflow-Push secara berulang-ulang menggunakan dua operasi dasar,
yaitu Push dan Relabel yang bekerja sebagai berikut.
Push ( , )
Applicability. is active, ( , ) and = + 1. Action. Set = { , , } and do the following.
1. Increase ( , ) by if , is a forward edge, otherwise decrease
( , ) by .
2. Decrease ( ) by and increase ( ) by .
(Note: > 0 because both ( ) and ( , ) are positive). Relabel ( )
Applicability. is active, and for every , , ( ) ( ). Action. Set = ( , ) { + 1}(Thulasiraman, 1992: 412).
Misalkan titik (bukan titik sumber maupun titik tujuan) yang aktif
( > 0), maka pilih titik tersebut dan lakukan push dan relabel secara berulang
sebagai berikut.
Langkah 1: jika ada busur ( , ) yang admissible = + 1 , maka
lakukan push = min{ , , }
(1) tingkatkan aliran ( , ) sebesar jika ( , ) busur maju, dan
penurunan aliran ( , ) sebesar jika ( , ) busur balik,
(2) turunkan ( ) sebesar dan tingkatkan ( ) sebesar , dengan
Langkah 2: jika tidak ada busur ( , ) yang admissible ( ) ( ), maka
lakukan relabel, dengan mengganti ( ) dengan label jarak sebesar
= min{ + 1}.
Lakukan push dan relabel secara berulang sehingga tidak ada lagi titik yang aktif.
Pendorongan preflow f dari ke meningkatkan aliran ( , ) dan ( )
dengan peningkatan sebesar = min{ , , }, dan penurunan ( , ) dan
( ) dengan nilai yang sama. Setelah dilakukan pendorongan preflow f dari
ke , jika , = 0dikatakan jenuh (f saturated), selainnya dikatakan tak
jenuh (f unsaturated). Algoritma Preflow-Push akan berhenti ketika tidak ada lagi
titik aktif.
4.5 Algoritma
Preflow-Push
dengan
Software
GIDEN
Untuk mempermudah menyelesaikan masalah aliran maksimum dengan
algoritma Preflow-Push, maka akan digunakan alat bantu yaitu software GIDEN.
Menurut Coullard et al. (2003: 48-49), pelabelan busur pada software GIDEN
yaitu ( , − ), di mana adalah preflow f dengan nilai awal nol ( = 0)
dan ( − ) merupakan kapasitas sisa busur yang biasa dilambangkan .
Software GIDEN ini mengimplementasikan aturan “highest label” pada pemilihan titik aktif. Menurut Ahuja et al. (1993: 230), cara bekerja algoritma
Preflow-Push dengan aturan “highest label” yaitu “this algorithm always pushes
from an active node with the highest value of the distance label”, menjelaskan bahwa algoritma ini bekerja dengan mendorong preflow dengan nilai label
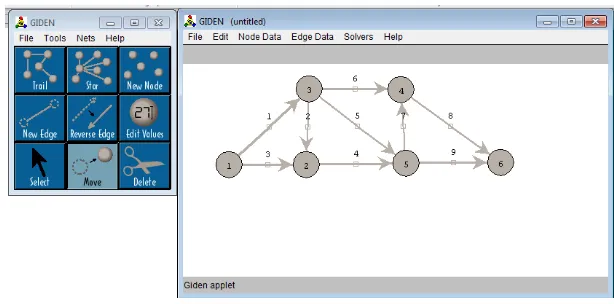
Langkah-langkah penggunaan software GIDEN seperti yang telah
dijelaskan pada bab sebelumnya. Untuk menyelesaikan masalah aliran maksimum
dengan algoritma Preflow-Push, klik solvers, pilih maximum flow, kemudian pilih
[image:60.595.163.464.216.412.2]Preflow-Push. Seperti pada gambar berikut.
Gambar 4.6. Tampilan cara menggunakan algoritma Preflow-Push.
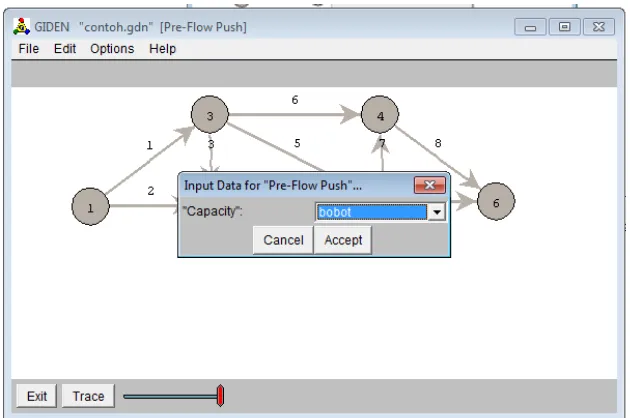
Kemudian akan muncul kotak pertanyaan, pilih “bobot”, klik accept.
[image:60.595.152.467.473.682.2]Kemudian klik trace, klik sink, klik source, kemudian enter “YES”. Klik trace berulang kali sampai iterasi berhenti dengan berubahnya trace menjadi
[image:61.595.177.479.183.381.2]reset.
Gambar 4.8. Tampilan untuk proses iterasi