Implementasi Minimal Cost Pada Network Flow Dengan Pendekatan Algoritma Out-Of-Kilter

IMPLEMENTASI MINIMAL COST PADA NETWORK FLOW

DENGAN PENDEKATAN ALGORITMA

OUT-OF-KILTER

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana

HEPPY SUHERI

041421010

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

ABSTRAK

IMPLEMENTATION OF MINIMUM COST AT NETWORK FLOW WITH

OUT-OF-KILTER ALGORITHM APPROACH

ABSTRACT

DAFTAR ISI

HALAMAN

Abstrak ... ii

Abstract ... iii

Daftar Isi ... iv

Daftar Tabel ... v

Daftar Gambar ... vi

Bab 1 Pendahuluan

1.1

Latar Belakang ... 1

1.2

Perumusan Masalah ... 2

1.3

Tujuan Penelitian ... 2

1.4

Metodologi Penelitian ... 3

1.5

Tujuan Pustaka ... 3

Bab 2 Landasan Teori

2.1 Konsep Dasar Graph ... 5

2.2 Graph Berlabel ... 6

2.3 Path Minimum ... 9

2.4 Representasi Graph Dalam Matriks ... 11

2.5 Shortest Path ... 13

2.6 Linear Programming ... 14

2.7 Flow ... 15

2.8 Minimal Cost Flow ... 16

Bab 3 Pembahasan

3.1 Out-Of-Kilter pada Permasalahan Minimal Cost dalam

Network Flow ... 18

3.1.1 Dual pada Aliran Jaringan ... 18

3.1.2 Kondisi-kondisi Complementary Slackness ... 19

3.1.3 Satus Kilter dan Bilangan Kilter pada Arc ... 20

3.2 Strategi Out-Of-Kilter ... 26

3.2.1 Tahap Permulaan(Initiation Phase) ... 26

3.2.2 Tahap Primal: Merubah Aliran ... 27

3.2.3 Tahap Dual ... 29

3.3 Contoh Algoritma Out-Of-Kilter ... 32

3.4 Prosedur Label pada Algoritma Out-Of-Kilter ... 34

3.4.1 Tahap Inisialisasi ... 34

3.4.2 Tahap Utama ... 34

Bab 4 Kesimpulan dan Saran

4.1 Kesimpulan ... 38

4.2 Saran ... 39

Daftar Pustaka ... 40

DAFTAR TABEL

DAFTAR GAMBAR

HALAMAN

Gambar 2.1 Graph dengan lima verteks dan enam edge ... 5

Gambar 2.2 Graph jaringan listrik di 8 kota ... 7

Gambar 2.3 Graph G dengan 7 verteks ... 9

Gambar 2.4 Graph dengan 6 verteks dan 10 edge ... 10

Gambar 2.5 Graph dengan 5 verteks dan 8 edge ... 12

Gambar 2.6 Shortest path ... 14

Gambar 2.7 Flow dalam network ... 16

Gambar 3.1a Network ... 20

Gambar 3.1b W

i

, z

ij

– c

ij

, x

ij

... 20

Gambar 3.2 Status kilter pada arc ... 22

Gambar 3.3 Bilangan kilter kij ...

25

Gambar 3.4 Network G’ buatan dari gambar 3.1 ... 28

Gambar 3.5 Perubahan pada network G pada tahap primal ... 29

Gambar 3.6 Flowchart Out-of-kilter ... 31

Gambar 3.7 Contoh Network ... 32

Gambar 3.8a Breakthrough dalam tahap primal pertama ... 32

Gambar 3.8b Nonbreakthrough dan tahap dual pertama ... 33

Gambar 3.8c Nonbreakthrough dan tahap dual ke dua ... 33

ABSTRAK

IMPLEMENTATION OF MINIMUM COST AT NETWORK FLOW WITH

OUT-OF-KILTER ALGORITHM APPROACH

ABSTRACT

BAB 1

PENDAHULUAN

1.1. Latar Belakang

Suatu aliran adalah suatu perjalanan objek dari satu tempat ke tempat lain dalam

jaringan kerja (network). Banyak masalah penting yang perlu diperhatikan pada aliran

dalam network. Sebagai contoh, bagaimana memaksimalkan jumlah materi yang

dikirim dari satu tempat ke tempat lain, menentukan cost yang minimal untuk

mengirimkan sejumlah objek dari sumber s ke tujuan t

Hampir semua masalah optimisasi, biasanya bertujuan bagaimana

memaksimalkan flow dan meminimalkan cost, di mana nilai yang diukur berupa cost,

jarak, waktu, atau parameter relevan lainnya. Secara umum suatu network dapat

dinotasikan dengan himpunan G = (N,A), di mana N adalah n titik(node) dan A adalah

m busur (arc).

Persoalan minimal cost flow merupakan permasalahan yang utama dalam

network flow. Bentuk persoalan ini adalah menentukan cost pengiriman yang minimal

pada sebuah komoditas melalui jaringan yang harus memenuhi node permintaan dan

node persediaan. Diberikan G = (N,A) sebagai network, setiap node i dalam network

G, misalkan jumlah b

i

adalah ketersediaan barang (b

i

> 0) atau permintaan barang (b

i

< 0). Node dengan b

i

> 0 sering disebut sources (sumber), dan node dengan b

i

< 0

sering disebut tujuan (sinks). Jika b

i

= 0, maka tidak ada barang yang tersedia pada

Asumsikan bahwa total penyediaan barang sama dengan total permintaan

di dalam network. Secara matematika dapat dituliskan sebagai berikut.

Minimumkan

∑∑

= =

m

i m

j ij ij

x

c

1 1

Kendala

∑ ∑

=

−

=

=

m

j

m

k ki

ij

x

x

1 1

b

i

i = 1, 2, ...,m

x

ij

≥ 0

i,j = 1, 2, …,m

Melihat masalah-masalah tersebut banyak dikembangkan metode-metode

untuk memecahkan permasalahan distribusi aliran dalam network. Misalnya dengan

metode simpleks, augmenting path, out-of-kilter dan sebagainya. Dalam hal ini,

penulis akan meninjau algoritma out-of-kilter serta prosedur-prosedurnya untuk

menyelesaikan persoalan minimal cost dalam distribusi aliran. Pemilihan algoritma

out-of-kilter karena dapat dipergunakan untuk menyelesaikan beberapa persoalan

jaringan berkapasitas, yaitu persoalan transportasi, persoalan penugasan, persoalan

ongkos minimum/aliran maksimum, dan persoalan transshipment.

1.2. Perumusan Masalah

Permasalahan dalam tulisan ini adalah bagaimana algoritma out-of-kilter dapat

menyelesaikan permasalahan distribusi aliran dalam network khususnya dalam

mencari minimal cost.

1.3. Tujuan Penelitian

Tujuan dalam penelitian ini adalah untuk mendapatkan nilai minimal cost dari sumber

s sampai ke tujuan t pada suatu distribusi aliran dengan menggunakan algoritma

1.4. Metodologi Penelitian

Tulisan ini merupakan hasil studi literatur pada teori-teori network. Langkah-langkah

yang akan dilakukan adalah:

1.

Menguraikan tentang aliran serta minimal cost pada suatu network.

2.

Menjelaskan penggunaan algoritma out-of-kilter dalam mencari minimal cost.

3.

Menerapkan pada suatu program.

1.5. Tinjauan Pustaka

Untuk mewujudkan maksud dan tujuan dari penelitian ini, penulis memanfaatkan

buku-buku yang dipergunakan sebagai referensi salah satunya:

Bazaara, Mokhtar S. dan John J. Jarvis [3, bab 10] dalam bukunya “Linear

Programming and Network Flows”,memuat tentang, penyelesaian program integer

seperti program linier, dengan rumus seperti di bawah ini:

Minimumkan

∑∑

= =

m

i m

j ij ij

x

c

1 1

Kendala

∑ ∑

=

−

=

=

m

j

m

k ki

ij

x

x

1 1

0

i = 1, 2, …,m

x

ij

≥

l

ij

i,j = 1, 2, …,m

x

ij

≤

u

ij

i,j = 1, 2, …,m

Kekekalan aliran yang memenuhi pada batasan tetap l

ij

≤

x

ij

≤

u

ij

adalah feasible

flow(Aliran yang layak). Asumsikan c

ij

, l

ij

, dan u

ij

integer dan 0

≤

l

ij

≤

u

ij

.

(Jean-Marie PLA. 1971, hal.279) menyatakan karakteristik pemecahan

masalah optimal dalam network flow yang paling sederhana adalah memperkenalkan

masalah dual dan kondisi complementary slackness.

Dalam menyelesaikan persoalan network dengan algoritma out-of-kilter

digunakan asumsi bahwa setiap arc berarah dalam network jaringan mempunyai

kapasitas tertentu, atau mempunyai batas bawah dan batas atas bagi alirannya. Dalam

pemakaian algoritma out-of-kilter, ada 2 (dua) langkah penting yang diperlukan

untuk memformulasikan masalah yaitu:

1. permasalahan diformulasikan dalam bentuk network berkapasitas dengan

loop tertutup.

2. inisialisasi harga variabel dual

π

i

dan sejumlah aliran X

ij

sehingga pembatas

konservasi aliran terpenuhi.

BAB 2

LANDASAN TEORI

2.1. Konsep Dasar Graph

Sebelum sampai pada pendefinisian masalah network flow, terlebih dahulu pada

bagian ini akan diuraikan mengenai konsep-konsep dasar dari model graph dan

representasinya dalam memodelkan masalah network flow.

Definisi 2.1. Sebuah graph G adalah pasangan (V,E) di mana V adalah himpunan tak

kosong yang anggotanya disebut verteks dan E adalah himpunan yang anggotanya

adalah pasangan tak berurut dari verteks V yang disebut edge.

Secara umum graph dapat digambarkan dengan suatu diagram di mana verteks

ditunjukkan sebagai titik yang dinotasikan dengan v

i

, i = 1, 2, …,P dan edge

digambarkan dengan sebuah garis lurus atau garis lengkung yang menghubungkan dua

verteks (v

i

, v

j

) dan dinotasikan dengan e

k

. Sebagai ilustrasi dapat dilihat Gambar 2.1.

yaitu suatu graph yang mempunyai lima verteks dan enam edge.

Gambar 2.1. Graph dengan lima verteks dan enam edge

V

1

V2

e4

V4

V

5

V3

e

2

e

5

e3

e6

2.2.

Graph Berlabel

Hubungan antar verteks-verteks dalam graph perlu diperjelas. Hubungan tidak cukup

hanya menunjukkan verteks-verteks mana yang berhubungan langsung, tetapi juga

seberapa kuat hubungan itu. Sebagai contoh, andaikata suatu graph menyatakan “peta”

suatu daerah. Verteks-verteks graph menyatakan kota-kota yang ada di daerah

tersebut. Edge-edge dalam graph menyatakan jalan yang menghubungkan kota-kota

tersebut.

Informasi tentang peta daerah perlu diperjelas dengan mencantumkan jarak

antara 2 kota yang berhubungan. Informasi tentang jarak dibutuhkan karena dalam

graph, letak verteks dan panjang edgenya tidak menyatakan jarak 2 kota yang

sebenarnya seperti halnya dengan peta yang sebenarnya. Jadi setiap garis dalam graph

berhubungan dengan suatu label yang menyatakan bobot garis tersebut.

Definisi 2.2. Graph Berlabel (weighted graph) adalah suatu graph tanpa edge paralel

di mana setiap edgenya berhubungan dengan suatu bilangan riil tak negatif yang

menyatakan bobot edge (w(e)) tersebut. Jumlah bobot semua edge disebut Total

Bobot.

Matriks yang bersesuaian dengan graph berlabel G adalah matriks hubung

A = (aij) dengan a

ij = bobot edge yang menghubungkan verteks vi

dengan verteks vj.

Jika verteks vi

tidak berhubungan langsung dengan verteks vj, maka aij

= ∞, dan

aij = 0 di mana i = j.

Contoh 2.1.

Edge

Kota yang dihubungkan

Biaya per satuan

e

4

e7

e

2

e

8

e

9

e

1

e

3

e

10

e5

e

11

e6

v

2

– v

3

v4 – v6

v

1

– v

7

v

3

– v

4

v

3

– v

5

v

1

– v

2

v

1

– v

4

v

6

– v

8

v7 – v8

v

5

– v

6

v6 – v7

3

4

5

5

5

15

15

15

15

15

18

a.

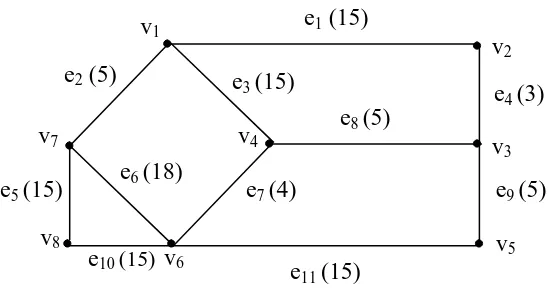
Graph berlabel untuk menyatakan jaringan listrik di 8 kota dapat digambarkan

pada Gambar 2.2. di bawah ini. Angka dalam kurung menyatakan bobot edge yang

bersangkutan. Bobot tersebut menyatakan biaya pengadaan jaringan listrik.

Gambar 2.2.Graph Jaringan listrik di 8 kota

v

1

v

4

v6

v8

v

7

v2

v

3

v

5

e

2

(5)

e3 (15)

e5 (15)

e

6

(18)

e7 (4)

e8 (5)

e9 (5)

e4 (3)

e1 (15)

e

10

(15)

b.

Matriks hubung untuk menyatakan graph berlabel pada Gambar 2.2. adalah

matriks A = (a

ij

) dengan a

ij

=

Jarak verteks vi dengan vj

di mana ada edge yang menghubungkan

verteks vi

dengan vj

∞

di mana tidak ada edge yang menghubungkan

verteks vi dengan vj

0

di mana i = j

v1

v2

v3

v4

v5

v6

v7

v8

v1

0

15

∞

15

∞

∞

∞

∞

v2

15

0

3

∞

∞

∞

∞

∞

v

3

∞

3

0

5

5

∞

∞

∞

A =

v4

15

∞

5

0

∞

4

∞

∞

v

5

∞

∞

5

∞

0

15

∞

∞

v

6

∞

∞

∞

4

15

0

18

15

v

7

5

∞

∞

∞

∞

18

0

15

v

8

∞

∞

∞

∞

∞

15

15

0

Misalkan G adalah sebuah graph berarah. Sebuah edge berarah e = [u,v]

dikatakan mulai pada verteks awal u dan berahkhir di verteks akhir v, u dan v

dikatakan adjacent.

Definisi 2.3. Derajat luar dari v, (outdeg (v)) adalah jumlah edge yang berawal pada v,

dan derajat dalam dari v (indeg (v)) adalah jumlah edge yang berakhir di v.

Jika setiap edge mulai dan berakhir pada suatu verteks, maka jumlah derajat-dalam

dan jumlah derajat-luar harus sama dengan n, yaitu jumlah edge pada G.

Definisi 2.4. Sebuah verteks v di G disebut sumber (source) bila mempunyai

derajat-luar positif tetapi derajat-dalam nol. Sedangkan, v disebut tujuan (sink) jika v

mempunyai derajat-dalam positif tetapi derajat-luar nol.

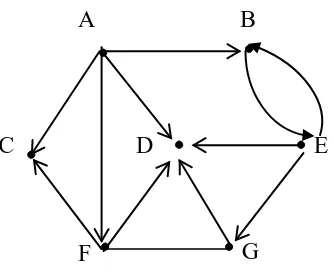
Gambar 2.3. Graph G dengan 7 verteks

Gambar 2.3. di atas terdiri dari:

Verteks

A

B

C

D

E

F

G

Derajat-dalam (indegree)

0

2

2

4

1

1

2

Derajat-luar (outdegree)

4

1

0

0

3

3

1

Jumlah derajat dalam dan jumlah derajat luar sama dengan 12 yaitu jumlah arc.

Pada Gambar 2.3. Verteks A adalah sumber (source) karena edgenya berawal

pada A tetapi tidak berakhir di A. Sedangkan C dan D adalah verteks tujuan (sink)

karena edgenya berakhir di C dan di D tetapi tidak berawal di verteks itu.

2.3.

Path Minimum

Salah satu aplikasi graph berarah berlabel yang sering dipakai adalah mencari path

terpendek diantara 2 verteks. Jika masalahnya adalah mencari jalur tercepat, maka

path terpendek tetap dapat digunakan dengan cara mengganti nilai edge.

A

B

G

E

D

Definisi 2.5. Misalkan G adalah suatu graph. Di mana v dan w adalah 2 verteks dalam

G. Suatu Walk dari v ke w adalah barisan verteks-verteks berhubungan dan edge

secara berselang-seling, diawali dari verteks v dan diakhiri pada verteks w. Walk

dengan panjang n dari v ke w ditulis: v0 e1

v1 e2

v2

… vn-1

en

vn dengan v0 = v; vn =

w; vi-1 dan v

i adalah verteks-verteks ujung edge ei.

Path dengan panjang n dari v ke w adalah walk dari v ke w yang semua edgenya

berbeda. Path dari v ke w dituliskan sebagai v = v0 e1

v1 e2

v2 … vn-1

en

vn = w

dengan ei

≠ e

j

untuk i ≠ j.

Definisi 2.6. Lintasan adalah suatu barisan edge

(

)

k

i i

i

e

e

e

,

,...

.,

2

1

sedemikian rupa

sehingga verteks terminal

j

i

e

berimpit dengan verteks awal

) 1 (j+

i

e

untuk 1 ≤ j ≤ k

– 1.

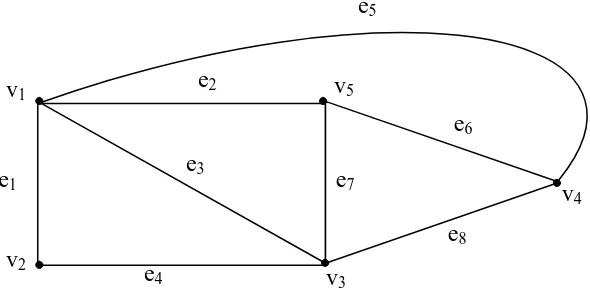
Contoh 2.2.

Gambar 2.4. Graph dengan 6 verteks dan 10 edge

Pada Gambar 2.4. di atas terdapat:

a.

Semua edge berbeda (e1, e3, e4, dan e

5

masing-masing muncul sekali). Ada

verteks yang berulang (v3 muncul 2 kali). Verteks awal dan verteks akhir tidak

sama (verteks awal = v1 dan verteks akhir = v

4). Barisan ini merupakan path dari

v1 ke v4 dengan panjang 4.

b.

Ada edge yang muncul lebih dari sekali, yaitu e5 (muncul 2 kali) berarti barisan

tersebut merupakan walk dari v1 ke v5 dengan panjang 5.

v

1

v2

v3

v6

v

5

v

4

e10

e9

e6

e5

e4

e7

e8

e

3

2.4.

Representasi Graph dalam Matriks

Matriks dapat digunakan untuk menyatakan suatu graph. Jika graph dinyatakan

sebagai suatu matriks, maka perhitungan-perhitungan yang diperlukan dapat dilakukan

dengan mudah.

Kesulitan utama merepresentasikan graph dalam suatu matriks adalah

keterbatasan matriks untuk mencakup semua informasi yang ada dalam graph.

Akibatnya ada bermacam-macam matriks untuk menyatakan suatu graph tertentu.

Tiap-tiap matriks tersebut mempunyai keuntungan yang berbeda-beda dalam

menyaring informasi yang dibutuhkan pada graph.

Misalkan G adalah sebuah graph dengan verteks-verteks v

1

, v

2,

…, v

m

dan

edge-edge e

1,

e

2,

…, e

n

.

Definisi 2.7. Matriks adjacency

Misalkan A = (a

ij

) adalah matriks m x m yang didefinisikan oleh

1

jika {u, v} adalah edge, yaitu v

i

adjacent terhadap v

j

0

lainnya

A disebut matriks adjacency dari G. Perhatikan a

ij

= a

ji

, sehingga A adalah sebuah

matriks simetris. (Didefinisikan sebuah matriks adjacency untuk sebuah multigraph

dengan pemisalan a

ij

menyatakan jumlah edge {v

i,

v

j

}.)

Definisi 2.8. Matriks Insiden

Misalkan M = (m

ij

) adalah matriks m x n yang didefinisikan oleh

1 verteks v

i

adalah incident pada edge e

j.

0 lainnya

M disebut matriks incidence dari G.

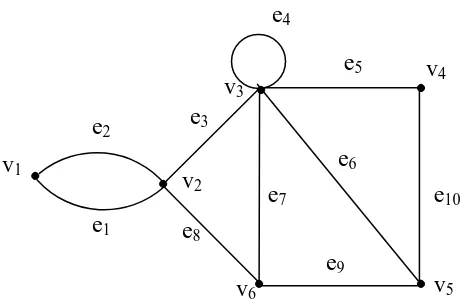
Perhatikan Gambar 2.5 berikut ini.

aij =

Gambar 2.5. Graph dengan 5 verteks dan 8 edge

Pada Gambar 2.5. Matriks adjacency A = (a

ij

) dari graph G.

Karena G mempunyai 5 verteks maka A akan menjadi matriks 5 x 5.

Jika ada sebuah edge antara v

i

dan v

j

, maka a

ij

=

1. Jika sebaliknya, maka a

ij

= 0. Ini

akan menghasilkan matriks berikut:

v

1

v

2

v

3

v

4

v

5

v1

0

1

1

1

1

A = v2

1

0

1

0

0

v3

1

1

0

1

1

v4

1

0

1

0

1

v5

1

0

1

1

0

Pada Gambar 2.5. Matriks Incidence M = (mij) dari graph G.

Jika G mempunyai 5 verteks dan 8 edge, maka M akan menjadi matris 5 x 8. Jika

verteks vi

anggota dari edge ej,

maka mij

=1, jika sebaliknya, maka mij

= 0 untuk

lainnya. Ini akan menghasilkan matriks berikut.

v

4

v

3

v

5

v2

v

1

e

5

e

8

e6

e7

e4

e3

e2

e1

e2

e3

e4

e5

e6

e7

e8

v1

1

1

1

0

1

0

0

0

v2

1

0

0

1

0

0

0

0

A =

v3

0

0

1

1

0

0

1

1

v4

0

0

0

0

1

1

0

1

v5

0

1

0

0

0

1

1

0

2.5.

Shortest Path

Setiap path dalam digraph mempunyai nilai yang dihubungkan dengan nilai path

tersebut, yang nilainya adalah jumlah dari nilai edge path tersebut. Dari ukuran dasar

ini dapat dirumuskan masalah seperti “ mencari lintasan terpendek antara dua verteks

dan meminimumkan biaya”.

Banyak bidang penerapan mensyaratkan untuk menentukan lintasan terpendek

berarah dari asal ke tujuan di dalam suatu distribusi aliran berarah. Algoritma yang

diberikan dapat dimodifikasi dengan mudah untuk menghadapi lintasan berarah pada

setiap iterasinya.

Suatu versi yang lebih umum dari masalah lintasan terpendek adalah

menentukan lintasan terpendek dari sembarang verteks menuju ke setiap verteks

lainnya. Pilihan lain adalah membuang kendala tak negatif bagi “jarak”. Suatu kendala

lain dapat juga diberlakukan dalam suatu masalah lintasan terpendek.

Definisi 2.10. Lintasan terpendek antara dua verteks dari s ke t dalam network adalah

Contoh 2.4.

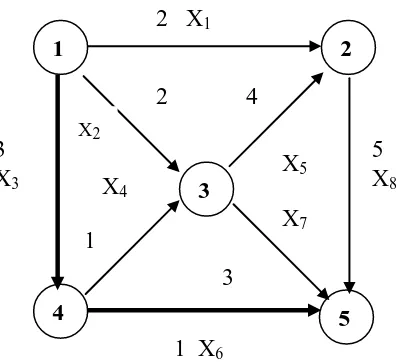
Gambar 2.6. Shortest path (garis tebal)

Pada Gambar 2.6. dapat dilihat bahwa setiap edge terletak pada path-path dari

titik 1 ke titik 5. Edge merepresentasikan saluran dengan kapasitas tertentu

(contohnya, air) dapat dialirkan melalui saluran. Sedangkan verteks merepresentasikan

persimpangan saluran. Air mengalir melalui verteks pada verteks yang dilalui

Lintasan terpendek dari verteks pada graph di atas adalah P = {1 – 4, 4 – 5} dengan

kapasitas 4.

2.6. Linear Programming

Perumusan linear programming dapat membantu prosedur penyelesaian lebih

efisien. Berikut ini adalah bentuk umum linear programming.

Minimumkan

c

1

x

1

+

c

2

x

2

+

...

+

c

n

x

n

(1)

Dengan kendala

1 1 2 12 1

11

x

a

x

...

a

x

b

a

+

+

+

n n

=

(2)

2 2

2 22 1

21

x

a

x

...

a

x

b

a

+

+

+

n n

=

.

.

m n mn m

m

x

a

x

a

x

b

a

1 1

+

2 2

+

...

+

=

0

...,

, 2 ,

1

x

x

n

≥

x

(3)

3

5

2

X7

3

X5

4

1

2

4

X2

X4

1

3

X

3

1 X6

Pada program linear ini, x1, x2, … , xn mewakili keputusan variabel yang tidak

diketahui; c

1,

c

2,

… , c

n

adalah biaya koefisien; b

1

, b

2,

… , b

n

adalah nilai di samping

kanan; dan aij, i = 1 sampai m dan j = 1 sampai n, dinamakan koefisien teknologi.

Pernyataan (1) dinamakan fungsi objektif; (2) dinamakan kendala; dan (3)

adalah kendala tidak negatif. Beberapa penyelesaian memenuhi semua kendala,

dinamakan feasible solution.

Pada perumusan ini, kendala ditulis dalam bentuk persamaan. Umumnya,

kendala linear programming mempunyai relasi ≥ atau ≤ tetapi selalu dapat diubah

dalam persamaan dengan penjumlahan slack variabel. Fungsi objektif (1) juga dapat

diekspresikan sebagai maksimum sebagai pengganti minimum.

Dapat dirumuskan menjadi:

Minimumkan

∑

=

n

j j j

x

c

1

Dengan kendala

,

1

i n

j j

ij

x

b

a

=

∑

₌

i

=

1

,

2

,...,

m

,

0

≥

j

x

j

=

1

,

2

,...,

m

2.7. Flow

Definisi 2.10 Suatu flow pada network G = (N,A) adalah suatu graph berarah dan

berkapasitas, di mana setap arc(x,y) Є A memiliki kapasitas nonnegative c(x,y) ≥ 0.

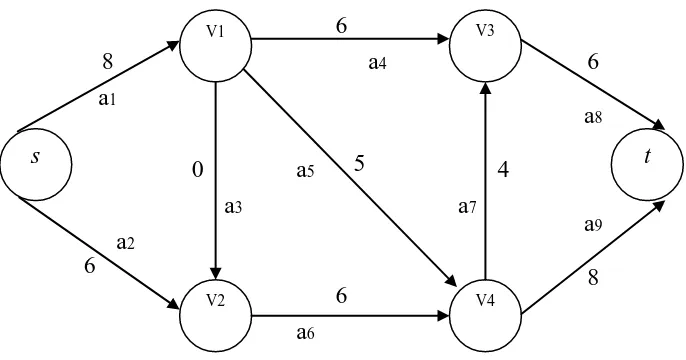
Gambar 2.7. Flow dalam network

Gambar 2.7 memperlihatkan bahwa setiap arc terletak pada tiap-tiap node dari

sumber s ke tujuan t. Arc menggambarkan saluran dengan kapasitas tertentu.

Kapasitas merupakan batas maksimal di mana setiap material (misalnya air, gas,

listrik) dapat dialirkan melalui saluran. Sedangkan node menggambarkan

persimpangan saluran. Material mengalir melalui node tanpa mengumpulkan material

tersebut pada node yang dilalui (kecuali pada node sumber dan node tujuan).

2.8. Minimal Cost Flow

Definisi 2.11 Cost flow pada arc dalam network flow dengan arc cost adalah perkalian

antara arc-arc flow dan cost. Cost pada flow adalah jumlah dari cost flow pada arc.

Andaikan sebuah directed network (jaringan berarah) G, terdiri atas beberapa

node (titik) N = {1,2,…,m) dan beberapa directed arcs (busur berarah) S = {(i,j),

(k,l),…,(s,t)} dan saling terhubung pada node N. Arc (i,j) disebut incident (peristiwa)

dari node i dan j dan terhubung dari node i ke node j. Dengan demikian diperoleh

bahwa network memiliki m node dan n arc.

Untuk setiap node i dalam network G, misalkan jumlah b

i

adalah ketersediaan

barang (b

i

> 0) atau permintaan barang (b

i

< 0). Node dengan b

i

> 0 sering disebut

sources (sumber), dan node dengan b

i

< 0 sering disebut tujuan (sinks). Jika b

i

= 0,

s

t

V2 V1

V4 V3

8

6

6

6

6

8

0

5

4

a2

a1

a3

a6

a5

a4

a7

maka tidak ada barang yang tersedia pada node i dan tidak diperlukan. Pada

permasalahan ini node i sering disebut intermediate (perantara) node. Untuk setiap arc

(i,j) pada x

ij

adalah jumlah aliran pada arc

(asumsikan 0 ≤

x

ij

) dan c

ij

adalah biaya

pengiriman sepanjang arc.

Asumsikan bahwa total penyediaan barang sama dengan total permintaan

di dalam network. Secara matematika dapat dituliskan sebagai berikut.

Minimumkan

∑∑

= = m i m j ij ij

x

c

1 1

Kendala

∑ ∑

=

−

=

=

m j m k ki ij

x

x

1 1

bi

i = 1, 2, ...,m

x

ij

≥ 0

i,j = 1, 2, …,m

(2.1)

Persamaan (2.1) disebut flow conservation atau persamaan Kirchhoff . Di dalam

persamaan kekekalan, menunjukkan jumlah aliran yang keluar dari node i

sedangkan

menunjukkan jumlah aliran yang masuk ke node i. Persamaan tersebut

mengharuskan aliran yang keluar dari node i,

, akan sama dengan b

i.

Jika b

i

< 0, maka akan lebih banyak aliran yang masuk pada node i dari pada yang

keluar.

∑

m₌ j

ij

x

1

∑

m₌ k

ki x 1

∑

m₌ −

∑

₌

BAB 3

PEMBAHASAN

3.1.

Out-Of-Kilter pada Permasalahan Minimal Cost Dalam Network Flow

Bentuk umum dari masalah aliran minimal cost dapat dituliskan sebagai

berikut.

Minimumkan

∑∑

= =

m

i m

j ij ij

x

c

1 1

Kendala

∑ ∑

=

−

=

=

m

j

m

k ki

ij

x

x

1 1

0

i = 1, 2, ...,m

x

ij

≥

l

ij

i,j = 1, 2, …,m

xij

≤

u

ij

i,j

= 1, 2, …,m

(3.1)

Kekekalan aliran yang memenuhi pada batasan tetap l

ij

≤

x

ij

≤

u

ij

adalah feasible

flow(Aliran yang layak). Asumsikan c

ij

, l

ij

, dan u

ij

integer dan 0

≤

l

ij

≤

u

ij

.

Karena semua nilai di sisi kanan pada persamaan kekekalan aliran adalah nol,

dapat disimpulkan bahwa aliran dalam network tidak mempunyai titik awal atau titik

akhir, tapi akan beredar/berputar terus-menerus sepanjang aliran pada network

tersebut. Dengan demikian kekekalan aliran dalam network akan membentuk directed

cycles.

3.1.1. Dual pada Aliran Network

Hubungkan variabel dual w

i

dengan beberapa node pada Persamaan 3.1, variabel dual

variabel dual v

ij

dengan batasan x

ij

≥

l

ij

, dual dari out-of-kilter pada permasalahan

aliran network minimal cost dituliskan sebagai berikut.

Minimumkan

∑∑

= =

m

i m

j ij ij

v

l

1 1

-

∑∑

= =

m

i m

j ij ij

h

u

1 1

Kendala

w

i

– w

j

+ v

ij

– h

ij

= c

ij

i, j = 1,…, m

h

ij

,v

ij

≥

0

i, j = 1,…, m

w

i

tak terbatas

i = 1,…, m

Jika w

i

(asumsikan semua w

i

integer), maka dual constraint untuk arc (i, j)

menjadi

v

ij

– h

ij

= c

ij

– w

i

+ w

j

, h

ij

≥

0, v

ij

≥

0

dan dapat dipenuhi oleh

v

ij

= Maksimum {0, c

ij

- w

i

+ w

j

}

h

ij

= Maksimum {0, - (c

ij

- w

i

+ w

j

}

3.1.2.

Kondisi-kondisi Complementary Slackness

Kondisi-kondisi complementary slackness untuk mendapatkan nilai yang optimal dari

perumusan out-of-kilter adalah sebagai berikut:

(x

ij

– l

ij

)v

ij

= 0

i,j = 1, 2,…, m

(3.2)

(u

ij

– x

ij

)v

ij

= 0

i,j = 1, 2,…, m

(3.3)

z

ij

– c

ij

≡ w

i

– w

j

- c

ij

. Kemudian dari definisi v

ij

dan h

ij

didapat

v

ij

= Maksimum {0, -(zij – c

ij

)}

(3.4)

h

ij

= Maksimum {0, zij – c

ij

}

(3.5)

Catatan bahwa z

ij

– c

ij

akan dikenal sebagai koefisien x

ij

dalam barisan fungsi objektif

pada tabel simpleks batas atas-batas bawah yang mempunyai solusi dasar pada

masalah primal.

Bila diberikan nilai pada w

i

, maka dapat dihitung z

ij

– c

ij

= w

i

– w

j

- c

ij.

Jika

z

ij

– c

ij

< 0 v

ij

> 0 x

ij

= l

ij

i, j = 1, 2,..., m

(3.6)

z

ij

– c

ij

> 0 h

ij

> 0 x

ij

= u

ij

i, j = 1, 2,..., m

(3.7)

Memasukkan kondisi tambahan

z

ij

– c

ij =

0 l

ij

≤

x

ij

≤

u

ij

i, j = 1, 2,..., m

(3.8)

Beberapa kekekalan aliran (conserving flow) yang memenuhi 3 (tiga) kondisi di atas

akan optimal. Permasalahannya, bagaimana mencari atas nilai-nilai dari w

i

kekekalan

x

ij

sampai tiga kondisi di atas terpenuhi. Lihat Gambar (3.1a). Ambil untuk tiap-tiap

w

i

= 0, dan kekekalan aliran tiap-tiap x

ij

, Agar dapat memeriksa nilai yang optimal.

Gambar (3.1b) memberikan nilai z

ij

– c

ij,

x

ij,

dan w

i

pada network yang ada di Gambar

(3.1a). Pada Gambar (3.1b) dapat dilihat bahwa z

12

– c

12

= -2 dan x

12

= 0 ( = l

12

) dan

demikian arc (1, 2) disebut menjadi in-kilter, pada sisi lain, z

23

– c

23

= 3 dan x

23

= 0

( < u

23

) dan karena itu arc (2, 3) disebut menjadi out-of-kilter.

(a)

(b)

Gambar (3.1a). Network

Gambar (3.1b) w

i

, z

ij

– c

ij

, x

ij

2

3

1

4

( 0, 2, 2 )

( 0, 5, -1 )

( 0, 6, -3 ) ( 0, 3, 0 )

(lij, uij, cij)

( 1, 2, 5 )

2

4

1

3

z12 – c12 = -2

z34 – c34 = 1

z23 – c23 = 3

z41 – c41 = 0

w1 = 0 w2 = 0

w3 = 0 w4 = 0

x12 = 0

x23 = 0

x34 = 0

x41 = 0

x13 = 0

3.1.3.

Status Kilter dan Bilangan Kilter pada Arc

Keadaan in-kilter dan out-of-kilter pada tiap-tiap arc dalam network dapat dilihat pada

Tabel (3.1). Dapat dilihat bahwa dikatakan in-kilter bila l

ij

≤

x

ij

≤

u

ij

. Ketika

mengubah aliran pada arc (i, j), bergerak naik dan turun pada kolom tertentu

tergantung apakah x

ij

dinaikkan atau diturunkan. Ketika mengubah w

i

, arc bergerak

maju dan mundur sepanjang baris. Gambar (3.2) dapat dilihat gambaran secara grafik

keadaan kilter pada arc.

Tabel 3.1. Status kilter pada arc

z

ij

– c

ij

< 0

z

ij

– c

ij

= 0

z

ij

– c

ij

> 0

x

ij

> u

ij

Out-of-kilter

Out-of-kilter

Out-of-kilter

x

ij

= u

ij

Out-of-kilter

In-kilter

In-kilter

l

ij

< x

ij

< u

ij

Out-of-kilter

In-kilter

Out-of-kilter

x

ij

= l

ij

In-kilter

In-kilter

Out-of-kilter

Gambar 3.2. Status kilter pada arc

In-kilter

In-kilter

In

-k

ilte

r

Out-of-kilter

Out-of-kilter

Out-of-kilter

l

ij

x

ij

u

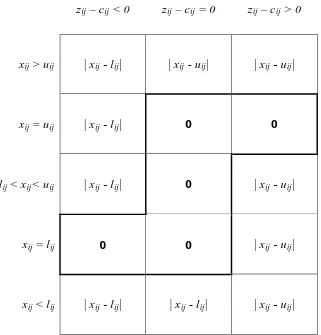
ij

Ada banyak perbedaan ukuran jarak untuk masalah out-of-kilter. Pada Tabel

(3.2) dijelaskan satu ukuran jarak yang disebut dengan bilangan kilter (Kilter number)

K

ij

pada arc (i, j). Bilangan kilter didefinisikan di sini untuk perubahan minimal dari

aliran pada arc yang dibutuhkan untuk membawanya kedalam kilter. Bilangan kilter

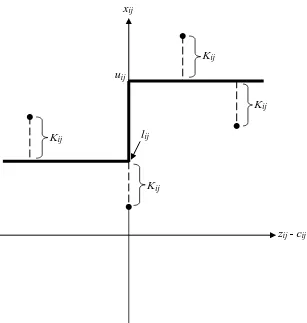
pada suatu arc diilustrasikan dalam bentuk grafik pada Gambar (3.3). Perlu diingat

bahwa karena syarat melibatkan nilai absolut, maka bilangan kilter pada arc harus non

negatif. Jika arc yang in-kilter, maka bilangan kilter adalah nol (0) dan jika arc

out-of-kilter, maka bilangan kilter adalah harus positif. Jika z

ij

– c

ij

< 0, maka arc (i, j)

adalah in-kilter jika dan hanya jika aliran adalah sama dengan l

ij

dan oleh sebab itu

bilangan kilter |x

ij

- l

ij

| menandai seberapa jauh arus aliran x

ij

adalah dari kasus ideal

l

ij

. Dengan cara yang sama, jika z

ij

– c

ij

> 0, maka bilangan kilter |x

ij

- u

ij

| memberi

jarak dari aliran ideal u

ij

. Terakhir, jika z

ij

– c

ij

= 0, maka arc adalah in-kilter bila l

ij

≤

x

ij

≤

u

ij

. Khususnya, jika x

ij

> u

ij

, maka arc dibawa ke in-kilter dan pengurangan

aliran oleh |x

ij

- u

ij

|, dan jika x

ij

< l

ij

, maka arc dibawa ke in-kilter dan peningkatan

aliran oleh |x

ij

- l

ij

|, dan karenanya masuk kedalam kolom z

ij

– c

ij

= 0 pada Tabel

[image:32.595.169.490.290.625.2]

Tabel 3.2 Bilangan kilter K

ij

z

ij

– c

ij

< 0

z

ij

– c

ij

= 0

z

ij

– c

ij

> 0

x

ij

> u

ij

| x

ij

- l

ij

|

| x

ij

- u

ij

|

| x

ij

- u

ij

|

x

ij

= u

ij

| x

ij

- l

ij

|

0

0

l

ij

< x

ij

< u

ij

| x

ij

- l

ij

|

0

| x

ij

- u

ij

|

x

ij

= l

ij

0

0

| x

ij

- u

ij

|

[image:33.595.186.493.261.584.2]

Gambar 3.3 Bilangan Kilter K

ij

x

ij

u

ij

l

ij

z

ij

- c

ij

K

ij

K

ij

K

ij

Satu metoda untuk meyakinkan batas pemusatan dari algoritma out-of-kilter

adalah sebagai berikut:

1.

Bilangan kilter pada arc tidak pernah meningkat

2.

Interval batas bilangan kilter pada beberapa arc menurun (dengan

bilangan integer).

3.2. Strategi Out-Of-Kilter

Langkah umum algoritma out-of-kilter adalah sebagai berikut

1.

Mulai dari kekekalan aliran, masing-masing x

ij

= 0, dan solusi yang layak

untuk dual, masing-masing w

i

= 0, dengan h

ij

, v

ij

seperti yang dijelaskan pada

Persamaan (3.4) dan (3.5). Identifikasi keadaan kilter dan hitung bilangan

kilter.

1.

Jika pada network memiliki arc out-of-kilter, maka lakukan tahap primal

algoritma. Selama tahap ini arc out-of-kilter terpilih dan mencoba membuat

bentuk kekekalan aliran baru sedemikian bilangan kilter tidak ada arc

memburuk dan arc yang terpilih ditingkatkan.

1.

Ketika ditentukan bahwa tidak ada aliran yang meningkat terbangun selama

tahap primal, algoritma membuat solusi dual yang baru sedemikian tidak ada

bilangan kilter yang memburuk dan ulangi tahap 2.

1.

Perulangan antara tahap 2 dan tahap 3, algoritma secepatnya membangun

solusi optimal atau menentukan tidak ada solusi yang layak.

3.2.1 Tahap Permulaan (Initiation Phase)

Dimulai dengan sebuah aliran, katakan untuk setiap x

ij

= 0, dan inisial dual variabel,

katakan w

i

= 0. Hitung z

ij

– c

ij

= w

i

– w

j

- c

ij.

3.2.2 Tahap Primal: Merubah Aliran

Tentukan status kilter dan bilangan kilter untuk setiap arc. Kemudian cari dalam

network yang membentuk sirkuit (cycle). Jika semua arc in-kilter, maka stop. Dengan

demikian diperoleh solusi optimal. Jika tidak, maka pilih atau lanjutkan dengan arc

out-of-kilter (p,q) yang sebelumnya terpilih. Dari network G membentuk network G’

menurut Tabel 3.3. Untuk setiap arc (i,j) pada G adalah salah satu dari status kilter

yang membolehkan aliran meningkat, tempatkan arc(i, j) di dalam G’ dengan arus

yang dibolehkan meningkatkan. Untuk setiap arc (i,j) pada G adalah salah satu dari

status kilter yang membolehkan aliran berkurang, selanjutnya tempatkan arc(j, i) di

dalam G’ dengan arus yang dibolehkan. Untuk arc-arc di dalam G yang bagian dari

status yang dibolehkan itu tidak ada aliran berubah, kemudian tempatkan tidak ada arc

di dalam G’. Penentuan sirkuit seperti itu disebut breakthrough. Jika sirkuit seperti itu

didapatkan, maka tentukan perubahan aliran

Δ

sama dengan minimum dari aliran yang

berubah pada arc dalam sirkuit. Ubah aliran pada setiap arc dari siklus berhubungan

dalam G dengan jumlah

Δ

menggunakan orientasi yang ditetapkan oleh sirkuit sebagai

arah peningkatan. Khususnya, misalkan x’

ij

= x

ij

+

Δ

jika (i, j) adalah anggota dari

sirkuit G’; misalkan x’

ij

= x

ij

-

Δ

jika (j, i) adalah anggota dari sirkuit G’; misalkan x’

ij

= x

ij

sebaliknya. Ulangi tahap primal. Jika tidak ada sirkuit berisi arc (p, q) ada

[image:36.595.182.470.284.552.2]

Tabel 3.3 Jumlah dan arah perubahan aliran yang diijinkan

.

Sebagai contoh lihat Gambar 3.1. Ambil salah satu arc, misalnya arc(1,3). x

13

< l

13

dan z

13

– c

13

< 0. Jika dilihat dari tabel pada Tabel 3.3, maka arc(1,3) adalah arc

out-of-kilter. Untuk itu aliran pada arc(1,3) harus ditingkatkan (increase) sebesar

| x

13

- l

13

| agar arc(1,3) menjadi in-kilter. Nilai yang diijinkan adalah sebesar nilai

l

13

= 1. Hasilnya dapat dilihat pada Gambar 3.4

z

ij

– c

ij

< 0

z

ij

– c

ij

= 0

z

ij

– c

ij

> 0

x

ij

> u

ij

x

ij

= u

ij

l

ij

< x

ij

<

u

ij

x

ij

= l

ij

x

ij

< l

ij

2

1

|x

– l

|

|x

– l

|

|x

– l

|

|x

– u

|

|x

– u

|

|x

– u

[image:37.595.235.502.83.193.2]

Gambar 3.4. Network G’ buatan dari Gambar 3.1.

Network G’ telah terbentuk dan out-of-kilter arc (p, q) telah ditentukan,

selanjutnya akan mencari sirkuit (directed cycle) yang ada pada arc G’. Jika tidak ada

sirkuit pada arc G’, maka harus melakukan proses tahap dual pada algoritma.

Pada arc(1,3) terdapat sirkuit, sebut saja C(circuit) = {(1 ,3), (3, 4), (4,1)}.

Tentukan jumlah dari permitted change pada aliran adalah

Δ

= Minimum {1, 5, 3}= 1.

Hasilnya dapat dilihat pada Gambar 3.3. Arc (2, 3) dan (3, 4) masih out-of-kilter pada

G. Karena tidak ada lagi sirkuit pada network G, maka lakukan tahap dual dari

algoritma out-of-kilter.

Gambar 3.5. Perubahan pada network G pada tahap primal

3.2.3 Tahap Dual

3

6

1

5

3

Permitted flow change

2

4

1

3

z12 – c12 = -2

x12 = 0

x23 = 0

x34 = 1

x13 = 1

x14 = 1

z13 – c13 = -5 _z

23 – c23 = 3

z41 – c41 = 0

z34 – c34 = 1

2

4

1

3

2 1

4

[image:37.595.123.520.473.624.2]

Menentukan satuan dari node X yang dapat dicapai dari node q sepanjang path pada

G’. Misalkan X = N – X. Dalam G, dapat digambarkan S

1

dan S

2

oleh

S

1

= {(i, j): i

Є

X, j

Є

X, z

ij

- c

ij

< 0, x

ij

≤

u

ij

}

S

2

= {(i, j): i

Є

X, j

Є

X, z

ij

- c

ij

> 0, x

ij

≥

l

ij

}

Ө

= Minimum {| z

ij

- c

ij

|,

∞ }

Jika

Ө

= ∞,

maka stop; tidak ada solusi yang layak. Sebaliknya, ubah w

i

dan z

ij

- c

ij

menurut

w

i

+

Ө

i

Є

X

w

i

=

w

i

i

Є

X

(z

ij

- c

ij

)

(i, j)

Є (

X, X)

U (

X, X)

(z

ij

- c

ij

)’ = (z

ij

- c

ij

) +

Ө

(i, j)

Є (

X, X)

(z

ij

- c

ij

) -

Ө

(i, j)

Є

(X, X)

dan lakukan tahap primal.

Begin

Misalkan x

ij

= 0 dan w

i

= 0

Hitung z

ij

– c

ij

= w

i

– w

j

- c

ij

Periksa status

kilter.Semua arc

inkilter?

Tentukan arc yang

out-of-kilter (p, q)

Bentuk Network G’

(Artificial Network)

Temukan sirkuit

(direct cycle) pada

network G’

Hitung S1 dan S2

Hitung Ө;

Jika Ө = ∞

Tidak ada

solusi yang

layak

Tidak

Tidak

Tidak

Ya

Stop

Hitung

∑∑

m_{= =} i

m

j ij ij

x

c

1 1

Ubah w

i

dan z

ij

- c

ij [image:40.595.107.556.89.727.2]

Dan simpan dalam network G

Gambar 3.6 Flowchart Out-of-kilter

Hitung Arc;

Ditingkatkan

/ diturunkan

3.3 Contoh Algoritma Out-Of-Kilter

Contoh permasalahan network dapat dilihat pada Gambar 3.6. Memulai algoritma

out-of-kilter dengan memberikan nilai setiap x

ij

= 0 dan setiap w

ij

= 0, sehingga didapat

[image:41.595.119.402.395.610.2]

rangkaian dari tahap primal dan dual yang ditunjukkan pada Gambar 3.6.

Gambar 3.7. Contoh Network.

(a)

Breakthrough dalam tahap primal pertama

(p,q) = (3,4)

X = {1, 2, 4, 5}, X = {3}

S

1

= {(2, 3)}, S

2

= {(3, 4)}

Ө

= 3

(3,4) adalah in-kilter

(p, q) = (4, 5)

X = {1, 5}, X = {2, 3, 4}

S

1

= {(1, 2), (5,2)}

S

2

= {(4, 5)}

Ө

= 1

(b)

Nonbreakthrough dan tahap dual pertama

(d) Solusi Optimal

Gambar 3.8(a,b,c,d). Solusi out-of-kilter dari Gambar 3.7.

3.4 Prosedur Label pada Algoritma Out-Of-Kilter

Misalkan untuk setiap node j label L( j ) = ( +

i, Δ

j

). Label (

i, Δ

j

) menunjukkan bahwa

aliran pada arc (i, j) dapat ditingkatkan dengan jumlah

Δ

j

tanpa memperburuk

bilangan kilter pada arc manapun

Δ

j

tanpa memperburuk bilangan kilter pada arc

manapun. Sebagai catatan bahwa

Δ

j

mewakili perkiraan aliran dari nilai aliran yang

diubah yang dapat berlangsung sepanjang siklus yang berisi arc out-of-kilter dan arc

(i, j) atau (j, i) dengan demikian bahwa bilangan kilter dari arc yang tidak ada

ditingkatkan. Algoritma label terdiri dari 2 (dua) tahap, yaitu tahap inisialisasi dan

tahap utama.

3.4.1 Tahap Inisialisasi

Tentukan sebuah aliran, sebagai contoh, setiap x

ij

= 0, dan nilai dari variabel dual,

misalkan setiap w

i

= 0.

1. Jika semua arc adalah in-kilter sesuai Tabel 3.2, maka stop; dengan demikian

nilai optimal diperoleh. Jika tidak, maka pilih (atau lanjutkan dengan pilihan

selanjutnya) arc out-of-kilter, misal(p, q). Hapus semua label-label. Jika (p, q)

adalah salah satu status di mana aliran meningkat.,

Δ

pq

, sesuai Tabel 3.3, maka

tetapkan s = q, t = p, dan L(s) = (+t,

Δ

pq

). Sebaliknya, jika (p, q) adalah salah

satu status di mana aliran berkurang,

Δ

pq

, sesuai Tabel 3.3, maka tetapkan

s = p, t = q, dan L(s) = (-t,

Δ

pq

).

2. Jika node i memiliki label, node j tidak memiliki label, dan aliran akan

ditingkatkan dengan jumlah

Δ

ij

sepanjang arc (i, j) sesuai dengan Tabel 3.3,

maka menetapkan node j label L(j) = (+i,

Δ

j

) di mana

Δ

j

= minimum{

Δ

i,

Δ

ij

}.

Jika node i memiliki label, node j tidak memiliki label, dan aliran dikurangi

dengan jumlah

Δ

ji

sepanjang arc (j, i) sesuai dengan Tabel 3.3, maka berikan

node j label L(j) = (-i,

Δ

j

) di mana

Δ

j

= minimum{

Δ

i,

Δ

ji

}. Ulangi langkah 2

sampai setiap node t diberi label atau sampai tidak ada lagi node-node yang

diberi label. Jika node t diberi label, maka lanjut ke langkah ke 3

(breakthrough telah terjadi); jika tidak, maka lanjut ke langkah ke 4

(nonbreakthrough telah terjadi).

3. Misalkan

Δ

=

Δ

t

. Ubah aliran sepanjang siklus yang dikenali sebagai berikut.

Mulai dari node t. Jika masukan pertama di L(t) adalah + k, maka tambahkan

Δ

ke x

kt

. Sebaliknya, jika masukan pertama L(t) adalah – k, maka kurangi

Δ

dari

x

tk

. Mundur ke node k dan ulangi proses sampai node t dicapai lagi dalam

proses mundur(backtrack process). Lakukan langkah 1.

1.

Misalkan X satuan node-node yang diberi label dan misalkan X = N - X .

Tetapkan S

1

= {(i, j): i

Є

X, j

Є

X, z

ij

- c

ij

< 0, x

ij

≤

u

ij

} dan S

2

= {(i, j) : i

Є

X, j

Є

X, z

ij

- c

ij

> 0, x

ij

≥

l

ij

}. Misalkan

Ө

= Minimum {| z

ij

- c

ij

|,

∞ : (

i, j)

Є

S

1

U

S

2

}. Jika

Ө

= ∞,

maka stop; tidak ada solusi yang layak. Sebaliknya,

misal

w

i

’ =

w

i

i

Є

X

dan

(z

ij

- c

ij

)

(i, j)

Є (

X, X)

U (

X, X)

(z

ij

- c

ij

)’ =

(z

ij

- c

ij

) +

Ө

(i, j)

Є (

X, X)

(z

ij

- c

ij

) -

Ө

(i, j)

Є (

X, X)

Lakukan langkah 1.

Metode label untuk algoritma out-of-kilter dapat dilihat pada Gambar 3.8 (a)

dan (b) yang melakukan pertama dengan dua iterasi. Dari Gambar 3.8(a) didapat arc

(1, 2) adalah arc out-of-kilter yang alirannya harus ditingkatkan.

Urutan operasi dari algoritma label adalah sebagai berikut:

1.

(p, q) = (1, 2), s = 2, t = 1, L(2) = (+1, 2)

2.

L(4) = (+2, 2)

3.

L(5) = (+4, 2)

4.

L(1) = (+5, 2)

5.

Breakthrough:

Δ

= 2

6.

L

1

(1) = +5



x′

51

= x

51

+

Δ

= 2

7.

L

1

(5) = +4



x′

45

= x

45

+

Δ

= 2

8.

L

1

(4) = +2



x′

24

= x

24

+

Δ

= 2

9.

L

1

(2) = +1



x′

12

= x12 +

Δ

= 2

10.

Hapus semua label, (p, q) = (3, 4), s = 4, t = 3, L(4) = (+3, 4)

11.

L(5) = (+4, 3)

14.

Nonbreakthrough: X = {1, 2, 4, 5}, X = {3},

Ө

= 3

15.

w

1

= w

2

= w

4

= w

5

= 3, w

3

= 0

BAB 4

KESIMPULAN DAN SARAN

4.1. Kesimpulan

Berdasarkan uraian-uraian dalam tulisan ini, penulis melihat bahwa algoritma

out-of-kilter berperan penting dalam menghasilkan minimal cost dalam network flow.

Kesimpulan yang diperoleh pada kajian ini adalah sebagai berikut:

1.

Untuk menentukan algoritma out-of-kilter, langkah pertama adalah tahap

initiation, yaitu menentukan x

ij

= 0 dan w

i

= 0. Kemudian masuk tahap

prima,yaitu menentukan status arc dan sirkuit (cycle) pada network. pada

tahap ini arc yang dalam status out-of-kilter akan dinaikkan atau

diturunkan agar status arc menjadi in-kilter. Selanjutnya membentuk

artificial network. Jika tidak ditemukan cycle dalam network, maka masuk

ke tahap dual. Pada tahap dual ini menghitung nilai z

ij

- c

ij

. Jika semua arc

statusnya sudah in-kilter, maka proses telah selesai. Kemudian akan

menghitung nilai nilai optimal pada network G.

2.

Di dalam algoritma out-of-kilter perlu diperhatikan nilai

Ө

. Ada dua

kemungkinan nilai

Ө

.

Jika 0 <

Ө

< ∞ , maka

w

i’

= w

i

+

Ө

i

Є

X dan w

i’

= w

i

i

Є

X .

4.2. Saran

Sebelum membaca karya ilmiah ini, penulis menyarankan kepada pembaca untuk

memahami terlebih dahulu algoritma out-of-kilter. Untuk selanjutnya penulis berharap

karya ilmiah ini dapat lebih dikembangkan di kemudian hari ke dalam

program-program komputer, khususnya yang berhubungan dengan optimisasi dan network

flow.

DAFTAR PUSTAKA

Aashtiani, H.A. June 1976. Implementing Primal-Dual Network Flow Algorithms.

Massachusetts Institute of Technology

Ahuja, Ravindra, K. 1998. Graph and Network Optimization. USA: University of

Florida.

Bazaara, Mokhtar S. dan Jhon J. Jarvis. 1977. Linear Programming and Network

Flows. Canada: John Wiley and Sons Inc.

Gibbens, R.J. 1997. Algorithms and Networks. Mathematical Tripos, Part IIA,

University of Cambridge.

Jean-Marie PLA. 1971. An ”Out-of-kilter” Algorithm For Solving Minimum Cost

Potential Problems. S.N.C.F. Paris, France. North-Holland Publishing

Company.

Jeremy F. Shapiro. 1975. A Note On The Primal-Dual And Out-Of-kilter Algorithms

For Network Optimization Problems. Mas

Liu, Jipping. 2003. Algorithm for Minimum-Cost Flow. Computer Science

Departement, The University Of Western Ontario.

LAMPIRAN A. LISTING PROGRAM

C INTEGER AAAA,NNNN PARAMETER (AAAA=12400,NNNN=1230) C INTEGER LNODE,MNODE

INTEGER DOWN(NNNN),NEXT(NNNN),LEVEL(NNNN)

INTEGER ARCID(NNNN),FLOW(NNNN),DUAL(NNNN),CAT(NNNN)

EQUIVALENCE (DUAL(1),CAT(1)) C C C NODE FORMAT C C C 1 - PREDECESSOR OR DOWN POINTER C 2 - THREAD OR NEXT POINTER C 3 - LEVEL NUMBER C 4 - ASSOCIATED ARC IDENTIFIER C (+=ORIENTATION OPPOSITE TO DOWN POINTER) C (-=ORIENTATION SAME AS DOWN POINTER) C 5 - FLOW ON ARC C 6 - DUAL VARIABLE VALUE C INTEGER LARC,MARC INTEGER FROM(AAAA),COST(AAAA),CAPAC(AAAA)

INTEGER FLOOR(AAAA),NAME(AAAA) INTEGER ARCNAM

C C ARC FORMAT C C 1 - FROM NODE C 2 - COST C 3 - CAPACITY(-,IF AT UB) C 4 - LOWER BOUND C 5 - NAME C C ARC(ARTY) IS GENERAL REFERENCE FOR ARTIFICIAL ARCS C INTEGER TO INTEGER SLACK,ARTIF,DUMMY,XCESS

INTEGER FLW,AID INTEGER Q1,Q2 INTEGER DIR,REF INTEGER U1,U2,U3,U4 LOGICAL INFEAS LOGICAL OPTIM LOGICAL DMP LOGICAL PPR LOGICAL PRES C DATA ITDOPT/ 1 / DATA ARTY/ 1 / DATA BIG/ 10000000 / DATA U1,U2,U3,U4/5,5,5,5/ C DATA SLACK/ 66666/ DATA ARTIF/ 99999/ DATA DUMMY/ 77777/ DATA XCESS/ 88888/ C 1000 FORMAT(8I10) 1001 FORMAT(1X,8I10) 1002 FORMAT(2X,I8,5I10) 1003 FORMAT(1X,I10,5I10) 1004 FORMAT(F10.0) 1005 FORMAT(1X,F10.5) 2001 FORMAT(1X,I5,1H,,4I15,1X,A10) 2002 FORMAT(1X,I5,1H,,6I15) 8910 FORMAT(8H0PROBLEM,I5) C C NSTOP - EXIT CONDITION C MNODE - NUMBER OF NODES C NET -TOTAL BALANCE IN NETWORK C MSORC - NUMBER OF SOURCES C MSINK - NUMBER OF SINKS C MARC - NUMBER OF ARCS C MTREE - NUMBER OF BRANCHES ON TREE(EXCLUDING ROOT) C THD - POINTER MOVING ALONG THREAD C TRY - VARIABLE ENCOUNTERED DURING SETUP OR PRICING C PRICE - REDUCED COST FOR TRY C NEWARC - BEST VARIABLE TO ENTER C NEWPR - PRICE FOR NEWARC C DW - DOWN PTRS FOR RATIO TEST(FROM STEM,TO STEM) C CH - PATH CONDITIONS FOR RATIO TEST (FROM STEM,TO STEM) C DWN - POINTER MOVING ALONG DOWN PATH C CHG - PATH CONDITION C THETA - MINIMUM RATIO IN RATIO TEST C JTHETA - UB (-) OR LB(+1) CONDITION FOR MIN THETA C KTHETA - MIN THETA OCCURS ON FROM STEM(1) OR TO STEM (2) C POSS - CANDIDATE FOR MIN THETA C JPOSS - UB (-1) OR LB(+1) CONDITION FOR CANDIDATE FOR MIN THETA C DWE - ROOT OF CYCLE C OPEN(5,FILE='NETFLO.INP')

OPEN(6,FILE='NETFLO.OUT') ARTYP1 = ARTY+1

LNODE = NNNN-2 LARC = AAAA-2

LNODP1 = LNODE+1 NPROB = 0 KARD = 0 5 CONTINUE PPR = .TRUE. PRES = .FALSE. NPROB = NPROB+1 C INPUT NUMBER OF REGULAR NODES NSTOP = 2 READ(U1,1000,END=999) I C C NUMBER OF NODES(I10) C KARD = KARD+1 IF(PPR) WRITE(6,8910) NPROB WRITE(6,1001) I NSTOP = 3 IF(I.LE.0) GO TO 999 MNODE = I MNODP1 = MNODE+1 MNODP2 = MNODE+2 NSTOP = 4 IF(MNODP1.GT.LNODE) GO TO 999 DUAL(MNODP1) = 0 C INITIALIZE NODE ARRAY DO 10 J10=1,MNODP1 DOWN(J10) = 0

NEXT(J10) = 0 LEVEL(J10) = 0 ARCID(J10) = 0 FLOW(J10) = 0 10 CONTINUE

20 CONTINUE IF(I.GT.MNODE) GO TO 999 NSTOP = 7 IF(FLOW(I).NE.0) GO TO 999 FLOW(I) = J NET = NET+J IF(J.LE.0) GO TO 15 MSORC = MSORC+1 C SAVE ORIGINAL SUPPLY IN LEVEL LEVEL(I) = J NEXT(I) = NEXT(MNODP1) NEXT(MNODP1) = I GO TO 15 60 CONTINUE C TEST FOR FEASIBILITY NSTOP = 8 IF(NET.LT.0) GO TO 999 C INPUT NUMBER OF ARCS TO EACH NODE(IN NUMERIC ORDER) NSTOP = 9 READ(U3,1000,END=999) (CAT(I),I=1,MNODE) C C NUMBER OF ARCS TO EACH NODE (8I10) C KARD = KARD+1 WRITE(6,1001) (CAT(I),I=1,MNODE) C C RESERVE LOCATIONS FOR INPUT ARCS BY FILLING WITH DUMMIES C CAT(N) WILL POINT TO THE NEXT OPEN LOCATION FOR STORING C ARCS WHOSE TERMINAL NODE IS N. C NSTOP = 10 I = 1 J = ARTY DO 80 J80 = 1,MNODE I = -I K70 = MAX0(1,CAT(J80))

IF(J+K70.GT.LARC) GO TO 999 CAT(J80) = ISIGN(J+1,I) DO 70 I70=1,K70 J = J+1 C NOTE THAT DUMMY ARCS HAVE SAME INITIAL AND TERMINAL NODE FROM(J) = ISIGN(J80,I) COST(J) = 0 CAPAC(J) = -BIG FLOOR(J) = 0

NAME(J) = DUMMY

C KARD = KARD+1 WRITE(6,1003) ARCNAM,I,J,K,L,M NSTOP = 12 IF(I) 999,150,100 100 CONTINUE IF(I.GT.MNODE) GO TO 999 IF(J.GT.MNODE) GO TO 999 IF(J.LE.0) GO TO 999 NSTOP = 13 IF(L.GE.BIG) GO TO 999 IF(L.EQ.0) L = BIG IF(L.LT.0) L = 0 IF(M.GE.BIG) GO TO 999 IF(M.LT.0) GO TO 999 IF(M.GT.L) GO TO 999 II = CAT(J) JJ = IABS(II) C TEST TO SEE IF CATEGORY IS FULL KK = ISIGN(LNODP1,II) IF(IEOR(KK,FROM(JJ)).GT.0) GO TO 140 C MOVE REST OF ARCS DOWN TO ACCOMODATE NSTOP = 14 IF(MARC.EQ.LARC) GO TO 999 MARC = MARC+1 K120 = MARC-JJ M120 = MARC DO 120 J120=1,K120 L120 = M120-1 FROM(M120) = FROM(L120)

COST(M120) = COST(L120) CAPAC(M120) = CAPAC(L120) FLOOR(M120) = FLOOR(L120) NAME(M120) = NAME(L120)

MARC = MARC-1 DO 190 J190=ARTYP1,MARC J = FROM(J190) IF(IEOR(I,J).GT.0) GO TO 160 I = -I L = L+1 CAT(L) = K+1 GO TO 170 160 IF(IABS(J).EQ.L) GO TO 190 170 K = K+1 IF(K.EQ.J190) GO TO 190 FROM(K) = FROM(J190)

COST(K) = COST(J190) CAPAC(K) = CAPAC(J190) FLOOR(K) = FLOOR(J190) NAME(K) = NAME(J190)

8000 FORMAT(1H+,20X,19H OPTIMAL INDICATION) C PRES = .TRUE. IF(.NOT.PRES) GO TO 885 C MOVE BASIC FLOWS TO CAPACITY CELLS FOR BASIC ARCS DO 884 I884=1,MNODE J884 = IABS(ARCID(I884)) CAPAC(J884) = -FLOW(I884) 884 CONTINUE 885 CONTINUE WRITE(6,8023) 8023 FORMAT(10H0ARC FLOWS/ *52H0ARC FROM TO FLOW COST ) TO = 1 TRY = ARTYP1 FRM = FROM(TRY) 8886 CONTINUE LST = ISIGN(LNODP1,FRM) 8888 CONTINUE FLW = MAX0(0,-CAPAC(TRY))+FLOOR(TRY) IF(FLW.EQ.0) GO TO 8889 FM = IABS(FRM) WRITE(6,8024) NAME(TRY),FM,TO,FLW,COST(TRY) 8024 FORMAT(1X,I10,1X,2I5,2I15)

* IF(NAME(TRY).LT.20000) WRITE(7,8025) NAME(TRY) 8025 FORMAT(I6)

8889 CONTINUE TRY = TRY+1 FRM = FROM(TRY) IF(IEOR(FRM,LST).GT.0) GO TO 8888 TO = TO+1 IF(TO.NE.MNODP1) GO TO 8886 CLOSE(5)

CLOSE(6)

STOP 12345 892 CONTINUE C C END OF PROBLEM C GO TO 5 C C EXIT C 999 CONTINUE WRITE(6,1999) NSTOP,KARD 1999 FORMAT(5H STOP,I5/1X,I10,16H DATA CARDS READ) STOP 77777