APLIKASI METODE BRANCH AND CUT DALAM OPTIMASI
PRODUKSI POT BUNGA
(Studi Kasus: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
SKRIPSI
NUSAIBAH KHOLILAH
100803035
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
APLIKASI METODE BRANCH AND CUT DALAM OPTIMASI
PRODUKSI POT BUNGA
(Studi Kasus: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat untuk mencapai gelar Sarjana Sains
NUSAIBAH KHOLLAH
100803035
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
i
PERSETUJUAN
Judul : Aplikasi Metode Branch and Cut Dalam
Optimasi Produksi Pot Bunga (Studi Kasus: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
Kategori : Skripsi
Nama : Nusaibah Kholilah
Nomor Induk Mahasiswa : 100803035
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika Dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Disetujui di Medan, April 2015
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Dr. Elly Rosmaini, M.Si. Dr. Faigiziduhu Bu’ulolo, M.Si.
NIP. 196005201985032002 NIP. 195312181980031003
Disetujui oleh:
Departemen Matematika FMIPA USU Ketua,
ii
PERNYATAAN
APLIKASI METODE BRANCH AND CUT DALAM OPTIMASI PRODUKSI POT BUNGA
(Studi Kasus: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, April 2015
iii
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Allah SWT Yang Maha Pemurah dan
Maha Penyayang, dengan limpahan karunia-Nya penulis dapat menyelesaikan
penyusunan skripsi ini dengan judul Aplikasi Metode Branch and Cut dalam
Optimasi Produksi Pot Bunga (Studi Kasus: UD. Pot Bunga Mukhlis Rangkuti,
Gelugur).
Terimakasih penulis sampaikan kepada Bapak Dr. Faigiziduhu Bu’ulolo,
M.Si selaku pembimbing 1 dan Ibu Dr. Elly Rosmaini, M.Si selaku pembimbing 2
yang telah meluangkan waktunya selama penulisan skripsi ini. Terimakasih
kepada dosen pembanding, Bapak Dr. Syahriol Sitorus, S.Si, M.IT dan Ibu Dra.
Asima Manurung, M.Si atas saran yang membangun dalam penulisan skripsi ini.
Terimakasih kepada Bapak Prof. Dr. Tulus, M.Si dan Ibu Dr. Mardiningsih, M.Si
selaku Ketua dan Sekretaris Departemen Matematika FMIPA USU. Terimakasih
kepada Bapak Dr. Sutarman, M.Sc selaku Dekan FMIPA USU, Pembantu Dekan
FMIPA USU, seluruh Staff dan Dosen Matematika serta rekan-rekan kuliah.
Akhirnya tidak terlupakan kepada Ayahanda Muhammad Dongan dan Ibunda
Hamidah serta saudara-saudari yang selama ini memberikan bantuan dan
iv
APLIKASI METODE BRANCH AND CUT DALAM OPTIMASI PRODUKSI POT BUNGA
(Studi Kasus: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
ABSTRAK
UD. Pot Bunga Mukhlis Rangkuti merupakan usaha kecil dan menengah yang memproduksi pot bunga dengan berbagai bentuk dan ukuran. Perusahaan ini melakukan produksi berdasarkan persediaan bahan baku dan jumlah permintaan yang ada. Oleh karena itu, perusahaan perlu melakukan perencanaan produksi agar dapat memproduksi pot bunga secara optimal. Metode yang digunakan untuk menentukan jumlah produksi optimal adalah metode branch and cut. Metode
branch and cut merupakan gabungan dari metode branch and bound dan metode
cutting plane. Metode ini mampu menyelesaikan permasalahan integer programming dengan lebih baik dibandingkan dengan metode branch and bound
murni. Hasil penelitian diperoleh bahwa terdapat 2 alternatif jumlah produksi optimal dari masing-masing pot bunga, yaitu 70 buah pot segi minimalis, 90 buah pot sampan minimalis, 117 buah pot petak segi besar bonsai, 99 buah pot bulat besar ukir bonsai, 77 buah pot segi ukir bonsai, 68 buah pot guci sedang dan 58 buah pot guci kecil, atau 70 buah pot segi minimalis, 92 buah pot sampan minimalis, 115 buah pot petak segi besar bonsai, 98 buah pot bulat besar ukir bonsai, 81 buah pot segi ukir bonsai, 68 buah pot guci sedang dan 58 buah pot guci kecil dengan kentungan sebesar Rp 11.554.000.
v
APLICATION OF BRANCH AND CUT METHOD IN OPTIMIZATION OF FLOWER POT PRODUCTION
(Case Study: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
ABSTRACT
UD. Pot Bunga Mukhlis Rangkuti are small and medium enterprises which produce the flower pot with a various of shapes and sizes. This company production based on inventory of raw materials and the amount of the demand. Therefore, companies need to make production planning in order to produce an optimal flower pots. The method used to determine the optimal production is the branch and cut method. Branch and cut method is a combination of branch and bound method and cutting plane method. This method is able to solve the integer programming problems better than pure branch and bound method. The results obtained that there are 2 alternative optimal production of each flowerpot, namely 70 pieces square minimalist pots, 90 pieces canoe minimalist pots, 117 pieces large square bonsai pots, 99 large round carved bonsai pots, 77 pieces square carved bonsai pots, 68 medium jar pots and 58 pieces small jar pots, or 70 pieces square minimalist pots, 92 pieces canoe minimalist pots, 115 pieces large square bonsai pots, 98 large round carved bonsai pots, 81 square carved bonsai pots, 68 pieces medium jar pots and 58 pieces small jar pots with profits at Rp 11.554.000.
vi
DAFTAR TABEL viii
DAFTAR LAMPIRAN ix
Bab 1. PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Batasan Masalah 2
1.4 Tinjauan Pustaka 3
1.5 Tujuan Penelitian 5
1.6 Manfaat Penelitian 5
1.7 Metodologi Penelitian 5
1.6.1 Studi Pendahuluan 5
1.6.2 Pengumpulan Data 5
1.6.3 Pengolahan Data 6
Bab 2. LANDASAN TEORI 7
2.1 Perencanaan Produksi 7
2.2 Program Linier 9
2.2.1 Unsur – Unsur Program Linier 10
2.2.2 Asumsi Dasar Program Linier 10
2.3 Program Bilangan Bulat Linier 11
2.4 Metode Simpleks 13
2.4.1 Langkah – Langkah Metode Simpleks 15
2.5 Metode Dual Simpleks 16
3.2.1 Perumusan Fungsi Tujuan 29
3.2.2 Perumusan Fungsi Kendala 30
vii
Bab 4. KESIMPULAN DAN SARAN 67
4.1 Kesimpulan 67
4.2 Saran 68
DAFTAR PUSTAKA 69
viii
DAFTAR TABEL
Nomor Judul Halaman
Tabel
2.1 Tabel Optimum Program Masalah Linier 20
2.2 Setelah Penambahan Pemotongan Fraksional 22
3.1 Data Volume Penjualan Pot Bunga Bulan Januari – Juni 2014 26
3.2 Komposisi Bahan Baku Produk 27
3.3 Persediaan Bahan Baku Selama Satu Bulan 27
3.4 Biaya Produksi Setiap Produk 28
3.5 Harga Jual Produk 28
3.6 Keuntungan Tiap Satu Unit Produk 29
3.7 Jumlah Produksi Pot Bunga Bulan Maret 2015 29
3.8 Iterasi Awal Metode Dual Simpleks 34
3.9 Iterasi 1 Metode Dual Simpleks 36
3.10 Iterasi 2 Metode Dual Simpleks 38
3.11 Iterasi 3 Metode Dual Simpleks 40
3.12 Iterasi 4 Metode Dual Simpleks 42
3.13 Iterasi 5 Metode Dual Simpleks 44
3.14 Iterasi 6 Metode Dual Simpleks 46
3.15 Iterasi 7 Metode Dual Simpleks 48
3.16 Iterasi 8 Metode Dual Simpleks 50
3.17 Iterasi 9 Metode Dual Simpleks 52
3.18 Tabel Simpleks Optimal Sub-Masalah 2 57
3.19 Tabel Simpleks Optimal Sub-Masalah 5 62
3.20 Solusi Optimal 65
ix
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lamp
1 Hasil Perhitungan Sub-Masalah 1 dengan Bantuan Software 70 POM-QM for Windows
2 Hasil Perhitungan Sub-Masalah 2 dengan Bantuan Software 71 POM-QM for Windows
3 Hasil Perhitungan Sub-Masalah 3 dengan Bantuan Software 72 POM-QM for Windows
4 Hasil Perhitungan Sub-Masalah 4 dengan Bantuan Software 73 POM-QM for Windows
5 Hasil Perhitungan Sub-Masalah 5 dengan Bantuan Software 74 POM-QM for Windows
6 Hasil Perhitungan Sub-Masalah 6 dengan Bantuan Software 75 POM-QM for Windows
7 Diagram Penyelesaian dengan Menggunakan Metode Branch 76
and Cut
8 Hasil Perhitungan dengan Metode Branch and Bound 77 Menggunakan Software POM-QM for Windows
iv
APLIKASI METODE BRANCH AND CUT DALAM OPTIMASI PRODUKSI POT BUNGA
(Studi Kasus: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
ABSTRAK
UD. Pot Bunga Mukhlis Rangkuti merupakan usaha kecil dan menengah yang memproduksi pot bunga dengan berbagai bentuk dan ukuran. Perusahaan ini melakukan produksi berdasarkan persediaan bahan baku dan jumlah permintaan yang ada. Oleh karena itu, perusahaan perlu melakukan perencanaan produksi agar dapat memproduksi pot bunga secara optimal. Metode yang digunakan untuk menentukan jumlah produksi optimal adalah metode branch and cut. Metode
branch and cut merupakan gabungan dari metode branch and bound dan metode
cutting plane. Metode ini mampu menyelesaikan permasalahan integer programming dengan lebih baik dibandingkan dengan metode branch and bound
murni. Hasil penelitian diperoleh bahwa terdapat 2 alternatif jumlah produksi optimal dari masing-masing pot bunga, yaitu 70 buah pot segi minimalis, 90 buah pot sampan minimalis, 117 buah pot petak segi besar bonsai, 99 buah pot bulat besar ukir bonsai, 77 buah pot segi ukir bonsai, 68 buah pot guci sedang dan 58 buah pot guci kecil, atau 70 buah pot segi minimalis, 92 buah pot sampan minimalis, 115 buah pot petak segi besar bonsai, 98 buah pot bulat besar ukir bonsai, 81 buah pot segi ukir bonsai, 68 buah pot guci sedang dan 58 buah pot guci kecil dengan kentungan sebesar Rp 11.554.000.
v
APLICATION OF BRANCH AND CUT METHOD IN OPTIMIZATION OF FLOWER POT PRODUCTION
(Case Study: UD. Pot Bunga Mukhlis Rangkuti, Gelugur)
ABSTRACT
UD. Pot Bunga Mukhlis Rangkuti are small and medium enterprises which produce the flower pot with a various of shapes and sizes. This company production based on inventory of raw materials and the amount of the demand. Therefore, companies need to make production planning in order to produce an optimal flower pots. The method used to determine the optimal production is the branch and cut method. Branch and cut method is a combination of branch and bound method and cutting plane method. This method is able to solve the integer programming problems better than pure branch and bound method. The results obtained that there are 2 alternative optimal production of each flowerpot, namely 70 pieces square minimalist pots, 90 pieces canoe minimalist pots, 117 pieces large square bonsai pots, 99 large round carved bonsai pots, 77 pieces square carved bonsai pots, 68 medium jar pots and 58 pieces small jar pots, or 70 pieces square minimalist pots, 92 pieces canoe minimalist pots, 115 pieces large square bonsai pots, 98 large round carved bonsai pots, 81 square carved bonsai pots, 68 pieces medium jar pots and 58 pieces small jar pots with profits at Rp 11.554.000.
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Persaingan pasar yang semakin meningkat menuntut perusahaan menyusun
strategi dengan baik agar mampu bertahan. Perusahaan harus membuat keputusan
yang tepat dengan mempertimbangkan batasan-batasan yang ada. Dalam suatu
usaha, batasan tersebut dapat berupa ketersediaan bahan baku, peralatan, mesin,
waktu, biaya, dan tenaga kerja. Keputusan-keputusan dalam dunia usaha
mengandung resiko besar yang perlu didukung oleh perhitungan-perhitungan yang
teliti untuk menghindari resiko kerugian. Dalam hal ini
pertimbangan-pertimbangan naluriah saja tidak cukup, sehingga diperlukan peralatan-peralatan,
teknik-teknik atau metode-metode kuantitatif yang lebih lengkap untuk
menyelesaikannya. Salah satu keputusan yang harus diambil adalah dalam hal
perencanaan produksi. Perencanaan produksi merupakan perencanaan tentang
produk apa saja dan berapa jumlah yang akan diproduksi oleh perusahaan dalam
waktu satu periode yang akan datang. Perencanaan produksi bertujuan untuk
optimasi produksi sehingga dapat memaksimalkan pendapatan. Salah satu cara
untuk optimasi perencanaan produksi adalah dengan menggunakan metode
branch and cut.
UD. Pot Bunga Mukhlis Rangkuti merupakan usaha kecil dan menengah
yang memproduksi pot bunga dengan berbagai bentuk dan ukuran. Usaha ini
merupakan usaha turun temurun yang pada awalnya dikelola oleh kakeknya alm.
Ali. Dalam proses produksi, pengusaha melakukan perencanaan produksi hanya
berdasarkan intuisi dan jumlah pesanan yang ada. Usaha ini sering dihadapkan
pada kondisi bahwa produk yang diminta pelanggan belum siap untuk dipakai
tetapi pelanggan tetap mendesak untuk membelinya. Hal ini menyebabkan produk
tersebut mudah rusak dan berpotensi membuat tingkat kepercayaan pelanggan
perencanaan produksi yang optimal. Untuk mengoptimalkan jumlah produksi
tersebut digunakan metode branch and cut.
Metode branch and cut adalah pendekatan yang dilakukan dengan
memadukan metode branch and bound dan cuting plane sebagai pendekatan
model program integer. Kombinasi kedua pendekatan tersebut merupakan
kombinasi yang baik untuk digunakan sebagai penyelesaian dalam persoalan
program integer (Taruna, 2011).
1.2 Perumusan Masalah
Berdasarkan latar belakang di atas maka yang menjadi rumusan masalah dalam
penelitian ini adalah bagaimana mengoptimalkan jumlah produksi pot bunga
dengan menggunakan metode branch and cut sehingga perusahaan dapat
memperoleh keuntungan yang maksimal.
1.3 Batasan Masalah
Batasan masalah dalam penelitian ini adalah:
1. Variabel keputusan dalam penelitian ini adalah jumlah masing-masing jenis
pot bunga yang akan diproduksi, yaitu:
�1 = Banyaknya pot bunga jenis segi minimalis diproduksi
�2 = Banyaknya pot bunga jenis sampan minimalis diproduksi
�3 = Banyaknya pot bunga jenis petak segi besar bonsai diproduksi
�4 = Banyaknya pot bunga jenis bulat besar ukir bonsai diproduksi
�5 = Banyaknya pot bunga jenis segi ukir bonsai diproduksi
�6 = Banyaknya pot bunga jenis guci sedang diproduksi
�7 = Banyaknya pot bunga jenis guci kecil diproduksi
2. Permasalahan optimalisasi produksi dalam penelitian ini dibatasi pada kendala
berupa ketersediaan bahan baku dan jumlah permintaan.
3. Data yang diambil adalah data satu kali tahapan produksi dan data bulan
4. Kondisi perusahaan dianggap dalam keadaan normal serta faktor-faktor lain
dianggap tidak mempengaruhi proses produksi.
5. Biaya penyimpanan dianggap tidak ada.
6. Waktu produksi produk tidak diperhitungkan.
1.4 Tinjauan Pustaka
Banyak metode yang dapat digunakan untuk menyelesaikan permasalahan linear
programming, di antaranya adalah metode grafik, metode interior point, metode
simpleks dan metode dual Simpleks. Dalam solusi yang diperoleh dengan
menggunakan metode tersebut terkadang masih terdapat beberapa variabel yang
tidak bernilai integer. Dalam kehidupan sehari-hari sering ditemukan
permasalahan optimasi yang mengandung kendala linier di mana seluruh atau
beberapa variabel keputusannya harus bernilai integer. Permasalahan ini
dinyatakan sebagai masalah integer linear programming. Permasalahan integer
linear programming tersebut dapat diselesaikan dengan berbagai metode di
antaranya adalah metode branch and bound, metode cuting plane dan metode
branch and cut.
Model awal dari Integer Linear Programming (ILP) dinyatakan dengan:
Maximum ���
Kendala: �� ≤ �
� ∈ �+ 1.1
di mana x dan c adalah vektor dengan jumlah elemen sebanyak n dan b adalah
vektor dengan jumlah elemen sebanyak m dan A adalah matriks ��, dan solusi
penyelesaian diperoleh dari variabel yang bersifat biner (Taruna, 2011).
Konsep dasar dari metode branch and bound adalah membagi dan
menyelesaikan. Karena masalah awal sulit untuk diselesaikan secara langsung,
maka masalah awal tersebut dibagi menjadi sub-masalah yang lebih kecil hingga
Operasi pencabangan pada metode branch and bound akan menelusuri
semua solusi integer fisibel yang mungkin, sedangkan konsep pembatasan dipakai
untuk mempersempit daerah yang layak penelusuran sehingga beberapa solusi
integer fisibel yang tidak potensial bisa dibuang. Dengan demikian, algoritma
pada teknik pencabangan dan pembatasan akan selalu konvergen dengan
ditemukannya solusi optimum integer atau diperoleh kesimpulan bahwa masalah
semula tidak fisibel (Sinurat, 2008).
Ide mendasar dari metode cutting plane adalah bahwa solusi integer
optimal berada dekat dengan solusi program linier, namun tidak berada pada
perpotongan kendala sehingga diperlukan kendala tambahan. Akibatnya, beberapa
kendala ditambahkan untuk menekan solusi program linier yang tidak integer
menjadi tidak layak tanpa menghilangkan setiap solusi integer. Hal ini dilakukan
dengan menambahkan sebuah kendala untuk menekan variabel nonbasis menjadi
lebih besar daripada sebuah nilai kecil tak nol (McCarl & Spreen, 1997).
Metode branch and cut dapat digunakan untuk menyelesaikan berbagai
masalah. Penelitian yang dilakukan oleh Amalia (2014) membahas tentang
implementasi metode branch and cut untuk menyelesaikan masalah multiobjektif
integer programming. Dalam penelitian ini diperoleh bahwa kinerja metode
branch and cut dalam menyelesaikan masalah multiobjektif integer programming
lebih efektif dibandingkan dengan metode branch and bound dan cutting plane.
Masalah lainnya yang dapat diselesaikan dengan metode branch and cut di
antaranya adalah masalah program stokastik biner campuran (Ardiana, 2012),
minimum cost multi-level network design (Chopra dan Tsai, 1998) dan traveling
1.5 Tujuan Penelitian
Tujuan dari penelitian ini adalah menentukan jumlah produksi pot bunga optimal
sehingga dapat memaksimalkan keuntungan dengan menggunakan metode branch
and cut.
1.6 Manfaat Penelitian
Manfaat dari penelitian ini adalah sebagai berikut:
1. Mengetahui jumlah produksi pot bunga yang optimal dengan menggunakan
metode branch and cut.
2. Hasil dari penelitian ini diharapkan dapat digunakan sebagai tambahan
referensi bagi pengusaha pot bunga untuk membuat keputusan yang lebih
baik dalam hal perencanaan produksi.
3. Hasil Penelitian ini diharapkan dapat digunakan sebagai tambahan informasi
dan referensi bacaan bagi peneliti selanjutnya yang akan
melakukan penelitian yang berkaitan.
1.7 Metodologi Penelitian 1.7.1 Studi Pendahuluan
Untuk memecahkan masalah yang ada sampai kepada tahap menganalisis dan
mengambil keputusan diperlukan studi pendahuluan berupa studi literatur.
1.7.2 Pengumpulan Data
Dalam melakukan penelitian, penulis mengumpulkan data sekunder yang
diperoleh dari perusahaan. Data-data yang dibutuhkan dalam penelitian ini adalah
sebagai berikut:
1. Data penjualan pot bunga pada bulan Januari – Juni 2014.
2. Data komposisi bahan baku yang diperlukan dari setiap jenis pot bunga.
3. Data biaya produksi pot bunga.
1.7.3 Pengolahan Data
1. Formulasi Fungsi
a. Penentuan Variabel Keputusan
Variabel keputusan merupakan output yang akan dioptimalkan sehingga
memenuhi kriteria tujuan dan kendala.
b. Perumusan Fungsi Tujuan
Dalam penelitian ini yang dijadikan sebagai fungsi tujuannya adalah
maksimasi keuntungan penjualan pot bunga. Koefisien dari variabel
keputusannya adalah keuntungan dari masing-masing jenis pot bunga.
c. Perumusan Fungsi Kendala
Fungsi kendala dirumuskan berdasarkan persediaan bahan baku yaitu
semen, pasir, kawat, cat hitam, cat wash, cat retak dan tiner serta jumlah
permintaan pot bunga.
2. Penyelesaian Model
Model diselesaikan secara iterative menggunakan metode branch and cut dan
bantuan software POM-QM for Windows.
3. Membuat Kesimpulan
Langkah terakhir dalam metode penelitian ini adalah membuat kesimpulan
BAB 2
LANDASAN TEORI
2.1 Perencanaan Produksi
Produksi yang dalam bahasa inggris disebut production adalah keseluruhan proses
yang dilakukan untuk menghasilkan produk atau jasa. Produk yang dihasilkan
sebagai output dari proses tersebut dapat berupa produk akhir (finished product)
yang sering disebut juga produk jadi, produk setengah jadi (work-in-process) atau
bahan baku (raw materials) yang semuanya bersifat tangible (berwujud fisik).
Jasa (services) adalah output yang bersifat intangible (berwujud non-fisik).
Aktifitas produksi sebagai suatu bagian dari fungsi organisasi perusahaan
bertanggung jawab terhadap pengolahan bahan baku menjadi produk jadi yang
dapat dijual. Untuk melaksanakan fungsi produksi tersebut diperlukan rangkaian
kegiatan yang akan membentuk suatu sistim produksi.
Sistim produksi merupakan kumpulan dari sub-sistim yang saling
berinteraksi dengan tujuan mentransformasi input produksi menjadi output
produksi. Input produksi ini dapat berupa bahan baku, mesin, tenaga kerja, modal
dan informasi sedangkan output produksi merupakan produk yang dihasilkan
berikut hasil sampingannya seperti limbah, informasi, dan sebagainya. Sub-sistim
dari sistim produksi tersebut antara lain adalah perencanaan dan pengendalian
produksi, pengendalian kualitas, penentuan standar-standar operasi, penentuan
fasilitas produksi, perawatan fasilitas produksi dan penentuan harga pokok
produksi.
Tujuan akhir dari suatu perusahaan adalah untuk memperoleh keuntungan
disamping tercapainya kelanjutan dan pengembangan usaha. Salah satu fungsi
yang terpenting dalam mendukung usaha untuk mencapai tujuan tersebut adalah
perencanaan produksi. Perencanaan produksi dapat didefinisikan sebagai proses
produksi atau operasi sehingga permintaan pasar dapat dipenuhi dengan jumlah
yang tepat.
The American Production and Inventory Control Society mendefinisikan
perencanaan produksi sebagai suatu kegiatan yang berkenaan dengan penentuan
apa yang harus diproduksi, berapa banyak diproduksi, kapan diproduksi, dan apa
sumber daya yang dibutuhkan untuk mendapatkan produk yang telah ditetapkan
(Sinulingga, 2009).
Perencanaan produksi dilakukan dengan tujuan menentukan arah awal dari
tindakan-tindakan yang harus dilakukan di masa mendatang, apa yang harus
dilakukan, berapa banyak melakukannya, dan kapan harus melakukan. Karena
perencanaan ini berkaitan dengan masa mendatang, maka perencanaan disusun
atas dasar perkiraan yang dibuat berdasarkan data masa lalu dengan menggunakan
beberapa asumsi.
Kegunaan dari pelaksanaan perencanaan produksi adalah:
1. Suatu perencanaan meliputi usaha untuk menetapkan tujuan yang dipilih
untuk dicapai sehingga dengan adanya perencanaan produksi dapat
memberikan arah bagi setiap kegiatan produksi. Dengan adanya kejelasan
arah tersebut maka kegiatan akan dapat dilaksanakan dengan efektif.
2. Dengan perencanaan produksi yang berisi formulasi tujuan yang hendak
dicapai maka akan memungkinkan untuk mengetahui apakah tujuan tersebut
telah tercapai atau tidak. Dengan demikian, koreksi-koreksi terhadap
penyimpangan dari tujuan yang telah ditetapkan dapat diketahui secepatnya
sehingga pemborosan dan usaha yang tidak menunjang pencapaian tujuan
dapat dihindari.
3. Memudahkan pelaksanaan kegiatan untuk mengidentifikasi
hambatan-hambatan yang mungkin muncul dalam usaha pencapaian tujuan tersebut.
4. Menghindarkan pertumbuhan dan perkembangan yang tidak terkendali.
selalu menambah jumlah dan jenis tenaga kerja yang sudah dimiliki untuk
memperbaiki mutu serta jumlah output.
2.2 Program Linier
Konsep linear programming ditemukan dan diperkenalkan pertama kali oleh
George Dantzig. Program linier merupakan suatu metode untuk membuat
keputusan di antara berbagai aternatif kegiatan dibatasi oleh kendala tertentu.
Keputusan yang diambil dinyatakan sebagai fungsi tujuan sedangkan
kendala-kendala yang dihadapi dalam membuat keputusan tersebut dinyatakan dalam
bentuk fungsi-fungsi kendala. Fungsi tujuan dan fungsi kendala tersebut berupa
fungsi linier, baik dalam bentuk persamaan maupun pertidaksamaan pada
variabel-variabel keputusannya.
Bentuk umum dari permasalahan LP adalah:
Maximum ���
Kendala: �� ≤ � 2.1
Beberapa contoh aplikasi LP yang telah berhasil diterapkan dalam bidang
militer, industri, dan sosial adalah:
1. Mengembangkan jadwal produksi yang bertujuan memuaskan konsumen
terhadap produk yang dikonsumsikan dan pada saat yang sama dapat
meminimalisasi biaya produksi dan persediaan.
2. Penentuan kombinasi produk (product-mix), yaitu menentukan produk mana
dari sejumlah alternatif kemungkinan produksi yang dapat memaksimalkan
keuntungan.
3. Penentuan sistim distribusi yang akan meminimalisasi biaya total pengiriman
dengan menggunakan mobil box dari gudang ke berbagai pasar.
4. Menganalisis portofolio investasi dari berbagai alternatif investasi dalam
saham dan obligasi sehingga seorang investor dapat menentukan portofolio
5. Menentuan penjadwalan untuk melakukan aktifitas produksi bagi tenaga kerja
di perusahaan.
2.2.1 Unsur – Unsur Program Linier
Adapun unsur-unsur dalam program linier adalah:
a. Variabel Keputusan
Variabel keputusan adalah variabel yang menguraikan secara lengkap
keputusan-keputusan yang akan dibuat. Variabel keputusan ini tidak negatif.
b. Fungsi Tujuan
Adapun tujuan dalam program linier adalah masalah optimasi yakni tujuan
memaksimumkan atau meminimumkan sesuatu di mana tingkat pencapaian
tujuan ini dibatasi oleh kendala yang mencerminkan keterbatasan yang
dimiliki.
c. Kendala Tujuan
Kendala merupakan batasan-batasan yang harus diperhatikan dalam
penyelesaian program linier. Kendala tersebut dibuat dalam fungsi linier.
2.2.2 Asumsi Dasar Program Linier
Dalam model program linier terdapat asumsi-asumsi yang harus dipenuhi agar
permasalahan program linier menjadi absah, adapun asumsi program linieradalah
sebagai berikut:
1. Asumsi kesebandingan (proposionality)
a. Kontribusi setiap variabel keputusan terhadap fungsi tujuan adalah
sebanding dengan nilai variabel keputusan.
b. Kontribusi suatu variabel keputusan terhadap ruas kiri dari setiap
pembatas juga sebanding dengan nilai variabel keputusan itu.
2. Asumsi penambahan (additivity)
a. Kontribusi setiap variabel keputusan terhadap fungsi tujuan tidak
b. Kontribusi suatu variabel keputusan terhadap ruas kiri dari setiap
pembatas bersifat tidak bergantung pada nilai dari variabel keputusan
yang lain.
3. Asumsi pembagian (divisibility)
Dalam persoalan program linier, variabel keputusan boleh diasumsikan
berupa bilangan pecahan.
4. Asumsi kepastian (certainty)
Setiap parameter, yaitu koefisien fungsi tujuan, ruas kanan, dan koefisien
teknologi, diasumsikan dapat diketahui secara pasti.
2.3 Program Bilangan Bulat Linier
Program bilangan bulat linier (Integer Linear Programming / ILP) adalah bentuk
khusus dari permasalahan program linier di mana pada solusi optimalnya
beberapa atau seluruh variabelnya dibatasi harus berupa bilangan bulat (integer)
tak negatif. ILP digunakan untuk memodelkan permasalahan yang mengandung
variabel keputusan yang harus bernilai integer, misalnya variabel yang
menggambarkan jumlah orang atau jumlah unit produk yang akan diproduksi.
Permasalahan di mana seluruh variabelnya dibatasi harus berupa integer
tak negatif disebut permasalahan program integer linier murni (Pure Integer
Linear Programming / PILP). Jika hanya beberapa variabel saja yang harus
bernilai integer, permasalahan ini disebut sebagai permasalahan integer linier
campuran (Mixed Integer Linear Programming / MILP). Dalam suatu kondisi
khusus di mana seluruh variabel keputusan dalam suatu masalah harus bernilai 0
atau 1 maka permasalahan tersebut disebut Binary Integer Linear Programming
�������: � �����
��� = Koefisien dari variabel keputusan dalam kendala ke-i
�� = Sumber daya yang tersedia dalam kendala ke-i
Banyak permasalahan yang dapat dimodelkan sebagai program integer,
misalnya dalam ilmu pengetahuan, teknologi, bisnis dan lingkungan, oleh karena
itu tidak mengherankan bahwa banyak metode penyelesaian dan kode yang
muncul untuk menyelesaikan program integer. Beberapa metode dapat digunakan
untuk seluruh tipe ILP dan beberapa metode hanya diperuntukkan untuk
menyelesaikan suatu masalah ILP tertentu.
Pada dasarnya, solusi integer optimal berada dekat dengan solusi program
linier. Titik-titik yang berada dalam daerah fisibel (feasible region) berupa
titik-titik yang fisibel sebagai koordinat yang bernilai integer disebut integer lattice
points. Pemecahan persoalan LP biasa terletak pada batas luar dari daerah
fisibelnya, khususnya pada titik-titik ekstrimnya yang disebut vertex.
Misalkan daerah fisibel tersebut dapat diciutkan menjadi convex hull of the
feasible lattice points, di mana convex hull merupakan daerah convex terkecil
yang memuat semua titik-titik lattice. Convex hull diperoleh sebagai hasil
modifikasi dari persoalan asli dengan jalan menambahkan kendala linier baru.
1. Mencakup setiap pemecahan integer yang fisibel terhadap persoalan asli. Jadi
pemecahan yang menghasilkan bilangan-bilangan bulat atau integer masih
merupakan penyelesaian dari persoalan LP yang asli.
2. Setiap pemecahan dasar dari persoalan baru merupakan pemecahan integer.
Pemecahan dasar optimal dari persoalan yang baru juga merupakan
pemecahan optimal dari permasalahan LP yang asli namun berupa integer.
Dalam prakteknya sukar untuk memotong daerah fisibel menjadi convex
hull of the feasible lattice points sehingga diperlukan metode yang terdiri dari
urutan langkah-langkah dengan jalan selalu menambahkan kendala baru terhadap
persoalan asli sebagai kelanjutan dari hasil perhitungan sebelumnya. Konsep
inilah yang diterapkan dalam metode branch and bound, cutting plane dan metode
branch and cut.
2.4 Metode Simpleks
Masalah program linier berkembang pesat setelah ditemukan suatu metode
penyelesaian program linier yaitu metode simpleks yang ditemukan oleh George
Dantzig pada tahun 1947. Permasalahan linier sederhana yang mengandung dua
atau tiga variabel dapat diselesaikan dengan menggunakan metode grafik. Namun
untuk masalah program linier yang mengandung lebih dari tiga variabel, metode
grafik tidak dapat digunakan sehingga diperlukan metode yang dapat digunakan
untuk menyelesaiakan masalah program linier yang rumit. Metode simpleks
adalah metode yang dapat menyelesaiakan masalah program linier dengan jumlah
variabel yang besar.
Penyelesaian model program linier dengan menggunakan metode simpleks
memerlukan pengubahan model formulasi ke dalam bentuk standar dengan syarat
sebagai berikut:
1. Semua kendala berbentuk pertidaksamaan yang dibatasi oleh kendala lebih
variable. Untuk pertidaksamaan yang dibatasi oleh tanda lebih besar (≥)
diubah ke dalam bentuk persamaan dengan menambahkan surplusvariable.
2. Nilai ruas kanan setiap kendala bertanda positif, jika nilai ruas kanan dari
suatu kendala bertanda negative maka harus diubah menjadi positif dengan
mengalikan pertidaksamaan dengan -1.
3. Semua variabel keputusan bernilai nonnegatif.
Ada beberapa istilah yang sangat sering digunakan dalam metode
simpleks, di antaranya:
1. Iterasi adalah tahapan perhitungan di mana nilai dalam perhitungan itu
tergantung dari nilai tabel sebelumnya.
2. Variabel nonbasis adalah variabel yang nilainya diatur menjadi nol pada
sembarang iterasi. Dalam terminologi umum, jumlah variabel nonbasis selalu
sama dengan derajat bebas dalam sistim persamaan.
3. Variabel basis merupakan variabel yang nilainya bukan nol pada sembarang
iterasi. Pada solusi awal, variabel basis merupakan variabel slack (jika fungsi
kendala merupakan pertidaksamaan ≤ ) atau variabel buatan (jika fungsi
kendala menggunakan pertidaksamaan ≥ atau =). Secara umum, jumlah
variabel basis selalu sama dengan jumlah fungsi pembatas (tanpa fungsi non
negatif).
4. Solusi atau nilai kanan merupakan nilai sumber daya pembatas yang masih
tersedia. Pada solusi awal, nilai kanan atau solusi sama dengan jumlah
sumber daya pembatas awal yang ada, karena aktivitas belum dilaksanakan.
5. Variabel slack adalah variabel yang ditambahkan ke model matematika
kendala untuk mengkonversikan pertidaksamaan ≤ menjadi persamaan (=).
Penambahan variabel ini terjadi pada tahap inisialisasi. Pada solusi awal,
variabel slack akan berfungsi sebagai variabel basis.
6. Variabel surplus adalah variabel yang dikurangkan dari model matematika
kendala untuk mengkonversikan pertidaksamaan ≥ menjadi persamaan (=).
Penambahan ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel
7. Variabel buatan adalah variabel yang ditambahkan ke model matematika
kendala dengan bentuk ≥ atau = untuk difungsikan sebagai variab el basis
awal. Penambahan variabel ini terjadi pada tahap inisialisasi. Variabel ini
harus bernilai 0 pada solusi optimal, karena kenyataannya variabel ini tidak
ada. Variabel hanya ada di atas kertas.
8. Kolom pivot (kolom kerja) adalah kolom yang memuat variabel masuk.
Koefisien pada kolom ini akan menjadi pembagi nilai kanan untuk
menentukan baris pivot (baris kerja).
9. Baris pivot (baris kerja) adalah salah satu baris dari antara variabel basis yang
memuat variabel keluar.
10. Elemen pivot (elemen kerja) adalah elemen yang terletak pada perpotongan
kolom dan baris pivot. Elemen pivot akan menjadi dasar perhitungan untuk
tabel simpleks berikutnya.
2.4.1 Langkah-Langkah Metode Simpleks
Algoritma metode simpleks untuk persoalan maksimasi:
1. Konversikan formulasi model program linier ke dalam bentuk standar.
2. Cari Solusi Basis Feasible (BFS).
3. Jika seluruh variabel nonbasis (NBV) mempunyai koefisien nonnegatif
(artinya berharga positif atau nol) pada baris fungsi tujuan [baris persamaan �
yang biasa disebut baris 0 atau baris (�� − ��)], maka BFS sudah optimal.
Jika pada baris 0 masih ada variabel dengan koefisien negatif, pilihlah salah
satu variabel yang mempunyai paling negatif pada baris 0 itu. Variabel ini
akan memasuki status variabel basis, karena itu variabel ini disebut sebagai
variabel yang masuk basis (entering variable, disingkat EV).
4. Hitung rasio dari ruas kanan atau (koefisien EV) pada setiap baris di mana
EV mempunyai koefisien positif. Variabel basis pada baris pembatas dengan
rasio positif terkecil akan berubah status menjadi variabel nonbasis. Variabel
ini kemudian disebut sebagai variabel yang meninggalkan basis (leaving
5. Lakukan operasi baris elementer (ERO) untuk membuat koefisien EV pada
baris dengan rasio positif terkecil ini menjadi bernilai 1 dan bernilai 0 pada
baris-baris lainnya.
6. Kembali ke langkah 3.
2.5 Metode Dual Simpleks
Apabila pada suatu iterasi diperoleh persoalan program linier yang sudah
optimum (berdasarkan kondisi optimalitas), tetapi belum fisibel (ada pembatas
nonnegatif yang tidak terpenuhi), maka persoalan tersebut harus diselesaikan
dengan menggunakan metode dual Simpleks. Syarat digunakannya metode ini
adalah bahwa seluruh pembatas harus merupakan ketidaksamaan yang bertanda
(≤), sedangkan fungsi tujuan bisa berupa maksimasi atau minimasi.
Pada dasarnya metode dual Simpleks ini menggunakan tabel yang sama
seperti metode simpleks pada primal, tetapi leaving dan entering variable-nya
ditentukan sebagai berikut:
1. Leaving variable (kondisi fisibilitas)
Yang menjadi leaving variable pada dual Simpleks adalah variabel basis yang
memiliki harga negatif terbesar. Jika semua variabel basis telah berharga
positif atau nol, berarti keadaan fisibel telah tercapai.
2. Entering variable (kondisi optimalitas)
a. Tentukan perbandingan (rasio) antara koefisien persamaan z dengan
koefisien persamaan leaving variable. Abaikan penyebut yang positif
atau nol. Jika semua penyebut berharga positif atau nol, berarti persoalan
yang bersangkutan tidak memiliki solusi fisibel.
b. Untuk persoalan minimasi, entering variable adalah variabel dengan
rasio terkecil, sedangkan persoalan maksimasi, entering variable adalah
2.6 Metode Branch and Bound
Metode branch and bound pertama kali dkembangkan pada tahun 1960 oleh Land
dan G. Doig yang digunakan untuk menyelesaikan masalah mixed integer linear
programming dan pure integer linear programming secara umum. Selanjutnya
pada tahun 1965 E. Balas mengembangkan algoritma tambahan untuk
menyelesaiakan masalah binary integer linear programming.
Metode branch and bound awalnya hanya digunakan untuk menyelesaikan
masalah program integer. Setelah diteliti lebih lanjut, ternyata metode ini juga
dapat digunakan untuk menyelesaikan masalah lainnya seperti traveling salesman
problem, scheduling dan sebagainya. Ide mendasar dari metode ini adalah
membagi daerah layak menjadi beberapa sub-bagian yang mengandung titk-titik
fisibel dengan koordinat integer dengan menambahkan kendala tambahan
kemudian menyelesaikannya.
Untuk menyelesaikan suatu masalah program integer dengan
menggunakan metode branch and bound, langkah pertama adalah mengabaikan
kendala integer dari permasalahan awal sehingga terbentuk permasalahan LP
relaksasi kemudian diselesaikan. Banyak metode yang dapat digunakan untuk
menyelesaiakan permasalahan LP relaksasi. Namun, metode yang umum
digunakan adalah metode simpleks. Jika permasalahan tersebut tidak mempunyai
penyelesaian optimum yang bernilai integer, maka dua kendala baru dibentuk.
Kendala tersebut adalah batas atas dan bawah dari variabel yang dibatasi harus
bernilai integer namun belum bernilai integer.
Konsep dasar dari metode branch and bound adalah pengamatan terhadap
tiap-tiap nilai ��, di mana �� adalah variabel yang dibatasi harus bernilai integer.
Jika nilai �� belum integer, maka masalah awal dibagi menjadi dua masalah baru
dengan menambahkan dua kendala baru yaitu, ���� ≤ �� dan �� ≤ ����+ 1 di
mana ���� adalah integer terdekat yang lebih kecil dari ��. Proses inilah yang
dinamakan branching (pencabangan). Dalam kasus maksimasi, solusi awal
pencabangan masalah akan mengakibatkan berkurangnya nilai fungsi tujuan pada
solusi optimal.
Sebagai salah satu hasil pencabangan variabel yang belum integer pada
setiap cabang, satu dari dua kejadian berikut akan terjadi. Yang pertama, solusi
yang diperoleh tidak memenuhi syarat integer dari variabel yang dicabangkan, dan
memperoleh nilai fungsi objektif yang kurang sesuai dibandingkan dengan
pencabangan lain yang semua solusinya sudah integer, dalam kasus ini
pencabangan dilanjutkan. Yang kedua, mungkin diperoleh solusi lain yang sudah
memenuhi syarat integer, dalam kasus ini pencabangan dihentikan.
Terdapat dua tahap yang dipakai dalam algoritma branch and bound,
yaitu:
1. Pencabangan, yaitu mempartisi masalah tersebut menjadi beberapa
sub-masalah dengan cara menambahkan kendala yang merupakan syarat perlu
untuk mencari solusi integer fisibel tanpa mengubah himpunan solusi integer
semula.
2. Pembatasan, yaitu nilai fungsi objektif dari suatu sub-masalah yang
mempunyai solusi integer dipakai sebagai batas nilai fungsi objektif dari
sub-masalah lainnya.
Branch and bound adalah algoritma yang paling umum digunakan untuk
menyelesaikan masalah integer programming. Algoritma branch and bound juga
telah banyak digunakan sebagai kode program computer, misalnya OSL,
LAMPU, dan LINDO.
Berikut ini adalah langkah-langkah penyelesaian suatu masalah
maksimisasi dengan metode branch and bound:
1. Selesaikan masalah program linier relaksasi dengan metode simpleks.
2. Teliti solusi optimalnya, jika variabel keputusan yang diharapkan adalah
integer, solusi optimum integer telah tercapai. Jika satu atau lebih variabel
3. Jadikan solusi pada penyelesaian langkah 1 menjadi batas atas dan untuk
batas bawahnya merupakan solusi yang variabel keputusannya telah
dibulatkan (rounded–down).
4. Pilih variabel yang mempunyai nilai pecahan terbesar (artinya bilangan
desimal terbesar) dari masing-masing variabel untuk dijadikan pencabangan
ke dalam sub-masalah. Tujuannya adalah untuk menghilangkan solusi yang
tidak memenuhi persyaratan integer dalam masalah itu. Pencabangan itu
dilakukan secara mutually exclusive untuk memenuhi persyaratan integer
dengan jaminan tidak ada solusi fisibel (layak) yang diikutsertakan.
5. Untuk setiap sub-masalah, nilai optimum fungsi tujuan ditetapkan sebagai
batas atas. Solusi optimum yang dibulatkan menjadi batas bawah (solusi yang
sebelumnya tidak bulat kemudian dibulatkan). Sub-masalah yang memiliki
batas atas kurang dari batas bawah yang ada, tidak diikutsertakan pada analisa
selanjutnya. Suatu solusi integer fisibel (layak) adalah sama baik atau lebih
baik dari batas atas untuk setiap sub-masalah yang dicari. Jika solusi yang
demikian terjadi, suatu sub-masalah dengan batas atas terbaik dipilih untuk
dicabangkan. Kembali ke langkah 4.
2.7 Metode Cutting Plane
Metode cutting plane yang digunakan untuk menyelesaikan masalah secara
umum, pertama kali dikemukakan oleh Gomory (1963). Metode cutting plane
merupakan metode yang digunakan untuk menyelesaikan program integer linier,
baik integer murni maupun campuran dengan penambahan batasan baru yang
disebut gomory. Batasan gomory diberikan jika nilai dari variabel keputusan
belum integer (bernilai pecahan). Batasan-batasan tersebut secara efektif akan
menyingkirkan beberapa ruang penyelesaian yang tidak berisi titik integer yang
layak, tetapi tidak pernah menyingkirkan satupun titik integer yang layak (Taha,
1996).
1. Selesaikan masalah program integer dengan menggunakan metode simpleks.
Masalah sederhana dapat diselesaikan dengan pendekatan grafik, sehingga
pendekatan gomory kurang efisien.
2. Periksa solusi optimum. Jika semua variabel basis memiliki nilai integer,
solusi optimum integer telah diperoleh dan proses solusi telah berakhir. Jika
satu atau lebih variabel basis masih meiliki nilai pecah, teruskan ke tahap 3.
3. Buatlah suatu batasan gomory dan cari solusi optimum melalui prosedur dual
Simpleks. Kembali ke tahap 2 (Taha, 1996).
Misalnya diberikan sebuah permasalahan integer programming berikut:
Tabel 2.1 Tabel Optimum Masalah Program Linier
Basis �1 … �� … �� �1 … �� … �� Hasil
Tentukan baris sumber dengan menentukan baris variabel keputusan yang
akan dibulatkan. Jika lebih dari satu, dipilih nilai pecahan terbesar.
Disimpulkan bahwa 0 <�� < 1 dan 0 <��� < 1, yang mana �� dan ���
adalah pecahan positif, sehingga:
�� = ��− � �����
Persamaan 2.4 haruslah integer yang berakibat sisi kiri juga harus integer. Karena
��� ≥0 dan �� ≥0 untuk semua i dan j maka:
batasannya dapat ditulis dalam bentuk:
��� =� �����
�
�=1
− ��
atau,
Tabel 2.2 Setelah Penambahan Pemotongan Fraksional
Basis �1 … �� … �� �1 … �� … �� ��� Hasil
di mana ��� adalah variabel slack nonnegatif yang berdasarkan definisinya
haruslah integer. Persamaan batasan ini mendefinisikan pemotong fraksional. Dari
Tabel 2.2 �� = 0 dan ��� =−�� tidak layak. Ini berarti bahwa batasan baru
tersebut tidak dipenuhi oleh solusi yang diberikan. Metode dual Simpleks dapat
dipergunakan untuk mengatasi ketidaklayakan ini yang setara dengan memotong
bidang solusi ke arah solusi integer optimal.
Jika solusi baru (setelah menerapkan metode dual Simpleks) adalah integer,
proses berakhir. Jika tidak, sebuah gomory baru ditambahkan dari tabel yang
dihasilkan dan metode dual Simpleks kembali digunakan untuk mengatasi
ketidaklayakan. Prosedur ini dilakukan sampai solusi integer dicapai. Jika di salah
satu iterasi metode dual Simpleks menunjukkan bahwa tidak ada solusi layak,
2.8 Metode Branch and Cut
Banyak permasalahan optimisasi dapat diformulasikan sebagai masalah Integer
Linear Programming (ILP). Masalah tersebut dapat diselesaikan dengan metode
branch and bound dan metode branch and cut. Algoritma metode branch and cut
dibuat dari kombinasi metode cutting-plane dengan metode branch and bound.
Prosedur metode branch and cut adalah menyelesaikan rangkaian relaksasi
program linier dari masalah integer linear programming. Metode cutting plane
memperbaharui relaksasi dari masalah untuk lebih mendekati penyelesaian berupa
integer, dan metode branch and bound memproses dengan membagi dan
menyelesaikan (devide and conquer) masalah.
Misalkan bahwa titik �∗ adalah solusi layak untuk linear programming. Jika
�∗ berada pada daerah integral, maka � merupakan solusi optimal untuk integer linear programming sudah diperoleh. Jika tidak, maka nilai fungsi objektif
merupakan batas atas dari nilai optimum, tetapi dibutuhkan penyelesaian lebih
lanjut untuk memperoleh nilai optimum berupa integer. Dengan penambahan
bidang pemotongan (cutting plane) atau membagi masalah tersebut menjadi
bagian-bagian masalah (branch).
Mitchell (1999) menjelaskan bahwa secara umum algoritma branch and
cut adalah sebagai berikut:
1. Inisialisasi: nyatakan persoalan awal ke dalam bentuk ILP0dan titik-titik aktif
menjadi �= {���0}. Tetapkan batas bawah menjadi �= −∞. Tetapkan
�� = +∞ untuk sebuah persoalan � ∈ �.
2. Penghentian proses: jika �= ∅ maka solusi �∗ yang menghasilkan nilai �
objektif yang terbaik merupakan solusi optimal. Jika tidak ditemukan �∗
(misalnya, �=−∞) maka ILP tidak layak.
3. Pemilihan masalah: pilih dan hilangkan masalah ���� dari L.
4. Relaksasi: selesaikan relaksasi program linier dari ����. Jika relaksasi tidak
layak, tetapkan �� = −∞ dan lanjut ke langkah 6. Misalkan � merupakan nilai
objektif optimal dari relaksasi dan misalkan ��� merupakan jawaban optimal.
5. Tambahkan bidang pemotongan: jika diinginkan carilah bidang pemotongan
yang akan memenuhi ���, jika sudah ditemukan, tambahkan bidang
pemotongan tersebut pada relaksasi dan kembali ke langkah 4.
6. Pengukuran dan pemangkasan:
a. Jika �� ≤ � kembali ke langkah 2.
b. Jika �� > � dan ��� adalah integer yang layak, perbaharui nilai �dengan
melakukan teknik rounded down berdasarkan nilai ��, kemudian buang
dari L seluruh masalah di mana �� ≤ �, dan lanjut ke langkah 2.
ILP0 = Bentuk ILP dari permasalahan awal
���� = Bentuk ILP dari sebuah permasalahan l∈L
L = Himpunan titik-titik aktif dari persoalan ILP
�� = Batas atas dari nilai fungsi tujuan suatu sub-masalah l∈L
Pada algoritma branch and cut, diberikan L yang merupakan himpunan
titik aktif pada pencabangan branch and cut. Nilai objektif terbaik yang diperoleh
dari titik layak dinotasikan sebagai �. Lebih lanjut, �� adalah batas atas nilai
memperbaharui ��. Dalam beberapa kondisi, sejumlah cutting plane ditemukan
pada langkah 5, biasanya cutting plane yang diperoleh dipilah dan yang
ditambahkan pada persamaan adalah subsetnya. Sub-masalah yang terbentuk pada
langkah 7 disebut sub-masalah anak dan sub-masalah pada node sebelumnya
sebagai sub-masalah induknya. Biasanya pembagian masalah tersebut
menggunakan bentuk dari variabel penghubung �� ≤ � dan �� ≥ � untuk suatu
variabel �� dan a merupakan integer. Kendala-kendala tersebut dapat diselesaikan
dengan berbagai metode untuk ILP. Secara khusus pada langkah awal
diselesaikan dengan metode simpleks, jawaban berikutnya diperoleh dengan
metode dual Simpleks. Solusi dual untuk jawaban sub-masalah akhir adalah layak
untuk sub-masalah awal. Lebih lanjut, ketika pemotongan (cut) ditambahkan pada
langkah 5, juga memanfaaatkan iterasi dual Simpleks untuk mendapatkan solusi
optimal yang integer. Cutting plane yang ditambahkan pada salah satu vertex dari
pohon branch and cut mungkin tidak berlaku untuk sub-masalah lain. Dalam hal
BAB 3
HASIL DAN PEMBAHASAN
3.1 Pengumpulan Data
Data yang diperlukan dalam penelitian ini adalah:
1. Data penjualan pot bunga pada bulan Januari-Juni 2014.
2. Data komposisi bahan baku yang diperlukan dari setiap jenis pot bunga.
3. Data biaya produksi pot bunga.
4. Data harga penjualan setiap jenis pot bunga pada UD. Mukhlis Rangkuti.
5. Data jumah produksi pot bunga pada bulan Maret 2015.
Berikut disajikan data volume penjualan pot bunga bulan Januari-Juni
2014 pada UD. Pot Bunga Mukhlis Rangkuti
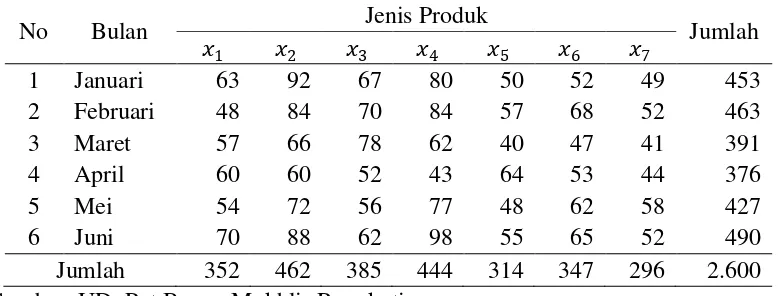
Tabel 3.1 Data Volume Penjualan Pot Bunga Bulan Januari – Juni 2014
No Bulan Jenis Produk Jumlah
Sumber: UD. Pot Bunga Mukhlis Rangkuti
Bahan baku yang diperlukan untuk memproduksi setiap satu buah pot
bunga disajikan dalam Tabel 3.2 berikut:
Tabel 3.2 Komposisi Bahan Baku Produk
No Bahan Jenis Produk Sumber: UD. Pot Bunga Mukhlis Rangkuti
Bahan baku pot bunga yang disediakan oleh UD. Pot bunga Mukhlis
Rangkuti ditampilkan dalam Tabel 3.3.
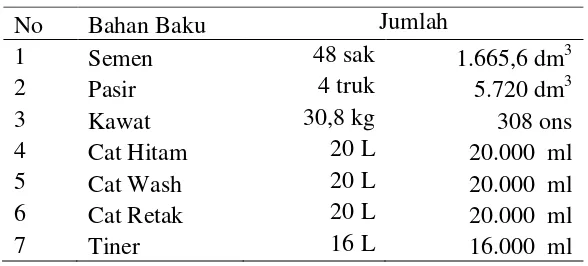
Tabel 3.3 Persediaan Bahan Baku Selama Satu Bulan
No Bahan Baku Jumlah
Sumber: UD. Pot Bunga Mukhlis Rangkuti
Keterangan:
1. 1 sak semen = 50 kg
Standard massa jenis semen = 1440 kg/m3
Dengan menggunakan persamaan 3.2 diperoleh:
Total biaya produksi dari masing-masing satu buah pot bunga termasuk
biaya bahan baku dan upah tenaga kerja disajikan dalam Tabel 3.4.
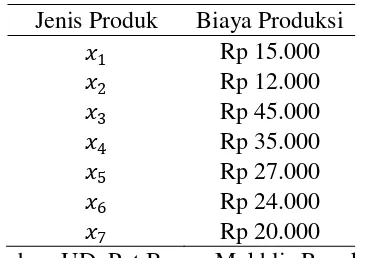
Tabel 3.4 Biaya Produksi Setiap Produk
Jenis Produk Biaya Produksi
�1 Rp 15.000
Sumber: UD. Pot Bunga Mukhlis Rangkuti
Harga jual setiap satu buah pot bunga ditampilkan dalam Tabel 3.5.
Tabel 3.5 Harga Jual Produk
Jenis Produk Harga Jual
�1 Rp 30.000
Sumber: UD. Pot Bunga Mukhlis Rangkuti
Besar keuntungan yang diperoleh dari setiap unit produk merupakan
selisih dari harga jual dengan besarnya biaya produksi yang dikeluarkan.
Tabel 3.6 Keuntungan Tiap Satu Unit Produk
Jenis Produk Keuntungan
�1 Rp 15.000
Sumber: UD. Pot Bunga Mukhlis Rangkuti
Berikut ditampilkan data volume produksi pot bunga bulan Maret 2015
pada UD. Pot Bunga Mukhlis Rangkuti.
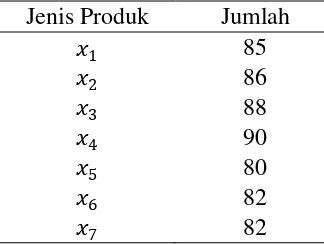
Tabel 3.7 Volume Produksi Pot Bunga Bulan Maret 2015
Jenis Produk Jumlah
Sumber: UD. Pot Bunga Mukhlis Rangkuti
Berdasarkan jumlah produksi tersebut, total biaya produksi yang dikeluarkan oleh
perusahaan adalah Rp15.185.000,- dan keuntungan yang diperoleh adalah
Rp11.311.000,-.
3.2 Pengolahan data
3.2.1 Perumusan Fungsi Tujuan
Keoptimalan jumlah pot bunga yang diproduksi akan seiring dengan keoptimalan
keuntungan yang diperoleh. Dalam penelitian ini yang dijadikan sebagai fungsi
objektifnya adalah maksimasi keuntungan penjualan pot bunga. Koefisien dari
variabel keputusannya adalah keuntungan dari masing-masing jenis pot bunga
Maksimum:
�= 15.000�1+ 15.000�2+ 30.000�3+ 20.000�4+ 20.000�5 +18.000�6+ 15.000�7
di mana:
�1 = Banyaknya pot bunga jenis segi minimalis diproduksi
�2 = Banyaknya pot bunga jenis sampan minimalis diproduksi
�3 = Banyaknya pot bunga jenis petak segi besar bonsai diproduksi
�4 = Banyaknya pot bunga jenis bulat besar ukir bonsai diproduksi
�5 = Banyaknya pot bunga jenis segi ukir bonsai diproduksi
�6 = Banyaknya pot bunga jenis guci sedang diproduksi
�7 = Banyaknya pot bunga jenis guci kecil diproduksi
3.2.2 Perumusan Fungsi Kendala
Fungsi kendala dalam permasalahan ini terdiri dari persediaan bahan baku dan
jumlah permintaan.
1. Model Fungsi Kendala Dari Persediaan Bahan Baku
Untuk memodelkan fungsi kendala dari persediaan bahan baku, data yang
digunakan adalah data pada Tabel 3.2 dan Tabel 3.3 sehingga dapat dimodelkan
sebagai berikut:
Semen : 2,41�1+ 2,17�2+ 3,61�3+ 2,41�4 + 1,97�5+ 1,81�6+
1,44�7 ≤ 1.665,60
Pasir :`7,22�1+ 6,50�2+ 10,83�3+ 7,22�4+ 5,91�5 + 5,42�6+
4,33�7 ≤ 5.720
Kawat : 0,60�1+ 0,60�2+ 0,70�3+ 0,60�4 + 0,50�5+ 0,50�6+ 0,50�7 ≤
340
Cat hitam : 50�1+ 41,67�2 ≤20.000
Cat wash : 55,56�5+ 55,56�6+ 41,67�7 ≤ 20.000
Cat retak : 100�3 + 83,33�4 ≤ 20.000
2. Model Fungsi Kendala dari Jumlah Permintaan
Data yang digunakan untuk memodelkan fungsi kendala dari jumlah permintaan
adalah data volume penjualan yang terdapat pada Tabel 3.1. Agar tidak terjadi
kondisi kekurangan barang, maka perusahaan harus memproduksi tiap jenis pot
bunga sekurang-kurangnya sama dengan jumlah penjualan terbanyak dari setiap
jenis pot bunga. Dimodelkan fungsi-fungsi kendala sebagai berikut:
Pot bunga jenis segi minimalis : �1 ≥ 70
Permasalahan ini dapat diformulasikan sebagai program integer dan akan
diselesaikan dengan menggunakan metode branch and cut. Dari permasalahan
diperoleh:
1. Kendala dari persediaan bahan baku
100�3 + 83,33�4 ≤ 20.000
33,33�3+ 33,33�4+ 33,33�5+ 33,33�6+ 33,33�7 ≤16.000
2. Kendala dari jumlah permintaan
�1 ≥70 �2 ≥92 �3 ≥78 �4 ≥98 �5 ≥64 �6 ≥68 �7 ≥58
Bentuk standarnya menjadi:
����= 15.000�1+ 15.000�2 + 30.000�3+ 20.000�4+ 20.000�5 +18.000�6+ 15.000�7
Dengan kendala:
2,41�1+ 2,17�2+ 3,61�3+ 2,41�4+ 1,97�5+ 1,81�6 + 1,44�7+�1 = 1.665,60
7,22�1+ 6,50�2+ 10,83�3+ 7,22�4 + 5,91�5+ 5,42�6+ 4,33�7+�2 = 5.720
0,60�1 + 0,60�2+ 0,70�3 + 0,60�4+ 0,50�5+ 0,50�6+ 0,50�7+�3 = 340
50�1+ 41,67�2+�4 = 20.000
55,56�5+ 55,56�6+ 41,67�7+�5= 20.000
100�3 + 83,33�4+�6 = 20.000
33,33�3 + 33,33�4+ 33,33�5+ 33,33�6+ 33,33�7+�7 = 16.000 −�1+�8 =−70
Setelah memformulasikan permasalahan produksi tersebut ke dalam model
integer programming, langkah selanjutnya adalah menyelesaikan model tersebut
dengan menggunakan metode dual Simpleks. Penyelesaian menggunakan metode
dual Simpleks yang ditampilkan hanya pada iterasi awal, pada iterasi berikutnya
penyelesaian model ini dilakukan dengan menggunakan bantuan komputer,
mengingat data yang akan dihitung secara iteratif cukup banyak. Persoalan model
integer programming tersebut akan diselesaikan dengan menggunakan software
POM-QM for Windows yang dapat dilihat pada Lampiran 5. Penyelesaian model
ini dimulai dengan merepresentasikan model ke dalam tabel simpleks sebagai
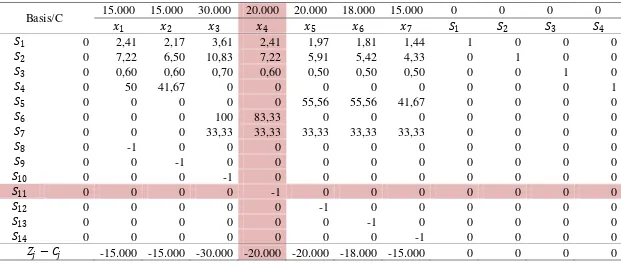
34 Tabel 3.8 Iterasi Awal Metode Dual Simpleks
Basis/C 15.000 15.000 30.000 20.000 20.000 18.000 15.000 0 0 0 0
�1 �2 �3 �4 �5 �6 �7 �1 �2 �3 �4
�1 0 2,41 2,17 3,61 2,41 1,97 1,81 1,44 1 0 0 0
�2 0 7,22 6,50 10,83 7,22 5,91 5,42 4,33 0 1 0 0
�3 0 0,60 0,60 0,70 0,60 0,50 0,50 0,50 0 0 1 0
�4 0 50 41,67 0 0 0 0 0 0 0 0 1
�5 0 0 0 0 0 55,56 55,56 41,67 0 0 0 0
�6 0 0 0 100 83,33 0 0 0 0 0 0 0
�7 0 0 0 33,33 33,33 33,33 33,33 33,33 0 0 0 0
�8 0 -1 0 0 0 0 0 0 0 0 0 0
�9 0 0 -1 0 0 0 0 0 0 0 0 0
�10 0 0 0 -1 0 0 0 0 0 0 0 0
�11 0 0 0 0 -1 0 0 0 0 0 0 0
�12 0 0 0 0 0 -1 0 0 0 0 0 0
�13 0 0 0 0 0 0 -1 0 0 0 0 0
�14 0 0 0 0 0 0 0 -1 0 0 0 0
35 Tabel 3.8 Lanjutan
0 0 0 0 0 0 0 0 0 0
Quantity
�5 �6 �7 �8 �9 �10 �11 �12 �13 �14
0 0 0 0 0 0 0 0 0 0 1.665,60
0 0 0 0 0 0 0 0 0 0 5.720
0 0 0 0 0 0 0 0 0 0 340
0 0 0 0 0 0 0 0 0 0 20.000
1 0 0 0 0 0 0 0 0 0 20.000
0 1 0 0 0 0 0 0 0 0 20.000
0 0 1 0 0 0 0 0 0 0 16.000
0 0 0 1 0 0 0 0 0 0 -70
0 0 0 0 1 0 0 0 0 0 -92
0 0 0 0 0 1 0 0 0 0 -78
0 0 0 0 0 0 1 0 0 0 -98
0 0 0 0 0 0 0 1 0 0 -64
0 0 0 0 0 0 0 0 1 0 -68
0 0 0 0 0 0 0 0 0 1 -58
0 0 0 0 0 0 0 0 0 0 0
Keterangan:
1. Pada iterasi Tabel 3.8 di atas, �11 = −98 terpilih sebagai leaving variable.
2. ���� =�−20.000−
1 �=20.000 (berarti �4 menjadi entering variable).
3. Baris pivot adalah baris �4 dikalikan -1.
36 5. Baris �2 yang baru: baris �2−7,22 kali baris �4.
6. Baris �3 yang baru: baris �3−0,60 kali baris �4.
7. Baris �6 yang baru: baris �6−83,33 kali baris �4.
8. Baris �7 yang baru: baris �7−33,33 kali baris �4.
9. Baris lainnya tetap karena elemen pada kolom pivot sudah bernilai 0 (nol).
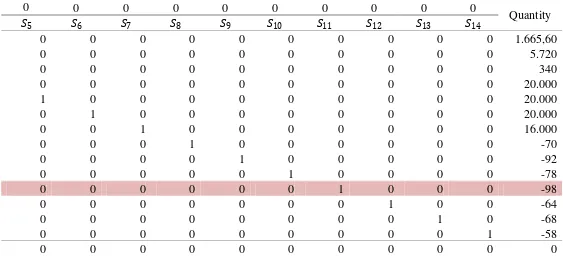
Tabel 3.9 Iterasi 1 Metode Dual Simpleks
Basis/C 15.000 15.000 30.000 20.000 20.000 18.000 15.000 0 0 0 0
�1 �2 �3 �4 �5 �6 �7 �1 �2 �3 �4
�1 0 2,41 2,17 3,61 0 1,97 1,81 1,44 1 0 0 0
�2 0 7,22 6,50 10,83 0 5,91 5,42 4,33 0 1 0 0
�3 0 0,60 0,60 0,70 0 0,50 0,50 0,50 0 0 1 0
�4 0 50 41,67 0 0 0 0 0 0 0 0 1
�5 0 0 0 0 0 55,56 55,56 41,67 0 0 0 0
�6 0 0 0 100 0 0 0 0 0 0 0 0
�7 0 0 0 33,33 0 33,33 33,33 33,33 0 0 0 0
�8 0 -1 0 0 0 0 0 0 0 0 0 0
�9 0 0 -1 0 0 0 0 0 0 0 0 0
�10 0 0 0 -1 0 0 0 0 0 0 0 0
�4 20.000 0 0 0 1 0 0 0 0 0 0 0
�12 0 0 0 0 0 -1 0 0 0 0 0 0
�13 0 0 0 0 0 0 -1 0 0 0 0 0
�14 0 0 0 0 0 0 0 -1 0 0 0 0
37 Tabel 3.9 Lanjutan
0 0 0 0 0 0 0 0 0 0
Quantity
�5 �6 �7 �8 �9 �10 �11 �12 �13 �14
0 0 0 0 0 0 2,41 0 0 0 1.429,42
0 0 0 0 0 0 7,22 0 0 0 5.012,44
0 0 0 0 0 0 0,60 0 0 0 281,20
0 0 0 0 0 0 0 0 0 0 20.000,00
1 0 0 0 0 0 0 0 0 0 20.000,00
0 1 0 0 0 0 83,33 0 0 0 11.833,66
0 0 1 0 0 0 33,33 0 0 0 12.733,66
0 0 0 1 0 0 0 0 0 0 -70
0 0 0 0 1 0 0 0 0 0 -92
0 0 0 0 0 1 0 0 0 0 -78
0 0 0 0 0 0 -1 0 0 0 98
0 0 0 0 0 0 0 1 0 0 -64
0 0 0 0 0 0 0 0 1 0 -68
0 0 0 0 0 0 0 0 0 1 -58
0 0 0 0 0 0 -20.000 0 0 0 1.960.000
Keterangan:
1. Pada iterasi Tabel 3.9 di atas, �9 =−92 terpilih sebagai leaving variable.
2. ���� =�−15.000−
1 �=15.000 (berarti �2 menjadi entering variable).
3. Baris pivot adalah baris �2 dikalikan -1.
38 5. Baris �2 yang baru: baris �2−6,50 kali baris �2.
6. Baris �3 yang baru: baris �3−0,60 kali baris �2.
7. Baris �4 yang baru: baris �4−41,67 kali baris �2.
8. Baris lainnya tetap karena elemen pada kolom pivot sudah bernilai 0 (nol).
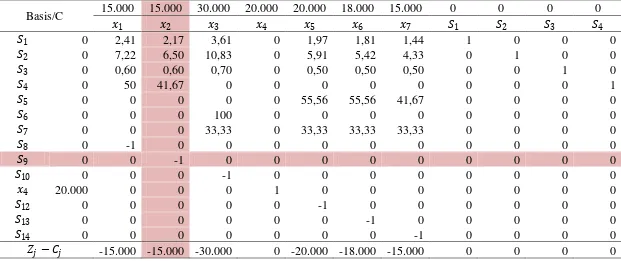
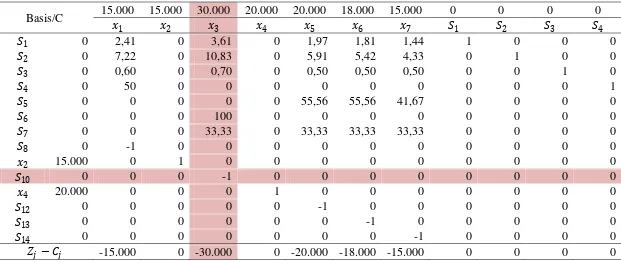
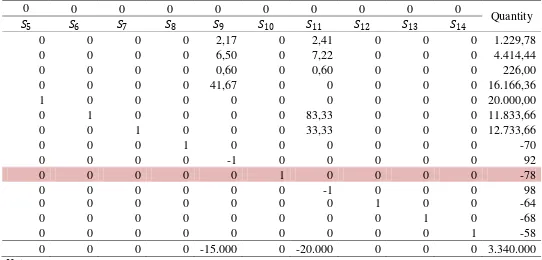
Tabel 3.10 Iterasi 2 Metode Dual Simpleks
Basis/C 15.000 15.000 30.000 20.000 20.000 18.000 15.000 0 0 0 0
�1 �2 �3 �4 �5 �6 �7 �1 �2 �3 �4
�1 0 2,41 0 3,61 0 1,97 1,81 1,44 1 0 0 0
�2 0 7,22 0 10,83 0 5,91 5,42 4,33 0 1 0 0
�3 0 0,60 0 0,70 0 0,50 0,50 0,50 0 0 1 0
�4 0 50 0 0 0 0 0 0 0 0 0 1
�5 0 0 0 0 0 55,56 55,56 41,67 0 0 0 0
�6 0 0 0 100 0 0 0 0 0 0 0 0
�7 0 0 0 33,33 0 33,33 33,33 33,33 0 0 0 0
�8 0 -1 0 0 0 0 0 0 0 0 0 0
�2 15.000 0 1 0 0 0 0 0 0 0 0 0
�10 0 0 0 -1 0 0 0 0 0 0 0 0
�4 20.000 0 0 0 1 0 0 0 0 0 0 0
�12 0 0 0 0 0 -1 0 0 0 0 0 0
�13 0 0 0 0 0 0 -1 0 0 0 0 0
�14 0 0 0 0 0 0 0 -1 0 0 0 0
39 Tabel 3.10 Lanjutan
0 0 0 0 0 0 0 0 0 0
Quantity
�5 �6 �7 �8 �9 �10 �11 �12 �13 �14
0 0 0 0 2,17 0 2,41 0 0 0 1.229,78
0 0 0 0 6,50 0 7,22 0 0 0 4.414,44
0 0 0 0 0,60 0 0,60 0 0 0 226,00
0 0 0 0 41,67 0 0 0 0 0 16.166,36
1 0 0 0 0 0 0 0 0 0 20.000,00
0 1 0 0 0 0 83,33 0 0 0 11.833,66
0 0 1 0 0 0 33,33 0 0 0 12.733,66
0 0 0 1 0 0 0 0 0 0 -70
0 0 0 0 -1 0 0 0 0 0 92
0 0 0 0 0 1 0 0 0 0 -78
0 0 0 0 0 0 -1 0 0 0 98
0 0 0 0 0 0 0 1 0 0 -64
0 0 0 0 0 0 0 0 1 0 -68
0 0 0 0 0 0 0 0 0 1 -58
0 0 0 0 -15.000 0 -20.000 0 0 0 3.340.000
Keterangan:
1. Pada iterasi Tabel 3.10 di atas, �10 =−78 terpilih sebagai leaving variable.
2. ���� = �−30.000
−1 �= 30.000 (berarti �3 menjadi entering variable).
3. Baris pivot adalah baris �3 dikalikan -1.
40 5. Baris �2 yang baru: baris �2−10,83 kali baris �3.
6. Baris �3 yang baru: baris �3−0,70 kali baris �3.
7. Baris �6 yang baru: baris �6−100 kali baris �3.
8. Baris �7 yang baru: baris �7−33,33 kali baris �3.
9. Baris lainnya tetap karena elemen pada kolom pivot sudah bernilai 0 (nol).
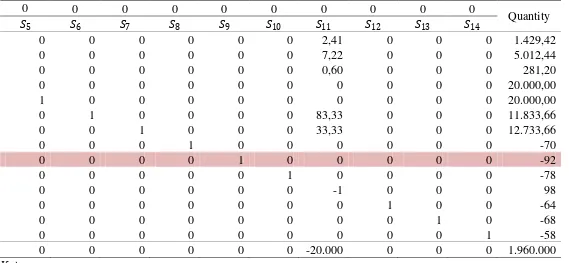
Tabel 3.11 Iterasi 3 Metode Dual Simpleks
Basis/C 15.000 15.000 30.000 20.000 20.000 18.000 15.000 0 0 0 0
�1 �2 �3 �4 �5 �6 �7 �1 �2 �3 �4
�1 0 2,41 0 0 0 1,97 1,81 1,44 1 0 0 0
�2 0 7,22 0 0 0 5,91 5,42 4,33 0 1 0 0
�3 0 0,60 0 0 0 0,50 0,50 0,50 0 0 1 0
�4 0 50 0 0 0 0 0 0 0 0 0 1
�5 0 0 0 0 0 55,56 55,56 41,67 0 0 0 0
�6 0 0 0 0 0 0 0 0 0 0 0 0
�7 0 0 0 0 0 33,33 33,33 33,33 0 0 0 0
�8 0 -1 0 0 0 0 0 0 0 0 0 0
�2 15.000 0 1 0 0 0 0 0 0 0 0 0
�3 30.000 0 0 1 0 0 0 0 0 0 0 0
�4 20.000 0 0 0 1 0 0 0 0 0 0 0
�12 0 0 0 0 0 -1 0 0 0 0 0 0
�13 0 0 0 0 0 0 -1 0 0 0 0 0
�14 0 0 0 0 0 0 0 -1 0 0 0 0
41 Tabel 3.11 Lanjutan
0 0 0 0 0 0 0 0 0 0
Quantity
�5 �6 �7 �8 �9 �10 �11 �12 �13 �14
0 0 0 0 2,17 3,61 2,41 0 0 0 948,20
0 0 0 0 6,50 10,83 7,22 0 0 0 3.569,70
0 0 0 0 0,60 0,70 0,60 0 0 0 171,40
0 0 0 0 41,67 0 0 0 0 0 16.166,36
1 0 0 0 0 0 0 0 0 0 20.000,00
0 1 0 0 0 100 83,33 0 0 0 4.033,66
0 0 1 0 0 33,33 33,33 0 0 0 10.133,92
0 0 0 1 0 0 0 0 0 0 -70
0 0 0 0 -1 0 0 0 0 0 92
0 0 0 0 0 -1 0 0 0 0 78
0 0 0 0 0 0 -1 0 0 0 98
0 0 0 0 0 0 0 1 0 0 -64
0 0 0 0 0 0 0 0 1 0 -68
0 0 0 0 0 0 0 0 0 1 -58
0 0 0 0 -15.000 -30.000 -20.000 0 0 0 5.680.000
Keterangan:
1. Pada iterasi Tabel 3.11 di atas, �8 =−70 terpilih sebagai leaving variable.
2. ���� = �−15.000−
1 �= 15.000 (berarti �1 menjadi entering variable).
3. Baris pivot adalah baris �1 dikalikan -1.