APLIKASI METODE BRANCH AND BOUND DALAM MENGOPTIMALKAN JUMLAH PRODUKSI (STUDI KASUS : PT. KANSAI PRAKARSA COATINGS) SKRIPSI

(1)

APLIKASI METODE BRANCH AND BOUND DALAM MENGOPTIMALKAN JUMLAH PRODUKSI

(STUDI KASUS : PT. KANSAI PRAKARSA COATINGS)

SKRIPSI

NOVIKA ELISABETH SIANTURI 120803044

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN

2016

(2)

APLIKASI METODE BRANCH AND BOUND DALAM MENGOPTIMALKAN JUMLAH PRODUKSI

(STUDI KASUS : PT. KANSAI PRAKARSA COATINGS)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

NOVIKA ELISABETH SIANTURI 120803044

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN

2016

(3)

PERSETUJUAN

Judul : Aplikasi Metode Branch And Bound dalam Pengoptimalan Jumlah Produksi (Studi Kasus PT.

Kansai Prakarsa Coatings) Kategori : Skripsi

Nama : Novika Elisabeth Sianturi Nomor Induk Mahasiswa : 120803044

Program Studi : Sarjana (S1) Matematika Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Disetujui di Medan, April 2016

Komisi Pembimbing :

Pembimbing 2, Pembimbing 1,

Dra. Normalina Napitupulu, M.Sc Drs. Partano Siagian, M.Sc NIP. 19631106 198902 2 001 NIP. 19511227 198003 1 001

Disetujui Oleh

DepartemenMatematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si. Ph.D NIP. 196209011988031002

(4)

PERNYATAAN

APLIKASI METODE BRANCH AND BOUND DALAM MENGOPTIMALKAN JUMLAH PRODUKSI (STUDI KASUS PT.

KANSAI PRAKARSA COATINGS)

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, April 2016

NOVIKA ELISABETH SIANTURI 120803044

(5)

PENGHARGAAN

Puji syukur kepada Tuhan Yesus Kristus atas anugerah dan penyertaanNya sehingga penulis dapat menyelesaikan skripsi yang berjudul: “Aplikasi Metode Branch and Bound dalam Pengoptimalan Jumlah Produksi (Studi Kasus PT. Kansai Prakarsa Coatings)” dapat diselesaikan dengan baik. Selama proses penyusunan skripsi ini, Penulis telah banyak mendapat bimbingan, bantuan dan doa dari berbagai pihak, sehingga skripsi ini dapat diselesaikan dengan baik. Penulis mengucapkan terimakasih kepada :

1. Bapak Drs. Partano Siagian, M.Sc dan Ibu Dra. Normalina Napitupulu, M.Sc selaku dosen pembimbing skripsi yang telah memberikan bimbingan dan arahan dalam penyusunan skripsi ini.

2. Bapak Drs. Marihat Situmorang, M.Kom dan Bapak Drs. Rosman Siregar, M.Si selaku dosen penguji skripsi atas kritik dan sarannya agar skripsi ini dapat disusun dengan baik.

3. Bapak Dr. Sutarman, M.Sc selaku Dekan dan Dosen Pembimbing Akademik, Bapak Prof. Drs. Tulus, Vordipl.Math, M.Si, Ph.D dan Ibu Dra. Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

4. Bapak dan Ibu dosen Pengajar yang sudah memberikan pengajaran dan ilmu pengetahuan, seluruh staf dan pegawai Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

5. Seluruh Staf, Pegawai, dan Karyawan di Pabrik Teh Bah Butong PTPN IV, terkhusus untuk Nantulang Ella yang telah berpartisipasi membantu memperoleh data riset serta mengarahkan penulis selama penelitian.

6. Teristimewa Penulis ucapkan terimakasih sebesar-besarnya kepada Bapak (Jonni Hamonangan Sianturi) , Mamak (Karnauli Sitorus) dan Adik (Andre Wiranta Sianturi) yang tak henti-hentinya memberikan dukungan, baik secara finansial maupun moril, semangat dan doa sejak perkuliahan hingga skripsi ini selesai.

7. Teman-teman d’angels (Theresia Simbolon, Kartika Cahaya Sirait, Tesi Almia Sembiring, Serli Waskitha Wiyata Manurung, dan Cristina Laura Marpaung) dan teman-teman d’wylipo ( Ruminy Manurung, Widya Simarmata, Elisa Librana Naibaho, S. Priya Darsini, dan Dessy Titien Sembiring) atas semangat dan doa yang terus menyertai Penulis.

8. Teman-teman Matematika 2012, Abang dan Kakak senior serta junior yang banyak membantu Penulis selama perkuliahan. Dan juga Saudara dan Saudari NHKBP Jl. Simalingkar yang terus mendoakan Penulis.

9. Semua pihak yang telah menolong dalam penyelesaian skripsi ini yang tidak dapat disebutkan satu per satu.

Masih terdapat banyak kekurangan dalam penyusunan skripsi ini, maka dari itu penulis mengharapkan kritik dan saran yang membangun dari pembaca demi kesempurnaan penelitian ini di masa yang akan datang. Semoga skripsi ini dapat berguna bagi pembaca.

(6)

APLIKASI METODE BRANCH AND BOUND DALAM MENGOPTIMALKAN JUMLAH PRODUKSI (STUDI KASUS PT.

KANSAI PRAKARSA COATINGS)

ABSTRAK

PT. Kansai Prakarsa Coatings adalah perusahaan yang bergerak dalam produksi berbagai jenis cat. Perusahaan ini memproduksi 3 jenis cat yaitu Short Oil Alkyd, Medium Oil Alkyd, dan Long Oil Alkyd. Masalah dalam pengoptimalan jumlah produksi akan diselesaikan dengan memodelkan ke dalam bentuk persamaan program linier. Untuk menghasilkan variabel-variabel keputusan yang integer karena jumlah produksi cat tidak memungkinkan berbentuk pecahan, maka digunakanlah program integer, dalam hal ini menggunakan metode Branch and Bound. Untuk menghitung nilai variabel keputusan, digunakan metode simpleks.

Sehingga dari analisis metode branch and bound diperoleh selisih nilai keuntungan sebesar 1,17% dari perkiraan keuntungan perusahaan.

Kata Kunci : Program Linier, Metode Simpleks, Program Integer dan Branch and Bound

(7)

APPLICATIONS BRANCH AND BOUND METHODS IN OPTIMIZING THE PRODUCTION QUANTITIES (CASE STUDY: PT. KANSAI

PRAKARSA COATINGS)

ABSTRACT

PT. Kansai Prakarsa Coatings is a company that moves on production various kinds of paint. This company produces 3 kinds of paints, those are Short Oil Alkyd, Medium Oil Alkyd, and Long Oil Alkyd. Problems in the optimization of production quantities will be resolved by modeled in the form of linear programming equation. To produce the decision variables are integer for the number of paint production is not possible in the form of fractions, it is used integer program, in this case using methods Branch and Bound. To calculate the value of decision variables, use the simplex method. So from the branch and bound method of analysis obtained by the difference value gain of 1.17% of the company's expected profits.

Keywords: Linear Programming, Simplex Method, Integer Programming and Branch and Bound

(8)

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel viii

Daftar Gambar ix

Bab 1. Pendahuluan 1.1 Latar Belakang 1

1.2 Rumusan Masalah 2

1.3 Batasan Masalah 3

1.4 Tujuan Penelitian 3

1.5 Manfaat Penelitian 3

1.6 Lokasi Penelitian 4

1.7 Metodologi Penelitian 4

Bab 2. Landasan Teori 2.1 Program Linier 5

2.1.1 Model Program Linier 7

2.1.2 Terminologi Umum dan Asumsi-Asumsi Dasar Program Linier 8

2.2 Program integer 9

2.3 Metode Branch and Bound (Pencabangan dan Pembatasan) 11

Bab 3. Hasil dan Pembahasan 3.1 Pengolahan data 15

3.1.1 Data Bahan Baku dan Persediaan Bahan Baku 15

3.1.2 Data Harga Jual, Biaya Produksi dan Keuntungan Penjualan 16

3.2 Perumusan Fungsi Tujuan 16

3.3 Perumusan Fungsi Kendala 16

3.4 Perumusan Fungsi Kendala 16

3.5 Pengolahan Data 18

3.6 Analisis Metode Branch and Bound 20

Bab 4. Kesimpulan dan Saran 4.1 Kesimpulan 62

4.2 Saran 62

Daftar Pustaka 63

(9)

DAFTAR TABEL

Nomor Judul Halaman

Tabel

3.1 Data Bahan Baku dan Persediaan Bahan Baku 15 3.2 Data Harga Jual, Biaya Produksi dan Keuntungan Penjualan 16 3.3 Iterasi I Metode Simpleks dengan Software QM 18 3.4 Iterasi II Metode Simpleks dengan Software QM 18 3.5 Iterasi III Metode Simpleks dengan Software QM 18 3.6 Iterasi I Metode Simpleks dengan Software QM 19 3.7 Solusi dari Hasil Iterasi dengan Software QM 19

(10)

DAFTAR GAMBAR

Nomor Judul Halaman

Gambar

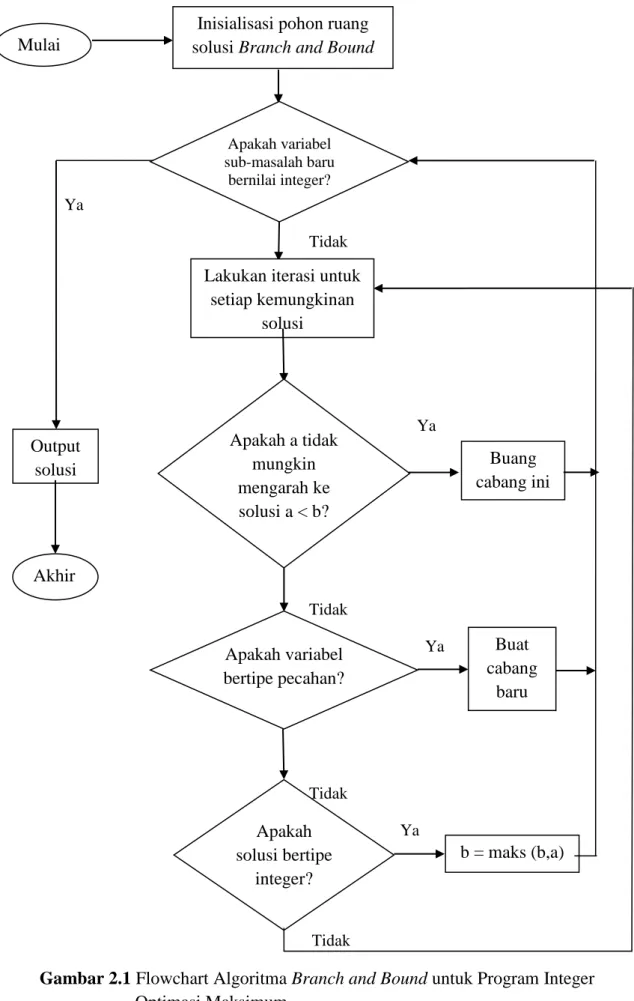
2.1 Flowchart Algoritma Branch and Bound untuk Program Integer

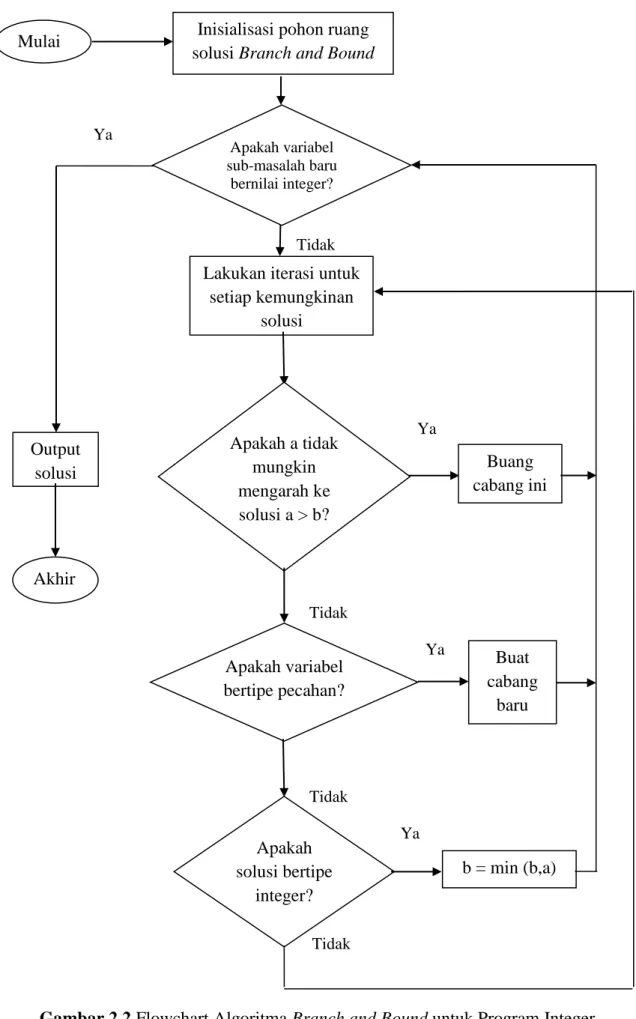
Optimasi Maksimum 13 2.2 Flowchart Algoritma Branch and Bound untuk Program Integer

Optimasi Minimum 14

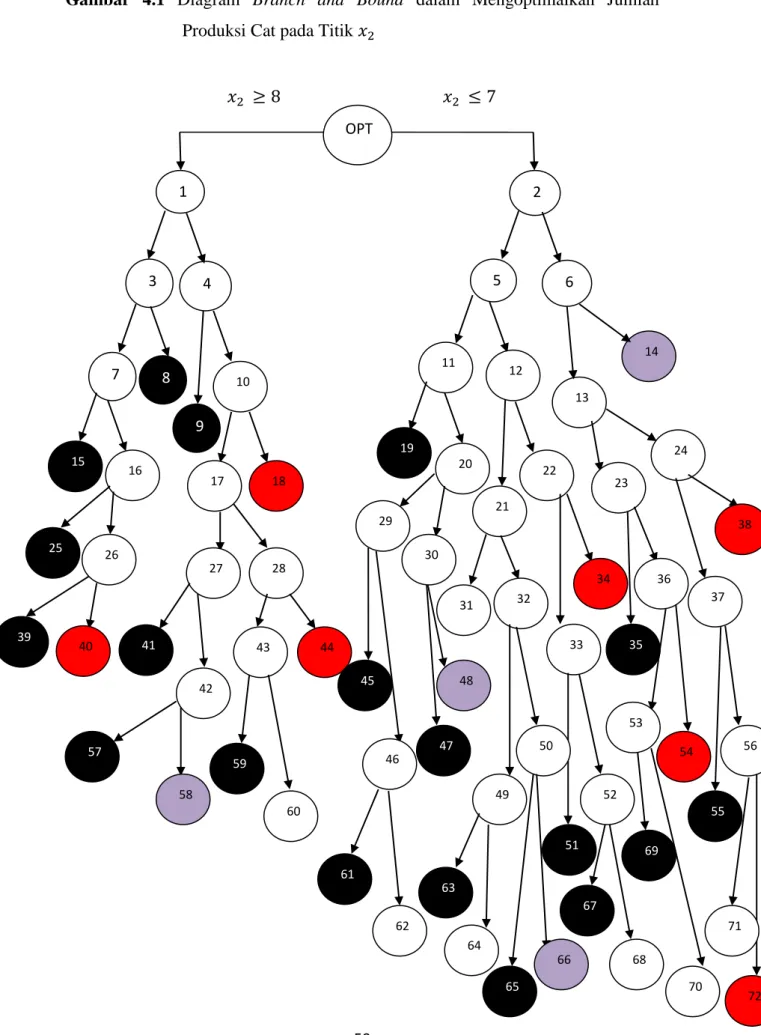
4.1 Diagram Branch and Bound dalam Mengoptimalkan Jumlah

Produksi Cat pada Titik 𝑥₂ 59

(11)

BAB I PENDAHULUAN

1.1 Latar Belakang

Saat ini terjadi perkembangan yang sangat pesat, salah satunya di bidang produksi. Dikarenakan kebutuhan manusia yang semakin banyak, seiring dengan pertumbuhan penduduk yang semakin meningkat menyebabkan jumlah produksi barang-barang semakin meningkat pula sesuai dengan kebutuhan. Dalam hal ini PT. Kansai Prakarsa Coatings menjadi salah satu perusahaan produksi cat yang besar di Indonesia yang memproduksi cat-cat untuk keperluan rumah tangga sampai kepada cat untuk konstruksi bangunan dan industri. Seiring dengan perkembangan teknologi, industri dan bisnis properti yang terus meningkat, ditambah dengan pembangunan yang semakin pesat di Indonesia, membuat pasar penjualan produksi cat pun semakin meningkat. Kenaikan permintaan akan cat dipicu oleh pesatnya pembangunan di sektor konstruksi, khususnya properti seperti real estate, apartemen, dan pusat perbelanjaan. Kenaikan permintaan juga terjadi di sektor otomotif untuk merakit kendaraan dan sektor industri lainnya.

Cat adalah suatu cairan yang digunakan untuk melindungi dan memberikan warna pada suatu obyek atau permukaan yang dilapisi dengan lapisan berpigmen dan dapat digunakan pada hampir semua jenis objek, antara lain untuk menghasilkan karya seni, salutan industri, pengawet untuk pencegah korosi, dan lain-lain.

Pada umumnya, setiap perusahaan ingin memperoleh laba sebesar-besarnya dan tentu saja dengan biaya produksi yang sekecil-kecilnya agar perusahaan dapat terus beroperasi dan berkembang. Namun pada kenyataannya, banyak perusahaan tidak mampu meningkatkan laba, bahkan mengalami kerugian. Hal ini diakibatkan oleh beberapa faktor, salah satunya kurangnya pengelolaan dalam hal produksi. Pengelolaan produksi yang tidak baik menyebabkan persediaan produk yang berlebihan atau produk yang diproduksi tidak mencukupi permintaan pasar.

(12)

Biasanya bahan baku sangat berpengaruh terhadap jumlah produk yang akan diproduksi. Maka dalam hal ini, pemanfaatkan energi dan pemakaian bahan baku yang optimal sangat diperlukan untuk memaksimalkan jumlah produksi yang akan menghasilkan keuntungan yang lebih besar. Agar jumlah produk cat yang diproduksi optimal, maka dapat digunakan pendekatan Linear Programming atau Program Linier sebagai cara untuk pengambilan keputusan dalam hal pengoptimalan produksi, dalam hal menggunakan metode Branch and Bound.

Program Linier (Linear Programming) merupakan alat yang ampuh bagi para pembuat keputusan untuk membuat keputusan yang paling baik (the best decision) berdasarkan hasil pemecahan yang terbaik dari persoalan optimisasi dan dapat digunakan sebagai suatu metode untuk memecahkan persoalan-persoalan optimisasi di dalam pembatasan-pembatasan.

Program Linier bilangan bulat atau Program Integer merupakan suatu model program linier yang khusus digunakan untuk menyesuaikan suatu masalah pada program linier dimana variabel-variabel keputusan dalam penyelesaian optimal harus merupakan bilangan bulat (integer). Kharakteristik model matematika Program Linier Integer adalah sama dengan model linier biasa, kecuali dalam Program Linier Integer harus ada memuat suatu persyaratan bahwa variabel keputusan harus bilangan integer. Dalam hal ini, metode penyelesaian masalah yang digunakan adalah metode Cabang dan Batas (Branch and Bound).

Dari uraian di atas, Penulis tertarik untuk melakukan penelitian di PT. Kansai Prakarsa Coatings dengan judul :

“APLIKASI METODE BRANCH AND BOUND DALAM

MENGOPTIMALKAN JUMLAH PRODUKSI (STUDI KASUS PT.

KANSAI PRAKARSA COATINGS)”

1.2 Rumusan Masalah

Yang menjadi permasalahan adalah biaya bahan baku yang besar sehingga tidak menghasilkan produk dengan keuntungan yang optimal. Untuk itu, perlu ditentukan bahan baku produk yang optimal sehingga dapat diperoleh jumlah

(13)

produk yang optimal dari masing-masing jenis cat dan dapat mengefisiensikan harga produksi sehingga menghasilkan keuntungan yang lebih besar, dengan asumsi semua pengadaan bahan baku dianggap berjalan dengan baik.

1.3 Batasan Masalah

Dalam penulisan ini Penulis hanya membatasi pada : 1. Dipilih 3 jenis cat yang diproduksi.

2. Proses kegiatan produksi dianggap berjalan lancar tanpa adanya gangguan.

3. Dalam menyelesaikan produksi, harga atau biaya bahan baku dianggap konstan, tidak terpengaruh oleh waktu dan faktor-faktor lain.

4. Hal-hal yang berhubungan dengan masalah pengadaan bahan baku dianggap selalu tersedia.

1.4 Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk menentukan bahan baku dalam mengoptimalkan jumlah produksi cat pada PT. Kansai Prakarsa Coatings dengan menggunakan metode Branch and Bound sehingga menghasilkan keuntungan yang maksimal.

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai alternatif cara yang dapat digunakan PT. Kansai Prakarsa Coatings untuk memecahkan persoalan dalam pengoptimalan produksi.

(14)

1.6 Lokasi Penelitian

Penelitian dilakukan di PT. Kansai Prakarsa Coatings, yang beralamat di Kompleks Industri Gajah Tunggal Jatake, Jalan Gatot Subroto Km.7, Jatiwung, Tangerang.

1.7 Metodologi Penelitian

Adapun metodologi yang digunakan dalam penelitian ini adalah :

1. Melakukan studi pembelajaran mengenai program linier yaitu program integer dengan menggunakan metode Branch and Bound melalui buku, artikel dan jurnal.

2. Mengambil data yang diperoleh dari catatan laporan produksi PT. Kansai Prakarsa Coatings, yaitu:

a. Data bahan baku dari 3 jenis cat.

b. persediaan bahan baku dari ketiga jenis cat di gudang selama seminggu.

c. Data harga jual, biaya produksi dan keuntungan penjualan dari 3 jenis cat.

3. Pengolahan data yang diperoleh dari PT. Kansai Prakarsa Coatings dengan:

a. Memodelkan fungsi tujuan dan fugsi kendala ke dalam bentuk Program Linier.

b. Menghitung nilai variabel keputusan dengan menggunakan Software QM.

c. Mencari nilai optimal dengan menggunakan metode Branch and Bound.

4. Membuat kesimpulan dari hasil perhitungan dan saran yang dapat menjadi masukan bagi pihak perusahaan.

(15)

BAB 2

LANDASAN TEORI

2.1 Program Linier atau Linear Programming (LP)

Menurut Rao (1987), program linier adalah sebuah metode optimisasi yang berlaku sebagai solusi permasalahan dimana fungsi tujuan dan kendala muncul sebagai fungsi linear dari variabel-variabel keputusan.

Sitorus (1997) juga mendefinisikan program linier sebagai suatu teknik penyelesaian optimal atas suatu problema keputusan dengan cara menentukan terlebih dahulu fungsi tujuan (memaksimalkan atau meminimalkan) dan kendala- kendala yang ada ke dalam model matematik persamaan linier. Program linier sering digunakan dalam menyelesaikan masalah-masalah alokasi sumber daya seperti dalam bidang manufacturing, pemasaran, keuangan, personalia, administrasi, dan lain sebagainya.

Siagian (2006) mengemukakan bahwa pokok pikiran yang paling utama dalam menggunakan program linier adalah merumuskan masalah dengan jelas menggunakan sejumlah informasi yang tersedia. Kemudian menerjemahkan masalah tersebut ke dalam model matematis, yang cara pemecahan masalahnya lebih mudah dan terstruktur agar didapatkan solusinya.

Suatu masalah dikatakan sebagai masalah program linier apabila :

1. Tujuan (objective) yang akan dicapai harus dapat dinyatakan dalam bentuk fungsi linier yang disebut sebagai fungsi tujuan (objective function).

2. Harus ada alternatif pemecahan. Pemecahan yang membuat fungsi tujuan optimum (laba yang maksimum, biaya yang minimum, dan sebagainya) yang harus dipilih.

3. Sumber-sumber tersedia dalam jumlah yang terbatas (bahan mentah terbatas, modal terbatas, ruangan untuk menyimpan barang terbatas, dan sebagainya). Pembatasan-pembatasan harus dinyatakan di dalam ketidaksamaan yang linier (linear inequality).

(16)

Menurut Mulyono (2004), setelah masalah diidentifikasikan, tujuan ditetapkan, langkah selanjutnya adalah formulasi model matematik yang meliputi :

1. Tentukan variabel yang tidak diketahui (variabel keputusan) dan nyatakan dalam simbol matematik.

2. Membentuk fungsi tujuan yang ditunjukkan sebagai suatu hubungan linier (bukan perkalian) dari variabel keputusan.

3. Menentukan semua kendala masalah tersebut dan mengekspresikan dalam persamaan atau pertidaksamaan yang juga merupakan hubungan linier dari variabel keputusan yang mencerminkan keterbatasan sumber daya masalah tersebut.

Umumnya masalah program linier dapat diselesaikan dengan menggunakan 2 metode, yaitu :

1. Metode grafik

Metode ini digunakan apabila jumlah variabel keputusan hanya dua dan jumlah kendala dalam model relatif sedikit (umumnya tidak lebih dari 4 kendala). Apabila jumlah kendalanya relatif banyak (> 4 kendala), maka akan sukar untuk melukiskan garis kendalanya dalam grafik.

2. Metode simpleks

Metode ini dapat digunakan untuk jumlah variabel keputusannya 2 atau lebih dan jumlah kendalanya 2 atau lebih. Metode simpleks adalah suatu prosedur ulang yang bergerak dari satu jawab layak basis ke jawab berikutnya sedemikian rupa hingga harga fungsi tujuan terus menaik (dalam persoalan maksimasi) dan akan berkelanjutan sampai dicapai jawab optimal (kalau ada) yang memberi harga maksimum. Metode simpleks didasarkan pada langkah seperti berikut :

a. Dimulai pada suatu titik pojok yang layak, biasanya titik asal ( yang disebut sebagai solusi awal).

b. Bergerak dari satu titik pojok layak ke titik pojok layak lain yang berdekatan. Pergerakan ini akan menghasilkan nilai fungsi tujuan yang lebih baik (meningkat untuk masalah maksimasi dan menurun untuk

(17)

masalah minimasi). Jika solusi yang lebih baik telah diperoleh, prosedur simpleks dengan sendirinya akan menghilangkan semua solusi-solusi lain yang kurang baik.

c. Proses ini diulang-ulang sampai suatu solusi yang lebih baik tak dapat ditemukan. Proses simpleks kemudian berhenti dan solusi optimum diperoleh.

2.1.1 Model Program Linier

Model persamaan umum dalam program linier dapat dirumuskan sebagai berikut :

Maksimalkan atau minimumkan : 𝑍 = ∑ 𝑐_𝑗𝑥_𝑗

𝑛

𝑗=1

Dengan kendala :

∑ 𝑎_𝑖𝑗𝑥_𝑗

𝑛

𝑗=1

≤ 𝑎𝑡𝑎𝑢 ≥ 𝑏_𝑖 𝑥_𝑗 ≥ 0

Untuk 𝑖 = 1, 2, 3, … , 𝑚 𝑗 = 1, 2, 3, … , 𝑛

Atau dapat ditulis secara lengkap sebagai berikut :

Maksimalkan atau minimumkan : 𝑍 = 𝑐₁𝑥₁+ 𝑐₂𝑥₂+ 𝑐₃𝑥₃+ … + 𝑐_𝑛𝑥_𝑛 Dengan kendala :

𝑎₁₁𝑥₁+ 𝑎₁₂𝑥₂ + 𝑎₁₃𝑥₃+ … + 𝑎_1𝑛𝑥_𝑛 ≤ 𝑎𝑡𝑎𝑢 ≥ 𝑏₁ 𝑎₂₁𝑥₁+ 𝑎₂₂𝑥₂ + 𝑎₂₃𝑥₃+ … + 𝑎_2𝑛𝑥_𝑛 ≤ 𝑎𝑡𝑎𝑢 ≥ 𝑏₂ . . . . . . . . . . . . . . . . . . . . .

(18)

𝑎_𝑚1𝑥₁ + 𝑎_𝑚2𝑥₂ + 𝑎_𝑚3𝑥₃ + … + 𝑎_𝑚𝑛𝑥_𝑛 ≤ 𝑎𝑡𝑎𝑢 ≥ 𝑏_𝑚 𝑥_𝑗 ≥ 0 untuk 𝑗 = 1, 2, 3, … , 𝑛

Dimana :

𝑍 = fungsi tujuan yang harus dicari nilai optimalnya (maksimal atau minimal)

𝑥_𝑗 = tingkat kegiatan ke- 𝑗

𝑐_𝑗 = kenaikan nilai 𝑍 terjadi apabila ada pertambahan tingkat kegiatan 𝑥_𝑗 dengan satu satuan unit atau sumbangan setiap satuan keluaran kegiatan 𝑍 terhadap 𝑗

𝑎_𝑖𝑗 = banyaknya sumber 𝑖 yang diperlukan untuk menghasilkan setiap unit keluaran kegiatan 𝑗

𝑏_𝑖 = kapasitas sumber 𝑖 yang tersedia untuk dialokasikan ke setiap unit kegiatan

𝑛 = macam kegiatan yang menggunakan sumber atau fasilitas yang tersedia

𝑚 = macam batasan sumber atau fasilitas yang tersedia (Aminudin, 2005)

2.1.2 Terminologi Umum dan Asumsi-Asumsi Dasar Program Linier Terminologi umum untuk model program linier dapat dirangkum sebagai berikut :

1. Fungsi yang akan dicari nilai optimalnya (Z) disebut sebagai fungsi tujuan (objective function).

2. Fungsi-fungsi batasan dapat dikelompokkan menjadi dua macam, yaitu : a. Fungsi batasan fungsional, yaitu fungsi-fungsi batasn sebanyak m.

b. Fungsi batasan non-negatif (non-negative constrains) yaitu variabel 𝑥_𝑗 ≥ 0.

3. Variabel-variabel 𝑥_𝑗 disebut sebagai variabel keputusan (decision variables).

(19)

4. Parameter model yaitu masukan konstan 𝑎_𝑖𝑗, 𝑏_𝑖, dan 𝑐_𝑗.

Agar penggunaan model program linier di atas memuaskan tanpa terbentur pada berbagai hal, makan diperlukan asumsi-asumsi dasar program linier sebagai berikut :

1. Proportionality, asumsi ini berarti naik turunnya nilai Z dan penggunaan sumber atau fasilitas yang tersedia akan berubah secara sebanding dengan perubahan tingkat kegiatan.

2. Additivity, berarti nilai tujuan tiap kegiatan tidak saling mempengaruhi, atau dalam program linier dianggap bahwa kenaikan suatu kegiatan dapat ditambahkan tanpa mempengaruhi bagian nilai Z yang diperoleh dari kegiatan lain.

3. Divisibility, berarti keluaran yang dihasilkan oleh setiap kegiatan dapat berupa bilangan pecahan.

4. Deterministic (certainty), berarti bahwa semua parameter ( 𝑎_𝑖𝑗, 𝑏_𝑖, dan 𝑐_𝑗) yang terdapat pada program linier dapat diperkirakan dengan pasti, meskipun dalam kenyataannya tidak sama persis.

2.2 Program Integer

Menurut Sitorus (1997), program linier bilangan bulat atau disebut juga sebagai program integer merupakan suatu model program linier yang khusus digunakan untuk menyesuaikan suatu masalah program linier dimana nilai variabel-variabel keputusan dalam menyelesaikan optimal harus merupakan bilangan integer (bulat). Karakteristik model matematika program linier integer adalah sama dengan model linier biasa, kecuali dalam program linier integer harus ada memuat suatu persyaratan bahwa variabel keputusan tertentu harus bilangan integer.

Apabila dalam Program Linier integer mensyaratkan bahwa :

1. Semua keputusan harus merupakan bilangan integer disebut All integer linear programming (AILP).

2. Hanya sebagian keputusan yang merupakan bilangan integer disebut Mixed integer linear programing (MILP).

(20)

3. Jika variabel keputusan harus bernilai 0 dan 1 disebut Zero one integer linear programming (ZOILP).

Ada banyak kasus dalam masalah program integer yang membatasi variabel model bernilai nol atau satu. Dalam kasus demikian, pengambil keputusan hanya memiliki dua pilihan yaitu menerima atau menolak suatu usulan kegiatan.

Penerimaan atau penolakan yang sifatnya parsial (sebagian) tidak diperbolehkan.

Jika variabel keputusan bernilai satu, kegiatan diterima. Dan jika variabel berilai nol, kegiatan ditolak. (Mulyono, 2004)

Bentuk umum program integer dapat dirumuskan sebagai berikut : Maksimumkan atau minimumkan :

𝑍 = ∑ 𝑐_𝑗𝑥_𝑗

𝑛

𝑗=1

Dengan kendala :

∑ 𝑎_𝑖𝑗𝑥_𝑗

𝑛

𝑗=1

(≥, =, ≤)𝑏_𝑖

𝑥_𝑗 ≥ 0 semua bilangan cacah Untuk 𝑖 = 1, 2, 3, … , 𝑚 𝑗 = 1, 2, 3, … , 𝑛 Dimana :

𝑍 = fungsi tujuan yang harus dicari nilai optimalnya (maksimal atau minimal)

𝑥_𝑗 = tingkat kegiatan ke- 𝑗

𝑐_𝑗 = kenaikan nilai 𝑍 apabila ada pertambahan tingkat kegiatan 𝑥_𝑗 dengan satu satuan unit atau sumbangan setiap satuan keluaran kegiatan 𝑍 terhadap 𝑗

𝑎_𝑖𝑗 = banyaknya sumber 𝑖 yang diperlukan untuk menghasilkan setiap unit keluaran kegiatan 𝑗

𝑏_𝑖 = kapasitas sumber 𝑖 yang tersedia untuk dialokasikan ke setiap unit kegiatan

𝑛 = macam kegiatan yang menggunakan sumber atau fasilitas yang tersedia

(21)

𝑚 = macam batasan sumber atau fasilitas yang tersedia

2.3 Metode Branch and Bound (Pencabangan dan Pembatasan)

Metode Branch and Bound pertama kali diperkenalkan oleh Land dan Doig (1960). Ide dasarnya adalah untuk membagi daerah solusi fisibel menjadi daerah solusi fisibel yang lebih kecil. Ini merupakan prosedur sederhana yang menetapkan batasan yang lebih tinggi dan rendah menjadi solusi saat menyelesaikan sub masalah secara sistematis. Kemudian metode ini dimodifikasi oleh Dakin (1965) dan dengan sukses menerapkannya di dalam kitab undang- undang hukum dagang banyak orang dalam memecahkan persoalan program integer.

Metode Branch and Bound adalah metode umum untuk mencari solusi optimal dari berbagai permasalahan optimasi. Pendekatan Branch and Bound didasarkan pada prinsip bahwa himpunan total solusi layak dapat dipartisi menjadi subset yang lebih kecil dari solusi. Subset yang lebih kecil ini kemudian dapat dievaluasi secara sistematis sampai solusi terbaik ditemukan.

Metode ini sering digunakan untuk menyelesaikan suatu masalah program integer karena hasil yang diperoleh dalam penyelesaian optimal lebih teliti dan lebih baik dari kedua metode lainnya. Kelemahan pokok metode ini adalah prosedur untuk mencapai hasil optimal sangat panjang. Prosedur penyelesaian masalah maksimasi program integer dengan metode Branch and Bound adalah sebagai berikut :

1. Langkah 1 : penyelesaian optimal dengan metode program linier biasa.

Masalah yang dihadapi diselesaikan terlebih dahulu menggunakan metode program linier biasa (menggunakan metode grafik atau metode simpleks) sampai diperoleh hasil yang optimal.

2. Langkah 2 : pemeriksaan penyelesaian optimal

Hasil optimal pada langkah 1 diperiksa apakah variabel keputusan yang diperoleh bernilai integer (bilangan bulat) atau pecahan. Apabila ternyata nilai semua variabel keputusan tersebut merupakan bilangan bulat positif

(22)

(nonnegative integer), maka penyelesaian optimal telah dicapai. Apabila tidak, maka proses iterasi dilanjutkan.

3. Langkah 3 : penyusunan sub masalah (branching)

Apabila penyelesaian optimal belum tercapai, maka masalah tersebut dimodifikasikan ke dalam dua sub masalah (branching) dengan memasukkan kendala baru ke masing-masing sub masalah tersebut.

Variabel kendala baru tersebut harus bersifat saling pengecualian (mutually exclusive constraints) sehingga memenuhi persyaratan penyelesaian integer.

4. Langkah 4 : penentuan nilai batas (bounding)

Hasil optimal yang diperoleh dengan metode program linier biasa (non integer) merupakan nilai batas atas (upper bound) bagi setiap sub masalah.

Sedangkan hasil optimal dengan penyelesaian integer merupakan nilai batas bawah (lower bound) bagi masing-masing sub masalah. Selanjutnya, apabila sub masalah yang memiliki batas atas yang lebih rendah dari batas bawah yang berlaku, maka sub masalah tersebut tidak perlu dianalisi lagi.

Apabila dalam penyelesaian integer menghasilkan hasil yang sama atau lebih baik daripada nilai batas atas dari setiap masalah, maka penyelesaian optimal integer telah tercapai. Apabila tidak, maka sub masalah yang memiliki nilai batas atas yang terbaik dipilih selanjutnya menjadi sub masalah baru. Proses iterasi ini kembali kepada langkah 2, sehingga demikian seterusnya. (sitorus, 1997)

(23)

Ya

Tidak

Ya

Tidak

Ya

Tidak

Ya

Tidak

Gambar 2.1 Flowchart Algoritma Branch and Bound untuk Program Integer Optimasi Maksimum

Mulai

Inisialisasi pohon ruang solusi Branch and Bound

Lakukan iterasi untuk setiap kemungkinan

solusi

Apakah a tidak mungkin mengarah ke solusi a < b?

Apakah variabel bertipe pecahan?

Apakah solusi bertipe

integer?

Output solusi

Akhir

Buang cabang ini

Buat cabang

baru

b = maks (b,a)

Apakah variabel sub-masalah baru

bernilai integer?

(24)

Ya

Tidak

Ya

Tidak

Ya

Tidak

Ya

Tidak

Gambar 2.2 Flowchart Algoritma Branch and Bound untuk Program Integer Optimasi Minimum

Mulai Inisialisasi pohon ruang solusi Branch and Bound

Lakukan iterasi untuk setiap kemungkinan

solusi

Apakah a tidak mungkin mengarah ke solusi a > b?

Apakah variabel bertipe pecahan?

Apakah solusi bertipe

integer?

Output solusi

Akhir

Buang cabang ini

Buat cabang

baru

b = min (b,a)

Apakah variabel sub-masalah baru

bernilai integer?

(25)

BAB 3

HASIL DAN PEMBAHASAN

3.1 Pengumpulan Data

Untuk menganalisis cara pengoptimalan jumlah produksi, diperlukan data dari PT. Kansai Prakarsa Coatings sebagai berikut :

a. Data bahan baku dan persediaan bahan baku dari 3 jenis cat.

b. Data harga jual, biaya produksi dan keuntungan penjualan dari 3 jenis cat.

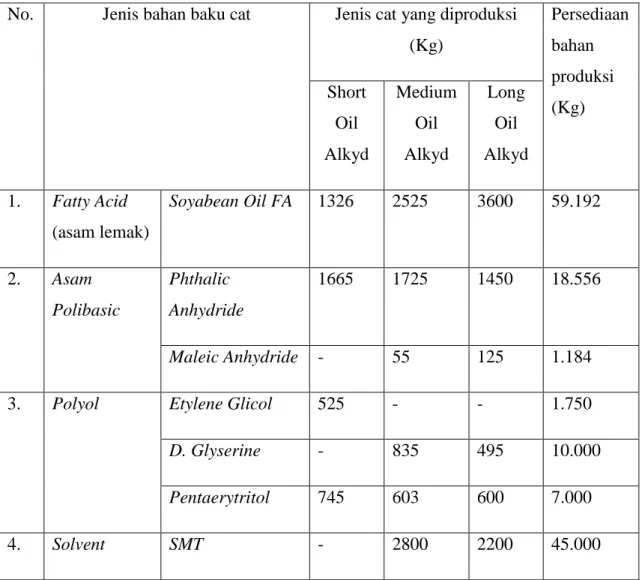
3.1.1. Data Bahan Baku dan Persediaan Bahan Baku

Tabel 3.1 Data Bahan Baku dan Persediaan Bahan Baku No. Jenis bahan baku cat Jenis cat yang diproduksi

(Kg)

Persediaan bahan produksi (Kg) Short

Oil Alkyd

Medium Oil Alkyd

Long Oil Alkyd 1. Fatty Acid

(asam lemak)

Soyabean Oil FA 1326 2525 3600 59.192

2. Asam Polibasic

Phthalic Anhydride

1665 1725 1450 18.556

Maleic Anhydride - 55 125 1.184

3. Polyol Etylene Glicol 525 - - 1.750

D. Glyserine - 835 495 10.000

Pentaerytritol 745 603 600 7.000

4. Solvent SMT - 2800 2200 45.000

(26)

(Pelarut) Xylene 3150 600 200 10.000

3.1.2 Data Harga Jual, Biaya Produksi dan Keuntungan Penjualan Data biaya yang diperoleh dengan modal awal perusahaan untuk sekali produksi adalah sebesar Rp. 1.003.000.000 Dengan banyak 8404 kg resin cat.

Tabel 3.2 Data Harga Jual, Biaya Produksi dan Keuntungan Penjualan No. Jenis cat Biaya produksi

dalam sekali produksi

Harga jual per Kg

Keuntungan penjualan dalam

sekali produksi 1. Short Oil Alkyd Rp. 96.251.012 Rp. 25.701 Rp. 119.740.192 2. Medium Oil Alkyd Rp. 88.872.300 Rp. 24.778 Rp. 119.362.012 3. Long Oil Alkyd Rp. 93.435.672 Rp. 23.724 Rp. 105.940.824

3.2 Perumusan Fungsi Tujuan

Yang menjadi fungsi tujuan adalah memaksimalkan keuntungan atau laba dari penjualan masing-masing jenis cat. Koefisien dari variabel-variabel keputusannya adalah keuntungan penjualan dari masing-masing resin cat.

Sehingga fungsi tujuannya dirumuskan sebagai berikut :

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Dimana : 𝑥₁ = variabel keputusan untuk cat Short Oil Alkyd

𝑥₂ = variabel keputusan untuk cat Medium Oil Alkyd 𝑥₃ = variabel keputusan untuk cat Long Oil Alkyd

(27)

3.3 Perumusan Fungsi Kendala

Yang menjadi fungsi kendala adalah biaya produksi setiap jenis cat dan bahan baku produksi dari 3 jenis cat tersebut.

1. Fungsi kendala dengan batasan bahan baku produksi cat dapat dibuat persamaan yaitu sebagai berikut :

1.326 𝑥₁+ 2.525 𝑥₂+ 3.600 𝑥₃ ≤ 59.192 1.665 𝑥₁+ 1.725 𝑥₂+ 1.450 𝑥₃ ≤ 18.556 55 𝑥₂+ 125 𝑥₃ ≤ 1.184

525 𝑥₁ ≤ 1.750

835 𝑥₂ + 495 𝑥₃ ≤ 10.000

745 𝑥₁+ 603 𝑥₂+ 600 𝑥₃ ≤ 7000 2.800 𝑥₂+ 2.200 𝑥₃ ≤ 45.000

3.150 𝑥₁+ 600 𝑥₂ + 200 𝑥₃ ≤ 10.000

2. Persamaan fungsi kendala dengan batasan biaya produksi setiap jenis cat adalah sebagai berikut :

96.251.012 𝑥₁+ 88.872.300 𝑥₂+ 93.435.672 𝑥₃ ≤ 1.003.000.000 Maka, permasalahan di atas antara lain sebagai berikut :

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : 1.326 𝑥₁+ 2.525 𝑥₂+ 3.600 𝑥₃ ≤ 59.192

1.665 𝑥₁+ 1.725 𝑥₂+ 1.450 𝑥₃ ≤ 18.556 55 𝑥₂+ 125 𝑥₃ ≤ 1.184

525 𝑥₁ ≤ 1.750

835 𝑥₂+ 495 𝑥₃ ≤ 10.000

745 𝑥₁+ 603 𝑥₂+ 600 𝑥₃ ≤ 7000 2.800 𝑥₂+ 2.200 𝑥₃ ≤ 45.000

3.150 𝑥₁+ 600 𝑥₂ + 200 𝑥₃ ≤ 10.000

96.251.012 𝑥₁ + 88.872.300 𝑥₂ + 93.435.672 𝑥₃ ≤ 1.003.000.000

(28)

3.4 Pengolahan Data

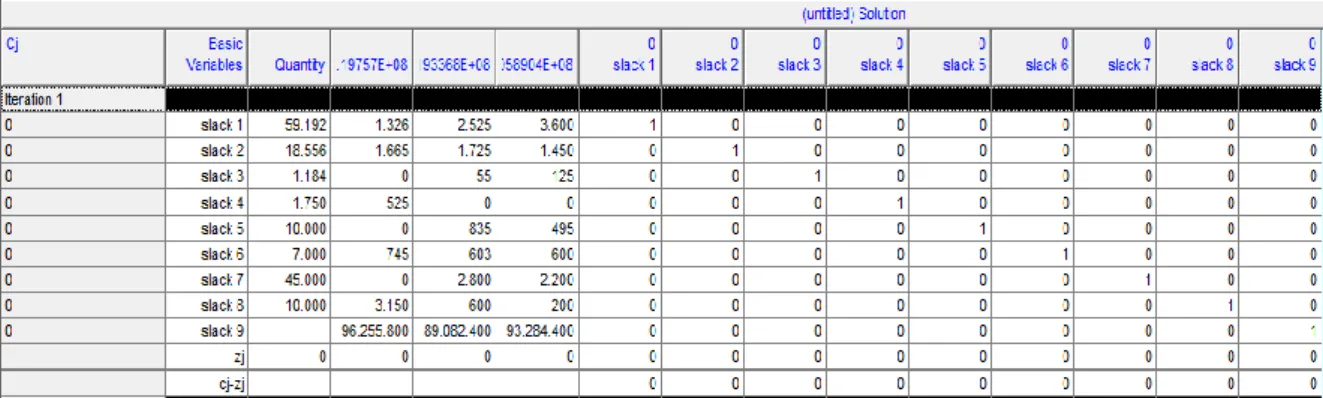
Tabel 3.3 Iterasi I Metode Simpleks dengan Software QM

Tabel 3.4 Iterasi II Metode Simpleks dengan Software QM

Tabel 3.5 Iterasi III Metode Simpleks dengan Software QM

(29)

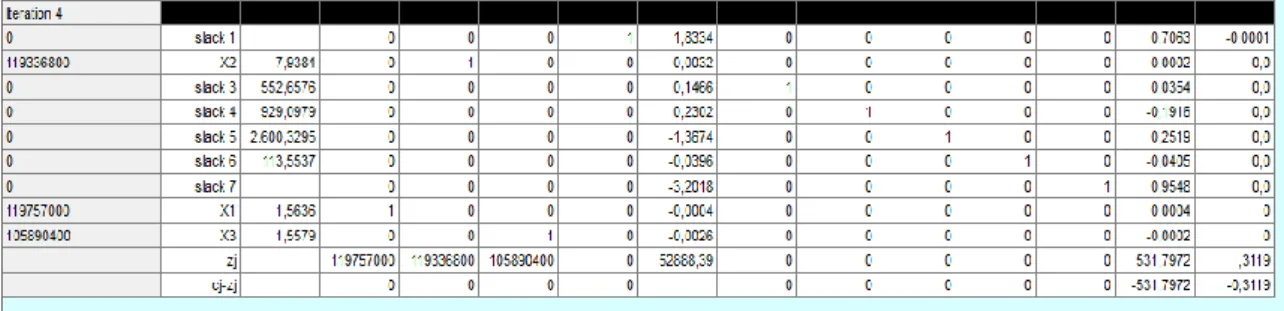
Tabel 3.6 Iterasi IV Metode Simpleks dengan Software QM

Tabel 3.7 Solusi dari Hasil Iterasi dengan Software QM

Dari hasil iterasi dengan menggunakan software QM, diperolehlah hasil yang optimal yaitu :

𝑥₁ = 1,5636 𝑥₂ = 7.9384 𝑥₃ = 1,5579

Sehingga cat Short Oil Alkyd yang harus diproduksi dalam sehari adalah sebanyak 1,5636 kali produksi, Medium Oil Alkyd sebanyak 7,9384 kali produksi, dan Long Oil Alkyd sebanyak 1,5579 kali produksi. Namun masalah ini belum valid karena solusi yang dibutuhkan adalah solusi berupa bilangan integer. Selanjutnya akan digunakan metode Branch and Bound agar solusi yang dihasilkan berupa bilangan integer.

(30)

3.5 Analisis Metode Branch and Bound

Yang pertama kali dilakukan adalah menentukan batas atas (BA) dan batas bawah (BB). Hasil yang diperoleh sebelumnya yaitu 𝑥₁ = 1,5636, 𝑥₂ = 7.9384, 𝑥₃ = 1,5579 dengan keuntungan sebesar Rp. 1.299.556.000 belum menjadi solusi yang valid karena 𝑥₁, 𝑥₂, dan 𝑥₃ bukan bilangan integer. Namun nilai keuntungannya yang menjadi batas atas (BA). Dengan metode pembulatan ke bawah, diperoleh : 𝑥₁ = 1, 𝑥₂ = 7, 𝑥₃ = 1 dengan keuntungan Rp. 1.061.005.000. Nilai keuntungan dengan pembulatan ke bawah dijadikan sebagai batas bawah (BB).

Setelah batas atas dan batas bawah ditentukan, maka selanjutnya memilih variabel keputusan untuk melakukan pencabangan (branching). Variabel keputusan memiliki nilai pecahan terbesar. Pecahan terbesar berada pada 𝑥₂ yaitu sebesar 0,9384, maka 𝑥₂ dicabangkan menjadi sub-masalah 1 dan sub-masalah 2 dengan tambahan kendala untuk sub-masalah 1 𝑥₂ ≥ 8 dan untuk sub-masalah 2 𝑥₂ ≤ 7.

Sehingga diperoleh :

Iterasi 1 :

1. Sub-masalah 1

1.665 𝑥₁+ 1.725 𝑥₂+ 1.450 𝑥₃ ≤ 18.556 55 𝑥₂+ 125 𝑥₃ ≤ 1.184

525 𝑥₁ ≤ 1.750

835 𝑥₂+ 495 𝑥₃ ≤ 10.000

745 𝑥₁+ 603 𝑥₂ + 600 𝑥₃ ≤ 7000 2.800 𝑥₂+ 2.200 𝑥₃ ≤ 45.000

3.150 𝑥₁+ 600 𝑥₂ + 200 𝑥₃ ≤ 10.000

96.251.012 𝑥₁+ 88.872.300 𝑥₂+ 93.435.672 𝑥₃ ≤ 1.003.000.000

𝑥₂ ≥ 8 Atau ringkasnya,

(31)

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala awal + kendala 𝑥₂ ≥ 8

2. Sub-masalah 2

1.665 𝑥₁+ 1.725 𝑥₂+ 1.450 𝑥₃ ≤ 18.556 55 𝑥₂+ 125 𝑥₃ ≤ 1.184

525 𝑥₁ ≤ 1.750

835 𝑥₂+ 495 𝑥₃ ≤ 10.000

745 𝑥₁+ 603 𝑥₂ + 600 𝑥₃ ≤ 7000 2.800 𝑥₂+ 2.200 𝑥₃ ≤ 45.000

3.150 𝑥₁+ 600 𝑥₂ + 200 𝑥₃ ≤ 10.000

96.251.012 𝑥₁+ 88.872.300 𝑥₂+ 93.435.672 𝑥₃ ≤ 1.003.000.000

𝑥₂ ≤ 7 Atau ringkasnya,

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala awal + kendala 𝑥₂ ≤ 7

Dengan menggunakan metode simpleks, diperoleh :

Solusi sub-masalah 1 : 𝑥₁ = 1,4354, 𝑥₂ = 8, 𝑥₃ = 1,6318, Z = Rp. 1.299.382.000 Solusi sub-masalah 2 : 𝑥₁ = 1,6976, 𝑥₂ = 7, 𝑥₃ = 2,2622, Z = Rp. 1.278.205.000

Selanjutnya adalah meneliti nilai solusi (Z) dari masing-masing sub- masalah apakah kurang dari nilai batas bawah dan lebih dari nilai batas atas. Jika nilai solusi yang diperoleh lebih besar dari batas atas, maka solusi tersebut tidak layak karena jika disubstitusikan ke dalam salah satu kendala, akan diperoleh kendala melebihi persediaan yang ada. Sedangkan jika nilai solusi yang diperoleh lebih kecil dari batas bawah, maka solusi tersebut tidak optimal.

(32)

Karena nilai solusi dari sub-masalah 1 dan sub-masalah 2 tidak lebih besar dari nilai batas atas dan tidak lebih kecil dari nilai batas bawah, serta nilai variabel keputusan sub-masalah 1 dan 2 masih ada yang tidak integer, maka sub-masalah 1 dan 2 dapat dicabangkan menjadi sub-masalah selanjutnya. Sub-masalah 1 dicabangkan menjadi sub-masalah 3 dan 4, sedangkan sub-masalah 2 dicabangkan menjadi sub-masalah 5 dan 6.

Iterasi 2

Sub-masalah 1 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp. 1.299.382.000 dengan 𝑥₁ = 1,4354, 𝑥₂ = 8, 𝑥₃ = 1,6318 BB = Rp. 1.180.341.800 dengan 𝑥₁ = 1, 𝑥₂ = 8, 𝑥₃ = 1

Karena pecahan terbesar terletak pada 𝑥₃ yaitu sebesar 0,6318 maka tambahan kendala untuk sub-masalah 3 adalah 𝑥₃ ≥ 2 dan 𝑥₃ ≤ 1 untuk sub-masalah 4.

Sehingga diperoleh : 1. Sub-masalah 3

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah l + kendala 𝑥₃ ≥ 2

2. Sub-masalah 4

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah l + kendala 𝑥₃ ≤ 1

Karena pecahan terbesar terletak pada 𝑥₁ yaitu sebesar 0,6976 maka tambahan kendala untuk sub-masalah 5 adalah 𝑥₁ ≥ 2 dan 𝑥₁ ≤ 1 untuk sub-masalah 6.

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah 2 + kendala 𝑥₁ ≥ 2

(33)

2. Sub-masalah 6

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah 2 + kendala 𝑥₁ ≤ 1

Dengan menggunakan metode simpleks pada Software QM, diperoleh :

Solusi sub-masalah 3 : 𝑥₁ = 0,1456, 𝑥₂ = 8,9354, 𝑥₃ = 2, Z = Rp. 1.295.540.800 Solusi sub-masalah 4 : 𝑥₁ = 1,4976, 𝑥₂ = 8,471, 𝑥₃ = 1, Z = Rp. 1.296.142.000 Solusi sub-masalah 5 : 𝑥₁ = 2, 𝑥₂ =4,8156, 𝑥₃ = 4,0531, Z = Rp. 1.243.383.000 Solusi sub-masalah 6 : 𝑥₁ = 1, 𝑥₂ = 7, 𝑥₃ = 2,9818, Z = Rp. 1.270.861.000

Karena nilai solusi sub-masalah 3, 4, 5, dan 6 tidak lebih besar dari batas atas dan tidak lebih kecil dari batas bawah, serta variabelnya belum seluruhnya bernilai integer, maka keempat sub-masalah ini dapat dicabangkan. Sub-masalah 3 dicabangkan menjadi sub-masalah 7 dan 8, sub-masalah 4 dicabangkan menjadi sub-masalah 9 dan 10, sub-masalah 5 dicabangkan menjadi sub-masalah 11 dan 12, dan sub-masalah 6 dicabangkan menjadi sub-masalah 13 dan 14.

Iterasi 3

Sub-masalah 3 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp. 1.295.540.800 dengan 𝑥₁ = 0,1456, 𝑥₂ = 8,9354, 𝑥₃ = 2 BB = Rp. 1.166.475.200 dengan 𝑥₁ = 1, 𝑥₂ = 8, 𝑥₃ = 2

Karena pecahan terbesar terletak pada 𝑥₂ yaitu sebesar 0,9354 maka tambahan kendala untuk sub-masalah 7 adalah 𝑥₂ ≥ 9 dan 𝑥₂ ≤ 8 untuk sub-masalah 8.

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah 3 + kendala 𝑥₂ ≥ 9

2. Sub-masalah 8

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah l + kendala 𝑥₂ ≤ 8

(34)

Sub-masalah 4 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp. 1.296.142.000 dengan 𝑥₁ = 1,4976, 𝑥₂ = 8,471, 𝑥₃ = 1 BB = Rp. 1.180.341.800 dengan 𝑥₁ = 1, 𝑥₂ = 8, 𝑥₃ = 1

2. Sub-masalah 10

Sub-masalah 5 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp. 1.243.383.000 dengan 𝑥₁ = 2, 𝑥₂ = 4,8156, 𝑥₃ = 4,0531 BB = Rp. 1.140.422.800 dengan 𝑥₁ = 2, 𝑥₂ = 4, 𝑥₃ = 4

2. Sub-masalah 12

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah 5 + kendala 𝑥₂ ≤ 4

Sub-masalah 6 memiliki batas atas (BA) dan batas bawah (BB) yaitu :

(35)

BA = Rp. 1.270.861.000 dengan 𝑥₁ = 1, 𝑥₂ = 7, 𝑥₃ = 2,9818 BB = Rp. 1.166.895.400 dengan 𝑥₁ = 1, 𝑥₂ = 7, 𝑥₃ = 2

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah 6 + kendala 𝑥₃ ≥ 3

2. Sub-masalah 14

Maksimalkan : 𝑍 = 119.740.192 𝑥₁+ 119.362.012 𝑥₂+ 105.940.824 𝑥₃ Kendala : Kendala sub-masalah 6 + kendala 𝑥₃ ≤ 2

Dengan menggunakan metode simpleks pada Software QM, diperoleh :

Solusi sub-masalah 7 : 𝑥₁ = 0,02, 𝑥₂ = 9, 𝑥₃ = 2,0673, Z = Rp. 1.295.342.000 Solusi sub-masalah 8 : 𝒙_𝟏 = 1,0186, 𝒙_𝟐 = 8, 𝒙_𝟑 = 2, Z = Rp. 1.298.455.000 (solusi tidak fisibel (tidak layak))

Solusi sub-masalah 9 : Tidak ada solusi fisibel

Solusi sub-masalah 10 : 𝑥₁ = 1, 𝑥₂ = 8,9513, 𝑥₃ = 1, Z = Rp. 1.293.867.000 Solusi sub-masalah 11 : 𝑥₁ = 2, 𝑥₂ = 5, 𝑥₃ = 3,5, Z = Rp. 1.206.814.000

Solusi sub-masalah 12 : 𝑥₁ = 2,1129, 𝑥₂ = 4, 𝑥₃ = 4,7219, Z = Rp.1.230.380.000 Solusi sub-masalah 13 : 𝑥₁ = 0,9824, 𝑥₂ = 7, 𝑥₃ = 3, Z = Rp. 1.270.675.000 Solusi sub-masalah 14 : 𝒙_𝟏 = 1, 𝒙_𝟐 = 7, 𝒙_𝟑 = 2 maka Z = Rp. 1.116.895.000 (seluruh variabel sudah bernilai integer namun solusi tidak fisibel)

Karena nilai solusi sub-masalah 7, 10, 11, 12, dan 13 tidak lebih besar dari batas atas dan tidak lebih kecil dari batas bawah, serta variabelnya belum seluruhnya bernilai integer, maka keempat sub-masalah ini dapat dicabangkan. Sedangkan ub-masalah 8, 9, dan 14 tidak bisa dicabangkan lagi. Sub-masalah 7 dicabangkan menjadi sub-masalah 15 dan 16, sub-masalah 10 dicabangkan menjadi sub- masalah 17 dan 18, sub-masalah 11 dicabangkan menjadi sub-masalah 19 dan 20,

(36)

sub-masalah 12 dicabangkan menjadi sub-masalah 21 dan 22, sub-masalah 13 dicabangkan menjadi sub-masalah 23 dan 24.

Iterasi 4

2. Sub-masalah 16

Sub-masalah 10 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp. 1.293.867.000dengan 𝑥₁ = 1, 𝑥₂ = 8,9513, 𝑥₃ = 1

BB = Rp. 1.180.341.800 dengan 𝑥₁ = 1, 𝑥₂ = 8, 𝑥₃ = 1

2. Sub-masalah 18

(37)

Sub-masalah 11 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp. 1.206.814.000 dengan 𝑥₁ = 2, 𝑥₂ = 5, 𝑥₃ = 3,5

BB = Rp. 1.153.869.200 dengan 𝑥₁ = 2, 𝑥₂ = 5, 𝑥₃ = 3

2. Sub-masalah 20

Sub-masalah 12 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp.1.230.380.000 dengan 𝑥₁ = 2,1129, 𝑥₂ = 4, 𝑥₃ = 4,7219 BB = Rp. 1.140.422.800 dengan 𝑥₁ = 2, 𝑥₂ = 4, 𝑥₃ = 4

2. Sub-masalah 20

Sub-masalah 13 memiliki batas atas (BA) dan batas bawah (BB) yaitu : BA = Rp. 1.270.675.000 dengan 𝑥₁ = 0,9824, 𝑥₂ = 7, 𝑥₃ = 3

BB = Rp. 1.153.028.800 dengan 𝑥₁ = 0, 𝑥₂ = 7, 𝑥₃ = 3

(38)

2. Sub-masalah 24

Dengan menggunakan metode simpleks pada Software QM, diperoleh : Solusi sub-masalah 15 : tidak ada solusi fisibel

Solusi sub-masalah 16 : 𝑥₁ = 0,787, 𝑥₂ = 8, 𝑥₃ = 2, Z = Rp. 1.295.234.000 Solusi sub-masalah 17 : 𝑥₁ = 0,9495, 𝑥₂ = 9, 𝑥₃ = 1, Z = Rp. 1.293.637.000 Solusi sub-masalah 18 : 𝒙_𝟏 = 1, 𝒙_𝟐 = 8, 𝒙_𝟑 = 1, Z = Rp. 1.180.342.000 (seluruh variabel sudah bernilai integer dan solusi fisibel)

Solusi sub-masalah 19 : tidak ada solusi fisibel

Solusi sub-masalah 20 : 𝑥₁ = 2, 𝑥₂ = 5,1667, 𝑥₃ = 3, Z = Rp.1.173.759.000 Solusi sub-masalah 21 : 𝑥₁ = 2, 𝑥₂ = 3,832, 𝑥₃ = 5, Z = Rp. 1.226.269.000 Solusi sub-masalah 22 : 𝑥₁ = 2,1587, 𝑥₂ = 4, 𝑥₃ = 4, Z = Rp. 1.116.895.000 Solusi sub-masalah 23 : 𝑥₁ = 1, 𝑥₂ = 6,9811, 𝑥₃ = 3, Z = Rp. 1.270.532.000 Solusi sub-masalah 24 : 𝑥₁ = 0, 𝑥₂ = 7, 𝑥₃ = 4,0134, Z = Rp. 1.260.330.000

Karena nilai solusi sub-masalah 16, 17, 20, 21, 22, 23 dan 24 tidak lebih besar dari batas atas dan tidak lebih kecil dari batas bawah, serta variabelnya belum seluruhnya bernilai integer, maka keempat sub-masalah ini dapat dicabangkan.

Sedangkan sub-masalah 15, 18, dan 19 tidak bisa dicabangkan lagi. Sub-masalah 16 dicabangkan menjadi sub-masalah 25 dan 26, sub-masalah 17 dicabangkan menjadi sub-masalah 27 dan 28, sub-masalah 20 dicabangkan menjadi sub- masalah 29 dan 30, sub-masalah 21 dicabangkan menjadi sub-masalah 31 dan 32, sub-masalah 22 dicabangkan menjadi sub-masalah 33 dan 34, sub-masalah 23

(39)

dicabangkan menjadi sub-masalah 35 dan 36, sub-masalah 24 dicabangkan menjadi sub-masalah 37 dan 38.

Iterasi 5

BB = Rp. 1.285.812.000 dengan 𝑥₁ = 0, 𝑥₂ = 8, 𝑥₃ = 2