Aplikasi Program Metode Elemen Hingga Pada Rangka Ruang (Space Truss) Dengan Program Matlab

(1)

APLIKASI PROGARAM METODE ELEMEN HINGGA PADA

RANGKA RUANG (SPACE TRUSS) DENGAN PROGRAM MATLAB

TUGAS AKHIR

Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil

Disusun oleh: ADE SATRIA 03 0404 012

BIDANG STUDI STRUKTUR

DEPARTEMEN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA

(2)

ABSTRAK

Pada perencanaan bangunan sipil saat ini banyak dipakai konstruksi rangka ruang,

seperti gedung pameran, hall dan lain-lain. Untuk itu penulis berkeinginan untuk

menganalisa struktur rangka tersebut.

Ada beberapa metode untuk menghitung dan menganalisa struktur rangka, antara

lain metode analitis dan metode numerik. Dalam tulisan ini, penulis akan manganalisa

secara numeric. Adapun metode yang akan di pakai adalah Metode Elemen Hingga

(M.E.H). Metode Elemen Hingga (M.E.H) adalah suatu metode numerik yang digunakan

untuk meyelesaikan problem dalam bidang engineering. Setelah dekade delapan puluhan

perkembangan metode ini sangat pesat karena pada saat itu juga telah dikembangkan dan

digunakan komputer untuk penyelesaian masalah numeriknya.

Pada tugas akhir ini akan dibuat suatu aplikasi program dengan menggunakan

Matlab (Matrix Laboratory) dimana MATLAB adalah sebuah program untuk analisis dan

komputasi numerik, yang merupakan suatu bahasa pemrograman matematika lanjutan

yang dibentuk dengan dasar pemikiran menggunakan sifat dan bentuk matriks, di sini

bentuk bangunan sipil yang dianalisis dimodelkan sebagai rangka ruang (space truss).

Pada perhitungan dengan momen, lintang dan normal dengan metode Matlab dan

SAP 2000 hasil yang diperoleh cukup akurat dengan perbedaan < 0.001 %. Pada

perhitungan deformasi dengan metode Matlab dan SAP 2000 hasil yang diperoleh cukup

(3)

1. Bap ak Prof. DR. Ing. Johannes Tarigan dan Bapak Ir. Sanci Barus, MT sebagai Dosen Pembimbing yang telah memberi bimbingan dan saran kepada penulis untuk menyelesaikan Tugas Akhir ini.

KATA PENGANTAR

Puji dan syukur penulis panjatkan kehadirat Allah SWT atas segala rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan Tugas Akhir ini, yang merupakan salah satu syarat untuk menyelesaikan pendidikan sarjana S1 pada Bidang Studi Struktur Jurusan Sipil Fakultas Teknik, Universitas Sumatera Utara, Medan.

Adapun judul Tugas Akhir ini adalah :

APLIKASI PROGRAM METODE ELEMEN HINGGA PADA RANGKA RUANG (SPACE TRUSS) DENGAN PROGRAM MATLAB

Pada kesempatan ini penulis ingin menyampaikan terima kasih yang sebesar-besarnya kepada :

2. Bap

ak Prof. DR. Ing. Johannes Tarigan sebagai Ketua Jurusan Teknik Sipil Fakultas Teknik Universitas Sumatera Medan.

3. Bap

ak Ir. Terunajaya, MSc sebagai Sekretaris Jurusan Teknik Sipil Fakultas Teknik Universitas Sumatera Medan.

4.

(4)

5. Bap ak dan Ibu staf pengajar dan seluruh pegawai Jurusan Teknik Sipil Fakultas Teknik Universitas Sumatera Medan.

6. Ora

ng tua dan saudara-saudara penulis yang telah memberikan dorongan semangat untuk menyelesaikan Tugas Akhir ini.

7. Tem

an-teman saya : Uus, Dani, Zul, Wira, Erwin dan Masana yang telah banyak membantu saya dalam menyelesaikan tugas akhir ini.

8. Rek

an-rekan mahasiswa yang telah memberikan motivasi serta bantuan moril dan segala kekerabatan dan kerja sama selama pendidikan Fakultas Teknik Universitas Sumatera Medan.

Penulis menyadari bahwa Tugas Akhir ini masih jauh dari sempurna, oleh karena itu penulis sangat mengharapkan kritik dan saran yang membangun dari Bapak dan Ibu Staf pengajar serta rekan-rekan mahasiswa demi penyempurnaan Tugas Akhir ini.

Akhir kata, penulis berharap Tugas Akhit ini dapat memberikan manfaat besar bagi kita semua.

Medan, Februari 2009 Penulis,

(5)

DAFTAR

ISI

Abstrak ... i

Kata pengantar ... ii

Daftar isi ... iv

Daftar notasi ... vii

Daftar tabel ... ix

Daftar gambar ... x

BAB I. PENDAHULUAN ... 1

1.1. Umum ... 1

1.2. Latar Belakang Masalah ... 3

1.3 Tujuan ... 4

1.4 Pembatasan Masalah ... 4

1.5 Metodologi ... 6

1.6 Sistematika Pembahasan ... 7

BAB II. METODE ELEMEN HINGGA PADA STRUKTUR TRUSS ... 8

(6)

II.1.1 Truss (rangka) ... 8

II.1.2 Beam ... 8

II.1.3 Spring Element ... 8

II.1.4. Grid ... 9

II.1.5. Frame (portal) ... 9

II.2 Metode Elemen Hingga ... 9

II. 3 Finite Element Method dan Methode Ritz ... 11

II.4 Penurunan matriks kekakuan batang ... 14

II. 5 Transformasi Pada Sistem Koordinat... 16

BAB III. DASAR-DASAR PEMROGRAMAN DENGAN MATLAB ... 38

III.1. Pendahuluan ... 38

III.2. Lingkungan Kerja Matlab ... 38

III.2.1 Beberapa Bagian dari Window Matlab ... 38

III.2.2 Getting Help ... 39

III.2.3 Interupting dan Terminating dalam Matlab ... 40

III.3. Variabel Pada Matlab ... 40

III.4. Operator ... 43

III.5. Fungsi Matematika lainnya ... 44

III.6. M File ... 44

III.6.1 Fungsi... 45

III.6.2 Flow Control ... 46

III.7 Langkah-langkah penyelesaian metode elemen hingga pada rangka ruang dengan Matlab ... 52

(7)

III.9 Perhitungan SAP2000 ... 54

BAB IV. APLIKASI ... 56

IV.1 Aplikasi 1 ... 56

IV.1.1 Perhitungan Dengan Program MATLAB ... 59

IV.1.2 Perhitungan dengan program SAP2000 ... 90

IV.2 Verifikasi Program ... 90

BAB V. KESIMPULAN DAN SARAN ... 106

V.1 Kesimpulan ... 106

V.2 Saran ... 107

DAFTAR PUSTAKA... 108

LAMPIRAN... 109

1. ... L ISTING PROGRAM MATLAB ... 109

(8)

DAFTAR NOTASI

A = Luas penampang

Cx = Kosinus arah x suatu batang Cy = Kosinus arah y suatu batang Cz = Kosinus arah z suatu batang

{d} = Vektor dari perpindahan (displacement) du = Perpindahan sejauh u

(9)

dz = Perpindahan titik kumpul arah z E = Modulus elastis

{f} = Vektor dari gaya-gaya luar pada titik simpul F = Gaya luar

Fx = Gaya sejajar sumbu x

Fy = Gaya sejajar sumbu y

Fz = Gaya sejajar sumbu z

i = Vektor satuan dalam arah sumbu x

j = Vektor satuan dalam arah sumbu y k = Vektor satuan dalam arah sumbu z

[K] = Matrix kekakuan

k = Koefisien kekakuan pegas

k = Vektor satuan dalam arah sumbu z

L = Panjang elemen M = Momen lentur P = Gaya batang

(10)

T = Torsi pada batang U = Energi

V = Potensial dari gaya luar = Energi potensial total

i = suatu fungsi

= Regangan

=

Tegangan

DAFTAR TABEL

Tabel II.1 : Penomoran Simpul Pada Elemen ... 24

Tabel IV.1 : Perpindahan Titik MATLAB ... 85

Tabel IV.2 : Reaksi Perletakan MATLAB ... 87

Tabel IV.3 : Gaya Batang MATLAB ... 87

Tabel IV.4 : Perpindahan Titik SAP2000 ... 93

Tabel IV.5 : Reaksi Tumpuan SAP2000 ... 94

Tabel IV.6 : Gaya Batang SAP2000 ... 94

Tabel IV.7 : Beda Absolut Perpindahan Titik ... 99

(11)

Tabel IV.9 : Beda Absolut Gaya Batang ... 101

DAFTAR GAMBAR

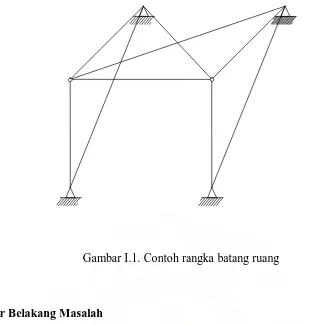
Gambar I.1 : Contoh rangka batang ruang ... 3

Gambar I.2 : Tumpuan sendi dan rol ... 4

Gambar I.3 : Menara Air ... 6

Gambar II.1 : Bentuk mesh pada metode elemen hingga ... 10

Gambar II.2 : Pemodelan Ritz ... 13

Gambar II.3 : Pemodelan FEM ... 13

Gambar II.4 : Elemen Rangka dibawah Pengaruh Gaya Luar F pada node 1 dan 2 ... 14

(12)

Gambar II.6 : Transformasi Sistem Koordinat Global ke Sistem Koordinat Lokal ... 19

Gambar II.7 : Penomoran untuk Nodal dan Batang ... 26

Gambar II.8 : Tanda dan Arah Gaya ... 29

Gambar III.1 : Tampilan Layar dari Matlab ... 43

Gambar III.2 : Contoh Gambar M-FILE ... 48

Gambar IV.1 : Menara Air ... 60

Gambar IV.2 : Pemodelan Gaya yang Bekerja ... 61

(13)

BAB I

PENDAHULUAN

1.1Umum

Seiring dengan perkembangan teknologi, maka perencanaan bangunan sipil juga semakin sulit. Ini dapat terlihat di kota-kota besar. Selain bangunan sipil yang berupa bangunan gedung, terdapat juga bangunan-bangunan sipil bukan gedung, misalnya jembatan, menara pemancar, atau rangka-rangka bangunan baja yang lain, yang memerlukan perhitungan dan perencanaan yang lebih matang.

Perkembangan teknologi komputer termasuk di dalamnya perkembangan software (perangkat lunak) yang sangat membantu guna memudahkan pekerjaan perhitungan dan perencanaan bangunan-bangunan yang kompleks. Perhitungan dengan menggunakan teknologi komputer mampu melakukan perhitungan dengan cepat, tepat, akurat serta efisien di dalam waktu dan saat ini telah banyak berkembang perangkat lunak yang profesional untuk membantu perhitungan dan perencanaan di bidang teknik sipil seperti SAP 2000, ETABS, STAAD PRO dan masih banyak lagi perangkat lunak yang sejenis. Pada umumnya perangkat lunak yang dikembangkan ini berbasis pada Metode Elemen Hingga (M.E.H) untuk memecahkan masalah mekanikanya.

(14)

(15)

Gambar I.1. Contoh rangka batang ruang

1.2Latar Belakang Masalah

(16)

1.3 Tujuan

Untuk mengembangkan suatu program analisa struktur untuk truss yang berbasis metode elemen hingga dengan menggunakan bahasa script programming yaitu Matlab serta membandingkan hasil yang diperoleh dengan software profesional untuk teknik sipil seperti SAP2000.

1.4 Pembatasan Masalah

Mengingat kompleksitas dari struktur, maka dalam kajian ini perlu adanya pembatasan permasalahan untuk menyederhanakan perhitungan dan mereduksi tingkat kesulitan, antara lain :

1. Struktur terdiri dari batang prismatis.

Batang memiliki sumbu yang lurus dan penampang lintang yang seragam di seluruh panjangnya

2. Titik kumpul dari rangka batang ruang dianggap sebagai sendi. 3. Jenis titik tumpuan yang ada di rangka adalah Sendi dan Rol.

Jenis tumpuan jepit tidak termasuk di rangka ruang, karena bisa menyebabkan momen, sehingga struktur tersebut harus di analisa sebagai portal.

Gambar I.2.tumpuan sendi dan rol

(17)

5. Praregang tidak diperhitungkan.

6. Penurunan atau perpindahan tumpuan tidak diperhitungkan.

7. Jenis material adalah homogen elastis, linier, homogen dan isotropis, yaitu pada setiap dan segala arah mempunyai modulus elastisitas yang sama.

8. Hasil keluaran dari program MATLAB untuk rangka ruang (space truss) berupa perpindahan titik (joint displacement), reaksi tumpuan (joint reaction), gaya batang dan tidak termasuk grafik.

(18)

Gambar I.3 Menara Air

tangki air

H = 3 m

d = 2.121 m

H = 3 m

L = 1.5 m

(19)

1.5 Metodologi

Metode yang dipakai dalam pembuatan program ini adalah berdasarkan metode Elemen Hingga (M.E.H) dengan menggunakan bahasa script programming dalam hal ini Matlab kemudian hasil yang diperoleh dibandingkan dengan program SAP 2000.

1.6 Sistematika Pembahasan

Penulisan tugas akhir ini dilakukan dengan sistematika pembahasan sebagai berikut: BAB I PENDAHULUAN

BAB II METODE ELEMEN HINGGA PADA STRUKTUR TRUSS

BAB III DASAR-DASAR PEMROGRAMAN DENGAN MATLAB

BAB IV APLIKASI

(20)

BAB II

METODE ELEMEN HINGGA PADA

STRUKTUR TRUSS

II.1 Jenis - Jenis Struktur dalam Elemen hingga II.1.1 Truss (rangka)

Definisi truss (rangka) adalah konstruksi yang tersusun dari batang-batang tarik dan batang-batang tekan saja, umumnya dari baja, kayu, atau paduan ringan guna mendukung atap atau jembatan, umumnya dapat menahan gaya aksial saja.

Truss 2 dimensi : truss yang dapat menahan beban pada arah datar saja (sumbu x, y) umumnya beban yang bekerja adalah beban terpusat nodal.

Truss 3 dimensi : himpunan batang yang dimana batang-batangnya berarah sembarang dalam ruang. yang dapat menahan beban pada semua arah (sumbu x, y dan z) umumnya beban yang bekerja adalah beban terpusat nodal.

II.1.2. Beam

Beam dapat menerima beban lateral atau beban yang tegak lurus pada beam.

II.1.3. Spring Element

(21)

II.1.4. Grid

Grid adalah struktur data yang dipersiapkan untuk menerima beban yang tegak lurus pada bidang datar struktur. Setiap penyusun struktur dianggap disambung (conected) secara rigid.

II.1.5. Frame (portal)

Definisi frame (portal) adalah kerangka yang terdiri dari dua atau lebih bagian konstruksi yang disambungkan guna stabilitas, umumnya dapat menahan gaya momen, gaya geser dan aksial.

Frame 2 dimensi : frame yang dapat menahan beban pada arah datar saja (sumbu x, y) umumnya beban yang bekerja adalah beban terpusat nodal dan beban batang.

Frame 3 dimensi : frame yang dapat menahan beban pada semua arah saja (sumbu x, y dan z) umumnya beban yang bekerja adalah beban terpusat nodal dan beban batang.

II.2 Metode Elemen Hingga

(22)

Bidang dengan dimensi tidak teratur menjadi bidang-bidang segiempat

beraturan

Kontinum Elemen

Hingga

Bidang dengan dimensi tidak teratur menjadi bidang-bidang segitiga

beraturan

Kontinum

Elemen Hingga

FEA

Exact

u

x

0

Batang bengkok menjadi batang pendek yang lurus

Sumber : Robert D Cook., David S. Malkus, Michael E. Palesha, Robert J. Witt Konsep dan aplikasi metode elemen hingga, Hal. 5

beraturan. Bidang yang dengan dimensi tidak beraturan tadi disebut kontinum, bidang segitiga atau segi empat beraturan disebut elemen hingga. Dan banyak lagi persoalan yang identik dengan hal diatas. Maka dari sini dapat dikatakan bahwa elemen hingga pasti mempunyai lebih kecil dari kontinumnya

Gambar II.1 Bentuk mesh pada metode elemen hingga

Sebaiknya pendekatan dengan metode elemen hingga merupakan suatu analisis pendekatan yang berdasarkan asumsi peralihan atau asumsi tegangan, bahkan dapat juga berdasarkan kombinasi kedua asumsi tadi dalam setiap elemennya.1

Tujuan utama analisis dengan metode elemen hingga adalah untuk memperoleh nilai pendekatan ( bukan eksak ) tegangan dan peralihan yang terjadi pada suatu struktur .

(23)

1

Sumber : William Weaver. JR, Paul R. Johnston.

Elemen Hingga Untuk Analisis Struktur. Hal. 3

dipakai, maka langkah-langkah berikut ini dapat digunakan sebagai pedoman bila menggunakan pendekatan berdasarkan asumsi tersebut :

1. Bagilah kontinum menjadi sejumlah elemen (Sub-region) yang berhingga dengan geometri yang sederhana (segitiga, segiempat. dan lain sebagainya).

2. Pada titik-titk pada elemen yang diperlakukan sebagai titik nodal, dimana syarat keseimbangan dan kompatibilitas dipenuhi.

3. Asumsikan fungsi peralihan pada setiap elemen sedemikian rupa sehingga peralihan pada setiap titik sembarangan dipengaruhi oleh nilai-nilai titik nodalnya.

4. Pada setiap elemen khusus yang dipilih tadi harus dipenuhi persyaratan hubungan regangan peralihan dan hubungan rengangan-tegangannya.

5. Tentukan kekakuan dan beban titik nodal ekivalen untuk setiap elemen dengan menggunakan prinsip usaha atau energi.

6. Turunkan persamaan keseimbangan ini untuk mencari peralihan titik nodal. 7. Selesaikan persamaan keseimbangan ini untuk mencari peralihan titik nodal. 8. Hitung tegangan pada titik tertentu pada elemen tadi.

9. Tentukan reaksi perletakan pada titik nodal yang tertahan bila diperlukan.

II. 3 Finite Element Method dan Methode Ritz

(24)

= U (v) + V (v) minimum …………... (2.1)

= Energi Potensial Total

V = Potensial dari gaya luar (terjadi bila gaya luar benda mempunyai arah)

U = Energi

Ritz V(x) =

∑ a

i

.

i

(x) = { }

T

{a}………... (2.2)

i = suatu fungsi

V = lendutan = minimum jika,

... (2.3)

pada suatu balok yang harus berlaku

= ½ ∫ E.I

... (2.4) V = - { ∫ q.v.dx + ∑ [Fj.vj + Mj .

... (2.5) = ½ ∫ (E v”2 – 2qv) dx - ∑ (Fj vj + Mj v’j) minimum ………...(2.6) dari (2.6) dan (2.2)

= ½ ∫ E (∑ ai . i”)2 dx - ∫ q ((∑ ai . i) dx - ∑[Fj ∑ai. i (xj) n

i=1

∂ _{= 0 (i = 1, 2, 3, …..,n) atau} ∂ _{= 0}

( )

d2V dx

( )2 . dx

( )

dV dx ( ) j]}

( ) (j)

( ) n

i=1 _i=₁ ₍_j₎ i=1

n n

(25)

+ j . ∑ ai . i (xj)]

= ½ ∫ E {a}T { ”}{ ”}T {a} dx - ∫ q{ }T {a} dx - ∑(Fj{ j}T{a}+Mj{ j}T{a})

= ½ {a}T∫E { ”}{ ”}T dx {a}- [∫q{ } dx + ∑(Fj { i}T + Mj { j}T)]{a}

= ½ {a}T [K] {a} – {f}T {a}

…….. (2.7)

Pada FEM balok akan dibagi dalam beberapa elemen untuk setiap elemen berlaku persamaan ke (2)

Ritz :

Gambar II.2 Pemodelan Ritz

FEM : i=1

( ) ( ) (j)

( )

( ) (j)

∂ ∂{a}

= [K] {a} – {f} = 0

[K] {a} f

X

V

V(x) = { }T {a}

. . . . . . . . . . . . = . . X

V

.

(26)

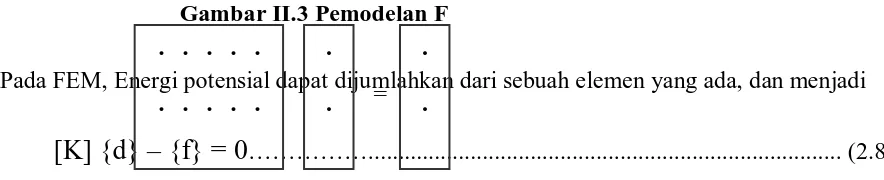
Gambar II.3 Pemodelan F

Pada FEM, Energi potensial dapat dijumlahkan dari sebuah elemen yang ada, dan menjadi

[K] {d} – {f} = 0………... (2.8)

II.4 Penurunan matriks kekakuan batang.

Pandanglah suatu elemen rangka dengan penampang melintang yang konstan, elastik dan linier, seperti ditunjukan dalam gambar.

A, E, L

d2x, f2x

d1x, f1x

1 2 F2 x y y x F1

Gambar II.4 Elemen Rangka dibawah Pengaruh Gaya Luar F pada Node 1 dan 2

Sumber : Ir. Yerri Susatio, MT

Dasar-Dasar Metode Elemen Hingga. Hal. 44

Sistem koordinat yang dipakai dalam gambar II.4 ada dua macam, yaitu :

Sistem koordinat lokal ( , ) yang berlaku hanya untuk elemen tersebut dan Sistem Global (x,y) yang berlaku untuk semua elemen yang ada (struktur).

Dengan anggapan bahwa elemen rangka memiliki penampang melintang A yang konstan, modulus elastis E, dan panjang L. Derajat kebebasan dari nodal adalah displacement lokal kearah axial (searah elemen rangka) berturut-turut adalah d1x, d2x

(27)

Berikut ini adalah beberapa asumsi yang digunakan untuk menurunkan persamaan matriks kekakuan elemen rangka.

1. Truss hanya menerima gaya pada arah axial (searah elemen) dan tidak menerima gaya pada arah lateral (tegak lurus elemen). Oleh karena itu F1y dan F2y masing-masing sama

dengan nol.

2. Semua perpindahan kearah selain arah penjang elemen diabaikan. 3. Elemen mengikuti hukum linier x = E x (pada arah axial)

Gunakan temuan Hooke bahwa perpindahan itu du akibat pengaruh gaya luar F.1

...(2.9)

...(2.10)

...(2.11) Dimana :

= koefisien kekakuan pegas

E = Modulus elastis

A = Luas penampang melintang L = Penjang elemen.

(28)

...……...(2.12)

1

Node 2 :

...(2.13)

Dalam bentuk matriks persamaan (2.12) dan (2.13) dapat dituliskan sebagai:

...(2.14) Matriks kekakuan lokal adalah:

...(2.15)

(29)

X

X Y

Y

Z

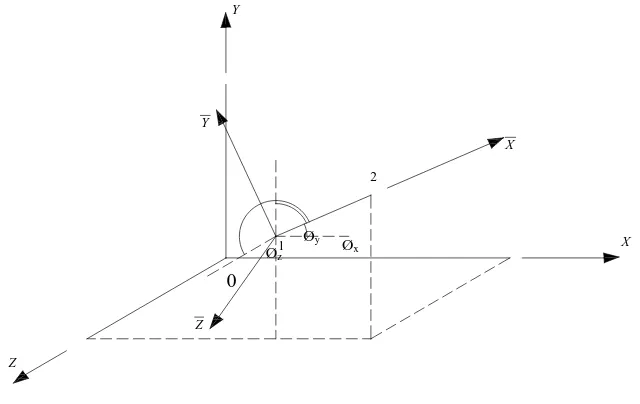
Gambar II.5 Elemen Dalam Ruang

1

2

Dalam gambar II.5 node 1 terletak pada titik O berada pada Sistem Koordinat Global dan node 2 pada titik A pada koordinat . Sudut antara

Koordinat Global dengan sumbu global x, y dan z berturut-turut adalah .

diambil pada arah longitudinal dari elemen rangka, dalam arah node 1 ke node 2.

Akan ditentukan Matriks Transformasi T* yang akan menghubungkan antara Sistem Koordinat Global dengan sistem koordinat Lokal:

...(2.16)

persamaan awal yang digunakan adalah:

...(2.17)

Dalam tiga dimensi persamaan ditulis sebagai berikut:

y z y z

...(2.18)

Øx Øy Øz

(30)

dimana :

, , : vektor satuan dalam arah sumbu lokal berturut-turut pada arah sumbu lokal , ,

i, j, k : vektor satuan dalam arah sumbu global berturut-turut pada arah sumbu lokal x, y, z.

Kalikan secara skalar (dot product) persamaan dengan i, akan dihasilkan persamaan:

y z ...(2.19)

dari definisi dot product :

...(2.20)

Dimana 2 1

2

2 1

2

2 1

2 1/2

Substitusikan harga-harga dari persamaan ke persamaan diperoleh:

(31)

...(2.21) Dimana [ T* ] adalah matriks transformasi.

Pada bagian ini akan diturunkan persamaan yang menghubungkan matriks kekakuan dalam koordinat global [ K ] dengan matriks kekakuan dalam koordinat lokal [ ].

Y

X X

D

B

E C

0 O

A (x,y)

GambarII.6 Transformasi sistem Koordinat Global ke Sistem Koordinat Lokal

(32)

Pengembangan dari Matriks Transformasi yang diperoleh, akan dikembangkan untuk kasus dalam ruang tiga dimensi.

Dalam Sistem Koordinat Global, koordinat A (x,y) Dalam Sistem Koordinat Lokal, koordinat A (OC,AC

...(2.22)

...(2.23)

Kedua persamaan (2.22) dan (2.23) ditulis dalam bentuk matriks ditulis sebagai:

...(2.24)

Jika Cos = dan Sin = µ maka Matriks Transformasi Koordinat Global ke Koordinat

Lokal adalah:

(33)

Satu titik (x1,y1) pada Koordinat Global dinyatakan dalam Koordinat Lokal yang

memebentuk sudut dengan sumbu Koordinat Global adalah:

...(2.26) Demikian juga titik (x2,y2) dalam Koordinat Global, jika dalam Koordinat Lokal menjadi:

...(2.27) Sebuah elemen dibatasi oleh dua buah node (x1,y1) dan (x2,y2) pada Koordinat Global, maka

elemen tersebut dalam Koordinat Lokal menjadi:

...(2.28) [ T2 ] adalah Matriks Transformasi elemen dengan dua node dari Koordinat Global ke Koordinat Lokal.

Catatan: x,y tanpa garis diatasnya (bar) menandakan Sistem Koordinat Global, sedangkan , (memakai garis diatas huruf menandakan Sistem Koordinat Lokal)

(34)

...(2.29) Matriks Transformasi Koordinat Global ke Koordinat Lokal adalah:

...(2.30) Seperti halnya dengan persamaan (2.28), maka Matriks Transformasi Koordinat Lokal ke Global adalah:

...(2.31) Dapat ditulis:

...(2.32) Persamaan (2.31) dapat ditulis dalam kaitannya dengan Displacement nodal sebagai:

...(2.33) Dalam bentuk simbol ditulis sebagai:

(35)

Rumus-rumus transformasi seperti diatas berlaku juga untuk mentransformasikan vektor gaya seperti dilakukan dibawah ini (lokal ke global).

Untuk node 1 yang dikenai gaya

Untuk node 2 yang dikenai gaya

Transformasi dari sebuah elemen yang berbatas dari dua buah node 1 dan 2, yang masing-masing dikenai gaya Fx1, Fy1 dan Fx2, Fy2 diperoleh hubungan:

...(2.35) Dalam bentuk simbol ditulis:

2 ...(2.36)

(lokal ke global) yang diketahui adalah vektor kolom pada ruas kanan. Dalam Sistem Koordinat Lokal berlaku

...(2.37)

(perhatikan x dan y memakai tanda garis diatas) Dalam Sistem Koordinat Global berlaku

(36)

Substitusi {q}xy dari persamaan (2.37) ke persamaan (2.38) diperoleh

...(2.39)

Dari persamaan (2.34)

maka;

...(2.40)

Karena matriks [T2] bersifat orthogonal, maka;

Persamaan terakhir menjadi

Substitusikan kembali hasil ini kepersamaan (2.38) dihasilkan

...(2.41)

Dari persamaan

...(2.42)

Kedua persamaan (2.41) dan (2.42) equivalen, maka:

(37)

Lihat kembali persamaan (2.38) Jadi:

... ...(2.43)

Persamaan (2.43) ini mentransformasikan matriks kekakuan dalam Koordinat Lokal ke Koordinat Global.

Sehingga dapat diturunkan persamaan matriks kekakuan dalam koordinat global sebagai berikut:

(38)

[image:38.595.155.506.282.555.2]

...(2.44)

Dimana:

II. 6 Kompatibilitas, keseimbangan, penentuan dari matriks kekakuan. Diketahui konstruklsi seperti gambar II.7

Gambar 2.7 Penomoran Untuk Nodal dan Batang

1

2

3

4

5

6

a

b

c

f

e

h

i

g

d

y

x

z

F

y

F

x

Tabel II. 1 Penomoran Simpul Pada Elemen Elemen Simpul 1 (awal) Simpul 2 (akhir)

a 1 2

b 2 3

c 1 3

d 4 5

(39)

f 4 6

g 2 5

h 2 6

i 3 5

Untuk elemen a (dibatasi oleh node 1 dan node 2),

matriks kekakuan elemen a adalah:

Untuk elemen b (dibatasi oleh node 2 dan node 3),

(40)

Untuk elemen c (dibatasi oleh node 1 dan node 3),

matriks kekakuan elemen c adalah:

Untuk elemen d (dibatasi oleh node 4 dan node 5),

(41)

Untuk elemen e (dibatasi oleh node 5 dan node 6),

matriks kekakuan elemen e adalah:

Untuk elemen f (dibatasi oleh node 4 dan node 6),

(42)

Untuk elemen g (dibatasi oleh node 2 dan node 5),

matriks kekakuan elemen g adalah:

Untuk elemen h (dibatasi oleh node 2 dan node 6),

(43)

Untuk elemen i (dibatasi oleh node 3 dan node 5),

matriks kekakuan elemen i adalah:

(44)

Sebagai syarat kompatibilitas maka, ditetapkan:

Dan dalam titik simpul harus memnuhi syarat keseimbangan. Pada titik simpul 1 berlaku:

(45)

+

-F

x

F

z

F

y

F

x

F

z

F

y

(46)

Dengan demikian didapat:

(47)

Dimana:

II. 7 Syarat batas (boundary cindition), perpindahan titik dan gaya batang.

Titik 1, 3, 4 dan 6 merupakan tumpuan sendi, maka tidak terjadi perpindahan

(48)

(49)

(50)

(51)

Dengan memasukan nilai , maka didapat reaksi tumpuan di titik 1, 3, 4 dan 6

(52)

Dimana:

Untuk gaya batang a:

Dimana:

(53)

Dengan memasukan nilai dari

dan

maka matriks menjadi:

(54)

BAB III

DASAR-DASAR PEMROGRAMAN

DENGAN MATLAB

III.1. Pendahuluan

Matlab merupakan bahasa pemrograman yang hadir dengan fungsi dan karakteristik yang berbeda dengan bahasa pemrograman lain yang sudah ada lebih dahulu seperti Delphi, Basic maupun C++. Matlab merupakan bahasa pemrograman level tinggi yang dikhususkan untuk kebutuhan komputasi teknis, visualisasi dan pemrograman seperti komputasi matematik, analisis data, pengembangan algoritma, simulasi dan pemodelan dan grafik-grafik perhitungan.

Matlab hadir dengan membawa warna yang berbeda. Hal ini karena matlab membawa keistimewaan dalam fungsi-fungsi matematika, fisika, statistik, dan visualisasi. Matlab dikembangkan oleh MathWorks, yang pada awalnya dibuat untuk memberikan kemudahan mengakses data matrik pada proyek LINPACK dan EISPACK. Saat ini matlab memiliki ratusan fungsi yang dapat digunakan sebagai problem solver mulai dari simple sampai masalah-masalah yang kompleks dari berbagai disiplin ilmu.

III.2. Lingkungan Kerja Matlab

(55)

Window ini menampilkan isi dari direktori kerja saat menggunakan matlab. Kita dapat mengganti direktori ini sesuai dengan tempat direktori kerja yang diinginkan. Default dari alamat direktori berada dalam folder works tempat program files Matlab berada.

• Command History

Window ini berfungsi untuk menyimpan perintah-perintah apa saja yang sebelumnya dilakukan oleh pengguna terhadap matlab.

• Command Window

Window ini adalah window utama dari Matlab. Disini adalah tempat untuk menjalankan fungsi, mendeklarasikan variable, menjalankan proses-proses , serta melihat isi variable.

• Workspace

Workspace berfungsi untuk menampilkan seluruh variabel-variabel yang sedang aktif pada saat pemakaian matlab. Apabila variabel berupa data matriks berukuran besar maka user dapat melihat isi dari seluruh data dengan melakukan double klik pada variabel tersebut. Matlab secara otomatis akan menampilkan window “array editor” yang berisikan data pada setiap variabel yang dipilih user .

III.2.2 Getting Help

(56)

menyediakan fungsi demos yang berisikan video tutorial matlab serta contoh-contoh program yang bisa dibuat dengan matlab

III.2.3 Interupting dan Terminating dalam Matlab

Untuk menghentikan proses yang sedang berjalan pada matlab dapat dilakukan dengan menekan tombol Ctrl-C. Sedangkan untuk keluar dari matlab dapat dilakukan dengan menuliskan perintah exit atau quit pada comamnd window atau dengan menekan menu exit pada bagian menu file dari menu bar.

(57)

III.3. Variabel Pada Matlab

Matlab hanya memiliki dua jenis tipe data yaitu Numeric dan String. Dalam matlab setiap variabel akan disimpan dalam bentuk matrik. User dapat langsung menuliskan variabel baru tanpa harus mendeklarasikannya terlebih dahulu pada command window

Contoh pembuatan variabel pada matlab:

>> varA = 1000 varA =

1000

>> varB = [45 2 35 45] varB =

45 2 35 45

>> varC = 'test variabel' varC =

test variabel

Penamaan variabel pada matlab bersifat caseSensitif karena itu perlu diperhatikan penggunaan huruf besar dan kecil pada penamaan variabel. Apabila terdapat variabel lama dengan nama yang sama maka matlab secara otomatis akan me-replace variabel lama tersebut dengan variabel baru yang dibuat user.

(58)

Contoh pembuatan data matriks pada matlab:

>> DataMatriks = [1 2 3;4 5 6] DataMatriks =

1 2 3 4 5 6

Matlab menyediakan beberapa fungsi yang dapat kita gunakan untuk menghasilkan bentuk-bentuk matriks yang diinginkan. Fungsi-fungsi tersebut antara lain:

• zeros : untuk membuat matriks yang semua datanya bernilai 0 • ones : matriks yang semua datanya bernilai 1

• rand : matriks dengan data random dengan menggunakan distribusi uniform • randn : matris dengan data random dengan menggunakan distribusi normal • eye : untuk menghasilkan matriks identitas

contoh penggunaan fungsi-fungsi diatas:

>> a = zeros(2,3) a =

0 0 0 0 0 0

>> b = ones(1,3) b =

1 1 1

(59)

0.9501 0.6068 0.2311 0.4860 >> d = rand (1,4) d =

0.8214 0.4447 0.6154 0.7919 >> e = eye(3,3)

e = 1 0 0 0 1 0 0 0 1

Untuk memanggil isi dari suatu data matriks, gunakan tanda kurung ‘()’ dengan isi indeks dari data yang akan dipanggil. Contoh penggunaan :

>> c(2,2) ans = 0.4860

Untuk pemanggilan data berurutan seperti a(1,2,3) dapat disingkat dengan menggunakan tanda titik dua ‘:’ sehingga menjadi a(1:2). Penggunaan tanda titik dua ‘:’ juga dapat digunakan untukmemanggil data matriks perbaris atau perkolom.

Contoh penggunaan:

(60)

III.4. Operator

Beberapa penggunaan operator aritmatika antara dua operand (A dan B) ditunjukkan berikut ini

Operasi Bentuk Aljabar Bentuk Matlab Contoh Perkalian A x B A * B 5*3

Pembagian A ÷ B A ¥ B 2¥3 Penambahan A + B A + B 1+2 Pengurangan A – B A – B 4-3 Eksponensial B A A ^ B 4^3

III.5. Fungsi Matematika lainnya

Beberapa fungsi matematika lainnya yang dapat kita gunakan untuk operasi matematika antara

lain sebagai berikut:

• abs(x) : fungsi untuk menghasilkan nilai absolut dari x

• sign(x) : fungsi untuk menghasilkan nilai -1 jika x<0, 0 jika x=0 dan 1 jika x>1 • exp(x) : untuk menghasilkan nilai eksponensian natural, x e

• log(x) : untuk menghasilkan nilai logaritma natural x, ln x

• log10(x) : untuk menghasilkan nilai logaritma dengan basis 10, x 10 log • sqrt(x) : untuk menghasilkan akar dari nilai x, x

(61)

III.6. M File

Di dalam matlab, kita dapat menyimpan semua script yang akan digunakan dalam file pada matlab dengan ekstensi .M. M-File dapat dipanggil dengan memilih menu file->new->M-File.

Gambar III.2 Contoh gambar M-File

(62)

Di dalam M File, kita dapat menuliskan fungsi-fungsi yang berisikan berbagai operasi sehingga menghasilkan data yang diinginkan.

Bentuk penulisan nama fungsi

Function [Nilai keluaran ] = namaFungsi (nilai masukan) % operasi dari fungsi

% … % …

Contoh penggunaan:

fungsi yang akan dibuat bernama ‘testfungsi’ memiliki tiga nilai masukan ‘c,d,e’ dan dua nilai

keluaran ‘a,b’:

function [a,b] = testFungsi(c,d,e) %operasi yang dijalankan

a = c + d +e; b = c * d *e;

Selanjutnya Fungsi tersebut akan dijalankan melalui command window dengan nilai

masukan ’10,2,4’. Perhatikan penulisan kurung siku ‘[ ]’ pada nilai keluaran dan kurung biasa

‘( )’ pada nilai masukan. >> [a,b] = testFungsi(10,2,3) a =

(63)

III.6.2 Flow Control

Matlab memiliki empat macam statement yang dapat digunakan untuk mengatur aliran data pada fungsi yang akan dibuat.

1. If, Else, Elseif

Bentuk dasar penggunaan statement jenis ini adalah sebagai berikut: if ekspresi1

statements1; elseif ekspresi2 statements2; else

statements3; end

Ekspresi akan bernilai 1 jika benar dan bernilai 0 jika salah. Contoh penggunaan:

function testFungsi(A,B) if A > B

disp('A lebih besar dari B') elseif A == B

disp('A sama dengan B') else

disp('A lebih kecil dari B') end

(64)

>> testFungsi(1,2) A lebih kecil dari B >> testFungsi(2,2) A sama dengan B >> testFungsi(2,3) A lebih kecil dari B

2. Switch

Bentuk dasar penggunaan statement switch switch switch_ekspresi

case case_ekspresi1 statement1

case case_ekspresi2 statement2

... ...

otherwise statementN end

Contoh penggunaan: function testFungsi(x) switch x

(65)

disp('x is 1') case {2,3,4} disp('x is 2, 3 or 4') case 5

disp('x is 5') otherwise

disp('x is not 1, 2, 3, 4 or 5') end

Hasil setelah dijalankan >> testFungsi(2)

x is 2, 3 or 4 >> testFungsi(1) x is 1

>> testFungsi(5) x is 5

>> testFungsi(6) x is not 1, 2, 3, 4 or 5

3. while

Statement while digunakan untuk aliran data yang bersifat perulangan. Bentuk dasar penggunaan while

(66)

Contoh penggunaan function testFungsi(x)

%selama nilai x kurang dari 10 while x < 10

disp('nilai saat ini : '); %tampilkan nilai x x

%increment nilai x x = x+1;

end

Hasil setelah dijalankan >> testFungsi(6)

nilai saat ini : x =

6

7

8

(67)

9

4. for

Bentuk dasar penggunaan bentuk for: for index = start:increment:stop statement

...

statement

end

Default dari nilai increment (penambahan nilai setiap perulangan) jika tidak ditentukan oleh user adalah 1.

Contoh fungsi :

function a = testFungsi for y = 1:10

a(y) = y^2; end

Hasil setelah fungsi dijalankan >> a = testFungsi

a =

1 4 9 16 25 36 49 64 81 100

(68)

Berikut ini adalah jenis-jenis operator pada matlab yang dapat digunakan untuk operasi ekspresi

pada statement yang membutuhkan perbandingan seperti if atau while.

Operator Keterangan A < B A lebih kecil dari B A > B A lebih besar dari B

A < = B A lebih kecil atau sama dengan B A > = B A lebih besar atau sama dengan B A = = B A sama dengan B

A ~ = B A tidak sama dengan B

Sebenarnya masih banyak fasilitas-fasilitas lain yang dimiliki oleh matlab. Tugas-tugas matematika yang membutuhkan analisis ataupun perhitungan yang kompleks dan rumit dapat kita implementasikan dengan mudah dengan memanfaatkan fasilitas yang tedapat di matlab.

III.7 Langkah-langkah penyelesaian metode elemen hingga pada rangka ruang dengan Matlab

1. Tentukan matriks kekakuan lokal dari struktur = [K]lokal

2. Transformasikan matriks untuk global ke sistem sumbu lokal = [T] 3. Konversi matriks untuk sumbu lokal ke sistem sumbu global 4. Bentuk matriks kekakuan sumbu global setiap elemen = [K]global

(69)

6. Bentuk matriks vektor beban dengan superposisi [Q]sis & [P]sis 7. Bentuk persamaan keseimbangan

[ ]

K (d)+(f)=(P)

[ ]

K sis*(D)=(P−Q)sis

8. Hitung reaksi dan perpindahan nodal per sistem sumbu global {P}global

9. Hitung reaksi dan perpindahan nodal per sistem sumbu lokal {P}lokal = [T].{P}global

10. Hitung gaya-gaya dalam struktur per elemen

III.8 File-file Matlab yang dibentuk pada waktu pemrograman File fungsi extract (extract.m)

File ini berfungsi untuk mengekstrak matriks (mxm) ke vektor matriks (mxm) x 1 dengan indeks informasi baris dan kolom

File fungsi aasembly (assembly.m)

File ini berfungsi untuk merangkai berdasarkan informasi baris dan kolom pada bahasa mesin (assembly) sehingga dapat mempercepat prose analisis matriks.

File fungsi sdata (sdata.m)

File ini berfungsi untuk membaca masukan data berupa jenis portal, koordinat, batang elastisitas, luas penampang dan inersia penampang)

(70)

File ini berfungsi untuk membaca masukan data berupa beban terpusat dan beban batang, serta kekangan dari perletakan

File fungsi t3d_stiff (t3d_stiff.m)

File ini berfungsi untuk membentuk matriks kekakuan sumbu lokal, matriks transformasi dan matriks kekakuan sumbu global.

File fungsi analysis_result (analysis_result..m)

File ini berfungsi untuk menganalisa matriks kekakuan sumbu kekakuan sumbu global dan matriks vektor beban dan dengan syarat batas dihitung reaksi perletakan dari struktur serta perpindahan nodal serta gaya-gaya dalam pada setiap elemen.

File fungsi print_result (print_result..m)

File ini berfungsi untuk menampilkan hasil berupa reaksi perletakan, perpindahan nodal, gaya momen, gaya geser dan gaya normal pada monitor dalam bentuk text.

III.9 Perhitungan SAP2000

(71)

SAP2000 benar-benar mampu mengambil tugas analisa struktur karena jika kita sudah melakukan input data dengan benar, maka proses analisa akan langsung diambil olah SAP2000 dan prosesnya pun tergolong sangat cepat.

Secara garis besar, perhitungan analisa struktur rangka dengan SAP2000 ini akan melaui beberapa tahap, yaitu:

1. Menentukan geometri model struktur 2. Mendefinisikan data-data.

a) Jenis dan kekuatan bahan.

b) Dimensi penampang elemen struktur. c) Macam beban.

d) Kombinasi pembebanan

3. Menempatkan (assign) data-data yang telah didefinisikan ke model struktur. a) Data penampang

b) Data beban 4. Memeriksa input data.

5. Analisa mekanika teknik (MT).

(72)

BAB IV

APLIKASI

Aplikasi penggunaan program Matlab dalam contoh ini adalah menara air yang menampung air dengan volume = 3 atau berat = 3 Ton. Hasil output kemudian dibandingkan

dengan output dari program analisa sruktur yang lain, dalam hal ini penulis menggunakan program SAP2000.

IV.1 APLIKASI 1

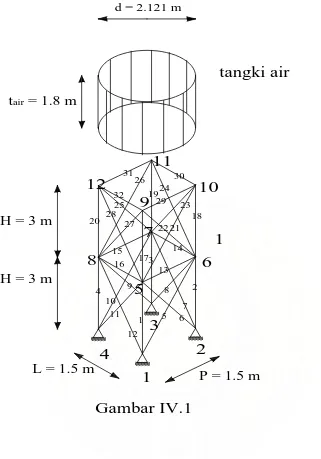
Gambar IV.I adalah rangka menara tangki air yangterdiri dari dua tingkat. Tingkat pertama dan kedua mempunyai ketinggian masing-masing sebesar H = 3 m. Panjang menara (P) = 1,5 m dan lebar (L) = 1,5 m. Tangki air dengan diameter (d) = 2.121 m dan tinggi (t) = 1.8 m. Rangka menara dibuat dengan profil baja siku 75.75.10 dengan luas profil A = 14.1 .

(73)

1

2

3

4

6

5

8

7

9

10

11

12

4 1 2 3 12 10

11 ₅ ₆

[image:73.595.122.443.92.551.2]

7 8 9 13 14 15 16 17 18 19 20 21 22 24 23 26 25 27 28 29 30 31 32

Gambar IV.1

tangki air

H = 3 m

d = 2.121 m

H = 3 m

L = 1.5 m

P = 1.5 m tair = 1.8 m

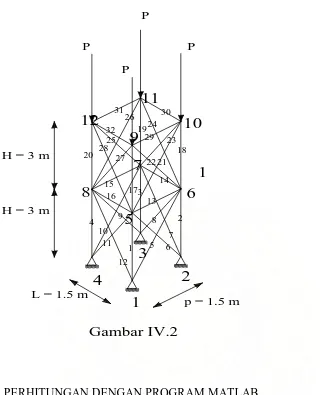
Perhitungan gaya – gaya yang bekerja pada tangki :

Tangki mempunyai diameter 2.121 m dengan tinggi 1.8 m. volume tangki adalah:

(74)

Besarnya gaya yang bekerja

gaya P didistribusikan ke empat titik maka setiap tititknya menahan gaya sebesar P = 0.75 Ton = 750 kg

(75)

[image:75.595.118.446.92.487.2]

1

2

3

4

6

5

8

7

9

10

11

12

4 1 2 3 12 10 11 ₅ 6 7 8 9 13 14 15 16 17 18 19 20 21 22 24 23 26 25 27 28 29 30 31 32 Gambar IV.2

H = 3 m H = 3 m

L = 1.5 m

p = 1.5 m P

P

IV.1.1 PERHITUNGAN DENGAN PROGRAM MATLAB

Dalam menjalankan program MATLAB diperlukan input data agar MATLAB dapat menjalankan perintah dengan benar. Adapun data-data yang dimasukan berupa material properti, koordinat dari struktur rangka, informasi elemen dan kondisi tumpuan. Untuk soal contoh 1, input datanya sebagai berikut:

(76)

%Prop i A E prop= [ 1 14.1 2100000 ]

%Koordinat grid:

% No.Joint absis-x ordinat-y ordinat-z coord= [ 1 0 0 0 2 150 0 0 3 150 150 0 4 0 150 0 5 0 0 300 6 150 0 300 7 150 150 300 8 0 150 300 9 0 0 600 10 150 0 600 11 150 150 600 12 0 150 600]

%Data Batang:

(77)

(78)

31 11 12 1 32 12 9 1]

%Kondisi Perletakan :

% Kekang Kekang Kekang % No.Joint Translasi-x Translasi-z Rotasi-y % lokal lokal lokal Support= [ 1 1 1 1 2 1 1 1 3 1 1 1 4 1 1 1]

%Joint Load:

% No.Joint Fx Fy Fz JL= [ 9 0 0 -750 10 0 0 -750 11 0 0 -750 12 0 0 -750]

(79)

(80)

0 0 0 0 0 0; 0 0 0 0 0 0; 0 0 0 0 0 0; 0 0 0 0 0 0; 0 0 0 0 0 0; 0 0 0 0 0 0; 0 0 0 0 0 0;]

Kemudian masih di dalam data masukan M-file TRUSS.m, lakukan analisa struktur dengan memanggil fungsi M-file yang telah dibuat sesuai dengan penjelasan pada Bab III.8 yaitu:

• extract.m

• assembly.m

• sdata.m

• ldata.m

• grid_stiff.m

• analysis_result..m

• print_result..m

(81)

%Analisa Struktur dengan memanggil fungsi M-file : [dof,index,coord,element]=...

sdata(prop,element,coord,type);

[S,Sm,SmS,Cx,Cy,Cxz,RT,L,A,Joint,Xj,Xk,Yj,Yk,Zj,Zk]=... t3d_stiff(prop,element,coord,index);

[IR,IF,Support]=ldata(Support,dof);

[DF,AR,AM]=analysis_result(element,dof,index,IF,IR,... S,SmS,JL,AML,RT,Support,type)

[joint_disp,support_reaction,beam_endforces]=...

print_result(dof,Support,element,IF,IR,DF,AR,AM,type); end

[image:81.595.89.505.375.745.2]

setelah M-file TRUSS.m dijalankan, didapat hasil keluaran dari program MATLAB untuk rangka ruang adalah :

Tabel IV.1 Perpindahan Titik MATLAB

titik Dx Dy Dz

cm cm cm

1 0.000000000 0.000000000 0.000000000

2 0.000000000 0.000000000 0.000000000

3 0.000000000 0.000000000 0.000000000

4 0.000000000 0.000000000 0.000000000

5 -0.000534597 -0.000534597 -0.003283026

(82)

7 0.000534597 0.000534597 -0.003283026

8 -0.000534597 0.000534597 -0.003283026

9 -0.000264863 -0.000264863 -0.006644010

10 0.000264863 -0.000264863 -0.006644010

11 0.000264863 0.000264863 -0.006644010

[image:82.595.171.473.70.245.2]

12 -0.000264863 0.000264863 -0.006644010

Tabel IV.2 Reaksi Perletakan MATLAB

titik Rx Ry Rz

kg kg kg

1 106.49133 106.49133 750.00000

2 -106.49133 106.49133 750.00000

3 -106.49133 -106.49133 750.00000

4 106.49133 -106.49133 750.00000

Tabel IV.3 Gaya Batang MATLAB

titik Fy1 Fx1 Fz1 Fy2 Fx2 Fz2

Kg Kg Kg Kg Kg Kg

1 324.03469 0 0 -324.03469 0 0

2 324.03469 0 0 -324.03469 0 0

3 324.03469 0 0 -324.03469 0 0

4 324.03469 0 0 -324.03469 0 0

5 238.12185 0 0 -238.12185 0 0

[image:82.595.90.540.288.742.2]

(83)

7 238.12185 0 0 -238.12185 0 0

8 238.12185 0 0 -238.12185 0 0

9 238.12185 0 0 -238.12185 0 0

10 238.12185 0 0 -238.12185 0 0

11 238.12185 0 0 -238.12185 0 0

12 238.12185 0 0 -238.12185 0 0

13 -211.05906 0 0 211.05906 0 0

14 -211.05906 0 0 211.05906 0 0

15 -211.05906 0 0 211.05906 0 0

16 -211.05906 0 0 211.05906 0 0

17 331.72906 0 0 -331.72906 0 0

18 331.72906 0 0 -331.72906 0 0

19 331.72906 0 0 -331.72906 0 0

20 331.72906 0 0 -331.72906 0 0

21 233.82057 0 0 -233.82057 0 0

22 233.82057 0 0 -233.82057 0 0

23 233.82057 0 0 -233.82057 0 0

24 233.82057 0 0 -233.82057 0 0

25 233.82057 0 0 -233.82057 0 0

26 233.82057 0 0 -233.82057 0 0

27 233.82057 0 0 -233.82057 0 0

28 233.82057 0 0 -233.82057 0 0

(84)

30 -104.56774 0 0 104.56774 0 0

31 -104.56774 0 0 104.56774 0 0

32 -104.56774 0 0 104.56774 0 0

IV.1.2 PERHITUNGAN DENGAN PROGRAM SAP2000

Dalam program SAP2000 sistem data masukan yang sering digunakan adalah dengan sistem GUI (Graphical User Interface), yaitu sistem dengan mendesain interface, yaitu memodelkan struktur dan kondisi pembebanannya dalam bentuk grafis. Tapi dalam tugas akhir ini, saya juga akan menyajikan masukan data dibuat dalam file program pengolah kata notepad dengan nama file berekstensi .$2K sebagai berikut:

TABLE: "JOINT COORDINATES"

Joint=1 CoordSys=GLOBAL CoordType=Cartesian XorR=0 Y=0 Z=0 SpecialJt=No GlobalX=0

GlobalY=0 GlobalZ=0

Joint=2 CoordSys=GLOBAL CoordType=Cartesian XorR=150 Y=0 Z=0 SpecialJt=No

GlobalX=150 GlobalY=0 GlobalZ=0

[image:84.595.87.541.71.158.2]

(85)

TABLE: "CONNECTIVITY - FRAME"

Frame=1 JointI=1 JointJ=5 IsCurved=No Length=300 CentroidX=0 CentroidY=0

CentroidZ=150

Frame=5 JointI=1 JointJ=6 IsCurved=No Length=335.410196624968 CentroidX=75

CentroidY=0 CentroidZ=150

[image:85.595.89.555.166.749.2]

(86)

CentroidZ=300

CentroidZ=450

(87)

CentroidZ=600

TABLE: "JOINT RESTRAINT ASSIGNMENTS"

Joint=1 U1=Yes U2=Yes U3=Yes R1=No R2=No R3=No

TABLE: "JOINT LOADS - FORCE"

Joint=9 LoadCase=DEAD CoordSys=GLOBAL F1=0 F2=0 F3=-750 M1=0 M2=0 M3=0

[image:87.595.88.555.69.511.2]

(88)

Dalam sistem GUI (Graphical User Interface),tampilan model rangka ruang, sebagai berikut:

Gamb ar IV.3 Tampilan Layar Pada SAP 2000

[image:88.595.91.544.122.519.2]

File hasil keluaran (output) dari program SAP2000 adalah:

Tabel IV.1 Perpindahan Titik SAP2000

TABLE: Joint Displacements

Joint OutputCase CaseType U1 U2 U3 R1 R2 R3

Text Text Text cm cm cm Radians Radians Radians

1 DEAD LinStatic 0 0 0 0 0 0

(89)

5 DEAD LinStatic -0.000535 -0.000535 -0.003283 0 0 0

6 DEAD LinStatic 0.000535 -0.000535 -0.003283 0 0 0

7 DEAD LinStatic 0.000535 0.000535 -0.003283 0 0 0

8 DEAD LinStatic -0.000535 0.000535 -0.003283 0 0 0

9 DEAD LinStatic -0.000265 -0.000265 -0.006644 0 0 0

10 DEAD LinStatic 0.000265 -0.000265 -0.006644 0 0 0

11 DEAD LinStatic 0.000265 0.000265 -0.006644 0 0 0

[image:89.595.87.550.66.656.2]

12 DEAD LinStatic -0.000265 0.000265 -0.006644 0 0 0

Tabel IV.2 Reaksi Perletakan SAP2000

TABLE: Joint Reactions

Joint OutputCase CaseType F1 F2 F3 M1 M2 M3

Text Text Text Kgf Kgf Kgf Kgf-cm Kgf-cm Kgf-cm

1 DEAD LinStatic 106.49 106.49 750 0 0 0

2 DEAD LinStatic -106.49 106.49 750 0 0 0

3 DEAD LinStatic -106.49 -106.49 750 0 0 0

4 DEAD LinStatic 106.49 -106.49 750 0 0 0

Tabel IV.3 Gaya Batang SAP2000

(90)

Fram e Statio n OutputCa se CaseTy pe P V 2 V 3

T M2 M3

FrameEl

em

ElemStati

on

Text cm Text Text Kgf Kg f Kg f Kgf-cm Kgf-cm Kgf-cm

Text cm

1 0 DEAD

LinStati

c

-324.0

3

0 0 0 0 0 1 0

1 300 DEAD

LinStati

c

-324.0

3

0 0 0 0 0 1 300

2 0 DEAD

LinStati

c

-324.0

3

0 0 0 0 0 2 0

2 300 DEAD

LinStati

c

-324.0

3

0 0 0 0 0 2 300

3 0 DEAD

LinStati

c

-324.0

3

0 0 0 0 0 3 0

3 300 DEAD

LinStati

c

-324.0

3

0 0 0 0 0 3 300

4 0 DEAD

LinStati

c

-324.0

(91)

3

4 300 DEAD

LinStati

c

-324.0

3

0 0 0 0 0 4 300

5 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 5 0

5 335.4 1 DEAD LinStati c -238.1 2

0 0 0 0 0 5 335.41

6 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 28 0

6 167.7 05 DEAD LinStati c -238.1 2

0 0 0 0 0 28 167.705

6 335.4 1 DEAD LinStati c -238.1 2

0 0 0 0 0 28 335.41

7 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 6 0

7 335.4 1 DEAD LinStati c -238.1

(92)

2

8 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 7 0

8 335.4 1 DEAD LinStati c -238.1 2

0 0 0 0 0 7 335.41

9 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 8 0

9 335.4 1 DEAD LinStati c -238.1 2

0 0 0 0 0 8 335.41

10 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 9 0

10 335.4 1 DEAD LinStati c -238.1 2

0 0 0 0 0 9 335.41

11 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 10 0

11 335.4 1 DEAD LinStati c -238.1

(93)

2

12 0 DEAD

LinStati

c

-238.1

2

0 0 0 0 0 11 0

12 335.4 1 DEAD LinStati c -238.1 2

0 0 0 0 0 11 335.41

13 0 DEAD

LinStati

c

211.0

6

0 0 0 0 0 12 0

13 150 DEAD

LinStati

c

211.0

6

0 0 0 0 0 12 150

14 0 DEAD

LinStati

c

211.0

6

0 0 0 0 0 13 0

14 150 DEAD

LinStati

c

211.0

6

0 0 0 0 0 13 150

15 0 DEAD

LinStati

c

211.0

6

0 0 0 0 0 14 0

15 150 DEAD

LinStati

c

211.0

6

0 0 0 0 0 14 150

16 0 DEAD

LinStati

c

211.0

6

0 0 0 0 0 15 0

16 150 DEAD

LinStati

c

211.0

6

0 0 0 0 0 15 150

(94)

c 331.7

3

17 300 DEAD

LinStati

c

-331.7

3

0 0 0 0 0 16 300

18 0 DEAD

LinStati

c

-331.7

3

0 0 0 0 0 17 0

18 300 DEAD

LinStati

c

-331.7

3

0 0 0 0 0 17 300

19 0 DEAD

LinStati

c

-331.7

3

0 0 0 0 0 18 0

19 300 DEAD

LinStati

c

-331.7

3

0 0 0 0 0 18 300

20 0 DEAD

LinStati

c

-331.7

3

0 0 0 0 0 19 0

20 300 DEAD

LinStati

c

-331.7

3

0 0 0 0 0 19 300

(95)

c 233.8 2 21 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 20 335.41

22 0 DEAD

LinStati

c

-233.8

2

0 0 0 0 0 21 0

22 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 21 335.41

23 0 DEAD

LinStati

c

-233.8

2

0 0 0 0 0 22 0

23 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 22 335.41

24 0 DEAD

LinStati

c

-233.8

2

0 0 0 0 0 23 0

24 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 23 335.41

(96)

c 233.8 2 25 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 24 335.41

26 0 DEAD

LinStati

c

-233.8

2

0 0 0 0 0 25 0

26 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 25 335.41

27 0 DEAD

LinStati

c

-233.8

2

0 0 0 0 0 26 0

27 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 26 335.41

28 0 DEAD

LinStati

c

-233.8

2

0 0 0 0 0 27 0

28 335.4 1 DEAD LinStati c -233.8 2

0 0 0 0 0 27 335.41

(97)

c 7

29 50 DEAD

LinStati

c

104.5

7

0 0 0 0 0 29 50

29 100 DEAD

LinStati

c

104.5

7

0 0 0 0 0 29 100

29 150 DEAD

LinStati

c

104.5

7

0 0 0 0 0 29 150

30 0 DEAD

LinStati

c

104.5

7

0 0 0 0 0 30 0

30 50 DEAD

LinStati

c

104.5

7

0 0 0 0 0 30 50

30 100 DEAD

LinStati

c

104.5

7

0 0 0 0 0 30 100

30 150 DEAD

LinStati

c

104.5

7

0 0 0 0 0 30 150

31 0 DEAD

LinStati

c

104.5

7

0 0 0 0 0 31 0

31 50 DEAD

LinStati

c

104.5

7

0 0 0 0 0 31 50

31 100 DEAD

LinStati

c

104.5

7

0 0 0 0 0 31 100

31 150 DEAD

LinStati

c

104.5

7

0 0 0 0 0 31 150

(98)

c 7

32 50 DEAD

LinStati

c

104.5

7

0 0 0 0 0 32 50

32 100 DEAD

LinStati

c

104.5

7

0 0 0 0 0 32 100

32 150 DEAD

LinStati

c

104.5

7

0 0 0 0 0 32 150

IV.2 VERIFIKASI PROGRAM

Karena program yang saya buat merupakan program buatan sendiri yang bersifat independent dan tahap pemula. Dan juga karena alasan bahwa yang sibuat merupakan aplikasi untuk teknik, dimana ketepatan perhitungansangat diperlukan. Maka perlu diadakan verifikasi atau uji check program dengan paket program yang telah dibuat oleh perusahaan kelas international.

Untuk verifikasi ini akan dipakai program SAP2000, dimana uji program dengan melihat selisih absolut hasil program yang dibuat dengan hasil program SAP2000.

Formula yang dipakai adalah:

[image:98.595.88.560.67.311.2]

Untuk aplikasi yang pertama

Tabel IV.7 Beda Absolut Perpindahan Titik titi

k program MATLAB6 SAP2000 BEDA ABSOLUT

(99)

cm cm cm cm cm cm cm cm cm

1 0 0 0 0 0 0 0 0 0

2 0 0 0 0 0 0 0 0 0

3 0 0 0 0 0 0 0 0 0

4 0 0 0 0 0 0 0 0 0

5 -0.0005345 97 -0.0005345 97 -0.0032830 26 -0.00053 5 -0.00053 5 -0.00328 3 4.03E-07 4.03E-07 -2.6E-08 6 0.0005345 97 -0.0005345 97 -0.0032830 26 0.00053 5 -0.00053 5 -0.00328 3 -4.03E-07 4.03E-07 -2.6E-08 7 0.0005345 97 0.0005345 97 -0.0032830 26 0.00053 5 0.00053 5 -0.00328 3 -4.03E-07 -4.03E-07 -2.6E-08 8 -0.0005345 97 0.0005345 97 -0.0032830 26 -0.00053 5 0.00053 5 -0.00328 3 4.03E-07 -4.03E-07 -2.6E-08 9 -0.0002648 63 -0.0002648 63 -0.0066440 1 -0.00026 5 -0.00026 5 -0.00664 4 1.37E-07

1.37E-07 -1E-08

10 0.0002648 63 -0.0002648 63 -0.0066440 1 0.00026 5 -0.00026 5 -0.00664 4 -1.37E-07

1.37E-07 -1E-08

(100)

63 63 0.0066440

1

5 5 0.00664

4

07 07

12 -0.0002648 63 0.0002648 63 -0.0066440 1 -0.00026 5 0.00026 5 -0.00664 4 1.37E-07

[image:100.595.86.559.71.211.2]

-1.37E-07 -1E-08

Tabel IV.8 Beda Absolut Reaksi Tumpuan

titik program MATLAB6 SAP2000 BEDA ABSOLUT

Rx Ry Rz Rx Ry Rz Rx Ry Rz

kg kg kg kg kg kg kg kg kg

1 106.49133 106.49133 750.00000 106.49 106.49 750 0.00133 0.00133 0

2 -106.49133 106.49133 750.00000 -106.49 106.49 750 -0.00133 0.00133 0

3 -106.49133 -106.49133 750.00000 -106.49 -106.49 750 -0.00133 -0.00133 0

4 106.49133 -106.49133 750.00000 106.49 -106.49 750 0.00133 -0.00133 0

[image:100.595.87.510.665.726.2]

Dapat dilihat dari tabel-tabel beda absolut untuk perpindahan titik dan reaksi tumpuan didapat sebagian besar sama. Adanya perbedaan hasil, terjadi karena pembulatan desimal yang dipakai, atau presisi (ketetapan perhitungan) yang dilakukan berbeda. Namun dengan berdasarkan nilai beda absolut yang mendekati 0 menunjukan program telah berjalan dengan semestinya.

Tabel IV.9 Beda Absolut Gaya Batang

titik program MATLAB6 SAP2000 BEDA ABSOLUT

(101)

Text Kg Kg Kg Kg Kg Kg Kg Kg Kg

1 324.03469 0 0 -324.03 0 0 648.06469 0 0

1 -324.03469 0 0 -324.03 0 0 -0.00469 0 0

2 324.03469 0 0 -324.03 0 0 648.06469 0 0

2 -324.03469 0 0 -324.03 0 0 -0.00469 0 0

3 324.03469 0 0 -324.03 0 0 648.06469 0 0

3 -324.03469 0 0 -324.03 0 0 -0.00469 0 0

4 324.03469 0 0 -324.03 0 0 648.06469 0 0

4 -324.03469 0 0 -324.03 0 0 -0.00469 0 0