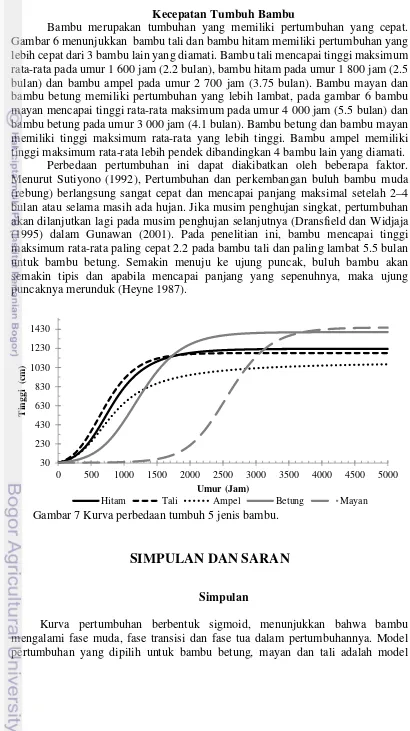
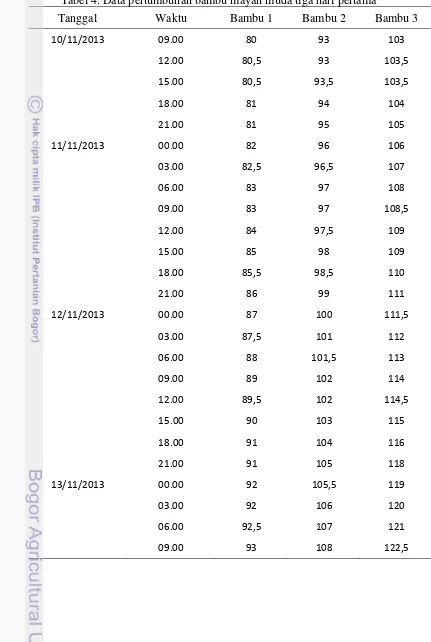
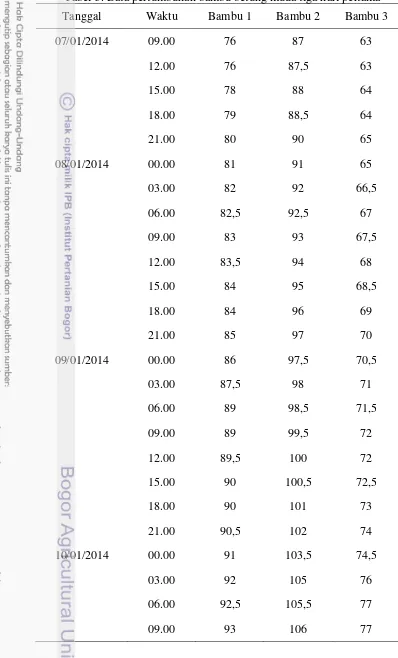
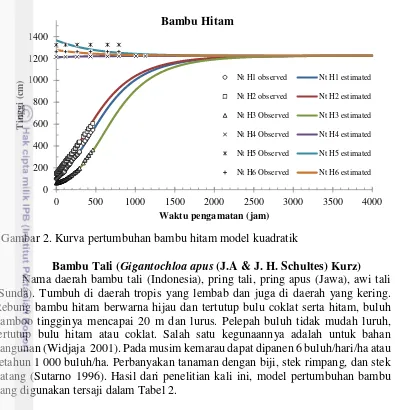
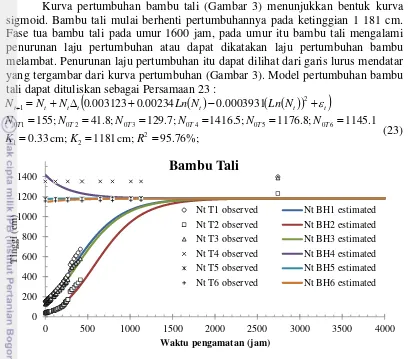
Kurva Pertumbuhan Lima Jenis Bambu
Teks penuh
Gambar
Garis besar
Dokumen terkait
Pada bab ini akan dibahas mengenai homomorfisma grup beserta sifat-sifatnya, termasuk diantaranya tiga Teorema Utama Homomorfisma.. termasuk diantaranya tiga Teorema
junk food disini merupakan makanan rendah gizi dan tidak sehat yang disajikan dengan cepat saji dan dikemas dalam bentuk yang menarik yang saat ini telah menjamur di
Cara berdagang yang dilakukan pedagang muslim di Kota Benteng sudah terbilang cukup baik, karena secara umum kebanyakan dari pedagang muslim yang ada di kota
Berangkat dari persoalan di atas, tulisan ini mendiskusikan konstruksi ketiga media cetak, yakni Kompas , Bola , dan Sindo dalam konflik PSSI dan KPSI,
Faktor risiko kejadian Leptospirosis pada pekerja sektor informal adalah umur dewasa (18-40 tahun), jenis kelamin laki-laki, riwayat mendapatkan luka selama bekerja,
berakti&itas untuk menyusun dan menyeles menyelesaikan makalah yang aikan makalah yang berjudul berjudul ''Me Membu mbuat at Bet Beton on De Denga ngan n Kin
Berdasarkan wawancara tersebut dapat diketahui bahwa peserta merasa puas terhadap inovasi-inovasi metode pembelajaran yang dijalankan instruktur dalam menyampaikan
Untuk mendapatkan gaya yang bekerja pada deck barge EASTERN NOVA, analisa yang dilakukan yaitu dengan menggunakan MOSES 6.0. Pada analisa ini gaya yang