SEM SERAH
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Bogor, Juli 2011
Sem Serah NRP G751090181 Dengan ini saya menyatakan bahwa tesis Model Minimal Kinetika Glukosa dan Insulin untuk mendeteksi Diabetes Tipe 2 adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
SEM SERAH. Minimal Model of Glucose and Insulin Kinetic to Detect Type 2 Diabetes. Under direction of AGUS KARTONO and AKHIRUDDIN.
Insulin sensitivity and pancreatic responsivity are two main factors controlling glucose tolerance. This research has proposed minimal model modified by rule introducing a mathematical model for describing the insulin infusion rate. The modified model was used to study three sets of published data including healthy human and type 2 diabetes with different types of insulin infusion rates. From the model parameter, it is possible to extract four indices: (1) SG, parameter discribes glucose effectiveness, which is the effect of glucose to
normalize the glucose concentration at basal insulin, (2) SI, the tissue insulin
sensitivity index, (3) ϕ1, first phase pancreatic responsitivity, and (4) ϕ2, second
phase pancreatic responsitivity. These four characteristic parameters have been shown to represent an integrated metabolic potrait of a single individual.
SEM SERAH. Model Minimal Kinetika Glukosa dan Insulin untuk Mendeteksi Diabetes Tipe 2. Dibimbing oleh AGUS KARTONO dan AKHIRUDDIN.
Diabetes Mellitus (DM) atau yang dikenal sebagai penyakit gula atau kencing manis adalah penyakit yang ditandai dengan kadar gula tinggi dalam darah dan urin. DM adalah penyakit kronis yang berhubungan dengan gangguan metabolisme karbohidrat yang disebabkan oleh gangguan sekresi insulin, ketidakmampuan tubuh untuk memproduksi hormon insulin atau karena penggunaan yang tidak efektif dari produksi insulin. Penyakit ini membutuhkan perhatian dan perawatan medis dalam waktu lama, baik untuk perawatan sakit maupun mencegah komplikasi dengan penyakit lain, seperti penyakit jantung koroner, stroke, kebutaan, gangguan ginjal kronik, gagal ginjal, dan luka yang sulit sembuh pada kaki sampai menjadi busuk. DM secara luas diklasifikasikan ke dalam dua kategori, yaitu diabetes tipe 1 dan diabetes tipe 2. Populasi diabetes tipe 2 di dunia hampir 90% dari seluruh populasi penderita DM, sedangkan diabetes tipe 1 sekitar 5-10% saja.
Pada DM, model matematika sederhana dan komprehensif yang berhubungan dengan aspek tinjauan yang berbeda dari penyakit ini telah digunakan selama tiga dekade terakhir. Banyak model matematika telah dikembangkan untuk lebih memahami mekanisme sistem pengaturan insulin. Model yang paling sesuai dengan mekanisme sistem pengaturan glukosa-insulin adalah Model Minimal Bergman. Model ini berisi jumlah parameter yang sedikit dan telah banyak digunakan dalam penelitian fisiologis untuk memperkirakan efektivitas glukosa (SG) dan sensitivitas insulin (SI) dari data tes toleransi glukosa intravena (IVGTT) selama periode tertentu.
perubahan konsentrasi glukosa dan insulin dari model yang dibuat. Model pada penelitian ini merupakan persamaan diferensial biasa, maka metode numerik yang paling akurat ialah Runge Kutta orde 45 atau ode45. Selanjutnya program divalidasi dengan data eksperimen yang diperoleh dari jurnal publikasi.
Nilai parameter yang digunakan untuk model minimal glukosa orang sehat
adalah G0 = 300 mg/dl, SG = 0.0026 menit-1, k3 = 0.025 menit-1,
SI = 0.0005 menit-1 (µU/ml)-1, sedangkan nilai parameter yang digunakan untuk
model minimal insulin orang sehat adalah k = 0.290 menit-1,
γ = 0.0055 menit-2 [(µU/ml) (mg/dl)]-1 , Gb = 92 mg/dl dan I0 = 410 µU/ml.
Sensitivitas insulin, SI, pada data diperkirakan 5.039×10-4 menit-1 (µU/ml)-1 yang berada dalam rentang normal, yaitu: 2.1 sampai 18.2×10-4 menit-1 (µU/ml)-1. Efektivitas glukosa, SG, untuk data diperkirakan 0.0265 menit-1, yang juga dalam rentang normal: 0.0026 sampai 0.039 menit-1. Responsivitas pankreas tahap pertama (ϕ1), diperkirakan 3.462 menit-1 [(µU/ml) (mg/dl)] -1. Ini tidak lebih dari kisaran normal untuk ϕ1 sebesar 2.0 sampai 4.0 menit-1 [(µU/ml) (mg/dl)] -1.
Responsivitas pankreas tahap kedua (ϕ2) diperkirakan sebesar 40,745 menit-2 [(µU/ml) (mg/dl)]-1. Hal ini sedikit lebih tinggi dari kisaran normal
untuk ϕ2 sebesar 20 sampai 35 menit-2 [(µU/ml) (mg/dl)]-1.
konsentrasi insulin terhadap waktu t. Fitting terbaik data eksperimen dengan plot grafik hasil simulasi model kinetika glukosa dihasilkan dengan nilai parameter:
Gb = 110 mg/dl, Ib = 20 µU/ml, I0 = 410 µU/ml, G0 = 360 mg/dl,
SG = 0.019 menit-1, k3 = 0.01 menit-1, SI = 0.00001 menit-1 (µU/ml)-1, sedangkan
fitting terbaik model kinetika insulin dihasilkan dengan nilai parameter: k = 0.27 menit-1, γ = 0.0055 menit-2 [(µU/ml) (mg/dl)]-1, G0 = 360 mg/dl dan
I0 = 80 µU/ml. Nilai SI yang ditunjukkan oleh model menyatakan bahwa pasien memiliki gangguan sensitivitas insulin, dengan kata lain pasien mengalami resistensi insulin. Efektivitas glukosa diprediksi dari model masih dalam rentang normal. Hal ini menunjukkan bahwa laju penyerapan glukosa pada jaringan tanpa bantuan insulin masih baik, dimana pada proses penyerapan glukosa untuk menghasilkan energi tidak memerlukan bantuan insulin. Konsentrasi insulin yang sesuai dirangsang oleh injeksi glukosa tidak begitu berpengaruh Ø1 ketika puncak pertama sekresi insulin tidak terlihat, dengan kata lain responsivitas insulin tahap pertama tidak mencukupi. Ø2 diperkirakan sebesar 55 menit-2 [(µU/ml) (mg/dl)]-1.
Hal ini lebih tinggi dari kisaran normal untuk Ø2 dilaporkan sebesar 20 sampai 35 menit-2 [(µU/ml) (mg/dl)]-1. Insulin eksogen diinjeksi dengan laju
28 (mU/kg menit).
© Hak Cipta milik IPB, tahun 2011
Hak Cipta dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan yang wajar IPB
SEM SERAH
Tesis
Sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Program Studi Biofisika
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
Judul : Model Minimal Kinetika Glukosa dan Insulin untuk Mendeteksi Diabetes Tipe 2
Nama : Sem Serah NRP : G751090181
Disetujui Komisi Pembimbing
Diketahui,
Tanggal Ujian: 11 Juli 2011 Tanggal Lulus:
Dr. Agus Kartono, M. Si Ketua
Dr. Akhiruddin, M. Si Anggota
Ketua Program Studi Biofisika
Dr. Agus Kartono, M. Si
Dekan Sekolah Pascasarjana
Puji dan syukur penulis panjatkan kepada Yesus Kristus Tuhan, atas kasih
karunia Allah yang dianugerahkan-Nya sehingga karya ilmiah ini dapat
diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan
Oktober 2010 ini adalah model minimal kinetika glukosa dan insulin untuk
mendeteksi diabetes tipe 2.
Terima kasih penulis ucapkan kepada Bapak Dr. Agus Kartono, M.Si dan
Bapak Dr. Akhiruddin, M.Si selaku komisi pembimbing yang telah banyak
memberi motivasi dan saran. Terima kasih kepada Bapak Dr. Ir. Irmansyah, M.Si
sebagai penguji Luar Komisi pada Ujian Tesis. Penghargaan kepada Pemerintah
Daerah Kabupaten Bulungan melalui Dinas Pendidikan Kabupaten Bulungan
Provinsi Kalimantan Timur sebagai sponsor biaya pendidikan dan penelitian.
Ungkapan terimakasih juga disampaikan kepada ibu, kakak, adik serta seluruh
keluarga atas segala dukungan doa dan kasih sayangnya. Akhirnya penulis
ucapkan terima kasih kepada pihak-pihak terkait yang tidak bisa penulis sebutkan
satu persatu termasuk teman-teman sejawat yang telah membantu penulis selama
menempuh Tugas Belajar di Institut Pertanian Bogor.
Semoga karya ilmiah ini bermanfaat.
Bogor, Juli 2011
Penulis dilahirkan di Pejalin pada tanggal 11 Desember 1978 dari seorang
ayah bernama Serah Laing dan ibu Tebai Luat. Penulis merupakan anak kedua
dari lima bersaudara.
Tahun 1997 penulis lulus dari SMAN 1 Tanjung Selor dan pada tahun yang
sama lulus seleksi Ujian Masuk Perguruan Tinggi Negeri (UMPTN) di
Universitas Mulawarman. Penulis memilih Program Studi Pendidikan Fisika,
Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan
dan Ilmu Pendidikan, lulus pada pendidikan sarjana tahun 2003. Tahun 2009,
penulis mendapat kesempatan untuk melanjutkan ke program Magister Sains
Program Studi Biofisika Sekolah Pascasarjana Institut Pertanian Bogor. Beasiswa
pendidikan pascasarjana diperoleh dari Pemerintah Daerah Kabupaten Bulungan
Provinsi Kalimantan Timur melalui program kerjasama Dinas Pendidikan
Bulungan dengan Sekolah Pascasarjana Institut Pertanian Bogor tahun 2009.
Penulis bekerja sebagai PNS, guru di SMA Negeri 1 Tanjung Palas
Halaman
DAFTAR TABEL ... xxi
DAFTAR GAMBAR ... xxiii
DAFTAR LAMPIRAN ... xxv
PENDAHULUAN ... 1
Latar Belakang ... 1
Perumusan masalah ... 4
Tujuan Penelitian ... 4
Manfaat Penelitian ... 4
Ruang lingkup penelitian ... 5
TINJAUAN PUSTAKA ... 7
Kinetika glukosa dan insulin ... 7
Model minimal Bergman ... 9
Model minimal Riel N Van ... 12
Model minimal Zheng dan Zhao ... 15
Model minmal yang diusulkan ... 18
METODE PENELITIAN ... 21
Waktu dan Tempat Penelitian ... 21
Peralatan ... 21
Studi pustaka ... 21
Pembuatan program ... 21
Analisis output ... 22
HASIL DAN PEMBAHASAN ... 23
Validasi model dengan data eksperimen ... 23
Solusi numerik untuk pasienkasus 1 ... 26
Solusi numerik untuk pasien kasus 2 ... 30
SIMPULAN DAN SARAN ... 37
DAFTAR PUTAKA ... 39
Halaman
1 Variabel dan parameter Model Bergman ... 10
2 Variabel dan parameter Model Minimal modifikasi Riel N Van ... 13
3 Variabel dan parameter Model Minimal Modifikasi Zheng dan Zhao ... 16
4 Nilai parameter profil metabolik orang sehat ... 26
5 Nilai parameter profil metabolik pasien kasus 1 ... 30
Halaman
1 Bagan sistem glukosa-insulin ... 8
2 Konsentrasi glukosa dan insulin yang disampel selama 180 menit setelah IVGTT pada subjek normal ... 12
3 Diagram model minimal kinetika glukosa ... 14
4 Diagram model minimal kinetika insulin ... 14
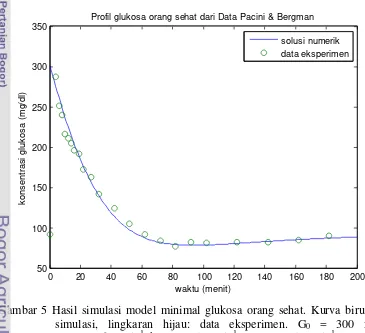
5 Hasil simulasi model minimal glukosa orang sehat. Kurva biru: hasil
simulasi, lingkaran hijau: data eksperimen. G0 = 300 mg/dl,
SG = 0.026 menit-1, k3 = 0.025 menit-1, SI = 0.0005 menit-1 (µU/ml) -1 ... 23
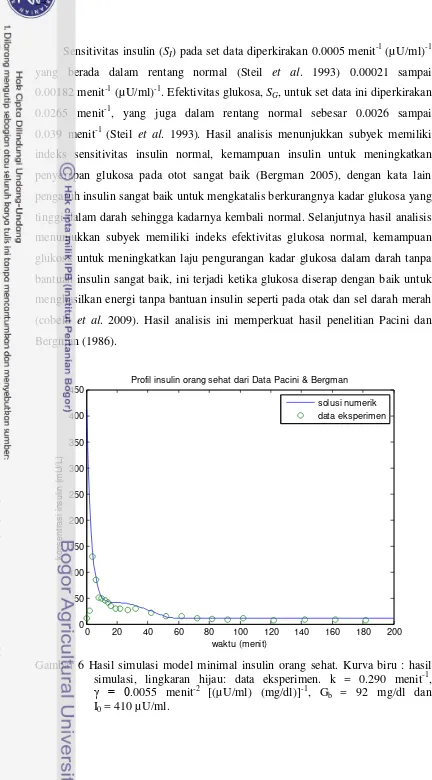
6 Hasil simulasi model minimal insulin orang sehat. Kurva biru : hasil
simulasi, lingkaran hijau: data eksperimen. k = 0.290 menit-1, = 0.0055 menit-2 [(µU/ml) (mg/dl)]-1, Gb = 92 mg/dl dan
I0 = 410 µU/ml ... 24
7 Hasil simulasi model minimal insulin orang sakit DM tipe 2 kasus 1.
Kurva Biru: hasil simulasi, lingkaran hijau: data eksperimen. k = 0.2 menit-1, = 0.0055 menit-2 [(µU/ml) (mg/dl)]-1, G0 = 230 mg/dl dan I0 = 12 µU/ml ... 27
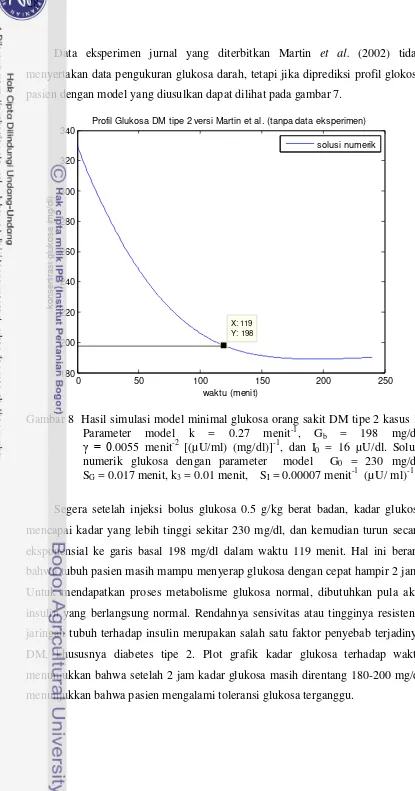
8 Hasil simulasi model minimal glukosa orang sakit DM tipe 2 kasus 1. Parameter model k = 0.27 menit-1, = 0.0055 menit-2 [(µU/ml) (mg/dl)]-1, Gb = 198 mg/dl dan I0 = 16 µU/dl. Solusi numerik glukosa dengan
parameter model G0 = 230 mg/dl, SG = 0.017 menit, k3 = 0.01 menit,
SI = 0.00007 menit-1 (µU/ ml)-1 ... 28
9 Hasil simulasi model minimal glukosa orang sakit DM tipe kasus 2. Kurva biru: hasil simulasi, lingkaran hijau: data eksperimen. Parameter model Gb = 110 mg/dl, Ib = 20 µU/ml, I0 = 410 µU/ml, G0 = 360 mg/dl,
SG = 0.019 menit-1, k3 = 0.01 menit-1, SI = 0.00001 menit-1 (µU/ml)-1 ... 31
10 Hasil simulasi model minimal insulin orang sakit DM tipe 2 kasus 2. Kurva biru: hasil simulasi, lingkaran hijau: data eksperimen. Parameter
Halaman
1 Diagram alir penelitian ... 43
2 Sintak simulasi model minimal glukosa orang sehat ... 45
3 Sintak simulasi model minimal insulin orang sehat ... 47
4 Sintak simulasi model minimal insulin DM tipe 2 kasus 1 ... 49
5 Sintak simulasi model minimal glukosa DM tipe 2 kasus 1 ... 51
6 Sintak simulasi model minimal glukosa DM tipe 2 kasus 2 ... 53
7 Sintak simulasi model minimal insulin DM tipe 2 kasus 2 ... 55
8 Data eksperimen IVGTT orang sehat dari Pacini dan Bergman (1986) ... 57
9 Data eksperimen IVGTT Pasien DM dari Martin et al. (2002) ... 59
PENDAHULUAN
Latar Belakang
Diabetes Melitus (DM) merupakan penyakit yang telah merambah ke
seluruh lapisan dunia. Prevalensi penyakit ini meningkat setiap tahunnya.
Organisasi Kesehatan Dunia (WHO) memperkirakan 194 juta jiwa atau 5,1% dari
3,8 miliar penduduk dunia usia 20-79 tahun menderita DM pada tahun 2003 dan
diperkirakan meningkat menjadi 333 juta jiwa pada tahun 2025. Di Indonesia,
WHO memprediksi kenaikan penderita diabetes dari 8,4 juta pada tahun 2000
menjadi 21,3 juta penderita pada tahun 2030. Sementara itu, data International
Diabetes Federation (IDF) menyebutkan, bahwa Indonesia merupakan negara ke-4
terbesar untuk prevalensi penyakit DM (PERKENI 2006).
Prevalensi Nasional DM berdasarkan hasil pengukuran gula darah pada
penduduk umur > 15 tahun bertempat tinggal di perkotaan adalah 5,7%.
Sebanyak 13 provinsi mempunyai prevalensi DM diatas prevalensi nasional,
yaitu Nanggroe Aceh Darussalam, Riau, Lampung, Bangka Belitung, DKI
Jakarta, Jawa Tengah, Jawa Timur, Banten, Kalimantan Barat, Kalimantan Timur,
Sulawesi Utara, Gorontalo, dan Maluku Utara (RISKESDAS 2007)
Prevalensi nasional toleransi glukosa terganggu berdasarkan hasil
pengukuran gula darah pada penduduk umur > 15 tahun, bertempat tinggal di
perkotaan adalah 10,2%. Sebanyak 13 provinsi mempunyai prevalensi Toleransi
Glukosa Terganggu diatas prevalensi nasional, yaitu Nanggroe Aceh Darussalam,
Sumatera Utara, DKI Jakarta, Jawa Tengah, Jawa Timur, Banten, Kalimantan
Barat, Kalimantan Selatan, Sulawesi Utara, Sulawesi Selatan, Sulawesi Barat,
Maluku, dan Papua Barat (RISKESDAS 2007).
DM atau yang dikenal sebagai penyakit gula atau penyakit kencing manis
adalah penyakit yang ditandai dengan kadar gula tinggi dalam darah dan urin
(Kwach et al. 2011). Di dalam darah, kadar gula fluktuatif dan mencapai kadar
tertinggi satu jam setelah makan, normalnya tidak melebihi 180 mg/dl. Kadar
180 mg/dl disebut nilai ambang ginjal dimana ginjal hanya mampu menahan gula
hanya sampai angka tersebut, lebih tinggi dari itu ginjal tidak dapat menahan gula
dan kelebihan gula akan keluar bersama urine sehingga terjadilah kencing manis
Seseorang tanpa gejala klasik seperti poliuri, polidipsi, polifagi, berat badan
turun dan menjadi kurus dapat diduga menderita DM jika hasil pemeriksaan kadar
gula darah sewaktu sama atau lebih dari 200 mg/dl tetapi belum pasti. Untuk
kepastiannya pemeriksaan dilakukan dengan tes toleransi glukosa (GTT).
Diagnosis DM dinyatakan pasti apabila kadar gula sesudah puasa 8-10 jam ≥ 1β6 mg/dl atau atau pada tes toleransi glukosa oral (TTGO) kadar gula darah 2 jam sesudah minum 75 gram glukosa khusus ≥ β00 mg/dl (Hartini 2009).
DM adalah penyakit kronis yang berhubungan dengan gangguan
metabolisme karbohidrat disebabkan oleh gangguan sekresi insulin, glukagon dan
epineprin (Choi dan Kang 2009) yang umumnya terjadi karena ketidakmampuan
tubuh untuk memproduksi hormon insulin atau karena penggunaan yang tidak
efektif dari produksi insulin. Penyakit ini membutuhkan perhatian dan perawatan
medis dalam waktu lama baik untuk perawatan sakit maupun mencegah
komplikasi seperti penyakit jantung koroner, stroke, kebutaan, gangguan ginjal
kronik, gagal ginjal, dan luka yang sulit sembuh pada kaki sampai menjadi busuk
(Hartini 2009).
Kadar glukosa darah normal pada manusia berada dalam kisaran yang
sempit yaitu 70-110 mg/dl. Faktor eksogen yang mempengaruhi tingkat kadar
glukosa darah termasuk asupan makanan, laju pencernaan, olahraga, status
reproduksi. Hormon endokrin insulin pankreas dan glukagon bertanggung jawab
untuk menjaga tingkat kadar glukosa. Insulin dan glukagon yang masing-masing mengeluarkan sel dan sel α, yang terdapat dalam pulau Langerhans yang tersebar di pankreas. Ketika tingkat kadar glukosa darah tinggi, sel melepaskan
insulin untuk menurunkan kadar kadar glukosa darah dengan mendorong
penyerapan kelebihan glukosa oleh hati dan sel-sel lain (misalnya, otot) dan menghambat produksi glukosa hati. Ketika kadar glukosa darah rendah, sel α melepaskan glukagon, yang menghasilkan peningkatan kadar glukosa darah
dengan bertindak pada sel hati dan menyebabkan mereka untuk melepaskan
glukosa ke dalam darah. Jika tingkat kadar glukosa seseorang selalu di luar
jangkauan 70-110 mg/dl, orang ini dianggap memiliki masalah glukosa darah
DM secara luas diklasifikasikan ke dalam dua kategori, diabetes tipe 1 dan
diabetes tipe 2. Kedua tipe ini timbul dari interaksi yang kompleks antara gen dan
lingkungan, namun patogenesis mereka berbeda. Populasi diabetes tipe 2 di dunia
hampir 90% sedangkan diabetes tipe 1 berisikan antara 5-10%. Hal ini masuk akal
bahwa frekuensi relatif tipe 1 dan diabetes tipe 2 akan berubah dengan
kecenderungan prevalensi diabetes tipe 2 semakin meningkat, obesitas, dan
prediabetes di negara berkembang (Cobelli et al. 2009).
Model matematika merupakan alat yang menarik bagi pemahaman tentang
penyakit. Model memberikan memberikan wawasan, meningkatkan intuisi,
mengklarifikasi asumsi-asumsi untuk teori formal, memungkinkan untuk studi
perencanaan, estimasi parameter, menentukan sensitivitas, menilai dugaan,
simulasi fenomena sederhana dan kompleks dan memberikan prediksi masa depan
(Boutayeb & Chetouani 2006). Dalam kasus diabetes, model sederhana dan
komprehensif berhubungan dengan aspek yang berbeda dari penyakit ini, telah
digunakan selama tiga dekade terakhir. Banyak model matematis telah
dikembangkan untuk lebih memahami mekanisme sistem pengaturan
insulin-glukosa. Model yang paling mencolok adalah yang model minimal yang berisi
jumlah parameter yang sedikit dan model ini banyak digunakan dalam pekerjaan
penelitian fisiologis untuk memperkirakan efektivitas glukosa (SG) dan sensitivitas insulin (SI) dari data tes toleransi glukosa intravena (IVGTT) selama periode tertentu (Makroglou et al. 2006).
Pada pasien dengan toleransi glukosa terganggu (pasien pradiabetes), respon
insulin terhadap glukosa mungkin ditekan sebagian atau seluruhnya. Tanpa respon
insulin, model minimal glukosa tidak dapat memberikan perkiraan parameter
metabolik, karena tidak ada input untuk model. Keadaan ini dapat diatasi dengan
menambah respon insulin melalui pemberian agen farmakologi (misalnya
tulbotamid) dengan tujuan respon insulin dapat cukup untuk mencapai perkiraan
yang akurat dari SI (Pacini & Bergman 1986)
DM jika tidak segera diatasi dapat menjadi penyakit yang paling banyak
komplikasinya oleh karena itu sangat penting untuk memprediksi dan
mengidentifikasi orang yang beresiko tinggi terhadap diabetes tipe 2 dengan
dipelajari kinetika glukosa dan insulin serta menganalisis penggunaan model
minimal yang diusulkan menggunakan model minimal yang sudah ada.
Penelitian ini akan memperkenalkan modifikasi model minimal untuk
membantu pemahaman kinetika glukosa dan insulin. Model yang diusulkan
mencoba menggabungkan laju infus insulin eksogen dari model minimal yang
dikembangkan (Zheng & Zhao 2005) pada model minimal yang dikembangkan
(Riel N Van 2004) khususnya pada model minimal insulin (persamaan ke-3).
Perumusan Masalah
1. Bagaimanakah mekanisme dari sistem pengaturan kadar gula darah ?
2. Bagaimanakah menjelaskan kinetika glukosa dan insulin ?
3. Apakah simulasi dari model yang digunakan dalam penelitian ini
memberikan hasil prediksi yang sesuai dengan hasil eksperimen?
Tujuan
Dalam penelitian ini dikaji kinetika glukosa dan insulin melalui penelusuran
jurnal kemudian dibuat simulasi model minimal kinetika glukosa dan insulin
untuk mendeteksi dibetes tipe 2 dengan menggunakan software Matlab.
Penelitian ini secara khusus bertujuan:
1. Menganalisis realitas fisiologis model yang diusulkan
2. Untuk mengestimasi profil metabolik satu individu dari model yang
diusulkan
3. Untuk mengetahui pengaruh laju infus insulin eksogen terhadap profil
metabolik satu individu dari model yang diusulkan
Manfaat Penelitian
Model minimal kinetika glukosa dan insulin yang diusulkan diharapkan
dapat berfungsi untuk menafsirkan hasil IVGTT pasien normal, pasien
pradiabetes, dan pasien diabetes tipe 2. Dengan demikian, model diharapkan
dapat memberikan pemahaman tentang kinetika glukosa dan insulin untuk
Ruang lingkup
Ruang lingkup dalam penelitian ini meliputi pemahaman sistem dinamika
nonliniear, persamaan diferensial biasa (ODE), teori tentang model matematika
kinetika glukosa dan insulin dan teori model minimal Bergman serta
TINJAUAN PUSTAKA
Kinetika Glukosa dan Insulin
Berbagai eksperimen in vivo dan in vitro menunjukkan bahwa laju sekresi
insulin dari pankreas, berosilasi dalam beberapa skala waktu yang berbeda.
Osilasi tercepat pertama memiliki jangka waktu puluhan detik dan mereka telah
terbukti berada dalam tahap dengan osilasi dalam kadar Ca2+ bebas dari sel ,
kemudian disusul oleh osilasi cepat kedua yang memiliki jangka waktu
5-15 menit dan osilasi lambat disebut biasanya sebagai osilasi ultradian, memiliki
periode dalam rentang 50-120 menit. Osilasi yang cepat disebabkan oleh insulin
keluar diatur secara periodik meledak dari sel . Semburan ini merupakan
mekanisme yang dominan melepaskan insulin pada keadaan basal. Dalam
beberapa senyawa kasus meledak terjadi, istilah yang dimaksud semburan
episodik terkumpul bersama dan senyawa meledak bertanggung jawab untuk
osilasi insulin dengan jangka waktu sekitar 5 menit. Osilasi ultradian kadar insulin
tersebut diasosiasikan dengan osilasi yang sama dengan kadar glukosa plasma,
dan terlihat sangat baik setelah konsumsi makan, asupan glukosa oral, nutrisi
enteralcontinue atau infus glukosa intravena (Makroglou et al. 2006).
Sistem kontrol glukosa-insulin tidak hanya paling banyak dipelajari dalam
hal pemodelan, tetapi pemodelan ini memiliki pengaruh besar pada riset dan terapi
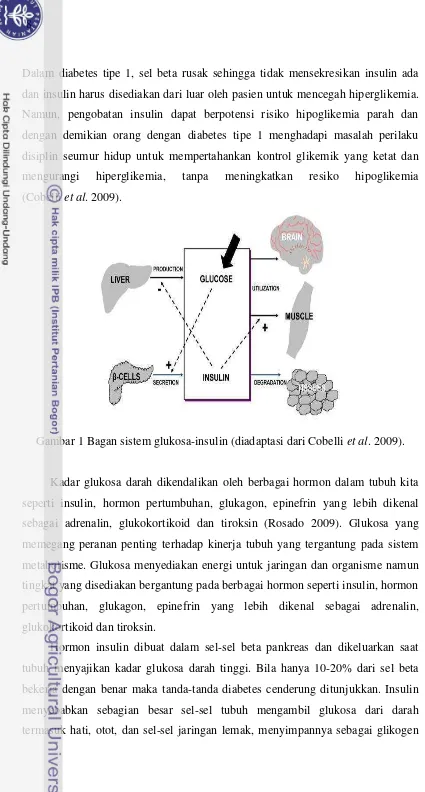
diabetes. Skema dari sistem ini seperti ditunjukkan pada Gambar 1. Glukosa
dihasilkan terutama oleh hati, didistribusikan, dan dimanfaatkan baik pada
jaringan tak tergantung insulin misalnya, sistem saraf pusat dan sel darah merah
dan pada jaringan tergantung insulin yaitu jaringan otot dan adiposa. Sistem
glukosa dan insulin berinteraksi dengan sinyal kontrol umpan balik, misalnya, jika
terjadi gangguan glukosa setelah makan, sel beta mensekresikan lebih banyak
insulin sebagai respon terhadap meningkat kadar glukosa plasma dan pada
gilirannya insulin signaling mempromosikan pemanfaatan glukosa dan
menghambat produksi glukosa sehingga membawa dengan cepat dan efektif
glukosa plasma ke kadar sebelum gangguan. Interaksi kontrol ini biasanya disebut
sebagai sensitivitas insulin dan responsivitas sel beta. Dalam diabetes tipe 2
penurunan ini awalnya hadir sebagai pradiabetes, dicirikan oleh kemunduran
Dalam diabetes tipe 1, sel beta rusak sehingga tidak mensekresikan insulin ada
dan insulin harus disediakan dari luar oleh pasien untuk mencegah hiperglikemia.
Namun, pengobatan insulin dapat berpotensi risiko hipoglikemia parah dan
dengan demikian orang dengan diabetes tipe 1 menghadapi masalah perilaku
disiplin seumur hidup untuk mempertahankan kontrol glikemik yang ketat dan
mengurangi hiperglikemia, tanpa meningkatkan resiko hipoglikemia
(Cobelli et al. 2009).
Gambar 1 Bagan sistem glukosa-insulin (diadaptasi dari Cobelli et al. 2009).
Kadar glukosa darah dikendalikan oleh berbagai hormon dalam tubuh kita
seperti insulin, hormon pertumbuhan, glukagon, epinefrin yang lebih dikenal
sebagai adrenalin, glukokortikoid dan tiroksin (Rosado 2009). Glukosa yang
memegang peranan penting terhadap kinerja tubuh yang tergantung pada sistem
metabolisme. Glukosa menyediakan energi untuk jaringan dan organisme namun
tingkat yang disediakan bergantung pada berbagai hormon seperti insulin, hormon
pertumbuhan, glukagon, epinefrin yang lebih dikenal sebagai adrenalin,
glukokortikoid dan tiroksin.
Hormon insulin dibuat dalam sel-sel beta pankreas dan dikeluarkan saat
tubuh menyajikan kadar glukosa darah tinggi. Bila hanya 10-20% dari sel beta
bekerja dengan benar maka tanda-tanda diabetes cenderung ditunjukkan. Insulin
menyebabkan sebagian besar sel-sel tubuh mengambil glukosa dari darah
di hati dan otot, dan berhenti menggunakan lemak sebagai sumber energi. Bila
insulin tidak ada atau rendah, glukosa tidak diambil oleh sel-sel tubuh dan tubuh
mulai menggunakan lemak sebagai sumber energi yaitu transfer lipid dari jaringan
adiposa ke hati untuk mobilisasi sebagai sumber energi. Ketika kadar glukosa
tinggi dalam tubuh maka hormon insulin dipisahkan. Ketika kontrol kadar insulin
gagal, hasilnya diabetes mellitus. Dengan kata lain, kelebihan insulin dihasilkan
dalam hipoglikemia (Rosado 2009).
Model Minimal Bergman
Model minimal diusulkan oleh tim dari Bergman dan Cobelli pada awal
tahun ’80-an (Boutayeb & Chetouani 2006). Walaupun atau karena
kesederhanaannya model minimal terus digunakan saat ini baik sebagai alat klinis
dan pendekatan untuk memahami efek gabungan sekresi insulin dan sensitivitas
insulin pada toleransi glukosa dan risiko pada diabetes mellitus tipe 2. Asumsi asli
model ini telah memberikan pemahaman tentang kinetika insulin in vivo, seperti kegagalan sel dalam patogenesis diabetes (Bergman 2005).
Model minimal telah digunakan secara luas untuk analisis data glukosa dan
insulin dari IVGTT untuk mengestimasi SI pada studi klinis dan epidemiologi (Morbiducci et al. 2007). Model minimal juga dikenal sebagai model Bergman,
digunakan untuk menafsirkan kadar glukosa dan insulin dari IVGTT yang terbagi
dalam dua bagian: (1) model minimal penghilangan glukosa, terdiri atas
persamaan diferensial pertama dan kedua, yang menyatakan pengaruh insulin
untuk mempercepat penyerapan glukosa dan (2) model minimal kinetika insulin,
persamaan diferensial ketiga, yang menyatakan pengaruh glukosa untuk
meningkatkan sekresi insulin (Bergman 2005). Model matematika dari model
minimal diuraikan di bawah ini (Pacini & Bergman 1986):
��
�� = − �1+� � ∙ � � +�1∙ ��, G 0 = G0 ... (1)
��
�� = −�2∙ � � + �3∙ � � − �� , X 0 = I0 ... (2)
��
Tabel 1 menunjukkan variabel, parameter, satuan, dan keterangan dari persamaan
di atas:
Tabel 1 Variabel dan Parameter Model Bergman
Simbol Satuan keterangan
G(t) mg/dl kadar glukosa pada saat t setelah injeksi glukosa I(t) µU/ml kadar insulin pada saat t setelah injeksi glukosa
X(t) menit -1 aksi insulin mengembalikan glukosa ke tingkat basal pada saat t setelah injeksi glukosa
Gb mg/dl kadar glukosa basal sebelum injeksi glukosa
Ib µU/ml kadar insulin basal sebelum injeksi glukosa
G0 mg/dl kadar glukosa teoritis dalam plasma pada saat t sama
dengan nol yaitu segera setelah injeksi glukosa
I0 µU/ml kadar insulin teoritis dalam plasma pada saat t sama
laju pankreas melepaskan insulin setelah injeksi glukosa, per menit dan per mg/dl dari kadar di atas “target” glikemia
h mg/dl “target glikemia” pankreatik, yang menggambarkan nilai kritis plasma glukosa dimana glukosa mulai memberi pengaruh pada besaran tahap kedua sekresi insulin. n menit -1 Time constant penghilangan insulin atau konstanta laju
fraksi penghilangan insulin endogen
p1 menit -1 SG = efektivitas glukosa, yaitu penyerapan glukosa tanpa
bantuan insulin pada jaringan
p2 menit -1 konstanta laju penurunan kemampuan penyerapan
glukosa, atau dengan kata lain laju fraksi insulin yang muncul dalam plasma interstitial
p3 menit-2
(µU/ml)-1
peningkatan kemampuan penyerapan glukosa-tergantung insulin dalam jaringan, per Unit kadar insulin di atas insulin basal, dengan kata lain fraksi pembersihan insulin dari kompartemen interstitial
Bergman (2005) menemukan bahwa realitas fisiologis tertentu yang sangat
mendasar harus diwakili dalam model: (1) glukosa, setelah ditinggikan oleh
injeksi, kembali ke tingkat basal kerena dua dampak yaitu pengaruh glukosa
sendiri untuk menormalkan kadar sendiri serta efek katalis insulin memungkinkan
glukosa untuk menormalkan diri, dan (2) pengaruh insulin pada hilangnya glukosa
total harus lamban yaitu insulin yang bertindak lambat kerena insulin pertama
harus berpindah dari plasma ke kompartemen larutan interstitial mengerahkan
Profil metabolik sebagai parameter deskriptif dapat muncul dari pemodelan
IVGTT, yang mungkin memiliki kegunaan untuk menetapkan resiko diabetes.
Faktor resiko penting untuk diabetes tipe 2 adalah resistensi insulin atau
kebalikannya sensitivitas insulin yang didefinisikan dalam istilah kuantitatif
sebagai pengaruh insulin untuk mengkatalisis hilangnya glukosa dari plasma
sehingga dengan mudah resistensi insulin dapat dihitung dari parameter model
minimal (Bergman 2005).
Model glukosa dan insulin minimal memungkinkan kita untuk menandai
data IVGTT dalam empat indeks metabolik (Pacini & Bergman 1986):
1. SI adalah sensitivitas insulin: kemampuan insulin untuk mempercepat
hilangnya glukosa dari plasma
2. SG adalah efektivitas glukosa: kemampuan glukosa untuk menurunkan kadar
sendiri dalam plasma tanpa bantuan insulin
3. Ø1 adalah responsivitas tahap pertama pankreas: ukuran dari tinggi puncak pertama
insulin akibat injeksi glukosa, dan
4. Ø2 adalah responsivitas tahap kedua pankreas: ukuran dari tinggi puncak kedua
insulin yang mengikuti puncak pertama dan periode refraktori.
Jadi, profil metabolik satu individu kemudian ditentukan oleh parameter berikut:
1. SensitivitasInsulin: SI=
P3
P2
2. EfektivitasGlukosa: SG= P1
3. Responsivitas tahap pertama pankreas: ∅1= Imax− Ib
n G0− Gb
4. Responsivitas tahap kedua pankreas: ∅2= γ × 104
Model minimal glukosa dan insulin biasanya digunakan untuk menganalisis
hasil tes toleransi glukosa pada manusia dan hewan laboratorium, sampel darah
diambil dari subyek puasa pada interval waktu yang teratur, setelah injeksi
intravena glukosa tunggal. Sampel darah kemudian dianalisis untuk mengetahui
kadar glukosa dan insulin (Andersen & Hojbjerre 2003). Respon khas dari subjek
Gambar 2 Kadar glukosa dan insulin yang disampel selama 180 menit setelah IVGTT pada subjek normal (Andersen & Hojbjerre 2003).
Dosis glukosa intravena segera meningkatkan kadar glukosa dalam plasma
memaksa sel pankreas untuk mensekresikan insulin. Insulin dalam plasma
dengan ini meningkat, dan pengambilan glukosa dalam otot, hati dan jaringan
meningkat oleh aksi insulin interstitial. Hal ini akan menurunkan kadar glukosa
dalam plasma, menyiratkan sel untuk mensekresikan insulin lebih sedikit, dari
efek umpan balik yang muncul (Andersen & Hojbjerre 2003).
Model minimal Bergman menggunakan kadar insulin yang diukur sebagai
input data untuk mendapatkan parameter pada persamaan pertama dan kedua,
kemudian menggunakan kadar glukosa diukur sebagai input data untuk
mendapatkan parameter pada persamaan ketiga (Boutayeb & Chetouani 2006).
Model minimal Bergman dalam perkembangannya banyak mengalami
modifikasi baik dalan teknik estimasi parameter maupun validasi model
(Boutayeb & Chetouani 2006), sebagai contoh Riel N Van (2004) dan Zheng &
Zhou (2005) menggunakan model minimal dengan mengupayakan beberapa
perbaikan.
Model Minimal Riel N Van
Riel N Van (2004) membagi model minimal dalam dua bagian yang sama
seperti model minimal klasik (model Bergman) yaitu model minimal untuk
kinetika glukosa, ditunjukkan pada persamaan (4) dan (5) dan model minimal
�� �
Tabel 2 Variabel dan Parameter Model Minimal modifikasi Riel N Van
Simbol Satuan keterangan
G(t) mg/dl kadar glukosa dalam plasma I(t) µU/ml kadar insulin dalam plasma
X(t) menit -1 aktivitas insulin interstitial (tidak menggambarkan fisiologis, kuantitas diukur, tetapi tetap merupakan variabel yang menirukan aktivitas insulin efektif
Gb mg/dl kadar glukosa basal
Ib µU/ml kadar insulin basal
G0 mg/dl kadar glukosa teoritis dalam plasma pada saat t sama
dengan nol yaitu segera setelah injeksi glukosa
I0 µU/ml kadar insulin teoritis dalam plasma pada saat t sama
dengan nol, di atas Ib, yaitu segera setelah injeksi glukosa
menit -2 (µU/ml) (mg/dl)-1
ukuran dari respon pankreas tahap kedua pada glukosa,
GT mg/dl kadar glukosa di atas ambang batas, kurang lebih
setingkat glukosa basal plasma
k menit -1 Konstanta laju fraksi penghilangan insulin endogen k1 menit -1 SG = efektivitas glukosa, yaitu penyerapan glukosa tanpa
bantuan insulin pada jaringan k2 menit-2
(µU/ml)-1
peningkatan kemampuan penyerapan glukosa-tergantung insulin dalam jaringan, per Unit kadar insulin di atas insulin basal, dengan kata lain pembersihan fraksi insulin dari kompartemen interstitial
k3 menit -1 konstanta laju penurunan kemampuan penyerapan
glukosa, atau dengan kata lain laju fraksi insulin yang muncul dalam plasma interstitial
t menit waktu
t0 menit waktu injeksi glukosa
Perhatikan bahwa dalam model ini, penambahan sejumlah insulin akan
menyebabkan jumlah insulin interstitial berubah, yang menyebabkan tingkat
pemanfaatan glukosa berubah. Sensitivitas insulin didefenisikan sebagai SI = k2/k3
Model minimal glukosa dan insulin memberikan kuantitatif dan diskripsi
kadar glukosa dan insulin dalam sampel darah setelah injeksi glukosa. Model
glukosa minimal melibatkan fisiologis dua kompartemen: kompartemen plasma
dan kompartemen jaringan interstitial, model insulin minimal hanya melibatkan
kompartemen plasma tunggal. Diagram yang ditunjukkan pada Gambar 3
merangkum model minimal untuk kinetika glukosa dan diagram yang ditunjukkan
pada Gambar 4 merangkum model minimal kinetika insulin.
Gambar 3 Diagram model minimal kinetika glukosa Riel N Van (2004)
Gambar 4 Diagram model minimal kinetika insulin Riel N Van (2004)
Glukosa meninggalkan atau memasuki kompartemen plasma pada tingkat
sebanding dengan perbedaan antara kadar glukosa plasma, G(t), dan tingkat
plasma basal, Gb, jika kadar glukosa plasma turun di bawah tingkat basal, glukosa
memasuki kompartemen plasma, dan jika tingkat glukosa naik di atas tingkat
basal, glukosa meninggalkan kompartemen plasma. Glukosa juga menghilang dari
kompartemen plasma melalui jalur kedua pada tingkat sebanding dengan 'aksi'
insulin dalam jaringan interstisial X(t).
Insulin meninggalkan atau memasuki kompartemen jaringan interstitial pada
tingkat sebanding dengan perbedaan antara tingkat insulin plasma, I(t), dan
plasma meningkat di atas tingkat basal, insulin memasuki kompartemen jaringan
interstisial. Insulin juga menghilang dari kompartemen jaringan interstitial melalui
jalur kedua pada tingkat sebanding dengan jumlah insulin dalam kompartemen
jaringan interstisial. I(t) adalah input model.
Insulin memasuki kompartemen plasma insulin pada tingkat proporsional
terhadap produk waktu dan kadar glukosa di atas ambang batas GT. Di sini, waktu adalah interval t-t0, dalam hitungan menit, dari injeksi glukosa. Jika kadar glukosa plasma turun di bawah nilai ambang batas, tingkat plasma insulin yang memasuki
kompartemen adalah nol. Insulin akan dihapus dari kompartemen plasma pada
tingkat sebanding dengan jumlah insulin dalam kompartemen plasma.
Riel N Van (2004) menunjukkan sebuah implementasi MATLAB untuk
mensimulasikan tingkat insulin dan glukosa plasma selama IVGTT dan
menentukan nilai-nilai dari indeks metabolisme (Pacini & Bergman 1986) dari
suatu kumpulan data melalui estimasi parameter pada kasus orang sehat.
Model Minimal Zheng dan Zhao
Model minimal telah dimodifikasi berdasarkan asumsi bahwa laju peluruhan
insulin akibat dirangsang oleh glukosa tidak selalu proses orde pertama, dan
pengenalan laju infus insulin. Modifikasi model menggunakan sistem
glukosa-insulin sebagai sistem yang terintegrasi dinamis dan, dikombinasikan dengan
proses single-step fitting, menghasilkan suatu pendekatan optimal pada
pengukuran data glukosa dan insulin. Model tetap memakai informasi insulin
pada respon pankreas untuk sirkulasi glukosa. Pengenalan fungsi untuk laju infus
insulin model yang diajukan mencerminkan situasi nyata IVGTT sebenarnya.
Suatu fungsi matematis yang mewakili proses infus insulin diperkenalkan ke
dalam model minimal Bergman (Zheng & Zhao 2005).
Model minimal modifikasi yang dikembangkan (Zheng & Zhao 2005)
Tabel 3 menunjukkan variabel, parameter, satuan, dan keterangan dari persamaan
di atas:
Tabel 3 Variabel dan Parameter Model Minimal modifikasi Zheng dan Zhao
Simbol Satuan keterangan
G(t) mmol/L kadar glukosa dalam plasma pada saat t I(t) µU/ml kadar insulin dalam plasma pada saat t
X(t) menit-1 ‘remote insulin’ sebanding dengan kadar insulin dalam kompartemen jauh
Gb mmol/L kadar glukosa basal
Ib µU/ml kadar insulin basal
p0 mmol/L kadar awal plasma glukosa segera setelah injeksi glukosa
p7 µU/ml kadar awal plasma insulin segera setelah injeksi glukosa
p4 (µU/mL)
((L/mmol)-1
menit -1)-1
laju pankreas melepaskan insulin setelah injeksi
p5 mmol/L nilai ambang pankreas
n menit-1 keadaan untuk orde proses ke-n pada laju peluruhan plasma insulin dan laju peningkatan remote insulin
p1 menit-1 SG = efektivitas glukosa, yaitu konstanta laju peluruhan
glukosa
p2 menit-1 laju hilangnya remote insulin
p3 menit-2
(mL/µU)n
laju peningkatan remote insulin oleh plasma insulin
p6 (µU/mL)1-n
(menit-1)
konstanta laju peluruhan untuk plasma insulin dan memainkan peran yang serupa untuk insulin sebagai p1
Hampir semua publikasi menggunakan model minimal untuk deskripsi
IVGTT diterapkan secara terpisah. Sebagaimana dinyatakan (Pacini & Bergman
1986), fitting model parameter harus dilakukan dalam dua tahap, pengukuran
kadar insulin digunakan sebagai data masukan untuk memperoleh parameter
dalam dua persamaan untuk profil glukosa dan remote insulin, dan kemudian
dicatat kadar glukosa digunakan sebagai data masukan untuk memperoleh
Menurut Zheng dan Zhao (2005), sistem glukosa-insulin sebagai suatu
sistem dinamis yang terintegrasi dalam fisiologis, bagaimanapun, harus
digambarkan secara matematis sebagai satu keseluruhan. Ketika sebuah sistem
yang dinamis terintegrasi dibagi menjadi dua interaksi sub-sistem, kemudian,
parameter sistem dioptimasi dengan fitting data diukur secara terpisah, parameter
yang dihasilkan tidak dapat dianggap sebagai yang optimal bagi keseluruhan
sistem. Dalam sistem fisiologis insulin-glukosa baik glukosa dan insulin memiliki
efek umpan balik satu sama lain melalui respon pankreas dan stimulasi. Proses
single-step fitting parameter menghasilkan pendekatan yang optimal nyata untuk
sistem dinamik terintegrasi glukosa-insulin tanpa kehilangan informasi interaksi
implisit yang terkandung dalam profil kadar diukur.
Pada DM tipe 2 biasanya didahului keadaan pradiabetes yaitu pasien dengan
toleransi glukosa terganggu, dimana respon insulin terhadap glukosa mungkin
ditekan sebagian atau seluruhnya. Tanpa respon insulin, model minimal tidak
dapat memberikan perkiraan metabolik yang tepat karena tidak ada input untuk
model penghilangan glukosa. Keadaan ini dapat diatasi dengan pemberian agen
farmakologik misalnya tulbotamid, dengan tujuan untuk mendapatkan respon
dinamika insulin yang cukup untuk mencapai perkiraan yang akurat dari SI (Pacini & Bergman 1986). Model minimal yang dikembangkan Riel N Van (2004) dapat
digunakan untuk memperoleh profil indeks metabolik orang sehat, model minimal
yang dikembangkan Zheng dan Zhao (2005) memberikan hasil yang bagus untuk
orang sehat dan orang sakit melalui single-step fitting. Model minimal yang
dikembangkan Riel N Van maupun model Zheng dan Zhao, memiliki kesamaan
dengan Model minimal klasik (model Bergman) yaitu pada persamaan model
minimal kinetika glukosa (persamaan 1 dan 2), yang berbeda hanya pada
persamaan model kinetika insulin. Oleh karena itu kami mengusulkan model
minimal yang dapat digunakan untuk mendeteksi profil indeks metabolik orang
sehat, orang dengan toleransi glukosa terganggu (pasien pradiabetes), dan pasien
DM tipe 2 dengan memodifikasi persamaan model minimal kinetika insulin Riel
Model Minimal yang diusulkan
Kami mengusulkan perluasan model minimal berdasarkan aspek laju infus
insulin eksogen dari model minimal yang dikembangkan Zheng dan Zhao (2005).
Infus insulin eksogen diperlukan ketika sekresi insulin endogen tidak cukup
meskipun dirangsang oleh injeksi glukosa. Kami ingin menunjukkan bahwa kami
tidak mengembangkan model baru atau estimasi nilai baru untuk parameter model
minimal yang dikembangkan Riel N Van (2004) tetapi kami menambahkan
bagian baru yaitu laju infus insulin eksogen U(t) dari model minimal yang
dikembangkan Zheng dan Zhao. Variable dan parameter yang kami gunakan
sesuai dengan variabel dan parameter model minimal yang dikembangkan Riel N
Van, sehingga persamaan model minimal yang diusulkan sebagai berikut: �� � tingkat glukosa basal. Efektifitas glukosa SG yang dinyatakan oleh k1 merupakan kemampuan glukosa untuk menurunkan kadar sendiri dalam plasma tanpa
bantuan insulin, yaitu laju pembuangan glukosa pada otot, hati dan jaringan
adipose. Bentuk γ [G(t) – GT] (t) menyatakan fungsi pengaturan internal yang meformulasikan sekresi insulin endogen, bernilai negatif untuk kasus DM tipe 1
dan bernilai positif untuk kasus DM tipe 2 yaitu ketika G(t) lebih besar daripada
GT (Yasini et al 2009).
Paremeter GT persisnya sama dengan kuantitas Gb pada pengamatan eksperimen, kenyataannya GT tidak diketahui tetapi merupakan nilai yang benar untuk parameter model, dalam banyak kasus GT = Gb adalah solusi yang mungkin (Gaetano & Arino 2000) oleh sebab itu, pada model yang kami usulkan nilai
parameter GT adalah sama dengan nilai Gb. Selanjutnya untuk mendeteksi seseorang sehat atau pasien pra diabetes dan pasien diabetes tipe 2 berdasarkan
(Pacini & Bergman 1986) di samping itu teori umum diabetologis yang
menyatakan bahwa periode alami tubuh orang sehat mampu menyerap glukosa
secara cepat setelah puasa 8-12 jam kurang dari 2 jam, dengan kata lain, kadar
glukosa kembali ke tingkat normal dalam waktu kurang dari 2 jam (Shiang et al
2010).
Parameter efektivitas glukosa SG pada orang sehat bernilai 0.0026-0.039 menit-1 dan parameter sensitivitas insulin SI orang sehat bernilai
0.00021-0.00182 menit-1 (µU/mL)-1 (Steil et al 1993). Parameter responsivitas
insulin tahap pertama Ø1 pada orang sehat bernilai 2.0 sampai
4.0 menit-1 [(µU/ml)(mg/dl)]-1 dan parameter responsivitas insulin tahap kedua Ø2
pada orang sehat bernilai 20-35 menit-2 [(µU/ml)(mg/dl)]-1 (Bergman et al 1981). Menurut penelitian (Chen & Tsai 2010), orang sehat memiliki kadar insulin
5-10 mU/l, produksi glukosa hati 5-10 menit, sekresi insulin dari sel karena
distimulasi oleh peningkatan glukosa 5-30 menit, pemanfaatan glukosa pada sel
otak dan sel saraf tanpa bantuan insulin 0.7-1 menit, pemanfaatan glukosa pada
lemak dan otot yang memerlukan insulin 0.5-1 menit, konstanta laju pembersihan
insulin pada otot, hati, ginjal 0.05–0.2 menit-1. Nilai parameter SI yang digunakan sebagai ambang batas antara orang pradiabetes (toleransi glukosa terganggu) dan
orang sehat adalah 0.00028 menit-1 (µU/ml)-1 dan nilai 0.00069 menit-1 (µU/ml)-1 sebagai ambang batas orang tanpa resistensi insulin (Morbiducci et al 2007).
Dalam keadaan fisiologis, insulin disekresikan sesuai dengan kebutuhan
tubuh normal oleh sel beta dalam dua tahap, sehingga sekresinya berbentuk
biphasic. Sekresi insulin normal yang biphasic ini akan terjadi setelah adanya
rangsangan seperti glukosa yang berasal dari makanan atau minuman atau berasal
dari injeksi bolus glukosa 300 (mg/kg berat badan) pada IVGTT standar. Insulin
yang dihasilkan ini, berfungsi mengatur regulasi glukosa darah agar selalu dalam
batas-batas fisiologis, baik saat puasa maupun setelah mendapat beban. Dengan
demikian, kedua tahap sekresi insulin yang berlangsung secara sinkron tersebut,
menjaga kadar glukosa darah selalu dalam batas-batas normal, sebagai cerminan
Sekresi tahap 1 (acute insulin secretion responce = AIR), ditunjukkan
dengan responsivitas insulin tahap pertama Ø1, adalah sekresi insulin yang terjadi
segera setelah ada rangsangan terhadap sel beta, muncul cepat dan berakhir juga
cepat. Sekresi tahap 1 biasanya mempunyai puncak yang relatif tinggi, karena hal
itu memang diperlukan untuk mengantisipasi kadar glukosa darah yang biasanya
meningkat tajam, segera setelah makan. Kinerja AIR yang cepat dan cukup
memadai ini sangat penting bagi pengaturan glukosa yang normal karena pada
gilirannya berkontribusi besar dalam pengendalian kadar glukosa darah setelah
makan. Dengan demikian, kehadiran AIR yang normal diperlukan untuk
mempertahankan berlangsungnya proses metabolisme glukosa secara fisiologis.
AIR yang berlangsung normal, bermanfaat dalam mencegah terjadinya
hiperglikemia akut setelah makan.
Selanjutnya, setelah sekresi tahap 1 berakhir, muncul sekresi tahap 2
(sustained phase, latent phase) ditunjukkan dengan responsivitas insulin tahap
pertama Ø2, dimana sekresi insulin kembali meningkat secara perlahan dan
bertahan dalam waktu relatif lebih lama. Setelah berakhirnya tahap 1, tugas
pengaturan glukosa darah selanjutnya diambil alih oleh sekresi tahap 2. Sekresi
insulin tahap 2 yang berlangsung relatif lebih lama, seberapa tinggi puncaknya
(secara kuantitatif) akan ditentukan oleh seberapa besar kadar glukosa darah di
akhir tahap 1, disamping faktor resistensi insulin. Jadi, terjadi semacam
mekanisme penyesuaian dari sekresi tahap 2 terhadap kinerja tahap 1 sebelumnya.
Apabila sekresi tahap 1 tidak cukup memadai, terjadi mekanisme mengimbangi
dalam bentuk peningkatan sekresi insulin pada tahap 2. Peningkatan produksi
insulin tersebut pada hakikatnya dimaksudkan memenuhi kebutuhan tubuh agar
kadar glukosa darah (setelah makan) tetap dalam batas batas normal. Dalam
prospektif perjalanan penyakit, tahap 2 sekresi insulin akan banyak dipengaruhi
oleh tahap 1.
Biasanya, dengan kinerja tahap 1 yang normal, disertai pula oleh aksi
insulin yang juga normal di jaringan (tanpa resistensi insulin), sekresi tahap 2 juga
akan berlangsung normal. Dengan demikian tidak dibutuhkan tambahan (ekstra)
sintesis maupun sekresi insulin pada tahap 2 diatas normal untuk dapat
METODOLOGI PENELITIAN
Waktu dan tempat penelitian
Penelitian dilakukan di Laboratorium Fisika Teori, Departemen Fisika,
FMIPA, Institut Pertanian Bogor di mulai pada bulan Oktober 2010 sampai
dengan bulan Juli 2011. Kegiatan meliputi penelitian pendahuluan, pembuatan
program, analisis output, pengolahan data dan penyusunan laporan.
Peralatan
Peralatan yang digunakan dalam penelitian ini adalah berupa laptop dengan
processor Intel Core i7-740QM, HDD 500GB, Memory 2GB. Software yang
digunakan untuk proses komputasi adalah bahasa pemprogaman Matlab R2010a
dari Mathwork, Inc. Pendukung penelitian ini berupa sumber pustaka, yaitu
jurnal-jurnal ilmiah Model Minimal juga berbagai informasi yang diperoleh dari
internet yang diakses dari Laboratorium.
Studi Pustaka
Studi pustaka dilakukan untuk memahami proses kinetika glukosa dan
insulin sehingga memudahkan perancangan program simulasinya. Studi pustaka
diperlukan untuk mengetahui sejauh mana perkembangan yang telah dicapai
dalam bidang yang diteliti. Studi pustaka akan membantu penulis dalam
menganalisis hasil yang didapat dari simulasi model minimal kinetika glukosa dan
insulin untuk mendeteksi diabetes. Data eksperimen yang digunakan dalam
penelitian diperoleh dari jurnal yang telah dipublikasi.
Pembuatan Program
Program simulasi dari model minimal gukosa dan insulin yang diusulkan
dibuat menggunakan software Matlab R2010a. Studi pustaka dilakukan untuk
memahami proses kinetika glukosa dan insulin, sehingga memudahkan
perancangan program simulasinya. Program dibuat dengan bahasa pemrograman
Matlab R2010a diperlukan untuk memudahkan perhitungan secara numerik dan
konsentrasi glukosa dan insulin dari model yang dibuat. Analisis numerik
dilakukan karena model ini sulit untuk diselesaikan secara analitik, sehingga
metode numerik diperlukan untuk memecahkan sistem persamaan tersebut. Model
matematika pada penelitian ini merupakan persamaan diferensial biasa, maka
metode numerik yang paling akurat ialah Runge Kutta orde 45 atau ode45.
Selanjutnya program divalidasi dengan data eksperimen yang digunakan dalam
penelitian diperoleh dari jurnal yang telah dipublikasi.
Analisis Output
Analisis output diperlukan untuk menguji apakah output yang didapat sesuai
dengan teori yang ada dalam jurnal. Sistematika penelitian secara lengkap dapat di
HASIL DAN PEMBAHASAN
Validasi model dengan data eksperimen.
Untuk lebih memahami kinetika glukosa dan insulin, sebuah model telah
diusulkan untuk modifikasi model minimal. Validasi model dilakukan dengan
membandingkan antara hasil simulasi model dan data eksperimen. Solusi numerik
yang diperoleh dengan cara mensubtitusikan nilai-nilai parameter ke persamaan
(10), (11) dan (12) sehingga diperoleh grafik hubungan antara konsentrasi glukosa
terhadap waktu t ditunjukkan pada Gambar 5 dan grafik hubungan antara
konsentrasi insulin terhadap waktu t ditunjukkan pada Gambar 6. Data
eksperimen diperoleh dari jurnal yang diterbitkan (Pacini & Bergman 1986). Laju
penurunan kadar glukosa orang sehat tanpa infus insulin ditunjukkan pada
Gambar 5 dan laju penurunan kadar Insulin orang sehat tanpa infus insulin
Profil glukosa orang sehat dari Data Pacini & Bergman
Sensitivitas insulin (SI) pada set data diperkirakan 0.0005 menit-1 (µU/ml)-1 yang berada dalam rentang normal (Steil et al. 1993) 0.00021 sampai
0.00182 menit-1 (µU/ml)-1. Efektivitas glukosa, SG, untuk set data ini diperkirakan 0.0265 menit-1, yang juga dalam rentang normal sebesar 0.0026 sampai 0.039 menit-1 (Steil et al. 1993). Hasil analisis menunjukkan subyek memiliki indeks sensitivitas insulin normal, kemampuan insulin untuk meningkatkan
penyerapan glukosa pada otot sangat baik (Bergman 2005), dengan kata lain
pengaruh insulin sangat baik untuk mengkatalis berkurangnya kadar glukosa yang
tinggi dalam darah sehingga kadarnya kembali normal. Selanjutnya hasil analisis
menunjukkan subyek memiliki indeks efektivitas glukosa normal, kemampuan
glukosa untuk meningkatkan laju pengurangan kadar glukosa dalam darah tanpa
bantuan insulin sangat baik, ini terjadi ketika glukosa diserap dengan baik untuk
menghasilkan energi tanpa bantuan insulin seperti pada otak dan sel darah merah
(cobelli et al. 2009). Hasil analisis ini memperkuat hasil penelitian Pacini dan
Profil insulin orang sehat dari Data Pacini & Bergman
Responsivitas pankreas tahap pertama (Ø1), diperkirakan 3.462 menit-1 [(µU/ml) (mg/dl)]-1 untuk set data. Ini tidak lebih dari kisaran
normal untuk Ø1 dilaporkan (Pacini & Bergman 1986) sebesar 2.0 sampai 4.0 menit-1 [(µU/ml) (mg/dl)]-1. Responsivitas pankreas tahap kedua (Ø2), diperkirakan sebesar 40.745 menit-2 [(µU/ml) (mg/dl)]-1. Hal ini sedikit lebih tinggi dari kisaran normal untuk Ø2 dilaporkan (Pacini & Bergman 1986) sebesar 20 sampai 35 menit-2 [(µU ml) (mg/dl)]-1. Hasil ini menunjukkan bahwa subyek secara keseluruhan memiliki responsivitas pankres yang baik. Responsivitas
pankreas yang baik ditunjukkan dengan sensivtivitas pankreas untuk merespon
setiap peningkatan kadar glukosa darah, ini berarti bahwa sel pankreas mampu
mensekresikan insulin yang cukup terhadap setiap rangsangan glukosa yang
meningkat dalam darah sehingga menjaga kadar glukosa darah tetap dalam
kondisi normal. Hasil analisis ini memperkuat hasil penelitian Pacini dan
Bergman (1986).
Laju perubahan kadar glukosa yang ditunjukkan pada Gambar 5, dan laju
perubahan kadar insulin yang ditunjukkan pada Gambar 6 adalah kasus orang
sehat tanpa infus insulin tambahan. Dalam IVGTT standar, setelah injeksi bolus
glukosa, kadar glukosa mencapai kadar yang lebih tinggi dan kemudian turun
secara eksponensial ke garis basal dalam waktu 62 menit. Penurunan itu
disebabkan oleh: (1) aksi insulin yaitu pengaruh insulin untuk mempercepat
penyerapan glukosa dan (2) responsivitas pankreas yaitu pengaruh glukosa untuk
meningkatkan sekresi insulin. Kadar insulin yang sesuai dirangsang oleh injeksi
glukosa naik membentuk puncak pertama, kemudian turun setelah itu, dan
akhirnya puncak kedua muncul. Hal ini tidak selalu terjadi bahwa pada orang
sehat hadir puncak kedua insulin (Riel N Van 2004). Nilai parameter yang
digunakan dalam model yang diusulkan sesuai dengan parameter Riel N Van
(2004), profil indeks metabolik orang sehat juga sesuai Pacini & Bergman (1986),
selain itu menurut teori umum diabetologi, orang sehat mampu menyerap glukosa
secara cepat kurang dari 2 jam setelah puasa 8 sampai 12 jam (Shiang et al. 2010)
sehingga dari kesesuaian visual empiris plot kurva simulasi dan data eksperimen
di atas dapat menunjukkan bahwa model yang kami diusulkan valid. Nilai
Tabel 4 Nilai parameter profil metabolik orang sehat
Indeks Nilai Satuan Status
SG 0.026 menit - 1 Normal
SI 0.0005 menit -1 (µU/ml) -1 Normal
ϕ1 3.4 menit-1 [(µU/ml) (mg/dl)] -1 Normal
ϕ2 40.7 menit -2 [(µU/ml) (mg/dl) ] -1 Normal
Solusi numerik untuk kasus pasien 1
Data eksperimen yang diperoleh dari publikasi Martin et al. (2002). Setelah
puasa 12 jam, pasien diinjeksi bolus glukosa (0.5 g/kg berat badan, dalam larutan
30%) secara perlahan. Sebelum diinjeksi, 15 menit dan 0 menit kadar glukosa
darah diukur sebagai kadar glukosa basal. Tepat pada 0 menit bolus glukosa
diinjeksi dan kemudian diukur pada 1, 3, 4, 6, 8, 10, 15, 19, 20, 22, 24, 30, 41, 70,
90, dan 180 menit. Insulin (0.02 U/kg berat badan) diinjeksi secara cepat setelah
19 menit. Kadar Insulin dari data eksperimen dan hasil simulasi numerik
ditunjukkan pada Gambar 6.
Prediksi sensivitas insulin SI dari data eksperimen Martin et al. (2002) diperoleh SI sebesar 0.00001 sampai 0.0006 menit-1 (µU/ml)-1. Sedangkan pada model kami SI = 0.00007 menit-1 (µU/ml)-1. Nilai SI yang ditunjukkan oleh model menyatakan bahwa pasien memiliki gangguan sensitivitas insulin, dengan kata
lain pasien mengalami resistensi insulin sesuai dengan nilai SI yang dilaporkan
(Morbiducci et al. 2007) bahwa nilai SI sebesar 0.0028 menit-1 (µU/ml)-1 dapat diasumsikan sebagai ambang batas antara pasien dengan gangguan SI dengan orang normal. Semakin tinggi tingkat resistensi insulin, rendahnya sensitivitas
insulin, berakibat glukosa sulit masuk ke dalam sel sehingga kadar glukosa di
dalam darah tetap tinggi dapat terlihat pada kadar glukosa darah puasa yang tinggi
mencapai 198 mg/dl. Kadar glukosa basal di sini menyatakan kadar glukosa puasa
Efektivitas glukosa diprediksi dari model SG = 0.017 menit-1, masih dalam
rentang normal seperti yang dilaporkan (Steil et al. 1993) sebesar 0.0026 sampai
0.039 menit-1. Hal ini menunjukkan bahwa laju penyerapan glukosa pada jaringan tanpa bantuan insulin masih baik, penyerapan glokosa tanpa respon insulin terjadi
pada otak dan sel darah merah, dimana pada proses penyerapan glukosa untuk
menghasilkan energi tidak memerlukan bantuan insulin.
Insulin eksogen dinjeksi dengan laju 20 mU/kg menit pada eksperimen
sedangkan pada model kami laju infus insulin eksogen 8 mU/kg menit. Pada
eksperimen IVGTT yang dimodifikasi dengan pemberian insulin dapat
merangsang peningkatan penggunaan glukosa pada jaringan otot untuk
mendapatkan kadar glukosa yang normal.
Gambar 7 Hasil simulasi model minimal insulin orang sakit DM tipe 2 kasus 1.
Kurva Biru: hasil simulasi, lingkaran hijau: data eksperimen.
Profil insulin DM tipe 2, laju infus 8 [mU/kg.menit], dari Data Martin et al
Data eksperimen jurnal yang diterbitkan Martin et al. (2002) tidak
menyertakan data pengukuran glukosa darah, tetapi jika diprediksi profil glokosa
pasien dengan model yang diusulkan dapat dilihat pada gambar 7.
Gambar 8 Hasil simulasi model minimal glukosa orang sakit DM tipe 2 kasus 1.
Parameter model k = 0.27 menit-1, Gb = 198 mg/dl,
bahwa tubuh pasien masih mampu menyerap glukosa dengan cepat hampir 2 jam.
Untuk mendapatkan proses metabolisme glukosa normal, dibutuhkan pula aksi
insulin yang berlangsung normal. Rendahnya sensivitas atau tingginya resistensi
jaringan tubuh terhadap insulin merupakan salah satu faktor penyebab terjadinya
DM, khususnya diabetes tipe 2. Plot grafik kadar glukosa terhadap waktu
menunjukkan bahwa setelah 2 jam kadar glukosa masih direntang 180-200 mg/dl
menunjukkan bahwa pasien mengalami toleransi glukosa terganggu.
0 50 100 150 200 250
Profil Glukosa DM tipe 2 versi Martin et al. (tanpa data eksperimen)
Kadar insulin yang sesuai dirangsang oleh injeksi glukosa tidak begitu
berpengaruh pada Ø1 adalah responsivitas tahap pertama pankreas: ukuran dari tinggi puncak pertama insulin akibat injeksi glukosa, dimana puncak pertama
sekresi insulin tidak terlihat, dengan kata lain responsivitas insulin tahap pertama
kurang mencukupi sehingga insulin di atas basal hanya dapat dijelaskan oleh
penambahan insulin eksogen selama IVGTT. Menurut Martin et al. (2002)
pengukuran sekresi insulin yang tepat pada eksperimen tidak diperlukan karena
respon insulin tahap pertama tumpul, sehingga kadar insulin selama IVGTT
paling hanya mencerminkan injeksi insulin pada menit ke-19, tentunya masih
mungkin untuk mengukur puncak tahap pertama dari sampel pada menit ke-1 dan
menit ke-3 jika dugaan sekresi insulin tahap pertama juga diinginkan.
Responsivitas insulin tahap pertama yang cacat adalah ciri-ciri yang hampir tetap
pada pasien diabetes tipe 2, secara klinis pada dasarnya bermula dari hambatan
dalam pemanfaatan glukosa yang kemudian diikuti oleh peningkatan kadar
glukosa darah. Hal ini terjadi karena gangguan, baik dari sekresi insulin pankreas
maupun aksi insulin. Sekresi insulin yang tidak mencukupi pada tahap pertama
yang kemudian diikiuti peningkatan kinerja sekresi insulin tahap kedua pada
awalnya belum akan menimbulkan gangguan terhadap kadar glukosa darah.
Secara klinis keadaan ini terdeteksi sebagai toleransi glukosa terganggu dan
glukosa darah puasa terganggu, kedua keadaan ini secara klinis mencerminkan
pasien pra diabetes.
Nilai Ø2 diperkirakan sebesar 55 menit-2 [(µU/ml) (mg/dl)]-1. Hal ini lebih tinggi dari kisaran Ø2 normal yang dilaporkan oleh Pacini & Bergman (1986) sebesar 20 sampai 35 menit-2 [(µU/ml) (mg/dl)]-1. Kadar insulin selama IVGTT hanya mencerminkan injeksi insulin eksogen pada menit ke-19, yang merupakan
puncak insulin buatan. Sekresi insulin tahap kedua muncul setelah tahap pertama
berakhir, dimana sekresi insulin kembali meningkat secara perlahan dan bertahan
dalam waktu yang relatif lebih lama. Setelah berakhirnya tahap pertama, tugas
pengaturan glukosa darah selanjutnya diambil alih oleh tahap kedua. Sekresi
insulin tahap kedua berlangsung relatif lebih lama, seberapa tinggi puncaknya
secara kuantitatif ditentukan oleh seberapa besar kadar glukosa darah di akhir
Apabila sekresi tahap pertama tidak mencukupi, terjadi mekanisme
penyeimbangan dalam bentuk peningkatan sekresi insulin tahap kedua.
Peningkatan produksi insulin tersebut pada prinsipnya dimaksudkan untuk
memenuhi kebutuhan tubuh agar kadar glukosa darah setelah makan tetap dalam
batas normal. Pada eksperimen, peningkatan sekresi insulin tahap kedua diberikan
secara buatan dengan injeksi insulin eksogen, dengan maksud memenuhi
kebutuhan tubuh agar kadar glukosa darah setelah injeksi bolus glukosa tetap
dalam batas normal.
Nilai parameter yang digunakan dalam Solusi numerik untuk IVGTT insulin
eksogen untuk orang sakit DM tipe 2 kasus 1 untuk menentukan profil indeks
metabolik pasien berada di luar rentang nilai parameter profil indeks metabolik
orang sehat (Pacini & Bergman 1986), selain itu menurut teori umum diabetologi,
orang sakit menyerap glukosa lebih dari 2 jam setelah puasa 8 sampai 12 jam
(Shiang et al. 2010) sehingga dari kesesuaian visual empiris plot kurva simulasi
dan data eksperimen di atas dengan sendirinya menunjukkan bahwa model yang
kami diusulkan valid. Nilai parameter profil metabolik pasien kasus 1
ditunjukkan pada Tabel 5.
Tabel 5 Nilai parameter profil metabolik pasien kasus 1
Indeks Nilai Satuan Status
SG 0.017 menit - 1 Normal
SI 0.00007 menit -1 (µU/ml) -1 Resistensi
Insulin
ϕ1 - menit-1 [(µU/ml) (mg/dl)] -1 Cacat
ϕ2 55 menit -2 [(µU/ml) (mg/dl) ] -1 Tidak Normal
Solusi numerik untuk kasus pasien 2
Data eksperimen diperoleh dari Mari (1998). Pasien puasa semalaman 8
sampai 12 jam, setelah 30 menit istirahat, sebelum diinjeksi, 30, 15 dan 0 menit
kadar plasma darah diukur sebagai kadar basal pasien. Tepat pada 0 menit, bolus
glukosa diinjeksi 0.3 g/kg berat badan secara cepat setelah pengukuran basal
diinfus dengan laju konstan selama 5 menit. Sampel darah sebanyak 3 ml dicuplik
diukur pada 2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 40, 60, 80, 100, 120, 140, 160, 180,
210, dan 240 menit. Kemudian, diukur kadar glukosa dan insulin. Plot dari data
eksperimen dan hasil simulasi ditunjukkan pada Gambar 9 dan kadar Insulin dari
data eksperimen dan hasil simulasi ditunjukkan pada Gambar 10.
Gambar 9 Hasil simulasi model minimal glukosa orang sakit DM tipe kasus 2. Kurva biru: hasil simulasi, lingkaran hijau: data eksperimen. Parameter model Gb = 110 mg/dl, Ib = 20 µU/ml, I0 = 410 µU/ml,
G0 = 360 mg/dl, SG = 0.019 menit-1, k3 = 0.01 menit-1,
SI = 0.00001 menit-1 (µU/ml)-1
Situasi Kasus 2 ditunjukkan dalam Gambar 8 dan 9. IVGTT dimodifikasi
dengan injeksi insulin pada menit ke- 20 selama 5 menit, kadar glukosa darah
orang yang sehat cepat kembali ke garis basal dalam 1 jam tetapi pada orang sakit
bisa lebih dari 2 jam untuk kembali ke tingkat basal setelah turun dengan cepat
melewati tingkat basal karena pengaruh pemberian insulin eksogen. Pada waktu
20 menit, kedua kadar glukosa eksperimen dan hasil simulasi menunjukkan
respon kecil untuk infus insulin.
Profil glukosa DM tipe 2 dari Data Mari (1998)