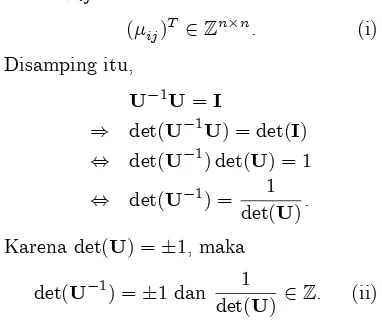ALGORITME LLL
DAN APLIKASINYA DALAM PEMBONGKARAN
SISTEMKRIPTO
KNAPSACK
MERKLE-HELLMAN
ARI AGUSTIANSA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
ARI AGUSTIANSA.Algoritme LLL dan Aplikasinya dalam Pembongkaran Sistemkripto
Knapsack Merkle-Hellman. Dibimbing olehSUGI GURITMANdanBIB PARUHUM SILALAHI.
ABSTRACT
ARI AGUSTIANSA. LLL Algorithm and Its Application in Breaking Merkle-Hellman Knapsack Cryptosystem. Supervised by SUGI GURITMAN and BIB PARUHUM SILALAHI.
LLL algorithm is an algorithm that can be used to determine an approximation of the shortest vector in a lattice. Size reduction algorithm is an important step of LLL algorithm. The LLL algorithm can be applied in many …elds. This paper shows how LLL algorithm can be used in breaking one of the famous cryptosystem, namely the Merkle-Hellman knapsack cryptosystem. Merkle-Hellman knapsack cryptosystem is an asymmetric cryptosystem using the subset sum problem as the support of security. Subset sum problem can be transformed into the problem of determining shortest vector in a lattice, so that LLL algorithm can also be used to solve the subset sum problem. Since the subset sum problem can be easily solved by applying LLL algorithm, then the Merkle-Hellman knapsack cryptosystem can also be easily be destructed.
ALGORITME LLL
DAN APLIKASINYA DALAM PEMBONGKARAN
SISTEMKRIPTO
KNAPSACK
MERKLE-HELLMAN
ARI AGUSTIANSA
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul Skripsi
: Algoritme LLL dan Aplikasinya dalam Pembongkaran Sistemkripto
Knapsack
Merkle-Hellman
Nama
: Ari Agustiansa
NIM
: G54080040
Menyetujui
Pembimbing I
Pembimbing II
Dr. Sugi Guritman
Dr. Ir. Bib Paruhum Silalahi, M.Kom.
NIP. 19620927 199203 1 004
NIP. 19670101 199203 1 004
Mengetahui
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS.
NIP. 19650505 198903 2 004
PRAKATA
Puji syukur penulis panjatkan ke hadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Penyusunan karya ilmiah ini juga tidak terlepas dari dukungan doa, moril dan materiil dari berbagai pihak. Pada kesempatan ini, penulis menyampaikan terima kasih kepada :
1. Dr. Sugi Guritman dan Dr. Ir. Bib Paruhum Silalahi, M.Kom. selaku pembimbing pertama dan kedua yang telah dengan sabar membimbing penulis dalam menyusun karya ilmiah ini,
2. Dr. Paian Sianturi selaku dosen pembimbing akademik, Muhamad Ilyas, M.Si. selaku dosen penguji, dan seluruh dosen Departemen Matematika FMIPA IPB,
3. Bapak dan almarhumah Ibu tercinta atas doa, dukungan, kasih sayang, nasihat, dan kepercayaannya,
4. Retno Wulandari, yang senantiasa menemani, mendukung, membantu, dan memberi semangat kepada penulis,
5. teman-teman Matematika 45 atas segala dukungan, bantuan, dan ketulusan hati yang telah diberikan,
6. seluruh staf Departemen Matematika : Bapak Yono, Mas Heri, Ibu Ade, Bapak Acep, Ibu Susi, Mas Bono (Alm), Mas Deni yang telah membantu penulis dalam administrasi dan sebagainya.
Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan, oleh kerena itu penulis mengharapkan saran dan kritik dari semua pihak. Semoga tulisan ini bermanfaat bagi semua pihak yang memerlukan.
Bogor, Oktober 2012
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta, pada tanggal 22 Agustus 1990 dari pasangan Hazarin dan Zubaidah. Penulis merupakan putra kedua dari tiga bersaudara. Pada tahun 2002, penulis lulus dari SD Negeri Sunter Agung 13 Jakarta. Pada tahun 2005, penulis lulus dari SMP Negeri 116 Jakarta. Pada tahun 2008, penulis lulus dari SMA Negeri 80 Jakarta dan pada tahun yang sama penulis diterima di Departemen Matematika IPB melalui jalur USMI (Undangan Seleksi Masuk IPB)
Disamping kegiatan akademis, penulis pernah menjadi asisten beberapa mata kuliah, diantaranya:
Pengantar Metode Komputasi pada tahun ajaran 2010-2011, Persamaan Diferensial Biasa pada tahun ajaran 2010-2011, Pemodelan Matematika pada tahun ajaran 2011-2012, Analisis Numerik pada tahun ajaran 2012-2013.
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... viii
I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
II LANDASAN TEORI ... 1
III PEMBAHASAN ... 3
3.1 Latis dan Basis ... 3
3.2 Gram-Schmidt dan Determinan ... 6
3.2.1 Kompleksitas Gram-Schmidt ... 8
3.3 Permasalahan dalam Latis ... 9
3.4 Algoritme LLL ... 10
3.4.1 Pengertian Basis Terreduksi ... 10
3.4.2 Reduksi Ukuran ... 11
3.4.3 Algoritme LLL dan Analisisnya ... 18
3.5 SistemkriptoKnapsack Merkle-Hellman ... 22
3.6 Pembongkaran Sistemkripto Knapsack Merkle-Hellman ... 24
IV SIMPULAN DAN SARAN ... 24
4.1 Simpulan ... 24
4.2 Saran ... 24
DAFTAR PUSTAKA ... 25
LAMPIRAN ... 26
DAFTAR GAMBAR
Halaman
Gambar 3.1: Latis dengan basisB=f(0;1);(1;0)g ... 3
Gambar 3.2: Latis dengan basisB=f(2;1);(3;1)g ... 3
Gambar 3.3: Latis dengan basisB=f(1;2);(2;1)g ... 4
Gambar 3.4: Latis dengan basisB=f(1;1)g ... 4
Gambar 3.5: Parallelepiped dasar denganB=f(2;1);(1;2)g... 6
DAFTAR LAMPIRAN
Halaman Lampiran 1: Sintaks Mathematica Algoritme LLL ... 27Lampiran 2: Sintaks Mathematica Pembangkitkan kunci ... 28
Lampiran 3: Sintaks Mathematica Enkripsi ... 28
Lampiran 4: Sintaks Mathematica menentukan solusi masalah jumlah subhimpunan ... 28
Lampiran 5: Sintaks Mathematica Dekripsi ... 29
I PENDAHULUAN
1.1 Latar Belakang
Latis (lattice) merupakan obyek
geometrik dalam ruang dimensi-n yang
diilustasikan sebagai himpunan titik-titik dengan susunan yang teratur dan periodik (Guritman 2012).
Dalam latis, terdapat suatu
permasalahan yang sangat mendasar, yaitu masalah menentukan vektor terpendek (shortest vector problem) yang disingkat SVP. SVP adalah suatu masalah yang sangat sulit diselesaikan dalam komputasi. Hingga pada tahun 1982, A. K. Lenstra, H. W. Lenstra, Jr, dan L. Lovasz berhasil
menemukan sebuah algoritme untuk
menentukan hampiran dari masalah SVP yang bernama algoritme LLL. Walaupun algoritme LLL tidak dapat menyelesaikan
masalah SVP secara eksak, algoritme
ini cukup ampuh dalam menjawab SVP. Sehingga algoritme ini lebih disukai karena memiliki wakturunning polinomial.
Setelah ditemukannya algoritme LLL,
bahasan tentang latis menjadi lebih
berwarna. Kini latis dapat diterapkan
pada banyak bidang ilmu komputer, seperti aljabar komputer (computer algebra), teori koding (coding theory), dan kriptologi (kriptogra… dan kriptanalisis).
Salah satu yang akan dibahas dalam karya ilmiah ini adalah penerapan latis
dalam membongkar sistemkripto knapsack
Merkle-Hellman. Terbukti bahwa masalah latis dapat diterapkan pada pembongkaran
sistemkripto knapsack Merkle-Hellman.
Hal ini membuat sistemkripto knapsack
Merkle-Hellman mengalami kejatuhan.
1.2 Tujuan
Tujuan dari penulisan karya ilmiah ini antara lain adalah :
1. merekonstruksi ulang dan melakukan analisa pada algoritme LLL.
2. mengaplikasikan algoritme LLL dalam
pembongkaran sistemkripto knapsack
Merkle-Hellman.
3. mengimplementasikan proses pembongkaran sistemkripto knapsack Merkle-Hellman dalamsoftware Mathematica 8.0.
II LANDASAN TEORI
De…nisi 2.1 Jika m adalah bilangan
bulat positif, maka sebuah m-tuple
terurut adalah barisan m bilangan real
(a1,a2,. . . ,am). Himpunan dari semua
m-tuple disebut m-ruang Euclidean dan dinotasikan sebagaiRm.
(Anton 2000)
De…nisi 2.2Jika u= (u1; u2; : : : ; um)dan
v = (v1; v2; : : : ; vm) adalah vektor-vektor yang berada dalam Rm, maka hasil kali dalam Euclideanu vdide…nisikan sebagai
u v=u1v1+u2v2+:::+umvm:
(Anton 2000)
De…nisi 2.3 Panjang Euclidean (atau
norm Euclidean) dari sebuah vektor u =
(u1; u2; : : : ; um) dalam Rm dide…nisikan sebagai
kuk= q
u2
1+u22+:::+u2m:
(Anton 2000)
De…nisi 2.4 Dua vektor u dan v disebut ortogonal jikau v= 0:
(Anton 2000)
De…nisi 2.5 Sebuah vektor w disebut
kombinasi linear dari vektor-vektor
v1;v2; :::vr jika dapat diekspresikan dalam bentuk
w=k1v1+k2v2+:::+krvr
dengank1; k2; :::kradalah skalar.
(Anton 2000)
De…nisi 2.6 Jika S = fv1;v2; : : : ;vrg adalah himpunan tak kosong yang berisi vektor-vektor, maka persamaan
k1v1+k2v2+:::+krvr=0
memiliki minimal satu solusi, yaitu:
k1= 0, k2= 0,..., kr= 0:
Jika hanya didapatkan satu solusi, maka
S disebut himpunan vektor bebas linear. Jika terdapat solusi lain maka S disebut himpunan vektor bergantung linear.
2
De…nisi 2.7 Jika a dan b adalah
bilangan bulat, dengan a 6= 0, dan
jika terdapat sebuah bilangan bulat c
sedemikian sehingga b = ac, maka kita
katakan bahwa a membagi b, dan ditulis
ajb. Jika a tidak membagi b, maka ditulis
a-b:
(Stark 1970)
De…nisi 2.8 Sebuah bilangan bulat yang nilainya lebih besar dari nol dan hanya memunyai satu pembagi positif yaitu bilangan itu sendiri, maka bilangan tersebut disebut bilangan prima. Sebuah bilangan yang lebih besar dari satu yang bukan merupakan bilangan prima disebut bilangan komposit.
(Stark 1970)
De…nisi 2.9 Misalkan a dan b adalah
bilangan positif tak nol. Dan misalkan
d adalah bilangan terbesar yang berada
dalam himpunan pembagi bersama dari
a dan b. Maka kita sebut d adalah
pembagi bersama terbesar (greatest
common divisor) dariadan b. Dan ditulis sebagaid= gcd(a; b):
(Stark 1970)
De…nisi 2.10 Misalkan a dan b adalah bilangan bulat tak nol. Jika gcd(a; b) = 1, maka kita katakan bahwa a dan b relatif prima.
(Stark 1970)
De…nisi 2.11 Misalkan a dan b adalah bilangan bulat dannsebuah bilangan bulat positif. Jika nj(a b), maka kita katakan bahwaa kongruen ke b modulondan kita tulis
a bmodn:
(Stark 1970)
De…nisi 2.12 Misalkan S adalah subhimpunan dariR. u2Rdisebut sebagai
batas atas dari S jika s u untuk semua
s2S. Serupa dengan sebelumnya, w2 R
disebut sebagai batas bawah dari S jika
w suntuk semuas2S.
(Bartle 1964)
De…nisi 2.13 Misalkan S adalah subhimpunan dariRyang terbatas di atas. Sebuah batas atas dari S disebut sebagai supremum (batas atas terkecil) dari S jika nilainya lebih kecil dari batas atas yang lain dari S. Serupa dengan sebelumnya, sebuah batas bawah dariS disebut sebagai in…mum (batas bawah terbesar) dariSjika nilainya lebih besar dari batas bawah yang lain dariS.
III PEMBAHASAN
3.1 Latis dan Basis
Seperti yang telah dijelaskan dalam pendahuluan bahwa latis merupakan obyek
geometrik dalam ruang dimensi-n yang
diilustasikan sebagai himpunan titik-titik dengan susunan yang teratur dan periodik.
Secara formal, de…nisi latis diberikan
sebagai berikut.
De…nisi 3.1 Misalkan B = fb1;b2; : : : ;
bng adalah himpunan n vektor bebas
linear dalam ruang vektor Rm. Latis
L(B) adalah subgrup aditif diskrit dari
Rm, yang beranggotakan semua kombinasi linear intejer dariB:
L(B) = 8 <
:
n
X
j=1
xjbj xj 2Z
9 =
;
dengan n m. Dalam hal ini B disebut
basis untukL(B).
Dalam karya ilmiah ini, notasi " " dibaca sebagai "dengan".
Seperti dalam ruang vektor, basis
B untuk latis L(B) dapat diperagakan
sebagai matriks B berukuran m n yang
kolom-kolomnya merupakan vektorbj:
B= b1 b2 bn .
Sehingga L(B) dapat dituliskan sebagai perkalian matriks
L(B) =fBx x2Zng.
Dalam hal ini, B merupakan bentuk
matriks dariB.
De…nisi 3.2 Dimensi atau rank pada latis L(B) dide…nisikan sebagai banyaknya anggota pada basisB. Untuk kasusm=n, maka latis L(B) dikatakan berdimensi penuh (full dimensional) atau disebut juga memilikirank penuh (full rank).
Terdapat kemiripan antara pengertian
latis yang dibangkitkan oleh B dengan
pengertian subruang vektor dalamRmyang direntang olehB:
hBi= 8 <
:
n
X
j=1
xjbj xj2R
9 =
;.
Perbedaannya hanya terdapat pada
bilangan yang dipakai pada kombinasi linear. Pada latis L(B), kombinasi linear
menggunakan koe…sien dalam rentang
intejer (Z R). Sedangkan pada hBi,
koe…sien pada kombinasi linear yang
digunakan adalah rentang bilangan real (R). Sehingga dapat disimpulkan jika B
adalah basis untukL(B), makaBpasti juga
merupakan basis untuk hBi. Namun hal
ini tidak berlaku sebaliknya, jikaB adalah basis untukhBi, belum tentu B juga basis untukL(B).
Berikut merupakan contoh latis dalam
R2.
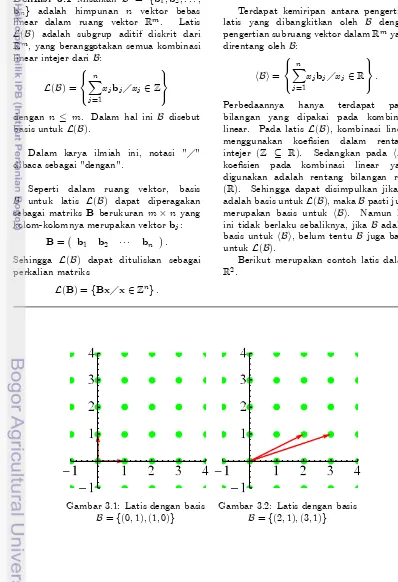
Gambar 3.1: Latis dengan basis
B=f(0;1);(1;0)g
Gambar 3.2: Latis dengan basis
4
Gambar 3.3: Latis dengan basis
B=f(1;2);(2;1)g
Gambar 3.4: Latis dengan basis
B=f(1;1)g
Gambar 3.1 dan gambar 3.2 merupakan latis Z2 yang dibangkitkan oleh basis baku
B1 = f(1;0);(0;1)g dan basis B2 =
f(2;1);(3;1)g. Hal ini memperlihatkan bahwa sama seperti ruang vektor, basis
untuk suatu latis tidak tunggal. Pada
gambar 3.3 merupakan contoh bahwa basis
B3=f(2;1);(1;2)gbukan merupakan basis
untuk Z2 walaupun B
3 memunyai rank
penuh di dalam R2. Selanjutnya gambar
3.4 merupakan sebuah contoh bahwa basis
B4=f(1;1)gmasih dapat membentuk latis
L(B4) walaupun B4 tidak memiliki rank
penuh di dalamR2.
Cara bagaimana menentukan basis lain dalam suatu latis akan dijelaskan setelah de…nisi berikut.
De…nisi 3.3Dua basisAdanBdikatakan ekuivalen, dinotasikan dengan A B, jhj
A dan B membangkitkan latis yang sama,
yaitu
L(A) =L(B).
De…nisi 3.4 Matriks U berukuran n n
disebut unimodular jika U 2 Zn n dan
det(U) = 1.
Proposisi 3.1 Invers dari matriks
unimodular juga merupakan matriks
unimodular.
Bukti:
Misalkan U = (uij) adalah matriks
unimodular berukuran n n, dari asumsi
diperoleh uij 2 Z dan det(U) = 1.
Berdasarkan rumus matriks invers, maka
U 1= 1
det(U)( ij)
T
dimana ij adalah kofaktor dari uij.
Karenauij 2Z, dari de…nisi kofaktor, jelas bahwa ij 2Zsehingga
( ij)T 2Zn n. (i)
Disamping itu,
U 1U=I
) det(U 1U) = det(I) , det(U 1) det(U) = 1
, det(U 1) = 1 det(U).
Karenadet(U) = 1, maka
det(U 1) = 1 dan 1
det(U) 2Z. (ii)
Dari (i) dan (ii), dapat disimpulkan bahwa
U 1 merupakan matriks unimodular.
Proposisi 3.2 Misalkan A = fa1;a2;
: : : ;ang adalah basis untukL(A)dan B=
fb1;b2; : : : ;bng adalah basis untuk L(B).
Maka A B jhj ada matriks unimodular
U 2 Zn n sehingga B = AU, dimana A
5
Bukti:
())Misalkan L(A) = L(B). Dari asumsi ini diperoleh bahwa untuk setiap
j= 1;2; : : : ; n,bj2 L(A), dan dari de…nisi
L(A) maka ada uj = (u1j; u2j; : : : ; unj) 2
Zn sehingga
bj= n
X
i=1
uijai. (i)
Dengan demikian, dapat dide…nisikan
matriks U 2 Zn n yang kolom-kolomnya
adalah vektoruj sebagai berikut.
U= u1 u2 un
Dan dari persamaan (i) diperoleh
persamaan matriks
B=AU (ii)
dimana
B = b1 b2 bn
A = a1 a2 an
U = u1 u2 un
Dengan langkah-langkah yang sama, dapat diperoleh matriksV2Zn n sehingga
A=BV (iii)
Dari persamaan (ii) dan (iii), didapatkan
A=BV
) det(A) = det(AUV) , det(U) det(V) = 1.
Disamping itu, karena U dan V adalah
matriks intejer, maka determinannya
juga intejer. Dengan demikian, dapat
disimpulkan bahwadet(U) = 1
(()Misalkan B = AU dengan U
unimodular. Dari asumsi ini diperoleh
bahwa untuk setiap j = 1;2; : : : ; n, bj 2
L(A), karena bj merupakan kombinasi
linear intejer dari A. Selanjutnya,
karena untuk setiap x 2 L(B) merupakan kombinasi linear intejer dariB, maka dapat
disimpulkan bahwa x juga merupakan
kombinasi linear intejer dari A (artinya,
x 2 L(A)). Dengan demikian diperoleh
L(B) L(A). Kemudian perhatikan
bahwa dari asumsi juga diperoleh A =
BU 1 dengan U 1 juga unimodular
(proposisi 3.1). Sehingga dengan
langkah-langkah yang serupa dengan
sebelumnya, diperolehL(A) L(B).
Cara yang lebih mudah dalam
menentukan dua basis yang ekuivalen adalah dengan menerapkan operasi kolom intejer (integer column operations)
De…nisi 3.5 Operasi kolom intejer (OKI) pada matriksBmemiliki 3 jenis berikut: 1. Kjk(B): menukar kolom ke-jdan kolom
ke-kpada matriksB
2. Kj(-1)(B): mengalikan kolom ke-j
dengan skalar -1 pada matriksB
3. Kjk( )(B): menambahkan kolom ke-j
dengan skalar 2 Z kali kolom ke-k
pada matriksB
OKI hampir sama dengan operasi kolom dasar (OKD) yang biasanya diterapkan pada ruang vektor. Hal yang membedakan
hanya terdapat pada jenis kedua. Pada
OKD, pengali yang digunakan adalah sembarang bilangan real taknol, sedangkan pada OKI pengali yang digunakan adalah -1.
Kemudian misalkan I adalah matriks
identitas dan K adalah serangkaian OKI
yang diterapkan pada suatu matriksBdan menghasilkan matriksC, maka berlaku
K(B) =C,BK(I) =C.
Serangkaian OKI yang diterapkan pada I
pasti akan menghasilkan matriks intejer, sehingga K(I) merupakan matriks intejer.
Disamping itu, karena det(I) = 1, OKI
jenis pertama dan kedua bersifat mengubah tanda determinan, dan OKI jenis ketiga bersifat tidak mengubah nilai determinan,
sehingga didapatkan det(K(I)) = 1.
Dengan demikian dapat disimpulkan bahwa
K(I) merupakan matriks unimodular.
Sehingga didapatkan proposisi berikut.
Proposisi 3.3 Dua basis dikatakan ekuivalen jhj yang satu merupakan hasil serangkaian OKI dari yang lain.
3.2 Gram-Schmidt dan Determinan
Salah satu bahasan dalam aljabar linear yang merupakan kunci penting dalam latis adalah proses ortogonalisasi
Gram-Schmidt. Proses ini yang akan
6
De…nisi 3.6 (Ortogonalisasi Gram-Schmidt (OGS)) Misalkan B = fb1;b2; : : : ;bngadalah himpunannvektor bebas linear dalam ruang vektorRm. Maka dapat dikonstruksi barisan n vektor yang saling ortogonal B = fb1;b2; : : : ;bng
dimana
b1 = b1,
bj = bj j 1
X
i=1
jibi,
dengan j= 2;3; : : : ; n, dan
ji=
bj bi
bi bi
Jika himpunan B = fb1;b2; : : : ;bng
adalah bebas linear, maka B merupakan
basis untuk hBi, dan jika B =
fb1;b2; : : : ;bng adalah hasil OGS dari B, maka B juga merupakan basis untuk hBi. Namun hal ini secara umum tidak berlaku dalam latis, jikaBadalah basis untukL(B)
tidak harus B merupakan basis untuk
L(B). Bahkan belum tentuB L(B).
Dalam ruang vektor, vektor
pj = Pji=11 jibi merupakan vektor
proyeksi dari bj pada subruang vektor
fb1;b2; : : : ;bj 1g darihB i. Sedangkan
bj merupakan vektor proyeksi daribjpada subruang vektor fbj;bj+1; : : : ;bng dari
hB i. Sehingga dapat dide…nisikan fungsi proyeksi sebagai berikut.
De…nisi 3.7 Untuk j = 1;2; : : : ; n,
fungsi proyeksi j dari ruang vektor
V = hB i = hBi ke subruang vektor
fbj;bj+1; : : : ;bng dide…nisikan sebagai
j(v) = n
X
i=j
v bi bi bi bi.
Jika diambil nilai v = bk, k =
1;2; : : : ; n, maka diperoleh
j(bk) =
8 <
:
0 jika k < j
bk jika k=j bk+Pki=j1 kibi jika k > j
Selanjutnya perhatikan de…nisi berikut.
De…nisi 3.8 Misalkan = L(B) adalah
latis yang dibangkitkan oleh basis B =
fb1;b2; : : : ;bng, maka dapat dide…nisikan himpunan
P(B) = 8 <
:
n
X
j=1
xjbj xj 2R;0 xj<1
9 =
;.
Dimana P(B) merupakan bangun
geometrik yang disebut parallelepiped
dasar atau daerah fundamental
(fundamental region). Berikut ilustrasi dariP(B).
7
Dari gambar 3.5 terlihat bahwa pada latis dalamR2,P(B)digambarkan sebagai
daerah arsir bidang jajaran genjang. Hasil dari luas jajaran genjang pada gambar 3.5 disebut vol(P(B)). Pada sembarang latis , dapat dide…nisikan nilai determinan dari latis , dinotasikan dengan det( ), yang merupakan nilai darivol(P(B)). Dari ilustrasi gambar 3.5, maka de…nisi det( )
dapat dinyatakan sebagai berikut.
De…nisi 3.9 Misalkan = L(B) adalah
latis yang dibangkitkan oleh basis B =
fb1;b2; : : : ;bngdanB =fb1;b2; : : : ;bng adalah hasil OGS dariB. Determinan dari
dide…nisikan sebagai
det( ) =
n
Y
i=1
kbik.
Cara menentukan determinan suatu latis tanpa melakukan OGS akan dijelaskan oleh proposisi setelah lemma berikut ini.
Lemma 3.1Jika matriks
B = b1 b2 bn
adalah matriks hasil OGS dari matriks
B= b1 b2 bn ,
maka ada matriksUdengan unsur diagonal adalah 1 sehingga
B=B U
Bukti:
Perhatikan bahwa rumus OGS dapat diubah menjadi
b1 = b1
b2 = b2+ 21b1
b3 = b3+ ( 31b1+ 32b2)
.. .
bn = bn+
n 1
X
i=1
nibi
Hal ini menunjukkan bahwa transformasi
balik OGS dari B ke B merupakan
serangkaian OKD yang dilakukan pada matriksB, yaitu
B=K(B ),B=B K(I).
Dengan demikian dapat dide…nisikan
sebuah matriksU=K(I), dimana
K(I) = 0 B B B @
1 21 n1
0 1 n2
..
. ... . .. ...
0 0 0 1
1
C C C A
Proposisi 3.4 Jika = L(B) adalah
latis yang dibangkitkan oleh basis B =
fb1;b2; : : : ;bng, maka
det( ) = q
det(BTB)
dimanaBadalah bentuk matriks dariB.
Bukti:
Misalkan
B = b1 b2 bn
adalah matriks hasil OGS dari matriks
B= b1 b2 bn ,
menurut lemma 2.1 terdapat sebuah
matriksU yang unsur diagonalnya adalah 1 sehingga
B=B U.
Dengan demikian diperoleh
BTB= (B U)T(B U) , BTB=UT (B )TB U
) det(BTB) = det UT (B )TB U , det(BTB) = det (B )TB
, det(BTB) =
n
Y
i=1
kbik !2
,
n
Y
i=1
kbik= q
det(BTB)
, det( ) = q
det(BTB)
Berikut merupakan proposisi yang
menjelaskan bahwa determinan suatu latis tidak bergantung pada pemilihan suatu basis.
Proposisi 3.5 Jika A B, maka
det(L(A)) = det(L(B)).
Bukti:
Misalkan A B, dengan A dan B
8
Berdasarkan proposisi 3.2 terdapat sebuah
matriks unimodular U sehingga A=BU.
Dengan demikian,
det(L(A)) = q
det(ATA)
= q
det((BU)T(BU))
= q
det(UT(BTB)U)
= q
det(BTB)
= det(L(B))
3.2.1 Kompleksitas Gram-Schmidt
Dalam OGS terlihat bahwa banyaknya operasi aritmetik yang dilibatkan dalam
OGS adalah O(n3). Namun belum dapat
disimpulkan bahwa waktu running pada
OGS adalah polinomial. Harus dipastikan terlebih dahulu bahwa bilangan-bilangan yang diproses pada OGS tidak tumbuh terlalu besar.
Diasumsikan bahwa matriks B yang
digunakan adalah matriks intejer.
Perhatikan bahwa langkah ke-j dari OGS dapat dirumuskan ulang sebagai
bj =bj+ j 1
X
i=1
vjibi untuk suatuvji2R
(3.1) Karena bj ortogonal ke bt untuk setiap
t < j, maka diperoleh
bt bj = (bt bj) + bt
j 1
X
i=1
vjibi
!
, 0 = (bt bj) + bt
j 1
X
i=1
vjibi
!
, bt j 1
X
i=1
vjibi= (bt bj) (3.2)
Untuk t = 1;2; : : : ; j 1, Persamaan tersebut bisa ditulis dalam bentuk matriks
0
B B B @
b1 Pji=11vjibi
b2 Pji=11vjibi .. .
bj 1 Pji=11vjibi
1 C C C A= 0 B B B @
b1 bj
b2 bj .. .
bj 1 bj
1
C C C A
Jika dide…nisikan matriks
Bj 1= b1 b2 bj 1
dan matriks
uj=
0
B B B @
vj1
vj2
.. .
vj;j 1
1
C C C A
maka persamaan (3.2) dapat ditulis sebagai
0
B B B @
b1 (Bj 1uj)
b2 (Bj 1uj) .. .
bj 1 (Bj 1uj)
1 C C C A= 0 B B B @
b1 bj
b2 bj .. .
bj 1 bj
1
C C C A
, BTj 1(Bj 1uj) = BTj 1bj
, (BTj 1Bj 1)uj = BTj 1bj(3.3)
Persamaan 3.3 merupakan SPL dengan matriks koe…sien BT
j 1Bj 1 dan vektor
BT
j 1bjadalah intejer. Dengan demikian, untuk s = 1;2; : : : ; j 1, berdasarkan aturan Cramer diperoleh
vjs2
Z det(BT
j 1Bj 1)
= Z
det(L(Bj 1))2
Hasil ini akan digunakan untuk memberi
batas pada koe…sien ji. Misalkan
Dj 1 = det(BTj 1Bj 1) dan dikalikan
nilainya kedua ruas dari persamaan 3.1 maka diperoleh
Dj 1bj =Dj 1bj+ j 1
X
i=1
(Dj 1vji)bi
merupakan persamaan yang semua
koe…sien vektornya adalah intejer. Ini
berarti semua penyebut dari bilangan dalam vektor bj adalah faktor dari Dj 1.
Kemudian
ji =
bj bi
bi bi
= Di 1(bj bi) Di 1(bi bi)
= ib1j (Di 1bi) Y
s=1
kbsk2 !
kbik2 2 DZ
i
Hasil ini menunjukkan bahwa penyebut dari
jiharus membagi Di.
Uraian di atas membuktikan bahwa bilangan-bilangan yang ada di dalam vektor
bi dan ji memunyai penyebut paling
banyak
max
k Dk n
Y
i=k
9
Akhirnya, besarnya bilangan juga
polinomial karena bj kbjk.
Dengan demikian secara keseluruhan
OGS memunyai kompleksitas waktu
running polinomial. Hasil ini bermanfaat untuk menganalisis algoritme LLL yang merupakan algoritme yang berbasiskan OGS.
3.3 Permasalahan dalam Latis
Berikut merupakan pengertian jarak minimum dan panjang vektor minimum dari suatu latis.
De…nisi 3.10 Jarak minimum antara
sembarang dua titik di dalam latis ,
dinotasikan dengan ( ), dide…nisikan
sebagai
( ) = inffkx yk x;y2 ;x6=yg
De…nisi 3.11 Panjang vektor minimum
di antara titik-titik di dalam latis ,
dinotasikan dengan ( ), dide…nisikan
sebagai
( ) = inffkxk x2 ;x6=0g
Dua pengertian di atas memiliki arti yang ekuivalen. Hal tersebut dinyatakan dalam proposisi berikut.
Proposisi 3.6 Untuk sembarang latis , berlaku
( ) = ( ).
Bukti:
Karena adalah grup, maka berlaku
( ) = inffkx yk x;y2 ;x6=yg = inffkzk z=x y2 ;x6=yg = inffkzk z2 ;z6=0g
= ( )
Berikut merupakan batas bawah dari .
Teorema 3.1 Jika = L(B) adalah
latis yang dibangkitkan oleh basis B =
fb1;b2; : : : ;bngdanB =fb1;b2; : : : ;bng adalah hasil ortogonalisasi dariB, maka
min
j2In
bj ( ),In=f1;2; : : : ; ng
Bukti:
Ambil sembarang v 2 L(B) dengan
v6=0, maka ada vektor x2Zn dengan
x6=0sehingga
v=Bx
dengan B adalah bentuk matriks dari B. Misalkanx=fx1; x2; : : : ; xngdankadalah indeks terbesar dari komponen x sehingga
xk 6= 0; Karena untuk setiap j < k, bk ortogonal ke bj dan juga ortogonal ke bj, maka
v bk = (Bx) bk
= 0
@
k
X
j=1
xjbj
1
A bk
= xk(bkbk)
dan
bk bk = 0
@bk k 1
X
j=1
kjbj
1
A bk
= bk bk.
Dengan demikian diperoleh
v bk = xk(bkbk)
= xkkbkk
2
) jv bkj=jxkj kbkk
2
Berdasarkan ketaksamaan Cauchy-Schwartz, maka diperoleh
jv bkj kvk kbkk , jxkj kbkk
2
kvk kbkk , jxkj kbkk kvk
Karena jxkj 1, untuk In = f1;2; : : : ; ng diperoleh
min
j2In
bj kbkk
kvk
Selanjutnya, karena v adalah sembarang
vektor dalam L(B), maka dapat
disimpulkan
min
j2In
bj ( )
10
Soal 3.1 (Pelacakan SVP) Diberikan
sebuah latis dengan basis B, carilah
x2L(B)sehingga
kxk= (L(B))
Soal 3.2 (Optimisasi SVP) Diberikan
sebuah latis dengan basis B, carilah
(L(B)).
Soal 3.3 (Pelacakan SVP) Diberikan sebuah latis dengan basis B dan bilangan rasionalq2Q, tentukan apakah
(L(B)) qatau (L(B))> q
Soal 3.4 (Pelacakan SVP) Diberikan
sebuah latis dengan basis B dan 1,
carilahx2L(B)dengan x6=0sehingga
kxk (L(B))
Soal 3.5 (Pelacakan SVP) Diberikan
sebuah latis dengan basis B dan 1,
carilahdsehingga
d (L(B)) d
3.4 Algoritme LLL
3.4.1 Pengertian Basis Terreduksi
Berikut merupakan de…nisi dari basis terreduksi .
De…nisi 3.12Suatu basisB= [b1;b2; : : : ;
bn] dalam Rm disebut terreduksi (atau terreduksi LLL dengan parameter ) jika memenuhi
1. ji 1
2, untuk setiap intejer i; j,
dengan1 i < j n,
2. k j(bj)k2 k j(bj+1)k2, untuk j =
1;2; : : : ; n 1,
dimana merupakan parameter reduksi
yang bernilai real dengan 14< <1.
Syarat pertama dalam de…nisi di
atas disebut dengan reduksi ukuran.
Syarat pertama mengatakan bahwa basis terreduksi harus "hampir ortogonal" dan dalam komputasinya syarat ini mudah dicapai OGS. Pembahasan mengenai syarat pertama akan dibahas pada subbab 3.4.2.
Sedangkan pada syarat kedua dari de…nisi di atas disebut syarat pertukaran, atau disebut juga kondisi Lovasz, yang
dapat ditulis ulang sebagai
bj 2 bj+1+ j+1;jbj
2
, ( 2j+1;j) bj
2
bj+1 2(3.5).
Ketaksamaan 3.5 menyatakan bahwa
vektor-vektor Gram-Schmidt dari basis terreduksi LLL harus terurut turun dengan
faktor penurunan sebesar 2
j+1;j. Jika terdapat pasangan vektor (bj;bj+1) yang tidak memenuhi kondisi Lovasz, maka dapat dilakukan pertukaran antara vektor tersebut kemudian OGS kembali dilakukan.
Selanjutnya dengan menerapkan
syarat-syarat yang terdapat pada de…nisi 3.12, maka didapatkan batas atas untuk
kb1k dari basis terreduksi .
Teorema 3.2 Jika B = [b1;b2; : : : ;bn] dalamRm adalah basis terreduksi , maka berlaku
kb1k
n 1 2 ( )
dengan = 11
4.
Bukti:
Misalkan B = [b1;b2; : : : ;bn] adalah basis terreduksi , dari de…nisi didapatkan
bj+1 2 ( 2
j+1;j) bj
2
1 4 bj
2
1 bj 2
, bj 2 bj+1 2 (i)
Maka dengan menerapkan ketaksamaan (i) secara berulang, diperoleh
kb1k2 kb2k2
2
kb3k2
.. .
n 1kb
nk
2
.
Atau dengan kata lain, secara umum untuk setiapj2In=f1;2; : : : ng, berlaku
kb1k2 j 1 bj 2 ) kb1k j21 b
j
, kb1k j 1
2 b
j
Karena berlaku untuk setiapj 2In, maka
kb1k
n 1
2 min
j2In
11
Misalkan B= [b1;b2; : : : ;bn] adalah basis
terreduksi LLL untuk latis = L(B),
menurut teorema 3.1 diperoleh
min
j2In
bj ( )
sehingga ketaksamaan (ii) menjadi
kb1k
n 1 2 ( )
Teorema 3.2 menyatakan bahwa vektor pertama pada basis terreduksi merupakan
jawaban dari soal 3.4 dengan nilai =
n 1 2 .
3.4.2 Reduksi Ukuran
Sebagaimana telah dinyatakan
sebelumnya bahwa syarat reduksi ukuran
(yaitu ji 12) mudah dicapai dengan
menggunakan OGS. Selanjutnya akan
dibahas syarat reduksi ukuran melalui interpretasi geometrik. Untuk akan dibahas terlebih dahulu de…nisi berikut.
De…nisi 3.13 Misalkan = L(B) adalah
latis yang dibangkitkan oleh basis B =
[b1;b2; : : : ;bn] dalam ruang vektor Rm.
Daerah fundamental terpusat (centered
fundamental region) dari , dinotasikan dengan C(B), dide…nisikan sebagai:
C(B) = 8 < : n X j=1
xjbj xj 2R;
1 2 xj
1 2
9 =
;.
C(B) juga disebut parallelepiped
dasar terpusat (centered fundamental
parallelepiped).
Proposisi 3.7 Jika = L(B) adalah
latis yang dibangkitkan oleh basis B =
[b1;b2; : : : ;bn] dalam ruang vektor Rm,
maka untuk setiap vektor w 2 hBi, ada
tepat satu vektort2 C(B)sehingga dapat dituliskanw=v+t
Bukti:
Karena B merupakan basis untuk ,
makaBjuga merupakan basis untuk ruang vektorhBi. Dan karenaw2 hBi, maka ada tepat satu (w1; w2; : : : ; wn)2Rn sehingga
w=
n
X
j=1
wjbj.
Kemudian, karena wj 2 R, maka ada
bwje 2Zsehingga
wj=bwje+tj, dengan
1 2 tj
1 2. Selanjutnya, w = n X j=1
(bwje+tj)bj
=
n
X
j=1
bwjebj+ n
X
j=1
tjbj
= v+t
Lemma 3.2 Misalkan B = [b1;b2; : : : ;
bn] adalah hasil proses ortogonalisasi Gram-Schmidt dari himpunan bebas linear
B = [b1;b2; : : : ;bn], dan diberikan sembarang w2 hBi. Jika w=Pnj=1wjbj, maka
wn =
w bn bn bn
Bukti:
Perhatikan bahwa
w bn = 0
@
n
X
j=1
wjbj
1
A bn
=
n
X
j=1
wj(bj bn)
= wn(bnbn)
,wn=
w bn bn bn
Selanjutnya akan ditunjukkan bahwa bn
bn =bn bn,
bn bn = bn+ n 1
X
i=1
nibi
!
bn
= bn bn+
nX1
i=1
ni(bi bn)
= bn bn
Sifat dari daerah fundamental terpusat dinyatakan dalam proposisi berikut.
Proposisi 3.9 Jika B = [b1;b2; : : : ;bn]
adalah hasil OGS dari basis latis B =
12
dituliskanw=v+t.
Bukti:
Demi kepentingan bagaimana
menentukan v dan t secara algoritmik,
proposisi akan dibuktikan secara instruktif. Kemudian, tanpa mengurangi keumuman,
akan diambil untuk kasus n = 3 sebagai
berikut.
1. De…nisikan w3 = w. Karena w3 2
hfb1;b2;b3gi, berarti ada tepat satu
(x31; x32; x33)2R3 sehingga
w3= 3
X
j=1
x3jbj
dan berdasarkan lemma 3.2, dapat
dituliskan
w3 = 2
X
j=1
x3jbj+
w3 b3
b3 b3b3
=
2
X
j=1
x3jbj+
w3 b3
b3 b3 +
t3b3)
dengan 1
2 t3 1
2. Selanjutnya,
w3 = 2
X
j=1
x3jbj+
w3 b3
b3 b3 b3+
t3b3)
=
2
X
j=1
x3jbj+
w3 b3
b3 b3 b3+
t3 b3+ 2
X
i=1 3ibi
!
, w3
w3 b3
b3 b3 b3+ (t3b3) =
2
X
j=1
x3jbj+
2
X
i=1
t3 3ibi (i)
2. De…nisikan
w2 = w3
w3 b3
b3 b3 b3+ t3b3).
Dari persamaan (i) dan karena
hfb1;b2gi = hfb1;b2gi, maka w2 2
hfb1;b2gi. Dengan ada tepat satu
(x21; x22)2R2 sehingga
w2=x21b1+x22b2
dan berdasarkan lemma 3.2, dapat
dituliskan
w2 = x21b1+
w2 b2
b2 b2b2
= x21b1+
w2 b2
b2 b2 + t2)b2
dengan 1
2 t2 1
2. Selanjutnya,
w2 = x21b1+
w2 b2
b2 b2 b2+ t2b2
= x21b1+
w2 b2
b2 b2 b2+ t2(b2+ 21b1)
, w2
w2 b2
b2 b2 b2+t2b2 = x21b1+t2 21b1=
(x21+t2 21)b1 (ii)
3. De…nisikan
w1=w2
w2 b2
b2 b2 b2+t2b2 .
Dari persamaan (ii), maka w1 2 hfb1gi
dan ada x11 2 R sehingga w1 =
x11b1. Berdasarkan lemma 3.2, dapat
dituliskan
w1 =
w1 b1
b1 b1b1
= w1 b1
b1 b1 +t1 b1
= w1 b1
b1 b1 b1+t1b1
dengan 12 t1 12. Dari ketiga
langkah di atas, didapatkan bahwa
w1 =
w1 b1
b1 b1 b1+t1b1
w2 = w1+
w2 b2
b2 b2 b2+t2b2
w3 = w2+
w3 b3
b3 b3 b3+t3b3
Karenaw=w3, maka dapat dituliskan
w=v+t
dimana
v = w1 b1 b1 b1 b1+
w2 b2
b2 b2 b2+ w3 b3
13
dan dapat dilihat bahwav 2 L(B) dan
t2 C(B )
Bukti dari proposisi sekaligus
merupakan bukti kebenaran dari algoritme berikut.
Algoritme 3.1
Input: B = [b1;b2; : : : ;bn] basis untuk
L(B)danw2 hBi.
Output: Vektor latisv2 L(B)dan vektor
t2 C(B ).
1. Dengan OGS, hitung [b1;b2; : : : ;bn] dengan input B.
2. v:=0
3. t:=0
4. Untuk i=n; n 1; : : : ;1, lakukan: a. xi:=
w b
i
b
i bi
b. vi:=bxie c. v:=v+vibi d. ti:=xi vi
e. t:=t+tibi
f. w:=w (vibi+tibi) 5. return(vdant)
Algoritme di atas dapat disederhanakan hanya untuk menentukan vektor vsebagai berikut.
Algoritme 3.2 (Menentukan vektor terdekat)
Input: B = [b1;b2; : : : ;bn] basis untuk
L(B)danw2 hBi.
Output: Vektor latisv2 L(B)
1. Dengan OGS, hitung [b1;b2; : : : ;bn] dengan input B.
2. v:=0
3. Untuk i=n; n 1; : : : ;1, lakukan: a. xi:=
w b
i
b
i bi
b. vi:=bxie c. v:=v+vibi d. ti:=xi vi
e. w:=w (vibi+tibi) 4. return(v)
Akibat dari proposisi 3.7 diberikan dalam teorema berikut.
Teorema 3.3 Jika B = [b1;b2; : : : ;bn]
adalah hasil proses ortogonalisasi
Gram-Scmidt dari basis latis B =
[b1;b2; : : : ;bn], maka B dapat
ditransformasikan menjadi B0
= [b0
1;b
0
2; : : : ;b
0
n]yang juga merupakan basis untuk L(B) dan B juga merupakan hasil
ortogonalisasi Gram-Scmidt dariB0. Dalam
hal ini,
b1 = b0
1
bj = b0
j j 1
X
i=1
0
jibi
untukj= 2;3; : : : ; n, dengan
0
ji=
b0
j bi
bi bi dan 0
ji
1 2:
Bukti:
Transformasi dari B ke B0
akan dilakukan secara instruktif sebagai berikut. 1. De…nisikan
b01=b1
Dalam hal ini, diperoleh subruang
vektor berdimensi-1, yaitu
S1 = hfb1gi
= hfb0
1gi
= hfb1gi
2. Dari proses ortogonalisasi b2 ke b2
berlaku hubungan
b2=b2 p1
dengan p1 = 21b1 =
b 2b1 b
1b1
b1 adalah vektor proyeksi dari b2 padaS1 berarti
p12 S1. Dengan demikian, berdasarkan
proposisi 3.6, ada vektor latis v1 2
L(fb1g) dan vektor t1 2 C(fb1g)
sehingga
p1=v1+t1
dan diperoleh
b2 = b2 (v1+t1)
= (b2 v1) t1.
Kemudian dari persamaan di atas dapat dide…nisikan
b02=b2 v1
sehingga jelas (karena latis adalah grup)
bahwa b0
2 2 L(B) dan diperoleh
persamaan
b2=b0
2 t1.
Hasil ini menunjukkan bahwa
ortogonalisasifb0
1;b02gjuga menghasilkan
fb1;b2gdengan vektor proyeksi darib0
14
padaS1 adalah
t1 = 021b1
= b 0
2 b1
b1 b1b1
dalam hal ini
0
21= 21 b 21e
sehinggaj 0
21j 12. Selanjutnya, untuk
menghitungb0
2berarti ukup menghitung
v1menggunakan algoritme 3.2 dan
b02=b2 v1
Sebelum ke langkah berikutnya,
dinotasikan terlebih dahulu subruang vektor berdimensi-2, yaitu
S2 = hfb1;b2gi
= hfb01;b02gi = hfb1;b2gi
3. Dari proses ortogonalisasi b3 ke b3
berlaku hubungan
b3=b3 p2
dengan
p2= 31b1+ 32b2
p2 dimana adalah vektor proyeksi dari
b3 pada S2 berarti p2 2 S2. Dengan
demikian,berdasarkan proposisi 3.6, ada vektor latisv22 L(fb1;b2g)dan vektor
t22 C(fb1;b2g)sehingga
p2=v2+t2
dan diperoleh
b3 = b3 (v2+t2)
= (b3 v2) t2.
Kemudian dari persamaan di atas dapat dide…nisikan
b0
3=b3 v2
sehingga jelas bahwa b0
3 2 L(B) dan
diperoleh persamaan
b3=b0
3 t3.
Hasil ini menunjukkan bahwa
ortogonalisasi b0
3 juga menghasilkan b3
dengan vektor proyeksi darib0
3 padaS2
adalah
t1 = 031b1+
0
32b2
= b 0
3 b1
b1 b1b1+ b0
3 b2
b2 b2b2
dalam hal ini, untuki= 1;2, berlaku
0
3i= 3i b 3ie sehingga j 0
3ij 12. Selanjutnya,
untuk menghitung b0
3 berarti cukup
menghitung v2 menggunakan algoritme
3.2 dan
b03=b3 v2
Demikian seterusnya, dari 3 langkah di atas secara rekursuf dapat dilanjutkan
sampai langkah ke-n untuk memperoleh
basis latis B0 hasil transformasi dari basis
latisB.
Makna geometrik dari transformasi B
ke B0
dalam teorema 3.3 beserta buktinya adalah memperkecil panjang vektor basis, yaitu untukj= 1;2; : : : ; n berlakukbjk
b0
j . Hal ini terlihat dari vektor proyeksi
pi 1hasil proyeksi daribike subruangSi 1
untuk i = 2;3; : : : ; n, ditransformasikan ke vektor proyeksi ti 1, hasil proyeksi
dari b0
i ke subruang Si 1. Jika pi 1 2
C([b1;b2; : : : ;bi 1]), maka bi b0i, tetapi jika pi 1 2 C= ([b1;b2; : : : ;bi 1]),
maka bi ditransformasikan b0i dengan
vektor proyeksi pada Si 1 adalah t 2
C([b1;b2; : : : ;bi 1])sehinggakbik kb0ik. Dengan demikian, teorema 3.3 beserta buktinya merupakan landasan teori yang
digunakan untuk menyusun algoritme
reduksi ukuran dari algoritme LLL berikut ini.
Algoritme 3.3 (Reduksi Ukuran LLL) Input: B = [b1;b2; : : : ;bn] basis untuk
L(B)
Output: B = [b1;b2; : : : ;bn] adalah hasil proses ortogonalisasi Gram-Schmidt dari B dan B0
= [b0
1;b
0
2; : : : ;b
0
n] adalah hasil reduksi ukuran dariB
1. b1:=b1
2. b0
1:=b1.
3. Untukj= 2;3; : : : ; n, lakukan: a. p:=0
b. Untuki= 1;2; : : : ; j 1, lakukan: i. ji:=
bjb
i
b
i bi
ii. p:=p+ jibi
c. Gunakan algoritme 3.2 untuk
menghitung vektorvdengan input
B = [b1;b2; : : : ;bn] dan B =
[b1;b2; : : : ;bn]sertap d. b0
15
dan[b0
1;b02; : : : ;b0n])
Berikut ini langkah-langkah ilustratif
penyusunan algoritme reduksi ukuran LLL yang sifatnya rekursif tanpa memanggil algoritme 3.2
1. Untuk j= 1, de…nisikan langsung
b1:=b1danb01:=b1
2. Untuk j= 2, perhatikan bahwap1= 21b1, berdasarkan algoritme 3.2, maka
v1 =
p b1 b1 b1 b1 = b 21eb1
Jadi, untuk menghitungb2 danb0
2, cukup menghitung dahulu 21, kemudian
b2 = b2 p1
= b2 21b1
dan
b2 = b2 v1
= b2 b 21eb1
3. Untuk j = 3, perhatikan bahwa p2 = 31b1 + 32b2, berdasarkan algoritme 3.2,
nyatakanv2=v22+v21 sehingga
v22 =
(p2 b2
b2 b2 b1 = b 32eb2
v21 =
p2 b 32eb2 032b2) b1
b1 b1 b1 = b 31 b 32e 21eb1
Jadi, untuk menghitungb3 danb0
3, dapat dilakukan secara rekursif sebagai berikut.
(a) untuki= 2, hitung 32, kemudian
b3=b3 32b2
dan
b03 = b3 v22
= b3 b 32eb2
(b) untuki= 1, hitung 31, kemudian
b3=b3 31b1
dan
b0
3 = b
0
3 v21
= b0
3 b 31 b 32e( 21)eb1
16
3.2, nyatakan v3=v33+v32+v31 sehingga
v33 =
p3 b3
b3 b3 b3
= ( 43b3) b3 b3 b3 b3 = b 43eb3
v32 =
(p (b 43eb3+ 043b3)) b2
b2 b2 b2 = b 42 b 43e( 32)eb2
v31 = (
p (b 43eb3+ 043b3) (b 42eb2+ 042b2) b1
b1 b1 b1
= b 41 b 43e 31 b 42e 21eb1
Jadi, untuk menghitungb4 danb0
4, dapat dilakukan secara rekursif sebagai berikut
(a) untuki= 3, hitung 43, kemudian
b4=b4 43b3
dan
b04=b4 b 43eb3
(b) untuki= 2, hitung 42, kemudian
b4=b4 42b2
dan
b0
4=b
0
4 b 42 b 43e 32eb3
(c) untuki= 1, hitung 41, kemudian
b4=b4 41b1
dan
b04=b04 b 41 b 43e 31 b 42e 21eb3
Berdasarkan pola dari 4 langkah di atas, berikut ini diberikan algoritme reduksi ukuran yang sifatnya rekursif.
Algoritme 3.4 (Reduksi Ukuran LLL) Input: B = [b1;b2; : : : ;bn] basis untuk
L(B)
Output: B = [b1;b2; : : : ;bn]adalah hasil proses ortogonalisasi Gram-Schmidt dari
B dan B0 = [b0
1;b
0
2; : : : ;b
0
n] adalah hasil reduksi ukuran dariB.
1. b1:=b1
2. b0
1:=b1
3. 21:=
b 2b1 b
1b1
4. b2:=b2 21b1
5. b0
2:=b2 b 21eb1
6. Untuk j= 3;4; : : : ; n, lakukan: (a) bj :=bj
(b) bj:=bj
(c) j;j 1:=
bjb
j 1 b
j 1bj 1
(d) bj :=bj j;j 1bj 1
(e) b0
j:=b
0
j j;j 1bj 1
(f) Untuk i = j 2; j 3; : : : ;1, lakukan:
i. ji:= bjbi
b
i bi
ii. bj :=bj jibi
iii. c:= ji
iv. Untuk k = i; i+ 1; : : : ; j 2, lakukan:
A. c:=c j;k+1 k+1;i v. b0
j:=b
0
j bcebi 7. return([b1;b2; : : : ;bn]
dan[b0
1;b
0
2; : : : ;b
0
n])
17
1. Untuk j= 1, de…nisikan langsung
b1=b1danb01=b1
2. Untuk j= 2, perhatikan bahwap1= 21b1, berdasarkan algoritme 3.2, maka
v1 =
p1 b1
b1 b1 b1 = b 21eb1
Jadi, untuk menghitungb2 danb0
2 cukup menghitung dahulu 21, kemudian
b2 = b2 p1
= b2 21b1
dan
b0
2 = b2 v1
= b2 b 21eb1
3. Untuk j= 3, dari uraian sebelumnya,
b0
3 = (b3 b 32eb2) b 31 b 32e 21eb1
= (b3 b 32eb2)
(b3 b 32eb2) b1
b1 b1 b1 = x y
x = b3 b 32e(b
0
2+b 21eb1)
= b3 b 32eb
0
2 b 32e b 21eb1
y = (b3 b 32e(b 0
2 b 21eb1)) b1
b1 b1 b1
= (b3 b 32eb 0
2 b 32e b 21eb1) b1
b1 b1 b1
= (b3 b 32eb 0
2) b1
b1 b1 b 32e b 21e b1
= (b3 b 32eb 0
2) b1
b1 b1 b1 b 32e b 21eb1
Dengan demikian, diperoleh
b0
3= (b3 b 32eb
0
2)
(b3 b 32eb
0
2) b1
b1 b1 b1
Jadi,untuk menghitung b3 danb0
3, dapat dilakukan secara rekursif sebagai berikut
(a) untuki= 2, hitung 32, kemudian
b3=b3 32b2
dan
b03=b3 b 32eb
0
2
(b) untuki= 1, hitung 31, kemudian
b3=b3 31b1
dan
b0
3=b
0
3
b0
3 b1
18
Berdasarkan pola dari 3 langkah di atas, berikut ini diberikan algoritme reduksi ukuran yang sifatnya rekursif
Algoritme 3.5 (Reduksi Ukuran LLL) Input: B = [b1;b2; : : : ;bn] basis untuk
L(B)
Output: B = [b1;b2; : : : ;bn] adalah hasil proses ortogonalisasi Gram-Schmidt dari B dan B0
= [b0
1;b
0
2; : : : ;b
0
n] adalah hasil reduksi ukuran dariB.
1. b1:=b1
2. b0
1:=b1
3. Untuk j= 2;3; : : : ; n, lakukan:
(a) Untuk i = j 1; j 2; : : : ;1,
lakukan: i. ji:= bjbi
b
i bi
ii. bj :=bj jibi
iii. 0
ji:=
b0 jbi
b
i bi
iv. b0
j:=b
0
j
0
ji bi 4. return([b1;b2; : : : ;bn]
dan[b0
1;b
0
2; : : : ;b
0
n])
3.4.3 Algoritme LLL dan Analisisnya
Dari pembahasan sebelumnya, dapat disimpulkan bahwa algoritme LLL adalah algoritme yang mentransformasikan basis
B menjadi basis B0
dengan menerapkan
algoritme reduksi ukuran. Kemudian,
ketika kondisi Lovasz tidak memenuhi, algoritme LLL akan melakukan penukaran pada vektor pasangan vektor(bj;bj+1)dan
reduksi ukuran kembali dilakukan. Jika
ada beberapa pasang vektor (bj;bj+1)
yang tidak memenuhi kondisi Lovasz, tidak ada masalah pasangan vektor yang
harus ditukar terlebih dahulu. Bahkan
pasangan vektor tersebut dapat ditukar secara bersamaan, yang mengarah pada varian algoritme LLL paralel. Algoritme yang asli akan melakukan penukaran pada pasangan vektor dengan nilai j terkecil. Berikut merupakan garis besar deskripsi algoritme LLL.
1. (Langkah Reduksi Ukuran)
Terapkan algoritme reduksi ukuran pada
B.
2. (Langkah Penukaran) Jika ada j 2 f2;3; : : : ; ngyang memenuhi
( j;j 1)2 bj 1 2
> bj 2
maka tukar bj 1 dan bj, kemudian
kembali ke langkah 1:
3. Jika tidak, algoritme selesai.
Sedangkan bentuk praktis algoritme LLL diberikan sebagai berikut.
Algoritme 3.6 (Algoritme LLL) Input: B = [b1;b2; : : : ;bn] basis untuk
L(B)dan 14 < <1.
Output: B = [b1;b2; : : : ;bn] adalah
basis terreduksi LLL untuk L(B) dan
B = [b1;b2; : : : ;bn] adalah hasil proses ortogonalisasi Gram-Schmidt dariB. 1. Inisialisasib1:=b1.
2. j:= 2.
3. Reduksi Ukuran. Sementara j n, hitung:
(a) bj :=bj.
(b) Untuki=j 1 s.d. i= 1, hitung: i. ji:= bjbi
b
i bi
ii. bj :=bj jibi. iii. bj:=bj ji bi. (c) Penukaran.
Jika ( j;j 1)2 bj 1
2
> bj 2, maka
i. jikaj= 2,
A. tukarb1 danb2
B. b1:=b2
ii. jikaj >2,
A. tukarbj 1 danbj
B. j :=j 1
Selainnya,j:=j+ 1
4. return([b1;b2; : : : ;bn] dan[b1;b2; : : : ;bn])
Algoritme LLL merupakan algoritme
yang mampu menghitung menghitung
vektor terpendek dalam suatu latis L(B).
Namun ketika n cukup besar dan basis
B cukup jauh dari ortogonal, maka
algoritme LLL sulit untuk menghasilkan
vektor terpendek. Hal ini disebabkan
karena prinsip algoritme LLL yang
mentransformasikanB ke suatu basis yang "hampir ortogonal". Sehingga jika basisB
jauh dari ortogonal, maka kerja algoritme LLL semakin berat.
Karena basis B memengaruhi kinerja
dari algoritme LLL, maka suatu basis dapat diklasi…kasikan berdasarkan jauh dekatnya basis tersebut dari ortogonal.
De…nisi 3.14Basis latisBdikatakan bagus
jika B mendekati ortogonal. Sedangkan
19
Suatu nilai yang dapat menjadi
indikator sebuah basis baik atau buruk dide…nisikan sebagai berikut.
De…nisi 3.15 Rasio Hadamard dari suatu basis latisB=fb1; b2; : : : ; bng, dinotasikan dengan H(B), dide…nisikan sebagai
H(B) = 0 B B B B @ det( ) n Y j=1
kbjk
1 C C C C A 1 n
Karena nilai 0 < H(B) 1 dan
memenuhi sifat "semakin dekat nilai H(B)
ke 1, semakin dekatBke ortogonal". Maka basis B dikatakan bagus jika nilai H(B)
dekat ke 1 dan basisBdikatakan buruk jika nilaiH(B)dekat ke 0.
Selanjutnya akan dilakukan analisis terhadap algoritme LLL dengan cara membatasi banyaknya iterasi dan dan
membatasi besarnya bilangan yang
dilibatkan.
Membatasi banyaknya iterasi
Diasumsikan bahwa basis latis yang digunakan dalah intejer, artinya B Zn.
Terlihat bahwa algoritme LLL cepat
selesai ketika langkah penukaran (swap)
yang dilakukan tidak terlalu banyak.
Oleh karena itu, hal pertama yang
perlu diperhatikan dalam menganalisis algoritme LLL adalah seberapa besar jumlah maksimum terjadinya penukaran. Dengan demikian, akan dide…nisikan suatu intejer positif yang terkait dengan basis B
berikut ini.
Ingat kembali de…nisi determinan suatu latis berikut.
det(L([b1;b2; : : : ;bj])) = j
Y
i=1
kbik
, det(L(Bj)) =
q det(BT
jBj)
dimana matriks
Bj= b1 b2 bj
Dari asumsiBjadalah matriks intejer, jelas bahwa
(det(L(Bj)))22Z
Dengan demikian, dapat dide…nisikan
intejer positif D yang terkait dengan
matriks, yaitu
D=
n
Y
j=1
det(L(Bj))2
dan kemudian berlaku sifat dalam proposisi berikut ini.
Proposisi 3.8 Langkah reduksi ukuran
tidak mengubah nilai D, tetapi setiap
terjadi penukaran mengakibatkan nilai D
menurun dengan faktor .
Bukti:
Berdasarkan teorema 3.3, perhatikan bahwa langkah reduksi ukuran tidak akan
mengubah nilai D. Dengan demikian,
selanjutnya tinggal ditunjukkan bahwa setiap terjadi penukaran, nilai D menurun
dengan faktor . Misalkan terjadi
penukaran bj dan bj+1, misalkan pula
intejer positifDterkait denganB sebelum
terjadinya penukaran, dan D0
terkait dengan B0
setelah bj dan bj+1 ditukar.
Sekarang perhatikan bahwa, jika i < j, maka basis [b1;b2; : : : ;bi] tidak berubah oleh terjadinya penukaran sehingga jelas bahwa
det(L(Bi))2= (det(L(B
0
i))
2
Ketika i > j, maka pada basis
[b1;b2; : : : ;bi]vektor bj danbj+1 ditukar
(menukar sepasang vektor kolom padaBi) sehingga
L(Bi) =L(B0i)
) (det(L(Bi))2= (det(L(B0i))
2
Di lain pihak, untuk i = j, maka
basis Bj = [b1;b2; : : : ;bj 1;bj] berubah menjadi B0
j = [b1;b2; : : : ;bj 1;bj+1]
sehingga
(det(L(Bj))2 = j
Y
i=1
kbik2
=
j 1
Y
i=1
kbik2 !
bj 2
Karena syarat pertukaran (
20
(det(L(Bj))2 >
jY1
i=1
kbik2 !
1 ( ( j+1;j)2)
bj+1 2
> 1
( ( j+1;j)2) jY1
i=1
kbik2 !
bj+1 2
> 1 det(L(B0
j))
2
, det(L(B 0
j))
2
(det(L(Bj)))2
< Akhirnya, D0 D = n Y j=1
det(L(B0
j)
2
n
Y
j=1
(det(L(Bj)))2
= det(L(B 0
j))
2
(det(L(Bj)))2
<
, D0 < D
, D>1D
, D 1D0
Berdasarkan proposisi di atas, sekarang akan dimisalkankbanyaknya iterasi dalam algoritme LLL dan D(j) menyatakan nilai
Dpada iterasi ke-j, maka
D 1D(1)
2
D(2)
.. .
k
D(k)
Karena untuk setiap j nilai D(j) adalah
intejer positif, maka
D(k) 1
) D k
, D 1
k
, k log1(D)
Hasil ini menunjukkan bahwa banyaknya iterasi terbatas ke atas pada fungsi yang nilainya bergantung pada nilai awal D, karena menghitung D = n Y j=1 0 @ j Y j=1
kbik2 1 A j Y j=1 0 @ n Y j=1
kbik2 1
A
membutuhkan waktu polinomial, maka dapat disimpulkan bahwa banayknya iterasi dalam algoritme LLL juga terbatas secara polinomial.
Membatasi besarnya bilangan yang terlibat
Sebelumnya telah ditunjukkan bahwa banyaknya iterasi dalam algoritme LLL terbatas secara polinomial dalam ukuran
input. Namun demikian, hal ini
belum cukup untuk menyimpulkan bahwa
algoritme LLL memunyai waktu running
polinomial. Perlu dipastikan bahwa
ukuran bilangan yang dilibatkan dalam keseluruhan komputasi juga terbatas secara polinomial. Algoritme LLL menggunakan aritmetik bilangan rasional, sehingga perlu dibatasi presisinya maupun besarannya.
Perhatikan bahwa langkah ke-j dari
proses Gram-Schmidt dapat dirumuskan ulang sebagai
bj =bj+
j 1
X
i=1
vjibi untuk suatuvji2R
(3.6) Karena bj ortogonal ke bt untuk setiap
t < j, maka diperoleh
(bt bj) = (bt bj) +bt j 1
X
i=1
vjibi
, 0= (bt bj) +bt j 1
X
i=1
vjibi
, bt j 1
X
i=1
vjibi= (bt bj) (3.7)
21
tersebut bisa ditulis dalam bentuk matriks
0 B B B B B B @ b1
Xj 1
i=1vjibi
b2
Xj 1
i=1vjibi
.. .
bj 1
Xj 1
i=1vjibi
1 C C C C C C A = 0 B B B @
b1 bj
b2 bj .. .
bj 1 bj
1
C C C A
Jika dide…nisikan matriks
Bj 1= b1 b2 bj 1
dan matriks
uj=
0
B B B @
vj1
vj2
.. .
vj;j 1
1
C C C A
maka persamaan (3.7) dapat ditulis sebagai
0
B B B @
b1 (Bj 1uj)
b2 (Bj 1uj) .. .
bj 1 (Bj 1uj)
1 C C C A= 0 B B B @
b1 bj
b2 bj .. .
bj 1 bj
1
C C C A
, BTj 1(Bj 1uj) = BTj 1bj
, (BT
j 1Bj 1)uj = BTj 1bj Persamaan terakhir tersebut merupakan
SPL dengan matriks koe…sien BT
j 1Bj 1
dan vektor BT
j 1bj adalah intejer. Dengan demikian, untuks= 1;2; : : : ; j 1, berdasarkan aturan Cramer diperoleh
vjs2
Z det(BT
j 1Bj 1)
= Z
det(L(Bj 1))2
Hasil ini akan digunakan untuk memberi batas pada koe…sien ji. Perhatikan lagi de…nisiDsebagai
D =
n
Y
j=1
(det(L(Bj)))2
=
n
Y
j=1
det(BT
j 1Bj 1)
, D =
n
Y
j=1
Dj dengan Dj= det(BTj 1Bj 1)
Kemudian, hitung Dj = det(BTj 1Bj 1)
dan dikalikan nilainya kedua ruas dari persamaan (3.6), maka diperoleh
Dj 1bj =Dj 1bj+ j 1
X
i=1
(Dj 1vji)bi
dan karena Dj 1vji 2 Z, maka diperoleh
Dj 1bj 2Zn. Ini berarti semua penyebut
dari bilangan dalam vektor bj adalah
faktor dariDj 1. Sekarang dihitung
ji =
bj bi
bi bi
= Di 1(bj bi)
Di 1(bi bi)
= ib1j (Di 1bi) Y
s=1
kbsk2 !
kbik2 2 Z
Di
Hasil ini menunjukkan bahwa penyebut dari
ji adalah Di. Oleh karena itu, bilangan rasional yang ada di dalam vektor
bj =bj j 1
X
i=1
jibi
dan ji dapat dituliskan dengan penyebut
D(Dmerupakan kelipatan setiapDi). Karena ji 12, maka ukuran bit yang
digunakan terbatas pada lgD. Kemudian dari
Dj= j
Y
s=1
kbsk2
diperoleh
bj 2= Dj
Dj 1 Dj D
Akhirnya,
kbjk2 = bj
2 + j 1 X i=1 2
jikbik
2
D+ (j 1) n 4 D nD
Dengan demikian, semua pembilang dan penyebut dari bilangan rasional yang terjadi di dalam eksekusi algoritme LLL memunyai ukuran bit yang terbatas secara polinomial dalamlgD.
3.5 Sistemkripto Knapsack Merkle-Hellman
SistemkriptoKnapsackMerkle-Hellman merupakan sistemkripto yang berlandaskan
kerumitan komputasi NP-complete.
Sistemkripto ini diperkenalkan oleh Merkle dan Hellman pada akhir 1970-an. Tumpuan
keamanan utamanya adalah problem
klasik matematika yang terkenal dengan
nama problem jumlah subhimpunan
22
keamanan sistem ini menjadi melemah secara signi…kan ketika tumpuan keamanan tersebut bisa dibawa ke masalah latis.
De…nisi 3.16 (Masalah jumlah subhimpunan)Diberikan list yang terdiri darinbilangan intejer positif
a=fa1; a2; : : : ang
dan suatu intejer positif lain s yang
ditetapkan. Masalah jumlah subhimpunan
adalah mencari subhimpunan dari a yang
jumlahnya sama dengans(diasumsikan ada sedikitnya satu sub-himpunan).
Deskripsi yang lain dari de…nisi di atas bisa dinyatakan adalah sebagai berikut. Diketahui vektor intejer a2Zn adalah bentuk vektor dari list intejer positif
a = fa1; a2; : : : ang dan intejer s 2 Z+. Tentukan vektor biner x= (x1; x2; : : : ; xn) dengan xi2Z2 sehingga
a x=s
,
n
X
i=1
aixi=s
Pelacakan brute force untuk
menyelesaikan problem ini adalah 2n.
Untuk n yang cukup besar, sulit
menentukan x pada masalah jumlah
subhimpunan (a;s). Namun sebagaimana layaknya paradigma kriptosistem, masalah ini dapat digunakan sebagai tumpuan
keamanan kalau dapat dide…nisika
informasi ekstra (trapdoor) pada a.
Sehingga dengan informasi ekstra tersebut masalah jumlah subhimpunan (a;s)dapat
diselesaikan dengan mudah. Untuk itu,
akan dide…nisikan suatu barisan dengan sifat khusus sebagai berikut.
De…nisi 3.17 Suatu barisan supernaik (superincreasing sequence) adalah suatu barisanr=fr1; r2; : : : ; r2g dengan sifat
ri+1 2ri,i= 1;2; : : : ; n 1
Lemma berikut ini akan digunakan untuk membuktikan suatu proposisi yang berkaitan dengan barisan supernaik.
Lemma 3.3 Misalkan r = fr1; r2; : : : ; r2g
adalah barisan supernaik, maka berlaku
sifat
rj > k 1
X
i=1
ri,j= 2;3; : : : ; n
Bukti:
Bukti akan dilakukan secara induktif.
Sebagai basis induksi, untuk k = 2,
berdasrkan de…nisi jelas benar bahwar2
2r1 > r1. Kemudian diasumsikan benar
untuk k = j, yaitu rj > Pji=11 dan
selanjutnya akan dibuktikan juga benar
untuk k = j + 1. Berdasarkan de…nisi
berlaku
rj+1 2rj
= rj+rj
> rj+ j 1
X
i=1
ri
=
j
X
i=1
ri
Proposisi 3.10 Misalkan (a; s) adalah
masalah jumlah subhimpunan dengan
a = fa1; a2; : : : ; ang adalah barisan
supernaik. Jika diasumsikan masalah
tersebut memiliki suatu solusi, yaitu x = fx1; x2; : : : ; xng. Maka nilai x dapat ditentukan dengan
xn = 1 , s an
xi = 1 , s n
X
j=i+1
xjaj ai
dimanai=n 1; n 2; : : : ;1.
Bukti:
Misalkan a = fa1; a2; : : : ; ang adalah
barisan supernaik. Dari de…nisi jumlah
subhimpunan diperoleh
s=
n
X
i=1
xiai
Lalu misalkans an, maka didapatkan
s an
,
n
X
i=1
xiai an
, xnan+ nX1
i=1
23
Jika nilaixn= 0, maka
n 1
X
i=1
xiai an
Hal ini kontradiksi dengan de…nisi barisan supernaik
an > nX1
i=1
ai
nX1
i=1
xiai
Sehingga haruslah xn = 1.Kemudian
misalkan dide…nisikan sebuah masalah subhimpunan yang baru, yaitu (bi; si) dimana
bi = fa1; a2; : : : ; aig
si = s n
X
j=i+1
xjaj
dengan i = n 1; n 2; : : : ;1. Dengan cara yang serupa didapatkan si ai jhj
xi= 1.
Berikut ini langkah-langkah ilustratif
dari proposisi 3.10. Tanpa mengurangi
keumuman, diambil nilain= 3
1. Untuk i = 3, dide…nisikan sebuah
masalah subhimpunan yang baru, yaitu
(b2; s2)
b2 = fa1; a2g
s2 = s x3a3
dari proposisi didapatkan jika s a3,
makax3= 1 sehingga
s2 = s x3a3
= s a3
Jikas < a3, makax3= 0 sehingga
s2 = s x3a3
= s
2. Untuk i = 2, dide…nisikan sebuah
masalah subhimpunan yang baru, yaitu
(b1; s1)
b1 = fa1g
s1 = s2 x2a2
dari proposisi didapatkan jika s2 a2,
makax2= 1 sehingga
s1 = s2 x2a2
= s2 a2
Jikas < a3, makax3= 0sehingga
s1 = s2 x2a2
= s2
3. Untuk i = 1, dari proposisi didapatkan jika s1 a1, maka x2 = 1 dan jika
s1< a1, makax2= 0.
Berdasarkan pola dari 3 langkah
tersebut, berikut merupakan algoritme
untuk menyelesaikan masalah jumlah
subhimpunan.
Algoritme 3.7
Input: Barisan supernaik yang terdiri
dari n bilangan intejer positif a =
fa1; a2; : : : ; ang dan intejer positifs.
Output: x = fx1; x2; : : : ; xng yang merupakan solusi dari masalah jumlah subhimpunan(a; s).
1. Untuki=n; n 1; : : : ;1, lakukan: (a) Jikas ai, maka lakukan:
i. xi:= 1 ii. s:=s ai (b) Selainnya,xi:= 0 2. return(x=fx1; x2; : : : ; xng)
Berikut merupakan deskripsi
sistemkriptoknapsack Merkle-Hellman.
Algoritme 3.8 (Pembangkitan Kunci)
Ringkasan: Entitas A membuat
kunci publik dan kunci privat dengan langka-langkah sebagai berikut,
1. Pilih barisan supernaik r =
fr1; r2; : : : ; rng
2. Pilih intejer positif p dan q dengan syaratq 2rn dangcd(p; q) = 1 3. Hitung barisan a = fa1; a2; : : : ; ang
dengan ai=primodq
4. Kunci publik: a; Kunci privat: (r; p; q)
Algoritme 3.9 (Enkripsi)
Ringkasan: Entitas B mengenkripsi pesan
bermakna m dengan kunci publik a
menjadi pesan tersandi c untuk dikirim ke entitas A.
B melakukan langkah-langkah berikut
1. Bentuk pesan bermakna m dalam
bentukn-bitm1m2: : : mn, dimanami2
f0;1g
2. Gunakan kunci publik a untuk
menghitung intejercdimana
c=
n
X
i=1
3. Kirim cke entitas A
Algoritme 3.10 (Dekripsi)
Ringkasan: Entitas A menerima pesan
tersandicdari B dan mendekripsicmenjadi
pesan bermakna m dengan kunci pribadi
(r; p; q)
A melakukan langkah-langkah berikut
1. Gunakan kunci p untuk menghitung
intejersdengans=p 1cmodq
2. Gunakan kuncirdan terapkan algoritme dengan inputrdansuntuk menghitung
b=fb1; b2; : : : ; bng
3. Pesan bermakna yang didapatkan
adalahb1b2: : : bn
3.6 Pembongkaran Sistemkripto
Knapsack Merkle-Hellman
Sekarang akan dibahas bagaimana
aplikasi algoritme LLL dalam pembongkaran
sistemkripto knapsack Merkle-Hellman.
Kembali pada de…nisi masalah jumlah subhimpunan
a1x1+a2x2+ +anxn=s.
Dengan mengasumsikan bahwa masalah jumlah subhimpunan di atas memiliki
minimal satu penyelesaian. Maka
penyelesaian yang didapat adalah sebuah vektor biner m = (m1; m2; : : : ; mn). Maka dengan demikian dapat dide…nisikan
sebuah matriks intejer
B= 0 B B B B B @
2 0 0 1
0 2 0 1
..
. ... . .. ... ...
0 0 2 1
a1 a2 an s
1 C C C C C A
Misalkan B = fb1;b2; : : : ;bn;sg adalah basis latis dengan bj adalah kolom ke-j dari matriks B untuk j = 1;2; : : : ; n dan
sadalah kolom ke-(n+ 1)matriksB, maka dalam latis tersebut jelas terdapat sebuah vektor
w= (m1b1+m1b1+ +mnbn s)2 L(B)
Kemudian perhatikan bahwa
w= 0 B B B B B @ w1 w2 .. . wn
wn+1
1 C C C C C A = 0 B B B B B @
2m1 1
2m2 1
.. .
2mn 1
0 1 C C C C C A
dan karena mj 2 Z2, maka wj 2 f 1;1g untuk j = 1;2; : : : ; n, sehingga didapatkan
kwk = pn. Hal ini mengakibatkan
bahwa w adalah vektor terpendek dalam
latis L(B) dan algoritme LLL dapat
diaplikasikan untuk mencari vektorw.
IV SIMPULAN DAN SARAN
4.1 Simpulan
Algoritme LLL merupakan algoritme
untuk mencari hampiran dari vektor
terpendek dalam suatu latis. Walaupun
demikian, algoritme LLL seringkali mampu
mencari solusi eksak dalam mencari
vektor terpendek. Hal ini membuat
algoritme LLL dapat digunakan sebagai
alat untuk membongkar sistemkripto
knapsack Merkle-Hellman. Sehingga
sistemkripto Merkle-Hellman sudah
mengalami keruntuhan.
4.2 Saran
Algoritme LLL terbukti dapat
digunakan dalam berbagai masalah.
Bagi yang berminat, dapat