PENJADWALAN PROYEK DENGAN
DURASI ACAK
TESIS
Oleh
JOHANNES KHO 107021022/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MAGISTER MATEMATIKA
UNIVERSITAS SUMATERA UTARA MEDAN
PENJADWALAN PROYEK DENGAN
DURASI ACAK
T E S I S
Diajukan Sebagai Salah Satu Syarat untuk Memperoleh Gelar Magister Sains dalam
Program Studi Magister Matematika pada
Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Oleh
JOHANNES KHO 107021022/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MAGISTER MATEMATIKA
Judul : PENJADWALAN PROYEK DENGAN DURASI ACAK
Nama : JOHANNES KHO
Nomor Induk Mahasiswa : 107021022 Program Studi : Matematika
Menyetujui, Komisi Pembimbing
Prof. Dr. Opim Salim S, M.Sc Prof. Dr. Herman Mawengkang
Ketua Anggota
Ketua Program Studi Dekan
Prof. Dr. Herman Mawengkang Dr. Sutarman, M.Sc
Telah diuji pada
Tanggal 11 Agustus 2012
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Opim Salim S, M.Sc Anggota : 1. Prof. Dr. Herman Mawengkang
ABSTRAK
Tesis ini membahas masalah pengaturan waktu selesai target dalam
aktivi-tas proyek dengan durasi acak dengan menggunakan program stokastik linier
integer dua tahap, yaitu pada tahap pertama ditentukan waktu target dan
kemudian tahap keduanya diikuti oleh pengembangan jadwal proyek secara
rinci dimana tujuannya untuk menyeimbangkan biaya penyelesaian proyek
se-bagai fungsi dari waktu aktivitas tujuan dan pinalti yang diharapkan dengan
deviasi dari nilai yang ditentukan. Bilamana deviasinya betul-betul
diper-timbangkan, hasilnya mungkin secara signifikan berbeda dibandingkan dengan
bilamana ketika aktivitas-aktivitas itu dijadwalkan sedini mungkin. Sebagai
contoh, waktu selesai target yang optimal untuk dibawah setiap suatu proyek
mungkin lebih baik daripada membuat rentang dari awal mulai jadwal dibawah
setiap skenario.
Kata kunci: Perencanaan Proyek, Penjadwalan Proyek, Pemrograman Stokastik, Manajemen Gangguan, Model Network,
ABSTRACT
This thesis studies the problem of setting target finish times for project
activi-ties with random durations. Using two-stage integer linear stochastic
program-ming, target times are determined in the first stage followed by the development
of a detailed project schedule in the second stage. The objective is to balance
the cost of project completion as a function of activity target times with the
expected penalty incurred by deviating from the specified values. When the
devi-ation is really considered, the result may significantly different from a situdevi-ation
when those activities was scheduled early. For instance, deciding the optimal
finish time under a whole project maybe better than deciding some time span
from the beginning under every scenario.
KATA PENGANTAR
Puji syukur kepada Tuhan yang Maha Pengasih dan Penyayang atas anugerah yang telah diberikanNya sehingga penulis dapat menyelesaikan tesis
ini dengan judul : PENJADWALAN PROYEK DENGAN DURASI ACAK
(PROJECT SCHEDULING WITH RANDOM DURATION). Penulis
menyam-paikan terima kasih yang sebesar-besarnya kepada :
Bapak Dr. Sutarman, M.Sc, Dekan Fakultas Matematika dan Ilmu Penge-tahuan Alam Universitas Sumatra Utara, yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Magister Matematika di FMIPA
Universitas Sumatera Utara.
Bapak Prof. Dr. Herman Mawengkang, Ketua Program Studi Magister Matematika FMIPA Universitas Sumatera Utara, yang juga sebagai Pembimb-ing II yang telah memberikan motivasi dan pengarahan sehPembimb-ingga selesainya
tesis ini.
Bapak Dr. Saib Suwilo, M.Sc, Sekretaris Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara, yang juga sebagai Anggota
Pengu-ji yang banyak memberi masukan dan saran dalam penyempurnaan tesis ini.
Bapak Prof. Dr. Opim Salim S, M.Sc, Ketua Komisi Pembimbing (Pem-bimbing I) yang telah mengarahkan dalam penulisan tesis ini.
Bapak Prof. Dr. Tulus, M.Si, sebagai Anggota Penguji yang telah mem-beri masukan dan saran dalam penyempurnaan tesis ini.
Bapak / Ibu Dosen Program Studi Magister Matematika FMIPA Universi-tas Sumatera Utara yang telah memberikan ilmunya selama masa perkuliahan.
Ibu Misiani, S.Si, Staf Administrasi Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang banyak membantu proses admini-strasi.
Ucapan terima kasih juga penulis sampaikan kepada semua pihak yang telah banyak memberi perhatian dan bantuan kepada penulis dalam
menyele-saikan tesis ini. Semoga Tuhan membalas segala kebaikan dan bantuan yang
telah diberikan kepada penulis.
Medan, Agustus 2012 Penulis
RIWAYAT HIDUP
Johannes Kho dilahirkan di Padang, Provinsi Sumatera Barat pada
tang-gal 21 Maret 1949, merupakan anak pertama dari enam bersaudara dari
Al-marhum ayahanda Gerard Kho dan AlAl-marhumah ibunda Nora. Penulis
menye-lesaikan pendidikan di SR ST. Joseph Medan pada tahun 1961, SMP Katolik
Budi Murni I Medan pada tahun 1964 dan SMA Katolik Medan pada tahun
1967.
Pada tahun 1968 penulis melanjutkan pendidikan Sarjana Strata I pada
jurusan matematika Fakultas Ilmu Pasti dan Ilmu Pengetahuan Alam
Univer-sitas Sumatera Utara dan memperoleh gelar sarjana matematika pada tahun
1978. Selama menjalani pendidikan Sarjana Strata I, penulis juga pernah
menjadi asisten dosen di FMIPA USU, Fakultas Teknik USU, Fakultas Teknik
IKIP Negeri Medan dan pernah menjadi guru di SMA WR Supratman Medan
serta SMA Katolik Medan.
Setelah menyelesaikan pendidikan Strata I jurusan Matematika di atas,
penulis pernah mengajar di SMP dan SMA Santa Maria Pekanbaru, Fakultas
Teknik dan Fakultas Pertaniaan Universitas Lancang Kuning dan sekarang
menjadi staf pengajar (PNS) di FMIPA Universitas Riau Jurusan Matematika
dari tahun 1979 sampai dengan sekarang.
Penulis telah dikaruniai 3 (tiga) orang putra yang sekarang 2 (dua) orang
sedang sekolah di Fakultas Kedokteran Universitas Indonesia dan 1 (satu)
orang lagi studi di Fakultas Kedokteran Universitas Padjadjaran, Bandung.
Pada tahun 2011, penulis melanjutkan studi pada Program Studi
DAFTAR ISI
HALAMAN
ABSTRAK . . . i
ABSTRACT. . . . ii
KATA PENGANTAR . . . iii
RIWAYAT HIDUP . . . iv
DAFTAR ISI . . . v
DAFTAR GAMBAR . . . vii
DAFTAR TABEL . . . viii
BAB 1 PENDAHULUAN . . . 1
1.1 Latar Belakang . . . 1
1.2 Rumusan Masalah . . . 3
1.3 Tujuan Penelitian . . . 3
1.4 Manfaat Penelitian . . . 3
1.5 Metode Penelitian . . . 3
BAB 2 KAJIAN LITERATUR TENTANG PENJADWALAN PROYEK . . . 5
BAB 3 PENJADWALAN PROYEK DAN PROGRAM STOKASTIK 10 3.1 Penjadwalan Proyek . . . 10
3.1.1 Diagram Jaringan dan Lintasan Kritis . . . 11
3.1.2 Waktu Mulai dan Selesai yang Tercepat dan yang Terlama . . . 13
3.2 Program Stokastik . . . 15
3.2.1 Pengertian Program Stokastik . . . 15
3.2.3 Pembentukan Skenario . . . 21
BAB 4 SOLUSI MODEL PEMROGRAMAN INTEGER . . 25
4.1 Model Pemrograman Integer . . . 25
4.2 Jaringan Aliran Formulasi Untuk Masalah Tahap Kedua 34 BAB 5 KESIMPULAN DAN RISET LANJUTAN . . . 38
5.1 Kesimpulan . . . 38
5.2 Riset Lanjutan . . . 38
DAFTAR GAMBAR
Gambar Judul Halaman
3.1 Diagram Jaringan Aktivitas . . . 12
3.2 Jaringan Proyek Untuk Proyek Sistem Informasi InterTrust . 12
3.3 Waktu Mulai dan Waktu Selesai dan Lintasan Kritis Untuk
InterTrust . . . 15
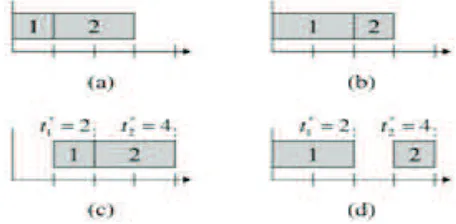
4.1 Jadwal: (a) jadwal awal untuk skenario 1; (b) jadwal awal
un-tuk skenario 2; (c) jadwal dengan waktu target unun-tuk skenario
1; (d) jadwal dengan waktu target untuk skenario 2 . . . 33
DAFTAR TABEL
Tabel Judul Halaman
3.1 Deskripsi dari Proyek Inter Trust Sistem Informasi . . . 11
ABSTRAK
Tesis ini membahas masalah pengaturan waktu selesai target dalam
aktivi-tas proyek dengan durasi acak dengan menggunakan program stokastik linier
integer dua tahap, yaitu pada tahap pertama ditentukan waktu target dan
kemudian tahap keduanya diikuti oleh pengembangan jadwal proyek secara
rinci dimana tujuannya untuk menyeimbangkan biaya penyelesaian proyek
se-bagai fungsi dari waktu aktivitas tujuan dan pinalti yang diharapkan dengan
deviasi dari nilai yang ditentukan. Bilamana deviasinya betul-betul
diper-timbangkan, hasilnya mungkin secara signifikan berbeda dibandingkan dengan
bilamana ketika aktivitas-aktivitas itu dijadwalkan sedini mungkin. Sebagai
contoh, waktu selesai target yang optimal untuk dibawah setiap suatu proyek
mungkin lebih baik daripada membuat rentang dari awal mulai jadwal dibawah
setiap skenario.
Kata kunci: Perencanaan Proyek, Penjadwalan Proyek, Pemrograman Stokastik, Manajemen Gangguan, Model Network,
ABSTRACT
This thesis studies the problem of setting target finish times for project
activi-ties with random durations. Using two-stage integer linear stochastic
program-ming, target times are determined in the first stage followed by the development
of a detailed project schedule in the second stage. The objective is to balance
the cost of project completion as a function of activity target times with the
expected penalty incurred by deviating from the specified values. When the
devi-ation is really considered, the result may significantly different from a situdevi-ation
when those activities was scheduled early. For instance, deciding the optimal
finish time under a whole project maybe better than deciding some time span
from the beginning under every scenario.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Pengelolaan proyek besar memerlukan alat analitik untuk menentukan
kegiatan penjadwalan dan pengolahan sumber daya sehingga diperolehnya
ke-seimbangan total biaya dan waktu penyelesaian proyek.
Apabila sumber daya, durasi aktivitas, biaya dan parameter lain yang
diketahui dengan kepastian, metode lintasan kritis (CPM/Critical Path Method)
dapat digunakan untuk mendapatkan jadwal proyek. Dalam kenyataannya,
bagaimanapun sering terjadi aktivitas proyek mengandung ketidakpastian yang
timbul dari faktor-faktor seperti teknologi, keragaman kinerja manusia dan
gangguan alam. Keacakan ini secara umum diakui menjadi bagian dari
man-ajemen proyek (Pitch et al, 2002).
Beberapa ketidakpastian biasanya dapat diselesaikan sebelum setiap
gang-guan besar terjadi, tetapi jarang dapat diprediksi bagaimana kejadian acak
akan terjadi. Namun demikian, banyak keputusan harus dibuat sebelum semua
ketidakpastian diselesaikan. Misalnya, ketika penawaran pada sebuah proyek,
kontraktor harus menyerahkan jadwal dan anggaran awal sebelum
informasi-informasi penting diperoleh.
Karena jadwal yang diusulkan mempengaruhi kemungkinan
memenang-kan tawaran proyek, mungkin ada kecenderungan untuk melampaui jadwal itu.
Jika kontrak telah dibuat, maka kinerja akan dinilai dengan seberapa
dekat jadwal diikuti, dengan penilaian pinalti akibat penundaan aktivitas dan
kegagalan untuk memenuhi syarat utama. Karena dalam perencanaan yang
mengandung ketidakpastian, keputusan tidak dapat diambil secara
meyakin-kan yang biasa dilakumeyakin-kan dalam praktek adalah hanya membuat keputusan
peruba-han. Setiap keputusan yang tersisa dibuat sebagai informasi yang lebih
defini-tif. Ini merupakan hal yang esensi dari pemrograman stokastik, yang telah
dit-erapkan dibanyak bidang perencanaan dibawah ketidakpastian (Birge, 1997).
Tesis ini membahas masalah bagaimana menetapkan waktu selesai target
(tanggal jatuh tempo) dari suatu kegiatan proyek dengan durasi yang tidak
pasti, dimana ketidakpastian diwakili oleh skenario-skenario diskrit untuk
di-analisis, dikembangkan sebuah model keputusan dua tahap, yang meliputi
pilihan sumber daya yang berkenaan dengan kendala anggaran. Jadi kalau
penelitian ini diandaikan durasi aktivitas sebagai peubah acak dan disebut
sebagai durasi acak.
Dalam kegiatan tahap pertama, target tetap didasarkan pada informasi
probabilistik yang dikenal, setelah semua ketidakpastian diselesaikan, jadwal
rinci diturunkan sebagai fungsi dari waktu target yang diusulkan. Solusi model
yang dirancang untuk menyeimbangkan biaya yang terkait dengan waktu
tar-get dan biaya penyimpangan yang diharapkan dari rencana semula. Tujuan
dari tahap kedua adalah untuk mendapatkan jadwal dengan biaya minimum
yang terkait pinalti akibat penyimpangan dari waktu target.
Karena dinamika yang mendasari, keputusan tahap pertama dapat
men-genakan tambahan kendala pada masalah penjadwalan tahap kedua. Sebagai
contoh, dalam suatu kegiatan mungkin diperlukan selesai dalam interval
wak-tu penyelesaian yang berpusat pada wakwak-tu target. Bahkan masalah
penjad-walan tahap kedua merupakan kasus khusus dari manajemen gangguan (Yu
dan Qi, 2004) yang mempelajari pengambilan keputusan yang optimal dalam
operasi yang tidak teratur. Dalam konteks ini, waktu target diperoleh pada
tahap pertama yang dapat dilihat sebagai rencana awal. Tesis ini memperluas
ide-ide manajemen gangguan dengan mempertimbangkan tidak hanya strategi
pemulihan terbaik untuk setiap skenario yang mungkin, tetapi juga
mengem-bangkan rencana awal yang mengoptimalkan kinerja yang diharapkan dibawah
Dengan adanya pengandaian bahwa waktu durasi aktivitas sebagai peubah
acak, teori peluang diaplikasikan pada persoalan penjadwalan proyek
(Free-man, 1960). Charnes dan Cooper (1962, 1963) mengkaji persoalan ini melalui
program kendala peluang. Ke dan Liu (2005) membentuk tiga model stokastik
untuk menyelesaikan suatu tipe persoalan penjadwalan proyek dengan waktu
durasi stokastik dengan adanya pembatasan waktu.
Teori ketidakpastian diajukan oleh Liu (2007) dan dipertajam oleh Liu
(2011) yang merupakan cabang dari aksiomatik matematika untuk
memodel-kan ketidakpastian manusia, Liu (2009) mengandaimemodel-kan bahwa waktu durasi
aktivitas merupakan variabel tak pasti dan menyajikan model ketidakpastian.
1.2 Rumusan Masalah
Dalam penelitian terdahulu, dalam model yang diajukan belum
mem-perhitungkan waktu target penyelesaian proyek. Pada penelitian ini diajukan
model program stokastik dua tahap untuk persoalan penjadwalan proyek
den-gan adanya durasi acak, dimana ketidakpastian disajikan oleh skenario diskrit.
Dalam model ikut diperhitungkan target waktu.
1.3 Tujuan Penelitian
Adapun yang menjadi tujuan dari penelitian ini adalah untuk
menye-lesaikan model program stokastik dua tahap persoalan penjadwalan proyek
dengan adanya durasi acak.
1.4 Manfaat Penelitian
Penelitian ini bermanfaat untuk memperluas aplikasi pemrograman stokastik.
1.5 Metode Penelitian
Metode penelitian ini bersifat studi kepustakaan (literatur) dengan menelaah
dan kajian terhadap beberapa jurnal/buku/disertasi pada kepustakaan yang
terlampir. Untuk menyelesaikan pemrograman linier stokastik dua tahap
a. Menyelesaikan masalah utama dan satu masalah tahap kedua untuk
masing-masing skenario.
b. Akan ditunjukkan juga bahwa dalam kasus ini masalah penjadwalan tahap
kedua dapat diselesaikan sebagai masalah jaringan arus biaya minimal.
c. Untuk kasus dengan kendala anggaran, akan ditunjukkan penyelesaian
BAB 2
KAJIAN LITERATUR TENTANG PENJADWALAN PROYEK
Ketidakpastian menambahkan tingkat kesulitan ekstra untuk masalah
penjad-walan apakah itu terdapat dalam struktur masalah atau dalam parameter
(Davenport dan Beck, 2000). Ketika jadwal proyek yang dihasilkan, tidak
hanya perawatan yang harus diambil tetapi juga rencana yang mungkin harus
dibuat untuk mengantisipasi adanya efek samping yang mungkin timbul
sela-ma pelaksanaan (eksekusi). Dalam berbagai situasi yang dapat dimodelkan
sebagai masalah optimisasi stokastik, kinerja rata-rata dan kekuatan (
robust-ness) adalah dua langkah utama yang digunakan untuk mengevaluasi hasil
(Kouvelis dan Yu, 1997).
Dalam penjadwalan proyek deterministik, tujuannya untuk
mengembang-kan rencana rinci dalam menentumengembang-kan waktu aktivitas dimulai dan berakhir
den-gan kendala sumber daya. Banyak perhatian telah diberikan kepada masalah
penjadwalan proyek dengan kendala sumber daya (RCPSP/Resource-Constrained
Project Scheduling Problem) dengan tujuan meminimalkan rentang (makespan),
tetapi kemungkinan lain termasuk meminimalkan biaya, memaksimalkan
be-berapa ukuran kualitas, atau kombinasi keduanya.
Meskipun ada kemajuan baru pada penyelesaian kasus yang lebih besar
dari RCPSP itu, beberapa aplikasi pada dunia real telah dikutip dalam
liter-atur. Alasan utama atas kekurangan ini adalah kurangnya alasan pembenaran
untuk asumsi deterministik diperlukan algoritma terbaik, apakah eksak atau
deterministik. Hal ini berarti bahwa solusi yang diberikan mungkin sangat
buruk dan bahkan dapat tidak layak. Ketidakpastian ini begitu umum
se-hingga beberapa proyek selesai tanpa menutupi biaya atau jadwal.
Keterlam-batan dalam satu aktivitas dapat mempengaruhi kinerja dari semua aktivitas
berikutnya, menyebabkan gangguan dalam pasokan materi, tugas pekerja, dan
Jenis-jenis ketidakpastian yang timbul dalam manajemen proyek dapat
dibagi menjadi tiga kategori (Miller dan Lessard, 2001) yaitu terkait:
1. pasar, seperti permintaan, persaingan dan rantai pasokan; 2. penyelesaian, seperti teknis, konstruksi dan operasional;
3. kelembagaan, seperti peraturan, budaya dan warganegara istimewa.
Pada tingkat proyek, setelah keputusan strategis telah dibuat,
tantan-gannya adalah untuk mencapai tujuan teknis dalam kendala waktu dan biaya
yang dibebankan oleh manajemen.
Untuk sebagian besar, ketidakpastian datang dalam sifat peristiwa stokastik.
Sebagai contoh, mungkin jarang untuk menentukan durasi tidak pasti dari
su-atu kegiatan jauh sebelum pelaksanaannya. Pendapat ahli, data historis, dan
metode teknik industri, umumnya digunakan untuk memperkirakan durasi.
Dari sudut pandang praktis, dimungkinkan untuk mengembangkan distribusi
probabilitas untuk beberapa peristiwa yang akan datang. Seiring dengan
ber-jalannya waktu dan pengalaman lebih yang diperoleh, jenis ketidakpastian
dapat diturunkan atau dihilangkan.
Cara khusus mengelola proyek ketidakpastian alamat adalah dengan
anal-isis parametrik yang dilengkapi dengan penilaian risiko (Chapman, 1977).
Ide umumnya adalah untuk mengidentifikasi dan mengevaluasi ketidakpastian
yang berhubungan dengan aspek-aspek berbeda dari proyek itu dan untuk
mengambil langkah-langkah pencegahan dalam dampaknya. Data historis
yang digunakan untuk mendapatkan statistik dan wawasan untuk menilai
akibat dari hasil yang tidak direncanakan. Sehubungan dengan pemodelan,
jaringan stokastik PERT (Adlakha dan Kulkarni, 1989) telah digunakan untuk
penyelesaian terbatas dan ukuran kinerja lainnya. Untuk masalah penjadwalan
mesin tunggal (Elmaghraby et al, 2000) disajikan skema pemrograman dinamik
untuk aktivitas yang layak dengan tanggal tertentu dan durasi stokastik.
Tu-juannya adalah untuk meminimalkan perbedaan antara waktu tertimbang dan
Sebuah asumsi umum dalam model jenis PERT adalah bahwa jadwal
awal harus yang terbaik untuk setiap realisasi ketidakpastian. Namun, ini
tidak selalu benar bilamana ukurunnya lain, seperti nilai sekarang bersih (Buss
dan Rosenblatt, 1997) dan deviasi digunakan (Zhu et al, 2005).
Herroelen dan Leus (2004b) memberikan sebuah review prosedur yang
berhubungan dengan ketidakpastian dalam penjadwalan proyek. Ada dua jenis
pendekatan utama.
1. Penjadwalan proaktif, yaitu mencoba untuk mengembangkan jadwal
aw-al yang memiliki penampilan kuat di bawah skenario pasti yang berbeda
(Herroelen dan Leus, 2004a),
2. Penjadwalan reaktif, yaitu mencoba untuk menanggapi seefektif mungkin
terhadap situasi yang realis (Yang, 1996). Jelas bahwa meskipun dua
pendekatan harus diintegrasikan, sedikit yang telah dilakukan dalam hal
ini.
Tipe kedua dari ketidakpastian dalam manajemen proyek adalah terkait
dengan peristiwa langka yang cenderung memiliki akibat besar. Contohnya
termasuk bencana alam, kebangkrutan pemasok, atau tiba-tiba kehilangan
personil kunci. Kejadian ini sulit diprediksi dan sulit untuk dihadapi. Yang
dirujuk kepadanya sebagai gangguan. Manajemen gangguan adalah sebuah
bidang yang muncul di mana operasi teknik penelitian yang diterapkan untuk
membantu mengatasi ketidakpastian sebagai pengembangan (Clausen et al,
2001; Yu dan Qi, 2004). Salah satu bidang yang paling aktif dimana
man-ajemen gangguan telah diterapkan yaitu yang berhubungan dengan operasi
penerbangan. Kinerja maskapai penerbangan sangat tergantung pada
sebera-pa baik dasebera-pat mengikuti jadwal yang dipublikasikan (Yu et al, 2003).
Pertimbangan biaya penyimpangan yang paling umum dalam masalah
penjadwalan mesin dimana sebuah pekerjaan adalah dipinalti karena
terlam-bat atau baik karena kecepatan (Baker dan Scudder, 1990). Sourd dan
penjadwalan mesin tunggal dengan pinalti kecepatan dan keterlambatan
di-mana batas bawah berasal dari jadwal terdahulu. Vanhoucke et al. (2001)
mempelajari masalah-masalah penjadwalan proyek dengan tanggal aktivitas
yang diberikan karena meminimalkan waktu total tertimbang dan
keterlam-batan. Chretienne dan Sourd (2003) secara umum masalah pembengkakan
biaya penjadwalan proyek tanpa kendala sumber daya.
Pemrograman stokastik telah digunakan secara luas untuk model
berba-gai jenis masalah yang tunduk pada ketidakpastian dan memerlukan kontribusi
dan keputusan akhir. Untuk mereview metode komputasi dan aplikasi, lihat
Birge (1997). Sebagaimana akan dilihat pada bagian berikutnya, dalam
tin-jauan model ada beberapa kesamaan dengan model keputusan stokastik yang
telah dikembangkan untuk manajemen kapasitas dalam rantai pasokan (Van
Mieghem, 2003), dimana ketidakpastian mungkin timbul di salah satu
dis-tribusi, produksi atau tahapan eceran (retail). Sejauh ini, masih sedikit sekali
riset yang telah dilakukan dalam hal menyelesaikan masalah penjadwalan
den-gan teknik pemrograman stokastik.
Hal ini diketahui bahwa masalah penjadwalan proyek adalah
menentu-kan jadwal mangalokasimenentu-kan sumber daya sehingga dapat menyeimbangmenentu-kan
to-tal biaya dan waktu penyelesaian karena dengan ketidakpastian waktu durasi
aktivitas proyek, masalah penjadwalan proyek selalu disertai dengan
ketidak-pastian. Dengan asumsi waktu durasi aktivitas proyek adalah variabel acak,
teori probabilitas adalah pendahuluan pertama untuk masalah penjadwalan
proyek oleh Freeman (1960a, 1960b), Kelley (1961) pertama
memperkenal-kan fungsi hubungan antara biaya proyek dan waktu durasi aktivitas proyek
dan menetapkan dasar matematika untuk masalah penjadwalan proyek.
Kel-ley (1963) awalnya merumuskan pendekatan untuk tipe masalah penjadwalan
proyek dengan tujuan untuk meminimalkan total biaya. Sejak itu, peneliti
lain seperti Kolisch dan Padman (2001), Maniezzo dan Mingozzi (1999) dan
lain-lain, memiliki partisipasi dalam mempelajari masalah penjadwalan proyek
1963) mempelajari masalah penjadwalan proyek melalui pemrograman
pergan-tian kendala di awal tahun 1960-an. Ke dan Liu (2005) membangun tiga
mod-el stokastik untuk menymod-elesaikan masalah penjadwalan proyek dengan durasi
aktivitas waktu stokastik dengan meminimalkan biaya total dengan waktu
ter-batas.
Namun, untuk beberapa proyek, aktivitas mungkin jarang atau tidak
pernah dilakukan sebelumnya dan karena kekurangan data statistik. Setelah
itu, dengan beberapa sarjana melalui pengetahuan ahli, waktu durasi
aktivi-tas proyek dalam masalah penjadwalan proyek, diasumsikan menjadi variabel
fuzzy. Prade (1979) pertama diterapkannya teori himpunan fuzzy kedalam
masalah penjadwalan proyek. Selanjutnya, Chanas dan Kamburowski (1981),
Dubios dan Prade (1979), Hapke dan Slowinski (1993), Kaufmann dan Gupta
(1988), dan Ke dan Liu (2010) membahas berbagai jenis masalah penjadwalan
proyek dengan durasi aktivitas waktu fuzzy. Selanjutnya, keacakan dan
keti-dakjelasan dapat berdampingan dalam masalah penjadwalan proyek. Ke dan
Liu (2007) mengemukakan model penjadwalan proyek dengan gabungan
keti-daktentuan dari keacakan dan ketidakjelasan menggunakan alat dari keacakan
BAB 3
PENJADWALAN PROYEK DAN PROGRAM STOKASTIK
3.1 Penjadwalan Proyek
Pengelolaan proyek besar membutuhkan alat-alat analisis untuk
aktivi-tas penjadwalan dan mengalokasikan sumber daya. Hal ini menggambarkan
satu himpunan alat yang telah terbukti secara konsisten berharga bagi
man-ajer proyek. Alat-alat yang secara kolektif dikenal sebagai Project
Evalua-tion and Review Technique (PERT) dan Critical Path Method (CPM). PERT
dikembangkan oleh angkatan laut AS sebagai konsultan Proyek Rudal Polaris,
sementaraCritical Path Method diciptakan olehDupont dan Remington Rand
Corporation untuk pengelolaan pabrik kimia besar. Aplikasi perangkat
terse-but termasuk dalam konstruksi untuk pengembangan perangkat lunak. Hal
ini menjelaskan konsep dasar dan perhitungan untuk penjadwalan proyek
den-gan PERT/CPM ini termasuk pembangunan diagram jarinden-gan, perhitunden-gan
penjadwalan proyek layak (feasible), menentukan efek ketidakpastian jadwal
proyek, dan menyesuaikan jadwal agar sesuai dengan waktu dan keterbatasan
sumber daya. Alat-alat yang penting untuk menjaganya agar tetap di jalur
setelah dimulai.
Sepanjang hal ini akan dirujuk pada suatu proyek tertentu. Instalasi
dari sistem informasi pada sebuah bank komersial yang besar seperti BANK
INTERTRUST. Waktu ditempat, sistem akan mengumpulkan entri akuntansi
yang dihasilkan oleh produk perbankan seperti rekening dan pinjaman
pe-rusahaan. Sekarang, bank sistemnya dioperasikan oleh kontraktor, dan sekali
sistem baru dibangun dan akan berjalan menghemat biaya kontrak sebesar
$3.000 per minggu.
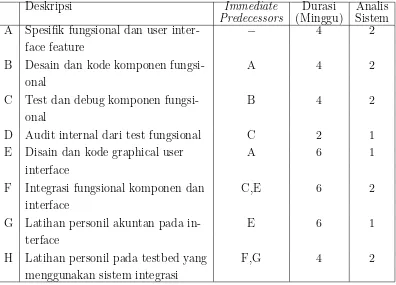
Tabel 3.1 menggambarkan aktivitas proyek dan durasi yang diharapkan.
Sistem akan dikembangkan dan diinstalasi oleh programmer komputer, analis
yang cukup dari akuntan, tapi para analis sistem memediasi antara teknisi
dan akuntan dalam memenuhi keterbatasan.
Saat ini, hanya tiga analis sistem yang tersedia untuk perusahaan, dan
sejumlah analis yang dibutuhkan untuk setiap aktivitas yang tercantum dalam
tabel. Tabel tersebut juga menentukan immediate predecessors, daftar tugas
terkecil yang mungkin yang harus diselesaikan sebelum memulai setiap
aktiv-itas.
Tabel 3.1 : Deskripsi dari Proyek Inter Trust Sistem Informasi
Deskripsi Immediate Durasi Analis
Predecessors (Minggu) Sistem
A Spesifik fungsional dan user inter- − 4 2
face feature
B Desain dan kode komponen fungsi- A 4 2
onal
C Test dan debug komponen fungsi- B 4 2
onal
D Audit internal dari test fungsional C 2 1
E Disain dan kode graphical user A 6 1
interface
F Integrasi fungsional komponen dan C,E 6 2
interface
G Latihan personil akuntan pada in- E 6 1
terface
H Latihan personil pada testbed yang F,G 4 2
menggunakan sistem integrasi
Diasumsikan bahwa proyek durasi yang tercantum dalam tabel 3.1
di-jamin, sehingga mereka tidak dikenakan keacakan. Dalam bab berikut akan
dipertimbangkan pengaruh acak waktu aktivitas pada proyek itu.
3.1.1 Diagram Jaringan dan Lintasan Kritis
Informasi dalam tabel diatas juga diwakili oleh diagram jaringan dibawah
ini seperti persegi panjang atau node yang menandakan aktivitas. Hubungan
antara aktivitas diwakili oleh panah antara node.
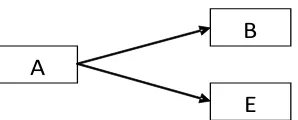
Untuk proyek InterTrust, aktivitas B dan E mungkin hanya setelah
A
B
E
Gambar 3.1 : Diagram Jaringan Aktivitas
Semua anak panah ke sebuah simpul dimulai pada immediate
predeces-sors node, menunjukkan bahwa aktivitas tidak dapat dimulai sampai seluruh
aktivitas sebelum itu node dalam jaringan selesai.
Gambar 3.2 menampilkan proyek jaringan lengkap InterTrust. Aktivitas
A harus diselesaikan sebelum aktivitas B dan E dimulai. Aktivitas F tidak
dapat dilaksanakan sebelum kedua aktivitas C dan E selesai.
C.4
A.4
B.4 D.2
E.6 F.6
G.6
H.4 END.0
Kunci
Aktivitas, Durasi
Gambar 3.2 : Jaringan Proyek Untuk Proyek Sistem Informasi InterTrust
Karena proyek itu sendiri tidak dapat diselesaikan sampai semua
aktivi-tas selesai END, dibuat node dummy dengan pendahulu sebelumnya D dan H.
Satu kemungkinan juga buat simpul dummy BEGIN jika beberapa aktivitas
bisa memulai proyek secara paralel.
Seorang manajer proyek sering memulai dengan pertanyaan sederhana.
Berapa lama proyek berakhir?. Setelah jaringan proyek digambarkan,
jawa-bannya juga sederhana: durasi proyek adalah sampai akhir jaringan. Karena
semua aktivitas disepanjang jalan ini harus diselesaikan, durasi proyek harus
berada setidaknya pada panjang jalan terpanjang. Karena semua jalan-jalan
Untuk InterTrust, jalan terpanjang dari A ke AKHIR (END) dapat
dite-mukan dengan mudah, dengan mencoba semua path (berapa banyak yang
ada?) dan memilih jalan yang terpanjang. Jalan ini adalah ABCFH-AKHIR
dan durasi adalah 4+ 4+ 4+ 6+ 4 = 22 minggu. Untuk proyek ini relatif
seder-hana, hanya ada beberapa jalan untuk membandingkan. Untuk yang lebih
besar, proyek dengan ribuan aktivitas, menemukan jalan terpanjang adalah
sulit kecuali metode terstruktur yang digunakan. Metode yang dijelaskan
disi-ni adalah salah satu metode terstruktur seperti itu, dan sepanjang jalan itu
berisi banyak informasi yang berguna selain panjang proyek.
3.1.2 Waktu Mulai dan Selesai yang Tercepat dan yang Terlama Untuk setiap aktivitas dihitung sebagai berikut:
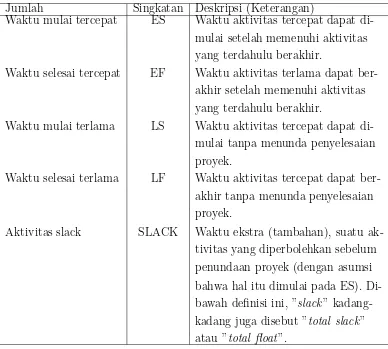
Tabel 3.2 : Singkatan dan Deskripsi Waktu Aktivitas
Jumlah Singkatan Deskripsi (Keterangan)
Waktu mulai tercepat ES Waktu aktivitas tercepat dapat di-mulai setelah memenuhi aktivitas yang terdahulu berakhir.
Waktu selesai tercepat EF Waktu aktivitas terlama dapat ber-akhir setelah memenuhi aktivitas yang terdahulu berakhir.
Waktu mulai terlama LS Waktu aktivitas tercepat dapat di-mulai tanpa menunda penyelesaian proyek.
Waktu selesai terlama LF Waktu aktivitas tercepat dapat ber-akhir tanpa menunda penyelesaian proyek.
Aktivitas slack SLACK Waktu ekstra (tambahan), suatu ak-tivitas yang diperbolehkan sebelum penundaan proyek (dengan asumsi bahwa hal itu dimulai pada ES). Di-bawah definisi ini, ”slack” kadang-kadang juga disebut ”total slack” atau ”total float”.
Dalam sebuah jaringan, waktu mulai dan selesai tercepat ditemukan
den-gan berulang kali menghitung dari awal proyek (node A) sampai akhir (END).
Waktu selesai terlama = ES = max[EF dariimmediate predecessors]
Waktu mulai tercepat = EF = ES + durasi aktivitas
Untuk InterTrust, dimulai dengan aktivitas A di ’nol’ minggu. Waktu
selesai tercepat untuk A adalah empat minggu kemudian, dan ini adalah waktu
mulai tercepat untuk aktivitas B dan E. Waktu selesai tercepat untuk B adalah
4 + 4 = 8 minggu, dan waktu mulai tercepat untuk penggantinya C adalah 8
minggu.
Gambar 3.2 menampilkan hasil dari perhitungan ini. Pertama-tama
harus hati-hati dengan aktivitas F karena memiliki dua pendahulunya. Waktu
mulai tercepat untuk F adalah waktu selesai tercepat terakhir dari
pendahu-lunya.
ES untuk aktivitas F = max(EF untuk aktivitas C, EF untuk aktivitas E) = max(8+4, 4+6)
= max (12, 10) = 12 minggu
Perhitungan serupa selesai untuk aktivitas yang tersisa sampai dicapai
AKHIR (END). Ditemukan bahwa proyek ini mengambil 22 minggu.
Wak-tu mulai dan selesai terlama unWak-tuk setiap aktivitas didapat dengan bekerja
mundur, dari akhir proyek ke awal.
Waktu selesai terlama = LF = min[LS dari immediate successors]
Waktu mulai terlama = LS = LF − durasi aktivitas
Untuk END, waktu mulai dan selesai terlama ditentukan sama dengan
waktu mulai dan selesai tercepat karena penundaan untuk END akan menunda
penyelesaian proyek.
Waktu selesai terlama aktivitas H adalah waktu mulai terlama untuk
END adalah 22 minggu, dan waktu mulai terlama untuk aktivitas H adalah
22−4 = 18 minggu. Waktu selesai terlama untuk D adalah juga 22 minggu,
sedangkan LF untuk F adalah LS untuk H adalah 18 minggu. Aktivitas C
memiliki dua immediate successors, sehingga:
LF untuk aktivitas C = min (LS untuk aktivitas D, LS untuk aktivitas F) = min (20, 12)
Perhitungan ini diulang sampai waktu terlama untuk aktivitas A
dite-mukan. Selanjutnya, aktivitas slack untuk tiap node dapat dengan mudah
dihitung yaitu: Aktivitas slack = SLACK = LS − ES = LF − EF. Lihat
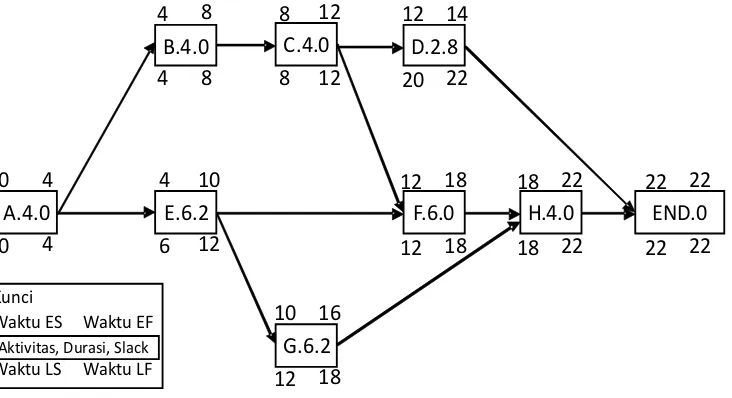
gambar 3.3 beserta hasilnya.
Gambar 3.3 : Waktu Mulai dan Waktu Selesai dan Lintasan Kritis Untuk InterTrust
3.2 Program Stokastik
3.2.1 Pengertian Program Stokastik
Banyak persoalan keputusan yang dapat dimodelkan dengan
menggu-nakan program matematika yang bertujuan menentukan nilai maksimum atau
minimum. Keputusan yang dihasilkan akan bergantung kepada kendala yang
dibatasi oleh sumber dana, persyaratan minimum dan lain-lain. Keputusan
yang dinyatakan oleh variabel dapat berupa bilangan cacah atau non negatif.
Tujuan dan kendala adalah fungsi dari variabel, dan persoalan data.
Seba-gai contoh dari persoalan data termasuk biaya persatuan, rata-rata produksi,
penjualan atau kapasitas.
Andaikan keputusan dinyatakan dengan variabel (x1, x2, . . . , xn).
matematikanya adalah :
Min Z =f(x)
Kendala gi(x)≥bi (3.1)
x1, x2, x3,· · · , xn≥0
x1, x2, x3,· · · , xn∈X
dimana X adalah himpunan bilangan real non negatif.
Program stokastik adalah sebuah nama yang menyatakan program
mate-matika yang dapat berupa linear, cacah, cacah campuran, non linear dengan
menampilkan elemen stokastik pada data. Sehingga program stokastik dapat
dinyata bahwa :
a. Pada program matematika deterministik, data adalah bilangan-bilangan
yang diketahui (tertentu).
b. Pada program stokastik, data merupakan bilangan tidak pasti yang
dis-ajikan sebagai distribusi peluang.
Program stokastik merupakan program matematika yang mengandung
ketidakpastian. Program stokastik adalah merupakan program matematika,
dimana beberapa data yang termuat pada tujuan atau kendala mengandung
ketidakpastian, ketidakpastian biasanya dicirikan oleh distribusi peluang pada
parameter. Walaupun ketidakpastian didefinisikan dengan tepat tetapi pada
prakteknya diberikan beberapa skenario yang spesifik dan distribusi peluang
gabungan yang tepat. Hasil-hasil secara umum digambarkan pada elemen
s∈S. Ketika beberapa data acak, maka penyelesaian dan nilai tujuan optimal
untuk masalah optimisasi juga acak.
Ada dua model dalam permasalahan program stokastik, yaitu :
1. Recourse Models
2. Model Kendala Berpeluang (Probabilistically Constrained Models)
Suatu cara logis yang diperlukan dalam persoalan adalah membuat
seba-Andaikan x adalah vektor keputusan yang diambil, dan y(w) adalah sebuah
vektor keputusan yang menyatakan aksi terbaru atau konsekuensi darix.
Him-punan berbeda yang berisiyakan dipilih dari tiap-tiap hasil yang mungkin dari
w. Formulasi dua tahapnya adalah
Min g1(x) +E[g2(y(w), w)]
Kendala f1(x)60,· · · , fm(x)60 (3.2)
h1(x, y(w))60,∀ w∈W
... ...
hk(x, y(w))6 0,∀ w∈W
x1, x2,· · · , xn∈X, y(w)∈Y.
Himpunan kendalah1, h2,· · ·, hk, menggambarkan hubungan antara
kepu-tusan tahap pertama x dan keputusan tahap kedua y(w). Dicatat bahwa
dipersyaratkan tiap-tiap kendala dipenuhi dengan peluang 1, atau untuk
se-tiap w ∈ W yang mungkin. Fungsi g2 merupakan penyelesaian yang sering
muncul dari persoalan matematika. Tidak dibutuhkan untuk membuat
ko-relasi yang berubah-ubah (recourse) untuk keputusan tahap pertama, perlu
untuk dibuat korelasi yang terbaik.
Recourse Models dapat diperluas dengan banyak cara. Untuk persoalan
tahap ganda, pengaruh keputusan sekarang akan ditunggu untuk beberapa
ketidakpastian yang diselesaikan kembali (direalisasikan), sehingga pembuatan
keputusan yang lain didasarkan pada apa yang terjadi. Tujuannya adalah
un-tuk meminimumkan biaya yang diharapkan dari semua keputusan yang
diam-bil.
Pada beberapa kasus, dapat digunakan suatu metode yang lebih tepat
untuk mencoba menentukan sebuah keputusan, yang mana keputusan
terse-but dijamin oleh himpunan kendala yang akan dipenuhi oleh sebuah peluang
probabilis-tically constrained models yang dirumuskan sebagai berikut :
Min Z =f(x)
Kendala P[g1(x)≤0,· · ·, gm(x)≤0]≥α (3.3)
h1(x)≤0
h2(x)≤0
x∈X.
3.2.2 Konsep Dasar Pembentukan Model Program Stokastik Dua Tahap
Banyak persoalan perencanaan dan manajemen yang mengandung
re-siko dan ketidakpastian dibahas dan diselesaikan dengan program stokastik
dua tahap. Persoalan stokastik dengan kompensasi dari divergensi pada
sis-tem dengan kendala mempunyai aplikasi yang lebih banyak dari pada model
program yang lain. Penyelesaian persoalan program stokastik dua tahap berisi
vektor acak dan vektor deterministik. Pada tahap pertama, penyelesaian
per-soalan rencana awal deterministik akan dibuat. Pembentukan rencana awal
deterministik dilakukan sebelum kondisi acak dari persoalan ditentukan.
Ji-ka persoalan program stoJi-kastik dengan model dua tahap dapat diselesaiJi-kan
maka pemilihan dari rencana awal deterministik akan menjamin keberadaan
(eksistensi) vektor acak di dalam kompensasi untuk sistem yang divergen.
Andaikan terdapat persoalan berikut :
Min (C, X) (3.4)
A0X =B0 (3.5)
AX =B (3.6)
dimana
C =cj, j = 1,2, ..., m
B = (bi), i= 1,2, ..., m
B0 = (b0k), k= 1,2, ..., m
A0 =ka0kjk, k = 1,2, ..., m;j = 1,2, ..., n
A=kaijk, i= 1,2, ..., m;j= 1,2, ..., n.
Andaikan elemen dari matriks A = A(ω), vektor B = B(ω) dan C = C(ω)
bernilai acak. Maka untuk proses penyelesaian dari persoalan (3.4− 3.7) akan
dibagi menjadi dua tahapan, sebelum pengamatan dari parameter acak pada
kondisi dari tahap pertama dipilih rencana non-negatif deterministikX0 yang
memenuhi kondisi (3.5). pada tahap kedua ditentukan spesifikasiω0dari setiap
kejadian acak yang bersamaan (sesuai) dengan nilaiA(ω0) danB(ω0). Hitung
divergensiB(ω0)− A(ω0)X0 yang muncul pada kondisi (3.6) setelah realisasi
ω0 ∈ Ω. Definisikan vektor kompensasi divergensi Y ≥ 0 yang sesuai dengan
hubungan berikut
D(ω0)Y(ω0) =B(ω0)−A(ω0)X0 (3.8)
dimana D = kdilk , i = 1,2,· · · , m;l = 1,2,· · · , n1 adalah sebuah matriks
kompensasi yang berisi elemen acak. Sehingga diasumsikan bahwa realisasi
acak ω yang diamati pada tahap kedua tidak bergantung pada pemilihan
ren-cana pendahuluan X0.
Perhatikan persoalan program matematika berikut :
Tentukan vektor X berdimensi n dan vektor Y(ω) berdimensi n1, ω0 ∈ Ω.
Yang menghasilkan
min
X Eω{(C(ω), X) + minY (H, Y(ω))} (3.9)
dengan kendala
A0X =B0 (3.10)
A(ω)X+D(ω)Y(ω) =B(ω), ω ∈Ω (3.11)
H adalah vektor penalti yang bergantung pada nilai komponen dari vektor
Y(ω) yang mana merupakan kompensasi divergensi. E adalah notasi
ekspek-tasi matematika setelah ditentukan rencana awalX0, dipilih komponen vektor
Y(ω) dengan cara menjamin penalti minimum untuk kompensasi divergensi
pada kondisi dari persoalan. Dengan kata lain, setelah ditentukan vektorX0,
perlu menyelesaikan persoalan
n min
Y (H, Y(ω))| D(ω)Y(ω) =B(ω)−A(ω)X
0, Y(ω)
≥ 0o (3.13)
Persoalan (3.13) akan menpunyai banyak rencana, vektor Y(ω) tidak dapat
ditentukan pada tiap ω0 ∈ Ω yang menjamin penemuan kondisi (3.11).
Per-soalan (3.9−3.12) dikenal sebagai persoalan program stokastik dua tahap dan
persoalan (3.13) adalah persoalan tahap kedua.
Model dan pendekatan dari penyelesaian persoalan program stokastik
dua tahap dapat digunakan untuk perspektif perencanaan dan operasional
manajemen, karena selalu terdapat keacakan yang mempengaruhi yang sudah
direncanakan dan sistem manajemen (pelaksanaan). Model dua tahap juga
kurang sensitif terhadap perubahan pada parameter dari kondisi persoalan,
yang menyebabkan lebih stabil. Akibatnya vektor dapat diterima untuk
ren-cana tahap pertama yang diperlukan untuk setiap ω0 ∈ Ω, terdapat vektor
Y ≥0 sedemikian hingga
D(ω)Y(ω) =B(ω)−A(ω)X (3.14)
Andaikan kendala tambahan yang disebutkan secara implisit pada (3.14)
muncul pada tahap kedua dari persoalan yang dihasilkan; dan andaikan
kon-disi yang ditentukan pada vektor non-negatif X dari persamaan (3.10) sudah
ditentukan.
Andaikan himpunan K1 = {X : A0 = B0, X ≥ 0} didefinisikan oleh
kendala yang sudah ditentukan tetapi K2 = {X : ∀ ω0 ∈ Ω,∃ Y ≥
persoalan (3.9 − 3.12). Jika X ∈ K, maka vektorX memenuhi kendala yang
sudah ditentukan A0X = B, X ≥ 0 dan sampai itu, persoalan tahap kedua
(3.6) akan memiliki banyak rencana.
Untuk perhitungan lanjutan diperlukan hasil berikut:
Teorema 3.2.1 HimpunanK dengan vektorXpada persoalan program stokastik dua tahap adalah konveks.
Bukti : K = K1 ∩K2 tetapi K1 ={X : A0 = B0, X ≥ 0} adalah konveks. Definisikan untuk ω ∈ Ω tertentu pada himpunan K2ω ={X | ∃ Y(ω)≥ 0}
sedemikian hinggaA(ω)X=B(ω)−D(ω)Y(ω) adalah konveks. Hal ini
meny-atakan bahwa K2 = ∩ω∈ΩK2ω dan K = K1 ∩K2 adalah himpunan konveks
sebagai pertolongan himpunan konveks.
3.2.3 Pembentukan Skenario
Dalam banyak aplikasi, sebaran peubah acak tidak diketahui atau
walau-pun diketahui, terlalu mahal untuk memperhatikan sebaran diskrit dengan
banyak hasil yang mungkin atau menangani sebaran kontinu dengan integrasi
numerik. Merupakan hal yang umum untuk memilih himpunan hasil
repre-sentatif yang relatif kecil yang disebut skenario untuk menyajikan kejadian
acak. Skenario dapat merupakan kuartil dari sebaran yang diketahui atau
data historis, prediksi dan beberapa pohon atau dibangun dengan simulasi.
Setiap skenario diberikan nilai probabilitas untuk merefleksikan kemungkinan
kejadiannya.
Simpul AKAR menyatakan waktu sekarang atau bagian dari data yang
diketahui. Pada tahap 2, terdapat 4 kemungkinan berbeda dan setiap dari
padanya mempunyai berbagai hasil berbeda yang mungkin di tahap 3 dan
seterusnya. Suatu skenario terdiri dari lintasan lengkap dari simpul akar
ke satu simpul daun, mendefinisikan realisasi tunggal dari himpunan peubah
acak. Untuk mengoperasikan model program stokastik, pembentukan skenario
metode pembentukan tersebut.
a. Bootstrap data historis
b. Pemodelan statistika dengan pendekatan”Value at Risk” c. Model vektor autoregressi
a. Bootstrap data historis
Pendekatan paling sederhana untuk membangun skenario hanya memakai
data yang ada tanpa pemodelan matematika. Setiap skenario merupakan
sam-pel dari perolehan aset yang diperoleh dengan mensampling perolehan yang
diamati di masa lalu. Waktu dari catatan historis yang tersedia dipilih secara
acak dan untuk setiap waktu dalam sampel dibawa perolehan dari semua
ke-las tersebut. Ini merupakan skenario perolehan bulanan. Jika ingin dibangun
skenario perolehan untuk horizon waktu panjang misalnya 1 tahun, disampel
perolehan 12 bulan dari titik waktu yang berbeda. Susunan perolehan dari
deretan yang disampel merupakan perolehan 1 tahun. Dengan pendekatan ini
korelasi diantara kelas aset dipertahankan.
b. Model Statistika dengan pendekatan Value at Risk
Analisis deret waktu dari data historis dapat dipakai untuk mengestimasi
perubahan dari matriks korelasi antara kelas aset. Matriks korelasi ini dipakai
untuk mengukur resiko dengan metode Value at Risk (VaR).
Nyatakan peubah acak dengan vektor acakk-dimensiw. Dimensiwsama
dengan jumlah faktor resiko yang ingin dimodelkan. Dengan mengandaikan
bahwa peubah acak secara gabungan bersebaran normal dapat didefinisikan
fungsi kepadatan peluang dari w sebagai
f(w) = (2π)−p/2|Q|1/2exp[−1
2(w−w¯) ′
Q−1
(w−w¯)]
disini ¯wadalah ekspektasi dari w danY matriks kovarian dan dapat dihitung
dari data historis.
dap-faktorisasi Cholesky atau prosedur pembentukan skenario yang didasarkan
pa-da analisis komponen utama yang diajukan oleh Jamshidian pa-dan Zhu (1997).
Simulasi dapat diterapkan secara berulang pada status berbeda dari
po-hon kejadian. Begitupun, mungkin saja ingin dipersyaratkan nilai acak yang
dibangun pada nilai-nilai yang diperoleh oleh beberapa peubah acak.
Sampling bersyarat dari peubah normal multivariat dilakukan seperti
berikut. Peubah w dipartisi menjadi 2 subvektor w1 dan w2 dengan w1
vek-tor dimensi K, dari peubah acak untuk nama beberapa informasi tambahan
tersedia danw2 adalah vektor dimensi K2−K−K1 dari peubah sisa. Vektor
nilai ekspektasi dan matriks kovarian dipartisi secara analog sebagai
¯
Fungsi kepadatan peluang marginal dari w2 dengan diketahui w1 = w∗1
diberikan oleh
dimana nilai ekspektasi bersyarat dan matriks kovarian diberikan oleh
¯
Skenario w2 untuk periode t dipersyaratkan pada nilai w1 diberikan oleh w1t
dapat dibangun dari peubah normal multivariat melalui pernyataan
wt2i=w02i exp[σi√tw2i]
dengan wt2i nilai hari ini dan σi adalah perubahan periode tunggal dari
c. Model Vektor Autoregressi
Model vektor autoregressi dapat dipakai untuk membentuk skenario.
Dalam hal ini diambil ilustrasi tentang sistem simulasi Asset Liability
Man-agement (ALM) untuk dana pensiun. Karena cakupan dari sistem ini selalu
dibatasi pada keputusan strategis jangka panjang model investasi hanya
mem-praktekkan kumpulan kecil dari kelas aset yang besar yaitu deposito, obligasi,
real estate dan saham. Terpisah dari perolehan atas aset-aset ini, setiap
ske-nario harus mengandung informasi tentang pertumbuhan gaji masa datang
untuk menghitung nilai masa datang pensiun.
Model vektor autoregressi untuk membentuk skenario perolehan aset dan
pertumbuhan gaji adalah
Rt=c+V ht−1+εt, ε∈N(o, Q), t= 1,2,· · · , T
Rit =ln(1 +πit), i= 1,2,· · · , m, t= 1,2,· · · , T.
Dengan m jumlah deret waktu aset, πit laju perubahan diskrit dari
peubah i ditahun t, Rt vektor dimensi-m dari laju majemuk, c vektor
koe-fisien berdimensi-m, V adalah matriks koefisien m x m, εt vektor dimensi m
dari pencilan dan Q matriks kovariansi m x m.
Spesifikasi model vektor autoregressi harus dipilih secara hati-hati,
walau-pun beberapa hubungan inter-temporal diantara perolehan mungkin signifikan
lemah yang didasarkan pada data historis, tidak berakibat bahwa hubungan
BAB 4
SOLUSI MODEL PEMROGRAMAN INTEGER
4.1 Model Pemrograman Integer
Dalam penelitian ini, akan diselidiki masalah pengaturan waktu
selesai-nya target untuk suatu kegiatan proyek dengan durasi (jangka waktu) acak,
dengan menggunakan pemrograman linier integer stokastik dua tahap yaitu
target ditentukan dan diikuti oleh penyeimbangan jadwal rinci proyek.
Untuk menggambarkan model, digunakan beberapa notasi sebagai berikut:
A : himpunan dari semua aktivitas aktual;
i, j : indeks aktivitas, i, j ∈A= 0,1,· · · , N+ 1, dimana 0 dan N + 1 adalah masing-masing kegiatan dummy yang menunjukkan awal dan penyelesaian proyek;
(i, j)∈P berarti aktivitasj hanya dapat dimulai setelah aktivitas
iselesai; |P|=m
(i, j) : indeks untuk hubungan precedence;
Ω = {ω1, ω2,· · · , ωS}, himpunan dari skenario yang terjadi dimana P rπs positif=P r(ω =ωs), danP
ω∈Ωπs = 1;
pi(ω) : durasi aktivitasi untuk skenario ω∈Ω, p0(ω) = 0, pn+1(ω) = 0;
ci : biaya per satuan waktu terkait dengan waktu target penyelesaian aktivitasi;
di : satuan biaya kendala dari aktivitasi;
qi+, q−
i : koefisien biaya penalti yang terkait dengan penyelesaian akhir, awal
aktivitasi;
B : anggaran total sebenarnya;
ti : waktu penyelesaian target untuk aktivitasi; ti∈Z+;
xi : variabel sebenarnya untuk aktivitas i;xi ∈[0, ui]∩Z+;
y+i , y−
i : jumlah satuan waktu terlambat aktivitasi, dari awal sehubungan
waktu penyelesaian targetyi+, y−
yang diharapkan dari suatu proyek adalah
(SP) Min {ct+Q(t) :t∈T∩Zn+2
+ } (4.1)
dengan t : waktu target penyelesaian, t∈Zn+2 T : daerah layak
c : biaya per satuan waktu terkait dengan waktu target penyelesaian
Q(t) : fungsi nilai optimal dari tahap kedua
Selanjutnya pada masalah tahap kedua diselesaikan fungsi nilai optimal
Q(t) =
S
X
s=1
πsv(t, ωs) (4.2)
dengan ωs : skenario
v(t, ωs) : fungsi nilai objektif optimal dari suatu penjad-walan tahap kedua
πs = Pr(ω=ωs)
P
ω∈Ωπs = 1
Untuk menyelesaikan waktu target t dengan skenario ω, dimiliki model pemrograman linier integer (ILP) dengan meminimalkan deviasi pinalti total:
v(t, ω) = MinX
Menggunakan notasi vektor yang didefinisikan di atas, model (4.3−4.7)
Minimalkan q−
dimana S adalah m x (n + 2) matriks sehingga jika k kendala utama adalah (i, j), maka Skj = 1 dan semua elemen lainnya di baris k dari S adalah 0.
Tujuan dalam (4.8) adalah untuk meminimalkan jumlah pinalti yang
dikelu-arkan deviasi waktu target. Kendala utama (4.9) menjamin jadwal layak, dan
(4.10) adalah kendala anggaran. Perhatikan bahwa waktu untuk 0 aktivitas
dummy, yang menunjukkan awal proyek, tidak diperbolehkan untuk diubah,
sehingga variabel yang sesuai dan dapat dihapus dari formulasi. Namun,
di-jaga agar mereka dihindari untuk mendefinisikan baris dari matriks utama.
Jika biaya tanpa kendala anggaran terbatas tetapi dipandang sebagai pinalti,
maka mereka dapat ditambahkan ke fungsi tujuan. Ini mengarah ke model LP
berikut untuk masalah tahap kedua:
Minimalkan q−
dan q+harus diatur untuk menyeimbangkan biaya d. Satu pertanyaan penting adalah bagaimana memperkirakan parameter dalam
mod-el. Meskipun proyek, untuk sebagian besar, adalah tunggal, ada beberapa
pe-doman umum untuk melakukan hal ini. Biaya waktu targetci, tergantung pada
persyaratan dari pelanggan. Dalam lingkungan penawaran, waktu
penyelesa-ian yang diusulkan dapat mempengaruhi probabilitas menang proyek. Setelah
pemangku kepentingan, sebagaimana dapat menyelesaikan kegiatan lebih awal
dari yang direncanakan. Hal ini terutama benar ketika konsep penjadwalan
tepat waktu yang digunakan. Bila diinginkan untuk mendorong secepatnya,
koefisien yang sesuai dapat diatur ke nilai negatif.
Estimasi koefisien penalti tidak hanya membutuhkan informasi kontrak
penuh, tetapi juga beberapa pemahaman tentang biaya yang terkait dengan
gangguan jadwal internal. Sebaliknya, biaya kendala umumnya terkait dengan
lembur, mempercepat, dan mungkin, biaya pemanfaatan sumber daya dari
luar (outsourcing fees).
Sekarang akan dibahas beberapa sifat dari relaksasi LP model integer
programming stokastik (4.1).
Adanya model solusi terbatas (4.8 − 4.12) menunjukkan bahwa untuk
masing-masing skenario, menyadari durasi p(ωs) muncul di sisi kanan dari
kendala (4.9) dalam program linier. Oleh karena itu, tahap kedua fungsi
ob-jektif yang optimalv(t, ωs) dapat dilihat hanya sebagai fungsi dariSp(ωs)−Pt.
Persamaan (4.2) ditulis ulang sebagai
Q(t) =
DimisalkanvLP(z) menjadi nilai dariv(z) bila kondisi integrabilitas padax,y+ dany−
sembarang, sekarang dibangun kondisi di manavLP(z) adalah terbatas
untuk setiap waktu tepat t dan setiap realisasi ketidakpastianω.
Proposisi 1 Nilai fungsi vLP(z) memenuhi ketaksamaan berikut:
(1)vLP(z)<∞,∀ z ∈Rm. (4.19)
(2)vLP(z)>−∞,∀ z ∈Rm jika q++q− ≥0.
Perhatikan bahwa biaya sesungguhnya karena selalu diasumsikan
non-negatif, baik (4.19) memiliki solusi optimal terbatas tidak terpengaruh oleh
kendala anggaran. Untuk setiap z ∈ Rm, daerah feasible dari masalah
du-al dari LP relaksasi dari (4.19) tanpa kenddu-ala anggaran dapat ditulis
seba-gai {λ ∈ Rm
} 6= φ dan karenanya (4.19) memiliki solusi optimal di-batasi, yaitu vLP(z)>−∞.
Mengingat bahwa z muncul di sisi kanan dari kendala pemrograman, diketahui bahwa vLP(z) adalah fungsi cembung dari z, atau t. Namun, ini tidak menjamin solusi terbatas untuk SP. Misalnya, jika ci +q−
i < 0 untuk
kegiatan i, maka ini optimal untuk menetapkan waktu ti selambat-lambat
mungkin dan jadwal aktivitas sedini mungkin. Jika c+q− <
0, itu adalah optimal untuk semua himpunan waktu target selambat-lambat mungkin (∞).
Akibatnya, dipunyai
Akibat 1. Pemograman Linier (LP) relaksasi SP (4.1) memiliki solusi opti-mal terbatas jika c+q−
≥0 dan q++q− ≥0.
Satu kasus sepele solusi dibatasi terjadi ketikaq+ ≤cdanq−
≥0, yang berarti bahwa pinalti keterlambatan tidak lebih besar daripada biaya target
waktu. Akibatnya, selalu optimal untuk menetapkan waktu target sebagai 0.
Analogi untuk masalah penjual surat kabar Pemrograman stokastik masalah
SP sisa biaya kelebihan waktu target dengan pinalti waktu target kekurangan.
Dengan ’waktu target berlebih’ berarti peningkatan nilai fungsi tujuan per
satuan waktu ketika waktu selesai diwujudkan dalam jadwal awal adalah
ku-rang dari waktu target. Dengan ’penalti kekuku-rangan waktu’ yang dimaksud
meningkatan nilai fungsi tujuan per satuan waktu ketika waktu selesai
diwu-judkan dalam jadwal awal adalah lebih besar dari waktu target. Hal ini mirip
dengan menjual surat kabar antara kelebihan dan kekurangan biaya dalam
masalah penjualan surat kabar tradisional (Porteus 1990). Dalam masalah
keputusan membeli harus dibuat sejumlah surat kabar (dengan biaya per
sat-uan c) sebelum realisasi permintaan yang tidak pasti x ≥ 0, yang dicirikan
oleh fungsi permintaan kumulatif (CDF/Cumulative Demand Function)F(x),
x ∈ R+. Setelah permintaan tersebut direalisasikan, loker (penjaja) yang
menjual surat kabar sebanyak mungkin pada harga satuan p (dengan asumsi
p ≥ c). Jika D permintaan lebih besar dari jumlah yang dibeli, maka semua
terjual. Jika D adalah kurang dari jumlah yang dibeli, maka kelebihannya
dijual dengan harga sisa satuan s (dengan asumsi s≥c). Misalkancs =p−c
menjadi kekurangan satuan biaya dan ce = c− s menjadi biaya kelebihan
satuan. Sangat mudah untuk menunjukkan bahwa kuantitas pembelian yang
optimal loker (penjaja) x∗
harus memenuhi
F(x∗
) = cs
cs+ce
Masalahnya jauh lebih rumit, meskipun, karena adanya beberapa
dimen-si dan kendala yang didahulukan. Untuk proyek dengan hanya satu aktivitas
(tiga kegiatan jika dua dummy yang dipertimbangkan), sekarang ditunjukkan
bahwa SP tanpa kendala setara dengan masalah penjual surat kabar
tradi-sional. Misalkan bahwa masalah 1-aktivitas memiliki biaya koefisien q+, q−
dan c, dan bahwa yang memiliki durasi pCDF F(p).
Proposisi 2 Versi 1-aktivitas SP tanpa kendala setara dengan masalah pen-jual surat kabar dengan ce satuan biaya kelebihan dan cs satuan kekurangan
biaya , sehingga jikaq+ ≤ 0, maka cs =q+−c, ce = q−+c dan jika q− ≥ 0,
Bukti: Solusi dengan informasi yang sempurna adalah untuk mengaturt=p. Jika q−
≤ 0, maka untuk setiap waktu tujuan t, solusi itu adalah optimal untuk jadwal aktivitas sedini mungkin. Untuk kasus ketika t > p (berlebih),
satuan biaya kelebihan c+q−
(yakni, satuan biaya waktu target ditambah
bonus menjadi awal oleh satu satuan waktu), jika t < p (kekurangan),
satuan waktu dikurangi satuan biaya waktu target). Jika q−
≤ 0, maka opti-mal untuk jadwal waktu penyelesaian aktivitas sedekat mungkin dengan target
waktut. Dalam situasi ini, jikat > p(berlebih), solusi itu adalah optimal
un-tuk jadwal aktivitas unun-tuk menyelesaikan padatkarena secepatnya dikenakan
pinalti. Dengan demikian, satuan biaya kelebihan hanya c. Di sisi lain, jika
t < p, satuan biaya kekurangan masih q+−c.
Nilai optimal dari t mengikuti solusi dari masalah penjual surat kabar
tradisional. Dalam masalah penjual surat kabar, diasumsikan bahwa ce > 0
dan cs > 0, yang menyatakan bahwa −q−
< c < q+ untuk suatu proyek
1 aktivitas. Memperluas kondisi biaya produk adalah antara nilai sisa dan
harga eceran untuk masalah ini, telah dikatakan bahwa biaya waktu target
yang telah ditentukan adalah tidak kurang dari bonus awal dan tidak lebih
besar dari pinalti keterlambatan dalam tahap pemulihan proyek. Diasumsikan
bahwa kondisi ini berlaku untuk setiap aktivitas, yaitu −q− <c<q+.
Batas untuk waktu target. Dalam masalah dengan ce dan cs > 0,
jum-lah pesanan optimal adajum-lah sama dengan permintaan untuk kasus dengan
informasi yang sempurna, dan adalah antara permintaan terbesar dan
terke-cil untuk kasus stokastik. Sekarang dianggap SP tanpa kendala dan dengan
parameter−q−
<c<q+. Masalah ini disebut SP (4.1), yang dapat dilihat se-bagai masalah multidimensi penjual surat kabar dengan kendala didahulukan.
Untuk waktu target SP (4.1) terbatas dalam kasus umum, pertama
didefin-isikan jadwal awal.
Definisi 1 Jadwal penjadwalan ES(p) adalah jadwal yang diperoleh dengan memulai semua aktivitas sedini mungkin, dimana aktivitas yang ditugaskan
pada durasi deterministikp.
Suatu kasus khusus SP (4.1) terjadi ketikaq−
<0. Kondisi ini mengimp-likasikan kehadiran awal yang selalu dihargai sebagai jadwal awal yang optimal
untuk semua skenario dan SP (4.1) dikomposis masalah individu penjual surat
aktivitasi, permintaan stokastik sesuai dengan waktu penyelesaian aktivitasi,
dan distribusi permintaan memiliki bentuk diskrit (fi(ωs), πs),s= 1,· · · , S, di
mana fi(ωs) adalah waktu penyelesaian aktivitas i di jadwal awal ES(p(ωs))
dengan skenario ωs. Satuan biaya kekurangan cs = q1+− ci sesuai dengan
masing-masing biaya kelebihan ce =q− i +ci.
Untuk SP (4.1) dengan realisasi tertentu dari jangka waktu (p(ωs)),
je-las bahwa solusi optimal diberikan oleh jadwal awal ES(p(ωs)). Misalkan
ti dan ti menjadi terlama dan tercepat waktu penyelesaian aktivitas i di
{ES(p(ω)) : ω ∈ Ω}. Misalkan ¯pi = max{p(ω)} dan ˆti menjadi waktu se-lesai untuk aktivitas i di jadwal awal ES(¯p). Selanjutnya diberikan proposisi berikut:
Proposisi 3 Untuk SP (4.1), waktu target yang optimal untuk memenuhi ak-tivitasti ≤t∗
i ≤ˆti.
Bukti: Untuk waktu targett, waktu penyelesaian yang sebenarnya untuk ak-tivitas i adalah tidak kurang dari ti untuk setiap skenario. Karena itu, jika
ti diatur kurang dari ti, selalu mungkin untuk meningkatkan ti untuk ti dan
menurunkan tujuan dengan (ti−ti) x (qi+−c). Jadi, t∗ i ≥ti.
Akan dibuktikan batas atas dengan induksi. Misalkan dimiliki suatu
proyek dengan satu aktivitas. Karena −q−
< c < q+, dari analogi untuk
masalah penjual surat kabar, waktu target yang optimal untuk aktivitas ini
adalah mungkin kurang dari durasi terpanjang p . Juga penyelesaian
sebe-narnya dari aktivitas ini tidak akan pernah lebih besar dari p. Sekarang
per-hatikan sebuah proyek parsial sehingga jika itu termasuk aktivitas j maka
semua pendahulu dari j juga disertakan. Misalkan waktu target untuk semua
aktivitas dalam proyek parsial memenuhi kondisi batas atas, dan waktu
penye-lesaian yang sebenarnya memenuhiti ≤ˆti untuk setiap aktivitasiyang selesai
dalam proyek parsial.
Selanjutnya ditambahkankaktivitas untuk proyek parsial sebagai penerus
ini tidak akan meningkatkan waktu target optimal dari aktivitas-aktivitas yang
sudah disertakan. Jika waktu target tk diatur yang lebih besar daripada ˆtk ,
selalu dapat diturunkan tk untuk ˆtk dan mengurangi tujuan oleh (tk −tkˆ) x
(¯qk+c). Oleh karena itu, t∗i ≤ˆti.
Menurut definisi, ˆti ≥ ¯ti untuk semua i. Jika durasi aktivitas adalah
variabel-variabel acak yang saling independen, maka ada satu skenario untuk
setiap kombinasi jangka waktu yang mungkin dan waktu penyelesaian di salah
satu jadwal awal adalah sama dengan batas atasnya, yaitu, ˆti = ¯ti untuk
semua i. Berikutnya karena akan ada satu skenario di mana semua aktivitas
mengambil durasi nilai terbesarnya. Ini adalah skenario yang menentukan ˆti.
Perhatikan bahwa dalam beberapa situasi bisa diperoleh t∗
i > tiˆ, yang
berarti bahwa waktu target yang optimal untuk aktivitas i adalah lebih
be-sar dari waktu selesai dalam setiap skenario. Hal ini disebabkan oleh pinalti
(deviasi) dalam tahap penjadwalan, seperti yang diilustrasikan dalam contoh
berikut
Contoh: Misalkan bahwa sebuah proyek terdiri dari dua aktivitas yaitu, aktiv-itas 1 dan aktivaktiv-itas 2 (aktivaktiv-itas 1 mendahului aktivaktiv-itas 2), dan bahwa ada dua
skenario secara total, masing-masing terjadi dengan probabilitas 0,5.
Misal-kan durasi aktivitasp1 = 1, p2 = 2 untuk skenario 1 dan p1 = 2,p2 = 1 untuk
skenario 2. Selain itu, misalkan biaya waktu target akan c1 = c2 = 1 dan
satuan tercepat dan pinalti keterlambatan akan q+i =q−
i = 5, i= 1,2. Solusi
optimal untuk masalah ini adalah t∗
1 = 2, t∗2= 4.
Gambar 4.1 menggambarkan jadwal awal untuk kedua skenario serta jadwal
aktual dengan waktu target yang optimal. Waktu target yang optimal
un-tuk aktivitas 2 adalah 4, tapi seperti yang dilihat, aktivitas 2 selalu selesai
sebelum 4 di jadwal awal untuk kedua skenario. Intuisi di balik ini adalah
sebagai berikut. Dalam urutan untuk menghindari pinalti keterlambatan
un-tuk aktivitas 1, waktu target diatur ke 2, ini adalah durasi maksimum yang
mungkin. Dalam skenario 1, untuk menghindari pinalti tercepat, itu adalah
optimal untuk jadwal aktivitas 1 untuk menyelesaikan pada waktu 2 meskipun
durasi disadari hanya 1. Sebagai akibatnya, aktivitas 2 selesai pada waktu 4
sehingga optimal untuk menetapkan waktu target aktivitas 2 sampai 4 untuk
menghindari pinalti keterlambatan.
4.2 Jaringan Aliran Formulasi Untuk Masalah Tahap Kedua
Sekarang ditunjukkan bahwa masalah tahap kedua diatas tanpa kendala
anggaran (4.13−4.16) adalah setara dengan masalah aliran jaringan biaya
min-imum (MCNFP/Minimum Cost Network Flow Problem). Ditulis variabel dual
untuk kendala utama (4.14) dan kendala batas atas (4.15) masing-masing
den-gan λ dan µ. Kemudian LP dual dari (4.13−4.16) dapat ditulis sebagai
Maksimalkan λ(Sp−Pt)−µu, (4.20)
Kendala λP≤q+, (4.21)
−λP≤q−
, (4.22)
λS−µ≤d, (4.23)
λ≥0, µ ≥0. (4.24)
Perhatikan bahwa, karena y0+ = y−
0 = 0, (4.21) dan (4.22) tidak diperlukan
untuk 0 aktivitas. Dalam sebuah jaringan proyek aktivitas-on-node (AON),
jika dilihatλsebagai aliran pada busur sebelumnya, makaλPberjangka meru-pakan arus bersih pada node. Kendala (4.21) dan (4.22) menunjukkan bahwa
aliran ini harus dibatasi.
men-ditentukan oleh kapasitas busur dan konservasi aliran kendala.
Prosedur: Membangun sebuah MCNFP untuk program linier (4.20−4.24).
Langkah 1. Membuat jaringan dengan 0 node dan dummy simpul d.
Langkah 2. Untuk setiap aktivitas i6= 0 denganui = 0 (yaitu,noncrushable): (a) Tambahkan node i ke jaringan.
(b) Tambahkan busur (i, d) dengan batas bawah −q−
i , batas atas qi+,
dan 0 aliran biaya.
Langkah 3. Untuk setiap aktivitas i6= 0 denganui >0 (yaitu,crushable): (a) Tambahkan tiga node i+, i, i− dengan batas bawah −∞, batas atas di, dan biaya aliran 0. (c) Tambahkan busur (i−, d
) dengan batas bawah −q−
i , batas atas qi+,
dan biaya aliran 0.
Langkah 4. Untuk setiap kendala diutamakan (i, j), tergantung dari tambahan node, tambahkan ke jaringan salah satu dari berikut busur: (i, j+), (i−, j
) atau (i−, j+
) (hanya salah satu dari tiga busur ada di jaringan) dengan batas atas ∞ dan biaya alirantj−ti−pj.
Gambar 4.2 : Struktur Jaringan; (a)ui = 0; (b) ui >0
Langkah 5. Tambahkan busur (d,0) ke jaringan dengan batas atas ∞ dan biaya aliran 0. Atur semua yang tidak spesifik batas bawah ke 0. Atur per-mintaan di semua node ke 0.
Menurut prosedur di atas, struktur jaringan dibuat untuk setiap aktivitas
sesuai salah satu dari dua situasi yang ditampilkan pada gambar 4.2,
tergan-tung pada apakah aktivitas tersebut crushable. Busur diberi label oleh [batas
bawah biaya, batas atas, aliran] pada gambar. Jaringan penuh diperoleh
dummy d untuk simpul (node) 0. Karena tidak ada permintaan eksternal di
simpul apapun, resultan MCNFP adalah masalah alur sirkulasi.
Misalkan zN F menjadi biaya minimum dari MCNFP dibangun dengan
prosedur di atas. Ditulis aliran optimal pada busur (i, j+), (i−, j
Proposisi 4 Fungsi nilai obyektif optimal dari LP (4.20−4.24) adalah−zN F
dan dalam penyelesaian optimal, λ∗ ij =f
adalah vektor darif∗
ij,(i, j)∈P dang
kendala (4.21−4.23) dan memaksimalkan fungsi tujuan dalam (4.20).
Dalam solusi yang optimal dari MCNFP, menyatakan aliran pada busur
(i, d) atau (i−, d
) (hanya salah satu dari dua busur ada di jaringan) denganα∗ i,
∀i6= 0. Konservasi aliran kondisi pada node iatau i−
(jika aktivitas i adalah
crushable) dapat ditulis sebagai
X
Batas-batas aliran didefinisikan sedemikian rupa sehingga −q−
i ≤ a∗i ≤ q+i ,
yang bila dikombinasikan dengan (4.25), memberikan
−q−
Dengan definisi dari matriksPsebelumnya, bagian kiri sisi (4.25) hanya baris ke f∗
P. Oleh karena itu, kendala (4.21) dan (4.22) dipenuhi oleh λ=f∗
.
Untuk aktivitas crushable i, g∗
i adalah aliran pada busur (i+, i).
Dit-ulis aliran pada busur (i+, i−
) dengan β∗
i dalam MCNFP yang optimal. Jadi
kondisi aliran konservasi pada node i+ memberikan solusi
dengan P
(k,i)∈Pf ∗
ki adalah baris ke f ∗
S dan β∗
i ≤ di. Jadi, kendala (4.23)
memenuhi λ=f∗ dan µ=g∗.
Akhirnya, diingat bahwa dalam prosedur untuk membangun jaringan
MCNFP, biaya aliran yang ditetapkan sedemikian rupa sehingga biaya jaringan
total −[f(Sp−Pt)−gu], yang diminimalkan pada f =f∗
,g=g∗
.
Akibat-nya, fungsi tujuanλ(Sp−Pt)−µu di (4.20) dimaksimalkan padaλ=f∗ dan
µ=g∗
, memberikan f∗
(Sp−Pt)−g∗
u, atau−zN F.
Sebuah masalah jaringan biaya aliran minimum biasanya dapat
disele-saikan lebih efisien dengan algoritma khusus seperti kode LP umum. Namun,
untuk setiap aktivitas crushable, perlu ditambahkan tiga node dan tiga atau
empat busur ke jaringan. Hal ini dapat membuat pendekatan yang diusulkan