Pendugaan Parameter Beberapa Sebaran Poisson Campuran dan Beberapa Sebaran Diskret dengan Menggunakan Algoritme EM

PENDUGAAN PARAMETER BEBERAPA SEBARAN POISSON

CAMPURAN DAN BEBERAPA SEBARAN DISKRET DENGAN

MENGGUNAKAN ALGORITME EM

ADE HARIS HIMAWAN

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Pendugaan Parameter Beberapa Sebaran Poisson Campuran dan Beberapa Sebaran Diskret dengan Menggunakan Algoritme EM adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2008

ABSTRACT

ADE HARIS HIMAWAN. Parameter Estimation of Some Mixed Poisson Distributions and Some Discrete Distributions Using EM Algorithm. Under direction of I GUSTI PUTU PURNABA and EFFENDI SYAHRIL.

Mixed Poisson distributions are widely used in various disciplines including actuarial applications. The family of mixed Poisson distributions contains several members according to the choice of mixing distribution to the Poisson distribution. The first objective of this thesis is to find explicit formula of mixed Poisson and some discrete distributions. The second objective is to search parameter estimation of these formulas using EM algorithm. The results show that general EM algorithm can be applied to the mixed Poisson distributions. The value of parameter estimator can be obtained by using EM algorithm in empirical data.

RINGKASAN

ADE HARIS HIMAWAN. Pendugaan Parameter Beberapa Sebaran Poisson Campuran dan Beberapa Sebaran Diskret dengan Menggunakan Algoritme EM. Dibimbing oleh I GUSTI PUTU PURNABA dan EFFENDI SYAHRIL.

Asuransi adalah transaksi pertanggungan yang melibatkan dua pihak, yaitu tertanggung dan penanggung. Perusahaan asuransi mengeluarkan polis yang berisi kesepakatan antara pihak tertanggung dan penanggung, dan menjanjikan akan membayar pemiliknya jika terjadi kerugian sepanjang waktu kontrak belum berakhir. Pembayaran kerugian disebut klaim sedang pengasuransi diwajibkan membayar premi.

Sebaran Poisson secara luas digunakan dalam masalah asuransi terutama untuk model proses klaim. Salah satu contohnya pada asuransi kendaraan bermotor, kejadian musibah seperti kecelakaan terjadi dalam waktu yang berbeda-beda merupakan kejadian acak, sehingga klaim yang datang tidak dapat diprediksi.

Adapun tujuan penelitian ini adalah: (1) Mencari formula eksplisit sebaran Poisson campuran dan beberapa sebaran diskret. (2) Menerapkan algoritme EM untuk menduga nilai parameter dari sebaran Poisson campuran dan beberapa sebaran diskret.

Metode yang digunakan dalam penelitian adalah studi pustaka disertai dengan perhitungan numerik untuk memperoleh nilai penduga parameter. Langkah-langkah yang akan dilakukan dalam penelitian adalah: (1) Penentuan formula eksplisit dari beberapa sebaran Poisson campuran dan beberapa sebaran diskret dengan menentukan fungsi sebaran geometri( ), sebaran Poisson-Lindley( )p , sebaran Poisson-Inverse Gaussian( , ), sebaran binomial negatif ( , ) , sebaran Neyman ( , ) , sebaran Poisson-lognormal ( , ) , sebaran Yule ( ) dan sebaran beta-binomial ( , ) , (2) Penentuan formula untuk tahap E dan M untuk setiap sebaran Poisson campuran dengan menggunakan algoritme EM, (3) Penentuan nilai dugaan parameter dengan menggunakan algoritme EM berdasarkan data empirik. Nilai penduga parameter ini dihitung secara numerik dengan menggunakan software Matlab 6.5. Untuk menguji kesesuaian sebaran hipotetik dengan sebaran data empirik digunakan uji Khi-kuadrat.

Formula eksplisit dari masing-masing sebaran Poisson campuran dan beberapa sebaran diskret telah berhasil diperoleh. Berdasarkan data empirik, diduga parameter dari setiap sebaran Poisson campuran dengan menggunakan algoritme EM.

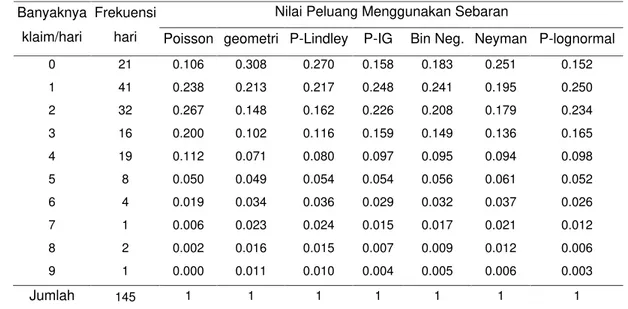
Nilai peluang dapat diperoleh dengan cara menyubstitusikan nilai penduga parameter ke fungsi kepekatan peluang dari beberapa sebaran Poisson. Setelah mendapatkan nilai peluang, nilai harapan juga dapat dicari dengan cara tiap nilai peluang dikalikan dengan total frekuensi hari. Dari frekuensi harapan dan frekuensi teramati dapat dicari nilai 2

hitung.

Dengan mengasumsikan parameter pada sebaran Poisson ( ) adalah suatu konstanta, maka didapatkan 2

hitung

2

tabel yang artinya sebaran Poisson ( ) ini

1

Poisson campuran yaitu sebaran sebaran geometri ( ) , sebaran Poisson-Lindley( )p , dan sebaran Neyman ( , ) .

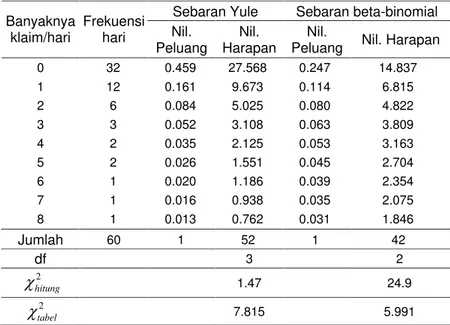
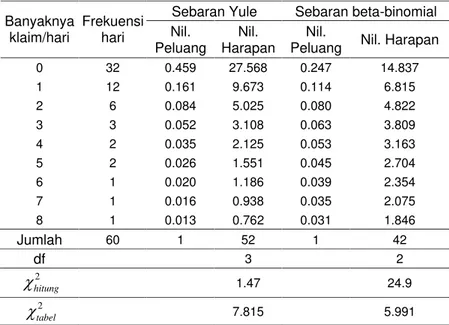
Untuk sebaran Poisson campuran berupa sebaran Poisson-Inverse Gaussian ( , ) , sebaran binomial negatif ( , ) , dan sebaran Poisson-lognormal ( , ) dengan _hitung2 _tabel2 yang artinya bahwa asumsi parameter pada sebaran Poisson ( ) menyebar menurut sebaran Inverse Gaussian, sebaran gamma atau sebaran lognormal menghasilkan sebaran Poisson campuran yang sesuai dengan sebaran data empirik. Untuk sebaran diskret yang sesuai dengan sebaran data empirik adalah sebaran Yule karena _hitung2 _tabel2 .

Berdasarkan data uji Khi-kuadrat, sebaran yang sesuai dengan data empirik adalah sebaran Poisson-Inverse Gaussian, sebaran binomial negatif, sebaran Poisson-lognormal dan sebaran Yule.

© Hak Cipta milik Institut Pertanian Bogor, tahun 2008

Hak Cipta dilindungi Undang-undang

1 Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber

a Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.

PENDUGAAN PARAMETER BEBERAPA SEBARAN POISSON

CAMPURAN DAN BEBERAPA SEBARAN DISKRET DENGAN

MENGGUNAKAN ALGORITME EM

ADE HARIS HIMAWAN

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Departemen Matematika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

Judul Tesis : Pendugaan Parameter Beberapa Sebaran Poisson Campuran dan Beberapa Sebaran Diskret dengan Menggunakan Algoritme EM

Nama : Ade Haris Himawan

NIM : G551060211

a

Disetujui Komisi Pembimbing

a

Dr. Ir. I Gusti Putu Purnaba, DEA Drs. Effendi Syahril, Grad.Dipl.

Ketua Anggota

A

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian dilaksanakan sejak bulan Nopember 2007 untuk mencari nilai penduga parameter, dengan judul Pendugaan Parameter Beberapa Sebaran Poisson Campuran dan Beberapa Sebaran Diskret dengan Menggunakan Algoritme EM.

Terima kasih penulis ucapkan kepada Bapak Dr. Ir. I Gusti Putu Purnaba, DEA dan Bapak Drs. Effendi Syahril, Grad.Dipl. selaku pembimbing, serta kepada Ibu Ir. Retno Budiarti, M.S. selaku penguji luar komisi. Di samping itu, penghargaan penulis sampaikan kepada Ibu Dr. Ir. Endar H. Nugrahani, M.S. sebagai ketua Program Studi Matematika Terapan dan Departemen Agama Republik Indonesia yang telah memberikan fasilitas berupa beasiswa. Ungkapan terima kasih juga disampaikan kepada istri dan anak serta seluruh keluarga, atas segala doa dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

RIWAYAT HIDUP

Penulis dilahirkan di Brebes pada tanggal 12 Juni 1975 dari ayah H. Kastum dan ibu Hj. Fasichah. Penulis merupakan putra kedua dari enam bersaudara.

Tahun 1993 penulis lulus dari SMA Negeri 2 Brebes dan pada tahun 1994 lulus seleksi masuk Universitas Muhammadiyah Surakarta (UMS). Penulis memilih Jurusan Pendidikan Matematika pada Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam dan selesai pada tahun 1998.

DAFTAR ISI

Halaman DAFTAR TABEL... DAFTAR LAMPIRAN... PENDAHULUAN………

Latar Belakang Masalah ………... Perumusan Masalah ……….………... Tujuan Penelitian ………... LANDASAN TEORI………...

Konsep Dasar Peluang ...………... Beberapa Jenis Sebaran Pencampur ...………... Sebaran Poisson Campuran ... Metode Pendugaan Parameter ………... Algoritme EM ………... METODOLOGI PENELITIAN ... SOLUSI EKSPLISIT BEBERAPA SEBARAN POISSON CAMPURAN DAN BEBERAPA SEBARAN DISKRET...

Beberapa Sebaran Poisson Campuran ………... Beberapa Sebaran Diskret ………... PENDUGAAN PARAMETER DENGAN ALGORITME EM...

Beberapa Sebaran Poisson Campuran ………... Beberapa Sebaran Diskret ………... NILAI PENDUGA PARAMETER ... KESIMPULAN DAN SARAN ... DAFTAR PUSTAKA... LAMPIRAN...

xii xiii 1 1 2 2 3 3 9 10 11 12 15

16 16 23 26 26 42 48 52 54 55

DAFTAR TABEL

Halaman Tabel 1 Banyaknya klaim dan frekuensi hari dalam rentang waktu

pengamatan 145 hari untuk sebaran Poisson campuran... Tabel 2 Nilai Penduga Parameter Beberapa Sebaran Poisson Campuran... Tabel 3 Nilai peluang sebaran Poisson campuran... Tabel 4 Nilai harapan sebaran Poisson campuran... Tabel 5 Banyaknya klaim dan frekuensi hari dalam rentang waktu

pengamatan 60 hari untuk beberapa sebaran diskret... Tabel 6 Nilai peluang dan nilai harapan beberapa sebaran diskret...

48 48 49 49

50 51

DAFTAR LAMPIRAN

Halaman

Lampiran 1 Bukti Lema 1... 56

Lampiran 2 Program sebaran geometri... 56

Lampiran 3 Program sebaran Poisson-Lindley... 57

Lampiran 4 Program sebaran Poisson-Inverse Gaussian... 58

Lampiran 5 Program sebaran binomial negatif... 59

Lampiran 6 Program sebaran Neyman……….. 60

Lampiran 7 Program sebaran Poisson-lognormal………. 61

Lampiran 8 Nilai peluang dan nilai harapan sebaran Poisson campuran……….. 61

Lampiran 9 Program sebaran Yule………...… 67

Lampiran 10 Program sebaran beta-binomial………... 67

Lampiran 11 Nilai peluang dan nilai harapan beberapa sebaran diskret……….. 68

Lampiran 12 Nilai Khi-kuadrat beberapa sebaran Poisson campuran dan beberapa sebaran diskret... 69

PENDAHULUAN Latar Belakang Masalah

Menurut Djojosoedarso (1999) dalam bukunya: “Prinsip-prinsip Manajemen Resiko dan Asuransi”, asuransi adalah transaksi pertanggungan yang melibatkan dua pihak, yaitu tertanggung dan penanggung. Perusahaan asuransi mengeluarkan polis yang berisi kesepakatan antara pihak tertanggung dan penanggung, dan menjanjikan akan membayar pemiliknya jika terjadi kerugian sepanjang waktu kontrak belum berakhir. Pembayaran kerugian disebut klaim sedang pengasuransi diwajibkan membayar premi.

Menurut Grandell (1997) sebaran Poisson secara luas digunakan dalam masalah asuransi terutama untuk model proses klaim. Salah satu contohnya pada asuransi kendaraan bermotor, kejadian musibah seperti kecelakaan terjadi dalam waktu yang berbeda-beda merupakan kejadian acak

, sehingga klaim yang datang

tidak dapat diprediksi dan biasanya kecelakaan sifatnya relatif jarang jika dibandingkan dengan jumlah yang diasuransikan. Ini dapat gambarkan dengan perusahaan asuransi yang memiliki nasabah ribuan dan peluang kecelakaannya kecil maka akan konvergen ke sebaran Poisson ( ) . Dengan demikian proses kedatangan klaim juga merupakan kejadian acak yang memiliki sebaran tertentu, salah satunya adalah sebaran Poisson ( ) .

Seringkali parameter dari sebaran Poisson ( ) merupakan nilai dari suatu peubah acak yang memiliki sebaran tertentu. Kombinasi dari dua sebaran ini membentuk sebaran baru yang dikenal dengan sebaran Poisson campuran. Berdasarkan sebaran , beberapa sebaran Poisson campuran antara lain sebaran geometri ( ) , sebaran Poisson-Lindley ( )p , sebaran Poisson-Inverse Gaussian ( , ) , sebaran binomial negatif ( , ) , sebaran Neyman ( , ) , sebaran Poisson-lognormal ( , ) , dan beberapa sebaran diskret lain seperti sebaran Yule ( ) dan sebaran beta-binomial ( , ) .

Permasalahan dalam pendugaan parameter dari beberapa sebaran Poisson campuran dan beberapa sebaran diskret terdapat parameter yang harus diduga.

2

(Maximum Likelihood, ML). Pendugaan parameter dengan menggunakan metode kemungkinan maksimum tidak bisa dilakukan secara langsung karena ada data yang tidak teramati sehingga perlu algoritme EM (Expectation Maximization) yang digunakan untuk data tidak teramati.

Dalam proses selanjutnya, peneliti mencoba menggunakan algoritme EM untuk mencari nilai penduga parameter dari beberapa sebaran Poisson campuran dan beberapa sebaran diskret. Untuk lebih jelasnya, hal ini akan dipelajari lebih dalam prinsip dari algoritme EM yang diterapkan pada beberapa sebaran Poisson campuran dan beberapa sebaran diskret.

Perumusan Masalah

Berdasarkan latar belakang di atas, maka dapat ditemukan beberapa permasalahan yang antara lain:

1 Karena parameter dari sebaran Poisson ( ) merupakan nilai dari suatu peubah acak yang menyebar menurut sebaran tertentu, maka akan terbentuk sebaran baru yang dikenal sebagai sebaran Poisson campuran. Berdasarkan asumsi sebaran dari , maka perlu dicari formula eksplisit dari sebaran Poisson campuran tersebut.

2 Sebaran Poisson campuran memiliki parameter baru yang perlu diduga, namun dalam pendugaan kemungkinan maksimum tidak bisa dilakukan secara langsung karena ada data yang tidak teramati sehingga perlu algoritme EM untuk mengatasi masalah ini.

Tujuan Penelitian

Penelitian ini bertujuan :

1 Mencari formula eksplisit sebaran Poisson campuran dan beberapa sebaran diskret.

LANDASAN TEORI Konsep Dasar Peluang

Ruang Contoh, Kejadian, dan Peluang

Suatu percobaan yang dapat diulang dalam kondisi yang sama, yang hasilnya tidak bisa diprediksi dengan tepat tapi kita bisa mengetahui semua kemungkinan hasil yang muncul disebut percobaan acak.

Definisi 1 (Ruang Contoh)

Ruang contoh adalah himpunan semua hasil yang mungkin dari suatu percobaan acak, dan dinotasikan dengan O.

(Grimmett dan Stirzaker 1992)

Definisi 2 (Kejadian)

Kejadian adalah suatu himpunan bagian dari ruang contoh O.

(Grimmett dan Stirzaker 1992)

Definisi 3 (Kejadian Saling Lepas)

Kejadian A dan B disebut saling lepas jika irisan dari keduanya adalah himpunan kosong yang dinotasikan dengan .

(Grimmett dan Stirzaker 1992)

Definisi 4 (Medan- )

Medan- adalah suatu himpunan yang anggotanya terdiri atas himpunan bagian ruang contoh O, yang memenuhi syarat berikut:

1 .

2 Jika A , maka Ac . 3 Jika A1, A2, … , maka

1

i i

A .

(Grimmett dan Stirzaker 1992)

Definisi 5 (Ukuran Peluang)

4

1 P tak negatif, yaitu untuk setiap A , P(A) = 0.

2 P bersifat aditif tak hingga, yaitu jika A1, A2, … dengan Aj Ak = , j?k,

maka

1 1

n n

n n

A A .

3 P bernorma satu, yaitu P(O) = 1.

Pasangan (O, , P) disebut ruang ukuran peluang atau ruang probabilitas.

(Hogg dan Craig 2005)

Definisi 6 (Kejadian Saling Bebas)

Kejadian A dan B dikatakan saling bebas jika:

A B A B .

Secara umum, himpunan kejadian {Ai; i I} dikatakan saling bebas jika:

i i

i J i J

A A

untuk setiap himpunan bagian J dari I.

(Grimmett dan Stirzaker 1992)

Peubah Acak dan Fungsi Sebaran Definisi 7 (Peubah Acak)

Misalkan O adalah ruang contoh dari suatu percobaan acak. Fungsi X yang terdefinisi pada O yang memetakan setiap unsur ? O ke satu dan hanya satu bilangan real X(? ) = x disebut peubah acak.

Ruang dari X adalah himpunan bagian bilangan real X(? ) = {x : x = X(? ), ? O}. (Hogg dan Craig 2005) Peubah acak dinotasikan dengan huruf kapital, misalnya X, Y, Z. Sedangkan nilai peubah acak dinotasikan dengan huruf kecil seperti x, y, z.

Definisi 8 (Peubah Acak Diskret)

Peubah acak X dikatakan diskret jika semua himpunan nilai dari peubah acak tersebut merupakan himpunan tercacah.

5

Definisi 9 (Fungsi Sebaran)

Misalkan X adalah peubah acak dengan ruang . Misalkan kejadian A=(-8,x] , maka peluang dari kejadian A adalah pX A X x FX x .

Fungsi FX disebut fungsi sebaran dari peubah acak X.

(Hogg dan Craig 2005)

Definisi 10 (Fungsi Kerapatan Peluang)

Fungsi kerapatan peluang dari peubah acak diskret X adalah fungsi p : ? [0,1] yang diberikan oleh:

X

p x X x .

(Hogg dan Craig 2005)

Definisi 11 (Peubah Acak Poisson)

Suatu peubah acak X disebut peubah acak Poisson dengan parameter ?, ?> 0, jika fungsi kerapatan peluangnya diberikan oleh

!

k X

p k X k e

k , untuk k = 0, 1, …

(Ross 2003)

Nilai Harapan, Ragam, dan Momen Definisi 12 (Nilai Harapan)

Misalkan X adalah peubah acak diskret dengan fungsi kerapatan peluang X

p x X x . Nilai harapan dari X, dinotasikan dengan E(X), adalah X

x x

X x X x x p x ,

jika jumlah di atas konvergen mutlak.

(Hogg dan Craig 2005)

Definisi 13 (Ragam)

Misalkan X adalah peubah acak diskret dengan fungsi kerapatan peluang pX x dan nilai harapan E(X). Maka ragam dari X, dinotasikan dengan Var X atau 2

X, adalah

2 2

2

X X

x

X X X X p x .

6

Definisi 14 (Momen ke-k)

Jika k adalah bilangan bulat positif, maka momen ke-k atau mkdari peubah acak X

adalah k k

m X .

(Hogg dan Craig 2005)

Definisi 15 (Momen Pusat ke-k₎

Jika k adalah bilangan bulat positif, maka momen pusat ke-k atau _k dari peubah acak X adalah

1

k k X m .

(Hogg dan Craig 2005) Nilai harapan dari peubah acak X juga merupakan rataan atau momen pertama dari X. Nilai harapan dari kuadrat perbedaan jarak antara peubah acak X dengan nilai harapannya disebut ragam atau variance dari X. Ragam merupakan momen pusat ke-2 dari peubah acak X.

Penduga

Definisi 16 (Statistik)

Statistik adalah suatu fungsi dari satu atau lebih peubah acak yang tidak tergantung pada satu atau beberapa parameter yang nilainya tidak diketahui.

(Hogg dan Craig 2005)

Definisi 17 (Penduga)

Misalkan X1, X2, …, Xnadalah contoh acak. Suatu statistik u(X1, X2, …, Xn) yang

digunakan untuk menduga fungsi parameter g(?), dikatakan sebagai penduga (estimator) bagi g(?), dilambangkan oleh gˆ .

Bilamana nilai X1 = x1, X2 = x2, …, Xn = xn, maka nilai u(x1, x2, …, xn) disebut

sebagai dugaan (estimate) bagi g(?).

7

Proses Poisson

Definisi 18 (Proses Stokastik)

Proses stokastik X X t,t T adalah suatu himpunan dari peubah acak yang memetakan suatu ruang contoh ke suatu ruang state S.

(Ross 1996) Jadi, untuk setiap t pada himpunan indeks T, X (t) adalah suatu peubah acak. Kita sering menginterpretasikan t sebagai waktu dan X(t) sebagai state (keadaan) dari proses pada waktu t.

Suatu proses stokastik X disebut proses stokastik dengan waktu diskret jika himpunan indeks T adalah himpunan tercacah, sedangkan X kita sebut proses stokastik dengan waktu kontinu jika T adalah suatu interval.

Definisi 19 (Inkremen Bebas)

Suatu proses stokastik dengan waktu kontinu X t , t T disebut memiliki inkremen bebas jika untuk semua t₀ t₁ t₂... t_n, peubah acak X t₁ X t₀ ,

1 2 X t t

X , . . ., X t_n X t_n1 adalah bebas.

(Ross 1996) Dengan kata lain, suatu proses stokastik dengan waktu kontinu X disebut memiliki inkremen bebas jika proses berubahnya nilai pada interval waktu yang tidak tumpang tindih (tidak overlap) adalah bebas.

Definisi 20 (Inkremen Stasioner)

Suatu proses stokastik dengan waktu kontinu X t ,t T disebut memiliki inkremen stasioner jika X t s X t memiliki sebaran yang sama untuk semua nilai t.

8

Definisi 21 (Proses Pencacahan)

Suatu proses stokastik N t,t 0 disebut proses pencacahan jika N t menyatakan banyaknya kejadian yang telah terjadi sampai waktu t.

Suatu proses pencacahan N t harus memenuhi syarat – syarat berikut: (i) N t 0 untuk semua t 0, .

(ii) Nilai N t adalah integer.

(iii) Jika s < t maka N s N t , s,t 0, .

(iv) Untuk s < t maka N t N s , sama dengan banyaknya kejadian yang terjadi pada selang s, . t

(Ross 1996)

Definisi 22 (Proses Poisson)

Suatu proses pencacahan N t,t 0 disebut proses Poisson dengan laju , 0 , jika dipenuhi tiga syarat berikut:

(i) N 0 0.

(ii) Proses tersebut memiliki inkremen bebas.

(iii) Banyaknya kejadian pada sembarang interval waktu dengan panjang t, memiliki sebaran (distribusi) Poisson dengan nilai harapan t. Jadi untuk semua t,s 0,

. . . 1, , 0 , !

P k

k t e k s N s t N

k t

9

Beberapa Jenis Sebaran Pencampur

Dalam beberapa sebaran Poisson campuran dan beberapa sebaran diskret digunakan sebaran pencampur antara lain:

Sebaran eksponensial

Suatu sebaran yang memiliki fungsi kepekatan peluang ( | ) exp( ) dengan , 0

g .

Sebaran Lindley

Suatu sebaran yang memiliki fungsi kepekatan peluang 2

( | ) ( 1) exp( ) dengan , 0 1

p

g p p p

p .

Sebaran Inverse Gaussian

Suatu sebaran yang memiliki fungsi kepekatan peluang 2

3/ 2 1 2

( | , ) exp( ) exp( ( )) dengan , , 0 2

2

g .

Sebaran gamma

Suatu sebaran yang memiliki fungsi kepekatan peluang 1

( | , ) e x p ( ) / ( ) d e n g a n , 0

g .

Sebuah fungsi yang digunakan dalam sebaran gamma adalah fungsi gamma yang didefinisikan dengan 1

0

( ) e d untuk 0

Sebaran lognormal

Suatu sebaran yang memiliki fungsi kepekatan peluang

2 2 2

2 ) (log

exp 2 1 )

, | (

g .

Sebaran beta

Suatu sebaran yang memiliki fungsi kepekatan peluang

1 1

( ) (1 ) / ( , )

g B dimana , 0, 0 1. Sebaran binomial

10

( ) N x(1 )N x h

x denganx 0,1,...,N dan 0 1 untuk nilai peluang sukses setiap kali percobaan.

Sebaran Poisson Campuran

Misalkan f x( | )adalah sebaran bersyarat dengan merupakan nilai dari peubah acak lain yang menyebar dengan fungsi sebaran G( | ). Gabungan dari kedua sebaran akan membentuk sebaran campuran:

) | ( ) | ( )

|

(x f x dG

f (1)

Dalam sebaran bersyarat ini, peneliti menggunakan kasus khusus yaitu sebaran Poisson dengan fungsi kerapatan masa f(x| ) exp( ) x/x!,x 0,1,... dimana 0 dan merupakan nilai dari peubah acak yang menyebar dengan fungsi sebaran G( | ). Gabungan dari kedua sebaran akan membentuk sebaran campuran:

0

exp( )

( | ) ( | )

!

x g

P x dG

x

(2)

yang dikenal dengan nama sebaran Poisson campuran.

Metode Pendugaan Parameter

Ada beberapa metode yang digunakan untuk pendugaan parameter, diantaranya adalah metode momen dan metode kemungkinan maksimum (Maximum Likelihood, ML)

Metode Momen

Menurut Nasoetion (1984), metode momen digunakan untuk menduga parameter suatu sebaran dengan memisalkan

1, 2,..., ( | )

bsi

n X

X X X f x dan untuk bilangan bulat positif r, ( r)

r E X dan

1 1 n

r

r i

m X

n dengan mr adalah momen contoh, sehingga pendugaan momen dari

11

Metode Kemungkinan Maksimum (Maximum Likelihood, ML)

Menurut Hogg dan Craig (2005), dengan memisalkanX X₁, ₂,...,X_n masing-masing peubah acak yang saling bebas dengan sebaran yang memiliki fungsi kepekatan peluang ( ; )f x dimana 0 1, dan adalah ruang contoh.

Fungsi kepekatan peluang bersama dari X X₁, ₂,...,X_n adalah

1 2 1 2

( ; , ,..., _n) ( ; ) ( ; )... ( ; )_n

L x x x f x f x f x yang disebut juga sebagai fungsi kemungkinan.

Andaikan dicari fungsi sederhana dari x x₁, ₂,...,x_n yaituu x x( ,_{1 2},...,x_n) sehingga u x x( ,_{1 2},...,x_n) membuat fungsi kemungkinan L maksimum untuk semua . Statistik u X X( ₁, ₂,...,X_n)disebut penduga kemungkinan maksimum dari yang dinotasikan dengan ˆ u X X( ₁, ₂,...,X_n).

Seringkali untuk pendugaan parameter dengan menggunakan metode Maximum Likelihood tidak bisa secara langsung karena datanya tidak lengkap, untuk itu dapat digunakan algoritme EM (Expectation Maximization). Hal ini sudah dibahas oleh Dimitris Karlis (2005) yang prinsip dasarnya digunakan untuk data tidak lengkap dengan cara memaksimumkan nilai harapan ke fungsi kemungkinannya.

Algoritme EM

Menurut Dempster (1977) algoritme EM adalah suatu algoritme yang sangat handal untuk pendugaan parameter dari fungsi kemungkinan pada data tidak teramati terutama digunakan untuk sebaran campuran karena dalam sebaran campuran ada data tidak teramati.

Ada dua tahap dalam menggunakan algoritme EM yaitu tahap E (Expectation) dan tahap M (Maximization). Dalam tahap E mencari nilai harapan penduga parameter dan tahap M memaksimumkan nilai harapan ke fungsi kemungkinan.

12

( ) ( )

( | k ) (log ( | ) | , k )

Q E p Y X dimana nilai harapan dihitung dengan menggunakan sebaran bersyarat f Y X( | , ( )k ).

Pada tahap M, nilai Q( | ( )k )dimaksimumkan terhadap dimana merupakan penduga parameter tertentu. Ketika model data lengkap berasal dari keluarga eksponensial, maka tahap E dihitung nilai harapan bersyarat dari statistik cukupnya. Ini sangat berguna dalam kasus yang akan dilakukan.

Dalam sebaran campuran, nilai-nilai data yang tidak teramati adalah realisasi dari _idimana _i adalah parameter yang tidak teramati untuk setiapX_i. Sehingga pada tahap E, kita perlu menghitung nilai harapan bersyarat dari fungsi _i(tidak teramati) dan memaksimumkan fungsi kemungkinan dari model data lengkap yang direduksi dari sebaran campuran.

Dalam kasus campuran yang berasal dari keluarga eksponensial, nilai harapan bersyarat diperlukan untuk pendugaan kemungkinan maksimum sebaran campuran.

Langkah-langkah untuk mencari nilai penduga kemungkinan maksimum dengan algoritme EM dapat diuraikan dengan beberapa tahap yaitu

1 Tahap E adalah tahapan yang menggunakan nilai dugaan terakhir atau saat ini (k)

dari iterasi ke-k, kemudian hitung nilai pseudo (samaran) ),

, | ) (

( _{j i} (k)

ij E h X

t dimana i 1,...,n,j 1,...,m ketika h_j(.)adalah fungsi sebaran tertentu dan adalah nilai penduga.

2 Tahap M adalah tahapan yang menggunakan nilai pseudo t_ijdari tahap E untuk memaksimumkan kemungkinan dari sebaran campuran dan diperoleh nilai terbaru dari yaitu (k 1)dari iterasi ke-k+1.

3 Iterasi akan berhenti ketika selisih (k) _dan (k 1) _{kurang dari suatu} bilangan yang sangat kecil, jika tidak iterasi berlanjut ke tahap E.

13

Definisi 23

Sebaran diskret dikatakan berasal dari keluarga sebaran deret kuasa jika fungsi peluang diberikan P(x| ) _x x(A( )) 1,x 0,1,...dengan _x 0 dan

0

( ) _x x

x

A ,suatu fungsi dari yang tidak tergantung pada x.

Jika sebaran g merupakan sebaran pencampur deret kuasa maka akan membentuk sebaran campuran yaitu

( | ) ( | )

( )

x x g

P x g d

A

(3)

Lema 1 (Sapatinas 1995)

Nilai harapan posteriorE( r|x) dimana x merupakan syarat dari yang menyebar sebaran diskret deret kuasa dan mempunyai fungsi kepekatan peluang g( )diberikan oleh

r x g x g r x P r x P x E ) | ( ) | ( ) | (

dengan P_g(x| )adalah sebaran campuran dari persamaan (3), bukti dapat dilihat pada Lampiran 1.

Sebagai contoh kasus khusus sebaran Poisson dengan _x 1/x! untuk Lema 1 sehingga nilai harapan diberikan:

) | ( ! ) | ( )! ( ) | ( x P x r x P r x x E g g

r ₍₄₎

dengan P_g(x| )diberikan dalam persamaan (2).

14

=

)! (

1 ) | (

! 1 ) | (

r x x P

x r x P

g g

) | ( !

) | ( )! (

x P x

r x P r x

g g

¦

METODOLOGI PENELITIAN

Metode yang digunakan dalam penelitian adalah studi pustaka disertai dengan perhitungan numerik untuk memperoleh penduga parameter. Langkah-langkah yang akan dilakukan dalam penelitian adalah: (1) Penentuan formula eksplisit dari beberapa sebaran Poisson campuran dan beberapa sebaran diskret dengan menentukan fungsi sebaran geometri ( ) , sebaran Poisson-Lindley ( )p , sebaran Poisson-Inverse Gaussian ( , ) , sebaran binomial negatif ( , ) , sebaran Neyman( , ) , sebaran Poisson-lognormal ( , ) , sebaran Yule ( ) dan sebaran beta-binomial ( , ) , (2) Penentuan formula untuk tahap E dan M untuk setiap sebaran Poisson campuran dan beberapa sebaran diskret dengan menggunakan algoritme EM, dan (3) Penentuan nilai dugaan parameter dengan menggunakan algoritme EM berdasarkan data empirik. Nilai dugaan parameter ini dihitung secara numerik dengan menggunakan software Matlab 6.5.

Untuk menguji kesesuaian sebaran hipotetik dengan sebaran data empirik digunakan uji Khi-kuadrat.

Formula uji Khi-kuadrat

Uji keselarasan (Goodness of Fit-Test) antara frekuensi teramati dengan frekuensi harapannya didasarkan pada besaran statistik uji:

2 2

1

( )

k

i i

i i

o e e

dengan 2adalah nilai sebaran Khi-kuadrat

i

o adalah frekuensi teramati untuk sel ke-i.

i

e adalah frekuensi harapan untuk sel ke-i.

SOLUSI EKSPLISIT BEBERAPA SEBARAN POISSON CAMPURAN DAN BEBERAPA SEBARAN DISKRET

Beberapa Sebaran Poisson Campuran

Gabungan sebaran Poisson dengan sebaran lain dari persamaan (2) akan membentuk sebaran Poisson campuran, antara lain:

Sebaran geometri( )

Sebaran eksponensial memiliki fungsi kepekatan peluang ( | ) exp( ) dengan , 0

g . Jika sebaran Poisson ( ) dimana

merupakan nilai dari peubah acak yang menyebar eskponensial maka dihasilkan sebaran Poisson campuran dengan fungsi kepekatan peluang bersyarat:

1

( | ) , 0,1,..., 0

1 1

x g

P x x (5)

yang dinamakan sebaran geometri ( ) .

Bukti: ) | (x P_g

0 !

x

e

e d x

e e d x

x

0 !

d e

x

x

0 ) 1 (

! (6)

Misalkan v ( 1) maka dv ( 1)d , dengan batasan v 0sampai v dari perubahan 0 sampai sehingga persamaan (6) menjadi

) | (x

P_g v e dv

x

v x

0 ( 1)

1 1

!

0 1 1 1

! v e dv

x

v x x

) 1 ( 1 1 !

1 x x

x

! 1 1 !

1 x x

17

x

1 1

1 ¦

Sebaran Poisson-Lindley ( )p

Sebaran Lindley memiliki fungsi kepekatan peluang 2

( | ) ( 1) exp( ) dengan , 0 1

p

g p p p

p . Jika sebaran Poisson ( )

dimana merupakan nilai dari peubah acak yang menyebar Lindley maka dihasilkan sebaran Poisson campuran dengan fungsi kepekatan peluang bersyarat:

2

3

( 2 )

( | ) , 0,1, ..., 0

( 1)

g x

p p x

P x p x p

p (7) yang dinamakan sebaran Poisson-Lindley ( )p .

Bukti: ) | (x p P_g

2

0

( 1) ! ( 1)

x p e p e d x p

2 ( 1) 0 ( 1) ( 1) !

x p p e d p x

0 0 ) 1 ( ) 1 ( 1 2 ! ) 1

(p x e d e d

p x p x p

(8) Misalkan v (p 1) maka dv (p 1)d , dengan batasan v 0sampai v dari perubahan 0 sampai sehingga persamaan (8) menjadi

) | (x p P_g 0 0 1 2 1 1 1 1 1 1 ! ) 1

( p e p dv

v dv p e p v x p p v x v x 0 0 1 1 2 1 1 1 1 1 1 1 1 ! ) 1

(p x p p v e dv p p v e dv

p x v

x v x x 0 0 1 1 2 1 1 1 1 ! ) 1

(p x p p v e dv v e dv

p x v x v

x ) 1 ( ) 2 ( 1 1 1 1 ! 2 2 x x p p x p x 2 2 1 1

( 1)! !

! 1 1

x

p

x x

18

2 2

1 1

! ( 1) 1

! 1 1

x

p

x x

x p p

1 2 1 1 2 2 p x p p p x 3 2 ) 1 ( ) 2 ( x p x p p ¦

Sebaran Poisson-Inverse Gaussian( , )

Sebaran Inverse Gaussian memiliki fungsi kepekatan peluang 2

3/ 2 1 2

( | , ) exp( ) exp( ( )) dengan , , 0 2

2

g .

Jika sebaran Poisson ( ) dimana merupakan nilai dari peubah acak yang menyebar Inverse Gaussian maka dihasilkan sebaran Poisson campuran dengan fungsi kepekatan peluang bersyarat dengan (2 2)1/2:

)), ( exp( ) , | 0 (

P P(1| , ) P(0 | , )

,... 3 , 2 , ) , | 2 ( 1 ) , | 1 ( ) 3 2 ( 1 ) , | ( 2

2 P x x

x x P x x x

P (9)

yang dinamakan sebaran Poisson-Inverse Gaussian ( , ) .

Bukti: Untuk x = 0

) , | 0 ( g P 2 2 1 3 ( ) 2 2 0 2

e e e d

d e e 0 2 2 1 2 3 2 2 2 2 2

2 2 2

1 (2 ) 3

2 2 0

2 e e d

2 2 2 2 1 2 2 3 ₂ 2 0

2 e e d

(10)

Misalkan 2

1 2 1 2 2

19

1 3

2 2 2

1 2 2

dz d atau 2

3 3

2 2

1 2 2

dz d d dengan

batasan z sampai z dari perubahan 0 sampai sehingga persamaan (10) menjadi

) , | 0 ( g

P e e z e dz

2 3 2 2 1 2 3 2 2 2

dz e

e z2

2 2 1 ) 2 (

2 2 2

) ( e

)) (

exp( dimana 2 2

¦

Untuk x = 1 (1| , )

g P 2 2 1 3 ( ) 2 2 0 2

e e e d

2 2 2 2

1 2

1 2 2 0

2 e e d

2 2 2

1 (2 ) 1

2 2 0

2 e e d

2 2 2 2 1 2 2 1 ₂ 2 0

2 e e d

(11)

Misalkan 2

1 2 1 2 2

z pada saat z = 0 maka 2 2 dan

1 3

2 2 2

1 2 2

dz d atau 2

3 3

2 2

1 2 2

dz d d dengan

batasan z sampai z dari perubahan 0 sampai sehingga persamaan (11) menjadi

(1| , )

g

P

2 2

3

1 1 ₂

2 2 2 2

z

e e e dz

2 2 1 2 2 2 z

e e e dz

2 2 1 2 2 2 2 2 z

e e e dz

2

2

1 ( 2 )

20

( ) 2 2 e

(0 | , ) P

¦

Sebaran binomial negatif( , )

Sebaran gamma memiliki fungsi kepekatan peluang 1

( | , ) e x p ( ) / ( ) d e n g a n , 0

g . Jika sebaran

Poisson ( ) dimana merupakan nilai dari peubah acak yang menyebar gamma maka dihasilkan sebaran Poisson campuran dengan fungsi kepekatan peluang bersyarat:

( ) 1

( | , )

! ( ) 1 1

x

g

x P x

x (12)

yang dinamakan sebaran binomial negatif ( , ) untuk i 0,1,..., , 0.

Bukti: ) , | (x P_g

1 ( )

0 ! ( )

x e e d x

0 1 ) 1 ( ) (

! e d

x

x

(13) Misalkan v (1 ) maka dv (1 )d , dengan batasan v 0sampai v dari perubahan 0 sampai sehingga persamaan (13) menjadi

) , | (x

P_g e v dv

x x v 1 1 1 ) ( ! 1 0 0 1 1 1 ) (

! e v dv

21

Sebaran Neyman( , )

Sebaran Poisson memiliki fungsi kepekatan peluang ( )

d e n g a n 0 !

k v x

e k v

v

x dimana merupakan nilai dari peubah acak. Jika k menyebar menurut sebaran Poisson ( ) dimana merupakan nilai dari peubah acak, maka dihasilkan sebaran Poisson campuran dengan fungsi kepekatan peluang bersyarat:

0

( ) ( | , )

! !

k v x k

g

k

e k v e

P x v

x k

(14) yang dinamakan sebaran Neyman ( , ) untuk x 0,1,... dan , 0, sehingga

(0 | , ) exp( )

g

P , dimana exp( v) dan

0

( 1) ( 1 | , ) ( | , )

! r x g g r v

x P x v P x r v

r

Bukti: Untuk x = 0

(0 | , )

g P v 0 ! kv k k e e k

( ) 0 ! kv k k e k

(2 ) 2 (3 ) 3 ( )

...

2! 3!

v v

v e e

e e

2 2 3 3

(1 ...)

2! 3!

v v

v e e

e e

2 3

(1 ...)

2! 3!

Ekspansi Deret Maclaurin

e dimana e v

e e

( ) e

exp ( )

¦ ( 1| , )

g

P x v

1 0

( ) ( 1)! !

kv x k

k

e kv e

22

0

( )

( 1) ! !

kv x k

k

e kv kv e

x x k

(x+1)P x_g( 1| , )v 0

( )

! !

kv x k

k

e kv e k

v

x k

1

( )

! ( 1)!

kv x k

k

k

e kv e v x k

1 1 ( )

! ( 1)!

kv x k

k

k

e kv e v

x k

(15) Misalkan n = k – 1 dengan batasan n = 0 sampai n = 8 dari perubahan k = 1 sampai k = 8 sehingga persamaan (15) menjadi

( 1) 0

(( 1) )

! !

n v x n

n

n

e n v e

v

x n

0

(( 1) )

! !

nv x n

n v

n

e n v e

v e

x n

( ) 0

(( 1) )

! !

nv n x

n

n

e n v

v n x ( ) 0 ( 1) ! !

nv n x x

n

n

e n v

v n x 0 ( | , ) ! r x g r v

v P x r v

r

¦

Sebaran Poisson-lognormal( , )

Sebaran lognormal memiliki fungsi kepekatan peluang

2 2 2 2 ) (log exp 2 1 ) , | (

g . Jika sebaran Poisson ( ) dimana

merupakan nilai dari peubah acak yang menyebar lognormal maka dihasilkan sebaran Poisson campuran dengan fungsi kepekatan peluang bersyarat:

2

2 1

2 0

1 (log )

( | , ) exp( ) exp

2 2 !

x

P x d

x (16)

23

Bukti:

) , | (x 2

P_g e d

x

e x 2

2

2 ) (log

0 2

1 !

d e

e x

x 2

2

2 ) (log

0 1 2

! 1

2

2 1

2 0

1 (log )

( | , ) exp( ) exp

2 2 !

x g

P x d

x ¦

Beberapa Sebaran Diskret Sebaran Yule( )

Sebaran beta memiliki fungsi kepekatan peluang

1 1

( ) (1 ) / ( , )

g B dimana , 0, 0 1 . Jika sebaran geometri dengan (1 ) 1 merupakan nilai peubah acak yang menyebar beta tipe I ( ,1) dengan fungsi kerapatan masa _{g( )} 1_{, maka dihasilkan sebaran} diskret dengan fungsi kepekatan peluang bersyarat:

( 1) ! ( )

( 2)

x P x

x

(17) yang dinamakan sebaran Yule ( ) untuk x 0,1,..., 0.

Bukti: Fungsi beta

1

1 1

0

( , ) (1 )

B d

beta I ( ,1)

1 1 0 ( ,1)

B d

1 1

0

1

beta I ( ,1) disubstitusikan ke g( )

1_{(1 )} 1 ( , ) B

1 1

24

Sebaran geometri , 0,1,..., 0

1 1 1

) |

(x x

P

x

dengan

parameter

1 sehingga ( | )P x

1 1

1 1

1 1

x

(1 )x

Sebaran Yule adalah gabungan antara sebaran beta I dengan sebaran geometri sehingga

( ) P x =

1 1 0

(1 )x_d

1

0

(1 )x_d

( 1, 1)

B x

( 1) ( 1)

( 2)

x x

( 1) !

( 2)

x x

Sebaran beta-binomial ( , )

Sebaran binomial memiliki fungsi kepekatan peluang (1 )

x N x

N

x denganx 0,1,...,N dan 0 1 untuk nilai peluang sukses setiap kali percobaan. Jika sebaran beta 1 1

( ) (1 ) / ( , )

g B dimana

merupakan nilai dari peubah acak yang menyebar binomial untuk , 0, 0 1 , maka dihasilkan sebaran diskret dengan fungsi kepekatan peluang bersyarat:

( , )

( | , )

( , )

N B x N x

P x

x B

(18)

25

Bukti: ( | , ) P x

1 1 1

0

(1 ) (1 )

( , )

x N x

N

x B

1 1 1

0

(1 ) ( , )

x N x

N

d

x B

( , )

( , )

N B x N x

x B

¦

PENDUGAAN PARAMETER DENGAN ALGORITME EM

Untuk pendugaan parameter yang baru dari beberapa sebaran Poisson campuran dan beberapa sebaran diskret dengan menggunakan algoritme EM. Dalam algoritme EM, pendugaan parameter diperoleh dengan cara memaksimumkan nilai harapan ke fungsi kemungkinan dari data tidak lengkap yang dilakukan secara iteratif (berulang).

Beberapa Sebaran Poisson Campuran Sebaran geometri( )

Pendugaan parameter sebaran geometri dapat diperoleh dengan menggunakan algoritme sebagai berikut:

Tahap E: hitung nilai pseudo

1 1 ) | ( ) | 1 ( ) 1 ( ) | ( lama i lama i lama i i i i i x x P x P x x E

t untuk i 1,...,n

Tahap M: temukan nilai penduga baru _baru

1 1 1 x t n _lama n i i baru

Bukti (Tahap E)

Tahap E dapat diperoleh dari persamaan (5) yang disubstitusikan ke persamaan (4) yaitu

1

( | ) , 0,1,..., 0

1 1

x g

P x x adalah sebaran geometri

disubstitusikan ke ) | ( ! ) | ( )! ( ) | ( x P x r x P r x x E g g

r _{untuk r = 1 dan sehingga}

( | )

i i i

t E x ( 1) ( 1| )

( | )

i i lama

i lama

x P x

27

1 1 ( 1) 1 1 i i lama lama x

x untuk i 1, 2,...,n

¦

Bukti (Tahap M) ( ) L 1 ( | ) n i i P t 1 1 1 1 n i i n t

log ( )L

1 1 log log 1 1 n i i n t 1 1 log log (1 ) log

1

n i i

n n t

Untuk memperoleh nilai penduga _baru yang memaksimumkan fungsi log-likelihood maka turunan pertama dari L( ) terhadap harus sama dengan 0 sehingga

log ( )L ₁

0 1 1 n i i t n n 1 1

(1 ) 0

n i

n n t

28

Sebaran Poisson-Lindley( )p

Pendugaan parameter sebaran Poisson-Lindley dapat diperoleh dengan menggunakan algoritme sebagai berikut:

Tahap E: hitung nilai pseudo

) 1 )( 2 ( ) 1 )( 3 ( ) | ( ) | 1 ( ) 1 ( ) | ( lama i lama i i lama lama i lama i i i i i p x p x x p p x P p x P x x E t

untuk i 1,...,n dan dari nilai tahap E hitung n

i ti n

t

1 / . Tahap M: temukan nilai penduga baru p _baru

t t t t p_baru 2 1 6 ) 1 ( 2

Bukti (Tahap E)

Tahap E dapat diperoleh dari persamaan (7) yang disubstitusikan ke persamaan (4) yaitu

2

3

( 2 )

( | ) , 0,1, ..., 0

( 1)

g x

p p x

P x p x p

p adalah sebaran Poisson-Lindley

disubstitusikan ke ) | ( ! ) | ( )! ( ) | ( x P x r x P r x x E g g r

untuk r = 1 dan psehingga

( | )

i i i

t E x

4 2

3 2

( 1) ( 2 1) /( 1)

( 2 ) /( 1)

i

i

x

i lama lama i lama

x

lama lama i lama

x p p x p

p p x p

( 1)( 3)

( 2)( 1)

i lama i

lama i lama

x p x

p x p

¦

Bukti (Tahap M) ( ) L p 1 ( | ) n i i

g t p

2

1 1

( 1) exp( ) 1

n _{n n}

i i

i i

p

t p t

p

log ( )L p

1 1

2 ln ln( 1) ln( 1)

n n

i i

i i

29

Untuk memperoleh nilai penduga p_baru yang memaksimumkan fungsi log-likelihood maka turunan pertama dari L p( ) terhadap p harus sama dengan 0 sehingga

log ( )L p

p 1

2

0 1

n i i

n n

t

p p

1

2 ( 1)

0 ( 1)

n i i

n np p p t

p p

2 ( 1)

0 ( 1)

p p p t p p

2 ( 1) p

t p p

Dengan menggunakan persamaan 2 ( 1) p

t

p p , dimana t rata-rata dari nilai harapan sehingga

2 2 p

t

p p

2

( 2) 0 p t pt p

2

( 1) 2 0 p t p t

2

( 1) ( 1) 4. .2 2

t t t

p

t

( 1) 2 1 8

2

t t t t

p

t

( 1) 6 1

2

baru

t t t

p

t

¦

Sebaran Poisson-Inverse Gaussian( , )

30

Tahap E: hitung nilai pseudo ( | )

i i i

t E X dan s_i E( _i1|X_i) untuk i 1,...,n dengan ( _i| _i 0)

E X dimana (2 2)1/2. Tahap M: temukan nilai penduga baru.

1

ˆ n _/

i i

M t ndan

1 1 1

ˆ n ₍ ˆ ₎

i i

n s M maka _baru ˆ1/ 2dan _{baru baru}/Mˆ

Bukti (Tahap E)

Sebaran Inverse Gaussian adalah kasus khusus dari sebaran Generalized Inverse Gaussian (GIG) dengan fungsi kepekatan peluang

1 2

2 1

( | , , ) exp

2 ( ) 2

g K

dimana 1 1 ( ) 1 2 0 1 ( ) 2 y y

K y e dyadalah modifikasi fungsi Bessel.

Untuk membuktikan E( _i|X_i)menggunakan momen dari sebaran GIG dengan persamaan

( ) ( )

( )

r

r K r

E

K

(19)

Bukti persamaan (19) ( r)

E 0 ( ) r g d

1 2 2 0 1 exp

2 ( ) 2

r d K 1 2 2 0 1 exp

2 ( ) 2

r

d K

Misalkan: sehingga

( r) E 2 1 2 2 0 1 exp

2 ( ) 2

r

31

2 1 2

2 0

1 exp

2 ( ) 2

r d K 2 1 1 2 2 0 1 exp

2 ( ) 2

r

d K

Misalkan: y 2 maka dy 2d sehingga

( r) E 1 2 1 2 0 1 exp

2 ( ) 2

r

y

y y d

K

1 1

2

2 2 2 1

2 0

1 1

exp

2 ( ) 2

r r

r

y y y dy

K 1 2 1 0 1 exp

2 ( ) 2

r

r r

y y y dy

K 2 ( ) ( ) r r r K K ( ) ( ) r r K K

¦

Jika GIG( , , ) maka |x GIG( x, 2 2, )sehingga untuk 1

0 dan 2

x maka (E _i|X_i 0)

( _i| _i 0)

E X 1( )

( ) K K

1/ 2 1/ 2 ( ) ( ) K K

1/ 2 1

0

3/ 2 1

0

1 1

exp ( )

2 2

1 1

exp ( )

2 2

y y y dy

y y y dy

32

untuk 1 dan 1 2

x maka (E _i|X_i 1) 2(1 )

( _i| _i 1)

E X 3/ 2

1/ 2 ( ) ( ) K K

1/ 2 1

0

1/ 2 1

0

1 1

exp ( )

2 2

1 1

exp ( )

2 2

y y y dy

y y y dy

3/ 2

1/ 2 2 (1 )

(1 ) ( )

2 ( ) e

e

2

(1 ) ¦

untuk 2 dan 3 2

x maka (E _i|X_i 2) 2

(3 (3 ))

(1 ) ( _i| _i 2)

E X 5 / 2

3/ 2 ( ) ( ) K K

3/ 2 1

0

1/ 2 1

0

1 1

exp ( )

2 2

1 1

exp ( )

2 2

y y y dy

y y y dy

5 / 2

3/ 2

2 (3 (3 ))

(3 (3 ))

( )

(1 ) 2 (1 )

( ) e

e

2

(3 (3 ))

(1 ) ¦

Bukti (Tahap M)

2

3/ 2 1 2

( | , ) exp( ) exp( ( )) dengan , , 0 2

33

( , ) L 1 ( | , ) n i i g

3 2 2 2 1 1 1 1

exp( ) exp

2 2

n _{n n}

i n i

i i

i i

n

ln ( , )L

2 2

1 1

1

3 1

ln ln 2 ln

2 2

n n

i n i

i i

i i

n n

Untuk memperoleh nilai penduga _baru yang memaksimumkan fungsi log-likelihood maka turunan pertama dari ( , )L terhadap harus sama dengan 0 sehingga

ln ( , )L

1 0 n i i n

1 n i i

n dimana ˆ M sehingga 1 ˆ n i i t M n ˆ baru baru M

¦ Untuk memperoleh nilai penduga _baru yang memaksimumkan fungsi log-likelihood maka turunan pertama dari L( , ) terhadap harus sama dengan 0 sehingga

ln ( , )L

34

2 2 1 1 ˆ n i i n M

2 2

1 ˆ 1

n n i i i i n M

2 2 1 1

ˆ n n ˆ ₀

i i

i i

nM M

2 1 1

1 1 ˆ ˆ ˆ ˆ 1 ˆ n n i i i i n n i i i i nM nM M M M

2 1 1 1 1 1 ˆ n i i n i n i i i n M

2 1 1 ˆ n i i n s M

1 2 1 1 ˆ n i i

n s M dimana 2 ˆ sehingga

1/ 2 ˆ baru

¦

Sebaran binomial negatif( , )

Pendugaan parameter sebaran binomial negatif dapat diperoleh dengan menggunakan algoritme sebagai berikut:

Tahap E: hitung nilai pseudo

lama lama i i i i x x E t 1 ) |

( dan

) 1 log(

)

( _{lama i lama}

i x

s

35

Tahap M: temukan nilai penduga baru t

lama

baru / dan

) ( ) log( ) ( 3 lama baru lama lama baru s

dimana ₃(x)notasi fungsi trigamma, (x)/ x turunan fungsi digamma.

Bukti (Tahap E)

Tahap E dapat diperoleh dari persamaan (12) yang disubstitusikan ke persamaan (4) yaitu

( ) 1

( | , )

! ( ) 1 1

x g

x P x

x adalah sebaran

binomial negatif disubstitusikan ke

) | ( ! ) | ( )! ( ) | ( x P x r x P r x x E g g

r _{untuk r = 1}

dan , sehingga

( | )

i i i

t E x

1

( 1)! ( 1) 1

( 1)! ( ) 1 1

! ( ) 1

! ( ) 1 1

i

i

x

i i lama lama

i lama lama lama

x

i i lama lama

i lama lama lama

x x

x

x x

x

( ) ( ) 1

( ) 1

i lama i lama

i lama lama

x x x

1 i lama lama x

¦ Berdasarkan sebaran gamma dengan parameter dan

1 0 1 1 ( ) x

x e dx

sehingga 1 0 ( ) ( ) x

x e dx

Kedua ruas diturunkan terhadap sehingga diperoleh 1

2 0

'( ) ( ) ln ln

( )

x

36

( ) 1

'( ) ln

( ) ( ) ln ( )

ln ( )

( ) ln

dimana ( ) ln ( ) sebagai fungsi digamma

Jadi 1

0 1

(ln ) ln ( ) ln

( )

x

E X x x e dx

Jika sebaran gamma dengan parameter xdan 1 maka (log | )

i i i

s E x ( _lama x_i) log(1 _lama)

¦

Bukti (Tahap M) ( , )

L

1

( | , )

n i i

g t

1

1 1

exp ( ( ))

n n n

i i

n

i i

t t

ln ( , )L

1 1

ln ln ( ) ( 1) ln

n n

i i

i i

n n t t

Untuk memperoleh nilai penduga _baru yang memaksimumkan fungsi log-likelihood maka turunan pertama dari ( , )L terhadap harus sama dengan 0 sehingga

log ( , )L ( ₁ )

0 1

n i i

n t

n

1 1

(1 ) ( ) 0

n i

n n t

1 1 0

n i

37

1 1 n n i i i i n t t t n

lama baru t

¦ Untuk memperoleh nilai penduga _barumenggunakan metode Newton Raphson dengan rumus:

1 '( ) ''( ) i i i i f x x x f x 1

ln ( , ) ln ( )

'( ) ln ln

n

i i

i

L

f x n n t

2 2

2 2

ln ( , ) ln ( ) ''( )

( ) ( )

i

L

f x n

Sehingga

1 2

2

ln ln ( )

(ln

ln ( ) ( ) n i i baru lama t n n n 3

ln ( )

( )

baru lama

s

3 ( ) ln

( ) baru lama s

¦

Sebaran Neyman( , )

Pendugaan parameter sebaran Neyman dapat diperoleh dengan menggunakan algoritme sebagai berikut:

Tahap E: hitung nilai pseudo

lama i i i i v x X E

t ( | ) ( 1)

38

Tahap M: temukan nilai penduga baru

1 /

n

baru t _i t ni dan vbaru x/ baru

Bukti (Tahap E)

Tahap E dapat diperoleh dari persamaan (14) yang disubstitusikan ke persamaan (4) yaitu

0

( ) ( | , )

! !

k v x k

g

k

e k v e

P x v

x k adalah sebaran Neyman disubstitusikan ke

) | ( ! ) | ( )! ( ) | ( x P x r x P r x x E g g r

untuk r = 1 dan ,

sehingga

( | )

i i i

t E X ( 1) ( 1| , )

( | , )

i i

i

x P x

P x

1 0 0 ( ) ( 1)

( 1)! !

( ) ( )! ! i i x kv k i k i x kv k k i

e kv e

x

x k

e kv e

x k

0 ( 1) ( 1) i k i kv x x

0 k kv

( | )

i i i

t E X ( 1) ( 1| , )

( | , )

i i lama lama

lama i lama lama

x P x

v P x

¦

Bukti (Tahap M) ( | )

!

k

e g k

k adalah sebaran Poisson dengan parameter sehingga

1

( ) ( | )

n i i

L g t

1 1 ! i n t n i n i i e t 1 1

ln ( ) ln ln !

n n

i i

i i

39

Untuk memperoleh nilai penduga _baru yang memaksimumkan fungsi log-likelihood maka turunan pertama dari L( ) terhadap harus sama dengan 0 sehingga

1 ln ( )

0

n i i

t L

n

1

n i i

t t n

¦

( ) ( | )

!

kv x

e kv g x v

x adalah sebaran Poisson dengan parameter vsehingga

1

( ) ( | )

n i i

L v g x v

1

1 ( )

! i

n x kvn

i n

i i

e kv

x

1 1

ln ( ) ln ln !

n n

i i

i i

L v kvn