Analisis pengelompokan objek dengan metode single linkage clustering dan Diskriminan Linear untuk kasus dua kelompok

ANALISIS PENGELOMPOKAN OBJEK

DENGAN METODE SINGLE LINKAGE CLUSTERING

DAN DISKRIMINAN LINEAR UNTUK KASUS DUA KELOMPOK

MELINDA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ANALISIS PENGELOMPOKAN OBJEK

DENGAN METODE SINGLE LINKAGE CLUSTERING

DAN DISKRIMINAN LINEAR UNTUK KASUS DUA KELOMPOK

MELINDA

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRAK

MELINDA. Analisis Pengelompokan Objek dengan Metode Single Linkage Clustering dan Diskriminan Linear untuk Kasus Dua Kelompok. Dibimbing oleh MUHAMMAD NUR AIDI dan RETNO BUDIARTI.

Banyak keragaman yang dapat dijumpai pada kehidupan ini sehingga pengelompokan suatu objek yang relatif homogen selalu menjadi permasalahan yang menarik. Analisis cluster merupakan teknik multivariat yang tujuan utamanya mengelompokkan objek-objek berdasarkan kesamaan karakteristik di antara objek-objek tersebut. Ciri pengelompokan yang baik, pertama terdapat kesamaan yang tinggi antar anggota dalam satu kelompok. Kedua, antar kelompok yang satu dengan kelompok lainnya memiliki perbedaan yang tinggi.

Terdapat beberapa metode dalam analisis cluster, salah satu diantaranya adalah metode hierarki yang akan mengelompokkan objek-objek secara bertingkat. Metode agglomeratif merupakan metode hierarki yang sering dipakai untuk suatu data metrik. Metode ini secara algoritma akan mengelompokkan objek-objek berdasarkan tingkat kesamaan antar objek-objek dari yang terdekat sampai akhirnya semua objek berada dalam sebuah kelompok. Jarak antara suatu kelompok terhadap kelompok lainnya dihitung sebagai jarak minimum antara anggota kelompok pertama dengan anggota kelompok lainnya, metode pengukuran ini disebut sebagai

single linkage clustering merupakan metode yang paling sederhana.

Kevalidan hasil pengelompokan dengan metode yang digunakan perlu agar tidak terjadi kesalahan (misklasifikasi) yang cukup besar terutama pada saat menentukan strategi dari tujuan dilakukannya analisis cluster. Analisis diskriminan merupakan metode yang dapat digunakan untuk menguji kevalidan hasil dari metode yang digunakan pada analisis cluster dan juga merupakan analisis lanjutan untuk menentukan fungsi setiap kelompok yang terbentuk (fungsi diskriminan). Dari fungsi diskriminan dapat dengan mudah menentukan kelompok untuk suatu objek baru. Fungsi ini dapat diperoleh dari persamaan yang akan meminimumkan nilai expected cost of misclassification (ECM).

Judul Skripsi : Analisis Pengelompokan Objek dengan Metode S

ingle Linkage

Clustering

dan Diskriminan Linear untuk Kasus Dua Kelompok

Nama : Melinda

NIM : G54101010

Menyetujui:

Pembimbing I Pembimbing II

Dr. Ir. Muhammad Nur Aidi, MS. Ir. Retno Budiarti, MS.

NIP. 131842408

NIP. 131842409

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, MS.

NIP. 131473999

PRAKATA

Alhamdulillah, puji dan syukur penulis panjatkan kepada Allah SWT atas segala limpahan rahmatNya sehingga karya ilmiah ini berhasil diselesaikan. Shalawat dan salam semoga tercurah kepada Rasulullah SAW.

Selama menyusun karya ilmiah, penulis banyak mendapatkan bimbingan dan bantuan dari

berbagai pihak. Dalam kesempatan ini, penulis mengucapkan terima kasih kepada Bapak Dr. Ir. Muhammad Nur Aidi, MS., dan Ibu Ir. Retno Budiarti, MS. selaku pembimbing serta Bapak Dr. Ir. I Gusti Putu Purnaba, DEA. selaku penguji. Ungkapan terima kasih juga disampaikan kepada kedua orang tua dan seluruh keluarga tercinta atas do’a dan kasih sayangnya. Selain itu, penulis juga menghaturkan terima kasih kepada seluruh staf dan dosen Departemen Matematika IPB. Terima kasih kepada semua teman Matematika 38, kost-an Al-Mardhiyah, dan semua pihak yang telah membantu kelancaran karya ilmiah ini atas do’a, perhatian, dan dukungan yang diberikan.

Semoga karya ilmiah ini bermanfaat dalam bidang ilmu pengetahuan.

Bogor, September 2006

RIWAYAT HIDUP

Penulis dilahirkan di Sumedang, 20 Oktober 1983 sebagai anak pertama dari 3 bersaudara dari pasangan Iman Arfiman dan Euis Suharyati.

Pada tahun 1995 penulis menyelesaikan sekolah di SDN Gudang Kopi 2 Sumedang dan tahun 1998 penulis menyelesaikan sekolahnya di SMPN 8 Sumedang. Pada tahun sama, penulis melanjutkan sekolah ke SMUN 2 Sumedang dan lulus pada tahun 2001. Pada tahun tersebut penulis diterima di IPB Departemen Matematika melalui jalur USMI.

DAFTAR ISI

Halaman

DAFTAR TABEL... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ...viii

PENDAHULUAN Latar Belakang ...1

Tujuan

...

1

LANDASAN TEORI

...

1

METODE DAN PEMBAHASAN Analisis Cluster ...5

Analisis Diskriminan ...7

Contoh Kasus ...11

SIMPULAN ...14

DAFTAR PUSTAKA ...15

DAFTAR TABEL

Halaman

1 Pengelompokan objek berdasarkan jumlah kelompok yang diinginkan... 6

2 Upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan ekonomi (LPE) 14 kabupaten/kota di Jawa Barat pada tahun 2002 ...11

3 Upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan ekonomi (LPE) Kab. Sumedang, Kab. Bogor, dan Kab. Purwakarta pada tahun 2002 ...13

4 Nilai diskriminan masing-masing kabupaten/kota...14

DAFTAR GAMBAR

Halaman 1 Jarak antar kelompok untuk single linkage clustering ... 5

2 Contoh Dendogram ... 6

DAFTAR LAMPIRAN

Halaman 1 ANALISIS CLUSTER 1.1 Nilai standarisasi upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan ekonomi (LPE) pada tahun 2002 ...16

1.2 Matriks jarak euclid antar kabupaten/kota ( matriks kasamaan)...17

1.3 Tabel tahap agglomeratif dengan single linkage clustering...19

1.4 Tabel anggota kelompok untuk 4, 3, dan 2 pengelompokan ...20

1.5 Gambar dendogram single linkage clustering untuk jarak antar kabupaten/kota ...21

1.6 Diagram pencar UMK, tingkat pengangguran, dan LPE...22

2 ANALISIS DISKRIMINAN 2.1 Nilai standarisasi upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan ekonomi (LPE) kelompok pertama dan kelompok kedua ...23

2.2 Hasil uji beda vektor rataan antar kelompok ...24

2.3 Hasil uji asumsi kenormalan variabel UMK, tingkat pengangguran, dan LPE ...25

PENDAHULUAN

Latar Belakang

Banyak keragaman yang dapat dijumpai pada kehidupan ini sehingga pengelompokan suatu objek yang relatif homogen selalu menjadi permasalahan yang menarik. Salah satu alasan pengelompokan adalah untuk memperoleh contoh data yang dapat mewakili populasi atau dapat menggambarkan karakteristik objek dalam populasi yang dikelompokkan.

Analisis cluster merupakan teknik multivariat yang tujuan utamanya mengelompokkan objek-objek berdasarkan kesamaan karakteristik di antara objek-objek tersebut. Analisis ini dapat bermanfaat dan diterapkan pada berbagai bidang ilmu, seperti : geografi, psikologi, biologi, manajemen dan lain sebagainya. Objek yang diamati dapat berupa produk (barang dan jasa), benda (tumbuhan atau lainnya) serta orang (responden, konsumen atau yang lain).

Ciri pengelompokan yang baik, pertama terdapat kesamaan yang tinggi antar anggota dalam satu kelompok (intra kelompok). Kedua, antar kelompok yang satu dengan kelompok lainnya (inter kelompok) memiliki perbedaan yang tinggi. Salah satu metode analisis cluster adalah dengan metode

hierarki. Metode hierarki yang banyak dipakai untuk suatu data metrik adalah metode agglomeratif. Adapun, setelah diperoleh hasil pengelompokan perlu dilakukan validasi dengan membandingkan hasil yang diperoleh terhadap metode lainnya ataupun dapat dilakukan suatu analisis lanjutan seperti analisis diskriminan. Analisis diskriminan selain itu berguna untuk memperoleh fungsi yang dapat menunjukkan perbedaan (diskriminasi) antar kelompok.

Pada tulisan ini akan dibahas proses pengelompokan objek secara agglomeratif dengan menggunakan metode paling sederhana yaitu, single linkage clustering

serta menguraikan analisis diskriminan untuk mengevaluasi objek pada kasus dua kelompok. Contoh pengolahan data pada tulisan ini menggunakan software SPSS.

Tujuan

Tujuan dari penulisan ini adalah menguraikan dan mempelajari proses pengelompokan suatu objek dengan menggunakan single linkage clustering. Serta bagaimana proses mengevalusi suatu objek pada kelompok yang terbentuk dengan analisis diskriminan.

LANDASAN TEORI

Berikut ini beberapa pokok bahasan

berupa definisi dan teorema yang dijadikan landasan dalam penyusunan tulisan ini. Definisi 1 (Analisis Cluster)

Analisis cluster merupakan alat untuk membangun kelompok-kelompok (cluster) dari objek data multivariat.

(Hä_{rdle & Simar 2003)}

Definisi 2 (Analisis Diskriminan)

Analisis diskriminan merupakan metode dan alat yang digunakan untuk membedakan antar kelompok serta berguna untuk menentukan proses mengalokasikan objek baru ke dalam kelompok.

(Hä_{rdle & Simar 2003)}

Definisi 3 (Single Linkage Clustering)

Single linkage clustering mendefinisikan bahwa jarak antar kelompok merupakan jarak terdekat dari anggota kelompok pertama dengan anggota kelompok lainnya.

(Hair, Anderson, Tatham, & Black 1998)

Definisi 4 (Ruang Contoh)

Ruang contoh adalah himpunan dari semua kemungkinan hasil suatu percobaan, dinotasikan Ω.

(Hogg & Craig 1995)

Definisi 5 (Peubah Acak)

Peubah acak X adalah suatu fungsi yang memetakan masing-masing elemen pada ruang contoh tepat satu ke bilangan real, dinotasikan X: Ω→R.

(Hogg & Craig 1995)

Definisi 6 (Jarak Euclid)

Jarak euclid untuk n objek dapat didefinisikan,

2 ...

2 2 2 2 1

1 ⎟_⎠⎞ +⎜⎛_⎝ − ⎟⎞_⎠ + +_⎝⎛⎜ − ⎟⎞_⎠

⎜ ⎝ ⎛ ₋

= x_i x_j x_i x_j x_ik x_jk dij

dimana:

i, j= 1, 2, ..., n

dij = jarak euclid antara objek ke-i dengan objek ke-j

xik = objek ke-i untuk variabel ke-k xjk = objek ke-j untuk variabel ke-k

Definisi 7 ( Rataan)

Misalkan x1, x2, ..., xn, objek pengamatan,

rataannya

n n

i i

x µ

∑ = = 1

dimana:

µ= rataan untuk n objek pengamatan

xi = objek pengamatan ke-i n = jumlah objek yang diamati

(Moore 1994)

Definisi 8 (Ragam)

Ragam untuk n objek pengamatan x1, x2, ..., xn didefinisikan sebagai

(

)

1 1

2 2

− ∑ = −µ =

n n

i i

x S

dimana:

S2 = ragam untuk n objek pengamatan

S = S2 = simpangan baku untuk n objek pengamatan

µ= rataan untuk n objek pengamatan

xi = objek pengamatan ke-i

(Moore 1994)

Definisi 9 (Koefisien Korelasi) Korelasi antara variabel xl dan xk,

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ −µ ∑ _⎟⎟

⎠ ⎞ ⎜⎜

⎝ ⎛ −µ −

=

= _k

k ik n

i _l l il lk

S x S x n

r

1 1 1

dimana:

rlk= korelasi antara variabel ke-l dan ke-k

Sl = simpangan baku untuk variabel ke-l Sk = simpangan baku untuk variabel ke-k

l

µ = rataan untuk variabel ke-l k

µ = rataan untuk variabel ke-k xil = objek ke i untuk variabel ke-l

xik = objek ke i untuk variabel ke-k

(Moore 1994)

Definisi 10 (Kovarian)

Kovarian antara variabel xl dan xk,

(

x_l,x_k

)

=r_lkS_lS_k

cov dimana:

cov(xl ,xk)= kovarian antara variabel ke-l dan ke-k

rlk= korelasi antara variabel ke-l dan ke-k

Sl = simpangan baku untuk variabel ke-l Sk = simpangan baku untuk variabel ke-k

(Hogg & Craig 1995)

Definisi 11 (z-skor)

Suatu pengamatan x dari suatu populasi yang mempunyai nilai tengah µdan simpangan baku S, mempunyai nilai z yang didefinisikan sebagai

S x−µ =

z

(Walpole 1995)

Definisi 12 (Fungsi Kepekatan Peluang) Misalkan X peubah acak dengan ruang contoh

Ωberdimensi satu, terdiri dari sebuah interval atau gabungan interval. Fungsi f(x) non negatif maka

( )

∫ =

Ωf xdx 1

Fungsi peluang P(R), R⊂Ω, dapat ditulis

P(R) = Pr(X∈R) = ∫

( )

R X dx x f

X disebut peubah acak kontinu dan fX(x) disebut fungsi kepekatan peluang bagi X.

(Hogg & Craig 1995)

Definisi 13 (Fungsi Likelihood)

Misalkan f

( )

x,θ fungsi kepekatan peluang dengan parameter θ, fungsi likelihood adalah

( )

θ f

(

x₁,θ

) (

f x₂,θ

)

f

(

x₃,θ

)

.

L = K

(Hogg & Craig 1995)

Definisi 14 (Aturan Diskriminan Maksimum Likelihood)

Aturan maksimum likelihood untuk mengalokasikan sebuah objek x ke salah satu kelompok Πg, dimana g = 1, 2,…,ng adalah mengalokasikan x ke kelompok yang memberikan likelihood terbesar ke x.

(Mardia, Kent & Bibby 1989)

Definisi 15 (Peluang Suatu Kejadian)

Peluang suatu kejadian A adalah jumlah peluang semua titik contoh dalam A. Apabila suatu percobaan mempunyai N hasil percobaan yang berbeda dan masing-masing mempunyai kemungkinan yang sama untuk terjadi, dan bila tepat n di antara hasil percobaan itu menyusun kejadian A, maka peluang kejadian A adalah

( )

N n A

P =

(Walpole 1995)

Definisi 16 (Peluang Bersyarat)

(

)

(

( )

)

A P B A P A | B

P = ∩ jika P(A) > 0

(Walpole 1995)

Definisi 17 (Distribusi Multinormal)

Misalkan X = [X1, X2, ..., Xk]' vektor acak

kontinu memiliki fungsi kepekatan peluang

fX(x), X berdistribusi normal dengan vektor rataan µ dan matriks kovarianΣ> 0. X ~ Nk( µ ,Σ ),

( )

= − _⎢⎣⎡−

(

−

)

−

(

−

)

_⎥⎦⎤ µ x Σ µ x Σ

x ' 1

2 1 exp 2 k/2

X

f π

(Hä_{rdle & Simar 2003)}

Definisi 18 (Distribusi Khi-kuadrat)

Fungsi kepekatan peluang untuk peubah acak kontinu X berdistribusi khi-kuadrat dengan derajat bebas r, X~χ_r2,

( )

( )

2 1 2 2

2 2

1 r x

r

X x e

r x

f − −

Γ

= , 0<x<∞. dimana:

( )

α = ∫ Γ ∞ α− − 0 1 dy e

y y , α>0.

(Hogg & Craig 1995)

Definisi 19 (Distribusi F)

Misalkan X1 dan X2 peubah acak bebas

masing-masing berdistribusi khi-kuadrat dengan derajat bebas r1 dan r2. Fungsí

kepekatan peluang bersama untuk X1 dan X2

berdistribusi F,

(

)

( ) (

)

( ) 222 1 (1 2)/2 1 2 1 1 2 / 2 1 2 1 2 1 2 1 2 2 / 2 / 1 , x x r r r r X X e x x r r x x f + − − − + Γ Γ = . x ,

x <∞ < <∞ < ₁ 0 ₂ 0

(Hogg & Craig 1995)

Definisi 20 (Modus)

Modus segugus pengamatan adalah nilai tengah yang terjadi paling sering atau yang mempunyai frekuensi paling tinggi.

(Walpole 1995)

Definisi 21 (Skewness)

Skewness adalah nilai ukuran kecondongan grafik.

Nilai skewness

= (rataan-modus)/simpangan baku

(Santoso 2000)

Definisi 22 (Kurtosis)

Kurtosis menunjukkan tinggi rendahnya atau runcing datarnya bentuk kurva model normal

atau distribusi normal. Koefisien kurtosis a4

dirumuskan

(

2

)

2 4 4 m /m

a = dimana:

(

)

n x x m r i r ∑ −

= , r = 0, 1, 2, ...

mr = momen ke r

xi= objek pengamatan ke-i

x= rataan variabel untuk n objek pengamatan (Sudjana 2000)

Uji beda 2 vektor rataan (T2 Hotelling) H0: µ1=µ2

H1: µ1≠µ2

T2 Hotelling didefinisikan,

(

)(

)

(

1 2

)

1 gabungan 2 1 2 1 2 1 2 'Σ µ µ µ µ − − + = − n n n n T

(

)

( , 1)

2 1 2 1 2 2 1 1 2 ~ _{+ − −} − − + − + k n n k F k n n k n n T dimana:

n1 = jumlah anggota kelompok pertama

n2 = jumlah anggota kelompok kedua

k = banyaknya variabel bebas H0 diterima jika:

(

)

( , 1)

2 2 1 2 1 2 1 1 2 − − + ≤ − − + − + k n n k F T k n n k n n

(Mardia, Kent & Bibby 1989)

Uji Kenormalan Multivariat (Skewness dan Kurtosis)

Misalkan X = [X1, X2, ..., Xk]' vektor acak dan

Σ matriks kovarian untuk contoh,

(

)(

)

' ' n

n

i

i

i x x x HD H x

Σ= ₋

∑

− − = u

=1 1 1

dimana:

H = (h1, h2, ..., hk) matriks ortogonal

Du = diag(u1, u2, ..., uk)

Skewness dan kurtosis untuk contoh data, didefinisikan

(

)

∑

∑

= = − ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − = k r n i r ri r

k u y y n

k b 1 2 1 3 2 3 1 1 dan

(

)

∑

∑

= = − ₋ = n i i ri k r r

k u y y

nk b 1 4 1 2 2 1 dimana:

r = 1, 2, ..., k i = 1, 2, ..., n

Data pengamatan tidak berdistribusi normal , jika

2 , 1 6 ⎟⎠ ≥χ α

⎞ ⎜ ⎝ ⎛ k k b nk

Tes kurtosis menolak normality, jika

(

2

)

2 2

1 3

24 b zα

nk

k − ≥ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

(Srivastava 2002)

Uji kehomogenan kovarian (Uji Box’s M) H0: Σ1=Σ2=...=Σn_g

H1: Σi ≠Σj , i≠j.

Box’s M dirumuskan sebagai berikut,

(

)

Σu Σu

1 log

1 −

∑ − γ

= n_{g g}

M , dimana:

(

)(

)

⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∑ − − − − + − + − = γ g n n g k k k g 1 1 1 1 1 6 1 3 2 1 2 Σ Σ g n n u= ₋

g g g ug n n Σ Σ 1 − =

Box’s M mempunyai distribusi khi-kuadrat asimtotik dengan derajat bebas

(

1

)(

1

)

2

1 _{+ −}

g k

k .

dimana:

g = 1, 2, ..., ng.

ng = jumlah objek dalam kelompok ke-g

Σ= matriks kovarian gabungan

g

Σ = matriks kovarian kelompok ke-g

H0 diterima jika M ≤χk2( )k+1

( )

ng−1 2

(Mardia, Kent & Bibby 1989)

Teorema Neyman-Pearson

Misalkan X1, X2,..., Xn, dimana n bilangan

bulat positif, merupakan contoh acak kontinu dari fungsi kepekatan peluang f

( )

x;θ . Maka fungsi kepekatan peluang bagi X1, X2,..., Xn

adalah

(

θ;x₁,x₂, ,x_n

) ( ) (

f x₁;θ f x₂;θ

) (

f x_n;θ

)

L K = K

Misalkan θ' dan θ" nilai tetap nyata bagi θ sehingga Ω=

{

θ:θ=θ',θ"

}

, dan k bilangan positif. Misalkan C himpunan bagian dari ruang contoh Ω dan C* komplemen dari C

sehingga,

(a)

(

(

)

)

k x x x L x x x L n n _≤ , , , ; " , , , ; ' 2 1 2 1 K K θ θ ,

dimana (x1, x2, ...., xn) ∈C.

(b)

(

(

)

)

k x x x L x x x L n n _≥ , , , ; " , , , ; ' 2 1 2 1 K K θ θ ,

dimana (x1, x2, ...., xn) ∈C*.

(c) α =Pr

[

(

X₁,X₂,K,X_n

)

∈C*;H₀

]

Maka C daerah kritis terbaik dengan ukuran α untuk menguji hipotesis H0: θ = θ' dan

H1: θ = θ".

Bukti:

Jika α ukuran daerah kritis C, dan terdapat daerah kritis lainnya berukuran α yaitu A. Maka,

(

)

∫ ∫ n n

R L x x x dx dx

L K

L θ; ₁, ₂, , ₁ dinotasikan oleh ∫RL

( )

θ . Akan ditunjukkan bahwa,

( )

( )

∫_CLθ" −∫_ALθ" ≥0.

Jika C gabungan dari irisan C∩A dan C∩A* dan A gabungan A∩C dan A ∩C*, maka

( )

−∫

( )

∫CLθ" ALθ"

( )

( )

( )

( )

∫ +∫ −∫ −∫

= _C∩ALθ" _C∩A*Lθ" _A∩CLθ" _A∩C*Lθ"

( )

−∫

( )

∫

= _C∩A*Lθ" _A∩C*Lθ" (1) Karena L

( ) ( ) ( )

θ" ≥ 1k Lθ' pada setiap titik di

C, dan setiap titik di C∩A*, maka

( )

( )

∫_C∩A* " ≥1∫_C∩A*L '

k

Lθ θ (2) Tetapi, L

( ) ( ) ( )

θ" ≤ 1k Lθ' pada setiap titik di

C*, dan setiap titik di A∩C*, maka

( )

( )

∫ ∩ * ≤ ∫ ∩ * ' 1

"

C

A A C L

k

Lθ θ (3) Dari persamaan (2) dan (3) dapat diperoleh suatu pertidaksamaan berikut,

( )

( )

( )

( )

∫_C∩A* "−∫_A∩C* "≥1∫_C∩A* '−1∫_A∩C*L '

k L k L

Lθ θ θ θ

dan dari persamaan (1), diperoleh

( )

( )

( )

( )

∫C −∫A ≥ ∫C∩A − ∫A∩C L k L k L

Lθ" θ" 1 _* θ' 1 _* θ' (4) Sehingga,

( )

−∫

( )

∫C∩A*Lθ' A∩C*Lθ'

( )

( )

( )

−∫

( )

∫ +∫ −∫

= _C∩A*Lθ' _C∩ALθ' _A∩CLθ' _A∩C*Lθ'

( )

( )

∫ −∫ = _CLθ' _ALθ'

. 0 = α − α =

Jika hasil disubstitusi ke persamaan (4), diperoleh

( )

" −∫

( )

" ≥0. ∫CLθ ALθ

METODE DAN PEMBAHASAN

Analisis Cluster

Proses pengelompokan melalui analisis cluster dapat dibagi ke dalam enam tahap:

Tahap pertama, memilih ataupun mengambil data yang akan digunakan sebagai objek pada analisis cluster. Misalkan, terdapat suatu data dengan n objek dan memiliki k

variabel. Matriks data:

⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ nk n n k x x x x x x x L L L M O M M M O M M M O M M M M L L L 2 1 22 1 12 11

Tahap kedua, memperhatikan apakah nilai variabel dari data mempunyai perbedaan yang besar. Jika terdapat perbedaan maka data harus dibakukan dengan mengubahnya ke nilai z.

(

)

l l il il S x −µ

= z

dimana:

zil = nilai z untuk objek ke-i variabel ke-l xil= objek ke-i variabel ke-l

l

µ = rataan untuk semua nilai variabel ke-l Sl = simpangan baku untuk variabel ke-l

Tahap ketiga, apabila data yang diambil berupa contoh maka harus diasumsikan bahwa contoh yang diambil benar-benar mewakili populasi yang ada. Asumsi lainnya yaitu, kemungkinan adanya korelasi antar variabel bebas sebaiknya tidak ada jika ada harus tidak besar (angka korelasi tidak mencapai 0,90). Asumsi ini harus dipenuhi agar hasil analisis yang diperoleh representatif, menggambarkan karakteristik dari populasi.

Tahap keempat, memilih algoritma pengelompokan yang akan dipakai. Metode hierarki tepat digunakan untuk suatu data metrik. Metode hierarki dengan menggunakan metode agglomeratif, mengalokasikan objek-objek yang terpisah ke suatu kelompok menurut tingkatan kesamaan sehingga akhirnya semua objek berada dalam satu kelompok. Jika ng menunjukkan banyaknya kelompok, maka n_g ≤n.

Algoritma agglomeratif untuk n objek :

Langkah pertama, membentuk matriks jarak simetri berukuran n x n,

{ }

⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = = nn n n n ij d d d d d d d d L L L M O M M M O M M M O M M M M L L L 2 1 22 1 12 11 D dimana:

i = 1, 2, ..., n

j = 1, 2, ..., n

dij jarak antara objek ke-i dan ke-j menunjukkan tingkat kesamaan atau ketidaksamaan antara n objek. Jarak antar objek tersebut menggunakan persamaan jarak euclid.

Langkah kedua, menentukan pasangan objek yang memiliki kesamaan paling besar, misalkan jarak objek U dan V paling minimum (dUV = min{dij}).

Langkah ketiga, menggabungkan objek U dan

V sebagai kelompok baru (UV). Membentuk kembali matriks baru berukuran (n-1)x(n-1) dengan menghapus baris dan kolom yang bersesuaian dengan objek U dan V dan menambah sebuah baris dan kolom yang terdiri dari elemen jarak antara kelompok (UV) dengan objek lain. Misalkan terdapat objek lain W, fungsi jarak antara kelompok (UV) dengan objek W yang didefinisikan oleh metode single linkage clustering adalah

( )UVW dUW dVW dUW dVW

d = + − −

2 1 2 1 2 1 (5)

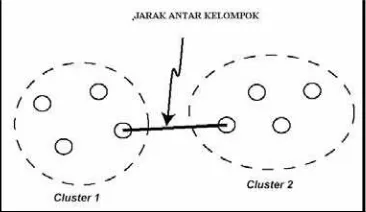
Single linkage clustering merupakan salah satu metode pengukuran jarak antar kelompok dimana jarak antara satu kelompok dengan kelompok lain merupakan jarak terpendek dari anggota kelompok yang satu terhadap anggota kelompok lainnya (lihat Gambar 1).

Jarak minimum di antara jarak U ke W

dengan jarak V ke W, dinotasikan sebagai

d(UV)W= min {dUW, dVW} (6) Maka dapat ditunjukkan bahwa,

d(UV)W = dUW + dVW − dUW −dVW

2 1 2

1 2

1

= min {dUW, dVW} Bukti :

Misalkan dUW > dVW,

VW UW VW

UW d d d

d − = −

substitusi ke persamaan (5), diperoleh

d(UV)W = dVW (7)

Misalkan dUW < dVW,

UW VW VW

UW d d d

d − = −

substitusi ke persamaan (5), diperoleh

d(UV)W = dUW (8)

Dari (7) dan (8) diperoleh bahwa

d(UV)W = min {dUW, dVW}.

Selanjutnya, ulangi langkah-langkah di atas sampai terbentuk satu kelompok yang terdiri dari semua objek yang dikelompokkan. Namun, pengelompokan dapat pula dihentikan pada saat min{dij}≤do, dimana do nilai batas jarak intra kelompok yang sudah ditentukan.

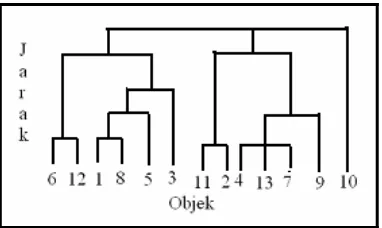
Tahapan metode hierarki ini dapat ditampilkan sebagai graf ataupun diagram pohon seperti gambar 2. Graf hierarki disebut juga dendogram.

Gambar 2 Contoh Dendogram.

Pada dendogram di atas terlihat jelas adanya tingkatan yang menunjukkan tahap pengelompokan. Jika dilihat pada Gambar 2, proses agglomeratif berjalan ke arah kanan menghasilkan beberapa kelompok sampai akhirnya semua objek bergabung menjadi satu kelompok. Jarak antar objek untuk setiap tahap pengelompokan secara hieraki akan semakin membesar atau jauh. Semakin besar jarak antar objek menunjukkan semakin besar perbedaan antar objek tersebut.

Dendogram dapat berfungsi untuk menunjukkan anggota kelompok yang sesuai dengan jumlah kelompok yang diinginkan.

Berdasarkan Gambar 2, dapat ditunjukkan anggota yang terdapat pada setiap kelompok berdasarkan jumlah kelompok yang diinginkan seperti yang ditampilkan pada Tabel 1.

Penentuan berapa jumlah kelompok biasanya berdasarkan pada tujuan dari dilakukannya proses analisis cluster (penelitian). Dalam hal ini, tidak ada ketentuan khusus berapa jumlah cluster yang ideal harus dibentuk. Adapun penentuan dari anggota untuk setiap kelompok berdasarkan pada tingkat kesamaan, dengan memperhatikan jarak antar objek. Setiap objek dalam satu kelompok harus memiliki tingkat kesamaan yang besar dan memiliki tingkat perbedaan yang jauh dengan kelompok lainnya. Dengan memperhatikan hal ini maka jumlah pengelompokan optimal dari Gambar 2 sebanyak tiga kelompok, dimana anggota kelompok pertama terdiri dari objek 6, 12, 1, 8, 5, dan 3. Sedangkan kelompok kedua terdiri dari objek 11, 2, 4, 13, 7, dan 9, serta objek 10 sebagai anggota kelompok ketiga.

Tabel 1 Pengelompokan objek berdasarkan jumlah kelompok yang diinginkan.

Jumlah kelompok Objek

4 3 2

1 2 1 1

2 3 2 2

3 2 1 1

4 3 2 2

5 2 1 1

6 1 1 1

7 3 2 2

8 2 1 1

9 3 2 2

10 4 3 1/2

11 3 2 2

12 1 1 1

13 3 2 2

Tahap kelima, setelah kelompok terbentuk maka tahap selanjutnya menginterpretasikan kelompok yang terbentuk, yaitu memberi nama spesifik untuk menggambarkan objek yang terdapat dalam kelompok tersebut. Pemberian nama terhadap kelompok sama halnya dengan penentuan jumlah kelompok yaitu, berdasarkan pada tujuan dilakukan analisis cluster.

Tahap keenam, melakukan profiling

kelompok. Pada saat profiling ditentukan persentase atas jumlah objek yang membentuk kelompok serta melihat perbedaan komposisi yang mencolok antar anggota kelompok. Perbedaan komposisi dapat dijelaskan secara lanjut melalui analisis diskriminan. Dari analisis diskriminan dapat ditemukan fungsi untuk kelompok yang terbentuk. Selain itu, dari fungsi yang dibuat dapat mempermudah pengelompokan objek yang baru. Kevalidan dari hasil dapat dilakukan dengan menggunakan analisis diskriminan. Apabila hasil dari evalusi objek terhadap diskriminan diperoleh nilai ketepatan lebih dari 50% maka dapat dikatakan bahwa model diskriminan yang diperoleh valid dan hasil dari pengelompokan analisis cluster juga valid.

Analisis Diskriminan

Analisis diskriminan digunakan sebagai metode dan alat untuk memisahkan objek-objek ke dalam kelompok secara tepat atau mengevaluasi apakah objek-objek yang telah dikelompokkan sudah tepat atau belum berada dalam kelompok yang diduga, dari fungsi diskriminan yang dicari. Fungsi diskriminan dapat berguna pula untuk mengalokasikan objek baru ke dalam kelompok yang sudah terbentuk sebelumnya saat analisis cluster. Dari fungsi diskriminan yang diperoleh, maka dapat diketahui hubungan antara variabel-variabel bebas yang bersifat metrik terhadap variabel terkait (kelompok) yang bersifat kategori. Fungsi diskriminan yang bersifat linear secara umum dituliskan,

k kx ... x x

y=λ_{1 1}+λ_{2 2}+ +λ

dimana:

y = nilai diskriminan (variabel terkait)

k

λ = nilai pembobot diskriminan untuk variabel ke-k

xk = variabel bebas ke-k

Asumsi yang diambil pada analisis diskriminan untuk memperoleh fungsi diskriminan linear yaitu: matriks kovarian dari semua variabel bebas dalam setiap kelompok sama (homogen). Apabila kehomogenan matriks kovarian tidak terpenuhi, akan menyebabkan fungsi atau model yang diperolehmenunjukkan hubungan yang kurang tepat antara variabel bebas dengan variabel terkait. Variabel bebas boleh diasumsikan atau tidak berdistribusi normal, namun akan lebih baik apabila diasumsikan berdistribusi normal sehingga dapat diperoleh

fungsi diskriminan yang memiliki ketepatan mengelompokkan lebih baik.

Sebelum melakukan analisis diskriminan lanjutan, dilakukan terlebih dahulu uji asumsi. Salah satu uji asumsi terhadap kenormalan data adalah dengan menggunakan statistik skewness dan kurtosis. Sedangkan untuk menguji asumsi kehomogenan matriks kovarian salah satunya dengan uji Box’s M. Selain melakukan kedua uji asumsi dapat pula diuji beda 2 vektor rataan salah satunya dengan menggunakan T2 Hotelling yang berguna untuk melihat apakah terdapat perbedaan yang nyata antara kelompok yang terbentuk dari masing-masing variabel bebas. Misalkan terdapat kelompok Πg, g = 1, 2, ...,

ng dan x sebagai objek yang akan dialokasikan ke salah satu kelompok sedangkan x0

merupakan objek baru. Aturan diskriminan, memisahkan ruang contoh Ω menjadi Rg sehingga jika x∈R_g, x diidentifikasikan sebagai anggota dari kelompok Πg dengan aturan diskriminan maksimum likelihood. Aturan maksimum likelihood mengalokasikan x ke Πg, dimana

( )

x

( )

x _g

( )

x g

g

g f L

L* = =maks (9) Sehingga diperoleh bahwa,

( )

( )

{

}

h g

n g

L L

Rg g h g

≠

= >

= x: x x untuk 1,2,K, ,

Jika Lg(x) = Lh(x), g ≠ h maka x dapat dialokasikan ke salah satu kelompok baik Πg

atau Πh karena peluang mengelompokkan x misklasifikasi ke salah satu kelompok baik ke Πg atau Πh adalah

P(Lg(x) = Lh(x), g≠h|Πg) = 0.

Misalkan g = 2, f1(x) dan f2(x)

masing-masing merupakan fungsi kepekatan peluang vektor acak X berdistribusi normal untuk kelompok Π1 dan Π2, ruang contoh

Ω= R1∪R2. Setiap objek hanya boleh

dikelompokkan ke dalam salah satu dari kedua kelompok.

Pada saat pengelompokan akan mungkin menemukan kesalahan pengelompokan (misklasifikasi). Peluang mengelompokkan sebuah objek x yang terdiri dari peubah acak kontinu yang berasal dari Π1 ke Π2, dapat

dihitung sebagai peluang bersyarat P(2|1) sebagai berikut,

( ) (

= ∈

)

=∫

( )

2 1 1

2| .

1 |

2 P R Π R f d

P X x x (10)

Hal sama, peluang mengelompokkan sebuah objek yang berasal dari Π2 ke Π1 adalah

( ) (

= ∈

)

=∫

( )

1 2 2

1| .

2 |

1 P R Π _R f d

Peluang pengelompokan objek-objek secara tepat atau tidak tepat dapat dirumuskan sebagai hasil kali peluang prior dengan peluang bersyarat :

P(objek tepat dikelompokkan sebagai Π1) =

P(objek berasal dari Π1 dan tepat

diklasifikasikan sebagai Π1) =

(

R1| 1

) ( ) ( )

P 1 P1|1 p1

P X∈ Π Π = (12)

P(objek tidak tepat dikelompokkan sebagai Π1) = P(objek berasal dari Π2 dan tidak tepat

diklasifikasikan sebagai Π1) =

(

R1| 2

) ( ) ( )

P 2 P1|2 p2

P X∈ Π Π = (13)

P(objek tepat dikelompokkan sebagai Π2) =

P(objek berasal dari Π2 dan tepat

diklasifikasikan sebagai Π2) =

(

R2| 2

) ( ) ( )

P 2 P 2|2 p2

P X∈ Π Π = (14)

P(objek tidak tepat dikelompokkan sebagai Π2) = P(objek berasal dari Π1 dan tidak tepat

diklasifikasikan sebagai Π2) =

(

R₂| ₁

) ( ) ( )

P ₁ P2|1 p₁

P X∈ Π Π = (15) Jumlah misklasifikasi objek pada setiap kelompok dapat ditampilkan berupa tabel berikut

Kelompok yang diduga

Π1 Π2

Π1 n1c n1m

= n1-n1c Kelompok

seharusnya _Π

2 n2m

= n2-n2c

n2c

Ketepatan prediksi pengelompokan secara

tepat = 100% 2 1 2 1 _× + + n n n n_{c c}

Besar misklasifikasi pengelompokan

= 100%

2 1 2 1 _× + + n n n

n_{m m}

dimana:

n1c = jumlah objek Π1 tepat dikelompokkan

sebagai anggota Π1

n1m = jumlah objek Π1 misklasifikasi sebagai

anggota Π2

n2c = jumlah objek Π2 tepat dikelompokkan

sebagai anggota Π2

n2m = jumlah objek Π2 misklasifikasi sebagai

anggota Π1

n1 = n1c+ n1m

n2 = n2c + n2m

Misklasifikasi akan membuat biaya sebesar

C(i | j). Matriks biaya tersebut :

Kelompok yang diduga

Π1 Π2

Π1 0 C(2|1)

Kelompok

seharusnya _{Π2 C(1|2) 0} Biaya sebesar nol terjadi apabila pengelompokan tepat, C(1|2) ketika objek dari Π2 tidak tepat dikelompokkan sebagai Π1,dan

C(2|1) ketika objek dari Π1 tidak tepat

dikelompokkan sebagai Π2.

Biaya yang diduga akibat misklasifikasi dirumuskan sebagai nilai expected cost of misclassification (ECM) yaitu,

( ) ( )

2|1P2|1p1 C

( ) ( )

1|2P1|2p2

C

ECM= + (16)

Dengan mensubstitusi persamaan (10) dan (11) ke persamaan (16) diperoleh,

( )

∫

( )

+

( )

∫

( )

=

1

2 1 2 2

1 1|2

1 |

2 p _R f d C p _R f d

C

ECM x x x x

karena Ω= R1 ∪ R2 , dimana

( )

( )

( )

1

1 2 1 1 Ω 1 = ∫ + ∫ = ∫ R R d f d f d

f x x x x x x

maka ECM dapat ditulis,

( )

[

( )

]

( )

( )

( )

( ) ( )

( )

[

2 2 1 1

]

( )

1 2 2 1 1 1 | 2 1 | 2 2 | 1 2 | 1 1 1 | 2 1 1 1 p C d f p C f p C d f p C d f p C ECM R R R + ∫ − = ∫ + ∫ − = x x x x x x x (17)

p1, p2 , C(1/2), C(2|1) nilainya diketahui dan

non negatif. f1(x) dan f2(x) juga diketahui dan

bernilai non negatif untuk semua nilai x. Pengelompokan dikatakan tepat apabila ECM

minimum atau kecil. ECM bernilai minimum apabila memenuhi aturan berikut :

( )

( )

( )

( )

_⎪⎭⎪⎬⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≥ = 1 2 2 1 1 1 | 2 2 | 1 : p p C C f f R x x

x (18)

( )

( )

( )

( )

_⎪⎭⎪⎬⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ < = 1 2 2 1 2 1 | 2 2 | 1 : p p C C f f R x x

Lemma Neyman-Pearson Bukti persamaan (18) dan (19):

Misalkan X = [X1, X2, ..., Xk]′ vektor acak, dan φ1

( )

x dan φ2

( )

x fungsi kontinu. Misalkan 2

1 ~ ~

R

R ∪ ruang contoh vektor acak X dan R~₁ dan R~₂ disjoint. Misalkan R1∪R2 ruang contoh X,

dimana R1={x|φ1

( )

x ≥φ2

( )

x } dan R2={x|φ1

( )

x <φ2

( )

x }. Jika diberikan bahwa,

( )

xdx

( )

xdx

I =∫ φ_R~_{1 1} +∫ φ_R~_{2 2} ~

, I=∫ φ_R

( )

xdx+∫ φ_R

( )

xdx

2

1 1 2

maka selisih keduanya

( )

xdx

( )

xdx

( )

xdx

( )

xdx

I

I− =∫ φ_R +∫ φ_R −∫ φ_R −∫ φ_R

2 1 2 1 ~ 2 ~ 1 2 1 ~ .

Jika 1

(

1 1

) (

1 2

)

~ ~ R R R R

R = ∩ ∪ ∩ , 2

(

2 1

) (

2 2

)

~ ~ R R R R

R = ∩ ∪ ∩ , 1

(

1 1

) (

1 2

)

~ ~ ~ R R R R

R = ∩ ∪ ∩ ,

(

2 1

) (

2 2

)

2 ~ ~ ~ R R R R

R = ∩ ∪ ∩

Maka selisih dapat ditulis

( )

( )

( )

( )

( )

( )

( )

x x

( )

x x

x x x x x x x x x x x x d d d d d d d d I I R R R R R R R R R R R R R R R R ∫ φ − ∫ φ − ∫ φ − ∫ φ − ∫ φ + ∫ φ + ∫ φ + ∫ φ = − ∩ ∩ ∩ ∩ ∩ ∩ ∩ ∩ 2 2 1 2 2 1 1 1 2 2 1 2 2 1 1 1 ~ 2 ~ 2 ~ ₁ ~ ₁ ~ ₂ ~ ₂ ~ ₁ ~ ₁ ~

=∫_R∩R φ

( )

xdx−∫_{R ∩R} φ

( )

xdx+∫_{R ∩R} φ

( )

xdx−∫_R∩R φ

( )

xdx

2 1 1 2 1 2 2 1 ~ 1 ~ 2 ~ 2 ~ 1

=∫_R∩R

[

φ

( )

x −φ

( )

x

]

dx+∫_R∩R

[

φ

( )

x −φ

( )

x

]

dx

1 2 2

1

~ _{2 1}

~ _{1 2}

Karena

(

R₁∩R~₂

)

⊂R₁dan φ₁

( )

x ≥φ₂

( )

x dalam R1 mengakibatkan

[

( )

( )

]

0 2

1 ~

2

1 ≥

∫_R∩R φ x −φ x dx . Sedangkan untuk

(

2 1

)

2

~

R R

R ∩ ⊂ dan φ₁

( )

x <φ₂

( )

x dalam R2 mengakibatkan

( )

( )

[

]

0

1 2

~

1

2 ≥

∫_R∩R φ x −φ x dx . Sehingga, I−~I ≥0. Jika φ₁

( ) ( )

x =C 2|1p₁f₁

( )

x dan

( )

x

( )

_{2 2}

( )

x

2 =C1|2 p f

φ , maka persamaan (17) bernilai minimum untukI≥I~ apabila memilih R1

dimana x memenuhi pertidaksamaan berikut

( )

( ) ( ) ( )

[

C1|2 p₁f₂ x −C 2|1 p₁f₁x

]

≤0

( )

( )

( )

( )

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≥ ⇔ 1 2 2 1 1 | 2 2 | 1 p p C C f f x x

untuk R2 = R1* komplemen dari R1 apabila x memenuhi pertidaksamaan berikut

( )

( ) ( )

( )

[

C1|2 p1f2 x −C 2|1 p1f1 x

]

>0

( )

( )

( )

( )

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ < ⇔ 1 2 2 1 1 | 2 2 | 1 p p C C f f x x Terbukti.ٱ

Dari kedua persamaan diatas (18) dan (19) dapat diperoleh ECM untuk beberapa kasus khusus.

Untuk p2/p1 = 1 (nilai peluang sama)

( )

( )

( )

( )

( )

( )

( )

( )

2 1 2 1 1 2 2 1 2 1 2 2 1 1 | C | C f f : R | C | C f f :

R ≥ <

x x

x

x

Untuk C(1|2)/C(2|1) = 1 (biaya akibat kesalahan pengelompokan sama)

( )

( )

( )

( )

1 2 2 1 2 1 2 2 1 1 p p f f : R p p f f :

R ≥ <

x x x

x

Untuk p2/p1 = C(1|2)/C(2|1) =1 atau p2/p1 =

1/(C(1|2)/C(2|1)) (nilai peluang sama dan biaya akibat kesalahan pengelompokan sama)

( )

( )

1

( )

( )

1 2 1 2 2

1

1 ≥ <

x x x x f f : R f f : R

Jika x0 sebagai objek baru yang ingin

dikelompokkan sedangkan nilai peluang dan biaya akibat kesalahan tidak diketahui maka x0 dikelompokkan ke Π1, jika

( )

₂

( )

1 1 x0 / f x0 ≥

f ⇔ f1

( )

x0 ≥ f2

( )

x0 x0 dikelompokkan ke Π2, jika

( )

₂

( )

1 1 x0 / f x0 <

f ⇔ f1

( )

x0 < f2

( )

x0

Kasus kelompok normal dan nilai µ1,µ2 , dan Σ = Σ1 = Σ2 diketahui

Misalkan fg(x) fungsi kepekatan normal dengan vektor rataan µg dan matriks

( )

( )

(

) (

)

⎥⎦ ⎤ ⎢⎣ ⎡_{− − −} π = − i i k g

f x µ Σ x µ

Σ x 1 2 / 1 2

/ ₂ '

1 exp 2

1 (20)

Dari persamaan (20), jika µ₁,µ₂ dan Σ = Σ1 = Σ2 nilainya sudah diketahui. Maka, hasil

substitusi terhadap persamaan (18) dan (19) akan diperoleh persamaan ECM sebagai berikut :

(

) (

) (

) (

)

( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≥ ⎥⎦ ⎤ − − + ⎢⎣ ⎡_{− −} − ₋ − 1 2 2 1 2 1 1 1 1 1 | 2 ) 2 | 1 ( ' 2 1 ' 2 1 exp : p p C C

R x µ Σ x µ x µ Σ x µ (21)

(

) (

) (

) (

)

( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ < ⎥⎦ ⎤ − − − + ⎢⎣ ⎡_{− −} − ₋ 1 2 1 | 2 ) 2 | 1 ( 2 1 ' 2 2 1 1 1 ' 1 2 1 exp : 2 _p p C C

R x µ Σ x µ x µ Σ x µ (22)

Sehingga, x0 sebagai objek baru dialokasikan ke Π1 jika

(

)

(

)

(

)

( )

( )

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≥ + − − − − − 1 2 2 1 1 2 1 0 1 2 1 1 | 2 2 | 1 ln ' 2 1 ' p p C C µ µ Σ µ µ x Σ µ

µ (23)

x0 dialokasikan ke Π2 jika selainnya.

(

) (

) (

) (

) (

)

(

) (

1 2

)

1 2 1 1 2 1 2 1 2 1 1 1 ' 2 1 ' ' 2 1 ' 2 1 µ µ Σ µ µ x Σ µ µ µ x Σ µ x µ x Σ µ

x− − + − − = − − − +

− − − − −

(24)

Bukti persamaan (24):

(

)

(

)

(

)

(

2

)

1 2 1 1 1 2 1 2 1 µ x Σ µ x µ x Σ µ

x− − + − −

− _' − _' −

(

)

(

)

[

(

)

(

2

)

]

1 2 1 1 1 1 1 2 1 µ x Σ µ Σ x µ x Σ µ Σ

x − − − − −

−

= − ' − − ' −

' '

[

' 1 1' 1 ' 1 1 1' 1 1 ' 1 ' 1 2 '2 1 2' 1 2

]

2 1 µ Σ µ x Σ µ µ Σ x x Σ x µ Σ µ µ Σ x x Σ µ x Σ

x − − − − − + − − − + − + − − −

− =

(

)

(

)

[

]

(

)

(

)

(

1 2

)

1 2 1 1 2 1 2 1 1 2 1 2 1 1 ' 1 ' 2 1 ' ' ' 2 2 2 1 µ µ Σ µ µ x Σ µ µ µ µ Σ µ µ µ Σ x x Σ µ + − − − = + − − − = − − − − − Terbukti.ٱ

Kasus kelompok normal dan nilai µ₁,µ₂, dan Σ = Σ1 = Σ2 belum diketahui

Misalkan X= [X1, X2, ...., Xk]' vektor acak, jumlah objek pada Π1 sebanyak n1 dan jumlah

objek pada Π2 sebanyak n2, dengan n1+ n2 – 2

≥k. Dan jika dari persamaan (21) dan (22) 1

µ ,µ₂ dan Σ1 , Σ2 nilainya belum diketahui.

Matriks data adalah

( ) ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ′ ′ ′ = × 1 1 12 11 1 x x x X n M k n1 (25) ( ) ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ′ ′ ′ = × 2 2 22 21 2 x x x X n M k n2 (26) dimana:

X1 = matriks yang berisi nilai objek untuk

kelompok pertama (Π1)

X2 = matriks yang berisi nilai objek untuk

kelompok kedua (Π2)

' 1 1

xn = vektor yang berisi nilai objek ke-n1 pada kelompok 1

' 2 2

x n = vektor yang berisi nilai objek ke-n2 pada kelompok 2

Dari matriks data, rataan dan mariks kovarian dihitung dengan rumus

( )×

∑

₌ = 1 1 1 1 1 1 n i i k n x

x₁ (27)

(× )= −

∑

₌

(

−

)(

−

)

1 1 1 1 1 1 1 n i i i k k '

n 1 1

1 x x x x

Σ (28)

( )×

∑

₌ = 2 1 2 2 1 1 n i i k n x

x₂ (29)

(× )= −

∑

₌

(

−

)(

−

)

2 1 2 2 2 1 1 n i i i k k '

n 2 2

2 x x x x

Σ (30)

dimana:

1

2

x = vektor yang terdiri dari nilai rataan variabel Π2

Σ1 = matriks kovarian Π1

Σ2 = matriks kovarian Π2

Dengan asumsi yang sama dimana Σ = Σ1 =

Σ2, matriks kovarianΣgabungan adalah gabungan

matriks kovarian Σ1 dan Σ2,

(

) (

)

(

) (

)

2 1 Σ Σ Σ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − − = 1 1 1 1 1 1 2 1 2 2 1 1 gabungan n n n n n n (31)

Substitusix1untuk µ1,x2untuk µ2 ,Σgabungan

untuk Σ ke dalam persamaan (23),

x0 sebagai objek baru dialokasikan ke Π1 jika

(

)

(

)

(

)

( )

( )

⎥⎥_⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≥ + − − − − − 1 2 2 1 1 gabungan 2 1 0 1 gabungan 2 1 1 | 2 2 | 1 ln ' 2 1 ' p p C C x x Σ x x x Σ x x (32)

x0 dialokasikan ke Π2 jika selainnya.

Jika

( )

( )

1 1 | 2 2 | 1 1 2 ₌ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ p p C C ,maka persamaan (32) menjadi

(

)

(

)

'

(

)

0

2 1 ' 2 1 1 gabungan 2 1 0 1 gabungan 2 1 ≥ + − − − − − x x Σ x x x Σ x x (33)

Misalkan dari persamaan (32) didefinisikan nilai diskriminan objek sebagai berikut

(

x1 x2

)

'Σ x aˆ'x

y

ˆ= − −1 =

gabungan (34) Maka selanjutnya x0 dievaluasi dengan nilai

tengah antara nilai diskriminan Π1 dan Π2,

(

x1−x2

)

Σ

(

x1 +x2

)

= −1

gabungan 2

1

' mˆ

=

(

y₁+y₂

)

2 1

(35)

dimana:

(

x x

)

'Σ x aˆ'x1

y₁= ₁− ₂ −_gabungan1 ₁=

(

x1 x2

)

'Σ x2 aˆ'x2

y₂= − −_gabungan1 =

1

y = nilai diskriminan untuk kelompok pertama

2

y = nilai diskriminan untuk kelompok kedua

Aturan minimum ECM untuk dua kelompok normal, yaitu

alokasikan x0 ke Π1 jika ˆy0 =ˆa'x≥mˆ

, dan

x0 dialokasikan ke Π2 jika ˆy0 =ˆa'x<mˆ

.

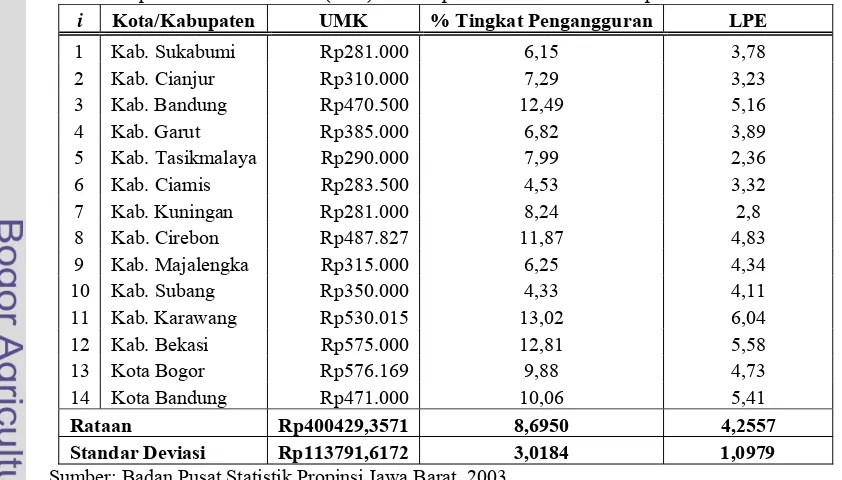
Tabel 2 Upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan ekonomi (LPE) 14 kabupaten/kota di Jawa Barat pada tahun 2002.

i Kota/Kabupaten UMK % Tingkat Pengangguran LPE 1 Kab. Sukabumi Rp281.000 6,15 3,78 2 Kab. Cianjur Rp310.000 7,29 3,23 3 Kab. Bandung Rp470.500 12,49 5,16 4 Kab. Garut Rp385.000 6,82 3,89 5 Kab. Tasikmalaya Rp290.000 7,99 2,36 6 Kab. Ciamis Rp283.500 4,53 3,32 7 Kab. Kuningan Rp281.000 8,24 2,8 8 Kab. Cirebon Rp487.827 11,87 4,83 9 Kab. Majalengka Rp315.000 6,25 4,34 10 Kab. Subang Rp350.000 4,33 4,11 11 Kab. Karawang Rp530.015 13,02 6,04 12 Kab. Bekasi Rp575.000 12,81 5,58 13 Kota Bogor Rp576.169 9,88 4,73 14 Kota Bandung Rp471.000 10,06 5,41

Rataan Rp400429,3571 8,6950 4,2557

Standar Deviasi Rp113791,6172 3,0184 1,0979

Contoh Kasus

Tabel 2 menyajikan data 14 kabupaten/kota di Jawa Barat yang terdiri dari tiga variabel bebas, yaitu upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan ekonomi (LPE) masing-masing kabupaten/kota. Tujuan yang ingin diperoleh adalah mengelompokkan keempatbelas kabupaten/kota kedalam dua kelompok sehingga dapat dibedakan kelompok dengan tingkat sosial ekonomi menengah ke bawah dan menengah ke atas diukur berdasarkan ketiga variabel bebas tersebut.

Analisis Cluster Diketahui: n =14 objek

k = 3 variabel bebas Misalkan:

x1 = upah minimum kabupaten/kota (Rupiah)

x2 = tingkat pengangguran (persen)

x3 = laju pertumbuhan ekonomi

Tahap kedua, standarisasi data dapat dilihat pada Lampiran 1.1.

Nilai z UMK Kabupaten Sukabumi:

0495 , 1 6172 , 113791 3571 , 400429 281000 1 1 11

11 =−

− = − = S x x z

Nilai z tingkat pengangguran Kabupaten Sukabumi: 8432 , 0 0184 , 3 6950 , 8 15 , 6 2 2 12

12 =−

− = − = S x x z

Nilai z LPE Sukabumi:

4333 , 0 0979 , 1 2557 , 4 78 , 3 3 3 13

13 =−

− = − = S x x z

Tahap ketiga, asumsi bahwa contoh yang diambil mewakili populasi yang ada, dan korelasi antara variabel bebas tidak besar.

Tahap keempat, membuat matriks jarak antar objek (Lampiran 1.2). Jarak antara Kabupaten Sukabumi dengan Kabupaten Cianjur sebesar 0,677 merupakan hasil perhitungan sebagai berikut:

2 23 13 2 22 12 2 21 11

12 z z z z z z

d = − + − + −

677 , 0 2 9342 , 0 4333 , 0 2 4655 , 0 8432 , 0 2 7947 , 0 0495 , 1 12 = + − + + − + + − = d

Pada matriks kesamaan, jarak terkecil antar objek sebesar 0,395 yaitu jarak antara Kabupaten Bandung dengan Kabupaten Cirebon.

min{dij}= d38 = dA = 0,395

Berikutnya membentuk matriks baru dengan menghilangkan baris dan kolom Kabupaten Bandung dan Kabupaten Cirebon, kemudian menambah baris dan kolom baru yang terdiri dari elemen jarak antara Kabupaten Bandung dan Kabupaten Cirebon dengan kabupaten/kota lainnya dengan menggunakan rumus jarak single linkage clustering. Sehingga terbentuk matriks berukuran 13×13. Tahap agglomeratif dapat dilihat pada Lampiran 1.3 dan dendogram pada Lampiran 1.5, sedangkan Lampiran 1.6 memperlihatkan diagram pencar data.

Pada langkah kesepuluh agglomeratif Kabupaten Bandung dan Kabupaten Cirebon dikelompokkan dengan Kota Bandung, seperti pada Lampiran 1.3 dengan koefisien jaraknya antara lain,

( )14 3( )14 8( )14 3( )14 8( )14 2 1 2 1 2 1 d d d d

d_A = + − −

( )

(

)

(

)

813 , 0 813 , 0 837 , 0 2 1 813 , 0 2 1 837 , 0 2 1 14 = − − + = A d Cara kedua: ( ) ( )

{

}

{

}

813 , 0 ;0,813 0,837 min ,

min _{314 814} 1

=

=

= d d

d_A

Hasil pengelompokan dapat dilihat pada Lampiran 1.4. Diperoleh hasil pengelompokan kabupaten/kota ke dalam dua kelompok , kelompok pertama terdiri dari, Kab.Sukabumi, Kab.Cianjur, Kab.Garut, Kab.Tasikmalaya, Kab.Ciamis, Kab.Kuningan, Kab.Majalengka, dan Kab.Subang. Kelompok kedua terdiri dari Kab.Bandung, Kab.Cirebon, Kab.Karawang, Kab.Bekasi, Kota Bogor dan Kota Bandung.

Tahap keenam, profiling, menguji kevalidan pengelompokan, dan mengetahui hubungan antara UMK, tingkat pengangguran, dan LPE dengan tingkat sosial ekonomi suatu kabupaten/kota menengah ke atas atau menengah ke bawah dilakukan melalui analisis diskriminan.

Analisis Diskriminan

Misalkan, terdapat tiga kabupaten sebagai objek baru yang ingin dievaluasi, yaitu Kab. Sumedang yang diduga termasuk ke dalam kelompok pertama, sedangkan Kab. Bogor, dan Kab. Purwakarta diduga termasuk kelompok kedua. Tabel 3 menampilkan data ketiga kabupaten tersebut. Standarisasi untuk data yang telah ditambahkan objek baru dapat dilihat pada Lampiran 2.1.

Hasil uji beda rataan dapat dilihat pada Lampiran 2.2, menunjukkan bahwa terdapat

perbedaan antara kelompok pertama dengan kelompok kedua. Besar kecilnya UMK, tingkat pengangguran, dan LPE mempengaruhi tingkat sosial ekonomi suatu kabupaten/kota. Pada Lampiran 2.2 ditunjukkan pula nilai F untuk ketiga variabel. UMK memiliki nilai F paling besar sehingga dapat dikatakan bahwa variabel ini paling besar mempengaruhi tingkat sosial ekonomi masyarakat suatu kabupaten/kota dibandingkan dengan pengaruh tingkat pengangguran. Sementara LPE pengaruhnya paling kecil.

Pada Lampiran 2.3 diperoleh bahwa data berdistribusi normal dengan melihat rasio skewness dan kurtosis diantara 2 dan -2. Lampiran 2.4 matriks kovarian kelompok cenderung homogen.

Tabel 3 Upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan ekonomi (LPE) Kab. Sumedang, Kab. Bogor, dan Kab. Purwakarta pada tahun 2002.

i Kota/Kabupaten UMK % Tingkat Pengangguran LPE 1 Kab. Sumedang Rp470.000 9,25 4,08 2 Kab. Bogor Rp576.169 9,69 2,93 3 Kab. Purwakarta Rp485.000 9,29 3,02 Sumber: Badan Pusat Statistik Propinsi Jawa Barat, 2003.

Apabila asumsi telah terpenuhi, maka dapat dicari fungsi diskriminan. Dengan asumsi lain

bahwa:

( )

( )

1 1 | 2 2 | 1 1 2 ₌ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ p p C C

Diketahui : n1 = 9, n2 = 8

Vektor rataan kelompok pertama dan kelompok kedua, ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = 5101 , 0 7528 , 0 7984 , 0 1

x ,

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 5738 , 0 8469 , 0 8982 , 0 2 x

Matriks kovarian kelompok pertama,

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − = 3797 , 0 1054 , 1 1664 , 0 1054 , 1 3622 , 0 1120 , 0 1664 , 0 1120 , 0 3146 , 0 1 Σ

Matriks kovarian kelompok kedua,

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − = 1410 , 1 4062 , 0 0400 , 0 4062 , 0 7951 , 0 0057 , 0 0400 , 0 0057 , 0 1845 , 0 2 Σ

Matriks kovarian gabungan ,

2 1 gabungan 15 7 15

8 _{Σ Σ}

Σ = +

Invers matriks kovarian gabungan,

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − = − 4482 , 1 3089 , 0 3302 , 0 3089 , 0 8795 , 1 3374 , 0 3302 , 0 3374 , 0 1063 , 4 1 gabungan Σ

Fungsi diskriminan adalah

[

x x

]

Σ x x

a = ₁− _{2 gabungan}−1 =ˆ' ' y ˆ

[

]

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − = 3 2 1 4482 , 1 3089 , 0 3302 , 0 3089 , 0 8795 , 1 3374 , 0 3302 , 0 3374 , 0 1063 , 4 0893 , 1 5997 , 1 6967 , 1 x x x 3 2

1 2,0993 0,5153 0694

,

6 x + x + x

Nilai diskriminan kelompok pertama,

[

]

7,5253

5101 , 0 7528 , 0 7984 , 0 0893 , 1 5997 , 1 6967 , 1 ' ˆ ₁ 1 = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − =

=a x y

Nilai diskriminan kelompok kedua,

[

]

6,6891

5738 , 0 8469 , 0 8982 , 0 0893 , 1 5997 , 1 6967 , 1 x ' aˆ ₂

2 =−

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = = y

Nilai tengah antara y1 dan y2,

(

)

(

7,5253 6,6891

)

0,4181 2 1 y y 2 1

ˆ= ₁+ ₂ = − =

m

Selanjutnya evaluasi objek dengan menghitung nilai diskriminan,yˆ dari masing-masing kabupaten/kota, Tabel 4 berikut menampilkan hasil perhitungan nilai yˆ untuk masing-masing kabupaten/kota. Dari Tabel 4 dapat diperkirakan terdapat satu misklasifikasi kabupaten/kota, Kab. Sumedang mempunyai nilai yˆ >mˆ = 0,4181 maka seharusnya kabupaten ini dikelompokkan ke kelompok kedua.

Ketepatan pengklasifikasian dari fungsi diskriminan yang diperoleh adalah

% 12 , 94 % 100 17 8

8+ _{× =}

Maka, hasil pengelompokan dapat dikatakan valid dengan fungsi diskriminan berikut,

3 2

1 2,0993 0,5153 0694

, 6

ˆ x x x

y= + +

.

Begitu pula hasil pengelompokan melalui analisis cluster valid karena setiap anggota tepat dikelompokkan sebagai kelompoknya. Berdasarkan Tabel 4 diperoleh bahwa dari ketujuhbelas kabupaten/kota di Jawa Barat 47,06% berada pada tingkat sosial ekonomi menengah ke bawah.

Tabel 4 Nilai diskriminan masing-masing kabupaten/kota.

Kabupaten/Kota ˆy Kelompok 1

Kab.Sukabumi -9,6476 Kab.Cianjur -7,4806 Kab.Garut -3,5019 Kab.Tasikmalaya -8,4329 Kab.Ciamis -10,9765 Kab.Kuningan -8,5133 Kab.Majalengka -7,4789 Kab.Subang -7,1843 Kab. Sumedang* 3,0131 Kelompok 2

Kab.Bandung 6,0423 Kab.Cirebon 6,3383 Kab.Karawang 10,0629 Kab.Bekasi 12,0948 Kota Bogor 9,5030 Kota Bandung 4,3247 Kab. Bogor 8,4957 Kab. Purwakarta 3,3411

SIMPULAN

Secara umum, analisis cluster mengelompokkan objek-objek yang memiliki kemiripan, dan setiap anggota kelompok akan berbeda dengan anggota kelompok yang lain. Salah satu cara mengukur tingkat kemiripannya yaitu dengan menghitung jarak antar objek dengan jarak euclid.

Metode agglomeratif akan mengelompokkan dua atau lebih kelompok dari yang memiliki kesamaan terdekat secara bertingkat sampai akhirnya diperoleh hanya satu kelompok. Setiap tahap algoritma agglomeratif jarak antar kelompok akan

semakin membesar. Semakin besar jarak antar kelompok menunjukkan semakin jauh tingkat kesamaan antar kelompok tersebut. Penentuan objek yang akan dikelompokkan sangat bergantung pada pendefinisian jarak antar kelompok. Single linkage clustering

Analisis diskriminan dapat digunakan untuk menguji kevalidan hasil analisis cluster karena hasil dapat berbeda berdasarkan metode yang dipilih pada analisis tersebut. Uji kevalidan dilakukan setelah menemukan fungsi diskriminan. Apabila fungsi kepekatan untuk kedua kelompok diketahui maka fungsi diskriminan dapat diperoleh melalui proses meminimumkan nilai expected cost of misclassification (ECM).

Dari hasil analisis diskriminan, pengelompokan tujuh belas kabupaten/kota di Jawa Barat berdasarkan tiga indikator sosial ekonomi pada tahun 2002, yaitu upah minimum kabupaten/kota (UMK), persentase tingkat pengangguran, dan laju pertumbuhan

ekonomi ke dalam dua kelompok diperoleh fungsi y=6,0694x₁+2,0993x₂ +0,5153x₃. Ketepatan pengklasifikasian kasus fungsi adalah sebesar 94,12%. Maka, fungsi ini dapat dianggap valid untuk mengelompokkan sebuah kabupaten/kota berdasarkan ketiga indikator tersebut ke dalam kelompok dengan tingkat sosial ekonomi menengah ke bawah atau menengah ke atas. Dengan membandingkan hasil pengelompokan analisis cl