Pengaruh Kesalahan Pembulatan Pada Metode Iterasi

PENGARUH KESALAHAN PEMBULATAN PADA

METODE ITERASI

TESIS

Oleh

TOHOM PAHA MEI BANJARNAHOR

097021074/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN

PENGARUH KESALAHAN PEMBULATAN PADA

METODE ITERASI

TESIS

Diajukan Sebagai Salah Satu Syarat

Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

TOHOM PAHA MEI BANJARNAHOR 097021074/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

Judul Tesis : PENGARUH KESALAHAN PEMBULATAN PADA METODE ITERASI

Nama Mahasiswa : Tohom Paha Mei Banjarnahor

Nomor Pokok : 097021074

Program Studi : Matematika

Menyetujui, Komisi Pembimbing

(Prof. Dr. Tulus, M.Si) (Prof. Dr. Drs. Iryanto, M.Si)

Ketua Anggota

Ketua Program Studi Dekan

(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)

Telah diuji pada Tanggal 15 Juni 2011

PANITIA PENGUJI TESIS

Ketua : Prof. Dr. Tulus, M.Si

Anggota : 1. Prof. Dr. Drs. Iryanto, M.Si

2. Prof. Dr. Opim Salim S, M.Sc

ABSTRAK

Tesis ini membahas tentang bagaimana memperkirakan solusi dari persamaan non linear pada ruang Banach dengan menggunakan metode Newton Raphson. Oleh karena adanya kesalahan pembulatan pada barisan yang dihasilkan oleh komputer sehingga berbeda dengan barisan yang dihasilkan secara teori, maka digunakan hipotesis Lipschitz pada turunan Frechet ke-m (m _≥ 2, bulat) sebagai pengganti dari barisan tersebut. Hal ini akan memenuhi syarat cukup konvergensi dan selan-jutnya akan dapat mempercepat rasio konvergensi.

Kata kunci : Ruang banach, Metode newton, Turunan frechet, Syarat lipschitz.

ABSTRACT

This thesis discusses how to estimate the solution of non linear equations in Ba-nach space using Newton Raphson method. Due to rounding errors in the sequence generated by a computer different with a sequence generated analytically, then used the hypothesis on the Lipschitz Frechet derivative mth (m _≥ 2, integer) instead of the sequence. This convergence will be qualified enough and then will be able to accelerate the convergence ratio.

KATA PENGANTAR

Puji dan syukur penulis panjatkan kehadirat Tuhan, karena berkat kasih dan karunia-Nya jualah penulis dapat menyelesaikan perkuliahan tepat waktu dan menyelesaikan Tesis dengan judul ”PENGARUH KESALAHAN

PEMBU-LATAN PADA METODE ITERASI”.

Pada kesempatan ini, penulis menyampaikan ucapan terima kasih dan peng-hargaan yang sebesar-besarnya kepada :

Bapak Prof. Dr.dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K), selaku Rektor Universitas Sumatera Utara.

Bapak Dr. Sutarman, M.Sc, selaku Dekan FMIPA Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti perkuliahan pada Program Studi Magister Matematika.

Bapak Prof. Dr. Herman Mawengkang, selaku Ketua Program Studi Magister Matematika pada Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara dan juga selaku Ketua Komisi Panitia Penguji tesis ini, yang telah dengan penuh kesabaran memotivasi dan membimbing penulis hingga selesainya tesis ini dengan baik.

Bapak Dr. Saib Suwilo, MSc, selaku Sekretaris Program Studi Magister Matema-tika pada Fakultas MatemaMatema-tika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara yang telah banyak memberikan saran dan masukan, juga motivasi belajar selama masa perkuliahan.

Bapak Prof. Dr. Tulus, M.Si dan Prof. Dr. Drs. Iryanto, M.Si, selaku pembimbing tesis yang telah banyak memberikan saran dan masukan, juga motivasi belajar masa perkuliahan.

Bapak Prof. Dr. Opim Salim, M.Sc dan Drs. Marwan Harahap, M.Eng, selaku pembanding dan penguji atas segala saran dan petunjuk yang diberikan.

Gubernur Sumatera Utara, yang telah memberi bantuan beasiswa pendidikan kepada penulis melalui BAPPEDASU.

Bapak Drs. Open Darnius, M.Sc ; Drs. Marihat Situmorang, Mkom; Drs. S. Arriswoyo, M.Si; Drs. Sawaluddin, M.IT dan Ibu Dra. Mardiningsih, M.Si sebagai staf pengajar yang telah memberikan ilmunya kepada penulis selama perkuliahan. Bapak Kepala Dinas Pendidikan, Sekretaris, Kabid SLTP / SM/PT dan jajarannya, Kepala UPT Disdik dan Camat Kecamatan Sirandorung dan rekan -rekan Kepala Sekolah dalam lingkungan dinas pendidikan Kabupaten Tapanuli Tengah

Rekan mahasiswa angkatan 2008 dan 2009 atas kerjasama dan kebersamaan yang indah selama perkuliahan dan rekan-rekan guru dan staf SMA Negeri 1 Siran-dorung Kabupaten Tapanuli Tengah yang turut memberi motivasi kepada penulis. Penulis juga mengucapkan terima kasih kepada istri tercinta Masda Br. Si-tumorang yang selalu mendukung penulis dalam menyelesaikan kuliah dan kepada Anak-anakku tersayang Teresia Imelda, Blessinta, Anugerah dan Ruth Realita.

Secara khusus penulis menyampaikan terima kasih dan sayang yang men-dalam kepada orangtua penulis ayahanda Alm. M. Banjarnahor dan Ibunda K. Br. Siregar, kakak, adik-adik, ipar dan semua keponakan saya yang senantiasa memberikan dukungan dan mendoakan keberhasilan penulis dalam menyelesaikan pendidikan ini.

Kepada seluruh pihak yang tidak dapat penulis sebutkan satu persatu, penulis berterima kasih atas semua bantuan yang diberikan, semoga Tuhan Yang Maha Kuasa membalaskan segala kebaikan yang telah diberikan, Amin.

Penulis menyadari tesis ini masih jauh dari sempurna, namun penulis berharap semoga tesis ini bermanfaat bagi pembaca dan pihak-pihak yang memerlukannya.

Medan, 15 Juni 2011 Penulis,

RIWAYAT HIDUP

Penulis bernama Tohom Paha Mei Banjarnahor dilahirkan di Bakara pada tanggal 15 Mei 1971 anak ke-7 dari 9 orang bersaudara. Nama Ayah Alm. Madang Banjarnahor dan Ibu Kristina Br. Siregar. Tamat dari Sekolah Dasar Negeri Marbun tahun 1984, melajutkan pendidikan ke Sekolah Menengah Pertama Negeri Bakara tamat tahun 1987, kemudian melanjut ke Sekolah Menengah Atas Negeri Barus dan tamat tahun 1990.

Pada tahun 1990 kuliah di Institut Keguruan dan ilmu Pendidikan Negeri Medan jurusan Pendidikan Matematika tamat tahun 1995. Pada tahun 1997 penulis menjadi guru di SLTP Negeri 2 Manduamas Kabupaten Tapanuli Tengah, dan pada tahun 2005 menjadi guru di SMA Negeri 1 Sirandorung dan mendapat tugas tambahan sebagai kepala sekolah sampai dengan sekarang.

Sebagai seorang kepala rumah tangga, penulis tinggal bersama isteri dan anak di Desa Siordang Kecamatan Sirandorung Kabupaten Tapanuli Tengah.

DAFTAR ISI

Halaman

ABSTRAK i

ABSTRACT ii

KATA PENGANTAR iii

RIWAYAT HIDUP v

DAFTAR ISI vi

DAFTAR TABEL viii

DAFTAR GAMBAR ix

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Kontribusi Penelitian 3

1.5 Metode Penelitian 3

BAB 2 TINJAUAN PUSTAKA 4

2.1 Aplikasi Metode Iterasi Variasional He dalam Menyelesaikan

Persamaan Orde ketujuh Swada-Kotera 4 2.2 Metode Iterasi Variasional He 4 2.3 Aplikasi Variational Iteration Method (VIM) untuk Ordo ke

7 Sawada Kotera (sSK) dan Lax’s Seventh Korteweg-de Vries

(LsKdV) 5

2.4 Penerapan dalam Contoh 6

BAB 3 LANDASAN TEORITIS 9

3.3 Metode Newton Rapshon dalam Sistem Persamaan Non Linier 14 3.3.1 Fungsi dan Himpunan Konveks 15 3.3.2 Ruang Banach (Banach Space) 16

3.3.3 Turunan Frechet 18

3.3.4 Lipschitz Kontinu 19

BAB 4 PEMBAHASAN 20

4.1 Pengaruh Kesalahan Pembulatan 20

4.2 Analisis Konvergensi 21

4.3 Penerapan dalam Kasus 25

BAB 5 KESIMPULAN DAN SARAN 30

5.1 Kesimpulan 30

5.2 Saran 30

DAFTAR PUSTAKA 31

DAFTAR TABEL

Nomor Judul Halaman

3.1 Representase Kesalahan 10

3.2 Jumlah Iterasi dan Kesalahan ε=_|xn−L| 12

4.1 Iterasi metode newton 27

DAFTAR GAMBAR

Nomor Judul Halaman

2.1 Solusi hampiran u(x, t) 7

2.2 Solusi eksak u(x, t) 7

2.3 Solusi hampiran u(x, t) 8

2.4 Solusi eksak u(x, t) 8

ABSTRAK

Tesis ini membahas tentang bagaimana memperkirakan solusi dari persamaan non linear pada ruang Banach dengan menggunakan metode Newton Raphson. Oleh karena adanya kesalahan pembulatan pada barisan yang dihasilkan oleh komputer sehingga berbeda dengan barisan yang dihasilkan secara teori, maka digunakan hipotesis Lipschitz pada turunan Frechet ke-m (m _≥ 2, bulat) sebagai pengganti dari barisan tersebut. Hal ini akan memenuhi syarat cukup konvergensi dan selan-jutnya akan dapat mempercepat rasio konvergensi.

ABSTRACT

This thesis discusses how to estimate the solution of non linear equations in Ba-nach space using Newton Raphson method. Due to rounding errors in the sequence generated by a computer different with a sequence generated analytically, then used the hypothesis on the Lipschitz Frechet derivative mth (m _≥ 2, integer) instead of the sequence. This convergence will be qualified enough and then will be able to accelerate the convergence ratio.

Keywords : Banach space, Newton’s method, Frechet derivative, Lipschitz condition.

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Dimulai pada tahun 1940-an, perkembangan dan ketersediaan komputer digi-tal telah menyebabkan peningkatan penggunaan model matematika realistik dalam ilmu pengetahuan, kedokteran, teknik, dan bisnis dimana analisa numerik diper-lukan untuk menyelesaikan model matematika yang semakin kompleks. (Atkin-son, 2007). Model matematika tersebut banyak yang sulit diselesaikan atau tidak mungkin diselesaikan maupun dengan metode analitik dengan penggunaan rumus-rumus aljabar. Untuk ini digunakan metode yang dapat menangani persoalan tersebut dengan menggunakan metode numerik. Beberapa permasalahan dalam bidang teknik yang sulit dapat diselesaikan dengan metode analitik karena sering dihadapkan pada sistem persamaan berskala besar, sangat tak linier dan cakupan yang lebih kompleks, persoalan demikian ini umumnya diselesaikan dengan metode numerik.

2

kesalahan pembulatan (round off error) dan kesalahan pemotongan (truncation error).

Kesalahan manusia merupakan kesalahan yang terjadi karena pengamatan yang kurang tepat, kesalahan menginterpretasi data, atau kesalahan membaca /menulis data. Kesalahan pemotongan adalah kesalahan karena pemenggalan data misalnya pada deret suku-suku tak hingga yang hanya suku pertamanya digu-nakan, sedangkan kesalahan pembulatan terjadi karena adanya pembulatan dan juga karena penggunaan digit yang terbatas pada mesin (kalkulator/komputer). Sebaga ilustrasi, andaikan kita akan menjumlahkan bilangan 9.26541 dan 7,16252 dengan menggunakan komputer dengan ketelitian 6 digit, maka penjumlahan ke-dua bilangan dengan komputer tersebut akan menghasilkan bilangan : 16,4279 yang seharusnya 16,42793 sehingga terdapat suatu kesalahan pembulatan sebe-sar 0,00003. Jika pekerjaan komputer dilakukan dengan banyak operasi bilangan, maka diperlukan pembulatan berkali-kali dan akibatnya terjadi kesalahan berulang kali sehingga dapat memperbesar kesalahan.

3

1.2 Perumusan Masalah

Masalah yang dibahas dalam penelitian ini yaitu ”Bagaimana menentukan so-lusi persamaan non linier pada ruang Banach dengan menggunakan metode Newton Raphson, sebagai akibat dari adanya kesalahan pembulatan pada metode iterasi”. 1.3 Tujuan Penelitian

Penelitian ini bertujuan untuk menentukan solusi persamaan non linier pada ruang Banach dengan menggunakan metode Newton Raphson, sebagai akibat dari adanya kesalahan pembulatan pada metode iterasi.

1.4 Kontribusi Penelitian

Manfaat dalam penelitian ini adalah membantu menyelesaikan suatu per-samaan non linier untuk mempercepat konvergensi.

1.5 Metode Penelitian

Penelitian ini menggunakan metode studi literatur dengan langkah-langkah sebagai berikut :

1. Mengumpulkan buku-buku, jurnal-jurnal, penelitian-penelitian maupun tulisan yang berkaitan dengan penelitian yang dilakukan.

2. Mempelajari dan memahami bahan-bahan studi yang telah terkumpul seperti Metode Newton Raphson

3. Membahas masalah persamaan non linier pada ruang Banach dengan meng-gunakan metode Newton Raphson untuk mempercepat konvergensi.

4. Mengecek validasi dari hasil yang diperoleh

BAB 2

TINJAUAN PUSTAKA

2.1 Aplikasi Metode Iterasi Variasional He dalam Menyelesaikan Per-samaan Orde ketujuh Swada-Kotera

Metode analisis yang umum digunakan untuk menyelesaikan persamaan non-linier sangat terbatas dan teknik numerik yang melibatkan variabel-variabel deskrit akan menimbulkan kesalahan pembulatan. Penelitian terbaru metode iterasi vari-asional oleh He memberikan pendekatan tentang kecepatan konvergensi dari solusi eksak dan telah terbukti berhasil dalam menurunkan solusi analitis persamaan diferensial nonliner dan linier. Metode ini lebih diminati karena bebas dari kesala-han pembulatan dan tidak memerlukan daya/memori yang besar pada komputer. He telah menerapkan metode ini untuk mendapatkan solusi analitik dari persamaan otonom diferensial. Metode iterasi variasional berhasil diterapkan oleh Burger’s dan persamaan Burger’s, Schruondinger-KdV, generalisasi Kdv dan persamaan peraian dangkal, persamaan differensial parsial Helmholtz, persamaan linier dan non linier, Kdv, dan persamaan Boussinesg (Hossein Jafari, dkk, 2008).

Untuk menentukan penyelesaian persamaan berikut digunakan metode VIM (Variational Iteration Method) :

ut+ (63u4+ 63(2u2uxx+uu2x) + 21(uuxxxx+u2xx+uxuxxx) +uxuxxx)x= 0, (2.1)

Ut+ (35u4+ 70(u2uxx+uu2x) + 7(2uuxxxx+ 3u2xx+ 4uxuxxx) +uxuxxx)x= 0, (2.2)

Persamaan (2.1) dikenal sebagai persamaan urutan ketujuh Sawada-Kotera (S.M. El-Sayed dan D. Kaya, 2004) dan Persamaan (2.2) sebagai persamaan Lax’s orde ketujuh KdV (E.J. Parkes dan B.R. Duffy, 1996).

2.2 Metode Iterasi Variasional He

Penggunaan metode iterasi variasional, diawali dengan menentukan persamaan differensial :

Lu+N u=g(x, t) (2.3)

5

dimanaL adalah operator linear,N operator nonlinear dan g(x, t) adalah bentuk persamaan. Metode iterasi variasional dapat dibentuk dan dianalisis dengan fungsi sebagai berikut:

un+ 1 (x, t) =un(x, t) +

Z t

0

λ(ξ) (Lun(ξ) +Nu˜(ξ)−g(ξ))dξ, n> 0, (2.4)

dimanaλ adalah pengali Lagrange (Inokuti, dkk, 1978), yang dapat diidentifikasi dengan teori variasional, subskrip n menunjukkan hampiran orde ˜un, ditentukan dengan batas variasional dan δ˜un= 0.

Hampiran un+1(x, t), n ≥0 dari solusi u(x, t) akan mudah diperoleh dengan

menggunakan pengali Lagrange dan dengan menggunakan fungsiu0

sehingga solusinya menjadi:

u(x, t) = lim

n→∞un(x, t) (2.5)

2.3 Aplikasi Variational Iteration Method (VIM) untuk Ordo ke 7 Sawada Kotera (sSK) dan Lax’s Seventh Korteweg-de Vries (LsKdV)

Untuk menerapkan VIM, pertama ditulis ulang persamaan (2.1) dalam ben-tuk :

Lt(u) + (63N1(u) + 63(2N2(u)) + 21(N4(u)) +Lx(u))x = 0, (2.6)

dimanaN1(u) =u4, N2(u) =u2uxx, N3(u) =uu2x, N4(u) =uuxxxx+u2xx+uxuxxxx,

melambangkan bentuk nonlinier. Lt = _∂t∂ dan Lx = ∂

6

∂x6 melambangkan operator

linier diferensial.

Ananlisis fungsi dari persamaan (2.6):

un+ 1 (x, t) =un(x, t) +

Z t

0

λ(ξ)

∂

∂ξ + (N(˜un))x

dξ, n>0, (2.7)

dimanaN(u) = (63N1(u) + 63(2N2(u) +N3(u)) + 21(N4(u)) +Lx(u). variasional

6

dengan λ(ξ) =₋1. Mensubstitusikan pengali Lagrange ke fungsi (2.7) akan mem-berikan rumus iterasi:

Menggunakan pendekatan u0(x, t) ke persamaan (2.10) diperoleh nilai hampiran.

Dengan cara yang sama untuk LsKdV diperoleh rumus iterasi berikut: un+1(x, t) =un(x, t)−

Dengan demikian diperoleh solusi hampiran u(x, t) = lim

n_→∞un(x, t)

2.4 Penerapan dalam Contoh

Untuk menunjukkan efekktivitas dari metode VIM ini, yang ditentukan dari persamaan (2.1) dan (2.2) dengan memberikan syarat awal, disajikan dalam contoh berikut.

Contoh 2.1. (Hossein Jafari, dkk, 2008). Tentukan SsK dari persamaan (2.1) dengan syarat awal: Substitusikan persamaan (2.12) ke dalam persamaan (2.10) akan diperoleh: u0(x, t) = 4₃k2 2−3 tanh2(kx)

u1(x, t) =u0(x, t) + 1₉k8sech2(kx)t[2176−896 cosh (2kx)],

7

(4kx)+24832 cosh (6kx)₋12544 cosh (8kx)]+1₃k6t2544812032₋2746548224 cosh (2kx) +305070080 cosh (4kx)+41746432 cosh (6kx)₋5619712 cosh (8kx)]+1

9k

12_t2_[50980192256

−23855104000 cosh(2kx)₋55593402368 cosh(4kx) + 17983078400 cosh(6kx)₋ 1258815488 cosh(8kx)]₁₃₅1 k18_t3_{[−238459436400640 + 291359575506944 cosh(2kx)}

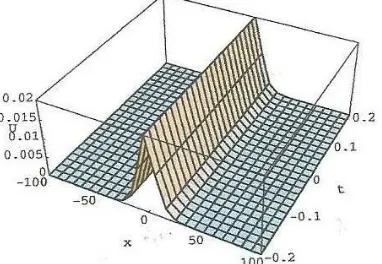
−8208301695232 cosh(kx) + 10956730007552 cosh(6kx)₋563949338624 cosh(8kx)]) Pada gambar 2.1, dan gambar 2.2 u3(x, t)dan solusi eksak

Gambar 2.1 Solusi hampiran u(x, t)

Gambar 2.2 Solusi eksak u(x, t)

Contoh 2.2. (Hossein Jafari, dkk, 2008). Perhatikan persamaan LsKdV dengan syarat awal yang diberikan :

8

dengan mensubstitusi persamaan (2.13) ke dalam persamaan (2.11) diperoleh ham-piran :

u0(x, t) = 2k2sek21(kx)

u1(x, t) = u0(x, t)−128k8tsech2(kx)

u2(x, t) = u1(x, t)−128₃ sech8(kx)k14t2(44040192t3k18+1720320t2k12+30464tk6

+(₋3440640t2_k12_−7168tk6_{+1803) cosh(2kx)+36(448k}6_{t−11) cosh}

(4kx)₋3 cosh(6kx)₋2004)

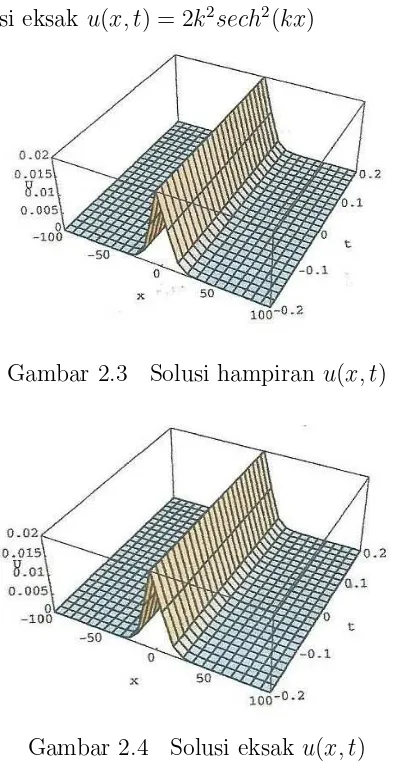
Pada gambar 2.3,u3(x, t) untukk= 0,1 dan x∈[−100,100].

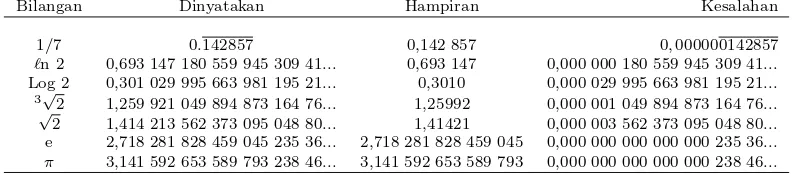
Pada gambar 2.4 solusi eksaku(x, t) = 2k2_sech2_(kx)

Gambar 2.3 Solusi hampiran u(x, t)

BAB 3

LANDASAN TEORITIS

3.1 Kesalahan Pembulatan (Round off error)

Solusi dengan metode numerik adalah solusi hampiran (aproksimasi) ter-hadap solusi eksak, dengan demikian solusi numerik mempunyai kesalahan yakni selisih antara solusi hampiran dengan solusi eksak. Rizwan Butt (2009) menje-laskan kesalahan (error) sebagai berikut :

Solusi hampiranp mendekati solusi eksakα ditulis sebagai :

p_≈α (3.1)

dengan kesalahan E terhadap solusi hampiran p, yaitu perbedaan antara solusi hampiran pdengan solusi eksak α yang didefenisikan

E =α₋p (3.2)

jika α > p maka E positif, dan jika α < p maka E negatif, sehingga kesalahan absolut/mutlak didefenisikan

|E_|=_|α₋p_| (3.3)

dengan kesalahan relatif (RE) terhadap solusi hampiran p yang merupakan rasio dari kesalahan absolut dengan solusi eksak, maka

RE = |α−p|

α α 6= 0 (3.4)

dan persentase kesalahan = |α−p|

α ×100% (3.5)

dengan :

E : Error (galat)

RE : Relative Error (galat relatif) p : Solusi hampiran

10

Secara umum terdapat tiga sumber utama penyebab kesalahan dalam per-hitungan numerik yaitu kesalahan manusia (human error), kesalahan pemotongan (truncation error) dan kesalahan pembulatan (round of error). Kesalahan dalam membulatkan sebuah bilangan disebut juga kesalahan pembulatan yaitu perbedaan solusi hampiaran dengan solusi eksak dalam perhitungan matematika. Analisis nu-merik secara khusus memperkirakan kesalahan dengan menggunakan pendekatan persamaan atau algoritma, terutama ketika banyak menggunakan angka terbatas untuk menyatakan bilangan riil (digit tak hingga) atau disebut kesalahan kuantitas. Kesalahan yang dihasilkan ketika sebuah kalkulator atau komputer digunakan untuk melakukan perhitungan bilangan riil disebut kesalahan pembulatan. Hal ini terjadi karena aritmatika dilakukan di mesin melibatkan angka dengan jumlah digit terbatas, dengan hasil perhitungan yang dilakukan hanya merupakan angka perkiraan dari angka yang sebenarnya. Komputer hanya sebagian kecil dari sis-tem bilangan digunakan untuk menyatakan bilangan riil positif atau negatif, dan menyimpan bagian pecahan bersama-sama dengan bagian eksponensial (Richard L. Burden dan J. Douglas Faires, 2005).

Representasi kesalahan diperkenalkan dengan menyatakan bilangan dalam komputer (kesalahan representasi), dapat ditunjukkan pada table berikut.

Tabel 3.1 Representase Kesalahan

Bilangan Dinyatakan Hampiran Kesalahan 1/7 0.142857 0,142 857 0,000000142857

ℓn 2 0,693 147 180 559 945 309 41... 0,693 147 0,000 000 180 559 945 309 41... Log 2 0,301 029 995 663 981 195 21... 0,3010 0,000 029 995 663 981 195 21...

3√_{2 1,259 921 049 894 873 164 76... 1,25992 0,000 001 049 894 873 164 76...}

√

2 1,414 213 562 373 095 048 80... 1,41421 0,000 003 562 373 095 048 80... e 2,718 281 828 459 045 235 36... 2,718 281 828 459 045 0,000 000 000 000 000 235 36...

π 3,141 592 653 589 793 238 46... 3,141 592 653 589 793 0,000 000 000 000 000 238 46...

Sumber : http://en.wikipedia.org/wiki/rounding error

Penambahan jumlah digit dapat dilakukan dalam representasi bilangan un-tuk mengurangi besarnya kesalahan pembulatan namun setiap representasi ter-batas pada digit terter-batas yang akan menyebabkan tingkat kesalahan pembulatan bilangan riil.

11

desimal (9,95) dengan tujuan entri data, dan kemudian dibulatkan lagi satu tempat desimal (10,0) untuk tujuan tampilan, kesalahan pembulatan adalah 0,054691. Jika bilangan 9,9 dibulatkan menjadi satu tempat desimal, kesalahan pembulatannya adalah 0,045309.

Menurut Frank R. Giardano, dkk (2009) kesalahan pembulatan disebabkan oleh penggunaan digit terbatas pada hitungan mesin. Karena semua bilangan tidak dapat dinyatakan dengan tepat penggunaannya hanya terbatas seharusnya diharapkan kesalahan pembulatan dapat dinyatakan. Contohnya dengan menggu-nakan kalkulator atau komputer digumenggu-nakan delapan digit aritmatik maka bilangan

1

3 dinyatakan dengan 0,33333333 juga bahwa 3x 1

3 adalah 0,99999999 kesalahan

10−8 _{oleh karena pembulatan. Bilangan riil} 1

3 adalah string tak hingga dari digit

desimal 0,333... namun pada kalkulator atau komputer dapat dihitung dengan ketelitian terbatas. Ketika beberapa operasi hitungan dilakukan berturut-turut, salah satunya dengan pembulatan, akumulasi pengaruh pembulatan sangat berarti terhadap hasil sebenaranya. Oleh karenanya kesalahan pembulatan merupakan hal yang harus diperhatikan ketika menggunakan mesin hitung.

Pembulatan dalam aritmatika menurut standar IEEE dilakukan dengan ke-tentuan sebagai berikut :

1. Pemotongan : hanya mengenal satu digit ; juga disebut pembulatan ke nol 0. 142.857_≈ 0,142 ; pengurangan angka signifikan setelah digit ke tiga 2. Bulat untuk terdekat ; bulat untuk nilai terdekat 0. 142.857 _≈ 0,143;

pem-bualatan angka signifikan keempat, dibualatkan ke atas karena 8>5

0. 142.857_≈ 0,14; pembulatan yang ketiga digit yang signifikan, dibulatkan ke bawah karena 2<5

3. Bulat untuk_−∞ ; selalu bulat ke kiri pada garis bilangan 4. Bulat untuk +_∞ ; selalu bulat ke kanan pada garis bilangan

12

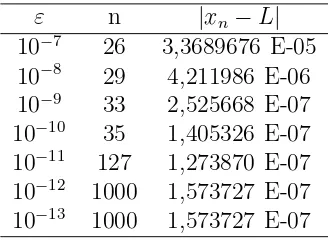
Pengaruh kesalahan pembulatan pada metode iterasi dapat ditunjukkan de-ngan menggunakan metode Newton’s dalam menghitung akar dari persamaan (J.M. Chesneaux, dkk, 2010) :

F(x) =x4₋1002x3 + 252001x2 ₋501000x+ 250000 (3.6)

dengan menentukan x0 = 11000 dan solusi eksak L = 500, kriteria penghentian

iterasi _|xn −xn₋1| ≤ ε|xn₋1| dimana jumlah iterasi maksimum 1000. Hasilnya

ditunjukkan dalam tabel berikut :

Tabel 3.2 Jumlah Iterasi dan Kesalahan ε=_|xn−L|

ε n _|xn−L|

10−7 _{26 3,3689676 E-05}

10−8 _{29 4,211986 E-06}

10−9 _{33 2,525668 E-07}

10−10 _{35 1,405326 E-07}

10−11 _{127 1,273870 E-07}

10−12 _{1000 1,573727 E-07}

10−13 _{1000 1,573727 E-07}

3.2 Metode Iterasi (Iterative Method)

Dalam matematika, iterasi dapat diartikan sebagai suatu proses perulangan atau metode yang digunakan secara berulang dalam menyelesaikan permasalahan matematika. Salah satu metode yang paling penting dalam perhitungan sekarang yaitu solusi dengan metode iterasi. Persamaan non linier antara lain persamaan kuadrat, persamaan trigonometri, persamaan yang memuat logaritma atau eks-ponen. Dalam kasus sederhana persamaan non linier dapat diselesaikan secara eksak atau analitik dengan menggunakan metode atau rumus tertentu, misalnya persamaan kuadrat diselesaikan dengan cara memfaktorkan atau menggunakan ru-mus. Namun secara umum persamaan non linier tidak dapat diselesaikan secara analitik, sehingga diperlukan metode iterasi untuk menyelesaikannya.

pe-13

rulangan perhitungan. Selanjutnya David H. Urmann (2008) meyatakan bahwa metode iterasi digunakan untuk memecahkan masalah matematika dengan men-cari solusi eksak, dengan memberikan pendekatan awal dan diulangi untuk langkah selanjutnya sampai diperoleh solusi akhir.

Dalam menentukan solusi persamaan non linier, misalnya masalah nilai batas dalam teori kinetik gas, elastisitas dan masalah menentukan akar persamaan non linier digunakan metode iterasi Newton (M. Heydari dkk, 2011). Metode Newton Raphson dapat digunakan untuk membahas salah satu masalah dalam aproksimasi (hampiran) numerik yaitu masalah penentuan akar persamaan non linier. Bentuk umum permasalahnya yaitu menentukan nilai variabel x sehingga F(x) = 0 di-mana F merupakan suatu fungsi non linier. Penyelesaian atau akar persamaan tersebut adalah semua nilai x yang memenuhi persamaan dimaksud. Akar suatu persamaan non linier dapat berupa nilai tunggal, lebih dari satu, atau bahkan tidak mempunyai akar sama sekali. Untuk mengidentifikasi ada tidaknya atau berapa banyak akar suatu persamaan non linier diperlukan syarat cukup agar su-atu persamaan non linier mempunyai akar di dalam susu-atu interval sehingga dapat dijadikan pedoman untuk melokalisir akar persamaan non linier tersebut. Pemili-han tebakan awal akan mempengaruhi kecepatan konvergensi barisan iterasi yang menjamin tidak akan terjadi derivatif nol.

14

3.3 Metode Newton Rapshon dalam Sistem Persamaan Non Linier

Generasi lain dari metode Newton Raphson adalah metode Newton-like (New-ton’s Method) yang digunakan untuk menentukan solusi dari suatu fungsi yang didefinisikan dalam ruang Banach atau dapat ditulis denganF(x) = 0 dimana F :Rn →Rm.

Modifikasi atau pengembangan metode Newton dalam menyelesaikan sistem persamaan non linier salah satunya metode inexact Newton-like. Metode Newton untuk menyelesaikan sistem persamaan nonlinier F(x) = 0 adalah xn+1 = xn −

(F(xn)−1)(F(xn) dimanaxberada padaRn. Fungsi F adalah fungsi dari himpunan

bagian pada Rn ke himpunan bagian Rn dan F′(x) adalah matriks Jacobian dari F(x). Pengembangan dari metode Newton yang disebut metode inexact Newton-like dalam menentukan solusi persamaan nonlinier F(x) = 0 adalah xn+1 = xn−

(A(xn))−1F(xn) (M. Podisuk, 2000).

Luca Bergamaschi (2008) menjelaskan metode Newton dalam sistem per-samaan non linier. Bentuk umum sistem perper-samaan non linier adalah sebagai

berikut : _

FungsiF dapat dideferensialkan dalam himpunan bagian terbukaD padaRn

.

Perhitungan skalar akan digunakan untuk menghitung solusi hampiran xn

15

misalkanF(xn+1) = 0 yang dikembangkan dari deret Taylor pada fungsiF(xn+1).

0 = F(xn+ 1) =F(xn) +F

′

(xn)y (3.8)

dimanaF′(xn) adalah sistem Jacobian yang dievaluasi pada xn.

(F′(x))ij =

∂Fi

∂xj

(x) (3.9)

sebelumnya akan dihitungy dalam vektor n

y=₋(F′(xn))−1F(xn) (3.10)

iterasi ke -n dalam metode Newton di tulis sebagai Xn+1 =xn−(F

′

(xn))−1F(xn) (3.11)

dengan beberapa asumsi :

1. Matriks JacobianF′(xn) saling invers

2. Konvergensi lokal pada metode Newton dapat menunjukkan bukti berupa harga tebakan awalx0 memenuhi syarat dekat dengan solusi

3. Perhitungan xn+1 dimulai dari xn memerlukan invers dan matrik Jacobian

dalam prakteknya vektorndievaluasi untuk menyelesaikan persamaan berikut F′(xn)y=−F(xn) (3.12)

4. F′ kebanyakan tidak simetrik, sehingga metode iteratif General Minimal Residual Solusion ( GMRES ) disarankan untuk solusi dari metode Newton.

3.3.1 Fungsi dan Himpunan Konveks

Definisi 3.1. (Robert Nurnberg, 2008) Sebuah himpunan S _⊂ Rn disebut himpunan konveks jika segmen garis lurus yang menghubungkan dua titik dalam himpunan S terletak di dalam himpunan S. Misalkan untuk dua titik x, y _∈ S terdapat

16

FungsiF :D _→R disebut fungsi konveks jika domain D _⊂Rn himpunan konveks dan jika untuk dua titikx, y_∈D,

f(<_∝x+ (1_{− ∝})_≤∝f(x) + (1_{− ∝}) +f(y) _∀x_∈[0,1] (3.14)

Misalkan D _⊂Rn adalah himpunan konveks terbuka jika :

a) f : D _→ Rn terdeferensialkan terus, maka f adalah konveks jika dan hanya jika

f(y)_≥f(x) +_∇f(x)T(y₋x) _∀x, y_∈D (3.15) b) f adalah turunan kedua, makaf adalah konveks jika dan hanya jika _∇2_f(x)

adalah definit positif untuk semuax pada domain.

3.3.2 Ruang Banach (Banach Space)

Ruang Banach adalah salah suatu objek pusat studi dalam analisis fung-sional. Banyak dimensi tak terbatas ruang-ruang fungsi yang dipelajari dalam analisis adalah ruang Banach, termasuk ruang dari fungsi kontinu fungsi kontinu pada ruang Hausdorff kompak, ruang-ruang Lebesgue dan ruang-ruang fungsi holo-morphic.

1. Norma Vektor (Vector Norm)

Menurut Mark Davis (2011) Sebuah vektor norma pada Rn adalah sebuah fungsi _k·kdari Rn keR dengan ketentuan

(a) _kx_{k ≥}0 untuk semua x_∈Rn dan _kx_k= 0 jika dan hanya jika x= 0 (b) _k∝k=_{| ∝ |}._kx_k untuk semua _∝∈Rn dan x_∈Rn

(c) _kx+y_{k ≤ k}x_k+_ky_kuntuk semua x, y_∈Rn

Selanjutnya vektor norma l1−l2−(Euclidean) dan l∞−norm:

kx_k1 =Pn

i=1kxik, kxk₂ ={

Pn

i=1xl2}

1_/

2_{, kxk}

17

0 untukn _{→ ∞}. Barisanxn disebut barisan Cauchy dixmerupakan barisan yang

konvergen (ke sebuah x∗ _{di X) maka X merupakan ruang lengkap dan disebut} ruang Banach. Jika T : X _→ Y merupakan operator terbatas dan yn konvergen

ke y maka konvergen ke T y, selanjutnya jika X merupakan ruang Banach dan T :X _→Y bersifat kontraktif yakni terdapat c <1 sehingga

kTy−Tyk ≤ k⊂kx−yk ∀x, y∈X (3.16)

maka T mempunyai titik tetap tunggal.

Ruang dari semua fungsi kontinu f : [a, b] _→ K yang didefinisikan pada sebuah interval tertutup [a, b] ruang ini menjadi ruang Banach jika sebuah norma yang sesuai_kf_k didefenisikan didalamnya. Seperti norma dapat didefinisikan pada sebuah_kf_k= sup_{|f(x)_{| ∈}[a, b]_}dikenal sebagai norma supremum.

2. Syarat Bilangan ( Condition Numbers)

Syarat bilangan dari sebuah matriks non singular A adalah relatif ke se-buah norma _k·k yang didefenisikan dengan K(A) = _kA_k._kA−1_{k dimana K(A) ≥}

kAA−1_k=_kI_k= max_kx_k=1 = 1 (Robert Nurnberg, 2008).

Misalkan _kδA_k < 1/_kA−1_{k maka solusi x}∗ _{pada (A+δA)x}∗ _{= b+δb yang} merupakan solusi hampiran X dari Ax =b dengan perkiraan kesalahan

18

3.3.3 Turunan Frechet

Turunan Frechet adalah turunan yang didefinisikan pada ruang Banach dan pada umumnya digunakan untuk merumuskan konsep turunan fungsional yang digunakan secara luas dalam kalkulus.

Definisi 3.2 (D. Behmardi dan E.D Nayeri, 2008) Misalkan f : D _⊆ Rn → Rm

dimanaD adalah himpunan terbuka. Fungsi f dapat diturunkan pada x0 ∈ ∪ jika

1. turunan parsial darif, δfi

δxj untuk i= 1, . . . , m dan j = 1, . . . , n pada x0

disebut matriks Jacobian J(x0) pada turunan f pada x0

Definisi 3.3. (Volker Pohl dan Holger Boche, 2009) MisalkanX dan Y dua buah ruang linier bernorn, dan misalkan D himpunan bagian terbuka dari x sebuah pemetaanF :D _→Y disebut turunan Frechet padax_∈Djika terdapat pemetaan linier terbatas ∆ :X _→Y yang memenuhi :

lim

h→0

kF(x)₋(x)₋∆h_ky

kh_kx = 0 (3.20)

Operator linier ∆ disebut turunan frechet dari F pada x dan solusi h ditulis dengan ∆h=F(x)h.

19

3.3.4 Lipschitz Kontinu

Masalah nilai awal adalah sebuah masalah yang melibatkan satu atau lebih fungsi yang tidak diketahui beserta turunannya dalam sebuah persamaan yang memenuhi syarat nilai awal. Menurut C.T Kelley (2009) Metode Newton dengan iterasixn+1 =xn−F

′

(xn)F(xn) memerlukan syarat sebagai berikut :

1. solusix∗ _ada

2. F′(x∗_{) non singular}

3. F′ adalah Lipschitz kontinu dekat dengan x∗

Lipschitz kontinu dari fungsi F′ berarti terdapat η_≥0 yang memenuhi

F

′

(x)₋F′(y)

≤ηkx−yk (3.21)

BAB 4

PEMBAHASAN

4.1 Pengaruh Kesalahan Pembulatan

Secara umum solusi eksak dari suatu persamaan non linier sulit ditentukan sehingga harus ditentukan solusi numeriknya yaitu solusi hampiran (aproksimasi) dengan metode iterasi Newton Raphson.

Solusi hampiran x∗_{dari persamaan non linier :}

F(x) = 0 (4.1)

dimana fungsi non linierF terdeferensialkan secara kontinu sebanyakm(m _≥ 2 bulat) yang didefenisikan pada himpunan bagian D konveks terbuka di ruang BanachE1 dengan nilai di ruang Banach E2.

Metode Newton menghasilkan barisan_{xn}(n ≥0) yang dalam teori memenuhi

Xn+1 =φ(xn) (n≥0) (4.2)

dimana

φ(x) =xn−(F

′

(xn))−1F(xn) (4.3)

F′(x)_∈D menunjukkan turunan pertama Fr’echet dari fungsi F yang dieva-luasi pada x_∈D.

Untuk menentukan solusi dari persamaan (4.2) dan (4.3), yaitu dengan menghi-tung F′(x) dan F(x)(n _≥ 0) selanjutnya menentukan solusi θ(xn)(n ≥ 0) dari

persamaan :

F′(xn)(y) =−F(xn), (n≥ 0) (4.4)

dan menyatakan

φ(xn) =xn+θ(xn) (n≥ 0) (4.5)

21

Karena adanya kesalahan pembulatan dalam perhitungan numerik, sebagai pengganti dari barisan _{xn}(n ≥ 0) dibentuk suatu barisan {x¯n} (I.K. Argyros,

2000) sedemikian hingga:

{x¯n} (I.K. Argyros, 2000) sedemikian hingga:

¯

xn+1 = ¯φ(¯xn) (n ≥0) (4.6)

¯

φ(x) = [I+E0(x)]ψ(x), ψ(x) =x+ ¯θ(x) (x∈D) (4.7)

dimana ¯θ(χn) adalah solusi eksak dari persamaan

h

ˆ

An+E1(¯xn)

i

(y) =₋[F(¯xn) +E2(¯xn)] (n≥0) (4.8)

untuk beberapa E0(x), E1(x), E2(x) ∈ L(E1, E2) ruang operator liniear terbatas

dari E1 keE2.

T.J. Ypma (1982) menganalisis kekonvergenan dari barisan eksak _{x¯n}(n ≥

0) apabila E1 = E2 = Ri(i ∈ N) menurut hipotesis Lipschitz pada turunan

per-tama Fr’echet. Dalam hal ini akan ditunjukkan syarat cukup untuk konvergensi lokal barisan eksak_{x¯n}(n≥0) pada keadaan yang lebih umum dalam ruang

Ba-nach, dengan menggunakan hipotesis Lipschitz pada turunan Fr’echet ke-m yang dapat meningkatkan rasio konvergensi dan pemilihan nilai tebakan awal.

4.2 Analisis Konvergensi

Misalkan F′_(x

n) dan ¯An merupakan dua hampiran dalam turunan Fr’echet

F′_{(xn) pada F untuk beberapa titik x(x ∈ D). Dapat ditulis bahwa ¯An ≡ A}¯_n+ E1(x) dan F(xn) ≡ F(xn) +E2(x). Selanjutnya terdapat hubungan ¯φ(¯xn)−x∗

diantarax∗ _{dan hampiran ¯φ(¯xn) seperti yang dihasilkan pada persamaan (4.6) dan} (4.8), dimana ¯φ(¯xn) dalam persamaan (4.3) merupakan solusi hampiran. Dengan

menggunakan notasi _k·k untuk beberapa norm padaRi _{untuk teorema berikut.}

22

Teorema 2. ( T.J.Ypma, 1982) Misalkan F sebanyak m(m _≥ 2 bulat) terdefe-rensialkan Frechet secara kontinu pada U(x∗_{, σ) = {x∈E}

dimanaδ0 merupakan positif nol dari persamaan

αm+1

23

maka metode Newton konvergen kuadratik kex∗

Teorema 3. (I.K. Argyros, 2000) Jika η0 = 0, w0 <1,x¯0 ∈U(x∗, σ) dengan

¯

x0 6=x∗, dankx¯0−x∗k<min{δ, δ0} (4.18)

dimanaδ0 adalah akar positif dari fungsi

f0(t)

pertidaksamaan pertama dalam (4.20) yang sebelumnya telah diketahui dalam (4.9) dengan menentukan n = 0 dan menggunakan (4.21), lambang kurung kurawal dalam (4.20) adalah kurang dari satu dengan menggunakan persamaan (4.18), se-hingga teorema 3 terbukti.

Berikut ini akan ditunjukkan syarat cukup konvergensi lokal dalam metode Newton.

Teorema 4. (I.K Argyros, 2000)

Jika ηn = 0, wn≤w <1 untuk setiapn ≥0 dan ¯x0 ∈U(x∗, σ) maka

24

dimanaδ(w) adalah akar positif dari fungsi (4.19) dengan w0 menjadi w,

f(t) = αm+1 Kemudian metode Newton pada persamaan (4.6) - (4.8) menghasilkan barisan

{x¯n}(n≥0) yang konvergen ke x∗.

Pernyataan 1. Syarat yang digunakan dalam penelitian ini berbeda dari hubungan pada persamaan (4.6) - (4.8) kecualiα= 0, dan E1 =E2 =Ri(i∈N)

Pernyataan 2. Teorema 4 memberikan syarat cukup untuk konvergensi lokal. Seperti yang dijelaskan oleh T.J. Ypma (1983),ηn 6= 0, mengakibatkan wn > 1, sehingga

konvergensi menurun. Oleh karena itu dalam teori diperkirakan menurun secara monoton pada barisan _{kxn−x∗k}(n ≥ 0) dalam prakteknya syarat

dalam teori ini tidak dapat digunakan untuk beberapa nilai sekitarx∗_{, dalam} nilai persekitaran pada _{x¯n}(n ≥0).

Untuk memperkirakan nilai persekitaran digunakan :

σn=wn+ (1 +wn) (4.24)

untuk n _≥ 0. Dengan menggunakan persamaan (4.9), (4.15) dan (4.24) dengan mudah diketahuiφ¯x¯_n)−x∗

Selanjutnya syarat perlu σn < 1, dan dengan persamaan (4.24) syarat tersebut

menyatakan

wn <1, kx¯n−x∗k<min{δ, δn}(n ≥0) (4.26)

25

Oleh karena itu, disimpulkan bahwa syarat cukup konvergensi:

4.3 Penerapan dalam Kasus

Contoh 4.1. (I.K. Argyros, 2000), misalkan sebuah operator F memenuhi : F′(x) =T(F(x)), x_∈U(x∗, σ), (4.29)

dimana T : E2 → E1 merupakan operator turunan Frechet, dengan

meng-gunakan persamaan (4.29) diperoleh F′(x∗_{) = T(F(x}∗_{)) = T(0), dan F}”_(x∗_{) =} F′(x∗_)Q′

(F(x∗_{)) =Q(0)Q}′

(F(0)).

Tanpa menentukan solusix∗_{, akan dapat digunakan hasil berikut untuk m= 2.} Misalkan E1 =E2 =R. fungdi F terdefinisi,T pada U(0,1) dengan

F(x) =e∗₋1 (x_∈U(0,1)), (4.30) T(x) =x+ 1 x_∈U(0,1)), (4.31)

yang diperoleh dari (4.30) dan (4.31) bahwa persamaan (4.29) telah dipenuhi. Dengan menggunakan persamaan (4.11), (4.12), (4.17), (4.18), (4.19), dan (4.30), ditetukan untuk ω0 = 1/2 yaitu α = e, β = 1, δ = .411255048 dan min {δ, δ0} =

δ0=.27587332, syarat konvergensi (4.16) dan (4.18) telah dipenuhi

kx¯0−x∗k< .411254048 (4.32)

dan

kx¯0−x∗k< .27587332, (4.33)

untuk membandingkannya dengan hasil yang diperoleh hasil yang terdapat pada T.J. Ypma (1982,1983) akan ditunjukkan

26

Syarat ini berhubungan dengan persamaan (4.16) dan (4.18)

kx¯0−x∗k<

Dapat dilihat dengan mudah dari (4.30) dan (4.34) bahwaµ =e, Oleh karena itu, syarat (4.35) dan (4.36) terpenuhi yang menunjukkan bahwa

kx¯0−x∗k< .245253 (4.37)

dan

kx¯0−x∗k< .1471518 (4.38)

Selanjutnya (4.32) dan (4.35) memberikan pilihan yang lebih banyak untuk x0dan ¯x0 dari pada syarat (4.37) dan (4.38), hal ini menunjukkan bahwa rasio

konvergensi yang lebih kecil. Seharusnya (4.15) dan (4.20) memberikan secara berturut-turut untuk_kx¯0−x∗k ≤2 dan kx¯0−x∗k ≤1, maka

Jika digunakan hasil (4.41) dan (4.42) memberikan

x₀−F′(x₀)−1F(x₀)−x∗

≤2.9783279kx₀−x∗k2 ≤.5956656kx₀−x∗k

27

Rasio konvergensi (4.39) dan (4.40) lebih kecil daripada (4.43) dan (4.44). Contoh 4.2. (Mark S. Gockenbach, 2003) Fungsi berikut didefinisikan dalam F : Rn

Untuk memperoleh solusi hampiran dari persamaan non linier tersebut de-ngan menggunakan tebakan awalx(0)_{= (0.5,0.5)}T _{dan dihitung dengan rumus:}

xn+1 =xn−(F

′

(xn))−1F(xn)

Hasil perhitungan disajikan dalam tabel 4.1. berikut. Tabel 4.1 Iterasi metode newton

n X₁(n) X₂(n)

0 0.50000000000000000 0.50000000000000000 5.5902.10−1 _3.0954.10−1

1 0.87500000000000000 0.62500000000000000 2.1021.10−1 _8.9121.10−2

2 0.79067460317460314 0.61805555555555558 1.0090.10−2 _4.5233.10−3

3 0.78616431593458214 0.61803398895790196 2.8769.10−5 _1.2938.10−5

4 0.78615137786388734 0.61803398874989490 2.3673.10−10 _1.0646.10−10

5 0.78615137775742328 0.61803398874989490 1.1102.10−16 _0.0000

Perhitungan dilakukan di IEEE aritmetika presisi ganda dengan 16 digit desi-mal. Hasil yang diperoleh menunjukkan bahwa x∗−x(5)

1.1102.10−16_{, sehingga terjadi perbedaan yang disebabkan oleh kesalahan}

pembu-latan. Solusi yang diperoleh hanya dengan 5 iterasi sudah mendekati solusi ek-sak, namun ketikaF(x(5)_{) dihitung dengan aritmatika floating point menyebabkan}

28

Konvergensix(n)−x∗

menuju nol, dengan pola yang pasti :

kx∗_−x(3)_k

kx∗_−x(2)_k2 = 0.6323,

kx∗_−x(4)_k

kx∗_−x(3)_k2 = 0.6360

yang menunjukkan rasio konvergensi

kx∗_−x(n+1)_k

kx∗_−x(n)_k2

asimtotis konstank _{→ ∞}. Sebagai contoh bahwa kesalahan menurun secara cepat akibat dari kesalahan pembulatan :

x∗−x(5)= 0.63

kesalahan ini dibawah presisi mesin.

Contoh 4.3. Tentukan akar hampiran persamaan non linierF(x) =x4 _−3x2

dengan nilai tebakan awal x0 = 2, pembulatan 3 tempat desimal dan 5 tempat

desimal.

Solusi hampiran dari persamaan non linier tersebut dihitung dengan rumus xn+1 =xn−(F

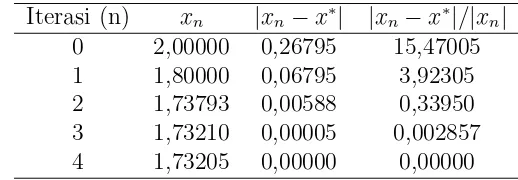
Hasil perhitungan disajikan dalam tabel 4.2 dan 4.3 sebagai berikut. Tabel 4.2 Iterasi newton Raphson (pembulatan 5 desimal)

Iterasi (n) xn |xn−x∗| |xn−x∗|/|xn|

0 2,00000 0,26795 15,47005 1 1,80000 0,06795 3,92305 2 1,73793 0,00588 0,33950 3 1,73210 0,00005 0,002857 4 1,73205 0,00000 0,00000

29

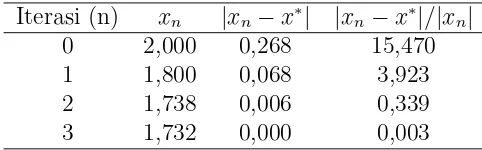
Tabel 4.3 Iterasi newton Raphson (pembulatan 5 desimal) Iterasi (n) xn |xn−x∗| |xn−x∗|/|xn|

0 2,000 0,268 15,470 1 1,800 0,068 3,923 2 1,738 0,006 0,339 3 1,732 0,000 0,003

Pada iterasi ke-3 diperoleh akar hampiran 1,732 dengan pembulatan 3 tempat desimal dimana kesalahan relatifnya sama dengan 0,003.

Dari tabel 4.2 dan 4.3 dapat disimpulkan bahwa :

1. Solusi hampiran pada pembulatan dengan jumlah digit desimal kecil lebih cepat diperoleh dibandingkan dengan solusi hampiran dengan pembulatan dengan jumlah digit desimal yang besar akan tetapi keakuratan solusi yang diperoleh lebih akurat pada pembulatan dengan junlah digit desimal yang besar.

BAB 5

KESIMPULAN DAN SARAN

5.1 Kesimpulan

Dalam menyelesaikan masalah numerik, khususnya dalam menentukan solusi persamaan non linier yaitu menentukan akar F(x) = 0 dilakukan secara iterasi dengan berbagai metode. Metode pencarian akar tersebut salah satunya adalah dengan menggunakan metode Newton Rapshon. Generalisasi lain dari metode Newton Rapshon yaitu menentukan akar fungsi F yang didefinisikan dalam ruang banach sehingga dapat mempercepat rasio konvergensi.

Metode Newton menghasilkan barisan_{xn}(n ≥0) yang dalam teori memenuhi

xn+1 =φ(xn)(n ≥0) dimana φ(x) =F

′

(x)−1_{F(x) dengan turunan fungsi F}′ (x)_∈ D merupakan turunan pertama Fr’echet dari fungsiF pada x_∈D.

Karena adanya kesalahan pembulatan dalam perhitungan numerik, sebagai pengganti dari barisan_{xn}(n ≥0) dibentuk suatu barisan{x¯n}sedemikian hingga

¯

xn+1 = ¯φ(¯xn)(n ≥0) dengan = ¯φ(x) = [I+E0(x)]ψ(x) dimanaψ(x) = ¯θ(x)(x∈D)

dan selanjutnya ¯θ(χn) adalah solusi eksak dari persamaan

h

ˆ

An+E1(¯xn)

i

(y) =

−[F(¯xn) +E2(¯xn)] (n≥0) untukE0(x), E1(x), E2(x) ∈L(E1, E2) ruang operator

liniear terbatas dari E1 keE2.

Metode Newton Rapshon memerlukan hipotesis lipshitz pada turunan Frechet ke-m (m _≥ 2 bulat). Dengan demikian syarat konvergensi dapat dipenuhi yang akhirnya dapat mempercepat rasio konvergensi.

5.2 Saran

Untuk peneliti selanjutnya, penulis menyarankan untuk melakukan penelitian yang mengkaji pengaruh kesalahan pembulatan pada metode iterasi yang dalam hal ini menentukan solusi hampiran dari persamaan non linier pada ruang banach dengan metode numerik lainnya.

DAFTAR PUSTAKA

Argyros. I.K. (2000). The Effect of Rounding Errors on a Certain Class of Iterative Methods, Applicationes. Mathematicae. 27,3 pp. 369-375.

Atkinson. E. Kendall. (2007). Scholarpedia. 2(8):3163. Departement of Computer Science, Departement of Mathematics. University of Loya

Behmardi. Daryoush dan Dehghan. Encyeh. Nayeri (2008). Introduction of Frechet and Gateaux Deritive. Mathematics Departement, Alzahra University Applied Mathematical Sciences, vol.2, no 2, 975-980

Bergamaschi. Luca. (2008). Iterative Methods for Sparse Linier System. Departe-ment of Mathematical Methods and Models for Scientific. Aplications. Uni-versity of Padova

Burden. L. Richard. Faires. J. Douglas. (2005). Numerical Analysis. Eight Edition. Belmont, CA 94602-3098. USA

Butt. Rizwan. (2009). Introduction to Numerical Analysis Using Matlab, U.S.A (page 10 - 11)

Chesneaux J.M, Graillat Stef, Jezequel Fabiene. (2010). Numerical Validation and Assessment. Laboratoire d’Informatique de Paris. France

Davis. Mark. (2011).Finite Difference Methods. Summer Term. Virginia Polytechnic Institute and State University. New York

Donald. W. Rogers. (2003).Computational Chemistry using the PC. Third Edition. ISBN. 0-471-42800-0. Copyrig. USA

E.J. Parkes and B.R. Duffy. (1996). An automated tanh-function method for fin-ding solitary wave solutions to non-linear evolution equations, Comput. Phys. Commun., 98 288-300

Giordano. R. Frank, Fox. P. William, Weir. D. Maurice. (2009). A First Course in Mathematical Modeling. Fourth Edition. Brooks/cole. Belmont. CA 94002-3098. USA

Gockenbach. S. Mark. (2003).Newton’s Method. Mathematical. Departement Michi-gan Technological University Houghton. MI

Heydari. M, Hosseini. S.M., Loghmani. G.B. (2011). One Two New Families of Iterative Methods for Solving Non Linier Equation with Optimal Rader. Appl. Anal. Discrette. Math. 5. Page. 93-109

Hossein. Jafari, Yazdani. Allahbakhsh, Vahidi. Javad, Ganji. D. Davood. (2008).

Application of He’s Variational Iteration Method for Solving Seventh Order Swada-Kotera Equations. Applied Mathematical Sciences, Vol. 2. No. 10, page. 471-477

32

L. V. Kantorovich and G. P. Akilov. (1982). Functional Analysis, Pergamon Press, Oxford.

M. Inokuti, et al., (1978). General use of the Lagrange multiplier in non-linear mathematical physics, in: S. Nemat-Nasser (Ed), Variational Metohd in the Mechanics of Solids, Pergamon Press, Oxford, pp. 156-162

Meza. C. Juan. (2010). Newton’s Method. Lawrence Berkeley National Laboratory. 94720. California

Nurnberg. Robert. (2008). Numerical Methods for Finance. Imperial College. Lon-don

Podisuk. M. (2000). Theorems on a Modified Method dor Solving System of non Linier Equations. Departement of Mathematical and Computer Science. Re-search Article. Science Asia. Thailand

Pohl. Volker dan Boche. Holger. (2009). Advanced Topics in system and signal The-ory. A. Mathematical Approach. Springer Heidelberg London New York. Page 9-10. S.M.El-Sayed and D.Kaya. (2004). Anapplication of the ADM to seven order Sawada-Kotera equations, Appl. Math. Comput., 157 93-101

Urman. H. David. (2008). Iterative Method. Obtaining Accurate Solution in Solving Linier Equation. Articlesbase, Free online Articles Directions. USA

Ypma. T.J. (1982). Numerical solution of systems of nonlinear algebraic equations. thesis, Oxford.