Stock Price Modelling Using ARIMA-GARCH Model

(1)

PEMODELAN HARGA SAHAM MENGGUNAKAN

MODEL ARIMA-GARCH

FITRIYAH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

ABSTRAK

FITRIYAH. Pemodelan Harga Saham Menggunakan Model ARIMA-GARCH. Dibimbing oleh RETNO BUDIARTI dan HADI SUMARNO.

Saham adalah nilai dengan berbagai instrumen finansial yang mengacu pada bagian kepemilikan sebuah perusahaan. Keuntungan yang menarik merupakan alasan seorang investor berinvestasi. Pergerakan harga saham berkaitan dengan faktor ketidakpastian sehingga investor harus terlebih dahulu mempertimbangkan dengan baik sebelum berinvestasi agar risiko yang ditanggung tidak terlalu besar. Pergerakan harga saham yang selalu berfluktuasi atau tidak berbentuk linear sehingga diperlukan metode khusus untuk memodelkan secara matematis. Model

autoregressive integrated moving average (ARIMA) merupakan salah satu model yang

menyatakan bahwa data saat sekarang dipengaruhi oleh data sebelumnya dan sisaan sebelumnya. Di sektor ekonomi, volatilitas yang tinggi menyebabkan munculnya masalah heteroskedastisitas yaitu di mana varian dari sisaan tidak konstan. Oleh karena itu, peramalan dengan menggunakan model ARIMA saja tidak cukup. Untuk itu diperlukan pemodelan ragam dengan model

generalized autoregressive conditional heteroscedasticity (GARCH) untuk menyelesaikan

masalah heteroskedastisitas.

Tujuan dari penulisan karya ilmiah ini adalah memodelkan harga saham menggunakan model ARIMA dan menyelesaikan keberadaan masalah heteroskesdasitisitas yang terjadi dengan menggunakan model GARCH. Hasil pemodelan yang didapatkan dari model ARIMA-GARCH adalah ragam dari sisaan sudah konstan. Ini berarti model ARIMA-ARIMA-GARCH dapat menyelesaikan masalah heteroskedastisitas.

(3)

ABSTRACT

FITRIYAH. Stock Price Modelling Using ARIMA-GARCH Model. Under supervision of RETNO BUDIARTI and HADI SUMARNO.

The stock is a value of financial instrument, which refers to the ownership of a company. An interesting advantage is the reason why an investor invests. The price movement of stocks are related to some uncertain factors, such that investors should first consider well before investing in order to limit the risk. Stock price are always fluctuating so that they require special method to model mathematically. Autoregressive integrated moving average (ARIMA) model defines that present data are influenced by earlier data and error. In economic sectors, high volatility tends to cause a problem of heteroscedasticity, i.e. nonconstant variance of error. Therefore, the use of an ARIMA model alone is not enough. The application of the generalized autoregressive conditional heteroscedasticity (GARCH) model to resolve the problem of heteroscedasticity is therefore recommended.

The purpose of this paper is to model stock prices using ARIMA model and to solve heteroscedasticity using the GARCH model. The result of simulation show that ARIMA-GARCH model gives constant variance. This means that ARIMA-ARIMA-GARCH model can solve the problem of heteroscedasticity.

(4)

PEMODELAN HARGA SAHAM MENGGUNAKAN

MODEL ARIMA-GARCH

FITRIYAH

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(5)

Judul Skripsi : Pemodelan Harga Saham Menggunakan Model ARIMA-GARCH Nama : Fitriyah

NIM : G54080073

Menyetujui Pembimbing I

Ir. Retno Budiarti, MS. NIP. 19610729 198903 2 001

Pembimbing II

Dr. Ir. Hadi Sumarno, MS. NIP. 19590926 198501 1 001

Tanggal Lulus : ... Mengetahui

Ketua Departemen Matematika

(6)

PRAKATA

Puji syukur penulis panjatkan ke hadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Penyusunan karya ilmiah ini juga tidak terlepas dari dukungan doa, moril dan materiil dari berbagai pihak. Pada kesempatan ini, penulis menyampaikan terima kasih kepada :

1 Keluarga penulis, Ayah, Ibu dan kakak-adik (Siti Khoirunnisa, Nur Sakinah, Muhamad Kholiq) beserta keluarga besar saya atas doa dan dukungan tiada henti yang diberikan sejak penulis menimba ilmu di IPB,

2 Ir. Retno Budiarti, MS. dan Dr. Ir. Hadi Sumarno, MS. selaku dosen pembimbing atas waktu dan bimbingannya selama penulis menyelesaikan karya ilmiah ini,

3 Dr. Ir. Endar H. Nugrahani, MS.selaku moderator seminar dan penguji sidang tugas akhir, 4 seluruh dosen TPB dan Departemen Matematika FMIPA IPB atas ilmu dan pengalaman

berharga yang telah diberikan selama penulis menimba ilmu di IPB,

5 seluruh staf/pegawai Departemen Matematika IPB yang telah membantu memperlancar kelengkapan administrasi dan membantu kelengkapan bahan karya ilmiah ini,

6 Teman-teman matematika 45: Putri, Nurul, Yunda, Dewi, Maya, Ana, Tya, Fuka, Fina, Ade dan seluruh teman mahasiswa matematika angkatan 45,

7 Kakak-kakak Matematika angkatan 44: Kak Shelvi, Kak Aswin, Kak Imam, Kak Mutia, Kak Della dkk atas bantuan serta dukungannya,

8 Adik-adik Matematika 46: Sevira, Widya dkk atas semangat serta dukungannya, 9 sahabat terbaik : Yayuk, Susan dan Nanda,

10 seluruh pihak yang tidak dapat disebutkan satu per satu.

Penulis menyadari karya ilmiah ini belum sempurna. Oleh karena itu, saran dan kritik yang membangun dibutuhkan dari para pembaca. Akhir kata, semoga karya ilmiah ini bermanfaat dan dapat menginspirasi kita semua khususnya untuk kemajuan ilmu Matematika.

Bogor, Desember 2012

(7)

RIWAYAT HIDUP

Penulis dilahirkan di kota Jakarta pada tanggal 27 April 1991 sebagai anak ketiga dari empat bersaudara, dari pasangan Sahid dan Sumarni. Pada tahun 2002, penulis lulus dari SD Raflesia Raya I Kota Bekasi. Pada tahun 2005, penulis lulus dari SMP Negeri 272 Kota Jakarta. Pada tahun 2008, penulis lulus dari SMA Negeri 62 Kota Jakarta dan pada tahun yang sama penulis diterima di Departemen Matematika IPB melalui jalur Seleksi Penerimaan Mahasiswa Baru (SPMB).

(8)

viii

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... viii

DAFTAR TABEL ... viii

DAFTAR LAMPIRAN ... viii

1 PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

1.3 Sistematika Penulisan ... 1

2 LANDASAN TEORI 2.1 Berbagai Definisi ... 1

2.1.1 Ruang Contoh ... 2

2.1.2 Peubah Acak ... 2

2.1.3 Peubah Acak Kontinu ... 2

2.1.4 Fungsi Sebaran ... 2

2.1.5 Fungsi Kepekatan Peluang ... 2

2.1.6 Nilai Harapan Peubah Acak Kontinu ... 2

2.1.7 Simpangan Baku dan Ragam Peubah Acak Kontinu ... 2

2.1.8 Sebaran Normal ... 3

2.2 Definisi Dasar Deret Waktu ... 3

2.2.1 Strict Stationarity ... 3

2.2.2 Covarian Stationarity ... 3

2.2.3 Autocorrelation Function ... 3

2.2.4 White Noise ... 3

2.2.5 Strict White Noise ... 3

2.3 Proses Analisis untuk Data Deret Waktu ... 3

2.3.1 Tren dan Kestasioneran ... 4

2.4 Model Deret Waktu ARIMA ... 4

2.4.1 Model ARMA (p,q) ... 4

2.4.2 Model ARIMA (p,d,q) ... 4

2.4.3 Metode Box dan Jenkins ... 5

2.5 Model Ragam Sisaan ARCH ... 5

2.6 Model Ragam Sisaan GARCH... 6

2.6.1 Pengepasan Model GARCH pada Data ... 6

3 HASIL DAN PEMBAHASAN 3.1 Data ... 8

3.2 Model ARIMA ... 8

3.3 Model ARIMA-GARCH ... 11

3.4 Peramalan ... 13

4 SIMPULAN DAN SARAN 4.1 Simpulan... 14

4.2 Saran ... 14

DAFTAR PUSTAKA ... 15

LAMPIRAN ... 16

(9)

DAFTAR GAMBAR

Halaman

1 Plot harga saham Sharp Corp.dari3 Januari 2011 s.d. 14 Maret 2012 ... 8

2 Plot ACF saham Sharp Corp. ... 8

3 Plot PACF saham Sharp Corp. ... 9

4 Plot setelah pembedaan satu kali ... 9

5 Plot ACF dari saham dengan pembedaan satu kali ... 9

6 Plot PACF dari saham dengan pembedaan satu kali ... 9

7 Plot kenormalan sisaan ... 10

8 Plot sisaan terhadap waktu ... 10

9 Plot residual ACF (RACF) ... 11

10 Plot residual PACF (RPACF) ... 11

11 Plot kenormalan sisaan ... 12

12 Plot data harga saham aktual dengan data ramalan ... 13

DAFTAR TABEL

1 Tabel alternatif model ARIMA tentatif ... 10

2 Tabel hasil analisis model ARIMA-GARCH ... 12

DAFTAR LAMPIRAN

Halaman 1 Data penutupan saham Sharp Corp. harian selama 3 Januari 2011 s.d. 14 Maret 2012 ... 17

2 Output uji ADF pada data asli ... 19

3 Output uji ADF setelah pembedaan satu kali ... 19

4 Output model ARIMA (2,1,5) ... 20

7 Output model ARIMA (2,1,5)-GARCH (0,2) ... 22

10 Output dari uji ARCH-LM ARIMA (2,1,5) ... 25

11 Output dari uji ARCH-LM ARIMA (2,1,5)-GARCH (1,3) ... 25

12 Output dari uji normalitas pada sisaan baku ARIMA (2,1,5)-GARCH (1,3) ... 25

13 Data peramalan selama 50 hari ke depan ... 26

(10)

1

I PENDAHULUAN

1.1 Latar Belakang

Bursa saham merupakan salah satu tempat kegiatan jual beli saham dalam sektor ekonomi. Saham adalah nilai atau pembukuan dengan berbagai instrumen finansial yang mengacu pada bagian kepemilikan sebuah perusahaan. Keuntungan yang menarik merupakan alasan seorang investor berinvestasi. Pergerakan harga saham berkaitan dengan faktor ketidakpastian sehingga investor harus terlebih dahulu mempertimbangkan dengan baik sebelum berinvestasi agar risiko yang ditanggung tidak terlalu besar.

Pergerakan harga saham yang naik turun disebabkan oleh permintaan dan penawaran atas saham tersebut. Semakin banyak investor yang membeli saham maka pergerakan harga saham akan cenderung naik. Sebaliknya, jika banyak investor yang menjual saham maka pergerakan harga saham akan cenderung turun. Namun pada kenyataannya, pergerakan harga saham tidak ada yang menerus naik atau terus-menerus turun.

Pergerakan harga saham yang selalu berfluktuasi atau tidak berbentuk linear sehingga diperlukan metode khusus untuk memodelkan secara matematis. Peramalan harga saham sangat dibutuhkan bagi para pelaku perdagangan saham, dimana besar keuntungan dari perdagangan tersebut memiliki risiko kerugian yang sama besar pula. Oleh karena itu, peramalan harga saham yang akurat diharapkan pelaku perdagangan saham akan memiliki risiko yang lebih kecil.

Pada kenyataannya, data di sektor keuangan sangat tinggi volatilitasnya. Kondisi tersebut menyebabkan terjadi masalah heteroskedastisitas dimana ragam sisaan tidak konstan. Oleh karena itu, peramalan dengan model ARIMA saja belum cukup. Sehingga diperlukan peramalan menggunakan model

ARIMA-GARCH dimana heteroskedastisitas diperhitungkan.

Selain memodelkan harga saham, dibutuhkan pula peramalan harga saham untuk memperoleh keuntungan yang maksimal. Bagi perusahaan, peramalan harga saham sangat dibutuhkan untuk meminimalkan risiko yang akan dihadapi dalam sebuah pengambilan keputusan. Sedangkan bagi investor, peramalan harga saham merupakan salah satu pertimbangan yang penting untuk melakukan investasi sehingga peramalan harga saham dibutuhkan untuk mengetahui fluktuasi harga saham yang ada di perusahaan tersebut ke depannya.

Ide karya ilmiah berasal dari tulisan Teguh Santoso pada tahun 2011 yang berjudul “Aplikasi Model GARCH pada Data Inflasi Bahan Makanan Indonesia Periode 2005.1-2010.6”. Karya ilmiah ini menggunakan model ARIMA-GARCH dengan aplikasi yang berbeda yaitu memodelkan harga saham.

1.2 Tujuan Penulisan

Tujuan utama dari penulisan karya ilmiah ini adalah

1. memodelkan harga saham menggunakan model ARIMA, 2. menyelesaikan keberadaan masalah

heteroskesdasitisitas yang terjadi dengan menggunakan model ARIMA-GARCH.

1.3 Sistematika Penulisan

Pada bab pertama dijelaskan latar belakang dan tujuan penulisan karya ilmiah ini. Bab dua berisi landasan teori yang menjadi konsep dasar dalam penyusunan pembahasan. Pada bab tiga dilakukan pemodelan harga saham dengan melakukan

model ARIMA-GARCH untuk

menyelesaikan masalah heteroskedastisitas. Pada bab empat akan dipaparkan simpulan serta saran dari karya ilmiah ini.

II LANDASAN TEORI

2.1 Berbagai Definisi

Suatu percobaan yang dapat diulang dalam kondisi yang sama dan semua kemungkinan hasil yang muncul dapat

diketahui tetapi hasilnya tidak dapat ditentukan dengan tepat disebut percobaan acak.

(11)

1

2.1.1 Ruang Contoh

Ruang contoh adalah himpunan semua hasil yang mungkin dari suatu percobaan acak dan dinotasikan dengan Ω.

(Grimmett & Stirzaker1992)

2.1.2 Peubah Acak

Suatu peubah acak (random variable) adalah suatu fungsi : Ω → dengan sifat bahwa{ Ω; ( ) ≤ } ℱ, untuk setiap

, dengan ℱ adalah sebuah medan- dari suatu ruang contoh Ω.

Peubah acak dinotasikan dengan huruf kapital, misalkan X,Y,Z. Sedangkan nilai peubah acak dinotasikan dengan huruf kecil seperti x,y,z.

2.1.3 Peubah Acak Kontinu

Peubah acak X dikatakan kontinu jika ada fungsi sehingga fungsi sebaran dapat dinyatakan sebagai

( ) = ( ) ,

∈ ℝ, dengan ∶ ℝ → [0, ∞) adalah fungsi yang terintegralkan. Fungsi disebut fungsi kepekatan peluang bagi peubah acak X.

2.1.4 Fungsi Sebaran

Fungsi sebaran dari suatu peubah acak X

adalah fungsi : ℝ → [0, 1] yang dinyatakan sebagai ( ) = ( ≤ ).

2.1.5 Fungsi Kepekatan Peluang

Peubah acak dikatakan kontinu jika fungsi

sebaran ( ) = ( ≤ ) dapat

diekspresikan sebagai

( ) = ( ) ,

untuk suatu fungsi ∶ → [0, ∞] yang dapat diintegralkan. Selanjutnya fungsi

= disebut juga fungsi kepekatan peluang (probability density function) bagi

.

2.1.6 Nilai Harapan untuk Peubah Acak Kontinu

Nilai harapan untuk peubah acak kontinu dengan fungsi kepekatan peluang adalah

( ) = ( ) ,

asalkan integral di atas konvergen.

Lema 1 (Sifat Nilai Harapan)

Beberapa sifat nilai harapan, antara lain: 1. Jika k adalah suatu konstanta, maka

( ) = .

(Hogg & Craig 1995)

2.1.7 Simpangan Baku dan Ragam Peubah Acak Kontinu

Misalkan X adalah peubah acak kontinu dengan ( ) = adalah nilai harapan dari , dengan fungsi kepekatan peluang ( ), maka ragam (variance) dan simpangan baku

(standard deviation) dari X dinotasikan

Lema 2 (Sifat Ragam)

Beberapa sifat dari ragam, antara lain : 1. Jika suatu konstanta, maka

( ) = ( ).

(12)

1

2.1.8 Sebaran Normal

Misalkan diberikan peubah acak .

Peubah acak dikatakan menyebar normal dengan rata-rata dan ragam jika memiliki fungsi kepekatan peluang

(probability density function) sebagai

berikut:

( ) = 1

√2 ( ) /( ).

Sebaran normal yang memiliki nilai rata-rata 0 dan ragam 1 disebut sebaran normal baku. Misalkan peubah acak menyebar normal baku, maka memiliki fungsi kepekatan peluang

( ) = 1

√2 .

2.2 Definisi Dasar Deret Waktu Strict stationarity

Deret waktu ( )∈ dikatakan strict

stationarity jika

, … , = , … ,

untuk semua , … , , ℤ dan untuk semua

ℤ.

(McNeil et al. 2005) 2.2.1 Covarian stationarity

Deret waktu ( )∈ dikatakan covarian

stationarity jika

( ) = , ( , ) = ( + , + ).

(McNeil et al.₂₀₀₅₎

2.2.2 Autocorelation Function (ACF)

Autocorelation funcion (ACF), (ℎ), dari

noise jika covarian stationary dengan fungsi

autokorelasi

peubah acak dengan ragam berhingga. Proses strict white noise (SWN) yang dipusatkan untuk mendapatkan rata-rata 0 dengan ragam akan dinotasikan SWN(0, ).

(McNeil et al.₂₀₀₅₎

2.3 Proses Analisis untuk Data Deret Waktu

Dalam analisis data deret waktu, proses baku yang harus dilakukan adalah

1. Memetakan nilai data terhadap waktu, hal ini dilakukan untuk menelaah kestasioneran data, sebab jika data tidak stasioner maka harus distasionerkan melalui proses stasioneritas.

(13)

1

dan lakukan penaksirannya baik dalam kawasan waktu maupun kawasan frekuensi.

4. Lakukan proses peramalan dengan metode yang sesuai dengan kondisi datanya, dan untuk mendapatkan hasil yang memuaskan, digunakan metode Box-Jenkins .

(Mulyana 2004)

2.3.1 Tren dan kestasioneran

Tren adalah komponen data deret waktu yang menunjukkan peningkatan atau penurunan dalam jangka panjang selama periode waktu yang diamati. Sebagai contoh data dengan tren diindikasikan antara lain dengan koefisien autokorelasi beberapa beda kala pertama tinggi dan berbeda dengan nol secara signifikan, lalu turun mendekati nol saat deret meningkat. Data dengan tren berarti data tidak stasioner.Data yang stasioner adalah data dengan rataan dan ragam konstan sepanjang waktu pengamatan. Data ini dicirikan oleh koefisien autokorelasi pada beberapa beda kala pertama mendekati nol atau tidak terdapat autokorelasi antar deret.

(Firdaus 2006)

2.4 Model Deret Waktu ARIMA

Model Autoregressive Integrated Moving

Average (ARIMA) diperkenalkan oleh Box

dan Jenkins. Pada model ini terjadi proses

Autoregressive (AR) berordo- atau proses

Moving Average (MA) berordo-q atau

merupakan kombinasi keduanya. Pembeda berordo-d dilakukan jika data deret waktu bersifat non-stasioner, padahal aspek-aspek AR dan MA dari model ARIMA menghendaki data yang stasioner. Bentuk umum model ARIMA ( , , ) adalah

( )(1 − ) =

dengan

= derajat autoregressive (AR) = derajat pembeda

= derajat moving average (MA) = waktu

= peubah acak ke-t

= parameter yang menjelaskan AR = (1 − − ⋯ − )

= parameter yang menjelaskan MA = (1 − − ⋯ − )

= sisaan acak pada waktu ke-t yang diasumsikan menyebar normal bebas stokastik

= operator backshift

= .

Jika ditetapkan nilai = 0 model tersebut menjadi model autoregressive ordo yang disingkat AR( ). Sebaliknya jika menyatakan bahwa data pada periode sekarang dipengaruhi oleh data p-periode sebelumnya dan q-periode sebelumnya. Model umum ARMA (p,q) adalah

Dengan operator pembeda, yaitu

= stasioner sehingga diperlukan pembedaan d

(14)

1

2.4.3 Metode Box dan Jenkins

Metode yang biasa digunakan dalam pembuatan model Autoregressive Moving

Average (ARMA) adalah metode Box dan

Jenkins (Makridaskis et al. 1983) dengan prosedur sebagai berikut:

1. Identifikasi model: Identifikasi model beranjak dari struktur data yang bersifat stasioner. Dari data yang stasioner dapat diperoleh model sementara dengan mengamati fungsi korelasi diri /

autocorrelation function (ACF) dan

fungsi korelasi diri parsialnya / Partial

autocorrelation function (PACF). Ordo

proses AR dapat ditentukan dengan melihat berapa banyak koefisien korelasi diri parsial (PACF) yang tidak nol. Sedangkan ordo proses MA ditentukan dengan melihat berapa banyak koefisien korelasi diri (ACF) pertama yang tidak nol (Bowerman & O’Connel 1987). Identifikasi proses ARMA dari plot autokorelasi dan plot korelasi parsialnya.

2. Pendugaan parameter: Banyaknya parameter yang akan diduga bergantung pada banyaknya koefisien model awal. Penduga parameter dikatakan berpengaruh jika nilai mutlak yang berpadanan dengan parameter tersebut lebih besar daripada nilai- tabel pada taraf nyata /2 berderajat bebas minus banyaknya parameter (Bowerman & O’Connel 1987).

3. Diagnostik model: Statistik uji Q Box- Pierce dapat digunakan untuk menguji kelayakan model, yaitu dengan menguji apakah sekumpulan korelasi diri untuk nilai sisa tersebut tidak nol. Statistik uji Q Box-Pierce menyebar mengikuti sebaran dengan derajat bebas

( − − ), dimana adalah lag maksimum yang diamati, adalah ordo AR, dan adalah ordo MA. JIka nilai Q lebih besar nilai ( − − ) untuk tingkat kepercayaan tertentu atau nilai peluang statistik Q lebih kecil dari taraf

nyata , maka dapat disimpulkan bahwa model tidak layak. Persamaan statistik uji Q Box-Pierce menurut Makridaskis

et al. (1983) adalah:

4. Peramalan: Peramalan merupakan suatu proses untuk memperoleh data beberapa periode waktu ke depan. Untuk memperoleh sejauh periode ke depan dari titik waktu ke , maka dipilih satu model yang memiliki nilai Kuadrat Tengah Galat (KTG) minimum. Perhitungan dilakukan secara rekursif, yaitu menghitung peramalan satu periode kemudian dua periode, dan seterusnya sampai periode ke depan. Setelah melakukan peramalan, ketepatan peramalan dapat dicari dengan menghitung

Mean Absolute Percentage Error (MAPE),

dengan rumus sebagai berikut:

MAPE =∑ | − |x 100.

Dengan adalah pengamatan pada waktu ke- dan adalah ramalan pada waktu ke- . Semakin kecil nilai MAPE menunjukkan data hasil peramalan semakin mendekati nilai aktual.

(Makridaskis et al. 1983)

2.5 Model Ragam Sisaan ARCH

Model Autoregressive Conditionally

Heteroscedastic (ARCH) diperkenalkan oleh

Engle pada tahun 1982. Modifikasi model AR (p) dengan mentransformasi sisaan menjadi bentuk sisaan kuadrat menghasilkan model ARCH.

Diberikan ( )∈ yang SWN(0,1). Proses ( )∈ adalah proses ARCH (p) jika

strictly stationary dan memenuhi persamaan

sisaan dan ragam sebagai berikut

(15)

=

= +

untuk semua ∈ ℤ dimana α > 0 dan

α ≥ 0, i = 1, … , p.

2.6 Model Ragam Sisaan GARCH

Pada tahun 1986, Bollerslev dan Taylor membuat bentuk umum dari ARCH dengan maksud menghindarkan struktur lag ragam sisaaan yang panjang pada model ARCH yang dibuat Engle. Model ini dikenal dengan

Generalized Autoregressive Conditionally

Heteroscedastic (GARCH).

Diberikan ( )∈ yang SWN (0,1). Proses ( )∈ adalah proses GARCH (p,q) jika proses tersebut adalah strictly stationary

dan jika memenuhi, untuk semua ∈ ℤ dan beberapa nilai positif sempurna yang mengolah ( )∈ , persamaan sisaan dan Jika terjadi pelanggaran dari asumsi tersebut dimana ragam sisaan tidak konstan yaitu

( ) = maka model tersebut masih mengandung masalah heteroskedasitisitas sehingga perlu pemodelan ragam sisaan dengan GARCH untuk menyelesaikannya.

Keberadaan heteroskedastisitas dapat dideteksi dengan uji LM yaitu

=

dengan

=∑ ( − ̅)_{∑ ( − ̅) .}

Jika > maka ( ) = yang berarti masih ada heteroskedastisitasdimana

= banyaknya data

= banyaknya data periode sebelumnya yang memengaruhi data sekarang

= besarnya kontribusi keragaman yang dapat dijelaskan data deret waktu sebelumnya.

(Simanjutak 2009)

2.6.2 Pengepasan Model GARCH pada Data

Untuk melakukan pengepasan model GARCH pada data diperlukan tiga tahap. Tiga tahap tersebut adalah membangun kemungkinan, mendapat estimasi parameter dan memeriksa model.

Menduga kemungkinan

Dalam prakteknya, pendekatan yang paling banyak digunakan untuk pengepasan model GARCH pada data adalah maximum

likelihood. Dengan menganggap pada

pengepasan model ARCH (1) dan GARCH (1,1) sebagai pengepasan umum dari model ARCH (p) dan GARCH (p, q), model akan lebih sederhana.

Untuk model ARCH (1) dan GARCH (1,1) anggap mempunyai total dari n+1 data nilai , , … , . Berdasarkan hal tersebut, fungsi kepekatan bersama dari peubah acak yang sesuai dapat ditulis seperti

,…, ( , …, )

= ( ) | …., ( | , … , ).

Model GARCH (p,q) dianggap memiliki

n+p nilai data yang berlabel

dimana σ mengikuti spesifikasi GARCH dan mengikuti spesifikasi ARMA.

(16)

1

Mendapatkan estimasi parameter Anggap fungsi likelihood sebagai berikut

( ; ) = ( ; )

dengan

( ; ) = 1 √2π ℯ

sehingga

( ; ) = 1

√2

= 1 (2 ) ( )

∑

( ) = ( ) = ( ; )

= −₂ 2 −₂ −₂1

Kemudian akan dicari nilai parameter dengan menggunakan turunan ( ) = 0.

( )

= − 2 + 2( ) = 0

↔ − + _{( ) = 0}

↔ − + = 0

↔∑ = .

Sehingga penaksir maksimum likelihood dari adalah :

= ∑ .

(Myers & Milton 1991)

Memeriksa model

Seperti model ARMA, memeriksa kecocokan model GARCH menggunakan sisaan juga. Dengan menganggap model umum ARMA-GARCH dari bentuk

− = = . Model dibedakan

antara sisaan unstandardized dan

standardized. Yang pertama adalah sisaan

̂ , … , ̂ dari bagian model ARMA. Selanjutnya realisasi yang direkonstruksi dari SWN yang diasumsikan mendorong bagian model GARCH, dan dihitung dari sebelumnya dengan

= ̂

= + ̂ + .

Untuk menggunakannya, perlu beberapa nilai awal yang satu solusinya adalah untuk menetapkan nilai awal ε sama dengan nol dan nilai awal volatilitas σ sama dengan ragam contoh atau nol. Karena beberapa nilai pertama akan dipengaruhi oleh nilai awal, serta nilai awal diperlukan untuk menghitung sisaan unstrandardized maka mungkin analisis selanjutnya akan diabaikan.

Sisaan standardized harus seperti SWN yang dapat diteliti dengan membangun

correlograms sisaan baku. Dengan

mengasumsikan bahwa hipotesis SWN tidak ditolak, validitas distribusi yang digunakan dalam pengepasan ML juga dapat diselidiki menggunakan QQplots dan goodness-of-fit test untuk sebaran normal atau sebaran-t.

(17)

8 2012 (www.finance.yahoo.com). Data tersebut terdapat pada Lampiran 1. Pengujian akan dilakukan dengan analisis deret waktu. Data penutupan harga saham yang didapatkan kemudian diplotkan dapat dilihat pada Gambar 1.

Gambar 1 Plot harga saham Sharp Corp. dari 1 Januari 2011 hingga 14 Maret 2012.

Data penutupan harga saham tersebut dibagi menjadi dua, yaitu data untuk pemodelan dan data untuk peramalan. Data untuk pemodelan adalah data penutupan harga saham selama tahun 2011, sedangkan data untuk peramalan adalah data penutupan harga saham awal tahun 2012.

3.2 Model ARIMA

Autoregressive Integrated Moving

Average (ARIMA) atau biasa disebut

dengan metode Box-Jenkins merupakan metode peramalan yang sangat baik ketepatannya untuk peramalan jangka pendek. ARIMA menganalisis data deret waktu dengan menggunakan nilai masa lalu dari nilai variabel dependen untuk menghasilkan peramalan jangka pendek yang akurat dengan mengabaikan variabel independennya dengan asumsi ragam sisaannya konstan.

Model umum ARIMA ( , , ) adalah

( )(1 − ) = ( )

dengan

= harga penutupan saham pada waktu ke-t

= derajat autoregressive (AR) = derajat pembeda

= derajat moving average (MA) = waktu

= parameter yang menjelaskan AR = (1 − − ⋯ − )

= parameter yang menjelaskan MA = (1 − − ⋯ − )

= sisaan acak pada waktu ke- yang diasumsikan menyebar normal bebas stokastik

= operator backshift

= .

Model umum ARIMA ( , , ) menyatakan bahwa data periode sekarang dipengaruhi oleh data periode sebelumnya dan nilai sisaan pada periode sebelumnya. Jika data tidak stasioner maka dilakukan pembedaan untuk membuat data stasioner dalam rata-rata.

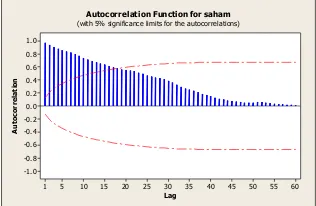
Untuk mengetahui apakah data tersebut dapat diprediksi dengan menggunakan masa lalu, maka harus melihat sifat pergerakan saham perusahaan tersebut stasioner atau tidak. Untuk mengetahui kestasioneran dari pergerakan saham, dilakukan dengan melihat plot dari korelasi diri (ACF) dan plot korelasi diri parsial (PACF). Hasil plot ACF dan PACF terdapat pada Gambar 2 dan Gambar 3.

Gambar 2 Plot ACF saham Sharp Corp. 60

Autocorrelation Function for saham (with 5% significance limits for the autocorrelations)

waktu

(18)

9

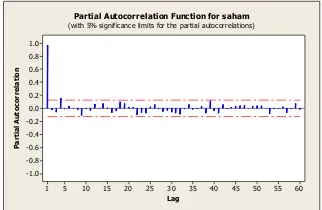
Gambar 3 Plot PACF saham Sharp Corp.

Pada plot ACF (Gambar 2) menunjukkan pola dies down atau turun secara eksponensial dan plot PACF (Gambar 3) yang menunjukkan pola terputus setelah lag -1. Menurut Wei (1994), data deret waktu tidak stasioner jika nilai autokorelasi mulai

lag-1 pada plot ACF turun dengan lamban dan nilai autokorelasi parsial pada plot PACF terputus (cut off) setelah lag-1. Pola

cut off adalah pola ketika garis ACF dan

PACF signifikan pada lag pertama atau kedua tetapi kemudian tidak ada garis ACF dan PACF yang signifikan pada lag berikutnya. Oleh karena itu, data tersebut tidak stasioner.

Pengujian stasioner secara statistik dapat dilakukan dengan Augmented Dickey Fuller Test (Uji ADF) dengan = 5%, dengan menggunakan hipotesis sebagai berikut

: data tidak bersifat stasioner : data bersifat stasioner

Berdasarkan uji ADF pada Lampiran 2 diperoleh hasil nilai probabilitasnya sebesar 0.2619. Nilai probabilitas yang lebih besar dari 0.05 artinya terima sehingga data tidak bersifat stasioner. Karena itu dilakukan pembedaan satu kali ( = 1) untuk mendapatkan output yang stasioner.

Gambar 4 Plot setelah pembedaan satu kali.

Gambar 5 Plot ACF dari saham dengan pembedaan satu kali.

Gambar 6 Plot PACF dari saham dengan pembedaan satu kali.

Hasil pembedaan satu kali dapat dilihat pada Gambar 4 yang menunjukkan bahwa data sudah memiliki kecenderungan berada di sekitar nilai tengah nol. Berdasarkan uji

Augmented Dickey-Fuller pada Lampiran 3,

nilai- yang kurang dari 0.05 artinya tolak yang menunjukkan data sudah stasioner.

Setelah data stasioner, tahap selanjutnya adalah mengidentifikasi model tentatif berdasarkan karakteristik ACF (Gambar 5) dan PACF (Gambar 6). Plot korelasi diri menunjukkan ordo- dan plot korelasi ordo parsial menunjukkan ordo- . Dari kedua plot tersebut ada tiga model yang teridentifikasi yaitu ARIMA (2,1,5), ARIMA (3,1,3), dan ARIMA (3,1,4). Tahap selanjutnya adalah pendugaan parameter dengan proses trial and error, yaitu dengan memperkecil ordo- atau yang mempunyai -hitung kecil atau menambah ordo- atau yang mempunyai

t-hitung besar sehingga memperoleh kandidat-kandidat model. Hasil pendugaan parameter dapat dilihat pada Lampiran 4, 5

Time Series Plot of d=1

60

Autocorrelation Function for d=1 (with 5% significance limits for the autocorrelations)

60

Partial Autocorrelation Function for saham (with 5% significance limits for the partial autocorrelations)

60

(19)

10

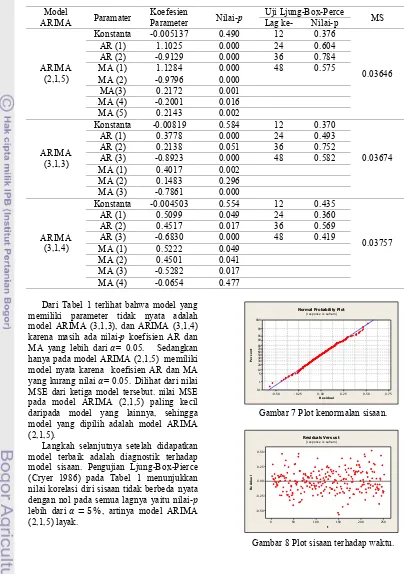
Tabel 1 Alternatif model ARIMA tentatif

Model

ARIMA Paramater Koefesien Parameter Nilai-p Uji Ljung-Box-Perce Lag ke- Nilai-p MS

ARIMA memiliki parameter tidak nyata adalah model ARIMA (3,1,3), dan ARIMA (3,1,4) karena masih ada nilai-p koefisien AR dan MA yang lebih dari = 0.05. Sedangkan hanya pada model ARIMA (2,1,5) memiliki model nyata karena koefisien AR dan MA yang kurang nilai = 0.05. Dilihat dari nilai MSE dari ketiga model tersebut. nilai MSE pada model ARIMA (2,1,5) paling kecil daripada model yang lainnya, sehingga model yang dipilih adalah model ARIMA (2,1,5).

Langkah selanjutnya setelah didapatkan model terbaik adalah diagnostik terhadap model sisaan. Pengujian Ljung-Box-Pierce (Cryer 1986) pada Tabel 1 menunjukkan nilai korelasi diri sisaan tidak berbeda nyata dengan nol pada semua lagnya yaitu nilai- lebih dari = 5%, artinya model ARIMA (2,1,5) layak.

Gambar 7 Plot kenormalan sisaan.

Gambar 8 Plot sisaan terhadap waktu.

(20)

11

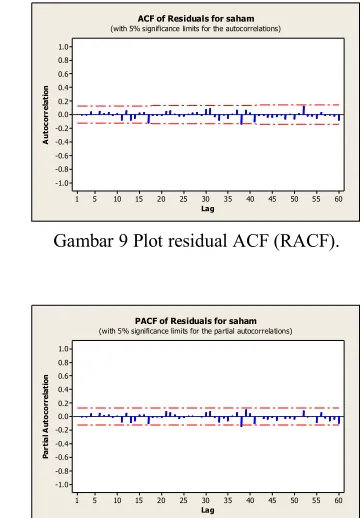
Gambar 9 Plot residual ACF (RACF).

Gambar 10 Plot residual PACF (RPACF).

Sisaan harus menyebar normal. Untuk mengecek kenormalan sisaan dapat dilihat dari Normal Probability Plot of the

Residuals pada Gambar 7. Nilai titik-titik

residual yang menempel atau sangat dekat dengan garis biru menunjukkan sisaan tersebut menyebar normal.

Selain menyebar normal, sisaan harus bersifat acak. Hal tersebut dapat dilihat juga tidak menunjukkan nilai autokorelasi yang nyata, artinya model sudah besifat acak. Dengan demikian asumsi keacakan dan kenormalan terpenuhi. Maka model ARIMA (2,1,5) merupakan model terbaik untuk meramalkan harga saham tersebut adalah

= −0.005137 + 2.1025

−2.0154 − 0.9129 − 1.1284

+0.9796 − 0.2172 + 0.2001 −

0.2143

3.3 Model ARIMA-GARCH

Setelah mendapatkan model ARIMA yang cocok, perlu mengecek apakah model ARIMA yang didapatkan tersebut memiliki ragam sisaan yang konstan atau tidak. Jika model menghasilkan ragam yang tidak konstan artinya model tersebut masih memiliki masalah heteroskedastisitas. Langkah yang bisa dilakukan untuk mengecek model tersebut adalah dengan menggunakan uji ARCH-LM.

Berdasarkan hasil uji ARCH-LM di Lampiran 10, pada saat lag 1 nilai

probability chi-square sebesar 0.0100.

Berdasarkan hasil ARCH-LM, nilai

probability chi-square kurang dari α = 5%.

sehingga dapat disimpulkan bahwa ragam dari harga saham mengandung efek ARCH/GARCH. Oleh karena itu, peramalan dengan model ARIMA terjadi pelanggaran asumsi sehingga yang sesuai berdasarkan asumsi bahwa ragamnya heteroskedastik yaitu peramalan model GARCH.

Persamaan ragam sisaan model GARCH

= + +

Dalam proses pengepasan model GARCH yang paling sering digunakan adalah metode maximum likelihood. Untuk membangun kemungkinan suatu model GARCH diperlukan beberapa iterasi untuk mendapatkan model yang paling baik.

Kemungkinan model yang akan digunakan adalah ARIMA (2,1,5)-GARCH (0,2), ARIMA (2,1,5)-GARCH (1,3) dan ARIMA (2,1,5)-GARCH (2,3). Didapatkan hasil estimasi model ARIMA (2,1,5)-GARCH (0,2), ARIMA (2,1,5)-(2,1,5)-GARCH (1,3) dan ARIMA (2,1,5)-GARCH (2,3) pada Lampiran 8, 9 dan 10. Secara ringkas, hasil telah dirangkum di Tabel 2.

60

PACF of Residuals for saham (with 5% significance limits for the partial autocorrelations)

60

(21)

12

Tabel 2 Hasil Analisis Model ARIMA-GARCH

Dilihat dari nilai probabilitasnya, ketiga model dari persamaan ragamnya sudah baik karena semua koefisien memiliki nilai probabilitas yang lebih kecil dari α = 5%. Namun pada koefisien MA (4) di model ARIMA (2,1,5)-GARCH (2,3) dan hampir seluruh koefesien AR dan MA di model ARIMA (2,1,5)-GARCH (0,2) masih belum signifikan karena nilainya lebih besar dari

α = 5%.

Oleh karena itu, model ARIMA (2,1,5)-GARCH (1,3) dipilih menjadi model yang terbaik. Setelah terpilih model yang terbaik, dilakukan pengujian keberadaan heteroskedastisitas kembali dengan ARCH-LM pada model ARIMA (2,1,5)-GARCH (1,3). Hasil dari ARCH-LM sudah tidak terdapat masalah heteroskedastisitas dengan nilai probability chi-square lebih besar dari

α = 5%yaitu sebesar 0.5374.

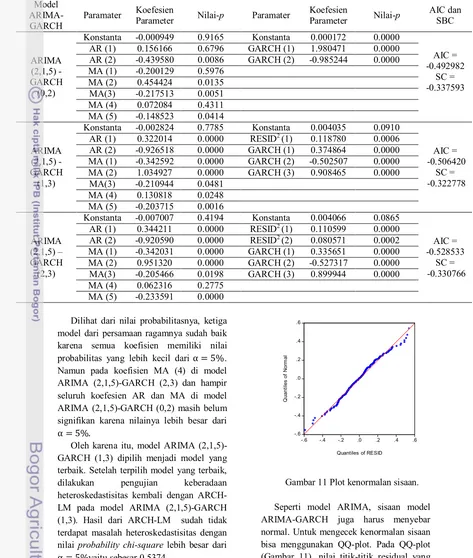
Gambar 11 Plot kenormalan sisaan.

Seperti model ARIMA, sisaan model ARIMA-GARCH juga harus menyebar normal. Untuk mengecek kenormalan sisaan bisa menggunakan QQ-plot. Pada QQ-plot (Gambar 11), nilai titik-titik residual yang Model

ARIMA-

GARCH Paramater Koefesien Parameter Nilai-p Paramater

Koefesien

Konstanta -0.000949 0.9165 Konstanta 0.000172 0.0000

AIC =

(22)

13

merah menunjukkan sisaan tersebut menyebar normal.

Secara statistik, uji kenormalan bisa digunakan dengan uji Jarque-Bera dengan

=5%, yang menggunakan hipotesis sebagai berikut

Ho : data menyebar normal

H1 : data tidak menyebar normal. Jika nilai JB < (,2) atau p-value > 

maka keputusannya terima Ho yang berarti

asumsi kenormalan terpenuhi. Berdasarkan hasil diperoleh pada Lampiran 12, nilai Jarque-Bera sebesar 1.856736, karena nilai ( . , ) = 5.99maka keputusannya terima Ho yaitu sisaan sudah menyebar normal.

Oleh karena itu, model yang terbaik adalah ARIMA (2,1,5)-GARCH (1,3) dengan model harga saham

= −0.002824 + 1.322014 −1.248532 − 0.926518 +0.342592 − 1.034927 +0.210944 − 0.130818 +0.203715

dan ragam sisaan

σ = 0.0040035 + 0.118780 +0.374864 − 0.502507

+0.908465

3.4 Peramalan

Peramalan harga saham dilakukan dengan menggunakan model dugaan ARIMA (2,1,5)-GARCH (1,3) selama periode 50 hari ke depan. Grafik hasil dari peramalan model tersebut terdapat pada Gambar 12 sedangkan data hasil peramalan terdapat pada Lampiran 13.

Gambar 12 Plot data harga saham aktual dengan data ramalan.

Secara statistik, MAPE yang diperoleh dari hasil peramalan model ARIMA (2,1,5)-GARCH (1,3) sebesar 2.2199. Dari plot data aktual dengan data peramalan model ARIMA (2,1,5)-GARCH (1,3) pada Gambar

(23)

14

IV SIMPULAN DAN SARAN

4.1 Simpulan

Harga saham dapat dimodelkan baik dengan menggunakan model ARIMA-GARCH. Model ARIMA merupakan pemodelan deret waktu dengan asumsi ragam konstan. Dalam kondisi ragam sisaan tidak konstan dapat digunakan model GARCH dengan cara mentransformasi sisaan.

Pada kenyataannya, di sektor keuangan volatilitasnya sangat tinggi yang menyebabkan munculnya masalah heteroskedastisitas dimana ragam sisaan tidak konstan. Karena itu, model ARIMA-GARCH lebih baik digunakan daripada hanya memodelkan ARIMA saja. Hasil estimasi dengan model ARIMA-GARCH pada dasarnya menunjukkan hasil yang tidak jauh berbeda dengan model ARIMA, namun

permasalahan utama yaitu keberadaan heteroskedastisitas yang masih ada pada model ARIMA.

Hasil peramalan dengan model ARIMA-GARCH terbukti lebih baik daripada menggunakan hanya model ARIMA karena plot data ramalan sudah hampir mengikuti pola data aktual. Jadi, model ARIMA-GARCH selain bisa menghilangkan masalah heteroskedastisitas juga dapat memodelkan ragam sisaannya dan memberikan peramalan yang baik.

4.2 Saran

(24)

15

DAFTAR PUSTAKA

Bowerman BL, O’Connell, RT. 1987. Time Series Forecasting. Inufied Concepts

and Computer Implementation.2nd

edition. Boston: Duxbury Press. Cryer JD. 1986. Time Series Analysis.

Boston: Duxbury Press.

Firdaus M. 2006. Analisis Deret Waktu Satu

Ragam. Bogor: IPB Press.

Ghahramani S. 2005. Fundamentals of

Probability. New Jersey: Prentice

Hall, Inc.

Grimmett GR, Stirzaker DR. 1992.

Probability and Random Processes.

2nd_{edition. Oxford: University Press.}

Gujarati D. 2003. Ekonometri Dasar.

Terjemahan Sumarno Zain. Jakarta: Erlangga.

Hogg RV, Craig AT. 1995. Introduction to

Mathematical Statistics. Ed. Ke-5.

Prentice Hall. Englewood Cliffs. New Jersey.

Makridaskis S, Whelwright SC, McGee VE. 1983. Forecasting: Methods and

Applications. 2nd_{edition. New York:}

John Wiley and Sons.

Makridaskis S, Whelwright SC, McGee VE. 1999. Metode dan Aplikasi

Peramalan. Terjemahan Sus

Andriyanto dan Abdul Basith. Jakarta: Erlangga.

McNeil AJ, Frey R, Embrechts P. 2005.

Quantitative Risk Management.

United Kingdom. Princeton University Press.

Mulyana. 2004. Analisis Data Deret Waktu.

http://resources.unpad.ac.id/unpad-content/uploads/publikasi_dosen/PEN GUJIAN%20AUTOKORELASI%20 PERIODIK%20UNTUK%20DATA

%20DERET%20WAKTU.PDF [13

Januari 2012].

Myers RH and Milton JS. 1991. A First

Course Linear Statistical Models.

Boston: PWS-Kent.

Ross SM. 2003. Introduction to Probability

Models. Burlington: Elsevier, Inc.

Simanjutak MA. 2009. Penanganan Masalah Heteroskedastisitas dengan Model ARCH-GARCH dan Model

Black-Scholes. Tesis Pasca Sarjana.

Bogor: Institut Pertanian Bogor. Wei WS. 1994. Time Series Analysis:

Univariate and Multivariate Method.

Addison: Wesley Publishing Company.

Santoso T. 2011. Aplikasi Model GARCH pada Data Inflasi Bahan Makanan Indonesia 2005.1-2010.6. Jurnal Organisasi dan Manajemen, Vol 7 No.1, hal. 38-52.

(25)

16

(26)

17

Lampiran 1 Data penutupan saham Sharp Corp. harian selama 3 Januari 2011 s.d. 14 Maret 2012

(27)

18

Tanggal Saham Tanggal Saham Tanggal Saham Tanggal Saham 7/29/2011 9.15 9/21/2011 8.10 11/11/2011 9.25 1/6/2012 8.45

(28)

19

Tanggal Saham 3/1/2012 6.81 3/2/2012 6.92 3/5/2012 6.83 3/6/2012 6.56 3/7/2012 6.75 3/8/2012 6.40 3/9/2012 6.33 3/12/2012 6.14 3/13/2012 6.20 3/14/2012 6.09

Sumber :

http://finance.yahoo.com/q/hp?s=SHCAY&a=11&b=30&c=2011&d=02&e=15&f=2012&g=d

Lampiran 2 Output uji ADF pada data asli

Null Hypothesis: SAHAM has a unit root Exogenous: Constant

Lag Length: 0 (Automatic based on SIC, MAXLAG=15)

t-Statistic Prob.*

Augmented Dickey-Fuller test statistic -2.058479 0.2619

Test critical values: 1% level -3.456302

5% level -2.872857

10% level -2.572875

.

Lampiran 3 Output uji ADF setelah pembedaan satu kali

Null Hypothesis: D(SAHAM) has a unit root Exogenous: Constant

Lag Length: 0 (Automatic based on SIC, MAXLAG=15)

t-Statistic Prob.*

Augmented Dickey-Fuller test statistic -15.92126 0.0000

Test critical values: 1% level -3.456408

5% level -2.872904

(29)

20

Lampiran 4 Output model ARIMA (2,1,5)

ARIMA Model: saham

Final Estimates of Parameters

Type Coef SE Coef T P AR 1 1.1025 0.0806 13.68 0.000 AR 2 -0.9129 0.0415 -22.00 0.000 MA 1 1.1284 0.0715 15.79 0.000 MA 2 -0.9796 0.0267 -36.75 0.000 MA 3 0.2172 0.0671 3.24 0.001 MA 4 -0.2001 0.0827 -2.42 0.016 MA 5 0.2143 0.0691 3.10 0.002 Constant -0.005137 0.007423 -0.69 0.490

Differencing: 1 regular difference

Number of observations: Original series 252, after differencing 251 Residuals: SS = 8.85880 (backforecasts excluded)

MS = 0.03646 DF = 243

Modified Box-Pierce (Ljung-Box) Chi-Square statistic Lag 12 24 36 48

Chi-Square 4.2 13.9 21.9 37.7 DF 4 16 28 40 P-Value 0.376 0.604 0.784 0.575

Type Coef SE Coef T P AR 1 0.3778 0.0950 3.98 0.000 AR 2 0.2138 0.1090 1.96 0.051 AR 3 -0.8923 0.0986 -9.05 0.000 MA 1 0.4017 0.1259 3.19 0.002 MA 2 0.1483 0.1416 1.05 0.296 MA 3 -0.7861 0.1279 -6.14 0.000 Constant -0.00819 0.01495 -0.55 0.584

MS = 0.03674 DF = 244

(30)

21

Type Coef SE Coef T P AR 1 0.5099 0.2577 1.98 0.049 AR 2 0.4517 0.1877 2.41 0.017 AR 3 -0.6830 0.1874 -3.64 0.000 MA 1 0.5222 0.2642 1.98 0.049 MA 2 0.4501 0.2190 2.06 0.041 MA 3 -0.5282 0.2201 -2.40 0.017 MA 4 -0.0654 0.0919 -0.71 0.477 Constant -0.004503 0.007605 -0.59 0.554

MS = 0.03757 DF = 243

(31)

22

Lampiran 7 Output pada model ARIMA (2,1,5)-GARCH (0,2)

Dependent Variable: D(SAHAM)

Method: ML - ARCH (Marquardt) - Normal distribution Date: 08/31/12 Time: 09:52

Sample (adjusted): 4 252

Included observations: 249 after adjustments Convergence achieved after 52 iterations MA Backcast: -1 3

Presample variance: backcast (parameter = 0.7)

GARCH = α + β*GARCH(1) + β *GARCH(2)

Variable Coefficient Std. Error z-Statistic Prob.

C -0.000949 0.009052 -0.104811 0.9165

AR(1) 0.156166 0.378180 0.412941 0.6796

AR(2) -0.439580 0.167227 -2.628645 0.0086

MA(1) -0.200129 0.379138 -0.527853 0.5976

MA(2) 0.454424 0.183857 2.471613 0.0135

MA(3) -0.217513 0.077689 -2.799793 0.0051

MA(4) 0.072084 0.091561 0.787284 0.4311

MA(5) -0.148523 0.072830 -2.039318 0.0414

Variance Equation

α 0.000172 2.15E-05 7.998596 0.0000

GARCH(1) 1.980471 0.005905 335.3836 0.0000

GARCH(2) -0.985244 0.005900 -166.9842 0.0000

R-squared 0.039402 Mean dependent var -0.007751

Adjusted R-squared -0.000960 S.D. dependent var 0.195749

S.E. of regression 0.195842 Akaike info criterion -0.492982

Sum squared resid 9.128318 Schwarz criterion -0.337593

Log likelihood 72.37630 Hannan-Quinn criter. -0.430436

F-statistic 0.976220 Durbin-Watson stat 1.927676

(32)

23

GARCH = α + α*RESID2_{(1) + β} _{*GARCH(1) + β}_{*GARCH(2) + β} _*GARCH(3)

C -0.002824 0.010037 -0.281318 0.7785

AR(1) 0.322014 0.022744 14.15789 0.0000

AR(2) -0.926518 0.018371 -50.43373 0.0000

MA(1) -0.342592 0.069277 -4.945249 0.0000

MA(2) 1.034927 0.059785 17.31085 0.0000

MA(3) -0.210944 0.106738 -1.976276 0.0481

MA(4) 0.130818 0.058272 2.244974 0.0248

MA(5) -0.203715 0.064712 -3.148009 0.0016

Variance Equation

α 0.004035 0.002387 1.690163 0.0910

RESID2₍₁₎ _0.118780 _0.034467 _3.446233 _0.0006

GARCH(1) 0.374864 0.032766 11.44046 0.0000

GARCH(2) -0.502507 0.019232 -26.12827 0.0000

GARCH(3) 0.908465 0.034189 26.57192 0.0000

Adjusted R-squared 0.004382 S.D. dependent var 0.195749

(33)

24

GARCH = α + α *RESID2_{(1) + α} _*RESID2_{(2) + β} _{*GARCH(1) + β} _{*GARCH(2) +}

β *GARCH(3)

C -0.007007 0.008678 -0.807506 0.4194

AR(1) 0.344211 0.027523 12.50646 0.0000

AR(2) -0.920590 0.015985 -57.58945 0.0000

MA(1) -0.342031 0.069539 -4.918521 0.0000

MA(2) 0.951320 0.054281 17.52580 0.0000

MA(3) -0.205466 0.088187 -2.329885 0.0198

MA(4) 0.062316 0.057388 1.085869 0.2775

MA(5) -0.233591 0.047613 -4.905995 0.0000

Variance Equation

α 0.004066 0.002372 1.714371 0.0865

RESID2₍₁₎ _0.110599 _0.021629 _5.113397 _0.0000

RESID2₍₂₎ _0.080571 _0.021821 _3.692317 _0.0002

GARCH(1) 0.335651 0.029165 11.50853 0.0000

GARCH(2) -0.527317 0.023118 -22.80960 0.0000

GARCH(3) 0.899944 0.025846 34.81984 0.0000

Adjusted R-squared 0.000574 S.D. dependent var 0.195749

(34)

25

Lampiran 10 Output dari uji ARCH-LM ARIMA (2,1,5)

Heteroskedasticity Test: ARCH

F-statistic 6.758334 Prob. F(1,246) 0.0099

Obs*R-squared 6.631104 Prob. Chi-Square(1) 0.0100

Lampiran 11 Output dari uji ARCH-LM ARIMA (2,1,5)-GARCH (1,3)

Heteroskedasticity Test: ARCH

F-statistic 0.377873 Prob. F(1,246) 0.5393

Obs*R-squared 0.380361 Prob. Chi-Square(1) 0.5374

Lampiran 12 Output dari uji normalitas pada sisaan baku ARIMA (2,1,5)-GARCH (1,3)

0 5 10 15 20 25 30

-3 -2 -1 0 1 2 3

Series: Standardized Residuals Sample 4 252

Observations 249

Mean -0.025137 Median -0.036890 Maximum 2.771287 Minimum -2.891404 Std. Dev. 0.999368 Skewness 0.209159 Kurtosis 3.063032

(35)

26

Lampiran 13 Data peramalan selama 50 hari ke depan

Waktu ke- Aktual GARCH Waktu ke- Aktual GARCH

1 8.82 8.684838 26 6.95 6.977552

2 8.69 8.85209 27 6.88 7.072523

3 8.56 8.714375 28 6.85 6.797131

4 8.45 8.563129 29 6.85 6.860665

5 8.46 8.425241 30 6.77 6.894828

6 8.61 8.436848 31 6.77 6.757831

7 8.55 8.633724 32 7.00 6.769778

8 8.30 8.571493 33 7.03 6.983386

9 8.39 8.287015 34 6.83 7.015004

10 8.23 8.361592 35 6.78 6.819085

11 8.21 8.234831 36 6.97 6.758644

12 8.46 8.202382 37 6.99 6.930926

13 8.71 8.489768 38 7.16 6.976939

14 8.68 8.676722 39 7.11 7.147829

15 8.39 8.643238 40 6.99 7.101244

16 8.50 8.370892 41 6.81 6.923246

17 8.49 8.439553 42 6.92 6.793055

18 8.53 8.474618 43 6.83 6.899902

19 8.57 8.511967 44 6.56 6.846554

20 8.48 8.590436 45 6.75 6.567707

21 7.42 8.449445 46 6.40 6.74202

22 6.75 7.437041 47 6.33 6.422691

23 7.17 6.771776 48 6.14 6.303989

24 6.81 7.246539 49 6.20 6.217455