Proyeksi Jumlah Kendaraan Bermotor Menurut Jenisnya Kotamadya Binjai Pada Tahun

(1)

PROYEKSI JUMLAH KENDARAAN BERMOTOR MENURUT JENISNYA DI KOTAMADYA BINJAI PADA TAHUN 2012

TUGAS AKHIR

FRISKA HANAYA 072407002

PROGRAM STUDI DIPLOMA III STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

PROYEKSI JUMLAH KENDARAAN BERMOTOR MENURUT JENISNYA

DI KOTAMADYA BINJAI PADA TAHUN 2012

TUGAS AKHIR

Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar Ahli Madya

FRISKA HANAYA

072407002

PROGRAM STUDI DIPLOMA III STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(3)

PERSETUJUAN

Judul : PROYEKSI JUMLAH KENDARAAN BERMOTOR

MENURUT JENISNYA KOTAMDYA BINJAI PADA TAHUN 2012

Kategori : TUGAS AKHIR

Nama : FRISKA HANAYA

Nomor Induk Mahasiswa : 072407002

Program Studi : DIPLOMA (D3) STATISTIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Disetujui di

Medan, Juni 2010

Diketahui

Departemen Matematika FMIPA USU Pembimbing 1

Ketua,

Dr. Saib Suwilo, M.Sc Drs. Suwarno Arriswoyo, M.Si

(4)

PERNYATAAN

PERAMALAN PRODUK DOMESTIK REGIONAL BRUTO (PDRB) KABUPATEN LABUHANBATU PADA SEKTOR PERTANIAN TAHUN 2011

TUGAS AKHIR

Saya mengakui bahwa Tugas Akhir ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Mei 2010

UCI SUPRIANA

(5)

PENGHARGAAN

Bismillahirrahmanirrahim,

Puji dan syukur penulis panjatkan kehadirat Allah SWT yang telah memberikan rahmat dan karunianya kepada penulis sehingga penulis dapat menyelesaikan tugas Akhir dengan judul ”PROYEKSI JUMLAH KENDARAAN BERMOTOR

MENURUT JENISNYA KOTAMDYA BINJAI PADA TAHUN 2012” tepat pada

waktunya.

Pada kesempatan ini penulis mengucapkan terima kasih atas bantuan, petunjuk dan bimbingan yang berharga yang telah diberikan kepada penulis sehingga akhirnya penulis dapat menyelesaikan Tugas Akhir ini terutama kepada : Bapak Prof. Dr. Eddy Marlianto, M.Sc, selaku Dekan FMIPA USU, Bapak Drs. Saib Suwilo, M.Sc, selaku ketua Departemen matematika, Bapak Drs. Suwarno Ariswoyo, M.Si, selaku pembimbing yang tak henti-hentinya memberikan bantuan, bimbingan, pengarahan serta saran.

Terima kasih secara khusus penulis ucapkan kepada yang terkasih dan teristimewah Ayahanda Edy Subandi dan Ibunda Sri Hayuni yang membesarkan dan mendidik penulis dengan penuh kasih sayang dan cinta kasih dari kecil hingga saat ini, serta banyak memberikan dukungan, baik itu motivasi, materi dan doa yang tak ternilai harganya.

Ucapan terima kasih yang tidak kalah pentingnya juga penulis ucapkan buat seluruh sahabat- sahabat penulis, Uci, Nisfi, Tika, Desi, Dedi, Defi, Budi, Amai, dan yang lainnya. Yang telah memberikan semangat dan menjadi tempat penulis mengaduh dalam menghadapi kesulitan, Semoga kita tetap menjadi sahabat selama- lamanya.

(6)

membangun demi peningkatan ilmu penulis dan mutu penulisan Tugas Akhir di masa yang akan datang.

Akhirnya penulis berharap semoga Tugas Akhir ini dapat memberikan manfaat kepada semua pihak yang memerlukannya.

Medan, Mei 2010

Penulis

(7)

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Daftar Isi v

Daftar Tabel vi

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Identifikasi Masalah 2

1.3 Batasan Masalah 2

1.4 Maksud dan Tujuan 3

1.5 Metodelogi Penelitian 3

1.6 Lokasi dan Waktu 4

1.7 Sistematika Penulisan 5

BAB 2 TINJAUAN TEORITIS 6

2.1 Pengertian Ramalan 6

2.2 Jenis- Jenis Peramalan 6

2.3 Langkah-langkah Peramalan 9

2.4 Metode Peramalan 10

2.5 Metode Penelitian 10

BAB 3 ANALISIS DATA 16

3.1 Analisis Data Jumlah Kendaraan Bermotor Menurut Jenisnya di

Kotamadya Binjai 16

3.2 Proyeksi Jumlah Mobil Penumpang di Binjai Tahun 2012 18

(8)

3.4 Proyeksi Jumlah Bus di Kotamadya Binjai Tahun 2001-2012 37 3.5 Proyeksi Jumlah Sepedamotor di Binjai Tahun 2001-2012 46

BAB 4 IMPLEMENTASI SISTEM 56

4.1 Pengertian Implementasi Sistem 56

4.2 Mengoperasikan Excel 56

4.3 Penggunaan Excel Pada Contoh Data 62

4.4 Menghitung Nilai Kesalahan Pada Contoh Data 63

BAB 5 KESIMPULAN DAN SARAN 65

5.1 Kesimpulan 65

5.2 Saran 66

Daftar Pustaka

(9)

DAFTAR TABEL

Halaman

Tabel 3.1 Jumlah kendaraan Bermotor Menurut Jenisnya di Binjai Mulai tahun

2001 sampai dengan 2008 17

Tabel 3.2.1 Jumlah Mobil Penumpang di Binjai Tahun 2001 – 2012 18

Tabel 3.2.2 Nilai kesalahan peramalan jumlah mobil penumpang di Kotamadya

Binjai tahun (2008 – 2012) 27

Tabel 3.3.1 Jumlah Mobil Gerobak Di Kotamadya Binjai Tahun 2001-2012 29

Tabel 3.3.2 Nilai kesalahan peramalan jumlah mobil gerobak di Kotamadya

Binjai pada tahun (2009 – 2012) 37

Tabel 3.4.1 Jumlah Bus Di Kotamadya Binjai Tahun 2001-2012 39

Tabel 3.4.2 Nilai kesalahan peramalan jumlah bus di Kotamadya Binjai pada

tahun (2009 – 2012) 46

Tabel 3.5.1 Jumlah Sepedamotor Di Kotamadya Binjai Tahun 2001-2012 49

Tabel 3.5.2 Nilai kesalahan peramalan jumlah sepedamotor di Kotamadya Binjai

(10)

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Setiap Negara mengalami keuntungan dan kerugian pada perekonomian.

Perkembangan perekonomian suatu Negara dapat diukur dengan berbagai cara, salah

satunya dengan mengetahui tingkat perkembangan dunia industri di Negara tersebut.

Contohnya yaitu dalam perindustrian otomotif atau dilihat dari meningkat atau

menurunnya minat masyarakat dalam memiliki kendaraan bermotor.

Dilihat dari perkembangan penduduk pada Negara Indonesia bahwa minat

masyarakat dalam memiliki kendaraan bermotor semakin meningkatkan pesat seiring

dengan semakin mudahnya untuk memiliki kendaraan bermotor melalui jasa

perbankan dalam bentuk kredit.

Oleh karena itu penulis mencoba untuk memproyeksikan banyaknya

kendaraan bermotor di kotamadya Binjai pada tahun 2012, untuk mengetahui apakah

proyeksi yang diperoleh dapat menggambarkan jumlah kendaraan bermotor di

kotamadya Binjai pada tahun 2012 mengalami peningkatan dan sesuai dengan kondisi

(11)

1.2 Identifikasi Masasalah

Penyusunan Tugas Akhir ini akan menguraikan tentang aspek-aspek jumlah

kendaraan bermotor di kotamadya Binjai serta metode-metode perhitunganya, maka

permasalahan yang dikaji dalam Tugas Akhir ini adalah :

1. Berapa Banyak Kendaraan Bermotor Menurut Jenisnya di Kotamadya Binjai pada

tahun 2012.

2. Jenis Kendaraan Bermotor manakah yang paling banyak terdapat di kotamadya

Binjai pada tahun 2012.

1.3 Batasan Masalah

Untuk memperjelas dan mempermudah penelitian ini agar tidak menyimpang dari

sasaran yang dituju, maka penulis melakukan pembatasan masalah sebagai berikut :

1. Dikarenakan dalam menetapkan peramalan kendaraan bermotor di kotamadya

Binjai penulis ingin meramalkan jumlah kendaraan bermotor pada tahun 2012

pada kota tersebut, berdasarkan data tahun 2001 - 2008.

2. Untuk periode waktu dalam memperoleh nilai paramalan dipergunakan data-data

yang berkaitan dengan jumlah kendaraan bermotor, dimana data yang diperoleh

(12)

1.4 Maksud dan Tujuan

Adapun maksud dan tujuan Penulis “Tugas Akhir” ini adalah ingin melihat banyak

kendaraan bermotor menurut jenisnya di kotamadya Binjai pada tahun 2012 dan jenis

kendaraan bermotor manakah yang paling banyak terdapat di kotamadya Binjai pada

tahun 2012 dengan menggunakan metode-metode Rata-rata Bergerak Linier (Linier

Moving Avarage).

1.5 Metodologi Penelitian

Untuk mendukung penyusunan Tugas Akhir, maka penulis membutuhkan data-data

yang diperoleh melalui serangkaian tinjauan, penelitian, riset maupun pengambilan

data. Data di dalam riset tersebut penulis menggunakan beberapa metode diantaranya :

1. Metode Penelitian Keputuskaan (Studi Literatur)

Dalam hal ini pengumpulan data serta keterangan-keterangan dapat dilakukan dengan

membaca serta mempelajari buku-buku ataupun literature pelajaran yang didapat

diperkuliahan ataupun umum, serta sumber informasi lainnya yang berhubungan

dengan objek yang diteliti.

2. Metode Pengumpulan Data

Pengumpulan data untuk keperluan riset ini penulis lakukan dengan menggunakan

(13)

Utara. Data yang dikumpulkan tersebut kemudian diatur, disusun dan disajikan dalam

bentuk angka-angka dengan tujuan untuk mendapatkan gambaran yang jelas tentang

sekumpulan data tersebut.

3. Metode Pengolahan Data

Adapun pengolahan data dalam meramalkan Jumlah Kendaraan Bermotor di

kotamadya Binjai pada tahun 2012 dengan menggunakan perumusan :

a. Menentukan smoothing pertama (S’t)

b. Menentukan smoothing kedua (S”t)

c. Menentukan besarnya konstanta (at)

d. Menentukan besarnya Slope (bt)

e. Menentukan besarnya forecast (f)

1.6 Lokasi dan Waktu

Dalam melakukan peninjaun untuk penyusunan Tugas Akhir ini penulis mengambil

data yang sudah ada pada Badan Pusat Statistika (BPS) Provinsi Sumatera Utara.

Penulis mengambil data dari tahun 2001 sampai tahun 2008 guna melakukan analisis.

(14)

1.7 Sistematika Penulisan

Seluruh penulisan dari Tugas Akhir ini disusun dalam beberapa bab yang setiap bab

tersebut berisiskan sub-sub bab, disusun guna memudahkan pembaca untuk mengerti

dan memahami isi penulisan ini. Adapun sistematika penulisannya adalah sebagai

berikut :

BAB 1 PENDAHULUAN

Bab ini mengutarakan tentang Latar Belakang. Identifikasi Masalah,

Maksud dan Tujuan, Metode Penelitian yang mencakup lokasi serta

waktu pengambilan data Sistematika Penulisan.

BAB 2 TINJAUAN TEORITIS

Bab ini menjelaskan tentang segala sesuatu yang mencakup

penyelesaian masalah sesuai dengan judul dan permasalahan yang

diutarakan.

BAB 3 PEMBAHASAN

Bab ini menerangkan penganalisisan data yang telah diamati dan

dikumpulkan.

BAB 4 IMPLEMENTASI SISTEM

Bab ini menerangkan tentang implementasi sistem yang digunakan.

BAB 5 KESIMPULAN

(15)

BAB 2

TINJAUAN TEORITIS

2.1 Pengertian Peramalan

Dalam melakukan analisis ekonomi atau analisis kegiatan perusahaan, haruslah

diperkirakan apa yang akan terjadi dalam bidang ekonomi atau dalam dunia usaha

pada masa yang akan datang. Kegiatan memperkirakan apa yang akan terjadi pada

masa yang akan datang, kita kenal dengan sebutan peramalan (forecasting). Setiap

kebijakan ekonomi maupun kebijakan perusahaan tidak akan terlepas dari usaha untuk

meningkatkan kesejahteraan masyarakat atau meningkatkan keberhasilan perusahaan

untuk mencapai tujuan pada masa yang akan datang dimana kebijakan tersebut

dilaksanakan. Usaha untuk melihat dan mengkaji situasi dan kondisi tersebut tidak

terlepas dari kegiatan peramalan.

2.2 Jenis - Jenis Peramalan

Pada umunnya peramalan dapat dibedakan dari beberapa segi, tergantung dari cara

melihatnya. Apabila dilihat dari sifat penyusunnya, maka peramalan dapat dibedakan

(16)

1. Peramalan yang subjektif, yaitu peramalan yang didasarkan atas perasaan

atau intuisi dari orang yang menyusunnya. Dalam hal ini pandangan atau

“judgment” dari orang yang menyusunnya sangat menentukan baik

tidaknya hasil ramalan tersebut.

2. Peramalan yang objektif, peramalan yang didasarkan atas data yang

relevan pada masa lalu, dengan menggunakan teknik-teknik dan metode

dalam penganalisaan data tersebut.

Disamping dilihat dari jangka waktu ramalan yang disusun. Maka peramalan

dapat dibedakan atas dua macam, yaitu :

1. Peramalan jangka panjang, yaitu peramalan yang dilakukan untuk

penyusunan hasil ramalan jangka waktunya lebih dari satu setengah tahun

atau tiga semester. Peramalan seperti ini misalnya diperlukan dalam

penyusunan rencana pembangunan suatu Negara atau suatu daerah,

corporate planning, rencana investasi atau rencana ekspansi dari suatu

perusahaan.

2. Peramalan jangka pendek, yaitu peramalan yang dilakukan penyusunan

hasil ramalan dalam jangka waktu yang kurang dari satu setengah tahun,

atau tiga semester. Peramalan seperti ini diperlukan dalam penyusunan

rencana tahunan, rencana kerja operasional, dan anggaran contoh

penyusunan rencana produksi, rencana penjualan, rencana persediaan, dan

(17)

Berdasarkan sifat ramalan yang telah disusun, maka peramalan dapat

dibedakan atas dua macam, yaitu :

1. Peramalan kualitatif, yaitu peramalan yang didasarkan atas data kualitatif

pada masa lalu. Hasil peramalan yang dibuat sangat tergantung pada orang

yang menyusunnya. Hal ini penting karena hasil peramalan tersebut

ditentukan berdasarkan pemikiran yang bersifat intuisi, judgment atau

pendapat, dan pengetahuan serta pengalaman dari penyusunnya. Biasanya

peramalan secara kualitatif ini didasarkan atas hasil penyelidikan.

2. Peramalan kuantitatif, yaitu peramalan yang didasarkan atas data

kuantitatif pada masa lalu. Hasil peramalan yang dibuat sangat tergantung

pada metode yang digunakan dalam peramalan tersebut. Dengan

peramalan yang berbeda akan diperoleh hasil peramalan yang berbeda.

Adapun yang perlu diperhatikan dari penggunaan metode-metode tersebut,

adalah baik tidaknya metode yang dipergunakan, sangat ditentukan oleh

perbedaan atau penyimpangan antara hasil peramalan dengan kenyataan

yang terjadi. Metode yang baik adalah metode yang memberikan nilai-nilai

perbedaan atau penyimpangan yang mungkin terjadi. Peramalan kuantitatif

hanya dapat digunakan apabila terdapat tiga kondisi sebagai berikut :

a. Adanya informasi tentang keadaan yang lain.

b. Informasi tersebut dapat dikuantifikasikan dalam bentuk data.

c. Dapat diasumsikan bahwa pola yang lalu akan berkelanjutan

(18)

Dari uraian di atas dapatlah diketahui bahwa jenis-jenis peramalan sangat

tergantung dari segi mana kita memandangnya.

2.3 Langkah-Langkah Peramalan

Kualitas atau mutu dari hasil peramalan yang di susun, sangat ditentukan oleh proses

pelaksanaan penyusunnya. Peramalan yang baik adalah peramalan yang dilakukan

dengan mengikuti langkah – langkah atau prosedur penyusunan yang baik. Pada

dasarnya ada tiga langkah peramalan yang penting, yaitu:

1. Menganalisa data yang lalu. Tahap ini benguna untuk pola yang terjadi pada masa

yang lalu. Analisa ini dilakukan dengan cara membuat tabulasi data maka dapat di

ketahui pola data tersebut.

2. Menentukan metode yang digunakan. Masing-masing merode akan memberikan

hasil peramalan yang berbeda. Dimana metode peramalan yang baik adalah

metode yang menghasilkan penyimpangan antara hasil peramalan dengan nilai

kenyataan yang sekecil mungkin.

3. Memproyeksikan data yang lalu dengan menggunakan metode yang dipergunakan,

dan mempertimbangkan adanya beberapa faktor perubahan. Faktor - faktor

perubahan tersebut antara lain terdiri dari perubahan kebijakan - kebijakan yang

(19)

Proyeksi adalah adanya suatu kecendrungan sesuatu hal pada masa yang akan

datang masih belum diketahui dan mempunyai nilai pada masa yang akan datang yang

merupakan petunjuk tentang jumlah sesuatu hal tersebut pada, masa yang akan datang.

2.4 Metode Peramalan

Peramalan adalah kegiatan memperkirakan apa yang terjadi pada masa yang akan

datang. Sedangkan ramalan adalah suatau situasi atau kondisi yang diperkirakan akan

terjadi pada masa yang akan datang. Metode peramalan adalah cara memperkirakan

secara kuantitatif apa yang akan terjadi pada masa depan, berdasarkan data yang

relevan pada masa lalu. Oleh karena metode peramalan ini dipergunakan dalam

peramalan yang objektif. Perlu diketahui bahwa, keberhasilan peramalan didasarkan

atas :

1. Pengetahuan teknik tentang informasi yang lalu dibutuhkan.

2. Teknik dan metode peramalan.

2.5 Metode Penelitian

2.5.1 Metode Smoothing

Metode smoothing merupakan teknik meramal dengan cara mengambil rata – rata dari

beberapa priode yang lalu untuk menaksir nilai pada masa atau priode yang akan

datang. Dalam metode smoothing ini data historis di gunakan untuk memperoleh

(20)

Metode smoothing ini dibagi menjadi dua, yaitu :

1. Moving Averanges (MOVA) / rata – rata bergerak

2. Eksponensial Smoothing

1. Moving Averange

Metode ini di lakukan dengan mengambil sekelompok nilai pengamatan, mencari

rata– ratanya kemudian menggunakan rata – rata tersebut sebagai ramalan untuk

priode yang akan datang. Metode ini disebut rata – rata bergerak karena setiap kali

data observasi baru tersedia, maka angka rata – rata baru dihitung dan digunakan

sebagai ramalan (forecast).

Metode moving average ini di bagi menjadi dua, yaitu :

1. Rata – rata Bergerak tunggal (Single Moving Averages)

Metode ini mempunyai karakteristik khusus, yaitu :

a. Untuk menentukan ramalan pada priode yang akan datang memerlukan

data historis selama jangka waktu tertentu. Misalnya, dengan 4 bulan

moving average, maka ramalan ke 5 baru bisa dibuat setelah bulan ke 4

selesai. Jika 6 bulan moving average, ramalan bulan ke 7 baru bisa

dibuat setelah bulan ke 6 selesai.

b. Semakin panjang jangka waktu moving average, efek pelicinan

semakin terlihat dalam ramalan atau menghasilkan moving average

(21)

2. Rata-rata Bergerak Ganda (Double Moving Average)

Dasar dari metode ini adalah menghitung rata-rata bergerak yang kedua.

Rata-rata bergerak ganda ini merupakan Rata-rata-Rata-rata bergerak dari Rata-rata-Rata-rata bergerak,

dan menurut simbol ditulis sebagai MA(M x N) dimana artinya adalah MA M

periode MA N periode.

Adapun prosedur peramalan rata-rata bergerak linier meliputi tiga

aspek:

1. Penggunaan rata-rata bergerak tunggal pada waktu (ditullis S’t)

2. Penyesuaian, yang merupakan perbedaan antara rata-rata bergerak tunggal

dan ganda pada waktu t (ditulis S’t - S”t), dan

3. Penyesuaian untuk kecenderungan dari periode t ke periode t +1 (atau

keperiode t + m jika kita meramalkan M periode ke muka).

Secara umum pembahasan tersebut dapat dilakukan sebagai berikut : Prosedur

rata-rata bergerak linier secara umum dapat diterangkan melalui persamaan berikut :

a. Menentukan smoothing pertama (S’t), persamaan ini mempunyai asumsi

bahwa saat ini kita berada periode waktu t dan mempunyai nilai masa lalu

sebanyak N, sebagai berikut :

N

X X

S t t t t N

t

1 2

1 ...

' = + − + − + + − +

(22)

Xt = nilai real periode t

N = jumlah periode

b. Menentukan smoothing kedua (S”t), persamaan ini menganggap bahwa semua

rata - rata bergerak tunggal (S’t) telah dihitung. Persamaan ini kita menghitung

rata – rata bergerak N periode dari nilai –nilai S’t tersebut.

N

S”t = smoothing kedua periode t

c. Menentukan besarnya konstanta (at), persamaan ini mengacu terhadap

penyesuaian MA tunggal S’t, dengan persamaan sebagai berikut :

at = S’t + (S’t-S”t) =2S’t - S”t

at = besarnya konstanta periode t

d. Menentukan besarnya slope (bt), persamaan ini menentukan taksiran

kecenderungan dari periode waktu yang satu ke periode waktu berikutnya,

persamaannya sebagai berikut :

bt =

(

' "

)

bt = slope /nilai trend dari data yang sesuai

e. Menentukan besarnya forecast, persamaan ini menunjukkan bagaimana

memoeroleh ramalan untuk m periode ke muka dari t. Ramalan untuk m

(23)

sesuaikan untuk periode t ditambah m kali komponen kecenderungan bt,

persamaannya sebagai berikut :

Ft+m = at + bt (m)

Ft+m = besarnya forecast

m = jangka waktu forecast

Hasil peramalan yang akurat adalah peramalan yang bias meminimalkan

kesalahan meramal. Karena itu adalah menghitung kesalahan meramal digunakan :

a. Mean Absolute Error (MAE)

Mean Absolute Error adalah rata – rata absolute dari kesalahan meramal ,tanpa

menghiraukan tanda negative.

MAE =

n F

X_t _t

∑

− 2

b. Mean Squared Error (MSE)

Mean Squared Error adalah rata – rata kesalahan meramal yang dikuadratkan.

MSE =

(

)

n F

X_t _t

∑

−

c. Mean Absolute Percentage Erroa (MAPE)

Mean Absolute Percentage Error merupakan nilai tengah kesalahan persentase

(24)

MAPE =

n APE

∑

d) Percentage Error (PE)

Percentage Error merupakan Kesalahan persentase dari suatu peramalan,

PE = x100

X F X

t t t

  

 −

dimana :

xt =nilai data ke periode ke-t

ft =nilai ramalan periode ke-t

n =banyaknya data

(25)

BAB 3

PEMBAHASAN

3.1 Analisa Data Jumlah Kendaraaan Bermotor Menurut Jenisnya di Kotamadya Binjai

Salah satu perbedaan manusia dengan makhluk lainnya adalah karena kemampuan dan

kemauannya untuk meramalkan/ memperkirakan keadaan yang akan datang. Hal ini

disebabkan oleh adanya perubahan yang cepat pada masa sekarang ini, sehingga

kebutuhan untuk meramalkan/ memperkirakan itu sangat penting dan sangat

diperlukan.

Seringkali dalam proses peramalan/ perkiraan terjadi pertentangan mengenai

apa yang akan terjadi di waktu yang akan datang, lebih – lebih setelah hasil

kenyataannya berbeda dengan apa yang sebelumnya diramalkan/ diperkirakan. Untuk

menghindari pertentangan yang mungkin terjadi, maka sebagai peramal (forecaster)

tidak boleh merasa cepat puas dengan hasil peramalan yang diperoleh, hal ini

biasanya dipengaruhi oleh terlalu banyaknya faktor yang mempengaruhi keadaan yang

(26)

Karena peramalan ini pada hakekatnya berhubungan dengan hal – hal yang

penuh ketidak pastian, maka perlu merubah situasi kedalam situasi yang setara dengan

keadaan yang pasti atau kedalam situasi yang berdasarkan berbagai kemungkinan

pernyataan bahwa peristiwa yang akan terjadi tersebut akan jatuh pada daerah tertentu

yang masih berada didaerah toleransi. Misalnya dengan mengasumsikan bahwa situasi

dan kondisi cenderung konstan.

Tabel 3.1 Jumlah kendaraan Bermotor Menurut Jenisnya di Binjai Mulai tahun 2001 sampai dengan 2008

Tahun

Jenis Kendaraan Mobil

Penumpang

Mobil

Gerobak Bus

Sepeda motor

2001 3565 1309 81 19041

2002 3647 1377 86 23067

2003 3922 1652 91 25314

2004 4124 1729 97 28590

2005 4260 1869 103 32665

2006 4681 2207 127 38182

2007 5100 2490 136 47485

2008 7560 6874 378 67420

Sumber: Badan Pusat Statistik (BPS) Sumatera Utara

Setelah melihat data yang ada, maka dapat diramalkan jumlah kendaraan bermotor

menurut jenisnya di Kotamadya Binjai dari tahun 2008 – 2012 yang akan datang

(27)

3.2 Proyeksi Jumlah Mobil Penumpang di Binjai Tahun 2012

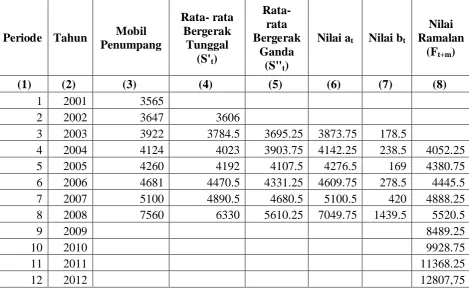
Tabel 3.2.1 Jumlah Mobil Penumpang di Binjai Tahun 2001 – 2012

Pada tabel 3.2 menunjukkan hasil proyeksi dengan menggunakan metode Rata- rata

Bergerak Ganda 2 Tahunan (Double Moving Average) terhadap jumlah mobil

penumpang di Binjai untuk tahun 2009 – 2012.

Untuk Rata- rata Bergerak Tunggal ( dua tahunan) dapat dilakukan dengan

menggunakan rumus :

Maka dari rumus diatas dapat dihitung Rata- rata bergerak Tunggal untuk:

(28)

(29)

=

Kemudian untuk rata - rata Bergerak Ganda (dua tahunan) dapat dilakukan dengan

menggunakan rumus yaitu:

N

Maka dari rumus itu dapat dihitung rata- rata bergerak ganda untuk:

(30)

(31)

= 5610,25

Setelah itu menghitung nilai konstan m periode ke muka (at) dengan persamaan rumus

yaitu:

at = 2S’t – S”t

Maka nilai konstan m periode ke muka (at) untuk:

a2003 = 2S’2003 - S”2003

= 2(3784,5)-3695,25

= 3873,75

a2004 = 2S’2004 - S”2004

= 2(4023) - 3903,75

= 4142,25

a2005 = 2S’2005 - S”2005

= 2(4192)-4107,5

= 4276,5

a2006 = 2S’2006 - S”2006

= 2(4470,5)-4331,25

= 4609,75

a2007 = 2S’2007 - S”2007

(32)

= 5100,5

a2008 = 2S’2008 - S”2008

= 2(6330)-5610,25

= 7049,75

Lalu menghitung nilai bt ( komponen kecendrungan) dengan rumus :

bt = ( ' " )

Maka didapat nilai bt ( komponen kecendrungan) untuk:

(33)

= 169

Sehingga dapat dihitung nilai ramalan Ft+1 dengan menggunakan rumus:

Ft+1 = at + bt.m

Maka didapat nilai ramalan (F) mobil penumpang untuk:

F2008+1 = a8 + b8(1)

F2009 = 7049,75+1439,5(1)

(34)

F2008+2 = a8 + b8(2)

F2010 = 7049,75+1439,5(2)

= 9928,75

F2008+3 = a8 + b8(3)

F2011 = 7049,75+1439,5(3)

= 11368,25

F2008+4 = a8 + b8(4)

F2012 = 7049,75+1439,5(4)

= 12807,75

Dari hasil perhitungan diatas maka diramalkan banyaknya mobil penumpang

di Kotamadya Binjai untuk tahun 2009 sebanyak 8489,25, tahun 2010 sebanyak

9928,75, tahun 2011 sebanyak 11368,25, tahun 2012 sebanyak 15182,75.

Hasil peramalan yang akurat adalah peramalan yang bisa meminimumkan

kesalahan meramal. Tabel dibawah ini menunjukkan besarnya kesalahan peramalan

jumlah mobil penumpang di Kotamadya Binjai berdasarkan data hasil peramalan

(35)

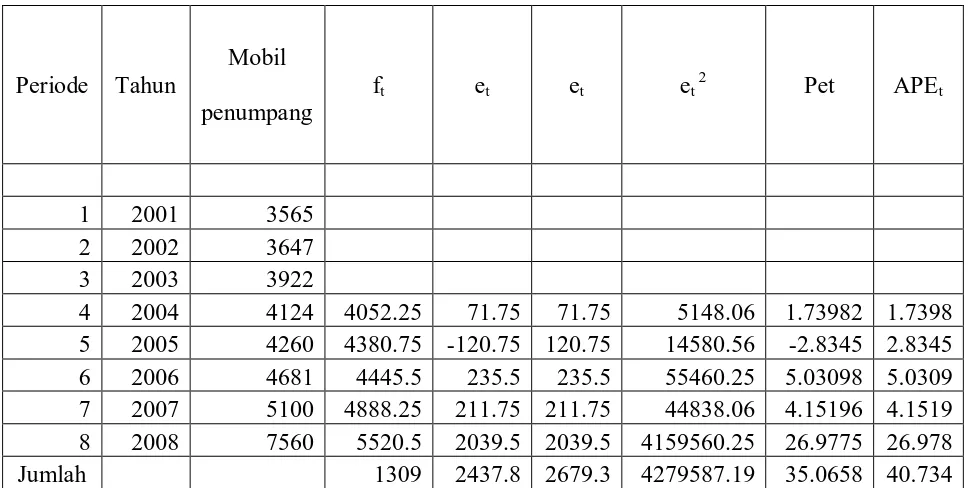
Tabel 3.2.2 Nilai kesalahan peramalan jumlah mobil penumpang di Kotamadya

Maka didapat kesalahan peramalan dengan menggunakan persamaan rumus tersebut

sebagai berikut : Periode Tahun

(36)

Mean Absoulute Error =

Mean Absoulute percentage Error =

n

3.3 Proyeksi Jumlah Mobil Gerobak Di Kotamadya Binjai Tahun 2001-2012

Table 3.3.1 Jumlah Mobil Gerobak Di Kotamadya Binjai Tahun 2001-2012

(37)

Pada tabel 3.3.1 menunjukan hasil proyeksi dengan menggunakan metode Rata-rata

Bergerak Ganda 2 tahunan (Double Moving Avarage) terhadap jumlah Mobil Gerobak

di Kotamadya Binjai pada tahun 2001-2012.

Untuk Rata- rata Bergerak Tunggal (dua tahunan) dapat dilakukan dengan

menggunakan rumus :

(38)

(39)

Kemudian untuk rata- rata Bergerak Ganda (dua tahunan) dapat dilakukan dengan

N

(40)

=1918,5

yaitu:

a2003 =2S’2003 - S”2003

=2(1514,5)-1428,75

=1600,25

a2004 =2S’2004 - S”2004

(41)

=1778,5

a2005 =2S’2005 - S”2005

=2(1799)-1744,75

=1853,25

a2006 =2S’2006 - S”2006

=2(2038)-1918,5

=2157,5

a2007 =2S’2007 - S”2007

=2(2348,5)-2193,25

=2503,75

a2008 =2S’2008 - S”2008

=2(4682)-3515,25

=5848,75

bt = ( ' " )

1 2

t t S S N− −

(42)

(43)

=310,5

b2008 = 1 2

−

N (S’2008 – S"2008)

=

1 2

2

− (4682 – 3515,25)

=2333,5

Ft+1 = at + bt.m

Maka didapat nilai ramalan (F) mobil penumpang untuk:

F2008+1 = a8 + b8(1)

F2009 =5848,75+2333,5(1)

= 8182,25

F2008+2 = a8 + b8(2)

F2010 =5848,75+2333,25(2)

= 10515,75

F2008+3 = a8 + b8(3)

F2011 =5848,75+2333,25(3)

= 12849,25

(44)

F2012 =5848,75+2333,25(4)

= 15182,75

Dari hasil perhitungan diatas maka diramalkan banyaknya mobil gerobak di

Kotamadya Binjai untuk tahun 2009 sebanyak 8182,25, tahun 2010 sebanyak

10515,75, tahun 2011 sebanyak 12849,25, tahun 2012 sebanyak 15182,75.

jumlah mobil gerobak di Kotamadya Binjai berdasarkan data hasil peramalan tahun

2004 -2008.

Tabel 3.3.2 Nilai kesalahan peramalan jumlah mobil gerobak di Kotamadya Binjai pada tahun (2009 – 2012).

Dimana :

Periode Tahun Mobil

Gerobak ft et et et

2

Pet APEt

1 2001 1309

2 2002 1377

3 2003 1652

4 2004 1729 1771.75 -42.75 42.75 1827.5625 -2.47253 2.47253 5 2005 1869 1954.5 -85.5 85.5 7310.25 -4.57464 4.57464 6 2006 2207 1961.75 245.25 245.25 60147.5625 11.11237 11.1124 7 2007 2490 2396.5 93.5 93.5 8742.25 3.75502 3.75502 8 2008 6874 2814.25 4059.75 4059.75 16481570.06 59.0595 59.0595

(45)

Error (et) =

(

xt − f t

)

sebagai berikut :

n

(46)

3.4 Proksi Jumlah Bus Di Kotamadya Binjai Tahun 2001-2012

Table 3.4.1 Jumlah Bus Di Kotamadya Binjai Tahun 2001-2012

Periode Tahun Bus

Bergerak Ganda 2 tahunan (Double Moving Avarage) terhadap jumlah Bus di

Kotamadya Binjai pada tahun 2001-2012.

menggunakan rumus :

(47)

(48)

=115

N

(49)

(50)

yaitu:

a2003 =2S’2003 - S”2003

=2(88,5) - 86

=91

a2004 =2S’2004 - S”2004

=2(94) – 91,25

=96,75

a2005 =2S’2005 - S”2005

=2(100) - 97

=103

a2006 =2S’2006 - S”2006

=2(115) – 107,5

=122,5

a2007 =2S’2007 - S”2007

(51)

=139,75

a2008 =2S’2008 - S”2008

=2(257) – 194,25

=319,75

bt = ( ' " )

(52)

=

Ft+1 = at + bt.m

Maka didapat nilai ramalan (F) bus untuk:

(53)

F2009 =319,75+125,5(1)

= 445,25

F2008+2 = a8 + b8(2)

F2010 =319,75+125,5(2)

= 570,75

F2008+3 = a8 + b8(3)

F2011 =319,75+125,5(3)

= 696,25

F2008+4 = a8 + b8(4)

F2012 =319,75+125,5(4)

= 821,75

Dari hasil perhitungan diatas maka diramalkan banyaknya bus di Kotamadya Binjai

untuk tahun 2009 sebanyak 445,25, tahun 2010 sebanyak 570,75, tahun 2011

sebanyak 696,25, tahun 2012 sebanyak 821,75.

(54)

Tabel 3.4.2 Nilai kesalahan peramalan jumlah bus di Kotamadya Binjai pada

Maka didapat kesalahan peramalan dengan menggunakan persamaan rumus

tersebut sebagai berikut :

(55)

Mean Squered Error =

n

3.5 Proyeksi Jumlah Sepedamotor Di Kotamadya Binjai Tahun 2001-2012

Tabel 3.5.1 Jumlah Sepedamotor Di Kotamadya Binjai Tahun 2001-2012

Periode Tahun Sepeda motor

Bergerak Ganda 2 tahunan (Double Moving Avarage) terhadap jumlah Sepedamotor

(56)

menggunakan rumus :

(57)

=30627,5

N

S”2003 =

(58)

(59)

S”2008 =

N S S'₂₀₀₇+ '₂₀₀₈

=

2

5 , 57452 5

,

42833 +

=50413

yaitu:

a2003 =2S’2003 - S”2003

=2(24190,5) – 22622,3

=25758,8

a2004 =2S’2004 - S”2004

=2(26592) – 25571,3

=20332,8

a2005 =2S’2005 - S”2005

=2(30627,5) – 28789,8

=32465,3

(60)

=2(35423,5) – 33025,5

=37821,5

a2007 =2S’2007 - S”2007

=2(42833,5) – 39128,5

=46538,5

a2008 =2S’2008 - S”2008

=2(57452,5) – 50143

=64762

bt = ( ' " )

(61)

(62)

Ft+1 = at + bt.m

Maka didapat nilai ramalan (F) bus untuk:

F2008+1 = a8 + b8(1)

F2009 =64672+14619(1)

= 79831

F2008+2 = a8 + b8(2)

F2010 =64672+14619(2)

= 94000

F2008+3 = a8 + b8(3)

F2011 =64672+14619(3)

= 108619

F2008+4 = a8 + b8(4)

F2012 =64672+14619(4)

= 123238

Dari hasil perhitungan diatas maka diramalkan banyaknya sepedamotor di

Kotamadya Binjai untuk tahun 2009 sebanyak 79831, tahun 2010 sebanyak 94000,

(63)

jumlah sepedamotor di Kotamadya Binjai berdasarkan data hasil peramalan tahun

2004 -2008.

Tabel 3.5.2 Nilai kesalahan peramalan jumlah sepedamotor di Kotamadya Binjai pada tahun (2009 – 2012).

Periode tahun Sepeda

(64)

sebagai berikut :

n

(65)

BAB 4

IMPLEMENTASI SISTEM

4.1 Pengertian Implementasi Sistem

Implementasi Sistem adalah prosedur yang dilakukan untuk menyesuaikan desain

yang ada dalam desain sistem yang disetujui, menginstal dan memulai sistem baru

yang diperbaiki.

Tahapan implementasi merupakan tahapan penerapan hasil desain tertulis ke

dalam programming (coding). Dalam pengolahan data pada tugas akhir ini penulis

menggunakan satu perangkat lunak (software) sebagai implementasi system yaitu

program Excel dalam masalah memperoleh hasil perhitungan.

5.2 Mengoperasikan Excel

Sebelum mengoperasikan software ini. Pastikan bahwa pada komputer Anda telah

terpasang program Excel. Setelah Komputer terpasang program, selanjutnya Anda

dapat menjalankan program ini dengan langkah- langkah sebagai berikut:

1. Setelah komputer dalam posisi hidup, klik tombol Start

(66)

3. Klik Microsoft Excel untuk memulai program, selanjutnya Excel akan

menampilkan buku kerja (Workbook) yang kosong

Selain cara tersebut di atas, ada cara lain untuk menjalankan program ini, yaitu jika

pada komputer anda telah diinstal office Shortcut, untuk memulai Excel akan

menampilkan buku kerja seperti gambar berikut:

Tampilan Excel di layar akan bervariasi tergantung pasa jenis monitornya yang

dipakai. Ketika Anda memulai program Excel, workbook Excel yang pertama disebut

Book 1. Jika anda membuka workbook lainnya saat itu juga, Excel secara otomatis

(67)

a) Aturan pengoperasian

Untuk mempermudah pengoperasian Excel dengan mudah ada beberapa istilah yang

perlu kami ulas, diantaranya adalah:

Klik : menekan tombol kiri mouse satu kali kemudian melepaskan.

Klik ganda : menekan dan melepas tombol kiri mouse sebanyak dua kali

secara cepat dan berurutan.

Geser : menekan dan menggeser tombol kiri mouse sambil menggerakan pointer mouse ke arah yang dikehendaki.

Ctrl + C : menekan tombol Ctrl, selanjutnya tekan C dan lepaskan kedua

tombol tersebut.

Icon : gambar grafis yang terdapat pada layar dan biasa diklik untuk

melakukan suatu perintah atau program tertentu.

b) Jendela Workbook

Bagian layar yang digunakan oleh suatu program disebut jendela. Jendela workbook

Ecxel terdidi dari banyak elemen windows.

c) Workbook

Workbook atau sering disebut buku kerja adalah dokumen yang terdapat pada Ecxel

yang setiap buku kerja terdiri dari tiga lembar kerja atau sering disebut sheet, dimana

(68)

Umunya jika Anda memulai Excel, sebuah workbook kosong akan terbuka dengan

judul sementara Book 1 kecuali jika Anda memulai Excel berserta sebuah file yang

telah ada.

Untuk membuka file-file tambahan, pilih New atau Open dari menu file atau

gunakan tombol Newbook dan Open pada Toolbar standart. Anda juga dapat

membuka workbook sebanyak yang di inginkan sampai computer anda kehabisan

memori. Workbook yang baru tampil di atas jendela workbook yang terakhir aktif dan

menjadi jendela workbook aktif.

d) Lembar kerja (Sheet)

Seperti dijelaskan di atas bahwa pada saat anda mengaktifkan Excel, maka secara

otomatis sebuah buku kerja akan tampil. Buku kerja tersebut terdiri atas tiga lembar

kerja atau Sheet. Lembar kerja Excel terdiri dari 256 kolom dan 65536 baris. Kolom

diberi nama A, B, C,…,Z dilanjutkan dengan AA, BB, CC,…,ZZ dan baris di tandai

dengan angka 1, 2, 3,……..sampai 65536.

Perpotongan antara kolom dan baris biasa disebut sel (cell). Sel diberi nama

menurut lokasi dan koordinat, misalnya Sel C20 ini artinya perpotongan antara kolom

pada C dengan baris ke 20, sel yang aktif ditandai dengan sel pointer/petunjuk sel.

Petunjuk sel yang terdapat pada lembar kerja dapat dipindahkan dari satu sel

ke sel yang lain. Untuk memindahkan satu sel ke sel yang lain gunakan tombol dalam

(69)

Tombol Keterangan

. . . . Menggeser pointer ke kiri, atas, kanan atau ke bawah suatu sel

HOME memindahkan pointer mouse ke awal baris

CTRL+HOME berpindah ke awal keja

PAGE DOWN berpindah satu layar ke bawah

PAGE UP berpindah satu layar ke atas

ALT+PAGE DOWN berpindah satu layar ke kanan

ALT+PAGE UP berpindah satu layar ke kiri

CTRL+F6 berpindah ke buku kerja atau jendela lain

CTRL+SHIF+F6 berpindah ke buku kerja atau jendela sebelumnya

F6 berpindah antara pane pada workbook yang di split

SHIF+F6 berpindah ke pane awal dalam workbook yang displit

TAB pindah antara sel yang tidak terprotek pada lembar kerja yang diprotek

END tanda panah berpindah antar blok baik di dalam maupun baris

HOME berpindah ke sel sebelah kiri

END berpindah ke sel di jendela sebelah kanan

e) Sel

Sel dibagi menjadi tiga kelompok, yaitu :

1. Sel relative

Sel relative adalah sel yang jika disalin akan menyasuaikan dengan tempat atau lokasi

(70)

2. Sel Semi Absolute

Sel semi absolute adalah sel tempat salah satu posisi (baris atau kolom) bertanda $.

Absoulute kolom misalnya pada sel A1 berisi $A1 artinya jika sel tersebut dikopi ke

posisi baru kolom tersebut akan selalu tetap sedangkan barisnya akan menyesuaikan.

Sedangkan absolute baris penulisannya adalah A$1, artinya jika sel tersebut dikopi,

baris yang bersangkutan akan selalu tetap sedangkan kolom akan menyesuaikan.

3. Sel Absolute

Sel absolute adalah sel baik kolom maupun barisnya terkunci, misalnya pada sel A1

berisi $A$9, artinya jika sel tersebut disalin atau dikopi baik baris ataupun kolom akan

terkunci.

f) Memasukan Program Excel

Setelah anda selesai bekerja dengan Excel dan ingin keluar dari Excel, pilih perintah

Exit dari menu File atau klik tombol close (X) dalam jendela Excel. Selanjutnya ,

Excel akan menanyakan apakah Anda akan menyimpan setiap perubahan yang telah

dilakukan pada setiap buku kerja yang terbuka. Jika Anda mengklik Yes, Anda dapat

menentukan nama file yang baru untuk setiap workbook yang belum disimpan

kemudian menyimpannya. Jika Anda mengklik No, setiap perubahan yang Anda

lakukan akan hilang ketika Anda keluar dari Excel. Mengklik tombol Cancel akan

(71)

5.3 Penggunaan Excel Pada Contoh Data

Pada tampilan di atas Anda dapat menyaksikan juga perhitungan moving average

pertama (S’t), moving average kedua (S”t), nilai konstanta (a), slope (b) dari analisa

proyeksi kendaraan bermotor (sebagai contoh analisa proyeksi Mobil Penumpang)

dengan cara :

a) S’t yaitu pada tahun 2002 (sel D4) dengan menggunakan rumus:

= SUM (C3:C4)/2

Untuk tahun berikutnya tinggal mengkopi rumus di atas.

b) S”t yaitu pada tahun 2003 (sel E5) dengan menggunakan rumus :

= SUM(D4:D5)/2

c) at besarnya bisa dicari pada tahun 2003 (sel F5) dengan menngunakan rumus :

(72)

Untuk tahun berikutnya tinggal mengkopi rumus di atas

d) b besarnya bisa dicari pada tahun 2003 (sel G5) dengan menggunakan rumus :

= (2*(D5-F5))/1

e) Nilai peramalannya {a+b(m)}bisa dicari pada tahun 2004 (sel H6) dengan

menggunakan rumus :

=F5+(E5*1)

(73)

Pada tampilan di atas Anda dapat menyaksikan juga hasil perhitungan kesalahan

meramal Mean Square Error dan Mean Absoulute Persentage Error dari analisis

proyek kendaraan bermotor (sebagai contoh nilai error untuk mobil penumpang)

dengan cara:

a) Mencari nilai error mulai tahun 2004 (sel E6) yaitu dengan menggunakan rumus :

=C6-D6

b) Nilai absoulute Error yaitu menunjukan absoulute dari nilai kesalahan meramal

(sel F6) yaitu dengan menggunakan rumus :

=ABS(E6)

c) Square Error menunjukkan kesalahan meramal dikuadratkan (sel G6) yaitu dengan

menggunakan rumus :

= G6^2

d) APE (Absoulute Persentage Error) menunjukan nilai tengah kesalahan percentage

absoulute (sel I 11) yaitu dengan menggunakan rumus :

(74)

BAB 5

IMPLEMENTASI SISTEM

5.1 Pengertian Implementasi Sistem

Implementasi Sistem adalah prosedur yang dilakukan untuk menyesuaikan desain

yang ada dalam desain system yang disetujui, menginstal dan memulai system baru

yang diperbaiki.

Tahapan implementasi merupakan tahapan penerapan hasil desain tertulis ke dalam

programming ( coding). Dalam pengolahan data pada tugas akhir ini penulis

menggunakan satu perangkat lunak (software) sebagai implementasi system yaitu

(75)

5.2 Mengoperasikan Excel

Sebelum mengoperasikan software ini. Pastikan bahwa pada computer Anda telah

terpasang program Excel. Setelah Komputer terpasang program, selanjutnya Anda

dapat menjalankan program ini dengan langkah- langkah sebagai berikut:

4. Setelah computer dalam posisi hidup, klik tombol Start

5. Pilih Programs

6. Klik Microsoft Excel untuk memulai program, selanjutnya Excel akan

menampilkan buku kerja( Workbook) yang kosong

Selain cara tersebut di atas, ada cara lain untuk menjalankan program ini, yaitu jika

pada computer anda telah diinstal office Shirtcut, untuk memulai Excel akan

(76)

Tampilan Excel di layar akan bervariasi tergantung pasa jenis monitornya yang

dipakai. Ketika Anda memulai program Excel, workbook Excel yang pertama disebut

Book 1. Jika anda membuka workbook lainnya saat itu juga, Excel secara otomatis

akan menamai book 2, demikian seterusnya.

g) Aturan pengoperasian

Untuk mempermudah pengomperasian Excel dengan mudah ada beberapa

istilah yang perlu kami ulas, diantaranya adalah:

Klik : menekan tombol kiri mouse satu kali kemudian melepaskan.

Klik ganda : menekan dan melepas tombol kiri mouse sebanyak dua kali

secara cepat dan berurutan.

Geser : menekan dan menggeser tombol kiri mouse sambil menggerakan

pointer mouse ke arah yang dikehendaki.

Ctrl + C : menekan tombol Ctrl, selanjutnya tekan C dan lepaskan kedua

tombol tersebut.

Icon : gambar grafis yang terdapat pada layar dan biasa diklik untuk

(77)

h) Jendela Workbook

Bagian layar yang digunakan oleh suatu program disebut jendela. Jendela

workbook Ecxel terdidi dari banyak elemen windows.

i) Workbook

Workbook atau sering disebut buku kerja adalah dokumen yang terdapat

pada Ecxel yang setiap buku kerja terdiri dari tiga lembar kerja atau sering

disebut sheet, dimana jumlah sheet ini bisa ditambah atau dikurangi sesuai

kebutuhan anda.

Umunya jika anda memulai Ecxel, sebuah workbook kosong akan

terbuka dengan judul sementara Book 1 kecuali jika anda memulai Excel

berserta sebuah file yang telah anda.

Untuk membuka file-file tambahan, pilih New atau Open dari menu

file atau gunakan tombol Newbook dan Open pada Toolbar standart.

Anda juga dapat membuka workbook sebanyak yang di inginkan

sampai computer anda kehabisan memori. Workbook yang baru tampil di

atas jendela workbook yang terakhir aktif dan menjadi jendela workbook

(78)

j) Lembar kerja (Sheet)

Seperti dijelaskan di atas bahwa pada saat anda mengaktifkan Excel, maka

secara otomatis sebuah buku kerja akan tampil. Buku kerja tersebut terdiri

atas tiga lembar kerja atau Sheet. Lembar kerja Excel terdiri dari 256

kolom dan 65536 baris. Kolom diberi nama A, B, C,…,Z dilanjutkan

dengan AA, BB, CC,…,ZZ dan baris di tandai dengan angka 1, 2,

3,……..sampai 65536.

Perpotongan antara kolom dan baris biasa disebut sel (cell). Sel diberi

nama menurut lokasi dan koordinat, misalnya Sel C20 ini artinya

perpotongan antara kolom pada C dengan baris ke 20, sel yang aktif

ditandai dengan sel pointer/petunjuk sel.

Petunjuk sel yang terdapat pada lembar kerja dapat dipindahkan dari

satu sel ke sel yang lain. Untuk memindahkan satu sel ke sel yang lain

gunakan tombol dalam keyboard seperti yang berikut ini :

Tombol Keterangan

. . . . Menggeser pointer ke kiri, atas, kanan

atau ke bawah suatu sel

HOME memindahkan pointer mouse ke awal

baris

CTRL+HOME berpindah ke awal keja

PAGE DOWN berpindah satu layar ke bawah

(79)

ALT+PAGE DOWN berpindah satu layar ke kanan

ALT+PAGE UP berpindah satu layar ke kiri

CTRL+F6 berpindah ke buku kerja atau jendela lain

CTRL+SHIF+F6 berpindah ke buku kerja atau jendela sebelumnya

F6 berpindah antara pane pada workbook

yang di split

SHIF+F6 berpindah ke pane awal dalam workbook yang

displit

TAB pindah antara sel yang tidak terprotek

pada lembar

kerja yang diprotek

END tanda panah berpindah antar blok baik di dalam maupun baris

HOME berpindah ke sel sebelah kiri

(80)

k) Sel

Sel dibagi menjadi tiga kelompok, yaitu :

4. Sel relative

Sel relative adalah sel yang jika disalin akan menyasuaikan dengan

tempat atau lokasi yang baru.

5. Sel semiabsoulute

Sel semiabsoulte adalah sel tempat salah satu posisi (baris atau

kolom) bertanda $. Absoulute kolom misalnya pada sel A1 berisi

$A1 artinya jika sel tersebut dikopi ke posisi baru kolom tersebut

akan selalu tetap sedangkan barisnya akan menyesuaikan.

Sedangkan absouluet baris penulisannya adalah A$1, artinya jikia

sel tersebut dikopi, baris yang bersangkutanakan selalu tetap

sedangkan kolom akan menyesuaikan.

6. Sel absoulute

Sel absoulute adalah sel baik kolom maupun barisnya terkunci,

misalnya pada sel A1 berisi $A$9, artinya jika sel tersebut disalin

atau dikopi baik baris ataupun kolom akan terkunci.

l) Memasukan Program Excel

Setelah anda selesai bekerja dengan Excel dan ingin keluar dari Excel,

pilih perintah Exit dari menu File atau klik tombol close (X) dalam jendela

Excel. Selanjutnya , Excel akan menanyakan apakah anda akan

(81)

yang terbuka. Jika anda mengklik Yes, anda dapat menentukan nama file

yang baru untuk setiap workbook yang belum disimpan kemudian

menyimpannya. Jika anda mengklik No, setiap perubahan yang anda

lakukan akan hilang ketika anda keluar dari Excel. Mengklik tombol

Cancel akan membatalkan perintah Exit dan mengembalikan anda dalam

program Excel.

(82)

Pada saat di atas anda dapat menyaksikan juga perhitungan moving average

pertama (S’t), moving average kedua (S”t), nilai konstanta (a), slope (b) dari

analisa proyeksi kendaraan bermotor (sebagai contoh analisa proyeksi

penumpang) dengan cara :

f) S’t yaitu pada tahun 2002 (sel D4) dengan menggunakan rumus:

=SUM (C3:C4)/2

g) S”t yaitu pada tahun 2003 (sel E5) dengan menggunakan rumus :

=SUM(D4:D5)/2

h) a besarnya bisa dicari pada tahun 2003 (sel F5) dengan

menngunakan rumus :

=(2*D5)-E5

i) b besarnya bisa dicari pada tahun 2003 (sel G5) dengan

menggunakan rumus :

=(2*(D5-F5))/1

j) Nilai peramalannya {a+b(m)}bisa dicari pada tahun 2004 (sel H6)

dengan menggunakan rumus :

=F5+(E5*1)

(83)

5.4 Menghitung Nilai Kesalahan pada contoh Data

Pada tampilan di atas anda dapat menyaksikan juga hasil perhitungan kesalahan

meramal Mean Square Error dan Mean Absoulute Persentage Error dari analisis

proyek kendaraan bermotor (sebagai contoh nilai error untuk mobil penumpang)

dengan cara:

e) Mencari nilai error mulai tahun 2004 (sel E6) yaitu dengan menggunakan

rumus :

=C6-D6

f) Nilai absoulute Error yaitu menunjukan absoulute dari nilai kesalahan

(84)

=ABS(E6)

g) Square Error menunjukkan kesalahan meramal dikuadratkan (sel G6) yaitu

dengan menggunakan rumus :

=G6^2

h) APE (Absoulute Persentage Error) menunjukan nilai tengah kesalahan

percentage absoulute (sel I 11) yaitu dengan menggunakan rumus :

(85)

BAB 6

KESIMPULAN

6.1 Kesimpulan

Berdasarkan hasil pengelohan data dan analisis data yang dilakukan

sebelumnya pada bab 4 maka kesimpulan yang diperoleh aadalah sebagai

berikut :

1. Dari hasil perhitungan jumlah kendaraan bermotor menurut

jenisnya, dapat dilihat perkembangan jumlah mobil penumpang,

mobil gerobak, bus, dan sepeda motor mengalami peningkatan pada

tahun 2012,yaitu mobil penumpang sebanyak 12807,75 unit, mobil

gerobak sebanyak 15182,75 unit, bus sebanyak 821,75 unit, dan

(86)

2. Penulis dapat mengetahui jumlah kendaraan bermotor mana yang

paling banyak terdapat di kotamadya Binjai pada tahun 2012, yaitu

(87)

DAFTAR PUSTAKA

Assaori, Sofyan.1984.Teknik dan Metode Peramalan. Jakarta: Fakultas Ekonomi

Universitas Indonesia.

Haymans, Adler. 1989. Tekhnik Peramalan Bisnis dan Ekonomi. Jakarta: Rineka

Cipta.