Hamiltonian Dengan Beberapa loop yang Diletakkan Berdekatan

Akelbek, Mahmud dan Kirkland, Steve. 2008. Coefficient of Egrodicity and The Scrambling Index. Linear Algebra And Its Application. 430: 1111-1130.

Akelbek, Mahmud dan Kirkland, Steve. 2009. Primitive digraphs with The Largest Scrambling Index. Linear Algebra And Its Application. 430: 1099-1110.

Chen, Shexi dan Liu, Bolian. 2010. The Scrambling Index Of Symmetric Primi-tive Matrices. Linear Algebra Application And Its Application. 433: 1110-1126.

Cho, Hyuk Han., Kim, Suh-Ryung dan Nam, Yunsun. 2000. The m-Step Comp-etition Graf of Digraf. Discrete Applied Mathematics. 105: 115-127.

Kim, Kyung Hwa. 2010. Generalized Competition Index of Primitive digraph. Linear Algebra Application And Its Application. 433: 72-79.

Shao, Yanling., Gao, Yubin dan Li, Zhongshan. 2012. The M-Competition Indices Of Symmetric Primitive Digraphs Whitout Loops. A Publication of The International Linear Algebra Society. Vol 23: 457-472.

West, B Douglas. 2002. Introduction to Graph Theory: Second Edition. Univer-sity of Illnois, Urbana.

18

BAB 3

METODOLOGI PENELITIAN

Pada bagian ini dipaparkan langkah-langkah untuk memperoleh batas atas m -kompetisi indeks dari digraf primitif dengan n buah titik v1, v2,· · · , vn di digraf

D yang terdiri atas lingkaran hamiltonian v1 → v2 → v3 → · · · → vn → v1 dan s buah loop diletakkan berdekatan yang disimbolkan dengan sDn. Adapun langkah-langkah yang dilakukan adalah

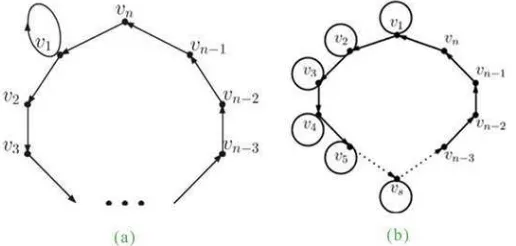
Gambar 3.1. (a) Digraf 1Dn (b) Digraf sDn

1. Ditentukan bentuk rumus umum dari batas atasm-kompetisi indeks untuk digraf 1Dn yaitu sebuah digraf terdiri atas lingkaran Hamiltonian v1 →

v2 → v3 → · · · → vn → v1 dan sebuah loop diletakkan di titik v1 yang diilustrasikan pada gambar 3.1.a. Adapun cara yang dilakukan yaitu,

1.1 Menentukan nilai batas atas m-kompetisi indeks dari 1D3 hingga 1Dn lalu menentukan bentuk rumus umumnya yang berbentuk km(1Dn) ≤

f(m, n).

2. Ditentukan bentuk rumus umum dari batas atasm-kompetisi indeks untuk digrafsDnyaitu sebuah digraf terdiri atas lingkaran Hamiltonianv1 →v2 →

v3 → · · · →vn →v1 dan s buah loop diletakkan pada titik v1, v2, · · ·, dan

vs seperti diilustrasikan pada gambar 3.1.b. Adapun cara yang dilakukan yaitu,

2.1 Menentukan nilai batas atas m-kompetisi indeks dari 2Dn hingga sDn lalu menentukan bentuk rumus umumnya yang berbentuk km(sDn) ≤

f(m, n, s)

2.2 Membuktikan bentuk rumus umum dari batas atasm-kompetisi indeks dari digraf sDn. Yaitu, cukup memperlihatkan bahwa untuk masing-masing pasangan titik vi dan vj di sDn terdapat sebuah jalan dengan panjangf(m, n, s) yang menghubungkan titikvi ke masing-masing titik

20

BAB 4

BATAS ATAS M-KOMPETISI INDEKS DARI DIGRAF HAMILTONIAN DENGAN BEBERAPA BUAH LOOP

Pada bagian ini akan dipaparkan hasil penelitian dari digraf sDn yaitu digraf lingkaran hamiltonian dengan s buah loop yang diletakkan saling berdekatan. Hal-hal yang akan dipaparkan adalah batas atas darim-kompetisi indeks dari di-graf1Dn dilanjutkan dengan batas atas digrafsDn dengann∈Z+ dan 1 ≤s≤n dilengkapi dengan pembuktian untuk masing-masing kasus.

4.1 Batas Atas M-kompetisi Indeks Digraf Hamiltonian 1 buah loop

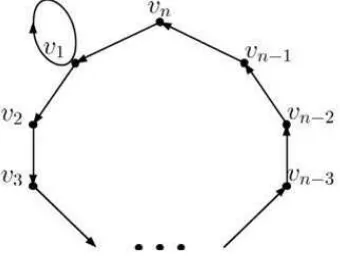
Gambar 4.1. Digraf 1Dn

Didefinisikan sebuah digraf 1Dn seperti pada gambar 4.1 yaitu digraf dengan se-buah lingkaran hamiltonian v1 → v2 → v3 → · · · → vn → v1 dengan sebuah loop yang diletakkan pada titik v1. Untuk mendapatkan batas atas m-kompetisi indeks dari digraf 1Dn dan proses untuk mendapatkan buktinya semua dilakukan secara induksi yaitu mengambil seluruh informasi dari m-kompetisi indeks dari digraf 1D3 hingga 1Dt untuk t= 1,2,3,· · · , n.

Teorema 4.1. Jika n ≥ 3 dan 1 ≤ m ≤ n dimana n, m adalah bilangan bulat maka

Bukti. Dari definisi digraf 1Dn, setiap titik pada digraf 1Dn terletak di dalam sebuah lingkaran dan panjang semua lingkaran yang ada di 1Dn adalah 1 dan n yang mengakibatkan digraf1Dn terhubung kuat dan pembagi persekutuan terke-cil untuk setiap panjang lingkaran di 1Dn adalah 1. Sehingga, digraf 1Dn adalah digraf primitif.

Selanjutnya, akan dibuktikan km(1Dn) ≤ m+n−2, yaitu cukup diperlihatkan bahwa untuk setiap titik vi di 1Dn terdapat jalan dari titikvi ke masing-masing titik vt, t= 1,2,3,· · · , m dengan panjang m+n−2.

Semua komposisi jalanWvi,vt akan diperlihatkan dalam 2 kasus berdasarkan letak titik asal vi. Sehingga semua komposisi jalannya adalah sebagai berikut

Kasus 1. Titikvi =v1.

Jalan yang dimulai dari titik vi = v1, lalu mengitari loop v1 → v1 sebanyak

m+n−1−t kali, lalu bergerak ke titik vt sepanjang lintasan Pv1,vt dengan pan-jangt−1 adalah sebuah jalan dari titikv1 ke titikvt, 1≤t ≤mdengan panjang

m+n−2.

Kasus 2. Titikvi terletak di lintasan v2 →v3 → · · · →vn.

Jalan yang dimulai dari titikvi, lalu bergerak ke titik v1 sepanjang lintasan Pvi,v1 dengan panjangn+ 1−i, lalu mengitari loopv1 →v1 sebanyak m+i−t−2 kali, lalu bergerak ke titik vt sepanjang lintasan Pv1,vt dengan panjang t−1 adalah sebuah jalan dari titik vi ke titik vt, 1≤t ≤m dengan panjang m+n−2.

22

4.2 Batas Atas M-kompetisi Indeks Digraf Hamiltonian s buah loop

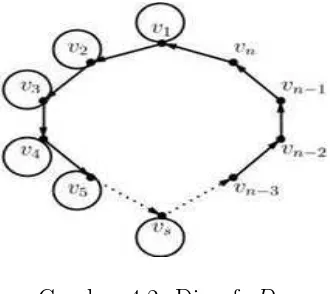
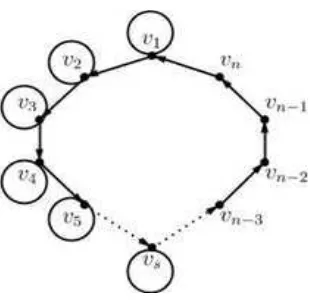
Gambar 4.2. Digraf sDn

Didefinisikan sebuah digraf sDn seperti pada gambar 4.2 yaitu digraf dengan se-buah lingkaran hamiltonian v1 → v2 → v3 → · · · → vn → v1 dengan s buah loop yang diletakkan pada titik v1, v2, v3, v4,· · · , vs. Untuk mendapatkan batas atasm-kompetisi indeks dari digrafsDn dan proses untuk mendapatkan buktinya semua dilakukan secara induksi.

Teorema 4.2. Untuk s sebuah bilangan bulat dimana 1 < s ≤ n. Jika n ≥ 3

dan 1≤m≤n dimana m, n adalah bilangan bulat maka

km(sDn)≤n+m− ⌈s+ 2 2 ⌉

Bukti. Dari definisi digraf sDn, setiap titik pada digraf sDn terletak di dalam sebuah lingkaran dan panjang semua lingkaran yang ada di sDn adalah 1 dan n yang mengakibatkan digraf sDn terhubung kuat dan pembagi persekutuan terke-cil untuk setiap panjang lingkaran di sDn adalah 1. Sehingga, digraf sDn adalah digraf primitif.

Selanjutnya, akan dibuktikankm(sDn)≤n+m−⌈s+2

2 ⌉, yaitu cukup diperlihatkan bahwa untuk setiap pasangan titik (vi, vj) di sDn terdapat jalan dari titik vi ke masing-masing titikvtdan vj ke masing-masing titikvt,t= 1,2,3,· · ·, m dengan panjang n+m− ⌈s+2

Semua komposisi jalan Wvi,vt dan Wvj,vt akan diperlihatkan dalam 3 buah kasus berdasarkan letak titik asal vi dan vj. Sehingga semua komposisi jalannya adalah sebagai berikut.

Kasus 1. Pasangan titik (vi, vj) dimana titik vi dan vj terletak di lintasan

vs→vs+1 → · · · →vn.

Jalan yang dimulai dari titikvi, lalu bergerak ke titik v1 sepanjang lintasan Pvi,v1 dengan panjang n−i+ 1 lalu mengitari loop v1 →v1 sebanyak m+i− ⌈s

+2 2 ⌉ −t kali, lalu bergerak ke titik vt sepanjang lintasan Pvt,v1 dengan panjang t − 1 adalah sebuah jalan dari titik vi ke titik vt dimana 1 ≤ t ≤ m dengan pan-jang n+m− ⌈s+2

2 ⌉ dan jalan yang dimulai dari titik vj, lalu bergerak ke titik v1 sepanjang lintasan Pvj,v1 dengan panjang n−j + 1 lalu mengitari loop v1 → v1 sebanyak m+j− ⌈s+2

2 ⌉ −tkali, lalu bergerak ke titik vt sepanjang lintasanPvt,v1 dengan panjangt−1 adalah sebuah jalan dari titikvj ke titikvtdimana 1≤t≤m dengan panjang n+m− ⌈s+2

2 ⌉.

Akibatnya, dengan menggunakan jalan tersebut, setiap pasangan titik (vi, vj) di-mana vi dan vj terletak di lintasan vs+1 →vs+2 → · · · → vn, terdapat jalan dari

24

Jika m > n−j+ 1, maka jalan yang dimulai dari titik vi, lalu bergerak ke titik

vj sepanjang lintasan Pvi,vj dengan panjang j −i, lalu mengitari loop vj → vj sebanyak n+m+i−t− ⌈s+2

2 ⌉ kali, lalu bergerak ke titik vt sepanjang lintasan

Pvj,vt dengan panjang t−j untuk j ≤t≤n dan jalan yang dimulai dari titik vi, lalu bergerak ke titik v1 sepanjang lintasan Pvi,v1 dengan panjangn−i+ 1, lalu mengitari loop v1 →v1 sebanyak m+i−t− ⌈s+2₂ ⌉ kali, lalu bergerak ke titik vt sepanjang lintasanPv1,vt dengan panjangt−1 untuk 1 ≤t≤m−n+j−1 adalah jalan dari titik vi ke titikvt dengan panjang n+m− ⌈s+22 ⌉.

Jalan yang dimulai dari titik vj, lalu mengitari loop vj → vj sebanyak n+m− ⌈s+2

2 ⌉+j−tkali, lalu bergerak ke titikvtsepanjang lintasanPvj,vt dengan panjang

t−j untuk j ≤ t≤ n dan jalan yang dimulai dari titik vj, lalu bergerak ke titik

v1 sepanjang lintasanPvj,v1 dengan panjangn−j+ 1, lalu mengitari loopv1 →v1 sebanyak m+j−t− ⌈s+2

2 ⌉kali, lalu bergerak ke titik vt sepanjang lintasanPv1,vt dengan panjang t−1 untuk 1 ≤ t ≤ m−n+j −1 adalah jalan dari titik vj ke dan jalan yang dimulai dari titik vj, lalu bergerak ke titik vi sepanjang lintasan

Pvj,vi dengan panjangn−j+i, lalu mengitari loopvi →visebanyakm−⌈ s+2

2 ⌉+j−t kali, lalu bergerak ke titikvt sepanjang lintasanPvi,vt dengan panjangt−iadalah jalan dari titikvj ke titikvtuntuki≤t≤m+i−1 dengan panjangn+m−⌈s+22 ⌉.

Jika m > n −i+ 1, maka jalan yang dimulai dari titik vi, lalu mengitari loop

vi → vi sebanyak n+m− ⌈s +2

2 ⌉+i−t kali, lalu bergerak ke titik vt sepanjang lintasan Pvi,vt dengan panjang t−i untuk i≤ t≤ n dan jalan yang dimulai dari titikvi, lalu bergerak ke titikv1sepanjang lintasanPvi,v1 dengan panjangn−i+1, lalu mengitari loop v1 →v1 sebanyak m+i−t− ⌈s+2₂ ⌉, lalu bergerak ke titik vt sepanjang lintasanPv1,vt dengan panjangt−1 untuk 1≤t≤m−n+i−1 adalah jalan dari titik vi ke titikvt dengan panjang m+n− ⌈s+22 ⌉.

dengan panjangn−j+i, lalu mengitari loopvi →vi sebanyakn+m+j−t−⌈s +2

2 ⌉ kali, lalu bergerak ke titik vt sepanjang lintasanPvi,vt dengan panjangt−i untuk

i≤t≤n dan jalan yang dimulai dari titik vj, lalu bergerak ke titik v1 sepanjang lintasan Pvj,v1 dengan panjang n−j + 1, lalu mengitari loop v1 → v1 sebanyak m+j−t− ⌈s+2

2 ⌉ kali, lalu bergerak ke titik vt sepanjang lintasan Pv1,vt dengan panjang t−1 untuk 1 ≤ t ≤ m−n+i−1 adalah jalan dari titik vi ke titik vt dengan panjang n+m− ⌈s+2

2 ⌉.

Akibatnya, dengan menggunakan jalan tersebut, setiap pasangan titik (vi, vj) di-mana titik vi dan titik vj terletak di lintasan vs+1 → vs+2 → · · · → vn terdapat

Komposisi jalan pada kasus ini terbagi ke dalam 2 subkasus berdasarkan letak posisi titik vi. Yaitu,

Subkasus 3.1 Untuk titikvi terletak di lintasan v1 →v2 → · · · →v_⌈s+1 2 ⌉ Jika m ≤ n − ⌈s

2⌉, maka jalan yang dimulai dari titik vi, lalu bergerak ke titik v_⌈s+1 adalah jalan yang menghubungkan titikvi ke titikvtdengan panjangm+n−⌈s+22 ⌉ dan jalan yang dimulai dari titik vj lalu menuju titik v⌈s+1

26 jalan yang dimulai dari titik vi, lalu bergerak ke titikv1 sepanjang lintasan Pvi,v1 sepanjang n− i+ 1 lalu mengitari loop v1 → v1 sebanyak m − ⌈s+2₂ ⌉+i−t, lalu bergerak ke titik vt sepanjang lintasan Pv1,vt dengan panjang t −1 untuk 1≤t≤m+⌈s

2⌉ −nadalah jalan yang menghubungkan titik vi ke titikvt dengan panjang m+n− ⌈s+2

2 ⌉.

Jalan yang dimulai dari titikvj, lalu menuju titikv_⌈s+1

2 ⌉sepanjang lintasanPvj,v⌈s+1₂ ⌉

2 ⌉ −t, lalu bergerak ke titik vt sepanjang lintasanPvt,v1 dengan pan-jang t−1 untuk 1≤t ≤m+⌈s

2⌉ −n adalah jalan yang menghubungkan titikvj ke titik vt dengan panjang m+n− ⌈s+22 ⌉.

Akibatnya, dengan menggunakan jalan tersebut, setiap pasangan titik (vi, vj) pa-da subkasus 3.1 terpa-dapat jalan pa-dari titik vi ke masing-masing titik vt dan vj ke masing-masing titikvt,⌈s+1

2 ⌉ ≤t≤ ⌈ s+1

2 ⌉+m−1 dengan panjangm+n− ⌈ s+2

2 ⌉.

Subkasus 3.2 Untuk titikvi terletak di lintasan v_⌈s+3 2 ⌉→v⌈

s+5

2 ⌉→ · · · →vs Jalan yang dimulai dari titik vi, lalu bergerak menuju titik v1 sepanjang lin-tasan Pvi,v1 dengan panjang n + 1 − i, lalu mengitari loop v1 → v1 sebanyak m+i− ⌈s+2

2 ⌉ −t, lalu bergerak ke titik vt sepanjang lintasan Pv1,vt dengan pan-jangt−1 adalah sebuah jalan dari titik vi ke titikvt, 1≤t≤m dengan panjang

m+n− ⌈s+2

2 ⌉ dan jalan yang dimulai dari titikvj, lalu bergerak menuju titik v1 sepanjang lintasan Pvj,v1 dengan panjang n+ 1−j, lalu mengitari loop v1 → v1

pa-da subkasus 3.2 terpa-dapat jalan pa-dari titik vi ke masing-masing titikvt, 1≤t ≤m danvj ke masing-masing titikvt, 1≤t≤mdengan panjangm+n−⌈s+22 ⌉. Sehing-ga, dari kasus 1, kasus 2, dan kasus 3, terbukti bahwa km(sDn)≤m+n− ⌈s+2

BAB 5

KESIMPULAN DAN SARAN

5.1 Kesimpulan

Penelitian ini membahas mengenai batas atas m-kompetisi indeks dari kelas di-graf sDn yaitu digraf lingkaran hamiltonian terdiri dari n titik dan s loop yang diletakkan berdekatan. Hasil yang diperoleh adalah sebagai berikut :

1. Jika n ≥3 dan 1≤m ≤n dimanan, m adalah bilangan bulat maka

km(1Dn)≤m+n−2

2. Jika n ≥3 dan 1≤m ≤n dimanam, n adalah bilangan bulat. Untuk sebuah bilangan bulat positif 1< s≤n maka

km(sDn)≤n+m− ⌈s+ 2 2 ⌉

Dari hasil tersebut, diperoleh bahwa digraf 1Dn adalah digraf yang memiliki batas atas m-kompetisi indeks yang terbesar.

5.2 Saran

BAB 2

DIGRAF PRIMITIF

Pada bagian ini, peneliti akan menjelaskan bahwa digraf kDn merupakan sebuah digraf primitif. Penjelasan tersebut diperkuat dengan memaparkan beberapa definisi digraf dan beberapa unsur-unsur lainnya. Lalu dilanjutkan dengan penje-lasan digraf dikatakan primitif, Definisi dari pembagi persekutuan terbesar, dan pemaparan dari m-kompetisi indeks.

2.1 Definisi Digraf

Digraf D adalah sebuah objek yang terdiri atas sebuah himpunan V(D) berjum-lah n buah dan tak kosong yang unsur-unsurnya merupakan semua titik vi untuk

i = 1,2,3,· · · , n di digraf D dan sebuah himpunan A(D) yaitu sebuah pasan-gan berurut V × V yang terdiri atas semua unsur (vi, vj) dimana vi ∈ V dan

vj ∈ V. Sehingga secara umum, digraf merupakan sebuah objek yang tersusun atas elemen-elemen titik yang tidak kosong dimana setiap titik dapat dihubungkan oleh sebuah penghubung berarah yang dinamakan busur.

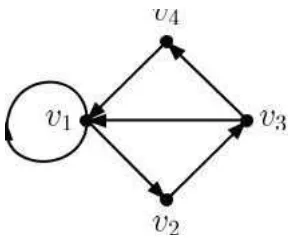
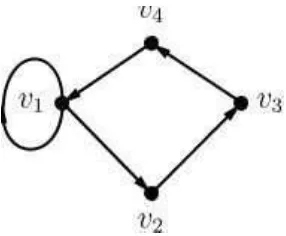
Sebagai contoh, gambar 2.1 akan menjadi ilustrasi pendukung untuk memahami pengertian dari digraf D. diberikan sebuah digraf D seperti pada gambar 2.1

7

Maka digraf D terdiri atas himpunan V(D) = {v1, v2, v3, v4} dan himpunan

A(D) = {(v1, v1),(v1, v2),(v2, v3),(v3, v1),(v3, v4),(v4, v1)}.

Terdapat beberapa istilah penting yang mendukung dalam penelitian ini,

a. Jika v ∈ V(D) maka himpunan k-step out-neighborhood dari titik v didefin-isikan sebagai N+_(Dk _{: v) = {x ∈ V(G) : v →}k _{x} atau semua titik} tu-juan dari titik v di D dengan panjang jalan k. Seperti pada contoh diatas, perhatikan titik v1, N+_{(D : v1) = {v1, v2} , N}+_(D2 _{: v1) = {v1, v2, v3},} N+_(D3 _{:v1) = {v1, v2, v3, v4} .}

b. Jalan pada digrafDmerupakan sebuah barisan antara busur di Ddinotasikan dengan W tersusun atas barisan (u, v1),(v1, v2),· · · ,(vn−1, vn), (vn, v). bi-asanya penulisan pada barisan Wuv dapat diilustrasikan dengan u → v1 →

v2 → v3 → · · · → vn → v dan panjang dari jalan Wuv dinotasikan dengan

ord(Wuv). Seperti pada contoh diatas, beberapa jalan untuk titik asal adalah

v2 dan titik tujuan v1 yaitu (1) Wv2,v1 : v2 → v3 → v1, (2) Wv2,v1 : v2 →

v3 → v4 → v1, (3) Wv2,v1 : v2 → v3 → v4 → v1 → v1 → v1. Perhatikan

bah-wa banyaknya jalan dengan titik asal v2 dan titik tujuan v1 dapat lebih dari satu selama ada busur yang menghubungkan setiap titik yang dikehendaki. Untuk jalan pada poin 1, panjangnya adalah ord(Wv2,v1) = 2, panjang jalan

pada poin 2 adalah ord(Wv2,v1) = 3, dan panjang jalan pada poin 3 adalah

ord(Wv2,v1) = 5

c. Lintasan pada digraf D merupakan sebuah jalan tanpa perulangan titik dino-tasikan dengan P. Pada dasarnya jalan di digraf D tidak memperhatikan adanya perulangan titik pada busurnya, tetapi pada lintasan sebuah barisan busur tidak memperbolehkan adanya perulangan titik pada titik asal hingga titik tujuan. Perhatikan contoh jalan pada bagian c, jalan pada poin 1 dan poin 2 merupakan sebuah lintasan tetapi jalan pada poin 3 bukan merupakan lintasan.

d. Lingkaran pada digraf D merupakan sebuah lintasan tertutup yang tersusun atas barisan (u, v1),(v1, v2),· · · ,(vn−1, vn),(vn, u). Perhatikan contoh pada gambar 2.1, Wv1v1 : v1 → v2 → v3 → v1 merupakan lingkaran pada digraf

e. Lingkaran Hamiltonian pada digraf D merupakan sebuah lintasan tertutup dimana lintasan tersebut melalui semua titik yang ada diD. Pada gambar 2.1,

Wv1,v1 :v1 →v2 →v3 →v4 →v1.

f. Loop pada digraf D merupakan sebuah lintasan tertutup dengan panjang 1. Pada gambar 2.1,Wv1,v1 :v1 →v1 merupakan loop.

g. jarak antara 2 buah titik u dan w di D adalah panjang jalan terpendek yang bisa ditempuh oleh titik awal u ke titik tujuan w yang dinotasikan dengan

d(u, w).

h. Girthpada sebuah digraf D adalah panjang dari sebuah lingkaran terpendek dari semua lingkaran di D. Maka, sebuah digraf D yang memiliki loop mem-punyai girthsebesar 1.

Sebuah digraf dapat direpresentasikan ke dalam sebuah matriks ketetanggan dengan definisi matriks bujursangkar A = (aij) dengan besar ordo A merupakan banyak titik pada digraf D yang setiap entri pada matriks A adalah

aij =

berdasarkan definisi digraf, tidak ada jaminan bahwa aij =aji untuk semua 1≤

i, j ≤n. Ini mengakibatkan bahwa representasi matriks ketetanggaan di digrafD

bukan merupakan matriks simetris. Perhatikan digraf pada contoh 5, Representasi matriks ketetanggaan untuk digraf pada gambar 2.1 adalah

A=

9

2.1 merupakan matriks non negatif. untuk matriks A5 _yaitu,

A5 =

merupakan matriks positif, karena tidak ada entri pada matriksA5 yang bernilai 0.

Selanjutnya pengertian dari sebuah digraf yang dikatakan terhubung kuat. Sebuah digraf D dikatakan terhubung kuat jika dan hanya jika setiap pasang

u, v ∈ V(D), terdapat sebuah lintasan berarah dari titik u ke v dan dari titik v

ke u. Perhatikan contoh gambar 2.2 berikut,

e. pasangan titik (v1, v3) terdapat sebuah lintasan yaitu Pv2,v4 : v2 → v3 → v4

dan Pv4,v2 :v4 →v1 →v2

f. pasangan titik (v1, v3) terdapat sebuah lintasan yaitu Pv3,v4 : v1 → v3 → v4

dan Pv4,v3 :v4 →v1 →v2 →v3

Karena setiap pasang (vi, vj) di digrafDv1 memenuhi definisi dari terhubung kuat,

maka digraf Dv1 merupakan sebuah digraf yang terhubung kuat.

Teorema 2.1: Andaikan sebuah digrafDdenganntitikv1, v2,· · · ,danvn, setiap

titik diD terletak dalam sebuah lingkaran jika dan hanya jika digraf Dterhubung kuat

Bukti. Diberikan sebuah digraf D dengan n titik v1, v2,· · · , dan vn. Perhatikan

karena semua titikvi diDuntuki= 1,2,· · · , nberada di sebuah lingkaran, maka dapat dibentuk sebuah jalan dimisalkan dengan Wv1,v1 : v1 → v2 → v3 → · · · →

vn → v1. Didapat bahwa untuk sembarang pasangan vi, vj di D, maka didapat lingkaran dengan jalan yaitu Wvi,vi danWvj,vj. KarenaWvi,vi dan Wvj,vj ada,

ma-ka pasti terdapat sebuah jalan darivi kevj dengan memanfaatkan lingkaranWvi,vi

dan sebuah jalan dari vj ke vi dengan memanfaatkan lingkaran Wvj,vj. Sehingga

karena setiap pasang titik vi, vj di D mempunyai jalan dari titik vi kevj dan dari titik vj kevi maka digraf D terhubung kuat.

Akan dibentuk lingkaran dengan setiap titik di D terletak didalamnya. Kare-naDterhubung kuat, maka setiap pasang titik (u, v) diD, terdapat sebuah jalan berarah sederhana dari ukev dan dariv keu. Sehingga dengan menghubungkan jalan berarah pada jalanWu,v denganWv,u maka akan terbentuk sebuah lingkaran

Wu,uyang memuat seluruh titik di D. Ini merupakan akhir dari pembuktian pada teorema ini.

2.2 Definisi digraf Primitif

11

merupakan sebuah digraf primitif karena setiap pasangan titik (vi, vj) diD mem-punyai jalan dengan panjang yang sama dengan panjang jalan terpendek adalah 6. Sebuah digraf D dikatakan primitif jika dan hanya jika D adalah terhubung kuat dan pembagian persekutuan terkecil untuk setiap lingkaran di D adalah 1 (Shao et al, 2012).

Proposisi 2.2 : (Akelbek dan Kirkland, 2008) Andaikan D merupakan sebuah digraf primitif dengan n titik dan s merupaka girth pada D. Maka exp(D) ≤ n+s(n−2).

Proposisi 2.3: Andaikan D merupakan sebuah digraf primitif dengan n titik dan memiliki loop didalamnya. Maka exp(D)≤2n−2

Bukti. Dengan menggunakan proposisi 2.2. Diketahui bahwa loop merupakan lingkaran terpendek di Dsehingga girthpada D adalah 1. Maka dengan mensu-btitusikan s= 1 ke pertidaksamaan di proposisi 2 didapat exp(D)≤2n−2

2.3 Digraf sDn Sebagai Digraf Primitif

Setelah beberapa pemaparan tentang bagaimana cara sebuah digraf dikatakan primitif maka akan dibuktikan bahwa digraf sDn merupakan sebuah digraf prim-itif. Didefinisikan bahwa digraf sDn adalah digraf dengan lingkaran Hamiltonian dimana terdapat s buah loop yang diletakkan saling berdekatan. Sehingga,

Akibat 2.7 Jika k merupakan banyak loop yang diletakkan berdekatan dan n merupakan banyak titik di sDn Maka sDn merupakan digraf primitif.

Bukti. Untuk membuktikan bahwasDnmerupakan digraf primitif hanya perlu dibuktikan bahwasDnmerupakan digraf yang terhubung kuat dan semua panjang setiap lingkaran pada sDn saling relatif prima. Berdasarkan teorema 2.1 digraf

sDn merupakan digraf yang terhubung kuat. Perhatikan bahwa semua lingkaran yang dimiliki digraf sDn adalah v1 → v1, v2 → v2, v3 → v3, · · ·, vi → vi dan

2.4 Definisi M-Kompetisi Indeks

Definisi 2.8 : Untuk bilangan bulat positif m dan n dengan 1 ≤ m ≤ n, didefinisikan m-kompetisi indeks dari sebuah digraf primitif D, dinotasikan den-gan km(D) adalah bilangan bulat positif terkecil k sehingga untuk setiap pasang x dan y, terdapat m titik berbeda yaitu v1, v2, v3,· · · , vm sehingga x

k

→ vi dan

y →k vi, dalam artian ada jalan Wxvi dan Wyvi dengan panjang yang sama untuk setiap i= 1,2,· · · , m.

Sebelum memasuki contoh, diperkenalkan terlebih dahulu beberapa definisi pem-bantu dalam pengerjaan m-kompetisi indeks.

Definisi 2.9 : MisalkanD merupakan sebuah digraf primitif. Indeksm-kompetisi lokal pada sebuah titik x dan y di D adalah panjang jalan terpendek k untuk sebuah pasangan titik (x, y) sehingga terdapat m titik berbeda v1, v2, v3,· · · , vm

dari x→vt dan y→vt untuk t = 1,2,3,· · · , m, dinotasikan dengan

km(D:x, y) = min{k|x→k vtdan y k

→vt, t≥k}

Maka dari definisi 2.9, nilai dari m-kompetisi indeks km(D) dari digrafD adalah

km(D) = max

x,y∈V(D)km(D:x, y)

sehingga dari definisi 2.8, untuk setiap m= 1,2,3,· · · , n didapat

km(D :x, y)≤km(D)

Definisi 2.10 : k-step common out-neighborhood titik x dan y adalah semua him-punan titik vt di D terdiri atas n buah titik yang bisa dikunjungi dengan panjang

13

dari D. Maka,

k(D) = k1(D)≤k2(D)≤k3(D)≤ · · · ≤kn(D) =exp(D)

Akibatnya scrambling indexmerupakan 1-kompetisi indeks dari sebuah digrafD

dan n-kompetisi indeks merupakan eksponen dari digrafD.

Sebagai contoh perhatikan kembali gambar 2.2. Untuk mendapatkan nilai dari

m-kompetisi indeks dari digraf tersebut terlebih dahulu dicari nilai m-kompetisi indeks lokalnya dan untuk mendapatkan m-kompetisi indeksnya, diambil nilai

m-kompetisi lokal terbesar. Maka,

a. Untuk 1-kompetisi indeks didapat,

v1 v2 v3 v4 min(km(vi, vj))

k1(v1, v2) = 3 4 5 6 3

k1(v1, v3) = 2 3 4 5 2

k1(v1, v4) = 1 2 3 4 1

k1(v2, v3) = 3 4 5 6 3

k1(v2, v4) = 3 4 5 6 3

k1(v3, v4) = 2 3 4 5 2

Sehingga, k(D) = max{3,2,1,3,3,2}= 3.

b. Untuk 2-kompetisi indeks didapat,

(v1, v2) (v1, v3) (v1, v4) (v2, v3) (v2, v4) (v3, v4) (km(vi, vj))

k1(v1, v2) = 4 5 6 4 4 5 4

k1(v1, v3) = 3 4 5 4 5 4 3

k1(v1, v4) = 2 3 4 3 4 4 2

k1(v2, v3) = 4 5 6 4 4 5 4

k1(v2, v4) = 4 5 6 4 4 5 4

Sehingga, k2(D) = max{4,3,2,4,4,3}= 4

c. Untuk 3-kompetisi indeks didapat,

(v1, v2.v3) (v1, v3, v4) (v2, v3, v4) (v1, v2, v4) (km(vi, vj))k1(v1, v2) = 5

k1(v1, v3) = 4 5 5 5 4

k1(v1, v4) = 3 4 4 4 5

k1(v2, v3) = 5 6 6 6 5

k1(v2, v4) = 5 6 6 6 5

k1(v3, v4) = 4 5 5 5 4

Sehingga, k3(D) = max{5,4,3,5,5,4}= 5.

d. Untuk 4-kompetisi indeks didapat,

(v1, v2.v3, v4) (km(vi, vj))

k1(v1, v2) = 6 6

k1(v1, v3) = 5 5

k1(v1, v4) = 4 4

k1(v2, v3) = 6 6

k1(v2, v4) = 6 6

k1(v3, v4) = 6 5

Sehingga, k4(D) = max{6,5,4,6,6,5}= 6. Ini merupakan akhir dari tinjauan

pustaka pada penelitian ini.

2.5 Batas Atas M-Kompetisi Indeks Digraf Primitif.

15

tasan berarah, jalan yang mengililingi lingkaran, dan jalan yang mengelilingi loop. Untuk membuktikan batas atas km(sDn) ≤ f(m, n, s) cukup dibuktikan bahwa untuk setiap pasangan titik (vi, vj) di sDn terdapat sebuah jalan dengan panjang

f(m, n, s) dari titik vi ke masing-masing titik vt,t= 1,2,3,· · · , vm dan dari titik

vj ke masing-masing titik vt, t= 1,2,3,· · · , vm.

Dengan menggunakan gambar 2.2 sebagai contoh, akan dibuktikan masing-masing batas atas dari digraf 1D4.

1. Untuk k1(1D4)≤4.

Cukup dengan membuktikan bahwa setiap titikv1, v2, v3 danv4 ada jalan den-gan panjang 4 ke titikv1. Sehingga setiap titik v1, v2, v3 dan v4 dengan meng-gunakan jalan yaitu :

a. v1 →v1 →v1 →v1

b. v2 →v3 →v4 →v1

c. v3 →v4 →v1 →v1

d. v4 →v1 →v1 →v1

ada jalan dengan panjang 4 ke titikv1.

2. Untuk k2(1D4)≤5.

3. Untuk k3(1D4)≤6.

Cukup dengan membuktikan bahwa setiap titikv1, v2, v3 danv4 ada jalan den-gan panjang 5 ke titik v1, v2 dan v3. Sehingga setiap titik v1, v2, v3 dan v4

dengan menggunakan jalan yaitu :

a. v1 →v1 →v1 →v1 →v1 →v1 v1 →v1 →v1 →v1 →v1 →v2 v1 →v1 →v1 →v1 →v2 →v3

b. v2 →v3 →v4 →v1 →v1 →v1 v2 →v3 →v4 →v1 →v1 →v2 v2 →v3 →v4 →v1 →v2 →v3

c. v3 →v4 →v1 →v1 →v1 →v1 v3 →v4 →v1 →v1 →v1 →v2 v3 →v4 →v1 →v1 →v2 →v3

d. v4 →v1 →v1 →v1 →v1 →v1 v4 →v1 →v1 →v1 →v1 →v2 v4 →v1 →v1 →v1 →v2 →v3

ada jalan dengan panjang 6 ke titikv1, v2 dan v3.

4. Untuk k4(1D4)≤6.

Cukup dengan membuktikan bahwa setiap titikv1, v2, v3 danv4 ada jalan den-gan panjang 5 ke titik v1, v2, v3 dan v4. Sehingga setiap titik v1, v2, v3 dan v4

dengan menggunakan jalan yaitu :

a. v1 →v1 →v1 →v1 →v1 →v1 →v1 v1 →v1 →v1 →v1 →v1 →v1 →v2 v1 →v1 →v1 →v1 →v1 →v2 →v3 v1 →v1 →v1 →v1 →v2 →v3 →v4

17

v3 →v4 →v1 →v1 →v1 →v2 →v3 v3 →v4 →v1 →v1 →v2 →v3 →v4

d. v4 →v1 →v1 →v1 →v1 →v1 →v1 v4 →v1 →v1 →v1 →v1 →v1 →v2 v4 →v1 →v1 →v1 →v1 →v2 →v3 v4 →v1 →v1 →v1 →v2 →v3 →v4

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Teori graf merupakan sebuah cabang ilmu pengetahuan yang mempelajari sifat-sifat, bentuk, dan ciri umum suatu graf . Banyak permasalahan dapat dimodelkan dan direpresentasikan ke dalam bentuk sebuah graf dan diselesaikan dengan ban-tuan graf. Sebagai contoh, Jejaring sosial seperti facebook,twitter, instagramdan lainnya dapat direpresentasikan ke dalam sebuah graf dengan memberikan bobot pertemanan sebagai sisi dan pengguna sebagai titik. Sehingga secara singkat graf yang dinotasikan dengan simbol G merupakan sebuah objek yang tersusun atas elemen-elemen titik yang tidak kosong dimana setiap titik dapat dihubungkan oleh sebuah penghubung yang dinamakan sisi.

Jika setiap sisi pada sebuah graf G sembarang diberikan sebuah arah dengan tidak mempengaruhi titik-titik di Gakan memberikan sebuah defiinisi baru yang dinamakan digraf yang dinotasikan sebagai D. Penggunaan definisi digraf sudah banyak digunakan dalam pengembangan teorema-teorema yang berguna. Joel E. Cohen (1968) memperkenalkan sebuah definisi kompetisi graf untuk penggunaan pada sistem ekologi yang berhubungan dengan rantai makanan. Beliau mendefin-isikan kompetisi graf C(D) adalah sebuah graf yang memiliki titik yang sama dengan D dan sisi merupakan pasangan (x, y) dimana x, y ∈ D jika dan hanya jika terdapat sebuah titik z ∈ D dimana (x, z) dan (y, z) merupakan arc di D

(Cho et all, 2000).

se-2

u, v ∈V(D) maka (u, v),(v, u)∈E(D) dengan menggunakan definisi yang sama.

Penelitian selanjutnya berkembang menjadi mencari sebuah generalisasi dari scrambling indeks dinamakan m-kompetisi indeks. Definisi dari m-kompetisi in-deks yang simbolkan dengankm(D) yaitu sebuah jalan terpendek dengan panjang

k sehingga setiap pasang titik x dan y yang berada di digraf primitifD terdapat

m titik yang berbeda yaitu v1, v2, v3,· · · , vm di D dimana x

Kim (2010) menelitim-kompetisi indeks dari sebuah digraf primitif dan mene-tapkan batas atas dari m-kompetisi indeks digraf tersebut. Jika Wn merupakan

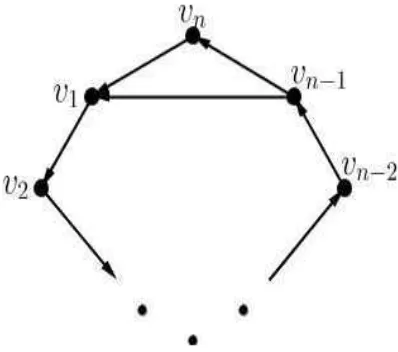
graf Wielandt seperti yang ditunjukkan pada gambar 1

Gambar 1.1. Graf Wielandt Wn

Beliau memaparkan bahwa, untuk 1 ≤ m ≤ n (n ≥ 3), maka m-kompetisi indeks graf pada gambar 1.1 adalah

km(Wn) =

Pada teorema selanjutnya, diberikan batas atas untuk kelas-kelas himpunan di-graph primitif yang dipengaruhi panjang lingkaran terpendekgirthsebesar s den-gan orde n ≥ 3. Andaikan D merupakan digraf primitif dengan orde n ≥ 3 dan

m-kompetisi indeks km(D) dari digraf D

Sehingga memberikan kesimpulan bahwa digraf Wielandt merupakanm-kompetisi terbesar untuk kelas himpunan digraf primitif yang dipengaruhi oleh panjang lingkaran terpendek girth.

Shaoet al(2012) menelitim-kompetisi indeks dari digraf primitif yang simetris

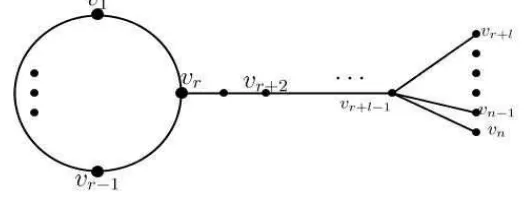
tanpa menggunakan loop dan menetapkan batas atas dari m-kompetisi indeks dari digraf tersebut. Pada penelitian tersebut, diteliti sebuah graf Sn(r) yang

dinotasikan sebagai semua digraf simetris primitif dengan banyaknya titik adalah

nyang memiliki lingkaran ganjil dengan panjangrtetapi tidak ada lingkaran dari panjang ganjil tersebut yang lebih kecil dari pada r. Andaikan Gr,l merupakan

4

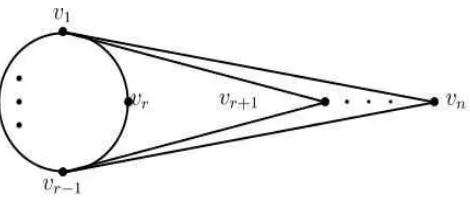
Kesimpulan yang dihasilkan, batas atas dari kelas graf Sn(r) adalah untuk

graf G∈ Sn(r), 3≤r≤n−1 dan 2≤m≤n−1. Maka,

graf primitif dengan banyaknya titik adalahnyang memiliki lingkaran ganjil den-gan panjang r tetapi tidak ada lingkaran dari panjang ganjil tersebut yang lebih kecil dari pada r.

Informasi diatas menjadi latar belakang peneliti untuk mengembangkan m -kompetisi indeks dari sebuah digraf primitif yang terdiri atas sebuah lingkaran hamiltonian dengan beberapa loop didalamnya.

1.2 Perumusan Masalah

Pembahasan digraf primitif sendiri karena definisi darim-kompetisi indeks meng-haruskan digraf tersebut terhubung kuat dan untuk setiap pasangan titik vi dan

vj harus mempunyaioutdegreeyang sama. Peneliti sebelumnya telah menelitim

sebuah lingkaran Hamiltonian dengan beberapaloop yang saling lepas diletakkan berdekatan. Secara khusus rumusan masalah dalam penelitian ini adalah sebagai berikut:

Gambar 1.4. Digraf sDn

Andaikan digraf sDn adalah sebuah digraf dengan banyak titik adalah n buah

terdiri atas sebuah lingkaran Hamiltonian yaitu v1 → v2 → v3 → · · · → vn → v1 dan s buah loop yang diletakkan berdekatan. Apakah f(km(sDn))≤f(s, m, n)?

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk menentukan bentuk rumus umum dari batas atas m-kompetisi indeks untuk kelas digraf primitif dengan n ∈ Z+

titik

v1, v2,· · · , vndi digrafDyang mempunyai lingkaran hamiltonianv1 →v2 →v3 → · · · → vn → v1 dan beberapa loop sebanyak s yang diletakkan berdekatan untuk 1≤s≤n.

1.4 Manfaat Penelitian

BATAS ATAS _M-KOMPETISI INDEKS DARI DIGRAF LINGKARAN

HAMILTONIAN DENGAN BEBERAPA LOOP YANG DILETAKKAN

BERDEKATAN

ABSTRAK

Untuk bilangan bulat positifmdanndengan 1≤m≤n,m-kompetisi indeks dari sebuah digraf primitifD, dinotasikan dengankm(D) adalah bilangan bulat positif terkecil k sehingga untuk setiap pasang x dan y, terdapatm titik berbeda yaitu v1, v2, v3,· · · , vm di D sehingga x

k

→ vi dan y →k vi untuk setiap i = 1,2,· · · , m. Tulisan ini membahas mengenai batas atas m-kompetisi indeks dari kelas digraf primitif sDn yaitu digraf dengan n buah titik yang terdiri atas sebuah lingkaran Hamiltonian dan s buah loop yang diletakkan saling berdekatan. Untuk setiap digraf sDn, diperoleh batas atas km(sDn)≤ f(s, n, m) yaitu fungsi yang bergan-tung pada s, ndan m.

ABSTRACT

For positive integers m and n with 1≤m≤n, m-competition indices of a prim-itive digraph D, notated with km(D) is a smallest positive integer such that for each pairs x dan y, there exist m distinct vertices v1, v2, v3,· · · , vm in D such

that x →k vi and y →k vi for each i = 1,2,· · · , m. This paper discuss an up-per bound of m-competition indices from a class of primitive digraph sDn which is digraph with n vertices consist of a Hamiltonian cylce and s loops put adje-cent. For every digraph sDn, we have an upper bound with inequality function km(sDn)≤f(s, n, m), a function depends on a value of s, nand m.

BATAS ATAS M-KOMPETISI INDEKS DARI DIGRAF

LINGKARAN HAMILTONIAN DENGAN BEBERAPA

LOOP

YANG DILETAKKAN BERDEKATAN

SKRIPSI

BIMA SATRYA SEBAYANG

120803026

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

LOOP

_{YANG DILETAKKAN BERDEKATAN}

SKRIPSI

Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar sarjana sains

BIMA SATRYA SEBAYANG

120803026

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

PERSETUJUAN

Judul : Batas AtasM-Kompetisi Indeks Dari Digraf Lingkaran

Hamiltonian Dengan Beberapaloop yang Diletakkan Berdekatan

Kategori : Skripsi

Nama : Bima Satrya Sebayang

Nomor Induk Mahasiswa : 120803026

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Disetujui di

Medan, Juli 2016

Komisi Pembimbing :

Pembimbing 2, Pembimbing 1,

Dr. Mardiningsih, M.Si Prof. Dr.Saib Suwilo, M.Sc

NIP.19630405 198811 2 001 NIP.19640109 198803 1 004

Disetujui Oleh

Departemen Matematika FMIPA USU Ketua,

BATAS ATAS _M-KOMPETISI INDEKS DARI DIGRAF

LINGKARAN HAMILTONIAN DENGAN BEBERAPA

LOOP YANG DILETAKKAN BERDEKATAN

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan penting yang masing-masing disebutkan sumbernya.

Medan, Juli 2016

PENGHARGAAN

Puji Syukur penulis ucapkan kehadirat Allah Subhanahu wa Ta’ala, sang pen-cipta langit dan bumi serta segala isinya yang telah melimpahkan rahmat, hi-dayah serta kasih sayang-Nya sehingga penulis dapat menyelesaikan penyusunan skripsi ini dengan judul m-kompetisi indeks dari Digraf Lingkaran Hamlitonian Dengan Beberapa Loop yang diletakkan Berdekatan. Shalawat dan salam penulis ucapkan kepada Rasulullah ShallAllahu’Alaihi wa Sallam, keluarga, para sahabat dan orang-orang yang mengikutinya.

Penulis ingin mengucapkan terima kasih sebesar-besarmya kepada :

1. Ibunda tercinta Nurhalimah Br Tarigan yang selalu memberikan dorongan dan semangat serta doa yang tak henti-hentinya diberikan kepada penulis se-hingga penulis merasa tidak terbebani dalam penyelesaian skripsi ini.

2. Bapak Prof. Dr. Saib Suwilo, M.Sc selaku pembimbing 1 dan Ibu Dr. Mardiningsih, M.Si selaku pembimbing 2 yang telah memberikan ilmu yang bermanfaat kepada penulis serta dapat meluangkan waktu, tenaga, dan piki-ran untuk penyusunan skripsi ini.

3. Bapak Prof. Dr. Tulus, M.Si dan Bapak Drs. Marihat Situmorang, M.Kom selaku dosen penguji yang telah memberikan masukan dan saran bermanfaat selama penyusunan skripsi ini.

4. Seluruh Dosen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara yang telah memberikan ilmu yang bermanfaat kepada penulis selam 4 tahun menimba ilmu dikampus ini.

5. Seluruh staff administrasi Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Uatara yang telah membantu penulis dalam menyelesa-iakn urusan-urusan terkait seminar proposal, seminar hasil, dan ujian skripsi.

kata-kata yang tepat dalam penyelesaian skripsi ini. Serta semua adik-adik junior yang selalu memberikan semangat kepada penulis. Terima kasih juga kepada kak Ratih, kak Merryanti, kak Mantari yang telah membagikan ilmu terkait dengan materi ini.

Penulis menyadari bahwa masih terdapat banyak kekurangan dalam penulisan skripsi ini. Maka dari itu, diperlukan kritik dan saran dari pembaca untuk penyempurnaan skripsi ini.

Medan, Juli 2016

BATAS ATAS _M-KOMPETISI INDEKS DARI DIGRAF LINGKARAN

HAMILTONIAN DENGAN BEBERAPA LOOP YANG DILETAKKAN

BERDEKATAN

ABSTRAK

Untuk bilangan bulat positifmdanndengan 1≤m≤n,m-kompetisi indeks dari sebuah digraf primitifD, dinotasikan dengankm(D) adalah bilangan bulat positif terkecil k sehingga untuk setiap pasang x dan y, terdapatm titik berbeda yaitu

v1, v2, v3,· · · , v_m di D sehingga x

k

→ vi dan y k

→ vi untuk setiap i = 1,2,· · · , m.

Tulisan ini membahas mengenai batas atas m-kompetisi indeks dari kelas digraf primitif sDn yaitu digraf dengan n buah titik yang terdiri atas sebuah lingkaran Hamiltonian dan s buah loop yang diletakkan saling berdekatan. Untuk setiap digraf sDn, diperoleh batas atas km(sDn)≤ f(s, n, m) yaitu fungsi yang bergan-tung pada s, ndan m.

ABSTRACT

For positive integers m and n with 1≤m≤n, m-competition indices of a prim-itive digraph D, notated with km(D) is a smallest positive integer such that for each pairs x dan y, there exist m distinct vertices v1, v2, v3,· · · , v_m in D such

that x →k vi and y k

→ vi for each i = 1,2,· · · , m. This paper discuss an

up-per bound of m-competition indices from a class of primitive digraph sDn which is digraph with n vertices consist of a Hamiltonian cylce and s loops put adje-cent. For every digraph sDn, we have an upper bound with inequality function

km(sDn)≤f(s, n, m), a function depends on a value of s, nand m.

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT vi

DAFTAR ISI vii

DAFTAR GAMBAR viii

BAB 1. PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 4

1.3 Tujuan Penelitian 5

1.4 Manfaat Penelitan 5

BAB 2. DIGRAF PRIMITIF 6

2.1 Definisi Digraf 6

2.2 Definisi Digraf Primitif 10

2.3 DigrafsDn Sebagai Digraf Primitif 11

2.4 Definisi M-Kompetisi Indeks 12

2.5 Batas AtasM-Kompetisi Indeks Digraf Primitif 14

BAB 3. METODOLOGI PENELITIAN 18

BAB 4. HASIL DAN PEMBAHASAN 18

4.1 Batas AtasM-Kompetisi Indeks Digraf Hamiltonian 1 buah loop 20 4.2 Batas AtasM-Kompetisi Indeks Digraf Hamiltoniansbuah loop 22

BAB 5. KESIMPULAN DAN SARAN 28

5.1 Kesimpulan 28

5.2 Saran 28

Nomor Judul Halaman Gambar

1.1 Graf Wielandt 2

1.2 Graf Gr,l 3

1.3 Graf Gr 4

1.4 Digraf sDn 5

2.1 Contoh Digraf D 6

2.2 Digraf 1D4 9

3.1 (a) Digraf 1D_n (b) Digraf _sD_n 18

4.1 Digraf 1D_n 20