ANALISIS KUALITATIF GEJALA CHAOS PADA GERAK PENDULUM SEDERHANA NONLINIER TEREDAM DAN TERKENDALI
SKRIPSI
SITI UTARI RAHAYU 060801030
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
ANALISIS KUALITATIF GEJALA CHAOS PADA GERAK PENDULUM SEDERHANA NONLINIER TEREDAM DAN TERKENDALI
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
SITI UTARI RAHAYU 060801030
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : ANALISIS KUALITATIF GEJALA CHAOS PADA
GERAK PENDULUM SEDERHANA NONLINIER TEREDAM DAN TERKENDALI
Kategori : SKRIPSI
Nama : SITI UTARI RAHAYU NIM : 060801030
Program Study : SARJANA (S1) FISIKA Departemen : FISIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, 04 Desember 2010
Diketahui/disetujui oleh
Departemen Fisika FMIPA USU
Ketua, Pembimbing,
PERNYATAAN
ANALISIS KUALITATIF GEJALA CHAOS PADA GERAK PENDULUM SEDERHANA NONLINIER TEREDAM DAN TERKENDALI
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya
Medan, 04 Desember 2010
PENGHARGAAN
Puji dan Syukur penulis persembahkan kepada Allah SWT yang telah melimpahkan kasih sayang serta karunia-Nya kepada penulis hingga skripsi yang berjudul: “Analisis Kualitatif Gejala Chaos Pada Gerak Pendulum Sederhana Nonlinier Teredam dan Terkendali” berhasil diselesaikan dengan baik dan tepat pada waktu yang telah ditetapkan. Shalawat dan salam kepada Nabi Muhammad SAW sebagai suri teladan terbaik di muka bumi.
Ucapan terima kasih penulis sampaikan kepada Dr. Mester Sitepu, M.Sc, M.Phil, selaku pembimbing yang telah memberikan panduan, bantuan, serta segenap perhatian dan dorongan kepada penulis dalam menyempurnakan skripsi ini. Paduan ringkas dan padat serta profesional telah diberikan kepada penulis sehingga penulis dapat menyelesaikan tugas ini. Ucapan terimakasih juga ditujukan kepada Ketua dan Sekretaris Departemen Fisika Dr. Marhaposan Situmorang dan Dra.Justinon, M.Si, serta Dekan dan Pembantu Dekan Fakultas MIPA USU. Ucapan terimakasih jugadiberikan kepada Dr. Kerista Tarigan, M.Eng.Sc, Drs. Takdir Tamba, M.Eng.Sc, dan Drs. Luhut Sihombing, MS, selaku dosen pembanding yang telah banyak memberikan saran dan masukan dalam penyempurnaan skripsi ini. Kemudian ucapan terimakasih kepada Bapak Drs. Setia Sembiring selaku dosen wali yang telah memperhatikan kemajuan studi penulis, serta Bapak dan Ibu Staf Pengajar Departemen Fisika FMIPA USU terima kasih atas ilmu yang diberikan selama ini, semoga menjadi ilmu yang bermanfaat, dan tak lupa pula kepada seluruh staff pegawai pada departemen Fisika FMIPA USU.
Ucapan terimakasih terbesar penulis sampaikan kepada Ibunda tercinta Siti Maryam atas segala cinta kasih dan do’a yang selalu dihadiahkan kepada penulis tanpa henti, juga tak lupa kepada saudara terbaik penulis Edi Sucipto yang selalu memotivasi penulis dalam menyelesaikan skripsi ini. Tak lupa pula terimakasih kepada sahabat-sahabat terbaik penulis Vika, Tika, Kak Aisyah, Kak Dewi, Kak Lili, Kak Novi, Ulan (Terima kasih atas pinjaman buku-bukunya), Winda, Dian, Farida, Nova, Muti, Linda, Yuni, Fuji, Mutia, Laila, Gina, Imah, Diah, Kata, Mey, Derlina, Heber, Trisno, Kiki, Eva dan semua rekan-rekan fisika angkatan 2006, abang kakak senior dan juga adik-adik junior departemen Fisika. Tak lupa pula terima kasih kepada saudara-saudara seperjuangan di UKMI AL-FALAK FMIPA USU. Semoga Allah SWT akan membalasnya.
ABSTRAK
QUALITATIVE ANALYSIS OF CHAOS BEHAVIOUR ON DAMPED DRIVEN NONLINEAR SIMPLE PENDULUM MOTION
ABSTRACT
DAFTAR ISI
1.3 Manfaat Penelitian 3 1.4 Batasan Masalah 4
1.5 Sistematika Penulisan 4 Bab 2 Tinjauan Pustaka 6 2.1 Teori Chaos 6 2.1.1 Studi Chaos Secara Numerik 7
2.1.1.1 Ruang Fasa 9 2.1.1.2 Belahan Poincaré 11 2.1.1.3 Penggandaan Perioda 12
2.1.2 Chaos dan Pengaruhnya Dalam Sains 13
2.2 Pendulum Sederhana 15 2.2.1 Pendulum Sederhana Linier 18 2.2.2 Pendulum Sederhana Nonlinier 20 2.2.3 Pendulum Sederhana Nonlinier Teredam 22 2.2.4 Pendulum Sederhana Nonlinier Teredam dan Terkendali 24 2.3 Metode Runge-Kutta 26 Bab 3 Analisis Masalah dan Perancangan Program 29
3.1 Analisis Masalah 29
3.1.1 Persamaan Gerak Pendulum Sederhana Nonlinier Teredam dan Terkendali 29 3.1.2 Penyelesaian dengan Metode Runge-Kutta Orde Empat 31 3.1.3 Penentuan Ruang Fasa dan Belahan Poincarè 32
4.2 Keadaan Kuasiperiodik 47
4.3 Keadaan Chaos 50
4.4 Perbandingan Keadaan Sistem Untuk Variasi Nilai
Beberapa Parameter 55
Bab 5 Kesimpulan dan Saran 58
5.1 Kesimpulan 58
5.2 Saran 59
Daftar Pustaka 60
DAFTAR TABEL
Halaman Tabel.4.1. Hasil Pengujian Keadaan Sistem Untuk Variasi Nilai Koefisien
Redaman, q dan Amplitudo Gaya Pengendali Eksternal, a 56 Tabel.4.2. Hasil Pengujian Keadaan Sistem Untuk Variasi Nilai Panjang
DAFTAR GAMBAR
Halaman Gambar 2.1. Ruang fasa dari rotor dengan kondisi batas periodik. 10
Lintasan fasa bergerak dari kanan ke kiri dan
Gambar 2.3 Gaya-gaya yang bekerja pada pendulum, tegangan tali 16 dan gaya berat, gaya peredam, dan gaya pengendali eksternal.
Gambar 2.4 Grafik θ Vs t untuk θo = π/4 dan L = 0,5 m. 19
Gambar 2.5 Grafik θ Vs θ
dari pendulum sederhana merupakan 19 gambar fasa pendulum dengan bentuk elips.
Gambar 2.6 Perbandingan Grafik θ Vs t untuk θo = π/4 dan θo = π/3.5 20
Gambar 2.7 Grafik θ Vs t untuk θo = 0 dan θ = 1.95 rad/s. 21
Gambar 2.8 Grafik θ Vs θ
dari pendulum sederhana nonlinier 21 merupakan gambar fasa pendulum nonlinier
Gambar 2.9 Perbandingan Grafik θ Vs t untuk θo= 1.95 rad/s 22 dan θ
o = 1.9 rad/s
Gambar 2.10 Grafik θ Vs t untuk kondisi awal θo = 0; q=0.08; θo = 3 rad/s 23 Gambar 2.11 Grafik θ Vs θ
untuk pendulum nonlinier teredam dengan 23 orbit yang berpilin menuju satu titik.
Gambar 2.12 Perbandingan Grafik θ Vs t untuk kondisi awal q=0.04 24 dan q=0.081
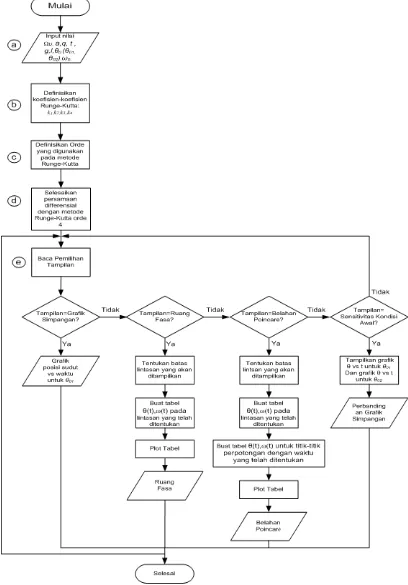
Gambar 3.1 Diagram Alir Simulasi persamaan gerak pendulum 35 sederhana nonlinier teredam dan terkendali dengan metode
Runge-Kutta Orde 4.
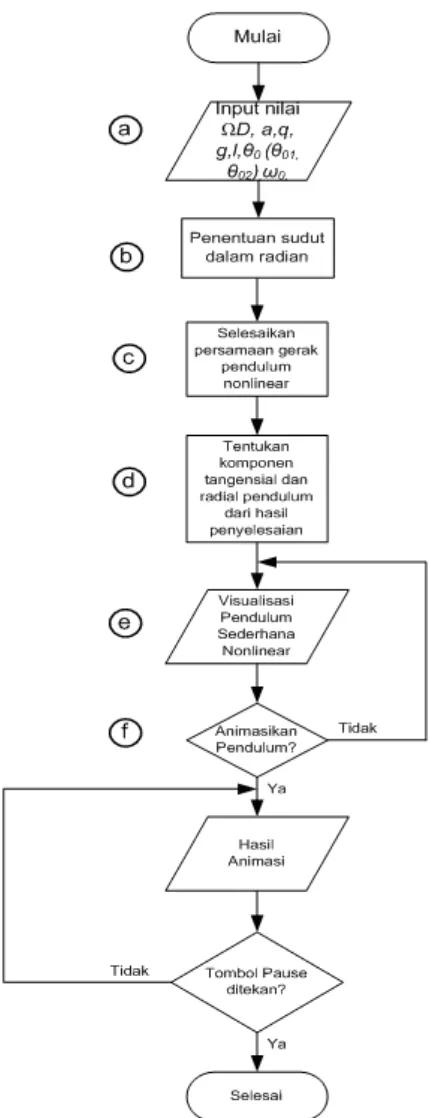
Gambar 3.2. Diagram Alir Animasi persamaan gerak pendulum 37 sederhana nonlinier teredam dan terkendali.
Gambar 4.1 Hasil eksekusi Program “Simulasi Gerak Pendulum 43 Sederhana Nonlinier Teredam Dan Terkendali“ pada
Lampiran A
Gambar 4.2 Hasil eksekusi program “Animasi Gerak Pendulum 44 Sederhana Nonlinier” pada Lampiran B
ABSTRAK
QUALITATIVE ANALYSIS OF CHAOS BEHAVIOUR ON DAMPED DRIVEN NONLINEAR SIMPLE PENDULUM MOTION
ABSTRACT
BAB 1
PENDAHULUAN
1.1. Latar Belakang
Berbagai gejala alam menampilkan perilaku yang rumit, tidak dapat diramalkan dan tampak acak (random). Keacakan ini merupakan suatu yang mendasar, dan tidak akan hilang walaupun informasi tentang sistem itu bertambah. Keacakan yang dihasilkan dengan cara seperti itulah yang dikatakan sebagai chaos. Akan tetapi, menurut teori
chaos, apabila keacakan tersebut kita perhatikan dalam waktu yang cukup lama
dengan mempertimbangkan dimensi waktu, maka akan ditemukan keteraturan dalam keacakan tersebut. Dengan demikian, chaos memungkinkan ditemukannya keteraturan dalam sistem-sistem yang tampaknya tidak beraturan, dan hal ini memiliki dampak besar pada banyak cabang ilmu pengetahuan. Pemanfaatan chaos antara lain pada analisis pergerakan saham pada bidang fisika ekonomi, kriptografi, dinamika atmosfer dan lautan, vibrasi molekul, ekologi, bahkan dalam bidang dinamika sosial. Untuk itu pemahaman yang jelas terhadap gejala chaos sangat diperlukan untuk dapat diterapkan pada berbagai bidang ilmu.
Deskripsi teoritik sering tidak mampu mengungkap gejala chaos ini. Karakter tak linier persamaan matematika yang muncul merupakan kesulitan utama. Dan dengan adanya kemajuan teknologi, maka permasalahan ini dapat diselesaikan dengan penggunaan komputer digital. Grafik komputer dengan resolusi tinggi memungkinkan para peneliti untuk menyelidiki gejala chaos yang terbentuk dari pola keluaran suatu sistem yang disimulasi (Setiawan, 1991).
sederhana ini karena merupakan sistem paling sederhana yang dapat mendemonstrasikan perilaku chaos, dan karena sistem ini secara matematika sama dengan persoalan-persoalan yang melibatkan getaran. Pendulum ini berupa sistem mekanik yang tersusun atas sebuah massa yang terikat oleh sebuah tali yang dapat berayun bebas sebagai respon terhadap gaya grafitasi. Dalam kasus sederhana, gerakan pendulum mengabaikan kehadiran gaya gesekan dan diasumsikan bahwa sudut simpangan sangat kecil. Gerakan yang dihasilkan dari pendulum dengan kondisi semacam ini berupa gerak harmonik sederhana. Sedangkan pendulum yang sebenarnya memiliki gesekan dengan medium saat berayun, pengendalian sistem melalui gaya pengendali eksternal dan dimungkinkan untuk berayun dengan sudut simpangan berapapun. Fitur inilah yang kemudian mengantarkan kepada perilaku
chaos.
Titik tekan penelitian gejala chaos ini adalah pada penggambaran yang jelas dinamika sistem secara nyata. Oleh karena itu perangkat-perangkat analisis gejala
chaos yang akan digunakan dalam penelitian ini berupa perangkat analisis secara
kualitatif, yang meliputi grafik lintasan, ruang fasa, belahan Poincarè, dan perbandingan grafik lintasan. Selain itu pemahaman terhadap keadaan fisis secara riil terhadap persamaan gerak pendulum adalah hal yang sangat penting, maka penelitian ini juga menampilkan animasi gerak pendulum.
Adapun perangkat lunak yang digunakan pada simulasi ini adalah
Mathematica versi 6. Digunakanya Mathematica versi 6 karena merupakan perangkat
1.2. Tujuan Penelitian
Tujuan dari penelitian ini adalah:
1. Menganalisis gejala chaos pada sistem pendulum sederhana berdasarkan grafik keluaran simulasi penyelesaian persamaan gerak pendulum sederhana nonlinier teredam dan terkendali yang terdiri dari grafik lintasan, ruang fasa, belahan Poincaré, dan perbandingan grafik lintasan untuk dua kondisi awal yang berbeda.
2. Merancang program bantu untuk mensimulasikan penyelesaian persamaan gerak pendulum sederhana nonlinier teredam dan terkendali dengan menggunakan bahasa pemrograman Mathematica
Versi 6.
3. Merancang program bantu untuk menganimasikan gerak pendulum sederhana nonlinier teredam dan terkendali dengan menggunakan bahasa pemrograman Mathematica Versi 6.
4. Menggunakan metode Runge-Kutta orde 4 untuk menyelesaikan persamaan gerak pendulum sederhana nonlinier teredam dan terkendali yang berupa persamaan differensial orde 2.
1.3. Manfaat Penelitian
1.4. Batasan Masalah
Penelitian ini dibatasi pada:
1. Model yang digunakan untuk menganalisis perilaku chaos pada sistem dinamis adalah pendulum sederhana nonlinier teredam dan terkendali dengan frekuensi alami pendulum, Ω2 = 1 dan massa pendulum, m = 1 (Dimensionless) pada kondisi awal ω0 = 0.8 rad/s dan θ0 = 0.8 rad serta
koefisien redaman, q = 0.4.
2. Gejala chaos pada sistem pendulum sederhana nonlinier dianalisis secara kualitatif menggunakan belahan Poincaré, ruang fasa, grafik lintasan, dan perbandingan grafik lintasan untuk dua kondisi awal yang berbeda dengan memvariasikan amplitudo gaya pengendali eksternal.
3. Penyelesaian persamaan differensial pendulum sederhana teredam dan terkendali dengan menggunakan metode Runge-Kutta orde 4.
4. Simulasi dilakukan dengan menggunakan bahasa pemrograman
Mathematica versi 6.
1.5. Sistematika Penulisan
Laporan tugas akhir ini disusun dalam lima bab yaitu sebagai berikut:
Bab 1 Pendahuluan
Bab 2 Tinjauan Pustaka
Bab ini menjelaskan landasan teori yang digunakan dalam penelitian, yaitu dasar teori pendulum sederhana, chaos, dan Metode Runge-Kutta, yang digunakan untuk mengolah informasi yang akan diimplementasikan dalam simulasi.
Bab 3 Analisis Masalah Dan Perancangan Program
Bab ini membahas penyelesaian masalah yang akan disimulasi, dan algoritma program yang akan digunakan.
Bab 4 Hasil Dan Pembahasan
Bab ini memberikan hasil uji coba simulasi gejala chaos pada pendulum sederhana nonlinier teredam dan terkendali untuk beberapa variasi amplitudo gaya pengendali eksternal, kemudian membandingkan hasil yang diperoleh antara keadaan tanpa chaos dengan keadaan chaos.
Bab 5 Kesimpulan Dan Saran
BAB 2
TINJAUAN PUSTAKA
2.1. Teori Chaos
Penemuan chaos dimulai ketika para matematisi dan fisikawan melakukan analisis dari suatu sistem dinamis yang berbentuk persamaan differensial dan menemukan keganjilan dalam perilakunya. Sistem persamaan differensial yang merupakan model dari sistem dinamis dapat dipandang sebagai suatu mesin yang menerima input dari beberapa nilai awal dari variabel yang terkait, kemudian menghasilkan nilai baru setelah dioperasikan beberapa saat. Setiap langkah penyelesaiannya dapat direkam dalam bentuk titik koordinat dari suatu bidang grafis, yang bila di-plot dari awal hingga akhir menampakkan jejak perilaku dari sistem dinamis tersebut.
Suatu keadaan chaos dapat diartikan sebagai keadaan di mana jejak perilaku sistem susah diprediksi (Surga,2007). Para ahli dinamika nonlinier juga menggunakan istilah chaos untuk tingkah laku tak teratur dan tak terprakirakan dalam sistem nonlinier deterministik. Sistem seperti ini tidak pernah mengulang dirinya sendiri, melainkan secara terus-menerus melakukan sesuatu yang berbeda, sehingga gerakannya tampak acak dan tak teratur (Walker, 1991). Chaos menunjukkan bahwa sebuah sistem dapat memiliki tingkah laku kompleks yang muncul sebagai konsekuensi interaksi sederhana, tak linier beberapa komponen saja. Bahkan diketahui pula bahwa sistem-sistem sederhana dengan hanya satu atau dua derajat kebebasan saja dapat bersifat chaos (Setiawan,1991).
penting. Model-model yang sederhana dapat menghasilkan tingkah laku kompleks dan tidak teratur (Setiawan, 1991), hal ini menyiratkan bahwa gerakan yang bersifat chaos ternyata jauh dari ketidakteraturan total dan malah menampilkan suatu pola tertentu yang dapat terlihat dengan mudah (Walker, 1991). Berdasarkan kenyataan ini. maka kita dapat mengharapkan penggambaran teoritis sejumlah besar gejala alam yang acak dan tak dapat diperkirakan dengan menggunakan model matematika yang menunjukkan perilaku chaos deterministik (Setiawan, 1991).
Aspek lain tentang chaos, ketika muncul dalam fisika, adalah suatu sensitivitas ekstrim terhadap kondisi awal. Aspek ini dapat diandaikan sebagai keadaan ketika kita hendak menegakkan sebuah pena tegak lurus pada salah satu ujungnya. Jika ditempatkan secara vertikal, pena tersebut akan berada dalam keseimbangan. Namun, keseimbangan tersebut tidak stabil, bahkan suatu gangguan yang kecil seperti hembusan udara yang ringan, atau suara buku jatuh dapat menyebabkan pena tersebut jatuh ke arah yang lain. Posisi vertikal pena merupakan suatu contoh keadaan yang menunjukkan sensitivitas ekstrim terhadap kondisi awal. Keadaan yang bersifat chaos adalah seperti ini, dimana semua bagian geraknya sama sensitifnya seperti pada pena vertikal. Akibatnya, kesalahan yang sangat kecil sekalipun dalam pengukuran suatu sistem chaos dapat menyebabkan kesalahan yang luar biasa. Hal inilah yang terjadi pada peramalan cuaca, ketidakmampuan peramalan ini diakui sebagai contoh gerak
chaos yang bersangkutan dengan transfer panas di atmosfer (Walker, 1991).
2.1.1. Studi Chaos Secara Numerik
Namun, bilangan bilangan irasional dapat didekati dengan bilangan rasional, atau dengan kata lain daerah chaos dikelilingi oleh daerah-daerah periodik. Strategi yang benar dalam studi komputer adalah dengan mengidentifikasi orbit periodik dengan tepat dan mencirikan gerak tak periodik. Selain itu, sistematika orbit periodik banyak sekali memberitahukan sifat gerak tak periodik yang berdekatan (Dalam ruang parameter). Dan telah dibuktikan bahwa setiap periode orbit pseudo-chaos dibayangi dengan orbit chaos yang sebenarnya.
Pengamatan lintasan secara langsung merupakan sebuah metode dengan resolusi paling rendah. Sedangkan penentuan belahan Poincaré (Bagian ini akan dijelaskan lebih lanjut pada subbab 2.1.1.2) memberikan suatu cara efektif untuk mengungkap sifat gerak (Setiawan, 1991).
Studi chaos secara numeris bahkan dapat dilakukan dengan menggunakan kalkulator tangan, yaitu untuk persamaan logistik yang diberikan pada persamaan 2.1.
) 1
( x
wx
x′= − (2.1)
Dengan rentang 0 x 1 dan w adalah parameter yang dapat diatur. Untuk nilai x = 0,4 dan nilai w = 2,9 maka dari persamaan 2.1. diperoleh x’ = 0,696, kemudian nilai x’ menjadi nilai awal dan diperoleh x’’ = 0,614, hal ini dilakukan seterusnya untuk beberapa iterasi sehingga akan ditemukan bahwa nilai x akan dibatasi pada nilai 0,655 dan berulang lagi. Hal ini yang dikatakan sebagai keadaan periodik.
2.1.1.1. Ruang Fasa
Ruang fasa (phase space) merupakan sarana yang bermanfaat untuk menggambarkan tingkah laku sistem-sistem yang bersifat chaos dalam bentuk geometri. Adapun yang dimaksud dengan ruang fasa dari suatu sistem dinamis adalah ruang yang secara matematika memiliki arah koordinat tegak lurus, dimana masing-masing koordinat mewakili variabel-variabel yang diperlukan untuk menentukan keadaan sistem pada saat tersebut (Baker et al, 1996). Sebagai contoh, keadaan dari suatu Partikel yang bergerak pada satu dimensi ditentukan oleh posisinya (x) dan kecepatannya (v), karena itu ruang fasanya berupa bidang. Sedangkan untuk partikel yang bergerak pada tiga dimensi akan memiliki enam dimensi ruang fasa, yaitu tiga arah untuk posisi dan tiga arah untuk kecepatan. Sebuah ruang fasa dapat dibentuk dengan beberapa variabel yang berbeda. Misalnya pada contoh ini momentum dapat digunakan untuk menggantikan kecepatan.
Sebagai contoh dari penentuan ruang fasa ini misalnya pada rotor berkecepatan konstan. Persamaan geraknya yaitu persamaan 2.2 dan 2.3.
0 =
dt dω
(2.2)
0 ω θ =
dt d
(2.3)
ω
θ π
-π
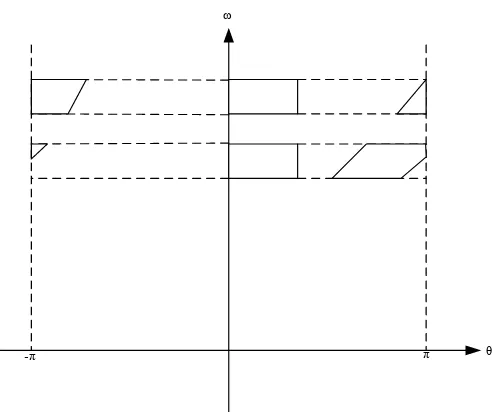
Gambar 2.1. Ruang fasa dari rotor dengan kondisi batas periodik. Lintasan fasa bergerak dari kanan ke kiri dan menghilang pada θ = π dan muncul kembali
pada θ =- π.
Lintasan yang bergantung pada θ dan ω memastikan bahwa daerah bujur sangkar awal bertransformasi menjadi daerah berbentuk jajaran genjang dengan tinggi konstan, dengan demikian luasan daerah asal tetap terjaga. Koordinat sudut, θ dari rotor dapat dinaikkan ( secara positif atau secara negatif) tanpa batas. Namun, θ adalah periodik secara fisika. Dari ruang fasa ini dapat ditentukan apakah sistem bersifat disipatif atau konservatif. Caranya adalah dengan mengidentifikasi variabel-variabel pada persamaan sistem dan menghitung nilai perubahan volum yang diberikan oleh persamaan 2.4. (Baker et al, 1996).
F dt dV
V =∇
1
(2.4)
Dan nilai turunan logaritma hanya bergantung pada kuantitas ∇F, jika nilainya 0 maka sistem bersifat konservatif dan jika nilainya negative maka sistem bersifat disipatif.
seperti ini juga disebut sebagai penarik (attractor), sebagai contoh adalah pendulum sederhana nonlinier teredam.
2.1.1.2. Belahan Poincaré
Salah satu karakteristik dari sistem chaos adalah bahwa sistem tersebut sangat sensitif terhadap kondisi awal. Misalkan untuk dua kondisi awal dengan selisih yang sangat kecil, maka lintasannya menyimpang secara eksponensial terhadap waktu. Salah satu cara untuk menentukan karakteristik ini yaitu eksponensial Lyapunov, suatu perhitungan rerata dari divergensi dan konvergensi dari dua lintasan yang berdekatan. Namun, hasil dari perhitungan eksponensial ini adalah berupa angka, sedangkan penelitian ini mengharapkan penggambaran dinamika sistem melalui suatu pola keluaran. Maka perangkat analisis lain yang digunakan pada penelitian ini adalah Belahan Poincaré.
Belahan Poincaré adalah sebuah bidang potong berdimensi dua (Representasi dua dimensi dari ruang fasa) tempat dimana lintasan-lintasan (Trajectories) dari sebuah penyelesaian sistem dinamik melewatinya. Dari belahan Poincaré akan diperoleh sebuah foto fasa (phase portrait) yang di dalam ilmu fisika disebut juga dengan photo stroboscopic. Belahan Poincaré secara umum diperlukan untuk menyederhanakan proses penganalisaan suatu sistem dinamik yang berdimensi tiga atau empat guna mendapatkan informasi sebanyak-banyaknya mengenai sifat-sifat sistem tersebut (sifat stabil atau tidak stabilnya orbit-orbit periodik, misalnya) (Zakaria, 2002).
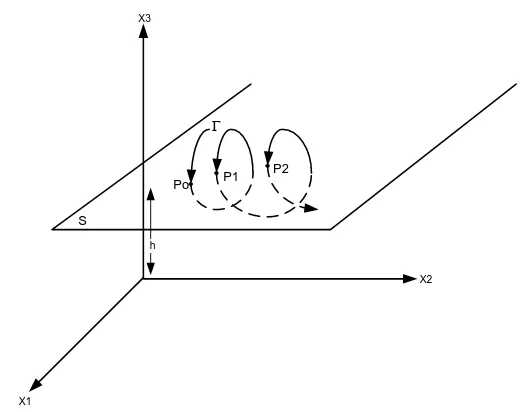
P0, P1, P2, …. Titik-titik ini merupakan belahan Poincaré dari Г pada bidang S (Berge
et al, 1984).
Po P1 P2
S
Г
X3
h
X2
X1
Gambar 2.2. Ilustrasi Belahan Poincaré. Lintasan fasa Г memotong bidang S ( Dengan x3< 0) pada titik-titik yang berurutan P0, P1, P2, …. Titik-titik ini
merupakan Belahan Poincaré dari Г pada bidang S.
Sistem chaos selain memiliki gerakan yang bersifat deterministik (Jika diberikan suatu keadaan awal yang telah diketahui sebelumnya, maka gerakannya yang akan datang dapat diuraikan secara tepat dengan menggunakan perhitungan matematika), juga bersifat tak periodik (Gerakannya tidak pernah berulang secara tepat). Dalam kasus pendulum sederhana, jika gerakannya bersifat tak periodik (chaos) maka akan terbentuk titik-titik tak berhingga pada ruang fasa. Hal ini yang dianalisis dengan menggunakan Belahan Poincaré, yaitu menentukan perilaku sistem pendulum sederhana pada ruang fasa secara periodik.
2.1.1.3. Penggandaan Perioda
yang pada akhirnya mengakibatkan kondisi chaos. Beberapa ahli dinamika nonlinier mengemukakan bahwa salah satu jenis bifurkasi yang terkenal adalah penggandaan perioda (period doubling), yakni suatu gerakan periodik yang mengalami bifurkasi dan “melontarkan” gerakan periodik lain yang periodenya dua kali lebih besar dari periode semula. Kemudian masing-masing gerakan periodik itu mengalami bifurkasi lagi yang sama dan begitu proses seterusnya. Masing-masing gerakan periodik yang terlontar biasanya tidak stabil, akibatnya pada suatu nilai parameter tertentu akan sangat banyak gerakan periodik yang tidak stabil dalam suatu sistem. Ketika hal ini terjadi, dinamika sistem sudah sangat kompleks dan kondisi chaos terjadi lagi.
Untuk lebih jelasnya, ditinjau sebuah sistem dinamis yang diatur oleh satu set persamaan differensial, yaitu persamaan 2.5.
) ,...,
(x m
f dt dX
= (2.5)
Dengan m merupakan sebuah parameter, sistem ini akan mengalami serangkaian perubahan kualitatif ketika nilai parameter m divariasikan, perubahan ini terjadi sebelum sistem tersebut menunjukkan perilaku chaos.
Ketika nilai m dinaikkan, satu nilai Eigen dari sistem yang dilinierkan akan meninggalkan lintasan lingkaran, melewati nilai -1. Dan ketika nilai Eigen sama dengan -1, sebuah orbit dengan perioda yang baru akan muncul, dimana perioda orbit ini dua kali lebih besar dari orbit awalnya. Jadi, ruang fasa akan terlihat seperti osilasi yang periodik dengan bentuk yang berbeda dari lingkaran awal. Hal ini yang disebut dengan penggandaan perioda. Jika nilai m lebih dinaikkan maka akan terbentuk orbit periodik yang baru terbentuk akan menjadi tidak stabil, dan penggandaan perioda berikutnya akan terjadi kembali. Dan hal inilah yang dikatakan bahwa sistem tersebut mengalami keadaan chaos.
2.1.2. Chaos dan Pengaruhnya Dalam Sains
mendorong lahirnya “paradigma ilmu pengetahuan baru”. Selain itu, menurut mereka teori chaos ini juga dapat merepresentasikan ilmu pengetahuan baru yang lebih unggul ketimbang metode reduksionis Newton, Einstein dan Darwin yang kurang menarik (Kusmarni, 2008). Chaos tidak hanya memberi para ilmuwan suatu cara baru untuk melihat dunia, menjelaskan perilaku dalam ragam sistem yang luas, namun juga memahami daya tarik estetik yang besar dalam bentuk geometri kompleks yang fantastik (Walker, 1991). Studi chaos juga memiliki dua tujuan, yaitu untuk membuktikan pemahaman teoritik yang diperoleh dari studi model dan untuk membangun teori baru dengan menantang teori yang ada dengan penemuan-penemuan yang tidak diharapkan (oleh teori yang sudah ada) (Setiawan, 1991).
Beberapa bentuk gejala chaos yang timbul dalam beberapa bidang sains, yaitu:
a. Dalam bidang mekanika, Lorenz dan Duffing berhasil memodelkan sistem mekanik sederhana. Vibrasi yang bersifat chaos pada tiang penyangga pengeboran minyak lepas pantai juga merupakan persoalan teknik penting yang giat ditangani saat ini.
b. Dalam bidang geofisika, selain prakiraan cuaca, dinamika atmosfer dan lautan juga merupakan bagian dari dinamika nonlinier (chaos). Salah satu contohnya adalah fenomena gelombang El-Nino yang terjadi pada lautan pasifik. Model dinamo geomagnetik yang melibatkan persamaan differensial biasa juga menampakkan tingkah laku bersifat chaos.
d. Dalam bidang kedokteran, dinamika jantung yang dimodelkan dengan osilator periodik terkendala, serta ritmik jantung dan berbagai praktek klinik ternyata mengalami gejala chaos. Selain itu, gejala chaos dalam jaringan saraf dan EEG (Electroencephalographic) dan dalam aktivitas otak telah mendapat banyak perhatian beberapa tahun belakangan ini.
e. Dalam bidang ekologi dan ekonomi, dinamika chaos juga terus dikembangkan untuk dapat diterapkan dalam bidang ilmu tersebut. Salah satu fenomena chaos yang telah diteliti dalam bidang ini yaitu fenomena beruntun. Beberapa ahli fisika ekonomi telah melaporkan bahwa penyebab krisis negara-negara asia termasuk Indonesia di tahun 1997 merupakan efek beruntun dari kegagalan sistem ekonomi di beberapa titik. Dengan teori Chaos ini dapat membantu melihat skenario-skenario mana yang berpeluang lebih besar menimbulkan krisis dan mana yang tidak (Situngkir et al, 2010).
2.2. Pendulum Sederhana
θ
l
mg F O
T
D
θ
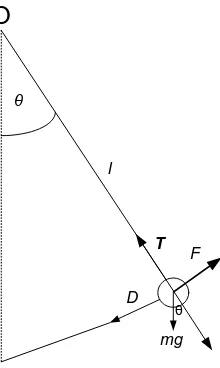
Gambar 2.3. Gaya-gaya yang bekerja pada pendulum, tegangan tali dan gaya berat, gaya peredam, dan gaya pengendali eksternal.
Karena massa yang terikat dapat bergerak bebas sepanjang lingkaran berjari-jari l disekitar sumbu O, maka massa tersebut dapat mengalami gerak rotasi dengan percepatan sudut α, atau θ yang merupakan turunan kedua dari posisi sudut,θ terhadap waktu. Sedangkan kecepatan tranlasinya adalah persamaan 2.6.
θ ω l l
v= = (2.6)
Dari gambar 2.2. terlihat bahwa gaya F bekerja pada massa, m yang posisinya terhadap titik asal O adalah l, maka torka yang bekerja pada massa tersebut adalah persamaan 2.7.
τ = l × F (2.7)
Torka adalah besaran vector yang besarnya diberikan oleh persamaan 2.8.
τ =lF sin θ (2.8)
Sedangkan hukum kedua Newton untuk gerak rotasi adalah persamaan 2.9.
Στ = I θ (2.9)
Dengan I adalah momen inersia yang besarnya adalah persamaan 2.10.
I = ml2 (2.10)
Gaya D pada gambar 2.3 adalah persamaan 2.11.
D = bv (2.11)
D = blθ (2.12)
Berdasarkan persamaan 2.8, 2.9, dan gambar 2.3. maka dapat diperoleh persamaan gerak pendulum dengan menganalisis gaya-gaya yang bekerja pada massa,m, yaitu gaya peredam, gaya gravitasi dan gaya pengendali. Hal ini diberikan oleh persamaan 2.13.
-Dl sin θ + (-mgl sin θ) + Fl sin θ = I θ (2.13) Kemudian ditetapkan bahwa gaya pengendali adalah fungsi waktu dan D bergantung pada kecepatan. Dengan mensibstitusi persamaan 2.10 dan 2.12 ke persamaan 2.13 dan menyusun ulang persamaan tersebut, maka diperoleh persamaan 2.14.
ml2θ+ bl2θ + mgl sin θ =F(t)l (2.14) Persamaan 2.15 merupakan persamaan differensial orde dua yang menggambarkan gerak pendulum sederhana.
Penyelesaian persamaan 2.15 terdiri dari dua bagian, yaitu penyelesaian transien dan penyelesaian keadaan tunak. Penyelesaian transien merupakan penyelesaian ketika sistem masih bergantung pada syarat-syarat awal (dengan sistem yang mendapat pengaruh redaman). Setelah sistem berjalan beberapa detik, penyelesaikan ini menjadi diabaikan karena penurunan amplitudo yang eksponensial, sehingga diperoleh penyelesaian keadaan tunak (Tipler, 1998).
2.2.1.Pendulum Sederhana Linier
Persamaan 2.15. pada subbab 2.2. merupakan persamaan gerak pendulum sederhana dengan memperhatikan seluruh gaya yang bekerja pada pendulum. Sedangkan persamaan gerak pendulum sederhana yang terdapat pada buku ajar fisika dasar biasanya hanya memperhatikan gaya gravitasi untuk gerak pendulum sederhana, dengan mengabaikan gaya peredam dan gaya pengendali. Atau dengan kata lain, F(t)
= 0 dan b = 0, sehingga persamaan 2.15. menjadi persamaan 2.16.
θ+ l g
sin θ = 0 (2.16)
Persamaan (2.15) merupakan persamaan nonlinier dan untuk simpangan yang kecil, θ << 1 radian maka sin θ≈ θ, maka persamaan (2.16) menjadi persamaan 2.17.
θ
Persamaan 2.17 merupakan persamaan differensial linier orde kedua yang menggambarkan persamaan gerak pendulum sederhana linier dengan
l g
merupakan frekuensi alami pendulum (frekuensi ketika tidak ada gaya redaman dan gaya pengendali). Penyelesaian persamaan 2.17 secara analitis diberikan oleh persamaan 2.18
θ(t) = θo cos t l g
(2.18) Dengan periode diberikan oleh persamaan 2.19.
g l
T =2π (2.19)
Gerak osilasi yang terjadi berupa sinusoidal terhadap waktu dan terus-menerus sepanjang waktu tanpa pelemahan. Sebagai contoh diberikan Grafik θ Vs t untuk θo =
Gambar 2.4. Grafik θ Vs t untuk θo = π/4 dan L = 0,5 m.
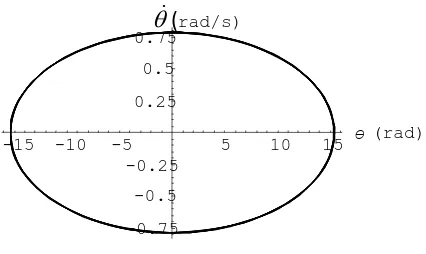
Dan grafik antara θ Vs θ menghasilkan gambar fasa dari pendulum ini, dengan bentuk elips tertutup seperti pada gambar 2.5. Dengan dimulai dari titik koordinat (15,0), titik yang yang disebut sebagai keadaan (state) akan bergerak melingkar membentuk sebuah orbit bebentuk elips hingga waktu yang tak berhingga.
Gambar 2.5. Grafik θ Vs θ dari pendulum sederhana merupakan gambar fasa pendulum dengan bentuk elips
Jika kondisi awal diubah sedikit, misalkan θo = π/3.5 maka akan diperoleh
perbandingan grafik Grafik θ Vs t seperti gambar 2.5. Pada grafik tersebut dapat dilihat bahwa dua gelombang sinusoidal berjalan dengan sedikit perbedaan amplitudo, dan kondisi ini tidak berubah hingga waktu yang tak berhingga.
-15 -10 -5 5 10 15 (rad)
-0.75 -0.5 -0.25 0.25 0.5 0.75θ
(rad/s)
0.5 1 1.5 2 t(s)
-0.75 -0.5 -0.25
0.25 0.5 0.75
0.5 1 1.5 2 t
s
Model pendulum ini tidak riil untuk dua hal penting, yaitu:
a. Sistem ini mengabaikan redaman yang mengakibatkan hilangnya gaya gerak pendulum secara berangsur-angsur, misalnya gaya gesek dengan udara. Sedangkan gerak sistem mekanika yang riil akan memperlihatkan adanya redaman jika tidak ada pengaruh gaya pengendali eksternal seperti yang telah dijelaskan pada subbab 2.2. Jadi, persamaan 2.17 telah gagal menjelaskan aspek penting ini.
b. Semua sistem yang riil akan memiliki beberapa derajat ketidaklinieran, yang menyebabkan adanya perilaku khusus pada sistem (Thompson et al,1986).
2.2.2. Pendulum Sederhana Nonlinier
Gerak pendulum yang sudah dibicarakan pada subbab 2.2.1 masih dengan asumsi bahwa sin θ ≈ θ yang memberikan hasil yang secara kualitatif benar. Tetapi, jika sudut simpangan pada pendulum sembarang atau tidak dibatasi dengan asumsi tersebut maka persamaan dari pendulum adalah persamaan 2.16 yang merupakan persamaan nonlinier. Sedangkan periode untuk pendulum ini diberikan oleh persamaan 2.20.
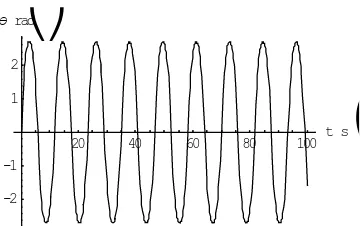
Penyelesaian persamaan 2.16 dapat dilakukan dengan metode Euler atau dengan Integral Eliptik. Persamaan ini juga dapat diselesaikan secara numerik dengan bantuan komputer digital. Sebagai contoh diberikan grafik-grafik penyelesaian persamaan 2.16 untuk θo = 0 dan θ = 1.95 rad/s dengan menggunakan Mathematica.
Grafik θ Vs t yang merupakan grafik simpangan pendulum ditunjukkan pada gambar 2.7.
20 40 60 80 100 t
s
-2 -1 1 2
rad
Gambar 2.7. Grafik θ Vs t untuk θo = 0 dan θ = 1.95 rad/s.
Sedangkan grafik θ Vs θ yang merupakan gambar fasa pendulum diberikan pada gambar 2.8.
Gambar 2.8. Grafik θ Vs θ dari pendulum sederhana nonlinier merupakan gambar fasa pendulum nonlinier
Dari gambar 2.7 dan 2.8 dapat terlihat bahwa pendulum juga tidak mengalami redaman sehingga gelombang yang dihasilkan berlangsung terus-menerus dengan
2
2
(rad)
-2 -1 1 2
amplitudo konstan dan perioda yang juga konstan. Dan dari persamaan 2.16 juga
= 0, maka sistem ini bersifat konservatif.
Jika kondisi awal diubah sedikit, yaitu θ = 1.9 rad/s, akan diperoleh perbandingan grafik θ Vs t seperti gambar 2.9. Dari grafik ini, diketahui bahwa dengan perubahan kondisi awal yang kecil ini menghasilkan amplitudo yang berbeda, dan karena perbedaan amplitudo ini maka akan dihasilkan sedikit perbedaan perioda juga, tetapi perbedaan gelombang ini juga bersifat periodik (Thompson et al,1986).
20 40 60 80 100 t
s
2.2.3. Pendulum Sederhana Nonlinier Teredam
Pada Subbab 2.2.2 telah diberikan penjelasan mengenai gerak pendulum sederhana nonlinier dengan mengabaikan efek redaman. Untuk gerak pendulum sederhana nonlinier teredam, persamaan geraknya adalah persamaan 2.15. dengan F(t) = 0, atau persamaan 2.21.
Dengan membuat pemisalan q =
m
maka persamaan 2.21 menjadi persamaan 2.22.
θ+ qθ+ 2
Penyelesaian persamaan 2.22 dapat dilakukan dengan menggunakan metode numerik seperti yang telah disebutkan pada subbab 2.2.2 atau dengan bantuan komputer digital. Sebagai contoh diberikan grafik-grafik hasil penyelesaian persamaan 2.22 dengan menggunakan Mathematica. Grafik θ Vs t untuk kondisi awal θo = 0; q=0.08; θo = 3 rad/s ditunjukkan pada gambar 2.10.
20 40 60 80 100 t
s
18 19 20 21
rad
Gambar 2.10. Grafik θ Vs t untuk kondisi awal θo = 0; q=0.08; θo = 3 rad/s. Dari gambar 2.10 ini dapat terlihat bahwa amplitudo berkurang secara lambat terhadap waktu, penurunan amplitudo ini merupakan penuruan eksponensial. Bila redaman kecil, pendulum berosilasi dengan frekuensi sudut mendekati frekuensi tak teredam. Sedangkan grafik θ Vs θ diberikan pada gambar 2.11.
2 3 4
rad-1 1 2 3
rad
s
Gambar 2.11.Grafik θ Vs θ untuk pendulum nonlinier teredam dengan orbit yang berpilin menuju satu titik.
diramalkan dengan tepat (Setiawan, 1991). Sifat disifatif dari sistem ini juga dapat
maka akan diperoleh perbandingan grafik seperti gambar 2.12.
20 40 60 80 100
Gambar 2.12. Perbandingan Grafik θ Vs t untuk kondisi awal q=0.08 dan q=0.081
2.2.4. Pendulum Sederhana Nonlinier Teredam dan Terkendali
Setelah gerak nonlinier teredam tetapi tak terkendali, masalah yang muncul kemudian adalah bagaimana jika gerak pendulum nonlinier tersebut terkendali melalui pengaruh luar. Dengan kehadiran pengaruh luar yang diberikan kepada sistem akan membuat sistem menjadi tak terprediksi.
Misalkan bahwa gaya luar yang bekerja pada sistem adalah persamaan 2.23
F(t) = A cos ΩD t (2.23)
Dengan mensubstitusikan persamaan 2.23 ke persamaan 2.15 maka diperoleh persamaan 2.24.
Dengan permisalan q =
m
, maka persamaan 2.24 dapat
θ+qθ+ Ω2sin θ
= aΩ2cosΩDt (2.25)
Persamaan 2.25 merupakan persamaan gerak untuk sistem pendulum nonlinier teredam dan terkendali. Gaya pengendali eksternal yang bekerja pada sistem ini dapat diperoleh dengan menggunakan arus bolak-balik (AC) yang diberikan secara horizontal (Pada sumbu x), jika massa, m berupa magnet yang dipasang secara vertikal. Sistem seperti ini biasa digunakan misalnya pada lengan robot (Hubbard, 2010).
Untuk sebuah sistem dinamis yang digambarkan melalui persamaan differensial orde dua, maka beberapa syarat penting yang harus dipenuhi, yaitu:
a. Sistem tersebut harus memiliki setidaknya tiga variabel dinamis.
b. Persamaan gerak harus memiliki suku nonlinier yang menggabungkan beberapa variabel.
Dan persamaan 2.26 dapat dipecah menjadi beberapa persamaan differensial orde pertama, yaitu:
D
Persamaan 2.26 merupakan suku nonlinier dari persamaan gerak sistem ini. Jadi, dengan nilai tertentu dari parameter-parameternya sistem ini akan menunjukkan gejala
chaos (Baker et al, 1996).
memotong dirinya sendiri hanya dapat terjadi pada ruang berdimensi tiga atau lebih (Setiawan, 1991).
Sistem pendulum seperti ini banyak dimanfaatkan pada robot, peredam massa-tertala pada bangunan untuk mereduksi hempasan angin keras, dan peredam massa pasif untuk beban gempa.
2.3. Metode Runge-Kutta
Salah satu metode numerik yang digunakan dalam penyelesaian persamaan differesial adalah metode Runge-Kutta. Metode ini mencapai ketelitian suatu pendekatan deret Taylor tanpa memerlukan kalkulasi turunan yang lebih tinggi. Banyak perubahan terjadi, tetapi semuanya dapat ditampung dalam bentuk umum dari persamaan 2.27.
yi+1 = yi + f (xi, yi, h) h (2.27)
dimana f (xi, yi, h) disebut suatu fungsi yang dapat diinterpretasikan sebagai sebuah slope rata-rata sepanjang interval. Fungsi tersebut dapat ditulis dalam bentuk umum
dalam persamaan 2.28.
f = a1 k1 + a2 k2 + … + an kn (2.28)
dimana setiap a adalah konstanta dan setiap k besarnya adalah persamaan-persamaan 2.29.
k1 = f(xi , yi )
k2 = f(xi + p1h, yi + q11 k1h)
k3 = f(xi + p2h, yi + q21 k1h + q22k2h) (2.29)
kn = f(xi + pn-1h, yi + qn-1,1 k1h + qn-1,2 k2h + ...+ qn-1,n-1 kn-1h)
Semua harga k berhubungan secara rekurensi. Artinya k1 muncul dalam persamaan untuk k2, yang muncul lagi dalam persamaan untuk k3, dan seterusnya. Rekurensi ini membuat metode RK efisien untuk kalkulasi oleh komputer (Raymond
et al, 1991).
Berbagai jenis metode Runge-Kutta dapat direncanakan dengan melaksanakan jumlah suku-suku yang berbeda pada fungsi tersebut seperti dinyatakan oleh n. untuk
y1 = y0+ h f(x0,y0) (2.30)
Dalam deret Taylor didapatkan persamaan 2.31.
...
Untuk metode RK orde kedua diberikan oleh persamaan-persamaan 2.32.
Metode RK orde tiga diberikan oleh persamaan-persamaan 2.33.
)
Metode RK orde empat diberikan oleh persamaan-persamaan 2.34.
y
Sedangkan untuk menyelesaikan persamaan differensial orde dua digunakan metode RK orde empat dengan terlebih dahulu membuat permisalan. Ditinjau persamaan differensial orde dua seperti pada persamaan 2.35.
Dengan y(x0) = y0, dan y’(x0)= y0’ . Persamaan 2.35. dibuat permisalan sehingga
diperoleh persamaan-persamaan 2.36.
)
Persamaan-persamaan 2.36. merupakan persamaan-persamaan simultan yang dapat juga dituliskan sebagai f1(x,y,z)=z dan f2(x,y,z)=f(x,y,z). Berdasarkan
persamaan-persamaan 2.36 tersebut, persamaan-persamaan differensial orde tersebut diselesaikan dengan mengikuti aturan metode RK orde empat pada persamaan 2.34 (Kandasamy et
al,1997).
BAB 3
ANALISIS MASALAH DAN PERANCANGAN PROGRAM
3.1. Analisis Masalah
3.1.1.Persamaan Gerak Pendulum Sederhana Nonlinier Teredam dan Terkendali
Persamaan differensial yang akan diselesaikan adalah persamaan gerak pendulum sederhana nonlinier teredam dan terkendali adalah persamaan 2.21. pada subbab 2.2.4. yang juga dapat dituliskan dengan persamaan 3.1.
t
pendulum dengan garis vertikal, b adalah koefisien redaman, Ω2 merupakan frekuensi alami (Seperti yang telah dijelaskan pada subbab 2.2.1) dari osilasi pendulum, ΩD dan A masing-masing adalah frekuensi dan amplitudo gaya pengendali eksternal. Dengan catatan bahwa efek dari percepatan vertikal sumbu adalah sebanding dengan medan gravitasi bergantung waktu (Gould et al, 1988).
D
Berdasarkan persamaan 3.2, maka dapat dikatakan bahwa sistem pendulum sederhana ini memiliki tiga variabel, maka lintasannya terletak pada ruang fasa 3 dimensi, ruang minimum terbentuknya gejala chaos. Dari persamaan 3.2. ini juga diketahui bahwa
F
sehingga ∇F=-q berarti sistem bersifat disipatif.
Agar sistem dapat menampilkan gejala chaos dengan jelas, maka ditentukan dalam keadaan tanpa dimensi (Dimensionless) yaitu m = g = l = 1 sehingga Ω2
=1. (Baker et al, 1996), berdasarkan hal ini, maka ditetapkan percepatan gravitasi, g sebesar 9,8 m/s2 dengan panjang tali, l sebesar 9,8 m sehingga tercapai keadaan Ω2=1 dan massa beban, m dianggap sama dengan 1 (Dimensionless) yang merupakan suatu bentuk penyederhaan yang sering digunakan dalam simulasi.
Persamaan 3.1. juga memiliki beberapa parameter yang nilainya dapat divariasikan, yaitu ΩD, A, dan b. Dalam hal ini, suatu ruang parameter tiga dimensi yang setiap titiknya mewakili ketiga parameter tersebut dapat ditentukan. Namun, penyelidikan menyeluruh terhadap perilaku sistem sebagai fungsi ketiga parameter tersebut tidak dapat dilakukan (Baker et al, 1996). Untuk itu dalam penelitian ini parameter yang divariasikan nilainya dalam menganalisis gejala chaos adalah amplitudo gaya pengendali eksternal, A, dengan memvariasikan a sementara ΩD dipertahankan konstan. Nilai ΩD ditentukan pada ΩD≈ Ω2 atau ΩD≈1 agar pendulum dapat menampilkan gejala chaos dengan jelas (Baker et al, 1996). Maka, dalam penelitian ini diberikan nilai ΩD=
3 2
.
Nilai kecepatan sudut awal pendulum, ω0 pada program dapat divariasikan,
rad/s, hal ini dimaksudkan agar ω0 > ΩD sehingga keadaan chaos dianalisis dengan jelas. Sedangkan nilai θ0 pada program terdiri dari dua, yaitu θ01 dan θ02. Hal ini
dimaksudkan untuk melihat perbandingan gerak pendulum jika kondisi awalnya diubah sedikit (0.01 rad). Adapun nilai yang dipakai sebenarnya adalah pada θ0 = θ01
= 0.8 rad.
Selanjutnya ditentukan nilai koefisien redaman, q < ω0 sehingga pendulum
tidak teredam kritis (Kembali ke keadaan seimbang tanpa osilasi), dalam penelitian ini ditentukan nilai q =
2
0
ω = 0.4.
Seperti yang telah dijelaskan sebelumnya, bahwa penentuan parameter-parameter di atas dimaksdukan agar keadaan-keadaan periodik, kuasiperiodik, dan
chaos pada sistem dapat dianalisis dengan jelas. Namun, sebagai perbandingan akan
diteliti pula keadaan-keadaan sistem bila nilai koefisien redaman, q dan panjang tali, l juga divariasikan (Hal ini diberikan pada subbab 4.4).
3.1.2. Penyelesaian dengan Metode Runge-Kutta Orde Empat
Persamaan 3.1. merupakan persamaan differensial biasa orde dua, untuk itu dalam menyelesaikanya dengan menggunakan metode Runge-Kutta orde empat, persamaan 3.1. dimisalkan dengan persamaan 3.3. dan persamaan 3.4.
ω
Persamaan 3.2. dan persamaan 3.3. merupakan persamaan-persamaan simultan dengan f1(t,θ,ω) = ω dan f2(t, θ,ω) = f(t, θ,ω). Dengan memberikan syarat awal θ0
k1n =f1 (tn,θn,ωn)
Setelah mendapatkan harga-harga k dan l pada persamaan 3.5. maka selanjutnya dihitung nilai-nilai θ dan ω.
Langkah-langkah pada persamaan 3.5 diulang sampai dengan tmax yang diberikan.
3.1.3. Penentuan Ruang Fasa dan Belahan Poincarè
Pada ruang fasa yang telah dijelaskan di atas, koordinat ω(t), dan θ(t) ditentukan pada t= 0, Δt, 2 Δt, 3 Δt, dan seterusnya, dengan Δt= T/150, T adalah
periode gaya pengendali eksternal dengan nilai, T = D Ωπ
2
. Agar dapat memperlihatkan
karakteristik sistem dinamis dengan baik, maka jejak lintasan yang muncul harus ditampilkan dengan jelas. Untuk itu ditentukan belahan Poincarè, dengan memplot titik-titik potong lintasan pada bidang setiap t = mT (m = 0,1,2,3,...). Dan dalam penelitian ini, titik pada dua langkah pertama dihilangkan untuk menghindari efek transien sistem. Dari hasil plot titik-titik tersebut, dapat ditentukan periodik atau tidaknya sistem. Jika lintasan-lintasannya yang berulang pada periode T, maka dapat dikatakan bahwa sistem tersebut periodik, sedangkan jika lintasannya tidak tepat berulang maka sistem tersebut dapat dikatakan tidak periodik.
3.2. Perancangan Program
Simulasi gerak pendulum sederhana nonlinier teredam dan terkendali ini diraancang dengan menggunakan seperangkat notebook yang menggunakan prosesor Intel Core 2
Duo dengan menggunakan bahasa pemrograman Mathematica Versi 6.
Adapun Proses perancangan program penelitian ini dirancang melalui tahapan-tahapan sebagai berikut:
a. Perancangan diagram alir (flowchart) dan algoritma simulasi penyelesaian persamaan gerak pendulum sederhana nonlinier teredam dan terkendali dengan metode Runge-Kutta orde 4.
3.2.1. Perancangan Diagram Alir (Flowchart)
Keterangan Gambar:
a. Input Data.
Simulasi dimulai dengan memberikan data-data input terlebih dahulu. Data input pada simulasi ini yaitu, frekuensi, percepatan gravitasi bumi, panjang tali pendulum, a, rentang waktu, dan syarat awal persamaan gerak pendulum, θ0 (θ01 dan θ02 ) dan ω0 serta nilai amplitudo gaya pengendali eksternal divariasikan.
b. Pendefinisian koefisien-koefisien Runge-Kutta orde 4.
Koefisien-koefisien Runge-Kutta orde 4 didefinisikan berdasarkan persamaan-persamaan 3.5.
c. Pendefinisian Orde Runge-Kutta.
Orde yang digunakan pada penelitian ini adalah orde 4.
d. Menyelesaikan Persamaan Gerak Pendulum dengan metode Runge-Kutta. Persamaan gerak pendulum nonlinier teredam dan terkendali diselesaikan dengan menggunakan langkah-langkah penyelesaian yang telah didefinisikan pada point c.
e. Membaca pemilihan tampilan.
Keterangan Gambar:
a. Input Data.
Simulasi dimulai dengan memberikan data-data input terlebih dahulu. Data input pada simulasi ini yaitu, frekuensi, percepatan gravitasi bumi, panjang tali pendulum, a, dan syarat awal persamaan gerak pendulum, θ0 dan ω0 serta nilai amplitudo gaya pengendali eksternal divariasikan.
b. Penentuan Sudut awal (dalam radian).
Sudut awal masukan adalah dalam derajat sehingga perlu dikonversi dalam radian, dengan
180 ) (
)
( 0
0
π θ
θ rad = derajat × .
c. Penyelesaian Persamaan gerak Pendulum Nonlinier Teredam dan Terkendali. Persamaan Gerak Pendulum yang merupakan persamaan differensial orde dua diselesaikan dengan menggunakan fungsi NDSolve yang terdapat pada bahasa pemrograman Mathematica Versi 6. Persamaan gerak yang diselesaikan ada dua, yaitu untuk nilai θ0 = θ01 dan θ0 =θ02.
d. Penentuan Komponen Tangensial dan Radial Pendulum.
Komponen tangensial dari pendulum yaitu, sin θ dan komponen radial pendulum, yaitu cos θ berdasarkan hasil penyelesaian persamaan gerak pendulum.
e. Menampilkan hasil visualisasi dari Pendulum sederhana.
Hasil visualisasi diperoleh dari fungsi Graphics yang terdapat pada bahasa pemrograman Mathematica Versi 6 berdasarkan komponen tangensial dan radial pada point d. Untuk nilai θ0 = θ01 warna pendulum adalah biru, dan
untuk θ0 = θ02 warna pendulum adalah hijau. Jika θ01= θ02 maka yang tampak
f. Menganimasikan visualisasi pendulum.
Hasil visualisasi dianimasikan sesuai dengan penyelesaian persamaan gerak pendulum sederhana nonlinier teredam dan terkendali dengan menggunakan fungsi Trigger pada bahasa pemrograman Mathematica Versi 6. Jika terdapat perbedaan yang kecil pada keadaan chaos, maka pendulum biru dan pendulum hijau akan memiliki gerak yang berbeda.
3.2.2. Algoritma Program Bantu
Adapun algoritma program bantu yang digunakan dalam penyelesaian persamaan gerak pendulum dengan metode Runge-Kutta orde 4 adalah sebagai berikut:
INPUT
a. ΩD = Frekuensi gaya pengendali eksternal
b. a = Variabel untuk memvariasikan amplitudo gaya pengendali eksternal
c. q = Variabel untuk merepresentasikan koefisien redaman
d. g = Percepatan gravitasi bumi
e. l = Panjang Tali Pendulum
f. θo = Sudut awal pendulum (θ pada t = 0) dalam program terdiri dari θ01 dan
θ02.
g. ω0 = Kecepatan sudut awal pendulum (ω pada t = 0)
h. p = Waktu maksimum terjadinya osilasi pendulum
PROSES
a. Membaca data masukan berupa , frekuensi gaya pengendali eksternal, percepatan gravitasi bumi, panjang tali pendulum, amplitudo gaya pengendali eksternal, koefisien redaman, waktu maksimum, dan syarat awal persamaan gerak pendulum, θ0 dan ω0.
b. Menentukan koefisien-koefisien Runge-Kutta orde 4.
d. Menyelesaikan persamaan gerak pendulum nonlinier teredam dan terkendali dengan metode Runge-Kutta orde 4 yang telah didefinisikan pada langkah point b.
e. Menentukan potongan lintasan pada rentang –π sampai +π sebagai ruang fasa. f. Menentukan titik-titik potong lintasan pada bidang setiap t = mT (m =
0,1,2,3,...) sebagai Belahan Poincarè.
OUTPUT
a. Hasil ditampilkan dengan menekan tombol Shift + Enter. b. Mem-plot hasil penyelesaian, yaitu plot posisi sudut vs waktu. c. Mem-plot kecepatan sudut vs posisi sudut (ruang fasa).
d. Mem-plot belahan Poincaré.
e. Mem-plot hasil penyelesaian, yaitu plot posisi sudut vs waktu untuk θ01 dan
θ02.
Sedangkan algoritma program bantu yang digunakan dalam animasi gerak pendulum adalah sebagai berikut:
INPUT
a. ΩD = Frekuensi gaya pengendali eksternal
b. a = Variabel untuk memvariasikan amplitudo gaya pengendali eksternal
c. q = Variabel untuk merepresentasikan koefisien redaman
d. g = Percepatan gravitasi bumi
e. l = Panjang Tali Pendulum
f. θo = Sudut awal pendulum (θ pada t = 0) dengan satuan derajat dalam
program terdiri dari θ01 dan θ02.
g. ω0 = Kecepatan sudut awal pendulum (ω pada t = 0) dengan satuan rad/s
PROSES
a. Membaca data masukan berupa frekuensi gaya pengendali eksternal,
b. Menkonversi nilai sudut awal ke dalam radian.
c. Menyelesaikan persamaan gerak pendulum nonlinier teredam dan terkendali dengan fungsi NDSolve.
d. Menentukan komponen tangensial dan radial dari pendulum.
e. Memvisualisasikan pendulum sederhana dengan fungsi Graphics berdasarkan komponen tangensial dan radial.
f. Menganimasikan visualisasi pendulum dengan fungsi Trigger.
OUTPUT
a. Hasil ditampilkan dengan menekan tombol Shift + Enter. b. Menampilkan hasil visualisasi pendulum sederhana.
BAB 4
HASIL DAN PEMBAHASAN
Hasil eksekusi program simulasi pada Lampiran A adalah berupa grafik-grafik keluaran dari penyelesaian persamaan gerak pendulum sederhana nonlinier teredam dan terkendali dengan metode Runge-Kutta orde 4 yang terintegrasi pada suatu tampilan GUI seperti yang ditunjukkan pada gambar 4.1. Tampilan grafik pada hasil eksekusi program tersebut dapat diganti dengan mengubah menu “Tampilan” yang berbentuk Pop Up Menu. Grafik-grafik keluaran tersebut meliputi Grafik Simpangan ( Plot posisi sudut vs waktu ), ruang fasa ( Plot kecepatan sudut vs posisi sudut ), dan belahan Poincarè. Ketiga grafik keluaran ini digunakan untuk menganalisis perilaku sistem pendulum sederhana nonlinier, yaitu periodik, kuasiperiodik, atau chaos secara kualitatif. Analisis kualitatif tersebut diperkuat oleh perbandingan plot posisi sudut vs waktu yang menunjukkan sensitivitas sistem terhadap kondisi awal dan menunjukkan karakteristik chaos deterministik dalam sistem, yaitu perubahan yang kecil pada kondisi awal dapat menyebabkan perubahan besar dan tak terprediksi untuk sistem
chaos.
Pada gambar 4.1. dapat dilihat bahwa nilai – nilai dari ω0, θ0, l, q, dan a dapat
divariasikan, tetapi dalam analisis gejala chaos nilai yang dipakai pada subbab 4.1, 4.2, dan 4.3 adalah ω0 = 0.8, dan θ0 = 0.8, nilai q = 0.4, Ω2= 1, ΩD=
3 2
dengan memvariasikan nilai dari amplitudo gaya eksternal yang direpresentasikan oleh a. Dan untuk melihat karakteristik sensitivitas terhadap kondisi awal, nilai θ02 dapat
Gambar 4.1. Hasil eksekusi Program “Simulasi Gerak Pendulum Sederhana Nonlinier Teredam Dan Terkendali” pada Lampiran A
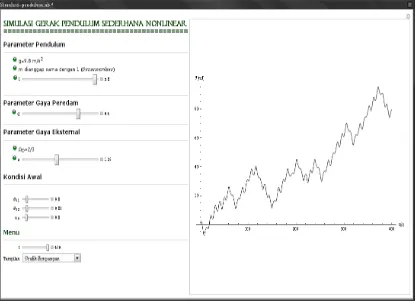
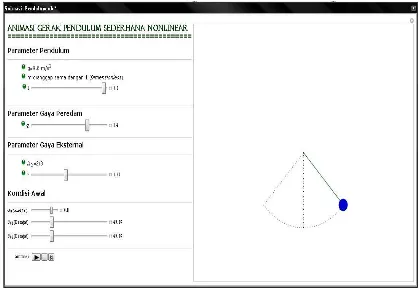
Sedangkan hasil eksekusi program animasi gerak pendulum sederhana nonlinier yang terdapat pada Lampiran B ditunjukkan pada gambar 4.2. Pada gambar 4.2 dapat dilihat bahwa nilai dari ω0, θ0, l, q, dan a, tetapi nilai yang dipakai dalam
Gambar 4.2. Hasil eksekusi program “Animasi Gerak Pendulum Sederhana
Nonlinier” pada lampiran B.
4.1. Keadaan Periodik
Keadaan periodik dari pendulum sederhana nonlinier teredam dan terkendali dengan ω0 = 0.8, dan θ0 = 0.8, nilai q = 0.4, Ω2= 1, ΩD=
3 2
Gambar 4.3. Grafik θ Vs t dengan a = 0.3, q = 0.4, Ω2= 1, ΩD=
3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
Gambar 4.3. menunjukkan perilaku simpangan θ pada setiap saat (t) untuk pemilihan amplitudo gaya pengendali eksternal yang kecil yaitu pada a = 0,3. Dalam kondisi ini terdapat dua daerah osilasi. Osilasi yang pertama terjadi pada rentang waktu, 0-20 s, pada kondisi ini pengaruh redaman masih berpengaruh sehingga osilasi mengarah ke keadaan transien dengan amplitudonya mengalami penurunan secara ekponensial. Pengaruh redaman ini selanjutnya dapat diantisipasi oleh gaya pengendali eksternal sehingga pendulum mengalami osilasi yang kedua pada keadaan tunak, yaitu pada rentang waktu 20 s sampai waktu tak berhingga (Osilasi harmonik) dengan frekuensi gaya pengendali eksternal, ΩD. Jika keadaan awal diubah sedikit, yaitu θ0 menjadi 0.81, maka perbandingan plot posisi sudut vs waktu yang
ditunjukkan pada gambar 4.4 untuk θ01 = 0.8 (Hitam) dan θ02 = 0.81 (Hijau)
menunjukkan bahwa grafik yang tampak hanya untuk θ02 = 0.81 karena kedua lintasan
Gambar 4.4. Grafik θ Vs t dengan a = 0.3, q = 0.4, Ω2= 1, ΩD= 3 2
pada dua kondisi awal ω0 = 0.8, dan θ01 = 0.8 dan θ01 = 0.81 berjalan selaras.
Gambar 4.5. Ruang fasa dengan a = 0.3, q = 0.4, Ω2= 1, ΩD= 3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
menandakan bahwa pendulum bersifat periodik, dengan keadaan akhirnya datang dengan keadaan awalnya.
Gambar 4.6. Belahan Poincarè dengan a = 0.3, q = 0.4, Ω2
= 1, ΩD=
3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
Untuk dapat memperlihatkan jejak lintasan dalam kasus ini secara lebih jelas, maka dipergunakan belahan Poincarè. Dalam kasus periodik belahan Poincarè diberikan pada gambar 4.6. Berdasarkan gambar 4.5. telah diketahui bahwa lintasan dari pendulum sederhana adalah orbit tertutup, maka belahan Poincarè yang terbentuk hanya satu titik, artinya lintasan-lintasan pendulum sederhana hanya memotong bidang pada satu titik tetap.
Hasil animasi untuk a = 0.3 juga menunjukkan bahwa pendulum sederhana pada awalnya berayun dengan sudut simpangan lebih dari 0.8 rad, tetapi kemudian mengalami osilasi harmonis pada sudut lebih kecil dari 0.8 rad, atau berdasarkan gambar 4.3, berada pada sudut simpangan 0.5 rad. Dan keadaan tersebut berlangsung terus-menerus hingga waktu tak berhingga.
4.2. Keadaan Kuasiperiodik
chaos itu sendiri terjadi bila suatu sistem mengalami penggandaan perioda beberapa
kali. Pada penelitian ini, keadaan kuasiperiodik tercapai pada a=1.23 untuk ω0 = 0.8,
dan θ0 = 0.8, nilai q = 0.4, Ω2= 1, ΩD=
3 2
. Hal ini ditunjukkan pada gambar 4.7, 4.8, 4.9 dan 4.10.
Gambar 4.7. Grafik θ Vs t dengan a = 1.23, q = 0.4, Ω2= 1, ΩD=
3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
Hasil yang ditunjukkan pada gambar 4.7. memperlihatkan bahwa pendulum bergerak berlawanan arah awal pendulum dan mengalami gerakan yang tidak harmonik lagi. Pada grafik ini juga terlihat keadaan transien dari sistem terjadi pada 60 s pertama, selanjutnya posisi sudut bergerak berlawanan arah dengan dua daerah osilasi, yaitu pada rentang 60 s – 250 s dan pada rentang 250 s – 400 s, artinya lintasan tetap mengalami perulangan tetapi butuh waktu lebih lama untuk melihat perulangan tersebut, sehingga tampak lebih kompleks. Hal tersebut dikatakan sebagai penggandaan periode, namun sistem ini masih bersifat periodik.
Jika keadaan awal diubah sedikit, yaitu θ0 menjadi 0.81, maka perbandingan
plot posisi sudut vs waktu untuk θ01 = 0.8 dan θ02 = 0.81 menunjukkan bahwa kedua
Gambar 4.8. Grafik θ Vs t dengan a = 1.23, q = 0.4, Ω2= 1, ΩD=
3 2
pada dua kondisi awal ω0 = 0.8, dan θ01 = 0.8 dan θ01 = 0.81 masih berjalan selaras.
Gambar 4.9. Ruang fasa dengan a = 1.23, q = 0.4, Ω2= 1, ΩD= 3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
juga menyebabkan perubahan keadaan yang drastis dari pendulum, hal ini menyebabkan pecahnya orbit awal. sehingga lintasan bergerak dengan dua periode yang berbeda, atau mengalami penggandaan periode.
Gambar 4.10. Belahan Poincarè dengan a = 1.23, q = 0.4, Ω2
= 1, ΩD=
3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
Dari gambar 4.10. dapat dilihat bahwa titik potong yang terbentuk adalah dua titik tetap, artinya lintasan-lintasan gerak pendulum sederhana tidak hanya bergerak memotong bidang pada satu titik, tetapi juga memotong bidang pada titik koordinat lain pada beberapa waktu kemudian (Dua periode). Untuk titik pada koordinat (0.5 , 1), mengindikasikan bahwa terdapat lintasan-lintasan yang memotong bidang tidak tepat pada titik tersebut. Hal ini terjadi karena adanya efek transien sistem seperti yang juga terlihat pada ruang fasa.
Hasil animasi juga menunjukkan bahwa pendulum terus bergerak berlawanan arah awal posisi sudut pendulum. Hal sesuai dengan penjelasan tentang grafik θ vs t untuk a = 1.23.
4.3. Keadaan Chaos.
chaos sudah tercapai pada a = 1.36 untuk ω0 = 0.8, dan θ0 = 0.8, nilai q = 0.4, Ω2= 1,
D Ω =
3 2
. Hal ini ditunjukkan pada gambar 4.11, 4.12, 4.13 dan 4.14.
Gambar 4.11. Grafik θ Vs t dengan a = 1.36, q = 0.4, Ω2
= 1, ΩD=
3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
Seperti yang telah dijelaskan pada subbab 2.1, bahwa kondisi chaos selain memiliki gerakan yang kompleks juga memiliki kesensitifan yang ekstrim terhadap kondisi awal. Hal ini ditunjukkan pada gambar 4.12, dimana terdapat dua keadaan awal yang berbeda sedikit yaitu senilai 0.01 yang pada awalnya bergerak selaras, namun pada 20 sekon kemudian kedua gerakan akan berubah dan menyebar makin jauh satu dengan yang lainnya. Menurut Walker (1991, hal: 460) hal ini dapat diandaikan seperti mengurai seutas tali menjadi dua helai individual. Sehingga dapat dikatakan bahwa sistem yang bersifat chaos menjadi tidak dapat diprediksi, karena dengan adanya gangguan sekecil apapun, gerakan sistem akan berubah jauh dari perkiraan awal.
Gambar 4.12. Grafik θ Vs t dengan a = 1.36, q = 0.4, Ω2= 1, ΩD=
3 2
pada dua kondisi awal ω0 = 0.8, θ01 = 0.8 (Hitam) dan ω0 = 0.8, θ02 = 0.81 (Hijau).
bergantung pada masing-masing sistem. Dalam gambar 4.12. terlihat bahwa prediksi untuk sistem pendulum sederhana ini dapat diketahui pada sekitar 20 sekon pertama.
Gambar 4.13. Ruang fasa dengan a = 1.36, q = 0.4, Ω2
= 1, ΩD=
3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
Gambar 4.14. Belahan Poincarè dengan a = 1.36, q = 0.4, Ω2= 1, ΩD= 3 2
pada kondisi awal ω0 = 0.8, dan θ0 = 0.8.
Lintasan-lintasan pendulum sederhana yang ditunjukkan pada gambar 4.13 diperjelas dengan belahan Poincarè pada gambar 4.14. Dapat dianalisis bahwa Lintasan-lintasan pendulum sederhana memotong bidang pada titik-titik yang jumlahnya sangat banyak dan membentuk suatu pola, dari hal ini dapat dikatakan bahwa periode sistem sangat banyak bahkan tak berhingga untuk waktu tak hingga.
Dari gambar 4.14 juga dapat dijelaskan salah satu kunci untuk memahami tingkah laku chaos -sensitivitas terhadap kondisi awal- yaitu penjelasan mengenai operasi mengulur (stretching) dan melipat (folding). Operasi mengulur terjadi antara
1
Hasil animasi juga menunjukkan gerakan pendulum sederhana yang berayun dengan tidak beraturan. Pendulum berputar hingga melewati titik maksimum, hal ini terjadi karena energi yang besar yang diserap pendulum dari gaya pengendali eksternal menyebabkan pendulum memiliki energi mekanik yang besar hingga dapat melewati titik maksimum. Namun, gerakan dari pendulum ini tak pernah berulang. Selain itu kecepatan pendulum juga tidak pernah mengalami keadaan tunak. Untuk dua kondisi awal yang hanya berbeda 0,01, yaitu θ01 = 0.8 (Pendulum Hitam) dan θ02
= 0.81 (Pendulum Hijau) pada t < 20 sekon maka lintasan dua pendulum akan berubah jauh.
4.4. Perbandingan Keadaan Sistem Untuk Variasi Nilai Beberapa Parameter
Selain analisis gejala chaos untuk nilai kondisi awal (θ0=0.8 rad dan ω0 = 0.8 rad/s),
D Ω =
3 2
, Ω2
=1, dan q = 0.4 seperti yang telah dijelaskan pada subbab-subbab sebelumnya, maka sebagai perbandingan diteliti juga beberapa keadaan sistem untuk beberapa variasi nilai parameter-parameter lainnya, yaitu:
a. Koefisien Redaman, q ( 0.1 – 0.5 dengan interval 0.1) untuk kondisi awal yang sama (θ0=0.8 rad dan ω0 = 0.8 rad/s), frekuensi gaya eksternal, ΩD=
3 2
,
Tabel.4.1. Hasil Pengujian Keadaan Sistem Untuk Variasi Nilai Koefisien Redaman, q dan Amplitudo Gaya Pengendali Eksternal, a
No. θ0 ω0 Ω2 q ΩD a Keadaan
Sistem 1. 0.8 0.8 1 0.1
3
2 0.1-0.3 Periodik 0.37-0.45 Kuasiperiodik 0.46-3.0 Chaos
2. 0.8 0.8 1 0.2
3
2 0.1-0.45 Periodik 0.46-0.49 Kuasiperiodik 0.5-3.0 Chaos
3. 0.8 0.8 1 0.3
3
2 0.1-0.62 Periodik 0.63-0.75 Kuasiperiodik 0.76-3.0 Chaos
4. 0.8 0.8 1 0.4
3
2 0.1-1.22 Periodik 1.23-1.35 Kuasiperiodik 1.35-3.0 Chaos
5. 0.8 0.8 1 0.5
3
2 0.1-1.3 Periodik 1.31-1.49 Kuasiperiodik
1.5-3 Chaos
Dari tabel 4.41. dapat terlihat bahwa nilai koefisien redaman, q juga mempengaruhi perubahan keadaan sistem dari periodik ke chaos. Pada nilai q yang kecil, keadaan chaos sudah tercapai bahkan sebelum amplitudo gaya pengendali eksternal, a mencapai nilai 1.0 dan semakin besar nilai koefisien radaman, q maka semakin besar pula nilai amplitudo gaya pengendali eksternal yang dibutuhkan untuk mencapai keadaan chaos. Hal ini karena semakin kecil koefisien redaman maka semakin kecil pula dibutuhkannya energi gaya pengendali eksternal yang diberikan untuk mengisi kembali energi yang terdisipasi.
b. Panjang tali, l (1.8-9.8 dengan interval 2) untuk kondisi awal yang sama (θ0=0.8 rad dan ω0 = 0.8 rad/s), dan frekuensi gaya eksternal,ΩD=
3 2