ﻳﺤرﻟاﻦ ﺤرﻟاﷲا ﺳﺑ
Alhamdulillah segala puji kehadirat illahirabbi Allah SWT yang telah
memberikan segala karunia, nikmat iman, nikmat islam, dan nikmat kesehatan
yang berlimpah dari dunia sampai akhirat. Shalawat dan Salam senantiasa
dicurahkan kepada Nabi Muhammad SAW beserta seluruh keluarga, sahabat, dan
para pengikutnya sampai akhir zaman.
Selama penulisan skripsi ini, penulis menyadari sepenuhnya bahwa tidak
sedikit kesulitan dan hambatan yang dialami. Namun, berkat kerja keras, doa,
perjuangan, kesungguhan hati dan dorongan serta masukan-masukan yang positif
dari berbagai pihak untuk penyelesaian skripsi ini, semua dapat teratasi. Oleh
sebab itu penulis mengucapkan terimakasih kepada:
1. Prof. Dr. Dede Rosyada, MA., Dekan Fakultas Ilmu Tarbiyah dan Keguruan
UIN Syarif Hidayatullah Jakarta.
2. Ibu Maifalinda Fatra, M.Pd., Ketua Jurusan Pendidikan Matematika Fakultas
Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
3. Bapak. Otong Suhyanto, M.Si., Sekretaris Jurusan Pendidikan Matematika
Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
4. Bapak Dr. Kadir, M.Pd., Dosen Pembimbing I yang penuh kesabaran,
bimbingan, waktu, arahan dan semangat dalam membimbing penulis selama
ini.
5. Bapak Abdul Muin, S.Si, M.Pd., sebagai dosen pembimbing II yang telah
memberikan bimbingan, kesabaran, arahan, waktu dan semangat dalam
membimbing penulis selama ini.
6. Seluruh Dosen Jurusan Pendidikan Matematika UIN Syarif Hidayatullah
Jakarta yang telah memberikan ilmu pengetahuan serta bimbingan kepada
penulis selama mengikuti perkuliahan, semoga ilmu yang telah Bapak dan Ibu
berikan mendapatkan keberkahan dari Allah SWT.
S.Pd yang telah memberikan izin untuk melakukan penelitian di Madrasah
Ibtidaiyah Pembangunan Ciputat, Ibu Lulu, S.Pd yang telah membantu penulis
melaksanakan penelitian di kelas IV-G dan IV-H. Seluruh karyawan dan guru
Madrasah Ibtidaiyah Pembangunan yang telah membantu melaksanakan
penelitian.
9. Pimpinan dan staff Perpustakaan Umum dan Perpustakaan Fakultas Ilmu
Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta yang telah
membantu penulis dalam menyediakan serta meberikan pinjaman literatur
yang dibutuhkan.
10.Keluarga tercinta Ayahanda Suparno, Ibunda Suryatin yang tak henti-hentinya
mendoakan, melimpahkan kasih sayang dan memberikan dukungan moril dan
materil kepada penulis. Kakanda tercinta Heru Suparyanto, S.E dan Hetty
Sumayanti, serta semua keluarga yang selalu mendoakan, mendorong penulis
untuk tetap semangat dalam mengejar dan meraih cita-cita.
11.Teman-teman seperjuangan Jurusan Pendidikan Matematika Angkatan ’06,
kelas A dan B terutama Cucu Suryani, Tri Nopriana, Lidiya Ekawati,
Rahmawati, Desy Bangkit Arihati, Priska Sri Hardiana, Lilis Marina Angraini
dan Isti Pramita
12.Kakak Kelas angkatan ’04, angkatan ’05 khususnya Kak Fajrina, Kak
Sarmadan, Kak Roslani, S.Pd yang membantu dan mempermudah penulis
dalam menyusun skripsi.
Ucapan terima kasih juga ditunjukan kepada semua pihak yang namanya
tidak dapat penulis sebutkan satu persatu. Penulis hanya dapat memohon dan
berdoa mudah-mudahan bantuan, bimbingan, dukungan, semangat, masukan dan
doa yang telah diberikan menjadi pintu datangnya ridho dan kasih sayang Allah
SWT di dunia dan akhirat. Amin yaa robbal’alamin.
yang membaca skripsi ini akan penulis terima dengan hati terbuka.
Penulis berharap semoga skripsi ini akan membawa manfaat yang
sebesar-besarnya bagi penulis khususnya dan bagi pembaca sekalian umumnya.
Jakarta, Oktober 2010
Penulis
ABSTRAK ... i
KATA PENGANTAR ... ii
DAFTAR ISI ... v
DAFTAR TABEL ... vii
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... ix
BAB I PENDAHULUAN ... 1
A. Latar belakang masalah ... 1
B. Identifikasi Masalah ... 5
C. Pembatasan Masalah ... 5
D. Perumusan Masalah ... 6
E. Tujuan Penelitian ... 6
F. Kegunaan Penelitian ... 6
BAB II Deskripsi Teoritik, Kerangka Berpikir dan Hipotesis Penelitian ... 8
A. Deskripsi Teoritik ... 8
1. Hasil Belajar Matematika ... 8
a. Pengertian Belajar ... ... 8
b. Pengertian Matematika ... ... 10
c. Konsep Pembagian Bilangan cacah ... 11
d. Hasil Belajar Matematika ... 14
2. B. Hasil C. Keran Pola Bilangan ... 17
a. Pengertian Teknik Pola Bilangan ... 17
b. Pembagian Bilangan Cacah dengan Pola Bilangan ... 20
1. Pembagian dengan Satuan ... 20
2. Pembagian dengan Puluhan ... 23
3. Pembagian Bersisa ... 25
Penelitian Relevan ... 27
gka Berpikir ... 27
BA
DA LA
C. Populasi dan Sampel ... 31
D. Instrumen Penelitian ... 31
E. Teknik Pengumpulan Data ... 32
F. Analisis Instrumen ... 32
G. Teknik Analisis Data ... 37
1. Uji Prasyarat ... 37
2. Uji Perbedaan Dua Rata-rata ... 39
3. Analisis Deskriptif ... 40
BAB IV HASIL PENELITIAN DAN PEMBAHASAN ... 42
A. Deskripsi Data ... 42
1. Hasil Belajar Matematika Siswa Kelas Eksperimen ... 43
2. Hasil Belajar Matematika Siswa Kelas Kontrol ... 45
B. Hasil Pengujian Prasyarat Analisis ... 50
1. Uji Normalitas Tes Hasil Belajar Matematika Siswa ... 50
a. Uji Normalitas Kelas Eksperimen ... 50
b. Uji Normalitas Kelas Kontrol ... 50
2. Uji Homogenitas Tes Hasil Belajar Matematika Siswa ... 51
C. Pengujian Hipotesis dan Pembahasan ... 52
D. Keterbatasan Penelitian ... 62
B V KESIMPULAN DAN SARAN ... 64
A. Kesimpulan ... 64
B. Saran ... 65
FTAR PUSTAKA ... 66 MPIRAN-LAMPIRAN
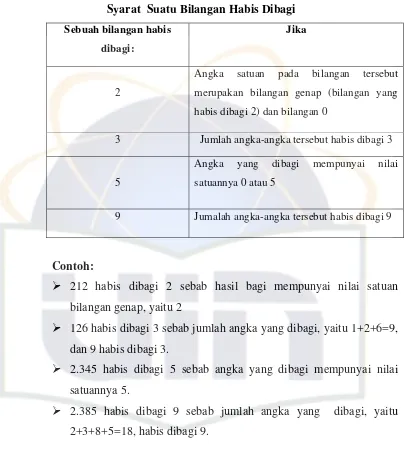
Tabel 1 Syarat Suatu Bilangan Habis Dibagi ... 14
Tabel 2 Rekapitulasi Hasil Uji Validitas, Daya Pembeda dan Tingkat Kesukaran ... 36
Tabel 3 Katagori Skor Penilaian Hasil Observasi ... 40
Tabel 4 Katagori Jumlah Skor Penilaian Hasil Observasi ... 41
Tabel 5 Rangkuman Skor Akhir Hasil Belajar Siswa Kelas Eksperimen .... 43
abel 6 Distribus Frekuensi Hasil Belajar Matematika Siswa Kelas Eksperimen ... 44
abel 7 Rangkuman Skor Akhir Hasil Belajar Siswa Kelas Kontrol ... 46
Tabel 8 Distribusi Freku atika Siswa Kelas Kontrol ... 47
Tabel 9 Perbandingan Hasil Belajar Matematika Siswa Antara Eksperimen ... 51
abel 11 T T ensi Hasil Belajar Matem dan Kelas Kontrol ... 49
Tabel 10 Rangkuman Hasil Uji Normalitas ... T Rangkuman Hasil Uji Homogenitas ... 51
Tabel 12 Hasil Uji-t ... 52
Tabel 13 Deskriptor Penilaian Observasi ... 54
Tabel 13 Hasil Pengamatan Proses Pembelajaran Siswa ... 55
ambar 1 Kolom Pola Bilangan Pembagian ... 19
ambar 2 Grafik Pemikiran ... 28
ambar 3 Grafik Histogram dan Poligon Distribusi Frekuensi Hasil Belajar
Matematika Siswa Kelompok Eksperimen ... 45
Gambar 4 Grafik Histogram dan Poligon Distribusi Frekuensi Hasil Belajar
Matematika Siswa Kelompok Kontrol ... 48
Gambar 5 Kurva Uji Perbedaan Data Kelas Ekperimen dan Kelas Kontrol ... 52
Gambar 6 Pekerjaan Kelompok Pada LKS 3 ... 58
Gambar 7 Pekerjaan Kelompok Pada LKS 4 ... 60
Gambar 8 Perbandingan Hasil Pengerjaan Ujian Postes siswa ... 61 G
G
G
ampiran 2 RPP Kelas Eksperimen dan Kelas Kontrol ... 69
ampiran 3 Lembar Kerja Siswa (LKS) ... 98
ampiran 4 Kisi-kisi Soal Uji Coba Instrumen Tes Hasil Belajar Sebelum Validitas ... 138
ampiran 5 Soal Uji Coba Instrumen ... 140
ampiran 6 Kisi-kisi Soal Uji Coba Instrumen Tes Hasil Belajar Setelah Validitas ... 143
ampiran 7 Soal Instrumen Tes Hasil Belajar ... 145
Lampiran 8 Kunci Jawaban Belajar ... 148
Lampiran 9 Perhitungan Validitas Tes Pilihan Ganda ... 149
Lampiran 10 Perhitungan Reliabilitas Tes Pilihan Ganda ... 150
... 153
dus, bagian L L L L L L Soal Instrumen Tes Hasil Lampiran 11 Perhitungan Tingkat Kesukaran Tes Pilihan Ganda ... 151
Lampiran 12 Perhitungan Daya Pembeda Tes Pilihan Ganda ... 152
Lampiran 13 Hasil Perhitungan Validitas, Daya Pembeda dan Tingkat Kesukaran Tes ... Lampiran 14 Perhitungan Distribusi Frekuensi, Mean, Median, Modus, Varians dan Simpangan Baku Kelas Eksperimen ... 157
Lampiran 15 Perhitungan Distribusi Frekuensi, Mean, Median, Mo Varians dan Simpangan Baku Kelas Kontrol ... 161
Lampiran 16 Uji Normalitas Kelas Eksperimen ... 165
Lampiran 17 Uji Normalitas Kelas Kontrol ... 166
Lampiran 18 Perhitungan Uji Homogenitas ... 167
Lampiran 19 Perhitungan Pengujian Hipotesis ... 168
Lampiran 20 Meletakkan Hasil Bagi dan Sisa Bagi dengan Menggunakan Teknik Pola Bilangan ... 169
Lampiran 21 Perbandingan Mengerjakan Soal Operasi Pem
Dengan Menggunakan Teknik Pola Bilangan dan Teknik
x
Lampiran 25 Tabel Nilai Kritis Distribusi Kai Kuadrat (Chi Square) ... 177 Lampiran 26 Tabel Nilai Kritis Distribusi F ... 179
A. Latar Belakang Masalah
Pendidikan merupakan hal yang sangat penting bagi setiap
manusia, karena pendidikan mempunyai peranan yang sangat penting
dalam menunjang segala aspek di kehidupan manusia. Salah satunya
terlihat dari kemajuan teknologi, sekarang ini penggunaan teknologi
semakin canggih, hal ini tidak terlepas dari peran pendidikan itu sendiri,
yang memberikan kemudahan-kemudahan bagi manusia.
Kecanggihan teknologi juga memberikan kemudahan pada proses
pembelajaran matematika di sekolah, pada contoh yang sangat real yaitu
hampir keseluruhan proses pembelajaran di sekolah guru menggunakan
laptop dan LCD (liquid crystal display). Bahkan bukan hanya laptop dan LCD (liquid crystal display) saja yang dijadikan alat teknologi dalam proses pembelajaran, tetapi internet adalah kecanggihan teknologi yang
menjadi acuan para guru dalam mengumpulkan atau menilai tugas siswa
dalam pelajaran matematika.
Meskipun kecanggihan teknologi dapat memberikan kemudahan
pada pelajaran matematika, tidak menutupi kemungkinan bahwa beberapa
siswa mengalami kesulitan dalam belajar matematika. Hal ini didukung di
dalam buku Cara Genius Menguasai Tabel Perkalian, Gunawan
menuliskan, “anak pasti akan berpikir bahwa belajar matematika itu sangat
sulit dan membosankan dan akhirnya dia tidak suka dengan pelajaran
matematika.”1
Dampak dari siswa yang tidak suka dengan pelajaran matematika
dapat dilihat dari hasil belajar matematika. Masalah utama dalam
pendidikan di Indonesia adalah rendahnya hasil belajar siswa di sekolah.
1
Adi W. Gunawan, Cara Genius menguasai Tabel Perkalian, (Jakarta: PT Gramedia Pustaka Utama, 2007), hal.7
Terutama yang paling mencolok adalah rendahnya prestasi siswa dalam
bidang matematika. Padahal jam pengajaran matematika di Indonesia tidak
digolongkan sedikit dari negara-negara lain. Pernyataan ini didukung oleh
hasil penelitian TIMMS yang dilakukan oleh Frederick K. S. Leung pada
2003, “jumlah jam pengajaran matematika di Indonesia jauh lebih banyak
dibandingkan Malaysia dan Singapura. Selama satu tahun, siswa di
Indonesia rata-rata mendapat 169 jam pelajaran matematika. Sementara di
Malaysia hanya mendapat 120 jam dan Singapura 112 jam.” 2. Walaupun jam pengajaran matematika di Indonesia jauh lebih banyak dari
negara-negara lain, termasuk negara-negara Malaysia dan Singapura, tetap tidak
menutupi kemungkinan bahwa hasil belajar matematika di Indonesia lebih
rendah dari negara-negara lain, bahkan negara tetangga pun sendiri yaitu
negara Malaysia dan negara Singapura. Peneliti mencari sumber tentang
perbandingan prestasi matematika siswa di Indonesia dan kedua negara
Asia tersebut, yaitu negara Malaysia dan Singapura. Hasil penelitian di
situs internet yang dipublikasikan di Jakarta pada 21 Desember 2006 itu
menyebutkan, “prestasi Indonesia berada jauh di bawah kedua negara
tersebut. Prestasi matematika siswa Indonesia hanya menembus skor
rata-rata 411. Sementara itu, Malaysia mencapai 508 dan Singapura 605 (400 =
rendah, 475 = menengah, 550 = tinggi, dan 625 = tingkat lanjut).”3. Posisi negara Indonesia dari pernyataan tersebut mengalami prestasi matematika
siswa jauh lebih rendah dibandingkan dengan negara Malaysia dan negara
Singapura. Maka dapat disimpulkan bahwa waktu yang dihabiskan siswa
Indonesia di sekolah tidak sebanding dengan prestasi yang diraih, itu
artinya, ada sesuatu dengan metode atau teknik pengajaran matematika di
negara Indonesia yang harus diperbaiki.
2
Firman, Syah Noor, Rendah, Prestasi Matematika Indonesia Jumlah Jam Pelajaran dan Prestasi tak Sebanding. Bandung, 2007. Dari
http://www.topix.com/forum/world/indonesia/T36OLENKQ6R3G1130 . Bandung, 2007 akses 18 Agustus 2010 14:27
3
Salah satu prestasi matematika siswa rendah di Indonesia selain
dari aspek guru yang kurang menggunakan metode dan teknik pengajaran
pada saat proses pembelajaran, yaitu aspek siswa. Siswa cenderung tidak
suka atau bahkan takut terhadap mata pelajaran matematika. Hal ini bukan
rahasia umum lagi siswa sering kali merasa bosan dan menganggap
matematika sebagai pelajaran yang tidak menyenangkan. Padahal
matematika merupakan salah satu mata pelajaran yang penting, yang
selalu diberikan kepada siswa mulai dari pendidikan dasar sampai
pendidikan tinggi.
Pertanyaannya adalah mengapa banyak sekali anak Indonesia yang
tidak menyukai pelajaran matematika, padahal pelajaran itu adalah dasar
untuk mempelajari pelajaran lain, misalnya pada pelajaran fisika dan
kimia, sebelum belajar pelajaran fisika dan kimia, siswa harus punya dasar
kemampuan matematika yaitu bagaimana cara mengoperasikan
penjumlahan, pengurangan, perkalian, dan pembagian.
Beberapa informasi menunjukkan bahwa kemampuan siswa
Sekolah Dasar (SD) dan sederatnya dalam mengerjakan operasi
pembagian belum memuaskan, bahkan hal tersebut juga dialami oleh
siswa pada tingkat-tingkat kelas yang lebih tinggi. Sekolah Madrasah
Ibtidaiyah Pembangunan sebagai contoh, nilai matematika pada materi
operasi pembagian mempunyai nilai rata-rata 5,28. Rata-rata hasil belajar
matematika yang diperoleh masih kurang dari KKM yang ditentukan,
yaitu 6,50. Keadaan ini sebenarnya tidak boleh terjadi sebab dengan
selesainya siswa mengikuti pelajaran matematika di Sekolah Dasar dan
sederajatnya, mereka harus telah memiliki kemampuan yang cukup dalam
mengerjakan operasi pembagian, karena keterampilan berhitung
merupakan salah satu sasaran pengajaran matematika.
Penjelasan di atas dapat diasumsikan bahwa matematika adalah
suatu mata pelajaran yang membuat banyak anak tertekan bahkan malas
untuk mempelajarinya. Bahkan ini bisa terjadi sampai anak tersebut
penting. Matematika adalah pintu gerbang menuju ilmu pengetahuan
lainnya, karena itu setiap manusia termasuk siswa perlu menguasai
matematika sebagai bekal hidupnya dalam memasuki era globalisasi ini.
Pembagian merupakan operasi aritmatika yang terbilang sulit
dikuasai oleh siswa. Kemampuan siswa Sekolah Dasar dan sederajatnya
untuk menghafal pembagian hanya sampai pembagian 2 digit dengan
bilangan pembagi 1-9 saja. Penyelesaian pembagian dengan teknik
bersusun seperti yang selama ini digunakan, memerlukan waktu yang
cukup lama untuk mengerjakannya. Siswa seringkali keliru untuk
menempatkan letak angka ratusan, puluhan, atau satuan. Teknik berhitung
cepat yang diajarkan di lembaga-lembaga kursus, juga butuh waktu lama
(sekitar 1 tahun) bagi siswa untuk menguasai pembagian.
Berdasarkan dari kesulitan siswa dalam mengoperasikan
pembagian tersebut maka dengan menggunakan teknik pola bilangan,
siswa dapat mengerjakan operasi pembagian dengan mudah dan cepat.
Pada buku Polamatika, Premadi mengemukakan bahwa:
Penggunaan pola bilangan ini terbukti cukup efektif untuk dipelajari siswa karena sangat mudah dan sangat cepat. Hal ini disebabkan siswa hanya menghafalkan satu pola untuk semua soal pembagian sampai 6 digit (bahkan digit tak terbatas) dengan bilangan pembaginya dari 2-99. Jika pola pembagian ini digunakan untuk bilangan yang pembaginya ratusan (101-999) atau bahkan ribuan (1001-9999), tetap menggunakan satu pola yang sama dengan yang digunakan pada pembagian satuan.4 Berdasarkan latar belakang masalah yang telah diuraikan di atas,
peneliti tertarik untuk menjadikannya sebagai penelitian yang berjudul,
“Pengaruh Penggunaan Teknik Pola Bilangan Terhadap Hasil Belajar Matematika.”
4
B. Identifikasi Masalah
Berdasarkan uraian pada latar belakang masalah di atas, masalah
yang dapat diidentifikasi menjadi pertanyaan-pertanyaan penelitian
sebagai berikut:
1. Faktor-faktor apa saja yang mempengaruhi hasil belajar matematika
siswa?
2. Upaya-upaya apa saja yang dapat dilakukan oleh guru untuk
meningkatkan hasil belajar matematika siswa?
3. Apakah penerapan perhitungan biasa (cara bersusun) cukup efektif
untuk meningkatkan hasil belajar siswa pada pokok bahasan operasi
pembagian?
4. Apakah penerapan perhitungan dengan teknik pola bilangan cukup
efektif untuk meningkatkan hasil belajar siswa pada pokok bahasan
operasi pembagian?
5. Apakah hasil belajar matematika siswa yang diajarkan dengan
menggunakan teknik pola bilangan pada operasi pembagian terdapat
perbedaan dengan siswa yang diajarkan dengan tidak menggunakan
teknik pola bilangan pada operasi pembagian?
6. Apakah terdapat pengaruh dalam penerapan teknik pola bilangan pada
operasi pembagian terhadap hasil belajar matematika siswa?
C. Pembatasan Masalah
Peneliti berharap agar tujuan penelitian ini menjadi jelas dan
terarah, maka dalam penelitian ini akan difokuskan dan diukur pada ada
atau tidaknya perbedaan hasil belajar matematika siswa, antara siswa yang
diajarkan teknik pola bilangan pada operasi pembagian bilanga cacah
dengan siswa yang diajarkan teknik bersusun pada operasi pembagian
bilangan cacah. Operasi hitung yang dibahas adalah operasi hitung
pembagian satu digit (satuan), dua digit (puluhan), dan pembagian bersisa.
Hasil belajar matematika yang dimaksud dalam penelitian ini adalah hasil
digit (puluhan), dan operasi pembagian bersisa sesuai dengan kurikulum
dan silabus Sekolah Dasar dan sederajatnya di Kelas IV pada semester
satu tahun ajaran 2010/2011.
D. Perumusan Masalah
Berdasarkan latar belakang masalah, identifikasi serta pembatasan
masalah yang telah dipaparkan di atas maka dapat dirumuskan masalahnya
sebagai berikut:
1. Bagaimana deskripsi kemampuan siswa dalam materi operasi
pembagian bilangan cacah dengan menggunakan teknik pola bilangan?
2. Apakah terdapat pengaruh dalam penerapan teknik pola bilangan pada
operasi pembagian bilangan cacah terhadap hasil belajar matematika
siswa?
E. Tujuan Penelitian
Tujuan dari penelitian ini adalah sebagai berikut:
1. Mengetahui kemampuan siswa dalam materi operasi pembagian
bilangan cacah dengan menggunakan teknik pola bilangan.
2. Mengetahui apakah terdapat pengaruh antara hasil belajar matematika
siswa dengan menggunakan teknik pola bilangan pada operasi
pembagian bilangan cacah terhadap hasil belajar matematika siswa.
F. Kegunaan Penelitian
Kegunaan dari penelitian ini adalah sebagai berikut:
1. Bagi siswa diharapkan dapat meningkatkan hasil belajar matematika
siswa dengan menggunakan teknik pola bilangan pada materi operasi
pembagian bilangan cacah.
2. Bagi guru sebagai alternatif teknik pembelajaran dalam upaya
meningkatkan hasil belajar matematika pada materi operasi pembagian
3. Bagi pengguna secara umum dapat menambah referensi baru dalam
menggunakan teknik pola bilangan pada materi operasi pembagian
A. Deskripsi Teoretik
1. Hasil Belajar Matematika
a. Pengertian Belajar
Belajar adalah suatu proses kegiatan yang bisa dilakukan secara
informal maupun formal. Belajar bukan hanya bisa dilakukan di
sekolah, tetapi bisa juga dilakukan di luar sekolah, seperti di rumah, di
jalan ataupun di sekeliling kita. Belajar adalah suatu proses yang
memperoleh pengetahuan. Pengetahuan yang kita dapat bukan hanya
dari sekolah tetapi di luar sekolah pun pengetahuan bisa didapatkan.
Hal ini sesuai dengan apa yang dikemukakan oleh Robbins yang
mendefinisikan bahwa “belajar sebagai proses menciptakan hubungan
antara sesuatu (pengetahuan) yang sudah dipahami dan sesuatu
(pengetahuan) baru.”1. Pandangan Robbins dalam pengertian belajar senada dengan yang dikemukakan oleh Brunner bahwa, “belajar adalah
suatu proses aktif di mana siswa membangun (mengkonstruk)
pengetahuan baru berdasarkan pada pengalaman/pengetahuan yang
sudah dimilikinya.”2
Pengetahuan yang diperoleh manusia bisa didapatkan dari setiap
jenjang pendidikan, jadi bisa dikatakan bahwa belajar merupakan
proses kegiatan yang dapat dilakukan oleh manusia pada jenjang
pendidikan dasar sampai jenjang perkuliahan. Pernyataan tersebut
sesuai dengan teori belajar yang terdapat di dalam buku Muhibbin yang
mendefinisikan bahwa, “belajar adalah kegiatan yang berproses dan
1
Trianto, Mendesain Model Pembelajaran Inovatif Progresif, (Jakarta: Kencana, 2009), Cet ke-1, hal 15
2
Trianto, Mendesain Model…, hal 15
merupakan unsur yang sangat fundamental dalam setiap
penyelenggaraan jenis dan jenjang pendidikan.”3
Kehidupan seseorang dikatakan belajar, bila dapat diasumsikan
bahwa dalam diri seseorang itu terjadi suatu proses kegiatan yang
mengakibatkan perubahan tingkah laku. Hal ini sesuai dengan apa yang
di kemukakan oleh “Skinner mengartikan belajar sebagai suatu proses
adaptasi atau penyesuaian tingkah laku yang berlangsung secara
progresif.”4, serta pendapat dari “Morgan mengartikan belajar sebagai suatu perubahan yang relatif menetap dalam tingkah laku sebagai akibat
atau hasil dari pengalaman yang lalu.”5
Pengalaman yang lalu pada proses pembelajaran adalah konsep
awal yang sudah dimiliki oleh siswa, dan guru sebagai fasilitator
membantu siswa menanamkan atau menambah pengetahuan baru dari
suatu materi, sehingga pengetahuan yang dimiliki oleh siswa
berkembang. Hal ini sesuai dengan pernyataan dari teori belajar
bermakna Ausubel yang menyatakan bahwa “belajar bermakna
merupakan proses dikaitkannya informasi baru pada konsep-konsep
relevan yang terdapat dalam struktur kognitif seseorang.”6
Ausubel menyarankan bahwa guru mencoba mengikatkan
informasi baru ke dalam stuktur yang telah direncanakan di dalam
permulaan pelajaran, dengan cara mengingatkan siswa bahwa rincian
yang bersifat spesifik itu berkaitan dengan gambaran informasi yang
bersifat umum. Akhir pembelajaran siswa diminta mengajukan
pertanyaan pada diri sendiri mengenai tingkat pemahamannya terhadap
pelajaran yang baru dipelajari, menghubungkannya dengan
pengetahuan yang telah dimiliki dan pengorganisasian materi
pembelajaran dan juga memberikan pertanyaan kepada siswa dalam
3
Muhibbin Syah, Psikologi Pendidikan dengan Pendekatan Baru, (Bandung: PT Remaja Rosdakarya, 2007), Cet ke-13. hal 89
4
Sobry Sutikno, Belajar dan Pembelajaran Upaya Kreatif dalam Mewujudkan Pembelajaran yang Berhasil, (Bandung: Prospect, 2009), Cet ke-5. Hal 3
5
Sobry Sutikno, Belajar dan Pembelajaran…, hal 4
6
rangka keluasan pemahaman siswa tentang isi pelajaran. Sesuai
pernyataan Winkel yang menyatakan tentang pembelajaran, yaitu
“pembelajaran sebagai seperangkat tindakan yang dirancang untuk
mendukung proses belajar peserta didik, dengan memperhitungkan
kejadian-kejadian eksternal yang berperanan terhadap rangkaian
kejadian-kejadian internal yang berlangsung di dalam diri peserta
didik.”7
Definsi-definisi belajar yang dijelaskan di atas, maka dapat
disimpulkan bahwa teori Ausubel yang lebih tepat dalam proses
pembelajaran matematika, karena jika siswa hanya mencoba-coba
menghafal informasi baru tanpa menghubungkan dengan
konsep-konsep yang telah ada dalam struktur kognitifnya, maka dalam hal ini
terjadi belajar hafalan, padahal dalam pembelajaran matematika suatu
konsep yang ada tidak bisa di hafalkan begitu saja, akan tetapi siswa
harus mengetahui struktur dari konsep tersebut.
b. Pengertian Matematika
Penjelasan pengertian matematika tidak dapat dijawab dengan
mudah, karena pasti pandangan masing-masing terhadap matematika
itu berbeda-beda. Seperti yang terdapat pada buku Model Pembelajaran
Matematika yang mengatakan bahwa, “matematika merupakan bahasa
simbol, matematika adalah bahasa numerik, matematika adalah ilmu
yang abstrak dan deduktif, matematika adalah metode berpikir logis,
matematika adalah ilmu yang mempelajari hubungan pola, bentuk dan
struktur, matematika adalah ratunya ilmu dan juga menjadi pelayan
ilmu yang lain.”8
Pernyataan di atas sudah dijelaskan mengenai pengertian
matematika. Peneliti dalam hal ini peneliti akan mencari tahu asal kata
matematika, di buku Model Pembelajaran Matematika berpendapat
7
Sobry Sutikno, Belajar dan Pembelajaran…, hal 31
8
bahwa matematika berasal dari “kata mathein atau mathenein yang
artinya belajar (berpikir). Jadi, berdasarkan asal katanya, maka
perkataan matematika berarti ilmu pengetahuan yang didapat dengan
berpikir(bernalar).”9
Jadi dari penjelasan di atas bahwa ilmu matematika adalah ilmu
dasar yang sangat penting untuk mempelajari ilmu lain, karena
matematika merupakan ratunya ilmu. Matematika juga merupakan
suatu ilmu yang menggunakan lambang-lambang matematika. Ilmu
matematika bukanlah sekadar berhitung, tetapi matematika merupakan
kegiatan menemukan dan mempelajari pola serta hubungan.
Matematika memiliki simbol, gambar, atau pola yang bersifat efisien
dan padat makna.
c. Konsep Pembagian Bilangan Cacah
Pembahasan matematika tentang angka dan bilangan masih
banyak yang keliru, angka dan bilangan seringkali dianggap dua entitas
yang sama. Mereka pun umumnya menganggap angka dan bilangan
sebagai bagian dari matematika. Padahal sebuah angka digunakan
untuk melambangkan bilangan, sedangkan bilangan adalah suatu
konsep matematika yang digunakan untuk pencacahan dan pengukuran.
Matematika mempunyai bermacam-macam bilangan, seperti yang
telah dijelaskan oleh Ruseffendi, “terdapat bermacam-macam yaitu
bilangan kardinal, bilangan asli, bilangan cacah, bilangan bulat,
bilangan rasional, bilangan irrasional, bilangan real, dan bilangan
kompleks.”10. Ensiklopedia Matematika menjelaskan bahwa, “bilangan adalah suatu idea. Sifatnya abstrak. Bilangan bukan simbol atau
9
Erna Suwangsih dan Tiurlina, Model Pembelajaran…, hal 3
10
lambang dan bukan lambang bilangan. Bilangan memberikan
keterangan mengenai banyaknya anggota suatu himpunan.”11
Macam-macam bilangan terdapat salah satu macam bilangan,
yaitu bilangan cacah. Bilangan cacah adalah sub bagian dari bilangan
kompleks, real, rasional serta bilangan bulat, hal ini sesuai dengan
pernyataan di dalam buku Catur Supatmono bahwa, “bilangan cacah
adalah bilangan asli yang ditambah unsur bilangan nol.” 12. Jadi yang termasuk bilangan cacah yaitu 0, 1, 2, 3, dan seterusnya. Pernyataan ini
juga didukung oleh penjelasan dalam Ensiklopedia Matematika bahwa,
“semua anggota himpunan bilangan asli adalah anggota himpunan
bilangan cacah, tetapi tidak semua anggota himpunan bilangan cacah
menjadi anggota himpunan bilangan asli. Satu-satunya anggota
himpunan bilangan cacah yang bukan anggota himpunan bilangan asli
adalah bilangan nol.”13
Tingkat Sekolah Dasar terdapat beberapa operasi hitung
bilangan cacah yang biasa diajarkan, salah satunya adalah operasi
pembagian. Pengertian pembagian dalam ilmu matematika adalah
invers dari perkalian. Berdasarkan kurikulum Sekolah Dasar (SD)
bahwa, “pembagian adalah suatu operasi yang digunakan untuk
menentukan suatu faktor, apabila suatu hasil kali dan satu faktor
diketahui. Atau suatu operasi untuk menentukan banyaknya himpunan
obyek, apabila banyaknya seluruh obyek dan banyaknya obyek dalam
setiap himpunan diketahui atau sebaliknya.”14 Bentuk umumnya adalah
dengan syarat . Dibaca
dibagi sama dengan . Dengan disebut yang dibagi, disebut
11
ST. Negoro, B. Harahap, Ensiklopedia Matematika, (Jakarta: Ghalia Indonesia, 1998), hal 36
12
Catur Supatmono, Matematika Asyik, (Jakarta: PT Grafindo, 2009), hal 77
13
ST. Negoro, B. Harahap, Ensiklopedia…, hal 41
14
pembagi, dan disebut hasil bagi. Beberapa buku menulis pembagian
dengan
¾ Sifat komutatif tidak berlaku pada pembagian, sebab
, atau . Ada beberapa sifat pembagian, yaitu:
, secara
umum:
tidak berlaku pada pembagian, sebab 8: :
¾ Bilangan bera akan me ¾ Sifat asosiatif
8: : , secara umum: a: b : c a: b: c
papun jika dibagi nol nghasilkan sesuatu
yang tidak terdefinisi. tidak terdefinisi. Dan jika =∞
→ x x
lim
0
karena tidak ada nilai da
1
lam limit mendekati x=0 dengan fungsi ,
sehingga nilai dari =∞ x
1
lim
Contoh:
→ x 0
tidak terdefinisi
¾ Nol dibagi berapapun hasilnya selalu nol.
Contoh: ,
a i lis:
, dengan disebut yang dibagi, disebut pembagi, disebut hasil
bagi, disebut sisa.
Contoh:
dan memiliki sisa 3. Jadi 23=(5x4)+3.
Jika s = 0, maka dikatakan habis dibagi , contoh: 110 habis dibagi
11 sebab 110 dibagi 11 akan meghasilkan sisa sama dengan nol. Secara umum, pembagian bersisa dap t d tu
Tabel 1
Syarat Suatu Bilangan Habis Dibagi
Sebuah bilangan habis
dibagi:
Jika
satuan pada bilangan tersebut
enap (bilangan yang
habis dibagi 2) dan b n 0 2 merupakan bilangan g
Angka
ilanga
3 Jumlah angka-angka tersebut habis dibagi 3
5
Angka yang dibagi mempunyai nilai
satuannya 0 atau 5
9 Jumalah angka-angka tersebut habis dibagi 9
Contoh:
¾ 212 habis dibagi 2 sebab hasil bagi mempunyai nilai satuan
bilangan genap, yaitu 2
126 habis dibagi 3 sebab jumlah angka yang dibagi, yaitu 1+2+6=9,
habis dibagi 3.
bagi 9.
Matematika
ya tujuan pembelajaran, dan tujuan
pem elajaran akan mencapai hasil yang maksimal apabila pembelajaran
pembelajaran yang sudah dicapai dapat
dilihat ¾
dan 9
¾ 2.345 habis dibagi 5 sebab angka yang dibagi mempunyai nilai
satuannya 5.
¾ 2.385 habis dibagi 9 sebab jumlah angka yang dibagi, yaitu
2+3+8+5=18, habis di
d. Hasil Belajar
Proses pembelajaran di kelas, baik guru maupun siswa
bersama-sama menjadi pelaku terlaksanan
b
berjalan secara efektif. Tujuan
dari keberhasilan siswa dalam belajar, yaitu dilihat dari hasil
belajar siswa. Definisi belajar yang telah dijelaskan oleh Morgan di atas
pengalaman yang lalu, maka dapat dikatakan bahwa hasil dari belajar
adalah ditandai dengan adanya perubahan yang dicapai. Hasil belajar
dapat dicapai oleh siswa apabila siswa tersebut telah melakukan
kegiatan belajar, hal ini sesuai dengan pendapat dari Abdurrahman
yang menyatakan bahwa, “hasil belajar adalah kemampuan yang
diperoleh anak setelah melalui kegiatan belajar.”15, serta didukung pula dengan pernyataan oleh Sudjana yang menyatakan bahwa, “hasil
belajar adalah kemampuan-kemampuan yang dimiliki siswa setelah ia
menerima pengalaman belajarnya.”16.
Arifin menjelaskan bahwa “indikator hasil belajar merupakan
uraian kemampuan yang harus dikuasai peserta didik dalam
berkomunikasi secara spesifik serta dapat dijadikan ukuran untuk
menilai ketercapaian hasil pembelajaran.”17. Peserta didik diberi kesemp
atan untuk menggunakan pengetahuan, keterampilan, sikap, dan
nilai-nilai yang sudah mereka kembangkan selama pembelajaran dan
dalam menyelesaikan tugas-tugas yang sudah ditentukan. Menurut
Arikunto, “hasil belajar adalah hasil akhir setelah mengalami proses
belajar dimana tingkah laku itu tampak dalam bentuk perbuatan yang
dapat diamati dan diukur.”18. Memperoleh hasil belajar siswa harus dilakukan evalusi atau penilaian guna mengukur tingkat keberhasilan
siswa atau penguasaan siswa, maupun perubahan siswa. Penilaian hasil
belajar siswa bisa mencakup pengetahuan, sikap dan keterampilan, tiga
ranah ini dikenal dengan Taksonomi Bloom. Bloom membagi hasil belajar menjadi tiga ranah, yaitu:
1. Ranah kognitif berkenaan dengan hasil belajar intelektual yang terdiri dari enam aspek, yakni pengetahuan atau
15
Asep Jihad dan Abdul Haris, Evaluasi Pembeelajaran, (Yogyakarta: Multi Pressindo, 2009), Cet ke-3, hal 14
16
Nana Sudjana, Penilaian Hasil Proses Belajar Mengajar, (Bandung: PT Remaja Rosdakarya, 2008), cet XI, hal.22
17
Zaenal Arifin, Evaluasi Pembelajaran Prinsip, Teknik, Prosedur, (Bandung: PT Remaja Rosdakarya, 2009), cet I, hal.27
18
ingatan, pemahaman, aplikasi, analisis, sintesis, dan evaluasi.
2. Ranah afektif berkenaan dengan sikap yang terdiri dari
ampuan bertindak. Ada enam
an keterampilan
penge
adalah enam taan ini
diduku
lima aspek, yakni penerimaan, jawaban atau reaksi, penilaian, organisasi, dan internalisasi.
3. Ranah psikomotorik berkenaan dengan hasil belajar keterampilan dan kem
aspek ranah psikomotorik, yakni gerakan releks, keterampilan gerakan dasar, kemampuan perceptual, keharmonisan atau ketepatan, gerak
kompleks, gerakan ekspresid dan interpretatif. 19
Ranah kognitif yang sudah disebutkan di atas, yaitu,
tahuan, pemahaman, penerapan, analisis, sintesis dan evaluasi
jenis perilaku yang bersifat hierarkis. Pernya
ng di dalam buku Dimyati yang menyatakan bahwa, “perilaku
yang terendah merupakan perilaku yang harus dimiliki terlebih dahulu
sebelum mempelajari perilaku yang lebih tinggi.”20Maka dapat diartikan bahwa hasil belajar adalah perubahan tingkah laku siswa
setelah dilakukan proses kegiatan belajar mengajar sesuai dengan
tujuan pembelajaran. Hal ini sesuai dengan pendapat Juliah yang
menyatakan bahwa, “hasil belajar adalah segala sesuatu yang menjadi
milik siswa sebagai akibat dari kegiatan belajar yang dilakukannya.”21 dan Hamalik yang menyatakan bahwa, “hasil belajar adalah pola-pola
perbuatan, nilai-nilai, pengertian-pengertian dan sikap-sikap, serta
apersepsi dan abilitas.”22, serta didukung pula dengan peryataan oleh Gagne yang menyatakan bahwa , “meninjau hasil belajar yang harus
dicapai oleh siswa dan juga meninjau proses belajar menuju ke hasil
belajar dan langkah-langkah instruksional yang dapat diambil oleh guru
dalam membantu siswa belajar.”23
19
Nana Sudjana, Penilaian Hasil…, hal.22-23
20
Dimyati dan Mudjiono, Belajar dan Pembelajaran, (Jakarta:Rineka Cipta, 2009), Cet IV, hal.2
p Jihad dan Abdul Haris, Evaluasi…, hal 15
an, (Jakarta: PT Grasindo, 2008), Cet ke-4, hal
7
21
Asep Jihad dan Abdul Haris, Evaluasi…, hal 15
22
Ase
23
Jika dikatakan bahwa hasil belajar adalah segala sesuatu yang
diperoleh oleh siswa setelah melakukan kegiatan belajar mengajar,
maka
ang belajar ru tentang
Jad
suatu nilai (angka) yang dicapai oleh siswa setelah melakukan proses
kegiata
2.
a. Pengertian Teknik Pola Bilangan
kita lebih jauh membahas pola bilangan, alangkah
lebih baik jika kita terlebih dahulu mengetahui tentang pola dan
hasil belajar matematika merupakan segala sesuatu yang
diperoleh oleh siswa setelah kegiatan belajar mengajar matematika.
Buku Pengembangan Kurikulum Matematika menjelaskan tentang
belajar matematika yang menyatakan bahwa “belajar matematika
adalah belajar tentang konsep-konsep dan struktur-struktur yang
terdapat di dalam bahasa yang dipelajari serta mencari
hubungan-hubungan antara konsep-konsep dan struktur-struktur tersebut.”24 Adapun penjelasan tentang hasil belajar matematika, yaitu:
Hasil belajar matematika di sekolah dasar umumnya dinyatakan dengan nilai (angka), sehingga siswa y
matematika akan mempunyai kemampuan ba
matematika sebagai tambahan dari kemampuan yang telah ada. Hasil belajar matematika adalah tolak ukur keberhasilan yang dicapai siswa dalam belajar matematika dengan tujuan kognitif, yaitu pengetahuan, pemahaman, penerapan, analisis, dan evaluasi.25
i, dapat disimpulkan bahwa hasil belajar matematika adalah
n belajar matematika dan pengetahuan tentang matematika yang
telah dimiliki oleh siswa akibat dari kegiatan belajar matematika yang
telah dilakukan serta hasil akhir setelah mengalami proses belajar
matematika dimana tingkah laku itu tampak dalam bentuk perbuatan
yang dapat diamati dan diukur.
Pola Bilangan
Sebelum
24
Asep Jihad, Pengembangan Kurikulum Matematika, (Yogyakarta:Multi Pressindo, 2008), Cet-1, hal 176
25
bilangan. Istilah pola dalam matematika adalah sebuah susunan. Dapat pula di yang diguna gan ditunjukkan dengan yang digunakan adalah nik lain y
ung. Hal ini sesuai dengan
pernya
pola bilangan.”29
nyatakan bahwa pola adalah sebuah susunan yang mempunyai
bentuk yang teratur dari bentuk yang satu ke bentuk berikutnya.
Hudojo menyatakan bahwa “pola adalah suatu sistem mengenai
hubungan-hubungan di antara perwujudan alamiah.”26
Pengertian bilangan dalam matematika adalah sesuatu
kan untuk menunjukkan kuantitas (banyak, sedikit) dan ukuran
(berat, ringan, panjang, pendek, luas) suatu objek. Bilan
suatu tanda atau lambang yang disebut angka.
Pola bilangan menurut Raharjo, adalah “pola bilangan yang
sajiannya dinyatakan dalam lambang-lambang dan angka-angka.”27 Teknik perhitungan pembagian pada umumnya
dengan cara bersusun. Cara bersusun bukanlah satu-satunya cara
dalam menyelesaikan suatu operasi hitung pembagian, tetapi ada tek
ang dapat digunakan dalam menyelesaikan operasi hitung
pembagian, yaitu teknik pola bilangan.
Teknik pola bilangan adalah teknik berhitung cepat dan mudah.
Dengan menggunakan teknik pola bilangan ini, siswa akan lebih mudah
untuk memahami suatu operasi hit
taan dari Premadi yang menyatakan bahwa, “penggunaan pola
bilangan ini terbukti cukup efektif untuk dipelajari siswa karena sangat
mudah dan sangat cepat.”28
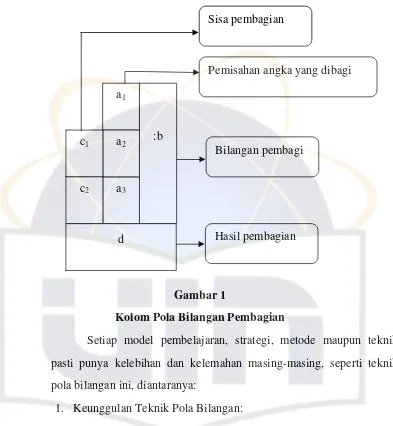
“Pola bilangan ini diperlukan kolom bantu. Kolom ini adalah
alat bantu perhitungan operasi hitung, seperti pada operasi pembagian.
Adapun contoh kolom teknik
26
Herman Hudojo, Strategi Mengajar Belajar Matematika, (Malang: IKIP Malang,1990), Cet ke-2
udi Raharjo, Bilangan Asli, Cacah dan Bulat, (Widyaiswara PPPG Matematika Yogyaka
arta: PT Wahyu Media, 2007), Cet ke-1, hal 2 , hal 3
27
Mars
rta: Tidak Diterbitkan), 2004, hal 36
28
Dradjad Premadi, Polamatika, (Jak
29
Gambar 1
Kolom Pola Bilangan Pembagian
Setiap model pe strategi, metode maupun teknik
pasti punya asing, seperti teknik
pola bi
mempunyai cara yang berbeda dari
meyelesaikan operasi hitung
rasi pembagian, kolom dibentuk kotak-kotak
matematika, bahkan dari sini bisa dijadikan suatu permainan Sisa pembagian
mbelajaran,
kelebihan dan kelemahan masing-m
langan ini, diantaranya:
1. Keunggulan Teknik Pola Bilangan:
a. Teknik pola bilangan
perhitungan cara bersusun dalam
pembagian, sehingga membuat siswa tidak bosan dalam belajar
operasi hitung.
b. Teknik pola bilangan mempunyai kolom untuk menyelesaikan
perhitungan ope
seperti sebuah permainan, dengan hal ini siswa akan senang,
karena ia merasa tidak terbebani dalam situasi belajar a3
a 1
a2
c1
c2
Pemisahan angka yang dibagi
:b
Bilangan pembagi
operasi pembagian yang menarik dengan alat bantu kolom.
c. Teknik pola bilangan tidak melakukan sistem simpan yang
dilakukan dengan metode bersusun, dengan ini siswa tidak
akan keliru dalam menghitung.
d. Tidak menggunakan alat bantu hitung, seperti sempoa.
2. Kelemahan Teknik Pola Bilangan
a. Teknik ini hanya cocok untuk siswa sekolah dasar dan
g yang
bagi
bagian besar siswa SD, SMP, maupun SMA. Mereka seringkali
, dengan pola
bilanga
dibagi, kemudian
alam kolom pola bilangan.
sedarajatnya, maka tidak bisa dikembangkan ke jenjan
lebih tinggi.
b. Siswa harus hapal perkalian 1 sampai perkalian 10.
c. Siswa harus hapal terlebih dahulu pembagian sampai 100.
b. Pembagian Bilangan Cacah dengan Pola Bilangan
Pembagian bilangan matematika sesuatu yang sulit
se
mengalami kesulitan untuk menyelesaikan pembagian
n, semua persoalan pembagian bilangan akan menjadi mudah.
1. Pembagian dengan Satuan
a. Dengan bilangan pertama bisa dibagi
56 : 2 =…
Langkah pertama
pisahkan angka pada bilangan yang
masukkan d
5 6 : 2 =
Langkah kedua
¾ Bagilah nilai a1 dengan bilangan pembagi (b)
¾ Tuliskan hasilnya di kolom d dan sisanya di kolom c1
5 : 2 = 2 sisa 1
Lan kah ketiga
¾ c1 dengan kolom sebelahnya (a2).
¾ b.
kem d (sebelah hasil pertama). : 2
5
6
5
: 2
g
Gabungkan kolom
Hasil penggabungan bagilah dengan nilai kolom
udian hasilnya di kolom
Hasil penggabungan 1 dan 6 adalah 16
Sehingga 16 : 2 = 8 1 6
2
5
: 2 1 6
Langkah keempat
¾ Hasil pembagian dapat diketahui di kolom d, nilainya
adalah 28
Jadi, 56 : 2 = 28
Lan
Pisahkan angka pada bilangan yang dibagi, kemudian
b. Dengan bilangan pertama tidak bisa dibagi
148 : 2 = …
gkah pertama
masukkan dalam kolom pola bilangan.
Catatan : Jika angka hasil pemisahan bilangan tidak dapat
ngan pembagi maka angka tersebut
angkah kedua
Bagilah nilai a1 dengan bilangan pembagi (b)
Tuliskan hasilnya di kolom d dan sisanya di kolom c1.
14 : 2 = 7 sisa 0 dibagi dengan bila
digabung dengan angka sesudahnya.
14 8 : 2 =
a1 a2 b
: 2 14
8
L
¾
angkah ketiga
Gabungkan kolom c1 dengan kolom sebelahnya (a2).
Hasilnya penggabungan, bagilah dengan nilai kolom b.
kemudian hasilnya tulis di kolom d (sebelah hasil
Langkah keempat
¾ Hasil pembagian dapat diketahui di kolom d, nilainya
adalah 74. Jadi, 148 : 2 = 74.
2. Pembagian dengan Puluhan
te Tahap selanjutnya adalah
mempelajari pembagian dengan puluhan. : 2 14
0
7 8
L
¾
¾
pertama).
Hasil penggabungan 0 dan 8 adalah 08 atau 8.
Sehingga 8 : 2 = 4
14
: 2
Setelah mempelajari pembagian bilangan dengan satuan,
ntunya kita telah menguasainya. 0 8
672 : 12 =…
Lan
angkah kedua
¾ agilah nilai a1 dengan bilangan pembagi (b)
¾ uliskan hasilnya di kolom d dan sisanya di kolom c1
7 : 12 = 5 sisa 7
angkah ketiga
¾ abungkan kolom c1 dengan kolom sebelahnya (a2).
¾ asil penggabungan bagilah dengan nilai kolom b, kemudian
asilnya tulis di kolom d (sebelah hasil pertama).
an 7 dan 2 adalah 72
gkah pertama
Pisahkan angka pada bilangan yang dibagi, kemudian
masukkan dalam kolom pola bilangan.
L
B
T
6
L
G
H
h
Hasil penggabung
Sehinga 72 : 12 = 6 67 2 : 12 =
a1 a2 b
: 12 67
2
67
: 12 7 2
L
: 12 67
7
angkah keempat
¾ asil pembagian dapat diketahui di kolom d, nilainya 56.
adi, 672 : 12 = 56
3.
ilkan
sisa hasilkan sisa terjadi jika bilangan tersebut
tidak habis dibagi.
Lan
H
J
Pembagian Bersisa
Pembagian bersisa adalah pembagian yang menghas
. Pembagian meng
89 : 7 =…
gkah pertama
Pisahkan angka pada bilangan yang dibagi, kemudian
masukkan dalam kolom pola bilangan. 2
56
8 9 : 7 =
a1 a2 b
: 7 8
Langkah kedua
¾ Bagilah nilai a1 dengan bilangan pembagi (b)
¾ Tuliskan hasilnya di kolom d dan sisanya di kolom c1.
8 : 7 = 1 sisa 1
Langkah ketiga
¾ Gabungkan kolom sebelahnya (a2).
¾ mudian
hasilnya tulis di kolom a).
Langkah keempat
¾ Karena bilangan di kolom a (bilangan utama) tidak ada, 8
: 7 1 9
c1 dengan kolom
Hasil penggabungan bagilah dengan nilai kolom b. ke
d (sebelah hasil pertam
an 1 dan 9 adalah 19 Hasil penggabung
Sehingga 19 : 7 = 2 sisa 5
sedangkan di kolom c masih ada sisa, berarti pembagian 1
8
: 7 1 9
5
tersebut menghasilkan sisa pembagian yaitu 5.
¾ Hasil pembagian dapat diketahui di kolom d, nilainya 12 dan
sisanya 5 atau dapat dituliskan dengan
Jadi, 89 : 7 =
e B. Hasil P
Penelitian yang berhubungan dengan pengaruh penerapan teknik berhitung
lainnya terhadap hasil belajar matematika siswa, salah satunya adalah hasil
elit ji Gojali tentang Pengaruh Penerapan Teknik Berhitu
ngan pada siswa maka siswa akan cepat dan
udah dalam penggunaan pola bilangan pada penyelesaian soal pembagian,
gan ini terbukti cukup efektif untuk dipelajari
siswa k
dengan bentuk diagram sebagai berikut : nelitian Relevan
pen ian yang dilakukan oleh Pu
ng Perkalian Polamatika Terhadap Hasil Belajar Matematika Siswa.
Penelitian ini mengungkapkan bahwa teknik polamatika dalam perkalian dapat
memberikan dampak positif terhadap hasil belajar siswa. Dari hasil penelitian ini
dapat disimpulkan bahwa terdapat perbedaan rata-rata hasil belajar matematika
yang signifikan antara kelompok eksperimen dan kelompok kontrol. Perbedaan
tersebut disebabkan karena pada saat berlangsungnya proses belajar, kelas
eksperimen menerapkan teknik berhitung perkalian polamatika dengan
menggunakan kolomatika dan kelas kontrol tidak menggunakannya, sehingga
dengan kata lain penerapan teknik berhitung perkalian polamatika mempunyai
pengaruh terhadap hasil belajar siswa. Pola bilangan dalam operasi pembagian
adalah bagian teknik berhitung yang menggunakan kolomatika untuk
menyelesaikan operasi pembagian. Maka penelitian ini relevan dengan penelitian
yang telah dilakukan sebelumnya.
C. Kerangka Berpikir
Penerapan teknik pola bila
m
sehingga penggunaan pola bilan
arena sangat mudah dan sangat cepat.
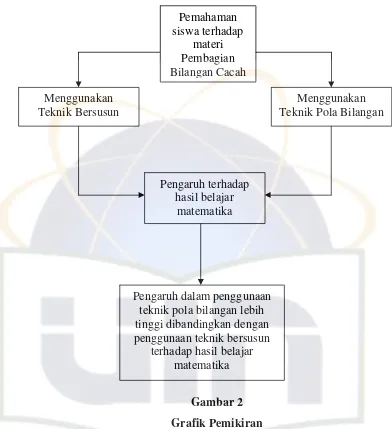
Pengaruh terhadap hasil belajar
matematika Pemahaman siswa terhadap
materi Pembagian Bilangan Cacah
Menggunakan Menggunakan Teknik Pola Bilangan Teknik Bersusun
Pengaruh dalam penggunaan teknik pola bilangan lebih tinggi dibandingkan dengan penggunaan teknik bersusun
[image:37.595.113.505.108.537.2]terhadap hasil belajar matematika
Gambar 2
Grafik Pemikiran
Maka melalui teknik pola bilangan, siswa diduga dapat meningkatkan
hasil belajar matematika, sehingga hasil belajar matematika siswa dalam
pem elajaran teknik pola bilangan menjadi lebih baik dibandingkan
pembelajaran teknik bersusun.
D. Hipotes
ada
pem tinggi dibandingkan dengan hasil belajar gan, siswa diduga dapat meningkatkan
hasil belajar matematika, sehingga hasil belajar matematika siswa dalam
pem elajaran teknik pola bilangan menjadi lebih baik dibandingkan
pembelajaran teknik bersusun.
D. Hipotes
ada
pem tinggi dibandingkan dengan hasil belajar b
b
is Penelitian
Berdasarkan kerangka berfikir di atas, maka hipotesis dalam penelitian ini
lah “Hasil belajar matematika siswa yang diajarkan teknik pola bilangan pada
bagian bilangan cacah lebih
is Penelitian
Berdasarkan kerangka berfikir di atas, maka hipotesis dalam penelitian ini
lah “Hasil belajar matematika siswa yang diajarkan teknik pola bilangan pada
menggunakan teknik bersusun pada pembagian bilangan
cacah.”
BAB III
METODE PENELITIAN
A. Tempat Dan Waktu Penelitian
Penelitian ini dilaksanakan di Madrasah Ibtidaiyah (MI)
Pembangunan beralamatkan di Jalan Ibnu Taimia IV Kompleks UIN
Syarif Hidayatullah Jakarta. Penelitian dilakukan pada siswa kelas IV
semester ganjil tahun ajaran 2010/2011, tanggal 26 Juli 2010 – 18 Agustus
2010.
B. Variabel dan Desain Penelitian
Penelitian ini terdapat dua variabel, yaitu variabel bebas dan
varibel terikat. Variabel terikatnya adalah hasil belajar, dan variabel
bebasnya adalah teknik pola bilangan.
Metode yang digunakan dalam penelitian ini adalah metode
quasi-eksperimen yaitu metode yang tidak memungkinkan peneliti melakukan
pengontrolan secara penuh terhadap sampel penelitian. Kelas eksperimen
dalam proses pembelajarannya menggunakan teknik pola bilangan,
sedangkan pada kelas kontrol dalam proses pembelajarannya
menggunakan teknik bersusun (konvensional).
Desain eksperimen yang digunakan dalam penelitian ini berbentuk
Two Group Randomized Subjek Post Test Only. Rancangan Desain Penelitian
Kelompok Pengambilan Perlakuan Postes
Eksperimen A X O
Kontrol A O
Keterangan:
A = pengambilan sampel secara random/acak
O = postes
X = perlakuan dengan teknik pola bilangan
C. Populasi dan Sampel
Populasi target dalam penelitian ini adalah seluruh siswa Madrasah
Ibtidaiyah (MI) Pembangunan dan populasi terjangkau dalam penelitian
ini adalah seluruh siswa kelas IV pada semester Ganjil tahun ajaran
2010/2011 yang terbagi dalam 8 kelas. Jumlah siswa kelas IV Madrasah
Ibtidaiyah Pembangunan sebanyak 268 siswa yang terbagi atas 8 kelas.
Penempatan siswa Madrasah Ibtidaiyah Pembangunan dilakukan secara
merata dalam kemampuan, artinya tidak ada kelas unggulan serta
kurikulum yang diberikan juga sama, maka karakteristik antar kelas dapat
dikatakan homogen, sedangkan karakteristik dalam kelas cukup heterogen,
artinya ada siswa yang memiliki kemampuan tinggi, sedang dan rendah.
Sampel dalam penelitian diambil dari populasi terjangkau.
Berdasarkan karakteristik yang telah dijelaskan maka pemilihan sampel
dilakukan dengan teknik Cluster Random Sampling, dengan mengambil dua kelas secara acak dari 8 kelas yang memiliki karakteristik yang sama.
Satu kelas akan menjadi kelas eksperimen sebanyak 30 orang yang berasal
dari kelas IV–H dengan menggunakan teknik pola bilangan dan satu kelas
menjadi kelas kontrol sebanyak 30 orang yang berasal dari kelas IV–G
dengan menggunakan teknik bersusun (konvensional).
D. Instrumen Penelitian
1. Instrumen Tes
Instrumen yang digunakan untuk mengukur kemampuan hasil
belajar adalah tes objektif dalam bentuk pilihan ganda sebanyak 21 soal
yang valid dari 30 soal uji coba, dengan empat pilihan yang mempunyai
skala ukur berupa skor 1 untuk jawaban yang benar dan diberi skor 0
untuk jawaban yang salah. Soal-soal tersebut mengacu pada aspek kognitif
yang meliputi pemahaman dan aplikasi.
Instrumen tersebut diujicobakan terlebih dahulu sebelum instrumen
dapat diketahui dengan melakukan pengujian validitas, daya pembeda
soal, taraf kesukaran dan reliabilitas.
2. Instrumen Non Tes
Instrumen non tes yang digunakan untuk melihat proses
pembelajaran berlangsung adalah sebagai berikut:
a. Lembar observasi siswa. Pengamatan yang dinilai meliputi
aktivitas siswa dalam pembelajaran dan hasil pembelajaran siswa.
b. Dokumentasi yang meliputi video dan foto.
E. Teknik Pengumpulan Data
1. Pemberian tes dilakukan untuk memperoleh data tentang hasil belajar
matematika siswa kelas IV Madrasah Ibtidaiyah Pembangunan pada
pokok bahasan operasi pembagian.
2. Mengobservasi siswa dengan menggunakan lembar observasi proses
pembelajaran siswa. Pengamatan akan dilakukan pada pertemuan ke–2
dan ke–7 selama proses pembelajaran berlangsung.
3. Mendokumentasikan proses pembelajaran siswa melalui kumpulan
foto pada pertemuan ke–2 dan ke–7 , dan video pertemuan ke – 3
F. Analisis Instrumen
Instrumen terlebih dahulu diujicobakan sebelum digunakan
sehingga didapatkan instrumen yang baik. Uji coba ini dimaksudkan untuk
memperoleh validitas, daya pembeda, tingkat kesukaran, dan reliabilitas
instrument.
1. Validitas Instrumen
Menghitung validitas butir digunakan rumus koefisien korelasi
Poin Biserial, yaitu:1
1
Dimana:
= koefisien korelasi point biserial
= mean (nilai rata-rata) skor peserta tes (testi) yang menjawab
betul item yang dicari korelasinya dengan tes.
= mean (nilai rata-rata) skor total (skor rata-rata dari seluruh
peserta tes)
= Standar deviasi skor total
= proporsi peserta tes yang menjawab betul item tersebut
Kriteria validitas ditentukan berdasarkan .
Jika , maka butir soal dikatakan valid
Peneliti membuat 30 butir soal, ternyata setelah dikoreksi dan
dianalisis dengan perhitungan statistika, soal yang valid adalah 21 soal
yang terdiri dari nomor 2, 4, 5 mewakili indikator menghitung
pembagian bilangan tiga angka dengan bilangan satu angka. Nomor 6,
8, 10 mewakili indikator menghitung pembagian bilangan empat angka
dengan bilangan satu atau dua angka. Nomor 11, 12, 13, 14 mewakili
indikator menghitung pembagian sebuah bilangan tiga angka atau
empat angka dengan dua bilangan satu angka secara berturut-turut.
Nomor 16, 17, 18, 20 mewakili indikator menghitung pembagian
bilangan lima angka dengan bilangan satu angka atau dua angka.
Nomor 21, 22, 24, 25 mewakili indikator menyelesaikan soal cerita
yang mengandung pembagian. Nomor 27, 28, 30 mewakili indikator
menghitung pembagian dengan bersisa. Dapat dilihat dari 6 indikator
terdapat 3 indikator yang diwakili 3 butir soal dan 3 indikator lainnya
untuk menjadi instrumen, sehingga 21 butir soal yang akan digunakan
menjadi instrumen hasil belajar pada materi operasi pembagian (Lihat
Lampiran 9, hal.149).
2. Daya Pembeda dan Tingkat Kesukaran
Pengujian daya pembeda soal digunakan untuk mengetahui
kemampuan soal dalam membedakan antara peserta tes yang
berkemampuan tinggi dengan peserta tes yang berkemampuan rendah.
Rumus yang digunakan untuk pengujian daya pembeda adalah sebagai
berikut 2:
DP J J
Keterangan :
,
, ,
, ,
, ,7
,7 ,
= banyaknya peserta kelompok atas yang menjawab soal dengan
benar
= banyaknya peserta kelompok bawah yang menjawab soal
dengan benar
= banyaknya peserta kelompok atas
JB = banyaknya peserta kelompok bawah
= daya pembeda
Klasifikasi daya pembeda :
: sangat jelek
: jelek
: cukup
: baik
: sangat baik
Instrumen 21 soal yang sudah valid, setelah dikoreksi dan
dianalisis dengan perhitungan statistika, nomor 12 dan 30
2
diklasifikasikan daya pembeda jelek. Nomor 2, 4, 5, 6, 8, 10 dan 28
diklasifikasikan daya pembeda cukup. Nomor 11, 13, 14, 16, 17, 18,
20, 21, 22, 24 dan 27 diklasifikasikan daya pembeda baik. Nomor 25
diklasifikasikan daya pembeda sangat baik (Lihat Lampiran12,
hal.152).
Uji taraf kesukaran instrumen penelitian dihitung dengan
menghitung indeks besarannya dengan rumus3 :
, ,
, ,7
,7 ,
Keterangan :
= banyaknya siswa yang menjawab soal itu dengan benar
= jumlah seluruh siswa peserta tes
= indeks kesukaran
Klasifikasi tingkat kesukaran:
: soal sukar
: soal sedang
: soal mudah
Uji taraf kesukaran digunakan untuk mengetahui soal-soal yang
sukar, sedang dan mudah. Bilangan yang menunjukkan sukar, sedang
dan mudahnya suatu soal disebut indeks kesukaran.
Idealnya tingkat kesukaran soal sesuai dengan kemampuan
peserta tes, sehingga diperoleh informasi yang antara lain dapat
digunakan sebagai alat perbaikan atau peningkatan program
pembelajaran.
Instrumen 21 soal yang sudah valid, setelah dikoreksi dan
dianalisis dengan perhitungan statistika, nomor 2, 4, 5, 6 dan 8
diklasifikasikan tingkat kesukaran soal mudah. Nomor 10, 11, 13, 14,
16, 17, 18, 20, 21, 22, 24, 25 dan 28 diklasifikasikan tingkat kesukaran
3
soal sedang. Nomor 12, 27 dan 30 diklasifikasikan tingkat kesukaran
soal sukar (Lihat Lampiran11, hal.151).
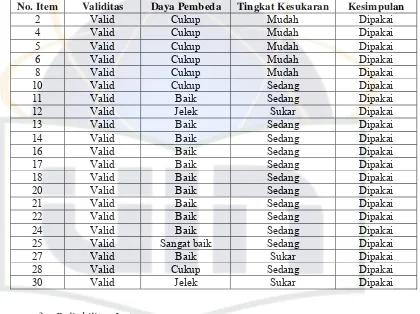
Uji validitas, daya pembeda dan tingkat kesukaran dapat
[image:45.595.112.532.238.552.2]dirangkum pada tabel berikut ini:
Tabel 2
Rekapitulasi Hasil Uji Validitas, Daya Pembeda dan Tingkat Kesukaran
No. Item Validitas Daya Pembeda Tingkat Kesukaran Kesimpulan
2 Valid Cukup Mudah Dipakai
4 Valid Cukup Mudah Dipakai
5 Valid Cukup Mudah Dipakai
6 Valid Cukup Mudah Dipakai
8 Valid Cukup Mudah Dipakai
10 Valid Cukup Sedang Dipakai
11 Valid Baik Sedang Dipakai
12 Valid Jelek Sukar Dipakai
13 Valid Baik Sedang Dipakai
14 Valid Baik Sedang Dipakai
16 Valid Baik Sedang Dipakai
17 Valid Baik Sedang Dipakai
18 Valid Baik Sedang Dipakai
20 Valid Baik Sedang Dipakai
21 Valid Baik Sedang Dipakai
22 Valid Baik Sedang Dipakai
24 Valid Baik Sedang Dipakai
25 Valid Sangat baik Sedang Dipakai
27 Valid Baik Sukar Dipakai
28 Valid Cukup Sedang Dipakai
30 Valid Jelek Sukar Dipakai
3. Reliabilitas Instrumen
Menentukan realiabilitas digunakan rumus Kuder Richardson-20 (KR-Richardson-20), yaitu :4
. ∑ dengan ∑ ∑
Dimana:
= reliabilitas tes secara kesuluruhan
= proporsi subjek yang menjawab item dengan benar
= proporsi subjek yang menjawab item yang salah
4
∑
2
,9 7
= reliabilitas tes secara kesuluruhan
= banyaknya item
= standar deviasi dari tes
Kriteria koefisien reliabilitas adalah sebagai berikut:
0,80 < ≤ 1,00 Derajat reliabilitas sangat baik
0,60 < ≤ 0,80 Derajat reliabilitas baik
0,40 < ≤ 0,60 Derajat reliabilitas cukup
0,20 < ≤ 0,40 Derajat reliabilitas rendah
0,00 < ≤ 0,20 Derajat reliabilitas sangat rendah
Berdasarkan kriteria koefisien reliabilitas, nilai
berada diantara kisaran mulai 0,80 < ≤ 1,00, maka dari 21 butir soal
memiliki derajat reliabilitas sangat baik (Lihat Lampiran 10, hal.150).
G. Teknik Analisis Data
1. Uji Prasyarat
Analisis data yang digunakan adalah pengujian hipotesis mengenai
perbedaan dua rata – rata populasi. Uji yang digunakan adalah uji – t.
Sebelum dilakukan pengujian hipotesis, terlebih dahulu dilakukan uji
persyaratan analisis, yaitu:
a. Uji Normalitas
Uji normalitas dilakukan untuk mengetahui apakah sampel
yang diteliti berasal dari populasi berdistribusi normal atau tidak.
Penelitian ini, pengujian normalitas menggunakan rumus chi square. Adapun prosedur pengujiannya adalah sebagai berikut5:
1. Menentukan hipotesis
H0 : data sampel berasal dari populasi berdistribusi normal
H1 : data sampel tidak berasal dari populasi berdistribusi normal
2. Menentukan rata-rata
5
3. Menentukan standar deviasi
1 3,3log
4. Membuat daftar frekuensi observasi dan frekuensi espektasi
a. Rumus banyak kelas interval (aturan Sturges)
, dengan banyaknya subjek
b. Rentang = skor terbesar – skor terkecil
c. Panjang kelas interval
5. Cari 2 dengan rumus: Ε Ε
Varians terbesar Varians terkecil
6. Cari dengan derajat kebebasan = banyaknya kelas
dan taraf kepercayaan 95% atau taraf signifikan %. 7. Kriteria pengujian:
Jika , maka H0 diterima dan H1 ditolak
Jika , maka H1 diterima dan H0 ditolak
b. Uji Homogenitas Varians
Uji homogenitas varians dilakukan untuk mengetahui
kesamaan antara dua keadaan atau populasi. Uji homogenitas varians
yang digunakan adalah uji Fisher, dengan langkah-langkah sebagai
berikut6: 1. Hipotesis
H0 :
H1 :
2. Cari dengan rumus:
3. Tetapkan taraf signifikan
/
4. Hitung dengan rumus
6
5. Tentukan kriterian pengujian H0 , yaitu:
Jika , maka H0 diterima dan H1 ditolak
Jika , maka H0 ditolak dan H1 diterima
2. Uji Perbedaan Dua Rata-rata
a. Uji-t
Apabila asumsi untuk uji-t telah terpenuhi, maka untuk menguji
hipotesis digunakan uji t dengan taraf signifikan α= 0,05.
Rumus uji t yang digunakan yaitu:7
2 1 2 1 1 1 n n S X X t gab + −
= di mana
(
)
(
)
2 1 1 2 1 2 2 2 2 1 1 2 − + − + − = n n S n S n Sgab Keterangan: 1
X : nilai rata-rata hasil belajar kelompok eksperimen
2
X : nilai rata-rata hasil belajar kelompok kontrol
n1 : jumlah sampel kelompok eksperimen
n2 : jumlah sampel kelompok kontrol
2 1
S : varians kelompok eksperimen
2 2
S : varians kelompok kontrol
b. Hipotesis Statistik
Adapun hipotesis statistik yang akan diuji adalah sebagai
berikut :
H0 : μ1 ≤μ2
H1 : μ1 >μ2
7
Keterangan :
=
1
μ rata-rata hasil belajar matematika dengan
menggunakan teknik pola bilangan
=
1
μ rata-rata hasil belajar matematika dengan
menggunakan teknik bersusun
Adapun kriteria pengujian untuk uji t ini adalah:
Terima Ho, apabila thitung ≤t(1−α;n1+n2−2)
Tolak Ho, apabila (1 ; 2 2 1+ − −
> n n
hitung t
t α )
3. Analisis Deskriptif
Analisis untuk data yang diperoleh dari lembar observasi yang
digunakan adalah analisis deskriptif. Analisis deskriptif adalah
menganalisis data dengan cara mendeskripsikan atau menggambarkan data
yang telah terkumpul sebagaimana adanya tanpa bermaksud membuat
kesimpulan yang berlaku untuk umum atau generalisasi.
Adapun rentang skor penilaian lembar observasi proses
[image:49.595.114.512.112.675.2]pembelajaran siswa, yaitu:
Tabel 3
Katagori Skor Penilaian Hasil Observasi
Skor Penilaian Katagori
1 Kurang
2 Cukup
3 Baik
4 Sangat Baik
Lembar observasi proses pembelajaran siswa mempunyai rentang
skor penilaian antara 1 sampai 4 dengan tujuh pernyataan, sehingga jumlah
minimum yang diperoleh setiap kali pengamatan adalah 7 dan jumlah
dilakukan di kelas eksperimen yang menggunakan teknik pola bilangan
pada materi operasi pembagian.
Jumlah skor penilaian dapat ditentukan dengan menjumlahkan skor
penilaian dari masing-masing aspek, yang diperoleh dari pengamatan.
Setelah didapat jumlah skor dari hasil observasi proses pembelajaran
[image:50.595.110.512.155.565.2]siswa, maka dapat dikatagorikan dari hasil tersebut sebagai berikut:
Tabel 4
Katagori Jumlah Skor Penilaian Hasil Observasi
Jumlah Skor Penilaian Katagori
7 < x ≤ 14 Kurang
14 < x ≤ 21 Cukup
21 < x ≤ 28 Baik
Dari katagori jumlah skor di atas, keaktivan siswa dalam proses
pembelajaran matematika pada materi operasi pembagian menggunakan
teknik pola bilangan dapat ditentukan. Lembar observasi pembelajaran
A. Deskripsi Data
Penelitian tentang hasil belajar matematika di Madrasah Ibtidaiyah
Pembangunan ini dilakukan terhadap dua kelas untuk dijadikan sebagai
sampel penelitian yaitu kelas IV-H sebagai kelas eksperimen, yang terdiri
dari 30 orang siswa yang diajarkan dengan menggunakan teknik pola
bilangan dan kelas IV-G sebagai kelas kontrol, yang terdiri dari 30 orang
siswa yang diajarkan dengan menggunakan teknik bersusun.
Pokok bahasan yang diajarkan pada penelitian ini adalah operasi
pembagian. Hasil belajar matematika kedua kelas tersebut dapat diukur
setelah diberikan perlakuan dengan menggunakan teknik pembelajaran
yang berbeda antara kelas eksperimen dan kelas kontrol, maka kedua kelas
tersebut diberikan tes berbentuk pilihan ganda. Sebelum tes tersebut
diberikan, terlebih dahulu dilakuan uji coba sebanyak 30 soal, uji coba
tersebut dilakuan pada 33 orang siswa di kelas IV-G angkatan 2009/2010
di Madrasah Ibtidaiyah Pembangunan.
Setelah dilakukan uji coba instrumen selanjutnya dilakuan uji
validitas, uji daya pembeda, uji taraf kesukaran dan uji reliabilitas.
Berdasarkan hasil perhitungan yang dilakukan diperoleh 21 butir soal yang
valid dengan reliabilitas soal sebesar 0,9037. Perhitungan uji daya
pembeda butir soal diperoleh 1 soal dengan kriteria sangat baik, 11 soal
dengan kriteria baik, 7 soal dengan kriteria cukup dan 2 soal dengan
kriteria jelek. Perhitungan uji taraf kesukaran butir soal diperoleh 5 soal
dengan kriteria mudah, 13 soal dengan kriteria sedang dan 3 soal dengan
kriteria sukar. Perhitungan selengkapnya dapat dilihat pada lampiran 13
hal 153.
Data pada penelitian ini ialah data yang terkumpul dari tes yang
telah diberikan kepada siswa Madrasah Ibtidaiyah Pembangunan Ciputat,
berupa data hasil tes hasil belajar siswa matematika siswa yang dilakukan
sesudah pembelajaran (posttes).
1. Hasil Belajar Matematika Siswa Kelas Eksperimen
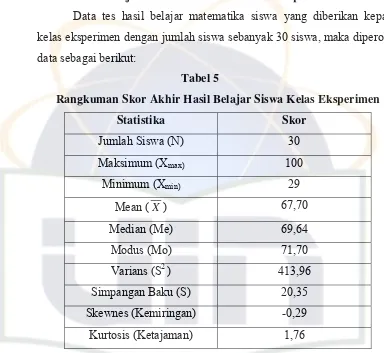
Data tes hasil belajar matematika siswa yang diberikan kepada
kelas eksperimen dengan jumlah siswa sebanyak 30 siswa, maka diperoleh
[image:52.595.112.496.187.540.2]data sebagai berikut:
Tabel 5
Rangkuman Skor Akhir Hasil Belajar Siswa Kelas Eksperimen
Statistika Skor
Jumlah Siswa (N) 30
Maksimum (Xmax) 100
Minimum (Xmin) 29
Mean (X ) 67,70
Median (Me) 69,64
Modus (Mo) 71,70
Varians (S2 ) 413,96
Simpangan Baku (S) 20,35
Skewnes (Kemiringan) -0,29
Kurtosis (Ketajaman) 1,76
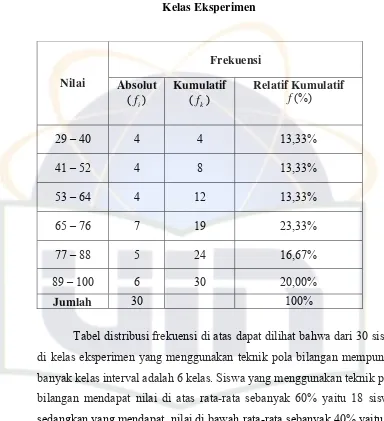
Tabel 5 dapat dilihat bahwa dari 30 siswa di kelas eksperimen
mendapatkan nilai rata-rata 67,70, nilai median 69,64, nilai modus 71,70
dan nilai simpangan baku 20,35. Tingkat kemiringan (sk) -0,29, karena nilai sk < 0, maka kurva memiliki ekor memanjang ke kiri atau miring ke
kanan, kurva menceng ke kanan, dan ketajaman/ kurtosis (α4)1,76 yang
berarti kurang dari 3 dengan kurva berbentuk platikurtik (mendatar)
sehingga ni