Konstruksi aritmetika kurva eliptik F(2m) supersingular dan non-supersingular untuk skema kunci publik ElGamal

(1)

ABSTACT

IRSYAD RAMLI. Constructions of Supersingular and Non-Supersingular Elliptic Curve Arithmetics for the ElGamal Public Key Scheme. Supervised by SUGI GURITMAN and NUR ALIATININGTYAS.

The ElGamal algorithm is one of the public key algorithms with modular arithmetic , which has the structure of the cyclic group . Security level of this algorithm depends on the solution of discrete logarithm problem. Unfortunately, this security level tends to decline recently because of the increase in ability of solving discrete logarithm. Moreover, to have an adequate level of security, very large value would be required, but this would cause the encryption and decryption process to be slow.

(2)

ABSTRAK

IRSYAD RAMLI. Konstruksi Aritmetika Kurva Eliptik Supersingular dan Non-Supersingular untuk Skema Kunci Publik ElGamal. Dibimbing oleh SUGI GURITMAN dan NUR ALIATININGTYAS.

Algoritme ElGamal adalah salah satu algoritme kunci publik dengan aritmetik modular yang mempunyai struktur grup siklik . Tingkat keamanan algoritme ini terletak pada pemecahan masalah logaritme diskret dari . Akan tetapi, tingkat keamanan dari tahun ke tahun semakin menurun yang disebabkan kemampuan pemecahan algoritme diskret semakin meningkat. Untuk memenuhi tingkat keamanan yang memadai dibutuhkan yang cukup besar yang menyebabkan proses enkripsi dan dekripsi menjadi lambat.

(3)

I PENDAHULUAN

1.1Latar Belakang

Komputer dan internet merupakan hasil karya manusia yang menggambarkan majunya teknologi saat ini. Komputer yang terhubung dengan internet dapat memberikan berbagai bentuk kemudahan untuk manusia dalam melakukan berbagai aktifitas. Salah satunya untuk berkomunikasi seperti pengiriman pesan penting yang harus dijaga kerahasiaannya. Keadaan ini tentu akan lebih nyaman apabila terdapat keamanan atau kerahasiaan pesan dalam proses tersebut. Hal ini bertujuan agar pesan tidak jatuh ke pihak yang tidak bertanggung jawab sehingga tidak terjadi hal-hal yang tidak diinginkan. Teknik untuk pengamanan tersebut adalah Kriptografi.

Kriptografi adalah studi teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasiaan, integritas data, otentikasi entitas, dan otentikasi data asli (Menezes 1997). Fungsi-fungsi matematika digunakan untuk melakukan penyandian (enkripsi) dan membuka sandi (dekripsi). Dalam melakukan proses enkripsi dan dekripsi tersebut, dibutuhkan suatu prinsip kunci (key). Inilah yang membedakan kriptografi menjadi dua bagian yaitu kunci simetrik dan kunci asimetrik atau yang lebih dikenal dengan kunci publik (public key).

Kunci simetrik merupakan jenis kriptografi yang paling umum digunakan. Untuk jenis ini, enkripsi dan dekripsi dilakukan dengan menggunakan kunci yang sama. Permasalahan yang muncul adalah bagaimana menyampaikan kunci tersebut ke penerima agar tidak diketahui oleh pihak-pihak yang tidak diinginkan karena siapapun yang memiliki kunci tersebut termasuk pihak-pihak yang tidak diinginkan juga dapat menyandi dan membongkar pesan dengan mudah. Oleh sebab itu, pada petengahan tahun 70-an Whitfield Diffie dan Martin Hellman menemukan teknik kunci asimetrik yang merevolusi dunia kriptografi.

Kunci asimetrik adalah pasangan-pasangan kunci kriptografi yang salah satunya digunakan untuk enkripsi (kunci publik) dan yang satunya lagi untuk dekripsi (kunci pribadi). Orang-orang yang memiliki kunci publik dapat menggunakannya untuk enkripsi, tetapi hanya satu orang (memiliki kunci pribadi) yang dapat membongkar pesan yang telah disandikan tersebut. Jenis ini

mempunyai tingkat keamanan yang lebih tinggi dari pada kunci simetrik. Contoh algoritme kunci asimetrik adalah RSA (singkatan Rivest, Shamir, Adleman), Rabin, ElGamal, dan lain-lain. Dalam tulisan ini, penulis menggunakan algoritme ElGamal.

Algoritme ElGamal ditemukan oleh Taher ElGamal yang dipublikasikan pada tahun 1985. Algoritme ini didasarkan pada aritmetik modular yang mempunyai struktur grup siklik dimana merupakan sembarang bilangan prima. Tingkat keamanannya didasarkan pada pemecahan masalah logaritme diskret .

Masalah logaritme diskret didefinisikan

dengan dimana yang akan

ditentukan adalah nilai . Sekilas, untuk menyelesaikan persamaan di atas terlihat mudah. Kita dapat mencoba menentukan nilai

sedemikian sehingga persamaan tersebut dipenuhi. Hal tersebut mungkin saja dengan mudah dilakukan apabila nilai kecil. Oleh sebab itu, untuk meningkatkan keamanan yang memadai dibutuhkan nilai yang cukup besar. Akan tetapi, dengan nilai yang cukup besar, dalam melakukan enkripsi dan dekripsi menjadi lambat, karena membutuhkan memori komputer yang besar. Akhirnya, para pakar Matematika dan Kriptografi untuk mencoba memperbaiki algoritme serta meningkatkan kemampuan komputer agar tingkat keamanan memadai tanpa membutuhkan memori komputer yang sangat besar.

Matematikawan asal Prancis yaitu Pierre Galois memperkenalkan konsep field yang dikenal dengan Galois Field dan disingkat dengan atau dengan prima. Kemudian field ini digabungkan dengan prinsip kurva eliptik yang kemudian diistilahkan dengan aritmetika kurva eliptik yang memiliki tiga karakteristik umum. Salah satunya, (dengan ) yang diharapkan mampu menggantikan struktur grup siklik pada algoritme ElGamal.

1.2 Tujuan

Tujuan penulisan ini adalah untuk mengonstruksi aritmetika kurva eliptik

Supersingular dan Non-Supersingular sehingga dapat disimulasikan pada algoritme ElGamal dengan menggunakan software

(4)

II LANDASAN TEORI

2.1Grup

Definisi 2.1.1 Diberikan sebarang himpunan tak kosong dan operasi biner pada .

Himpunan disebut grup terhadap operasi biner jika memenuhi

a. Operasi bersifat asosiatif.

, , , G

b. Terdapat unsur identitas untuk pada G sehingga berlaku

,

c. Untuk setiap terdapat unsur invers, yaitu sehingga berlaku

.

(Fraleigh 1994)

Definisi 2.1.2 Suatu grup (G, ) disebut grup komutatif jika operasi binernya bersifat

komutatif, yaitu , , G

(Fraleigh 1994)

Definisi 2.1.3 Suatu grup G dikatakan grup berhingga (finite group) jika banyak unsurnya berhingga dan banyaknya unsur G tersebut disebut orderG, ditulis o(G) atau |G|.

(Fraleigh 1994)

2.2 Grup Siklik

Definisi 2.2.1 Misalkan G grup dan G

dan n bilangan bulat positif, maka a. … , (sebanyak n kali) b. … , (sebanyak n kali).

c. .

(Aliatiningtyas 2002)

Teorema 2.2.2 Jika G suatu grup dan a G,

maka untuk setiap bilangan bulat m dan n

berlaku hukum eksponen : a.

b.

c.

(Guritman 2004)

Definisi 2.2.3 Misalkan G grup dan sebuah elemen . Jika | maka G

disebut grup siklik (cyclic group) dan disebut elemen pembangun yang dinotasikan . Jika G berhingga dan berorder m, maka terdapat m kuasa dari a yang masing-masing berbeda, yaitu

, , , …

Jika G adalah grup adisi (operasi penjumlahan), maka dapat dituliskan

|

dan jika berorder m, maka dapat ditunjukkan , , , … ,

(Guritman 2004)

2.3Ring

Definisi 2.3.1 Suatu grup dengan operasi + disebut operasi penjumlahan dan operasi · disebut operasi perkalian yang dinotasikan (R,+,·), disebut ring jika memenuhi aksioma-aksioma berikut

a. (R,+) grup komutatif.

b. Operasi perkalian bersifat asosiatif.

c. Hukum distributif kiri berlaku

, , ,

d. Hukum distributif kanan berlaku

, , ,

e. Unsur identitas terhadap “+” dinotasikan dengan 0 dan disebut unsur nol.

Selanjutnya,

a. Jika operasi perkalian bersifat komutatif, , , maka R disebut ring

komutatif.

b. Jika ada unsur identitas di bawah operasi perkalian (unsur ini disebut unsur kesatuan, dinotasikan dengan 1 dan disingkat dengan unkes), , ,

· · maka R disebut ring

dengan unsur kesatuan (unkes).

2.4Lapangan (Field)

Definisi 2.4.1 Suatu ring yang komutatif, ada unkes dan setiap unsur tak nolnya mempunyai invers (perkalian) disebut lapangan (field).

Salah satu contoh field adalah yang merupakan himpunan semua polinomial-polinomial berderajat paling banyak yang dinyatakan sebagai

| .

(5)

3 Contoh : 1. Penjumlahan 2. Perkalian

Suatu unsur biner di atas merepresentasikan polinomial basis yang di sebelah kanannya. Sehingga terlihat dengan

mudah, setara

dengan unsur biner yang dimulai dari

… sebanyak (dalam

penjumlahan di atas, unsurnya dimulai dari pangkat tertinggi ke pangkat terendah. Begitu pula dengan binernya). Misalkan, setara dengan

.

(Rosdiana 2009)

Aritmetik ini dijadikan acuan dalam perhitungan kurva eliptik atas .

Teorema 2.4.2 merupakan grup siklik multiplikatif berorder .

(Rosdiana 2009)

2.5 Pengenalan Kurva Eliptik

Definisi 2.5.1 Suatu kurva eliptik atas field

didefinisikan sebagai kurva dengan persamaan

(1)

dimana , , , , dan Δ

merupakan diskriminan dari yang di definisikan sebagai berikut:

∆

(2) Persamaan (1) disebut dengan persamaan

Weierstrass dan kurva eliptik dinotasikan ).

, |

∞ (Hankerson et al. 2004)

2.6 Penyederhanaan Persamaan Weierstrass

Definisi 2.6.1 Terkait dengan kriptografi, kurva eliptik

dikenakan atas field berhingga dimana p

prima. Berikut ini diberikan tiga kelompok besar kurva eliptik dibedakan atas field dasar

.

1. Jika dan , maka persamaan kurva eliptiknya adalah

:

dimana , dan diskriminan

kurva Δ .

2. Jika , maka terdapat dua kasus a. Non-Supersingular

Persamaan kurva eliptiknya adalah :

dimana , dan diskriminan kurva Δ .

b. Supersingular

dimana , , dan diskriminan kurva Δ .

(Hankerson et al. 2004)

2.7 Hukum Grup Kurva Eliptik

Misalkan E adalah kurva eliptik yang didefinisikan atas . Pada E diambil dua titik

yang berbeda , , , .

Maka garis memotong kurva di titik ketiga , kemudian diperoleh titik

, . Titik ini merupakan hasil dari pencerminan titik R’ terhadap sumbu x.

Proses ini disebut dengan proses adisi titik (penjumlahan titik).

(6)

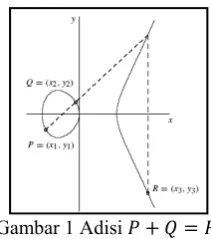
4

Gambar 1 Adisi

Jika sejajar dengan sumbu-y, maka titik yang ketiga didefinisikan sebagai titik di tak-hingga dengan notasi ∞, sehingga

∞

Jika , maka kondisi ini disebut adisi titik yang sama dan atau disebut juga pendobelan (doubling). Dinotasikan

,

Jadi, operasi adisi titik pada himpunan semua titik pada kurva dan titik di tak-hingga mempunyai struktur grup, disebut dengan grup kurva eliptik. Dalam hal ini, ∞ adalah unsur identitas. Untuk setiap pada , negatif dari yang dinotasikan dengan – yang merupakan hasil pencerminan dari pada terhadap sumbu-x.

Gambar 2 Doubling

Operasi grup kurva eliptik cukup mudah diilustrasikan secara geometri ketika didefinisikan atas bilangan real seperti gambar di atas. Akan tetapi, jika didefinisikan terhadap field berhingga dimana adalah karakteristik prima, maka secara geometrik, akan tersamarkan dan sulit dibayangkan. Oleh sebab itu, yang hanya bisa dilakukan adalah dengan pendekatan aksiomatik (aljabar). Sedangkan metodenya disebut dengan aritmetik kurva eliptik.

Dalam aritmetik pada , terdapat beberapa karakteristik prima yaitu biner

, terner dan karakteristik dan yang dinotasikan dengan . Sedangkan untuk biner dan terner, akan dibedakan lagi dengan Supersingular dan Non-Supersingular, dimana yang menjadi

pembeda adalah persamaan kurva eliptiknya .

2.8Pengenalan Algoritme ElGamal atas Algoritme ElGamal merupakan salah satu jenis kriptografi kunci publik. Algoritme ini aritmetikanya berbasis integer grup siklik pada grup multiplikatif .

Ada tiga algoritme untuk penyandian kunci Publik ElGamal. Algoritme 1 untuk pembangkitan kunci, Algoritme 2 untuk Enkripsi Kunci Publik, dan Algoritme 3 untuk Dekripsi.

Misalkan A mengirimkan pesan kepada B. Pesan tersebut ingin disandikan. Maka yang akan dilakukan adalah

1. Algoritme 1 Pembangkitan Kunci B membuat sebuah kunci publik dan kunci pribadi. Hal yang dilakukan adalah a. Dengan prima acak yang besar,

kemudian dilakukan pembangkitan generator dari grup dengan integer-integer modulo p.

b. Memilih suatu integer acak a, dengan positif.

c. Menghitung mod .

d. Kunci publik B adalah , , dan kunci pribadi B adalah a.

e. Memberikan kunci publik ke A.

Dalam algoritme pembangkitan kunci pada penyandian kunci publik ElGamal, dijelaskan membangkitkan suatu bilangan prima p yang besardan generator dari grup

. Ini bertujuan bahwa dengan mendapatkan bilangan yang memenuhi kriteria keamanan, maka p tersebut dapat digunakan untuk grup dari integer-integer suatu prima p (jika prima, maka mempunyai generator dan dikatakan siklik). Semakin besar , maka keamanannya semakin tinggi.

2. Algoritme 2 Enkripsi

A menyandikan atau me-enkripsi sebuah pesan m ke B. Langkah-langkah yang harus dilakukan oleh A adalah

a. Memperoleh kunci publik , , dan merepresentasikan pesan sebagai suatu integer m pada interval [0, .

b. Memilih integer acak k, dimana positif.

c. Menghitung mod dan mod .

(7)

enkripsi didefinisikan oleh mod dan menghasilkan siferteks c.

3. Algoritme 3 Dekripsi

Untuk menemukan kembali m dari c, B harus melakukan hal-hal berikut

a. Menggunakan kunci pribadi a untuk menghitung mod . Dengan

catatan .

b. Menemukan kembali m dengan menghitung mod .

Pada proses dekripsi, dengan dan didefinisikan : , sehingga fungsi dekripsi didefinisikan oleh

mod .

(Menezes et al. 1996)

Berikut ini diberikan suatu ilustrasi penyandian yang dihitung dengan menggunakan software Maple 12 dengan PC processor Intel Pentium Dual Core 1,73 GHz, Ram 512 MB.

Contoh ElGamal

A mengirim pesan kepada B. Pesan tersebut adalah 91819250104.

Langkah pertama, B membuat kunci publik dan kunci pribadi. Setelah melalui

Algoritme 1 Pembangkitan Kunci, diperoleh kunci publik , , (9574006709478958 762709029785327385064807, 5, 468663437 0436292147431903521064446370856) dan kunci pribadi (665638090635425982769 337333168305062441). Kemudian, kunci publik tersebut dikirim ke A.

Setelah A memperoleh kunci publik , , dari B, kemudian A memilih integer positif acak k dan menghitung

mod 52940576363150816401527749-6545355441362, dan mod = 598-510960553455680182318130888811111301. A mengirim pesan yang telah disandikan tadi (siferteks) kepada B dengan bentuk

, = (529405763631508164015277496-545355441362, 5985109605534556801823-18130888811111301).

Setelah B menerima siferteks tadi, maka B mendekripsikan siferteks tadi untuk menemukan kembali pesan m dengan menggunakan kunci pribadi,

mod , dimana pesan yang telah didekripsikan tadi sama dengan pesan yang sebelum dienkripsikan.

III PEMBAHASAN

Field dengan karakteristik prima merupakan suatu kasus khusus, dimana tidak ada pengurangan pada operasi aljabarnya.

Seperti yang telah dipaparkan pada bab 2, di bawah ini akan dibahas struktur grup kurva eliptik Supersingular dengan , dan Non-Supersingular sehingga titik (0,0) berada di luar kurva yang merepresentasikan titik ∞.

3.1 Aritmetika Kurva Eliptik Supersingular.

Misalkan adalah field dengan karakteristik prima Supersingular dengan bentuk sederhana dari persamaan kurva eliptiknya adalah

:

dengan , , dan ∆ ∆

.

Didefinisikan persamaan kurva eliptik Supersingular

, |

∞.

1. Misalkan terdapat titik , sembarang. Karena syarat

dan dengan , maka titik , dijamin tidak terletak pada kurva dan dapat digunakan untuk merepresentasikan ∞ , . Akibatnya,

∞ , ,

2. Dengan titik , yang direpresentasikan dengan titik di tak-hingga maka untuk

setiap , , terdapat

invers dari yang dinotasikan dengan

– , berlaku,

, ∞.

dimana ∞ ∞.

3. Untuk setiap , dimana

, , , dan

maka titik yang akan dicari adalah , .

Terdapat tiga titik pada E, maka berlaku tiga persamaan

(1.1)

(1.2) (1.3) Jika dilihat dari definisi secara geometri, maka , dan ,

(8)

3. Algoritme 3 Dekripsi

catatan .

mod .

Contoh ElGamal

, = (529405763631508164015277496-545355441362, 5985109605534556801823-18130888811111301).

III PEMBAHASAN

3.1 Aritmetika Kurva Eliptik Supersingular.

:

.

, |

∞.

∞ , ,

setiap , , terdapat

– , berlaku,

, ∞.

dimana ∞ ∞.

, , , dan

(1.1)

(9)

6

dimisalkan dengan maka diperoleh persamaan

(1.4) Kemudian apabila dari persamaan (1.1) dan (1.3) kita jumlahkan dan dimodulokan dengan dua, akan diperoleh

Apabila pada ruas kiri kita tambahkan nilai , maka persamaan di atas menjadi

Kemudian kedua ruas disederhanakan dan dibagi dengan diperoleh

(1.5) Setelah memperoleh persamaan (1.5) dengan dari persamaan (1.4), maka untuk persamaan (1.2), (1.3) akan diperoleh dengan cara yang sama, sehingga didapatkan

(1.6) Untuk memperoleh dan , akan dijumlahkan persamaan (1.5), (1.6) sehingga kita peroleh

Apabila kita bagi kedua ruas dengan maka didapatkan

dan dari dihasilkan

.

Jadi, dihasilkan , dengan dan

dengan .

4. Untuk setiap , dan

, titik yang ingin ditentukan

adalah , .

Apabila diperhatikan secara geometri, titik P dan R berada pada kurva E. Oleh sebab itu, terdapat dua persamaan

dan

. (1.7) Jika ditarik garis lurus P dan R’ (titik

sebelum dicerminkan terhadap sumbu-x), terlihat merupakan sebuah garis singgung. Dimisalkan gradiennya , maka

(1.8)

Kemudian, dengan turunan implisit

dengan memisalkan , ,

dapat kita peroleh nilai yaitu

, ,

(1.9) Sama halnya dengan penurunan kasus

(pada persamaan 1.5), diperoleh persamaan

Sehingga . Untuk diperoleh dari persamaan (1.8) yaitu

dengan .

Dari uraian di atas, diperoleh aritmetik pada kurva eliptik Supersingular sebagai berikut

1. Titik di luar kurva yang digunakan adalah

∞ , .

2. , dan – ,

apabila dijumlahkan menghasilkan titik ∞.

3. , dimana , ,

, dan maka, ,

dimana dan

dengan .

4. , dan ,

berlaku , dimana

dan

dengan .

Di bawah operasi di atas, maka kurva eliptik supersingular merupakan grup dengan unsur identitas ∞ , dan invers

(10)

7

3.2 Algoritme Aritmetik Kurva Eliptik Supersingular.

3.2.1 Pembangkitan Kurva Eliptik

K(a,b,c)

INPUT : Memasukkan nilai m

OUTPUT : nilai kurva , ,

Mulai

1. Pilih acak , , .

2. Lakukan sampai i proses jika ∞ dengan cara

a. Mengacak b. Selesai

3. Kemudian lakukan juga sampai i proses jika diperoleh ∞ dengan cara

a. Mengacak b. Selesai 4. Tampilkan , ,

3.2.2 Menentukan Titik P(x,y) INPUT : Nilai kurva , , OUTPUT : Titik ,

Mulai

1. Hitung

2. Lakukan sampai i proses jika diperoleh ∞dengan cara

a. Menentukan kembali

b. Selesai.

3. Tampilkan nilai , yang memenuhi

dengan ∞.

3.2.3 Adisi Titik , , INPUT : P , , Q ,

dengan , , OUTPUT : Titik ,

Mulai

1. Jika ∞ atau ∞, maka a.

b.

2. Jika dan , maka a.

b.

3. Jika . Maka a.

b. c.

4. Jika tidak , maka :

a. b. c.

5. Tampilkan ,

3.2.4 Menentukan Invers (Negatif) Titik INPUT : Titik P ,

dengan kurva eliptik , ,

OUPUT : P , c

Mulai

1. Dengan c

2. Tampilakan , .

3.2.5 Menentukan (Kelipatan sebanyak )

INPUT : Titik P , dan merupakan integer positif acak dengan , ,

OUPUT :

Mulai

1. Pilih suatu integer acak dan diubah menjadi basis 2

2. Misalkan

3. Jika hanya terdapat satu titik P, maka a. Nilai yaitu nilai P

b. Selesai

4. Untuk langkah kedua, lakukan sampai i

kali apabila terdapat beberapa titik yang sama dengan cara

a. Nilai yaitu nilai . Jadi apabila terdapat dua titik yang sama dan masing-masing bisa dipasangkan, titik tersebut digandakan sampai i sehingga ditemukan satu titik.

b. Jika operasi ke i kali yang nilai biner (terdapat satu titik yang tidak ada pasangan untuk digandakan), maka lakukan

1. Titik yang digandakan sebelumnya dijumlahkan dengan satu titik yang tidak mempunyai pasangan sehingga proses a

2. Selesai c. Selesai 5. Tampilkan titik

3.3 Aritmetika Kurva Eliptik Non-Supersingular.

Misalkan adalah field dengan karakteristik prima Non-Supersingular dengan bentuk sederhana dari persamaan kurva eliptiknya adalah

:

dengan , dan ∆ .

Didefinisikan persamaan kurva eliptik Non-Supersingular

, |

(11)

8

1. Misalkan terdapat titik , sembarang. Karena syarat , maka titik , dijamin tidak terletak pada kurva dan dapat digunakan untuk merepresentasikan ∞ , . Akibatnya,

∞ , , .

setiap , , terdapat

– , berlaku,

, ∞.

dimana ∞ ∞.

, , , dan

Apabila ditelaah pada tiga titik pada E, maka berlaku tiga persamaan

(2.1)

(2.2) (2.3) Jika dilihat dari definisi secara geometri, maka P, Q dan ,

adalah segaris. Jika gradiennya dimisalkan dengan λ maka diperoleh persamaan

(2.4) Kemudian dari penjumlahan persamaan (2.1) dan (2.3) yang kemudian dimodulokan dengan dua diperoleh

/

⁄

(2.5) Dengan cara yang sama dari persamaan (2.2), (2.3), dan (2.4) diperoleh

(2.6)

Dengan nilai gradien seperti pada (2.4), sehingga penjumlahan dari (2.5) dan (2.6) menghasilkan

dan dari persamaan (2.4) diperoleh

Dengan demikian, diperoleh , dimana

dan dengan

.

adalah , .

Dilihat secara geometri, titik dan , segaris. Titik dan , merupakan garis singgung kurva pada titik . Maka berlaku persamaan

(2.7) (2.8) Dimisalkan gradiennya dengan

(2.9) Kemudian, dengan turunan implisit

(3.0) karena dalam biner, maka (2.8) menjadi

, ,

(3.1) Seperti pada penurunan persamaan

(2.5), dari persamaan (2.7), (2.8), dan (2.9) diperoleh

(12)

9

dengan menerapkan persamaan (3.1) maka diperoleh

Selanjutnya, dengan membagi kedua ruas dengan dan diterapkan juga persamaan (2.9) diperoleh

Untuk mendapatkan nilai digunakan persamaan (2.9), maka diperoleh

dengan persamaan (3.1) persamaan di atas menjadi

Akhirnya diperoleh

, dimana dan

dengan .

Dari uraian di atas, diperoleh aritmetik pada kurva eliptik Non-Supersingular sebagai berikut

a. Titik di luar kurva yang digunakan adalah

∞ , .

b. , dan – ,

c. , sembarang. Misalkan

, , , dan

maka,

, dimana dan adalah

dan

dengan .

d. Untuk setiap , dan

, berlaku ,

dimana dan

dengan .

Di bawah operasi di atas, maka kurva eliptik Non-Supersingular merupakan grup dengan unsur identitas ∞ , dan

invers dari adalah – , .

3.4 Algoritme Aritmetika Kurva Eliptik Non-Supersingular

3.4.1 Pembangkitan Kurva K(a,b) INPUT : Memasukkan nilai m

OUTPUT : Nilai kurva ,

Mulai

1. Pilih acak , .

2. Lakukan sampai i proses dengan syarat ∞ dengan cara

a. Mengacak b. Selesai 3. Tampilkan ,

3.4.2 Menentukan Titik P(x,y) INPUT : Nilai kurva , OUTPUT : Titik ,

Mulai

1. Hitung

2. Lakukan sampai i proses apabila ∞ dengan cara

a. Hitung

b. Selesai.

3. Tampilkan , dengan dan ∞.

dengan , OUTPUT : Titik ,

Mulai

b.

2. Jika dan , maka

a. b.

3. Jika . Maka a.

b. c.

4. Jika tidak , maka : a.

b. c.

(13)

10

3.4.4 Menentukan Invers (Negatif) Titik INPUT : Titik P , dengan

, OUPUT : P ,

Mulai

1. Hitung 2. Tampilkan ,

3.4.5 Menentukan (kelipatan sebanyak k kali)

OUPUT :

Mulai

2. Misalkan

b. Selesai

3.5 ElGamal Kurva Eliptik atas

Untuk penerapan kurva eliptik dalam algoritme ElGamal, maka terdapat beberapa perubahan yang terjadi dalam algoritme tersebut. Perubahannya dari grup multiplikatif yang digeneralisasi menjadi aritmetik kurva eliptik .

Berikut langkah-langkah penyandian dengan grup multiplikatif digeneralisasi. Diilustrasikan A mengirim pesan kepada B.

1. Algoritme 1 Pembangkitan Kunci B membuat sebuah kunci publik dan kunci pribadi. Hal yang dilakukan adalah

a. Memilih suatu grup siklik berorder dengan generator .

b. Memilih suatu integer acak a dalam

.

c. Menghitung .

d. Kunci publik B adalah , dan kunci pribadi B adalah a.

e. Kemudian kunci publik tersebut dikirimkan ke A.

2. Algoritme 2 Enkripsi

a. Memperoleh kunci publik , . b. Merepresentasikan pesan tersebut

sebagai suatu integer

c. Memilih integer acak k, dimana positif.

d. Menghitung dan . e. Mengirim siferteks , ke B. 3. Algoritme 3 Dekripsi

a. Menggunakan kunci pribadi a untuk menghitung . Dengan catatan

.

b. Menemukan kembali m dengan menghitung , sehingga diperoleh

. (Menezes et al. 1996)

Sedangkan untuk aritmetika kurva eliptik digunakan aturan definisi grup kurva eliptik dengan menggunakan proses adisi. Perubahan yang terjadi adalah

a. menjadi

Sebanyak kali b. menjadi .

Oleh karena itu, algoritme ElGamal dalam grup multiplikatif diatas diganti menjadi aritmetika kurva eliptik (diilustrasikan A mengirim pesan ke B).

1. Algoritme 1 Pembangkitan Kunci B membuat sebuah kunci publik dan kunci pribadi. Hal yang dilakukan adalah

a. Memilih suatu generator , yang merupakan titik pada kurva eliptik. .

b. Memilih suatu integer acak a dalam

.

c. Menghitung .

d. Kunci publik B adalah , dan kunci pribadi B adalah a.

(14)

11

2. Algoritme 2 Enkripsi

a. Memperoleh kunci publik , . b. Merepresentasikan pesan tersebut

sebagai suatu titik . c. Memilih integer acak k,

d. Menghitung dan .

e. Mengirim siferteks , ke B. 3. Algoritme 3 Dekripsi

a. Menggunakan kunci pribadi a untuk menghitung .

b. Menemukan kembali pesan m dengan

menghitung , sehingga

diperoleh

.

Contoh ElGamal Kurva Eliptik (Lihat

Lampiran 4):

Diilustrasikan Andi mengirim pesan kepada Beni. Hal pertama yang dilakukan Beni adalah membuat kunci pribadi dan kunci publik. Dimisalkan menggunakan aritmetik kurva eliptik Non-Supersingular. Hal ini dikarenakan langkah-langkah yang dilakukan sama.

1. Algoritme 1 Pembangkitan Kunci.

a. Beni memilih generator yang merupakan suatu titik pada kurva eliptik. , , , , , , , ,

, , , .

b. Beni memilih integer acak yang nantinya merupakan kunci pribadi

.

c. Kemudian menghitung , , , , , , , .

d. Kunci Publik adalah , dengan nilai , , , , , , , , , , ,

, , , , , , , .

2. Algoritme 2 Enkripsi

Setelah menerima kunci publik dari Beni, Andi menyandi pesan tersebut dengan

menggunakan kunci tersebut. Kemudian yang dilakukan Andi adalah

a. Membangkitkan pesan. Di sini dimisalkan pesan yang dibangkitkan Andi adalah suatu titik

, , , , , , , , , .

b. Kemudian Andi memilih sembarang integer .

c. Setelah itu Andi mencari nilai , , , , , , , , , , . Kemudian, mencari nilai

, , , , , , , , , .

d. Nilai yang diperoleh tersebut dikirim kepada Beni dalam bentuk siferteks

, , , , , , , , , , , , , , , , , , , , , .

3. Algoritme 3 Dekripsi

Setelah Beni menerima siferteks, barulah dia menemukan kembali pesan yang telah disandikan tersebut dengan menggunakan kunci pribadi yang hanya dia sendiri yang mengetahuinya dengan cara

a. Mencari – dimana a merupakan kunci pribadi, sehingga diperoleh –

, , , , , , , , , , .

b. Menemukan kembali m dengan

menghitung sehingga

diperoleh pesan yang sama seperti pesan yang belum disandikan

, , , , , , , , , .

Terlihat dengan jelas bahwa dalam melakukan penyandian tersebut, digunakan empat prinsip hukum grup dari kurva eliptik

. Titik yang diperoleh di atas merupakan suatu himpunan. Himpunan-himpunan tersebut merupakan pangkat dari definisi

. Misalkan contoh pesan yang digunakan pada contoh di atas. Pasangan titik

, , , , , , , , , sama dengan pasangan polinomial . . .

. . . , . . .

. . Sedangkan untuk nilai merupakan nilai untuk a. Ini dikarenakan berapapun nilai

(15)

IV SIMPULAN DAN SARAN

4.1 Simpulan

Terdapat dua kasus untuk kurva eliptik dalam field biner yaitu Supersingular dan Non-Supersingular. Aritmetik baru yang diperoleh dari kurva eliptik field biner ini merupakan proses adisi yang disebut dengan hukum grup kurva eliptik. Proses adisi tersebut adalah penjumlahan dengan suatu titik dengan unsur identitas, penjumlahan suatu titik dengan invers titik tersebut, penjumlahan dua titik yang berbeda, dan

doubling.

Aritmetik yang diperoleh dari penjumlahan tersebut adalah

1. Kurva eliptik Supersingular

a. Terdapatnya identitas ∞, sehingga

∞ .

b. Adanya invers, , .

c. Untuk adisi, , ,

diperoleh dan

dengan .

d. Untuk doubling,

, , nilai dan nilai dengan

.

2. Kurva eliptik Non-Supersingular a. Terdapatnya identitas ∞, sehingga

∞ .

c. Untuk adisi, , ,

nilai dan

dengan .

, dimana nilai dan nilai

dengan .

Dari hukum grup ini dapat dibentuk prosedur dalam Maple 12 dan juga dapat digabung dengan ElGamal.

Dalam penggabungan ini, dihasilkan pesan yang sebelum disandikan identik dengan pesan yang telah disandikan. Ini menunjukkan ElGamal yang semula dalam grup multiplikatif digeneralisasi menjadi ElGamal Kurva Eliptik dalam field .

4.2 Saran

Dalam karya ilmiah ini, penulis hanya melakukan pencarian titik pada kurva dan melakukan proses adisi struktur grup kurva eliptik. Di samping itu juga, penulis hanya mencoba menggabungkan aritmetik ini dengan ElGamal. Jadi, masih terdapat kekurangan diantaranya membandingkan keamanan suatu pesan pada ElGamal kurva eliptik Supersingular dengan Non-Supersingular. Semoga tulisan ini dapat menjadi inspirasi.

DAFTAR PUSTAKA

Aliatiningtyas N. 2002. Struktur Aljabar.

Bogor: Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Fraleigh. 1994. Abstract Algebra. United States of America: Addison-Wesley Publishing Company.

Guritman S. 2004. Struktur Aljabar. Bogor: Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Hankerson, Menezes, Vanstone.2004. Guide to Elliptic Curve Cryptography. New York: Springer-Verlag Inc.

Menezes, Oorschot Van, Vanstone. 1996.

Handbook of Applied Cyrptography.

Massachusetts Institute of Technology.

(16)

KONSTRUKSI ARITMETIKA KURVA ELIPTIK

SUPERSINGULAR DAN NON-SUPERSINGULAR

UNTUK SKEMA KUNCI PUBLIK ELGAMAL

IRSYAD RAMLI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(17)

IV SIMPULAN DAN SARAN

4.1 Simpulan

Terdapat dua kasus untuk kurva eliptik dalam field biner yaitu Supersingular dan Non-Supersingular. Aritmetik baru yang diperoleh dari kurva eliptik field biner ini merupakan proses adisi yang disebut dengan hukum grup kurva eliptik. Proses adisi tersebut adalah penjumlahan dengan suatu titik dengan unsur identitas, penjumlahan suatu titik dengan invers titik tersebut, penjumlahan dua titik yang berbeda, dan

doubling.

Aritmetik yang diperoleh dari penjumlahan tersebut adalah

1. Kurva eliptik Supersingular

a. Terdapatnya identitas ∞, sehingga

∞ .

c. Untuk adisi, , ,

diperoleh dan

dengan .

, , nilai dan nilai dengan

.

2. Kurva eliptik Non-Supersingular a. Terdapatnya identitas ∞, sehingga

∞ .

c. Untuk adisi, , ,

nilai dan

dengan .

, dimana nilai dan nilai

dengan .

Dari hukum grup ini dapat dibentuk prosedur dalam Maple 12 dan juga dapat digabung dengan ElGamal.

Dalam penggabungan ini, dihasilkan pesan yang sebelum disandikan identik dengan pesan yang telah disandikan. Ini menunjukkan ElGamal yang semula dalam grup multiplikatif digeneralisasi menjadi ElGamal Kurva Eliptik dalam field .

4.2 Saran

Dalam karya ilmiah ini, penulis hanya melakukan pencarian titik pada kurva dan melakukan proses adisi struktur grup kurva eliptik. Di samping itu juga, penulis hanya mencoba menggabungkan aritmetik ini dengan ElGamal. Jadi, masih terdapat kekurangan diantaranya membandingkan keamanan suatu pesan pada ElGamal kurva eliptik Supersingular dengan Non-Supersingular. Semoga tulisan ini dapat menjadi inspirasi.

DAFTAR PUSTAKA

Aliatiningtyas N. 2002. Struktur Aljabar.

Bogor: Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Fraleigh. 1994. Abstract Algebra. United States of America: Addison-Wesley Publishing Company.

Guritman S. 2004. Struktur Aljabar. Bogor: Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Hankerson, Menezes, Vanstone.2004. Guide to Elliptic Curve Cryptography. New York: Springer-Verlag Inc.

Menezes, Oorschot Van, Vanstone. 1996.

Handbook of Applied Cyrptography.

Massachusetts Institute of Technology.

(18)

KONSTRUKSI ARITMETIKA KURVA ELIPTIK

UNTUK SKEMA KUNCI PUBLIK ELGAMAL

IRSYAD RAMLI

(19)

ABSTACT

IRSYAD RAMLI. Constructions of Supersingular and Non-Supersingular Elliptic Curve Arithmetics for the ElGamal Public Key Scheme. Supervised by SUGI GURITMAN and NUR ALIATININGTYAS.

The ElGamal algorithm is one of the public key algorithms with modular arithmetic , which has the structure of the cyclic group . Security level of this algorithm depends on the solution of discrete logarithm problem. Unfortunately, this security level tends to decline recently because of the increase in ability of solving discrete logarithm. Moreover, to have an adequate level of security, very large value would be required, but this would cause the encryption and decryption process to be slow.

(20)

ABSTRAK

IRSYAD RAMLI. Konstruksi Aritmetika Kurva Eliptik Supersingular dan Non-Supersingular untuk Skema Kunci Publik ElGamal. Dibimbing oleh SUGI GURITMAN dan NUR ALIATININGTYAS.

Algoritme ElGamal adalah salah satu algoritme kunci publik dengan aritmetik modular yang mempunyai struktur grup siklik . Tingkat keamanan algoritme ini terletak pada pemecahan masalah logaritme diskret dari . Akan tetapi, tingkat keamanan dari tahun ke tahun semakin menurun yang disebabkan kemampuan pemecahan algoritme diskret semakin meningkat. Untuk memenuhi tingkat keamanan yang memadai dibutuhkan yang cukup besar yang menyebabkan proses enkripsi dan dekripsi menjadi lambat.

(21)

KONSTRUKSI ARITMETIKA KURVA ELIPTIK

UNTUK SKEMA KUNCI PUBLIK ELGAMAL

IRSYAD RAMLI

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

(22)

Judul

: Konstruksi Aritmetika Kurva Eliptik

Supersingular dan

Non-Supersingular untuk Skema Kunci Publik ElGamal

Nama :

Irsyad

Ramli

NIM :

G54063001

Menyetujui

Pembimbing I,

Dr. Sugi Guritman

NIP : 19620927 199203 1 004

Pembimbing II,

Dra. Nur Aliatiningtyas, M.Si

NIP : 19610104 198803 2 002

Mengetahui :

Ketua Departemen,

Dr. Berlian Setiawaty, MS

NIP : 19650505 198903 2 004

(23)

KATA PENGANTAR

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala nikmat, karunia, izin, dan pertolongan-Nya sehingga penulisan karya ilmiah ini berhasil diselesaikan. Shalawat serta salam tercurah kepada nabi Muhammad SAW sebagai suri tauladan terbaik bagi umatnya hingga akhir zaman. Karya ilmiah ini berjudul “Konstruksi Aritmetika Kurva Eliptik Supersingular dan Non-Supersingular untuk Skema Kunci Publik ElGamal”

Penyusunan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu, penulis mengucapkan terima kasih yang sebesar-besarnya kepada

1. Bapak Dr. Sugi Guritman selaku dosen pembimbing I (terima kasih atas semua ilmu, kesabaran, motivasi dan bantuannya selama penulisan skripsi ini).

2. Ibu Dra. Nur Aliatiningtyas, M.Si selaku dosen pembimbing II (terima kasih atas semua ilmu, kesabaran, dan motivasinya).

3. Semua dosen Departemen Matematika (terima kasih atas semua ilmu dan sarannya). 4. Terima kasih atas bantuannya kepada Mas Yono, Mas Bono, Mas Deni, Mas Heri, Bu

Susi, Bu Ade.

5. Keluargaku tercinta : ayahanda (terima kasih atas doa, dukungan, motivasi, kerja keras dan kesabarannya menyekolahkan ananda. Ayahanda adalah ayah yang penuh semangat walaupun harus membanting tulang untuk menafkahi keluarga. Ayah adalah ayah yang paling terbaik sedunia), Ibunda (terima kasih atas doa, didikan, motivasi dan kasih sayangnya. Ibunda adalah ibu yang paling terbaik sedunia). Kakakku tercinta (Rahmawita) yang tak henti-hentinya memotivasi. Adik-adikku tercinta (Hamdan, Hafizh) yang menjadi motivasiku dan membangkitkan semangatku.

6. Bibi-bibiku : Bibi Risyda, Bibi Arma Suari, Bibi Irawati (terima kasih atas tempat tinggalnya, doa, kasih sayang, dan perhatiannya kepadaku selama di sini).

7. Kakak-kakak sepupuku : Yessi Adjisir, Andry Adjisir, Haryenni Adjisir, Gafrian Abrar, Zamakhsyari Abrar, Amalia Fitri, Haikal Abrar, Denny Ismayadin (terima kasih atas bantuan, motivasi, dan kasih sayangnya).

8. Ro’fah Nur Rachmawati (terima kasih atas bimbingan, motivasi, ilmu, dan sarannya). 9. Teman-teman kontrakan Kahfi 43 : Deni Hamdan Permana, Yogi Nur Anggowo, Slamet

Riyadi, Slamet Aprian Utomo, Agung Surya Permadi, Martono (terima kasih atas dukungannya).

10. Teman-teman : Retwando, Dorisman, Dian Fernanda, Chawen, Ira, Hanif, Dya, Rezki Anandra.

11. Kakak-kakak Math 41 : Mora, Chubby, Jali, Cumi, dan lainnya (terima kasih atas dukungan dan bantuannya).

12. Kakak-kakak Math 42 : Djawa, Acuy, Iput, Ilyas, Danu, Eko, Eyyi, Zil, Mocco, Sapto, Danu dan lainnya (terima kasih atas dukungannya).

13. Teman-teman Math 43 : Ucok, Andrew, Sabar, Cici, Desi, Gandi, Fitria, Margie, Rias, Erni, Ratna, Sunarsih, Rizki NS, Rizki SN, Zul, Paisol, Nanu, Wira, Sofyan, Nia, Tami, Nenek, Destya, Putri, Vera, Suci, Hermalina, Nurmalina, Kiki, Arif, David, Adi, Fardan dan lainnya (terima kasih atas dukungannya).

14. Adik-adik Math 44 : Cristoper, Fani, Selvie dan lainnya (terima kasih atas dukungannya). 15. Adik-adik Math 45 terima kasih atas bantuannya.

Semoga karya ilmiah ini bermanfaat bagi dunia ilmu pengetahuan.

Bogor, November 2010

(24)

DAFTAR ISI

Halaman DAFTAR LAMPIRAN ... viii

I PENDAHULUAN

1.1 Latar Belakang ... 1 1.2 Tujuan ... 1

II LANDASAN TEORI

2.1 Grup ... 2 2.2 Grup Siklik ... 2 2.3 Ring ... 2 2.4 Lapangan (field) ... 2 2.5 Pengenalan Kurva Eliptik ... 3 2.6 Penyederhanaan Persamaan Weierstrass ... 3 2.7 Hukum Grup Kurva Eliptik ... 3 2.8 Pengenalan Algoritme ElGamal atas ... 4

III PEMBAHASAN

3.1 Aritmetik Kurva Eliptik Supersingular ... 5 3.2 Algoritme Aritmetik Kurva Eliptik Supersingular ... 7 3.2.1 Pembangkitan Kurva K(a,b,c) ... 7 3.2.2 Menentukan Titik P(x,y) ... 7 3.2.3 Adisi Titik P( , ) + Q( , ) ... 7 3.2.4 Menentukan Invers Titik ... 7 3.2.5 Menentukan Q P (Kelipatan Sebanyak k) ... 7 3.3 Aritmetik Kurva Eliptik Non-Supersingular ... 7 3.4 Algoritme Aritmetik Kurva Eliptik Non-Supersingular ... 9 3.4.1 Pembangkitan Kurva K(a,b) ... 9 3.4.2 Menentukan Titik P(x,y) ... 9 3.4.3 Adisi Titik P( , ) + Q( , ) ... 9 3.4.4 Menentukan Invers Titik ... 10 3.4.5 Menentukan Q P (Kelipatan Sebanyak k) ... 10 3.5 ElGamal Kurva Eliptik atas ... 10

IV SIMPULAN DAN SARAN

4.1 Simpulan ... 12 4.2 Saran ... 12

DAFTAR PUSTAKA ... 12 LAMPIRAN ... 14

(25)

DAFTAR GAMBAR

Halaman 1 Adisi ... 4 2 Doubling ... 4

DAFTAR LAMPIRAN

Halaman 1 Program Aritmetika ... 14 2 Program Konstruksi Aritmetika Kurva Eliptik ... 17 3 Program ElGamal ... 22 4 Program ElGamal Kurva Eliptik atas ... 23

(26)

RIWAYAT HIDUP

Penulis dilahirkan di Bukittinggi pada tanggal 28 November 1988 sebagai anak kedua dari empat bersaudara, anak dari pasangan Dt. Ramli dan Hanifah.

Tahun 2006 penulis lulus dari SMA Negeri 1 Matur Sumatera Barat dan pada tahun yang sama menempuh pendidikan sarjana melalui Undangan Seleksi Masuk IPB (USMI) di Program Studi Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam IPB.

(27)

I PENDAHULUAN

1.1Latar Belakang

Komputer dan internet merupakan hasil karya manusia yang menggambarkan majunya teknologi saat ini. Komputer yang terhubung dengan internet dapat memberikan berbagai bentuk kemudahan untuk manusia dalam melakukan berbagai aktifitas. Salah satunya untuk berkomunikasi seperti pengiriman pesan penting yang harus dijaga kerahasiaannya. Keadaan ini tentu akan lebih nyaman apabila terdapat keamanan atau kerahasiaan pesan dalam proses tersebut. Hal ini bertujuan agar pesan tidak jatuh ke pihak yang tidak bertanggung jawab sehingga tidak terjadi hal-hal yang tidak diinginkan. Teknik untuk pengamanan tersebut adalah Kriptografi.

Kriptografi adalah studi teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasiaan, integritas data, otentikasi entitas, dan otentikasi data asli (Menezes 1997). Fungsi-fungsi matematika digunakan untuk melakukan penyandian (enkripsi) dan membuka sandi (dekripsi). Dalam melakukan proses enkripsi dan dekripsi tersebut, dibutuhkan suatu prinsip kunci (key). Inilah yang membedakan kriptografi menjadi dua bagian yaitu kunci simetrik dan kunci asimetrik atau yang lebih dikenal dengan kunci publik (public key).

Kunci simetrik merupakan jenis kriptografi yang paling umum digunakan. Untuk jenis ini, enkripsi dan dekripsi dilakukan dengan menggunakan kunci yang sama. Permasalahan yang muncul adalah bagaimana menyampaikan kunci tersebut ke penerima agar tidak diketahui oleh pihak-pihak yang tidak diinginkan karena siapapun yang memiliki kunci tersebut termasuk pihak-pihak yang tidak diinginkan juga dapat menyandi dan membongkar pesan dengan mudah. Oleh sebab itu, pada petengahan tahun 70-an Whitfield Diffie dan Martin Hellman menemukan teknik kunci asimetrik yang merevolusi dunia kriptografi.

Kunci asimetrik adalah pasangan-pasangan kunci kriptografi yang salah satunya digunakan untuk enkripsi (kunci publik) dan yang satunya lagi untuk dekripsi (kunci pribadi). Orang-orang yang memiliki kunci publik dapat menggunakannya untuk enkripsi, tetapi hanya satu orang (memiliki kunci pribadi) yang dapat membongkar pesan yang telah disandikan tersebut. Jenis ini

mempunyai tingkat keamanan yang lebih tinggi dari pada kunci simetrik. Contoh algoritme kunci asimetrik adalah RSA (singkatan Rivest, Shamir, Adleman), Rabin, ElGamal, dan lain-lain. Dalam tulisan ini, penulis menggunakan algoritme ElGamal.

Algoritme ElGamal ditemukan oleh Taher ElGamal yang dipublikasikan pada tahun 1985. Algoritme ini didasarkan pada aritmetik modular yang mempunyai struktur grup siklik dimana merupakan sembarang bilangan prima. Tingkat keamanannya didasarkan pada pemecahan masalah logaritme diskret .

Masalah logaritme diskret didefinisikan

dengan dimana yang akan

ditentukan adalah nilai . Sekilas, untuk menyelesaikan persamaan di atas terlihat mudah. Kita dapat mencoba menentukan nilai

sedemikian sehingga persamaan tersebut dipenuhi. Hal tersebut mungkin saja dengan mudah dilakukan apabila nilai kecil. Oleh sebab itu, untuk meningkatkan keamanan yang memadai dibutuhkan nilai yang cukup besar. Akan tetapi, dengan nilai yang cukup besar, dalam melakukan enkripsi dan dekripsi menjadi lambat, karena membutuhkan memori komputer yang besar. Akhirnya, para pakar Matematika dan Kriptografi untuk mencoba memperbaiki algoritme serta meningkatkan kemampuan komputer agar tingkat keamanan memadai tanpa membutuhkan memori komputer yang sangat besar.

Matematikawan asal Prancis yaitu Pierre Galois memperkenalkan konsep field yang dikenal dengan Galois Field dan disingkat dengan atau dengan prima. Kemudian field ini digabungkan dengan prinsip kurva eliptik yang kemudian diistilahkan dengan aritmetika kurva eliptik yang memiliki tiga karakteristik umum. Salah satunya, (dengan ) yang diharapkan mampu menggantikan struktur grup siklik pada algoritme ElGamal.

1.2 Tujuan

Tujuan penulisan ini adalah untuk mengonstruksi aritmetika kurva eliptik

Supersingular dan Non-Supersingular sehingga dapat disimulasikan pada algoritme ElGamal dengan menggunakan software

(28)

II LANDASAN TEORI

2.1Grup

Definisi 2.1.1 Diberikan sebarang himpunan tak kosong dan operasi biner pada .

Himpunan disebut grup terhadap operasi biner jika memenuhi

a. Operasi bersifat asosiatif.

, , , G

b. Terdapat unsur identitas untuk pada G sehingga berlaku

,

c. Untuk setiap terdapat unsur invers, yaitu sehingga berlaku

.

(Fraleigh 1994)

Definisi 2.1.2 Suatu grup (G, ) disebut grup komutatif jika operasi binernya bersifat

komutatif, yaitu , , G

(Fraleigh 1994)

Definisi 2.1.3 Suatu grup G dikatakan grup berhingga (finite group) jika banyak unsurnya berhingga dan banyaknya unsur G tersebut disebut orderG, ditulis o(G) atau |G|.

(Fraleigh 1994)

2.2 Grup Siklik

Definisi 2.2.1 Misalkan G grup dan G

dan n bilangan bulat positif, maka a. … , (sebanyak n kali) b. … , (sebanyak n kali).

c. .

Teorema 2.2.2 Jika G suatu grup dan a G,

maka untuk setiap bilangan bulat m dan n

berlaku hukum eksponen : a.

b.

c.

(Guritman 2004)

Definisi 2.2.3 Misalkan G grup dan sebuah elemen . Jika | maka G

disebut grup siklik (cyclic group) dan disebut elemen pembangun yang dinotasikan . Jika G berhingga dan berorder m, maka terdapat m kuasa dari a yang masing-masing berbeda, yaitu

, , , …

Jika G adalah grup adisi (operasi penjumlahan), maka dapat dituliskan

|

dan jika berorder m, maka dapat ditunjukkan , , , … ,

(Guritman 2004)

2.3Ring

Definisi 2.3.1 Suatu grup dengan operasi + disebut operasi penjumlahan dan operasi · disebut operasi perkalian yang dinotasikan (R,+,·), disebut ring jika memenuhi aksioma-aksioma berikut

a. (R,+) grup komutatif.

b. Operasi perkalian bersifat asosiatif.

c. Hukum distributif kiri berlaku

, , ,

d. Hukum distributif kanan berlaku

, , ,

e. Unsur identitas terhadap “+” dinotasikan dengan 0 dan disebut unsur nol.

Selanjutnya,

a. Jika operasi perkalian bersifat komutatif, , , maka R disebut ring

komutatif.

b. Jika ada unsur identitas di bawah operasi perkalian (unsur ini disebut unsur kesatuan, dinotasikan dengan 1 dan disingkat dengan unkes), , ,

· · maka R disebut ring

dengan unsur kesatuan (unkes).

2.4Lapangan (Field)

Definisi 2.4.1 Suatu ring yang komutatif, ada unkes dan setiap unsur tak nolnya mempunyai invers (perkalian) disebut lapangan (field).

Salah satu contoh field adalah yang merupakan himpunan semua polinomial-polinomial berderajat paling banyak yang dinyatakan sebagai

| .

(29)

3 Contoh : 1. Penjumlahan 2. Perkalian

Suatu unsur biner di atas merepresentasikan polinomial basis yang di sebelah kanannya. Sehingga terlihat dengan

mudah, setara

dengan unsur biner yang dimulai dari

… sebanyak (dalam

penjumlahan di atas, unsurnya dimulai dari pangkat tertinggi ke pangkat terendah. Begitu pula dengan binernya). Misalkan, setara dengan

.

(Rosdiana 2009)

Aritmetik ini dijadikan acuan dalam perhitungan kurva eliptik atas .

Teorema 2.4.2 merupakan grup siklik multiplikatif berorder .

(Rosdiana 2009)

2.5 Pengenalan Kurva Eliptik

Definisi 2.5.1 Suatu kurva eliptik atas field

didefinisikan sebagai kurva dengan persamaan

(1)

dimana , , , , dan Δ

merupakan diskriminan dari yang di definisikan sebagai berikut:

∆

(2) Persamaan (1) disebut dengan persamaan

Weierstrass dan kurva eliptik dinotasikan ).

, |

∞ (Hankerson et al. 2004)

2.6 Penyederhanaan Persamaan Weierstrass

Definisi 2.6.1 Terkait dengan kriptografi, kurva eliptik

dikenakan atas field berhingga dimana p

prima. Berikut ini diberikan tiga kelompok besar kurva eliptik dibedakan atas field dasar

.

1. Jika dan , maka persamaan kurva eliptiknya adalah

:

dimana , dan diskriminan

kurva Δ .

2.7 Hukum Grup Kurva Eliptik

Misalkan E adalah kurva eliptik yang didefinisikan atas . Pada E diambil dua titik

yang berbeda , , , .

Maka garis memotong kurva di titik ketiga , kemudian diperoleh titik

, . Titik ini merupakan hasil dari pencerminan titik R’ terhadap sumbu x.

Proses ini disebut dengan proses adisi titik (penjumlahan titik).

(30)

[image:30.595.152.258.82.202.2]

4

Gambar 1 Adisi

Jika sejajar dengan sumbu-y, maka titik yang ketiga didefinisikan sebagai titik di tak-hingga dengan notasi ∞, sehingga

∞

Jika , maka kondisi ini disebut adisi titik yang sama dan atau disebut juga pendobelan (doubling). Dinotasikan

,

[image:30.595.142.266.404.520.2]

Jadi, operasi adisi titik pada himpunan semua titik pada kurva dan titik di tak-hingga mempunyai struktur grup, disebut dengan grup kurva eliptik. Dalam hal ini, ∞ adalah unsur identitas. Untuk setiap pada , negatif dari yang dinotasikan dengan – yang merupakan hasil pencerminan dari pada terhadap sumbu-x.

Gambar 2 Doubling

Operasi grup kurva eliptik cukup mudah diilustrasikan secara geometri ketika didefinisikan atas bilangan real seperti gambar di atas. Akan tetapi, jika didefinisikan terhadap field berhingga dimana adalah karakteristik prima, maka secara geometrik, akan tersamarkan dan sulit dibayangkan. Oleh sebab itu, yang hanya bisa dilakukan adalah dengan pendekatan aksiomatik (aljabar). Sedangkan metodenya disebut dengan aritmetik kurva eliptik.

Dalam aritmetik pada , terdapat beberapa karakteristik prima yaitu biner

, terner dan karakteristik dan yang dinotasikan dengan . Sedangkan untuk biner dan terner, akan dibedakan lagi dengan Supersingular dan Non-Supersingular, dimana yang menjadi

pembeda adalah persamaan kurva eliptiknya .

2.8Pengenalan Algoritme ElGamal atas Algoritme ElGamal merupakan salah satu jenis kriptografi kunci publik. Algoritme ini aritmetikanya berbasis integer grup siklik pada grup multiplikatif .

Ada tiga algoritme untuk penyandian kunci Publik ElGamal. Algoritme 1 untuk pembangkitan kunci, Algoritme 2 untuk Enkripsi Kunci Publik, dan Algoritme 3 untuk Dekripsi.

Misalkan A mengirimkan pesan kepada B. Pesan tersebut ingin disandikan. Maka yang akan dilakukan adalah

1. Algoritme 1 Pembangkitan Kunci B membuat sebuah kunci publik dan kunci pribadi. Hal yang dilakukan adalah a. Dengan prima acak yang besar,

kemudian dilakukan pembangkitan generator dari grup dengan integer-integer modulo p.

b. Memilih suatu integer acak a, dengan positif.

c. Menghitung mod .

d. Kunci publik B adalah , , dan kunci pribadi B adalah a.

e. Memberikan kunci publik ke A.

Dalam algoritme pembangkitan kunci pada penyandian kunci publik ElGamal, dijelaskan membangkitkan suatu bilangan prima p yang besardan generator dari grup

. Ini bertujuan bahwa dengan mendapatkan bilangan yang memenuhi kriteria keamanan, maka p tersebut dapat digunakan untuk grup dari integer-integer suatu prima p (jika prima, maka mempunyai generator dan dikatakan siklik). Semakin besar , maka keamanannya semakin tinggi.

2. Algoritme 2 Enkripsi

a. Memperoleh kunci publik , , dan merepresentasikan pesan sebagai suatu integer m pada interval [0, .

b. Memilih integer acak k, dimana positif.

c. Menghitung mod dan mod .

(31)

3. Algoritme 3 Dekripsi

catatan .

mod .

Contoh ElGamal

, = (529405763631508164015277496-545355441362, 5985109605534556801823-18130888811111301).

III PEMBAHASAN

3.1 Aritmetika Kurva Eliptik Supersingular.

:

.

, |

∞.

∞ , ,

setiap , , terdapat

– , berlaku,

, ∞.

dimana ∞ ∞.

, , , dan

(1.1)

(32)

6

dimisalkan dengan maka diperoleh persamaan

(1.4) Kemudian apabila dari persamaan (1.1) dan (1.3) kita jumlahkan dan dimodulokan dengan dua, akan diperoleh

Apabila pada ruas kiri kita tambahkan nilai , maka persamaan di atas menjadi

Kemudian kedua ruas disederhanakan dan dibagi dengan diperoleh

(1.5) Setelah memperoleh persamaan (1.5) dengan dari persamaan (1.4), maka untuk persamaan (1.2), (1.3) akan diperoleh dengan cara yang sama, sehingga didapatkan

(1.6) Untuk memperoleh dan , akan dijumlahkan persamaan (1.5), (1.6) sehingga kita peroleh

Apabila kita bagi kedua ruas dengan maka didapatkan

dan dari dihasilkan

.

Jadi, dihasilkan , dengan dan

dengan .

adalah , .

Apabila diperhatikan secara geometri, titik P dan R berada pada kurva E. Oleh sebab itu, terdapat dua persamaan

dan

. (1.7) Jika ditarik garis lurus P dan R’ (titik

sebelum dicerminkan terhadap sumbu-x), terlihat merupakan sebuah garis singgung. Dimisalkan gradiennya , maka

(1.8)

Kemudian, dengan turunan implisit

, ,

(1.9) Sama halnya dengan penurunan kasus

(pada persamaan 1.5), diperoleh persamaan

Sehingga . Untuk diperoleh dari persamaan (1.8) yaitu

dengan .

Dari uraian di atas, diperoleh aritmetik pada kurva eliptik Supersingular sebagai berikut

1. Titik di luar kurva yang digunakan adalah

∞ , .

2. , dan – ,

3. , dimana , ,

, dan maka, ,

dimana dan

dengan .

4. , dan ,

berlaku , dimana

dan

dengan .

Di bawah operasi di atas, maka kurva eliptik supersingular merupakan grup dengan unsur identitas ∞ , dan invers

(33)

7

3.2 Algoritme Aritmetik Kurva Eliptik Supersingular.

3.2.1 Pembangkitan Kurva Eliptik

K(a,b,c)

INPUT : Memasukkan nilai m

OUTPUT : nilai kurva , ,

Mulai

1. Pilih acak , , .

2. Lakukan sampai i proses jika ∞ dengan cara

a. Mengacak b. Selesai

3. Kemudian lakukan juga sampai i proses jika diperoleh ∞ dengan cara

a. Mengacak b. Selesai 4. Tampilkan , ,

3.2.2 Menentukan Titik P(x,y) INPUT : Nilai kurva , , OUTPUT : Titik ,

Mulai

1. Hitung

2. Lakukan sampai i proses jika diperoleh ∞dengan cara

a. Menentukan kembali

b. Selesai.

3. Tampilkan nilai , yang memenuhi

dengan ∞.

dengan , , OUTPUT : Titik ,

Mulai

b.

2. Jika dan , maka a.

b.

3. Jika . Maka a.

b. c.

4. Jika tidak , maka :

a. b. c.

5. Tampilkan ,

3.2.4 Menentukan Invers (Negatif) Titik INPUT : Titik P ,

dengan kurva eliptik , ,

OUPUT : P , c

Mulai

1. Dengan c

2. Tampilakan , .

3.2.5 Menentukan (Kelipatan sebanyak )

OUPUT :

Mulai

2. Misalkan

b. Selesai

3.3 Aritmetika Kurva Eliptik Non-Supersingular.

Misalkan adalah field dengan karakteristik prima Non-Supersingular dengan bentuk sederhana dari persamaan kurva eliptiknya adalah

:

dengan , dan ∆ .

Didefinisikan persamaan kurva eliptik Non-Supersingular

, |

(34)

8

1. Misalkan terdapat titik , sembarang. Karena syarat , maka titik , dijamin tidak terletak pada kurva dan dapat digunakan untuk merepresentasikan ∞ , . Akibatnya,

∞ , , .

setiap , , terdapat

– , berlaku,

, ∞.

dimana ∞ ∞.

, , , dan

Apabila ditelaah pada tiga titik pada E, maka berlaku tiga persamaan

(2.1)

(2.2) (2.3) Jika dilihat dari definisi secara geometri, maka P, Q dan ,

adalah segaris. Jika gradiennya dimisalkan dengan λ maka diperoleh persamaan

(2.4) Kemudian dari penjumlahan persamaan (2.1) dan (2.3) yang kemudian dimodulokan dengan dua diperoleh

/

⁄

(2.5) Dengan cara yang sama dari persamaan (2.2), (2.3), dan (2.4) diperoleh