Informasi Dokumen
- Penulis:
- Desi Ratna Sari Aritonang
- Pengajar:
- Prof. Dr. Tulus, M.Si. Ph.D
- Dra. Elly Rosmaini, M.Si
- Sekolah: Universitas Sumatera Utara
- Mata Pelajaran: Matematika
- Topik: Analisis Metode Branch and Bound Dalam Mengoptimalkan Jumlah Produksi Roti (Studi Kasus: PT. Ramah Jaya Bakery)
- Tipe: skripsi
- Tahun: 2013
- Kota: Medan
Ringkasan Dokumen
I. Pendahuluan
Bagian ini menjelaskan latar belakang penelitian mengenai pentingnya optimasi dalam produksi roti di PT. Ramah Jaya Bakery. Penulis menguraikan bahwa industri makanan, khususnya roti, terus berkembang dan memerlukan strategi efisien untuk memaksimalkan keuntungan. Metode Branch and Bound dipilih sebagai solusi untuk permasalahan pengalokasian sumber daya yang terbatas. Penelitian ini bertujuan untuk menunjukkan bagaimana metode ini dapat digunakan untuk menentukan jumlah produksi yang optimal.
1.1 Latar Belakang
Latar belakang penelitian ini menyoroti pertumbuhan industri roti di Indonesia dan tantangan yang dihadapi oleh perusahaan dalam mengoptimalkan produksi. Penelitian ini penting untuk memberikan wawasan tentang cara meningkatkan efisiensi dan keuntungan melalui penerapan metode matematika dalam pengambilan keputusan.
1.2 Perumusan Masalah
Permasalahan yang dihadapi oleh PT. Ramah Jaya Bakery adalah keterbatasan modal awal yang mempengaruhi jumlah produksi roti. Oleh karena itu, penting untuk menentukan jumlah bahan baku yang optimal untuk memproduksi berbagai jenis roti agar biaya produksi dapat diminimalkan dan keuntungan maksimal.
1.3 Batasan Masalah
Dalam penelitian ini, batasan masalah ditetapkan untuk fokus pada tiga jenis rasa roti yang diproduksi, yaitu kelapa, cokelat, dan melon. Penelitian ini juga mengasumsikan bahwa harga bahan baku konstan dan selalu tersedia.
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah untuk menunjukkan bagaimana metode Branch and Bound dapat digunakan untuk efisiensi dalam pengelolaan bahan baku dalam produksi roti, serta untuk memberikan alternatif solusi dalam pengambilan keputusan di perusahaan.
1.5 Tinjauan Pustaka
Tinjauan pustaka mencakup teori-teori tentang program linier dan metode pemrograman integer. Penulis menjelaskan bahwa program linier adalah teknik untuk menyelesaikan masalah alokasi sumber daya, dan program integer adalah model yang memerlukan solusi dalam bentuk bilangan bulat.
1.6 Kontribusi Penelitian
Penelitian ini memberikan kontribusi bagi pembaca dalam memahami metode Branch and Bound dan aplikasinya dalam optimasi produksi. Selain itu, penelitian ini juga dapat menjadi referensi bagi peneliti lain dan perusahaan dalam pengambilan keputusan terkait produksi.
1.7 Metodologi Penelitian
Metodologi penelitian ini menggunakan studi kasus di PT. Ramah Jaya Bakery dengan pengumpulan data melalui observasi dan wawancara. Data yang diambil mencakup bahan baku, proses produksi, dan harga jual roti untuk menganalisis optimasi produksi.
II. Landasan Teori
Bagian ini membahas teori-teori yang mendasari penelitian, termasuk program linier, program integer, dan metode Branch and Bound. Penjelasan ini penting untuk memahami dasar-dasar matematis yang digunakan dalam penelitian.
2.1 Program Linier
Program linier adalah model matematis untuk mengoptimalkan penggunaan sumber daya terbatas. Penelitian ini menggunakan program linier untuk memformulasikan masalah produksi roti dengan tujuan memaksimalkan keuntungan dari setiap jenis roti.
2.1.1 Model Program Linier
Model program linier menyajikan fungsi tujuan dan kendala dalam bentuk persamaan linier. Ini merupakan langkah awal dalam menganalisis dan menyelesaikan masalah optimasi di perusahaan.
2.1.2 Terminologi Program Linier
Terminologi ini mencakup istilah-istilah penting dalam program linier, seperti fungsi tujuan, kendala, dan variabel keputusan. Memahami istilah ini membantu dalam merumuskan model yang tepat untuk penelitian.
2.1.3 Asumsi-Asumsi Dasar Program Linier
Asumsi dasar program linier mencakup kesebandingan, penambahan, pembagian, dan kepastian. Asumsi ini penting untuk memastikan bahwa model yang dibangun dapat menghasilkan solusi yang valid.
2.1.4 Unsur-Unsur Program Linier
Unsur-unsur penting dalam program linier adalah variabel keputusan, fungsi tujuan, dan kendala. Masing-masing unsur ini berperan dalam menentukan hasil optimal dari model yang dibangun.
2.2 Program Integer
Program integer adalah jenis program linier di mana variabel keputusannya harus bernilai integer. Ini sangat relevan dalam konteks produksi roti, di mana jumlah produk tidak dapat berupa pecahan.
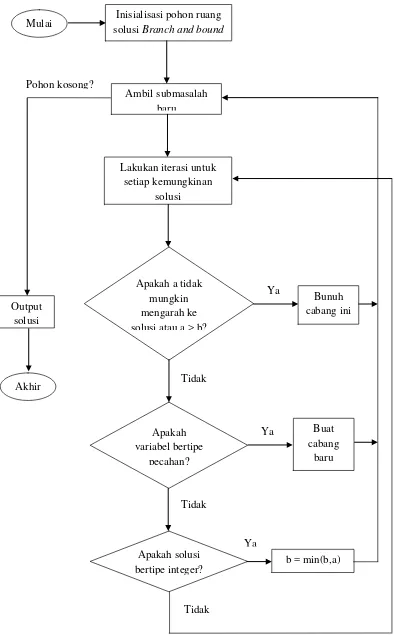
2.3 Pencabangan dan Pembatasan (Branch and Bound)
Metode Branch and Bound adalah algoritma untuk mencari solusi optimal dari masalah optimasi. Metode ini digunakan untuk menyelesaikan program integer dengan cara membagi masalah menjadi sub-masalah yang lebih kecil.
III. Metode Penelitian
Bagian ini menjelaskan langkah-langkah yang diambil dalam penelitian, mulai dari merumuskan masalah hingga analisis data menggunakan metode yang telah ditentukan.
3.1 Merumuskan Masalah
Merumuskan masalah penting untuk memahami tujuan penelitian dan memfokuskan analisis pada optimasi jumlah produksi roti di PT. Ramah Jaya Bakery. Hal ini membantu dalam menyusun strategi yang tepat untuk mencapai tujuan.
3.2 Studi Literatur dan Studi Kasus
Studi literatur dilakukan untuk memahami teori yang berkaitan dengan program linier dan metode Branch and Bound. Studi kasus di PT. Ramah Jaya Bakery memberikan konteks praktis untuk menerapkan teori-teori tersebut.
3.3 Pengamatan dan Pengumpulan Data
Pengamatan dilakukan untuk memahami proses produksi dan bahan baku yang digunakan. Data yang dikumpulkan mencakup informasi tentang jenis roti, bahan baku, dan waktu produksi yang diperlukan.
3.4 Pengolahan Data
Data yang diperoleh diolah untuk memodelkan fungsi tujuan dan kendala dalam bentuk program linier. Penggunaan software QM membantu dalam menghitung nilai variabel keputusan dan mencari solusi optimal.
3.5 Penarikan Kesimpulan
Kesimpulan diambil berdasarkan hasil analisis data untuk memberikan rekomendasi tentang jumlah produksi roti yang optimal. Penarikan kesimpulan ini penting untuk memberikan arahan bagi perusahaan.
3.6 Skema Pengolahan Data
Skema pengolahan data memberikan gambaran jelas tentang langkah-langkah yang diambil dalam penelitian, mulai dari formulasi masalah hingga analisis hasil yang diperoleh.
IV. Pembahasan
Bagian ini membahas hasil analisis data yang diperoleh dari penelitian dan bagaimana metode Branch and Bound diterapkan untuk mencapai solusi optimal dalam produksi roti.
4.1 Merumuskan Data ke dalam Model Matematika
Data yang diperoleh dari perusahaan dirumuskan dalam model matematika untuk menentukan jumlah produksi yang optimal. Fungsi tujuan di formulasi untuk memaksimalkan keuntungan dari setiap jenis roti yang diproduksi.
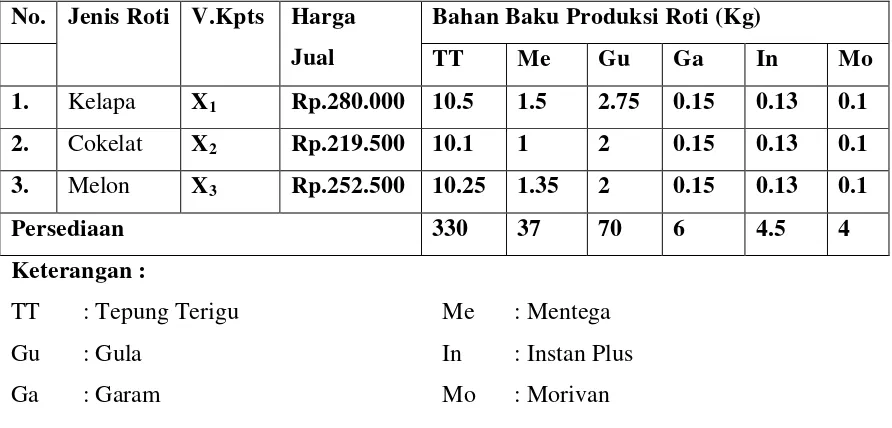
4.1.1 Perumusan Fungsi Tujuan
Fungsi tujuan yang dirumuskan adalah untuk memaksimalkan laba dari penjualan roti. Penentuan koefisien dari variabel keputusan dilakukan berdasarkan data biaya produksi dan harga jual.
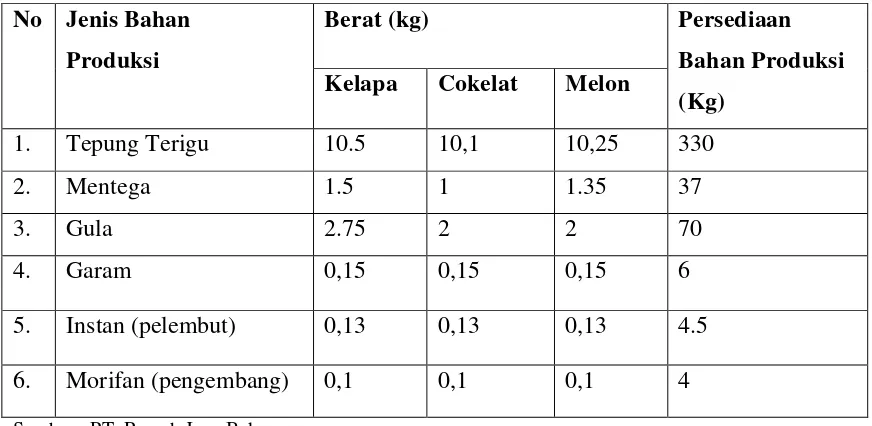
4.1.2 Perumusan Fungsi Kendala
Fungsi kendala terdiri dari batasan bahan baku dan biaya produksi. Kendala ini penting untuk memastikan bahwa model yang dibangun realistis dan dapat diterapkan dalam konteks produksi.
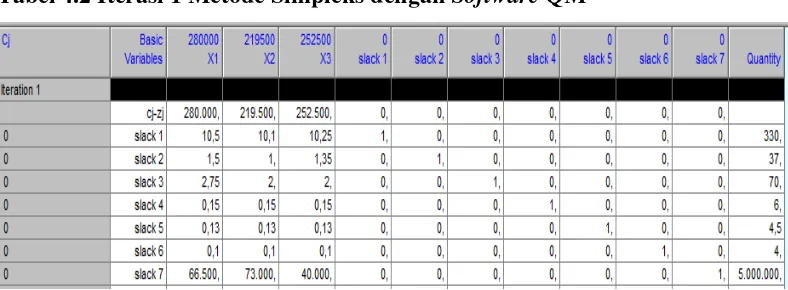
4.2 Pengolahan Data
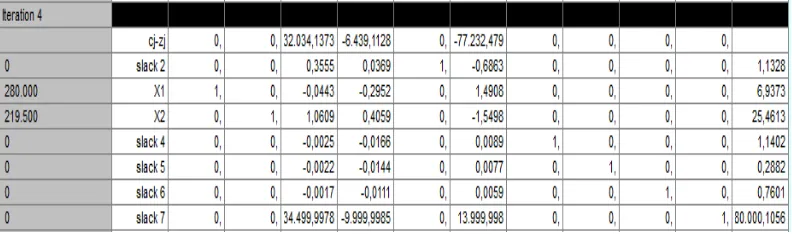
Data yang telah diformulasikan dalam model matematika kemudian diolah dengan menggunakan software QM. Hasil olahan data memberikan solusi optimal untuk jumlah produksi roti yang harus diproduksi.
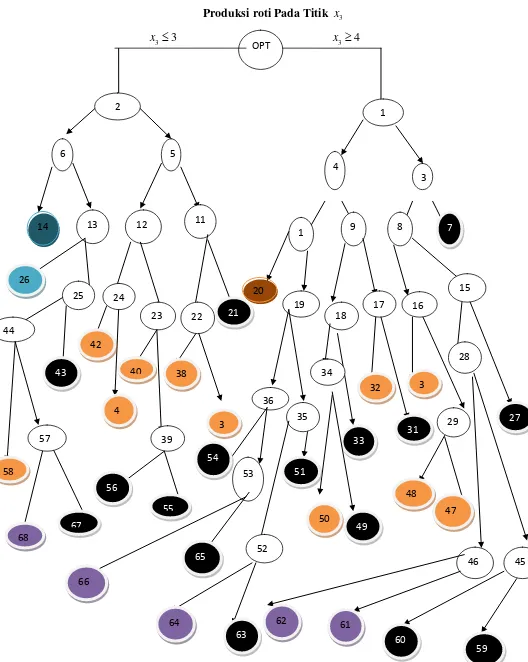
4.3 Analisis Metode Branch and Bound
Analisis dilakukan untuk mengevaluasi hasil yang diperoleh dari metode Branch and Bound. Proses ini melibatkan pencabangan untuk menemukan solusi integer yang optimal, serta perbandingan antara batas atas dan batas bawah.
V. Kesimpulan dan Saran
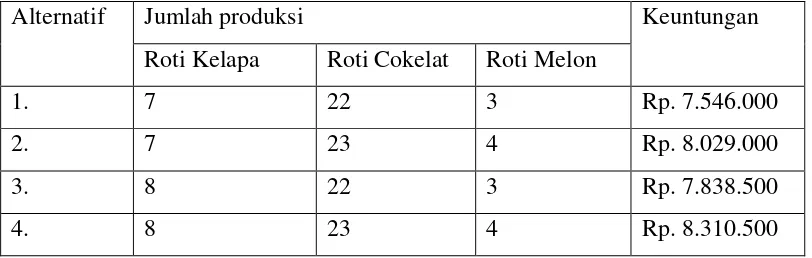
Kesimpulan dari penelitian ini menegaskan bahwa metode Branch and Bound efektif dalam mengoptimalkan jumlah produksi roti. Penelitian ini juga memberikan saran untuk implementasi lebih lanjut dari metode ini dalam konteks industri makanan.
5.1 Kesimpulan
Kesimpulan dari penelitian ini menunjukkan bahwa penerapan metode Branch and Bound dapat meningkatkan efisiensi dalam produksi roti di PT. Ramah Jaya Bakery, serta memberikan keuntungan yang lebih optimal.
5.2 Saran
Saran untuk perusahaan adalah untuk terus menerapkan metode ini dalam proses produksi dan mempertimbangkan variabel lain yang mungkin mempengaruhi hasil. Penelitian lebih lanjut juga disarankan untuk mengeksplorasi metode lain dalam optimasi produksi.