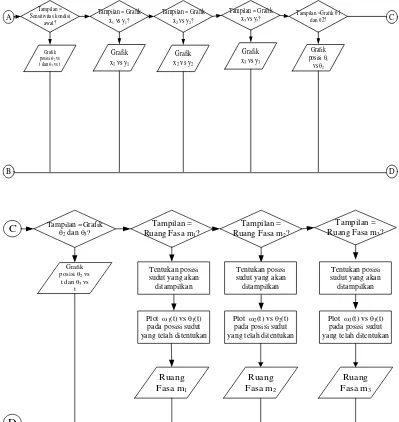
LAMPIRAN A : MENTERJEMAHKAN SETIAP LANGKAH DEMI LANGKAH KE BAHASA MATHEMATICA 9
Persaman gerak untuk θ1 adalah
+ + � + + � − � � + � −
� � + + � � � − � + � � � − � + + +
� � � = (2.19)
Diubah dalam program menjadi
g (m1+m2+m3) Sin[θ1[t]]+θ2’[t]^2 l2 (m2+m3) Sin[θ1[t] -θ2[t]]+θ3’[t]^2 l3 m3 Sin[θ1[t]-θ3[t]]+l1 m1 θ1’’[t]+(m2+m3)
sol=NDSolve[eqns, (θ1,θ2}, {t,0,p}, Maxsteps->Infinity, PrecisionGoal->4];pq=sol[[1,1,2,1,1,2]];
Posisi Persamaan pendulum :
pos2[t_]:={(l1 Sin[θ1[t]]+l2 Sin[θ2[t]]),(-l1 Cos[θ1[t]]-l2 Cos[θ2[t]])};
pos3[t_]:={(l1 Sin[θ1[t]]+l2 Sin[θ2[t]]+l3 Sin[θ3[t]]),(-l1 Cos[θ1[t]]-l2 Cos[θ2[t]]-l3 Cos[θ3[t]])};
Jejak persamaan Gerak Pendulum dalam simulasi:
path=ParametricPlot[Evaluate[pos3[t]/.sol[[1]],{t,p-Tombol Pemilihan Grafik hasil animasi Pendulum : Switch[plottype,
(*Tampilan plot simpangan x m1 dan m2 terhadap t*)
x1x2, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Green, Blue}, Axes->False,PlotLabel->Style{“x(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan y m1 dan m2 terhadap t*)
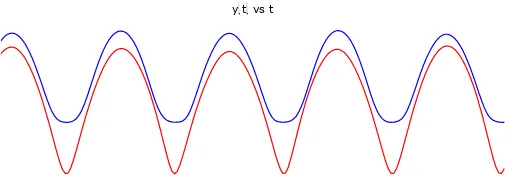
y1y2, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Green, Blue}, Axes->False,PlotLabel->Style{“x(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan x m2 dan m3 terhadap t*)
x2x3, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Blue, Red}, Axes->False,PlotLabel->Style{“x(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan y m2 dan m3 terhadap t*)
y2y3, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Blue, Red}, Axes->False,PlotLabel->Style{“x(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan θ m1 dan m2 terhadap t*)
->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan θ m2 dan m3 terhadap t*)
θ2θ3, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Blue, Red}, Axes->False,PlotLabel->Style{“θ(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan Plot x1 vs y1*)
x1y1, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion-
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[x,1],” vs “, Subscript[y,1]}],PlotRange->{{-3Pi/4,3Pi/4}, Automatic}, ImageSize->{420,150},PlotStyle->Darker[Green,.1],AspectRatio->32/100.],
(*Tampilan Plot x2 vs y2*)
x2y2, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion-
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[x,2],” vs “, Subscript[y,2]}],PlotRange ->{{-3Pi/2,3Pi/2}, Automatic}, ImageSize->{420,150},PlotStyle->Darker[Blue,.1],AspectRatio->32/100.],
(*Tampilan Plot x3 vs y3*)
x3y3, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion-
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[x,3],” vs “, Subscript[y,3]}],PlotRange ->{{-3Pi/2,3Pi/2}, Automatic}, ImageSize->{420,150},PlotStyle->Darker[Blue,.1],AspectRatio->32/100.],
(*Tampilan Plot θ1 vs θ2*)
θθ, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion -
->{{-Pi,Pi}, Automatic}, ImageSize->{420,150},ColorFunction->(Blend[{Blue, Green}, #1]&),AspectRatio->32/100.],
(*Tampilan Plot θ2 vs θ3*)
θϕ, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion -
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[θ,2],” vs “, Subscript[θ,3]}],PlotRange ->{{-Pi,Pi}, Automatic}, ImageSize->{420,150},ColorFunction->(Blend[{Red, Blue}, #1]&),AspectRatio->32/100.],
(*Tampilan plot ω1 vs θ1*)
θθPrime1, ParametricPlot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion ->ControlActive[3,4], Axes->False,PlotLabel->Row[{Subscript[OverDot[θ],1],” vs “,Subscript[θ,1]}],Plot Range->{{-Pi,Pi}, Automatic},ImageSize{420,150},AspectRatio->32/100., PlotStyle->Darker[Green,.2]],
(*Tampilan plot ω2 vs θ2*)
θθPrime2, ParametricPlot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion ->ControlActive[3,4], Axes->False,PlotLabel->Row[{Subscript[OverDot[θ],2],” vs “,Subscript[θ,2]}],PlotRange ->{{-Pi,Pi}, Automatic},ImageSize{420,150},AspectRatio->32/100., PlotStyle->Darker[Blue,.2]],
(*Tampilan plot ω3 vs θ3*)
θθPrime2, ParametricPlot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion ->ControlActive[3,4],
Style[“***********************************************”, Bold,16, Darker[Black, .1], “Label”],
Style[“PENDULUM NONLINIER”, Bold, 18, Darker[Black, .1], “Label”],
Style[“******************************************”, Bold, 12, Darker[Black, .1], “Label”],
Style[“ “, Bold, 12, Darker[Green,.8], “Label”],
Style[“Parameter Pendulum”,”Subsection”, Bold, 12,
Darker[Black,.1], “Label”],
Tampilan Parameter massa pendulum hijau, biru, merah, panjang pendulum hijau, biru, merah, gravitasi, sudut pendulum hijau, biru, merah, kecepatan sudut pendulum hijau, biru, merah, dan waktu (Berurutan):
{{m1, 1, “Green mass (m1)”},1,5,ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
{{m2,1,”Blue mass (m2)”},1,5, ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
{{m3,1,”Red mass (m3)”},1,5, ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
{{l1,1,”Green length (l1)”},1,5,ImageSize->Tiny,
ContinuousAction->False, Appearance->”Labeled”},
{{l2,1,”Blue length (l2)”},1,5, ImageSize->Tiny,
ContinuousAction->False, Appearance->”Labeled”},
{{l3,1,”Red length (l3)”},1,5, ImageSize->Tiny,
ContinuousAction->False, Appearance->”Labeled”},
{{g,1,”Gravity (g)”},1,9.8, ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
Delimiter,
Style[“Kondisi Awal”, “Subsection”, Bold, 12,
Darker[Black,.1],”Label”],
{{init1,Pi/2,”green angle(θ1)
“},-Pi/2, Pi/2, Appearance->”Labeled”, ImageSize->Tiny},
{{init2,0,”blue angle(θ2)
{{init3,0,”red angle(θ3) “},-Pi/2, Pi/2, Appearance->”Labeled”, ImageSize->Tiny},
{{initprime1,0,”green velocity(ω1)”},0,5,ImageSize
->Tiny,Appearance->”Labeled”},
{{initprime2,0,”blue velocity(ω2)”},0,
5,ImageSize->Tiny,Appearance->”Labeled”},
{{initprime3,0,”red velocity(ω3)”},0,5,ImageSize
->Tiny,Appearance->”Labeled”},
Delimiter,{{p, 12,”Waktu”},0.001,100,ImageSize ->Tiny,Appearance->”Labeled”},
Tombol Pemilihan Tampilan Grafik:
[{plottype, x1x2, “Grafik”}, {x1x2->”Simpangan x m1 dan m2”,y1y2->” Simpangan y m1 dan m2”, x2x3->” Simpangan x m2 dan m3”, y2y3->” Simpangan y m2 dan m3”,θ1θ2->”Sensitivitas Kondisi Awal θ1 dan θ2”, θ2θ3->”Sensitivitas Kondisi Awal θ2 dan θ3”,x1y1->”x1 vs. y1”, x2y2->”x2 vs. y2”, x3y3->”x3 vs. y3”,θθ->”θ1 vs. θ2”, θϕ->”θ2 vs. θ3”, θθprime1->” � vs θ1”, θθprime2->” � vs θ2”, θθprime3->” � vs θ3”} ”},ControlType->PopupMenu}
Tombol untuk menganimasikan pendulum terhadap waktu:
{{p,0.001,”Animasi”},0.001,100,1.0, ControlType->Trigger},
AutorunSequencing->All,TrackedSymbols:->Manipulate,Initialization:->Get[“Barcharts”],
LAMPIRAN B: LISTING PROGRAM SIMULASI GERAK TRIPLE PENDULUM NONLINIER
Berikut ini merupakan listing program untukanimasi dan visualisasi gerakan triple pendulum nonlinier
sol=NDSolve[eqns, (θ1,θ2}, {t,0,p}, Maxsteps->Infinity, PrecisionGoal->4];pq=sol[[1,1,2,1,1,2]];
pos1[t_]:={l1 Sin[θ1[t]],-l1 Cos[θ1[t]]};
pos2[t_]:={(l1 Sin[θ1[t]]+l2 Sin[θ2[t]]),(-l1 Cos[θ1[t]]-l2 Cos[θ2[t]])};
pos3[t_]:={(l1 Sin[θ1[t]]+l2 Sin[θ2[t]]+l3 Sin[θ3[t]]),(-l1 Cos[θ1[t]]-l2 Cos[θ2[t]]-l3 Cos[θ3[t]])};
path=ParametricPlot[Evaluate[pos3[t]/.sol[[1]],{t,p-
path1=ParametricPlot[Evaluate[pos2[t]/.sol[[1]],{t,p-p/5,p}, Sin[θ2[t]],y1y2,(-l1 Cos[θ1[t]]-l2 Cos[θ2[t]]),x2x3,(l1
Sin[θ1[t]+l2 Sin[θ2[t]]+l3 Sin[θ3[t]]),y2y3,(-l1 Cos[θ1[t]-l2 Cos[t]]-l3
Cos[t]]),x1y1,pos1[t][[2]],x2y2,pos2[t][[2]],pos3[t][[2]],θ1θ2, θ2[t],θ2θ3,θ3[t],θθ,θ2[t],θϕ,θ3[t],θθprime1,θ1’[t],θθprime2, θ2’[t],θθprime3,θ3’[t],_,1]/.sol[[1]];
Switch[plottype,
(*Tampilan plot simpangan x m1 dan m2 terhadap t*)
(*Tampilan plot simpangan y m1 dan m2 terhadap t*)
y1y2, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Green, Blue}, Axes->False,PlotLabel->Style{“x(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan x m2 dan m3 terhadap t*)
x2x3, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Blue, Red}, Axes->False,PlotLabel->Style{“x(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan y m2 dan m3 terhadap t*)
y2y3, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Blue, Red}, Axes->False,PlotLabel->Style{“x(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan θ m1 dan m2 terhadap t*)
θ1θ2, Plot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3, 4], PlotStyle->{Green, Blue}, Axes->False,PlotLabel->Style{“θ(t)vs t”, “Label”], PlotRange ->{{pq-25,pq}, Automatic}, ImageSize->{420, 150}, AspectRatio->32/100.],
(*Tampilan plot simpangan θ m2 dan m3 terhadap t*)
(*Tampilan Plot x1 vs y1*)
x1y1, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion-
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[x,1],” vs “, Subscript[y,1]}],PlotRange ->{{-3Pi/4,3Pi/4}, Automatic}, ImageSize->{420,150},PlotStyle->Darker[Green,.1],AspectRatio->32/100.],
(*Tampilan Plot x2 vs y2*)
x2y2, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion-
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[x,2],” vs “, Subscript[y,2]}],PlotRange ->{{-3Pi/2,3Pi/2}, Automatic}, ImageSize->{420,150},PlotStyle->Darker[Blue,.1],AspectRatio->32/100.],
(*Tampilan Plot x3 vs y3*)
x3y3, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion-
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[x,3],” vs “, Subscript[y,3]}],PlotRange ->{{-3Pi/2,3Pi/2}, Automatic}, ImageSize->{420,150},PlotStyle->Darker[Blue,.1],AspectRatio->32/100.],
(*Tampilan Plot θ1 vs θ2*)
θθ, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion -
>ControlActive[3,4],Axes->False,PlotLabel->Rown[{Subscript[θ,1],” vs “, Subscript[θ,2]}],PlotRange ->{{-Pi,Pi}, Automatic}, ImageSize->{420,150},ColorFunction->(Blend[{Blue, Green}, #1]&),AspectRatio->32/100.],
(*Tampilan Plot θ2 vs θ3*)
θϕ, ParametricPlot[{g1[t],g2[t]},{t,0,p},MaxRecursion -
(*Tampilan plot ω1 vs θ1*)
θθPrime1, ParametricPlot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion ->ControlActive[3,4], Axes->False,PlotLabel->Row[{Subscript[OverDot[θ],1],” vs “,Subscript[θ ,1]}],PlotRange->{{-Pi,Pi}, Automatic},ImageSize{420,150},AspectRatio->32/100., PlotStyle->Darker[Green,.2]],
(*Tampilan plot ω2 vs θ2*)
θθPrime2, ParametricPlot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3,4], Axes->False,PlotLabel->Row[{Subscript[OverDot[θ],2],” vs “,Subscript[θ,2]}],PlotRange ->{{-Pi,Pi}, Automatic},ImageSize{420,150},AspectRatio->32/100., PlotStyle->Darker[Blue,.2]],
(*Tampilan plot ω3 vs θ3*)
θθPrime2, ParametricPlot[{g1[t], g2[t]}, {t,0,p}, MaxRecursion->ControlActive[3,4],
Axes->False,PlotLabel-Style[“ANIMASI GERAK TRIPLE”, Bold, 18, Darker[Black,.1], “Label”],
Style[“***********************************************”, Bold,16, Darker[Black, .1], “Label”],
Style[“PENDULUM NONLINIER”, Bold, 18, Darker[Black, .1], “Label”],
Style[“******************************************”, Bold, 12, Darker[Black, .1], “Label”],
Style[“ “, Bold, 12, Darker[Green,.8], “Label”],
Style[“Parameter Pendulum”,”Subsection”, Bold, 12,
{{m1, 1, “Green mass (m1)”},1,5,ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
{{m2,1,”Blue mass (m2)”},1,5, ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
{{m3,1,”Red mass (m3)”},1,5, ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
{{l1,1,”Green length (l1)”},1,5,ImageSize->Tiny,
ContinuousAction->False, Appearance->”Labeled”},
{{l2,1,”Blue length (l2)”},1,5, ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
{{l3,1,”Red length (l3)”},1,5, ImageSize->Tiny,
ContinuousAction->False, Appearance->”Labeled”},
{{g,1,”Gravity (g)”},1,9.8, ImageSize->Tiny, ContinuousAction->False, Appearance->”Labeled”},
Delimiter,
Style[“Kondisi Awal”, “Subsection”, Bold, 12,
Darker[Black,.1],”Label”],
{{init1,Pi/2,”green angle(θ1)
“},-Pi/2, Pi/2, Appearance->”Labeled”, ImageSize->Tiny},
{{init2,0,”blue angle(θ2)
“},-Pi/2, Pi/2, Appearance->”Labeled”, ImageSize->Tiny},
{{init3,0,”red angle(θ3)
“},-Pi/2, Pi/2, Appearance->”Labeled”, ImageSize->Tiny},
-m3”, y2y3->” Simpangan y m2 dan m3”,θ1θ2->”Sensitivitas Kondisi Awal θ1 dan θ2”, θ2θ3->”Sensitivitas Kondisi Awal θ2 dan θ3”,x1y1->”x1 vs. y1”, x2y2->”x2 vs. y2”, x3y3->”x3 vs. y3”,θθ->”θ1 vs. θ2”, θϕ->”θ2 vs. θ3”, θθprime1->” � vs θ1”, θθprime2->” � vs θ2”, θθprime3->” � vs θ3”},
ControlType->PopupMenu},{{p,0.001,”Animasi”},0.001,100,1.0, ControlType->Trigger}, AutorunSequencing->All,TrackedSymbols:->Manipulate,Initialization:->Get[“Barcharts”],
LAMPIRAN C: PENJABARAN PERSAMAAN GERAK SISTEM TRIPLE PENDULUM NONLINIER
Koordinat – koordinat posisi tiap pendulum :
x1 = l1 + l2 + l3– l1cos θ1 (2.2) Kemudian, setiap koordinat diatas akan diturunkan terhadap waktu untuk memperoleh kecepatan. Hasil dari turunan menghasilkan
= − � sin � trigonometri untuk selisih dua sudut diperoleh energi kinetik :
T = x + y + x + y + x + y
cos (α –β) = cosα cosβ + sinα sinβ
T = � + [� + � + � � cos � − � ] +
[� + � + � + � � cos � − � + � � cos � − � + � � cos � − � ] (2.16)
Energi potensial diperoleh dengan mensubsitusikan persamaan 2.2, 2.4, 2.6 ke persamaan 2.9 :
V = m1gx1 + m2gx2 + m3gx3
Sehingga Fungsi Lagrangian Triple Pendulum Nonlinier:
Persamaan diatas adalah Fungsi Lagrangian dari triple pendulum, persamaan diatas akan diselesaikan dengan persamaan Lagrange agar diperoleh posisi masing-masing pendulum. Persamaan gerak untuk pendulum pertama:
� + � + � + � � − �
Untuk lebih sederhananya maka persamaan diatas dibagi l1 diperoleh hasil:
+ + � + + � − � � + � − � � +
+ � � � − � + � � � − � + + + � � � =
(2.19)
Persamaan gerak untuk pendulum kedua:
Untuk lebih sederhananya maka persamaan diatas dibagi l2 diperoleh hasil:
+ � − � � + + � + � − � � −
+ � � � − � + � � � − � + + � � � =
(2.20)
Persamaan gerak untuk pendulum ketiga:
��
�� = � � sin � − � + � � sin � − � − � sin �
��
�� = � + � � − � + � � − �
��
�� = � + � � − � − � (� − � ) � � − �
+ � � − � − � (� − � )sin � − �
Kemudian dengan persamaan Lagrange,
��
�� =
�� ��
� + � � − � − � (� − � ) � � − �
+ � � − � − � (� − � ) sin � − �
= � � sin � − � + � � sin � − � − � sin �
Untuk lebih sederhananya maka persamaan diatas dibagi l3 diperoleh hasil:
� − � � + � − � � + � − � � � −
LAMPIRAN D: GRAFIK RUANG FASA UNTUK PERBANDINGAN SISTEM DENGAN VARIASI NILAI BEBERAPA PARAMETER
Grafik diagram fasa untuk Tabel 4.1 (Hasil pengujian keadaan sistem untuk variasi sudut simpangan awal, m1 = m2 = m3 = 1 dan l1 = l2 = l3 = 1)
Gambar C.1, Ruang fasa dengan θ1 = 1.15-1.57, θ2 = 1.31, dan θ3 = 1.17
Gambar C.2, Ruang fasa dengan θ1 = 0.85-1.14, θ2 = 1.31, dan θ3 = 1.17
Gambar C.3, Ruang fasa dengan θ1 = 0-0.85, θ2 = 1.31, dan θ3 = 1.17
Gambar C.4, Ruang fasa dengan θ1 = 1.0-1.14, θ2 = 1.2, dan θ3 = 1.65
1vs. 1
1vs. 1
1vs. 1
Gambar C.5, Ruang fasa dengan θ1 = 0.9-0.99, θ2 = 1.2, dan θ3 = 1.65
Gambar C.6, Ruang fasa dengan θ1 = 0-0.89, θ2 = 1.2, dan θ3 = 1.65
Gambar C.7, Ruang fasa dengan θ1 = 0-0.89, θ2 = 1.05, dan θ3 = 1.05
Gambar C.8, Ruang fasa dengan θ1 = 0.7-0.79, θ2 = 1.05, dan θ3 = 1.05
1vs. 1
1vs. 1
1vs. 1
Gambar C.9, Ruang fasa dengan θ1 = 0-0.69, θ2 = 1.05, dan θ3 = 1.05
Gambar C.10, Ruang fasa dengan θ1 = 0.62-0.69, θ2 = 0.86, dan θ3 = 0.95
Gambar C.11, Ruang fasa dengan θ1 = 0.5-0.61, θ2 = 0.86, dan θ3 = 0.95
Gambar C.12, Ruang fasa dengan θ1 = 0-0.49, θ2 = 0.86, dan θ3 = 0.95
1vs. 1
1vs. 1
1vs. 1
Gambar C.13, Ruang fasa dengan θ1 = 0.4-0.49, θ2 = 0.48, dan θ3 = 0.7
Gambar C.14, Ruang fasa dengan θ1 = 0.28-0.39, θ2 = 0.48, dan θ3 = 0.7
Gambar C.15, Ruang fasa dengan θ1 = 0-0.27, θ2 = 0.48, dan θ3 = 0.7
Grafik diagram fasa untuk Tabel 4.2 (Hasil pengujian keadaan sistem untuk variasi panjang tali pendulum1, m1 = m2 = m3 = 1, l2 = l3 = 1, dan θ1 = Pi/2)
Gambar C.16, Ruang fasa dengan l1 = 1-1.5, θ2 = 1.31, dan θ3 = 1.17
1vs. 1
1vs. 1
1vs. 1
Gambar C.17, Ruang fasa dengan l1 = 1.6-1.9, θ2 = 1.31, dan θ3 = 1.17
Gambar C.18, Ruang fasa dengan l1 = 2-5, θ2 = 1.31, dan θ3 = 1.17
Gambar C.19, Ruang fasa dengan l1 = 2-2.2, θ2 = 1.15, dan θ3 = 1
Gambar C.20, Ruang fasa dengan l1 = 2.3-2.4, θ2 = 1.15, dan θ3 = 1
Gambar C.21, Ruang fasa dengan l1 = 2.5-5, θ2 = 1.15, dan θ3 = 1
1vs. 1
1vs. 1
1vs. 1
1vs. 1
Gambar C.22, Ruang fasa dengan l1 = 2.5-3, θ2 = 0.98, dan θ3 = 0.98
Gambar C.23, Ruang fasa dengan l1 = 3.1-5, θ2 = 0.98, dan θ3 = 0.98
Grafik diagram fasa untuk Tabel 4.3 (Hasil pengujian keadaan sistem untuk variasi panjang tali pendulum2, m1 = m2 = m3 =1, l1 = l3 = 1, dan θ1 = Pi/2)
Gambar C.24, Ruang fasa dengan l2 = 2, θ2 = 0-1.57, dan θ3 = 0-1.57
Grafik diagram fasa untuk Tabel 4.4 (Hasil pengujian keadaan sistem untuk variasi panjang tali pendulum3, m1 = m2 = m3 =1, l1 = l2 = 1, dan θ1 = Pi/2)
Gambar C.25, Ruang fasa dengan l3 = 1.1-1.2, θ2 = 1.31, dan θ3 = 1.17 1vs. 1
1vs. 1
Gambar C.26, Ruang fasa dengan l3 = 1.3-5, θ2 = 1.31, dan θ3 = 1.17
Gambar C.27, Ruang fasa dengan l3 = 1.3-1.6, θ2 = 1.35, dan θ3 = 1.4
Gambar C.28, Ruang fasa dengan l3 = 1.7-2, θ2 = 1.35, dan θ3 = 1.4
Gambar C.29, Ruang fasa dengan l3 = 2.1-5, θ2 = 1.35, dan θ3 = 1.4
Gambar C.30, Ruang fasa dengan l3 = 2.1-2.8, θ2 = 1.15, dan θ3 = 1.57 3vs. 3
3vs. 3
3vs. 3
3vs. 3
Gambar C.31, Ruang fasa dengan l3 = 2.9-3.2, θ2 = 1.15, dan θ3 = 1.57
Gambar C.32, Ruang fasa dengan l3 = 3.3-5, θ2 = 1.15, dan θ3 = 1.57
Gambar C.33, Ruang fasa dengan l3 = 3.3-4, θ2 = 0.78, dan θ3 = 1.57
Gambar C.34, Ruang fasa dengan l3 = 4.1-4.4, θ2 = 0.78, dan θ3 = 1.57
Gambar C.35, Ruang fasa dengan l3 = 4.5-5, θ2 = 0.78, dan θ3 = 1.57
3vs. 3
3vs. 3
3vs. 3
3vs. 3
Grafik diagram fasa untuk Tabel 4.5 (Hasil pengujian keadaan sistem untuk variasi massa pendulum1, m2 = m3 = 1, l1 = l2 = l3 = 1, dan θ1 = Pi/2)
Gambar C.36, Ruang fasa dengan, m1 = 1-1.1, θ2 = 1.31, dan θ3 = 1.17
Gambar C.37, Ruang fasa dengan, m1 = 1.2-1.9, θ2 = 1.31, dan θ3 = 1.17
Gambar C.38, Ruang fasa dengan, m1 = 2-5, θ2 = 1.31, dan θ3 = 1.17
Gambar C.39, Ruang fasa dengan, m1 = 2-2.2, θ2 = 1.44, dan θ3 = 1.57
Gambar C.40, Ruang fasa dengan, m1 = 2.3-5, θ2 = 1.44, dan θ3 = 1.57
1vs. 1
1vs. 1
1vs. 1
1vs. 1
Grafik diagram fasa untuk Tabel 4.6 (Hasil pengujian keadaan sistem untuk variasi massa pendulum2, m1 = m3 = 1, l1 = l2 = l3 = 1, dan θ1 = Pi/2)
Gambar C.41, Ruang fasa dengan, m2 = 1-2, θ2 = 1.31, dan θ3 = 1.17
Gambar C.42, Ruang fasa dengan, m2 = 2.1-2.4, θ2 = 1.31, dan θ3 = 1.17
Gambar C.43, Ruang fasa dengan, m2 = 2.5-5, θ2 = 1.31, dan θ3 = 1.17
Gambar C.44, Ruang fasa dengan, m2 = 3, θ2 = 1.17, dan θ3 = 1
Gambar C.45, Ruang fasa dengan, m2 = 3.1-5, θ2 = 1.17, dan θ3 = 1
2vs. 2
2vs. 2
2vs. 2
2vs. 2
Grafik diagram fasa untuk Tabel 4.7 (Hasil pengujian keadaan sistem untuk variasi massa pendulum3, m1 = m2 = 1, l1 = l2 = l3 = 1, dan θ1 = Pi/2)
Gambar C.46, Ruang fasa dengan, m3 = 1-1.2, θ2 = 1.31, dan θ3 = 1.17
Gambar C.47, Ruang fasa dengan, m3 = 1.3, θ2 = 1.31, dan θ3 = 1.17
Gambar C.48, Ruang fasa dengan, m3 = 1.4-5, θ2 = 1.31, dan θ3 = 1.17
Gambar C.49, Ruang fasa dengan, m3 = 2, θ2 = 0.9, dan θ3 = 0.9
Gambar C.50, Ruang fasa dengan, m3 = 2.1-2.2, θ2 = 0.9, dan θ3 = 0.9
3vs. 3
3vs. 3
3vs. 3
3vs. 3
Gambar C.51, Ruang fasa dengan, m3 = 2.3-5, θ2 = 0.9, dan θ3 = 0.9
Gambar C.52, Ruang fasa dengan, m3 = 2.3-2.5, θ2 = 0.78, dan θ3 = 0.69
Gambar C.53, Ruang fasa dengan, m3 = 2.6-5, θ2 = 0.78, dan θ3 = 0.69
Grafik diagram fasa untuk Tabel 4.8 (Hasil pengujian sistem untuk massa dan tali yang sama)
Gambar C.54, Ruang fasa dengan m1 = m2 = m3 = 2, l1 = l2 = l3 = 1, θ1 = 1.15-1.57, θ2 = 1.31, dan θ3 = 1.17
Gambar C.55, Ruang fasa dengan m1 = m2 = m3 = 3, l1 = l2 = l3 = 1, θ1 = 1.15-1.57, θ2 = 1.31, dan θ3 = 1.17
3vs. 3
3vs. 3
3vs. 3
1vs. 1
Gambar C.56, Ruang fasa dengan m1 = m2 = m3 = 1, l1 = l2 = l3 = 2, θ1 = 1.15-1.57, θ2 = 1.31, dan θ3 = 1.17
Gambar C.57, Ruang fasa dengan m1 = m2 = m3 = 1, l1 = l2 = l3 = 3, θ1 = 1.15-1.57, θ2 = 1.31, dan θ3 = 1.17
Gambar C.58, Ruang fasa dengan m1 = m2 = m3 = l1 = l2 = l3 = 2, θ1 = 1.15-1.57, θ2 = 1.31, dan θ3 = 1.17
1vs. 1
1vs. 1
50
DAFTAR PUSTAKA
Baker, G.L. and Gollub,J.P. 1996. Chaotic Dynamics: An Introduction. 2nd Edition. New York: Cambridge Unversity Press.
Deserio, Robert. 2004. Chaotic Pendulum: The Complete Attractor. Florida: University of Florida.
Kusmarni, Yani. 2008. Teori Chaos Sebuah Keteraturan Dalam Keacakan. Bandung: Universitas Pendidikan Indonesia.
McCrummen, John. 2015. The Double Pendulum Differential Equations. Flathead Valley: Community College.
Panggabean, Eva Suraya. 2011. Analisis dan Visualisasi Gerak Pendulum Ganda Nonlinier. Medan: Universitas Sumatera Utara.
Rahayu, Siti Utari. 2010. Analisis Kualitatif Gejala Chaos Pada Gerak Pendulum Sederhana Nonlinier Teredam dan Terkendali. Medan: Universitas
Sumatera Utara.
Sahid, 2003. Teori Keos (Chaos Theory) : Dapatkah Gejala Dinamika Alam dan Sosial Diprediksi dalam Jangka Panjang?. Yogyakarta: Universitas
Negeri Yogyakarta.
Setiawan, Sandi. 1991. Chaos Gelora Sains Baru. Yogyakarta: Andi. Situngkir, H., Surya, Y. 24 Juli 2010. Teori Chaos dan Bank Century.
http://www.yohanessurya.com/chaosekonom.htm
Spigel, Murray. 1967. Schaums’s Outlines Series: Theory and Problems of Theoretical Mechanics. Toronto: Mc-Graw Hill Book Company.
Stroup, Adrianne. 2004. The Dynamics of Pendula: An Introduction to Hamiltonian System and Chaos. California: California Institute of
Technology
Raharjo, Agus. 2007. Fenomena Chaos dalam Kehidupan Hukum Indonesia. Jakarta: Universitas Indonesia.
Tel, H. and Gruiz M. 2006. Chaotic Dynamics An Introduction based on Classical Mechanics. 1st Edition. New York: Cambridge University Press.
51
Tipler, A.P. 1998. Fisika untuk Sains dan Teknik. Edisi Ketiga, Jilid 1. Jakarta: Erlangga.
17
BAB 3
ANALISIS MASALAH DAN PERANCANGAN PROGRAM
3.1 Analisis Masalah
3.1.1 Persamaan Gerak Triple Pendulum Nonlinier
Persamaan gerak triple pendulum nonlinier adalah persamaan 2.19, 2.20, dan 2.21 pada subbab 2.4. Berdasarkan ketiga persamaan maka dapat dikatakan bahwa sistem triple pendulum memiliki tiga variabel, maka lintasannya terletak pada ruang fasa 3 dimensi, ruang minimum terbentuknya gejala chaos.
Agar sistem dapat menampilkan gejala chaos dengan jelas, maka ditentukan dalam keadaan tanpa dimensi (Dimensionless) yaitu m = l = g = 1 (Baker et al, 1996), berdasarkan hal ini, maka ditetapkan m1 = m2 = m3 = l1 = l2 = l3 = g = 1, yang merupakan bentuk penyederhanaan yang sering digunakan dalam
simulasi.
Nilai kecepatan awal pendulum, ω1, ω2, dan ω3 pada program dapat divariasikan, tetapi dalam menganalisis gejala chaos nilai ω1, ω2, dan ω3 yang dipakai adalah pada ω1= ω2 = ω3 = 0 rad/s, hal ini dimaksudkan agar pendulum tidak berputar sehingga keadaan chaos dapat dianalisis dengan jelas. Sedangkan nilai θ pada program terdiri dari tiga, yaitu θ1, θ2, dan θ3. Hal ini dimaksudkan untuk menguji sesitivitas kondisi awal dari setiap gejala dari periodik hingga chaos jik kondisi awal ketiga pendulum diubah sedikit (Pi/12 rad). Adapun nilai dipakai sebenarnya adalah pada θ0 = Pi/2 rad, hal ini juga dimaksudkan agar diperoleh keadaan dimensionless.
18
Namun, sebagai perbandingan akan diteliti pula keadaan-keadaan sistem selain pengujian secara dimensionless. Pengujian akan dilakukan dengan beberapa variabel parameter yang nilainya dapat divariasikan, yaitu m1,m2,m3, l1,l2,l3, dan θ1(simpangan awal) untuk mengetahui keterkaitan hubungan varibel tersebut dengan keadaan periodik atau chaos. Dalam hal ini, suatu ruang parameter tiga dimensi yang setiap titiknya mewakili ketiga parameter tersebut dapat ditentukan. Penyelidikan yang akan dilakukan untuk mengamati pengaruh variasi:
1. θ1 sedangkan l1, m1, l2, m2, l3, dan m3 dianggap konstan. mempertahankan keperiodikan. Demikian metode tersebut dilakukan karena penyelidikan menyeluruh terhadap perilaku sistem sebagai fungsi ketiga variabel parameter tersebut tidak dapat dilakukan (Baker et al, 1996).
3.1.2 Penentuan Ruang Fasa
Seperti yang telah dijelaskan pada subbab 2.1.1.1 bahwa ruang fasa memiliki koordinat-koordinat yang mewakili variabel-variabel yang diperlukan untuk menentukan keadaan sistem pada saat tersebut. Dalam penelitian ini variabel-variabel yang digunakan sebagai analisis terhadap ruang fasa adalah kecepatan sudut, ω(t), dan posisi sudut, θ(t), dan ruang fasanya berbentuk bidang.
19
Pada ruang fasa yang telah dijelaskan di atas, koordinat ω(t), dan θ(t) ditentukan pada t = 1, 2, 3 dan seterusnya, hingga tmax yakni t = 100. Hal ini agar dapat memperlihatkan karakteristik sistem dinamis dengan baik, maka jejak lintasan yang muncul harus ditampilkan dengan jelas. Jika lintasan pada ruang fasa ini berulang, maka dapat dikatakan bahwa sistem tersebut periodik, sedangkan jika lintasannya tidak tepat berulang maka sistem tersebut dapat dikatakan tidak periodik.
3.2 Perancangan Program
Simulasi gerak triple pendulum nonlinier ini dirancang dengan menggunakan seperangkat laptop yang menggunakan prosesor AMD E-300 APU with Radeon(tm) HD Graphics 1.30 Ghz dengan menggunakan software Wolfram
Mathematica versi 9.
Adapun proses perancangan program penelitian ini dirancang melalui tahapan-tahapan sebagai berikut:
a. Perancangan diagram alir (flowchart) dan algoritma simulasi penyelesaian persamaan gerak triple pendulum nonlinier dengan metode Euler-Lagrange
b. Pembuatan program lengkap berdasarkan rancangan diagram alir dan algoritma dengan menggunakan bahasa pemrograman Mathematica versi 9.
3.2.1 Perancangan Diagram Alir (Flowchart)
21
Gambar 3.1 Diagram alir simulasi dan animasi persamaan gerak triple pendulum nonlinier dengan metode Euler-Lagrange
Keterangan Gambar: a. Input Data.
22
rentang waktu, t, dan syarat awal persamaan gerak pendulum, θ (θ1, θ2 dan θ3) dan ω (ω1, ω2, dan ω3).
Dalam program ini, rentang nilai massa, panjang, dan kecepatan sudut masing-masing pendulum dibatasi dari 0 sampai 5. Untuk gravitasi, rentang nilai yang dibatasi antara 1 sampai 9,8, sedangkan untuk rentang sudut masing-masing pendulum dibatasi dari 0 sampai π/2.
b. Menyelesaikan Persamaan Gerak Triple Pendulum
Persamaan gerak triple pendulum diselesaikan dengan menggunakan operasi numerik dengan fungsi NDSolve yang terdapat pada pemrograman pada Mathematica.
c. Penentuan Komponen Tangensial dan Radial Pendulum
Komponen tangensial dari pendulum yaitu, sin θ dan komponen radial pendulum, yaitu cos θ berdasarkan hasil penyelesaian persamaan gerak pendulum.
d. Menampilkan Hasil Visualisasi dari Triple Pendulum
Hasil visualisasi diperoleh dari fungsi Graphics yang terdapat pada bahasa pemrograman Mathematica versi 9 berdasarkan komponen tangensial dan radial pada point c. Untuk pendulum1 warna pendulum adalah hijau, untuk pendulum2 warna pendulum adalah biru, dan untuk pendulum3 warna pendulum adalah merah.
e. Membaca pemilihan tampilan
Program membaca pemilihan tampilan yang dipiliah oleh pengguna, jika tampilan yang diinginkan adalah ”Simpangan x m1 dan m2” atau
”Simpangan x m2 dan m3”, maka plot yang ditampilkan adalah x(t) vs t. Jika
tampilan yang diinginkan adalah ”Simpangan y m1 dan m2” atau
”Simpangan y m2 dan m3” maka plot yang ditampilkan adalah plot y(t) vs t.
Jika tampilan yang diinginkan ”Sensitivitas kondisi awal θ1 dan θ2” atau
23 ditampilkan adalah θ2 vs θ3. Jika tampilan yang diinginkan adalah ”ruang fasa
m1” maka plot yang dihasilkan adalah pada rentang-rentang –π sampai +π,
dan memplot titik lintasan ω1(t), dan θ1(t) pada t = 0,1,2,3 dan seterusnya, hingga tmax. Jika tampilan yang diinginkan adalah ”ruang fasa m2” maka plot yang dihasilkan adalah pada rentang-rentang –π sampai +π, dan memplot titik lintasan ω2(t), dan θ2(t) pada t = 0,1,2,3 dan seterusnya, hingga tmax. Dan jika tampilan yang diinginkan adalah ”ruang fasa m3” maka plot yang dihasilkan adalah pada rentang-rentang –π sampai +π, dan memplot titik lintasan ω3(t), dan θ3(t) pada t = 0,1,2,3 dan seterusnya, hingga tmax.
f. Menganimasikan Visualisasi Triple Pendulum
Hasil visualisasi dianimasikan sesuai dengan penyelesaian persamaan gerak triple pendulum nonlinier dengan menggunakan fungsi Trigger pada bahasa
pemrograman Mathematica 9. Jika terdapat perbedaan pada keadaan pendulum, maka pendulum hijau, pendulum biru, dan pendulum merah akan memiliki gerak yang berbeda.
3.2.2 Algoritma Program Bantu
Adapun algoritma program bantu yang digunakan dalam penyelesaian persamaan gerak pendulum adalah sebagai berikut:
INPUT
a. m1, m2 dan m3 = Massa masing-masing pendulum 1, pendulum 2, dan pendulum 3.
24 f. p = Waktu maksimum terjadinya osilasi pendulum
PROSES
a. Membaca data masukkan berupa, percepatan gravitasi bumi, panjang tali masing-masing pendulum, massa masing-masing pendulum, waktu maksimum, dan syarat awal persamaan gerak pendulum, θ1, θ2, θ3, ω1, ω2, dan ω3.
b. Menyelesaikan persamaan gerak triple pendulum nonlinier dengan fungsi NDSolve.
c. Menentukan komponen tangensial dan radial dari pendulum.
d. Memvisualisasikan triple pendulum dengan fungsi Graphics berdasarkan komponen tangensial dan radial.
e. Menentukan potongan lintasan pada rentang –π sampai +π sebagai ruang fasa.
f. Menentukan titik-titik lintasan pada setiap lintasan grafik yang diinginkan. g. Menganimasikan visualisasi triple pendulum dengan fungsi Trigger.
OUTPUT
a. Hasil ditampilkan dengan menekan tombol Shift + Enter. b. Menampilkan hasil visualisasi triple pendulum
c. Menganimasikan visualisasi triple pendulum ganda dengan menekan
tombol ”animasi” pada setiap setiap hasil eksekusi
d. Hasil grafik-grafik yang ditampilkan setelah animasi:
25
3. Memplot hasil penyelesaian yaitu plot θ(t) vs t, (sensitivitas kondisi awal).
26
BAB 4
HASIL DAN PEMBAHASAN
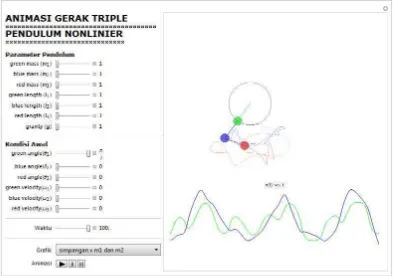
Hasil eksekusi simulasi pada Lampiran adalah berupa grafik-grafik keluaran dari penyelesaian persamaan gerak triple pendulum nonlinier yang terintegrasi pada suatu tampilan GUI seperti yang ditunjukkan pada gambar 4.1. Tampilan grafik pada hasil eksekusi program tersebut dapat diganti dengan mengubah menu
”Tampilan” yang berbentuk Pop Up Menu. Grafik-grafik keluaran tersebut
meliputi Grafik Simpangan x (plot x(t) vs t), grafik simpangan y (plot y(t) vs t), grafik x1 vs y1 (plot x1 vs y1), grafik sensitivitas terhadap kondisi awal(plot θ(t) vs t), grafik x2 vs y2 (plot x2 vs y2), grafik x3 vs y3 (plot x3 vs y3), grafik θ1 vs θ2 (plot
θ1 vs θ2), grafik θ2 vs θ3 (plot θ2 vs θ3), ruang fasa m1 (plot ω1 vs θ1), ruang fasa
m1 (plot ω2 vs θ2), dan ruang fasa m1 (plot ω3 vs θ3). Grafik keluaran ini digunakan untuk menganalisis perilaku sistem triple pendulum nonlinier, yaitu periodik, kuasiperiodik, atau chaos. Analisis tersebut diperkuat oleh perbandingan plot posisi terhadap sudut vs waktu yang menunjukkan sensitivitas sistem terhadap kondisi awal dan menujukkan karakteristik chaos deterministik dalam sistem, yaitu perubahan yang kecil pada kondisi awal dapat menyebabkan perubahan besar dan tak terprediksi untuk sistem chaos.
Pada gambar 4.1 dapat dilihat bahwa nilai-nilai dari m1, m2, m3, l1, l2, l3, θ1, θ2, θ3, ω1, ω2, ω3, dan t dapat divariasikan, tetapi dalam analisis gejala chaos nilai yang dipakai pada subbab 4.1, 4.2, dan 4.3 adalah, m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1 = ω2 = ω3 = 0, dan θ1 = Pi/2, dengan memvariasikan nilai θ2 dan θ3. Kemudian, untuk melihat karakteristik sensitivitas terhadap kondisi awal, nilai θ1 dapat diubah sedikit sebesar Pi/12 rad.
Sedangkan hasil ekesekusi program animasi gerak triple pendulum nonlinier yang ditunjukkan pada gambar 4.1. Hasil eksekusi berupa visualisasi triple pendulum. Animasi Triple pendulum dapat dianimasikan dengan
27
Gambar 4.1 Hasil eksekusi program ”Animasi & Visualisasi Gerak Triple Pendulum Nonlinier” pada lampiran
4.1 Keadaan Periodik
Keadaan Periodik dari triple pendulum nonlinier dengan m1 = m2 = m3 =1, l1 = l2 = l3 = 1, g = 1, ω1 = ω2 = ω3 = 0, θ1 = Pi/2, tercapai pada nilai θ2 = 5Pi/12
dan nilai θ3 = 3Pi/8. Hal ini dianalisis dari grafik-grafik keluaran yang ditunjukkan
pada gambar 4.2 hingga gambar 4.17.
Gambar 4.2 Ruang fasa pada m1 dengan m1 = m2 = m3 = 1, l1 = l2 = l3 =1, g =
28
Gambar 4.3 Ruang fasa pada m2 dengan m1 = m2 = m3 = 1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8.
Gambar 4.4 Ruang fasa pada m3 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8.
Pada gambar 4.2, 4.3 dan 4.4 menunjukkan keadaan triple pendulum (ditentukan oleh koordinat posisi–kecepatan sudut) yang bergerak sepanjang suatu lintasan pada bidang fasa sementara pendulum berayun. Karena adanya penurunan energi akibat pengaruh redaman dari masing-masing pendulum yang saling mempengaruhi sehingga lintasan pada keadaan transien terpilin ke pusat bidang. Selanjutnya efek redaman diantisipasi oleh energi yang diserap oleh pengaruh redaman sehingga keadaan menjadi tunak dengan bentuk lintasan tertutup. Lintasan tertutup ini menandakan bahwa pendulum bersifat periodik, dengan keadaan akhirnya datang dengan keadaan awalnya.
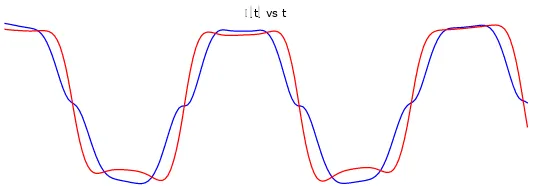
Gambar 4.5 Grafik Sensitivitas kondisi awal θ(t) vs t denganm1 = m2 = m3
=1, l1 = l2 = l3 = 1, g = 1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 =
3Pi/8. 2vs. 2
3vs. 3
29
Gambar 4.6 Grafik Sensitivitas kondisi awal θ1(t) vs t dengan m1 = m2 = m3
=1, l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = 5Pi/12, θ2 = 5Pi/12, dan θ3 =
3Pi/8.
Gambar 4.7 Grafik Sensitivitas kondisi awal θ(t) vs t denganm1 = m2 = m3
=1, l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8.
Gambar 4.8 Grafik Sensitivitas kondisi awal θ(t) vs t denganm1 = m2 = m3
=1, l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = 5Pi/2, θ2 = 5Pi/12, dan θ3 =
3Pi/8.
Pada gambar 4.5 dan 4.7 menunjukkan perilaku simpangan θ setiap saat
(t). Dalam keadaan ini terdapat dua daerah osilasi yakni osilasi yang terjadi pada pendulum1 dan pendulum2 beserta pendulum2 dan pendulum3. Jika keadaan ini
diubah sedikit yaitu θ1 menjadi 5Pi/12, maka perbandingan plot posisi sudut vs
waktu yang ditunjukkan pada gambar 4.6 dan 4.8 menunjukkan grafik yang t vs t
t vs t
30
tampak bahwa kedua posisi sudut berjalan selaras, berarti sistem ini tidak sensitif terhadap kondisi awal karena sifatnya yang periodik.
Berikut juga ditampilkan beberapa tampilan simpangan pada keadaan periodik ini, yang dapat dilihat pada gambar 4.9, 4.10, 4.11, 4.12, 4.13, 4.14, 4.15, 4.16, 4.17.
Gambar 4.9 Grafik x(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8 (Pendulum1 dan
pendulum2)
Gambar 4.10 Grafik x(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8 (Pendulum2 &
pendulum3)
Gambar 4.11 Grafik y(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8 (Pendulum1 &
pendulum2)
x t vs t
x t vs t
31
Gambar 4.12 Grafik y(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8 (Pendulum2 &
pendulum3)
Gambar 4.13 Grafik x1 vs y1 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8
Gambar 4.14 Grafik x2 vs y2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8
Gambar 4.15 Grafik x3 vs y3 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8
y t vs t
x1vs.y1
x2vs.y2
32
Gambar 4.16 Grafik θ1 vs θ2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8
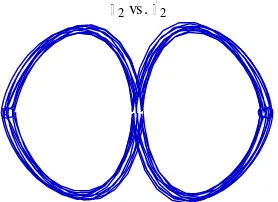
Gambar 4.17 Grafik θ2 vs θ3 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/8
4.2 Keadaan Kuasiperiodik
Keadaan ini adalah keadaan dimana suatu sistem dinamis mengalami penggandaan perioda. Keadaan ini merupakan jalan ke arah terjadinya chaos, dimana chaos itu sendiri terjadi bila suatu sistem mengalami penggandaan perioda beberapa kali. Pada penelitian ini, keadaan kuasiperiodik dengan m1 = m2 = m3 = l1 = l2 = l3 = g = 1, ω1 = ω2 = ω3 = 0, θ1 = Pi/2, tercapai ketika nilai θ2 atau nilai
θ3 digeser dari sudut periodik dengan range waktu sekitar 1s - 15s. Sebagai contoh diambil sudut θ2 = 5Pi/12 dan nilai θ3 = 3Pi/7. Hal ini ditunjukkan pada gambar 4.18 sampai 4.33
Gambar 4.18 Ruang fasa pada m1 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada saat range
33
Pada gambar 4.18, 4.19 dan 4.20 menunjukkan koordinat posisi–kecepatan sudut. Dalam keadaan terlihat bahwa lintasam tidak bergerak lagi dengan lintasan tertutup. Lintasan pada keadaan transien tertartik ke satu titik ruang fasa, tetapi karena amplitudo pendulum yang cukup besar maka energi diserap oleh pendulum pun cukup besar. Energi ini mengantisipasi redaman juga menyebabkan perubahan drastis dari pendulum, hal ini menyebabkan pecahnya orbit awal sehingga lintasan bergerak dengan dua periode yang berbeda atau menggalami penggandaan periode.
Gambar 4.19 Ruang fasa pada m2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada saat range
waktu 1s - 15s.
Gambar 4.20 Ruang fasa pada m2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada saat range
waktu 1s - 15s.
2vs. 2
34
Gambar 4.21 Grafik Sensitivitas kondisi awal θ(t) vs t denganm1 = m2 = m3
=1, l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7
pada range waktu 1s-35s.
Gambar 4.22 Grafik Sensitivitas kondisi awal θ(t) vs t denganm1 = m2 = m3
=1, l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = 7Pi/12, θ2 = 5Pi/12, dan θ3 =
3Pi/7 pada range waktu 1s-35s.
Hasil yang ditunjukkan pada gambar 4.21 memperlihatkan bahwa pendulum bergerak berlawanan arah awal pendulum dan mulai mengalami gerakan yang tidak harmonik lagi. Pada grafik juga terlihat bahwa lintasan tetap mengalami pengulangan tetapi butuh waktu yang lebih lama untuk melihat pengulangan tersebut, sehingga tampak lebih kompleks. Hal ini dikatakan sebagai penggandaan periode, namun sistem ini masih bersifat periodik.
Jika keadaan awal diubah sedikit yaitu θ1 = menjadi 7Pi/12, maka
perbandingan plot posisi sudutn vs waktu menunjuukkan bahwa kedua lintasan masih berjalan selaras, artinya sistem pada kondisi ini juga belum menunjukkan karakteristik kesensitifan terhadap kondisi awal yang ditunjukkan pada gamabr 4.22. Berikut ini juga ditampilkan simpangan pada keadaan kuasiperiodik ini, yang dapat dilihat pada gambar 4.23, 4.24, 4.25, 4.26, 4.27, 4.28, 4.29, dan 4.30.
t vs t
35
Gambar 4.23 Grafik x(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
(Pendulum1 dan pendulum2)
Gambar 4.24 Grafik x(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
(Pendulum2 dan pendulum3)
Gambar 4.25 Grafik y(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
(Pendulum1 dan pendulum2)
Gambar 4.26 Grafik y(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
(Pendulum2 dan pendulum3)
x t vs t
x t vs t
y t vs t
36
Gambar 4.27 Grafik x2 vs y2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
Gambar 4.28 Grafik x3 vs y3 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
Gambar 4.29 Grafik θ1 vs θ2 dengan m1 = m2 = m3 = l1 = l2 = l3 = g = 1, ω1 =
ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
Gambar 4.30 Grafik θ1 vs θ2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/7 pada range waktu 1s-35s
x2vs.y2
37
4.3 Keadaan Chaos
Seperti yang telah dijelaskan sebelulmnya bahwa keadaan chaos terjadi bila suatu sistem mengalami penggandaan periode beberapa kali. Pada penelitian ini kondisi chaos sudah tercapai pada keadaan dimensionless ketika range waktu dari 1s-90s.
Sebagai contoh diambil sudut θ2 = 5Pi/12 dan θ3 = 3Pi/11.
Gambar 4.31 Ruang fasa pada m1 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11 pada saat range
waktu 1s - 90s.
Gambar 4.32 Ruang fasa pada m2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11 pada saat range
waktu 1s - 90s.
Gambar 4.33 Ruang fasa pada m2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g =
1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11 pada saat range
waktu 1s - 90s. 1vs. 1
2vs. 2
38
Pada gambar 4.31, 4.32, dan 4.33 memperlihatkan lintasan-lintasan gerak pendulum ganda yang sudah kompleks dengan memiliki banyak perioda. Berbeda dengan ruang fasa pada keadaan kuasiperiodik yang masih dapat ditinjau lintasan-lintasannya. Lintasan-lintasan pada ruang fasa ini menjadi sulit untuk diidentifikasi karena geometri lintasan yang kompleks. Hal ini disebabkan energi yang besar dari pendulum menyebabkan ketidaklinearan dari sistem dan menyebabkan lintasan pecah dan kemudian pecah lahi menjadi beberapa lintasam, begitu seterusnya. Namun, menurut setiawan (1991) karena ukurannya yang tak terhingga maka lintasan-lintasan tersebut tidak dapat dipisahkan secara eksponensial, dan melipat kearahnya sendiri, dan terbentuklah lipatan-lipatan, hal inilah yang menyebabkan geometri yang kompleks.
Gambar 4.34 Grafik Sensitivitas kondisi awal θ(t) vs t denganm1 = m2 = m3 =
l1 = l2 = l3 = g = 1, ω1= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11
Gambar 4.35 Grafik Sensitivitas kondisi awal θ(t) vs t denganm1 = m2 = m3
=1, l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = 7Pi/12, θ2 = 5Pi/12, dan θ3 =
3Pi/11
Pada gambar 4.34 dan gambar 4.35 terlihat bahwa gerak triple pendulum sudah tidak beraturan, terdapat lonjakan-lonjakan dan penurunan-penurunan posisi sudut dengan pola yang tidak beraturan atau dengan kata lain geraknya tidak pernah berulang dan terus-menerus melakukan gerakan yang berbeda. Hal ini menyebabkan penggandaan periode terjadi dalam selang frekuensi yang lebih rapat dari keadaan kuasi periodik. Dalam hal ini langkah yang tak hingga hanya
t vs t
39
menempuh suatu jarak yang berhingga sehinga periodenya menjadi tak berhingga. Hal inilah yang dikatakan sebagai chaos.
Salah satu hal yang menarik yang dapat dituliskan disini adalah gerakan akhir dari sistem ini bergantung secara pasti pasti bagaimana sistem dimulai atau bersifat deterministik. Oleh sebab itu keadaan seperti ini disebut sebagai chaos deterministik. Sebagai sistem yang determinsitik, sistem itu dapat diprediksi sebagai suatu sistem yang bersifat chaos maka sistem ini menjadi tidak dapat diprediksi untuk jangka waktu yang panjang. Dan rentang waktu ini bergantung pada masing-masing sistem.
Berikut juga ditampilkan beberapa tampilan pada keadaan chaos, yang dapat dilihat pada gambar 4.36 – 4.43.
Gambar 4.36 Grafik x(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2 = ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11 (Pendulum1 dan
pendulum2)
Gambar 4.37 Grafik x(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2 = ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11 (Pendulum2 dan
pendulum3)
Gambar 4.38 Grafik y(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2 = ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11 (Pendulum1 dan
pendulum2)
x t vs t
x t vs t
40
Gambar 4.39 Grafik y(t) vs t dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2 = ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11 (Pendulum1 dan
pendulum2)
Gambar 4.40 Grafik x2 vs y2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11
Gambar 4.41 Grafik x3 vs y3 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11
Gambar 4.42 Grafik θ1 vs θ2 dengan m1 = m2 = m3 =1, l1 = l2 = l3 =1, g = 1, ω1
= ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11
Gambar 4.43 Grafik θ1 vs θ2 dengan m1 = m2 = m3 = l1 = l2 = l3 = g = 1, ω1 =
ω2= ω3 = 0, θ1 = Pi/2, θ2 = 5Pi/12, dan θ3 = 3Pi/11
y t vs t
x2vs.y2
41
4.4 Perbandingan Keadaan Sistem Untuk Variasi Nilai Beberapa Parameter Selain dilakukannya analisis gejala chaos untuk nilai kondisi dimensionless, maka sebagai perbandingan diteliti juga beberapa keadaan sistem untuk variasi nilai parameter-parameter lainnya untuk mengetahui keterkaitannnya dengan gerakan periodik dan chaos. Semua pengujian diambil saat t = 100 s, yaitu :
a. sudut simpangan awal, θ1(0 – 1.57 ) radian untuk kondisi m,l, dan g = 1, sudut pendulum2 dan sudut pendulum3 divariasikan antara sudut 0 sampai sudut 90o. Hasil dari syarat-syarat kondisi tersebut ditunjukkan pada tabel 4.1. (Program ini hanya dibatasi sampai maksimum sudut 90o)
Tabel 4.1 Hasil pengujian keadaan sistem untuk variasi sudut simpangan awal, sudut pendulum2 dan sudut pendulum3
No. m1 m2 m3 l1 l2 l3 θ1(rad) θ2(rad) θ3(rad) Keterangan
42
Gambar 4.44 Animasi Pendulum saat gerakan chaos dengan m1 = m2 = m3 =1,
l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = 0-0.84, θ2 = 1.31, dan θ3 = 1.17
Gambar 4.45 Animasi Pendulum saat gerakan kuasiperiodik dengan m1 = m2
= m3 =1, l1 = l2 = l3 = 1, g = 1, ω1= ω2= ω3 = 0, θ1 = 0.85-1.14, θ2 = 1.31, dan
θ3 = 1.17
Gambar 4.46 Animasi Pendulum saat gerakan periodik dengan m1 = m2 = m3
=1, l1 = l2 = l3 =1, g = 1, ω1= ω2= ω3 = 0, θ1 = 1.15-1.57, θ2 = 1.31, dan θ3 =
43
Dari tabel 4.1 terlihat bahwa sudut simpangan awal juga mempengaruhi keadaan sistem dari keadaan periodik ke chaos. Pada sudut simpangan yang kecil, sementara sudut pendulum2 dan pendulum3 dipertahankan konstan dari sudut 1.308 rad dan 1.177 rad, maka keadaan chaos akan muncul karena pendulum tidak bisa lagi bergerak bersama-sama secara linier karena pendulum2 dan pendulum3 sudah berotasi sebelum pendulum1 berotasi. Agar gerakan periodik muncul ketika sudut simpangan awal diperkecil dari 90o, maka sudut pendulum2 dan sudut pendulum3 juga ikut diperkecil dari sudut sebelumnya.
b. panjang tali pendulum1, l1 (1.0-5.0), untuk kondisi m dan g = 1, sudut simpangan awal = 90o, sudut pendulum2 dan pendulum3 bisa divariasikan antara 0 sampai 90o.
Tabel 4.2 Hasil pengujian keadaan sistem untuk variasi panjang tali pendulum1, sudut pendulum2 dan sudut pendulum3
No. m1 m2 m3 l1 l2 l3 θ1(rad) θ2(rad) θ3(rad) Keterangan
44
kuasiperiodik langsung. Hal disebabkan karena ketika panjang pendulum1 terlalu panjang sehingga pendulum3 akan berotasi terlebih dahulu.
c. panjang tali pendulum2, l2 (1.0-5.0), untuk kondisi m dan g=1, sudut simpangan awal = 90o dan sudut pendulum2 dan pendulum3 bisa divariasikan antara 0 sampai 90o.
Tabel 4.3 Hasil pengujian keadaan sistem untuk variasi panjang tali pendulum2, sudut pendulum2 dan sudut pendulum3
No. m1 m2 m3 l1 l2 l3 θ1(rad) θ2(rad) θ3(rad) Keterangan
1. 1 1 1 1 2 1 1.57 0-1.57 0-1.57 Chaos
Dari tabel diatas dapat terlihat bahwa jika kita memanjangkan panjang tali pendulum2 membuat keadaan chaos walaupun hanya bertambah 1 karena pendulum2 terletak di tengah sehingga pendulum1 akan mencapai ujung sebelum pendulum2.
d. panjang tali pendulum3, l3 (1.0-5.0), untuk kondisi m dan g=1, sudut simpangan awal = 90o, sudut pendulum2 dan pendulum3 bisaa divariasikan antara 0 sampai 90o.
Tabel 4.4 Hasil pengujian keadaan sistem untuk variasi panjang tali pendulum3, sudut pendulum2 dan sudut pendulum3
45
3.1-5 Chaos
4. 1 1 1 1 1 3.2-4 1.57 0.78 1.57 Periodik
4.1-4.4 Kuasiperiodik
4.5-5 Chaos
Dari tabel diatas terlihat bahwa panjang tali pendulum3 juga mempengaruhi keadaan sistem dari keadaan periodik ke chaos. Untuk sudut pendulum2 yang diperkecil sementara sudut pendulum3 yang diperbesar, maka keadaan chaos akan muncul untuk panjang tali yang lebih panjang atau yang sangat pendek. Namun, ketika panjang tali pendulum3 bernilai 5, maka keadaan periodik tidak nampak lagi hal ini dikarenakan pendulum 1 sudah mencapai ujung sebelum pendulum3.
e. massa pendulum1, m1 (1.0-5.0), untuk kondisi l dan g=1, sudut simpangan awal = 90o dan sudut pendulum2 dan pendulum3 bisa divariasikan antara 0 sampai 90o.
Tabel 4.5 Hasil pengujian keadaan sistem untuk variasi massa pendulum1, sudut pendulum2 dan sudut pendulum3
Tabel diatas menunjukkan bahwa ketika massa pendulum1 ditambah sementara sudut pendulum2 dan pendulum3 divariasikan maka keadaan pendulum akan mengalami keadaan chaos karena pendulum1 yang berat sehingga pendulum3 akan terayun lebih tinggi dibandingkan pendulum1.
46
Tabel 4.6 Hasil pengujian keadaan sistem untuk variasi massa pendulum2, sudut pendulum2 dan sudut pendulum3 keadaan pendulum sangat chaos karena beratnya pendulum2 sehingga pendulum1 dan pendulum3 tidak mampu mengikuti pergerakan pendulum2 bahkan pendulum3 akan mencapai titik tertinggi ketika pendulum2 mencapai ujung.
g. massa pendulum 3, m3 (1.0-5.0), untuk kondisi l dan g=1, sudut simpangan awal = 90o, sudut pendulum2 dan pendulum3 bisa divariasikan antara 0 sampai 90o.
47
Tabel diatas menunjukkan bahwa ketika massa pendulum3 dinaikkan maka pendulum akan mengalami keadaan yang chaos karena beratnya pendulum3 sehingga pendulum1 dan pendulum2 akan mencapai ujung sebelum pendulum3.
Walaupun massa bandul bertambah sangat besar atau panjang tali bertambah sangat panjang, pendulum tetap akan berada dalam keadaan periodik selama nilai massa atau panjang mempunyai nilai yang sama tiap pendulum.
48
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
1. Sistem triple pendulum ternyata merupakan sistem yang dapat menampilkan gejala chaos setelah mengalami beberapa penggandaan
perioda ketika nilai θ2 atau θ3 dinaikkan atau diturunkan dengan parameter
yang lain dipertahankan konstan.
2. Munculnya gejala chaos pada sistem triple pendulum ditandai oleh grafik posisi sudut yang tidak beraturan, lintasan-lintasan pada ruang fasa yang membentk sudut geometri yang kompleks, perbedaan grafik lintasan yang besar untuk kondisi awal yang diubah sedikit.
3. Pada analisis chaos untuk keadaan dimensionless dengan nilai m1 = m2 = m3 = l1 = l2 = l3 = g = 1, ω1 = ω2 = ω3 = 0, θ1 = Pi/2. keadaan chaos
tercapai tercapai ketika nilai θ2 digeser dari sudut 5Pi/12 atau nilai θ3
digeser dari sudut 3Pi/8.
4. Semakin besar nilai panjang atau massa tali pendulum, maka sudut pendulum2 dan sudut pendulum3 harus diubah untuk mempertahankan keperiodikkan, akan tetapi pada nilai yang terlalu besar maka keadaan pendulum akan selalu chaos. Untuk mempertahankan keadaan periodik, maka nilai massa tiap pendulum atau panjang tali tiap pendulum harus dibuat sama.
49
5.2 Saran
1. Pada peneliti selanjutnya dapat menganalisis gejala chaos sistem triple pendulum secara kuantitatif dengan menggunakan eksponensial Lyapunov. 2. Pada peneliti selanjutnya dapat mengganalisis gejala chaos pada sistem mekanika yang lain seperti pada quadruple pendulum atau triple pendulum elastik.
5
BAB 2
TINJAUAN PUSTAKA
2.1. Teori Chaos
Jacques Hadamard pada tahun 1898 menerbitkan suatu tulisan tentang gerakan yang tidak stabil atau acak dari suatu “arah peluru”. Ia menunjukkan bahwa semua arah peluru yang ditembakkan dari senapan memiliki arah yang berbeda dan menyimpang dari senapan memiliki arah yang berbeda dan menyimpang satu sama lainnya. sementara itu istilah “chaos” dirumuskan pertama kali oleh Henri Poincare (1854-1912), seorang ahli matematika perancis. Ia menemukan bukti bahwa sistem tata surya tidak bekerja secara teratur dan dapat diprediksi dengan pasti. Ia mengungkapkan bahwa “dapat terjadi perbedaan kecil pada kondisi awal menghasilkan peristiwa yang berdampak sangat besar. Sebuah kesalahan kecil pada permulaannya akan menghasilkan peristiwa yang berdampak sangat besar. Sebuah kesalahan kecil pada permulaannya akan menghasilkan penyimpangan yang lebih besar. Semula gagasan Henri Poincare tidak terlalu dihargai oleh para ilmuan pada saat itu, sampai penemuan computer yang memungkinkan pada ahli membuat model dan menggambarkan sistem chaostik.
Gambar 2.1 Model Cuaca Edward Loretz (Sahid, 2003)