Evaluasi Numerik dari Metode Aproksimasi dalam Program Stokastik

(1)

EVALUASI NUMERIK DARI METODE APROKSIMASI

DALAM PROGRAM STOKASTIK

TESIS

Oleh

MUHAMMAD ISMAIL 127021006/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

EVALUASI NUMERIK DARI METODE APROKSIMASI

DALAM PROGRAM STOKASTIK

T E S I S

Diajukan Sebagai Salah Satu Syarat

Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

(3)

Judul Tesis : EVALUASI NUMERIK DARI METODE APROKSIMASI DALAM PROGRAM STOKASTIK

Nama Mahasiswa : Muhammad Ismail Nomor Pokok : 127021006

Program Studi : Magister Matematika

Menyetujui, Komisi Pembimbing

(Prof. Dr. Tulus, M.Si) (Prof. Dr. Opim Salim S, M.Sc)

Ketua Anggota

Ketua Program Studi Dekan

(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)

(4)

Telah diuji pada Tanggal 4 Juni 2014

PANITIA PENGUJI TESIS

Ketua : Prof. Dr. Tulus, M.Si

(5)

PERNYATAAN

EVALUASI NUMERIK DARI METODE APROKSIMASI DALAM PROGRAM STOKASTIK

TESIS

Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing dituliskan sumbernya.

Medan, Juni 2014 Penulis,

(6)

ABSTRAK

Perbedaan sifat dasar masalah program stokastik dengan masalah optimisasi lainnya adalah pada cara mendefinisikan fungsi tujuan atau fungsi kendala. Pada program stokastik nilai dari beberapa fungsi ini bersifat numerik dan tergantung pada pengambilan random dalam variabel keputusan. Secara khusus, hal ini berar-ti bahwa ekspektasi matemaberar-tika dari fungsi bergantung pada variabel keputusan dan beberapa parameter random atau probabilitas dari beberapa kejadian random dikendalikan oleh variabel keputusan. Program stokastik hanya dapat diselesaikan dengan distribusi diskrit dari kardinalitas terbatas. Biasanya, data input berbentuk distribusi kontinu atau himpunan data yang besar. Pembangkit skenario memben-tuk distribusi diskrit terbatas dari data input tersebut. Tesis ini akan memfokuskan evaluasi numerik dengan metode pohon skenario dari metode aproksimasi dalam program stokastik. Prosedur untuk mengevaluasi metode pohon skenario diilus-trasikan pada kasus portfolio manajemen.

(7)

ABSTRACT

The difference nature problem of stochastic programs with other optimization pro-blem is on how to define objective function or constraint function. The stochastic program value of some numerical function and depends in random decision-making variables. In particular, this means that mathematical expectation of function de-pends in decision variables and random parameters or probability of some random events is controlled by the decision variables. The program can only be solved with a stochastic discrete distribution of limited cardinality. Typically, the input data form of a continuous distribution or a large data set. Generating scenarios form a finite discrete distribution of the input data. This thesis will focus on the nume-rical evaluation of scenario tree method or approximation omethods in stochastic programs. Procedures for evaluating the scenario tree method is illustrated in case of portfolio management.

(8)

KATA PENGANTAR

Puji syukur kepada Allah SWT memberikan anugrah yang luar biasa sehing-ga penulis dapat menyelesaikan tesis densehing-gan judul: EVALUASI NUMERIK DARI METODE APROKSIMASI DALAM PROGRAM STOKASTIK. Penulis menyampaikan terima kasih yang sebesar-besarnya kepada :

Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara.

Bapak Dr. Sutarman, M.Sc, Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Magister Matematika di FMIPA Universitas Su-matera Utara.

Bapak Prof. Dr. Herman Mawengkang, Ketua Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara sekaligus pembanding II yang telah memberikan saran dan kritik dalam menyelesaikan tesis ini.

Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Sekretaris Program Studi Magister Matematika FMIPA Universitas Sumatera Utara sekaligus pembanding I yang telah banyak memberikan bimbingan dan arahan dalam menyelesaikan tesis ini.

Bapak Prof. Dr. Tulus, M.Si, Pembimbing-I yang telah banyak memberikan bimbingan dan arahan dalam menyelesaikan tesis ini.

Bapak Prof. Dr. Opim Salim S, M.Sc, Pembimbing-II yang memberikan saran dan kritik dalam penyempurnaan tesis ini.

Bapak / Ibu Dosen Program Studi Magister Matematika FMIPA Universitas Su-matera Utara yang telah memberikan ilmunya selama masa perkuliahan.

(9)

Ucapan terimakasih juga penulis sampaikan kepada :

Istri tercinta Laila Wanna Hari Rangkuti, S.Pd. dan kedua anak saya Muhammad Herza Ismail dan Muhammad Al Khaliifi Zikri Ismail, ayahanda dan ibunda ter-cinta Suparman dan Siti Aminah, serta kakak terter-cinta Siti Mariyam, abang-abang tersayang Muhammad Ali dan Muhammad Razali dan adik-adik tercinta Muham-mad Zulham, Siti Masitha dan Rahmat Shaleh yang telah memberikan kasih sayang dan dukungan baik moril maupun materiil selama penulis dalam pendidikan dan penyelesaian tesis ini.

Rekan-rekan mahasiswa Program Studi Magister Matematika FMIPA Universitas Sumatera Utara khususnya angkatan reguler tahun 2012, dan semua pihak yang tidak dapat penulis sebutkan satu persatu pada tesis ini. Semoga Tuhan Yang Maha Kuasa membalas segala kebaikan dan bantuan yang telah diberikan.

(10)

RIWAYAT HIDUP

Muhammad Ismail, dilahirkan di Suka Damai, Langkat, pada tanggal 29 Ja-nuari 1977, merupakan anak keempat dari enam bersaudara dari ayah Suparman dan Siti Aminah. Penulis menyelesaikan pendidikan Sekolah Dasar (SD) di SD Negeri di Suka Damai Langkat tahun 1990, Sekolah Lanjutan tingkat Pertama (SLTP) di Madrasah Tsanawiyah Negeri (MTsN) Tanjung Pura tahun 1994,dan Sekolah Menengah Atas (SMA) di Madrasah Aliyah Negeri 1 (MAN 1) Tanjung Pura pada tahun 1997.

(11)

DAFTAR ISI

Halaman

PERNYATAAN i

ABSTRAK ii

ABSTRACT iii

KATA PENGANTAR iv

RIWAYAT HIDUP vi

DAFTAR ISI vii

DAFTAR TABEL ix

DAFTAR GAMBAR x

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Manfaat Penelitian 3

1.5 Metode Penelitian 3

BAB 2 TINJAUAN PUSTAKA 5

2.1 Program Stokastik 5

2.2 Metode Aproksimasi 7

2.3 Metode Numerik 13

BAB 3 POHON SKENARIO 15

(12)

3.2 Membangkitkan Pohon Skenario 16

BAB 4 EVALUASI NUMERIK 22

4.1 Model Statistik 22

4.2 Konstruksi Pohon Skenario 23

BAB 5 KESIMPULAN 26

(13)

DAFTAR TABEL

Nomor Judul Halaman

4.1 Dimensi input skenario yang disimulasi 23

4.2 Hasil numerik algoritma 3.2 untuk pohon skenario harga permintaan

(14)

DAFTAR GAMBAR

Nomor Judul Halaman

3.1 Ilustrasi konstruksi pohon untuk contoh dengan periode waktu

T = 5 20

4.1 Harga permintaan tahunan pohon skenario dengan tingkat reduk-si εrel = 0,4 yang diperoleh dengan Algoritma 3.2 24

(15)

EVALUASI NUMERIK DARI METODE APROKSIMASI

DALAM PROGRAM STOKASTIK

T E S I S

Oleh

(16)

Ketua Anggota

(17)

EVALUASI NUMERIK DARI METODE APROKSIMASI

DALAM PROGRAM STOKASTIK

TESIS

Oleh

(18)

EVALUASI NUMERIK DARI METODE APROKSIMASI

DALAM PROGRAM STOKASTIK

T E S I S

Oleh

(19)

Ketua Anggota

(20)

Telah diuji pada Tanggal 4 Juni 2014

PANITIA PENGUJI TESIS

Ketua : Prof. Dr. Tulus, M.Si

(21)

Ucapan terimakasih juga penulis sampaikan kepada :

Istri tercinta Laila Wanna Hari Rangkuti, S.Pd. dan kedua anak saya Muhammad Herza Ismail dan Muhammad Al Khaliifi Zikri Ismail, ayahanda dan ibunda ter-cinta Suparman dan Siti Aminah, serta kakak terter-cinta Siti Mariyam, abang-abang tersayang Muhammad Ali dan Muhammad Razali dan adik-adik tercinta Muham-mad Zulham, Siti Masitha dan Rahmat Shaleh yang telah memberikan kasih sayang dan dukungan baik moril maupun materiil selama penulis dalam pendidikan dan penyelesaian tesis ini.

Rekan-rekan mahasiswa Program Studi Magister Matematika FMIPA Universitas Sumatera Utara khususnya angkatan reguler tahun 2012, dan semua pihak yang tidak dapat penulis sebutkan satu persatu pada tesis ini. Semoga Tuhan Yang Maha Kuasa membalas segala kebaikan dan bantuan yang telah diberikan.

(22)

RIWAYAT HIDUP

Muhammad Ismail, dilahirkan di Suka Damai, Langkat, pada tanggal 29 Ja-nuari 1977, merupakan anak keempat dari enam bersaudara dari ayah Suparman dan Siti Aminah. Penulis menyelesaikan pendidikan Sekolah Dasar (SD) di SD Negeri di Suka Damai Langkat tahun 1990, Sekolah Lanjutan tingkat Pertama (SLTP) di Madrasah Tsanawiyah Negeri (MTsN) Tanjung Pura tahun 1994,dan Sekolah Menengah Atas (SMA) di Madrasah Aliyah Negeri 1 (MAN 1) Tanjung Pura pada tahun 1997.

(23)

DAFTAR ISI

Halaman

PERNYATAAN i

ABSTRAK ii

ABSTRACT iii

KATA PENGANTAR iv

RIWAYAT HIDUP vi

DAFTAR ISI vii

DAFTAR TABEL ix

DAFTAR GAMBAR x

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Manfaat Penelitian 3

1.5 Metode Penelitian 3

BAB 2 TINJAUAN PUSTAKA 5

2.1 Program Stokastik 5

2.2 Metode Aproksimasi 7

2.3 Metode Numerik 13

BAB 3 POHON SKENARIO 15

(24)

3.2 Membangkitkan Pohon Skenario 16

BAB 4 EVALUASI NUMERIK 22

4.1 Model Statistik 22

4.2 Konstruksi Pohon Skenario 23

BAB 5 KESIMPULAN 26

(25)

DAFTAR TABEL

Nomor Judul Halaman

4.1 Dimensi input skenario yang disimulasi 23

4.2 Hasil numerik algoritma 3.2 untuk pohon skenario harga permintaan

(26)

DAFTAR GAMBAR

Nomor Judul Halaman

3.1 Ilustrasi konstruksi pohon untuk contoh dengan periode waktu

T = 5 20

4.1 Harga permintaan tahunan pohon skenario dengan tingkat reduk-si εrel = 0,4 yang diperoleh dengan Algoritma 3.2 24

(27)

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Dalam beberapa tahun terakhir, program stokastik memiliki popularitas yang semakin meningkat dalam komunitas pemograman matematika. Model pemogra-man stokastik dapat dilihat sebagai model pemograpemogra-man matematika dengan keti-dakpastian nilai beberapa parameter. Pada nilai tunggal, parameter ini kemudi-an dijelaskkemudi-an dengkemudi-an distribusi (pada kasus periode tunggal), atau dengkemudi-an proses stokastik (pada kasus multi periode). Kesulitan utama dalam masalah program stokastik adalah dalam menghitung nilai dan gradien (atau subgradien) fungsi ma-salah.

Untuk membahas hal seperti ini lebih rinci, anggap bahwa fungsi objektif

F(x) dalam masalah program stokastik didefinisikan sebagai ekspektasi matema-tika fungsi f(x,ξ), dimana x ∈ Rn adalah vektor dari variabel keputusan dan ξ

adalah vektor berdimensimdari parameter random. Secara umum, fungsi objektif dapat dinyatakan sebagai berikut :

F(x) =Ef(x,ξ) =fΩf(x,ξ(w))P(dω) (1.1)

dimana Ω menunjukkan ruang probabilitas abstrak danP adalah ukuran probabi-litas.

Menurut Kall et al., (1984) ada 2 pendekatan utama yang dapat digunakan untuk mengatasi kesulitan ini, yaitu metode aproksimasi dan metode stokastik quasigradien.

(28)

2

metode ini adalah membuat langkah random dalam aturan perhitungan dasar dari beberapa informasi statistik tentang masalah yang diperoleh pada setiap langkah.

Kebaikan dari metode aproksimasi adalah tidak cenderung untuk mendapat-kan gambaran umum dari F(x), tetapi menggunakan nilai random f(x,ξk) dan penyesuaian gradien (atau subgradien dalam kasus nondiferensiasi) dihitung pada beberapa realisasi sampelξk _dari _ξ_{, k = 0, 1, 2, ... (Kall}_{et al}_{., 1984).}

Kuchler dan Vigerske (2009) menyatakan bahwa ketika membentuk aproksi-masi untuk masalah program stokastik, harus dianalisis hal-hal yang saling terkait berikut.

1. Harus menemukan cara yang tepat untuk menggantikan vektor random sebe-narnya ξ dengan sesuatu yang diskrit.

2. Mempelajari hubungan antara masalah sebenarnya dan masalah aproksimasi dan memperkirakan aproksimasi yang tepat.

3. Membutuhkan suatu metode untuk meningkatkan akurasi, dengan memben-tuk aproksimasi yang lebih baik unmemben-tuk ξ.

Metode solusi numerik untuk masalah optimisasi stokastik memerlukan dasar ukuran probabilitas untuk mendapatkan dukungan terbatas. Dengan demikian, teknik yang berbeda telah dikembangkan untuk variabel random aproksimasi atau proses stokastik dengan dibatasi beberapa skenario. Teknik ini mengikuti prinsip-prinsip yang berbeda seperti Random Sampling, Ukuran Probabilitas, Quasi Monte-Carlo Sampling (Kuchler dan Vigerske, 2009).

(29)

3

Tesis ini akan fokus pada evaluasi numerik dari metode aproksimasi dalam program stokastik yang diberikan. Pendekatan ini tidak menghasilkan metode yang terbaik, tetapi mencoba menemukan cara yang netral dalam mengevaluasi metode yang disarankan.

1.2 Perumusan Masalah

Dengan melakukan evaluasi numerik dari metode aproksimasi, persoalan pada tesis ini adalah bagaimana penggunaan pohon skenario untuk mempelajari perilaku dari metode aproksimasi untuk program stokastik.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah melakukan evaluasi menggunakan pohon skenario untuk program stokastik yang diilustrasikan dengan evaluasi numerik pada kasus portfolio manajemen.

1.4 Manfaat Penelitian

Hasil penelitian ini penting untuk menunjukkan bahwa terdapat persyaratan-persyaratan minimal yang harus dikenakan pada metode pohon skenario sebelum dapat digunakan untuk menyelesaikan program stokastik.

1.5 Metode Penelitian

Metode penelitian ini bersifat literatur dan kepustakaan dengan mengum-pulkan informasi dari berbagai jurnal. Langkah-langkah yang digunakan adalah sebagai berikut :

1. Menjelaskan program stokastik;

2. Menjelaskan metode aproksimasi;

(30)

4

(a) Ukuran kualitas pohon skenario; (b) Pengujian metode pohon skenario.

4. Membuat evaluasi numerik pada kasus portfolio manajemen;

5. Membahas beberapa aspek dan persyaratan pada metode pohon skenario;

(31)

BAB 2

TINJAUAN PUSTAKA

2.1 Program Stokastik

Persoalan keputusan dapat dimodelkan dengan menggunakan program sto-kastik dengan tujuan menentukan nilai maksimum atau minimum. Tujuan dan kendala dari sebuah program stokastik adalah fungsi dari variabel, dan persoalan data yang berasal dari permasalahan yang sebenarnya.

Andaikan keputusan dinyatakan oleh variabel (x1, x2, ..., xn). Sebagai contoh

xi menyatakan produksi ke-i dari n produk. Bentuk umum program matematika adalah :

Min f(x1, x2, x3, ..., xn)

Kendala :g1(x1, x2, x3, ..., xn)≤0

g2(x1, x2, x3, ..., xn)≤0

.

gn(x1, x2, x3, ..., xn)≤0

(x1, x2, x3, ..., xn)∈X

dimana X adalah himpunan bilangan real non negatif serta g1, g2, ...gn adalah kendala yang dihadapi dalam program stokastik.

(32)

6

Oleh karena itu dapat dinyatakan bahwa:

1. Program stokastik deterministik, data (koefisien) adalah bilangan-bilangan yang diketahui (tertentu);

2. Program stokastik, data (koefisien) merupakan bilangan yang tidak diketahui (tidak pasti) yang disajikan sebagai distribusi peluang.

Program stokastik adalah merupakan program matematika, dimana beberapa data yang termuat pada tujuan atau kendala mengandung ketidakpastian. Keti-dakpastian biasanya dicirikan oleh distribusi peluang pada parameter. Walaupun ketidakpastian didefinisikan dengan tepat tetapi pada prakteknya diberikan bebe-rapa skenario (hasil yang mungkin dari data) yang spesifik dan distribusi peluang gabungan yang cepat. Hasil-hasil secara umum digambarkan pada elemenw∈W. Ketika beberapa data acak, maka penyelesaian dan nilai tujuan optimal untuk masalah optimisasi juga acak (Kall dan Wallace, 1994).

Model pemograman stokastik periode tunggal dapat dirumuskan sebagai

z∗

dimana ξ˜adalah vektor random, dan distribusi G harus independen dari vektor keputusan x. Diasumsikan bahwa daerah layak X independen dari ξ˜, yaitu dia-sumsikan secara relatif merupakan jalan yang komplit.

Notasi topi digunakan untuk membedakan antara masalah sebenarnya dan masalah berbasis skenario, sehingga ˆG, ˆF, dan ˆx∗ _{masing-masing digunakan untuk}

fungsi distribusi, fungsi objektif, dan solusi optimal berbasis skenario. Selain itu, huruf tebal menunjukkan vektor, sehinggaξˆmenyatakan vektor stokastik. Sehing-ga, versi berbasis skenario dari masalah optimisasi adalah

(33)

7

2.2 Metode Aproksimasi

Dalam kasus tertentu, jika ξ pada (1.1) adalah vektor random diskrit yang hanya mencapai nilai terbatas dari nilai-nilaiξ1

,ξ2

jadi bentuk integral Riemann

F(x) =

Untuk mengevaluasi fungsi objektif F pada titik x tertentu perlu menghi-tung integral ganda yang berhubungan dengan mengukur gambaran ξ. Jika tidak mungkin melakukan integrasi analitis, maka harus digunakan metode numerik, yang biasanya membutuhkan banyak usaha komputasi, yang meningkat pesat de-ngan dimensiξ dan dengan akurasi yang dibutuhkan.

Menurut Bazaraa dan Shetty (1979), aplikasi dari metode umum pemogra-man nonlinier untuk masalah pemograpemogra-man stokastik akan memerlukan perhitung-an integral dari bentuk (1.1) pada setiap titik xk_{, k} _{= 0}_,₁_,₂_{, ...}_{, yang dihasilkan} dari algoritma optimisasi. Kesulitan meningkat jika teknik yang dihasilkan dari algoritma optimisasi juga memerlukan gradien∇F(xk₎_{, k} _{= 0}_,₁_,₂_{, ...}_{, yang dalam} kasus ini menjadi lebih sulit untuk evaluasi secara objektif. Fungsi f(x,ξ) pada (1.1) secara terus-menerus dideferensialkan terhadap x untuk setiap ξ, kemudian, di bawah kondisi tambahan yang wajarF(x) secara terus-menerus dideferensialkan dan

∇F(x) =

Z

Ω

∇xf(x,ξ(ω))P(dω) (2.5)

dimana ∇xf(x,ξ) menunjukkan gradien dari f terhadap x. Dalam dua kasus tertentu di atas diperoleh

∇F(x) = L

X

(34)

8

Karena metode pemrograman nonlinier biasanya memerlukan banyak peru-langan untuk mencapai daerah hasil, upaya perhitungan total diperlukan di luar biaya yang dapat diberikan.

Ada dua pendekatan pokok dalam mengatasi kesulitan di atas : teknik aprok-simasi dan metode stokastik quasigradient.

Pada teknik aproksimasi masalah sebenarnya diganti dengan hal sederhana melalui mengaproksimasi vektor random ξ dengan vektor random lain ξ˜agar in-tegral pada (1.1) lebih mudah digunakan. Secara khusus, dipilih ξ˜sebagai vektor random diskrit dan digunakan pada (2.1).

Metode stokastik quasigradient tidak menggunakan perhitungan integral pa-da (1.1). Ide pokok pa-dari metode ini apa-dalah membuat langkah-langkah random dalam perhitungan berdasarkan beberapa informasi statistik tentang masalah yang diperoleh pada tiap langkah. Kebalikan dari teknik aproksimasi, metode ini cen-derung tidak mendapatkan gambaran umum dari F(x), tetapi menggunakan nilai random f(x,ξk) dan menyesuaikan gradien ∇xf(x,ξk) (atau subgradien pada ka-sus nondiferensial) dihitung pada beberapa realisasi sampelξk_dari_ξ_{, k}_{= 0}_,₁_,₂_{, ...}_.

Beberapa jenis metode self-learning dibangun, dimana setiap langkah tertentu mungkin tidak efisien, tetapi nilai yang besar menunjukkan sifat umum statistik yang berarti konvergen dengan satu solusi aproksimasi.

Ketika membentuk aproksimasi untuk masalah pemorgraman stokastik harus dianalisis pertanyaan yang saling terkait berikut.

1. Harus ditemukan cara yang tepat untuk menggantikan vektor random asli ξ

dengan yang diskrit;

(35)

9

3. Dibutuhkan suatu metode untuk meningkatkan akurasi, jika tidak cukup, dengan membangun aproksimasi yang lebih baik untukξ.

Sebelum menyelidiki masalah ini secara detil, berikut beberapa ide dasar dan bentuk matematika dari pendekatan ini.

Misalkan Ξ⊂Rm _{menjadi pendukung dari vektor random}_ξ_{(yaitu himpunan} terkecil tertutup diRm _sehingga_P_{_ξ_ε_Ξ}_{= 1), dan misalkan}_SL_{adalah koleksi}

ter-Dinyatakan bahwa SL _{adalah partisi dari Ξ.}

Untuk setiap partisi dapat menggunakan integral (1.1) sebagai berikut

F(x) =

dimana integrasi melalui dukungan Ξ⊂ Rm _{dan menggunakan deskripsi dari} dis-tribusiξ pada rentang nilai-nilainya.

Pada kasus tertentu (2.2), yang secara khusus berguna, (2.8) menjadi

F(x) =

Metode yang paling sederhana untuk menghitung integral pada perkiraan masing-masing integral melalui Ξl sebagai berikut

(36)

10

dimana ξl dipilih mewakili subset Ξl. Dengan kata lain, diaproksimasi fungsi

f(x,ξ) dengan fungsi berikutnya pada ξ, yang bernilai konstan pada setiap him-punan Ξl, l = 1,2, ..., L. Dengan demikian diperoleh aproksimasi F(x):

Dari (2.6) dan (2.7) diperoleh PL

l=1pl = 1, aproksimasi ini dapat diinter-pretasikan secara ekuivalen sebagai aproksimasi ξ dengan sebuah vektor random diskritξ˜mencapai nilaiξl_{dengan probabilitas}_p

l, l= 1,2, ..., L, dan formula aprok-simasi (2.11) tepat berbentuk (2.1).

Pada umumnya, jika bentuk Ξ terbatas dan jika max

1≤l≤LP{ξεΞl} →0 sampai

L → ∞, kemudian untuk setiap x, berdasarkan asumsi yang tepat pada f(x,ξ) diperoleh titik konvergen dari nilai fungsi : FL₍_x₎_→_F₍_x_{) sampai}_L_{→ ∞. Hal ini} menjadi dasar dan sangat diperlukan, akan tetapi, tidak cukup, karena terdapat konvergensi dari urutan solusi ˆxL dari masalah aproksimasi, atau paling tidak bagian urutan konvergen untuk solusi yang sebenarnya dari masalah optimisasi. Beberapa kondisi tambahan, misalnya kepadatan dari himpunan yang mungkin dari x dengan konvergensi seragam dari FL _ke _F_{, dibutuhkan untuk kepastian} jenis konvergensi. Hal yang sering terjadi, yaitu bahwa dalam prakteknya nilai ˜x

memuaskan, dimana nilai objektif terletak antara nilai toleransi tertentu dengan tujuan ke nilai minimum, dan hal ini mungkin tercapai pada masalah yang lebih luas.

Akan tetapi, masih sangat sulit untuk menentukan terlebih dahulu bagai-mana sebaiknya partisi dapat memastikan keakuratan aproksimasi. Pembagian Ξ ke dalam beberapa bentuk kecil Ξl, l = 1,2, ..., L, tanpa strategi apapun se-cara langsung dapat meningkatkan kompleksitas komputasi dari masalah aprok-simasi. Untuk mengilustrasikan kesulitan yang mungkin timbul, andaikan bahwa terdapat 10 variabel acak skalar bebas dalam masalah yang sebenarnya, sehingga

(37)

11

10 subinterval, diperoleh 1010himpunan bagian Ξldari dukungan Ξ padaξ, jumlah yang nyata di luar kemampuan komputasi.

Untuk menghindari jumlah berlebihan dari subset Ξlharus digunakan partisi yang tidak seragam yang sesuai untuk sifat darif(x,ξ) sebagai fungsi ξ. Masalah membentuk beberapa partisi berkaitan erat dengan cara memilih titik-titikξlεΞl. Dari segi konvergensi, ini dapat menjadi titik bebas; namun, jika lebih berhati-hati dalam memilih, dinamakan ekspektasi bersyarat

ξl =E{ξ(ω)/ξ(ω)εΞl} (2.15)

dengan probabilitas

pl =P{ξ(ω)εΞl} (2.16)

maka dapat meningkatkan akurasi aproksimasi pada banyak kasus, tetapi juga memperoleh informasi yang dapat membantu untuk memperbaiki partisi yang be-nar jika akurasi tidak mencukupi.

Memang, jika fungsi f(x,ξ) linier terhadap ξ pada himpunan Ξl, maka de-nganξl _{didefinisikan oleh (2.13) diperoleh kesetaraan pada (2.10),}

Z

Ξl

f(x,ξ)P(dξ) =f(x,ξl)P{ξεΞl} (2.17)

Ini berarti bahwa pembagian selanjutnya dari subset Ξl tidak menggunakan peningkatan akurasi dari aproksimasi pada x. Di sisi lain, jika f(x, .) nonlinier pada Ξl, aproksimasi pada Ξldapat agak kasar dan partisi halus dari Ξldiinginkan. Oleh karena itu, kepadatan partisi pada berbagai sub-wilayah dari bentuk Ξlharus terkait dengan sifat nonlinier dari f(x, .).

Umumnya, tidak diketahui sifat rinci fungsif(x,ξ), beberapa informasi dapat diperoleh dalam memecahkan masalah aproksimasi yang pasti. Selain itu, sifat dari fungsi f(x, .) berubah ketika x berubah, dan perlu untuk memiliki partisi yang baikmdarix mendekati solusi masalah.

(38)

12

1. Pilih partisi awal Ξl, l= 1,2, ..., Lyang memenuhi (2.6) dan (2.7);

2. Pilih titik ξl_ε_{Ξ dan probabilitas} _p

l, l = 1,2, ..., L sesuai dengan (2.13) dan (2.14);

3. Memecahkan masalah aproksimasi;

4. Pada solusi ˜xL dianalisis akurasi aproksimasi dengan menyelidiki sifat fungsi

f(˜xL,ξ) pada masing-masing subset Ξl, l = 1,2, ..., L, memilih hal-hal yang harus dibagi lagi, jika akurasi tidak cukup, dan ulangi langkah 3.

Realisasi rinci dari prosedur ini tergantung pada sifat dari kelas masalah yang diterapkan.

Pendekatan untuk evaluasi aproksimasi dan metode solusi untuk multi stage linier program stokastik dengan mengukur kinerja solusi yang diperoleh pada su-atu himpunan skenario out-of-sample. Titik utama dari pendekatan adalah un-tuk mengembalikan kelayakan solusi unun-tuk masalah aproksimasi sepanjang snario out-of-sample. Untuk tujuan ini, dipertimbangkan dan dibandingkan ke-layakan yang berbeda dan mengoptimalkan berdasarkan metode proyeksi. De-ngan demikian, dipelajari bahwa kualitas solusi untuk tes model berdasarkan pada keklasikkan serta mengkombinasikan pohon skenario.

Secara umum, metode solusi numerik untuk masalah optimisasi stokastik memerlukan dasar ukuran probabilitas untuk memiliki dukungan terbatas. Dengan demikian, teknik yang berbeda telah dikembangkan untuk variabel random aprok-simasi atau proses stokastik dengan dibatasi beberapa skenario atau pohon ske-nario terbatas. Teknik ini mengikuti prinsip-prinsip yang berbeda seperti random sampling, momen pencocokan, ukuran probabilitas, Quasi Monte-Carlo sampling. Konvergensi nilai optimal dan/atau himpunan solusi telah terbukti untuk teknik tertentu dan sifat perkiraan statistik dan berbatas telah ditetapkan. Analisis sta-bilitas program stokastik menghasilkan petunjuk lanjutan bagaimana aproksimasi akan terlibat.

(39)

13

praktis. Di sisi lain, kuantitatif batas kesalahan dan sifat statistik tidak tersedia untuk semua kelas masalah. Selanjutnya, karena kompleksitas numerik dari model program stokastik. kadang-kadang perlu menggunakan aproksimasi yang terlalu kasar untuk mendapatkan batas kesalahan yang berarti atau interval kepercayaan melalui hasil asimtotik.

Dalam kasus tersebut, harus menggunakan metode numerik untuk mengukur kinerja dan kualitas dari metode aproksimsi dan solusi. Karena tugas utama pro-gram stokastik adalah untuk memberikan strategi keputusan yang cukup kuat yang dapat diterapkan dalam skenario kehidupan nyata, hal itu menunjukkan program tersebut untuk mengukur kualitas suatu metode aproksimsi dengan mengevaluasi solusi (optimal) diperoleh dari pemecahan masalah aproksimasi. Hal ini dapat di-lakukan, misalnya, dengan mengevaluasi solusi ini bersama metode pohon skenario.

2.3 Metode Numerik

Menurut Ralston dan Rabinowitz (1978) metode numerik adalah teknik di-mana masalah matematika diformulasikan sedemikian sehingga dapat diselesaikan oleh pengoperasian Aritmetika. Atau bisa dikatakan bahwa metode numerik adalah cara penyelesaian matematis yang dikembangkan dari cara analitis, dan memasuki wilayah simulasi. Salah satu metode numerik yang sering digunakan adalah metode Deret Taylor.

Aproksimasi orde ke-0 dilakukan dengan mengambil 1 suku pertama, yaitu nilai sebelumnya.

f(xi+1)≈f(xi) (2.18)

Aproksimasi orde ke-1 dilakukan dengan menambahi suku lainnya.

f(xi+1)≈f(xi) +f′(xi)(xi+1−xi) → f′(xi) adalah kemiringan/slope (2.19)

Aproksimasi orde ke-2 dilakukan dengan menambahi lagi suku lainnya.

f(xi+1)≈f(xi) +f′(xi)(xi+1−xi) +

f′′₍_x_i)

2! (xi+1−xi)

(40)

14

Sehingga Deret Taylor selengkapnya adalah sebagai berikut:

f(xi+1) = f(xi) +f′(xi)(xi+1−xi) +

Seringkali ada baiknya untuk memudahkan Deret Taylor dengan mendefinisikan suatu ukuran langkahh =xi+1−xi dan menyatakan persamaan (2.4) sebagai :

f(xi+1) =f(xi) +f′(xi)h+

Dimana suku sisa sekarang adalah

Rn=

fn+1₍_ξ₎

(n+ 1)!h

(41)

BAB 3

POHON SKENARIO

3.1 Ukuran Kualitas Pohon Skenario

Kesalahan aproksimasi vektor randomξ˜dengan distribusiGoleh diskritisasi ˆ

ξ dengan distribusi ˆG, untuk masalah pemograman stokastik pada (2.1), mengak-ibatkan kesenjangan optimal, yaitu perbedaan antara nilai fungsi objektif sebe-narnya pada solusi optimal dari masalah masalah sebesebe-narnya dan masalah aprok-simasi: Jika terdapat beberapa solusi optimal yang lebih baik,xˆ∗ _{dan fungsi arg min harus} dipahami sebagai salah satu solusi optimal. Bentuk f pada ef(G,Gˆ) digunakan untuk menekankan ketergantungan pada masalah optimisasi.

Perhatikan bahwaef(G,Gˆ)≥0, karena bentuk kedua adalah minimum sebe-narnya, sedangkan yang pertama adalah nilai fungsi objektif (sebenarnya) pada so-lusi aproksimasi. Perhatikan juga bahwa soso-lusi optimal tidak dibandingkan, tetapi membandingkan nilai-nilai yang sesuai dari fungsi objektif. Alasannya adalah bah-wa fungsi objektif masalah pemograman stokastik biasanya datar, sehingga terda-pat solusi berbeda yang memberikan nilai objektif yang sangat mirip. Tapi bukan berarti solusi yang mengarah ke fungsi objektif (hampir) sama dan mewakili nilai-nilai ketidakstabilan.

Definisi (3.1) memiliki satu masalah agak jelas: kesenjangan optimal, yaitu pada banyak masalah praktis mustahil untuk dikalkulasi. Pflug (2001) memecah-kan hal ini dengan membuktimemecah-kan bahwa persamaan 3.2 kondisi Lipshitz seragam tertentu,

(42)

16

Ladalah konstanta Lipshitz darif dand( ˆG, G) adalah jarak (transportasi) Wasser-stein dari fungsi distribusi ˆG dan G. Sebuah algoritma kemudian dikembangkan untuk membangun pohon skenario yang meminimalkan batas atas, yaitu jarak Wassersteind( ˆG, G).

Perlu dicatat bahwa secara umum batas ini cukup renggang, sehingga wa-laupun ditemukan pohon skenario yang meminimalkan batas atas, tidak menjamin akan mendekati nilai minimumef. Alasannya adalah bahwa meminimalkan batas atas tidak bergantung pada masalah optimisasi, jadi hubungan generasi skenario dan masalah telah hilang. Hanya konstantaL, yaitu keketatan batas yang tergan-tung pada masalah. Dalam konteks ini, metode generasi skenario dapat dipandang sebagai heuristik untuk meminimalkan kesenjangan optimalitas ef. Tentu saja, metode yang ditetapkan untuk meminimalkan batas atas pada ef mungkin diuji.

3.2 Membangkitkan Pohon Skenario

Misalkan ξ proses stokastik asli pada ruang probabilitas (Ω,F,P) dengan parameter{1, ..., T}dan ruang semestaRd. Tujuannya untuk menghasilkan pohon skenarioξtr sehingga jarak

kξ−ξtrkr dan Df∗(ξ, ξtr) (3.3)

adalah kecil dan karenanya, nilai optimal υ(ξ) dan υ(ξtr), dan solusi aproksimasi menetapkan Sε(ξ) dan Sε(ξtr) saling berdekatan.

Idenya adalah untuk memulai dengan aproksimasi awal yang baik ˆξ dari ξ

memiliki jumlah terbatas skenarioξi _{= (}_ξi

1, ..., ξiT)∈RT d dengan probabilitas pi > 0, i= 1, ..., N, dan akar umum, misalnya,ξ1

1 =...=ξ1N =:ξ∗1. Skenario ini mungkin

diperoleh dengan teknik kuantisasi, seperti yang dinyatakan oleh Graf dan Luschgy (2000), atau dengan teknik sampling atau resampling berdasarkan model stokastik parametrik dan nonparametrik ξ.

Berikut ini diasumsikan bahwa

kξ−ξˆkr+D∗

(43)

17

berlaku untuk beberapa toleransi (awal) yang diberikan ε > 0. Sebagai contoh, kondisi (3.4) mungkin cukup untuk D∗

f dan untuk setiap toleransi ε > 0 jika ˆξ diperoleh dengan sampling dari himpunan berhingga dengan ukuran sampel yang cukup besar. Heitsch dan Romisch (2009) memberikan contoh mengenai masalah ini.

Selanjutnya digambarkan prosedur algoritma yang dimulai dengan ξ dan be-rakhir dengan proses pohon skenario ξtr memiliki node (simpul) akar yang sama

ξ∗

1, mengurangi node dari ˆξ dan memungkinkan untuk perkiraan konstruktif dari

kξˆ−ξtrkr (3.5)

Menurut Heitsch dan Rmisch (2008) ide dari algoritma ini adalah membentuk kelompok skenario berdasarkan pada reduksi skenario pada waktu hirizon{1, ..., t} secara rekursif untuk meningkatkan waktu t.

Untuk itu, bentuk semi Lr kkr,t pada Lr(Ω,F,P;Rs) (dengan s = T d)

digunakan pada langkah t, dimana kkt adalah nilai semi pada Rs , untuk setiap

ξ= (ξ1, ..., ξT ∈Rs, diberikan oleh|ξ|t:=|(ξ1, ..., ξt,0, ...,0)|.

Prosedur berikut menentukan proses rekursif stokastik ˆξt _{memiliki skenario} ˆ

ξt,i_{diberikan dengan probabilitas}_p

i, i∈I :={1, ..., N}, dan, di samping itu, partisi C ={C1

t, ..., C Kt

t } dari himpunan indeksI, yaitu,

Ck

Indeks menghasilkan Ck

t ∈ Ct, k = 1, ..., Kt, mencirikan kelompok skenario. Ini-sialisasi prosedur terdiri dari membentuk ˆξ1 _{:= ˆ}_ξ_{, yaitu, ˆ}_ξ1,i ₌ _ξi_{, i} _∈ _I_{, dan} C1 ={I}. Pada langkah t(dengan t >1) dipertimbangkan bahwa setiap kelompok

Ctk−1, yaitu, setiap subset skenario {ξˆt−1,i}i∈Ck

t₋1, secara terpisah dan menghapus

skenario{ξˆt−1,j_} j∈Jk

t dengan algoritma seleksi sehingga

(44)

18

dibatasi dari atas oleh beberapa toleransi yang dibutuhkan. Disini, himpunan indeksIk

t skenario yang tersisa diberikan oleh

Ik

t =Ctk−1\Jtk (3.9)

Seperti dalam prosedur reduksi skenario umum, himpunan indeks Jk

t dibagi ke dalam himpunan indeksJk

t,i, i∈Itk sehingga

Selanjutnya didefinisikan pemetaan αt:I →I sehingga

αt(j) =

τ=1 didefinisikan oleh

ˆ

dengan probabilitas pi untuk setiap i ∈ I. Proses ˆξt diilustrasikan pada Gambar 3.1, dimana ˆξt _{sesuai dengan gambar ke-t untuk} _t _{= 1}_{, ..., T}_{. Partisi} _Ct _pada _t

yaitu, setiap elemen himpunan indeks Ik

t mendefinisikan sebuah kelompok baru dan partisi baruCt adalah penyempurnaan dari bentuk partisi Ct−1.

Skenario dan probabilitas dari pohon skenario final ξtr := ˆξT diberikan oleh sruktur partisi final CT, yaitu, memiliki bentuk

ξk

untuk setiapk = 1, ..., KT. Himpunan indeks It dari realisasiξttr diberikan oleh

(45)

19 untuk setiap i ∈ It. Probabilitas realisasi ke-i dari ξtr

t adalah πti =

P

j∈Ctkt(i)pj. Derajat percabangan skenarioi ∈It−1 bertepatan dengan kardinilitas Ik

t(i) t . Hasil berikutnya mengkuantisasi kesalahan relatif dari langkah konstruksi ke-t.

Teorema 3.1 Misalkan proses stokastik ξˆdengan node awal ξ∗

1, skenario ξi dan probabilitas pi, i = 1, ..., N, diberikan. Misalkan ξtr proses stokastik dengan

ske-nario ξk

Kemudian, disediakan sebuah algoritma fleksibel yang memungkinkan un-tuk membenun-tuk berbagai pohon skenario yang menunjukkan toleransi aproksimasi dengan hubungan ke jarak Lr.

Algoritma 3.2 Misalkan N skenario ξi _{dengan probabilitas} _p

i, i = 1, ..., N, akar

t−1 }. Tentukan adjoin himpunan in-deks Ik

t dan Jtk sehingga Itk ∪Jtk = Ctk−1, pemetaan αt() sesuai persamaan (3.11) dan proses stokastikξˆt _memiliki _N _skenario _ξˆt,i _{dengan probabilitas} _p

i

sesuai persamaan (3.12) dan sehingga

(46)

20

Langkah t + 1 : Misalkan Ct = {CT1, ..., C Kt

T }. Buatlah sebuah proses stokastik

ξtr memiliki KT skenario ξtrk sehingga ξtr,tk := ξ αt(i)

t , t = 1, ..., T jika i ∈ CTk

dengan probabilitas πk

T sesuai persamaan (3.12),k = 1, ..., KT.

Gambar 3.1 Ilustrasi konstruksi pohon untuk contoh dengan periode waktuT = 5

Sumber : Heitsch dan Romisch (2008)

Gambar pertama pada Gambar 3.1 mengilustrasikan proses ˆξ, gambar ke-t

sesuai dengan Langkah 6 dan mengilustrasikan pohon skenario final ξtr.

Akibat 3.3 Misalkan proses stokastik ξˆ dengan node awal ξ∗

1, skenario ξi dan probabilitas pi, i = 1, ..., N, diberikan. Jika ξtr dibentuk dengan Algoritma 3.2,

diperoleh

kξˆ−ξtrkr≤ T

X

t=2

(47)

21

Hasil selanjutnya menyatakan bahwa jarak |υ(ξ)−υ(ξtr)| dari nilai optimal akan kecil jika toleransi awalε pada (3.4) serta εr kecil.

Teorema 3.4 Misalkan (A1), (A2) dan (A3) dinyatakan dengan r′ _∈

[1,∞) dan himpunan X1( ˆξ1) tidak kosong dan seragam dibatasi pada Rm1 jika |ξˆ1 −ξ1| ≤ δ. Misalkan L > 0, δ > 0 dan C > 0 menjadi konstanta. Jika (ε(rn)) adalah urutan

yang cenderung menuju 0 sehingga toleransi yang sesuai ε(tn) pada Algoritma 3.2

tidak meningkat untuk semuat = 2, ..., T, urutan yang sesuai(ξtr(n))memiliki bentuk

lim sup n→∞

|υ(ξ)−υ(ξt(n))| ≤Lmax{1, C}ε (3.19)

dimanaε >0 adalah toleransi awal pada (3.4).

Bukti :Estimasi

|υ(ξ)−υ(ξtr(n))| ≤L(ε( n)

r +kξ−ξˆkr+CD

∗

f(ξ,ξˆ) +CD

∗

f( ˆξ, ξ

(n)

tr )) (3.20)

adalah sah dan bahwaD∗

f( ˆξ, ξ

(n)

tr )cenderung menuju 0 sebagain → ∞. Disimpulkan

(48)

BAB 4

EVALUASI NUMERIK

Model optimisasi rata-rata resiko dari perusahaan listrik terdiri dari produk-si listrik sendiri, kontrak pasar spot, kontrak penyediaan dan listrik berjangka. Stokastik memasukkan model melalui permintaan listrik, perilaku konsumsi, dan harga listrik. Pendekatan menghasilkan skenario dalam bentuk pohon skenario terdiri dari mengembangkan model statistik untuk semua komponen stokastik dan dalam menggunakan Algoritma 3.2 dimulai dengan jumlah terbatas skenario yang disimulasikan dari model statistik.

4.1 Model Statistik

Untuk memasukkan data stokastik dari meodel optimisasi (yaitu, permintaan listrik, perilaku konsumsi, dan harga listrik), digunakan data historis yang telah ada (dari periode tahunan pengamatan per jam). Permintaan listrik dipengaruhi oleh iklim yang ditandai dengan siklus khas tahunan dengan permintaan tinggi (rendah) selama musim hujan (musim kemarau). Selain itu permintaan listrik mengandung siklus mingguan karena berbagai konsumsi perilaku konsumen swasta dan industri pada akhir kerja dan akhir pekan. Perilaku konsumsi konsumen mencerminkan perbedaan musiman. Dapat diamati pada hari libur, pada hari-hari kerja, dan pada hari-hari dengan kondisi iklim ekstrim. Harga listrik dipengaruhi oleh kondisi iklim, aktivitas ekonomi, produsen listrik lokal, perilaku konsumen, dan lain-lain. Harga listrik juga ditandai oleh siklus tahunan khas dengan harga tinggi (rendah) selama musim hujan (kemarau) dan menunjukkan siklus mingguan dan harian juga

(49)

23

Kemudian jumlah dari skenario tiga dimensi dapat dengan mudah diper-oleh dengan mensimulasikan proses white noise untuk model ARMA dan dengan menambahkan pada fungsi tren, kecocokan profil intra-day dari cluster dan harga yang dikeluarkan dimodelkan oleh proses lompatan difusi diskrit dengan parameter waktu lompatan yang bervariasi. Skenario harga listrik mendatang secara langsung berasal dari harga listrik saat ini (Heitsch dan Romisch).

4.2 Konstruksi Pohon Skenario

Skenario tiga dimensi (permintaan listrik, perilaku konsumsi, dan harga lis-trik) dari penetapan bagian skenario awal dan berfungsi sebagai masukan untuk konstruksi pohon selanjutnya (Algoritma 3.2). Dalam seri pengujian dimulai de-ngan jumlah total dari 120 sampel skenario untuk satu tahun dede-ngan diskritisasi per jam. Tabel 4.1 menampilkan dimensi input skenario yang disimulasi. Karena pada kenyataannya produksi listrik hanya dapat diperdagangkan bulanan, perca-bangan ditetapkan pada akhir setiap bulan.

Tabel 4.1 Dimensi input skenario yang disimulasi

Komponen Horizon Skenario Waktu Node

3 (tiga variasi) 1 tahun 120 8760 880 906

Pohon skenario yang dihasilkan Algoritma 3.2 untuk r =r′_{= 2 dan tingkat}

reduksi relatif yang berbeda εrel. Tingkat relatif diberikan oleh

εrel :=

dimana εmax menyatakan maksimum kemungkinan terbaik jarak Lr dari ˆξ dan salah satu skenario yang dinotasikan dengan satuan massa. Toleransi individualεt pada titik-titik percabangan diproleh sedemikian rupa sehingga

εt

(50)

24

sedikit menurun. Tabel 4.2 menunjukkan hasil pengujian tes-run dengan tingkat reduksi relatif berbeda. Seperti yang diperkirakan, untuk tingkat reduksi yang sangat kecil, reduksi hanya mempengaruhi beberapa skenario.

Tabel 4.2 Hasil numerik algoritma 3.2 untuk pohon skenario harga permintaan tahunan

εrel Skenario Node Tingkat Waktu (detik)

inisial pohon inisial pohon

0,20 120 120 880 906 780 997 4 24,55

0,25 120 120 880 906 757 141 5 25,56

0,30 120 120 880 906 724 477 7 25,57

0,35 120 114 880 906 681 421 8 26,63

0,40 120 116 880 906 650 677 10 26,66

0,45 120 112 880 906 603 709 10 26,77

0,50 120 110 880 906 570 805 9 27,76

0,55 120 96 880 906 457 189 10 27,77

0,60 120 94 880 906 342 733 11 27,91

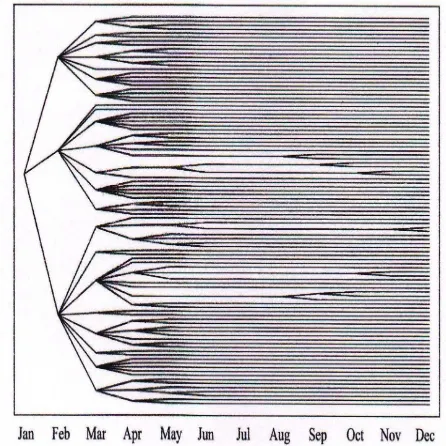
Selain itu, jumlah node berkurang jauh jika tingkat reduksi meningkat. Wak-tu komputasi kurang dari 30 detik sudah termasuk sekitar 20 detik unWak-tuk menghi-tung jarak dari semua pasangan skenario yang diperlukan pada semua kalkulasi. Gambar 4.1 dan Gambar 4.2 mengilustrasikan pohon skenario yang diperoleh untuk tingkat reduksi masing-masing 40% dan 55%.

Gambar 4.1 Harga permintaan tahunan pohon skenario dengan tingkat reduksi

(51)

25

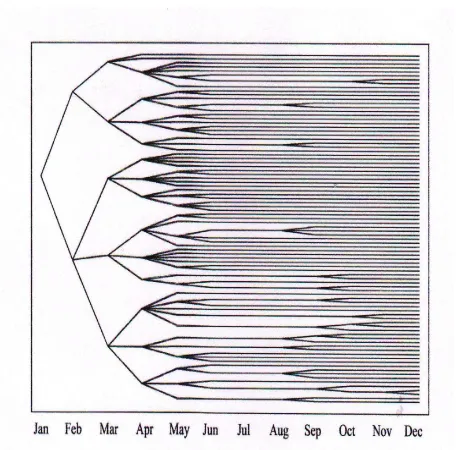
Gambar 4.2 Harga permintaan tahunan pohon skenario dengan tingkat reduksi

(52)

BAB 5 KESIMPULAN

Evaluasi numerik telah dilakukan dengan ilustrasi pada portfolio manajemen dari data yang sudah ada. Di sini, diasumsikan bahwa semua distribusi diketahui, walaupun tidak terjadi di banyak aplikasi.

Simulasi adalah cara untuk mengevaluasi nilai sebenarnya dari keputusan tertentu. Aspek yang baik dari model simulasi adalah terdapat rincian jika hasil tersebut tidak dapat dimasukkan dalam model optimisasi, tetapi semua masalah yang ada pada penyelidikan ini adalah tetap. Dalam model simulasi diperlukan sampel dari distribusi dan biasanya tidak sepenuhnya diketahui.

Pada kenyataannya, sifat konvergensi tidak terlalu berpengaruh pada po-hon skenario. Lebih penting untuk mempunyai alat pembangkit skenario yang memberi kendali atas pohon dengan jumlah skenario terbatas. Tujuannya adalah untuk memiliki metode yang stabil dan memiliki kesenjangan optimalitas kecil ser-ta menghasilkan pohon kecil. Karena itu ada baser-tas yang dibutuhkan dalam hal akurasi.

Dari evaluasi numerik diperoleh bahwa untuk tingkat reduksi yang sangat kecil reduksi hanya mempengaruhi beberapa skenario, dan jika tingkat reduksi meningkat maka jumlah node berkurang.

(53)

DAFTAR PUSTAKA

Bazaraa, M. S., dan Shetty, C. M. (1979). Nonlinear Programming : Theory and Algorithms. John Wiley, New York.

Graf, S., dan Luschgy, H. (2000). Foundations of Quantization for Probability Dis-tributions. Lecture Notes in Mathematics, Vol. 1730. Springer, Berlin.

Heitsch, H., dan Romisch, W. (2008). Scenario Tree Reduction for Multistage Stochastic Programs. Springer-Verlag.

Heitsch, H., dan Romisch, W. (2009). Scenario Tree Modelling for Multistage Stochastic Programs. Mathematical Programming, 118 : 371-406.

Heitsch, H., Romisch, W., dan Strugarek, C. (2006). Stability of Multistage Stochas-tic Programs.SIAM Journal on Optimization, 17:511-525.

Heitsch, H., dan Romisch, W. (2011). Stability and Scenario Trees for Multistage Stochastic Programs. www.math.hu-berlin.de/.../HR05brev.pdf Springer-Verlag.

Juditsky, A., Lan, G., Nemirovskiz, A., dan Shapiro, A. (2006). Stochastic Approxi-mation Approach to Stochastic Programming. Georgia Institute of Technology, Atlanta, Georgia.

Kall, P., Frauendorfer, K., dan Ruszczynski, A. (1984). Approximation Techniques in Stochastic Programming. Institut fur Operations Research der Universitat Zurich.

Kall, P., Wallace, S.W. (1994).Stochastic Programming, Second Edition. John Wiley and Sons, Chichester.

Kuchler, C., dan Vigerske, S. (2009).Numerical Evaluation of Approximation Meth-ods in Stochastic Programming. HumboldtUniversiti at zu Berlin, Unter den Linden 6, D10099 Berlin, Germany.

Mirkov, R., dan Pflug, G.C. (2007). Tree Approximations of Dynamic Stochastic Programs. SIAM Journal on Optimization, 18(3):1082-1105.