PENGGUNAAN METODE
AUTOMATIC CLUSTERING
DAN
FUZZY LOGICAL RELATIONSHIPS
UNTUK PREDIKSI
JUMLAH MAHASISWA BARU IPB
MUHAMMAD FAHMI ABDULLOH
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penggunaan Metode
Automatic Clustering dan Fuzzy Logical Relationships untuk Prediksi Jumlah Mahasiswa Baru IPB adalah benar karya saya dengan arahan dari dosen pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka dibagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya saya kepada Institut Pertanian Bogor.
Bogor, Februari 2015
Muhammad Fahmi Abdulloh
ABSTRAK
MUHAMMAD FAHMI ABDULLOH. PenggunaanMetode Automatic Clustering
dan Fuzzy Logical Relationships untuk Prediksi Jumlah Mahasiswa Baru IPB. Dibimbing oleh SRI NURDIATI dan MUHAMMAD ILYAS.
Pada tahun-tahun sebelumnya telah diterapkan metode fuzzy time series
untuk prediksi jumlah mahasiswa baru IPB. Ketika digunakan metode fuzzy time series untuk prediksi, penentuan panjang interval sangat berpengaruh dalam pembentukan fuzzy relationships yang akan menentukan hasil perhitungan prediksi. Penelitian fuzzy time series sebelumnyamenggunakan interval statis, yaitu panjang setiap interval dibuat sama. Pada penelitian sekarang ini diterapkan metode baru untuk prediksi menggunakan fuzzy time series dengan interval tak statis, yaitu dengan automatic clustering dan fuzzy logical relationships. Tujuan dari penelitian ini ialah memperkirakan jumlah mahasiswa baru IPB menggunakan metode
automatic clustering dan fuzzy logical relationships serta membandingkan keakuratan hasil prediksi antara metode automatic clustering dan fuzzy logical relationships dengan metode fuzzy time series pada penelitian sebelumnya. Hasil penelitian menunjukkan prediksi jumlah mahasiswa baru IPB menggunakan metode automatic clustering dan fuzzy logical relationships memiliki tingkat akurasi lebih tinggi daripada metode fuzzy time series sebelumnya.
Kata kunci: automatic clustering, fuzzy logical relationships, fuzzy time series,
himpunan fuzzy, prediksi
ABSTRACT
MUHAMMAD FAHMI ABDULLOH. The Use of Automatic Clustering and Fuzzy Logical Relationships Methods for Prediction the Number of New Students at IPB. Supervised by SRI NURDIATI and MUHAMMAD ILYAS.
In previous years it has been applied fuzzy time series methods for predicting the number of new students at IPB. When using fuzzy time series methods for prediction, determination of the length of the interval affect in the formation of fuzzy relationships that will determine the outcome of the prediction calculations. Research of fuzzy time series used a static interval which is the interval with equal length. This current research applied a new method for prediction using fuzzy time series with no static interval with automatic clustering and fuzzy logical relationships. The purpose of this research is to estimate the number of new students at IPB using automatic clustering and fuzzy logical relationships methods and to compare the accuracy of the prediction results between the method of automatic clustering and fuzzy logical relationships with fuzzy time series methods in previous research. The results showed that the prediction of new students at IPB using automatic clustering and fuzzy logical relationships method gives a higher degree of accuracy than that of previous methods using fuzzy time series.
PENGGUNAAN METODE
AUTOMATIC CLUSTERING
DAN
FUZZY LOGICAL RELATIONSHIPS
UNTUK PREDIKSI
JUMLAH MAHASISWA BARU IPB
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2015
MUHAMMAD FAHMI ABDULLOH
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Shalawat serta salam penulis sampaikan kepada Baginda Nabi Muhammad shallallahu ‘alaihi wa
sallam beserta keluarganya dan para sahabatnya. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Juli 2014 sampai Desember 2014 ini ialah PenggunaanMetode Automatic Clustering dan Fuzzy Logical Relationships untuk PrediksiJumlah Mahasiswa Baru IPB.
Terima kasih penulis ucapkan kepada Ibu Dr Ir Sri Nurdiati, MSc dan Bapak Muhammad Ilyas, MSi, MSc selaku pembimbing skripsi yang telah memberikan bimbingan dan pengarahan untuk kegiatan penelitian ini. Terima kasih penulis ucapkan juga kepada Bapak Dr Ir Fahren Bukhari, MSc selaku dosen penguji. Ucapan terima kasih juga disampaikan kepada ayah, ibu, serta seluruh keluarga atas doa dan kasih sayangnya. Ucapan terima kasih juga disampaikan kepada Ust. Drs Romli, MAg selaku pengasuh PPM Al-Inayah atas doa dan dukungannya. Ucapan terima kasih juga disampaikan kepada teman-teman Matematika 47, teman- teman santri Al-Inayah, teman-teman KMNU dan teman-teman lain yang tidak bisa penulis sebutkan satu persatu.
Semoga karya ilmiah ini bermanfaat.
Bogor, Februari 2015
DAFTAR ISI
DAFTAR TABEL xi
DAFTAR LAMPIRAN xi
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
Ruang Lingkup Penelitian 2
TINJAUAN PUSTAKA 2
Fuzzy Time Series 2
Ukuran Kesalahan 3
METODE 3
Algoritme Automatic Clustering 4
Metode Automatic Clustering dan Fuzzy Logical Relationships 8
HASIL DAN PEMBAHASAN 10
Algoritme Automatic Clustering 10
Metode Automatic Clustering dan Fuzzy Logical Relationships 11
Himpunan semesta 11
Proses fuzzifikasi 15
Fuzzy Logical Relationships 15
Proses defuzzifikasi 16
Prediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2012 17 Prediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2013 18 Prediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2014 23 Prediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2015 29
Perbandingan Hasil Prediksi 35
Perbandingan hasil prediksi metode Automatic Clustering dan Fuzzy
Logical Relationships dengan nilai p berbeda 35 Perbandingan hasil prediksi metode Automatic Clustering dan Fuzzy
Logical Relationships dengan metode pada penelitian sebelumnya 37
SIMPULAN DAN SARAN 38
Simpulan 38
DAFTAR PUSTAKA 39
DAFTAR TABEL
1 Jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 –
2012 3
2 Data fuzzifikasi jumlah mahasiswa baru Institut Pertanian Bogor
tahun 1992 – 2011 15
3 Fuzzy logical relationships jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 - 2011 16
4 Fuzzy logical relationship groups jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 – 2011 16
5 Hasil prediksi jumlah mahasiswa baru Institutut Pertanian Bogor
tahun 1992 – 2011 17
6 Data fuzzifikasi jumlah mahasiswa baru Institut Pertanian Bogor
tahun 1992 – 2012 22
7 Fuzzy logical relationships jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 – 2012 23
8 Fuzzy logical relationship groups jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 – 2012 23
9 Data fuzzifikasi jumlah mahasiswa baru Institut Pertanian Bogor
tahun 1992 – 2013 28
10 Fuzzy logical relationships jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 - 2013 28
11 Fuzzy logical relationship groups jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 – 2013 29
12 Data fuzzifikasi jumlah mahasiswa baru Institut Pertanian Bogor
tahun 1992 – 2014 34
13 Fuzzy logical relationships jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 – 2014 34
14 Fuzzy logical relationship groups jumlah mahasiswa baru Institut
Pertanian Bogor tahun 1992 – 2014 35
15 Perbandingan hasil prediksi metode automatic clustering dan fuzzy logical relationships dengan nilai p berbeda. 36 16 Perbandingan hasil prediksi metode fuzzy time series Hsu et al.
yang telah dideskripsikan oleh Steven (2013), metode fuzzy time series Chen dan Hsu yang telah dideskripsikan oleh Permana (2014), dan metode automatic clustering dan fuzzy logical
relationships 37
DAFTAR LAMPIRAN
1 Perhitungan hasil prediksi di setiap tahun 40
PENDAHULUAN
Latar Belakang
Prediksi jumlah mahasiwa baru Institutut Pertanian Bogor secara akurat penting untuk dilakukan karena dari hasil prediksi tersebut bisa diambil banyak keputusan seperti penyesuaian ruang kelas yang diperlukan mahasiswa, penyesuaian jumlah dosen, dan penyesuaian sarana pendukung kegiatan belajar mengajar lainnya. Beberapa penelitian telah dilakukan untuk memperkirakan jumlah mahasiswa baru Institutut Pertanian Bogor, antara lain oleh Steven (2013) dengan metode holt double exponential smoothing dan fuzzy time series Hsu et al., dan oleh Permana (2014) dengan metode fuzzy time series Chen dan Hsu.
Dalam perhitungan prediksi menggunakan fuzzy time series, panjang interval dari semesta pembicaraan telah ditentukan di awal proses perhitungan. Penentuan panjang interval sangat berpengaruh dalam pembentukan fuzzy relationships yang akan menentukan hasil perhitungan prediksi. Oleh karena itu, pembentukan fuzzy relationship haruslah tepat dan hal ini mengharuskan penentuan panjang setiap interval yang sesuai. Penelitian fuzzy time series sebelumnya oleh Steven (2013) dan Permana (2014) menggunakan interval statis yaitu panjang setiap interval dibuat sama. Kekurangan penggunaan interval statis diantaranya data historis dikelompokkan ke dalam interval-interval secara kasar sehingga hasil prediksi kurang baik. Oleh karena itu Chen et al. (2009, 2011) mengembangkan metode baru untuk prediksi menggunakan fuzzy time series dengan interval tak statis yaitu dengan
automatic clustering.
Menurut Song dan Chissom (1993), sistem prediksi dengan metode fuzzy time series dilakukan dengan cara menangkap pola dari data sebelumnya kemudian data tersebut digunakan untuk memproyeksikan data yang akan datang. Prosesnya juga tidak membutuhkan suatu sistem pembelajaran dari suatu sistem yang rumit seperti yang ada pada algoritme genetika dan jaringan syaraf sehingga mudah untuk dikembangkan dan tidak memerlukan adanya pola trend untuk melakukan proses prediksi.
Penelitian yang dilakukan oleh Chen et al. (2009) memperkenalkan sebuah metode automatic clustering dan fuzzy logical relationships untuk memperkirakan pendaftaran di Universitas Alabama. Penelitian tersebut memberikan hasil MSE (Mean Square Error) lebih rendah daripada penelitian sebelumnya yang menggunakan metode Chen (1996), metode Cheng et al. (2006, 2008), metode Huarg (2001b), metode Song dan Chissom (1993a), dan metode Sullivan dan Woodall (1994) pada kasus yang sama.
2
Tujuan Penelitian
Tujuan dari penelitian ini ialah memperkirakan jumlah mahasiswa baru Institut Pertanian Bogor menggunakan metode automatic clustering dan fuzzy logical relationships serta membandingkan keakuratan hasil prediksi menggunakan MAPE (Mean Absolute Percentage Error) antara metode automatic clustering dan
fuzzy logical relationships dengan metode fuzzy time series Hsu et al. yang dideskripsikan oleh Steven (2013) dan metode fuzzy time series Chen dan Hsu yang dideskripsikan oleh Permana (2014).
Ruang Lingkup Penelitian
Ruang lingkup penelitian ini antara lain:
1. Metode yang digunakan adalah metode automatic clustering dan fuzzy logical relationships, metode fuzzy time series Hsu et al. yang dideskripsikan oleh Steven (2013), dan metode fuzzy time series Chen dan Hsu yang dideskripsikan oleh Permana (2014).
2. Data yang digunakan adalah data sekunder jumlah mahasiswa baru di Institut Pertanian Bogor sejak tahun 1992 – 2012.
3. Penghitungan besarnya error menggunakan MAPE (Mean Absolute Percentage Error).
TINJAUAN PUSTAKA
Fuzzy Time Series
Akan dibahas secara singkat beberapa konsep dasar fuzzy time series yang diperkenalkan oleh Song dan Chissom ( 1993a, 1993b, 1994 ) yang nilai fuzzy time series direpresentasikan dengan himpunan fuzzy (Chen 1998, Zadeh 1965). Didefinisikan � adalah semesta pembicaraan dengan � = { , , … , �}. Sebuah himpunan fuzzy � dalam semesta pembicaraan � dapat direpresentasikan sebagai
� = � / + � / + + � � / �, dengan � adalah fungsi
keanggotaan dari himpunan fuzzy �, � ∶ � → [ , ], � merupakan tingkat keanggotaan dari dalam himpunan fuzzyA, dan � .
Misalkan � = . . . , , , , . . . adalah himpunan bagian dari R, yang menjadi himpunan semesta dengan himpunan fuzzy � = , , . . . telah didefinisikan sebelumnya dan dijadikan menjadi kumpulan dari
� = , , . . . , maka F(t) dinyatakan sebagai fuzzy time series terhadap � = . . . , , , . . . .
Jika ada sebuah fuzzy logical relationship � , − sedemikian sehingga = − � , − , dengan dan − merupakan himpunan
fuzzy dan merupakan operator komposisi maks-min, maka disebut diperoleh dari − , dilambangkan oleh fuzzy logical relationship sebagai
3 himpunan fuzzy, maka fuzzy logical relationship antara − dan dapat ditunjukkan oleh � → �, dengan � disebut current state dan � disebut next state.
Ukuran Kesalahan
MAPE (Mean Absolute Percentage Error) merupakan salah satu alat ukur kesalahan yang bisa digunakan untuk menentukan tingkat keakuratan hasil penelitian. Semakin kecil nilai MAPE dari suatu hasil penelitian berarti tingkat keakuratan semakin baik. Cara menghitung MAPE menurut Makridakis et al. (1998) sebagai berikut:
MAPE = ∑ │�
�│,
�
�= dengan
� �= (��−� �
� ) × .
Ket:
�� : Data aktual pada periode ke-t, � : Nilai prediksi pada periode ke-t,
: Banyaknya periode waktu.
METODE
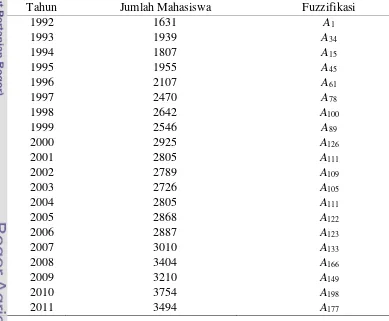
Data yang digunakan dalam karya ilmiah ini adalah data jumlah mahasiswa baru Institut Pertanian Bogor dari tahun 1992 – 2012 (21 tahun). Data jumlah mahasiswa baru Institut Pertanian Bogor sejak tahun 1992 – 2012 dapat dilihat pada Tabel 1.
Tabel 1 Jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 – 2012 Tahun Jumlah Mahasiswa Tahun Jumlah Mahasiswa
1992 1631 2003 2726
1993 1939 2004 2805
1994 1807 2005 2868
1995 1955 2006 2887
1996 2107 2007 3010
1997 2470 2008 3404
1998 2642 2009 3210
1999 2546 2010 3754
2000 2925 2011 3494
2001 2805 2012 3868
2002 2789
4
Algoritme Automatic Clustering
Sebuah cluster adalah sebuah himpunan yang elemen-elemennya memiliki sifat yang mirip dalam hal tertentu. Elemen-elemen dari cluster yang sama memiliki sifat yang mirip, sementara elemen-elemen dari cluster berbeda memiliki sifat berbeda. Jika elemen-elemen dari sebuah cluster adalah nilai-nilai numerik, maka semakin kecil jarak selisih antara dua elemen berarti tingkat kesamaan dua elemen tersebut semakin tinggi (Chen dan Hisau 2007).
Diasumsikan ada data numerik yang diurutkan dalam urutan menaik seperti berikut:
d1,0 = d1,1 = . . . <d2,0 = d2,1 = . . . <dn - 1,0 = dn - 1,1= . . . <dn ,0 = dn ,1= . . . , dengan di,0 , di,1 , . . . , dan di,jmerupakan data numerik dengan nilai sama, 1 i n , dan j 0. Terlihat bahwa ada n data numerik berbeda dalam data urutan menaik. Proses clustering mengikuti prinsip-prinsip berikut:
Prinsip 1: JIKA xj– xi average_diff
MAKA letakkan xj ke dalam cluster yang memuat xi, Prinsip 2: JIKA xj– xi average_diff DAN xj– xi cluster_diff
MAKA letakkan xj ke dalam cluster yang memuat xi, Prinsip 3: JIKA xk–xj average_diff DAN xk–xj<xj–xi
MAKA letakkan xk ke dalam cluster yang memuat xj,
dengan xi xj xk. Average_diff menunjukkan jarak selisih rata-rata antar setiap dua data berdekatan dalam data urutan menaik. Cluster_diff menunjukkan jarak selisih rata-rata antar setiap dua data berdekatan dalam current cluster. Dalam perhitungan average_diff dan cluster_diff data yang sama dalam data urutan menaik hanya dihitung satu kali.
Nilai average_diff dihitung sebagai berikut:
� � _ � = ∑�−= −+ − .
Nilai cluster_diff dihitung sebagai berikut:
_ � =∑�−= −+ − ,
dengan ,, , … dan � menunjukkan data di dalam current cluster.
Berdasarkan Prinsip 1, dua data numerik yang adjacentxidan xj dalam urutan menaikdapat diletakkan ke dalam satu cluster jika jarak selisih mereka lebih kecil atau sama dengan average_diff. Tetapi jika hanya menggunakan Prinsip 1 masih kurang beralasan. Sebagai contoh, diasumsikan ada data numerik dalam barisan menaik yang memiliki nilai average_diff = 30. Diasumsikan pula ada sebuah cluster
5 . . . , 71, 71, 72, 73, 74, 74, 100, 130, . . .
Akan ditentukan apakah 100 dapat diletakkan ke dalam cluster {71, 71, 72, 73, 74, 74}. Jika hanya menggunakan Prinsip 1, 100 – 74 average_diff, dengan
average_diff = 30, maka 100 akan diletakkan ke dalam cluster dan akan diperoleh
cluster baru {71, 71, 72, 73, 74, 74, 100}. Tetapi menurut persepsi manusia, 100 tidak akan ditempatkan ke dalam cluster {71, 71, 72, 73, 74, 74} karena fakta bahwa hal tersebut akan meningkatkan jarak rata-rata dalam cluster. Dengan demikian, diperlukan prinsip clustering baru yaitu Prinsip 2.
Dari contoh sebelumnya, nilai cluster_diff dari {71, 71, 72, 73, 74, 74} dihitung sebagai berikut:
cluster_diff = [(72 - 71) + (73 – 72) + (74 – 73)] / 3 = 1.
Perlu diperhatikan bahwa data yang sama dalam sebuah cluster hanya dihitung satu kali. Diketahui xi = 74, xj = 100, average_diff = 30, dan cluster_diff = 1. Setelah diterapkan Prinsip 2 diperoleh
JIKA 100 – 74 30 DAN 100 – 74 1
MAKA letakkan 100 ke dalam cluster yang memuat 74.
Jelas, karena ekspresi 100 – 74 1 adalah salah, 100 tidak dapat diletakkan ke dalam
cluster yang memuat 74. Oleh karena itu hasil clustering seperti berikut: . . . , {71, 71, 72, 73, 74, 74}, {100}, 130, . . .
Maka, 100 merupakan elemen tunggal dalam cluster {100}. Setelah diterapkan Prinsip 1 diperoleh
JIKA 130 – 100 30
MAKA letakkan 130 ke dalam cluster yang memuat 100.
Karena “130 – 100 average_diff” adalah benar, dengan average_diff = 30,
berdasarkan Prinsip 1, 130 akan diletakkan ke dalam cluster {100}, dan akan diperoleh cluster baru {100, 130}. Akan tetapi jika 100 dan 130 diletakkan ke dalam satu cluster kurang beralasan karena fakta bahwa jarak selisih antara 100 dan 130 lebih besar dari pada jarak selisih antara 74 dan 100. Dengan demikian, diperlukan prinsip clustering baru yaitu Prinsip 3.
Dari contoh sebelumnya, diketahui xi = 74, xj = 100, xk = 130, dan
average_diff = 30. Berdasarkan Prinsip 3 diperoleh hasil sebagai berikut: JIKA 130 – 100 30 DAN 130 – 100 < 100 – 74 MAKA letakkan 130 ke dalam cluster yang memuat 100.
Jelas, karena ekspresi “130 – 100 < 100 – 74” adalah salah, 130 tidak dapat
diletakkan ke dalam cluster yang memuat 100. Oleh karena ini hasil clustering seperti berikut:
6
Terlihat bahwa sekarang hasil clustering dari data numeriktersebut lebih beralasan (Chen dan Hisau 2007).
Elemen-elemen dalam setiap cluster hasil clustering perlu disesuaikan lagi karena akan dibentuk interval-interval. Dalam setiap cluster sebisa mungkin hanya memuat dua elemen agar mudah dilakukan transformasi dari cluster-cluster ke dalam interval-interval. Jika sebuah cluster memiliki lebih dari dua elemen maka hanya perlu dipertahankan elemen terkecil dan elemen terbesar. Jika sebuah cluster tepat memiliki dua elemen maka dipertahankan elemen-elemen tersebut. Jika sebuah
cluster hanya memiliki satu elemen misal dq maka “dq –average_diff ” dan “dq +
average_diff” diletakkan ke dalam cluster dan dq dihapus dari cluster. Karena tidak ada cluster sebelum cluster pertama maka jika cluster pertama hanya memiliki satu elemen misal dq, elemen cluster diubah menjadi dqdan “dq + average_diff”. Karena tidak ada cluster setelah cluster terakhir maka jika cluster terakhir hanya memiliki satu elemen misal dq,elemen cluster diubah menjadi “dq– average_diff” dan dq. Jika
nilai dari “dq – average_diff “ lebih kecil dari pada nilai terkecil dalam cluster
sebelumnya, maka cluster dibiarkan tetap. Selanjutnya dilakukan transformasi dari
cluster-cluster ke dalam interval-interval.
Dari penjelasan-penjelasan di atas dapat disajikan langkah-langkah algoritme
automatic clustering sebagai berikut (Chen, et al. 2009):
Langkah 1: Data yang terdiri atas n data numerik berbeda diurutkan dalam urutan data menaik. Diasumsikan bahwa urutan data menaik tanpa data ganda ditunjukkan sebagai berikut:
d1 , d 2 , d3 , . . . , di , . . . , dn.
Berdasarkan barisan di atas, dihitung nilai dari “average_diff” sebagai berikut:
� � _ � =∑�−= −+ − , (1)
dengan “average_diff” menunjukkan rata-rata perbedaan antara setiap data yang berdekatan dalam urutan menaik.
Langkah 2: : Datum pertama dalam urutan data menaik ditetapkan sebagai current cluster. Berdasakan nilai average_diff ditentukan apakah datum berikutnya dalam urutan data menaik dapat dimasukkan ke dalam current cluster atau perlu dimasukkan ke dalam new cluster didasarkan pada prinsip berikut:
Prinsip 1: Diasumsikan bahwa current cluster adalalah cluster pertama dan di dalamnya hanya ada satu datum d1 dan diasumsikan bahwa d2 adalah datum adjacent dari d1, ditampilkan sebagai berikut:
{d1}, d2, d3, . . . , dn.
Jika d2 – d1 average_diff, makad2 diletakkan ke dalam current cluster yang memuat d1. Jika tidak, dibentuk newcluster untuk d2 dan ditetapkan new cluster yang memuat d2 menjadi currentcluster.
7 pada current cluster dan diasumsikan bahwa dj adalah datum adjacent dari di yang ditampilkan sebagai berikut:
{d1, . . .}, . . . , {. . .},{. . . , di}, dj , . . . , dn.
Jika dj– di average_diff dan dj– di cluster_diff , maka dj diletakkan ke dalam
current cluster yang memuat di. Jika tidak, dibentuk new cluster untuk dj dan ditetapkan new cluster yang memuat dj menjadi current cluster, dengan
''cluster_diff " menunjukkan perbedaan rata-rata jarak antar setiap pasangan data yang berdekatan dalam cluster yang dihitung sebagai berikut:
_ � = ∑�−= −+ − , (2)
dengan ,, , … dan � menunjukkan data di dalam current cluster.
Prinsip 3: Diasumsikan current cluster bukan cluster pertama dan hanya ada satu
datumdjpada currentcluster. Diasumsikan dkadalah datumadjacent dari dj dan diasumsikan di adalah datum terbesar dalam cluster yang merupakan antecedent
cluster dari current cluster, ditampilkan sebagai berikut: {d1, . . .}, . . . , {. . . , di}, {dj}, dk , . . . , dn.
Jika dk – dj average_diff dan dk – dj< dj – di, maka dk diletakkan ke dalam
current cluster yang memuat dj. Jika tidak, dibentuk new cluster untuk dk dan ditetapkan new cluster yang memuat dk menjadi currentcluster.
Langkah 3: Berdasarkan hasil clustering yang diperoleh pada Langkah 2, isi cluster
disesuaikan dengan prinsip-prinsip berikut:
Prinsip 1: Jika sebuah cluster memiliki lebih dari dua data, maka datum terkecil,
datum terbesar dipertahankan dan data yang lain dihapus.
Prinsip 2: Jika sebuah cluster hanya memiliki dua data, maka dua data tersebut dipertahankan.
Prinsip 3: Jika sebuah cluster hanya memiliki satu datum dq, maka nilai-nilai dari
“dq – average_diff ” dan “dq + average_diff” diletakkan ke dalam cluster dan dq dihapus dari cluster. Jika situasi berikut terjadi, cluster perlu disesuaikan lagi:
Situasi 1: Jika situasi terjadi di cluster pertama, maka hapus nilai dari “dq –
average_diff” dan ditetapkan dq sebagai penggantinya.
Situasi 2: Jika situasi terjadi di cluster terakhir, maka hapus nilai dari “dq +
average_diff” dan ditetapkan dq sebagai penggantinya.
Situasi 3: Jika nilai dari “dq– average_diff“ lebih kecil dari pada nilai terkecil dalam antecedent cluster, maka semua tindakan dalam Prinsip 3 dibatalkan. Langkah 4: Diasumsikan bahwa hasil clustering yang diperoleh dari Langkah 3 ditampilkan sebagai berikut:
{d1, d2}, {d3, d4}, {d5, d6}, … , {dr}, {ds, dt}, . . . , {dn-1, dn}.
8 yangditetapkan menjadi current interval dan cluster selanjutnya ditetapkan menjadi current cluster.
(3) Interval terakhir merupakan interval selang tutup [dm, dn]
Langkah 4.3: Current interval dan current cluster diperiksa berulang kali sampai semua cluster telah berubah menjadi interval-interval.
Langkah 5: Untuk setiap interval yang diperoleh pada Langkah 4, bagi masing-masing interval ke dalam p sub-interval, dengan p 1.
Metode Automatic Clustering dan Fuzzy Logical Relationships
Pada bagian ini, disajikan metode prediksi oleh Chen, et al. (2009) yaitu metode automatic clustering dan fuzzy logical relationships sebagai berikut:
1. Himpunan semesta
Himpunan semesta U = [Dmin, Dmax] ditentukan sesuai data historis yang ada. Algoritme automatic clustering diterapkan untuk membuat interval-interval dari data historis. Kemudian setiap interval yang terbentuk dihitung titik tengahnya.
2. Proses fuzzifikasi
Diasumsikan ada n interval yang didapatkan dari langkah pertama yaitu , , . . . , dan �, kemudian didefinisikan setiap himpunan fuzzy � , dengan
Fuzzifikasi setiap datum ke dalam himpunan fuzzy. Jika datum masuk dalam interval , dengan � , maka datum difuzzifikasi ke dalam himpunan
fuzzy � . Himpunan fuzzy � , � , � , . . . , �� merupakan suatu himpunan-himpunan fuzzy yang variabel linguistiknya ditentukan sesuai dengan keadaan semesta. Himpunan fuzzy � merupakan himpunan fuzzy jumlah mahasiswa paling sedikit sedangkan himpunan fuzzy �� merupakan himpunan fuzzy jumlah mahasiswa paling banyak.
9
3. Fuzzy logical relationship
Membuat fuzzy logical relationships berdasarkan pada fuzzifikasi yang diperoleh pada langkah 2. Jika hasil fuzzifikasi tahun dan + adalah Ai dan Ak, maka terbentuk fuzzy logical relationship“� → � ”, dengan � dan � berturut-turut disebut current state dan next state dari fuzzy logical relationship. Berdasarkan current state dari fuzzy logical relationships,
dibuat fuzzy logical relationship groups, yaitu fuzzy logical relationships
yang memiliki current state sama dimasukkan ke dalam fuzzy logical relationshipgroup yang sama.
4. Proses defuzzifikasi
Proses defuzzifikasi mengubah suatu besaran fuzzy menjadi besaran tegas. Keluaran dalam proses ini yaitu suatu nilai prediksi yang ditentukan dengan menggunakan aturan-aturan berikut:
(1) Jika hasil fuzzifikasi pada tahun t adalah Aj dan hanya ada satu fuzzy
logical relationship di dalam fuzzy logical relationship group yang memiliki current state Aj ditunjukkan sebagai berikut:
Aj→Ak ,
maka prediksi pada tahun + adalah , dengan adalah titik tengah dari interval dan nilai keanggotaan maksimum dari himpunan
fuzzyAk terjadi pada interval .
(2) Jika hasil fuzzifikasi pada tahun t adalah Aj dan ada fuzzy logical
relationships berikut di dalam grup fuzzy logical relationship yang memiliki current state Aj, ditunjukkan sebagai berikut:
� → � � , � � , . .. , � � �� ,
maka prediksi pada tahun t + 1 dihitung sebagai berikut:
� × + � × + + �� × �
� + � + + �� , (4)
dengan � menunjukkan jumlah dari fuzzy logical relationships
“Aj→Aki” di dalam fuzzy logical relationship group, � �, ,
, . . . , dan � berturut-turut adalah titik tengah dari interval , , . . . , dan �, dan nilai keanggotaan maksimum dari himpunan fuzzy � , � , . . . , dan � � berturut-turut terjadi pada interval
, , . . . , dan �.
(3) Jika hasil fuzzifikasi pada tahun t adalah Aj dan ada fuzzy logical
relationship di dalam fuzzy logical relationship group yang memiliki
current state Aj ditunjukkan sebagai berikut:
Aj →#,
10
HASIL DAN PEMBAHASAN
Algoritme Automatic Clustering
Tabel 1 menunjukkan data historis jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 sampai tahun 2012. Algoritme automatic clustering akan diterapkan untuk clustering data historis jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 sampai tahun 2011 ke dalam interval-interval. Langkah-langkah penerapan Algoritme automatic clustering sebagiai berikut:
[Langkah 1]: hasil dari pengurutan data historis tahun 1992 sampai tahun 2011 dalam urutan menaik sebagai berikut:
1631, 1807, 1939, 1955, 2107, 2470, 2546, 2642, 2726, 2789, 2805, 2805, 2868,2887, 2925, 3010, 3210, 3404, 3494, 3754.
Data yang nilainya sama cukup dituliskan satu kali, hasilnya sebagai berikut:
1631, 1807, 1939, 1955, 2107, 2470, 2546, 2642, 2726, 2789, 2805, 2868, 2887, 2925, 3010, 3210, 3404, 3494, 3754.
Berdasarkan persamaan (1) dapat dihitung nilai average_diffsebagai berikut:
average_diff = [(1807 – 1631) + (1939 – 1807) + (1939 – 1807) + (1955 – 1939) + (2107 – 1955) + (2470 – 2107) + (2546 – 2470) + (2642 – 2546) + (2726 – 2642) + (2789 – 2726) + (2805 – 2789) + (2868 – 2805) + (2887 – 2868) + (2925 – 2887) + (3010 – 2925) + (3210 – 3010) + (3494 – 3404) + (3754 – 3494)]/18
= 2123/18 = 117.94
[Langkah 2]: Berdasakan nilai average_diff dan tiga prinsip pada Langkah 2, dapat dibuat cluster dari data urutan menaik sehingga diperoleh hasil clustering sebagai berikut:
{1631}, {1807}, {1939, 1955}, {2107}, {2470, 2546}, {2642, 2726, 2789, 2805}, {2868, 2887}, {2925}, {3010}, {3210}, {3404, 3494}, {3754}.
[Langkah 3]: Berdasarkan tiga prinsip pada Langkah 3, hasil clustering yang diperoleh pada Langkah 2 disesuaikan lagi, sehingga diperoleh hasil clustering
sebagai berikut:
{1631, 1749}, {1689, 1925}, {1939, 1955}, {1989, 2225}, {2470, 2546}, {2642, 2805}, {2868, 2887}, {2925}, {3010}, {3092, 3328}, {3404, 3494}, {3636, 3754}. [Langkah 4]: Dengan menggunakan sub-langkah pada Langkah 4, diperoleh interval-interval sebagai berikut:
u1 = [1631, 1749)
u2 = [1749, 1925)
u7 = [2225, 2470)
u8 = [2470, 2546)
u13 = [3010, 3092)
11 dibagi ke dalam 2 sub-interval. Hasilnya sebagai berikut:
u1 = [1631, 1690) u13 = [2255, 2347) u25 = [3010, 3051)
Metode Automatic Clustering dan Fuzzy Logical Relationships
Pada bagian ini akan diterapkan metode automatic clustering dan fuzzy logical relationships untuk perkiraan jumlah mahasiswa baru Institut Pertanian Bogor.
Himpunan semesta
Berdasarkan data historis jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 sampai tahun 2011 diketahui data terkecil adalah 1631 (data tahun 1992) sedangkan data terbesar adalah 3754 (data tahun 2010) maka dapat ditentukan himpunan semesta U = [1631, 3754]. Setelah diterapkan algoritme automatic clustering dengan memilih p = 11, diperoleh interval-interval sebagai berikut:
12
u12 = [1748.74, 1764.74) u78 = [2470, 2476.91) u144 = [3092.26, 3113.67)
u13 = [1764.74, 1780.74) u79 = [2476.91, 2483.82) u145 = [3113.67, 3135.08)
u14 = [1780.74, 1796.74) u80 = [2483.82, 2490.73) u146 = [3135.08, 3156.48)
u15 = [1796.74, 1812.74) u81 = [2490.73, 2497.64) u147 = [3156.48, 3177.89)
u16 = [1812.74, 1828.74) u82 = [2497.64, 2504.55) u148 = [3177.89, 3199.3)
u17 = [1828.74, 1844.74) u83 = [2504.55, 2511.45) u149 = [3199.3, 3220.7)
u18 = [1844.74, 1860.74) u84 = [2511.45, 2518.36) u150 = [3220.7, 3242.11)
u19 = [1860.74, 1876.74) u85 = [2518.36, 2525.27) u151 = [3242.11, 3263.52)
u20 = [1876.74, 1892.74) u86 = [2525.27, 2532.18) u152 = [3263.52, 3284.92)
u21 = [1892.74, 1908.74) u87 = [2532.18, 2539.09) u153 = [3284.92, 3306.33)
u22 = [1908.74, 1924.74) u88 = [2539.09, 2546) u154 = [3306.33, 3327.74)
u23 = [1924.74, 1926.03) u89 = [2546, 2554.73) u155 = [3327.74, 3334.67)
u24 = [1926.03, 1927.33) u90 = [2554.73, 2563.45) u156 = [3334.67, 3341.6)
u25 = [1927.33, 1928.63) u91 = [2563.45, 2572.18) u157 = [3341.6, 3348.54)
u26 = [1928.63, 1929.92) u92 = [2572.18, 2580.91) u158 = [3348.54, 3355.47)
u27 = [1929.92, 1931.22) u93 = [2580.91, 2589.64) u159 = [3355.47, 3362.4)
u28 = [1931.22, 1932.52) u94 = [2589.64, 2598.36) u160 = [3362.4, 3369.33)
u29 = [1932.52, 1933.81) u95 = [2598.36, 2607.09) u161 = [3369.33, 3376.27)
u30 = [1933.81, 1935.11) u96 = [2607.09, 2615.82) u162 = [3376.27, 3383.2)
u31 = [1935.11, 1936.41) u97 = [2615.82, 2624.55) u163 = [3383.2, 3390.13)
u32 = [1936.41, 1937.7) u98 = [2624.55, 2633.27) u164 = [3390.13, 3397.07)
u33 = [1937.7, 1939) u99 = [2633.27, 2642) u165 = [3397.07, 3404)
u34 = [1939, 1940.45) u100 = [2642, 2656.82) u166 = [3404, 3412.18)
u35 = [1940.45, 1941.91) u101 = [2656.82, 2671.64) u167 = [3412.18, 3420.36)
u36 = [1941.91, 1943.36) u102 = [2671.64, 2686.45) u168 = [3420.36, 3428.55)
u37 = [1943.36, 1944.82) u103 = [2686.45, 2701.27) u169 = [3428.55, 3436.73)
u38 = [1944.82, 1946.27) u104 = [2701.27, 2716.09) u170 = [3436.73, 3444.91)
u39 = [1946.27, 1947.73) u105 = [2716.09, 2730.91) u171 = [3444.91, 3453.09)
u40 = [1947.73, 1949.18) u106 = [2730.91, 2745.73) u172 = [3453.09, 3461.27)
u41 = [1949.18, 1950.64) u107 = [2745.73, 2760.55) u173 = [3461.27, 3469.45)
u42 = [1950.64, 1952.09) u108 = [2760.55, 2775.36) u174 = [3469.45, 3477.64)
u43 = [1952.09, 1953.55) u109 = [2775.36, 2790.18) u175 = [3477.64, 3485.82)
u44 = [1953.55, 1955) u110 = [2790.18, 2805) u176 = [3485.82, 3494)
u45 = [1955, 1958.11) u111 = [2805, 2810.73) u177 = [3494, 3506.91)
u46 = [1958.11, 1961.23) u112 = [2810.73, 2816.45) u178 = [3506.91, 3519.83)
u47 = [1961.23, 1964.34) u113 = [2816.45, 2822.18) u179 = [3519.83, 3532.74)
u48 = [1964.34, 1967.46) u114 = [2822.18, 2827.91) u180 = [3532.74, 3545.66)
u49 = [1967.46, 1970.57) u115 = [2827.91, 2833.64) u181 = [3545.66, 3558.57)
u50 = [1970.57, 1973.69) u116 = [2833.64, 2839.36) u182 = [3558.57, 3571.48)
u51 = [1973.69, 1976.8) u117 = [2839.36, 2845.09) u183 = [3571.48, 3584.4)
u52 = [1976.8, 1979.92) u118 = [2845.09, 2850.82) u184 = [3584.4, 3597.31)
13
u54 = [1983.03, 1986.15) u120 = [2856.55, 2862.27) u186 = [3610.23, 3623.14)
u55 = [1986.15, 1989.26) u121 = [2862.27, 2868) u187 = [3623.14, 3636.06)
u56 = [1989.26, 2010.67) u122 = [2868, 2880.91) u188 = [3636.06, 3646.78)
u57 = [2010.67, 2032.08) u123 = [2880.91, 2893.82) u189 = [3646.78, 3657.5)
u58 = [2032.08, 2053.48) u124 = [2893.82, 2906.73) u190 = [3657.5, 3668.22)
u59 = [2053.48, 2074.89) u125 = [2906.73, 2919.64) u191 = [3668.22, 3678.94)
u60 = [2074.89, 2096.3) u126 = [2919.64, 2932.55) u192 = [3678.94, 3689.67)
u61 = [2096.3, 2117.7) u127 = [2932.55, 2945.45) u193 = [3689.67, 3700.39)
u62 = [2117.7, 2139.11) u128 = [2945.45, 2958.36) u194 = [3700.39, 3711.11)
u63 = [2139.11, 2160.52) u129 = [2958.36, 2971.27) u195 = [3711.11, 3721.83)
u64 = [2160.52, 2181.92) u130 = [2971.27, 2984.18) u196 = [3721.83, 3732.56)
u65 = [2181.92, 2203.33) u131 = [2984.18, 2997.09) u197 = [3732.56, 3743.28)
u66 = [2203.33, 2224.74) u132 = [2997.09, 3010) u198 = [3743.28, 3754]
Setelah dihitung nilai tengah mi untuk setiap interval ui dengan � , diperoleh hasil sebagai berikut:
m1 = 1636.35 m67 = 2235.89 m133 = 3013.74
m2 = 1647.06 m68 = 2258.18 m134 = 3021.22
m3 = 1657.76 m69 = 2280.48 m135 = 3028.7
m4 = 1668.46 m70 = 2302.78 m136 = 3036.17
m5 = 1679.17 m71 = 2325.07 m137 = 3043.65
m6 = 1689.87 m72 = 2347.37 m138 = 3051.13
m7 = 1700.57 m73 = 2369.67 m139 = 3058.61
m8 = 1711.28 m74 = 2391.96 m140 = 3066.09
m9 = 1721.98 m75 = 2414.26 m141 = 3073.57
m10 = 1732.68 m76 = 2436.56 m142 = 3081.05
m11 = 1743.39 m77 = 2458.85 m143 = 3088.52
m12 = 1756.74 m78 = 2473.45 m144 = 3102.97
m13 = 1772.74 m79 = 2480.36 m145 = 3124.37
m14 = 1788.74 m80 = 2487.27 m146 = 3145.78
m15 = 1804.74 m81 = 2494.18 m147 = 3167.19
m16 = 1820.74 m82 = 2501.09 m148 = 3188.59
m17 = 1836.74 m83 = 2508 m149 = 3210
m18 = 1852.74 m84 = 2514.91 m150 = 3231.41
m19 = 1868.74 m85 = 2521.82 m151 = 3252.81
m20 = 1884.74 m86 = 2528.73 m152 = 3274.22
m21 = 1900.74 m87 = 2535.64 m153 = 3295.63
m22 = 1916.74 m88 = 2542.55 m154 = 3317.03
m23 = 1925.39 m89 = 2550.36 m155 = 3331.2
m24 = 1926.68 m90 = 2559.09 m156 = 3338.14
m25 = 1927.98 m91 = 2567.82 m157 = 3345.07
m26 = 1929.28 m92 = 2576.55 m158 = 3352
14
m28 = 1931.87 m94 = 2594 m160 = 3365.87
m29 = 1933.17 m95 = 2602.73 m161 = 3372.8
m30 = 1934.46 m96 = 2611.45 m162 = 3379.73
m31 = 1935.76 m97 = 2620.18 m163 = 3386.67
m32 = 1937.06 m98 = 2628.91 m164 = 3393.6
m33 = 1938.35 m99 = 2637.64 m165 = 3400.53
m34 = 1939.73 m100 = 2649.41 m166 = 3408.09
m35 = 1941.18 m101 = 2664.23 m167 = 3416.27
m36 = 1942.64 m102 = 2679.05 m168 = 3424.45
m37 = 1944.09 m103 = 2693.86 m169 = 3432.64
m38 = 1945.55 m104 = 2708.68 m170 = 3440.82
m39 = 1947 m105 = 2723.5 m171 = 3449
m40 = 1948.45 m106 = 2738.32 m172 = 3457.18
m41 = 1949.91 m107 = 2753.14 m173 = 3465.36
m42 = 1951.36 m108 = 2767.95 m174 = 3473.55
m43 = 1952.82 m109 = 2782.77 m175 = 3481.73
m44 = 1954.27 m110 = 2797.59 m176 = 3489.91
m45 = 1956.56 m111 = 2807.86 m177 = 3500.46
m46 = 1959.67 m112 = 2813.59 m178 = 3513.37
m47 = 1962.79 m113 = 2819.32 m179 = 3526.29
m48 = 1965.9 m114 = 2825.05 m180 = 3539.2
m49 = 1969.02 m115 = 2830.77 m181 = 3552.11
m50 = 1972.13 m116 = 2836.5 m182 = 3565.03
m51 = 1975.25 m117 = 2842.23 m183 = 3577.94
m52 = 1978.36 m118 = 2847.95 m184 = 3590.86
m53 = 1981.48 m119 = 2853.68 m185 = 3603.77
m54 = 1984.59 m120 = 2859.41 m186 = 3616.68
m55 = 1987.71 m121 = 2865.14 m187 = 3629.6
m56 = 1999.97 m122 = 2874.45 m188 = 3641.42
m57 = 2021.37 m123 = 2887.36 m189 = 3652.14
m58 = 2042.78 m124 = 2900.27 m190 = 3662.86
m59 = 2064.19 m125 = 2913.18 m191 = 3673.58
m60 = 2085.59 m126 = 2926.09 m192 = 3684.31
m61 = 2107 m127 = 2939 m193 = 3695.03
m62 = 2128.41 m128 = 2951.91 m194 = 3705.75
m63 = 2149.81 m129 = 2964.82 m195 = 3716.47
m64 = 2171.22 m130 = 2977.73 m196 = 3727.19
m65 = 2192.63 m131 = 2990.64 m197 = 3737.92
15 Proses fuzzifikasi
Didefinisikan himpunan fuzzyA1, A2, . . . , dan A198 sebagai berikut:
A1 = ⁄ + . ⁄ + ⁄ + ⁄ + ⋅ ⋅ ⋅ +
�−
⁄ + ⁄ ,
A2 = . ⁄ + ⁄ + . ⁄ + ⁄ + ⋅ ⋅ ⋅ +
�−
⁄ + ⁄ ,
A198 = ⁄ + ⁄ + ⁄ + ⁄ + ⋅ ⋅ ⋅ + .
�−
⁄ + ⁄ .
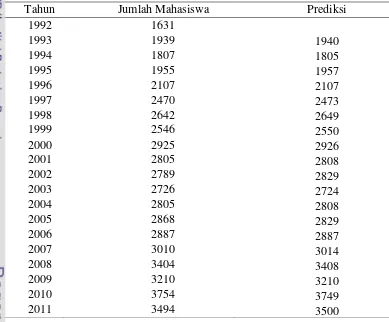
Berdasarkan definisi himpunan fuzzy tersebut jumlah mahasiswa baru Institut Pertanian Bogor dapat difuzzifikasi seperti dalam Tabel 2. Sebagai contoh, dari Tabel 1, jumlah mahasiswa baru IPB pada tahun 1992 adalah 1631 yang teletak di dalam interval u1 = [1631, 1641.7), maka jumlah mahasiswa IPB pada tahun 1992 yaitu 1631 difuzzifikasi ke dalam A1.
Tabel 2 Data fuzzifikasi jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 – 2011
Fuzzy Logical Relationships
Berdasarkan Tabel 2, fuzzy logical relationships dapat dibuat. Sebagai contoh, karena hasil fuzzifikasi jumlah mahasiswa pada tahun 1994 adalah A15 dan hasil fuzzifikasi jumlah mahasiswa pada tahun 1993 adalah A34, fuzzy logical relationship
Tahun Jumlah Mahasiswa Fuzzifikasi
1992 1631 A1
1993 1939 A34
1994 1807 A15
1995 1955 A45
1996 2107 A61
1997 2470 A78
1998 2642 A100
1999 2546 A89
2000 2925 A126
2001 2805 A111
2002 2789 A109
2003 2726 A105
2004 2805 A111
2005 2868 A122
2006 2887 A123
2007 3010 A133
2008 3404 A166
2009 3210 A149
2010 3754 A198
16
antara tahun 1993 dan 1994 dapat dibuat “A34 →A15”, dengan“A34” dan “A15” secara
berturut-turut disebut current state dan next state dari fuzzy logical relationship.
Tabel 3 Fuzzy logical relationships jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 - 2011
A1→A34 A34→A15 A15→A45 A45→A61 A61→A78
A78→A100 A100→A89 A89→A126 A126→A111 A111→A109
A109→A105 A105→A111 A111→A122 A122→A123 A123→A133
A133→A166 A166→A149 A149→A198 A198→A177 A177→#
Berdasarkan current state pada fuzzy logical relationships yang ditunjukkan dalam Tabel 3, dapat diperoleh fuzzy logical relationship groups, seperti ditunjukkan dalam Tabel 4.
Tabel 4 Fuzzy logical relationship groups jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 – 2011
Group 1: A1→A34
Group 2: A15→A45
Group 3: A34→A15
Group 4: A45→A61
Group 5: A61→A78
Group 6: A78→A100
Group 7: A89→A126
Group 8: A100→A89
Group 9: A105→A111
Group 10: A109→A105
Group 11: A111→A109 (1), A122 (1)
Group 12: A122→A123
Group 13: A123→A133
Group 14: A126→A111
Group 15: A133→A166
Group 16: A149→A198
Group 17: A166→A149
Group 18: A177→#
Group 19: A198→A177
Fuzzy logical relationship group“A111→A109 (1), A122 (1)” (Group 11) menunjukkan ada fuzzy logical relationships:
A111→A109,
A111→A122.
Proses defuzzifikasi
17 tengah dari interval u34 adalah 1939.73, maka hasil prediksi mahasiswa pada tahun 1993 sama dengan 1940.
Diasumsikan akan dilakukan prediksi mahasiswa pada tahun 2002, maka berdasarkan Tabel 2, dapat dilihat hasil fuzzifikasi jumlah mahasiswa pada tahun 2001 adalah A111. Dari Tabel 4, dapat dilihat ada fuzzy logical relationship
“A111→A109 (1), A122 (1)” pada Group 11. Berdasarkan persamaan (4), prediksi jumlah mahasiswa pada tahun 2002 dapat dihitung sebagai berikut:
. × + . ×
+ = . ≈
dengan . , . secara berturut-turut merupakan titik tengah dari interval u109 dan u122.
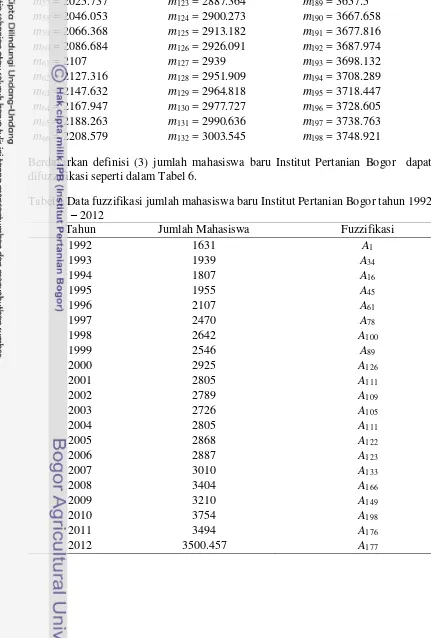
Dengan cara yang sama akan diperoleh hasil perediksi jumlah mahasiswa baru Institut Pertanian Bogor pada tahun yang lain seperti ditunjukkan pada Tabel 5. Perhitungan tahun lainnya dapat dilihat pada Lampiran 1.
Tabel 5 Hasil prediksi jumlah mahasiswa baru Institutut Pertanian Bogor tahun 1992 – 2011
Berdasasrkan Metode automatic clustering dan fuzzy logical relationships
akan diprediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2012 sampai tahun 2015.
Prediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2012
Berdasarkan Tabel 2, dapat dilihat hasil fuzzifikasi jumlah mahasiswa pada tahun 2011 adalah A177. Dari Tabel 4, dapat dilihat ada fuzzy logical relationship
Tahun Jumlah Mahasiswa Prediksi
1992 1631
1993 1939 1940
1994 1807 1805
1995 1955 1957
1996 2107 2107
1997 2470 2473
1998 2642 2649
1999 2546 2550
2000 2925 2926
2001 2805 2808
2002 2789 2829
2003 2726 2724
2004 2805 2808
2005 2868 2829
2006 2887 2887
2007 3010 3014
2008 3404 3408
2009 3210 3210
2010 3754 3749
18
“A177→#” pada Group 18. Oleh karena itu hasil prediksi jumlah mahasiswa pada
tahun 2012 merupakan nilai tengah dari interval u177. Karena u177 = [3494, 3506.91) dan nilai tengah dari interval u177 adalah 3500.46, maka hasil prediksi mahasiswa pada tahun 2012 sama dengan 3500.
Prediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2013
Jumlah mahasiswa tahun 2012 hasil prediksi dimasukkan ke dalam data historis terlebih dahulu, selanjutnya diterapkan algoritme automatic clustering. [Langkah 1]: hasil dari pengurutan data historis tahun 1992 sampai tahun 2012 dalam urutan menaik sebagai berikut:
1631, 1807, 1939, 1955, 2107, 2470, 2546, 2642, 2726, 2789, 2805, 2805, 2868, 2887, 2925, 3010, 3210, 3404, 3494, 3500.457, 3754.
Data yang nilainya sama cukup dituliskan satu kali, hasilnya sebagai berikut:
1631, 1807, 1939, 1955, 2107, 2470, 2546, 2642, 2726, 2789, 2805, 2868,2887, 2925, 3010, 3210, 3404, 3494, 3500.457, 3754.
Berdasarkan persamaan (1) dapat dihitung nilai average_diffsebagai berikut:
average_diff = [(1807 – 1631) + (1939 – 1807) + (1939 – 1807) + (1955 – 1939) + (2107 – 1955) + (2470 – 2107) + (2546 – 2470) + (2642 – 2546) + (2726 – 2642) + (2789 – 2726) + (2805 – 2789) + (2868 – 2805) + (2887 – 2868) + (2925 – 2887) + (3010 – 2925) + (3210 – 3010) + (3494 – 3404) + (3500.457 – 3494) + (3754 – 3500.457)]/1
= 2123/19 = 111.737
[Langkah 2]: Berdasakan nilai average_diff dan tiga prinsip pada Langkah 2, dapat dibuat cluster dari data urutan menaik sehingga diperoleh hasil clustering sebagai berikut:
{1631}, {1807}, {1939, 1955}, {2107}, {2470, 2546}, {2642, 2726, 2789, 2805}, {2868, 2887}, {2925}, {3010}, {3210}, {3404, 3494, 3500.457}, {3754}.
[Langkah 3]: Berdasarkan tiga prinsip pada Langkah 3, hasil clustering yang diperoleh pada Langkah 2 disesuaikan lagi, sehingga diperoleh hasil clustering
sebagai berikut:
{1631, 1749}, {1689, 1925}, {1939, 1955}, {1989, 2225}, {2470, 2546}, {2642, 2805}, {2868, 2887}, {2925}, {3010}, {3092, 3328}, {3404, 3500.457}, {3642.263, 3754}.
[Langkah 4]: Dengan menggunakan sub-langkah pada Langkah 4, diperoleh interval-interval sebagai berikut:
u1 = [1631, 1742.737) u7 = [2218.737, 2470) u13 = [3010, 3098.263)
19
u3 = [1918.737, 1939) u9 = [2546, 2642) u15 = [3321.737, 3404)
u4 = [1939, 1955) u10 = [2642, 2805) u16 = [3404, 3500.457)
u5 = [1955, 1995.263) u11 = [2805, 2868) u17 = [3500.457, 3642.263)
u6 = [1995.263, 2218.737) u12 = [2868, 3010) u18 = [3642.263, 3754]
Berdasarkan data historis jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 sampai tahun 2011 diketahui data terkecil adalah 1631 (data tahun 1992) sedangkan data terbesar adalah 3754 (data tahun 2010) maka dapat ditentukan himpunan semesta U = [1631, 3754]. Setelah diterapkan algoritme automatic clustering dengan memilih p = 11, diperoleh interval-interval sebagai berikut:
u1 = [1631, 1641.158) u67 = [2218.737, 2241.579) u133 = [3010, 3018.024)
u2 = [1641.158, 1651.316) u68 = [2241.579, 2264.421) u134 = [3018.024, 3026.048)
u3 = [1651.316, 1661.474) u69 = [2264.421, 2287.263) u135 = [3026.048, 3034.072)
u4 = [1661.474, 1671.632) u70 = [2287.263, 2310.105) u136 = [3034.072, 3042.096)
u5 = [1671.632, 1681.789) u71 = [2310.105, 2332.947) u137 = [3042.096, 3050.12)
u6 = [1681.789, 1691.947) u72 = [2332.947, 2355.789) u138 = [3050.12, 3058.144)
u7 = [1691.947, 1702.105) u73 = [2355.789, 2378.632) u139 = [3058.144, 3066.167)
u8 = [1702.105, 1712.263) u74 = [2378.632, 2401.474) u140 = [3066.167, 3074.191)
u9 = [1712.263, 1722.421) u75 = [2401.474, 2424.316) u141 = [3074.191, 3082.215)
u10 = [1722.421, 1732.579) u76 = [2424.316, 2447.158) u142 = [3082.215, 3090.239)
u11 = [1732.579, 1742.737) u77 = [2447.158, 2470) u143 = [3090.239, 3098.263)
u12 = [1742.737, 1758.737) u78 = [2470, 2476.909) u144 = [3098.263, 3118.579)
u13 = [1758.737, 1774.737) u79 = [2476.909, 2483.818) u145 = [3118.579, 3138.895)
u14 = [1774.737, 1790.737) u80 = [2483.818, 2490.727) u146 = [3138.895, 3159.211)
u15 = [1790.737, 1806.737) u81 = [2490.727, 2497.636) u147 = [3159.211, 3179.526)
u16 = [1806.737, 1822.737) u82 = [2497.636, 2504.545) u148 = [3179.526, 3199.842)
u17 = [1822.737, 1838.737) u83 = [2504.545, 2511.455) u149 = [3199.842, 3220.158)
u18 = [1838.737, 1854.737) u84 = [2511.455, 2518.364) u150 = [3220.158, 3240.474)
u19 = [1854.737, 1870.737) u85 = [2518.364, 2525.273) u151 = [3240.474, 3260.789)
u20 = [1870.737, 1886.737) u86 = [2525.273, 2532.182) u152 = [3260.789, 3281.105)
u21 = [1886.737, 1902.737) u87 = [2532.182, 2539.091) u153 = [3281.105, 3301.421)
u22 = [1902.737, 1918.737) u88 = [2539.091, 2546) u154 = [3301.421, 3321.737)
u23 = [1918.737, 1920.579) u89 = [2546, 2554.727) u155 = [3321.737, 3329.215)
u24 = [1920.579, 1922.421) u90 = [2554.727, 2563.455) u156 = [3329.215, 3336.694)
u25 = [1922.421, 1924.263) u91 = [2563.455, 2572.182) u157 = [3336.694, 3344.172)
u26 = [1924.263, 1926.105) u92 = [2572.182, 2580.909) u158 = [3344.172, 3351.651)
u27 = [1926.105, 1927.947) u93 = [2580.909, 2589.636) u159 = [3351.651, 3359.129)
u28 = [1927.947, 1929.789) u94 = [2589.636, 2598.364) u160 = [3359.129, 3366.608)
u29 = [1929.789, 1931.632) u95 = [2598.364, 2607.091) u161 = [3366.608, 3374.086)
u30 = [1931.632, 1933.474) u96 = [2607.091, 2615.818) u162 = [3374.086, 3381.565)
u31 = [1933.474, 1935.316) u97 = [2615.818, 2624.545) u163 = [3381.565, 3389.043)
u32 = [1935.316, 1937.158) u98 = [2624.545, 2633.273) u164 = [3389.043, 3396.522)
u33 = [1937.158, 1939) u99 = [2633.273, 2642) u165 = [3396.522, 3404)
20
u35 = [1940.455, 1941.909) u101 = [2656.818, 2671.636) u167 = [3412.769, 3421.538)
u36 = [1941.909, 1943.364) u102 = [2671.636, 2686.455) u168 = [3421.538, 3430.306)
u37 = [1943.364, 1944.818) u103 = [2686.455, 2701.273) u169 = [3430.306, 3439.075)
u38 = [1944.818, 1946.273) u104 = [2701.273, 2716.091) u170 = [3439.075, 3447.844)
u39 = [1946.273, 1947.727) u105 = [2716.091, 2730.909) u171 = [3447.844, 3456.613)
u40 = [1947.727, 1949.182) u106 = [2730.909, 2745.727) u172 = [3456.613, 3465.382)
u41 = [1949.182, 1950.636) u107 = [2745.727, 2760.545) u173 = [3465.382, 3474.151)
u42 = [1950.636, 1952.091) u108 = [2760.545, 2775.364) u174 = [3474.151, 3482.919)
u43 = [1952.091, 1953.545) u109 = [2775.364, 2790.182) u175 = [3482.919, 3491.688)
u44 = [1953.545, 1955) u110 = [2790.182, 2805) u176 = [3491.688, 3500.457)
u45 = [1955, 1958.66) u111 = [2805, 2810.727) u177 = [3500.457, 3513.349)
u46 = [1958.66, 1962.321) u112 = [2810.727, 2816.455) u178 = [3513.349, 3526.24)
u47 = [1962.321, 1965.981) u113 = [2816.455, 2822.182) u179 = [3526.24, 3539.131)
u48 = [1965.981, 1969.641) u114 = [2822.182, 2827.909) u180 = [3539.131, 3552.023)
u49 = [1969.641, 1973.301) u115 = [2827.909, 2833.636) u181 = [3552.023, 3564.914)
u50 = [1973.301, 1976.962) u116 = [2833.636, 2839.364) u182 = [3564.914, 3577.806)
u51 = [1976.962, 1980.622) u117 = [2839.364, 2845.091) u183 = [3577.806, 3590.697)
u52 = [1980.622, 1984.282) u118 = [2845.091, 2850.818) u184 = [3590.697, 3603.589)
u53 = [1984.282, 1987.943) u119 = [2850.818, 2856.545) u185 = [3603.589, 3616.48)
u54 = [1987.943, 1991.603) u120 = [2856.545, 2862.273) u186 = [3616.48, 3629.372)
u55 = [1991.603, 1995.263) u121 = [2862.273, 2868) u187 = [3629.372, 3642.263)
u56 = [1995.263, 2015.579) u122 = [2868, 2880.909) u188 = [3642.263, 3652.421)
u57 = [2015.579, 2035.895) u123 = [2880.909, 2893.818) u189 = [3652.421, 3662.579)
u58 = [2035.895, 2056.211) u124 = [2893.818, 2906.727) u190 = [3662.579, 3672.737)
u59 = [2056.211, 2076.526) u125 = [2906.727, 2919.636) u191 = [3672.737, 3682.895)
u60 = [2076.526, 2096.842) u126 = [2919.636, 2932.545) u192 = [3682.895, 3693.053)
u61 = [2096.842, 2117.158) u127 = [2932.545, 2945.455) u193 = [3693.053, 3703.211)
u62 = [2117.158, 2137.474) u128 = [2945.455, 2958.364) u194 = [3703.211, 3713.368)
u63 = [2137.474, 2157.789) u129 = [2958.364, 2971.273) u195 = [3713.368, 3723.526)
u64 = [2157.789, 2178.105) u130 = [2971.273, 2984.182) u196 = [3723.526, 3733.684)
u65 = [2178.105, 2198.421) u131 = [2984.182, 2997.091) u197 = [3733.684, 3743.842)
u66 = [2198.421, 2218.737) u132 = [2997.091, 3010) u198 = [3743.842, 3754)
Setelah dihitung nilai tengah mi untuk setiap interval ui dengan � , diperoleh hasil sebagai berikut:
m1 = 1636.079 m67 = 2230.158 m133 = 3014.012
m2 = 1646.237 m68 = 2253 m134 = 3022.036
m3 = 1656.395 m69 = 2275.842 m135 = 3030.06
m4 = 1666.553 m70 = 2298.684 m136 = 3038.084
m5 = 1676.711 m71 = 2321.526 m137 = 3046.108
m6 = 1686.868 m72 = 2344.368 m138 = 3054.132
m7 = 1697.026 m73 = 2367.211 m139 = 3062.156
m8 = 1707.184 m74 = 2390.053 m140 = 3070.179
21
m10 = 1727.5 m76 = 2435.737 m142 = 3086.227
m11 = 1737.658 m77 = 2458.579 m143 = 3094.251
m12 = 1750.737 m78 = 2473.455 m144 = 3108.421
m13 = 1766.737 m79 = 2480.364 m145 = 3128.737
m14 = 1782.737 m80 = 2487.273 m146 = 3149.053
m15 = 1798.737 m81 = 2494.182 m147 = 3169.368
m16 = 1814.737 m82 = 2501.091 m148 = 3189.684
m17 = 1830.737 m83 = 2508 m149 = 3210
m18 = 1846.737 m84 = 2514.909 m150 = 3230.316
m19 = 1862.737 m85 = 2521.818 m151 = 3250.632
m20 = 1878.737 m86 = 2528.727 m152 = 3270.947
m21 = 1894.737 m87 = 2535.636 m153 = 3291.263
m22 = 1910.737 m88 = 2542.545 m154 = 3311.579
m23 = 1919.658 m89 = 2550.364 m155 = 3325.476
m24 = 1921.5 m90 = 2559.091 m156 = 3332.955
m25 = 1923.342 m91 = 2567.818 m157 = 3340.433
m26 = 1925.184 m92 = 2576.545 m158 = 3347.911
m27 = 1927.026 m93 = 2585.273 m159 = 3355.39
m28 = 1928.868 m94 = 2594 m160 = 3362.868
m29 = 1930.711 m95 = 2602.727 m161 = 3370.347
m30 = 1932.553 m96 = 2611.455 m162 = 3377.825
m31 = 1934.395 m97 = 2620.182 m163 = 3385.304
m32 = 1936.237 m98 = 2628.909 m164 = 3392.782
m33 = 1938.079 m99 = 2637.636 m165 = 3400.261
m34 = 1939.727 m100 = 2649.409 m166 = 3408.384
m35 = 1941.182 m101 = 2664.227 m167 = 3417.153
m36 = 1942.636 m102 = 2679.045 m168 = 3425.922
m37 = 1944.091 m103 = 2693.864 m169 = 3434.691
m38 = 1945.545 m104 = 2708.682 m170 = 3443.46
m39 = 1947 m105 = 2723.5 m171 = 3452.229
m40 = 1948.455 m106 = 2738.318 m172 = 3460.997
m41 = 1949.909 m107 = 2753.136 m173 = 3469.766
m42 = 1951.364 m108 = 2767.955 m174 = 3478.535
m43 = 1952.818 m109 = 2782.773 m175 = 3487.304
m44 = 1954.273 m110 = 2797.591 m176 = 3496.073
m45 = 1956.83 m111 = 2807.864 m177 = 3506.903
m46 = 1960.49 m112 = 2813.591 m178 = 3519.794
m47 = 1964.151 m113 = 2819.318 m179 = 3532.686
m48 = 1967.811 m114 = 2825.045 m180 = 3545.577
m49 = 1971.471 m115 = 2830.773 m181 = 3558.469
m50 = 1975.132 m116 = 2836.5 m182 = 3571.36
m51 = 1978.792 m117 = 2842.227 m183 = 3584.252
m52 = 1982.452 m118 = 2847.955 m184 = 3597.143
22
m54 = 1989.773 m120 = 2859.409 m186 = 3622.926
m55 = 1993.433 m121 = 2865.136 m187 = 3635.817
m56 = 2005.421 m122 = 2874.455 m188 = 3647.342
m57 = 2025.737 m123 = 2887.364 m189 = 3657.5
m58 = 2046.053 m124 = 2900.273 m190 = 3667.658
m59 = 2066.368 m125 = 2913.182 m191 = 3677.816
m60 = 2086.684 m126 = 2926.091 m192 = 3687.974
m61 = 2107 m127 = 2939 m193 = 3698.132
m62 = 2127.316 m128 = 2951.909 m194 = 3708.289
m63 = 2147.632 m129 = 2964.818 m195 = 3718.447
m64 = 2167.947 m130 = 2977.727 m196 = 3728.605
m65 = 2188.263 m131 = 2990.636 m197 = 3738.763
m66 = 2208.579 m132 = 3003.545 m198 = 3748.921
Berdasarkan definisi (3) jumlah mahasiswa baru Institut Pertanian Bogor dapat difuzzifikasi seperti dalam Tabel 6.
Tabel 6 Data fuzzifikasi jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992
– 2012
Tahun Jumlah Mahasiswa Fuzzifikasi
1992 1631 A1
1993 1939 A34
1994 1807 A16
1995 1955 A45
1996 2107 A61
1997 2470 A78
1998 2642 A100
1999 2546 A89
2000 2925 A126
2001 2805 A111
2002 2789 A109
2003 2726 A105
2004 2805 A111
2005 2868 A122
2006 2887 A123
2007 3010 A133
2008 3404 A166
2009 3210 A149
2010 3754 A198
2011 3494 A176
23 Berdasarkan Tabel 6, fuzzy logical relationships dapat dibuat.
Tabel 7 Fuzzy logical relationships jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 – 2012
A1→A34 A34→A16 A16→A45 A45→A61 A61→A78
A78→A100 A100→A89 A89→A126 A126→A111 A111→A109
A109→A105 A105→A111 A111→A122 A122→A123 A123→A133
A133→A166 A166→A149 A149→A198 A198→A176 A176→ A177
A177→#
Berdasarkan current state pada fuzzy logical relationships yang ditunjukkan dalam Tabel 7, dapat diperoleh fuzzy logical relationship groups, seperti ditunjukkan dalam Tabel 8.
Tabel 8 Fuzzy logical relationship groups jumlah mahasiswa baru Institut Pertanian Bogor tahun 1992 – 2012
Group 1: A1→A34
Group 2: A16→A45
Group 3: A34→A15
Group 4: A45→A61
Group 5: A61→A78
Group 6: A78→A100
Group 7: A89→A126
Group 8: A100→A89
Group 9: A105→A111
Group 10: A109→A105
Group 11: A111→A109 (1), A122 (1)
Group 12: A122→A123
Group 13: A123→A133
Group 14: A126→A111
Group 15: A133→A166
Group 16: A149→A198
Group 17: A166→A149
Group 18: A176→ A177
Group 19: A177→#
Group 20: A198→ A176
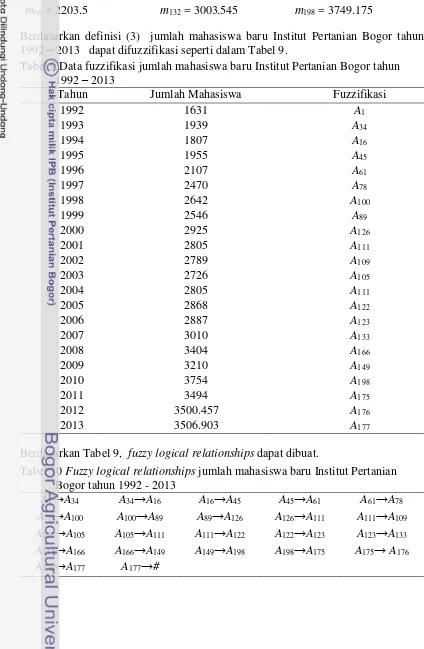
Berdasarkan Tabel 6, dapat dilihat hasil fuzzifikasi jumlah mahasiswa pada tahun 2012 adalah A177. Dari Tabel 8, dapat dilihat ada fuzzy logical relationship“A177→#” pada Group 19. Oleh karena itu hasil prediksi jumlah mahasiswa pada tahun 2013 merupakan nilai tengah dari interval u177. Karena u177 = [3500.457, 3513.349) dan nilai tengah dari interval u177 adalah 3506.903, maka hasil prediksi mahasiswa pada tahun 2013 sama dengan 3507.
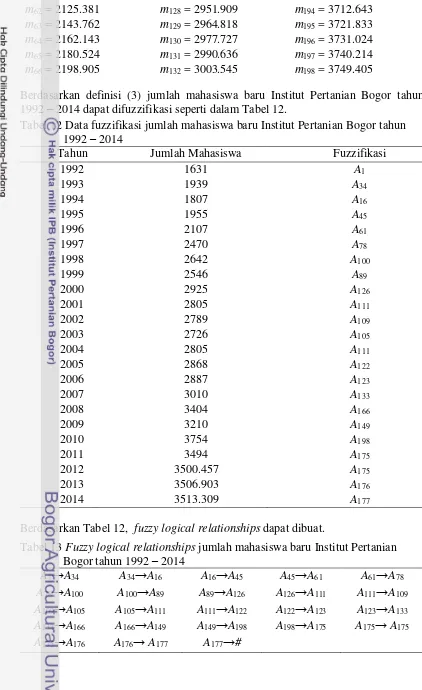
Prediksi jumlah mahasiswa baru Institut Pertanian Bogor tahun 2014