METODE AUTOMATIC CLUSTERING-RELASI LOGIKA FUZZY DAN METODE FUZZY TIME SERIES DALAM MERAMAL JUMLAH
PEMINAT DEPARTEMEN S1 MATEMATIKA USU TAHUN 2014 MELALUI JALUR TERTULIS
SKRIPSI
WINDA ASTARY
100803005
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
METODE AUTOMATIC CLUSTERING-RELASI LOGIKA FUZZY DAN METODE FUZZY TIME SERIES DALAM MERAMAL JUMLAH
PEMINAT DEPARTEMEN S1 MATEMATIKA USU TAHUN 2014 MELALUI JALUR TERTULIS
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat untuk mencapai gelar sarjana
sains
WINDA ASTARY 100803005
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Metode Automatic Clustering-Relasi Logka Fuzzy dan
Metode Fuzzy Time Series Dalam Meramal Jumlah Peminat Departemen S1 Matematika USU Tahun 2014 Melalui Jalur
Tertulis
Kategori : Skripsi
Nama : Winda Astary
Nomor Induk Mahasiswa : 100803005
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam (FMIPA)
Universitas Sumatera Utara
Diluluskan di
Medan, Mei 2014
Komisi pembimbing :
Pembimbing 2, Pembimbing 1,
Drs. Partano Siagian, M.Sc. Dr. Suwarno Ariswoyo, M.Si. NIP. 19511227 198003 1 001 NIP. 19500321 198003 1 001
Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
METODE AUTOMATIC CLUSTERING-RELASI LOGIKA FUZZY DAN METODE FUZZY TIME SERIES DALAM MERAMAL JUMLAH PEMINAT
DEPARTEMEN S1 MATEMATIKAUSU TAHUN 2014 MELALUI JALUR TERTULIS
SKRIPSI
Saya mengaku bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing–masing disebutkan sumbernya.
Medan, Juni 2014
PENGHARGAAN
Assalamu‟alaikum Wr.Wb
Puji dan syukur penulis ucapkan kepada Allah SWT Yang Maha Esa dan Kuasa atas limpahan rahmat dan karuniaNYA sehingga skripsi ini dapat diselesaikan.
Pada skripsi ini, penulis mengambil judul Metode Automatic Clustering-Relasi Logika Fuzzy dan Metode Fuzzy Time Series Dalam Meramal Jumlah Peminat Departemen S1 Matematika USU Tahun 2014 Melalui Jalur Tertulis.
Dalam penyusunan skripsi ini banyak pihak yang membantu, sehingga dengan segala rasa hormat penulis mengucapkan terima kasih kepada:
1. Bapak Dr. Suwarno Ariswoyo, M.Si selaku dosen pembimbing 1 yang berkenan dan rela mengorbankan waktu, tenaga, dan fikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.
2. Bapak Drs. Partano Siagian, M.Sc. selaku dosen pembimbing 2 yang juga berkenan dan rela mengorbankan waktu, tenaga, dan fikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.
3. Bapak Drs.Marihat Situmorang, M.kom. dan Ibu Normalina Napitupulu, M.Sc. selaku komisi penguji atas saran yang talah diberikan demi perbaikan skripsi ini.
4. Bapak Dr. Sutarman, M.Sc selaku dekan FMIPA USU
5. Bapak Prof. Dr. Tulus, M.Si dan Ibu Dr. Mardiningsih, M.Si selaku ketua dan sekretaris Departemen Matematika FMIPA USU.
6. Ibunda tercinta Enyzar, Ayahanda tercinta Alwan dan adikku Mhd.Reza Fahnial tersayang atas segala pengertian, kesabaran, dukungan dan kasih sayang yang telah diberikan kepada penulis selama di bangku perkuliahan hingga akhirnya menyelesaikan skripsi ini.
7. Untuk orang – orang tersayang khususnya Kesebelasan, Reno Sulbakti, Lia Purwanti, Salwa, SATELIT GRADE dan ANAK JENDRAL 2010 yang telah
membantu penulis dengan memberikan semangat dan do‟a dalam menyelesaikan
8. Untuk semua senior dan junior khususnya Kak isna, Bang romi dan masih banyak lagi yang tak tersebutkan namanya yang telah membantu penulis dengan
memberikan semangat dan do‟a dalam menyelesaikan tulisan ini.
Penulis juga menyadari masih banyak kekurangan dalam skripsi ini, baik dalam teori maupun penulisannya. Oleh karena itu, penulis mengharapkan saran dari pembaca demi perbaikan bagi penulis. Semoga segala bentuk bantuan yang telah diberikan kepada penulis mendapatkan balasan yang lebih baik dari Allah SWT. Akhir kata penulis berharap semoga tulisan ini bermanfaat bagi para pembaca.
Medan, Mei 2014 Penulis,
METODE AUTOMATIC CLUSTERING-RELASI LOGIKA FUZZY DAN METODE FUZZY TIME SERIES DALAM MERAMAL JUMLAH
PEMINAT DEPARTEMEN S1 MATEMATIKA USU TAHUN 2014 MELALUI JALUR TERTULIS
ABSTRAK
Berbagai jenis model peramalan telah banyak dikembangkan untuk meningkatkan akurasi peramalan yang diukur berdasarkan nilai MSE. Pada tulisan ini diterapkan metode automatic clustering-relasi logika fuzzy untuk meramal jumlah peminat Departemen S1 Matematika USU Tahun 2014 melalui jalur tertulis. Hasil peramalan yang diperoleh, kemudian dibandingkan dengan metode fuzzy time series. Berdasarkan MSE dan rata – rata error dari masing – masing metode dapat disimpulkan bahwa metode automatic clustering-relasi logika fuzzy memiliki tingkat arurasi yang labih tinggi dibandingkan dengan metode fuzzy time series. Dari hasil peramalan dengan menggunakan metode automatic clustering-relasi logika fuzzy didapatkan peramalan jumlah peminat melalui jalur tertulis Departemen S1 Matematika USU adalah sejumlah 614 orang.
AUTOMATIC CLUSTERING METHODS-RELATION OF FUZZY LOGIC AND FUZZY TIME SERIES METHOD IN FORECASTING TOTAL
INTEREST USU DEPARTMENT OF MATHEMATICS S1 2014 THROUGHT THE WRITTEN PATH
ABSTRACT
Various types of forecasting models have been developed to improve the forecasting accuracy is measured based on the MSE. In this paper applied automatic clustering method-relation fuzzy logic to predict the number of applicants USU Department of Mathematics S1 2014 through written path. Forecasting results obtained, and then compared with the fuzzy time series method. Based on the MSE and average error of each method can be concluded that the method of automatic clustering- fuzzy logic relationship have level higher accuracy rate than the fuzzy time series method. From the results of forecasting by using automatic clustering- fuzzy logic relationship forecasting the number of applicants obtained through written USU Department of Mathematics S1 is the number of 614 people.
BAB 1 PENDAHULUAN
1.1 Latar Belakang Masalah
Peramalan merupakan hal penting dalam kehidupan sehari-hari. Orang-orang telah
terbiasa berhadapan dengan banyak aktifitas peramalan misal, peramalan cuaca,
peramalan persediaan, peramalan gempa bumi, peramalan harga saham dan sebagainya.
Seiring dengan berbagai aktifitas yang memerlukan peramalan tersebut, maka metode
peramalan banyak dikembangkan oleh para peneliti. Salah satunya adalah metode
automatic clustering-relasi logika fuzzy.
Metode automatic clustering-relasi logika fuzzy pertama kali diperkenalkan oleh Wang, Chen dan Pan (2009). Metode ini mereka gunakan untuk meramalkan jumlah
mahasiswa yang akan mendaftar di Universitas Alabama. Penelitian tersebut
memberikan hasil Mean Square Error (MSE) yang lebih rendah dibanding penelitian sebelumnya yang diterapkan pada kasus yang sama dengan metode yang berbeda.
Selain metode automatic clustering-relasi logika fuzzy, metode peramalan lain yang biasa digunakan adalah metode fuzzy time series. Namun tingkat akurasi hasil peramalan belum optimal. Metode fuzzy time series pertama kali diperkenalkan oleh Song, dkk(1993). Chen (1996) juga memaparkan tentang metode fuzzy time series
menggunakan metode aritmatika sederhana. Metode fuzzy time series ini mampu menangani data fuzzy dan tidak lengkap yang dipresentasikan sebagai nilai-nilai
linguistik dalam keadaan tertentu. Kemudian pada tahun 2006, Chen dan Chung
melakukan peramalan menggunakan metode fuzzy time series dan genetic algorithm,
sehingga diperoleh hasil bahwa dengan menaikkan nilai Dmin 10% dan menurunkan
Dmax 10% mengasilkan kromosom terbaik untuk pembentukan interval, sehingga
Dalam peramalan, hal terpenting yang akan dicapai adalah hasil peramalan
dengan nilai error yang minimum. Semakin kecil nilai error maka semakin akurat hasil peramalan yang diperoleh. Lee, dkk (2007) menyatakan bahwa hasil peramalan
menggunakan metode fuzzy time series yang sudah ada masih memberikan nilai MSE yang relatif besar sehingga metode peramalan yang sudah ada terus dikembangkan
untuk mendapatkan metode peramalan yang memiliki tingkat akurasi lebih tinggi.
Hingga pada akhirnya, Wang, Chen dan Pan (2009) memperkenalkan sebuah metode
peramalan yaitu metode automatic clustering-relasi logika fuzzy yang memiliki tingkat akurasi lebih tinggi dalam meramalkan data dibanding dengan metode yang telah ada.
Metode ini dapat digunakan untuk data yang relatif sedikit. Hanya saja metode ini tidak
memperhatikan fenomena yang terjadi pada data.
1.2 Rumusan Masalah
Bagaimana menerapkan metode automatic clustering-relasi logika fuzzy dan metode
fuzzy time series dalam meramal jumlah peminat departemen S1 Matematika USU tahun 2014 melalui jalur tertulis.
1.3 Batasan Masalah
Masalah yang diteliti dibatasi dalam perhitungan MSE. Data yang digunakan adalah
data jumlah peminat Departemen S1 Matematika USU melalui jalur tertulis mulai tahun
2006 sampai dengan tahun 2013. Dalam hal ini data hanya sebagai bahan untuk
perhitungannya dan tidak memperhatikan bagaimana pengaruh dan fenomena yang
1.4 Tinjauan Pustaka
Peramalan adalah kegiatan untuk memperkirakan apa yang akan terjadi pada masa yang
akan datang. Dalam usaha mengetahui atau melihat perkembangan di masa depan,
peramalan dibutuhkan untuk menentukan kapan suatu peristiwa akan terjadi atau suatu
kebutuhan akan timbul, sehingga dapat dipersiapkan kebijakan atau tindakan-tindakan
yang perlu dilakukan. Peramalan merupakan bagian integral dari kegiatan pengambilan
keputusan menejemen.
Metode peramalan merupakan bagian dari ilmu statistika. Salah satu metode
peramalan adalah deret waktu. Metode ini disebut sebagai metode peramalan deret
waktu karena memiliki karakteristik bahwa data yang di analisis bersifat deret waktu.
Periode deret waktu dapat berupa tahunan, mingguan, bulanan, semesteran, kuartal dan
lain-lain. Jenis pola data sangat penting untuk diketahui karena akan berpengaruh
terhadap hasilan ramalan.
Menurut Assauri (1984), metode peramalan adalah cara memperkirakan secara
kuantitatif apa yang akan terjadi pada masa depan, berdasarkan pada data yang relevan
pada masa lalu. Oleh karena metode peramalan didasarkan atas data yang relevan pada
masa lalu, maka metode peramalan ini dipergunakan dalam peramalan yang objektif.
Metode peramalan fuzzy time series adalah metode peramalan yang menggunakan prinsip-prinsip fuzzy sebagai dasarnya. Konsep dasar fuzzy time series
yang diperkenalkan oleh Song dan Chissom (1993a, 1993b, 1994) dengan nilai fuzzy time series direpresentasikan dengan himpunan fuzzy (Chen 1998) :
Didefenisikan U adalah semesta pembicaraan dengan U = { u1, u2, u3, ... , un}.
Ahmad Amiruddin Anwary (2011) dalam penelitiannya untuk meramal kurs
Rupiah terhadap terhadap Dollar Amerika menggunakan metode fuzzy time series. Dalam peramalan tersebut dilakukan upaya untuk memprediksi besarnya kurs untuk
satu hari ke depan. Permasalahan yang dihadapi adalah cara untuk memprediksi
besarnya kurs yaang menghasilkan nilai prediksi dengan tingkat kesalahan minimal.
depan. Tingkat keakuratan hasil prediksi diukur dengan nilai AFER (Average Forecasting Error).
Robert Kurniawan pada penelitiannya menggunakan metode automatic clustering-relasi logika fuzzy untuk peramalan data unvariat. Robert Kurniawan menerapkannya untuk Data Kunjungan Wisatawan Mancanegara ke Indonesia melalui
Bandara Ngurah Rai Bali (Januari 1989 – Februari 2009) dan Data Simulasi.
1.5 Tujuan Penelitian
Tujuan dari penelitian ini adalah mengetahui perbandingan metode automatic clustering-relasi logika fuzzy dan metode fuzzy time series dalam meramalkan jumlah peminat Departemen S1 Matematika USU melalui jalur tertulis mulai tahun 2006
sampai dengan tahun 2013.
1.6 Kontribusi Penelitian
1. Memberi informasi tentang jumlah peminat Departemen S1 Matematika USU
melalui jalur tertulis pada tahun 2014.
BAB 2
LANDASAN TEORI
2.1Metode Peramalan
Peramalan (forecasting) adalah kegiatan untuk memperkirakan apa yang akan terjadi di masa yang akan datang. Sedangkan ramalan adalah situasi atau kondisi yang
diperkirakan akan terjadi pada masa yang akan datang.
Metode peramalan merupakan cara untuk memperkirakan secara kuantitatif apa
yang akan terjadi pada masa yang akan datang dengan dasar data yang relevan pada
masa lalu. Dengan kata lain metode peramalan yang bersifat objektif. Oleh karena itu,
metode peramalan termasuk dalam kegiatan kuantitatif. Keberhasilan dari suatu
peramalan sangat ditentukan oleh pengetahuan teknik tentang informasi lalu yang
dibutuhkan yaitu informasi yang bersifat kuantitatif serta teknik dan metode
peramalannya.
Baik tidaknya suatu peramalan yang disusun, di samping ditentukan oleh metode yang
digunakan juga ditentukan oleh baik tidaknya informasi maupun data yang digunakan.
Selama data maupun informasi yang digunakan tidak dapat meyakinkan, maka hasil
peramalan yang disusun juga akan sukar dipercaya akan ketepatannya. Dalam
melakukan analisa ekonomi atau analisa kegiatan perusahaan, haruslah di perkirakan
apa yang terjadi dalam bidang ekonomi atau di dalam dunia usaha pada masa yang akan
datang. Kegiatan memperkirakan apa yang akan terjadi pada masa yang akan datang,
dikenal dengan sebutan peramalan.
Kualitas atau mutu dari hasil peramalan yang disusun, sangat ditentukan oleh
dilakukan dengan mengikuti langkah-langkah atau prosedur penyusunan yang baik.
Pada dasarnya ada tiga langkah peramalan yang penting yaitu :
1. Menganalisa data yang lalu.
Tahap ini berguna untuk pola yang terjadi pada masa yang lalu. Analisa ini
dilakukan dengan cara membuat tabulasi data maka dapat diketahui pola data
tersebut.
2. Menentukan metode yang digunakan.
Masing-masing metode akan memberikan hasil peramalan yang berbeda.
Dimana metode peramalan yang baik adalah metode yang menghasilkan
penyimpangan antara hasil peramalan dengan nilai kenyataan yang sekecil
mungkin.
3. Memproyeksikan data yang lalu dengan menggunakan metode yang
dipergunakan, dan mempertimbangkan adanya beberapa faktor perubahan.
Faktor-faktor perubahan tersebut antara lain terdiri dari perubahan
kebijakan-kebijakan yang mungkin terjadi, termasuk kebijakan-kebijakan pemerintah. Proyeksi
adalah adanya suatu kecendrungan sesuatu hal pada masa yang akan datang yang
masih belum diketahui dan mempunyai nilai pada masa yang akan datang yang
merupakan petunjuk tentang jumlah sesuatu hal tersebut di masa yang akan
datang.
2.1.1 Jenis – jenis Peramalan
Menurut Assauri (1984) peramalan dapat dibedakan dari beberapa segi tergantung dari
cara melihatnya, yaitu dilihat dari jangka waktu ramalan dan dilihat dari sifat ramalan.
Jika dilihat dari jangka waktu ramalan yang disusun, maka ramalan dapat dibedakan
1. Peramalan jangka panjang
Yaitu peramalan yang dilakukan untuk penyusunan hasil ramalan jangka
waktunya lebih dari satu setengah tahun atau tiga semester. Peramalan jangka
panjang digunakan untuk pengambilan keputusan mengenai perencanaan produk
dan perencanaan pasar, pengeluaran biaya perusahaan, studi kelayakan pabrik,
anggaran, purchase order, perencanaan tenaga kerja serta perencanaan kapasitas kerja.
2. Peramalan jangka pendek
Yaitu peramalan yang dilakukan untuk penyusunan hasil ramalan dalam jangka
waktu yang kurang dari satu setengah tahun atau tiga semester. Peramalan
seperti ini diperlukan dalam penyusunan rencana tahunan, rencana kerja
operasional, dan anggaran contoh penyusunan rencana produksi, rencana
penjualan, rencana persediaan, anggaran produksi, dan anggaran perusahaan.
Berdasarkan dari sifat penyusunnya, maka peramalan dapat dibedakan atas dua
macam, yaitu:
1. Peramalan yang subjektif
Yaitu peramalan yang didasarkan atas perasaan atau intuasi dari orang yang
menyusunnya. Dalam hal ini pandangan atau judgement dari orang yang
menyusunnya sangat menetukan baik tidaknya hasil ramalan tersebut.
2. Peramalan yang objektif
Yaitu peramalan yang didasarkan atas data yang relevan pada masa lalu, dengan
menggunakan teknik-teknik dan metode dalam penganalisaan data tersebut.
Berdasarkan beberapa teknik yang telah dikembangkan dalam peramalan
dibedakan atas dua yaitu:
1. Peramalan kualitatif
Yaitu peramalan yang didasarkan atas dua kualitatif pada masa lalu. Hasil
penting karena hasil peramalan tersebut ditentukan berdasarkan pemikiran yang
bersifat intuisi, judgement atau pendapat, dan pengetahuan serta pengalaman dari penyusunnya. Biasanya peramalan secara kualitatif ini didasarkan atas hasil
penyelidikan.
2. Peramalan kuantitatif
Yaitu peramalan didasarkan atas data kuantitatif pada masa lalu. Hasil
peramalan dibuat sangat bergantung pada metode yang digunakan dalam
peramalan tersebut. Dengan peramalan yang berbeda akan diperoleh hasil
peramalan yang berbeda.
Hal yang perlu diperhatikan dari penggunaan metode-metode tersebut, adalah
baik tidaknya metode yang dipergunakan, sangat ditentukan oleh perbedaan atau
penyimpangan antara hasil peramalan dengan kenyataan yang terjadi. Metode yang baik
adalah metode yang memberikan nilai-nilai perbedaan atau penyimpangan yang
mungkin terjadi.
Peramalan kuantitatif hanya dapat digunakan apabila terdapat tiga kondisi
sebagai berikut :
1. Adanya informasi tentang keadaan yang lain.
2. Informasi tersebut dapat dikuantifikasikan dalam bentuk data.
3. Dapat diasumsikan bahwa pola yang lalu akan berkelanjutan pada masa yang
akan datang.
Dalam pemilihan teknik dan metode peramalan, pertama-tama perlu diketahui ciri-ciri
penting yang perlu diperhatikan bagi pengambil keputusan dan analisa keadaan dalam
mempersiapkan peramalan .
Ada enam faktor utama yang diidentifikasi sebagai teknik dan metode paramalan,
yaitu :
1. Horizon waktu
Ada dua aspek dari horizon waktu yang berhubungan dengan masing-masing
metode peramalan. Pertama adalah cakupan waktu di masa yang akan datang.
Aspek kedua adalah periode untuk peramalan yang diinginkan.
2. Pola data
Dasar utama dari metode peramalan adalah anggapan bahwa macam dari pola
yang didapati di dalam data yang diramalkan akan berkelanjutan.
3. Jenis dan model
Model-model merupakan suatu deret dimana waktu digambarkan sebagai unsur
yang penting untuk menentukan perubahan-perubahan dalam pola. Model-model
perlu diperhatikan karena masing-masing model mempunyai kemampuan yang
berbeda dalam analisa keadaan untuk pengambilan keputusan.
4. Biaya yang dibutuhkan
Umumnya ada empat unsur biaya yang tercakup dalam penggunaan suatu
prosedur peramalan yaitu: biaya-biaya pengembangan, penyimpanan (storage) data, operasi pelaksanaan, kesempatan dalam penggunaan teknik-teknik dan
metode peramalan.
5. Ketepatan metode peramalan
Tingkat ketepatan yang dibutuhkan sangat erat kaitannya dengan tingkat
6. Kemudahan dalam penerapan
Metode-metode yang dapat dimengerti dan mudah diaplikasikan sudah
merupakan suatu prinsip umum bagi pengambil keputusan.
2.1.3 Metode Fuzzy Time Series
Fuzzy time series (FTS) adalah metode peramalan data yang menggunakan prinsip– prinsip fuzzy sebagai dasarnya. Sistem peramalan dengan FTS menangkap pola dari data yang telah lalu kemudian digunakan untuk memproyeksikan data yang akan datang.
Pertama kali dikembangkan oleh Q. Song dan B.S Chissom pada tahun 1993. Metode
ini sering kali digunakan oleh para peneliti untuk menyelesaikan masalah peramalan.
Metode peramalan fuzzy time series adalah metode peramalan yang menggunakan prinsip-prinsip fuzzy sebagai dasarnya. Konsep dasar fuzzy time series
yang diperkenalkan oleh Song dan Chissom (1993a, 1993b, 1994) dengan nilai fuzzy time series direpresentasikan dengan himpunan fuzzy (Chen 1998): Didefenisikan U
adalah semesta pembicaraan dengan U = { u1, u2, u3, ... , un}.
Sebuah himpunan fuzzy dalam semesta pembiracaraan U dapat direpresentasikan
sebagai berikut:
A = fA(u1) / u1 + fA(u2) / u2+ … + fA(un) / un dengan fA adalah fungsi
keanggotaan dari himpunan fuzzy A, fA : U → [0, 1], fA(ui) merupakan tingkat
keanggotan ui dalam himpunan fuzzy A, dan 1≤ i ≤ n.
Ahmad Amiruddin Anwary (2011) dalam penelitiannya untuk meramal kurs
Rupiah terhadap terhadap Dollar Amerika menggunakan metode fuzzy time series. Dalam peramalan tersebut dilakukan upaya untuk memprediksi besarnya kurs untuk
satu hari ke depan. Permasalahan yang dihadapi adalah cara untuk memprediksi
besarnya kurs yaang menghasilkan nilai prediksi dengan tingkat kesalahan minimal.
Hasilnya berupa data kurs yang terprediksi untuk tiap jenis kurs sampai satu hari ke
depan. Tingkat keakuratan hasil prediksi diukur dengan nilai AFER (Average Forecasting Error).
Algoritma fuzzy time series dalam menyelesaikan masalah prediksi adalah sebagai berikut (Pousen 2009):
1. Menentukan himpunan semesta (universe of discourse) dan membaginya ke dalam interval yang panjangnya sama. Pada tahap ini dicari nilai minimum dan
maksimum dari data aktual [ ] yang akan dijadikan sebagai
himpunan semesta data aktual dan kemudian membaginya ke dalam interval
yang sama panjangnya.
2. Mendefenisikan himpunan fuzzy pada himpunan semesta. Tahap ini mengubah himpunan semesta yang telah terbagi dan masih berupa himpunan bilangan crips
menjadi himpunan fuzzy berdasarkan interval.
3. Melakukan fuzzifikasi pada data historis. Tahap ini menentukan nilai
keanggotaan pada masing-masing himpunan fuzzy dari data historis, dengan nilai keanggotaan 0 sampai 1. Nilai keanggotaan ini diperoleh dari fungsi
keanggotaan yang telah dibuat sebelumnya.
4. Memilih basis model w (orde) yang paling sesuai dan menghitung operasi fuzzy. Tahap ini menentukan nilai hasil inferensi fuzzy berdasarkan basis model w (orde) dengan rumus:
dimana n=w dan m1, m2, ... , mn adalah nilai keanggotaan dari data historis.
Rahamini (2010) dalam tulisannya memaparkan algoritma metode automatic clustering
relasi logika fuzzy adalah sebagai berikut:
Langkah 1 : Memasukkan data yang akan dilakukan peramalan.
Langkah 2 : Menentukan interval dengan menggunakan algoritma automatic clustering.
Langkah 3 : Membentuk dan menentukan relasi logika fuzzy dari interval yang sudah terbentuk.
Langkah 4 : Menghitung nilai ramalannya dari hasil logika fuzzy.
Langkah 5 : Mencari nilai MSE dari hasil peramalan dibandingkan dengan data
aktual.
2.2Kegunaan Metode Peramalan
Saat ini banyak teknik-teknik peramalan digunakan. Dengan semakin canggihnya
teknik-teknik peramalan yang melibatkan kemampuan komputer, peramalan makin
diterima dan makin mendapat perhatian. Hampir setiap pengambil keputusan saat ini
mempunyai kemampuan menggunakan teknik analisis data dalam kegiatan pramalan,
dan pengertian dari teknik tersebut saat ini menjadi suatu hal terpenting bagi para
pengambil keputusan dalam kegiatan peramalan.
Sejalan dengan semakin diperlukannya proses peramalan dalam berbagai
kegiatan, banyak teknik–teknik baru untuk peramalan juga dikembangkan. Perhatian khusus dalam pengambangan metode peramalan adalah nilai error yang merupakan bagian penting pada setiap prosedur peramalan. Prediksi sebagai output masa depan memang jarang di dapat secara akurat. Peramal hanya dapat berusaha membuat
Sehubungan dengan ketidak akuratan dalam suatu proses, peramalan sangat
diperlukan karena setiap organisasi bekerja dalam situasi ketidakpastian. Walaupun
demikian keputusan–keputusan harus tetap dibuat untuk keperluan organisasi di masa yang akan datang. Selain itu dalam dunia organisasi seringkali dihadapkan pada
keadaan yang selalu berubah–ubah, sehingga ramalan juga selalu diperlukan.
Metode peramalan merupakan cara memperkirakan apa yang akan terjadi pada
masa depan secara sistimatis dan pragmatis atas dasar data yang relevan pada masa lalu.
Selain itu kegunaan metode peramalan adalah untuk membantu dalam
mengadakan pendekatan analisa terhadap tingkah laku atau pola data yang lalu,
sehingga dapat memberikan cara pemikiran, pengerjaan dan pemecahan yang sistimatis
dan pragmatis serta memberikan tingkat keyakinan atas ketepatan hasil ramalan yang
dibuat.
2.3Keakuratan Metode Peramalan
Seorang perencana tentu menginginkan hasil perkiraan ramalan yang tepat atau paling
tidak dapat memberikan gambaran yang paling mendekati sehingga rencana yang
dibuatnya merupakan rencana yang realistis. Ketepatan atau ketelitian inilah yang
menjadi kriteria performance suatu metode peramalan. Ketepatan atau ketelitian
tersebut dapat dinyatakan sebagai kesalahan peramalan (forecast error). Kesalahan yang kecil memberikan arti ketelitian peramalan yang tinggi, dengan kata lain keakuratan
hasil peramalan tinggi, begitu pula sebaliknya. Ada beberapa perhitungan yang biasa
digunakan untuk membandingkan model peramalan yang berbeda, mengawasi
peramalan, dan untuk memastikan peramalan dengan baik, antara lain:
1. Deviasi absolut rata-rata (mean absolute deviation - MAD) Membagi jumlah total kesalahan absolut dengan jumlah periode.
∑ | |
2. Persentase deviasi absolut rata-rata (mean absolute precente deviation - MAPD) Membagi jumlah total kesalahan absolut dengan jumlah data aktual yang
ditampilkan dalam bentuk persentase.
Pada umumnya, semakin kecil nilai MAPD maka ramalan semakin akurat.
∑ | ∑ |
3. Kesalahan kumulatif (cummulative error - E)
Diperoleh dari total kesalahan. Nilai positif berarti ramalan cenderung lebih
rendah dibandingkan data aktual (mengalami bias rendah). Sebaliknya, nilai
negatif berarti ramalan cenderung lebih tinggi dibandingkan data aktual
(mengalami bias tinggi). Tidak digunakan untuk metode regresi (garis trend
linier), karena nilai E akan mendekati nol.
∑
dimana:
4. Kesalahan rata-rata (avverage error - ̅ (E bar))
Diperoleh dari total kesalahan dibagi dengan jumlah periode. Nilai positif berarti
ramalan cenderung lebih rendah dibandungkan data aktual (mengalami bias
rendah). Sebaliknya, nilai negatif berarti nilai ramalan cenderung lebih tinggi
dibandingkan data aktual (mengalami bias tinggi). Tinggi digunakan untuk
peramalan Metode regresi (garis tren linier), karena nilai E akan mendekati nol.
̅ ∑
dimana:
E = et = Dt - Ft n = total jumlah periode
5. Kesalahan kuadrat rata-rata (mean square error - MSE)
Diperoleh dari jumlah seluuruh nilai kesalahan setiap periode yang dikuadratkan
lalu dibagi dengan jumlah periode. Pada umumnya, semakin kecil nilai MSE
maka ramalan semakin akurat.
∑
dimana:
et = Dt - Ft
n = total jumlah periode
2.4Data Berkala (Time Series)
Data berkala (time series) adalah data yang dikumpulkan dari waktu ke waktu untuk menggambarkan perkembangan suatu kegiatan atau sekumpulan hasil observasi yang
diatur dan didapat menurut urutan kronoligis waktu. Waktu yang digunakan dapat
berhubungan dengan data statistik yang dicatat dan diselidiki dalam bats-bats interval
waktu tertentu, seperti perkembangan produksi, harga barang, jumlah penduduk, hasil
penjualan, harga saham, nilai tukar kurs.
Dengan adanya data time series maka pola gerakan data dapat diketahui. Dengan
demikian data time series dapat dijadikan dasar untuk :
1. Pembuatan keputusan pada saat ini
2. Peramalan keadaan perdagangan
3. Perencanaan kegiatan untuk masa depan
2.5Logika Fuzzy
2.5.1 Pengertian Logika fuzzy
Fuzzy secara bahasa diartikan sebagai kabur atau samar-samar. Suatu nilai dapat bernilai besar atau salah secara bersamaan. Dalam fuzzy dikenal derajat keanggotaan yang memiliki rentang nilai 0 (nol) hingga 1 (satu). Berbeda dengan himpunan tegas yang
memiliki nilai 1 atau 0 (ya atau tidak).
Logika fuzzy pertama sekali diperkenalkan oleh Lotfi. A. Zadeh pada thaun 1965. Dasar logika fuzzy adalah teori himpunan fuzzy. Dalam teori himpunan dikenal fungsi karakteristik yaitu fungsi dari himpunan semesta X ke himpunan {0,1}
Defenisi: Himpunan A dalam semesta X dapat dinyatakan dengan fungsi karakteristik
yang didefinisikan dengan aturan:
Logika fuzzy merupakan suatu logika yang memiliki nilai kekaburan atau kesamaran (fuzzyness) antara benar atau salah. Dalam teori logika fuzzy suatu nilai bisa bernilai benar atau salah secar bersama. Namun berapa besar keberadaan dan kesalahan
derajat keanggotaan dalam rentang 0 hingga 1. Berbeda dengan logika digital yang
hanya memiliki dua nilai 0 atau 1. Logika fuzzy digunakan untuk menterjemahkan suatu besaran yang di ekspresikan menggunakan bahasa (linguistic), misalkan kecepatan laju kendaraan yang diekspresikan dengan pelan, lebih cepat, cepat, dan sangat cepat. Dan
logika fuzzy menunnjukkan sejauh mana suatu nilai itu benar dan sejauh mana suatu nilai itu salah. Tidak seperti logika klasik (crips) atau tegas, suatu nilai hanya mempunyai 2 kemungkinan yaitu merupakan suatu anggota himpunan atau tidak.
Derajat keanggotaan 0 (nol) artinya nilai bukan merupakan anggota himpunan dan 1
(satu) berarti nilai tersebut adalah anggota himpunan.
Sri kusumadewi (2004) mengatakan bahwa logika fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input kedalam suatu ruang output, mempunyai nilai kontinu. Fuzzy dinyatakan dalam derajat dari suatu keanggotaan dan derajat dari kebenaran. Oleh sebab itu sesuatu dapat dikatakahn sebagian benar dan sebagian salah
dalam waktu yang sama.
Logika fuzzy memungkinkan nilai keanggotaan antara 0 dan 1, tingkat keabuan
juga hitam dan putih, dan dalam bentuk linguistik, konsep tidak pasti seperti “sedikit”, “lumayan” dan “sangat”. (Zadeh 1995).
Himpunan fuzzy memperluas jangkauan fungsi karakteristik pada himpunan crips sehingga fungsi tersebut mencakup bilangan riil pada interval [0.1]. Fungsi itu
memetakan setiap unsur dalam himpunan semesta X ke suatu nilai pada interval [0,1]
yang selanjutnya disebut dengan derajat keanggotaan dari suatu himpunan kabur A
dalam semesta X adalah pemetaan [ ] Nilai menyatakan derajat
keanggotaan dalam himpunan kabur A.
Misalkan diketahui data IPK mahasiswa pada inteval [0,00, 4,00]. Akan dibuat
himpunan mahasiswa pandai. Kata “pandai” menunjukkan seberapa besar seorang mahasiswa dikatakan pandai.
Dengan menggunakan crips seorang mahasiswa dikatakan Pandai jika memiliki IPK diatas atau sama dengan 3,00 dengan derajat keanggotaan sebaliknya jika
memiliki IPK 3,01 maka akan dikatakan „Pandai‟. Sedangkan mahasiswa B dengan IPK 2,99 dikatakan „Tidak Pandai‟.
Sedangkan dengan menggunakan fuzzy set, suatu fungsi keanggotaan menjadi bersifat kontinu. Seorang mahasiswa dengan IPK 2,5 dikatakan mendekati Pandai
dengan dan mahasiswa dengan IPK 1,25 memang kurang Pandai dengan
Kelebihan dari teori logika fuzzy adalah kemampuan dalam proses penalaran secara bahasa (linguistic reasoning). Sehingga dalam perancangannya tidak memrlukan persamaan matematik dari objek yang akan dikendalikan.
2.5.2 Notasi Himpunan fuzzy
Himpunan fuzzy memiliki 2atribut, yaitu:
1. Linguistik
Yaitu penamaan suatu grup yang memiliki suatu keadaan atau kondisi
tertentu dengan menggunakan bahasa alami, seperti: MUDA, PAROBAYA,
TUA, PANAS, DINGIN.
2. Numerik
Yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu variabel,
contoh: 40, 25, 50 dan sebagainya.
Ada beberapa hal yang perlu diketahui dalam memahami sistem fuzzy, yaitu:
a. Variabel fuzzy
Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu system
fuzzy.
umur, temperatur, permintaan, dsb.
b. Himpunan fuzzy
Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy.
Contoh:
1. Variabel umur, terbagi menjadi 3 himpunan fuzzy, yaitu: MUDA, PAROBAYA, dan TUA.
2. Variabel temperatur, terbagi menjadi 5 himpunan fuzzy, yaitu: DINGIN, SEJUK, NORMAL, HANGAT, dan PANAS.
c. Semesta pembicaraan
Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk
dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan
himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif
maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi
batas atasnya.
Contoh:
1. Semesta pembicaraan untuk variabel umur: [0 , +∞) 2. Semesta pembicaraan untuk variabel temperatur: [0 , 40]
d. Domain himpunan fuzzy
Domain himpunan fuzzy adalah keseluruhan nilai yang diijinkan dalam semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy. Seperti halnya semesta pembicaraan, domain merupakan himpunan bilangan
real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan.
Nilai domain dapat berupa bilangan positif maupun negatif.
Contoh:
2. PAROBAYA = [35,55]
3. TUA = [45,+∞] 4. DINGIN = [0,20]
5. SEJUK = [15,25]
6. NORMAL = [20,30]
7. HANGAT = [25,35]
8. PANAS = [30,40]
2.5.3 Fungsi Keanggotaan Fuzzy
Fungsi keanggotaan adalah suatu kurva yang menunjukkan pemetaan titik-titik input
data ke dalam nilai keanggotaannya (derajat keanggotaan) yang memiliki interval antara
0 sampai 1. Salah satu cara yang dapat digunakan untuk mendapatkan nilai keanggotaan
adalah dengan melalui pendekatan fungsi.
Adapun beberapa jenis fungsi yang dapat digunakan untuk mendapat nilai keanggotaan
yaitu:
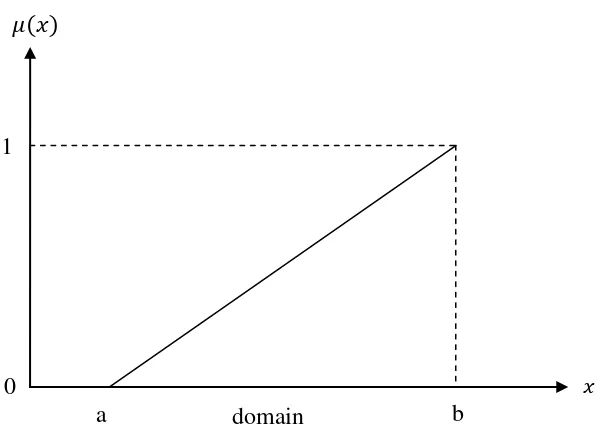
1. Representasi linier
Pada representasi linier, permukaan digambarkan sebagai suatu garis lurus.
Bentuk ini paling sederhanadan menjadi pilihan yang baik untuk mendekati
konsep yang kurang jelas.
Ada 2 kemungkinan himpunan fuzzy linier: 1) Linier naik
Kenaikan himpunan dimulai pada nilai domain yang memiliki derajat
keanggotaan 0 (nol) bergerak ke kanan menuju domain yang memiliki
Gambar 2.1 Grafik fungsi keanggotaan representasi linier naik (Sumber: Sri Kusumadewi, 2002)
Fungsi keanggotaan:
{
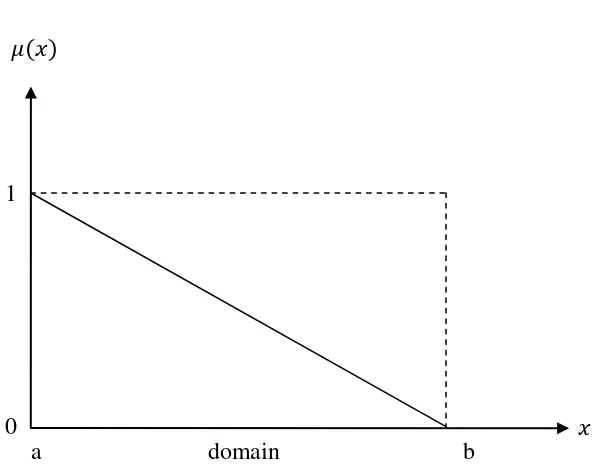
2) Linier turun
Garis lurus dimulai dari domain dengan derajat keanggotaan tertinggi
pada sisi kiri, kemudian bergerak menurun ke nilai domain yang
memiliki derajat keanggotaan lebih rendah. 0
a b
1
Gambar 2.2 Grafik fungsi keanggotaan pada representasi linier turun (Sumber: Sri Kusumadewi, 2002)
Fungsi keanggotaan:
{
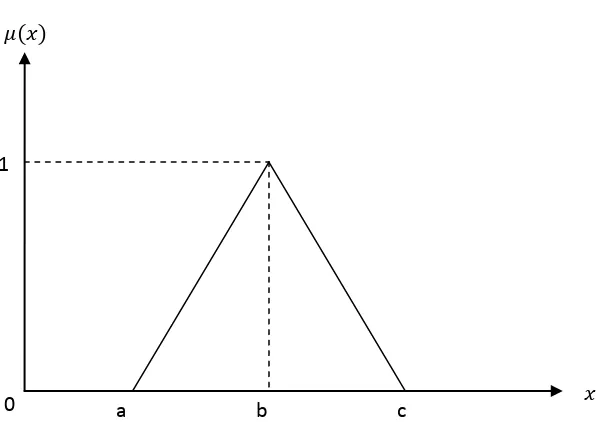
2. Representasi kurva segitiga
Kurva segitiga pada dasarnya merupakan gabungan antara dua garis (linier) serta
ditandai oleh adanya tiga parameter {a,b,c}yang menentukan koordinat x dari
tiga sudut. 0
a b
1
Gambar 2.3 Grafik fungsi keanggotaan pada representasi kurva segitiga (Sumber: Sri Kusumadewi, 2002)
{
3. Representasi kurva trapesium
Kurva trapesium pada dasarnya seperti bentuk segitiga, hanya saja ada beberapa
titik yang memiliki nilai keanggotaan 1.
1
a b c
Gambar 2.4 Grafik fungsi keanggotaan pada representasi kurva trapesium (Sumber: Sri Kusumadewi, 2002)
{
4. Representasi kurva bahu
Suatu kurva yang letak daerahnya terletak ditengah-tengah satu variabel yang di
representasikan dalam bentuk segitiga, pada sisi kanan dan kirinya akan naik dan
turun (misalkan dingin bergerak ke sejuk bergerak ke hangat bergerak ke panas).
Tetapi terkadang satu sisi dari variabel tersebut tidak mengalami perubahan. 1
0
a b c d
tetap pada kondisi panas. Himpunan fuzzy „bahu‟ bukan segitiga, digunakan
untuk mengakhiri variabel suatu daerah fuzzy. Bahu kiri bergerak dari benar ke salah, demikian juga bahu kanan bergerak dari salah ke benar.
Normal:
Seperti halnya himpunan konvensional, ada beberapa operasi yang didefinisikan secara
khusus untuk mengkombinasi dan memodifikasi himpunan fuzzy. Nilai keanggotaan sebagai hasil dari operasi 2 himpunan sering dikenal dengan nama fire strengthatau α–
Ada 3 operator dasar yang diciptakan oleh Zadeh, yaitu:
1. Operator AND
Operator ini berhubungan dengan operasi interseksi pada himpunan. α–predikat sebagai hasil operasi dengan operator AND diperoleh denganmengambil nilai
keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan.
( )
2. Operator OR
Operator ini berhubungan dengan operasi union pada himpunan. α–predikat sebagai hasil operasi dengan operator OR diperoleh dengan mengambil nilai
keanggotaan terbesar antar elemen pada himpunan-himpunan yang
bersangkutan.
3. Operator NOT
Operator ini berhubungan dengan operasi komplemen pada himpunan. α– predikat sebagai hasil operasi dengan operator NOT diperoleh dengan
mengurangkan nilai keanggotaan elemen pada himpunan yang bersangkutan dari
1.
BAB 3
METODE PENELITIAN
Metode penelitian yang digunakan untuk memecahkan permasalahan dalam tugas akhir
ini adalah sebagai berikut:
1. Studi literatur.
Tahap ini dilakukan dengan mengidentifikasi permasalahan, mengkaji dan
memahami teori-teori yang dipelajari diantaranya mengenai konsep dasar
metode automatic clustering-relasi logika fuzzy dan metode fuzzy time series
yang menjadi metode peramalan. Penelusuran referensi ini bersumber dari buku,
jurnal maupun penelitian yang telah ada sebelumnya mengenai hal-hal yang
berhubungan dangan metode automatic clustering-relasi logika fuzzy dan metode
fuzzy time series.
2. Pengumpulan data.
Pada tahap ini dilakukan pengambilan data jumlah peminat Departemen S1
Matematika USU melalui jalur tertulis mulai tahun 2006 sampai dengan tahun
2013.
3. Peramalan jumlah peminat dengan metode automatic clustering-relasi logika
fuzzy.
Pada tahap ini dilakukan peramalan jumlah peminat Departemen S1 Matematika
4. Membandingkan hasil peramalan.
Pada tahap ini dilakukan peramalan dengan metode fuzzy time series kemudian hasil yang diperoleh dibandingkan dengan hasil peramalan metode automatic clustering-relasi logika fuzzy dilihat dari MSE. Jika MSE lebih kecil berarti metode tersebut lebih akurat.
5. Pengambilan kesimpulan.
Pada tahap ini dilakukan penarikan kesimpulan hasil analisa data sekaligus
memberikan saran yang berkaitan dengan pengembangan penellitian
BAB 4 PEMBAHASAN
4.1 Pengumpulan data
Data yang digunakan adalah data jumlah peminat pada departemen S1 Matematika USU
melalui jalur tertulis yaitu jalur SPMB, SNMPTN dan SBMPTN (tidak termasuk jalur
UMB dan Undangan). Data diperoleh dari Biro Rektor USU Bagian Pendidikan sesuai
dengan izin yang diberikan oleh pihak terkait. Data yang digunakan mulai dari data
jumlah peminat pada tahun 2006 – 2013.
Tabel 4.1 Data Jumlah Peminat S1 Matematika USU Melalui Jalur Tertulis Tahun 2006
– 2013
Tahun Jumlah peminat
2006 466
2007 507
2008 211
2009 320
2010 309
2011 442
2012 536
2013 617
Sumber: Biro Akademik USU
4.2 Metode Automatic Clustering-Relasi Logika Fuzzy
Pada bagian ini, disajikan metode untuk peramalan jumlah peminat didasarkan pada
metode automatic clustering-relasi logika fuzzy.
Langkah 1: Menerapkan metode automatic clustering untuk klaster data historis menjadi bentuk interval kemudian hitung titik tengah masing-masing intervalnya.
Langkah 2: Mengasumsikan bahwa terdapat n interval , kemudian mendefenisikan setiap fuzzy set , di mana dan .
Langkah 3: Fuzzifikasi setiap data historis, menjadi himpunan fuzzy. Jika data terletak pada interval , dengan , maka data difuzzifikasi ke .
Langkah 4: Membentuk relasi logika fuzzy yang didasarkan pada data historis yang diperoleh dari Langkah 3. Fuzzifikasi data jumlah peminat tahun t dan t+1 adalah dan yang masing-masing kemudian membangun relasi logika fuzzy
dimana dan adalah keadaan sekarang dan keadaan mendatang dari hasil logika
fuzzy. Berdasarkan keadaan saat ini pada relasi logika fuzzy, relasi logika fuzzy dibagi ke dalam kelompok relasi logika fuzzy, di mana relasi logika fuzzy yang memiliki keadaan saat ini yang sama di masukkan ke dalam kelompok relasi logika fuzzy yang sama.
Langkah 5: Menghitung nilai peramalan jumlah peminat, sesuai prinsip berikut:
Prinsip 1: Jika fuzzifikasi jumlah peminatdari tahun t adalah dan hanya ada satu relasi logika fuzzy pada kelompok relasi logika fuzzy yang memiliki keadaan saat ini
ditunjukkan sebagai berikut:
Prinsip 2: jika fuzzifikasi jumlah peminat dari tahun t adalah Aj dan ada relasi logika
fuzzy yang memiliki keadaan sekarang Aj, yang ditunjukkan sebagai berikut:
( )
Maka nilai peramalan dari tahun t+1 dihitung sebagai berikut:
Dimana xi menggambarkan angka dari Relasi Logika Fuzzy pada kelompok
Relasi Logika fuzzy, adalah titik tengah dari
interval-interval berturut-turut, dan nilai keanggotaan maksimum dari
himpunan fuzzy terjadi pada interval
berturut-turut.
Prinsip 3: jika fuzzifikasi jumlah peminat pada tahun t adalah Aj dn ada relasi logika fuzzy yang memiliki keadaan saat ini Aj yang di ganbarkan seperti berikut:
Dengan simbol “ ≠ “ merupakan sebuah nilai yang tidak diketahui, maka nilai
peramalan pada tahun t+1 adalah mj, dengan mj adalah titik tengah dari interval ui dan nilai keanggotaan maksimal dari himpunan fuzzyAj terjadi pada ui.
4.3 Algoritma automatic clustering
Langkah 1: Mengurutkan data numerik dalam urutan menaik sehingga memiliki n data yang berbeda. Diasumsikan bahawa data yang telah terurut tanpa data ganda akan
ditampilkan sebagai berikut:
Berdasarkan data yang telah terurut, maka hitung nilai “average_dif” dengan rumus
sebagai berikut:
∑
Langkah 2: Mengambil data angka pertama (data terkecil dalam bariran terurut naik) ke dalam klaster sekarang. Berdasarkan nilai dari “average_diff”, ditentukan apakah data angka mengikuti data pada pengelompokan sekarang pada barisan data terurut naik
dapat diletakkan pada klaster baru berdasarkan pada beberapa prinsip berikut:
Prinsip 1: asumsikan bahwa saat ini klaster pertamanya adalah klaster pertama dan hanya ada satu data d1 di dalamnya dan menganggap bahwa data d2 adalah yang berdekatan dengan d1, ditampilkan sebagai berikut:
JIKA MAKA d2 diletakkan ke dalam klaster sekarang dimana d1termasuk.
Sebaliknya, dibentuk kelompok untuk d2 dan biarkan klaster baru yang baru dibangun
yang mana d2 termasuk ke dalam klaster sekarang.
Prinsip 2: Asumsikan bahwa klaster yang sekarang bukan klaster yang pertama dan ada lebih satu data di klaster saat ini. Diasumsikan bahwa di adalah data terbesar di klaster saat ini dan diasumsikan bahwa dj adalah data yang berdekatan di sebelah di, yang ditampilkan sebagai berikut:
MAKA dj diletakkan ke dalam klaster yang sama dengan di. Dalam hal ini .
Diberikan rumus mencari nilai cluster_diff:
∑
dimana menunjukkan data dalam klaster sekarang.
Cluster_diff menunjukkan jarak dari average_diff antara elemen – elemen yang berada dalam klaster yang sama. Jika di membentuk sebuah klaster yang memilik
elemen tunggal, maka Prinsip 2 tidak berlaku.
Prinsip 3: Asumsikan bahwa di adalah elemen terakhir dari sebuah klaster, dj adalah
elemen pertama dari klaster berikutnya, dan dk adalah sebuah angka yang mengikuti dj
yang ditampilkan sebagai berikut:
{ }
JIKA DAN MAKA letakkan dk ke dalam klaster yang sama dengan dj.
Langkah 3: Berdasarkan hasil pengklasteran pada Langkah 2, sesuaikan isi klaster menurut beberapa prinsip berikut:
Prinsip 1: Jika sebuah klaster memiliki lebih dari dua elemen, maka di ambil elemen terkecil dan terbesar serta menghapus elemen yang lain.
Prinsip 2: Jika sebuah klaster memiliki tepat dua elemen, maka klaster dibiarkan (tidak berubah)
Prinsip 3: jika sebuah klaster hanya memiliki satu elemen dq, maka letakkan nilai–nilai
dari dan ke dalam klaster dan
Kondisi 1: jika kondisi terjadi di klaster pertama, maka hapus nilai sebagai ganti dari .
Kondisi 2: jika kondisi terjadi di klaster terakhir, maka nilai dari dihapus sebagai ganti dari dq dari klaster ini.
Kondisi 3: jika nilai dari lebih besar daripada nilai terkecil dalam klaster terdahulu, maka semua tindakan dalam Prinsip 3 dibatalkan.
Langkah 4: Asumsikan bahwa hasil klaster yang diperoleh pada Langkah 3 adalah ditampilkan sebagai berikut:
Kemudian ubah kelompok ini ke dalam interval yang bersebelahan dengan sub-langkah
berikut:
interval sekarang dan biarkan klaster menjadi klaster sekarang.
3. Jika interval sekarang adalah [ ) dan klaster sekarang adalah {dk}, maka
ubahlah interval sekarang [ ) ke dalam [ . Biarkan [ menjadi
interval sekarang dan biarkan klaster selanjutnya menjadi klaster sekarang.
4.4. Algoritma Metode Fuzzy Time Series
Langkah–langkah peramalan menggunakan metode fuzzy time series adalah:
1. Mendefenisikan semesta pembicaraan U dengan data historis dalam himpunan
fuzzy yang akan didefinisikan. Biasanya ketika mendefinikan semesta, pertama harus ditemukan data peminat tertinggi Dmaks dan terendah Dmin dari data
historis. Berdasarkan pada data Dmin dan Dmaks mendefenisikan semesta U
sebagai [ ] dengan D1 dan D2 adalah dua bilangan positif yang tepat.
2. Membagi semesta U ke dalam beberapa panjang interval.
3. Mendefinisikan himpunan fuzzy pada semesta U. Pertama, menentukan beberapa nilai linguistik. Tidak ada batasan pada angka himpunan fuzzy pada yang didefinisikan. Kedua, mendefinisikan himpunan fuzzy pada U. Semua himpunan
fuzzy akan diberi nama dengan nilai linguistik yang mungkin.
4. Fuzzifikasi data historis, temukan sebuah himpunan fuzzy yang sesuai dengan jumlah peminat setiap tahun.
5. Menghitung nilai peramalan dengan beberapa aturan seperti berikut:
Aturan 1: Jika himpunan fuzzy sekarang adalah Ai, Relasi Logika kelompok
adalah kosong,
Maka nilai peramalannya adalah miyang merupakan titik tengah ui.
Aturan 2: Jika himpunan fuzzy sekarang adalah Ai dan ada relasi logika fuzzy
terhadap Aj,
Maka nilai peramalannya adalah mj dan mj merupakan nilai titik tengah dari uj. Aturan 3: Jika himpunan fuzzy sekarang adalah Ai dan ada Relasi Logika Fuzzy
lebih dari satu,
4.5 Pengolahan data
4.5.1 Peramalan dengan Metode Automatic Clustering-Relasi Logika Fuzzy
Data setelah terurut naik: 211, 309, 320, 442, 466, 507, 536, 617.
Kemudian cari beda rata – rata dari data dengan menggunakan rumus:
∑
Diperoleh:
[
Selanjutnya pengklasteran menggunakan metode automatic clustering:
Berdasarkan Prinsip 1, diperoleh: Klaster1 = {211}
Klaster2 = {309, 320}
Klaster3 = {442, 446, 507, 536}
Kalster4 = {617}
Klaster2 = {309, 320}
Klaster3 = {442, 466, 507, 536}
Klaster4 = {617}
Diperiksa kembali berdasarkan Prinsip 3, diperoleh: Klaster1 = {211}
Klaster2 = {309, 320}
Klaster3 = {442, 466}
Klaster4 = {507, 536}
Klaster5 = {617}
Klaster – klaster yang sudah terbentuk diperiksa kembali berdasarkan Langkah 3, diperoleh:
Klaster1 = {211, 269}
Klaster2 = {309, 320}
Klaster3 = {442, 466}
Klaster4 = {507, 536}
Klaster5 = {617}
Kemudian berdasarkan Langkah 4 ubah klaster – klaster tersebut menjadi interval yang bersebelahan diperoleh:
u1 = [211, 269)
u2 = [269, 309)
u3 = [309, 320)
u6 = [466, 507)
u7 = [507, 536)
u8 = [536, 617)
Setelah interval diperoleh, bagi setiap interval dalam p sub-inteval dengan p ≥ 1.
Diambil p = 10. Sehingga diperoleh interval baru, diperoleh;
u1 = [211,000 , 214,625) u21 = [279,000 , 281.500)
u2 = [214,625 , 218.250) u22 = [281,500 , 284,000)
u3 = [218,250 , 221,875) u23 = [284,000 , 286,500)
u4 = [221,875 , 225,500) u24 = [286,500 , 289,000)
u5 = [225,500 , 229,125) u25 = [289,000 , 291,500)
u6 = [229,125 , 232,750) u26 = [291,500 , 294,000)
u7 = [232,750 , 236,375) u27 = [294,000 , 296,500)
u8 = [236,375 , 240,000) u28 = [296,500 , 299,000)
u9 = [240,000 , 243,625) u29 = [299,000 , 301,500)
u10 = [243,625 , 247,250) u30 = [301,500 , 304,000)
u11 = [247,250 , 250,875) u31 = [304,000 , 306,500)
u12 = [250,875 , 254,500) u32 = [306,500 , 309,000)
u13 = [254,500 , 258,125) u33 = [309,000 , 309,688)
u14 = [258,125 , 261,750) u34 = [309,688 , 310,375)
u15 = [261,750 , 265,375) u35 = [310,375 , 311,063)
u16 = [263,375 , 269,000) u36 = [311,063 , 311,750)
u18 = [271,500 , 274,000) u38 = [312,438 , 313,125)
u19 = [274,000 , 276,500) u39 = [313,125 , 313,813)
u20 = [276,500 , 279,000) u40 = [313,813 , 314,500)
u41 = [314,500 , 315,188) u61 = [411,500 , 419,125)
u42 = [315,188 , 315,875) u62 = [419,125 , 426,750)
u43 = [315,875 , 316,563) u63 = [426,750 , 434,375)
u44 = [316,563 , 317,250) u64 = [434,375 , 442,000)
u45 = [317,250 , 317,938) u65 = [442,000 , 443,500)
u46 = [317,938 , 318,625) u66 = [443,500 , 445,000)
u47 = [318,625 , 319,313) u67 = [445,000 , 446,500)
u48 = [319,313 , 320,000) u68 = [446,500 , 448,000)
u49 = [320,000 , 327,625) u69 = [448,000 , 449,500)
u50 = [327,625 , 335,250) u70 = [449,500 , 451,000)
u51 = [335,250 , 342,875) u71 = [451,000 , 452,500)
u52 = [342,875 , 350,500) u72 = [452,500 , 454,000)
u53 = [350,500 , 358,125) u73 = [454,000 , 455,500)
u55 = [358,125 , 365,750) u74 = [455,500 , 457,000)
u54 = [365,750 , 373,375) u75 = [457,000 , 458,500)
u56 = [373,375 , 381,000) u76 = [458,500 , 460,000)
u57 = [381,000 , 388,625) u77 = [460,000 , 461,500)
u59 = [369,250 , 403,875) u79 = [463,000 , 464,500)
u60 = [403,875 , 411,500) u80 = [464,500 , 466,000)
u81 = [466,000 , 468,563) u101= [514,250 , 516,063)
u82 = [468,563 , 471,125) u102 = [516,063 , 517,875)
u83 = [471,125 , 473,688) u103 = [517,875 , 519,688)
u84 = [473,688 , 476,250) u104 = [519,688 , 521,500)
u85 = [476,250 , 478,813) u105 = [521,500 , 523,313)
u86 = [478,813 , 481,375) u106 = [523,313 , 525,125)
u87 = [481,375 , 483,938) u107 = [525,125 , 526,938)
u88 = [483,938 , 486,500) u108 = [526,938 , 528,750)
u89 = [486,500 , 489,063) u109 = [528,750 , 530,563)
u90 = [489,063 , 491,625) u110 = [530,563 , 532,375)
u91 = [491,625 , 494,188) u111 = [532,375 , 534,188)
u92 = [494,188 , 496,750) u112 = [534,188 , 536,000)
u93 = [496,750 , 499,313) u113 = [536,000 , 541,063)
u94 = [499,313 , 501,875) u114 = [541,063 , 546,125)
u95 = [501,875 , 504,438) u115 = [546,125 , 551,188)
u96 = [504,438 , 507,000) u116 = [551,188 , 556,250)
u97 = [507,000 , 508,813) u117 = [556,250 , 561,313)
u98 = [508,813 , 510,625) u118 = [561,313 , 566,375)
u100 = [512,438 , 514,250) u120 = [571,438 , 576,500)
u121 = [576,500 , 581,563) u125 = [596,750 , 601.813)
u122 = [581,563 , 586,625) u126 = [601,813 , 606,875)
u123 = [586,625 , 591,688) u127 = [606,875 , 611,938)
u124 = [591,688 , 596,750) u128 = [611.938 , 617,000 )
Selanjutnya cari titik tengah dari masing – masing interval, diperoleh:
m1 = 212,813 m21 = 280,250 m41 = 314,844
m2 = 216,438 m22 = 282,750 m42 = 315,531
m3 = 220,063 m23 = 285,250 m43 = 316,219
m4 = 223,689 m24 = 287,750 m44 = 316,906
m5 = 227,313 m25 = 290,250 m45 = 317,594
m6 = 230,938 m26 = 292,750 m46 = 318,281
m7 = 234,563 m27 = 295,250 m47 = 318,969
m8 = 238,188 m28 = 297,705 m48 = 319,656
m9 = 241,813 m29 = 300,250 m49 = 323,813
m10 = 245,438 m30 = 302,750 m50 = 331,438
m11 = 249,063 m31 = 305,250 m51 = 339,063
m12 = 252,688 m32 = 307,750 m52 = 346,688
m13 = 256,313 m33 = 309,344 m53 = 354,313
m14 = 259,938 m34 = 310,031 m54 = 361,938
m15 = 263,563 m35 = 310,719 m55 = 369,563
m17 = 270,250 m37 = 312,094 m57 = 384,183
m18 = 272,750 m38 = 312,781 m58 = 393,438
m19 = 275,250 m39 = 313,469 m59 = 400,063
m20 =277,750 m40 = 314,156 m60 = 407,688
m61 = 415,313 m85 = 477,531 m109= 529,656
m62 = 422,938 m85 = 480,094 m110= 531,469
m63 = 430,563 m87 = 482,656 m111= 533,281
m64 = 438,188 m88 = 485,219 m112= 535,094
m65 = 442,750 m89 = 487,781 m113= 538,531
m66 = 444,250 m90 = 490,343 m114= 543,594
m67 = 444,750 m91 = 492,906 m115= 548,656
m68 = 447,250 m92 = 495,469 m116= 553,719
m69 = 448,750 m93 = 498,031 m117= 558,781
m70 = 450,250 m94 = 500,599 m118= 563,844
m71 = 451,750 m95 = 503,156 m119= 568,906
m72 = 453,250 m96 = 505,719 m120= 573,969
m73 = 454,750 m97 = 507,906 m121= 579,061
m74 = 456,250 m98 = 509,719 m122= 584,094
m75 = 457,750 m99 = 511,531 m123= 589,156
m76 = 459,250 m100 = 513,344 m124= 594,219
m78 = 462,250 m102= 516,969 m126= 604,344
m79 = 463,750 m103= 518,781 m127= 609,406
m80 = 465,250 m104= 520,594 m128= 614,469
m81 = 467,281 m105= 522,406
m82 = 469,844 m106= 524,219
m83 = 472,406 m107= 526,031
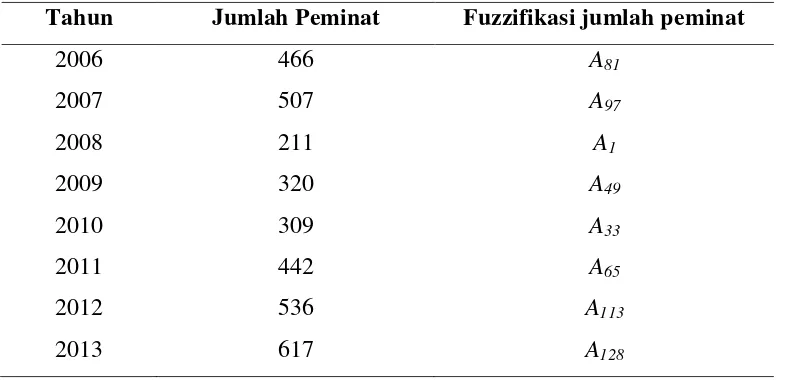
Tabel 4.2 Hasil Fuzzifikasi Jumlah Peminat dengan Metode Automatic Clustering -Relasi Logika Fuzzy
Pada Tabel 4.2 dapat dilihat bahwa jumlah peminat pada tahun 2006 adalah 466 yang
berada pada interval u81 = [466.000 , 468.563) maka jumlah peminat pada tahun 2006 difuzzifikasikan ke dalam A81.
Dari Tabel 4.2 dapat ditentukan relasi logika fuzzy. Misalnya, hasil fuzzifikasi pada tahun 2006 adalah A81 dan hasil fuzzifikasi data pada tahun 2007 adalah A97. Maka relasi logika fuzzy antara tahun 2006 dan 2007 adalah . A51 adalah keadaan sekarang dan A61 adalah keadaan mendatang pada relasi logika fuzzy. Maka relasi logika fuzzy setiap tahun jumlah peminat adalah sebagai berikut:
Tahun Jumlah Peminat Fuzzifikasi jumlah peminat
Karena tidak terdapat relasi logika fuzzy yang sama, maka tidak perlu dilakukan pengelompokan. Selanjutnya perhitungan peramalan, diperoleh:
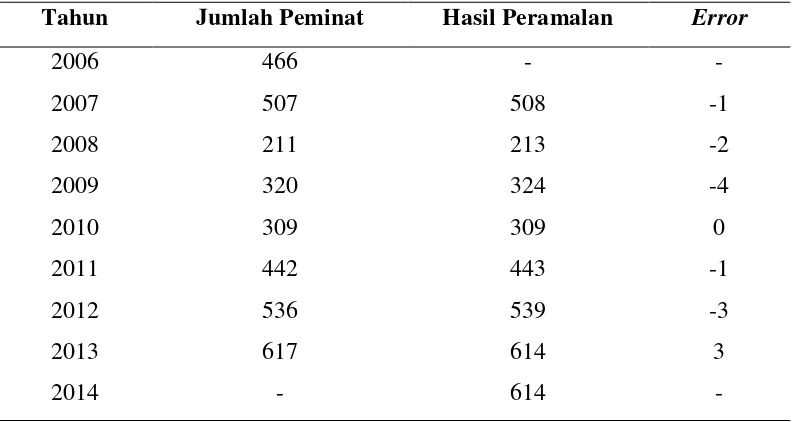
Tabel 4.3 Hasil Peramalan Jumlah Peminat dengan Metode Automatic Clustering-Relasi Logika Fuzzy
Tahun Jumlah Peminat Hasil Peramalan Error
2006 466 - -
2007 507 508 -1
2008 211 213 -2
2009 320 324 -4
2010 309 309 0
2011 442 443 -1
2012 536 539 -3
2013 617 614 3
2014 - 614 -
Kemudian hitung nilai Mean Square Error (MSE) dari hasil peramalan menggunakan metode automatic clustering-relasi logika fuzzy pada Tabel 4.3, diperoleh :
∑
Nilai MSE 5.71 menunjukkan bahwa hasil peramalan data tahun 2007 – 2013 tidak jauh berbeda dari data sebenarnya.
4.5.2 Peramalan dengan Metode Fuzzy Time Series
Defenisikan semesta U sebagai [Dmin – D1, Dmax + D2] dengan Dmin = 211 dan Dmax = 617. Dipilih D1 = 11 dan D2 = 3.
Sehingga didefinikan semesta U sebagai [200 , 620]
Kemudian bagi semesta U kedalam p panjang interval.
Dipilih p = 20.
u1 = [200, 221) u11 = [410, 431)
u2 = [221, 242) u12 = [431, 452)
u3 = [242, 263) u13 = [452, 473)
u4 = [263, 284) u14 = [473, 494)
u5 = [284, 305) u15 = [494, 515)
u6 = [305, 326) u16 = [515, 536)
u7 = [326, 347) u17 = [536, 557)
u8 = [347, 368) u18 = [557, 578)
u9 = [368, 389) u19 = [578, 599)
Kemudian cari titik tengah dari masing – masing interval di atas:
m1 = 210,5 m11 = 420,5
m2 = 231,5 m12 = 441,5
m3 = 252,5 m13 = 462,5
m4 = 273,5 m14 = 483,5
m5 = 294,5 m15 = 504,5
m6 = 315,5 m16 = 525,5
m7 = 336,5 m17 = 546,5
m8 = 357,5 m18 = 567,5
m9 = 378,5 m19 = 588,5
m10 = 399,5 m20 = 609,5
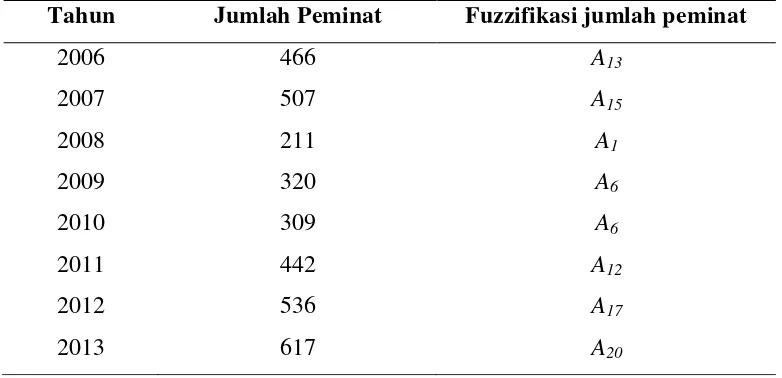
Tabel 4.4 Hasil Fuzzifikasi Jumlah Peminat dengan Metode Fuzzy Time Series
Dari Tabel 4.4 dapat ditentukan relasi logika fuzzy. Misalnya, hasil fuzzifikasi pada
tahun 2006 adalah A13 dan hasil fuzzifikasi data pada tahun 2007 adalah A15. Maka relasi logika fuzzy antara tahun 2006 dan 2007 adalah . A13 adalah keadaan sekarang
Tahun Jumlah Peminat Fuzzifikasi jumlah peminat
2006 466 A13
2007 507 A15
2008 211 A1
2009 320 A6
2010 309 A6
2011 442 A12
2012 536 A17
dan A15 adalah keadaan mendatang pada relasi logika fuzzy. Maka relasi logika fuzzy
setiap tahun jumlah peminat adalah sebagai berikut:
Karena terdapat relasi logika fuzzy yang sama, maka perlu dilakukan pengelompokan:
Kelompok 1:
Kelompok 2:
Kelompok 3:
Kelompok 4:
Kelompok 5:
Kelompok 6:
Kelompok 7:
Kemudian cari nilai peramalannya, seperti pada Tabel 4.5.
Kemudian hitung nilai MSE dari nilai error yang didapat dari Tabel 4.5, diperoleh:
∑
Nilai MSE 1293.8 menggambarkan bahwa hasil peramalan data tahun 2007 – 2013 masih jauh dari data sebenarnya.
Perbandingan peramalan menggunakan Metode Automatic Clustering-Relasi Logika
Fuzzy dengan Metode Fuzzy Time Series dapat dilihat pada Tabel 4.6.
Tabel 4.6 Perbandingan Hasil Peramalan Antara Metode Automatic Clustering-Relasi Logika Fuzzy dengan Metode Fuzzy Time Series
Tahun Jumlah Peminat Hasil Peramalan Error
2006 466 - -
2007 507 505 2
2008 211 211 0
2009 320 316 4
2010 309 379 -70
2011 442 379 63
2012 536 547 -11
2013 617 610 7
Tahun Jumlah peminat
Hasil peramalan dengan Metode Automatic Clustering-Relasi Logika
Fuzzy
Hasil peramalan dengan Metode Fuzzy Time
Series
Ft et Ft et
2006 466 -
2007 507 508 -1 505 2
2008 211 213 -2 211 0
2009 320 324 -4 316 4
2010 309 309 0 379 -70
2011 442 443 -1 379 63
2012 536 539 -3 547 -11
2013 617 614 -3 610 7
2014 - 614 610
0 100 200 300 400 500 600 700
2006 2007 2008 2009 2010 2011 2012 2013 2014
Data Jumlah Peminat
Hasil peramalan metode automatic clustering-relasi logika fuzzy
Hasil peramalan metode fuzzy time series
Gambar 4.1. Grafik Perbandingan Hasil Peramalan Antara Metode Automatic Clustering-Relasi Logika Fuzzy dengan Metode Fuzzy Time Series
Jumlah Peminat