AKMAL IDRIS
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
AKMAL IDRIS. Penentuan Harga Obligasi untuk Beberapa Nilai Parameter. Dibimbing oleh DONNY CITRA LESMANAdan ENDAR HASAFAH NUGRAHANI.
Obligasi merupakan sekuritas yang diterbitkan sehubungan dengan perjanjian pinjaman. Pihak peminjam menerbitkan (menjual) obligasi kepada pihak pemilik dana dengan imbalan sejumlah uang. Perjanjian tersebut mewajibkan penerbit obligasi (pihak peminjam) untuk melakukan pembayaran tertentu kepada pemegang obligasi pada waktu yang telah ditentukan. Penerbit obligasi akan membayar seluruh utangnya pada saat jatuh tempo sesuai dengan nilai nominal obligasi tersebut.
Seorang investor yang mempertimbangkan pembelian obligasi tidak diberi tahu secara langsung tingkat imbal hasil yang dijanjikan. Tetapi investor tersebut harus menggunakan harga obligasi, jangka waktu, dan pembayaran bunga untuk kemudian menghitung imbal hasil yang ditawarkan obligasi tersebut sepanjang waktunya. Imbal hasil ini disebut yield to maturity.
Hubungan antara yield to maturity dan harga obligasi ditunjukkan oleh Malkiel dalam teoremanya. Malkiel menunjukkan bagaimana yield to maturitydan harga obligasi berubah yang bergantung pada tingkat kupon, waktu hingga jatuh tempo, dan keadaan yield to maturity. Pada karya ilmiah ini kita dibuktikan teorema-teorema Malikiel menggunakan aljabar sederhana. Bukti-bukti tersebut akan dapat menjelaskan dengan lebih baik hubungan perubahan pada yield to maturitydan harga obligasi.
AKMAL IDRIS. Determination of Bond Prices for Some Parameter Values. Under supervision of DONNY CITRA LESMANAand ENDAR HASAFAH NUGRAHANI.
A bond is a security that is issued in connection with a borrowing arrangement. The borrower issues (i.e. sells) a bond to the lender for some amount of cash. The arrangement obligates the issuer to make specified payments to the bondholder on specified dates. When the bond matures, the issuer repays the debt by paying the bondholder the bond’s par value (equivalently, its face value).
An investor considering the purchase of a bond is usually not quoted a promised rate of return. Instead, the investor must use the bond price, maturity date, and coupon payments to infer the return offered by the bond over its life, which is called the yield to maturity.
The relationship between yield to maturity and bond price were proved by Malkiel in his theorems. He showed how yield to maturity and bond prices movements depend on coupon rate, the time to maturity, and the existing yield to maturity. In this paper we prove the Malkiel theorems using simple algebra. The proofs will give a better understanding about the relationship of the movements in yield to maturity and bond prices.
AKMAL IDRIS
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
NIM
: G54104017
Disetujui
Donny C. Lesmana, S.Si., M.Fin.Math.
Pembimbing I
Dr. Ir. Endar H. Nugrahani, MS.
Pembimbing II
Diketahui
Dr. Drh. Hasim, DEA.
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan tugas akhir yang berjudul Penentuan Harga Obligasi untuk Beberapa Nilai Parameter. Shalawat serta salam senantiasa tercurah kepada Rasulullah SAW beserta keluarga, sahabat dan umatnya hingga akhir zaman.
Penulis mengucapkan terima kasih kepada Bapak Donny Citra Lesmana dan Ibu Endar Hasafah Nugrahani selaku dosen pembimbing atas waktu, bimbingan dan saran yang telah diberikan, serta Ibu Retno Budiarti atas kesediaannya menjadi penguji yang juga telah memberikan masukan yang dibutuhkan penulis. Ungkapan terima kasih juga disampaikan kepada:
1. Kedua orang tua tercinta, adik-adikku: Silfia, Fauziah, Irsyad, Annisa yang tersayang, serta seluruh keluarga atas doa, kasih sayang, serta dukungan yang telah diberikan kepada penulis. 2. Seluruh dosen Departemen Matematika IPB atas segala ilmu dan nasehat yang diberikan, serta
kepada staf Departemen Matematika (terima kasih atas bantuan yang telah diberikan kepada penulis).
3. Nur Armi, Yaya Sukarya, dan Nidia Rosita atas kesediaannya menjadi pembahas dalam seminar tugas akhir penulis.
4. Semua teman seperjuangan, senasib, dan sepenanggungan, Matematika 41. Terima kasih atas kenangan dan kebersamaan dalam segala suasana hati. Kebersamaan kita selama kuliah akan selalu menjadi kenangan terindah dalam hidupku.
5. Kakak-kakak kelas Matematika angkatan 38, 39 dan 40, serta adik-adik Matematika angkatan 42 dan 43.
6. Semua pihak yang telah memberikan dukungan kepada penulis yang tidak dapat disebutkan satu persatu sehingga tugas akhir ini dapat diselesaikan.
Penulis menyadari bahwa tugas akhir ini masih jauh dari kesempurnaan. Semoga tugas akhir ini dapat bermanfaat bagi penulis khususnya dan bagi pihak lain umumnya yang membutuhkan.
Bogor, Agustus 2009
Penulis dilahirkan di Bukittinggi pada tanggal 23 November 1985 dari pasangan Majusar dan Elya. Penulis merupakan anak pertama dari lima bersaudara.
Pada tahun 1998 penulis menyelesaikan pendidikan dasar di SDN 08 Muaralabuh, kemudian melanjutkan studi ke SLTPN 1 Muaralabuh hingga tahun 2001. Pada tahun 2004 penulis menyelesaikan pendidikan di SMUN 1 Muaralabuh dan pada tahun yang sama diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB (USMI).
Halaman
DAFTAR GAMBAR ...viii
DAFTAR TABEL ...viii
DAFTAR LAMPIRAN ...viii
PENDAHULUAN ... 1
Latar Belakang ... 1
Tujuan Penulisan ... 1
LANDASAN TEORI ... 1
PEMODELAN ... 3
PEMBAHASAN ... 4
Teorema 1 ... 4
Teorema 2 ... 4
Teorema 3 ... 4
Teorema 4 ... 5
Teorema 5 ... 6
ILUSTRASI ... 7
SIMPULAN ... 9
DAFTAR PUSTAKA ... 10
Halaman
1 Harga obligasi dengan kupon 10% ... 7
2 Harga obligasi ketika maturitas 20 tahun ... 8
DAFTAR GAMBAR
Halaman
1 Grafik perbandingan harga obligasi premi, pari dan diskonto ... 7
2 Grafik perbandingan harga obligasi dengan yield dan maturitas yang berbeda ... 8
3 Grafik perbandingan harga obligasi dengan yield dan kupon yang berbeda ... 9
DAFTAR LAMPIRAN
Halaman
1 Bukti persamaan (6) ... 12
2 Bukti hasil bagi persamaan (13) dengan persamaan (12) ... 13
PENDAHULUAN
Latar Belakang
Obligasi adalah surat hutang yang diterbitkan pemerintah atau perusahaan dalam rangka memenuhi kebutuhan dana. Setiap obligasi yang diterbitkan harus memuat nilai nominal, waktu jatuh tempo, tingkat bunga obligasi atau kupon dan waktu pembayaran bunga. Hal tersebut kemudian disebut sebagai karakteristik obligasi.
Dilihat dari kepentingan investor, obligasi termasuk jenis investasi yang relatif aman karena memiliki kepastian keuntungan yang diperoleh dari pendapatan tetap yang akan diterimanya selama waktu kepemilikan. Pendapatan tetap ini merupakan nilai pari, yaitu pendapatan sebesar jumlah modal pada awal investasi yang diterima pemegang obligasi pada waktu jatuh tempo dan kupon, yaitu bunga dari investasi yang diterima pemegang obligasi setiap tahun atau tengahtahunan selama kepemilikan obligasi.
Jenis obligasi yang akan dibahas dalam karya ilmiah ini adalah coupon bond atau obligasi berbunga. Obligasi berbunga pada umumnya mewajibkan pihak penerbit untuk melakukan pembayaran bunga hingga masa jatuh tempo kepada pemegang obligasi atau investor. Pada praktiknya, seorang investor yang mempertimbangkan pembelian obligasi tidak diberikan tingkat imbal hasil yang dijanjikan. Tetapi investor tersebut harus menggunakan harga obligasi, jangka waktu dan pembayaran bunga untuk kemudian menghitung imbal hasil yang ditawarkan obligasi tersebut sepanjang waktunya atau
hingga jatuh tempo (yield to maturity). Imbal hasil hingga jatuh tempo ini merupakan tingkat bunga yang menjadikan nilai sekarang dari pembayaran obligasi sama dengan harganya.
Hubungan antara harga obligasi dan imbal hasil hingga jatuh tempo telah ditunjukkan oleh Malkiel dalam teorema-teoremanya (Lawrence dan Shankar 2007). Bahkan teorema tersebut banyak digunakan atau dijadikan rujukan dalam buku-buku keuangan. Tapi, buku tersebut hanya menggunakan gambar dan contoh numerik untuk menunjukkan teorema Malkiel. Sebagai contoh, Corrado dan Jordan (2002, hal. 296) yang hanya memberikan contoh numerik; Bodie, Kane, dan Markus (2006, hal. 106-107), dan Charles P. Jones (2000, hal. 202) yang memberikan gambar dan contoh numerik, tanpa menunjukkan bukti logis. Tanpa bukti logis akan sulit untuk memahami hasil teorema-teorema tersebut. Oleh karena itu, dalam karya ilmiah ini akan dibahas cara alternatif berupa pendekatan teoretis yang menggunakan aljabar sederhana untuk membuktikan teorema-teorema Malkiel yang pada akhirnya akan membantu pemahaman teorema-teorema tersebut.
Tujuan Penulisan
Tujuan penulisan karya ilmiah ini adalah: 1. mempelajari hubungan antara yield to
maturitydan harga obligasi.
2. memberikan bukti logis dari teorema-teorema Malkiel dengan menggunakan aljabar sederhana.
LANDASAN TEORI
Karakteristik obligasi meliputi nilai obligasi (nilai nominal), tingkat suku bunga, jadwal pembayaran dan jangka waktu obligasi.
Nilai Nominal
Nilai nominal adalah nilai yang ditetapkan atas obligasi. Nilai tersebut menunjukkan jumlah uang yang dipinjam dan dibayar kembali oleh perusahaan pada tanggal jatuh tempo. Misalkan, bila perusahaan membutuhkan dana sebesar Rp
500 miliar maka akan diterbitkan obligasi bernilai Rp 500 miliar.
Tingkat Kupon
dapat menarik minat investor. Tentunya juga harus dipertimbangkan kemampuan perusahaan untuk membayar kupon tersebut sampai jatuh tempo.
Jadwal Pembayaran
Jadwal pembayaran adalah periode waktu yang mewajibkan perusahaan penerbit membayar kupon obligasi. Pembayaran dilakukan secara berkala dengan kesepakatan sebelumnya, bisa dilakukan triwulanan, semesteran atau tahunan. Ketepatan pembayaran kupon obligasi kepada investor merupakan aspek penting dalam menjaga reputasi perusahaan penerbit obligasi.
Jangka Waktu Obligasi
Jangka waktu obligasi adalah masa jatuh tempo atau berakhirnya masa pinjaman. Masa jatuh tempo obligasi di Indonesia satu sampai sepuluh tahun. Pada saat jatuh tempo, pihak penerbit berkewajiban untuk melunasi pokok investasi di dalam obligasi tersebut. Sebagai contoh, perusahaan mengeluarkan obligasi dengan nilai Rp 500 miliar untuk jangka waktu lima tahun. Saat memasuki masa jatuh tempo, perusahaan wajib membayar pinjaman sebesar Rp 500 miliar kepada investor beserta bunganya.
Definisi 1 (Present Value/Nilai Sekarang) Present valuemerupakan nilai sekarang dari sejumlah aliran kas di masa akan datang melalui pendiskontoan atas aliran kas di masa yang akan datang dengan tingkat bunga yang diharapkan, selama periode tertentu, yaitu:
nilai akan datang (1 )t
PV
r
dengan PV adalah nilai sekarang, t menyatakan waktu, dan r adalah suku bunga.
[Sundjaja dan Barlian, 2003]
Definisi 2 (Harga Obligasi)
1(1 ) (1 )
T t T t Cpn FV P r r
dengan P adalah harga obligasi, T adalah waktu jatuh tempo, r adalah suku bunga,
Cpnadalah pembayaran kupon, dan FV adalah Face Value(nilai pari atau nilai nominal).
[Bodie, Kane dan Marcus, 2006]
Definisi 3 (Yield to maturity)
Yield to maturity radalah suku bunga selama periode T yang membuat nilai sekarang dari pembayaran obligasi sama dengan harganya. Suku bunga ini sering kali dipandang sebagai sebuah ukuran atas tingkat imbal hasil rata-rata yang didapat dari sebuah obligasi jika dibeli saat ini dan dipegang hingga jatuh temponya. Untuk menghitung yield to maturity r, digunakan rumus harga obligasi untuk tingkat bunga tertentu dan pada harga yang telah ditentukan.
[Bodie, Kane dan Marcus, 2006]
Definisi 4 (Coupon Rate)
Coupon rate c (tingkat kupon atau bunga) merupakan pembayaran kupon per nilai nominalnya. Jadi:
Cpn c
FV
.
[Corrado dan Jordan, 2002]
Definisi 5 (Nilai Sekarang dari Anuitas) Nilai sekarang dari pembayaran tahunan sebesar $1 yang berjangka waktuTketika tingkat bunga radalah:
1 1
(1 )T
r r r
.
[Bodie, Kane dan Marcus, 2006] Atau secara umum:
1 1
(1 )T
PV A
r r r
,
dengan Aadalah besarnya pembayaran.
[Frensidy, 2007]
Premium bonds(obligasi premi)
Obligasi premi memiliki harga yang lebih besar daripada nilai parinya. Yield to maturitynya lebih kecil dari tingkat kuponnya.
Discount bonds(obligasi diskonto)
Obligasi diskonto memiliki harga yang lebih rendah daripada nilai parinya. Yield to maturitynya lebih besar dari tingkat kuponnya.
[Corrado dan Jordan, 2002]
Par bonds(obligasi pari)
Obligasi pari memiliki harga yang sama dengan nilai parinya. Yield to maturitynya juga sama dengan tingkat kuponnya.
[Corrado dan Jordan, 2002]
PEMODELAN
Diketahui dari definisi bahwa harga pasar sebuah obligasi adalah:
1(1 ) (1 )
T t T t Cpn FV P r r
.Bentuk di atas bila dijabarkan menjadi:
2
1 (1 ) (1 )T (1 )T
Cpn Cpn Cpn FV
P
r r r r
.
(1)
Dari persamaan di atas,FVadalah face value (nilai pari atau nilai nominal),radalah yield to maturity dan Cpn adalah pembayaran kupon. Jika cadalah tingkat kupon dan dari Definisi 4:
Cpn c
FV
,
maka tingkat kupon ditulis sebagai:
CpnFV c
. (2)
Substitusikan persamaan (2) ke persamaan (1), diperoeh harga obligasi:2
1 (1 ) (1 )T (1 )T
FV c FV c FV c FV
P
r r r r
.
(3)
Tingkat kupon c dan yield to maturity r adalah dua pecahan dan dapat dinyatakan sebagai:
c r x (4) dengan x adalah sebarang bilangan. Tingkat kupon cdari obligasi adalah tetap. Kemudian, x akan meningkat (menurun) dengan penurunan (peningkatan) pada yield to maturity r. Substitusikan persamaan (4) ke persamaan (3), diperoleh:
2 .
1 (1 ) (1 )T (1 )T
r x r x r x FV
P FV
r r r r
(5)
Dengan menggunakan formula nilai sekarang (present value) dari sebuah anuitas maka persamaan (5) menjadi (bukti di Lampiran 1):
1 1
(1 )T
P FV FV x
r r r
. (6) Hitungan dalam tanda kurung besar pada persamaan (6) di atas merupakan nilai sekarang dari anuitas sebesar $1 dan akan selalu taknegatif. Dari persamaan (6) bisa diketahui hubungan umum dan sederhana berikut:
a. Ketika x = 0, tingkat kupon sama dengan yield to maturity dan harga obligasi sama dengan nilai parinya. Obligasi seperti ini disebut dengan par bonds(obligasi pari). b. Untuk x > 0, yakni ketika tingkat kupon
obligasi lebih besar dibandingkan dengan yield to maturity, maka harga obligasi adalah:
P = FV + sebuah bilangan positif.
Selanjutnya, harga obligasi lebih besar daripada nilai parinya. Obligasi seperti ini disebut dengan premium bonds (obligasi premi).
c. Untuk x < 0, yakni ketika tingkat kupon lebih rendah dari yield to maturity, maka harga obligasi adalah:
P = FV+ sebuah bilangan negatif.
PEMBAHASAN
Teorema 1
Harga dan yield to maturity obligasi berhubungan terbalik.
Untuk membuktikan teorema di atas, harus ditunjukkan bahwa untuk peningkatan pada yield to maturity, harga obligasi akan menurun dan sebaliknya. Teorema 1 bisa dibuktikan dari persamaan (6), dengan harga obligasi diberikan oleh:
1 1
(1 )T
P FV FV x
r r r
.
Ketika yield to maturity dari obligasi meningkat, nilai sekarang dari anuitas sebesar $1 menurun dan nilai x pada persamaan (4) menurun (untuk obligasi premi, nilai x yang baru lebih rendah dari nilai sebelumnya, dan untuk obligasi diskonto, nilai x yang baru makin kecil dari nilai sebelumnya). Jadi dengan meningkatnya yield to maturity akan mengurangi harga obligasi. Sebaliknya, ketika yield to maturity menurun, nilai dari anuitas $1 meningkat dan nilai xjuga meningkat (nilai xyang baru lebih dari nilai sebelumnya untuk obligasi premi, dan nilai x yang baru kurang negatif untuk obligasi diskonto). Jadi dengan adanya penurunan pada yield to maturityakan meningkatkan harga obligasi. Karena itu, apakah obligasi tersebut obligasi premi atau diskonto, maka harga obligasi dan yield to maturityberhubungan terbalik.
Teorema 2
Untuk perubahan yang diberikan pada yield to maturity, perubahan pada harga obligasi lebih besar untuk waktu jatuh tempo yang lebih lama.
Asumsikan ada dua obligasi (obligasi 1 dan obligasi 2) dengan tingkat kupon dan nilai pari yang sama tapi berbeda jangka waktunya (T1 dan T2), denganT1> T2. Perubahan yang
sama pada yield to maturity yakni untuk r yang sama maka harga obligasi adalah:
1 1
1 1
(1 )T
P FV FV x
r r r
(7)
2 2
1 1
(1 )T
P FV FV x
r r r
. (8)
Jelas, semakin lama jangka waktu sebuah anuitas makin tinggi nilai anuitas yang akanterjadi. Karena hitungan pada tanda kurung besar dari persamaan (7) dan (8) di atas adalah nilai sekarang dari anuitas sebesar $1, diperolehP1> P2.
Ketika obligasi diperdagangkan pada nilai pari setelah adanya perubahan pada yield, nilai mutlak perubahan harga obligasi 1 lebih besar daripada nilai mutlak perubahan harga obligasi 2, yakni P1FV P2FV .
Nilai mutlak digunakan karena perubahan pada obligasi premi dan obligasi diskonto berlawanan arah. Untuk obligasi premi, x positif dan dari persamaan (7) dan (8), harga obligasi dengan jangka waktu yang lebih lama menjadi lebih besar dibandingkan dengan harga obligasi dengan jangka waktu yang lebih singkat, yakni P1 > P2. Karena pada
obligasi premi PFV maka
1 2
PFV P FV
.
Untuk obligasi diskonto, x negatif. Karena itu, suku kedua pada nilai sisi kanan persamaan (7) lebih negatif (nilainya lebih kecil) daripada suku kedua pada persamaan (8), sehingga mengakibatkan P1 < P2. Karena pada obligasi diskontoPFV maka P1FV P2FV yang kedua ruasnya bernilai negatif. Karena yang diukur perubahannya, maka masing-masing ruas tersebut harus dimutlakkan sehingga diperoleh
1 2
PFV P FV .
Berdasarkan bukti di atas, untuk obligasi premi: harga obligasi dengan kupon tengah tahunan akan jadi lebih besar dibandingkan dengan harga obligasi dengan kupon tahunan. Dengan cara yang sama, untuk obligasi diskonto: harga obligasi dengan kupon tengah tahunan akan jadi lebih rendah dibandingkan dengan harga obligasi dengan kupon tahunan.
Teorema 3
Persentase perubahan harga obligasi karena perubahan pada yield to maturity meningkat pada tingkat yang semakin berkurang ketika jangka waktu bertambah.
T + 1 ke T + 2. Dengan menggunakan persamaan (6), harga tiga obligasi (dengan jatuh tempo T, T + 1, T + 2) adalah:
1
1 1
(1 )T
P FV FV x
r r r
(9)
2 1
1 1
(1 )T
P FV FV x
r r r
(10)
3 2
1 1
(1 )T
P FV FV x
r r r
. (11) Persentase perubahan harga ketiga obligasi yang diperdagangkan adalah:
1
P FV FV
, P2 FV
FV
danP3 FV
FV
,
masing-masing untuk obligasi dengan jangka waktu T, T + 1 dan T + 2. Untuk menunjukkan bahwa persentase perubahan harga meningkat pada tingkat yang semakin berkurang ketika jangka waktu obligasi bertambah, harus ditunjukkan bahwa selisih P2– P1lebih besar
daripada selisih P3 – P2. Dari persamaan (9),
(10), dan (11):
2 1 1
1 1
(1 )T (1 )T
P P FV x
r r r r
(12)
3 2 1 2
1 1
(1 )T (1 )T
P P FV x
r r r r
.(13)
Dengan membagi persamaan (13) dengan persamaan (12), kita peroleh (bukti di Lampiran 2): 3 2 2 1 1 1 P P
P P r
.
Karena r > 0, penyebut dalam persamaan di atas lebih besar daripada 1 dan P2– P1 lebih
besar daripada P3 – P2 menandakan bahwa
persentase perubahan harga meningkat pada tingkat yang semakin berkurang ketika jangka waktu obligasi bertambah.
Teorema 4
Nilai mutlak dari perubahan harga sebagai akibat dari peningkatan dan penurunan dengan besaran yang sama pada yield to maturity adalah tidak simetris (penurunan pada yield to maturity obligasi menghasilkan perubahan harga yang lebih besar dibandingkan dengan peningkatan pada yield to maturity dengan besaran yang sama).
Dari persamaan (4) dan (6), peningkatan sebesar k pada yield to maturity maka harga obligasi yang baru adalah:
1 1
( ) .
( )(1 )
k T
P FV FV x k
r k r k r k
Kurangi persamaan di atas dengan persamaan (6), kita dapatkan perubahan pada harga sebagai berikut:
1 1
( )
( )(1 )
k T
P FV x k
r k r k r k
1 1
(1 )T
FV x
r r r
(14) Dengan cara yang sama dengan peningkatan yield to maturity sebesar k, untuk penurunan sebesar kdalam yield to maturity, perubahan harga obligasi menjadi:
1 1
( ) .
( )(1 )
k T
P FV FV x k
r k r k r k
Kurangi persamaan di atas dengan persamaan (6), diperoleh perubahan pada harga sebagai berikut:
1 1
( )
( )(1 )
k T
P FV x k
r k r k r k
1 1 (1 )T
FV x
r r r
. (15)
Harus ditunjukkan bahwa nilai mutlak dari perubahan harga sebagai akibat dari peningkatan dan penurunan dengan besaran yang sama pada yield to maturityadalah tidak simetris (tidak sama) dan penurunan pada yield to maturity menghasilkan perubahan harga yang lebih besar dibandingkan dengan peningkatan pada yield to maturity dengan besaran yang sama, yakni Pk < Pk . Sukukedua dari persamaan (14) dan (15) adalah sama. Oleh karena itu:
( ) ( )
FV x k AFV x k B.
Dengan 1 1
( )(1 )T
A
r k r k r k
dan
1 1
( )(1 )T
B
r k r k r k
.
di atas bernilai positif dan nilai suku pertama lebih besar daripada nilai suku kedua; lebih tinggi untuk yield to maturity yang lebih rendah dan lebih rendah untuk yield to maturityyang lebih tinggi karena suku kedua pada ruas kanan didiskontokan pada tingkat yang lebih rendah sehingga nilainya lebih besar daripada suku kedua ruas kiri dan juga nilai suku pertama ruas kanan lebih besar daripada suku pertama ruas kiri; dan (x + k) lebih besar daripada (x – k). Sebab itu, ruas kanan lebih besar daripada ruas kiri, menandakan bahwa nilai mutlak perubahan harga sebagai akibat dari peningkatan dan penurunan dengan besaran yang sama pada yield to maturity adalah tidak simetris dan penurunan pada yield to maturity menghasilkan perubahan harga lebih besar dibandingkan peningkatan pada yield to maturitydengan besaran yang sama.
Teorema 5
Obligasi dengan tingkat kupon yang lebih tinggi akan menghasilkan persentase perubahan harga yang lebih kecil akibat adanya perubahan pada yield to maturity dibandingkan dengan obligasi dengan tingkat kupon yang lebih rendah.
Misalkan dua oligasi (obligasi 1 dan obligasi 2) dengan tingkat kupon obligasi 1 (c1) lebih
besar daripada tingkat kupon obligasi 2 (c2).
Dengan menggunakan hubungan pada persamaan (4) dan (6), harga obligasi adalah:
1 1
1 1
( )
(1 )T
P FV FV c r
r r r
(16)
2 2
1 1
( )
(1 )T
P FV FV c r
r r r
. (17)
Karena c1 > c2, dari persamaan (16) dan (17)
jelas bahwa P1 > P2. Untuk penurunan sebesar
pada yield to maturity, harga dari obligasi 1 dan 2 diberikan oleh:
1 ( 1 )
P FVFV c r (18)
2 ( 2 )
P FVFV c r
(19)
dengan 1 1
( )(1 )T
r r r
.
Perbedaan dalam harga obligasi berkaitan dengan perbedaan dalam kedua hubungan dari persamaan harga (16), (17), (18), (19). Hitungan pertama FV adalah sama di setiap persamaan tersebut. Sebab itu, dengan membuang FV, persentase perubahan harga untuk dua obligasi dapat ditulis sebagai: a. Persentase perubahan harga obligasi 1:
1
1
1 1
( )
( )(1 )
1 1 1 ( ) (1 ) T T c r
r r r
c r
r r r .
b. Persentase perubahan harga obligasi 2:
2
2
1 1
( )
( )(1 )
1 1 1 ( ) (1 ) T T c r
r r r
c r
r r r .
Untuk menunjukan bahwa tingkat kupon yang lebih tinggi menghasilkan persentase perubahan harga yang lebih kecil, harus ditunjukkan bahwa persentase perubahan harga obligasi 2 lebih besar daripada persentase perubahan obligasi 1. Pada dasarnya harus ditunjukkan bahwa:
1 2
1 2
( ) ( )
( ) ( )
c r c r
c r c r
. (20) Untuk menunjukkan hubungan di atas, bisa dengan menggunakan sifat dasar bilangan asli. Jika ada dua bilangan pdan q, dengan p > q, maka (bukti di Lampiran 3):
p k q k
p q
.
ILUSTRASI
Untuk mengilustrasikan teorema-teorema Malkiel, digunakan dua tabel di bawah. Tabel 1 digunakan untuk ilustrasi Teorema 1 sampai Teorema 3 dan Tabel 2 untuk Teorema 4 dan Teorema 5. Pada masing-masing tabel diasumsikan nilai nominal obligasi adalah $1,000.00.
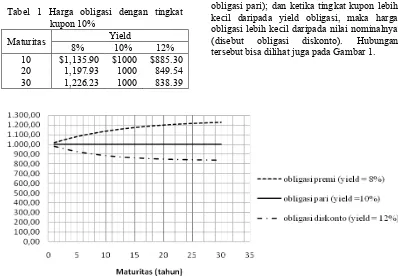
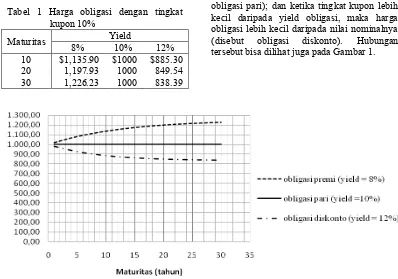
Tabel 1 Harga obligasi dengan tingkat kupon 10%
Maturitas Yield
8% 10% 12%
10 $1,135.90 $1000 $885.30 20 1,197.93 1000 849.54 30 1,226.23 1000 838.39
Dari Tabel 1 bisa diketahui beberapa hubungan berikut: ketika tingkat kupon lebih besar daripada yield obligasi, maka harga obligasi lebih besar daripada nilai nominalnya (disebut obligasi premi); ketika tingkat kupon dan yield obligasi sama, maka harga obligasi sama dengan nilai nominalnya (disebut obligasi pari); dan ketika tingkat kupon lebih kecil daripada yield obligasi, maka harga obligasi lebih kecil daripada nilai nominalnya (disebut obligasi diskonto). Hubungan tersebut bisa dilihat juga pada Gambar 1.
Gambar 1 Grafik perbandingan harga obligasi premi, pari dan diskonto.
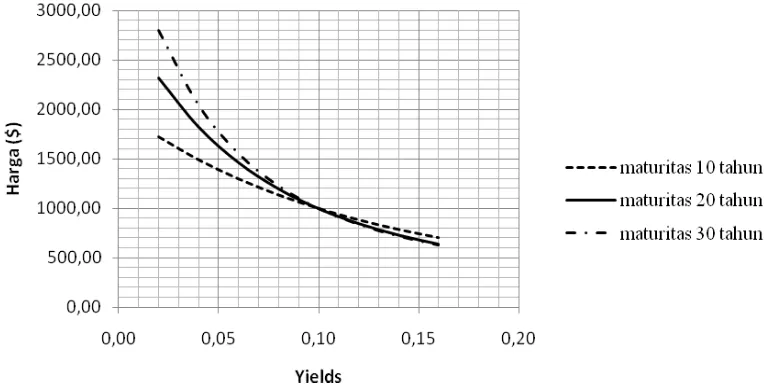
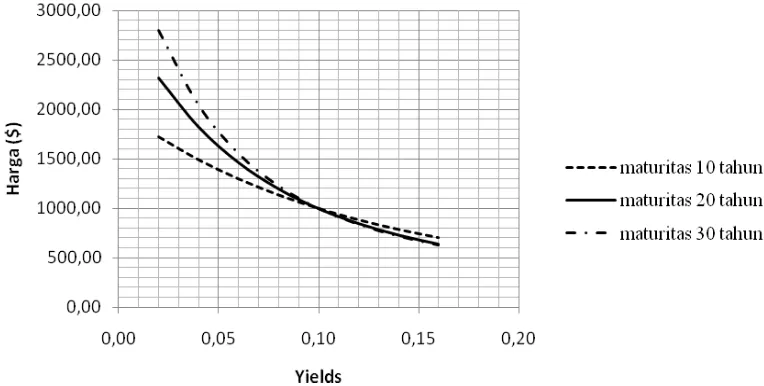
Teorema 1 menyatakan bahwa harga dan yield to maturityobligasi berbanding terbalik. Misalkan yieldawal adalah 10%. Dari tabel di atas bisa dilihat, ketika yield meningkat menjadi 12%, harga obligasi menurun. Sebaliknya, ketika yield menurun dari 10% menjadi 8%, harga obligasi meningkat (Gambar 2).
Ilustrasi untuk Teorema 2, misalkan ada dua obligasi dengan yield awal 10% dan maturitas 10 dan 20 tahun. Ketika yield berubah menjadi 8%, harga masing-masing obligasi juga berubah. Perubahan harga masingmasing obligasi adalah $1,135.90 -$1000 = $135.90 (untuk maturitas 10 tahun) dan $1,197.93 - $1000 = $197.93 (untuk maturitas 20 tahun). Jadi, obligasi dengan jangka waktu yang lebih lama memiliki perubahan harga yang lebih besar ketika yield berubah (Gambar 2). Cara yang sama bisa dilakukan ketika yield berubah menjadi 12%.
Tapi, perubahan harga masing-masing obligasi harus dimutlakkan karena bernilai negatif.
Gambar 2 Grafik perbandingan harga obligasi dengan yield dan maturitas yang berbeda.
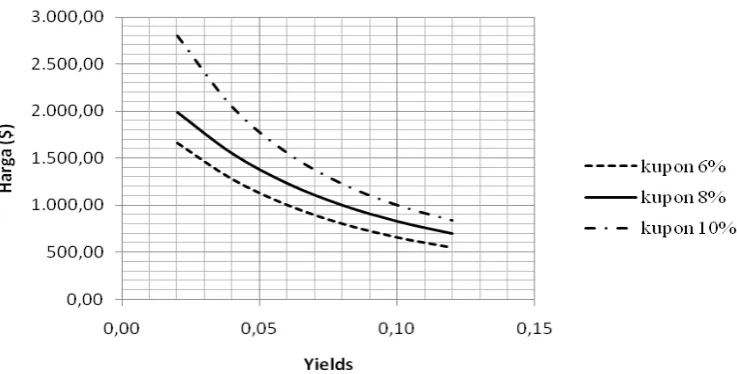
Tabel 2 Harga obligasi ($) ketika maturitas 20 tahun
Yield Tingkat Kupon
6% 8% 10%
6% 1,000.00 1,231.15 1,462.30 8% 802.07 1,000.00 1,197.93 10% 656.82 828.41 1,000.00
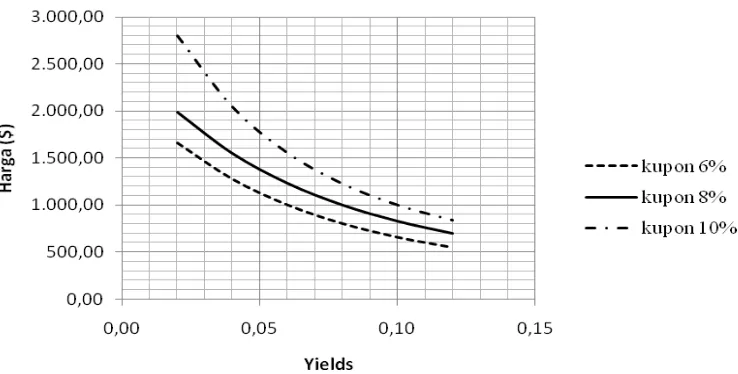
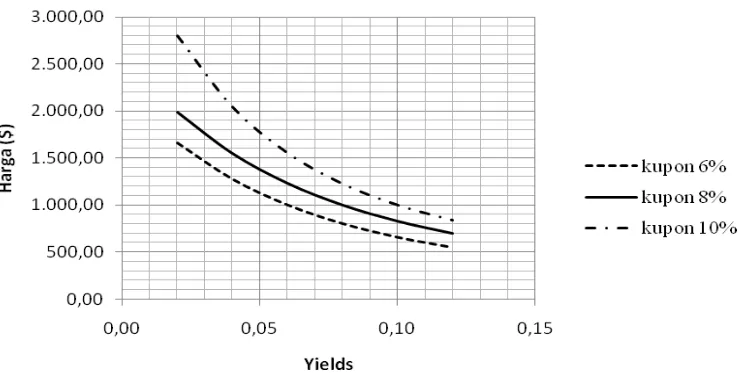
Teorema 4 menyatakan bahwa nilai mutlak dari perubahan harga sebagai akibat dari peningkatan dan penurunan dengan besaran yang sama pada yield to maturity adalah tidak simetris. Dengan kata lain, penurunan pada yield to maturity obligasi menghasilkan perubahan harga yang lebih besar dibandingkan dengan peningkatan pada yield to maturity dengan besaran yang sama. Misalkan obligasi dengan harga $1,000.00, yield 8% dan tingkat kupon 8%. Ketika yield menurun 2% dari 8% menjadi 6%, harga obligasi menjadi $1,231.15. Maka terjadi perubahan harga sebesar $231.15. Ketika yield meningkat 2% dari 8% menjadi 10%, harga obligasi menjadi $828.41. Maka terjadi perubahan harga sebesar $171.59. Jadi dengan adanya penurunan pada yield to maturity obligasi menghasilkan perubahan harga yang lebih besar dibandingkan dengan peningkatan
pada yield to maturity dengan besaran yang sama.
Gambar 3 Grafik perbandingan harga obligasi dengan yield dan kupon yang berbeda.
SIMPULAN
Hubungan antara perubahan harga dan yield to maturity obligasi telah lama dibuktikan oleh Malkiel dalam teorema-teoremanya. Hubungan tersebut bergantung pada kupon, waktu hingga jatuh tempo dan keadaan yield to maturity.
Adanya perubahan yang terjadi pada yield to maturity dan perbedaan pada jangka waktu obligasi akan mempengaruhi nilai sekarang dari sebuah anuitas. Nilai anuitas tersebut merupakan komponen dalam penentuan harga obligasi.
Dari bukti-bukti logis yang telah diberikan dapat diketahui bahwa:
1. yield to maturity dan harga obligasi berbanding terbalik. Dengan adanya peningkatan pada yield to maturity maka harga obligasi akan menurun dan sebaliknya.
2. Harga obligasi dengan waktu jatuh tempo yang lebih lama lebih sensitif dengan adanya perubahan pada yield to maturity dibandingkan dengan harga obligasi
dengan waktu jatuh tempo yang lebih singkat. Artinya, perubahan harga yang terjadi akan lebih besar pada obligasi dengan waktu jatuh tempo yang lebih lama.
3. Persentase perubahan harga akan meningkat pada tingkat yang semakin berkurang ketika jangka waktu jatuh tempo bertambah akibatnya berubahnya yield to maturity.
4. Penurunan pada yield to maturity obligasi menghasilkan perubahan harga yang lebih besar dibandingkan dengan peningkatan pada yield to maturity.
DAFTAR PUSTAKA
Bodie, Z., A. Kane, danA. J. Marcus.2006. Investments, 6th ed. New York: McGraw-Hill.
Corrado, C. J. dan B. D. Jordan. 2002. Fundamentals of Investments: Valuation and Management, 2nd ed. New York: McGraw-Hill.
Frensidy, B. 2007. Matematika Keuangan. Jakarta: Salemba Empat.
Jones, C. P.2000. Investments: Analysis and Management, 7th ed. New York: John Wiley & Sons, Inc.
Lawrence, E. R. dan S. Shankar. 2007. A Simple and Student-Friendly Approach to the Mathematics of Bond Prices. Quarterly Journal of Business and Economics,46: 91-99.
Lampiran 1 Bukti persamaan (6)
Dari persamaan (5):
2
2
1 (1 ) (1 ) (1 )
1 1 1
( ) .
1 (1 ) (1 ) (1 )
T T
T T
r x r x r x FV
P FV
r r r r
FV
P FV r x
r r r r
Dengan menggunakan formula nilai sekarang (present value) dari sebuah anuitas maka menjadi:
(1 ) (1 )
(1 ) (1 ) (1 )
1
1
(1 ) (1 ) (1 )
(1 ) (1 ) (1 )
(1 )
1 1
(1
T T
T T T
T T T
T T T
T
r x r x FV
P FV
r r r r
r x r x FV
FV
r r r r r r r
x x FV
FV
r r r r r
FV x FV FV x FV
FV
r r r r r
FV x FV x
FV
r r r
P FV FV x
r r r
)T .
Lampiran 2Bukti hasil bagi persamaan (13) dengan persamaan (12) 1 2 3 2 2 1 1 1 1
(1 ) (1 )
1 1
(1 ) (1 )
T T
T T
FV x
r r r r
P P P P
FV x
r r r r
2 1 2 3 1 2 1
(1 ) (1 )
(1 )
(1 ) (1 )
(1 ) T T T T T T r r r r r r
2 1 2 1
2 3 1
(1 ) (1 ) (1 )
(1 ) (1 ) (1 )
T T T
T T T
r r r
r r r
2 1 2 1
(1 ) (1 ) 1
(1 ) (1 ) (1 )
T T
T T
r r
r r r
2 1 3 2
(1 ) (1 )
(1 ) (1 )
T T T T r r r r
2
(1 ) 1 (1 ) (1 )
r r r
2
(1 2 ) (1 )
r
r r r
2 r r r
(1 ) r r r 3 2 2 1 1 1 P P
P P r
Lampiran 3Bukti persamaan (20)
1 1 p q
p q
, dengan 0
1 1
. k k
k p q
k k
p q
p k q k p p q q p k q k
p q
AKMAL IDRIS
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
AKMAL IDRIS. Determination of Bond Prices for Some Parameter Values. Under supervision of
DONNY CITRA LESMANAandENDAR HASAFAH NUGRAHANI.
A bond is a security that is issued in connection with a borrowing arrangement. The borrower issues (i.e. sells) a bond to the lender for some amount of cash. The arrangement obligates the issuer to make specified payments to the bondholder on specified dates. When the bond matures, the issuer repays the debt by paying the bondholder the bond’s par value (equivalently, its face value).
An investor considering the purchase of a bond is usually not quoted a promised rate of return. Instead, the investor must use the bond price, maturity date, and coupon payments to infer the return offered by the bond over its life, which is called the yield to maturity.
The relationship between yield to maturity and bond price were proved by Malkiel in his theorems. He showed how yield to maturity and bond prices movements depend on coupon rate, the time to maturity, and the existing yield to maturity. In this paper we prove the Malkiel theorems using simple algebra. The proofs will give a better understanding about the relationship of the movements in yield to maturity and bond prices.
PENDAHULUAN
Latar Belakang
Obligasi adalah surat hutang yang diterbitkan pemerintah atau perusahaan dalam rangka memenuhi kebutuhan dana. Setiap obligasi yang diterbitkan harus memuat nilai nominal, waktu jatuh tempo, tingkat bunga obligasi atau kupon dan waktu pembayaran bunga. Hal tersebut kemudian disebut sebagai karakteristik obligasi.
Dilihat dari kepentingan investor, obligasi termasuk jenis investasi yang relatif aman karena memiliki kepastian keuntungan yang diperoleh dari pendapatan tetap yang akan diterimanya selama waktu kepemilikan. Pendapatan tetap ini merupakan nilai pari, yaitu pendapatan sebesar jumlah modal pada awal investasi yang diterima pemegang obligasi pada waktu jatuh tempo dan kupon, yaitu bunga dari investasi yang diterima pemegang obligasi setiap tahun atau tengahtahunan selama kepemilikan obligasi.
Jenis obligasi yang akan dibahas dalam karya ilmiah ini adalah coupon bond atau obligasi berbunga. Obligasi berbunga pada umumnya mewajibkan pihak penerbit untuk melakukan pembayaran bunga hingga masa jatuh tempo kepada pemegang obligasi atau investor. Pada praktiknya, seorang investor yang mempertimbangkan pembelian obligasi tidak diberikan tingkat imbal hasil yang dijanjikan. Tetapi investor tersebut harus menggunakan harga obligasi, jangka waktu dan pembayaran bunga untuk kemudian menghitung imbal hasil yang ditawarkan obligasi tersebut sepanjang waktunya atau
hingga jatuh tempo (yield to maturity). Imbal hasil hingga jatuh tempo ini merupakan tingkat bunga yang menjadikan nilai sekarang dari pembayaran obligasi sama dengan harganya.
Hubungan antara harga obligasi dan imbal hasil hingga jatuh tempo telah ditunjukkan oleh Malkiel dalam teorema-teoremanya (Lawrence dan Shankar 2007). Bahkan teorema tersebut banyak digunakan atau dijadikan rujukan dalam buku-buku keuangan. Tapi, buku tersebut hanya menggunakan gambar dan contoh numerik untuk menunjukkan teorema Malkiel. Sebagai contoh, Corrado dan Jordan (2002, hal. 296) yang hanya memberikan contoh numerik; Bodie, Kane, dan Markus (2006, hal. 106-107), dan Charles P. Jones (2000, hal. 202) yang memberikan gambar dan contoh numerik, tanpa menunjukkan bukti logis. Tanpa bukti logis akan sulit untuk memahami hasil teorema-teorema tersebut. Oleh karena itu, dalam karya ilmiah ini akan dibahas cara alternatif berupa pendekatan teoretis yang menggunakan aljabar sederhana untuk membuktikan teorema-teorema Malkiel yang pada akhirnya akan membantu pemahaman teorema-teorema tersebut.
Tujuan Penulisan
Tujuan penulisan karya ilmiah ini adalah: 1. mempelajari hubungan antara yield to
maturitydan harga obligasi.
2. memberikan bukti logis dari teorema-teorema Malkiel dengan menggunakan aljabar sederhana.
LANDASAN TEORI
Karakteristik obligasi meliputi nilai obligasi (nilai nominal), tingkat suku bunga, jadwal pembayaran dan jangka waktu obligasi.
Nilai Nominal
Nilai nominal adalah nilai yang ditetapkan atas obligasi. Nilai tersebut menunjukkan jumlah uang yang dipinjam dan dibayar kembali oleh perusahaan pada tanggal jatuh tempo. Misalkan, bila perusahaan membutuhkan dana sebesar Rp
500 miliar maka akan diterbitkan obligasi bernilai Rp 500 miliar.
Tingkat Kupon
PENDAHULUAN
Latar Belakang
Obligasi adalah surat hutang yang diterbitkan pemerintah atau perusahaan dalam rangka memenuhi kebutuhan dana. Setiap obligasi yang diterbitkan harus memuat nilai nominal, waktu jatuh tempo, tingkat bunga obligasi atau kupon dan waktu pembayaran bunga. Hal tersebut kemudian disebut sebagai karakteristik obligasi.
Dilihat dari kepentingan investor, obligasi termasuk jenis investasi yang relatif aman karena memiliki kepastian keuntungan yang diperoleh dari pendapatan tetap yang akan diterimanya selama waktu kepemilikan. Pendapatan tetap ini merupakan nilai pari, yaitu pendapatan sebesar jumlah modal pada awal investasi yang diterima pemegang obligasi pada waktu jatuh tempo dan kupon, yaitu bunga dari investasi yang diterima pemegang obligasi setiap tahun atau tengahtahunan selama kepemilikan obligasi.
Jenis obligasi yang akan dibahas dalam karya ilmiah ini adalah coupon bond atau obligasi berbunga. Obligasi berbunga pada umumnya mewajibkan pihak penerbit untuk melakukan pembayaran bunga hingga masa jatuh tempo kepada pemegang obligasi atau investor. Pada praktiknya, seorang investor yang mempertimbangkan pembelian obligasi tidak diberikan tingkat imbal hasil yang dijanjikan. Tetapi investor tersebut harus menggunakan harga obligasi, jangka waktu dan pembayaran bunga untuk kemudian menghitung imbal hasil yang ditawarkan obligasi tersebut sepanjang waktunya atau
hingga jatuh tempo (yield to maturity). Imbal hasil hingga jatuh tempo ini merupakan tingkat bunga yang menjadikan nilai sekarang dari pembayaran obligasi sama dengan harganya.
Hubungan antara harga obligasi dan imbal hasil hingga jatuh tempo telah ditunjukkan oleh Malkiel dalam teorema-teoremanya (Lawrence dan Shankar 2007). Bahkan teorema tersebut banyak digunakan atau dijadikan rujukan dalam buku-buku keuangan. Tapi, buku tersebut hanya menggunakan gambar dan contoh numerik untuk menunjukkan teorema Malkiel. Sebagai contoh, Corrado dan Jordan (2002, hal. 296) yang hanya memberikan contoh numerik; Bodie, Kane, dan Markus (2006, hal. 106-107), dan Charles P. Jones (2000, hal. 202) yang memberikan gambar dan contoh numerik, tanpa menunjukkan bukti logis. Tanpa bukti logis akan sulit untuk memahami hasil teorema-teorema tersebut. Oleh karena itu, dalam karya ilmiah ini akan dibahas cara alternatif berupa pendekatan teoretis yang menggunakan aljabar sederhana untuk membuktikan teorema-teorema Malkiel yang pada akhirnya akan membantu pemahaman teorema-teorema tersebut.
Tujuan Penulisan
Tujuan penulisan karya ilmiah ini adalah: 1. mempelajari hubungan antara yield to
maturitydan harga obligasi.
2. memberikan bukti logis dari teorema-teorema Malkiel dengan menggunakan aljabar sederhana.
LANDASAN TEORI
Karakteristik obligasi meliputi nilai obligasi (nilai nominal), tingkat suku bunga, jadwal pembayaran dan jangka waktu obligasi.
Nilai Nominal
Nilai nominal adalah nilai yang ditetapkan atas obligasi. Nilai tersebut menunjukkan jumlah uang yang dipinjam dan dibayar kembali oleh perusahaan pada tanggal jatuh tempo. Misalkan, bila perusahaan membutuhkan dana sebesar Rp
500 miliar maka akan diterbitkan obligasi bernilai Rp 500 miliar.
Tingkat Kupon
dapat menarik minat investor. Tentunya juga harus dipertimbangkan kemampuan perusahaan untuk membayar kupon tersebut sampai jatuh tempo.
Jadwal Pembayaran
Jadwal pembayaran adalah periode waktu yang mewajibkan perusahaan penerbit membayar kupon obligasi. Pembayaran dilakukan secara berkala dengan kesepakatan sebelumnya, bisa dilakukan triwulanan, semesteran atau tahunan. Ketepatan pembayaran kupon obligasi kepada investor merupakan aspek penting dalam menjaga reputasi perusahaan penerbit obligasi.
Jangka Waktu Obligasi
Jangka waktu obligasi adalah masa jatuh tempo atau berakhirnya masa pinjaman. Masa jatuh tempo obligasi di Indonesia satu sampai sepuluh tahun. Pada saat jatuh tempo, pihak penerbit berkewajiban untuk melunasi pokok investasi di dalam obligasi tersebut. Sebagai contoh, perusahaan mengeluarkan obligasi dengan nilai Rp 500 miliar untuk jangka waktu lima tahun. Saat memasuki masa jatuh tempo, perusahaan wajib membayar pinjaman sebesar Rp 500 miliar kepada investor beserta bunganya.
Definisi 1 (Present Value/Nilai Sekarang) Present valuemerupakan nilai sekarang dari sejumlah aliran kas di masa akan datang melalui pendiskontoan atas aliran kas di masa yang akan datang dengan tingkat bunga yang diharapkan, selama periode tertentu, yaitu:
nilai akan datang (1 )t
PV
r
dengan PV adalah nilai sekarang, t menyatakan waktu, dan r adalah suku bunga.
[Sundjaja dan Barlian, 2003]
Definisi 2 (Harga Obligasi)
1(1 ) (1 )
T t T t Cpn FV P r r
dengan P adalah harga obligasi, T adalah waktu jatuh tempo, r adalah suku bunga,
Cpnadalah pembayaran kupon, dan FV adalah Face Value(nilai pari atau nilai nominal).
[Bodie, Kane dan Marcus, 2006]
Definisi 3 (Yield to maturity)
Yield to maturity radalah suku bunga selama periode T yang membuat nilai sekarang dari pembayaran obligasi sama dengan harganya. Suku bunga ini sering kali dipandang sebagai sebuah ukuran atas tingkat imbal hasil rata-rata yang didapat dari sebuah obligasi jika dibeli saat ini dan dipegang hingga jatuh temponya. Untuk menghitung yield to maturity r, digunakan rumus harga obligasi untuk tingkat bunga tertentu dan pada harga yang telah ditentukan.
[Bodie, Kane dan Marcus, 2006]
Definisi 4 (Coupon Rate)
Coupon rate c (tingkat kupon atau bunga) merupakan pembayaran kupon per nilai nominalnya. Jadi:
Cpn c
FV
.
[Corrado dan Jordan, 2002]
Definisi 5 (Nilai Sekarang dari Anuitas) Nilai sekarang dari pembayaran tahunan sebesar $1 yang berjangka waktuTketika tingkat bunga radalah:
1 1
(1 )T
r r r
.
[Bodie, Kane dan Marcus, 2006] Atau secara umum:
1 1
(1 )T
PV A
r r r
,
dengan Aadalah besarnya pembayaran.
[Frensidy, 2007]
Premium bonds(obligasi premi)
Obligasi premi memiliki harga yang lebih besar daripada nilai parinya. Yield to maturitynya lebih kecil dari tingkat kuponnya.
Discount bonds(obligasi diskonto)
Obligasi diskonto memiliki harga yang lebih rendah daripada nilai parinya. Yield to maturitynya lebih besar dari tingkat kuponnya.
[Corrado dan Jordan, 2002]
Par bonds(obligasi pari)
Obligasi pari memiliki harga yang sama dengan nilai parinya. Yield to maturitynya juga sama dengan tingkat kuponnya.
[Corrado dan Jordan, 2002]
PEMODELAN
Diketahui dari definisi bahwa harga pasar sebuah obligasi adalah:
1(1 ) (1 )
T t T t Cpn FV P r r
.Bentuk di atas bila dijabarkan menjadi:
2
1 (1 ) (1 )T (1 )T
Cpn Cpn Cpn FV
P
r r r r
.
(1)
Dari persamaan di atas,FVadalah face value (nilai pari atau nilai nominal),radalah yield to maturity dan Cpn adalah pembayaran kupon. Jika cadalah tingkat kupon dan dari Definisi 4:
Cpn c
FV
,
maka tingkat kupon ditulis sebagai:
CpnFV c
. (2)
Substitusikan persamaan (2) ke persamaan (1), diperoeh harga obligasi:2
1 (1 ) (1 )T (1 )T
FV c FV c FV c FV
P
r r r r
.
(3)
Tingkat kupon c dan yield to maturity r adalah dua pecahan dan dapat dinyatakan sebagai:
c r x (4) dengan x adalah sebarang bilangan. Tingkat kupon cdari obligasi adalah tetap. Kemudian, x akan meningkat (menurun) dengan penurunan (peningkatan) pada yield to maturity r. Substitusikan persamaan (4) ke persamaan (3), diperoleh:
2 .
1 (1 ) (1 )T (1 )T
r x r x r x FV
P FV
r r r r
(5)
Dengan menggunakan formula nilai sekarang (present value) dari sebuah anuitas maka persamaan (5) menjadi (bukti di Lampiran 1):
1 1
(1 )T
P FV FV x
r r r
. (6) Hitungan dalam tanda kurung besar pada persamaan (6) di atas merupakan nilai sekarang dari anuitas sebesar $1 dan akan selalu taknegatif. Dari persamaan (6) bisa diketahui hubungan umum dan sederhana berikut:
a. Ketika x = 0, tingkat kupon sama dengan yield to maturity dan harga obligasi sama dengan nilai parinya. Obligasi seperti ini disebut dengan par bonds(obligasi pari). b. Untuk x > 0, yakni ketika tingkat kupon
obligasi lebih besar dibandingkan dengan yield to maturity, maka harga obligasi adalah:
P = FV + sebuah bilangan positif.
Selanjutnya, harga obligasi lebih besar daripada nilai parinya. Obligasi seperti ini disebut dengan premium bonds (obligasi premi).
c. Untuk x < 0, yakni ketika tingkat kupon lebih rendah dari yield to maturity, maka harga obligasi adalah:
P = FV+ sebuah bilangan negatif.
Discount bonds(obligasi diskonto)
Obligasi diskonto memiliki harga yang lebih rendah daripada nilai parinya. Yield to maturitynya lebih besar dari tingkat kuponnya.
[Corrado dan Jordan, 2002]
Par bonds(obligasi pari)
Obligasi pari memiliki harga yang sama dengan nilai parinya. Yield to maturitynya juga sama dengan tingkat kuponnya.
[Corrado dan Jordan, 2002]
PEMODELAN
Diketahui dari definisi bahwa harga pasar sebuah obligasi adalah:
1(1 ) (1 )
T t T t Cpn FV P r r
.Bentuk di atas bila dijabarkan menjadi:
2
1 (1 ) (1 )T (1 )T
Cpn Cpn Cpn FV
P
r r r r
.
(1)
Dari persamaan di atas,FVadalah face value (nilai pari atau nilai nominal),radalah yield to maturity dan Cpn adalah pembayaran kupon. Jika cadalah tingkat kupon dan dari Definisi 4:
Cpn c
FV
,
maka tingkat kupon ditulis sebagai:
CpnFV c
. (2)
Substitusikan persamaan (2) ke persamaan (1), diperoeh harga obligasi:2
1 (1 ) (1 )T (1 )T
FV c FV c FV c FV
P
r r r r
.
(3)
Tingkat kupon c dan yield to maturity r adalah dua pecahan dan dapat dinyatakan sebagai:
c r x (4) dengan x adalah sebarang bilangan. Tingkat kupon cdari obligasi adalah tetap. Kemudian, x akan meningkat (menurun) dengan penurunan (peningkatan) pada yield to maturity r. Substitusikan persamaan (4) ke persamaan (3), diperoleh:
2 .
1 (1 ) (1 )T (1 )T
r x r x r x FV
P FV
r r r r
(5)
Dengan menggunakan formula nilai sekarang (present value) dari sebuah anuitas maka persamaan (5) menjadi (bukti di Lampiran 1):
1 1
(1 )T
P FV FV x
r r r
. (6) Hitungan dalam tanda kurung besar pada persamaan (6) di atas merupakan nilai sekarang dari anuitas sebesar $1 dan akan selalu taknegatif. Dari persamaan (6) bisa diketahui hubungan umum dan sederhana berikut:
a. Ketika x = 0, tingkat kupon sama dengan yield to maturity dan harga obligasi sama dengan nilai parinya. Obligasi seperti ini disebut dengan par bonds(obligasi pari). b. Untuk x > 0, yakni ketika tingkat kupon
obligasi lebih besar dibandingkan dengan yield to maturity, maka harga obligasi adalah:
P = FV + sebuah bilangan positif.
Selanjutnya, harga obligasi lebih besar daripada nilai parinya. Obligasi seperti ini disebut dengan premium bonds (obligasi premi).
c. Untuk x < 0, yakni ketika tingkat kupon lebih rendah dari yield to maturity, maka harga obligasi adalah:
P = FV+ sebuah bilangan negatif.
PEMBAHASAN
Teorema 1
Harga dan yield to maturity obligasi berhubungan terbalik.
Untuk membuktikan teorema di atas, harus ditunjukkan bahwa untuk peningkatan pada yield to maturity, harga obligasi akan menurun dan sebaliknya. Teorema 1 bisa dibuktikan dari persamaan (6), dengan harga obligasi diberikan oleh:
1 1
(1 )T
P FV FV x
r r r
.
Ketika yield to maturity dari obligasi meningkat, nilai sekarang dari anuitas sebesar $1 menurun dan nilai x pada persamaan (4) menurun (untuk obligasi premi, nilai x yang baru lebih rendah dari nilai sebelumnya, dan untuk obligasi diskonto, nilai x yang baru makin kecil dari nilai sebelumnya). Jadi dengan meningkatnya yield to maturity akan mengurangi harga obligasi. Sebaliknya, ketika yield to maturity menurun, nilai dari anuitas $1 meningkat dan nilai xjuga meningkat (nilai xyang baru lebih dari nilai sebelumnya untuk obligasi premi, dan nilai x yang baru kurang negatif untuk obligasi diskonto). Jadi dengan adanya penurunan pada yield to maturityakan meningkatkan harga obligasi. Karena itu, apakah obligasi tersebut obligasi premi atau diskonto, maka harga obligasi dan yield to maturityberhubungan terbalik.
Teorema 2
Untuk perubahan yang diberikan pada yield to maturity, perubahan pada harga obligasi lebih besar untuk waktu jatuh tempo yang lebih lama.
Asumsikan ada dua obligasi (obligasi 1 dan obligasi 2) dengan tingkat kupon dan nilai pari yang sama tapi berbeda jangka waktunya (T1 dan T2), denganT1> T2. Perubahan yang
sama pada yield to maturity yakni untuk r yang sama maka harga obligasi adalah:
1 1
1 1
(1 )T
P FV FV x
r r r
(7)
2 2
1 1
(1 )T
P FV FV x
r r r
. (8)
Jelas, semakin lama jangka waktu sebuah anuitas makin tinggi nilai anuitas yang akanterjadi. Karena hitungan pada tanda kurung besar dari persamaan (7) dan (8) di atas adalah nilai sekarang dari anuitas sebesar $1, diperolehP1> P2.
Ketika obligasi diperdagangkan pada nilai pari setelah adanya perubahan pada yield, nilai mutlak perubahan harga obligasi 1 lebih besar daripada nilai mutlak perubahan harga obligasi 2, yakni P1FV P2FV .
Nilai mutlak digunakan karena perubahan pada obligasi premi dan obligasi diskonto berlawanan arah. Untuk obligasi premi, x positif dan dari persamaan (7) dan (8), harga obligasi dengan jangka waktu yang lebih lama menjadi lebih besar dibandingkan dengan harga obligasi dengan jangka waktu yang lebih singkat, yakni P1 > P2. Karena pada
obligasi premi PFV maka
1 2
PFV P FV
.
Untuk obligasi diskonto, x negatif. Karena itu, suku kedua pada nilai sisi kanan persamaan (7) lebih negatif (nilainya lebih kecil) daripada suku kedua pada persamaan (8), sehingga mengakibatkan P1 < P2. Karena pada obligasi diskontoPFV maka P1FV P2FV yang kedua ruasnya bernilai negatif. Karena yang diukur perubahannya, maka masing-masing ruas tersebut harus dimutlakkan sehingga diperoleh
1 2
PFV P FV .
Berdasarkan bukti di atas, untuk obligasi premi: harga obligasi dengan kupon tengah tahunan akan jadi lebih besar dibandingkan dengan harga obligasi dengan kupon tahunan. Dengan cara yang sama, untuk obligasi diskonto: harga obligasi dengan kupon tengah tahunan akan jadi lebih rendah dibandingkan dengan harga obligasi dengan kupon tahunan.
Teorema 3
Persentase perubahan harga obligasi karena perubahan pada yield to maturity meningkat pada tingkat yang semakin berkurang ketika jangka waktu bertambah.
T + 1 ke T + 2. Dengan menggunakan persamaan (6), harga tiga obligasi (dengan jatuh tempo T, T + 1, T + 2) adalah:
1
1 1
(1 )T
P FV FV x
r r r
(9)
2 1
1 1
(1 )T
P FV FV x
r r r
(10)
3 2
1 1
(1 )T
P FV FV x
r r r
. (11) Persentase perubahan harga ketiga obligasi yang diperdagangkan adalah:
1
P FV FV
, P2 FV
FV
danP3 FV
FV
,
masing-masing untuk obligasi dengan jangka waktu T, T + 1 dan T + 2. Untuk menunjukkan bahwa persentase perubahan harga meningkat pada tingkat yang semakin berkurang ketika jangka waktu obligasi bertambah, harus ditunjukkan bahwa selisih P2– P1lebih besar
daripada selisih P3 – P2. Dari persamaan (9),
(10), dan (11):
2 1 1
1 1
(1 )T (1 )T
P P FV x
r r r r
(12)
3 2 1 2
1 1
(1 )T (1 )T
P P FV x
r r r r
.(13)
Dengan membagi persamaan (13) dengan persamaan (12), kita peroleh (bukti di Lampiran 2): 3 2 2 1 1 1 P P
P P r
.
Karena r > 0, penyebut dalam persamaan di atas lebih besar daripada 1 dan P2– P1 lebih
besar daripada P3 – P2 menandakan bahwa
persentase perubahan harga meningkat pada tingkat yang semakin berkurang ketika jangka waktu obligasi bertambah.
Teorema 4
Nilai mutlak dari perubahan harga sebagai akibat dari peningkatan dan penurunan dengan besaran yang sama pada yield to maturity adalah tidak simetris (penurunan pada yield to maturity obligasi menghasilkan perubahan harga yang lebih besar dibandingkan dengan peningkatan pada yield to maturity dengan besaran yang sama).
Dari persamaan (4) dan (6), peningkatan sebesar k pada yield to maturity maka harga obligasi yang baru adalah:
1 1
( ) .
( )(1 )
k T
P FV FV x k
r k r k r k
Kurangi persamaan di atas dengan persamaan (6), kita dapatkan perubahan pada harga sebagai berikut:
1 1
( )
( )(1 )
k T
P FV x k
r k r k r k
1 1
(1 )T
FV x
r r r
(14) Dengan cara yang sama dengan peningkatan yield to maturity sebesar k, untuk penurunan sebesar kdalam yield to maturity, perubahan harga obligasi menjadi:
1 1
( ) .
( )(1 )
k T
P FV FV x k
r k r k r k
Kurangi persamaan di atas dengan persamaan (6), diperoleh perubahan pada harga sebagai berikut:
1 1
( )
( )(1 )
k T
P FV x k
r k r k r k
1 1 (1 )T
FV x
r r r
. (15)
Harus ditunjukkan bahwa nilai mutlak dari perubahan harga sebagai akibat dari peningkatan dan penurunan dengan besaran yang sama pada yield to maturityadalah tidak simetris (tidak sama) dan penurunan pada yield to maturity menghasilkan perubahan harga yang lebih besar dibandingkan dengan peningkatan pada yield to maturity dengan besaran yang sama, yakni Pk < Pk . Sukukedua dari persamaan (14) dan (15) adalah sama. Oleh karena itu:
( ) ( )
FV x k AFV x k B.
Dengan 1 1
( )(1 )T
A
r k r k r k