Penentuan Rute Bus Karyawan Menggunakan Pemrograman Linear Integer

(1)

ZIL’ARIFAH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

ZIL’ARIFAH

G54050899

(3)

Dibimbing oleh PRAPTO TRI SUPRIYO dan FARIDA HANUM.

(4)

Supervised by PRAPTO TRI SUPRIYO and FARIDA HANUM.

(5)

ZIL’ARIFAH

G54050899

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada

Departemen Matematika

(6)

NIM

: G54050899

Menyetujui,

Mengetahui:

Ketua Departemen

Dr. Berlian Setiawaty, M.S.

NIP. 19650505 198903 2 004

Tanggal Lulus :

Pembimbing I

Drs. Prapto Tri Supriyo, M.Kom.

NIP. 19630715 199002 1 002

Pembimbing II

(7)

pertolongan-Nya, sehingga penulis dapat menyelesaikan karya ilmiah yang berjudul “Penentuan Rute Bus Karyawan Menggunakan Pemrograman Linear Integer”. Karya ilmiah ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Terima kasih penulis ucapkan kepada:

1. _{Sang pencipta, Tuhan semesta alam Allah SWT, atas maha karya-Nya,} 2. _{Nabi besar Muhammad SAW sebagai penutup para nabi,}

3. _{Bapak dan Ibu tercinta; Drs. Ermasdi dan Brata Graha, atas segala dukungan, motivasi,} pembelajaran, masukan, dan segala kasih sayang yang diberikan kepada penulis, juga adik-adikku tersayang, Rozaanah, Fauzan Aziman, dan Hanifatul Khairiyah, atas segala kasih sayangnya dan keceriaannya,

4. _{Bapak Drs. Prapto Tri Supriyo, M. Kom dan Ibu Dra. Farida Hanum, M.Si, selaku dosen} pembimbing, atas segala kesabaran dan masukan serta doanya selama membimbing penulis, tak lupa kepada Bapak Drs. Siswandi, M. Si selaku penguji yang telah memberikan ilmu, saran, dan doanya,

5. _{semua dosen Departemen Matematika, terima kasih atas semua ilmu yang telah diberikan,} 6. _{staf Departemen Matematika: Bapak Yono, Bapak Hery, Bapak Deni, Ibu Ade, Bapak Epul,}

Bapak Bono dan Ibu Susi atas semangat dan doanya,

7. _{keluarga besar Ibu Sulastri, Mama El, Mama Af,}_Etek_Am,_Om_Eri,_Etek_Pit,_Etek_Ira,_Etek_Eda,

Etek Nel, Etek Adek, Pa Etek Razak, Pa Etek Am, dan Pa Etek Fadly,

8. _{keluarga besar Bapak M. Yusuf, terutama Ibu Maemunah,}_Mamang_Sabeni,_Bibi_Lilis,_Uwa Isah, Siska, Syukri, dan Fajar,

9. _{keluarga besar Bapak Mardani, terutama Ibu Hj. Masna Ulyanah Mardani,}_Aa_Dicky,_Mas Risyad, Aa Fikri, Kang Ade, Wildan, dan Algifari,

10._{Chandra yang selalu mendampingi serta memberikan semangat, dukungan, dan doanya,} 11._{Afat yang selalu memberikan semangat, dan doanya,}

12._{sahabat-sahabatku tersayang yang selalu memberi semangat; Kiky, Warno, Mega, Dhani, dan}

Aa Dede, atas segala tawa dan tangis, manis dan pahit, suka dan duka selama persahabatan kita, 13._{teman-teman mahasiswa angkatan 42: Riyu, Ricken, Agnes, Hikmah, Dian, Titi, Mira, Octa,} Rita, Vita, Vera, Gita, Luri, Rima, Hesti, Ayu, Nyoman, Lisda, Ida, Achi, Dewi, Septiwi, Erlin, Eyyi, Hapsari, Jane, Lela, Lina, Mega, Niken, Nola, Nofi, Oby, Ocoy, Pipit, Siti, Tia, Vino, Yuni, Ety, Yudi, Danu, Sapto, Dendi, Ardy, Septian, Awi, Eko, Rendy, Boy, Jawa, Arif, Makinun, Ridwan, Yusep, Bima, Ilyas, Iput, Fachri, Warno, Heri, Acuy, dan Bayu, atas segenap dukungan, suka duka dan keceriaan selama penulis menempuh studi di Departemen Matematika IPB,

14._{kakak-kakak mahasiswa matematika angkatan 40, terutama kak Rusli, atas segala bantuannya} dalam mengajarkan Lingo; kakak-kakak mahasiswa angkatan 41, terutama kak Aji, atas bantuannya; adik-adik mahasiswa angkatan 43, terutama Slamet atas bantuannya dan Faizal yang telah bersedia menjadi pembahas, dan adik-adik mahasiswa angkatan 44,

15._{keluarga besar BEM FMIPA IPB angkatan 2006-2007 dan angkatan 2007-2008, atas segenap} dukungan, doa, dorongan semangat, dan warna warni dalam kebersamaan kita,

16._{keluarga besar pengurus Gumatika IPB, atas dukungan dan doanya,}

17._{pembimbing dan asisten pengajar Kumon Taman Yasmin; bu Yani, pak Bambang,}_mbak_Berti,

mbak Eka, mbak Era, mbak Sri, mbak Iis, mbak Nining, mbak Mira, mbak Tina, mbak Titi,

mbak Oy, Susi, Roby, Mia, Dwi, Wiwi, Eyyi, dan Riska,

18._{teman-teman penghuni Maharlika Depan; Vina, Ayu, Veza, Yuyun, Icha, Ninu’, Almira dan} Isna,

19._{semua pihak yang telah membantu dalam penyusunan karya ilmiah ini.}

Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu penulis mengharapkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat.

Bogor, Februari 2012

(8)

Brata Graha. Penulis merupakan anak pertama dari empat bersaudara.

Pada tahun 1999 penulis lulus dari SD Negeri 22 Batusangkar kemudian tahun 2002 lulus dari SLTP Negeri 1 Batusangkar. Tahun 2005 penulis lulus dari SMA Negeri 1 Padang Panjang dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur USMI (Undangan Seleksi Masuk IPB). Pada tahun 2006, penulis memilih Mayor Matematika dan Minor Statistika Industri, Fakultas Matematika dan Ilmu Pengetahuan Alam.

(9)

vii

Halaman

DAFTAR TABEL viii

DAFTAR GAMBAR viii

DAFTARLAMPIRAN viii

I PENDAHULUAN

1.1 Latar Belakang 1

1.2 Tujuan 1

II LANDASAN TEORI

2.1 Fungsi Linear dan Pertidaksamaan Linear 1

2.2 Pemrograman Linear 1

2.3 Pemrograman Integer (Integer Programming) 3

2.4 Relaksasi Pemrograman Linear 3

2.5 Graf 3

2.6 Masalah Path Terpendek 4

2.7 Traveling Salesman Problem (TSP) 5

2.8 Metode Branch-and-Bound 6

III DESKRIPSI DAN FORMULASI MASALAH

3.1 Deskripsi Masalah Rute Bus Karyawan 9

3.2 Model Masalah Rute Bus Karyawan 9

IV STUDI KASUS 12

V SIMPULAN DAN SARAN

5.1 Simpulan 15

5.2 Saran 15

DAFTAR PUSTAKA 15

(10)

viii

1 Jarak antarpos penjemputan bus karyawan 12

2 Banyaknya karyawan yang dijemput pada setiap pos 13

3 Rute solusi optimal untuk bus Pertama 14

4 Rute solusi optimal untuk bus kedua 14

5 Rute solusi optimal untuk bus ketiga 14

6 Rute solusi optimal untuk bus keempat 14

DAFTAR GAMBAR

Halaman

1 Graf G = (V, E) 3

2 Graf G’ = (V, E) 4

3 Graf berbobot G’ =(V,A) 4

4 Contoh rute dalam traveling salesman problem (TSP) 5

5 Input dari sebuah VRP 5

6 Solusi yang mungkin dari VRP pada Gambar 5 dengan tiga kendaraan 6

7 Daerah fisibel untuk PL-relaksasi dan IP (2.7) 7

8 Daerah fisibel untuk Subproblem 2 dan Subproblem 3 dari IP (2.7) 8 9 Seluruh pencabangan pada metode branch-and-bound untuk menyelesaikan IP (2.7) 9

10 Perjalanan bus yang berupa subrute 11

11 Perjalanan bus yang berupa rute 11

12 Solusi rute perjalanan 14

DAFTAR LAMPIRAN

Halaman

1 Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode Branch-and-Bound Beserta Hasil yang Diperoleh 17 2 Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah Rute Bus Karyawan 21 3 Hasil Komputasi Program pada Lingo 8.0 untuk Menyelesaikan Masalah Rute Bus Karyawan

23

(11)

1.1Latar Belakang

Masalah penentuan rute bus karyawan mendapat perhatian dari para peneliti selama lebih kurang 30 tahun belakangan ini. Masalah optimisasi rute bus karyawan secara matematis termasuk dalam kelas permasalahan yang disebut Vehicle Routing Problem (VRP). Bentuk dasar VRP berkaitan dengan masalah penentuan suatu himpunan rute kendaraan (vehicle) yang melayani suatu himpunan pelanggan.

Dalam kehidupan sehari-hari banyak ditemukan terapan VRP, antara lain pendistribusian barang hasil produksi oleh produsen ke konsumen, pengambilan surat dari kotak-kotak pos yang tersebar di seluruh kota, pengantaran dan penjemputan anak sekolah dengan bus sekolah.

Karakteristik khusus yang diperhatikan dalam masalah bus karyawan di antaranya, bus tidak kembali ke pos yang sudah

dilewatinya setelah melengkapi rute perjalanannya tetapi bus mengakhiri perjalanannya di depot, serta banyaknya karyawan pada setiap bus tidak melebihi kapasitas bus.

Tulisan ini akan membahas bagaimana mengoptimalkan biaya yang berhubungan dengan pengangkutan karyawan dengan menggunakan PLI (pemrograman linear integer) sedemikian sehingga kendala-kendalanya dipenuhi. Model penentuan rute bus karyawan pada karya ilmiah ini berdasarkan pada artikel berjudul “Solving school bus routing problems through integer programming” yang ditulis oleh T Bektas dan Seda Elmastas tahun 2007.

1.2Tujuan

Tujuan penulisan ini adalah memodelkan dan menyelesaikan masalah penentuan rute bus karyawan dengan PLI.

II LANDASAN TEORI

Untuk membuat model penentuan rute bus karyawan dan teknik-teknik pemecahan yang digunakan dalam karya tulis ini, diperlukan pemahaman teori pemrograman linear (PL), Pemrograman Linear Integer (PLI) atau Integer Linear Programming (ILP), dan metode branch-and-bound.

2.1Fungsi Linear dan Pertidaksamaan Linear

Fungsi linear dan pertidaksamaan linear merupakan salah satu konsep dasar yang harus dipahami terkait dengan konsep pemrograman linear.

Definisi 1 (Fungsi Linear)

Misalkan f(x₁,x₂,...,x_n) menyatakan suatu fungsi dalam variabel-variabel

. Fungsi dikatakan linear jika dan hanya jika untuk suatu himpunan konstanta , fungsi f

dapat dituliskan sebagai

(Winston 2004)

Sebagai gambaran,

merupakan fungsi linear, sementara bukan fungsi linear.

Definisi 2 (Pertidaksamaan dan Persamaan Linear)

Untuk sembarang fungsi linear dan sembarang bilangan

pertidaksamaan dan

adalah pertidaksamaan linear; sedangkan

merupakan persamaan linear.

(Winston 2004)

2.2 Pemrograman Linear

Menurut Winston (2004), pemrograman linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut.

a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

n

x x

x1, 2,..., f(x1,x2,...,xn)

n

c c c1, 2,...,

. ... )

,..., ,

(x1 x2 xn c1x1 c2x2 cnxn

f = + + +

2 1 2 1, ) 2 (x x x x

f = +

2 2 1 2 1, ) (x x x x

f =

) ,..., , (x1 x2 xn

f b,

b x x x

f( 1, 2,..., n)≤

b x x x

f( 1, 2,..., n)≥

b x x x

(12)

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel , pembatasan tanda menentukan harus taknegatif

atau tidak dibatasi tandanya (unrestricted in sign).

Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 (Bentuk Standar PL) Pemrograman linear

min z = cTx terhadap Ax = b

x ≥ 0 (2.1)

dikatakan PL dalam bentuk standar, dengan x dan c vektor-vektor berukuran n, vektor b berukuran m, dan A matriks berukuran m × n yang disebut sebagai matriks kendala, dengan m ≤ n.

(Nash & Sofer 1996)

Sebagai catatan, yang dimaksud dengan vektor berukuran n adalah vektor yang memiliki dimensi (ukuran) n × 1.

Solusi Pemrograman Linear

Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimal bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947, dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.

Pada masalah PL (2.1), vektor x yang memenuhi kendala disebut solusi PL (2.1). Misalkan matriks A dapat dinyatakan sebagai , dengan B adalah

matriks berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks berukuran

yang elemen-elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks B disebut matriks basis untuk PL (2.1).

Misalkan x dapat dinyatakan sebagai

vektor , dengan adalah vektor

variabel basis dan adalah vektor variabel nonbasis, maka dapat dinyatakan

sebagai

(2.2) Karena matriks B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2.2) xB dapat dinyatakan sebagai:

xB = B-1b – B-1NxN. (2.3)

Definisi 4 (Daerah Fisibel)

Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.

(Winston 2004)

Definisi 5 (Solusi Basis)

Solusi dari suatu PL disebut solusi basis jika memenuhi syarat berikut:

i. solusi tersebut memenuhi kendala pesamaan pada PL,

ii. kolom-kolom dari matriks kendala yang berpadanan dengan komponen taknol dari solusi tersebut adalah bebas linear.

(Nash & Sofer 1996)

Definisi 6 (Solusi Fisibel Basis)

Solusi fisibel basis adalah solusi basis pada PL yang semua variabel-variabelnya taknegatif.

(Winston 2004)

Definisi 7 (Solusi Optimal)

Untuk masalah maksimisasi, solusi optimal suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimal suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston 2004)

Ilustrasi solusi basis dan solusi fisibel basis diberikan dalam Contoh 1.

Contoh 1

Misalkan diberikan PL (2.4) berikut: min z = −2x1 – 3x2

terhadap −2x1 + x2 + x3 = 4

−x1 + 2x2 + x4 = 11 (2.4) x1 + x5 = 5

x1, x2, x3, x4, x5≥ 0

Dari PL (2.4) diperoleh:

i

x

i

x (xi ≥0)

=

Ax b

(

)

=

A B N

( ) m× −n m

⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ B N x x

x xB

N x = Ax b

(

)

⎛ ⎞ = _⎜ _⎟ ⎝ ⎠ B N x

Ax B N

x

.

(13)

.

Misalkan dipilih

maka matriks basisnya adalah

.

Dengan menggunakan matriks basis di atas didapatkan

(2.5) Solusi (2.5) merupakan solusi basis, karena memenuhi kendala pada PL (2.4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (2.5), yaitu , bebas linear. Solusi (2.5) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

PL (2.1) dapat dinyatakan dalam bentuk dan sebagai berikut

(2.6)

dengan cB vektor koefisien variabel basis pada

fungsi objektif dan cN vektor koefisien

variabel nonbasis pada fungsi objektif. Jika persamaan (2.3) disubstitusikan ke dalam fungsi objektif PL (2.6) maka akan didapat

(Winston 2004)

2.3 Pemrograman Integer (Integer Programming)

pemrograman integer (PI) atau Integer programming (IP) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming. IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

(Garfinkel & Nemhauser 1972)

2.4 Relaksasi Pemrograman Linear

Konsep relaksasi pemrograman linear atau relaksasi-PL diberikan dalam definisi berikut ini.

Definisi 8 (Relaksasi Pemrograman Linear) Pemrograman linear relaksasi atau sering disebut relaksasi-PL merupakan suatu pemrograman linear yang diperoleh dari suatu IP dengan menghilangkan kendala integer atau kendala 0-1 pada setiap variabelnya.

Untuk masalah maksimisasi, nilai optimal fungsi objektif relaksasi-PL lebih besar atau sama dengan nilai optimal fungsi objektif IP, sedangkan untuk masalah minimisasi, nilai optimal fungsi objektif relaksasi-PL lebih kecil atau sama dengan nilai optimal fungsi objektif IP.

(Winston 1995)

2.5 Graf

Konsep graf yang digunakan dalam karya ilmiah ini meliputi definisi-definisi berikut ini.

Definisi 9 (Graf)

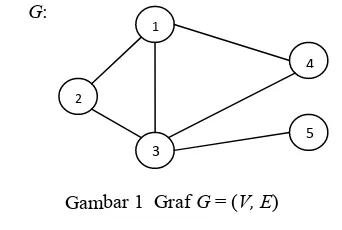
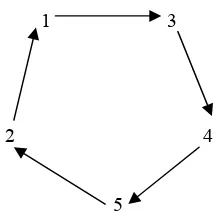
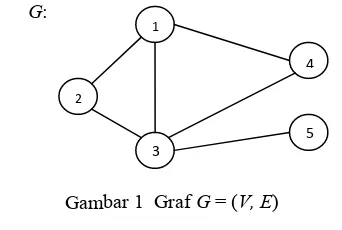
Suatu graf G adalah pasangan terurut (V, E) dengan V himpunan takkosong dan berhingga yang anggota-anggotanya disebut simpul (node/vertex) dan E merupakan himpunan berhingga garis yang menghubungkan simpul-simpul anggota V yang disebut dengan sisi (edge). Sisi yang menghubungkan simpul i dengan simpul j dinyatakan dengan {i, j}.

(Foulds 1992)

Graf seperti disebutkan pada definisi di atas disebut juga graf tak berarah. Ilustrasi graf tak berarah dapat dilihat pada Gambar 1 berikut:

Gambar 1 Graf G = (V, E)

Pada Gambar 1 di atas diperlihatkan bahwa dan

Definisi 10 (Graf Berarah)

Dalam suatu graf, jika sisi yang menghubungkan simpul-simpulnya berarah 2 1 1 0 0 4

1 2 0 1 0 , 11 1 0 0 0 1 5 − ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = −_⎜ _⎟ =_{⎜ ⎟} ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ A b

(

x3 x4 x5

)

dan

(

x1 x2

)

,

= T = T

B N

x x

1 0 0 0 1 0 0 0 1

⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ B

(

0 0

)

, −

(

4 11 5

)

.

= T = 1 = T

N B

x x B b

B

x x_N

min terhadap

, z= +

+ =

≥

T T

B B N N

B N

c x c x

Bx Nx b

x 0

( )

( ) .

z − −

− −

= − +

= + −

T 1 1 T

B N N N

T 1 T T 1

B N B N

c B b B Nx c x

c B b c c B N x

{1, 2, 3, 4,5} V =

(14)

maka graf tersebut dinamakan graf berarah (directed graph/digraph). Sisi yang menghubungkan simpul i dengan simpul j berarah dinyatakan dengan {i, j}.

(Foulds 1992)

Ilustrasi graf berarah dapat dilihat pada gambar berikut

Gambar 2 Graf

Pada Gambar 2 diperlihatkan bahwa dan

Definisi 11(Walk)

Suatu walk pada graf G = (V, E) adalah suatu barisan simpul dan sisi dari G dengan bentuk:

atau ditulis dengan ringkas :

atau Walk tersebut

menghubungkan simpul dengan simpul

(Foulds 1992)

Definisi 12 (Path)

Path pada suatu graf G adalah suatu walk dengan semua simpulnya berbeda.

(Foulds 1992)

Ilustrasi walk dan path diberikan sebagai berikut. Pada graf G yang terdapat dalam Gambar 1, salah satu contoh walk adalah , sedangkan adalah salah satu contoh path.

Definisi 13 (Walk Berarah)

Walk berarah pada suatu graf berarah adalah suatu barisan terurut simpul dan sisi pada yang berbentuk

dengan setiap sisi berarah ai menghubungkan simpul-simpul vi-1 dan vi secara berurutan.

(Foulds 1992)

Definisi 14 (Path Berarah)

Path berarah pada graf berarah G’ adalah suatu walk berarah yang semua simpulnya berbeda.

(Foulds 1992)

Ilustrasi walk dan path berarah diberikan sebagai berikut. Pada graf berarah yang terdapat dalam Gambar 2, contoh walk berarah adalah , dan contoh

path berarah adalah .

Definisi 15 (Graf Berbobot)

Suatu graf G = (V, E) atau graf berarah dikatakan berbobot jika terdapat fungsi atau (dengan

himpunan bilangan real) yang memberikan bobot pada setiap elemen E atau A.

(Foulds 1992)

Ilustrasi graf berbobot diberikan dalam Gambar 3.

Gambar 3 Graf berbobot

Misalkan diberikan untuk graf berbobot pada Gambar 3, maka

= 3 atau dapat pula ditulis

2.6 Masalah Path Terpendek

Masalah penentuan rute perjalanan dengan biaya minimum merupakan aplikasi dari masalah penentuan path terpendek dalam suatu graf berbobot. Didefinisikan panjang untuk sembarang path berarah dalam suatu network sebagai jumlah biaya semua sisi berarah dalam path tersebut. Dalam masalah ini akan dicari suatu path terpendek, yakni path berarah dari suatu simpul asal ke simpul tujuan dengan panjang terkecil.

Dalam bab ini, juga dijelaskan tentang traveling salesman problem (TSP) yang merupakan dasar dari vehicle routing problem (VRP), kemudian akan diperlihatkan ' ( , ).

G = V A

{1, 2, 3, 4,5} V =

{(1, 2), (1, 3), (1, 4), (2,1), (3, 2), (3, 5), (4, 3)}. A=

{

} {

}

1, 1, 2 , 2, 2, 3 ,..., n1, n , n , v v v v v v v₋ v v

1, ,...,2 n

v v v v v₁, ,..., .₂ v_n 1 v .

n v

1, 2,3, 4,3,5 1,2,3,5

' ( , ) G = V A

' G , , ,..., , , ₁ ₁

0 a v an vn

v

' G

1,3, 2,1, 4,3,5

2,1, 4,3,5

' ( , ) G = V A

:

w E→ ℜ l:A→ ℜ

ℜ

' ( , ). G = V A

:A→ ℜ

l

' ( , ) G = V A ((4,3))

l

4 ,3 2 ,1 1,3 3,5 3, 2

1, 4

3; 1; 0; 2;

2.

= = = = = −

=

l l l l l

(15)

penggunaan pemrograman linear integer (PLI) untuk mencari solusi dari kasus VRP.

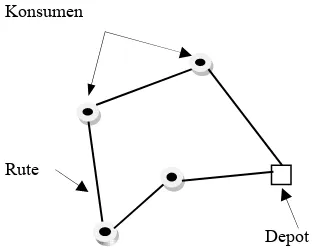
2.7 Traveling Salesman Problem (TSP) Dalam TSP, seorang salesman harus mengunjungi seluruh kota yang ada dan diharuskan kembali ke kota awal pada akhir perjalanannya. Tujuan dari TSP adalah menetukan rute perjalanan yang fisibel sedemikian sehingga jarak tempuh yang melalui rute tersebut minimum.

Definisi 16 (m-TSP)

m-TSP adalah salah satu variasi dari TSP. Dalam m-TSP terdapat m salesman mengunjungi seluruh kota tetapi setiap kota hanya dapat dikunjungi oleh tepat satu salesman saja. Setiap salesman berangkat dari suatu depot dan pada akhir perjalanannya juga harus kembali ke depot tersebut. Tujuan dari m-TSP adalah meminimumkan total jarak dari setiap rute.

Masalah m-TSP dikenal juga sebagai vehicle routing problem (VRP). Dalam masalah tersebut, sebuah kota diasosiasikan sebagai konsumen dan tiap kendaraan memiliki kapasitas tertentu. Total jumlah permintaan dalam suatu rute tidak boleh melebihi kapasitas dari kendaraan yang beroperasi.

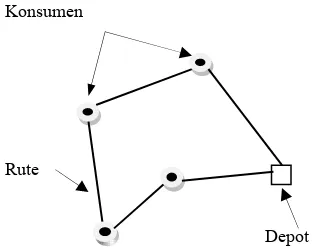
(Larsen 1999) Contoh solusi dari TSP dapat dilihat pada Gambar 4.

Konsumen

Rute

Depot

Gambar 4 Contoh rute dalam traveling salesman problem (TSP).

Vehicle Routing Problem (VRP)

VRP merupakan masalah pendistribusian setiap kendaraan yang terletak di depot untuk memenuhi permintaan para pelanggan yang tersebar di banyak tempat. Masalah utama dari VRP adalah membuat rute yang fisibel dengan biaya yang rendah untuk setiap kendaraan dengan ketentuan bahwa setiap kendaraan memulai dan mengakhiri perjalanan dari depot.

Misalkan V’ adalah himpunan pelanggan yang harus dilayani. Fungsi objektif dari sebuah VRP adalah mencari sebanyak m buah rute kendaraan dengan total biaya yang minimum sehingga setiap pelanggan di V’ dikunjungi oleh tepat satu kendaraan. Sebuah rute Ri dikatakan fisibel jika setiap pelanggan dikunjungi tepat satu kali oleh sebuah kendaraan.

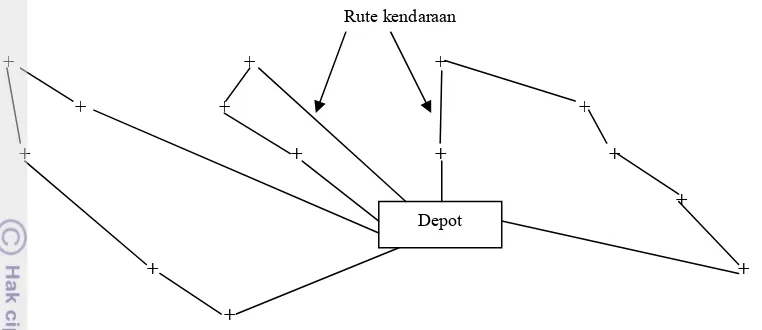
Gambar berikut mencoba menjelaskan input dari sebuah VRP dan solusi yang mungkin terjadi.

+ + + Pelanggan

+ + +

+ + + +

+

+ +

(16)

Rute kendaraan

+ + +

+ + + +

+

+ +

+

Gambar 6 Solusi yang mungkin dari VRP pada Gambar 5 dengan tiga kendaraan.

Tujuan dari VRP adalah menentukan sejumlah rute untuk melakukan pengiriman pada setiap konsumen, dengan mengikuti beberapa ketentuan antara lain :

1. setiap rute berawal dan berakhir di depot, 2. setiap konsumen dikunjungi tepat satu

kali oleh tepat satu kendaraan,

3. jumlah permintaan tiap rute tidak melebihi kapasitas kendaraan,

4. meminimumkan biaya perjalanan, (Cordeau et al. 2002)

Definisi 17 (Capacitated Vehicle Routing Problem)

Capacitated Vehicle Routing Problem (CVRP) merupakan salah satu variasi dari masalah VRP dengan penambahan kendala kapasitas kendaraan. Setiap kendaraan yang melayani konsumen disyaratkan memiliki batasan kapasitas sehingga banyaknya konsumen yang dilayani oleh setiap kendaraan dalam satu rute bergantung pada kapasitas kendaraan. CVRP bertujuan meminimumkan waktu tempuh rute perjalanan kendaraan dalam mendistribusikan barang dari tempat produksi yang dinamakan dengan depot ke sejumlah konsumen dan memenuhi batasan kapasitas.

2.8 Metode Branch-and-Bound

Dalam karya ilmiah ini, untuk memperoleh solusi optimum dari masalah PLI digunakan software LINGO 8.0, yaitu sebuah program yang dirancang untuk menentukan solusi model linear, taklinear, dan optimisasi integer. Software LINGO 8.0 ini menggunakan metode branch-and-bound untuk menyelesaikan masalah PLI.

Prinsip dasar metode branch-and-bound adalah memecah daerah fisibel dari masalah relaksasi-PL dengan membuat subproblem-subproblem. Terdapat dua konsep dasar dalam algoritme branch-and-bound.

• Branch (Cabang)

Branching (pencabangan) adalah proses membagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi fisibel.

• Bound (Batas)

Bounding (pembatasan) adalah suatu proses untuk mencari atau menghitung batas atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimum pada subproblem yang mengarah ke solusi.

(Taha 1975)

Metode branch-and-bound diawali dari menyelesaikan relaksasi-PL dari suatu pemrograman linear integer. Jika semua nilai variabel keputusan solusi optimal sudah berupa integer, maka solusi tersebut merupakan solusi optimal PLI. Jika tidak, dilakukan pencabangan dan penambahan batasan pada relaksasi-PLnya kemudian diselesaikan.

Winston (2004) menyebutkan bahwa untuk masalah maksimisasi nilai fungsi objektif optimum untuk PLI nilai fungsi objektif optimum untuk relaksasi-PL, sehingga nilai fungsi objektif optimum relaksasi-PL merupakan batas atas bagi nilai fungsi objektif optimum untuk masalah PLI. Diungkapkan pula oleh Winston (2004) untuk

(17)

masalah maksimisasi bahwa nilai fungsi objektif optimal untuk suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimum untuk masalah PLI asalnya. Suatu kandidat solusi diperoleh jika solusi dari suatu subproblem sudah memenuhi kendala integer pada masalah PLI, artinya fungsi objektif dan semua variabelnya sudah bernilai integer.

Sebelumnya akan dibahas terlebih dulu pengertian subproblem yang terukur. Menurut Winston (2004), suatu subproblem dikatakan terukur (fathomed) jika terdapat situasi sebagai berikut:

a. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimum untuk PLI.

b. Subproblem tersebut menghasilkan suatu solusi optimum dengan semua variabelnya bernilai integer. Jika solusi optimum ini mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimum dan nilai fungsi objektifnya menjadi batas bawah (dalam masalah maksimisasi) dan batas atas (dalam masalah minimisasi) nilai fungsi objektif optimum bagi masalah PLI pada saat itu, bisa jadi subproblem ini menghasilkan solusi optimum untuk masalah PLI.

c. Nilai fungsi objektif optimum untuk subproblem tersebut tidak melebihi batas bawah saat itu (untuk masalah maksimisasi), maka subproblem ini dapat dieliminasi.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound.

• Langkah 0

Didefinisikan z sebagai batas bawah dari nilai fungsi objektif (solusi) PLI yang optimum. Pada awalnya ditetapkan dan

• Langkah 1

Subproblem PL(i) dipilih sebagai bagian masalah berikutnya untuk diteliti. Subproblem PL(i) diselesaikan dan diukur dengan kondisi yang sesuai.

a) Jika PL(i) terukur, batas bawah z diperbarui jika solusi PLI yang lebih baik ditemukan. Jika tidak, bagian masalah (subproblem) baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah diteliti, maka proses dihentikan.

b) Jika PL(i) tidak terukur, proses dilanjutkan ke langkah 2 untuk melakukan pencabangan PL(i).

• Langkah 2

Dipilih salah satu variabel xj dengan nilai optimumnya adalah xj* yang tidak memenuhi batasan integer dalam solusi PL(i). Bidang [xj*] < xj <[xj*] + 1 disingkirkan dengan membuat dua subproblem PL yang berkaitan menjadi dua subproblem yang tidak dapat dipenuhi secara bersamaan, yaitu

xj≤ [xj*] dan xj≥[xj*] + 1,

dengan [xj*] didefinisikan sebagai integer terbesar yang kurang dari atau sama dengan xj*. Jika PL(i) masih tidak terukur, maka kembali ke Langkah 1.

(Taha 1996)

Untuk memudahkan pemahaman metode branch-and-bound diberikan contoh sebagai berikut.

Contoh 3 (Metode Branch-and-Bound) Misalkan diberikan integer programming (IP) berikut:

maks z = 5x1 + 4x2

terhadap x1 + x2≤ 5

10x1 + 6x2≤ 45 (2.7)

x1, x2≥ 0

x1, x2 integer.

Solusi optimal relaksasi-PL dari masalah IP (2.7) adalah dan

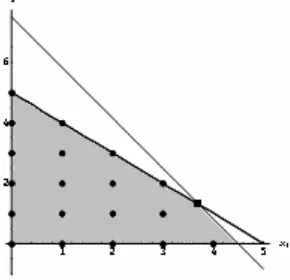
(yang dapat dilihat di Lampiran 1). Batas atas nilai optimal fungsi objektif masalah ini adalah Daerah fisibel masalah (2.7) ditunjukkan pada Gambar 7.

Gambar 7 Daerah fisibel untuk relaksasi-PL dari IP (2.7).

Keterangan :

= solusi optimal relaksasi-PL IP (2.7) = titik-titik fisibel bagi IP (2.7)

Langkah berikutnya adalah memartisi daerah fisibel relaksasi-PL menjadi dua bagian berdasarkan variabel yang bernilai

−∞ =

z i=0.

1 3.75,

x = x2 =1.25, 23.75

z=

(18)

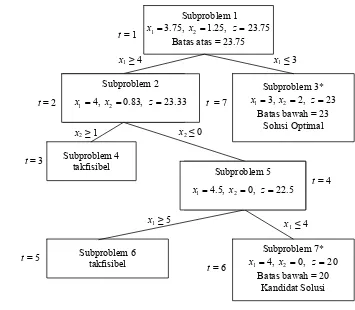
pecahan (non-integer). Karena nilai dari kedua variabel yang diperoleh bukan integer, maka dipilih salah satu variabel untuk dasar pencabangan. Misalkan dipilih x1 sebagai dasar pencabangan. Jika masalah relaksasi-PL diberi nama Subproblem 1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:

• Subproblem 2: Subproblem 1 ditambah kendala

• Subproblem 3: Subproblem 1 ditambah kendala Hal ini diilustrasikan secara grafis pada Gambar 8.

Gambar 8 Daerah fisibel untuk Subproblem 2 dan Subproblem 3 dari IP (2.7).

Setiap titik (solusi) fisibel dari IP (2.7) termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Subproblem 2 dan Subproblem 3 dikatakan dicabangkan oleh x1.

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih Subproblem 2, kemudian diselesaikan. Solusi optimal untuk Subproblem 2 ini adalah

dan (lihat Lampiran 1). Karena solusi optimal yang dihasilkan Subproblem 2 bukan solusi integer, maka dipilih pencabangan pada Subproblem 2 atas sehingga diperoleh dua subproblem lagi, yakni:

• Subproblem 5: Subproblem 2 ditambah kendala Saat ini subproblem yang belum diselesaikan adalah Subproblem 3, 4, dan 5. Salah satu subproblem dipilih, misalnya

dengan aturan LIFO (Last In First Out). Dengan adanya aturan ini berarti dipilih Subproblem 4 atau Subproblem 5. Karena Subproblem 4 takfisibel (lihat pada Lampiran 1), maka subproblem ini tidak dapat menghasilkan solusi optimal, yang tersisa adalah Subproblem 3 dan Subproblem 5.

Karena aturan LIFO, dipilih Subproblem 5, yang kemudian menghasilkan solusi optimal dan (lihat pada Lampiran 1). Karena bukan integer, maka dilakukan kembali pencabangan atas x1, sehingga diperoleh:

• Subproblem 7: Subproblem 5 ditambah kendala Misalkan dipilih Subproblem 6. Ternyata subproblem ini juga takfisibel (lihat pada Lampiran 1), sehingga tidak dapat menghasilkan solusi optimal. Dengan demikian subproblem-subproblem yang belum diselesaikan adalah Subproblem 3 dan Subproblem 7. Karena aturan LIFO, dipilih Subproblem 7. Subproblem ini kemudian menghasilkan solusi optimal

dan (lihat pada Lampiran 1). Dapat dilihat bahwa solusi optimal subproblem ini semuanya berupa integer, sehingga merupakan kandidat solusi untuk IP (2.7). Nilai z pada kandidat solusi ini merupakan batas bawah bagi nilai optimal IP. Penyelesaian Subproblem 3 menghasilkan solusi optimal dan

(lihat pada Lampiran 1). Batas bawah yang ditetapkan dari solusi optimal Subproblem 7 terlalu lemah dan tidak lebih baik dari nilai solusi optimal yang dihasilkan oleh Subproblem 3. Dengan demikian, nilai solusi optimal Subproblem 3, yakni menjadi batas bawah yang baru. Semua solusi optimal telah berupa integer dan tidak perlu lagi dilakukan pencabangan, sehingga solusi optimal dari Subproblem 3 merupakan solusi optimal IP (2.7), yakni dan

Pohon pencabangan yang menunjukkan penyelesaian masalah IP (2.7) secara keseluruhan ditunjukkan pada Gambar 9. 1 4; x ≥ 1 3. x ≤ 1 4,

x = x2 =0.83, 23.33 z= 2, x 2 1; x ≥ 2 0. x ≤ 1 4.5,

x = x2 =0, z=22.5

1 4.5 x = 1 5; x ≥ 1 4. x ≤

1 4, 0,2

x = x =

20 z=

1 3, 2,2

x = x = z=23

23 z=

1 3,

x = x2 =2, 23.

z=

Subproblem 2

(19)

Pada Gambar 9, solusi Subproblem 3 dan Subproblem 7 adalah kandidat solusi terbaik karena semua variabelnya bernilai integer. Namun, karena nilai z untuk Subproblem 3 lebih besar dari Subproblem 7 maka solusi

dari Subproblem 3 merupakan solusi optimum untuk masalah IP pada Contoh 3. Tanda (*) pada Subproblem 3 dan Subproblem 7 menyatakan kandidat solusi untuk masalah IP tersebut.

III DESKRIPSI DAN FORMULASI MASALAH

3.1 Deskripsi Masalah Rute Bus Karyawan Masalah rute bus karyawan adalah masalah penentuan rute bus untuk menjemput karyawan dari pos-pos yang sudah ditentukan menuju perusahaan dan mengantarkan karyawan dari perusahaan ke pos-pos, kemudian bus tersebut kembali ke tempat asalnya, yaitu perusahaan (depot), dengan biaya yang minimum sehingga kendala kapasitas atau kendala waktu tempuh terpenuhi.

Untuk meminimumkan biaya operasional bus, hal yang harus dipertimbangkan adalah biaya perjalanan setiap bus dan biaya tetap untuk mengirimkan bus.

3.2 Model Masalah Rute Bus Karyawan Dalam model ini, rute untuk menjemput karyawan dari pos-pos menuju perusahaan dan rute untuk mengantarkan karyawan dari perusahaan ke pos-pos, diasumsikan sama karena pos-pos penjemputan dan pengantaran karyawan adalah sama.

Masalah penentuan rute bus karyawan sangat berhubungan dengan VRP dan graf. Secara matematis VRP dapat dinyatakan sebagai suatu digraf G = (V, A) dengan V = {0, 1, ... , n} adalah himpunan simpul yang menunjukkan pos-pos antar-jemput karyawan dan A={(i, j) | i, j V, i ≠ j} yaitu himpunan sisi berarah yang menyatakan jalan penghubung antarpos. Pos 0 menunjukkan

∈

Gambar 9 Seluruh pencabangan pada metode branch-and-bound untuk menyelesaikan IP (2.7).

Subproblem 1

Batas atas = 23.75 1 3.75,

x = x2 =1.25, z=23.75

Subproblem 2

1 4,

x = x2 =0.83, z=23.33

Subproblem 3*

Batas bawah = 23 Solusi Optimal

1 3, 2,2 x = x = z=23

Subproblem 7*

Batas bawah = 20 Kandidat Solusi 1 4, 0, 2 20 x = x = z= Subproblem 5

2 0,

x =

1 4.5,

x = z=22.5

Subproblem 6 takfisibel Subproblem 4

takfisibel t = 1

t = 7

t = 4

t = 6 t = 2

t = 5 t = 3

x1≥ 4 x1≤ 3

x2≥ 1 x2≤ 0

x1≤ 4 x1≥ 5

Subproblem 2

1 4,

x = x2 =0.83, z=23.33

Subproblem 5

1 4.5,

(20)

depot, yaitu tempat menyimpan bus yang digunakan untuk mengangkut karyawan dan merupakan tempat dimulainya suatu rute bus. Intermediate node (simpul penghubung) menunjukkan pos ke-i yang dilewati oleh setiap bus untuk menjemput dan mengantarkan karyawan. Misalkan banyaknya bus yang tersedia di depot adalah k dengan kapasitas setiap bus diasumsikan sama, yaitu Q, dan jarak tempuh maksimum setiap bus adalah T. Permasalahannya ialah menentukan rute yang fisibel (yang mungkin dapat dilalui) sehingga biaya dari setiap bus yang melalui rute tersebut adalah minimum.

Toth dan Vigo (2002) memformulasikan VRP dalam bentuk ILP dengan tujuan meminimalkan total biaya atau total jarak tempuh dari rute perjalanan.

Untuk mendefinisikan masalah rute bus karyawan, dimisalkan:

Q = kapasitas bus

T = jarak tempuh maksimum dari setiap bus V = himpunan pos yang dilalui oleh bus I = himpunan intermediate node (simpul

penghubung)

k = banyaknya bus yang tersedia

f = biaya tetap untuk setiap pengiriman satu bus per hari

qi = banyaknya karyawan yang harus dijemput di pos i

ui = banyaknya karyawan di bus tepat setelah pos i

dij = jarak tempuh dari pos i ke pos j

vi = total panjang perjalanan bus dari depot sampai pada pos i

cij = biaya dari pos i ke pos j

α = biaya yang dikeluarkan tiap-tiap bus per kilometer

Variabel keputusan :

Fungsi objektif dari permasalahan ini adalah meminimumkan biaya yang dikeluarkan oleh pengelola bus karyawan. Setiap bus yang dijadwalkan berangkat dari depot ke pos-pos yang sudah ditentukan, akan dikenakan biaya sesuai dengan jauhnya perjalanan bus ditambah dengan biaya tetap untuk semua bus yang dikirim sehingga dimodelkan sebagai berikut: min z =

dengan cij = αdij dan V’ = V U {0}. Dalam model ini, yang dipakai hanya rute penjemputan saja karena diasumsikan bahwa rute penjemputan karyawan sama dengan rute pengantaran karyawan.

Kendala-kendala :

1. Setiap rute perjalanan bus berawal dari depot dengan pembatasan bahwa paling banyak k bus yang meninggalkan pos 0 menuju pos i

2. Setiap rute perjalanan bus berakhir di depot dengan pembatasan bahwa paling banyak k bus yang meninggalkan pos i menuju depot

3. Setiap pos hanya dapat dikunjungi tepat satu kali oleh satu bus

4. Kendala kapasitas

ui − uj + Qxij≤ Q − qj (3.1) i ≠ j I

ui≥ qi , _(3.2) ui − qix0i + Qx0i≤ Q _(3.3)

Variabel xij dan xji hanya akan terdefinisi jika qi + qj≤ Q. Jika xij= 0 maka kendala ui – uj + Qxij ≤ Q − qj akan menunjukkan bahwa ui + qj≤ Q + uj. Jika xij = 1 maka kendala tersebut menunjukkan bahwa uj≥ ui + qj.

Formulasi (3.1) dan (3.2) memastikan bahwa tidak terdapat subrute pada setiap rute yang terbentuk, karena kapasitas bus sangat mempengaruhi rute yang ada. Formulasi (3.3) menunjukkan kapasitas bus yang dimulai dari depot ke pos pertama dalam rute perjalanannya. Formulasi kendala (4) pada intinya menekankan pada batasan subrute yaitu mengeliminasi subrute supaya tidak terdapat subrute pada rute-rute yang terbentuk yang dikaitkan dengan batasan kapasitas bus. Perjalanan yang memuat suatu subrute merupakan solusi yang tidak fisibel. Variabel keputusan hanya akan terdefinisi jika banyaknya karyawan yang dijemput pada pos i dan pos j tidak melebihi kapasitas bus.

Ilustrasi :

Misalkan diberikan pos 1, 2, 3, 4, dan 5 yang akan dilalui oleh satu bus karyawan, 1 ; jika bus berangkat dari pos ke pos

0 ; jika selainnya ij

i j

x = ⎨⎧ ⎩

' '

. ij ij

i V j V

c x f k ∈ ∈ +

∑ ∑

0i i I x k ∈ ≤

∑

0 i i I x k ∈ ≤

∑

, 1 ij j I j i

x ∈ ≠

=

∑

∀ ∈i I

,

1 ij i I i j

x ∈ ≠

=

∑

∀ ∈j I

∀ ∈

i I

∀ ∈

i I

(21)

dan perjalanan bus yang diberikan seperti gambar berikut:

1 3

4

2 5

Gambar 10 Perjalanan bus yang berupa subrute.

Gambar 10 merupakan subrute yang terdiri atas (1-2-1) dan (1-3-4-5-1), dan diasumsikan bahwa pos 1 adalah depot. Pada Gambar 10, nilai x13 = x34 = x45 = x51 = x12 = x21 = 1. Misalkan diambil subrute (1-2-1) dengan q1 = 0, q2 = 15, q3 = 10, q4 = 21, q5 = 8, dengan Q = 40. q3 + q4 + q5 = 10 + 21 + 8 = 39. Sedangkan q2 = 15, sehingga q3 + q4 + q5 + q2 = 10 + 21 + 8 +15 = 54 > 40 (kapasitas bus). Akibatnya dari pos 5, bus harus kembali lagi ke depot untuk menurunkan karyawan terlebih dahulu baru menjemput karyawan lagi. Rute bus seperti ini tidak diinginkan, sehingga harus dieliminasi.

Representasi pertaksamaan kendala (4) terhadap sisi berarah dalam subcycle ini adalah :

u1 − u2 + Qx12 ≤ Q − q2 (1)

dan

u2 − u1+ Qx21≤ Q − q1 (2)

sehingga dari (1) dan (2) didapat :

Q(x12 + x21) ≤ 2Q − q2 − q1 (3)

Hasil (3) bertentangan dengan x12 = x21 = 1

yaitu, Q(1 + 1) ≤ 2Q − q2 – q1 2Q ≤ 2Q − q2 – q1 80 ≤ 80 – 15 – 0 80 ≤ 65

Berdasarkan hasil di atas perjalanan yang memuat suatu subrute merupakan solusi yang tidak fisibel.

Ilustrasi :

Misalkan diberikan pos 1, 2, 3, 4, dan 5 yang akan dilalui oleh satu bus karyawan, dan perjalanan bus yang diberikan seperti gambar berikut:

1 3

2 4

5

Gambar 11 Perjalanan bus yang berupa rute.

Dari Gambar 11 diasumsikan bahwa pos 1 merupakan pos pertama dari perjalanan bus (pada akhirnya semua pos akan dikunjungi). Misalkan ui = banyaknya karyawan di bus tepat setelah pos i dan qi = banyaknya karyawan yang harus dijemput di pos i.

Sebagai gambaran, akan dipertimbangkan rute yang diperoleh dari Gambar 11, yaitu 1-3-4-5-2-1, kemudian dipilih q1 = 0, q2 = 15, q3 = 10, q4 = 21, q5 = 8, dengan Q = 40 sehingga x13 = x34 = x45 = x52 = x21 = 1.

Dengan pemilihan tersebut akan dibuktikan pertidaksamaan (4) terpenuhi. Pertama, pemilihan tersebut sesuai untuk sebuah sisi berarah dengan xij = 1. Sebagai contoh, pembatasan untuk x34 adalah u3 – u4 + 40 x34≤ 40 – q4 dengan u3 = 10 dan u4 = 31 sehingga

10 − 31 + 40 x34≤ 40 – 21 10 − 31 + 40 (1) ≤ 40 − 21 19 ≤ 19

Kedua, pemilihan rute di atas juga memenuhi kendala xij = 0. Sebagai contoh untuk untuk x34 adalah u3 – u4 + 40 x34≤ 40 – q4 dengan u3 = 10 dan u4 = 31 sehingga

10 – 31 + 40 x34≤ 40 – 21 10 – 31 + 40 (0) ≤ 40 − 21 31 ≤ 71

5. Kendala Jarak

vi− vj + (T − di0− d0j + dij) xij + (T − di0− d0j− dji) xji ≤ T − dio− doj i ≠ j I vi− d0i x0i≥ 0, i I vi− d0i x0i + T x0i≤ T, i I

dengan d0i + dij + dj0 ≤ T bagi setiap pasangan (i, j).

Jika xij = 1 dan xji = 0, maka kendala tersebut menunjukkan bahwa vi – vj + dij ≤ 0 sehingga vi + dij≤ vj.Jika xji = 1 dan xij = 0, maka kendala ini menunjukkan

∀

∈

∀

∈

(22)

bahwa vi− vj− dji ≤ 0 sehingga vi≤ vj + dji.

Formulasi model pada kendala (5) memastikan bahwa panjang perjalanan bus tidak melebihi jarak tempuh maksimumnya sehingga dapat dipastikan bahwa bus akan kembali ke depot tepat sebelum jam kerja dimulai. Variabel keputusan hanya akan terdefinisi jika jauhnya perjalanan bus yang dimulai dari pos i ke pos j tidak melebihi jarak tempuh maksimum yang ditempuh oleh setiap bus.

Jarak sangat menentukan dalam menentukan waktu yang dibutuhkan untuk mengantarkan dan menjemput karyawan ke perusahaan. Semakin jauh jarak yang ditempuh, semakin lama waktu yang dibutuhkan bus dalam menjemput karyawan. Sebaliknya, semakin dekat jarak yang ditempuh, semakin sedikit waktu yang dibutuhkan bus dalam menjemput karyawan.

6. Variabel keputusan xij adalah integer biner.

xij {0, 1}, i, j V’

IV STUDI KASUS

Studi kasus berikut berdasarkan data hipotetik dengan kendala-kendala sebagai berikut:

1. Setiap pos hanya dikunjungi satu kali oleh satu bus.

2. Setiap bus mengangkut karyawan sesuai dengan batasan kapasitasnya. Setiap bus mempunyai kapasitas maksimum 40 orang.

3. Setiap rute bus berawal dari perusahaan. 4. Setiap rute bus berakhir di perusahaan. 5. Setelah menjemput karyawan dari pos, bus

akan meninggalkan pos tersebut.

6. Tidak terdapat subrute pada setiap rute yang ada.

7. Jarak maksimum yang ditempuh oleh setiap bus adalah 100 km.

8. Biaya tetap untuk setiap pengiriman satu bus per hari adalah 100000 rupiah.

9. Biaya yang dikeluarkan tiap-tiap bus per kilometer adalah 2000 rupiah.

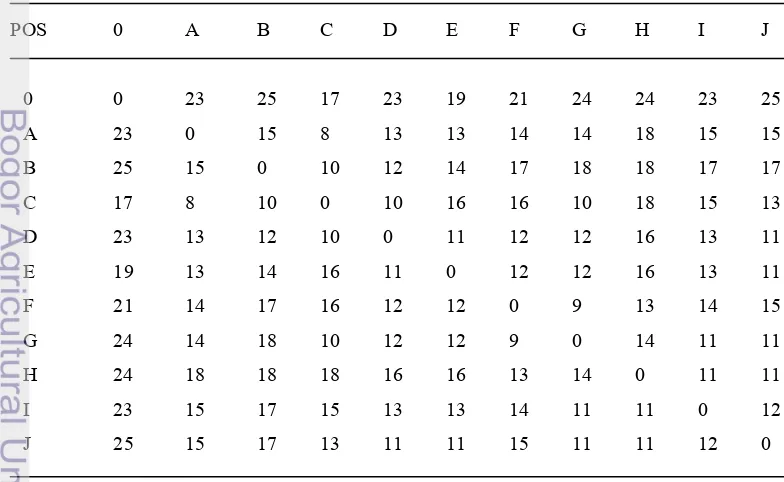
Pengelola bus karyawan tersebut telah melakukan survei ke beberapa tempat yang dianggap strategis untuk dijadikan pos sehingga semua karyawan dapat menjangkau pos tersebut dengan mudah. Pos-pos ini yang nantinya menjadi tempat bus untuk menjemput karyawan. Pos dibagi menjadi: Pos A, Pos B, Pos C, Pos D, Pos E, Pos F, Pos G, Pos H, Pos I, dan Pos J. Setiap pos hanya dikunjungi oleh satu bus. Data jarak antarpos dan jarak dari perusahaan ke setiap pos diberikan pada Tabel 1 (dalam kilometer).

Tabel 1 Jarak antarpos penjemputan bus karyawan

POS 0 A B C D E F G H I J

0 0 23 25 17 23 19 21 24 24 23 25

A 23 0 15 8 13 13 14 14 18 15 15

B 25 15 0 10 12 14 17 18 18 17 17

C 17 8 10 0 10 16 16 10 18 15 13

D 23 13 12 10 0 11 12 12 16 13 11

E 19 13 14 16 11 0 12 12 16 13 11

F 21 14 17 16 12 12 0 9 13 14 15

G 24 14 18 10 12 12 9 0 14 11 11

H 24 18 18 18 16 16 13 14 0 11 11

I 23 15 17 15 13 13 14 11 11 0 12

J 25 15 17 13 11 11 15 11 11 12 0

(23)

Tabel 2 Banyaknya karyawan yang dijemput pada setiap pos

POS Banyaknya karyawan yang dijemput di pos i

A 10

B 12

C 13

D 14

E 15

F 16

G 17

H 18

I 19

J 20

Formulasi model PLI dari data pada Tabel 1 adalah sebagai berikut:

Minimumkan

terhadap kendala berikut:

1. Setiap rute perjalanan bus berawal dari depot dengan pembatasan bahwa paling banyak k bus yang meninggalkan pos 0 menuju pos i

i = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

2. Setiap rute perjalanan bus berakhir di depot dengan pembatasan bahwa paling banyak k bus yang meninggalkan node i menuju depot

i = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

3. Setiap pos hanya dapat dikunjungi tepat satu kali oleh satu bus

i = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

4. Kendala Kapasitas ui− uj + Qxij≤ Q − qj

i ≠ j I ui≥ qi ,

ui− qix0i + Qx0i≤ Q

i = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

5. Kendala Jarak

vi− vj + (T − di0− d0j + dij) xij + (T − di0− d0j− dji) xji ≤ T − dio− doj i ≠ j I vi – d0i x0i≥ 0, i I vi – d0i x0i + T x0i≤ T, i I

i = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

6. Variabel keputusan xij merupakan integer biner.

Model dalam bentuk integer linear programming selanjutnya diselesaikan menggunakan software LINGO 8.0 dengan metode branch and bound (lihat Lampiran 2), sehingga dihasilkan rute kendaraan untuk menjemput dan mengantar karyawan yang meminimumkan total jarak tempuh. Setelah melakukan beberapa kali iterasi dengan mengganti nilai k, biaya yang paling minimum diperoleh jika digunakan 4 unit bus untuk dapat menjemput karyawan dengan rute setiap bus diberikan pada Tabel 3, Tabel 4, Tabel 5, Tabel 6, dan Gambar 12.

' '

. ij ij

i V j V

c x f k ∈ ∈ +

∑ ∑

0i i I x k ∈ ≤

∑

0 i i I x k ∈ ≤

∑

, 1 ij j I j i

x ∈ ≠

=

∑

∀ ∈i I

,

1 ij i I i j

x ∈ ≠

=

∑

∀ ∈j I

∀ ∈ i I ∀ ∈ i I ∀ ∈

∀

∈

∀

∈

∀

∈

1 ; jika bus berangkat dari pos ke pos 0 ; jika selainnya

ij

i j

(24)

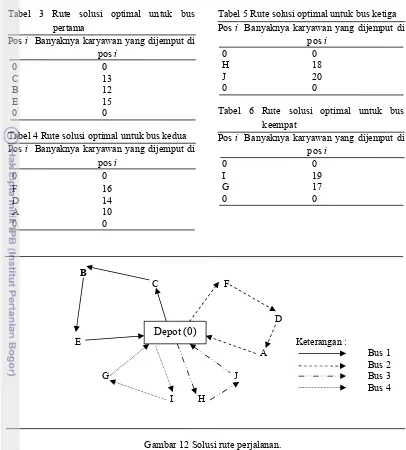
Tabel 3 Rute solusi optimal untuk bus pertama

Pos i Banyaknya karyawan yang dijemput di pos i

0 0 C 13 B 12 E 15 0 0

Tabel 4 Rute solusi optimal untuk bus kedua Pos i Banyaknya karyawan yang dijemput di

pos i

0 0 F 16 D 14 A 10 0 0

Tabel 5 Rute solusi optimal untuk bus ketiga Pos i Banyaknya karyawan yang dijemput di

pos i

0 0 H 18 J 20 0 0

Tabel 6 Rute solusi optimal untuk bus keempat

Pos i Banyaknya karyawan yang dijemput di pos i

0 0 I 19 G 17 0 0

B

C F

D

E Keterangan :

A Bus 1

Bus 2

G J Bus 3

Bus 4

I H

Gambar 12 Solusi rute perjalanan.

Rute yang dilalui bus pertama berawal dari depot, pos C, pos B, pos E, lalu kembali ke depot dengan total jarak tempuh 60 km dan mengangkut karyawan sejumlah 40 orang. Rute yang dilalui oleh bus kedua adalah meliputi depot, pos F, pos D, pos A, kemudian kembali ke depot dengan total jarak tempuh 69 km dan mengangkut karyawan sejumlah 40 orang. Rute yang dilalui oleh bus ketiga meliputi depot, pos H, pos J, dan kembali ke depot dengan total jarak tempuh 60 km dan mengangkut karyawan sejumlah 38 orang.

Sedangkan rute yang dilalui oleh bus keempat meliputi depot, pos I, pos G, dan kembali ke depot dengan total jarak tempuh 58 km dan mengangkut karyawan sejumlah 36 orang.

Total jarak yang ditempuh oleh keempat unit bus tersebut dalam menjemput atau mengantar karyawan adalah 247 km. Total biaya yang harus dikeluarkan untuk biaya operasional bus karyawan per harinya adalah 894000 rupiah.

(25)

V SIMPULAN DAN SARAN

5.1 Simpulan

Dalam karya ilmiah ini telah diperlihatkan masalah penentuan rute bus karyawan. Masalah ini dipandang sebagai masalah PLI dengan fungsi objektif meminimumkan biaya operasional bus.

Rute yang diperoleh sangat bergantung pada kapasitas bus dan jarak antarpos penjemputan karyawan. Penentuan rute bus

karyawan dengan menggunakan PLI sangat fleksibel, di mana pengguna dapat dengan mudah menambahkan data maupun kendala-kendala baru yang diperlukan.

. 5.2 Saran

Tulisan ini dapat dikembangkan untuk menyelesaikan masalah penentuan rute bus dengan mempertimbangkan kendala waktu.

DAFTAR PUSTAKA

Bektas T, Elmastas S. 2007. Solving school bus routing problems through integer programming. Journal of Operational Research Society 58: 1599-1604.

Cordeau JF, Gendreau M, Laporte, Potvin JY, Semet F. 2002. A guide to vehicle routing heuristics. Journal of Operational Research Society 53: 512-522.

Foulds LR. 1992. Graph Theory Applications. Springer-Verlag, New York.

Garfinkel RS, Nemhauser GL. 1972. Integer Programming. Jo Ghn Wiley & Sons, New York.

Larsen J. 1999. Vehicle routing with times windows [Ph. D Thesis]. Denmark : Department of Mathematical Modelling, University of Denmark.

Nash SG, Sofer A. 1996. Linear and Nonlinear Programming. McGraw-Hill, New York.

Taha HA. 1975. Integer Programming: Theory, Applications, and Computations. Academic Press, New York.

Taha HA. 1996. Pengantar Riset Operasi. Alih Bahasa: Daniel Wirajaya. Binarupa Aksara, Jakarta. Terjemahan dari: Operations Research.

Toth P, Vigo D. 2002. An overview of vehicle routing problems. Di dalam: Toth P, Vigo D, editor. The Vehicle Routing Problem. Philadelphia: Siam. Hlm. 1-26.

Winston WL. 1995. Introduction to Mathematical Programming 2nd ed. Duxbury, New York.

(26)

(27)

Lampiran 1.

Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode

Branch-and-Bound Beserta Hasil yang Diperoleh

1) PL‐relaksasi masalah (2.7)

max=5*x1+4*x2;

x1+x2<=5;

10*x1+6*x2<=45; x1>=0;

x2>=0;

Hasil yang diperoleh :

Global optimal solution found at iteration: 4

Objective value: 23.75000

Variable Value Reduced Cost X1 3.750000 0.000000 X2 1.250000 0.000000

Row Slack or Surplus Dual Price 1 23.75000 1.000000 2 0.000000 2.500000 3 0.000000 0.2500000 4 3.750000 0.000000 5 1.250000 0.000000

2) Subproblem 2:

max=5*x1+4*x2;

x1+x2<=5;

10*x1+6*x2<=45; x1>=4;

x2>=0;

Row Slack or Surplus Dual Price 1 23.33333 1.000000 2 0.1666667 0.000000 3 0.000000 0.6666667 4 0.000000 -1.666667 5 0.8333333 0.000000

3) Subproblem 4 :

max=5*x1+4*x2;

x1+x2<=5;

10*x1+6*x2<=45; x1>=4;

(28)

hasil yang diperoleh: takfisibel, sebagaimana ditunjukkan di bawah ini

4) Subproblem 5:

max=5*x1+4*x2;

x1+x2<=5;

10*x1+6*x2<=45; x1>=4;

x2<=0;

(29)

5) Subproblem 6:

max=5*x1+4*x2;

x1+x2<=5;

10*x1+6*x2<=45; x1>=5;

x2<=0;

hasil yang diperoleh: takfisibel, sebagaimana ditunjukkan di bawah ini

6) Subproblem 7:

max=5*x1+4*x2;

x1+x2<=5;

10*x1+6*x2<=45; x1<=4;

(30)

Row Slack or Surplus Dual Price 1 20.00000 1.000000 2 1.000000 0.000000 3 5.000000 0.000000 4 0.000000 5.000000 5 0.000000 4.000000

7) Subproblem 3:

max=5*x1+4*x2;

x1+x2<=5;

10*x1+6*x2<=45; x1<=3;

x2>=0;

(31)

Lampiran 2.

Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah Rute Bus Karyawan

SETS:

NODE/1..11/:KRWN,CAP,V; LINK(NODE,NODE):DIST,X,C; ENDSETS

DATA: DIST =

0 23 25 17 23 19 21 24 24 23 25

23 0 15 8 13 13 14 14 18 15 15

25 15 0 10 12 14 17 18 18 17 17

17 8 10 0 10 16 16 10 18 15 13

23 13 12 10 0 11 12 12 16 13 11

19 13 14 16 11 0 12 12 16 13 11

21 14 17 16 12 12 0 9 13 14 15

24 14 18 10 12 12 9 0 14 11 11

24 18 18 18 16 16 13 14 0 11 11

23 15 17 15 13 13 14 11 11 0 12

25 15 17 13 11 11 15 11 11 12 0

; KRWN=

0 10 12 13 14 15 16 17 18 19 20 ;

ALPHA = 2000;F = 100000;K = 4 ;T = 100;Q= 40;

ENDDATA

MAX = @SUM(LINK(I,J)|I#NE#J:C(I,J)*X(I,J))+ F*K;

!BIAYA;

@FOR(LINK(I,J)|I#NE#J:C(I,J) = ALPHA * DIST(I,J));

!KENDALA

!SETIAP RUTE BERAWAL DAN BERAKHIR DI DEPOT;

@FOR(NODE(I)|I#EQ#1:@SUM(NODE(J)| J#GT#1 : X(I,J))<=K);

@FOR(NODE(J)|J#EQ#1:@SUM(NODE(I)| I#GT#1 : X(I,J))<=K);

!SETIAP POS HANYA DAPAT DIKUNJUNGI TEPAT SATU KALI OLEH SATU BIS;

@FOR(NODE(I)|I#GT#1:@SUM(NODE(J) |I#NE#J: X(I,J))=1);

@FOR(NODE(J)|J#GT#1:@SUM(NODE(I) |J#NE#I: X(I,J))=1);

!VARIABEL KEPUTUSAN;

@FOR(LINK:@BIN(X));

!KAPASITAS;

@FOR(LINK(I,J)|I#GT#1 #AND# J#GT#1 #AND#

(32)

@FOR(NODE(I)|I#GT#1 : CAP(I) >= KRWN(I));

@FOR(LINK(I,J)|I#EQ#1 #AND# J#GT#1 : CAP(I)- KRWN(I)*X(I,J)+Q*X(I,J)<=Q);

@FOR(LINK(I,J)| I #NE# J : KRWN(I)+ KRWN(J)<=Q );

!JARAK;

@FOR(LINK(I,J)|I#GT#1 #AND# J#GT#1 #AND# I#NE#J:

V(I)-V(J)+(T-DIST(I,1)- DIST(1,I)+DIST(I,J))*X(I,J)+(T-DIST(I,1)-DIST(1,I)-DIST(J,I))*X(J,I)<=T-DIST(I,1)-DIST(1,J));

@FOR(NODE(I)|I#GT#1 :V(I)-DIST(1,I)*X(1,I)>=0);

@FOR(NODE(I)|I#GT#1 :V(I)-DIST(1,I)*X(1,I)+T*X(1,I)<=T);

@FOR(LINK(I,J)|I#GT#1 #AND# J#GT#1 #AND#

I#NE#J:DIST(1,J)+DIST(I,J)+DIST(I,1)<=T);

(33)

Lampiran 3

Hasil Komputasi Program pada LINGO 8.0 untuk Menyelesaikan Masalah Bus Karyawan

Global optimal solution found at iteration: 13357043 Objective value: 894000.0

(34)

(35)

(36)

(37)

(38)

X( 8, 10) 0.000000 22000.00 X( 8, 11) 1.000000 22000.00 X( 9, 1) 1.000000 48000.00 X( 9, 2) 0.000000 36000.00 X( 9, 3) 0.000000 36000.00 X( 9, 4) 0.000000 36000.00 X( 9, 5) 0.000000 32000.00 X( 9, 6) 0.000000 32000.00 X( 9, 7) 0.000000 26000.00 X( 9, 8) 0.000000 28000.00 X( 9, 9) 0.000000 0.000000 X( 9, 10) 0.000000 22000.00 X( 9, 11) 0.000000 22000.00 X( 10, 1) 0.000000 46000.00 X( 10, 2) 0.000000 30000.00 X( 10, 3) 0.000000 34000.00 X( 10, 4) 0.000000 30000.00 X( 10, 5) 0.000000 26000.00 X( 10, 6) 0.000000 26000.00 X( 10, 7) 0.000000 28000.00 X( 10, 8) 0.000000 22000.00 X( 10, 9) 1.000000 22000.00 X( 10, 10) 0.000000 0.000000 X( 10, 11) 0.000000 24000.00 X( 11, 1) 1.000000 50000.00 X( 11, 2) 0.000000 30000.00 X( 11, 3) 0.000000 34000.00 X( 11, 4) 0.000000 26000.00 X( 11, 5) 0.000000 22000.00 X( 11, 6) 0.000000 22000.00 X( 11, 7) 0.000000 30000.00 X( 11, 8) 0.000000 22000.00 X( 11, 9) 0.000000 22000.00 X( 11, 10) 0.000000 24000.00 X( 11, 11) 0.000000 0.000000 C( 1, 1) 0.000000 0.000000 C( 1, 2) 46000.00 0.000000 C( 1, 3) 50000.00 0.000000 C( 1, 4) 34000.00 0.000000 C( 1, 5) 46000.00 0.000000 C( 1, 6) 38000.00 0.000000 C( 1, 7) 42000.00 0.000000 C( 1, 8) 48000.00 0.000000 C( 1, 9) 48000.00 0.000000 C( 1, 10) 46000.00 0.000000 C( 1, 11) 50000.00 0.000000 C( 2, 1) 46000.00 0.000000 C( 2, 2) 0.000000 0.000000 C( 2, 3) 30000.00 0.000000

(39)

(40)

(41)

ZIL’ARIFAH

(42)

Dibimbing oleh PRAPTO TRI SUPRIYO dan FARIDA HANUM.

(43)

Supervised by PRAPTO TRI SUPRIYO and FARIDA HANUM.

(44)

1.1Latar Belakang

1.2Tujuan

II LANDASAN TEORI

2.1Fungsi Linear dan Pertidaksamaan Linear

(Winston 2004)

Sebagai gambaran,

Definisi 2 (Pertidaksamaan dan Persamaan Linear)

pertidaksamaan dan

(Winston 2004)

n

x x

x1, 2,..., f(x1,x2,...,xn)

n

c c c1, 2,...,

. ... )

,..., ,

(x1 x2 xn c1x1 c2x2 cnxn

f = + + +

2 1 2 1, ) 2 (x x x x

f = +

2 2 1 2 1, ) (x x x x

f =

) ,..., , (x1 x2 xn

f b,

b x x x

f( 1, 2,..., n)≤

b x x x

f( 1, 2,..., n)≥

b x x x

(45)

1.1Latar Belakang

1.2Tujuan

II LANDASAN TEORI

2.1Fungsi Linear dan Pertidaksamaan Linear

(Winston 2004)

Sebagai gambaran,

Definisi 2 (Pertidaksamaan dan Persamaan Linear)

pertidaksamaan dan

(Winston 2004)

n

x x

x1, 2,..., f(x1,x2,...,xn)

n

c c c1, 2,...,

. ... )