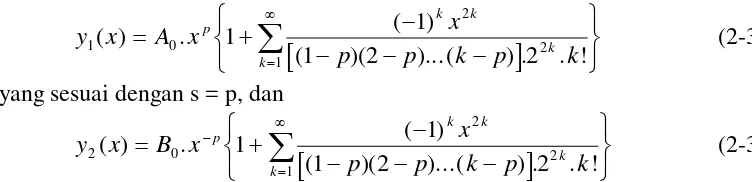MATEMATIKA TEKNIK KIMIA 2

MATEMATIKA TEKNIK KIMIA 2

Prof. Ali Altway, Dr. Tantular Nurtono

Pustaka :

1. Mickley, T.S. Sherwood, C.E. Reed,"Applied Mathematics in Chemical Engineering", McGraw Hill, 2nd. ed., New York, 1975.

2. Jonson, G.V. Jeffreys,"Mathematical Methods in Chemical Engineering", Academic Press, 2nd. Ed., London, 1977.

3. Richard G. Rice, Duong D. Do,”Applied Mathematics and Modeling for Chemical Engineers”, John Wiley & Sons, 1995.

Materi :

1. Perumusan Matematika untuk Persoalan-persoalan Fisik dan Kimia. 2. Penyelesaian Persamaan Differensial Biasa Secara Deret.

3. Fungsi-Fungsi Khusus. 4. Deret Fourier.

BAB I

Perumusan Matematika

untuk Persoalan-persoalan Fisik dan Kimia

I. Perumusan Matematika.

Ilmu-ilmu terapan hampir seluruhnya memerlukan pelaksanaan percobaan dan menginterpretasikan hasil percobaannya. Cara yang banyak diminati adalah dilaksanakan secara kuantitaif dengan melakukan pengukuran yang akurat dari variabel-variabel sistem, kemudian data hasil pengukuran ini dianalisa (diolah) dan dibuat korelasinya, atau dilaksanakan secara kualitatif dengan menyelidiki perilaku umum sistem yang dinyatakan sebagai suatu variabel yang mempengaruhi variabel yang lain.

Bila suatu penyelidikan kuantitatif akan dilaksanakan maka perlu dibuat model matematik untuk sistemnya sebelum melakukan eksperimen, karena model matematis ini bisa mempengaruhi jalannya eksperimen. Perumusan model matematika suatu sistem atau proses dibutuhkan juga pada perancangan peralatan-peralatan, misalnya menara distilasi, menara absorbsi, reaktor, ekstraktor, dsb.

Pembentukan model matematika suatu sistem (proses) dilakukan melalui tiga tahap dasar yaitu :

1. Mengubah dari proses fisik/kimia menjadi bahasa matematika, sehingga didapat suatu persamaan matematis.

2. Menyelesaikan persamaan matematis yang diperoleh

3. Menginterpretasikan hasil penyelesaian yang diperoleh ke dalam istilah-istilah fisik/kimia.

atau digambarkan sbb. :

Proses fisik/kimia Jelas mekanismenya

Perumusan matematis/modelling berupa PD/pers. aljabar/transendental

Penyelesaian rumusan/model matematika

II. Hukum-hukum dasar yang dipakai.

1. Hukum Kekekalan :

a. massa : 1. overall :

laju akumulasi massa dalam sistem = laju massa masuk ke sistem - laju massa keluar dari sistem 2. komponen :

laju akumulasi mssa komponen i dalam sistem = laju massa komponen i masuk ke sistem - laju massa komponen i keluar dari sistem + laju massa komponen i yang timbul dalam sistem - laju massa komponen i yang terpakai dalam sistem

b. energi :

laju akumulasi energi dalam sistem = laju energi masuk ke sistem - laju energi keluar dari sistem + laju energi yang timbul dalam sistem - laju energi yang terpakai dalam sistem

c. momentum :

laju akumulasi i momentum dalam sistem = laju i momentum i masuk ke sistem - laju i momenutm keluar dari sistem + gaya-gaya ke arah i yang bekerja dalam sistem

2. Hukum untuk proses kecepatan :

a. perpindahan panas : 1. konduksi :

Q = -k.A.T/x (hk. Fourier), dimana : k = thermal konduktifity A = luas perpindahan panas T/x = gradien suhu ke arah x 2. konveksi antar fasa :

Q = h.A.(TS - Tf), dimana :

h = koeffisien perpindahan panas A = luas perpindahan panas

(TS Tf) = perbedaan suhu antara permukaan dengan badan fluida

b. perpindahan massa

1. secara molekuler (diffusi) :

Ni = -Di.S. Ci (hk. Fick), dimana :

Di = koeffisien diffusi komponen i S = luas perpindahan massa

Ci = gradien konsentrasi komponen i 2. antar fasa :

Ni = Kc.S.(Cs - Cb), dimana :

Kc = koeffisien perpindahan massa

xy = -.Vx/y (hk. newton untuk viskositas), dimana : xy = fluks perpindahan x momentum ke arah y Vx = kecepatan ke arah x

 = viskositas d. reaksi kimia :

aA + bB  cC

kecepatan A bereaksi dinyatakan dengan : rA k C. A.CB

 

mol A bereaksi/(volume . waktu), dimana :

k = konstanta kecepatan reaksi  = orde reaksi terhadap A  = orde reaksi terhadap B

3. Hukum kesetimbangan :

a. kesetimbangan fasa : uap-cair, cair-cair, gas/uap-padat, cair-padat b. kesetimbangan kimia :

aA + bB  cC, maka K =

 

   

C

C C

C c

A a

B b .

III. Contoh Soal.

A. Hk. Kekekalan Massa.

1. Dua buah tangki (masing-masing 100 l), mula-mula penuh dengan larutan garam berkonsentrasi 20 gr/l. Ke dalam tangki I dialirkan air dengan laju 5 l/min, dan pada saat yang sama dikeluarkan dari tangki I, larutan dengan laju 8 l/min ke tangki II. Dari tangki II dikeluarkan larutan dengan laju 8 l/min, dimana 3 l/min ke tangki I dan 5 l/min dibuang. Tentukan konsentrasi garam (gr/l) di tangki I dan II sebagai fungsi waktu. Asumsi  sama diseluruh aliran.

Jawab :

I II

V1 dan C1 V2 dan C2 air

5 l/min lar._{3 l/min}

lar 8 l/min

lar. 5 l/min

Tangki I :

neraca massa total : akumulasi = input - output





d V dt

1

5 3 8

.

  

    dV

dt

1 ₀  V





d V C

dt C C

1 1

2 1

5 0 3 8

.

.

  

 C dV dt V

dC

dt C C

1 1

1 1

2 1

3 8

  

 100 1 3 8

2 1

dC

dt  C  C (1)

Tangki II :

neraca massa total : akumulasi = input - output  dV

dt

2 ₀  V

2 konstan = 100 l neraca massa garam : akumulasi = input - output





d V C

dt C C

2 2

1 2

8 8

.

 

 C dV dt V

dC

dt C C

2 2

2 2

1 2

8 8

  

 100 2 8 8

1 2

dC

dt  C  C  C C

dC dt

1 2

2

12 5

  . (2)

Pers. (2) didefferensialkan : dC dt

dC dt

d C dt

1 2

2 2 2

12 5

  . (3)

Substitusi pers.(2) + (3) ke pers. (1) :

100 2 1250 3 8 100

2 2

2 2 2

2

dC dt

d C

dt C C

dC dt

   

 1250 200 5 0

2 2 2

2 2

d C dt

dC

dt C

  

 250 40 0

2 2 2

2 2

d C dt

dC dt C

   , diselesaikan dengan P.D. linier tereduksi tingkat n

 250 m2

+ 40 m + 1 = 0, diperoleh m1 = -0.031 dan m2 = -0.129, maka penyelesaiannya adalah : C2 = K1.e-0.031 t + K2.e-0.129 t (4)

t t

e K e

K dt

dC _0.129

2 031

. 0 1

2 _{0.031. .}  _0.129.  ₍₅₎

Kondisi awal, t = 0 : - pers. (4) 20 = K1 + K2 - pers. (5) 0 = -0.031 K1 - 0.129 K2

dari kedua persamaan ini didapat harga K₁ = 26.33 dan K₂ = -6.33, jadi penyelesaian untuk tangki II adalah : C2 = 26.326.e-0.031 t - 6.33.e-0.129 t (6) Substitusi pers. (5) + (6) ke pers. (2) :

C₁ = 26.33.e-0.031 t - 6.33.e-0.129 t + 12.5(-0.031.26.33.e-0.031 t + 0.129.6.33.e-0.129 t

)

= 16.e-0.031 t + 3.875.e-0.129 t Dengan cara Transformasi Laplace :

100 1 3 8

2 1

dC

 

 

100 1 3 8

2 1

.L dC . .

dt L C L C

  

 

 

 100s C s.~₁( )C₁20( )0 3.C s~₂( ) 8.C s~₁( ) 

 



  

 (100.s8)C s~₁( )3.C s~₂( )2000 (1) 100dC2 8 ₁ 8 ₂

dt  C  C , dilakukan transformasi Laplace :

 

 

100.L dC2 8. ₁ 8. ₂

dt L C L C

  

 

 

 100s C s.~₂( )C₂20( )0 8.C s~₁( ) 8.C s~₂( ) 

 



  

 8.C s~₁( )(100.s8)C s~₂( )2000 (2)

Penyelesaian pers. (1) dan (2) :

~

( ) ( . )

( . )

( . )

. .

. . .

. .

( . )( . )

C s s

s

s

s

s s

s

s s

1 2

2000 3

2000 100 8

100 8 3

8 100 8

20 2 2 016 0 004

20 2 2 0129 0 031 

 

 

 

 

  



 

C L

s s

1

1 3875

0129

16 0 031 

  

  

  

 .

( . ) ( . ) 16.e

-0.031 t

+ 3.875.e-0.129 t

~ ( )

( . )

( . )

( . )

. .

. . .

. .

( . )( . )

C s

s

s

s

s

s s

s

s s

2 2

100 8 2000

8 2000

100 8 3

8 100 8

20 3 2 016 0 004

20 3 2 0129 0 031 

 

 

 

 

  



 

C L

s s

2

1 6 33

0129

26 33 0 031

 

  

  

  

 .

( . )

.

( . ) 26.326.K1.e -0.031 t

- 6.33.K2.e-0.129 t

2. 5 m3/jam larutan yang berisi reaktan A dengan konsentrasi 2 kgmol/m3 untuk reaktor alir berpengaduk yang mula-mula berisi pelarut murni 2 m3. Dalam reaktor terjadi reaksi peruraian : A  R + S (reaksi order 1 irreversible). Dari reaktor keluar larutan dengan laju alir 5 m3/jam.

a. Tentukan persamaan yang menyatakan konsentrasi A (CA) sebagai fungsi waktu (t), dimana k = 6/jam.

b. Tentukan waktu yang dibutuhkan agar konsentrasi A dalam cairan keluar reaktor mencapai 0.518 kgmol/m3. Pada saat itu tentukan CR dan CS.

c. Bila keadaan mantap tercapai, tentukan CA yang keluar reaktor. Jawab :

A 5 m3/jam 2 kgmol/m3

A R S

5 m3/jam V

a. rA =- k. jam

1

CA ₃ A m kgmol

= -6.CA

jam m kgmol . A 3

neraca massa total : akumulasi = input - output

dV  

dt 5 5 0 , V konstan = 2 m 3

neraca massa komponen A : akumulasi = input - output





V r C dt C V d A A

A _{5.2 5. .}

.

  

 2dC 10 5 6 2 10 17

dt C C C

A

A A A

  .  ( . . ) 

 2

10 17 C_AdCA dt, diintegralkan :

2

10 17

0  0





_C dC



dt

A A

CA t

  2  

17ln(10 17CA)₀ t

CA

 ln 10 17 .

10 8 5

      C t A

 1-1,7CA = e-8.5t  CA



e



t

 1  

17 1

8 5

.

.

kgmol/m3

b. 0 518 1





17 1 8 5 . . .   

e t  t   1







8 5. ln1 17. . 0 518. = 0.25 jam.

neraca massa komponen R :



R



_{R A A R}

C C V r C dt C V d 5 12 . . 5 0 . 5 . _{    }













A R A R A R R A R R R R C C V kC C V r C dt C V d r r ana V r C dt C V d 12 5 5 5 . , : dim ; . . 5 0 . 5 .               

 2 12 1

17 1 5

8 5

dC

dt e C

R t R     . . ( ) .

 dC

dt C e _{x e} t

R

R

t

   

2 5 6

17 1 2 5

8 5

.

. ( ) .

 e t dC

dt e t C e

t _e

R

R

t

2 5 _{2 5 2 5} 6

17 2 5 1

8 5

. _. .

. . ( )

.

   

 d e t C

dt e

t _e

R

t

2 5

6 17

2 5 6

. .

. (

. ₎



 _{  } 

,diintegralkan :

d e t C_R e t e dt

e C

t t

t R

2 5

0

6 17

2 5

0 2 5

6

. .

. (

. ₎

.

.



  







 e2 5t C_R 6 e t e t k 17

1 2 5

2 5 1 6

6

. .

. ( .

. ₎

    _{, t = 0  C}

R = 0  0 6

17 1 2 5

1

6 2

     

. ( . ) k k , maka :

C_R  6  e t  e t 17

1 2 5

1

6 2

2 5

8 5

. ( . ) .

.

.

,

Saat t = 0.25  CR = 0.4115 kgmol/m3, dan dari pers. reaksi CS = CR = 0.4115 kgmol/m3.

c. Keadaan mantap tercapai saat t = , maka CA = 1

17. (1 0 )= 0.588 kgmol/m 3

.

3. Reaksi peruraian zat A menjadi B, dalam reaktor bertekanan yang ishotermal dirumuskan sebagai 2A  B. Reaksi ini irreversibel dan mengikuti kinetika reaksi order 2, dengan konstanta kecepatan reaksi 1000 ft3/(lbmol.menit). Reaktor beroperasi pada suhu 800 oF dan tekanan 3 atm yang dijaga tetap, dimana gas A murni masuk dengan laju alir 1 lbmol/menit. Karena suhu operasi yang rendah, dianggap tidak ada reaksi didalam sistem perpipaan, dan kedua gas mengikuti sifat gas ideal.

a. Pada keadaan steady state, gas keluar reaktor mengandung 1/3 bagian gas B, tentukan volume reaktor tersebut.

b. Setelah keadaan steady tercapai, tiba-tiba valve keluar reaktor ditutup dan laju alir gas A diatur agar tekanan di dalam reaktor tetap 3 atm. Tentukan waktu yang diperlukan mulai valve ditutup sampai konsentrasi B di dalam reaktor 9/10 bagian.

Jawab : a./

Feed A

Product A, B P = 3 atm

rA = -kC

2A  B

awal nAo 0

reaksi nAo.x 0.5 nAo.x akhir nAo.(1- x) 0.5 nAo.x

(x = konversi reaksi)

Jumlah mol gas di dalam reaktor = nAo.(1- x) + 0.5 nAo.x = nAo.(1- 0.5 x) Konsentrasi gas A di dalam reaktor = (1 - 1/3) = 2/3 = nAo.(1- x)/(nAo.(1- 0.5 x))

= (1 - x)/(1 - 0.5 x) 3 - 3x = 2 - x

1 = 2x , maka x = 0.5 n_A = n_Ao(1 - x) = 1(1 - 0.5) = 0.5

Neraca massa komponen A di dalam reaktor : dnA/dt = nAo - nA– k(nA/V)2v

dn_A/dt = n_Ao - n_A - kn_A2/V (steady state)

0 = 1 - 0.5 - 1000 . 0.52/V ====> V = 500 ft3 b./

Feed A

P = 3 atm T = 800 oF V = 500 ft3 P

n P V R T

 .  

. .

3

163034 . 500

0.7302 . 1260 lbmol nA = 0.1 x 1.63034 = 0.163 lbmol neraca massa komponen A :

dn dt

k n V

k n V

dn dt

k n V

A   . A  _. . A  A   _. . A

2 2 2

1 2

1

2  dt

V k

dn n

t

A A 0

2 0 5 0 163

2



  . .



. .

 t V k n_A   

  



   _  _

2 1 2 1

0163 1

0 5 4 135

0 5 0 163

. .

. . .

. .

. 500

1000 min

B. Hk. Kekekalan Energi.

Jawab :

x

q k S T

x

x x x

x x 



  . . 

X

Ts _T

0

.q k S. . T x

x x x x

x x x  

 

 





 

Asumsi :

 konveksi di permukaan slab bersuhu Ts diabaikan.  arah perambatan panas hanya pada arah x.

 k dan Cp tak tergantung suhu. Neraca panas pada elemen setebal x :

akumulasi = input - output

 

 

  _

Q

t k S

T

x k S

T x

x x x x x

   



 

 

  

. . . .









 

  _

m C T

t k S

T

x k S

T x

p

x x x x x

. .

. . . .



   



 

 

  

  







 

  _

. . . .(

. . . .

S x C T T

t k S

T

x k S

T x

p ref

x x x x x



   



 

 

  

  



 



  

. .S x C. T . . . .

t k S

T x k S

T

x k S x T x

p    

2 2

  

  

. .S x C. T . . t k S x

T x

p 

2

2 

  

 

T t

k C

T x

p

 .

2

2 



  

T t

T x  2

2 2

Untuk menyelesaikan diperlukan batasan masalah sbb. : - t = 0 : 0  x  L  T = T0

- t > 0 : x = 0  T = Ts dan x =   T = T0.

a r L r r r r T L r k    . . . . 2 . r r r r T L r k       . . . . 2 . Asumsi :

 konveksi di permukaan slab bersuhu Ts diabaikan.  arah perambatan panas hanya pada arah r.

 k dan Cp tak tergantung suhu. Neraca panas pada elemen setebal r :

akumulasi = input - output

r r r r r r T L r k r T L r k t Q                     . . . . 2 . . . . . 2 . 





r r r r r p r T L r k r T L r k t T C m                      . . . . 2 . . . . . 2 . . . 









r r r r r ref p r T L r k r T L r k t T T C r L r                          . . . . 2 . . . . . 2 . . . . . . . 2 .                  . . . . . .

2 r L x C T 2 2 2

t k r L

T

r k r L

T

r L r

k r T

r r

p    

               . . . . . .

2 r L r C T 2

t L r

k r T

r r p     _       . . . . C T t r

k r T

r r p      1  _         r T r r T k t T C_p     

. . . ₂ 1.

2  _         r T r r T C k t T p       . 1 . . 2 2  _         r T r r T t T       . 1 . ₂ 2 2

- t = 0 : 0  r  a  T = T0 - t > 0 : r = a  T = Ts.

3. Suatu bola terbuat dari logam dengan jari-jari a, yang mula-mula bersuhu T0. Tiba-tiba bola ini dimasukkan ke dalam cairan pada suhu Ts. Dianggap sejak saat itu suhu permukaan bola selalu tetap pada Ts. Jabarkan PD yang menyatakan distribusi suhu di dalam bola.

Jawab :

r



 

k r T

r _{r r r} .( . .4 2).

 _





k r T

r _{r r} .( . .4 2).



r

Asumsi :

 konveksi di permukaan slab bersuhu Ts diabaikan.  arah perambatan panas hanya pada arah r.

 k dan Cp tak tergantung suhu. Neraca panas pada elemen setebal r :

akumulasi = input - output





   

 



 

  _

4

4 4

2

2 2

. . . .( )

. . . .

r r Cp T T

t k r

T

r k r

T r

ref

r r r r r



   



 

 

  



 

 

 

 

T

t r

T r

T r

  



 

 

2

2 2

2 . .

Untuk menyelesaikan diperlukan batasan masalah sbb. : - t = 0 : 0  r  a  T = T0

- t > 0 : r = a  T = Ts.

1. Diinginkan untuk menghasilkan suatu zat B dari bahan baku A didalam reaktor tangki teraduk dengan volume efektif V m3. Bila Q m3/detik suatu larutan A dengan konsentrasi Co dialirkan ke reaktor yang semula kosong, dan reaksi yang terjadi dalam reaktor :

A B C

K

K

K

1

2

3

 

   

dimana semua reaksi berorder 1. Jabarkan PD yang menunjukkan jumlah mol B didalam reaktor sebelum cairan tumpah.

2. Suatu aliran liquida dengan densitas, , dan panas jenis, Cp, mengalir melalui pipa dengan jari-jari dalam, a m. Kecepatan linier cairan didalam, U m/jam. Dinding pipa dipertahankan pada suhu, T1 oC, dan suhu liquida masuk, T0oC, (T1 > T0). Koeffisien perpindahan panas secara konveksi pada dinding pipa, h kcal/(m2.jam.oC). Konduksi didalam cairan diabaikan dan perubahan suhu ke arah radial diabaikan. Pada keadaan steady state :

a. Tunjukkan PD yang menggambarkan peristiwa perpindahan panas di dalam cairan.

b. Tentukan kondisi batas PD pada soal a). c. Bila diketahui :

Cp = 1 kcal/(m2.jam.oC)  = 1000 kg/m3

U = 6000 m/jam a = 0.025 m

L = panjang pipa = 5 m T0 = 40 oC

T1 = 100 oC h = 500 kcal/(m2.jam.oC) tentukan suhu cairan keluar pipa.

3. Turunkan distribusi suhu pada keadaan steady state pada suatu silinder berongga dengan jari-jari dalam, r = a, dan jari-jari luar, r = b. Pada badan silinder yang bersuhu seragam dan selalu tetap, T, terdapat sumber panas, yang mengalir secara radial sebagai fungsi jari-jari dengan kecepatan Q(r) = Q₀.r, dan konduktifitas panas bahan silinder berubah menurut fungsi waktu, k = k0.r, dimana Q0 dan k0 adalah konstanta. Permukaan batas dalam suhunya dijaga 0, pada permukaan batas luar terjadi perpindahan panas secara konveksi ke udara sekitarnya yang bersuhu Ts, dengan koeffisien perpindahan panas, h.

4. Sebuah metal berpenampang segi empat dengan lebar 3 inchi dan tebal 0.2 inchi) dan panjang 4 ft. Pada salah satu ujungnya dipanaskan pada suhu tetap 600 o

Qin

Qout

Qout

Qout

4"

0.2" 3"

5. Oksigen cair produksi PT. Aneka Gas Industri disimpan dalam tangki berbentuk bola, yang berventilasi ke udara atmosfer. Jari-jari dalam tangki, r = r0, bersuhu T0, dan jari-jari luar, r = r1, bersuhu T1. Kondutifitas panas bahan tangki tergantung dari suhu, dengan fungsi sbb. : k = k0 + (k1 - k0).((T - T0)/(T1 - T0)). a. Tentukan laju perpindahan panas yang melalui bahan tangki sebagai fungsi jari-jari dan suhu pada keadaan stady state, Q = f(r,T).

b. Tentukan laju penguapan oksigen dari dalam tangki yang berdiameter dalam 6 ft dengan tebal 1 ft, dimana kondisi tangki sbb. :

- suhu permukaan dalam tangki, T0 = -183 oC - suhu permukaan luar tangki, T1 = 0

o C - titik didih normal O2 = -183 oC - panas penguapan normal oksigen = 1636 cal/mol - k, pada suhu : 0 oC = 0.090 Btu/(hr.ft2/ft.oF)

-183 oC = 0.072 Btu/(hr.ft2/ft.oF) (Bird, soal 9.F2)

6. Suatu larutan yang mengandung 20 % reaktan A pada 30 oC dialirkan ke suatu reaktor tangki teraduk dengan laju 10000 kg/jam. Reaktor dilengkapi dengan suatu koil pemanas dengan luas 3 m2. Koil ini dialiri uap air yang mengembun pada suhu 149 oC. Didalam reaktor terjadi reaksi kimia sangat cepat yang endotermis dengan panas reaksi 20 Kcal/(kg A yang bereaksi). Cairan panas (yang praktis tak mengandung A) keluar dari reaktor dengan laju 10000 kg/jam. Pada saat awal terdapat 2500 kg larutan pada suhu 30 oC didalam tangki. Harga koefisien perpindahan panas total adalah 350 Kcal/(jam.m2.oC) dan kapasitas panas larutan adalah 1 kcal/(kg.oC). Hitung suhu cairan keluar sesudah : a) 10 menit ,b) 1 jam , c) 2 jam.

7. Suatu tangki berisi N2 (anggap sebagai gas ideal) pada tekanan 780 kPa dan suhu 30 oC, dengan volume tangki adalah 28 m3. Tiba-tiba terjadi sedikit kebocoran pada tangki. Laju alir gas melalui lubang bocor pada saat itu adalah 0.1 kgmole/jam. Selanjutnya laju alir gas melalui lubang bocor dinyatakan sebagai berikut,

F = Cd P Patm kgmole/jam

dimana ,

Patm = Tekanan atmosfir = 1.013 x 105 Pa Cd = suatu konstanta

Anggap selama kebocoran tak ada perubahan suhu pada tangki. Tentukan tekanan pada tangki 15 menit setelah kebocoran terjadi.

BAB II

PENYELESAIAN PERSAMAAN DIFFERENSIAL

BIASA DENGAN DERET

Sebagian tipe persamaan-persamaan differensial yang penyelesaiannya dapat dinyatakan dalam bentuk tertutup telah dibicarakan pada mata kuliah matematika di semester-semester yang terdahulu. Bahkan untuk hal-hal tersebut di atas, banyak penyelesaian-penyelesaian tertutup diperoleh (dinyatakan) sebagai fungsi-fungsi yang sebenarnya menyatakan deret tak berhingga.

(Contoh : fungsi-fungsi logaritmik, trigonometri, dan hiperbolic). Penyelesaian sebagian besar persamaan-persamaan differensial biasa diperoleh dalam bentuk deret tak berhingga. Pernyataan berikut :

A0 + A1(x - x0) + ... + An(x - xn)n + ... = n





0

An(x - xn)n (2-1) disebut deret Pangkat. Deret ini disebut memusat bila deret ini mendekati suatu harga yang berhingga bila n mendekati tak berhingga. Pengujian yang paling sederhana untuk kondisi memusat adalah rasio test, yaitu bila :

lim n

n n

A

A x x J L x x



1 _{    }

0 0 1 (2-2)

maka deret ini memusat, namun bila J > 1, deret menjadi tak memusat. Pengujian ini tak dapat digunakan bila J = 1. Besaran : 1 1

L

A A

n n

n 

 

lim sering disebut jari-jari pemusatan. Di dalam selang pemusatan, suatu deret pangkat bisa diperlakukan sebagai fungsi kontinyu dengan turunan-turunannya untuk semua tingkat juga kontinyu. Berikut ini sifat-sifat penting dari deret pangkat :

1. Di dalam selang pemusatan deret pangkat awal, deret yang dibentuk dengan cara differensiasi atau integrasi suku persuku deret awal juga memusat.

2. Hasil kali dua deret pangkat memusat di dalam selang pemusatan yang bersamaan dari pada kedua deret asal.

3. Perbandingan dua deret pangkat memusat di dalam selang pemusatan yang bersamaan kedua deret asal, asalkan penyebut mempunyai harga yang tidak nol di dalam selang ini.

Operasi dengan deret lebih mudah dilaksanakan bila notasinya disingkat. Bila y menyatakan suatu fungsi x [f(x)] yang disajikan dalam selang pemusatan sebagai deret pangkat :

y = f(x) = A₀ + A₁(x - x₀) + ... + A_n(x - x_n)n + ... = n





0

A_n(x - x_n)n (2-3) maka,

dy

dx = A1 + 2A2(x - x0) + ... + n.An(x - x0)

n - 1

+ ... = n





0

n.An(x - xn) n - 1

(2-4)

d y dx

2

2 = 2A2 + 6A3(x - x0) + ... + n.(n - 1).An(x - x0)

= n





0

n.(n - 1).An(x - xn)n - 2 (2-5)

d y dx

k k =

n





0

n.(n - 1)....(n - k + 1).An.(x - xn) n - k

(2-6) Deret pangkat I seperti pada pers. (2-3), bisa diajdikan bentuk yang lebih bermanfaat yang dikenal sebagai "Deret Taylor" sebagai berikut : differensiasikan pers.(2-3) n kali dan tetapkan x = x0. Masing-masing anggota daripada sistem persamaan-persamaan yang dihasilkan akan menentukan satu konstanta :

A0 = y0 = f(x0) (2-7)

A1 =

dy dx x  



 ₀= f '(x0) (2-8)

An =

f x

n

n ( )

!

0 _(2-9)

akibatnya, pers.(2-3) menjadi : y = f(x) = f x

n n

n

( ) !

0 0  



(x - x0)n (2-10)

supaya pers.(2-10) valid, seluruh turunan-turunan f(x) harus ada pada x = x0. Suatu fungsi yang dapat disajikan dengan deret Taylor di sekitar x = x0 dikatakan sebagai regular pada x = x0. Penyelesaian suatu PD orde dua homogen linier seringkali bisa diperoleh dengan metoda deret pangkat. Dalam bentuk standart, PD ini bisa ditulis sbb. :

d y

dx a x dy

dx a x y

2

2  1( )  1( ) 0 (2-11)

Sifat-sifat koeffisien-koeffisien a1(x) dan a2(x) mempunyai arti yang penting pada karakteristik penyelesaian deret pangkatnya. Apabila fungsi a1(x) dan a2(x) tak dapat dinyatakan dengan deret pangkat yang memusat dalam selang tertentu, maka penyelesaian deret pangkatnya akan sulit dikerjakan.

Karakteristik penyelesaian deretnya disekitar x0 dapat diperkirakan dari sifat-sifat fungsi a1(x) dan a2(x) didekat x0. Titik x0 dapat diklasifikasikan sbb. :

1. x₀ disebut titik ordinary PD bila a₁(x) dan a₂(x) dapat disajikan sebagai deret pangkat yang memusat yang meliputi x = x0 di dalam selang pemusatannya, artinya a1(x) dan a2(x) regular pada x = x0.

2. x0 disebut titik singular PD bila salah satu a1(x) atau a2(x) tak regular pada x = x0.

3. x0 disebut titik regular singular PD bila klasifikasi 2 berlaku tetapi hasilkali (x - x0).a1(x) dan (x - x0)2.a2(x) kedua-duanya regular pada x = x0.

4. x0 disebut titik irregular singular PD bila klasifikasi 2 berlaku tetapi 3 tidak berlaku.

Contoh :

 a(x) = x hanya mempunyai titik-titik ordinary

 a(x) = 1 1

x( x)mempunyai titik singular pada x = 0 dan x = 1

Contoh : [Mickley, 5-3]

x x d y

dx x x dy dx y

2 2 2

2 2

1 2 1 0

(  )  (  )  

Identifikasikan jenis titik dan lokasinya.

Jawab :

 d y

dx

x x

x x

dy

dx x x y

2

2 2 2 2 2 2 2

2 1

1

1

1 0

 

   

( )

( ) ( )

 d y

dx

x x

x x x

dy

dx x x y

2

2 2 2 2 2 2 2

2 1

1 1

1

1 0

 

    

( )

( ) ( ) ( )

 d y

dx x x x

dy

dx x x y

2

2 2 2 2 2

2

1 1

1

1 0



    

( )( ) ( )

maka : a1(x) =

2

1 2 1

x.( x )( x) dan a2(x) =

1 1

2 2 2

x ( x )  x0 = 0 : - a1(x) dan a2(x) : tidak regular

- x.a1(x) :

2

1 2 1

.( x )( x) : regular - x2.a2(x) :

1

1 2 2

( x ) : regular

x0 = 0 : titik regular singular  x0 = 1 : - a1(x) dan a2(x) : tidak regular

- (x-1).a1(x) :

2 1

1 1

2 1

1 1 1

2

( )

.( )( )

( )

.( )( )( )

x

x x x

x

x x x x



  

 

   =



 2

1 2

. .(x x) : regular - (x-1)2.a2(x) :

( )

.( )

( )

.( ) .( )

x

x x

x

x x x



 



  

1 1

1

1 1

2

2 2 2

2

2 2 2

1

1

2 2

x .( x) : regular x₀ = 1 : titik regular singular

 x0 = 2 : ordinary  ... : ordinary  x0 =  : ordinary

Penyelesaian secara deret pangkat dengan pers.(2-11) diterangkan sbb. :

1. Bila x0 adalah titik ordinary pers.(2-11), maka akan diperoleh dua penyelesaian deret pangkat yang linier independent yang regular pada x = x0. Masing-masing penyelesaian mempunyai bentuk :

y = n





0

2. Bila x0 adalah titik regular singular pers.(2-11), maka penyelesaian deret pangkat yang regular pada x = x0 tak dapat dijamin. Tetapi metoda yang akan dijelaskan sesudah ini akan selalu menghasilkan setidak-tidaknya sebuah penyelesaian dengan bentuk :

y = (x - x0)s n





0

An(x - x0)n (2-13) dimana s adalah sebuah bilangan yang harganya dapat ditentukan.

3. Bila x0 adalah titik irregular singular pers.(2-11), maka penyelesaian deret pangkatnya mungkin ada atau mungkin tidak ada.

Contoh : [Titik Ordinary]

Selesaikan PD berikut yang valid disekitar x = 0 :

d y dx x

dy dx y

2

2   0

Jawab :

Fungsi a1(x) = x dan a2(x) = 1 adalah regular untuk x0 = 0, jadi titik x0 = 0 adalah ordinary, sehingga penyelesaian deret pangkatnya adalah : Y x A xn

n n

( ) ( )

 



0

.

Dimana turunannya adalah : dy

dx nA xn n n

 

 



( ) 1

0

dan d y

dx n n A xn

n n

2 2

2 0

1

  

 



( ) ( ) , yang disubstitusikan ke PD diatas. PD menjadi :

 n n A xn x n A x A x n

n

n n

n n n

n

.(  ). .   . .  . 

 

  

 



1 2





0

0

1 0 0

 [2A2 + 6A3.x + 12A4.x 2

+ 20A5.x 3

+ 30A6.x 4

+ 42A7.x 5

+ ...] + [A1.x + 2A2.x 2 + 3A3.x3 + 4A4.x4 + 5A5.x5 + ...] + [A0 + A1.x + A2.x2 + A3.x3 + A4.x4 + A5.x5 + ...] = 0

identity :

2A2 + A0 = 0  A2 = -1/2 A0 6A3 + 2A1 = 0  A3 = -1/3 A1

12A₄ + 3A₂ = 0  A₄ = -1/4 A₂ = 1/8 A₀ 20A5 + 4A3 = 0  A5 = -1/5 A3 = 1/15 A1 30A6 + 5A4 = 0  A6 = -1/6 A4 = -1/48 A0 42A7 + 6A5 = 0  A7 = -1/7 A5 = -1/105 A1 ....

....

A

n A n

n n

2 0

1 2  ( )

. !

Jadi penyelesaian PD adalah :

Y x A

n x A x x x x

n n

n n

( )` ( )

. !. . ...

       



 

 



0

2 1

3 5 7

0

1 2

1 3

1 15

I. METODA FROBENIUS

.

Metoda ini dimulai dengan mencari penyelesaian-penyelesaian yang valid di daerah titik x = 0. Penyelesaian-penyelesaian yang valid di daerah suatu titik x = x0 bisa diperoleh dengan transformasi persamaan differensial itu dengan menggunakan variabel baru z = x - x0. Pembahasan berikut ini menganggap bahwa transformasi ini telah dilaksanakan. Pers.(2-11) ditulis dalam bentuk berikut :

Ly  R(x)d y

dx 2

2   

1 1

0

2 xP x

dy

dx x V x y

( ) ( ) (2-14)

dianggap :

1. R(x) 0 di dalam interval sekitar x = 0.

2. persamaan telah dibagi dengan suatu konstanta yang membuat R(0) = 1. 3. R(x), P(x), dan V(x) adalah regular pada x = 0.

maka x.a1(x)  P(x)/R(x) dan x 2

.a2(x)  V(x)/R(x) adalah regular pada x = 0, dan titik x = 0 adalah seburuk-buruknya merupakan titik regular singular.

Fungsi-fungsi R(x), P(x), dan V(x) disajikan sebagai deret pangkat : R(x) =

k





0

Rk.xk (2-15)

P(x) = k





0

Pk.xk (2-16)

V(x) = k





0

Vk.xk (2-17)

Harga-harga numerik koeffisien R_k, P_k, dan V_k dapat ditentukan dalam setiap persoalan-persoalan praktis. Penyelesaian pers.(2-14) dianggap berbentuk :

y = xs. n





0

An.xn (2-18)

dimana A0 tidak boleh nol. Pers,(2-18) didefferensialkan untuk menentukan deret yang menyajikan dy/dx dan d2y/dx2 dan hasil-hasilnya bersama-sama dengan deret yang menyatakan R(x), P(x), dan V(x) disubstitusikan dalam pers.(2-14). Hasilnya adalah :

L(y) = R x_k k n s n s A x

k

n n s n

 

  







 

 



   



 

  

0

2 0

1

( ).( )

P x_k k n s A x

k

n n s n

 

  







 

 



  

 

  

0

2 0

( ) V x_k k A x

k

n n s n

 

  







 

 

 



 

 

0

2 0

=



(n s).(n s )R_k (n s P) _k V_k



.A x_n k n s n

k

        

 

 





1 2

0 0

= 0 (2-19)

Pers.(2-19) akan dipenuhi bila koeffisien-koeffisien xl adalah nol (dimana l adalah

maka koeffisien-koeffisien xl+s-2 diinginkan bila l mempunyai suatu harga tertentu. Pandanglah suku, V A xk n

k n s n

k

. .   

 

 





2

0 0

(2-21)

untuk l = 0, harga-harga n = 0 dan k = 0 merupakan satu-satunya pasangan yang memenuhi pers.(2-20). Sehingga koeffisien xs-2 dalah V0.A0. Untuk l = 1, pasangan-pasangan n = 0, k = 1,dan n = 1, k = 0 yang memenuhi pers.(2-20). Koeffisien-koeffisien xs-1 adalah V1.A0 + V0.A1. Bila proses ini dilanjutkan, ternyata koeffisien-koeffisien ini diperoleh dari pernyataan :

.V A_k. _{l k}xl s k

l l

   

 





2

0 0

(2-22)

Kondisi yang memenuhi pers.(2-19) adalah :



(l s k).(l s k )Rk (l s k P). k Vk



.Al k k

         _ 

 



1 0

0

(2-23) untuk masing-masing harga l antara 0 dan . Karena Al-k = An, pers.(2-23) menentukan koeffisien-koeffisien di dalam penyelesaian deret pangkat (pers. 2-18) dari PD (pers.2-14). Hubungan yang timbul dari l = 0 akan menentukan harga s. Jadi, untuk l = 0, pers.(2-23) menjadi, s(s-1)R0 + s.P0 + V0 = 0 (2-24).

Pada umumnya, pers.(2-24) akan menentukan dua harga s yaitu s1 dan s2, sehingga diperoleh dua penyelesaian deret (yang berbeda satu sama lain) dari PD (pers.2-14). Suku A₀ adalah sembarang dan harganya dapat ditentukan dari kondisi batas untuk persamaan differensial ini. Koeffisien-koeffisien yang lain A1, A2,..., An dapat dinyatakan dalam A0 untuk harga s tertentu. Sehingga, untuk l = 1, pers.(2-23) memberikan :

A s s R s P V

s s s P V A

1

1 1 1

0 0

0

1

1 1

    

   

( ). .

( ) ( ). .

Kondisi untuk l = 2, akan memberikan A2 dinyatakan dalam A1, dan seterusnya. Dengan notasi :

f(s) = s2 + (P0 - 1)s + V0 (2-25) qk(s) = Rk(s-k)

2

+ (Pk - Rk).(s-k) + Vk (2-26) rumus rekurensi yang menghubungkan An dengan koeffisien-koeffisien dengan indeks yang lebih kecil, jadi juga dengan A0 mudah diperoleh dari pers.(2-23) sebagai :

A

q s n A f s n

n

k n k

k n



 



 



( ).

( )

1 _(2-27)

dimana n  1. Pers.(2-27) tak berlaku bila f(s+n) sama dengan nol. Keadaan khusus ini dibicarakan berikut ini.

II. KEADAAN-KEADAAN KHUSUS.

pada pers.(2-27) menjadi nol untuk suatu harga n tertentu, katakanlah n = N, dan AN tak dapat ditentukan.

Oleh karena itu dapat disimpulkan bahwa bila metoda Frobenius digunakan untuk menentukan penyelesaian deret suatu PD linier homogen, timbul beberapa alternatif berikut :

1. Bila s1 - s2  0 dan juga bukan bilangan bulat, maka metoda Frobenius memberikan dua buah penyelesaian yang independent dalam bentuk pers.(2-18).

2. Bila s1 - s2 = 0, maka metoda Frobenius hanya memberikan sebuah penyelesaian dengan bentuk pers.(2-18)

3. Bila s1 - s2 = N, dimana N adalah bilangan bulat real, maka pemakaian harga s yang lebih besar (yaitu s₁) akan selalu memberikan sebuah penyelesaian dengan bentuk pers.(2-18). Bila harga s yang lebih kecil yang digunakan (yaitu s2). maka mungkin tak diperoleh penyelesaian dengan bentuk pers.(2-18) atau mungkin juga diperoleh dua penyelesaian independent dengan bentuk pers.(2-18), salah satu dari padanya adalah identitas dengan yang diperoleh dari harga s1. Yang terakhir ini terjadi bila x = 0, merupakan ordinary point.

4. Dalam semua keadaan dimana dapat diperoleh hanya sebuah penyelesaian dengan bentuk :

y1 = A xn A u x n s

n

.  . ( )

 





1

0 1 0

(2-28)

Penyelesaian independent kedua adalah dalam bentuk : y2 = c u x x B xn

n s n

. ₁( ).ln( ) .

0

2

 

 



(2-29)

Differensiasi pers.(2-29) dilanjutkan dengan substitusi ke persamaan differensial semula, akan menentukan keffisien Bn dinyatakan dalam suatu konstanta sembarang c.

Contoh : [s1 - s2 0 dan juga bukan bilangan bulat, Mickley 5-4a]

Selesaikan PD berikut dengan metode Frobenius yang valid disekitar x = 0 :

2 1 2 0

2 2

xd y

dx x

dy dx y

 ( )  

Jawab :

PD diubah ke bentuk PD Frobenius : R x d y

dx x P x dy

dx x V x y

( ). . ( ) . ( ).

2

2 2

1 1

0

   ,

yaitu :

d y

dx x

x dy

dx x x y

2

2 2

1 1 2

2

1 1

2 0

  

     

. . .

dimana : R(x) = 1  R(0) = 1 P(x) = 1 2

2 1 2 

 

x

x

R(x) = R x_k k n

.

 



0

= R0 + R1.x + R2.x2 + R3.x3 + ... R0 = 1, R1 = R2 = R3 = ... = 0 P(x) = P xk

k n

.

 



0

= P₀ + P₁.x + P₂.x2 + P₃.x3 + ... P0 = 1/2, P1 = -1, P2 = P3 = ... = 0 V(x) = V x_k k

n

.

 



0

= V0 + V1.x + V2.x2 + V3.x3 + ... V0 = 0, V1 = -1/2, V2 = V3 = ... = 0 Pers. Indicial : R₀ = 1, maka pers. indicialnya :

s2 + (P0 - 1)s + V0 = 0 s2 + (1/2 - 1)s + 0 = 0

s(s - 1/2) = 0  s1 = 0 dan s2 = 1/2

Penyelesaian secara deret : Y = Y1 + Y2

= xs A x_n n x A x n

s

n n n

1 2

0 0

. . . '.

 

 







Pers. rekurensi : A

q s n A

f s n n

k n k

k n



 



 



( ).

( )

1 _,

dimana : - qk(s) = Rk.(s-k)2 + (Pk - Rk).(s - k) + Vk - f(s) = s2 + (P0 - 1)s + V0

untuk s = s1 = 0 :

n = 1  A q A

f

1

1 1 0

1  [ ( ). ]

( )

q1(1) = R1.(1 - 1)2 + (P1 - R1).(1 - 1) + V1 = -1/2 f(1) = 12 + (P0 - 1).1 + V0 = 1 + (1/2 - 1).1 + 0 = 1/2

A₁ 1 2 A0 A₀

1 2   [ / . ]

/

n = 2  A q A q A

f

2

1 2 1 2 2 0

2

 [ ( ).  ( ). ] ( )

q1(2) = R1.(2 - 1) 2

+ (P1 - R1).(2 - 1) + V1 = -3/2 q2(2) = R2.(2 - 2)2 + (P2 - R2).(2 - 2) + V2 = 0 f(2) = 22 + (P0 - 1).2 + V0 = 4 + (1/2 - 1).2 + 0 = 3

A₂ A1 A A

1 0

3 2 3

1 2

1 2   [ / . ] 

n = 3  A q A q A q A

f

3

1 3 2 2 3 1 3 3 0

3

q1(3) = R1.(3 - 1)2 + (P1 - R1).(3 - 1) + V1 = -5/2 q2(3) = R2.(3 - 2)

2

+ (P2 - R2).(3 - 2) + V2 = 0 q3(3) = R3.(3 - 3)2 + (P3 - R3).(3 - 3) + V3 = 0

f(3) = 32 + (P0 - 1).3 + V0 = 9 + (1/2 - 1).3 + 0 = 15/2

A₃ A1 A A

2 0

5 2 15 2

1 3

1 6   [ / . ] 

/ n = ....

n = n  A

n A n 

1

0

!.

Jadi : Y xs A xn n n

1

0

1 

 



. . = x

n A x A n x n

n

n n

0

0 0

0 0

1 1

.

! . . !

 

 







untuk s = s2 = 1/2 :

n = 1  A q A

f

1

1 1 5 0

1 5

` '

'

[ ( , ). ] ( , )

 

q1(1,5) = R1.(1,5 - 1)2 + (P1 - R1).(1,5 - 1) + V1 = -1 f(1,5) = 1,52 + (P0 - 1).1,5 + V0 = 3/2

A₁ A0 A

0

3 2 2 3

' '

'

/

 

n = 2  A q A q A

f

2

1 2 5 1 2 2 5 0

2 5

'

' '

[ ( , ). ( , ). ]

( , )

  

q1(2,5) = R1.(2,5 - 1) 2

+ (P1 - R1).(2,5 - 1) + V1 = -2 q2(2,5) = R2.(2,5 - 2)2 + (P2 - R2).(2,5 - 2) + V2 = 0 f(2,5) = 2,52 + (P₀ - 1).2,5 + V₀ = 5

A₂ A1 A A

0 2

0

2 5

4 15

2 35

'

'

' '

.

.

  

n = 3  A q A q A q A

f

3

1 3 5 2 2 3 5 1 3 3 5 0

3 5

'

' ' '

[ ( , ). ( , ). ( , ). ]

( , )

   

q1(3,5) = R1.(3,5 - 1)2 + (P1 - R1).(3,5 - 1) + V1 = -3 q2(3,5) = R2.(3,5 - 2)2 + (P2 - R2).(3,5 - 2) + V2 = 0 q3(3,5) = R3.(3,5 - 3)

2

+ (P3 - R3).(3,5 - 3) + V3 = 0 f(3,5) = 3,52 + (P0 - 1).3,5 + V0 = 21/2

A₃ A₂ A A

2 0

3 0

3 21 2

21 7

2 35

2 35 7

' ' ' '

/ . . . .

  

  

  

Jadi : Y₂ = xs A x_n n x A A x A x n

2

0

0 5

0 1 2

2

. '.  , .[ '  '.  '. ...]

 

= x0 5 A₀ x x x

2 2

3 3

1 2 3

2 35

2 35 7

, '

. [ .

. . . ...]

   

Sehingga : Y(x) = A

n x n n

0 0

1 .

!

 



+x0 5 A₀ x x x

2 2

3 3

1 2

3 2 35

2 35 7

, '

. [ .

. . . ...]

Contoh : [s1 - s2 0 tetapi bilangan bulat, Mickley 5-4c]

Selesaikan PD berikut dengan metode Frobenius yang valid disekitar x = 0 : xd y

dx

dy dx xy

2

2 2  0 ...(A)

Jawab :

PD diubah ke bentuk PD Frobenius : R x d y

dx x P x dy

dx x V x y

( ). . ( ) . ( ).

2

2 2

1 1

0

   ,

yaitu :

d y dx x

dy dx

x x y

2 2

2 2

2

0

  

dimana : R(x) = 1  R(0) = 1 P(x) = 2

V(x) = x2 Identity :

R(x) = R xk k n

.

 



0

= R0 + R1.x + R2.x 2

+ R3.x 3

+ ... R0 = 1, R1 = R2 = R3 = ... = 0 P(x) = P x_k k

n

.

 



0

= P0 + P1.x + P2.x2 + P3.x3 + ... P0 = 2, P1 = P2 = P3 = ... = 0 V(x) = V x_k k

n

.

 



0

= V0 + V1.x + V2.x2 + V3.x3 + ...

V0 = 0, V1 = 0, V2 = 2, V3 = V4 = ... = 0 Pers. Indicial : R0 = 1, maka pers. indicialnya :

s2 + (P0 - 1)s + V0 = 0 s2 + (2 - 1)s + 0 = 0

s(s + 1) = 0  s1 = 0 dan s2 = -1

Penyelesaian secara deret : Y = Y₁ + Y₂

= xs A x c u x x B x

n n n

n n s n

1 2

0

1

0

. . . ( ).ln( ) .

 

 





 



untuk s = s1 = 0 :

Pers. rekurensi : A

q s n A

f s n n

k n k

k n



 



 



( ).

( )

1 _,

dimana : - qk(s) = Rk.(s-k) 2

+ (Pk - Rk).(s - k) + Vk - f(s) = s2 + (P0 - 1)s + V0

n = 1  A q A

f

1

1 1 0

1  [ ( ). ]

( ) q1(1) = R1.(1 - 1)

2

A₁ 0 A0

2 0

 [ . ]

n = 2  A q A q A

f

2

1 2 1 2 2 0

2

 [ ( ).  ( ). ] ( )

q1(2) = R1.(2 - 1) 2

+ (P1 - R1).(2 - 1) + V1 = 0 q2(2) = R2.(2 - 2)2 + (P2 - R2).(2 - 2) + V2 = 1 f(2) = 22 + (P0 - 1).2 + V0 = 4 + (2 - 1).2 + 0 = 6

A₂ A0 A

0

0 0 1 6

1 6  [ .  . ] 

n = 3  A q A q A q A

f

3

1 3 2 2 3 1 3 3 0

3

 [ ( ).  ( ).  ( ). ] ( )

q1(3) = R1.(3 - 1)2 + (P1 - R1).(3 - 1) + V1 = 0 q2(3) = R2.(3 - 2)2 + (P2 - R2).(3 - 2) + V2 = 1 q₃(3) = R₃.(3 - 3)2 + (P₃ - R₃).(3 - 3) + V₃ = 0 f(3) = 32 + (P0 - 1).3 + V0 = 9 + (2 - 1).3 + 0 = 12

A₃ 0 A2 10 0 A0

12

0 12 0  [ .  .  . ] 

n = 4  A q A q A q A q A

f

4

1 4 2 2 4 1 3 4 1 4 4 0

4

 [ ( ).  ( ).  ( ).  ( ). ] ( )

q1(4) = R1.(4 - 1)2 + (P1 - R1).(4 - 1) + V1 = 0 q2(4) = R2.(4 - 2)

2

+ (P2 - R2).(4 - 2) + V2 = 1 q3(4) = R3.(4 - 3)2 + (P3 - R3).(4 - 3) + V3 = 0 q4(4) = R4.(4 - 4)2 + (P4 - R4).(4 - 4) + V4 = 0 f(4) = 42 + (P0 - 1).4 + V0 = 16 + (2 - 1).4 + 0 = 20

A₄ 0 A3 1 A2 0 A1 0 A0 A2 A0

20 20 120

 [ .  .  .  . ]    n = ....

n = n  generalisasi : - suku ganjil : A2n+1 = 0 - suku genap :A

n A

n

n

2 0

1

2 1

 



( )

( )!.

Jadi : Y xs A xn n n

1

0

1 

 



. . = x

n A x A n x

n

n n

n n n

0

0 2 0

0

2 0

1

2 1

1

2 1

. ( )

( )! . .

( )

( )!



 

 

 

 





dimana : u1(x) = .

( )

( )!

 

 



1

2 1

2 0

n n

n n

x

untuk s = s2 = -1 :

y c u x x B x_n n s

n

2 1

0

2

  

 



. ( ).ln( ) .

y c x

n x B x

n n n

n n n

2

2 0

1 0

1

2 1

 

 

 

 







.ln( ). ( )

dy

dx c x

n

n x c n x B n x

n n n n n n n n n

2 2 1

0 2 1 0 2 0 1 2 2 1 1

2 1 1

                







.ln( ). ( ) .

( )!. .

( )

( )!. .( ).

...(C)

d y

dx c x

n n

n x c

n n x n n n n n n 2 2 2 2 2 0 2 2 0

1 2 2 1

2 1 1 2 2 1             





.ln( ). ( ) . .( )

( )! . . ( ) . ( )!.             





c n

n x B n n x

n n n n n n . ( ) .( ) ( )! . .( ).( ).

1 2 1

2 1 1 2

2 2 0

3 0

...(D) Pers.(B), (C), dan (D)  (A) :

c x n n

n x c

n n x n n n n n n

.ln( ). ( ) . .( )

( )! . . ( ) . ( )!.            



1 2 2 1



2 1 1 2 2 1 2 1 0 2 1 0             





c n

n x B n n x

n n n n n n . ( ) .( ) ( )! . .( ).( ).

1 2 1

2 1 1 2

2 1 0 2 0                 







c x n

n x c n x B n x

n n n n n n n n n

.ln( ). ( ) .

( )!. . ( ) . ( )!. . .( ). 1 4 2 1 1 2

2 1 2 1

2 1 0 2 1 0 2 0          





c x

n x B x

n n n n n n

.ln( ). ( )

( )! .

1

2 1 0

2 1

0 0

 c x n n

n x c

n n x n n n n n n

.ln( ). ( ) .( )

( )! . . ( ) .( ) ( )! .             



1 4 2



2 1

1 4 1

2 1 2 2 1 0 2 1 0               







c x

n x B n n x B x

n n n n n n n n n

.ln( ). ( )

( )! .( ). . .

1

2 1 1 0

2 1 0

2

0 0

 c x x  x x  x x 

     16 3 120 5 142 7 3 5

. . .ln( ) !

. . .ln( ) !

. . .ln( )

! ...            

c x 1 x x x

3 5 15 3 9 5 13 7 . . ! . ! . ! ...            c x.ln( )x x .ln( )x x x x x

!

. .ln( ) !

.ln( ) ! ...

3 5 7

3 5 7

+ [2B2 + 6B3.x + 12B4.x 2

+ 20B5.x 3

+ 30B6.x 4

+ 42B7.x 5

+ ...] + [B0 + B1.x + B2.x2 + B3.x3 + B4.x4 + B5.x5 + ...] = 0

identity : - suku : x-1  c = 0

- suku : x.ln(x)  c{-6/3! + 1] = 0  c = 0 - suku : x3.ln(x)  c(20/5! - 1/3!] = 0  c = 0 jadi c = 0

- suku : x0  2B2 + B0 = 0  B2 = -B0/2 - suku : x1  6B3 + B1 = 0  B3 = -B1/6

- suku : x3  20B5 + B3 = 0  B5 = -B3/20 = B1/120

generalisasi : - suku ganjil : B B n n n 2 1 1 1 2 1     ( ) . ( )!

- suku genap : B B

n n n 2 0 1 2  ( ) . ( )! y B

n x B n x

n n n n n n 2 0 2 1 0 1 2 0 1 2 1 2 1          



( )



( )!. ( ) ( )!.

Jadi : y A

n x n n n      



0 2 0 1 2 1 . ( )

( )! B n x B n x

n n n n n n 0 2 1 0 1 2 0 1 2 1 2 1 ( ) ( )!. ( ) ( )!.  _       





y B

n x A B n x

n n n n n n           





0 2 1 0 0 1 2 0 1 2 1 2 1 ( ) ( )!. ( ) ( ) ( )!.

III. PERSAMAAN BESSEL.

Persamaan differensial linier orde dua berikut : x d y

dx x dy

dx x p y

2 2

2

2 2

0

 (  )  (2-30)

dikenal sebagai pers. Bessel dan penyelesaiannya disebut fungsi Bessel. Penyelesaian pers.(2-30) dengan bentuk :

y xs A x

n n n   



. 0 (2-18) bisa diperoleh dengan menggunakan metoda Frobenius. Mula-mula pers.(2-30) ditulis dalam bentuk :

d y dx x

dy

dx x x p y

2

2 2

2 2

1 1

0

  (  )  (2-31)

Bila dibandingkan dengan pers.(2-14) maka : R(x) = 1

P(x) = 1

V(x) = x2 - p2 (2-32)

Ekspansi deret pers.(2-32) yang sesuai dengan pers.(2-15) s/d pers.(2-17) memberikan harga koeffisien-koeffisiennya sbb. :

R₀ = 1, R₁ = R₂ = ....= R_n = 0 P0 = 1, P1 = P2 = ...= Pn = 0

V0 = -p2, V1 = 0, V2 = 1, V3 = V4 = ...=Vn = 0 (2-33)

Persamaan indicial (2-24), memberikan :





y x A x x

p p k p k

p

k k

k k

1 0

2

2 1

1 1

1 2 2

( ) . ( )

( )( )...( ) . . !

  

  

  

  

 



(2-35)

yang sesuai dengan s = p, dan





y x B x x

p p k p k

p

k k

k k

2 0

2

2 1

1 1

1 2 2

( ) . ( )

( )( )...( ) . . !

  

  

  

  



 



(2-36)

yang sesuai untuk s = -p.

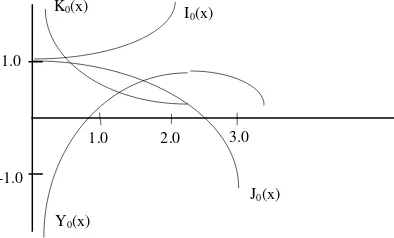
Pers.(2-35) dan (2-36) bisa ditulis dalam bentuk yang lebih sering digunakan dengan memperkenalkan suatu fungsi khusus yang disebut fungsi Gamma. Untuk harga-harga p yang positif, integral : (p) = ex xpdx





. 1 0 [image:30.595.114.490.86.177.2]

; p > 0 (2-37) disebut fungsi Gamma. Harga-harga fungsi Gamma diberikan didalam banyak tabel-tabel di literatur-literatur. Sifat-sifat penting fungsi ini adalah :

(p+1) = p.(p) ; p > 0 (2-38)

Bila N adalah bilangan bulat positif, maka :

(p+N) = (p+N-1)(P+N-2...(p+1)(p) (p) ; p > 0 (2-39) (p-1) = 1

1

(p ) (p) ; p > 1 (2-40) Bila p adalah bilangan bulat positif n, maka :

(n+1) = n! (2-41)

(1) = 0! = 1 (2-42)

Biasanya pers.(2-41) dikembangkan untuk harga-harga p yang bukan bulat dan mendefinisikan faktorial suatu bilangan positif dengan hubungan :