Crashing Optimal Pada CPM Dengan Pendekatan Linear Programing (Studi Kasus di STMIK Kristen Neumann Indonesia

CRASHING OPTIMAL PADA CPM DENGAN PENDEKATAN LINEAR PROGRAMMING

(Studi Kasus di STMIK Kristen Neumann Indonesia)

SKRIPSI

AGUSTINUS SIANTURI 030803015

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

CRASHING OPTIMAL PADA CPM DENGAN PENDEKATAN LINEAR PROGRAMMING

(Studi Kasus di STMIK Kristen Neumann Indonesia)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

AGUSTINUS SIANTURI 030803015

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : CRASHING OPTIMAL PADA CPM DENGAN PENDEKATAN LINEAR PROGRAMMING (Studi Kasus di STMIK Kristen Neumann Indonesia)

Kategori : SKRIPSI

Nama : AGUSTINUS SIANTURI

Nomor Induk Mahasiswa : 030803015

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Januari 2009

Komisi Pembimbing :

Pembimbing II Pembimbing I

Drs.Henry Rani Sitepu, M.Si Dra. Suwarno Ariswoyo, M.Si

NIP. 131 283 729 NIP. 130 810 774

Diketahui/Disetujui Oleh

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

CRASHING OPTIMAL PADA CPM DENGAN PENDEKATAN LINEAR PROGRAMMING

(Studi Kasus di STMIK Kristen Neumann Indonesia)

SKRIPSI

Saya mengakui bahwa Skripsi ini adalah hasil kerja saya sendiri kecuali beberapa kutipan dan ringkasan yang masing – masing disebutkan sumbernya.

Medan, Januari 2009

PENGHARGAAN

Segala puji dan syukur penulis ucapkan kepada Tuhan Yang Maha Esa atas berkat dan rahmat-Nya yang telah membimbing dan menyertai penulis selama proses pengerjaan sampai akhirnya dapat menyelesaikan Skripsi ini dengan baik.

Adapun penulisaan Skripsi ini dimaksudkan untuk memenuhi syarat untuk mencapai gelar Sarjana Sains. Terkait dengan keberadaan penulis di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, maka penulis

dalam hal ini memilih judul “CRASHING OPTIMAL PADA CPM DENGAN

PENDEKATAN LINEAR PROGRAMMING (Studi Kasus di STMIK Kristen Neumann Indonesia)”

Penulis mengucapkan terima kasih yang sebesar-besarnya kepada Bapak Drs.Suwarno Ariswoyo, MSi selaku Pembimbing 1 atas segala bimbingan, arahan dan kebaikan untuk meluangkan waktu, tenaga, pikiran dan bantuan pengetahuan kepada penulis. Ucapan terima kasih juga ditujukan kepada Bapak Drs. Henry Rani Sitepu, MSi selaku Pembimbing 2 atas segala nasehat dan saran yang berharga dalam penyelesaian skripsi ini.

Dalam penulisan skripsi ini, penulis banyak menerima bantuan, dorongan serta fasilitas dari berbagai pihak. Oleh karena itu, penulis juga mengucapkan terima kasih kepada :

1. Bapak Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas

Sumatera Utara Medan.

2. Bapak Dr. Saib Suwilo, Msc dan Bapak Drs. Henry Rani Sitepu, Msc selaku Ketua

dan Sekretaris Departemen Matematika FMIPA USU yang membantu kelancaran studi penulis.

3. Seluruh Staff Pengajar Departemen Matematika FMIPA USU atas segala ilmu dan

bimbingan yang telah diberikan kepada penulis selama mengikuti perkuliahan.

4. Bapak Ir. Petra Sibero atas bimbingan yang diberikan selama pengambilan data di

STMIK Kristen Neumann Indonesia.

5. Andi Sijabat, Jeffrey, Sutrisno, Santi, Maranatha, Saut Dame, Pudan, Natra,

Gunawan, Richie, Anggiat dan Rekan-rekan mahasiswa Departemen Matematika stambuk 2003 atas dorongan yang diberikan kepada penulis.

Penulis menyadari bahwa Skripsi ini masih jauh dari kesempurnaan, oleh karena itu demi perbaikan dan penyempurnaan, penulis terbuka atas kritik dan saran yang bersifat membangun dari berbagai pihak. Mudah-mudahan Skripsi ini bermanfaat bagi para pembaca.

Medan, Januari 2009 Penulis,

ABSTRAK

CPM adalah metode yang digunakan pada jaringan kerja (network) untuk perencanaan dan penjadwalan kegiatan, yang menghasilkan sebuah jalur yang tidak boleh diperlambat, karena akan memperlambat kegiatan secara keseluruhan, jalur ini disebut jalur kritis.

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak vi Daftar Isi vii Daftar Tabel ix

Daftar Gambar x Bab 1 Pendahuluan 1.1Latar Belakang 1 1.2Perumusan Masalah 2

1.3Pembatasan Masalah 2

1.4Tujuan Penelitian 3

1.5Manfaat Penelitian 3

1.6Tinjauan Pustaka 3

1.7Metodologi Penelitian 7

Bab 2 Landasan Teori 2.1 Analisa Jaringan Kerja 8 2.2 Sistematika Menyusun Jaringan Kerja 10

2.3 Diagram Jaringan Kerja 11

2.4 Menyusun Urutan Kegiatan 15

2.5 Metode Yang Digunakan 17

2.5.1 CPM (Critical Path Method) 17

2.5.1.1 Cara Menghitung Jalur Kritis 21

2.5.1.1.1 Cara Forward Pass 22

2.5.1.1.2 Cara Backward Pass 24

2.5.2 Metode Simpleks 25

2.6 Model Linear Programming 26

2.7 Penentuan Biaya Dalam CPM 27 2.8 Waktu Aktivitas Crashing 28

2.8.1 Crashing Dengan Model Linear Programming 31 Bab 3 Pembahasan 3.1 Bentuk Permasalahan 48 3.2 Cara Penyelesaian 51 3.2.1 Penentuan jalur Kritis 53 3.2.1.1 Cara Forward Pass 53

3.2.1.2 Cara Backward Pass 58

Bab 4 Kesimpulan dan Saran

4.1 Kesimpulan 71

4.2 Saran 71

Daftar Pustaka 72

DAFTRAR TABEL

Halaman

Tabel 2.1 Proyek Pembangunan Gudang Kerangka Besi 16

Tabel 2.2 Bentuk Umum Tabel Simpleks 26

Tabel 2.3 Logika Ketergantungan Pembangunan Ruko 33

Tabel 2.4 Estimasi biaya Pembangunan Ruko 33

Tabel 2.5 Tabel Simpleks Pertama (Pendahuluan) 37

Tabel 2.6 Tabel Simpleks Kedua 38

Tabel 2.7 Tabel Simpleks Ketiga 39

Tabel 2.8 Tabel Simpleks Keempat 40

Tabel 2.9 Tabel Simpleks Kelima 41

Tabel 2.10 Tabel Simpleks Keenam 42

Tabel 2.11 Tabel Simpleks Ketujuh 43

Tabel 2.12 Tabel Simpleks Kedelapan 44

Tabel 2.13 Tabel Simpleks Kesembilan 45

Tabel 2.14 Final Tabel 46

Tabel 3.1 Logika Ketergantungan Pembangunan STMIK KNI 49

DAFTAR GAMBAR

Halaman

Gambar 1.1 Hubungan Antara Waktu dan Biaya Pada Keadaan

Normal dan Crash 3

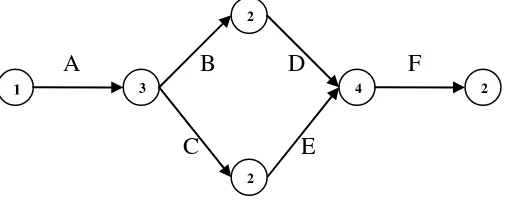
Gambar 1.2 Contoh Jaringan Kerja 4

Gambar 2.1 Jaringan Kerja Proyek Pembangunan Kerangka Besi 17

Gambar 2.2 Posisi dan Hubungan antara ES, LS, LF, EF, D dan Slack 20

Gambar 2.3 Pembentukan Jalur Kritis 22

Gambar 2.4 Hubungan Antara Waktu dan Biaya Pada Keadaan

Normal dan Crash 30

Gambar 2.5 Jaringan Kerja Pembangunan Ruko 34

Gambar 2.6 Jalur Kritis Pembangunan Ruko 35

Gambar 3.1 Diagram Jaringan Kerja Pembangunan Gedung STMIK KNI 52

Gambar 3.2 Diagram Jaringan Kerja Dengan Forward Pass 57

Gambar 3.3 Diagram Jaringan kerja Dengan Backward Pass 62

Gambar 3.4 Jalur Kritis Pembangunan Gegung STMIK KNI 65

ABSTRAK

CPM adalah metode yang digunakan pada jaringan kerja (network) untuk perencanaan dan penjadwalan kegiatan, yang menghasilkan sebuah jalur yang tidak boleh diperlambat, karena akan memperlambat kegiatan secara keseluruhan, jalur ini disebut jalur kritis.

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Dalam pelaksanaan proyek sering kali mengalami suatu hambatan atau penyimpangan

sehingga sering terjadi kerugian bagi penyelesaian proyek tersebut. Untuk itu perlu

adanya suatu perencanaan (planning) sebaik-baiknya yang disusun secara sistematis.

Perencanaan adalah penentuan mengenai apa yang harus dicapai, kapan dan bagaimana

hal tersebut dilaksanakan. Perencanaan merupakan salah satu fungsi manajemen yang

bertujuan untuk memecahkan masalah.

Metode jaringan kerja yang cukup dikenal akhir-akhir ini mampu menyuguhkan

teknik dasar dalam menentukan urutan dan kurun waktu kegiatan proyek. Dan pada

giliran selanjutnya dapat dipakai memperkirakan waktu penyelesaian proyek secara

keseluruhan. Dua teknik perencanaan yaitu CPM (Critical Path Method) dan PERT

(Project Evaluation and Review Thecnique) yang sangat berguna untuk menyusun

perencanaan, penjadwalan, dan pengawasan atau pengontrolan proyek, telah

dipergunakan secara meluas oleh para manager terutama untuk proyek-proyek besar.

Critical Path Method pada mulanya dikembangkan untuk memecahkan

Scheduling Problems dalam lingkungan industri. CPM berbeda dengan PERT, yang

mana CPM tidak mempergunakan Probabilistic Job Times, karena ini adalah suatu

deterministic model.

Model ini mempunyai variasi-variasi waktu (variations in job times) bukan

sebagai akibat dari random faktors (seperti good luck atau bad luck) melainkan sebagai

akibat dari pada hasil alokasi-alokasi sumber yang direncanakan dan diharapkan

Didalam CPM, kebanyakan pekerjaan dapat dikurangi waktu pelaksanaannya

jika sumber-sumber (tenaga manusia, mesin-mesin, uang dan sebagainya) ekstra

ditambah untuk melakasanakannya. Biaya untuk menyelesaikan tersebut mungkin naik,

tetapi jika ini lebih menguntungkan, maka pekerjaan tersebut harus dilaksanakan secara

biasa, dengan alokasi sumber-sumber semestinya. Kegiatan inilah yang dinamakan

percepatan (Crashing). Pekerjaan-pekerjaan yang mana yang harus diajukan dan secepat

manakah pekerjaan-pekerjaan tersebut harus diusahakan, merupakan

problema-problema yang harus dipecahkan.

Untuk melakukan percepatan (Crashing) inilah dibutuhkan model Program

Linear. Hal inilah yang mendasari penulis menggunakan pendekatan program Linear.

Dari uraian diatas penulis memilih judul ”Crashing Optimal Pada CPM Dengan Pendekatan Linear Programming (Studi Kasus di STMIK Kristen Neumann Indonesia)”.

1.2 Perumusan Masalah

Yang menjadi masalah dalam tulisan ini adalah bagaimana menentukan penyelesaian

proyek dan menentukan biaya optimum percepatan (crashing) menggunakan metode

CPM dengan pendekatan Linear Programming.

1.3 Pembatasan Masalah

Untuk mewujudkan tujuan dari penelitian ini penulis membatasi masalah yang dibahas

sebagai berikut :

1. Penulis hanya menggunakan metode CPM dengan pendekatan Program Linear

(dengan penggunaan Metode Simpleks) dalam menentukan biaya optimum setelah

dilakukan percepatan (crashing)

2. Data berupa biaya yang dipergunakan dalam penelitian hanya berupa biaya upah

tukang/ pekerja.

3. Setiap kegiatan untuk melakukan pembangunan gedung berlangsung dalam keadaan

cuaca yang baik.

1.4 Tujuan Penelitian

Adapun tujuan penulis membuat tulisan ini adalah untuk mengetahui kapan proyek akan

selesai dan berapa biaya optimum setelah dilakukan percepatan (crashing) dari sebuah

jaringan kerja.

1.5 Manfaat Penelitian

Manfaat penelitian ini adalah untuk mengetahui kapan proyek dapat diselesaikan secara

keseluruhan dan berapa biaya yang dibutuhkan untuk penyelesaian proyek tersebut.

1.6 Tinjauan Pustaka

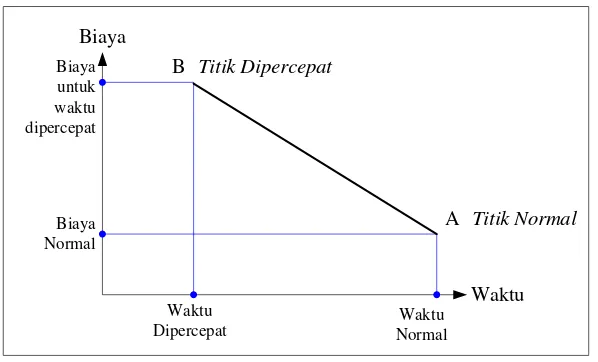
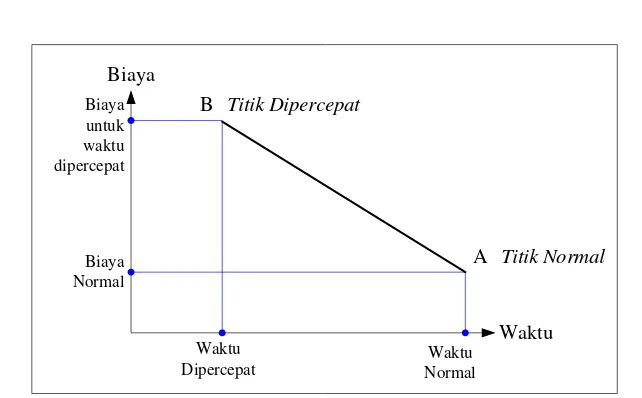
Santosa, Budi, 2003. Dalam buku ini dijelaskan hubungan waktu dan biaya pada keadaan normal dan crash sehingga umur proyek dapat dipersingkat dengan

penambahan sumber daya tenaga kerja, peralatan, modal untuk kegiatan-kegiatan

tertentu (crashing).

Biaya

Waktu A B

Waktu Normal Biaya

Normal

Titik Normal

Biaya untuk waktu dipercepat

Waktu Dipercepat

Titik Dipercepat

Siagian P., 1987. Dalam buku ini dikatakan bahwa dalam diagram kerja mempunyai dua peranan yakni, sebagai alat perencanaan proyek dan sebagai ilustrasi

secara grafik dari kegiatan-kegiatan suatu proyek. Oleh karena itu, jaringan kerja harus

mampu memberikan gambaran tentang hubungan antara komponen-komponen kegiatan

secara keseluruhan, serta arus operasi yang dijalankan sejak awal sampai berakhirnya

suatu proyek.

Siswojo, 1981. Dalam buku ini dikatakan bahwa dengan menggunakan crash schedule, tentu saja biayanya akan jauh lebih besar dibandingkan dengan normal

schedule. Dalam crash schedule akan dipilih kegiatan-kegiatan kritis dengan tingkat

kemiringan terkecil untuk mempercepat pelaksanaannya. Langkah ini dilakukan sampai

seluruh kegiatan mencapai nilai crash time-nya. Perhitungan yang dilakukan untuk

menentukan sudut kemiringan (waktu dan biaya suatu kegiatan) atau lebih dikenal

dengan slope adalah:

Biaya Dipercepat – Biaya Normal Slope Biaya =

Waktu Normal – Waktu Dipercepat

Soeharto, Iman, 1995. Dalam buku ini ditinjau cara mencari jalur kritis dengan perhitungan maju. Dimana dapat diilustrasikan pada gambar berikut :

1

B

3 2 A

3 2

0 0

C

D

E

F

G

H 2

4

3

4

5

2 d1

4

5

6 7

2 4

3 8

13 15

15 13

8 4 2

4

Keterangan :

ES LF

: Node menyatakan suatu kejadian atau peristiwa.

• ES (Earliest Start Time) adalah waktu mulai paling awal kegiatan

• LF (Latest Allowable Finish Time) adalah waktu paling akhir

kegiatan boleh selesai tanpa memperlambat penyelesaian proyek.

: Arrow menyatakan kegiatan.

: Dummy menyatakan kegiatan semu.

: Jalur kritis

Dimana dalam perhitungan maju, waktu terpanjang dalam rangkaian kegiatan

adalah jalur kritis. Yang mana jika jalur kritis diperlambat, maka akan memperlambat

kegiatan proyek keseluruhan.

Starr, Martin K, 2002, dalam buku ini dijelaskan pengambilan waktu percepatan (crash) yang optimal dengan pendekatan program linear.

Jika x_i = waktu untuk kejadian i

j

x = waktu untuk kejadian j

m

x = waktu untuk kejadian pada simpul terakhir

( )

m

ij

t = waktu normal untuk aktivitas i→ j

ij

tc = waktu crashing aktivitas i→ j

ij

τ = kemungkinan maksimum pengurangan waktu untuk

aktivitas i→ j karena crashing maksimum

ij

C = biaya untuk aktivitas normal i→ j

ij

Cc = biaya untuk aktivitas i→ j dengan crashing

ij

Model umum program linear untuk jaringan ini adalah

Min Z = S_mτ_m

Untuk kendala yang menjelaskan struktur jaringan, dimulai dari event i dengan asumsi

bahwa x_i=0

Untuk event berikutnya

i A A

j t x

x ≥ −τ +

j B B

k t x

x ≥ −τ +

. . .

1

−

+ −

≥ _{Z Z m}

m t x

x τ

Selanjutnya dengan dengan menggunakan metode simpleks dapat diperoleh jawaban

optimalnya.

Taylor III, Bernard W, 2001, dalam buku ini dijelaskan pendekatan program linear terhadap jaringan kerja. Dimana jaringan kerja dapat dimodelkan kedalam bentuk

program linear.

Jika kita menganggap x_m adalah waktu kejadian simpul terakhir dalam jaringan tersebut

diatas, ditunjuk pada simpul m, maka fungsi objektif dapat dinyatakan sebagai

Minimum Z=xm

Selanjutnya kita mengembangkan hambatan model tersebut. Maka kita menentukan

waktu untuk aktifitas i→ j sebagai t_ij. Kumpulan hambatan yang menyatakan kondisi

ini adalah

ij i

j x t

x − ≥

Maka model umum program linear untuk jaringan ini dapat dirangkum sebagai

Minimum Z=x_m

Ditujukan

ij i

j x t

x − ≥ untuk seluruh aktivitas i→ j

0 , _j≥

i x

Diketahui

i

x = waktu kejadian pada simpul i

j

x = waktu kejadian pada simpul j

ij

t = waktu aktifitas i→ j

m = simpul terakhir dalam jaringan

1.7 Metodologi Penelitian

Metode penelitian yang akan digunakan adalah studi literatur dan studi kasus, yang akan

dilakukan sebagai berikut :

1. Pengambilan data

Data yang diambil adalah :

a. Jadwal kegiatan pembangunan gedung STMIK Kristen Neumann Indonesia

b. Biaya untuk upah tukang/pekerja

2. Pengolahan data

Data yang diperoleh nantinya akan diolah untuk

a. Membuat tabel logika ketergantungan kegiatan proyek

b. Membuat diagram jaringan kerja

c. Penentuan jalur kritis

d. Penentuan waktu crashing optimal

e. Pendekatan Linear programming untuk penentuan biaya yang optimum

BAB 2

LANDASAN TEORI

2.1 Analisa Jaringan Kerja

Metode jaringan kerja diperkenalkan menjelang decade 50-an, oleh satu tim engineer

dan ahli matematika dari perusahaan Du Pont bekerja sama dengan Rand Corporation,

dalam usaha mengembangkan sistem kontrol manajemen. Sistem ini dimaksudkan

untuk merencanakan dan mengendalikan sejumlah besar kegiatan yang memiliki

hubungan ketergantungan yang kompleks dalam masalah desain, engineering,

konstruksi dan pemeliharaan. Usaha-usaha ditekankan untuk mencari metode yang

dapat meminimalkan biaya, dalam hubungannya dengan kurun waktu penyelesaian

suatu kegiatan.

Jaringan kerja dapat didefenisikan sebagai kumpulan dari kejadian-kejadian

dan kegiatan-kegiatan yang menggambarkan tinjauan waktu dari susunan proyek.

Jaringan kerja muncul pada sejumlah perencanaan dan dalam berbagai bidang.

Perencanaan jaringan kerja merupakan suatu alat manajemen yang memungkinkan

dapat lebih luas dan lebih lengkap untuk perencanaan dan pengawasan suatu proyek.

Dalam banyak situasi, manager bertanggung jawab untuk perencanaan dan

menjadwalkan dan mengendalikan proyek yang terdiri dari berbagai pekerjaan atau

aktivitas terpisah yang dilakukan oleh berbagai departemen dan individu. Dalam hal

ini manager harus mengadakan pendekatan secara kuantitatif dalam pengambilan

suatu keputusan. Cara ini penting sekali digunakan oleh manager yang bertanggung

jawab atas bidang engineering, production, administration, dan penelitian operasional.

Penerapan pengambilan keputusan secara pendekatan kuantitatif dalam berbagai

bidang pada kenyataannya prosedurnya tidaklah begitu kompleks. Oleh karena cara

ini dapat dianalisa secara sistematis dan sederhana dengan menggunakan metode

Teknik jaringan kerja menunjukkan manfaat nyata bila digunakan membantu

atau melengkapi perencanaan dan pengendalian proyek baru. Sedangkan untuk proyek

yang sedang berjalan penerapan analisa jaringan kerja akan terkait pada persyaratan

atau ketentuan semula yang ditetapkan atau yang sedang berjalan.

Penggambaran jaringan kerja merupakan suatu teknik jaringan kerja yang

digunakan secara luas untuk masalah-masalah seperti produksi, distribusi,

perencanaan proyek, perencanaan keuangan dan lain sebagainya. Sesungguhnya

penggambaran jaringan kerja menyediakan bantuan secara visual dan konseptual yang

sangat berharga dalam menggambarkan hubungan antara komponen-komponen dalam

suatu sistem. Hal ini sangat bermanfaat bagi para pengambil keputusan.

Menggambarkan jaringan kerja dari tiap awal kegiatan sangat bermanfaat

untuk mempermudah pengawasan serta pengumpulan, penetapan dan penganalisaan

informasi yang sesuai dengan tujuan yang diharapkan, sehingga keputusan-keputusan

dalam pemilihan alternatif dengan mudah dapat dilaksanakan untuk mencapai tujuan

proyek. Didalam penyusunan perencanaan suatu jaringan kerja suatu proyek, harus

ada logika ketergantungan dari suatu kegiatan dengan kegiatan yang lain, serta

menggunakan simbol-simbol kegiatan maupun simbol-simbol peristiwa. Dengan

demikian diharapkan teori jaringan kerja dapat mengatur rangkaian dari

kegiatan-kegiatan, sehingga benar-benar dapat dilaksanakan secara efektif dan efisien.

Pemakaian analisa jaringan kerja dalam suatu proyek dimaksudkan untuk

mengkoordinir semua unsur proyek kedalam suatu rencana utama, dengan

menciptakan suatu modal kerja untuk melengkapi proyek sehingga diperoleh waktu

terbaik melakukan pekerjaan atau kegiatan, penekanan biaya, pengurangan resiko,

penggunaan sumber-sumber secara efektif dan efisien, mendapatkan atau

mengembangkan schedule yang optimum, memudahkan revisi atau perbaikan

terhadap penyimpangan yang terjadi.

Jadi, kunci keberhasilan pendekatan jaringan kerja untuk menyelesaikan suatu

suatu model jaringan. Dengan demikian permasalahan yang kompleks dapat

diselesaikan lebih sederhana dan lebih sistematis.

2.2 Sistematika Menyusun Jaringan Kerja

Sistematika lengkap dari proses menyusun jaringan kerja adalah sebagai berikut :

1. Langkah Pertama

Mengkaji dan mengidentifikasi lingkup proyek, menguraikan atau

memecahkannya menjadi kegiatan-kegiatan atau kelompok kegiatan yang

merupakan komponen proyek. Pengkajian yang dimaksud adalah untuk

mengetahui kegiatan-kegiatan apa yang merupakan bagian atau komponen dari

proyek yang bisa dibedakan satu sama lain.

2. Langkah kedua

Menyusun kembali komponen-komponen tersebut pada butir pertama, menjadi

mata rantai dengan urutan yang sesuai dengan logika ketergantungan. Urutan ini

dapat berbentuk pararel atau seri. Menyusun urutan ketergantungan dituntut

berpikir secara analitis, sehingga akan diperoleh urutan yang benar-benar dapat

mempermudah permasalahan.

3. Langkah ketiga

Memberikan perkiraan kurun waktu bagi masing-masing kegiatan yang dihasilkan

dari penguraian lingkup proyek. Dengan memasukkan unsur kurun waktu ke

analisis jaringan kerja, berarti perencanaan telah memasuki taraf yang lebih

spesifik, yaitu membuat jadwal kegiatan proyek.

4. Langkah keempat

Mengidentifikasi jalur kritis (critical path) pada jaringan kerja. Jalur kritis adalah

jalur yang terdiri dari rangkaian kegiatan dari lingkup proyek, yang bila terlambat

akan menyebabkan keterlambatan proyek secara keseluruhan. Masalah jalur kritis

akan penulis sajikan pada sub bab dalam bagian ini secara lengkap.

5. langkah kelima

Bila semua langkah-langkah diatas diselesaikan, dilanjutkan dengan usaha-usaha

meningkatkan daya guna dan hasil guna pemakaian sumber daya, yang meliputi

a. menentukan jadwal yang paling ekonomis

b. meminimalkan fluktuasi pemakaian sumber daya

Setelah tersusun rencana dan jadwal proyek yang cukup realistik, kemudian

dapat dipakai diantaranya sebagai tolak ukur atau alat pembanding dalam kegiatan

pengendalian pada tahap inplementasi fisik, yaitu dengan memperbandingkan antara

perencanaan atau jadwal dengan hasil pelaksanaan nyata dilapangan.

2.3 Diagram Jaringan kerja

Diagram jaringan kerja merupakan logika model yang menggambarkan hubungan

antara masing-masing kegiatan dan menjelaskan arus dari operasi sejak awal hingga

selesainya kegiatan-kegiatan proyek.

Diagram jaringan kerja mempunyai dua peranan. Yakni, pertama sebagai alat

perencanaan proyek dan yang kedua sebagai ilustrasi secara grafik dari

kegiatan-kegiatan suatu proyek. Oleh karena itu diagram suatu jaringan kerja harus mampu

memberi gambaran tentang dimulainya dari awal kegiatan sampai diselesaikannya

kegiatan tersebut.

Untuk itu diagram jaringan kerja memerlukan beberapa lambang khusus untuk

memberikan keterangan yang jelas tentang suatu proyek, yaitu :

1. Anak panah (arrow) menyatakan kegiatan dengan ketentuan bahwa

panjang dan arah panah tidak mempunyai arti khusus. Pangkal dan

ujung panah menerangkan kegiatan mulai dan berakhir dengan arah

kekanan (positif). Kegiatan harus berlangsung terus dalam jangka

waktu tertentu (duration) dengan pemakaian sejumlah sumber seperti

manusia, alat, bahan dan dana. Pada umumnya kegiatan diberikan

huruf kode huruf besar A, B, C, dan seterusnya.

2. Lingkaran kecil atau node menyatakan suatu kejadian atau peristiwa.

1

2

3 4

1

3

4

2 5

kegiatan. Umumnya kegiatan diberi kode dengan angka 1, 2, 3, dan

seterusnya yang disebut dengan nomor kejadian.

3. Anak panah terputus-putus menyatakan kegiatan semu atau dummy.

Dummy sebagai pemberitahuan bahwa terjadi perpindahan dari satu

kejadian ke kejadian yang lain pada saat yang sama. Oleh karena itu

dummy tidak memerlukan waktu dan tidak menghabiskan sumber.

Panjang dan arah dummy tidak mempunyai arti khusus.

Untuk menyatakan saling ketergantungan logika dari kegiatan-kegiatan

berikut ini dijelaskan beberapa ketentuan sebagai berikut :

A B

1. 1 2 3 : Kegiatan B hanya dapat dimulai setelah kegiatan A

selesai. Perlu diperhatikan bahwa kejadian merupakan

awal dan akhir suatu kegiatan. Jadi kegiatan B mulai

pada dimana kejadian A berakhir.

1. kegiatan C hanya dapat dimulai setelah kegiatan A dan selesai. Kegiatan A dan B

boleh berlangsung bersama-sama ; A dan B berakhir pada kegiatan yang sama.

A C

B

3. kegiatan C dan D dapat dimulai setelah kegiatan A dan B berakhir, dan selesai

pada kejadian yang berbeda.

A C

1

2

3 4

1

2

3

4 5

1

2

5 3

6 4

1

2

3 4

4. Dalam diagram ini (a), (b), (c) terdapat dua kejadian yang saling bergantungan

tanpa dihubungkan dengan kegiatan, tapi dihubungkan dengan dummy.

A A

B C

C

B D

(a) (b)

(c)

5.

A

C

B

Dalam hal terdapat kejadian menyatu (merge event) seperti ini maka ada dua

pertimbangan yaitu :

a. Kegiatan C tergantung pada selesainya seluruh kegiatan A dan B.

b. Kegiatan C tergantung pada selesainya kegiatan A dan sebagian kegiatan B

atau sebaliknya. Dalam hal seperti ini rangkaian kegiatan dapat disusun dalam

1

2

5 3

6 4

1

2

5 3

6 4

1

2

4 3

1

2

5 3

4

A C

B1 B

A

2

Atau

1 A

A

B C

7. Dalam suatu jaringan kerja tidak boleh terjadi suatu loop atau arus putar, misalnya

2

B C

6. Bila ada dua kegiatan berbeda yang mulai pada kejadian yang sama dan berakhir

pada kejadian yang sama pula, maka pekerjaan tersebut tidak boleh dibuat

berimpit, misalnya

A D

B

C

8. Nomor kejadian terkecil adalah nomor dari kejadian awal dan nomor kejadian

terbesar adalah nomor kejadian akhir. Nomor kejadian ditulis di dalam lingkaran

kejadian.

9. Tiap kegiatan diberi kode berupa huruf besar juga diberi kode dengan simbol (i, j)

; i menyatakan nomor kejadian awal kegiatan dan j menyatakan nomor kejadian

2.4 Menyusun Urutan Kegiatan

Menyusun urutan kegiatan atau hubungan kegiatan yang satu dengan yang lain dalam

proses pembuatan jaringan kerja, didasarkan atas logika ketergantungan. Hal ini

merupakan salah satu aturan dasar dalam menyusun jaringan kerja. Ketergantungan

ini dikelompokkan menjadi dua golongan yaitu :

a. Ketergantungan Alamiah

Sebagian besar ketergantungan disebabkan oleh sifat kegiatan itu sendiri. Misalnya

kasus untuk pendirian sebuah rumah. Kegiatan untuk menaikkan atap belum dapat

dilakukan sebelum pekerjaan mendirikan tiang penyangga diselesaikan.

Ketergantungan demikian disebut ketergantungan alamiah, karena meskipun

seandainya tersedia cukup tenaga atau sumber daya lain, tetapi tiang belum berdiri dan

siap menyangga atap, maka pelaksanaan pekerjaan menaikkan atap belum dapat

dimulai.

b. Ketergantungan Sumber Daya

Jenis lain dari ketergantungan adalah ketergantungan sumber daya. Sebagai contoh

pekerjaan membuat pondasi tidak dapat dilakukan bersamaan waktunya dengan

pekerjaan pabrikasi tiang atau kerangka atap, karena kurangnya tenaga kerja, sehingga

harus dilakukan secara berurutab atau seri. Dalam contoh ini ketergantungan tersebut

disebabkan oleh terbatasnya dana atau sumber daya.

Menyusun jaringan kerja pada awalnya hendaknya didasarkan atas

ketergantungan alamiah. Pada taraf selanjutnya nanti bila sampai pada analisa

keperluan sumber daya, mungkin penyesuaian atau revisi dilakukan.

Usaha menyusun urutan kegiatan yang mengikuti logika ketergantungan akan

dipermudah dengan menjawab pertanyaan berikut :

• Kegiatan apa yang dimulai terlebih dahulu

• Mana kegiatan berikutnya yang akan dilakukan

• Adakah kegiatan-kegiatan yang berlangsung sejajar

Contoh 1

Sebagai gambaran dalam menyusun komponen-komponen kegiatan proyek menjadi

jaringan kerja, berikut ini adalah contoh proyek pembangunan gudang kerangka besi,

seperti yang terdapat pada tabel 2.1 dibawah ini.

Tabel 2.1. Proyek Pembangunan Gudang kerangka besi Kegiatan

Keterangan

Kegiatan

Yang

Mendahului

i j

(1) (2) (3) (4)

1

2

3

4

5

6

A

B

C

D

E

F

Membuat gambar desain

Membeli material

Menyiapkan lahan

Pabrikasi (tiang dan atap)

Membuat pondasi

Mendirikan bangunan

A

A

B

C

B,C

Proyek dipecah menjadi 6 komponen pekerjaan dan ditentukan urutannya.

Pada langkah ini, yang diberi perhatian hanyalah menyusun kegiatan-kegiatan tersebut

berdasarkan hubungan ketergantungan, sedangkan hal-hal lain akan ditinjau pada

tahap berikutnya. Terlihat bahwa kegiatan pembelian material (B) harus menunggu

selesainya pembuatan gambar desain (A), karena sebelum desain diselesaikan belum

diketahui jumlah maupun macam material secara tepat. Demikian pula halnya dengan

pekerjaan menyiapkan lahan (C) harus menunggu sampai gambar desain selesai untuk

mengetahui misalnya berapa ukuran penggalian tanah untuk pondasi yang harus

disiapkan. Dari analisis diketahui bahwa kegiatan pembelian material (B) dapat

dilakukan bersamaan waktunya dengan kegiatan menyiapkan lahan (C). Selanjutnya

mudah dimengerti bahwa pekerjaan pabrikasi (3-5) harus menunggu tersedianya

material. Sedangkan mengecor pondasi (4-5) menunggu selesainya menyiapkan lahan

(C). Pekerjaan mendirikan bangunan (F) baru dapat dimulai bila dua pekerjaan yang

1 3 4 2 2

2

telah dikerjakan (D). Bila kegiatan-kegiatan diatas disusun dalam diagram jaringan

kerja kan terlihat seperti pada gambar 2.3 dibawah ini :

A B D F

C E

Gambar 2.1. Jaringan Kerja Proyek Pembangunan Kerangka besi

2.5 Metode yang Digunakan

Pengolahan proyek berskala besar membutuhkan suatu perencanaan, penjadwalan dan

koordinasi sejumlah kegiatan yang saling berkaitan. Untuk membantu tugas ini, suatu

prosedur formal yang didasarkan pada penggunaan jaringan kerja dan teknik jaringan

kerja telah dikembangkan sejak akhir tahun 1950 – an. Beberapa teknik berdasarkan

analisa jaringan kerja yang sudah berkembang luas diantaranya yang paling terkenal

adalah metode lintasan kritis dan teknik penilaian dan peninjauan program serta

beberapa modifikasi lain untuk keperluan khusus. Teknik-teknik ini pada umumnya

bertujuan menguraikan dan menentukan hubungan antara berbagai kegiatan dalam

perencanaan proyek secara menyeluruh untuk merencanakan dan pengendalian

proyek.

Dalam tulisan ini penulis menggunakan teknik analisa jaringan kerja yaitu

CPM (Critical Path Metod). Untuk lebih jelasnya, CPM akan penulis terangkan dalam

sub bab berikut ini.

2.5.1 CPM (Critical Path Method)

Metode CPM adalah metode yang digunakan untuk merencanakan dan mengendalikan

proyek, merupakan sistem yang paling banyak dipergunakan diantara sistem lain yang

memakai prinsip pembentukan jaringan kerja. Metode CPM sering dipergunakan pada

jembatan layang dan lain-lain. Metode CPM lebih menitikberatkan pada persoalan

keseimbangan antara biaya dan waktu penyelesaian.

Jika dalam suatu proyek, waktu yang dibutuhkan untuk menyelesaikannya

dapat diperkirakan terlebih dahulu dan biaya-biaya proyek dapat dihitung sejak

semula, maka dengan mempergunakan metode CPM pelaksanaan proyek akan lebih

terarah dan sistematis. Dalam pelaksanaan proyek dengan menggunakan metode CPM

dikenal adanya jalur kritis, yaitu jalur yang memiliki rangkaian komponen-komponen

kegiatan, dengan total jumlah waktu terlama dan menunjukkan kurun waktu

penyelesaian proyek yang tercepat. Jadi jalur kritis terdiri dari rangkaian kegiatan

kritis, dimulai dari kegiatan pertama sampai kegiatan terakhir proyek. Makna jalur

kritis penting bagi pelaksanaan proyek, karena pada jalur terletak kegiatan-kegiatan

yang bila pelaksanaannya terlambat maka akan menyebabkan keterlambatan proyek

secara keseluruhan. Maka perlu adanya perhatian penuh pada jalur kritis tersebut,

karena cepat lambatnya suatu proyek selesai terletak pada jalur kritis.

Dalam metode CPM digunakan dua buah perkiraan waktu untuk setiap

kegiatan yang terdapat pada jaringan kerja yakni:

a. Perkiraan Normal (Normal Estimates)

Perkiraan normal adalah waktu yang dibutuhkan untuk menyelesaikan aktivitas

proyek jika proses pelaksanaannya berjalan normal.

b. Perkiraan Cepat.

Perkiraan cepat adalah waktu yang dibutuhkan oleh proyek yang

sesingkat-singkatnya untuk penyelesaian proyek tanpa memperhitungkan biaya.

A. Terminologi dan Defenisi

Dalam proses identifikasi jalur kritis, dikenal beberapa terminology dan defenisi

sebagai berikut :

a. ES (Earliest Start Time)

Earliest Start time adalah waktu mulai paling awal suatu kegiatan. Bila waktu

kegiatan dinyatakan atau berlangsung dalam jam, maka waktu ini adalah jam

b. EF (Earliest Finish Time)

Earliest Finish Time adalah waktu selesai paling awal suatu kegiatan.

c. LS (Lates Allowable Start Time)

Lates Allowable Start Time adalah waktu paling akhir kegiatan boleh dimulai

tanpa memperlambat penyelesaian proyek secara keseluruhan.

d. LF (Latest Allowable Finish Time)

Latest Allowable Finish Time adalah waktu paling akhir kegiatan boleh selesai

tanpa memperlambat penyelesaian proyek.

e. Duration

Duration adalah waktu kegiatan, umumnya dengan satuan hari, minggu, bulan, dan

lain-lain.

B. Pengertian Slack

Slack didefenisikan sebagai panjang waktu suatu aktivitas dapat ditunda tanpa

mempengaruhi waktu yang dibutuhkan untuk menyelesaikan suatu proyek. Jumlah

waktu slack untuk setiap aktivitas dapat dihitung sebagai berikut :

Slack = LS – ES = LF – EF………...(2.1)

Pada perencanaan dan penyusunan jadwal proyek, arti penting daripada slack

adalah menunjukkan jumlah waktu yang diperkenankan suatu kegiatan boleh ditunda,

tanpa mempengaruhi jadwal penyelesaian proyek secara keseluruhan. Jumlah waktu

tersebut sama dengan waktu yang didapat bila semua kegiatan terlebih dahulu dimulai

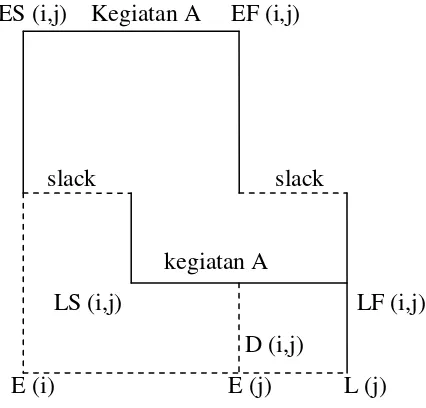
Berikut ini ditunjukkan posisi dan hubungan slack dan parameter-parameter

yang lain.

ES (i,j) Kegiatan A EF (i,j)

slack slack

kegiatan A

LS (i,j) LF (i,j)

D (i,j)

E (i) E (j) L (j)

Gambar 2.2 Posisi dan hubungan antara ES, LS, LF, EF, D dan Slack

Dari gambar diatas terlihat bahwa slack dapat berada dibagian awal mulainya

kegiatan (ES) atau di ujung waktu penyelesaian paling akhir (LS), bahkan dapat

dipecah-pecah sesuai kebutuhan, asalkan masih dalam batas L (j) dan E (i).

Bagi pengelola proyek memahami pengertian diatas akan sangat berguna,

terutama untuk memecahkan masalah pemerataan sumber daya (resource leveling).

C. Perhitungan Maju (Forward Pass)

Dalam mengidentifikasi jalur kritis dipakai suatu cara yang disebut hitungan maju.

Hitungan maju dimulai dari kiri kekanan sampai kegiatan terakhir, atau dengan kata

lain dimulai dari kegiatan paling awal kegiatan sampai pada kegiatan yang terakhir.

Tujuan dari forward pass adalah menghitung earliest start time dan earliest finish time

untuk setiap aktivitas dalam suatu proyek. Forward pass kemudian dikerjakan dengan

anggapan bahwa aktivitas mulai secepat mungkin yaitu setelah aktivitas-aktivitas yang

[image:32.595.204.417.127.331.2]

Adapun langkah-langkah forward pass adalah :

a. Tentukan ES_i = 0 untuk kejadian paling awal dari suatu jaringan kerja. Hal ini

logis sebab belum ada kegiatan yang sudah dikerjakan, artinya kegiatan pertama

baru akan dimulai.

b. Aturan selanjutnya adalah menghitung :

j

ES = maks

{

ESi +Dij

}

dan untuk semua kegiatan

( )

i,j . Agar dapat menghitung

j

ES untuk kejadian j, semua ESi harus dihitung terlebih dahulu.

D. Perhitungan Mundur (Backward Pass)

Selain perhitungan maju, akan digunakan perhitungan mundur untuk mengidentifikasi

jalur kritis. Perhitungan mundur bergerak dari kanan ke kiri, atau dengan kata lain dari

kegiatan paling terakhir sampai kegiatan paling awal. Tujuan dari backward pass

adalah untuk menghitung latest alloweable start time dan finish time untuk setiap

kegiatan.

Adapun langkah-langkah untuk menghitung backward pass adalah:

a. Tentukan harga LF untuk kejadian yang terakhir yang besarnya sama dengan ES

pada kejadian tersebut, dimana LF_i=ES_i.

b. Aturan selanjutnya adalah menghitung:

{

i ij

}

i LF D

LF =min − untuk semua kegiatan

( )

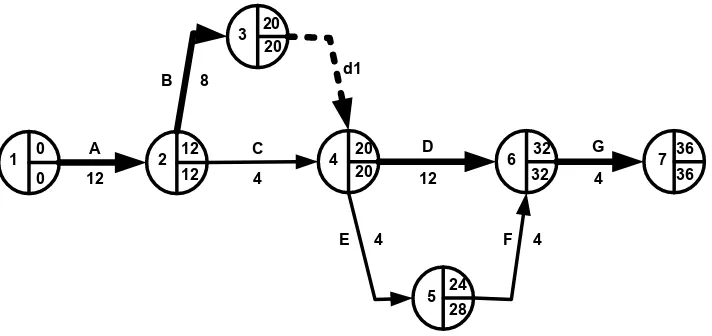
i, j .

2.5.1.1 Cara Menghitung Jalur Kritis

Untuk menentukan jalur kritis, harus dilakukan dua macam perhitungan yaitu

perhitungan maju (forward pass) dan perhitungan mundur (backward pass). Untuk

lebih memahami cara menghitung jalur kritis dengan menggunakan perhitungan maju

dan perhitungan mundur yang telah dijelaskan diatas, berikut akan diberikan

gambaran suatu kegiatan yang telah dibuat kedalam suatu jaringan kerja. Dari jaringan

1 0 0

A

12

B 8

C

4

D

12

E 4 F 4

G

4 d1

2

3

4 12

12

20 20

20 20

24

32 32

36 36

5

6 7

28

Gambar 2.3 Pembentukan Jalur Kritis

2.5.1.1.1 Cara forward pass

i

ES = 0 dimana kejadian pertama kali belum ada kegiatan, baru akan dimulai.

ij

D = lamanya waktu yang diperlukan kegiatan

( )

i, j

j

ES = maks

{

ES_i+D_ij

}

Perhatikan gambar 2.2. diatas, hanya ada satu kegiatan yang mulai dari node 1

menuju ke 2 yaitu kegiatan A. Dimana ES₁ = 0, oleh karena itu hanya ada satu

kegiatan saja dari node 1, yaitu kegiatan A dan D_A = 3, maka

2

ES =

{

ES₁+D₁₂

}

=

{

0+12

}

= 12

Nilai ini dimasukkan dalam bujur sangkar diatas node 2. Event berikutnya

adalah event 3 (perhatikan event 4 belum bisa dihitung, sebab untuk menghitung

diperlukan nilai ES₃ yang harus dihitung terlebih dahulu.

3

ES =

{

ES₂+D₂₃

}

=

{

12+8

}

= 20

[image:34.595.138.494.86.254.2]

Sekarang ES₄ baru bisa dihitung sebab ada dua kegiatan yang menuju

ke-node 4 yaitu kegiatan B dan C.

4

ES =

{

_{i ij}

}

i ES D

maks +

=2,3

= maks

{

ES₂+D₃₄,ES₃+D₂₄

}

= maks

{

20+0,12+4

}

= maks

{

20,16

}

= 20

(nilai ini dimasukkan kedalam node 4).

5

ES =

{

ES_i+D_ij

}

=

{

ES₄+D₄₅

}

=

{

20+4

}

= 24

(nilai ini dimasukkan kedalam node 5).

6

ES =

{

_{i ij}

}

i ES D

maks +

=4,5

= maks

{

ES₄+D₄₆,ES₅+D₅₆

}

= maks

{

20+12,24+4

}

= maks

{

32,28

}

= 32

(nilai ini dimasukkan kedalam node 6).

7

ES =

{

ES_i+D_ij

}

=

{

32+4

}

= 36

Perhitungan dengan forward pass sudah selesai, semua waktu paling awal

2.5.1.1.2. Cara Backward pass

Berikut ini adalah menghitung waktu penyelesaian paling akhir dengan cara sebagai

berikut :

{

j ij

}

j

i LF D

LF =min − , untuk semua kegiatan

( )

i, j

Semua nilai LF_i kemudian dimasukkan dalam masing masing node.

36

7 7 =ES =

LF

6

LF =

{

LF₇−D₆₇

}

=

{

36−4

}

= 32

5

LF =

{

LF_j −D_ij

}

=

{

LF₆−D₅₆

}

=

{

32−4

}

= 28

4

LF =

{

_{j ij}

}

i=5,6 LF −D

min

= min

{

LF₆−D₄₆,LF₅−D₄₅

}

= min

{

32−12,28−4

}

= min

{

20,24

}

= 20

3

LF =

{

LF₄−D₃₄

}

=

{

20−0

}

= 20

2

LF = min

{

LF₃−D₂₃,LF₄−D₂₄

}

= min

{

20−8,20−4

}

= min

{

12,16

}

= 12

1

LF =

{

LF₂−D₁₂

}

=

{

12−12

}

Setelah semua nilai ES dan LF sudah dihitung untuk semua node, maka suatu

kegiatan

( )

i, j dikatakan terletak pada jalur kritis dan merupakan kegiatan kritis

jikalau memenuhi syarat berikut :

I. ES_i=LF_i

II. ES_j =LF_j

III. ES_j −ES_i=LF_j−LF_i=D_ij...(2.2)

Dengan menggunakan syarat diatas, ternyata kegiatan atau aktivitas (1,2),

(2,3), (3,4), (4,6) dan (6,7) merupakan kegiatan-kegiatan kritis. Ini merupakan waktu

yang paling pendek atau paling cepat penyelesaian proyek tersebut, dimana jumlah

waktu yang diperlukan

= D₁₂+D₂₃+D₃₄+D₄₆+D₆₇

= 12 + 8 + 0 + 12 + 4

= 36

Yaitu sebesar LF₆ yaitu waktu penyelesaian paling akhir atau paling lambat.

Perhatikan : kegiatan (2,4), (4,5) dan (5,6) memenuhi syarat I dan II tetapi tidak

memenuhi syarat III, jadi tidak merupakan jalur kritis. Jalur kritis

selain memenuhi syarat I, II, dan III juga harus membentang

(membentuk mata rantai) dari node awal sampai dengan node yang

terakhir.

2.5.2 Metode Simpleks

Metode simpleks untuk penyelesaian persoalan optimasi menggunakan tabel

terstruktur pengolahan data dengan algoritma khusus penyusunan tabel-tabel optimasi

sebagai penjabaran dari langkah-langkah eliminasi Gauss-Jordan dan subtitusi yang

digunakan pada teknik program linear.

Tabel simpleks terdiri dari baris dan kolom yang memuat simbol dan nilai

koevisien dari variabel-variabel yang digunakan pada fungsi tujuan dan

[image:38.595.108.522.101.335.2]

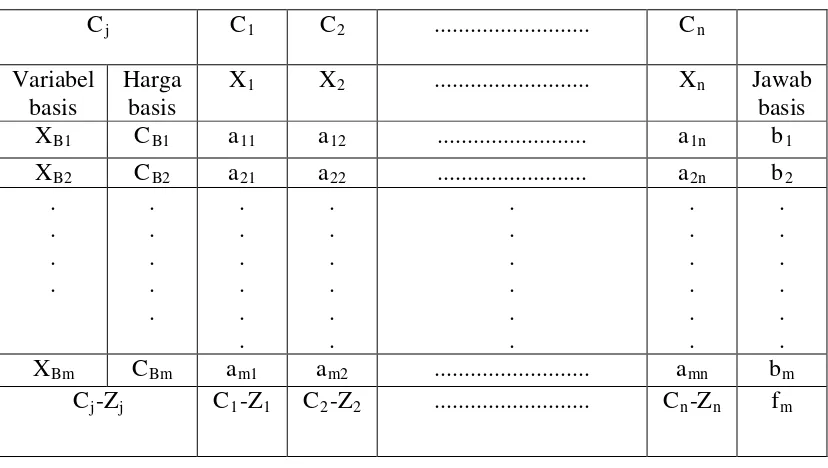
Tabel 2.2. Bentuk umum tabel Simpleks

Cj C1 C2 ... Cn

Variabel basis

Harga basis

X1 X2 ... X Jawab

basis

n

XB1 CB1 a11 a12 ... a1n b1

XB2 CB2 a21 a22 ... a2n b2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . XBm CBm am1 am2 ... amn bm

Cj-Zj C1-Z1 C2-Z2 ... Cn-Zn fm

2.6 Model Linear Programming

Sebagai langkah awal dalam merumuskan model program linier, harus terlebih dahulu

ditentukan variabel-variabel keputusan. Penandaan suatu aktivitas dengan angka node

awal dan akhirnya, maka suatu aktivitas yang dimulai pada node 1 dan berakhir pada

node 2 disebut sebagai aktivitas 1→2. Penandaan seperti ini akan digunakan sebagai

penandaan yang sama untuk menentukan variabel-variabel keputusan dari program

linear. Untuk aktivitas i→j, waktu untuk kejadian i akan sebesar x_i, dan waktu

untuk kejadian j akan sebesar x_j.

Tujuan dari jaringan proyek adalah untuk menentukan waktu tercepat suatu

proyek dapat diselesaikan (waktu garis edar kritis). Waktu garis edar kritis merupakan

waktu tercepat kejadian node terakhir. Jika x_m adalah waktu tercepat kejadian node

terakhir dalam jaringan kerja, ditunjuk pada node m, maka fungsi objektif dapat

dinyatakan sebagai :

Selanjutnya dapat dikembangkan hambatan model tersebut. Pertama,

menentukan waktu aktivitas i→j sebagai t_ij, dimana perbedaan antara waktu

kejadian pada node j dan waktu kejadian pada node i harus paling tidak sama

dengan waktu aktivitas tij. Sebuah kumpulan hambatan yang menyatakan kondisi

adalah :

ij i

j x t

x − ≥

Model umum program linear untuk perumusan jaringan CPM ini dapat

dirangkum sebagai

Minimum Z=xm

Dengan kendala

ij i

j x t

x − ≥ untuk seluruh aktivitas i→j

0 , _j≥

i x

x

Diketahui

i

x = waktu kejadian pada node i

j

x = waktu kejadian pada node j

ij

t = waktu aktivitas i→j

m = node terakhir dalam jaringan

Solusi untuk model program linear ini akan mengindikasikan waku tercepat kejadian

setiap simpul dalam jaringan serta lamanya waktu proyek tersebut.

2.7 Penentuan Biaya Dalam CPM

Selain CPM dapat digunakan untuk menentukan waktu paling cepat sebuah proyek

dapat terselesaikan dan mengidentifikasi waktu kelonggaran (Slack) paling lambat

sebuah kegiatan dapat dimulai tanpa menghambat jadwal proyek keseluruhan, metode

ini juga mampu melakukan analisis terhadap sumber daya yang dipakai dalam proyek

(biaya) agar jadwal yang dihasilkan akan jauh lebih optimal dan ekonomis.

Suatu proyek menggambarkan hubungan antara waktu terhadap biaya. Perlu

pembelian material dan peralatan) tanpa memasukkan biaya tidak langsung seperti

biaya administrasi, dan lain-lain. Adapun istilah-istilah dari hubungan antara waktu

penyelesaian proyek dengan biaya yang dikeluarkan adalah sebagai berikut:

1. Waktu Normal

Adalah waktu yang diperlukan bagi sebuah proyek untuk melakukan rangkaian

kegiatan sampai selesai tanpa ada pertimbangan terhadap penggunaan sumber

daya.

2. Biaya Normal

Adalah biaya langsung yang dikeluarkan selama penyelesaian kegiatan-kegiatan

proyek sesuai dengan waktu normalnya.

3. Waktu Dipercepat

Waktu dipercepat atau lebih dikenal dengan Crash Time adalah waktu paling

singkat untuk menyelesaikan seluruh kegiatan yang secara teknis pelaksanaannnya

masing mungkin dilakukan. Dalam hal ini penggunaan sumber daya bukan

hambatan.

4. Biaya untuk Waktu Dipercepat

Atau Crash Cost merupakan biaya langsung yang dikeluarkan untuk

menyelesaikan kegiatan dengan waktu yang dipercepat.

2.8. Waktu Aktivitas Crashing

Waktu yang sudah dicapai dalam penjadwalan suatu proyek merupakan waktu normal.

Namun waktu normal ini masih dapat diperpendek lagi guna mencapai waktu

penyelesaian yang paling singkat. Usaha untuk memperpendek waktu aktivitas ini

disebut Crashing. Untuk mencapai waktu crashing ini biasanya akan menambah

sumber daya seperti tenaga kerja dan lembur, sehingga akan memperbanyak biaya

proyek. Semakin cepat suatu proyek selesai maka semakin banyak biaya yang

dibutuhkan untuk menyelesaikan proyek tersebut. Oleh karena penambahan sumber

perlu mengidentifikasi aktivitas yang paling sedikit biayanya untuk dicrash dan

kemudian meng-crash aktivitas itu hanya sejumlah yang diperlukan untuk memenuhi

waktu penyelesaian proyek yang diinginkan.

Untuk menentukan dimana dan berapa banyak crash waktu aktivitas, maka

diperlukan informasi mengenai berapa banyak setiap aktivitas dapat dicrash dan

berapa banyak biaya proses crashing itu.

Untuk mendapatkan informasi ini, maka perlu mengistemasi biaya aktivitas di

bawah waktu normal, mengistemasi waktu untuk menyelesaikan aktivitas itu dengan

crashing maksimum.

Tujuan pokok untuk mempercepat waktu penyelesaian adalah memperpendek

waktu penyelesaian proyek dengan kenaikan biaya yang seminimal mungkin. Proses

mempercepat waktu penyelesaian proyek dinamakan Crash Program. Akan tetapi,

terdapat batas waktu percepatan (crash time) yaitu suatu batas dimana dilakukan

pengurangan waktu melewati batas waktu ini akan tidak efektif lagi.

Anggaplah t_ij = waktu normal untuk aktivitas i→ j

ij

tc = waktu untuk aktivitas i→ j dengan crashing masksimum

ij

τ = kemungkinan maksimum pengurangan waktu untuk

aktivitas i→ j karena crashing maksimum

Dengan t_ij dan tc_ij diketahui, maka τ_ij dapat dihitung sebagai berikut :

ij

τ = t_ij - tc_ij...(2.4)

Berikut jika dianggap :

C_ij = menyatakan biaya untuk aktivitas i→ j dalam waktu normal.

ij

Cc = menyatakan biaya dengan aktivitas i→ j dengan

Jadi berdasarkan waktu per unit, biaya crashing

( )

S_ij untuk setiap aktivitas

adalah :

ij

S =

ij ij

ij C

Cc

τ −

...(2.5)

Biaya

Waktu A B

Waktu Normal Biaya

Normal

Titik Normal

Biaya untuk waktu dipercepat

Waktu Dipercepat

[image:42.595.153.474.175.374.2]

Titik Dipercepat

Gambar 2.4. Hubungan antara waktu dan biaya pada keadaan normal dan crash

Dengan menggunakan crash schedule, tentu saja biayanya akan jauh lebih

besar dibandingkan dengan normal schedule. Dalam crash schedule akan dipilih

kegiatan-kegiatan kritis dengan tingkat kemiringan terkecil untuk mempercepat

pelaksanaannya. Langkah ini dilakukan sampai seluruh kegiatan mencapai nilai crash

time-nya. Perhitungan yang dilakukan untuk menentukan sudut kemiringan (waktu

dan biaya suatu kegiatan) atau lebih dikenal dengan slope adalah:

Biaya Dipercepat – Biaya Normal

Slope Biaya =

2.8.1. Crashing Dengan Model Linear Programming

Untuk jaringan yang besar maka diperlukan prosedur matematis untuk menentukan

keputusan crashing optimal. Dalam hal ini pemograman linear dapat digunakan untuk

menyelesaikan masalah crashing jaringan. Hal pertama yang dikerjakan dalam

menentukan keputusan crashing adalah menentukan variabel-variabel keputusan

sebagai berikut :

i

x = waktu terjadinya peristiwa i

j

x = waktu terjadinya peristiwa j

m

x = waktu terjadinya peristiwa paling akhir

( )

m

ij

t = waktu kegiatan i→ j

ij

tc = waktu crashing maksimum kegiatan i→ j

ij

τ = kemungkinan maksimum pengurangan waktu untuk

aktivitas i→ j karena crashing maksimum

C_ij = menyatakan biaya untuk aktivitas i→ j dalam waktu normal.

ij

Cc = menyatakan biaya dengan aktivitas i→ j dengan

crashing maksimum

j i

S_→ = Slope biaya untuk kegiatan i→ j

Dimana

i, j = node (1,2,3,...)

j

i→ = nama kegiatan (A,B,C,...)

Oleh karena tujuan yang terutama adalah memperpendek atau mempersingkat

waktu penyelesaian proyek dengan meminimalkan biaya crashing, maka fungsi tujuan

program linearnya adalah :

∑

m m m

S

Min τ ...(2.6)

Dimana S_ij = biaya crash untuk kegiatan i→ j berdasarkan waktu per unit.

Untuk kendala yang menjelaskan struktur jaringan, dimulai dari event i dengan asumsi bahwa x_i=0

Untuk event berikutnya

i A A

j t x

x ≥ −τ +

j B B

k t x

x ≥ −τ +

. . .

1

−

+ −

≥ Z Z m

m t x

x τ

Selanjutnya dengan dengan menggunakan metode simpleks dapat diperoleh jawaban

optimalnya.

Kendala untuk model ini mencakup penggambaran jaringan kerja dan

pembatasan waktu crash aktivitas. Dari semua ini, kendala yang digunakan untuk

menggambarkan jaringan mungkin merupakan kendala yang paling sulit. Kendala

kendala itu didasarkan pada persyaratan berikut ini :

1. waktu terjadinya peristiwa i

( )

x_i harus lebih besar daripada atau sama dengan

waktu penyelesaian aktivitas untuk semua aktivitas yang menuju node atau

peristiwa itu.

2. waktu awal suatu aktivitas sama dengan waktu terjadinya node atau peristiwa

pendahulunya.

3. waktu untuk menyelesaikan satu waktu aktivitas adalah sama dengan waktu

normalnya dikurang panjang waktu yang dicrash.

Dengan menambah batasan bahwa x_m≥0 maka dapat dicari waktu crashing

optimal dengan menggunakan metode simpleks.

Sebagai contoh diambil sebuah jaringan kerja pembangunan sebuah ruko,

dimana akan dicari waktu percepatan optimalnya dengan menggunakan metode

[image:45.595.101.535.145.298.2]

Contoh 2

Tabel 2.3. Logika ketergantunganPembangunan Ruko

Kode Nama Kegiatan Waktu

(hari)

Kegiatan yang mendahului

A Pembersihan 7 -

B Dinding 6 -

C Atap 8 A

D Lantai 5 B

E Cat + Keramik 7 C, D

Dengan estimasi biaya pembangunan ruko adalah sebagai berikut :

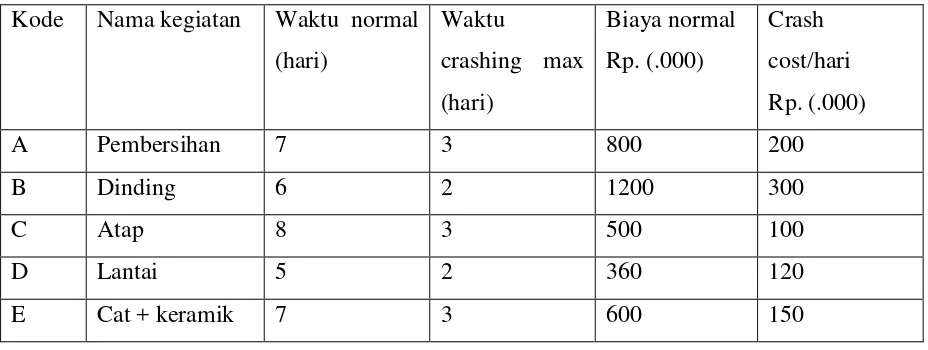
Tabel 2.4. Estimasi biaya

Kode Nama kegiatan Waktu normal

(hari)

Waktu

crashing max

(hari)

Biaya normal

Rp. (.000)

Crash

cost/hari

Rp. (.000)

A Pembersihan 7 3 800 200

B Dinding 6 2 1200 300

C Atap 8 3 500 100

D Lantai 5 2 360 120

E Cat + keramik 7 3 600 150

Penyelesaian:

Berdasarkan Tabel Logika ketergantungan diatas maka dapat digambarkan jaringan

[image:45.595.102.566.376.551.2]

1

C

D B

5 4

3 2 A

6

7 8

5

E

15 7

0

0

7 7

15 ₂₂

22

[image:46.595.186.445.84.234.2]

6 10

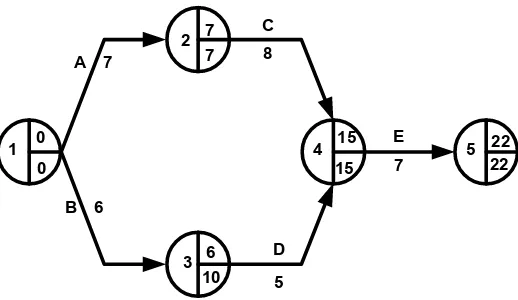
Gambar 2.5. Jaringan kerja pembangunan ruko

(i) Penentuan Jalur Kritis

Perhitungan maju

- ES₁ = 0

- ES₂ = maks

(

ES₁+D_A

)

= maks (0 + 7)

= 7

- ES₃ = maks

(

ES₁+D_B

)

= maks (0 + 8)

= 8

- ES₄ = maks

(

ES₂+D_C,ES₃+D_D

)

= maks

(

7+8,6+5

)

= maks

(

15,11

)

= 15

- ES₅ = maks

(

ES₄ +D_E

)

= maks (15 + 7)

= 22

Perhitungan mundur

- LF₅=ES₅=22

- LF₄ = min

(

LF₅−D_E

)

= min (22 – 7)

- LF₃ = min

(

LF₄ −D_D

)

= min (15 – 5)

= 10

- LF₂ = min

(

LF4−DC

)

= min (15 – 8)

= 7

- LF₁ = min

(

LF₃ −D_B,LF₂ −D_A

)

= min

(

10−6,7−7

)

= 0

Dengan menggunakan formulasi (2.2) yaitu :

ij i j i

j ES LF LF D

ES − = − =

Maka yang menjadi jalur kritis pada jaringan kerja pembangunan ruko adalah :

A – C – E

1

C

D B

5 4

3 2 A

6

7 8

5

E

15 7

0

0

7 7

15 ₂₂

22

[image:47.595.187.448.377.519.2]

6 10

Gambar. 2.6. Jalur kritis Pembangunan ruko

(ii) Penentuan Biaya Crashing Optimum dengan menggunakan pendekatan Program

Linear.

Data dari tabel dan gambar yang dilengkapi dengan informasi waktu penyelesaian,

dapat digunakan untuk memformulasikan model linear programming.

Jika x_i adalah waktu yang yang dibutuhkan untuk menyelesaikan event - i, dan τ_j

adalah waktu percepatan yang dapat dilakukan pada aktivitas j, maka untuk proyek

Min Z = 200.000 τ_A + 300.000 τ_B + 100.000 τ_C + 120.000 τ_D + 150.000 τ_E Dengan kendala time crash dan time normal selisih kendala E D C B A         ≤ ≤ ≤ ≤ ≤ 3 2 3 2 3 τ τ τ τ τ 13 6≤

x → kendala batas waktu percepatan

Untuk kendala yang menjelaskan struktur jaringan, dimulai dari event -1 dengan

asumsi bahwa x₁=0

Untuk event – 2 :

2 x ≥ A aktivitas normal waktu - ) percepatan (waktu A τ +

(

x 0

)

A aktivitas untuk awal Waktu 0 1= 2

x ≥ 7 - τ_A + 0 atau x₂+ τ_A-x₁ ≥ 7

Untuk event – 3 :

3

x ≥6−τ_B+0 atau x₃+τ_B−x₁≥6

Untuk event – 4, dibutuhkan dua kendala, yaitu jalur aktivitas C dan jalur aktivitas D :

4

x ≥8−τ_C +x₂ atau x₄+τ_C−x₂≥8

4

x ≥5−τ_D+x₃ atau x₄+τ_D−x₃≥5

Untuk event – 5 :

5

x ≥7−τE +x₄ atau x5+τE −x4≥7

Dengan menambah batasan x₁,x₂,x₃,x₄,x₅≥0, maka dengan menggunakan metode

[image:49.842.27.830.110.507.2]

Tabel 2.5. Tabel Simpleks pertama (pendahuluan)

A

τ τ_B τ_C τ_D τ_E x₁ x₂ x₃ x₄ x₅ s₁ s₂ s₃ s₄ s₅ s₆ A₇ s₈ A₈ s₉ A₉ s₁₀ A10 s11 A11 s12 A12 s13 s14 s15 s16 s17

Sol .

basis

C(j) 200 300 100 120 150 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1

s 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3

2

s 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2

3

s 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3

4

s 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2

5

s 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3

6

s 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13

7

A M 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

8

A M 1 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 7

9

A M 0 1 0 0 0 -1 0 1 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 6

10

A M 0 0 1 0 0 0 -1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 8

11

A M 0 0 0 1 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 5

12

A M 0 0 0 0 1 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 7

13

s 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0

14

s 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0

15

s 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0

16

s 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0

17

s 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 C(j) – Z(j) 200 300 100 120 150 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

[image:50.842.27.825.111.506.2]

Tabel 2.6. Tabel Simpleks kedua

A

τ τ_B τC τD τE x1 x2 x3 x4 x5 s1 s2 s3 s4 s5 s6 A7 s8 A8 s9 A9 s10 A10 s11 A11 s12 A12 s13 s14 s15 s16 s17

basis

C(j) 200 300 100 120 150 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Sol. Ras.

1

s 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 M

2

s 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 M

3

s 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 M

4

s 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 M

5

s 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 M

6

s 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13 M

7

A M 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 M

8

A M 1 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 7 M

9

A M 0 1 0 0 0 -1 0 1 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 6 M

10

A M 0 0 1 0 0 0 -1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 8 8

11

A M 0 0 0 1 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 5 5

12

A M 0 0 0 0 1 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 7 0

13

s 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 M

14

s 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 M

15

s 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 M

16

s 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0

17

s 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 M C(j) – Z(j) 200 300 100 120 150 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

M -1 -1 -1 -1 -1 1 0 0 -1 -1 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 33

Masuk : 4

x ; keluar 11

[image:51.842.27.815.111.505.2]

Tabel 2.7. Tabel Simpleks ketiga

A

τ τ_B τC τD τE x1 x2 x3 x4 x5 s1 s2 s3 s4 s5 s6 A7 s8 A8 s9 A9 s10 A10 s11 A11 s12 A12 s13 s14 s15 s16 s17

basis

C(j) 200 300 100 120 150 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0