Model SIRS-SI Penyebaran Penyakit Malaria dengan Pengobatan, Vaksinasi, dan Penyemprotan

MODEL SIRS-SI PENYEBARAN PENYAKIT MALARIA

DENGAN PENGOBATAN, VAKSINASI,

DAN PENYEMPROTAN

RANDITA GUSTIAN PUTRI

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa tesis berjudul Model SIRS-SI Penyebaran Penyakit Malaria dengan Pengobatan, Vaksinasi, dan Penyemprotan adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, September 2014

Randita Gustian Putri

RINGKASAN

RANDITA GUSTIAN PUTRI. Model SIRS-SI Penyebaran Penyakit Malaria dengan Pengobatan, Vaksinasi, dan Penyemprotan. Dibimbing oleh JAHARUDDIN dan TONI BAHKTIAR.

Malaria merupakan penyakit menular yang disebabkan oleh parasit yang dikenal dengan Plasmodium. Pembawa parasit Plasmodium adalah nyamuk

Anopheles betina yang menyebabkan rusaknya sel-sel darah merah pada manusia dan hewan melalui gigitannya. Malaria juga dapat ditularkan melalui transfusi darah, pemakaian jarum suntik, maupun bawaan. Malaria merupakan penyakit mematikan. Untuk itu, diperlukan perlakuan pencegahan untuk mengendalikan baik tingkat infeksi maupun tingkat penyebaran penyakit ini.

Dalam penelitian ini, dibahas sebuah model penyebaran penyakit malaria tipe SIR (Susceptible-Infected-Recovered) – SI (Susceptible-Infected). Modifikasi model dilakukan dengan menambahkan asumsi bahwa manusia yang pulih dapat rentan kembali terkena malaria akibat hilangnya kekebalan tubuh. Selain itu, modifikasi model juga dilakukan dengan pemberian perlakuan pada manusia dan nyamuk. Perlakuan yang diberikan adalah pengobatan dan vaksinasi pada manusia serta penyemprotan pada nyamuk. Dalam model ini, populasi manusia dibagi menjadi tiga kelas, yaitu rentan, terinfeksi, dan pulih. Sedangkan populasi nyamuk dibagi menjadi dua kelas, yaitu rentan dan terinfeksi. Manusia pada kelas rentan dapat berpindah ke kelas terinfeksi akibat gigitan nyamuk terinfeksi atau penularan dari manusia terinfeksi melalui transfusi darah dan kongenital. Manusia di kelas rentan juga dapat langsung berpindah ke kelas pulih karena vaksinasi. Manusia pada kelas terinfeksi dapat berpindah ke kelas pulih karena perlakuan pengobatan yang diberikan. Manusia di kelas pulih dapat kembali ke kelas rentan akibat hilangnya kekebalan tubuh. Nyamuk pada kelas rentan dapat berpindah ke kelas terinfeksi akibat menggigit manusia terinfeksi. Nyamuk di kelas rentan dan kelas terinfeksi dapat mati akibat penyemprotan.

Tujuan dari penelitian ini adalah mengonstruksi model tipe SIRS-SI, melakukan analisis kestabilan pada model, melihat pengaruh perlakuan terhadap dinamika populasi manusia dan populasi nyamuk, dan mendeskripsikan penggunaan metode homotopi untuk memperoleh pendekatan solusi dari model.

Terdapat dua titik tetap pada model: titik tetap tanpa penyakit dan titik tetap endemik. Simulasi numerik menunjukkan bahwa perlakuan yang diberikan memberikan pengaruh terhadap dinamika populasi manusia dan nyamuk yang ditunjukkan dengan bilangan reproduksi dasar. Bilangan reproduksi dasar merupakan nilai harapan banyaknya individu terinfeksi tiap satuan waktu. Infeksi ini terjadi pada populasi rentan yang diakibatkan oleh satu individu terinfeksi. Secara umum, jika efektivitas penggunaan perlakuan ditingkatkan, maka menyebabkan menurunnya bilangan reproduksi dasar. Itu artinya, jumlah individu yang terinfeksi semakin berkurang, sehingga penyakit tidak akan menyebar dan dalam jangka waktu tertentu penyakit akan menghilang dari populasi tersebut.

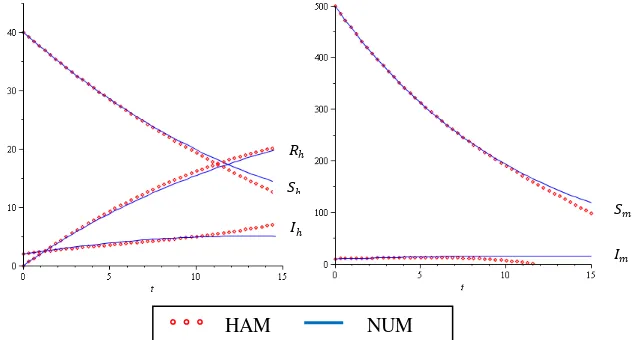
numerik. Diperoleh bahwa antara penyelesaian homotopi dan penyelesaian numerik memiliki absolute error yang cukup kecil hingga = 9. Itu artinya, metode homotopi merupakan metode pendekatan penyelesaian yang cukup baik.

SUMMARY

RANDITA GUSTIAN PUTRI. SIRS-SI Model of Malaria Spread with Drug Treatment, Vaccination, and Mosquito Spraying. Supervised by JAHARUDDIN and TONI BAHKTIAR.

Malaria is an infectious disease caused by a parasite known as plasmodium. Carrier of plasmodium parasite is the female anopheles mosquito that causes the destruction of red blood cells in humans and animals through bites. Malaria also can be transmitted through blood transfusion, sharing needles, or congenital. Malaria is a deadly disease. Therefore, preventive treatment is necessary to control the rate of infection and the rate of incidence of this disease.

This study discussed the spread of malaria in the framework of an SIR (Susceptible-Infected-Recovered) – SI (Susceptible-Infected) model. Modification of the model is done by considering the assumption that humans belong to recovered class have possibility to be susceptible due to loss of immunity. Moreover, modifications are also performed with treatments given to humans and mosquitoes. The treatments are drug treatment and vaccination to humans and spraying to mosquitoes. In this model, the human population is divided into three classes, namely susceptible, infected, and recovered classes. The mosquito population is divided into two classes, namely susceptible and infected classes. Human in susceptible class can moved into infected class by an infected mosquito bite or can be transmitted from infected human through blood transfusion and congenital. Human in susceptible class also can move into recovered class due to vaccination. Human in infected class can moved into recovered class due to drug treatment. Human in recovered class can moved into susceptible class due to loss of immunity. Mosquito in susceptible class can moved into infected class for biting infected human. Mosquito in susceptible and infected classes can die because of spraying.

The purpose of this study are to construct of SIRS-SI model, to analyze the stability on the model, to show the treatments effect on the dynamics of human and mosquito populations, and to describe the use of the homotopy analysis method in providing an approximate solution of the model.

There are two fixed points on the model: disease free and endemic equilibriums. Numerical simulation shows that treatments affect the dynamics of human and mosquito population characterized by a basic reproduction number. Basic reproduction number is denoted by the expectation value of the number of infections per unit time. This infection occurs in a susceptible population produced by one infected individual. In general, if the effectiveness of the use of treatment is increased, then it decreases the basic reproduction number. That means, the number of infected individuals is reduced, so that the disease will not spread and within a certain period of disease will disappear from the population.

numeric have quite small absolute error up to = 9. It means that homotopy method can approximate the solution quite well.

© Hak Cipta Milik IPB, Tahun 2014

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

MODEL SIRS-SI PENYEBARAN PENYAKIT MALARIA

DENGAN PENGOBATAN, VAKSINASI,

DAN PENYEMPROTAN

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2014

Judul Tesis : Model SIRS-SI Penyebaran Penyakit Malaria dengan Pengobatan, Vaksinasi, dan Penyemprotan

Nama : Randita Gustian Putri

NIM : G551130366

Disetujui oleh Komisi Pembimbing

Dr Jaharuddin, MS Ketua

Dr Toni Bakhtiar, MSc Anggota

Diketahui oleh

Ketua Program Studi Matematika Terapan

Dr Jaharuddin, MS

Dekan Sekolah Pascasarjana

Dr Ir Dahrul Syah, MScAgr

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah Subhanahu wa ta’ ala atas segala karunia-Nya sehingga tesis ini berhasil diselesaikan. Tema yang dipilih ialah model matematika pada penyakit malaria, dengan judul Model SIRS-SI Penyebaran Penyakit Malaria dengan Pengobata, Vaksinasi dan Penyemprotan.

Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis menyampaikan terima kasih kepada:

1. Bapak Ranu dan Ibu Lestari selaku orang tua serta Allif Ralestyo Laksono selaku adik penulis.

2. Dr. Jaharuddin, MS selaku ketua komisi pembimbing sekaligus Ketua Program Studi Pascasarjana Matematika Terapan Institut Pertanian Bogor. 3. Dr. Toni Bakhtiar, M.Sc selaku anggota komisi pembimbing sekaligus Ketua

Departemen Matematika Institut Pertanian Bogor.

4. Dr. Ir. Hadi Sumarno, MS selaku penguji luar komisi pembimbing.

5. Lestari Dwi Asih dan Windiani Erliana, M.Si sebagai partner penulis dalam Program Sinergi 2012-2014.

6. Seluruh mahasiswa Departemen Matematika khususnya teman-teman angkatan 2009 di program studi S1 Matematika dan angkatan 2012 di program studi S2 Matematika Terapan.

7. Seluruh keluarga yang selalu memberikan dorongan dan mendoakan untuk keberhasilan studi bagi penulis.

8. Sahabat-sahabat yang tidak dapat disebutkan satu persatu yang telah banyak membantu penulias dalam penyelesaian tesis ini.

Semoga segala bantuan, bimbingan, dan motivasi yang telah diberikan kepada penulis senantiasa mendapat balasan dari Allah Subhanahu wa ta’ ala.

Akhirnya, semoga penulisan tesis ini dapat memperkaya pengalaman belajar dan wawasan kita semua.

Bogor, September 2014

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

1 PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 2

2 TINJAUAN PUSTAKA 2

Sistem Persamaan Diferensial Biasa 2

Nilai Eigen dan Vektor Eigen 3

Pelinearan 3

Titik Tetap 3

Kestabilan Titik Tetap 4

Bilangan Reproduksi Dasar 4

Metode Homotopi 4

3 MODEL MATEMATIKA PENYEBARAN PENYAKIT MALARIA 6

Penelitian Sebelumnya 6

Modifikasi Model 7

4 HASIL DAN PEMBAHASAN 9

Penentuan Titik Tetap 9

Analisis Kestabilan Titik Tetap 10

Penentuan Bilangan Reproduksi Dasar 12

Simulasi 12

Metode Analisis Homotopi 18

Aplikasi Metode Homotopi 20

4 SIMPULAN DAN SARAN 21

Simpulan 21

Saran 22

DAFTAR PUSTAKA 22

LAMPIRAN 24

DAFTAR TABEL

1 Parameter pada model malaria tipe SIR-SI dan tipe SIRS-SI 8 2 Nilai parameter pada model malaria tipe SIRS-SI 13 3 Hasil simulasi efektivitas pengobatan pada manusia terhadap bilangan

reproduksi dasar 14

4 Hasil simulasi efektivitas vaksinasi pada manusia terhadap bilangan

reproduksi dasar 15

5 Hasil simulasi efektivitas penyemprotan pada nyamuk terhadap

bilangan reproduksi dasar 17

DAFTAR GAMBAR

1 Diagram kompartemen penyakit malaria tipe SIR-SI 7 2 Diagram kompartemen penyakit malaria tipe SIRS-SI 8 3 Dinamika populasi manusia karena pengobatan pada manusia 14 4 Dinamika populasi nyamuk karena pengobatan pada manusia 15 5 Dinamika populasi manusia karena vaksinasi pada manusia 16 6 Dinamika populasi nyamuk karena vaksinasi pada manusia 16 7 Dinamika populasi manusia karena penyemprotan pada nyamuk 17 8 Dinamika populasi nyamuk karena penyemprotan pada nyamuk 18

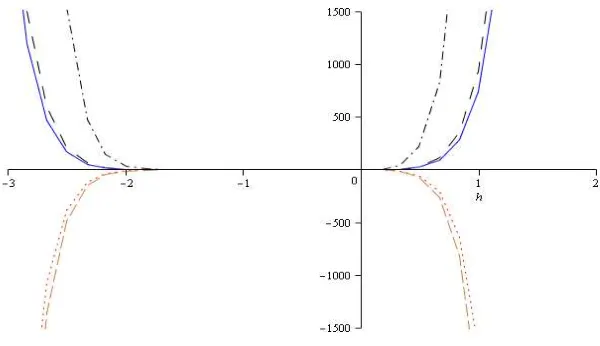
9 Kurva h hingga orde ke-10 20

10 Penyelesaian HAM dan NUM terhadap populasi manusia dan populasi

nyamuk hingga orde ke-10 dengan ℎ=−1 21

DAFTAR LAMPIRAN

1 Penentuan titik tetap 24

2 Penentuan matriks Jacobi 30

3 Penentuan matriks Jacobi untuk titik tetap tanpa penyakit 31

4 Penentuan nilai eigen 32

5 Penentuan bilangan reproduksi dasar 33

6 Simulasi efektivitas pengobatan pada manusia 34

7 Simulasi efektivitas vaksinasi pada manusia 35

8 Simulasi efektivitas penyemprotan pada nyamuk 36

9 Penurunan persamaan (4.8) 37

10 Penurunan persamaan (4.9) 39

11 Program untuk Gambar 9 44

1

PENDAHULUAN

Latar Belakang

Malaria merupakan penyakit menular yang disebabkan oleh parasit yang dikenal dengan Plasmodium. Perantara atau pembawa parasit Plasmodium ini adalah nyamuk Anopheles betina yang menyebabkan rusaknya sel-sel darah merah pada manusia dan hewan melalui gigitannya. Malaria dapat ditularkan melalui transfusi darah, pemakaian jarum suntik, maupun bawaan. Malaria merupakan penyakit mematikan. Di Indonesia, kelompok yang berisiko tinggi terkena malaria adalah bayi, anak balita, dan ibu hamil. Berdasarkan API (Annual Parasite Incidence), Indonesia bagian timur termasuk dalam wilayah risiko malaria tinggi, Kalimantan, Sulawesi, dan Sumatera termasuk dalam wilayah risiko malaria sedang, serta Jawa-Bali termasuk dalam wilayah risiko malaria rendah (Ditjen PP 2011). Pada tahun 2012, WHO menyatakan bahwa sekitar 3.4 milyar penduduk di dunia berisiko terkena malaria dengan 80% di antaranya merupakan penduduk benua Afrika dan Asia (WHO 2013).

Banyak peneliti yang telah mengembangkan model matematika dari transmisi penyakit malaria. Laarabi et al. (2012) memformulasikan model SIR dengan tingkat infeksi taklinear dan melihat akibat dari vaksinasi terhadap populasi manusia. Dalam model ini diasumsikan bahwa vaksinasi di waktu yang tepat dapat mangakibatkan manusia rentan yang memperoleh vaksinasi dapat langsung berpindah ke manusia pulih. Agusto et al. (2012) mengaplikasikan kontrol optimum dengan penggunaan treatment sebagai variabel kontrol pada sistem transmisi penyakit malaria. Abdullahi et al. (2013) mengembangkan model penyebaran penyakit malaria dengan mempertimbangkan adanya penularan dari manusia ke manusia melalui transfusi darah dan melalui ibu hamil yang terinfeksi malaria.

Dalam penelitian ini dibahas sebuah model penyebaran penyakit malaria dengan efektivitas penggunaan obat-obatan yang diperkenalkan oleh Abdullahi

et al. (2013). Model ini merupakan model SIR-SI. Modifikasi model dilakukan dengan menambahkan asumsi bahwa manusia yang pulih dapat rentan kembali terkena malaria akibat hilangnya kekebalan tubuh (Mandal et al. 2011), sehingga model ini disebut SIRS-SI. Selain itu, modifikasi model juga dilakukan dengan penambahan parameter pencegahan malaria yaitu vaksinasi pada manusia (Schwartz et al. 2012) dan penyemprotan pada nyamuk (Ratovonjato et al. 2014). Selanjutnya, dilakukan analisis kestabilan pada model dan melihat dinamika populasi dengan adanya treatment pencegahan malaria. Model SIRS-SI ini juga akan diselesaikan menggunakan metode homotopi kemudian dibandingkan galatnya dengan penyelesaian numerik.

2

analisis kestabilan pada model penyebaran penyakit malaria dan Khan et al.

(2013) yang menggunakan metode homotopi perturbasi pada model epidemik leptospirosis. Metode homotopi merupakan suatu pendekatan penyelesaian analitik dari masalah persamaan diferensial yang tak linear. Dalam metode ini, didefinisikan suatu operator linear dan operator taklinear yang didasarkan pada suatu bentuk persamaan diferensial. Kelebihan metode homotopi dibandingkan metode pendekatan penyelesaian analitik yang lain yaitu terdapat parameter bantu pada fungsi homotopi yang dapat mengontrol kekonvergenan dari penyelesaiannya dan kebebasan dalam pemilihan pendekatan awal (Liao 2004). Penerapan dari metode homotopi yang telah digunakan oleh para peneliti antara lain Jaharuddin (2014) pada model populasi spesies tunggal pada lingkungan yang tercemar, Paparao (2013) pada model ekologi tiga populasi, dan Padma (2013) pada model kualitas air.

Tujuan Penelitian

Berdasarkan uraian latar belakang di atas, maka penelitian ini bertujuan untuk

1 Mengonstruksi model penyakit malaria tipe SIRS-SI. 2 Melakukan analisis kestabilan pada model.

3 Melakukan simulasi numerik terhadap model untuk melihat pengaruh

treatment pencegahan dan penanganan malaria terhadap dinamika populasi manusia dan nyamuk.

4 Menggunakan metode homotopi untuk menyelesaikan model.

2

TINJAUAN PUSTAKA

Sistem Persamaan Diferensial Biasa

Sistem Persamaan Diferensial Biasa Taklinear

Misalkan suatu sistem persamaan diferensial biasa (PDB) dinyatakan sebagai (2.1) disebut sistem persamaan diferensial biasa taklinear (Tu 1994).

Sistem Persamaan Diferensial Biasa Mandiri

3

�= � ,� ∈ ℝ (2.2)

dengan f merupakan fungsi kontinu bernilai real dari �. Sistem persamaan (2.2) disebut sistem persamaan diferensial biasa mandiri (autonomous) karena tidak memuat t secara eksplisit di dalamnya (Tu 1994).

Nilai Eigen dan Vektor Eigen

Diberikan matriks koefisien konstan � berukuran × dan sistem

Untuk mencari nilai dari �, maka sistem persamaan (2.3) dapat ditulis

� − �=�, (2.4)

dengan adalah matriks identitas. Sistem persamaan (2.4) mempunyai penyelesaian taknol jika dan hanya jika

det � − =�. (2.5)

Persamaan (2.5) merupakan persamaan karakteristik matriks � (Leon 1998). Pelinearan

Misalkan diberikan sistem persamaa diferensial biasa tak linear sebagai berikut :

�= � ,� ∈ ℝ . (2.6)

Dengan menggunakan ekspansi deret Taylor di sekitar titik tetap � , maka sistem persamaan (2.6) dapat ditulis sebagai

�= �+ � , (2.7)

dengan adalah matriks Jacobi.

= (�)

4

Kestabilan Titik Tetap

Misalkan diberikan sistem persamaan diferensial biasa sebarang � =

� , � ∈ ℝ dengan � sebagai titik tetap. Kestabilan titik tetap � dapat ditentukan dengan memperhatikan nilai-nilai eigen, yaitu , = 1,2,…, , yang diperoleh dari persamaan karakteristik. Secara umum, kestabilan titik tetap mempunyai perilaku sebagai berikut :

1 Stabil, jika :

Bilangan reproduksi dasar ( ₀) merupakan nilai harapan terjadinya infeksi per satuan waktu. Infeksi ini terjadi pada suatu populasi yang seluruhnya rentan yang dihasilkan oleh satu jenis individu yang sudah terinfeksi. ₀ dalam penelitian ini ditentukan dengan menggunakan metode yang dikenalkan oleh van den Driessche dan Watmough (2008) yaitu mengonstruksi suatu matriks yang berasal dari subpopulasi-subpopulasi yang menyebabkan infeksi saja. Matriks tersebut dikenal dengan the next generation matrix. Nilai ₀ merupakan nilai eigen tak negatif terbesar dari matriks ini.

Kondisi yang memungkinkan dari bilangan reproduksi dasar menurut van den Driessche dan Watmough (2008) adalah

1 Jika ₀ < 1, maka jumlah individu yang terinfeksi akan menurun pada setiap generasi, sehingga penyakit tidak akan menyebar.

2 Jika ₀ > 1, maka jumlah individu yang terinfeksi akan meningkat pada setiap generasi, sehingga penyakit akan menyebar.

Metode Homotopi

Berikut ini diberikan ilustrasi konsep dasar metode homotopi. Misalkan diberikan persamaan diferensial berikut:

� = 0, (2.8)

dengan �operator turunan, t variabel bebas, dan u(t) fungsi yang akan ditentukan penyelesaiannya. Selanjutnya, didefinisikan pula suatu operator ℒ yang memenuhi

ℒ = 0, bila = 0. (2.9)

Didefinisikan suatu fungsi homotopi sebagai berikut:

ℋ , ; = 1− ℒ , − ₀ + � , , (2.10)

dengan fungsi yang akan ditentukan yang bergantung pada t dan parameter q. Fungsi u0(t) merupakan pendekatan awal dari penyelesaian persamaan (2.8) dan

q [0,1] suatu parameter. Berdasarkan persamaan (2.10), untuk q = 0 dan q = 1 masing-masing memberikan persamaan berikut:

5

Perluasan metode homotopi lebih lanjut dapat dituliskan dalam bentuk persamaan deformasi orde nol berikut :

1− ℒ , − ₀ = ℎ� � , , (2.11)

Kemudian dengan menurunkan persamaan (2.11) terhadap q hingga n kali serta dievaluasi pada q = 0 dan dibagi dengan n! akan diperoleh bentuk persamaan

6

3

MODEL MATEMATIKA PENYEBARAN

PENYAKIT MALARIA

Penelitian Sebelumnya

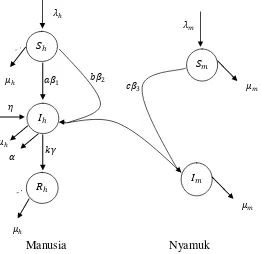
Abdullahi et al. (2013) merumuskan model penyebaran penyakit malaria tipe SIR-SI. Pada model ini, populasi manusia dibagi menjadi tiga kelas, yaitu manusia rentan (susceptible) _ℎ, manusia terinfeksi (infected) _ℎ, dan manusia pulih (recovered) _ℎ, sedangkan populasi nyamuk dibagi menjadi dua kelas, yaitu nyamuk rentan (susceptible) dan nyamuk terinfeksi (infected) .

Individu yang lahir dan bermigrasi pada kelas rentan _ℎ memiliki laju konstan sebesar _ℎ. Manusia yang berada di kelas rentan dapat berpindah ke kelas terinfeksi _ℎ akibat transfusi darah dengan laju ₁ atau akibat gigitan nyamuk terinfeksi dengan laju ₂. Manusia yang berada di kelas rentan dapat mati dengan laju kematian sebesar _ℎ. Lahirnya bayi yang terinfeksi malaria akibat bawaan pada kelas terinfeksi _ℎ memiliki laju sebesar . Manusia yang berada di kelas terinfeksi dapat berpindah ke kelas pulih _ℎ karena penggunaan obat-obatan anti-malaria dengan laju . Manusia di kelas terinfeksi dapat mati dengan laju kematian _ℎ dan mati akibat malaria dengan laju . Manusia di kelas pulih _ℎ dapat mati dengan laju _ℎ.

Nyamuk yang lahir dan bermigrasi pada kelas rentan memiliki laju konstan sebesar . Nyamuk di kelas rentan dapat berpindah ke kelas terinfeksi karena menggigit manusia terinfeksi dengan laju ₃ atau dapat mati dengan laju kematian sebesar . Selanjutnya, nyamuk di kelas terinfeksi dapat mati dengan laju kematian sebesar .

Persamaan dinamika sistem tersebut diformulasikan sebagai berikut ℎ

= _ℎ − 1 ℎ + 2 + ℎ ℎ,

ℎ

= _ℎ + 1 ℎ + 2 ℎ − ℎ + + ℎ,

ℎ ₌

ℎ − ℎ ℎ, (3.1)

= − _{3 ℎ} + ,

= 3 ℎ − .

7 Secara skematis, pola penyebaran penyakit malaria tipe SIRS-SI digambarkan dalam diagram kompartemen pada Gambar 1.

Modifikasi Model

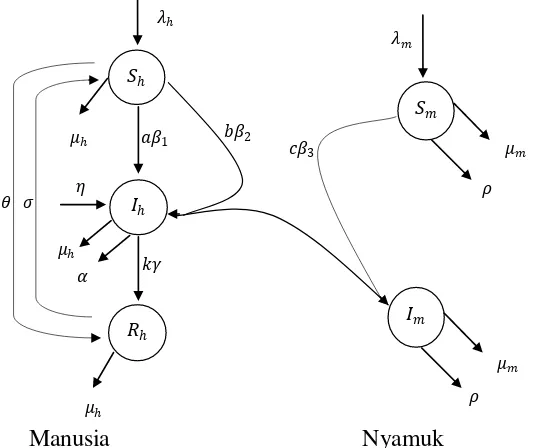
Model SIR-SI yang dirumuskan oleh Abdullahi et al. (2013) selanjutnya dimodifikasi dengan menambahkan asumsi bahwa manusia yang telah pulih dapat rentan kembali terkena malaria akibat hilangnya laju kekebalan tubuh dengan laju � (Mandal et al., 2011), sehingga model ini selanjutnya disebut SIRS-SI. Definisi kelas rentan pada model ini merupakan manusia yang belum tergigit nyamuk dan telah tergigit nyamuk namun parasit hanya berada di dalam darah. Vaksinasi yang diberikan dapat membuat manusia rentan yang telah tergigit dapat langsung berpindah ke manusia pulih. Kelas terinfeksi merupakan manusia yang telah tergigit nyamuk dan parasit telah berada di hati. Manusia yang telah pulih atau sembuh dari malaria karena perlakuan yang diberikan didifinisikan ke dalam kelas pulih. Modifikasi model juga dilakukan dengan menambahkan asumsi bahwa manusia pada kelas rentan ( _ℎ) dapat berpindah ke kelas pulih _ℎ karena adanya vaksinasi dengan laju (Schwartz et al. 2012) serta nyamuk pada kelas rentan dan kelas terinfeksi dapat mati karena penyemprotan dengan laju � (Ratovonjato et al. 2014).

Persamaan dinamika sistem tersebut diformulasikan sebagai berikut

ℎ ₌

ℎ +� ℎ − 1 ℎ + 2 ℎ − + ℎ ℎ,

Manusia Nyamuk

Gambar 1 Diagram kompartemen penyakit malaria tipe SIR-SI

2

3 1

ℎ ℎ

ℎ ℎ

ℎ ℎ

8

Keterangan parameter disajikan pada Tabel 1.

Secara skematis, pola penyebaran penyakit malaria dapat digambarkan dalam diagram kompartemen pada Gambar 2.

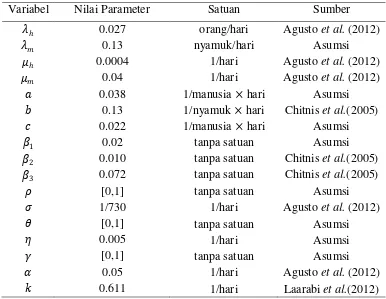
Tabel 1 Parameter pada model malaria tipe SIR-SI dan tipe SIRS-SI

Variabel Keterangan Satuan

ℎ Laju kelahiran dan migrasi manusia orang/waktu Laju kelahiran dan migrasi nyamuk orang/waktu ℎ Laju konstan kematian manusia secara alami 1/waktu

Laju konstan kematian nyamuk secara alami 1/waktu Rata-rata banyaknya transfusi darah tiap satuan

waktu

1/orang × waktu Rata-rata banyaknya gigitan nyamuk terinfeksi

pada manusia rentan tiap satuan waktu

1/nyamuk × waktu Rata-rata banyaknya gigitan nyamuk rentan pada

manusia terinfeksi tiap satuan waktu

1/orang × waktu

1 Peluang terjadinya transmisi penyakit dari manusia terinfeksi ke manusia rentan

tanpa satuan

2 Peluang terjadinya transmisi penyakit dari tanpa satuan Manusia Nyamuk

9 nyamuk terinfeksi ke manusia rentan

3 Peluang terjadinya tranmisi penyakit dari manusia terinfeksi ke nyamuk rentan

tanpa satuan � Efektivitas penyemprotan pada nyamuk 1/waktu � Laju konstan hilangnya kekebalan tubuh pada

manusia setelah pulih

1/waktu Efektivitas vaksinasi pada manusia 1/waktu Laju bayi yang lahir dari ibu yang terinfeksi

malaria

1/waktu Efektivitas pengobatan pada manusia tanpa satuan Laju kematian manusia akibat malaria 1/waktu

Laju pemulihan 1/waktu

4

HASIL DAN PEMBAHASAN

Penentuan Titik Tetap

Pada sub-bab ini akan dicari titik tetap berdasarkan persamaan (3.2). Titik tetap diperoleh dengan cara menyelesaikan persamaan

ℎ ₌ ℎ ₌ ℎ _{= = = 0.}

10

Analisis Kestabilan Titik Tetap

Pada bagian ini, dilakukan analisis untuk melihat sifat kestabilan pada titik tetap. Untuk selanjutnya hanya dilakukan analisis kestabilan untuk titik tetap tanpa penyakit � , sedangkan untuk titik tetap � tidak dilakukan analisis ketabilan karena bentuknya yang sangat kompleks.

Penentuan Matriks Jacobi

Misalkan diberikan sistem (3.2) didefinisikan sebagai fungsi berikut

�= � ,� ∈ ℝ5, (4.3)

dengan � ∈ ℝ5 adalah variabel-variabel yang terdapat pada sistem (3.2). Matriks Jacobi dari sistem (3.2) didefinisikan sebagai

=

Penentuan matriks Jacobi dapat dilihat pada Lampiran 2.

Penentuan Matriks Jacobi untuk Titik Tetap Tanpa Penyakit

Sifat kestabilan titik tetap � _ℎ, _ℎ, _ℎ, , = _ℎ∗, 0, _ℎ∗, ∗, 0 dapat dilakukan dengan melakukan pelinearan pada sistem persamaan diferensial (4.3) di sekitar � , sehingga diperoleh matriks Jacobi untuk titik tetap tanpa penyakit sebagai berikut

11

44 =− − �, 52 =

3

+�,

55 =− − �.

Penentuan matriks Jacobi untuk titik tetap tanpa penyakit dapat dilihat pada Lampiran 3.

Penentuan Nilai Eigen

Menurut Tu (1994), titik tetap � bersifat stabil jika dan hanya jika setiap nilai eigen dari matriks _� bernilai negatif dan tidak stabil jika dan hanya jika ada minimal satu nilai eigen dari matriks _� yang taknegatif. Berdasarkan matriks | _� − | diperoleh lima nilai eigen berikut :

1 = 44 =− − �,

Sistem akan stabil jika semua nilai eigen bernilai negatif.  Untuk nilai eigen ₂,

 ₁ < 0, karena semua parameter bernilai positif,

 ₂ bernilai negatif, jika ₁2 −₄

2 > 0 atau 12 > 4 2, Jika dua kondisi tersebut terpenuhi , maka mengakibatkan ₂ < 0.  Untuk nilai eigen ₃,

 3 bernilai negatif, jika 12 −4 2 < − 1,

 ₃ bernilai negatif, jika ₁2 ₋₄

2 > 0 atau 12 > 4 2, .Jika dua kondisi tersebut terpenuhi, maka mengakibatkan ₃ < 0.  Untuk nilai eigen ₄,

 ₃ < 0, jika + 1 ℎ ℎ+�

ℎ +�+ _ℎ < ℎ + + + +�,

12

Jika tiga kondisi tersebut terpenuhi, maka mengakibatkan ₅ < 0. Penentuan nilai eigen dapat dilihat pada Lampiran 4.

Penentuan Bilangan Reproduksi Dasar

Bilangan reproduksi dasar dinotasikan dengan ₀ adalah nilai harapan banyaknya infeksi tiap satuan waktu. Infeksi ini terjadi pada suatu populasi rentan yang dihasilkan oleh satu individu terinfeksi.

Untuk menentukan bilangan reproduksi dasar digunakan pendekatan the next generation matrix. Berdasarkan persamaan (3.2), maka diperoleh matriks � dan � sebagai berikut

Bilangan reproduksi dasar ₀ merupakan nilai eigen positif terbesar dari matriks =��−1_{, yaitu}

Penentuan bilangan reproduksi dapat dilihat pada Lampiran 5.

Kondisi yang memungkinkan dari bilangan reproduksi dasar menurut van den Driessche & Watmough (2008) adalah

1. Jika ₀ < 1, maka jumlah individu yang terinfeksi akan menurun pada setiap generasi, sehingga penyakit tidak akan menyebar.

2. Jika ₀ > 1, maka jumlah individu yang terinfeksi akan meningkat pada setiap generasi, sehingga penyakit akan menyebar.

Simulasi

13 pada persamaan (4.4). Simulasi ini diperlukan untuk menunjukkan pengaruh pengobatan dan vaksinasi pada manusia serta penyemprotan pada nyamuk terhadap dinamika populasi manusia dan populasi nyamuk.

Nilai Parameter

Pemilihan parameter didasarkan pada studi yang dilakukan oleh berbagai sumber terpercaya. Beberapa nilai parameter seperti yang menyangkut populasi, didasarkan pada asumsi tentang situasi penyakit yang paling umum. Nilai-nilai parameter yang diambil sehingga diperoleh ₀ < 1 disajikan pada Tabel 2.

Tabel 2 Nilai Parameter pada model malaria tipe SIRS-SI

Variabel Nilai Parameter Satuan Sumber

ℎ 0.027 orang/hari Agusto et al. (2012)

0.13 nyamuk/hari Asumsi

ℎ 0.0004 1/hari Agusto et al. (2012) Dengan linearisasi dan perhitungan terhadap sistem (3.2) di sekitar titik tetap, diperoleh matriks Jacobian dan nilai eigen untuk titik tetap tanpa penyakit. Selanjutnya dapat disimpulkan bahwa titik tetap tanpa penyakit memiliki sifat stabil karena semua nilai eigen bernilai negatif pada kondisi ₀ < 1. Simulasi dilakukan dengan menggunakan nilai parameter pada Tabel 2. Nilai awal populasi manusia rentan ( _ℎ) adalah 40, populasi manusia terinfeksi _ℎ adalah 2, populasi manusia pulih _ℎ adalah 0, populasi nyamuk rentan adalah 500, dan populasi nyamuk terinfeksi adalah 10. Simulasi ini diperlukan untuk menunjukkan pengaruh treatment yang diberikan.

Simulasi Efektivitas Pengobatan pada Manusia

14

mengubah bilangan reproduksi dasar ₀ yang didefinisikan pada persamaan (4.4). Terdapat tiga nilai yang diamati, diambil pada selang 0.10,0.30 dengan langkah 0.10. Nilai-nilai parameter lain dapat dilihat pada Tabel 2. Adapun perubahan nilai parameter yang menyebabkan terjadinya perubahan

0 dapat dilihat pada Tabel 3.

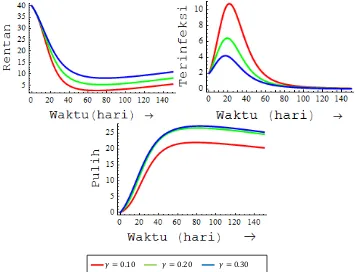
Tabel 3 Hasil simulasi efektivitas pengobatan pada manusia terhadap bilangan reproduksi dasar

Parameter Bilangan reproduksi dasar

= 0.10 ₀= 0.646

= 0.20 ₀= 0.454

= 0.30 _{0= 0.361}

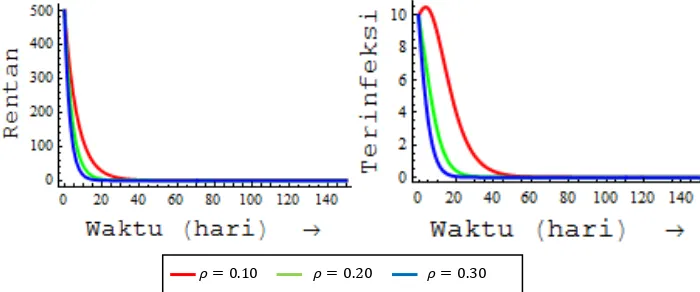
Pada populasi manusia sebagaimana ditunjukkan dalam Gambar 3, jika efektivitas pengobatan pada manusia diperbesar, maka menyebabkan semakin berkurangnya jumlah manusia di kelas terinfeksi dan semakin bertambahnya jumlah manusia di kelas pulih. Sedangkan jumlah manusia di kelas rentan mengalami penurunan.

Pengobatan yang diberikan kepada manusia memberikan dampak pada populasi nyamuk sebagaimana ditunjukkan dalam Gambar 4. Jika efektivitas pengobatan pada manusia diperbesar, maka menyebabkan menurunnya jumlah nyamuk di kelas terinfeksi dan menyebabkan bertambahnya jumlah nyamuk di kelas rentan. Hal ini dikarenakan peningkatan efektivitas pengobatan pada manusia menyebabkan penurunan pada jumlah manusia di kelas terinfeksi,

15 sehingga mengakibatkan penurunan pula pada jumlah nyamuk di kelas terinfeksi.

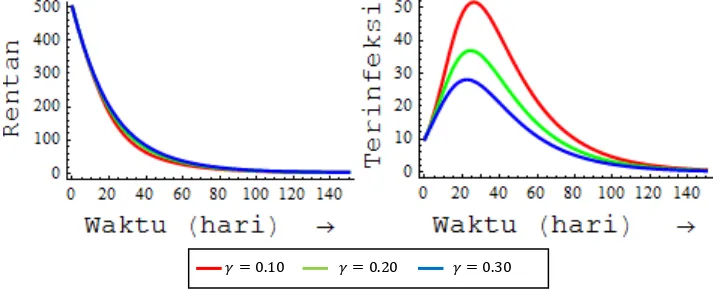
Bertambah atau berkurangnya jumlah manusia dan nyamuk di tiap kelas cenderung tidak sama untuk setiap kenaikan efektivitas pengobatan pada manusia. Maksimum jumlah manusia dan jumlah nyamuk di kelas terinfeksi terjadi pada saat = 25 hari. Pada saat = 25 hari, dengan efektivitas sebesar 20%, dapat menurunkan persentase manusia terinfeksi sebesar 23.81% dari total populasi manusia dan dapat menurunkan persentase nyamuk terinfeksi sebesar 5.88% dari total populasi nyamuk.

Program simulasi dapat dilihat pada Lampiran 6. Simulasi Efektivitas Vaksinasi pada Manusia

Dalam hal ini, dilakukan simulasi untuk menunjukkan efektivitas dari vaksinasi terhadap populasi manusia dan populasi nyamuk. Diasumsikan manusia terinfeksi diberikan pengobatan pada manusia sebesar 10%. Akan ditunjukkan bahwa peningkatan atau penurunan nilai parameter dapat mengubah bilangan reproduksi dasar ₀ yang didefinisikan pada persamaan (4.4). Perubahan nilai parameter yang menyebabkan terjadinya perubahan ₀ dapat dilihat pada Tabel 4.

Tabel 4 Hasil simulasi efektivitas vaksinasi pada manusia terhadap bilangan reproduksi dasar

Parameter Bilangan reproduksi dasar

= 0.10 ₀ = 0.047

= 0.20 ₀ = 0.039

= 0.30 _{0 = 0.027}

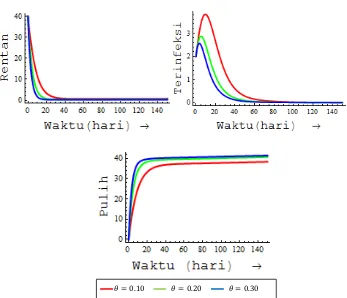
Gambar 5 menjelaskan bahwa jika efektivitas vaksinasi diperbesar dan nilai parameter yang lain tetap, maka jumlah manusia pada kelas rentan semakin berkurang dan jumlah manusia pada kelas pulih semakin bertambah. Hal ini secara tidak langsung menyebabkan penurunan jumlah manusia pada kelas terinfeksi.

16

Jika efektivitas vaksinasi diperbesar dan nilai parameter yang lain tetap, maka secara tidak langsung menyebabkan jumlah nyamuk pada kelas terinfeksi semakin berkurang sebagaimana yang dapat dilihat pada Gambar 6. Hal ini dikarenakan peningkatan efektivitas penggunaan vaksin menyebabkan semakin berkurangnya jumlah manusia di kelas terinfeksi.

Jumlah manusia dan nyamuk di tiap kelas berbeda untuk setiap kenaikan efektivitas vaksinasi pada manusia. Pada saat = 15 hari, dengan efektivitas sebesar 20%, dapat menurunkan persentase jumlah manusia di kelas rentan sebesar 14.29% dan meningkatkan persentase jumlah manusia di kelas pulih sebesar 21.43% dari total populasi manusia. Vaksinasi yang diberikan pada manusia memberikan pengaruh terhadap berkurangnya jumlah nyamuk di kelas

Gambar 5 Dinamika populasi manusia karena vaksinasi pada manusia = 0.10 = 0.20 = 0.30

17 terinfeksi. Persentase jumlah nyamuk di kelas terinfeksi berkurang sebesar 1,57% dari total populasi nyamuk saat = 15.

Program simulasi dapat dilihat pada Lampiran 7. Simulasi Efektivitas Penyemprotan pada Nyamuk

Efektivitas dari penggunaan spraying terhadap populasi manusia dan populasi nyamuk ditunjukkan pada simulasi ini. Diasumsikan manusia terinfeksi diberikan pengobatan sebesar 10%. Perubahan bilangan reproduksi dasar 0 dipengaruhi dengan peningkatan atau penurunan nilai parameter � dengan nilai � yang diamati, diambil pada selang 0.10,0.30 . Nilai-nilai parameter lain dapat dilihat pada Tabel 2. Perubahan nilai parameter � yang menyebabkan terjadinya perubahan ₀ dapat dilihat pada Tabel 5.

Tabel 5 Hasil simulasi efektivitas penyemprotan pada nyamuk terhadap bilangan reproduksi dasar

Parameter � Bilangan reproduksi dasar

�= 0.10 _{0 = 0.499}

�= 0.20 _{0 = 0.488}

�= 0.30 ₀ = 0.485

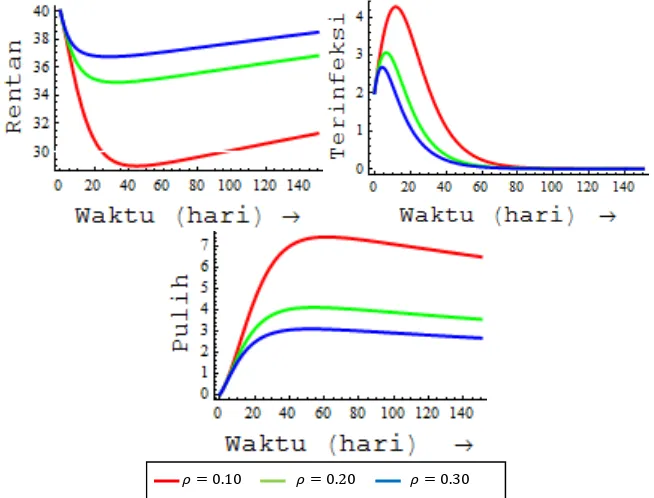
Penyemprotan pada nyamuk mengakibatkan perubahan pada populasi manusia di tiap-tiap kelas yang ditunjukkan dalam Gambar 7. Jika efektivitas penyemprotan pada nyamuk diperbesar dan nilai parameter yang lain tetap, maka jumlah manusia di kelas rentan semakin bertambah, jumlah manusia di kelas terinfeksi semakin berkurang sedangkan jumlah manusia di kelas pulih semakin berkurang pula.

18

Berdasarkan Gambar 8 dapat dijelaskan bahwa jika efektivitas penyemprotan pada nyamuk diperbesar, maka menyebabkan jumlah nyamuk di kelas rentan dan jumlah nyamuk di kelas terinfeksi semakin berkurang.

Persentase jumlah nyamuk di kelas rentan berkurang sebesar 19.8% dan persentase jumlah nyamuk di kelas terinfeksi pun berkurang sebesar 1.78% dari total populasi nyamuk pada saat = 10 dengan efektivitas peenyemprotan pada nyamuk sebesar 20%. Penyemprotan pada nyamuk juga memberikan dampak pada menurunnya persentase jumlah manusia di kelas terinfeksi sebesar 4.76% dari total populasi manusia.

Program simulasi dapat dilihat pada Lampiran 8. Metode Analisis Homotopi

Berikut ini akan dibahas penggunaan metode homotopi yang telah diuraikan sebelumnya untuk menyelesaikan model malaria tipe SIRS-SI. Berdasarkan persamaan (3.2), maka didefinisikan suatu operator linear ℒ1,ℒ2,ℒ3,ℒ4,ℒ5 dan operator nonlinear �1,�2,�3,�4, �5 sebagai berikut

Berdasarkan persamaan (4.5), maka dikonstruksikan persamaan deformasi orde ke-nol berikut

1− ℒ � , − �_,0 = ℎ� � , , = 1,2,3,4,5. (4.6) Gambar 8 Dinamika populasi nyamuk karena penyemprotan pada nyamuk

19 Jika q = 0 dan q = 1, maka berdasarkan persamaan (4.6) diperoleh

� , 0 =�,0 ; � , 1 = � , = 1,2,3,4,5.

Menggunakan konsep deret Taylor, � , dapat diuraikan menjadi � , = �,0 + �,

Kemudian, ditentukan persamaan orde ke-n sebagai berikut

ℒ �, − �, −1 =ℎ , � , −1 , = 1,2,3,4,5, (4.8)

(Penurunan dapat dilihat pada Lampiran 9)

dengan

(Penurunan dapat dilihat pada Lampiran 10) dan

�1,0 = ℎ 0 = 40, �2,0 = ℎ 0 = 2, �3,0 = ℎ 0 = 0

�4,0 = 0 = 500, �5,0 = 0 = 10. (4.10)

Solusi untuk orde ke-n dari persamaan (4.8) adalah

�, = �, ₋1 +ℎ , � , ₋1 . (4.11) dengan = 0 untuk ≤ 1 dan = 1 untuk > 1. Dengan demikian apabila diberikan masalah taklinear dengan persamaan diferensial pada persamaan (3.2), maka dengan metode homotopi diperoleh penyelesaian pendekatan masalah tak linear tersebut sebagai berikut

� = �_, ( )

10

=0

20 dengan

�1 = ℎ , �2 = ℎ , �3 = ℎ �4 = , �5 = .

Aplikasi Metode Homotopi

Berdasarkan uraian pada bagian analisis metode homotopi, berikut ini prosedur untuk menentukan penyelesaian dari sistem (3.2) :

1 Misalkan didefinisikan operator linear dan operator nonlinear pada persamaan (4.5).

2 Menentukan persamaan orde ke-n pada persamaan (4.8). 3 Misalkan diberikan pendekatan awal persamaan (4.10).

4 Menentukan pendekatan penyelesaian homotopi untuk orde ke-n pada persamaan (4.11) dengan _, � _{, −1} didefinisikan pada persamaan (4.9). 5 Menentukan penyelesaian sistem (3.2) dari persamaan (4.12).

Berdasarkan prosedur di atas, penyelesaian metode homotopi yang diperoleh bergantung pada variabel bantu h dan variabel waktu t. Oleh karena itu, diperlukan pemilihan variabel bantu h yang tepat agar menghasilkan penyelesaian pendekatan analitik yang sesuai. Pemilihan variabel bantu h

diperoleh dengan cara penyelesaian homotopi diturunkan dua kali terhadap q

kemudian dievaluasi pada saat q = 0. Kurva yang saling bersinggungan disuatu selang h akan menjadi nilai h yang diambil dalam penyelesaian metode homotopi.

Berdasarkan Gambar 10, kelima kurva bersinggungan pada selang h yaitu −1.8≤ ℎ ≤0.3. Berdasarkan selang ini, dapat dipilih suatu nilai h sehingga diperoleh penyelesaian dengan absolute error yang kecil bila dibandingkan dengan suatu penyelesaian numerik. Dalam hal ini, dipilih ℎ= −1. Dengan pemilihan ℎ =−1, maka diperoleh penyelesaian homotopi sebagai fungsi dari t. Dengan demikian diperoleh penyelesaian homotopi hingga orde ke-10

�1 = ℎ = �1,1 +�1,2 +�1,3 + +�1,10 , �2 = ℎ =�2,1 +�2,2 +�2,3 + +�2,10 , �3 = ℎ =�3,1 +�3,2 +�3,3 + +�3,10 ,

21 �4 = = �4,1 +�4,2 +�4,3 + +�4,10 ,

�5 = =�5,1 +�5,2 +�5,3 + +�5,10 .

Penyelesaian homotopi hingga orde ke-10 merupakan penyelesaian pendekatan analitik dari model SIRS-SI. Penyelesaian tersebut diperoleh secara eksplisit sebagai fungsi dari . Dalam hal ini, penyelesaian numerik yang diperoleh menggunakan software berbasis fungsional dianggap sebagai penyelesaian eksak dari model taklinear tersebut. Selanjutnya, dilakukan perbandingan kurva untuk melihat absolute error dari penyelesaian homotopi dan penyelesaian numerik.

Gambar 10 menunjukkan bahwa penyelesaian menggunakan metode homotopi (HAM) dan penyelesaian numerik (NUM) memiliki absolute error

yang kecil. Terlihat pada jarak kedua kurva penyelesaian yang cukup dekat. Artinya metode homotopi merupakan metode yang cukup baik digunakan untuk menyelesaikan suatu model taklinear.

5

SIMPULAN DAN SARAN

Simpulan

Pada model penyebaran penyakit malaria tipe SIRS-SI ini terdapat dua titik tetap yaitu titik tetap tanpa penyakit dan titik tetap endemik. Simulasi dilakukan untuk melihat perilaku sistem di sekitar titik tetap. Simulasi yang dilakukan menunjukkan bahwa perlakuan yang diberikan memiliki pengaruh terhadap dinamika populasi manusia dan nyamuk yang ditunjukkan dengan bilangan reproduksi dasar. Secara umum, jika efektivitas penggunaan perlakuan ditingkatkan, maka menyebabkan menurunnya bilangan reproduksi dasar. Itu artinya, jumlah individu yang terinfeksi semakin berkurang, sehingga penyakit

ℎ

Gambar 10 Penyelesaian HAM dan NUM terhadap populasi manusia dan populasi nyamuk hingga orde ke-10 dengan ℎ= −1.

ℎ

ℎ ℎ

22

tidak akan menyebar dan dalam jangka waktu tertentu penyakit akan menghilang dari populasi tersebut.

Dalam penelitian ini, digunakan pula metode homotopi untuk memperoleh pendekatan penyelesaian secara analitik dari model. Dalam metode homotopi didefinisikan suatu fungsi homotopi dengan parameter bantu ℎ yang dapat mengontrol daerah kekonvergenan penyelesaian homotopi. Penyelesaian homotopi diperoleh secara eksplisit sebagai fungsi dari hingga orde ke-10 dan parameter bantu ℎ= −1. Penyelesaian dari metode ini dibandingkan dengan penyelesaian numerik. Diperoleh bahwa antara penyelesaian homotopi dan penyelesaian numerik memiliki absolute error yang cukup kecil hingga = 9. Itu artinya, metode homotopi merupakan metode pendekatan penyelesaian masalah persamaan diferensial taklinear yang cukup baik.

Saran

Pada penelitian ini, di dalam model hanya digunakan tiga perlakuan untuk penyakit malaria yaitu pengobatan dan vaksinasi pada manusia dan penyemprotan pada nyamuk. Perlu dikaji lebih lanjut untuk perlakuan pencegahan yang lain seperti pemakaian lotion anti-nyamuk dan pemakaian kelambu.

DAFTAR PUSTAKA

Abdullahi MB, Hasan YA, Abdullah FA. 2013. A mathematical model of malaria and the effectiveness of drugs. Applied Mathematical Sciences. Vol. 7, 2013, No. 62, 3079-3095.

Agusto FB, Marcus N, Okosun KO. 2012. Application of optimal control to the epidemiology of malaria. Electronic Journal of Differential Equation. Vol. 2012(2012), No.81, pp. 1-22.

Chitnis NR. 2005. Using mathematical models in controlling the spread of malaria [disertasi]. Arizona (US) : The University of Arizona.

Jaharuddin. 2014. A single species population model in polluted environment solved by homotopy analysis method. Applied Mathematical Sciences. Vol.8, 2014, no.20, 951-961, http://dx.doi.org/10.12988/ams.2014.312728.

[Ditjen PP] Direktorat Jenderal Pengendalian Penyakit. 2011. Epidemiologi Malaria di Indonesia. Jakarta: Kementerian Kesehatan RI.

Khan MA, Islam S, Ullah M, Khan SA, Zaman G, Saddiq SF. 2013. Analytical solution of the leptospirosis epidemic model by homotopy perturbation method. Research Journal of Recent Sciences. Vol. 2(8), 66-71

Laarabi H, Labriji EH, Rachik M, Kaddar A. 2012. Optimal control of an epidemic model with a saturated incidence rate. Modelling and Control. Vol.17, No.4,448-459.

Leon SJ. 1998. Aljabar Linear dan Aplikasinya. Bondan A, penerjemah; Hardani HW, editor. Jakarta (ID): Penerbit Erlangga. Terjemahan dari:

23 Liao. 2004. Beyond Perturbation : Introduction to the homotopy analysis

method. New York (US) : Boca Raton.

Mandal S, Sarkar RR, Sinha S. 2011. Mathematical models of malaria - a review. Malaria Journal. Vol 10:202.

Padma S, Hariharan G, Kannan K, Srikanth R. 2013. Homotopy analysis method to water quality model in a uniform channel. Applied Mathematical Sciences. Vol.7, 2013, no.22, 1057-1066.

Paparao AV, Narayan LK, Bathul S. 2013. Computation of three species ecological model by homotopy analysis method. International Journal of Advanced Research in Computer Science and Software Engineering. Vol.3, Issue 6, June 2013.

Putri RG, Jaharuddin, Bakhtiar T. 2014. SIRS-SI Model of Malaria Disease with Application of Vaccines, Anti-malarial Drugs, and Spraying. Journal of Mathematics. [siap terbit]

Ratovonjato et al. 2014. Entomological and parasitological impacts of indoor residual spraying with DDT, alphacypermethrin and deltamethrin in the weaterd foothill area of Madagascar. Malaria Journal. 13:21

Schwartz L, Brown GV, Genton B, Moorthy VS. 2012. A reiew of malaria vaccine clinical projects based on the WHO rainbow table. Malaria Journal. 11:11

Tu PNV. 1994. Dynamical System, An Introduction with Applications in Economics and Biology. New York : Springer-Verlag.

Van Den Driessche P, Watmough J. 2008. Chapter 6: Further Notes on the Basic Reproduction Number. In: Brauer F, Van Den Driessche P, Wu, J.

Mathematical Epidemiology. 1945. Lecture Notes in Mathematics, Springer, pp. 159–178.

24

Lampiran 1 Penentuan titik tetap

Untuk persamaan di bawah ini

ℎ = 1 ; = 2 ; ℎ = 1 ; = 2 ; = ; =

Penentuan titik tetap tanpa penyakit �

25

Nilai _ℎ∗∗, _ℎ∗∗, _ℎ∗∗, ∗∗, dan ∗∗ yang hanya bergantung pada parameter-parameter diberikan sebagai berikut:

ℎ∗∗=

) + (

) _Z

) ((

26

)_Z

) ((

) (

)

) ((

27

)

) ((

) (

ℎ∗∗ =−( ((

) ( -

28

)

) ((+

)

ℎ∗∗ =−(

((

)

)

29

) (

)

∗∗ _{= ((}

) (

30

32

Lampiran 4 Penentuan nilai eigen

Nilai eigen diperoleh dengan cara

| _� − | = 0

Menggunakan konsep Minor-Kofaktor, diperoleh persamaan karakterisitik sebagai berikut Berdasarkan persamaan (1) diperoleh ₁ = ₄₄.

Berdasarkan persamaan (2) diperoleh 2₋ Berdasarkan persamaan (3) diperoleh

33 Lampiran 5 Penentuan bilangan reproduksi dasar

Berdasarkan persamaan (3.2) diperoleh ℎ

Bilangan reproduksi dasar merupakan nilai eigen positif terbesar dari matriks = ��−1.

Sehingga matriks menjadi

= 1 2

Sehingga diperoleh nilai eigen positif terbesar yang merupakan bilangan reproduksi dasar sebagai berikut

0 =

1+ 1 2+ 4 2 3

34

36

37 Lampiran 9 Penurunan persamaan (4.8)

Tinjau persamaan berikut :

1− ℒ � , − � _,0 = ℎ� � , , = 1,2,3,4,5 atau

ℒ � , − � _,0 − ℒ � , − �_,0 =− ℎ� � , Turunan pertama terhadap q dari persamaan diatas adalah

ℒ � , − �_,0 dengan langkah yang sama, turunan ke-n adalah

ℒ � , − �_,0

Untuk q = 0 dan kedua ruas dikalikan dengan 1

38

, � , −1 = 1 ( −1)!

−1_{� � ,} −1

=0

, = 1,2,3,4,5

39 Lampiran 10 Penurunan persamaan (4.9)

43

5,2 � ,1 =

�5( , 0)

− 3

�2( , 0)

�4− 3�2

�4( , 0)

+ �5( , 0)+� �5( , 0)

atau

5,2 � ,1 = �4,1 + 3�2,1 �4,1+ 3�2�4,1 + �5,1 +��5,1  Secara umum, untuk = 1,2,3,…

5, = �5, −1− 3 �4, �2, −1− +

−1

=0

44

Lampiran 11 Program untuk Gambar 9

46

Lampiran 12 Program untuk Gambar 10

47

> dsol := dsolve(sys, numeric, output = listprocedure, range = 0 .. 10):

> graf1:=plot([u_appr(-1,t), dsol1(t)],t=0..15,0..45,color = [red, blue],style=[point,line]):graf1;

> with(plots):

> graf2:=plot([v_appr(-1,t), dsol2(t)],t=0..15,0..2.5, color = [red, blue],style=[point,line]):graf2;

> with(plots):

> graf3:=plot([w_appr(-1,t), dsol3(t)],t=0..15,0..1, color = [red, blue],style=[point,line]):graf3;

> with(plots):

> graf4:=plot([x_appr(-1,t), dsol4(t)],t=0..15,0..500,color = [red, blue],style=[point,line]):graf4;

> with(plots):

> graf5:=plot([z_appr(-1,t), dsol5(t)],t=0..15,0..12,color = [red, blue],style=[point,line]):graf5;

48

RIWAYAT HIDUP

Penulis dilahirkan di Ponorogo tanggal 15 Agustus 1991 sebagai anak pertama dari 2 bersaudara dari pasangan Ranu dan Lestari. Pendidikan formal yang ditempuh penulis yaitu di SDN Ujung Menteng 01 Pagi lulus pada tahun 2003, SMP Negeri 193 Jakarta Timur lulus pada tahun 2006, SMA Negeri 89 Jakarta lulus pada tahun 2009. Penulis menyelesaikan studi S1 di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor (IPB) lulus pada tahun 2013. Penulis juga merupakan mahasiswa program Sinergi IPB 2012-2014 dengan mayor Matematika Terapan, Fakultas Matematika dan Ilmu Pengetahuan Alam, Pascasarjana Institut Pertanian Bogor.

Selama mengikuti perkuliahan penulis juga aktif dalam berbagai kegiatan baik akademik maupun nonakademik, diantaranya: Staf Kesekretariatan Matematika Ria 2011 dan 2012 yang diselenggerakan oleh Fakultas Matematika dan Ilmu Pengetahuan Alam IPB, Ketua Divisi Kesekretariatan IPB Mathematics Challenges 2012 (IMC) yang diselenggarakan oleh Departemen Matematika FMIPA IPB, Ketua Divisi Acara dalam Seminar Kewanitaan 2013 yang diadakan oleh Rohis Matematika angkatan 46 IPB, Peserta Pelatihan software MATLAB dan Mathematica 2012 yang diselenggarakan oleh GUMATIKA (Gugus Mahasiswa Matematika) IPB, Peserta Pelatihan ENTERPRISE (Enterpreunership Practice and Experience) 2010 yang diadakan oleh BEM TPB IPB, Peserta dalam Seminar Dunia Kerja 2012 yang diselenggarakan oleh IPB. Penulis mendapat beasiswa Peningkatan Prestasi Akademik (PPA) periode 2010-2013 dan beasiswa fresh graduate