Kajian pada Rancangan Fractional Factorial dan Fractional Factorial Split-Plot

KAJIAN PADA RANCANGAN

FRACTIONAL FACTORIAL

DAN

FRACTIONAL FACTORIAL SPLIT-PLOT

SRI WINARNI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

SURAT PERNYATAAN

Dengan ini saya menyatakan bahwa tesis yang berjudul : Kajian pada

Rancangan Fractional Factorial dan Fractional Factorial Split-Plot adalah benar merupakan hasil karya sendiri dan belum dipublikasikan. Semua sumber data dan

informasi telah dinyatakan dengan jelas dan dapat diperiksa kebenarannya.

Bogor, Agustus 2006

ABSTRAK

SRI WINARNI. Kajian pada Rancangan Fractional Factorial dan Fractional FactorialSplit-Plot. Dibimbing oleh BUDI SUSETYO dan BAGUS SARTONO

Rancangan faktorial lengkap yang mencobakan banyak faktor dengan ulangan tunggal membutuhkan satuan percobaan yang homogen sejumlah kombinasi perlakuan lengkapnya. Biaya yang besar untuk menyediakan satuan percob aan dan kesulitan dalam interpretasi hasil untuk pengaruh interaksi tingkat tinggi membuat rancangan ini sangat mahal untuk dilakukan. Rancangan Fractional factorial (FF) merupakan solusi bagi masalah tersebut. Jika teknik pengacakan lengkap sulit untuk dilakukan pada rancangan FF maka rancangan Fractional Factorial Split-Plot (FFSP) dapat digunakan.

Pembentukan struktur rancangan FF dan FFSP dapat dilakukan dengan menentukan banyaknya faktor yang akan dicobakan dan fraksi percobaan, struktur generator, defining relation, alias dan resolusi. Pemilihan struktur rancangan ditentukan oleh kriteria resolusi maksimum dan minimum aberration atau dengan menggunakan kriteria mampu menduga pengaruh faktor tertentu. Proses pembentukan struktur rancangan dan teknik analisis dapat dilakukan dengan mudah menggunakan perangkat lunak yang tersedia.

© Hak cipta milik Institut Pertanian Bogor, tahun 2006

Hak cipta dilindungi

KAJIAN PADA RANCANGAN

FRACTIONAL FACTORIAL

DAN

FRACTIONAL FACTORIAL SPLIT-PLOT

SRI WINARNI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Statistika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

Judul Tesis : Kajian pada Rancangan Fractional Factorial dan Fractional Factorial Split-Plot

Nama : Sri Winarni

NRP : G151020191

Program Studi : Statistika

Disetujui

Komisi Pembimbing

Diketahui

Tanggal lulus : 2 September 2006 Dr. Ir. Budi Susetyo, MS

Ketua

Bagus Sartono , M.Si Anggota

Ketua Program Studi Statistika

Dr. Ir. Aji Hamim Wigena, MSc

Dekan Sekolah Pascasarjana

RIWAYAT HIDUP

Penulis dilahirkan sebagai anak kedua dari pasangan Muryono dan Sri

Kamilah di Metro pada tanggal 4 Mei 1979. sebelum menjalani pendidikan

pascasarjana di program magister pada tahun 2002, penulis menjalani pendidikan

PRAKATA

Penghargaan yang setinggi-tingginya penulis sampaikan kepada Dr. Ir.

Budi Susetyo, MS. dan Bagus Sartono, Msi. selaku komisi pembimbing. Ucapan

terima kasih juga penulis sampaikan kepada rekan-rekan Statistika 2002 dan EPN

2004, keluarga Bagunde 12B, keluarga M20, dan sahabat-sahabat atas diskusi dan

semangat yang diberikan.

Karya ini penulis persembahkan kepada bapak dan mamak tercinta,

Luqman, Apri, Yayu’ Wati, Mas Nung dan Atha tersayang atas curahan kasih

sayang dan perhatiannya, baiti jannati.

Bogor, Agustus 2006

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... ix

DAFTAR LAMPIRAN ... x

PENDAHULUAN... 1

TINJAUAN PUSTAKA ... 4

Rancangan Fractional Factorial (FF) ... 4

Rancangan Fractional Factorial Split-Plot (FFSP) ... 9

Plot Kwantil Half-Normal ... 13

Analisis Regresi dengan Metode Forward Selection ... 16

Analisis Ragam pada Rancangan FF dan FFSP ... 17

BAHAN DAN METODE ... 20

HASIL ... ... 21

Penggunaan Rancangan FF dan FFSP ... 21

Teknik Pembentukan dan Pemilihan Struktur Rancangan ... 25

Teknik Analisis Data ... 40

Contoh Kasus untuk Percobaan dengan Rancangan FF ... 42

Contoh Kasus untuk Percobaan dengan Rancangan FFSP ... 47

SIMPULAN ... 52

DAFTAR PUSTAKA ... 53

DAFTAR TABEL

Halaman

1. Matriks rancangan 25V1

−

dengan defining relation I = ABCDE ... 5

2. Resolusi dan maknanya... 7

3. Tiga alternatif rancangan 7 2 IV 2− dengan defining relation berbeda ... 8

4. Karakteristik dua jenis proses pembauran pada rancangan FFSP ... 10

5. Generator untuk rancangan 25−2 ... 29

6. Generator pilihan untuk rancangan 25−2 ... 30

7. Struktur rancangan ₂5−2 _{yang dapat dibentuk dengan resolusi maksimum. 31} 8. Struktur rancangan 25−2 isomorphic... 33

9. Struktur rancangan 25−2 dengan generator D=AB dan E=AC... 32

10. Struktur rancangan 25−2 dengan generator D= AC; E=ABC ... 33

11. Matriks rancangan 25−2 dengan generator D=ABdan E=AC... 34

12. Matriks rancangan 25−2 dengan generator D=AC dan E=ABC ... 34

13. Generator rancangan 2(2+3)−(0+2)... 36

14. Generator pilihan untuk rancangan 2(2+3)−(0+2)... 36

15. Struktur rancangan MA 2(2+3)−(0+2) ... 37

16. Struktur rancangan MA ₂(2+3)−(0+2) _{isomorphic... 37}

17. Generator rancangan 2(2+3)−(1+1)... 38

18. Matriks rancangan 2(2+3)−(0+2) dengan generator Q=AP ;R=BP ... 38

19. Faktor dan taraf yang digunakan pada contoh kasus rancangan FF... 42

20. Data percobaan pada contoh kasus rancangan FF... 42

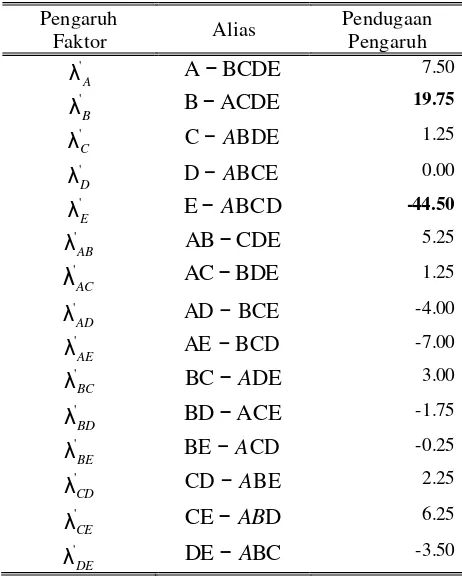
21. Struktur alias dan pendugaan pengaruh pada kasus rancangan FF ... 43

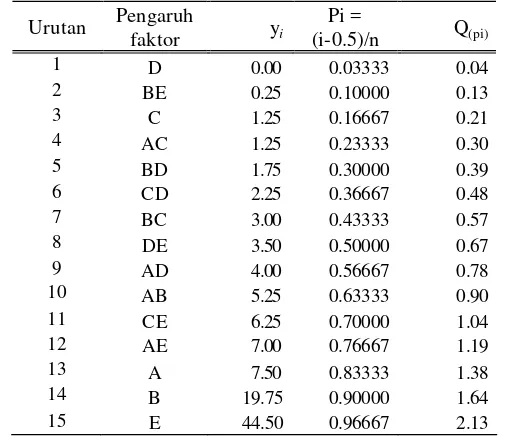
22. Nilai kwantil half-normal pada contoh kasus rancangan FF... 44

23. Tabel analisis ragam untuk contoh kasus rancangan FF... 46

24. Faktor dan taraf yang digunakan pada contoh kasus rancangan FFSP ... 47

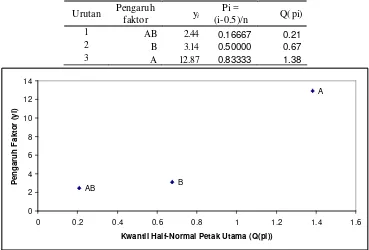
25. Nilai kwantil half-normal petak utama pada contoh kasus FFSP ... 48

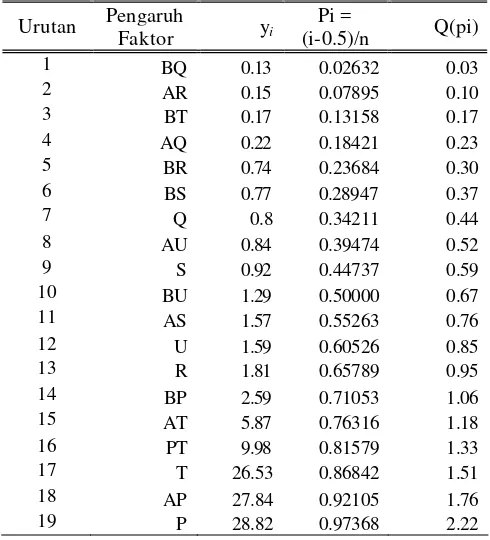
26. Nilai kwantil half-normal anak petak pada contoh kasus FFSP... 49

KAJIAN PADA RANCANGAN

FRACTIONAL FACTORIAL

DAN

FRACTIONAL FACTORIAL SPLIT-PLOT

SRI WINARNI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

SURAT PERNYATAAN

Dengan ini saya menyatakan bahwa tesis yang berjudul : Kajian pada

Rancangan Fractional Factorial dan Fractional Factorial Split-Plot adalah benar merupakan hasil karya sendiri dan belum dipublikasikan. Semua sumber data dan

informasi telah dinyatakan dengan jelas dan dapat diperiksa kebenarannya.

Bogor, Agustus 2006

ABSTRAK

SRI WINARNI. Kajian pada Rancangan Fractional Factorial dan Fractional FactorialSplit-Plot. Dibimbing oleh BUDI SUSETYO dan BAGUS SARTONO

Rancangan faktorial lengkap yang mencobakan banyak faktor dengan ulangan tunggal membutuhkan satuan percobaan yang homogen sejumlah kombinasi perlakuan lengkapnya. Biaya yang besar untuk menyediakan satuan percob aan dan kesulitan dalam interpretasi hasil untuk pengaruh interaksi tingkat tinggi membuat rancangan ini sangat mahal untuk dilakukan. Rancangan Fractional factorial (FF) merupakan solusi bagi masalah tersebut. Jika teknik pengacakan lengkap sulit untuk dilakukan pada rancangan FF maka rancangan Fractional Factorial Split-Plot (FFSP) dapat digunakan.

Pembentukan struktur rancangan FF dan FFSP dapat dilakukan dengan menentukan banyaknya faktor yang akan dicobakan dan fraksi percobaan, struktur generator, defining relation, alias dan resolusi. Pemilihan struktur rancangan ditentukan oleh kriteria resolusi maksimum dan minimum aberration atau dengan menggunakan kriteria mampu menduga pengaruh faktor tertentu. Proses pembentukan struktur rancangan dan teknik analisis dapat dilakukan dengan mudah menggunakan perangkat lunak yang tersedia.

© Hak cipta milik Institut Pertanian Bogor, tahun 2006

Hak cipta dilindungi

KAJIAN PADA RANCANGAN

FRACTIONAL FACTORIAL

DAN

FRACTIONAL FACTORIAL SPLIT-PLOT

SRI WINARNI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Statistika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

Judul Tesis : Kajian pada Rancangan Fractional Factorial dan Fractional Factorial Split-Plot

Nama : Sri Winarni

NRP : G151020191

Program Studi : Statistika

Disetujui

Komisi Pembimbing

Diketahui

Tanggal lulus : 2 September 2006 Dr. Ir. Budi Susetyo, MS

Ketua

Bagus Sartono , M.Si Anggota

Ketua Program Studi Statistika

Dr. Ir. Aji Hamim Wigena, MSc

Dekan Sekolah Pascasarjana

RIWAYAT HIDUP

Penulis dilahirkan sebagai anak kedua dari pasangan Muryono dan Sri

Kamilah di Metro pada tanggal 4 Mei 1979. sebelum menjalani pendidikan

pascasarjana di program magister pada tahun 2002, penulis menjalani pendidikan

PRAKATA

Penghargaan yang setinggi-tingginya penulis sampaikan kepada Dr. Ir.

Budi Susetyo, MS. dan Bagus Sartono, Msi. selaku komisi pembimbing. Ucapan

terima kasih juga penulis sampaikan kepada rekan-rekan Statistika 2002 dan EPN

2004, keluarga Bagunde 12B, keluarga M20, dan sahabat-sahabat atas diskusi dan

semangat yang diberikan.

Karya ini penulis persembahkan kepada bapak dan mamak tercinta,

Luqman, Apri, Yayu’ Wati, Mas Nung dan Atha tersayang atas curahan kasih

sayang dan perhatiannya, baiti jannati.

Bogor, Agustus 2006

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... ix

DAFTAR LAMPIRAN ... x

PENDAHULUAN... 1

TINJAUAN PUSTAKA ... 4

Rancangan Fractional Factorial (FF) ... 4

Rancangan Fractional Factorial Split-Plot (FFSP) ... 9

Plot Kwantil Half-Normal ... 13

Analisis Regresi dengan Metode Forward Selection ... 16

Analisis Ragam pada Rancangan FF dan FFSP ... 17

BAHAN DAN METODE ... 20

HASIL ... ... 21

Penggunaan Rancangan FF dan FFSP ... 21

Teknik Pembentukan dan Pemilihan Struktur Rancangan ... 25

Teknik Analisis Data ... 40

Contoh Kasus untuk Percobaan dengan Rancangan FF ... 42

Contoh Kasus untuk Percobaan dengan Rancangan FFSP ... 47

SIMPULAN ... 52

DAFTAR PUSTAKA ... 53

DAFTAR TABEL

Halaman

1. Matriks rancangan 25V1

−

dengan defining relation I = ABCDE ... 5

2. Resolusi dan maknanya... 7

3. Tiga alternatif rancangan 7 2 IV 2− dengan defining relation berbeda ... 8

4. Karakteristik dua jenis proses pembauran pada rancangan FFSP ... 10

5. Generator untuk rancangan 25−2 ... 29

6. Generator pilihan untuk rancangan 25−2 ... 30

7. Struktur rancangan ₂5−2 _{yang dapat dibentuk dengan resolusi maksimum. 31} 8. Struktur rancangan 25−2 isomorphic... 33

9. Struktur rancangan 25−2 dengan generator D=AB dan E=AC... 32

10. Struktur rancangan 25−2 dengan generator D= AC; E=ABC ... 33

11. Matriks rancangan 25−2 dengan generator D=ABdan E=AC... 34

12. Matriks rancangan 25−2 dengan generator D=AC dan E=ABC ... 34

13. Generator rancangan 2(2+3)−(0+2)... 36

14. Generator pilihan untuk rancangan 2(2+3)−(0+2)... 36

15. Struktur rancangan MA 2(2+3)−(0+2) ... 37

16. Struktur rancangan MA ₂(2+3)−(0+2) _{isomorphic... 37}

17. Generator rancangan 2(2+3)−(1+1)... 38

18. Matriks rancangan 2(2+3)−(0+2) dengan generator Q=AP ;R=BP ... 38

19. Faktor dan taraf yang digunakan pada contoh kasus rancangan FF... 42

20. Data percobaan pada contoh kasus rancangan FF... 42

21. Struktur alias dan pendugaan pengaruh pada kasus rancangan FF ... 43

22. Nilai kwantil half-normal pada contoh kasus rancangan FF... 44

23. Tabel analisis ragam untuk contoh kasus rancangan FF... 46

24. Faktor dan taraf yang digunakan pada contoh kasus rancangan FFSP ... 47

25. Nilai kwantil half-normal petak utama pada contoh kasus FFSP ... 48

26. Nilai kwantil half-normal anak petak pada contoh kasus FFSP... 49

DAFTAR GAMBAR

Halaman

1. Proses pembentukan struktur rancangan ... 28

2. Struktur pengacakan untuk rancangan 25−2... 34

3. Struktur pengacakan rancangan 2(2+3)−(0+2) dengan generator Q=AP ;R =BP ... 39

4. Plot kwantil half-normal untuk contoh kasus rancangan FF... 45

5. Proses penghalusan lapisan emas pada contoh kasus rancangan FFSP ... 47

6. Plot kwantil half-normal petak utama pada contoh kasus FFSP... 48

7. Plot kwantil half-normal anak petak untuk contoh kasus FFSP ... 49

DAFTAR LAMPIRAN

Halaman 1. Alias interaksi dua faktor untuk tiga rancangan 2IV7-2 ... 54

2. Struktur pembentukan rancangan FF 25−22 ... 55

3. Penggunaan SAS 9.1 untuk pembentukan struktur rancangan FF... 58

4. Penggunaan ADX SAS 9.1 untuk Pengacakan Rancangan FF... 62

5. Pembentukan struktur rancangan FFSP 2(2+3)−(0+2)... 63

6. Penggunaan SAS 9.1 untuk pembentukan struktur rancangan FFSP... 65

7. Penggunaan SAS 9.1 untuk pembentukan pengacakan struktur rancangan FFSP ... 68

8. Hasil analisis regresi dengan metode forward selection untuk percobaan pada contoh kasus rancangan FF... 69

9. Data percobaan pada contoh kasus rancangan FFSP ... 70

10. Struktur aliases untuk rancangan pada contoh kasus FFSP... 71

PENDAHULUAN

Pada perancangan percobaan dengan rancangan faktorial lengkap, jumlah

kombinasi perlakuan terus meningkat seiring dengan meningkatnya jumlah faktor

yang digunakan. Jika biaya yang dibutuhkan untuk menggunakan faktor-faktor

tersebut sangat besar, maka menambah jumlah faktor berarti juga menambah

biaya yang diperlukan dan hal ini tentu sangat tidak diharapkan. Selain itu,

kadangkala ditemui kesulitan dalam menginterpretasikan pengaruh interaksi

tingkat tinggi pada rancangan faktorial lengkap dengan banyak faktor. Rancangan

fractional factorial (FF) merupakan salah satu solusi untuk mengatasi masalah-masalah tersebut (Box & Hunter 1961).

Rancangan FF merupakan rancangan yang hanya melakukan sebagian dari

kombinasi perlakuan lengkap. Penerapan rancangan FF dapat menghilangkan

informasi tentang pengaruh interaksi tingkat tinggi, tetapi tidak menghilangkan

informasi tentang pengaruh faktor utama dan interaksi tingkat rendah yang

merupakan informasi penting dalam percobaan (Gomes & Gomes 1995).

Masalah yang dihadapi dalam rancangan FF adalah bagaimana memilih

sebagian dari kombinasi perlakuan lengkap yang akan dicobakan tetapi tetap

mendapatkan informasi penting yang diperlukan (Musa 1999). Pembentukan

struktur rancangan FF ditentukan oleh banyaknya faktor dan kombinasi perlakuan

yang dicobakan. Dengan jumlah faktor tertentu, dapat dibentuk beberapa struktur

rancangan FF yang berbeda. Perbedaan struktur rancangan tersebut ditentukan

oleh struktur generator, defining relation, alias, dan resolusi yang d igunakan. Pemilihan struktur rancangan terbaik dilakukan dengan kriteria resolusi

maksimum dan minimum-aberration (Fries & Hunter 1980). Pemilihan rancangan juga dapat ditentukan oleh pengaruh faktor tertentu atau pengaruh

interaksi faktor tertentu yang ingin diduga.

Kombinasi perlakuan yang digunakan pada rancangan FF ditempatkan

secara acak lengkap pada unit percobaan yang digunakan. Pengacakan lengkap

pada rancangan FF tersebut kadangkala sulit dilakukan. Dua hal yang membuat

1. Ada kendala teknis di lapang. Kendala teknis tersebut muncul ketika ada

faktor yang sulit untuk diubah pengaturan tarafnya berulang kali pada setiap

unit percobaan yang digunakan.

Contoh : Faktor suhu pemanasan. Tidak mudah untuk memberikan taraf suhu

yang berbeda dari unit percobaan yang satu ke unit percobaan yang

lain. Lebih mudah jika unit-unit percobaan yang mendapat taraf

suhu yang sama di kumpulkan, kemudian diberikan taraf suhu

tertentu secara bersamaan (Kulahci et al. 2006).

2. Secara teknis tidak ada masalah untuk melakukan pengacakan lengkap , tetapi

mengubah taraf faktor tertentu dari unit percobaan satu ke unit percobaan yang

lain dikhawatirkan akan mengganggu pengaruh dari faktor yang dicobakan.

Contoh : Faktor pemberian air. Jika dilakukan pengacakan lengkap ,

dikhawatirkan air yang diberikan pada beberapa unit percobaan

akan mengalir pada unit percobaan di sekitarnya yang seharusnya

tidak mendapat pemberian air. Akan lebih aman jika unit-unit

percobaan yang diberi air di p isah dengan unit -unit percobaan yang

tidak diberi air .

Rancangan fractional factorial split-plot (FFSP) merupakan solusi yang tepat digunakan untuk melakukan percobaan dengan kondisi tersebut di atas.

Pada rancangan FFSP terdapat petak utama dan anak petak. Faktor yang

sulit untuk diubah pengaturan tarafnya ditempatkan sebagai faktor petak utama

dan faktor lainnya ditempatkan sebagai faktor anak petak. Petak utama merupakan

kombinasi taraf dari faktor-faktor petak utama yang digunakan dan anak petak

merupakan kombinasi taraf dari faktor-faktor anak petak (Bingham & Sitter

2001).

Rancangan FF dan FFSP sangat berguna dalam proses penyeleksian faktor

(screening experiment), yaitu percobaan yang melibatkan banyak faktor dan bertujuan untuk mengidentifikasi faktor-faktor yang memiliki pengaruh besar.

Percobaan dilakukan dengan dua taraf, yaitu taraf tinggi (1) dan taraf rendah (-1).

Faktor-faktor yang teridentifikasi memiliki pengaruh besar akan diinvestigasi

Analisis yang digunakan dalam rancangan FF dan FFSP berupa

pendekatan analisis secara visual menggunakan plot kuantil half-normal yang kemudian dilanjutkan dengan analisis ragam (Box et al. 1978, Montgomery 2001). Pendekatan analisis regresi dengan metode forward selection (seleksi maju) juga dapat digunakan untuk penyeleksian pengaruh faktor.

Masalah umum yang dihadapi pada rancangan FF dan FFSP adalah teknik

pembentukan struktur rancangan yang relatif rumit dan ketersediaan perangkat

lunak yang langka untuk melakukan pembentukan struktur rancangan sekaligus

analisis data. Dengan pertimbangan sulitnya mendapatkan data sekunder dari

kasus riil dan tidak memungkinkan untuk melakukan percobaan, maka penelitian

ini lebih mengarah kepada kajian teori dan pustaka.

Tujuan penelitian ini adalah melakukan kajian teori terhadap dua jenis

rancangan percobaan , yaitu rancangan FF dan rancangan FFSP. Kajian teori

dilakukan terhadap proses pembentukan struktur rancangan dan teknik analisis

TINJAUAN PUSTAKA

Rancangan Fractional Factorial (FF)

Rancangan FF dengan dua taraf yang dinotasikan dengan 2n−p merupakan rancangan yang mencobakan hanya 2n−p kombinasi perlakuan dari selu ruh 2n

kombinasi perlakuan lengkap . Seberapa besar proporsi total kombinasi perlakuan

yang akan dicobakan dalam rancangan FF disebut dengan fraksi percobaan (Box

& Hunter 1961). Fraksi percobaan yang sering digunakan adalah :

Ø Fraksi setengah , mencobakan hanya setengah bagian dari kombinasi

perlakuan lengkap. Bentuk rancangan dari percobaan setengah fraksi ini

adalah 2n−1.

Contoh : percobaan ₂5−1 _{melakukan 16 kombinasi perlakuan dari 32}

kombinasi perlakuan lengkap.

Ø Fraksi seperempat, percobaan fraksi seperempat mencobakan hanya seperempat bagian dari kombinasi perlakuan lengkap dan bentuk

rancangan nya adalah 2n−2.

Contoh : percobaan 25−2 melakukan 8 dari 32 kombinasi perlakuan lengkap.

Secara umum percobaan FF dengan fraksi 1 2p mencobakan 1 2p bagian dari

jumlah kombinasi perlakuan lengkap . Bentuk umum dari rancangan ini adalah

p n−

2 . Penentuan fraksi percobaan yang digunakan harus menyeimbangkan antara

informasi yang ingin diperoleh dengan biaya yang tersedia (Hines & Montgomery

1996).

Struktur rancangan FF ditentukan oleh banyaknya faktor yang dicobakan

dan fraksi percobaan yang digunakan. Dengan jumlah faktor dan fraksi tertentu,

dapat dibentuk beberapa struktur rancangan FF yang berbeda. Perbedaan struktur

rancangan tersebut ditentukan oleh struktur generator, defining relation,alias, dan resolusi yang digunakan.

Sebuah ilustrasi rancangan FF yang mencobakan 5 faktor dengan fraksi

Ilustrasi : Sebuah percobaan fraksi setengah yang mencobakan 5 faktor (A, B, C,

D, dan E) masing-masing dengan dua taraf yaitu taraf tinggi (1) dan

taraf rendah (-1) dilakukan dengan 16 kombinasi perlakuan. Defining relation yang digunakan adalah I=ABCDE. Struktur rancangan dengan I=ABCDE pada ilustrasi ini merupakan salah satu dari

beberapa struktu r rancangan yang dapat dibentuk, matriks rancangan

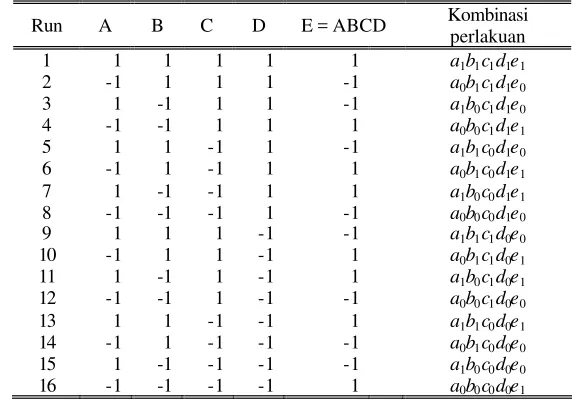
pada ilustrasi ini seperti pada Tabel 1.

.

Tabel 1. Matriks rancangan 25V1

−

dengan defining relation I=ABCDE

Run A B C D E = ABCD Kombinasi perlakuan 1 1 1 1 1 1 a1b1c1d1e1

2 -1 1 1 1 -1 a0b1c1d1e0

3 1 -1 1 1 -1 a1b0c1d1e0

4 -1 -1 1 1 1 a0b0c1d1e1

5 1 1 -1 1 -1 a1b1c0d1e0

6 -1 1 -1 1 1 a0b1c0d1e1

7 1 -1 -1 1 1 a1b0c0d1e1

8 -1 -1 -1 1 -1 a0b0c0d1e0

9 1 1 1 -1 -1 a1b1c1d0e0

10 -1 1 1 -1 1 a0b1c1d0e1

11 1 -1 1 -1 1 a1b0c1d0e1

12 -1 -1 1 -1 -1 a0b0c1d0e0

13 1 1 -1 -1 1 a1b1c0d0e1

14 -1 1 -1 -1 -1 a0b1c0d0e0

15 1 -1 -1 -1 -1 a1b0c0d0e0

16 -1 -1 -1 -1 1 a0b0c0d0e1

Taraf faktor E ditentukan oleh kombinasi taraf dari faktor A, B, C, dan D

melalui persamaan E=ABCD. Jika kedua ruas dikalikan dengan E akan didapat

persamaan :

ABCDE

E2 = menjadi I=ABCDE

Hubungan I=ABCDE disebut dengan defining relation dan interaksi ABCDE disebut sebagai generator. Cochran (1957) meny ebut defining relation dengan defining contrast. Jika terdapat lebih dari satu defining relation yang digunakan, misalnya pada rancangan dengan fraksi seperempat yang menggunakan dua

relation yang bertanda negatif. Struktur generator dan defining relation menentukan struktur alias yang berkaitan dengan pengaruh faktor yang dianalisis.

Alias merupakan hubungan pendugaan pengaruh yang saling terpaut

(confounded), hubungan tersebut didapatkan dari generalized interaction yang merupakan perkalian antara pengaruh faktor dengan defining relation yang digunakan. Pada ilustrasi diatas, dari defining relation yang digunakan

ABCDE

I= dapat ditentukan hubungan alias pengaruh faktor tertentu. Sebagai

contoh, generalized interaction pengaruh utama faktor A dengan defining relation sebagai berikut :

ABCDE

I= ; kedua ruas dikali dengan A

BCDE A

IA= 2 ; menjadi A =BCDE

Dengan demikian, pengaruh utama faktor A terpaut dengan pengaruh interaksi

BCDE. Begitu juga dengan pengaruh interaksi AB yang terpaut dengan pengaruh

interaksi CDE. Hubungan alias pengaruh yang lain dapat diperoleh dengan cara

yang sama.

Hubungan alias A =BCDE menunjukkan bahwa kombinasi pengaruh

perlakuan yang digunakan untuk menduga pengaruh utama faktor A sama dengan

kombinasi pengaruh perlakuan yang digunakan untuk menduga pengaruh interaksi

faktor BCDE. Menduga pengaruh utama A sebenarnya adalah menduga pengaruh faktor A+BCDE. Pengaruh utama faktor A tidak dapat diduga kecuali jika

pengaruh interaksi faktor BCDE dianggap bernilai nol atau diabaikan. Sama halnya dengan pengaruh interaksi faktor AB yang tidak dapat diduga kecuali

pengaruh interaksi faktor CDEdiabaikan.

Rancangan 2n-p memiliki p generator bebas yang membentuk defining relation. Struktur generator yang berbeda akan menghasilkan struktur alias yang berbeda, hal ini akan berpengaruh pada struktur pengaruh faktor tertentu yang

Sebuah rancangan dikatakan memiliki resolusi R jika tidak ada pengaruh i faktor yang ber-alias dengan pengaruh lain yang mengandung kurang dari R-i faktor (Box et al. 1978). Beberapa resolusi yang biasa digunakan dapat dilihat pada Tabel 2.

Tabel 2. Resolusi dan maknanya

Resolusi Keterangan

Resolusi III Pengaruh faktor utama tidak ber-alias dengan pengaruh faktor utama tetapi ber-alias dengan pengaruh interaksi dua faktor dan yang lebih tinggi.

Resolusi IV Pengaruh interaksi dua faktor tidak ber-alias dengan pengaruh faktor utama tetapi ber-alias dengan pengaruh interaksi dua faktor dan yang lebih tinggi .

Resolusi V Pengaruh interaksi dua faktor tidak ber-alias dengan pengaruh utama dan pengaruh interaksi dua faktor, tetapi ber-alias dengan interaksi tiga faktor dan yang lebih tinggi .

Secara umum resolusi dari rancangan FF sama dengan jumlah huruf terkecil pada

defining relation yang digunakan. Pada contoh sebelumnya, rancangan 25−1

dengan defining relation I=ABCDE memiliki resolusi V.

Pemilihan tingkat resolusi tergantung pada interaksi tingkat berapa yang

akan diabaikan dan tergantung dari banyaknya generator yang digunakan (p). Menurut Fries & Hunter (1980), tingkat resolusi maksimum yang dapat dicapai

untuk p =1 dan p =2 adalah sebagai berikut: • Untuk p=1 maka resolusi maksimum = n • Untuk p=2 maka resolusi maksimum = [2n/3]

Dengan n adalah banyaknya faktor yang dicobakan dan [x] adalah nilai bilangan bulat terbesar yang lebih besar dari x.

Kriteria resolusi tertinggi kadangkala tidak cukup karena beberapa

rancangan berbeda dapat memiliki resolusi yang sama. Sebagai contoh, pada

rancangan 27_IV−2 yang menggunakan 7 faktor, 2 generator dan memiliki resolusi IV terdapat tiga alternatif rancangan dengan generator yang berbeda. Ketiga alternatif

Tabel 3. Tiga alternatif rancangan 27_IV−2 dengan defining relation berbeda.

Kode Generator Defining relation

(D1) F=ABC dan G=BCD I=ABCF=BCDG =ADFG

(D2) F=ABC dan G=ADE I=ABCF =ADEG = BCDEFG

(D3) F=ABCD dan G=ABDE I=ABCDF=ABDEG =CEFG

Panjang huruf terkecil dari ketiga defining relation adalah 4, dengan begitu ketiga rancangan tersebut sama-sama memiliki resolusi IV. Pola panjang huruf

dari defining relation disebut dengan Word Length Pattern (WLP). WLP untuk rancangan D₁={4,4,4}, rancangan D₂={4,4,6}, dan rancangan D₃ ={4,5,5}.

Rancangan D1 memiliki panjang huruf 4 sebanyak 3, rancangan D2 sebanyak 2

dan rancangan D3 hanya 1. Rancangan D3 memiliki panjang huruf terkecil

minimum, dan dikatakan rancangan D3 merupakan rancangan yang memiliki minimum-aberration. Rancangan minimum -aberration (MA) adalah rancangan yang meminimalkan banyaknya kata dalam defin ing relation yang panjangnya minimum (Fries & Hunter 1980).

Rancangan minimum aberration meminimalkan banyaknya interaksi tingkat rendah (dua faktor) yang saling ber -confounded. Pada ilustrasi tiga rancangan di atas, rancangan D1 menyebabkan 15 pasang interaksi dua faktor

saling ber -confounded, rancangan D2 12 pasang, dan rancangan D3 hanya 6

pasang, hal ini dapat dilihat pada Lampiran 1.

Rancangan FF yang memenuhi kriteria resolusi maksimum dan minimum aberration dipilih sebagai rancangan terbaik. Pemilihan rancangan terbaik kadangkala tidak hanya didasarkan pada kriteria di atas, jika diinginkan untuk

mengetahui pengaruh faktor tertentu yang spesifik, maka pemilihan rancangan

dilakukan berdasarkan kemampuan rancangan untuk menduga pengaruh spesifik

Rancangan Fractional Factori al Split-Plot (FFSP)

Huang et al. (1998) menotasikan rancangan FFSP dua taraf dengan

) ( )

( 1 2 1 2

2 n+n − p+p _{. Rancangan ini dibentuk dengan mengkombinasikan rancangan}

petak utama (₂n1−p1_{) yang memiliki n}

1 faktor dan p1 generator dengan rancangan

anak petak (₂n2−p2_{) yang memiliki n}

2 faktor dan p2 generator. Ada 21 1

p n−

kombinasi perlakuan yang dilakukan pada rancangan petak utama, sedangkan

pada rancangan anak petak ada sebanyak ₂(n1+n2)−(p1+p2) _{kombinasi perlakuan yang}

dilakukan.

Pembentukan generator dalam rancangan FFSP dilakukan dengan

memperhatikan dua hal, yaitu : (Bingham & Sitter 1999).

1. Generator anak petak boleh mengandung beberapa faktor petak utama.

2. Generator petak utama harus bebas dari faktor anak petak dan generator

anak petak harus mengandung sedikitnya dua faktor anak petak .

Jika generator petak utama mengandung faktor anak petak maka sama halnya

dengan melibatkan taraf faktor anak petak ke dalam penentuan taraf faktor petak

utama. Sama dengan apa yang berlaku pada rancangan FF, generator yang

dibentuk akan menentukan defining relation yang digunakan. Defining relation pada rancangan FFSP disebut dengan defining contrast subgroup (DCS).

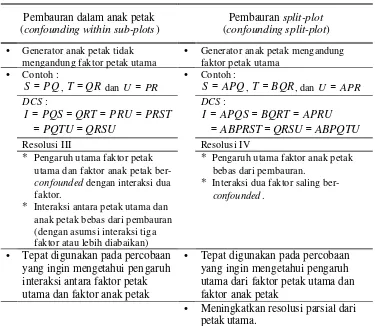
Nembehard et al. (2006) menjelaskan bahwa ada dua kemungkinan proses pembauran yang dapat terjadi pada rancangan FFSP, yaitu : pembauran dalam

anak petak (confounding within sub -plots) dan pembauran split-plot (confounding split-plot). Penggunaan dari pembauran dalam anak petak dan pembauran split-plot tergantung tujuan dari percobaan yang dilakukan. Pembauran dalam anak petak lebih mampu untuk menduga pengaruh interaksi antara faktor petak utama

dan faktor anak petak, sedangkan pembauran split -plot lebih mampu untuk menduga pengaruh utama faktor petak utama dan pengaruh utama faktor anaka

petak. Ilustrasi rancangan yang digunakan adalah sebuah rancangan FFSP dengan A

dan B sebagai faktor petak utama dan P, Q, R, S, T, U sebagai faktor anak petak.

[image:31.612.133.508.97.423.2]

Tabel 4. Karakteristik dua jenis proses pembauran pada rancangan FFSP

Pembauran dalam anak petak (confounding within sub-plots)

Pembauran split-plot (confounding split-plot) • Generator anak petak tidak

mengandung faktor petak utama

• Generator anak petak mengandung faktor petak utama

• Contoh :

PQ

S = , T =QR dan U = PR

• Contoh :

APQ

S = , T =BQR, dan U = APR

DCS :

PRST PRU

QRT PQS

I = = = =

=PQTU=QRSU

DCS :

APRU BQRT

APQS

I = = =

=ABPRST=QRSU=ABPQTU

Resolusi III Resolusi IV

* Pengaruh utama faktor petak utama dan faktor anak petak ber-confounded dengan interaksi dua faktor.

* Interaksi antara petak utama dan anak petak bebas dari pembauran (dengan asumsi interaksi tiga faktor atau lebih diabaikan)

* Pengaruh utama faktor anak petak bebas dari pembauran.

* Interaksi dua faktor saling ber-confounded.

• Tepat digunakan pada percobaan yang ingin mengetahui pen garuh interaksi antara faktor petak utama dan faktor anak petak

• Tepat digunakan pada percobaan yang ingin mengetahui pengaruh utama dari faktor petak utama dan faktor anak petak

• Meningkatkan resolusi parsial dari petak utama.

Generator dibangun dari beberapa huruf (letter) yang membentuk satu kata (word). Banyaknya kata yang memiliki panjang i dapat dituliskan dalam suatu pola yang disebut dengan word length pattern .

Misal Ai(D) merupakan banyaknya kata yang panjangnya i, yang

didefinisikan d alam defining contrast subgroup rancangan D, dan misal :

(

( ), ( ), ( ),..., ( )

)

2 1 5

4

3 D A D A D A D

A

WLP= _n+n

adalah word length pattern (panjang kata 1 dan 2 tidak digunakan). A3(D)

merupakan banyaknya kata dalam defining contrast subgroup rancangan D yang panjangnya 3 huruf, A4(D) dengan panjang 4 huruf, A5(D) dengan panjang 5

huruf, dan seterusnya sampai ( )

2

1 D

Resolusi merupakan panjang kata terpendek yang didefinisikan dalam

defining contrast subgroup. Sebagai contoh rancangan 2(5+3)−(1+1) dengan huruf kapital A, B, C, D dan E merupakan faktor-faktor petak utama dan huruf kecil p, q, r adalah faktor-faktor anak petak. Defining contrast subgroup yang dibentuk :

ABCDEpqr ABCDE

pqr

I = = =

memiliki WLP=(1,0,1,0,0,1)dan memiliki resolusi tingkat III karena panjang kata

terpendek adalah 3 (Bingham & Sitter 2001).

Sebuah rancangan FFSP ₂(n1+n2)−(p1+p2)

dikatakan memiliki resolusi

maksimum jika tidak ada rancangan FFSP lain ₂(n1+n2)−(p1+p2) _{yang memiliki}

resolusi lebih besar. Rancangan dengan resolusi yang sama bisa memiliki WLP yang berbeda. Dalam kondisi demikian, Fries & Hunter (1980) memperkenalkan

minimum-aberration sebagai kriteria untuk pemilihan rancangan terbaik.

Pertanyaan yang kemudian muncul adalah, yang mana dari banyak

kemungkinan rancangan FFSP yang sebaiknya digunakan? Penentuan ini

mempertimbangkan seberapa banyak unit percobaan yang digunakan, dan

faktor-faktor mana saja yang masuk sebagai petak utama dan faktor-faktor-faktor-faktor mana yang

masuk sebagai anak petak. Kebutuhan untuk mendapatkan informasi yang luas

harus diimbangi keinginan untuk mereduksi biaya percobaan. Bingham & Sitter

(2001) memberikan beberapa petunjuk yang bisa digunakan untuk melakukan

rancangan FFSP :

1. Menempatkan hard-to-change factors sebagai faktor petak utama dan menempatkan faktor-faktor sisanya sebagai faktor anak petak.

2. Memilih WLP terbaik, pada umumnya yaitu WLP yang menghasilkan resolusi tertinggi. Misalkan ada dua rancangan FFSP, yaitu :

BCpqr Apqr

ABC I

D1: = = =

BCqr ACpr

ABpq I

D₂ : = = =

) 0 , 1 , 1 , 1 ( ) (D₁ =

WLP dan WLP(D₂)=(0,3,0,0) sehingga D1 memiliki resolusi

3. Memilih rancangan minimum aberration.

4. Pertimbangan biaya dan run-size

Hal lain yang perlu dipertimbangkan selain minimum-aberration adalah pemilihan rancangan yang paling ekonomis. Perhitungan biaya dilakukan pada

unit percobaan yang digunakan.

Pertimbangan-pertimbangan tersebut di atas diselaraskan untuk mendapatkan

rancangan yang terbaik dengan tidak menentukan pengaruh faktor tertentu yang

ingin dianalisis.

Huang et al. (1998) menggunakan generating matrix yang merupakan matriks dari generator-generator yang digunakan. Generating matrix untuk

rancangan FF 2n−p dapat dituliskan secara umum dalam bentuk matriks :

G_FF =

(

I C

)

_{……… ..……….. (1)}

dengan I adalah matriks identitas p×p dan C adalah matriks p×(n− p) yang elemennya sama dengan 0 atau 1 dan setiap baris harus mengandung paling

sedikit satu elemen tak nol. Sebagai contoh rancangan 27−3 dengan generating relation I =ADEF =BDEG =CDFG bisa dijelaskan dengan:

          = 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 0 0 1 G F E D C B A FF G

Berdasarkan bentuk umum generating matrix untuk rancangan FF, dapat dibentuk generating matrix untuk rancangan FFSP dengan rancangan petak utama

)

( 1 1

2 n−p _{dan rancangan anak petak 2}(n2−p2) _{sebagai berikut:}

(

1 1

)

1 I C

G = adalah generating matrix petak utama, dan

(

2 2

)

2 I C

G = adalah generating matrix anak petak.

dengan I1 merupakan matriks identitas berukuran p1× p1 dan C1 merupakan

matriks berukuran p₁×(n₁−p₁), begitu juga dengan I2 merupakan matriks

) ( 2 2

2 n p

p × − . Jika generator anak petak tidak mengandung faktor petak utama,

maka generating matri x untuk rancangan FFSP berbentuk sebagai berikut:

2 1     = G O O G G_FFSP 2 1 2 2 2 1 4 1 3 1 p p p n p p n

p_{1 1 2 2 2}

    − − = C O I O O C O

I ….……….. (2)

Generating matrix untuk rancangan FFSP dengan generator anak petak yang mengandung faktor petak utama adalah :

2 1 2 2 2 1 2 1 1 1 p p p n p p n

p_{1 1 2 2 2}

FFSP     − − = C O I O B C B I

G ...……….. (3)

dengan B1 dan B2 adalah matriks dengan element 0 atau 1; (I1 C1) dinotasikan

dengan G1 menjelaskan generating matrix dari petak utama, dan

(

B1 B2 I2 C2

)

dinotasikan dengan G2 merupakan generating matrix dari

anak petak .

Jika pada awal percobaan telah ditentukan pengaruh faktor tertentu yang

ingin dianalisis, maka struktur rancangan FFSP dipilih berdasarkan kriteria

struktur rancangan yang dapat menduga pengaruh faktor yang diinginkan tersebut.

Plot kuantil Half-Normal

Plot kuantil half-normal merupakan plot antara nilai mutlak pengaruh faktor yang telah diurutkan dengan nilai kuantil half-normal dari masing-masing pengaruh faktor. Pengaruh faktor ke-i dapat diduga dengan persamaan :

) 2 ( kontras ) kontras ( 2 N N i i

i = =

λ

Kontrasi didapatkan dari penjumlahan respon menurut tanda plus dan minus pada

Menurut Aunuddin (1989), pengertian dari kuantil serupa dengan

pengertian persentil. Sebagai contoh adalah nilai kuantil 0.67 berarti bahwa ada

0.67 bagian data yang nilainya lebih kecil dari nilai kuantil dan 0.33 bagian

lainnya memiliki nilai yang lebih tinggi.

Penetapan nilai kuantil dilakukan dengan mengurutkan terlebih dahulu

data yang dimiliki dari data yang terkecil sampai dengan data yang terbesar.

Kumpulan data yang telah diurutkan tersebut membentuk suatu kumpulan data

baru yi dengan i adalah nomor urut besarnya data tersebut. Kuantil empirik

didefinisikan sebagai berikut :

i

p y

Q i = ∗

)

(

untuk i = 1,2,...,n dan p_i =(i−0.5)/n

Secara umum dapat dirumuskan bahwa :

i

p p

Q F

i }=

{ _{( )} dan Q_(p) F 1(p_i) i

− =

Dengan −1

F adalah kebalikan fungsi F yang merupakan fungsi sebaran kumulatif

yang digunakan, dan p_i =(i−0.5)/n.

Prosedur pembuatan plot kuantil-kuantil ini dapat dilakukan dengan

langkah-langkah sebagai berikut :

• Urutkan data menjadi y1,...,yi,...,yn

Dengan y1 adalah nilai y terkecil, yi adalah nilai y urutan ke-i, dan yn

adalah nilai y terbesar.

• Untuk setiap yi, tetapkan pi =(i−0.5)/n

• Untuk setiap pi, tetapkan ( ) ( )

1

i

i Q p

p

F− = . Nilai Q(p_i) adalah kuantil berdasarkan sebaran hipotetik.

• Plotkan antara yi dengan Q(pi).

Plot kuantil half-normal dapat digunakan untuk mendeteksi pengaruh faktor yang memiliki pengaruh besar. Pengaruh faktor yang berada diluar pola

pengaruh besar terhadap respon. Hal ini karena nilai mutlak dari pendugaan

pengaruh faktor tersebut relatif lebih besar dibandingkan dengan pengaruh faktor

lain.

Jika peubah x menyebar menurut sebaran normal dengan nilai tengah = 0

dan ragam σ2, maka |x| akan menyebar menurut sebaran half-normal dengan nilai tengah = 2 πσ dan ragam σ2. Fungsi sebaran half-normal dengan nilai tengah = 2 πσ dan ragam σ2 _{adalah sebagai berikut :}

0 untuk , 2 2 )

(_x = _e− 22 2 _x≥

f x σ

σ π

=0 untuk x<0

dengan demikian fungsi sebaran half-normal kumulatifnya adalah:

dx e x F x x

∫

− = 0 2 2 2 2 2 ) ( σ σ π _      − =

∫

∫

∞ − −∞ − − x x

x _{dx e dx}

e

0

2

2 2 2 2

2

2 1 2

1

2 σ σ

σ π σ π _      ₋       Φ

=2 0.5

σ

x

Dengan Φ(x) adalah sebaran normal baku yang dapat dengan mudah didapatkan

dengan bantuan tabel sebaran normal baku. Nilai kuantil half-normal merupakan nilai fungsi kebalikan dari fungsi half-normal kumulatif di atas.

Pengujian terhadap penentuan pengaruh faktor yang memiliki pengaruh

besar digunakan statistik uji modulus-ratio (Daniel 1959, Birnbaum 1959). Uji tersebut dapat diberikan sebagai berikut :

a n n y y t =

dengan y_n : nilai mutlak pengaruh terbesar

jika nilai n=15 maka y_a merupakan nilai mulak pengaruh pada urutan 11.

dengan n=31, y_a merupakan nilai mutlak pengaruh pada urutan 22. Nilai t_n

kemudian dibandingkan dengan nilai kritik k(n,α) yang didapat dengan

persamaan berikut :

    ₊ − Φ = − 2 ) 1 ( 2 1 ) , ( / 1 1 n n

k α α

Batas signifikan pengaruh faktor :

) , (nα k t_n >

) , (n α k y y a n > a

n k n y

y > ( ,α)

Pengaruh faktor yang bernilai lebih besar dari k(n,α)y_a diputuskan sebagai

pengaruh faktor yang signifikan.

Analisis Regresi dengan Metode Forward Selection

Analisis regresi merupakan hubungan antara peubah bebas dan peubah tak

bebas. Peubah bebas yang diamati tidak semuanya memiliki kontribusi yang

besar terhadap peubah tak bebas. Jika terdapat banyak peubah bebas yang diamati

maka perlu dilakukan penyeleksian untuk mendapatkan peubah bebas yang

memiliki kontribusi besar dalam menjelaskan keragaman yang terdapat pada

peubah tak bebas.

Penyeleksian peubah bebas dengan metode forward selection (seleksi maju) dilakukan dengan tahap pertama adalah memasukkan satu peubah bebas

yang memiliki nilai R2 terbesar diantara peubah bebas yang lain, misal peubah

tersebut adalah x1. Tahap kedua adalah memilih peubah bebas kedua yang

dengan memilih peubah bebas yang memiliki nilai F parsial terbesar. Pada tahap

kedua di atas, nilai F parsial dirumuskan dengan :

) , ( ) | ( 2 1 2 1 2 x x s x x R F =

Dimana R(x2 |x1) adalah jumlah kuadrat regresi parsial x2 pada saat x1

sudah ada di dalam model dan _s2(_x1,_x2)

adalah kuadrat tengah galat dari model

regresi yang peubah bebasnya terdiri dari x1 dan x2. Nilai R(x2 |x1) dirumuskan

dengan persamaan berikut :

) ( ) , ( ) |

(x₂ x₁ R x₂ x₁ R x₁

R = −

) , (x2 x1

R adalah jumlah kuadrat regresi dengan peubah bebas x1 dan x2, dan

) (x1

R merupakan jumlah kuadrat regresi dengan peubah bebas x1 (Myers 1990).

Proses pemilihan peubah bebas di atas sama juga halnya dengan memilih

peubah bebas dengan P-value terkecil. Proses pemilihan terus berlanjut sampai

tidak ada peubah bebas x yang memiliki P-value lebih kecil dari nilai alpha yang telah ditentukan. Jika tidak dibatasi pada sebuah nilai tertentu maka proses di atas

akan berlanjut sampai semua peubah bebas masuk ke dalam model.

Analisis Ragam pada Rancangan FF dan FFSP

Analisis ragam yang dilakukan pada rancangan FF dan FFSP sedikit

berbeda dengan analisis ragam yang dilakukan pada rancangan faktorial lengkap

dan rancangan split-plot lengkap. Pada percobaan FF dan FFSP, analisis ragam dilakukan hanya terhadap pengaruh faktor dan interaksi tertentu yang dianalisis,

tidak untuk semua pengaruh faktor dan interaksi. (Montgomery 2001, Nembhard

et al. 2006).

Model matematis yang digunakan dalam rancangan FF ini adalah sebagai

berikut :

Dengan y adalah respon, f(x) merupakan fungsi dari faktor pengaruh perlakuan yang signifikan dan ε adalah komponen galat yang diasumsikan merupakan

variabel acak yang saling bebas dan ε ∼N(0,σ2).

Berbeda dengan analisis ragam pada rancangan FF, analisis ragam pada

rancangan FFSP memiliki dua jenis galat yang dihasilkan dalam rancangan FFSP,

yaitu galat petak utama dan galat anak petak. Hal ini sama seperti pada rancangan

split-p lot lengkap. Perbedaannya adalah pada pengujian pengaruh faktor yang

ber-alias.

Model yang digunakan pada rancangan FFSP adalah :

ε

δ + +

+

= f(x) g(x) y

dimana δadalah galat petak utama dan ε adalah galat dari anak petak. f(x)dan

) (x

g merupakan fungsi parameter dari rancangan petak utama dan fungsi

parameter dari rancangan anak petak. Diasumsikan bahwa δ dan ε merupakan

variabel acak yang saling bebas , δ ∼N(0,σ_PU2 )dan ε∼N(0,σ2AP). Keragaman

antar plot (σ_PU2 ) diharapkan lebih besar daripada keragaman dalam plot (σ2_AP), atau σPU2 >σ2AP (Bingham & Sitter 2001, Loeppky & Sitter 2002).

Nembhard et a.l (2006) melakukan pendekatan analisis ragam pada rancangan FFSP dengan menggunakan pengaruh -pengaruh faktor tertentu sebagai

komponen ragam model dan pengaruh faktor yang diabaikan sebagai komponen

galat.

Ada beberapa aturan untuk pengujian pengaruh faktor pada rancangan

FFSP (Bingham & Sitter 2001):

1. Pengaruh petak utama dan interaksi antara faktor-faktor petak utama

dibandingkan dengan galat petak utama.

2. Pengaruh anak petak dan interaksi yang beralias dengan pengaruh petak

3. Pengaruh anak petak dan interaksi yang melibatkan paling tidak satu

faktor anak petak yang tidak beralias dengan pengaruh petak utama atau

tidak beralias dengan interaksi antara faktor-faktor petak utama

dibandingkan dengan galat anak petak.

Dalam rancangan ini galat petak utama lebih besar daripada galat anak petak, oleh

BAHAN DAN METODE

Data yang akan digunakan dalam penelitian ini berupa contoh kasus

percobaan yang diambil dari artikel Quality Engeenering (1988) dalam Montgomery (2001) untuk rancangan FF dan dari Nembhard et al. (2006) untuk rancangan FFSP. Dua contoh kasus tersebut diambil untuk memberikan gambaran

tentang penerapan rancangan FF dan rancangan FFSP beserta analisis nya untuk

mendapatkan faktor yang memiliki pengaruh besar.

Kajian teori yang dilakukan dalam penelitian ini mengikuti tahapan

metode sebagai berikut :

1. Pengkajian teori dan literatur terhadap rancangan FF dan FFSP , meliputi

kegunaan dan konsep-konsep penting yang terdapat pada kedua rancangan.

2. Menjelaskan proses pembentukan struktur rancangan dan ilustrasinya yang

diperoleh secara manual dan dengan bantuan modul ADX (Analysis Design of Experiments) yang terdapat pada paket software SAS 9.1. 3. Analisis data pada contoh kasus yang diambil dari Montgomery 2001

untuk rancangan FF dan dari Nembhard 2006 untuk rancangan FFSP.

Analisis secara visual dilakukan dengan plot kuantil half-normal yang diperoleh secara manual dan dengan bantuan modul ADX pada SAS 9.1.

Analisis secara formal dilakukan dengan pendekatan analisis regresi

menggunakan metode seleksi maju yang dilanjutkan dengan analisis

HASIL

Penggunaan Rancangan FF dan FFSP

Penggunaan rancangan FF muncul karena keterbatasan satuan percobaan

yang dimiliki. Satuan percobaan yang bersifat homogen hanya cukup untuk

melakukan sebagian dari kombinasi perlakuan lengkap. Keterbatasan juga bis a

muncul dari faktor waktu dan biaya yang tersedia.

Jumlah kombinasi perlakuan dari percobaan faktorial lengkap bertambah

dengan bertambahnya faktor perlakuan yang digunakan. Pengaruh faktor utama

dan interaksi h faktor yang diduga dari percobaan faktoria l lengkap 2n ada sebanyak :

n pengaruh faktor utama

2 ) 1 (n− n

pengaruh interaksi dua faktor

3 . 2 ) 2 )( 1 (n− n− n

pengaruh interaksi tiga faktor

. . . ! ) 1 )...( 2 )( 1 ( h h n n n

n − − − −

pengaruh interaksi h faktor.

Secara umum ada sebanyak n pengaruh faktor utama dan C(n,h) pengaruh

interaksi berordo h-1 yang dapat diduga pada percobaan faktorial lengkap 2n. Hal ini dapat terjadi karena kombinasi perlakuan yang dilakukan pada percobaan

faktorial lengk ap ada sebanyak 2n sehingga nilai rataan umum dan 2n −1

pengaruh faktor dapat diduga. Sebagai contoh adalah percobaan dengan

rancangan faktorial lengkap menggunakan 7 faktor yang melakukan 27 =128

kombinasi perlakuan dapat menduga 127 pengaruh faktor masing-masing adalah 7

pengaruh faktor utama, 21 pengaruh interaksi dua faktor, dan 99 sisanya adalah

pengaruh interaksi lebih besar dari tiga faktor.

Berdasarkan prinsip urutan pengaruh hirarki bahwa pengaruh faktor

tinggi. Pengaruh interaksi tingkat tinggi dapat dianggap memiliki pengaruh yang

kurang penting dalam analisis, sehingga pengaruh tersebut dapat diasumsikan

untuk diabaikan. Kehilangan informasi tentang pengaruh interaksi tingkat tinggi

ini merupakan kerugian yang harus dibayar dalam menggunakan rancangan FF.

Dalam percobaan yang melibatkan banyak faktor, kehilangan informasi tersebut

tidak begitu berarti karena informasi yang dibutuhkan lebih ditekankan pada

pengaruh faktor utama dan pengaruh interaksi tingkat rendah. Selain itu,

kadangkala ditemui kesulitan untuk mengintepretasikan interaksi tingkat tinggi.

Pada rancangan FF hanya sebanyak 2n−p kombinasi perlakuan yang dapat dilakukan, hal ini dikarenakan keterbat asan sumberdaya yang dimiliki, sehingga

tidak semua pengaruh faktor dapat diduga. Pengaruh faktor utama dan pengaruh

interaksi tingkat rendah lebih diutamakan untuk dilakukan pendugaan, sedangkan

pengaruh interaksi faktor tingkat tinggi diasumsikan untuk diabaikan.

Ketidakmampuan rancangan FF untuk menduga semua pengaruh faktor

merupakan salah satu kelemahan dalam penerapan rancangan ini.

Rancangan FF menduga nilai rataan dan 2n−p−1 pengaruh faktor, hal ini terjadi karena kombinasi perlakuan yang dicobakan hanya sebagian dari jumlah

kombinasi lengkap. Kesalahan dalam penafsiran penafsiran pengaruh faktor dapat

terjadi pada penerapan rancangan FF akibat adanya pengaruh faktor yang saling

terpaut (Cochran & Cox 1957). Pendugaan terhadap pengaruh faktor tertentu bisa

jadi adalah bukan pengaruh sebenarnya dari pengaruh faktor tersebut. Hal ini

berkaitan dengan clear effect s, yaitu pengaruh faktor penting yang tidak terpau t dengan pengaruh faktor penting yang lain. Pengaruh penting yang dimaksud

adalah pengaruh faktor utama dan pengaruh interaksi dua faktor, sedangkan

pengaruh yang tidak penting merupakan pengaruh interaksi tingkat tinggi yang

diabaikan. Clear effects dapat diduga apabila terdapat asumsi untuk mengabaikan pengaruh interaksi tiga faktor dan interaksi yang lebih tinggi. Jika pengaruh faktor

tersebut bukan suatu clear effects, maka pendugaan terhadap pengaruh faktor tersebut sebenarnya adalah pendugaan terhadap faktor itu sendiri dan pengaruh

faktor yang terpaut dengannya. Kesalahan dalam penafsiran pengaruh faktor ini

Kelebihan rancangan FF jika dibandingkan dengan rancangan faktorial

lengkap adalah rancangan FF mampu menduga pengaruh-pengaruh penting dari

banyak faktor yang digunakan dalam percobaan tanpa harus melakukan semua

kombinasi perlakuan lengkap . Hal ini tentu saja akan meningkatkan efisiensi

biaya dan waktu.

Rancangan FF digunakan secara luas dalam proses screening experiment. Screening experiment merupakan percobaan yang dilakukan dengan melibatkan banyak faktor perlakuan dengan tujuan mencari faktor-faktor yang memiliki

pengaruh besar terhadap respon yang diamati. Proses ini banyak digunakan pada

percobaan industri manufaktur dimana ingin diketahui faktor apa yang sebenarnya

berpengaruh terhadap respon dari banyak faktor yang dicobakan . Dalam proses

screening experiment, taraf yang digunakan untuk setiap faktor yang dicobakan idealnya terdiri dari dua taraf yaitu taraf tinggi dan taraf rendah. Jika telah

diketahui faktor-faktor yang berpengaruh terhadap respon, maka kemudian

dilakukan percobaan lanjutan dengan jumlah taraf yang lebih banyak untuk

mendapatkan informasi yang lebih luas.

Sebuah contoh percobaan yang dilakukan untuk proses screening experiment berupa percobaan pembuatan roti oleh Anderson (2005) dengan menggunakan rancangan FF dengan fraksi setengah . Percobaan dilakukan dengan

mencobakan empat faktor masing-masing dengan dua taraf, yaitu :

A. Pengencer: air (–) atau susu (+)

B. Minyak: margarin (–) atau mentega (+)

C. Tepung: tepung biasa (–) atau tepung roti (+)

D. Gandum: gandum biasa (–) atau gandum roti (+)

Hasilnya, tiga pengaruh faktor memiliki pengaruh yang besar yaitu pengaruh

faktor A, C dan AC. Artinya dari empat faktor yang dicobakan, faktor yang

berpengaruh adalah faktor A dan B. Kedua faktor tersebut diinvestigasi lebih

lanjut pada percobaan lanjutan.

Menurut montgomery (2001), keberhasilan dari penggunaan rancangan FF

didasarkan pada tiga ide dasar berikut:

pengaruh faktor utama dan pengaruh interaksi tingkat rendah lebih

memegang peranan.

2. The projection property. Rancangan FF dapat diproyeksikan menjadi rancangan yang lebih kuat dengan melibatkan faktor-faktor yang memiliki

pengaruh signifikan.

3. Sequential experimentation. Memungkinkan untuk menggabungkan dua atau lebih rancangan FF untuk membentuk rancangan yang lebih besar

untuk menduga pengaruh faktor dan interaksi yang menarik.

Rancangan FF yang dilakukan dengan mengutamakan pengaruh faktor

utama dan interaksi dua faktor diharapkan dapat menghasilkan pengaruh faktor

tertentu yang berpengaruh besar terhadap respon. Faktor-faktor yang memiliki

pengaruh besar kemudian digunakan dalam percobaan selanjutnya untuk

mendapatkan informasi yang lebih luas. Menggabungkan dua rancangan FF dapat

dilakukan untuk mendapatkan informasi yang menarik tentang pengaruh faktor

interaksi yang penting. Contoh penggabungan dua rancangan FF ini adalah pada

rancangan fractional factorial split-plot (FFSP) yang juga akan dikaji dalam penelitian ini.

Rancangan FFSP digunakan pada kondisi dimana terdapat kendala teknis

di lapang yang tidak memungkinkan untuk melakukan pengacakan lengkap.

Kendala teknis yang melatarbelakangi penggunaan rancangan FFSP ini sama

dengan kondisi yang terjadi pada rancangan split-plot. Perbedaan antara kedua rancangan ini terletak pada keterbatasan satuan percobaan yang tersedia. Pada

rancangan split-plot satuan percobaan yang tersedia mencukupi untuk mencobakan semua kombinasi perlakuan lengkap, sedangkan pada rancangan

FFSP keterbatasan satuan percobaan yang tersedia membuat percobaan yang

dilakukan hanya melakukan sebagian dari kombinasi perlakuan lengkap.

Kelebihan dari rancangan FFSP adalah bahwa rancangan ini secara teknis

memudahkan pelaksanaan percobaan di lapang ketimbang pelaksanaan rancangan

FF. Rancangan ini mampu menganalisis pengaruh anak petak dengan tingkat

ketelitian yang lebih tinggi dibandingkan dengan tingkat ketelitian untuk

menganalisis pengaruh petak utama. Kesulitan yang muncul adalah teknik analisis

Pengggunaan utama dari rancangan FFSP adalah pada proses screening experiment, hal ini sama dengan penggunaan rancangan FF. Faktor-faktor yang terlibat dalam rancangan FFSP ini dicobakan untuk dapat menentukan pengaruh

faktor tertentu yang memilik i pengaruh besar terhadap respon untuk kemudian

dilakukan percobaan lanjutan terhadap faktor-faktor yang memiliki pengaruh

besar tersebut.

Teknik Pembentukan dan Pemilihan Struktur Rancangan

Pembentukan struktur rancangan dilakukan untuk menentukan kombinasi

perlakuan yang akan dicobakan. Struktur rancangan yang berbeda akan

menghasilkan kombinasi perlakuan yang berbeda, dengan demikian akan berbeda

pula pengaruh faktor yang dapat diduga. Perbedaan struktur rancangan yang

terbentuk akan tergantung dari generator yang digunakan dalam rancangan.

Sebuah rancangan dapat dibentuk dalam beberapa struktur rancangan yang

berbeda, dengan demikian perlu dipilih struktur rancangan yang sesuai dengan

tujuan penelitian. Ada dua jenis pemilihan struktur rancangan (Bingham & Sitter

2001):

1. Pemilihan struktur rancangan berdasarkan kriteria terbaik

2. Pemilihan struktur rancangan berdasarkan pengaruh faktor tertentu yang

ingin diduga

Struktur rancangan terbaik merupakan struktur rancangan yang dapat menduga

pengaruh fakto r yang penting, yaitu pengaruh faktor utama dan pengaruh interaksi

dua faktor.

Pemilihan struktur rancangan berdasarkan kriteria rancangan terbaik

memiliki dua kriteria yang harus dipenuhi, yaitu :

1. Resolusi maksimum

2. Minimum aberration

Kedua kriteria ters ebut di atas diperlukan untuk mendapatkan struktur rancangan

terbaik (Montgomery 2001, Fries & Hunter 1980).

Kriteria resolusi maksimum diberikan agar pengaruh faktor yang penting

yang tidak terpaut dengan pengaruh faktor penting yang lain. Clear effects dapat diduga apabila terdapat asumsi untuk mengabaikan pengaruh interaksi tiga faktor

dan interaksi yang lebih tinggi. Beberapa hal tentang resolusi terkait dengan clear effects:

• Dalam rancangan dengan resolusi IV, pengaruh faktor utama merupakan clear effects.

• Dalam rancangan dengan resolusi V, pengaruh faktor utama dan interaksi dua faktor merupakan clear effects.

Pengaruh interaksi dua faktor bukan merupakan clear effects pada rancangan dengan resolusi IV karena pengaruh tersebut terpautdengan pengaruh interaksi

dua faktor yang lain. Semakin tinggi resolusi sebuah rancangan maka akan

semakin banyak clear effects, dengan demikian rancangan dengan resolusi tertinggi dipilih sebagai rancangan terbaik.

Resolusi maksimum dapat dicapai dengan pembentukan generator yang

tepat. Beberapa hal yang harus diperhatikan untuk mendapatkan struktur

rancangan dengan resolusi maksimum adalah sebagai berikut:

• Resolusi maksimum pada rancangan fraksi setengah diperoleh dengan cara membentuk defining relation yang melibatkan semua faktor yang

dicobakan. Rancangan dengan empat faktor 24 mencapai resolusi maksimum dengan defining relation I=ABCD yaitu resolusi IV dan

rancangan ₂5 _{mencapai resolusi V dengan defining relation}

ABCDE

I= .

Dengan membentuk defining relation di atas maka pengaruh faktor utama dan interaksi dua faktor akan terpaut dengan pengaruh interaksi tingkat

tinggi yang diasumsikan dapat diabaikan, sehingga pengaruh faktor utama

dan interaksi dua faktor dapat diduga. Pada contoh rancangan ₂5 _dengan

defining relation I=ABCDE akan didapatkan bahwa pengaruh faktor utama akan terpaut dengan pengaruh interaksi empat faktor dan pengaruh

interaksi dua faktor akan terpaut dengan pengaruh interaksi tiga faktor.

Karena pengaruh interaksi tiga dan empat faktor diasumsikan untuk

diabaikan, maka pengaruh faktor utama dan pengaruh interaksi dua faktor

• Penentuan resolusi maksimum pada rancangan fraksi seperempat yang menggunakan dua defining relation dan satu generalized defining relation dilakukan pemilihan defining relation dengan teknik trial and error. Dapat dipastikan bahwa untuk mendapatkan resolusi maksimum pada rancangan

fraksi setengah adalah dengan membentuk generator yang melibatkan semua

faktor yang dicobakan.

Rancangan minimum aberration merupakan rancangan yang meminimumkan defining relation terpendek. Defining relation terpendek merupakan penentu tingkat resolusi, untuk itu bisa jadi beberapa alternatif

rancangan terbaik memiliki tingkat resolusi yang sama. Meminimumkan defining relation terpendek berarti meminimumkan banyaknya pengaruh interaksi tingkat rendah yang saling terpaut.

Pemilihan struktur rancangan adakalanya tidak berdasarkan kriteria

rancangan terbaik tetapi berdasarkan kemampuan rancangan untuk menduga

pengaruh tertentu yang diinginkan. Pada struktur rancangan berdasarkan

pengaruh faktor yang ingin diduga, defining relation dibentuk sedemikian rupa sehingga pengaruh yang ingin diduga tidak terpaut dengan pengaruh lain yang

juga ingin diduga. Pengaruh yang ingin diduga diusahakan untuk terpaut dengan

hanya pengaruh lain yang diasumsikan untuk diabaikan.

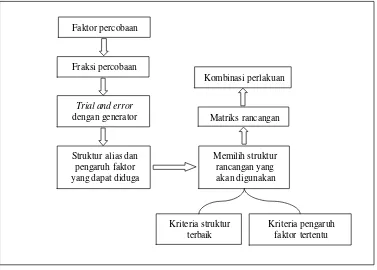
Pembentukan struktur rancangan dilakukan dengan trial and error. Proses pembentukan struktur rancangan dalam bagan di atas dapat dijelaskan oleh tahap

– tahap sebagai berikut (Cochran & Cox 1957) :

1. Menentukan banyaknya faktor yang akan dicobakan.

2. Menentukan ukuran percobaan yang terkait dengan fraksi percobaan

yang digunakan dengan mempertimbangkan jumlah satuan percobaan

yang tersedia.

3. Menentukan generator dan defining relation yang mungkin untuk dibentuk dengan trial and error.

4. Menentukan struktur alias berdasarkan defining relation yang mungkin untuk dibentuk untuk kemudian dapat menentukan pengaruh faktor

5. Memilih struktur rancangan yang sesuai dengan kriteria yang telah

ditentukan sehingga dapat ditentukan defining relation tertentu yang akan digunakan dalam percobaan.

6. Membentuk matriks rancangan untuk struktur yang sesuai dengan

defining relation yang telah ditentukan.

7. Menentukan kombinasi perlakuan yang akan dicobakan yang didapat

dari matriks percobaan.

Langkah -langkah yang dilakukan dalam pembentukan struktur rancangan jenis ini

[image:49.612.133.510.274.544.2]

dapat dijelaskan oleh bagan pada Gambar 1.

Gambar 1. Proses pembentukan struktur rancangan

Pemilihan defining relation yang menentukan struktur rancangan dipilih berdasarkan kriteria yang sesuai dengan tujuan penelitian. Jika penelitian ingin

menduga pengaruh faktor utama dan pengaruh interaksi dua faktor yang tidak

spesifik, maka pemilihan struktur rancangan didasarkan pada kriteria pemilihan

struktur rancangan terbaik. Tetapi jika ditentukan pengaruh faktor tertentu yang

Faktor percobaan

Fraksi percobaan

Trial and error

dengan generator

Struktur alias dan pengaruh faktor yang dapat diduga

Kriteria struktur terbaik

Kriteria pengaruh faktor tertentu Memilih struktur

ingin dianalisis maka pemilihan struktur rancangan didasarkan pada pengaruh

faktor spesifik tersebut.

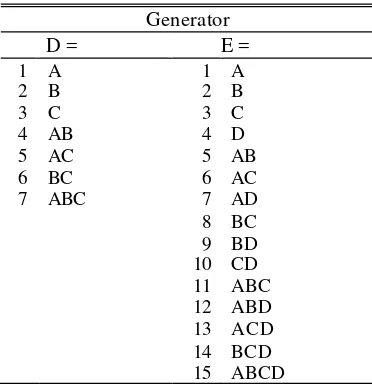
Sebuah contoh pembentukan struktur rancangan FF 25−2 dilakukan untuk memberikan ilustrasi proses pembentukan rancangan FF. Sebuah rancangan FF

dengan 5 faktor (A, B, C, D dan E) dilakukan dengan fraksi seperempat sehingga

bentuk rancangannya adalah 25−2. Dalam Tabel 5 disajikan kemungkinan -kemungkinan generator yang dapat dibentuk yang terdiri 7 -kemungkinan

generator yang dapat dibentuk untuk faktor D dan 15 untuk faktor E, sehingga ada

105 15

7× = struktur rancangan yang dapat dibentuk. Pembentukan struktur

[image:50.612.227.413.324.518.2]

rancangan tersebut dapat dilakukan dengan cara manual.

Tabel 5. Generator untuk rancangan 25−2

Generator D = E =

1 A 1 A

2 B 2 B

3 C 3 C

4 AB 4 D 5 AC 5 AB 6 BC 6 AC 7 ABC 7 AD

8 BC

9 BD

10 CD

11 ABC

12 ABD

13 ACD

14 BCD

15 ABCD

Beberapa hal yang perlu diperhatikan dalam membentuk generator agar

dapat mengurangi banyaknya kemungkinan yang mungkin dibentuk, yaitu :

• Tidak membentuk generator dengan hanya satu huruf yang membentuk defining relation yang terdiri dari dua huruf. Defining relation yang terdiri dari dua huruf akan menyebabkan pengaruh utama tertentu terpaut dengan

pengaruh utama yang lain, sedangkan kedua pengaruh faktor utama

tersebut ingin diduga. Pendugaan terhadap kedua pengaruh utama tersebut

Contoh : D=A dan E=C

I=AD=CE=ACDE

Pengaruh utama faktor A terpaut dengan faktor D

Pengaruh utama faktor C terpaut dengan faktor E

Dengan begitu pengaruh utama faktor A dan C tidak dapat

diduga kecuali pengaruh faktor D dan E diabaikan.

• Tidak membentuk generator kedua yang melibatkan faktor pada generator pertama, dalam kasus ini tidak melibatkan faktor D dalam generator E.

Melibatkan faktor D dal