Perbandingan Metode Least Trimmed Squares Dan Penduga-S Dalam Mengatasi Data Pencilan Dengan Simulasi Data

(1)

PERBANDINGAN METODE

LEAST TRIMMED SQUARES

DAN PENDUGA-S DALAM MENGATASI DATA

PENCILAN DENGAN SIMULASI DATA

SKRIPSI

ANDOS NIKI S. M. SEMBIRING

090803032

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN

ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(2)

PERBANDINGAN METODE LEAST TRIMMED SQUARES DAN PENDUGA-S DALAM MENGATASI DATA

PENCILAN DENGAN SIMULASI DATA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

ANDOS NIKI S. M. SEMBIRING 090803032

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : Perbandingan Metode Least Trimmed Squares dan Penduga-S dalam Mengatasi Data Pencilan dengan Simulasi Data

Kategori : Skripsi

Nama : Andos Niki S. M. Sembiring

Nomor Induk Mahasiswa : 090803032

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam

(FMIPA) Universitas Sumatera Utara

Disetujui di Medan, April 2015

Komisi Pembimbing:

Pembimbing 2, Pembimbing 1,

Asima Manurung, S.Si, M.Si NIP. 19730315 199903 2 001

Dr. Open Darnius, M.Sc NIP. 19641014 199103 1 004

Diketahui oleh:

Departemen Matematika FMIPA USU Ketua,

(4)

PERNYATAAN

PERBANDINGAN METODE LEAST TRIMMED SQUARES

DAN PENDUGA-S DALAM MENGATASI DATA PENCILAN DENGAN SIMULASI DATA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, April 2015

(5)

PENGHARGAAN

Pujian dan syukur penulis panjatkan kepada Tuhan Yesus atas kasih dan penyertaanNya yang dirasakan penulis dalam menyelesaikan penyusunan skripsi ini dengan judul Perbandingan Metode Least Trimmed Squares dan Penduga-S dalam Mengatasi Data Pencilan dengan Simulasi Data.

(6)

ABSTRAK

Analisis regresi digunakan untuk mengetahui hubungan antar variabel. Salah satu metode penduga parameter dalam model regresi adalah metode kuadrat terkecil (OLS). Dalam penelitian ini digunakan empat model kelompok data dengan letak pencilan berbeda-beda dengan lima kali perulangan setiap modelnya. Kemudian tulisan ini bertujuan untuk membandingkan dua metode regresi robust yaitu penduga least trimmed squares (LTS) dan penduga-S. Pada pencilan yang terletak di tengah garis regresi regresi robust penduga-LTS memberikan hasil yang lebih baik dari pada penduga-S, sebaliknya penduga-S lebih baik pada pencilan yang berada di ujung. Kriteria pembandingannya menggunakan rata-rata kuadrat sisa.

(7)

THE COMPARISON OF ROBUST REGRESSION LEAST TRIMMED SQUARES AND S-ESTIMATORS OVERCOMING OUTLIERS

WITH SIMULATION OF DATA

ABSTRACT

Regression analysis was used to determine the relationship between variables. One of method parameter estimator in the regression model is ordinary least squares (OLS). In this study used four groups of data models with different outlier layout with five repetitions of each model. Then, this paper aims to compare the two methods, namely robust regression of least trimmed squares (LTS) and S-estimators. In the outliers are located amid robust regression line regression LTS-estimators provides better results than the S-LTS-estimators, otherwise S-LTS-estimators is better at outliers are located end. The comparison criteria using the average squared residual.

(8)

DAFTAR ISI

DAFTAR TABEL viii

DAFTAR GAMBAR x

DAFTAR LAMPIRAN xi

BAB 1 Pendahuluan 1

1.1. Latar Belakang 1

1.2. Perumusan Masalah 2

1.3. Pembatasan Masalah 2

1.4. Tinjauan Pustaka 3

1.5. Tujuan Peneletian 4

1.6. Kontribusi Peneletian 4

1.7. Metodologi Peneletian 4

BAB 2 Landasan Teori 6

2.1. Regresi Linier 6

2.2. Metode Kuadrat Terkecil 7

2.3. Rataan Kuadrat Sisa (Mean Square Error) 8

2.4. Pencilan 9

2.4.1. Pengertian Pencilan 9

2.4.2. Dampak Pencilan 9

2.4.3. Pendeteksian Pencilan 10

2.5. Regresi Robust 12

2.5.1. Regresi Robust Penduga-S 13

2.5.2. Regresi Robust Penduga Least Trimmed Square (LTS)

17

BAB 3 Pembahasan 18

3.1. Data 18

3.2. Pendeteksian Pencilan/ Outlier 21

3.3. Metode Kuadrat Terkecil 24

3.4. Regresi Robust Penduga Least Trimmed Square

(LTS) 27

3.4.1. Rataan Kuadrat Sisa (Mean Square Error)

untuk Penduga-LTS 31

(9)

3.5.1. Rataan Kuadrat Sisa (Mean Square Error)

untuk Penduga-S 43

BAB 4 Kesimpulan dan Saran 50

4.1. Kesimpulan 50

4.2. Saran 50

FTAR PUSTAKA 51

(10)

DAFTAR TABEL

3.6 Perkalian Variabel Bebas dan Variabel Terikat untuk

Data 1 25

3.7 Sisaan Kuadrat Semua Data dengan Metode Kuadrat

Terkecil 26

3.8 Sisaaan Kuadrat yang Diurutkan 28

3.9 Data yang Terbentuk dari Sisaan Kuadrat Sudah Diurutkan

29

3.10 Perkalian Variabel untuk Data 1 dengan Penduga-LTS 30 3.11 Nilai Jumlah Kuadrat Regresi dan Jumlah Kuadrat Total

Menggunakan Penduga-LTS untuk Data 1 31

3.12 Nilai Jumlah Kuadrat Regresi dan Jumlah Kuadrat Total

3.15 Hasil Perhitungan Koefisien Regresi Iterasi ke-1 37 3.16 Hasil Perhitungan Koefisien Regresi Iterasi ke-2 37

3.17 Nilai Koefisien Regresi Penduga-M 38

3.18 Sisaan dari Persamaan Penduga-M 39

3.19 Hasil Perhitungan Koefisien Regresi Iterasi ke-1 40 3.20 Hasil Perhitungan Koefisien Regresi Iterasi ke-2 41

3.21 Nilai Koefisien Regresi Penduga-S 42

Menggunakan Penduga-S untuk Data 1 43

3.26 Hasil Estimasi Koefisien Regresi dan Rata-rata Kuadrat

(11)

3.27 Hasil Estimasi Koefisien Regresi dan Rata-rata Kuadrat

(12)

DAFTAR GAMBAR

Nomor Judul Halaman

Gambar

2.1 ma Identifikasi Data Pencilan dengan IQR atau Box Plot

11 2.2 Kriteria Pengambilan Keputusan Adanya Pencilan atau

Tidak 12

3.1 Scatterplot Data 1 21

(13)

DAFTAR LAMPIRAN

Nomor Judul Halaman

Lampiran

1 mbangkitkan Data dengan Program R 53

2 amaan dengan Metode Kuadrat Terkecil dan Mendeteksi

Pencilan dengan MINITAB 53

3 amaan Penduga-LTS dengan Metode Kuadrat Terkecil 54 4 gram Macro MINITAB Regresi Robust dengan Pembobot

Fungsi Huber (dengan r=1) 55

5 il Output Program macro MINITAB Data 1, Data 2, Data 3

dan Data 4 56

6 amaan Penduga-S Data 1, Data 2, Data 3 dan Data 4 dengan R

70

(14)

ABSTRAK

Analisis regresi digunakan untuk mengetahui hubungan antar variabel. Salah satu metode penduga parameter dalam model regresi adalah metode kuadrat terkecil (OLS). Dalam penelitian ini digunakan empat model kelompok data dengan letak pencilan berbeda-beda dengan lima kali perulangan setiap modelnya. Kemudian tulisan ini bertujuan untuk membandingkan dua metode regresi robust yaitu penduga least trimmed squares (LTS) dan penduga-S. Pada pencilan yang terletak di tengah garis regresi regresi robust penduga-LTS memberikan hasil yang lebih baik dari pada penduga-S, sebaliknya penduga-S lebih baik pada pencilan yang berada di ujung. Kriteria pembandingannya menggunakan rata-rata kuadrat sisa.

(15)

THE COMPARISON OF ROBUST REGRESSION LEAST TRIMMED SQUARES AND S-ESTIMATORS OVERCOMING OUTLIERS

WITH SIMULATION OF DATA

ABSTRACT

Regression analysis was used to determine the relationship between variables. One of method parameter estimator in the regression model is ordinary least squares (OLS). In this study used four groups of data models with different outlier layout with five repetitions of each model. Then, this paper aims to compare the two methods, namely robust regression of least trimmed squares (LTS) and S-estimators. In the outliers are located amid robust regression line regression LTS-estimators provides better results than the S-LTS-estimators, otherwise S-LTS-estimators is better at outliers are located end. The comparison criteria using the average squared residual.

(16)

BAB I

PENDAHULUAN

1.1 Latar Belakang

Analisis Regresi adalah metode statistika yang digunakan untuk mengetahui hubungan antara variabel terikat (dependen, respon, �) dengan satu atau lebih variabel bebas (independen, prediktor, �). Apabila banyaknya variabel bebas hanya ada satu maka disebut regresi linier sederhana, sedangkan apabila terdapat lebih dari satu variabel bebas maka disebut sebagai regresi linier berganda.

Salah satu metode penduga parameter dalam regresi linier yang sering digunakan adalah metode kuadrat terkecil (MKT) atau ordinary least squares (OLS). Penggunaan metode ini membutuhkan beberapa asumsi klasik yang harus dipenuhi untuk menghasilkan penduga linier tidak bias terbaik atau best linier unbiased estimator. Menurut Cahyawati dkk (2009) salah satu penyebab tidak terpenuhinya asumsi klasik tersebut adalah adanya pencilan (outlier) pada data amatan.

Metode kuadrat terkecil tidak dapat digunakan jika asumsinya tidak terpenuhi oleh karena itu selanjutnya diperlukan alternatif metode penduga parameter lain yang dapat mengatasi adanya pencilan dalam data amatan. Metode Robust dapat menjadi alternatif pilihan untuk menghasilkan model yang lebih baik dari hasil metode kuadrat terkecil berdasarkan kriteria mean square error (MSE) bagi masing-masing model.

(17)

median of square (LMS), penduga least trimmed squares (LTS), penduga-S dan penduga-MM. Dari ke-5 metode di atas, Penulis akan berfokus pada metode estimasi parameter dengan menggunakan metode penduga robust least trimmed square (LTS) dan penduga-S, di mana kedua metode ini memiliki nilai breakdown point yang tinggi yaitu hampir 50% (Rousseeuw, 1987).

Berdasarkan uraian di atas maka penulis memilih judul tugas akhir

“Perbandingan Metode Least Trimmed Squares dan Penduga-S dalam

Mengatasi Data Pencilan dengan Simulasi Data”.

1.2 Perumusan Masalah

Perumusan masalah yang akan diteliti dalam tulisan ini adalah bagaimana perbandingan dua regresi robust yakni metode penduga least trimmed squares (LTS) dan penduga-S dapat mengatasi data pencilan berdasarkan letak pencilan yang dibandingkan dengan suatu simulasi dalam empat posisi yakni di ujung bawah, ujung atas, tengah atas dan tengah bawah dalam model garis regresi sederhana.

1.3 Pembatasan Masalah

Agar pembatasan masalah lebih jelas, maka penulis memberikan batasan yang akan dilakukan yaitu:

1. Simulasi data yang diambil penulis adalah 4 model data bangkitan dari program R yang terdiri dari 20 observasi dengan ketentuan letak pencilan pada garis regresi yang berbeda-beda setiap model data.

2. Penulis menggunakan regresi robust dalam mengatasi data pencilan yaitu dengan metode penduga least trimmed squares (LTS) dan penduga-S.

(18)

1.4 Tinjuan Pustaka

Analisis regresi digunakan untuk mengetahui hubungan antara variabel terikat (�) dengan satu atau lebih variabel bebas (�). Model regresi linier yang memuat satu variabel terikat (�) dan satu variabel bebas (�) adalah model regresi linier sederhana.

Metode kuadrat terkecil (MKT) atau ordinary least squares (OLS) merupakan salah satu penduga parameter model regresi linier sederhana. Metode kuadrat terkecil membutuhkan asumsi klasik yang harus dipenuhi untuk menghasilkan penduga linier tidak bias terbaik atau bestlinier unbiased estimator. Adapun asumsi klasik yang harus dipenuhi adalah homokedastisitas, nonautokorelasi, nonmultikorelasi, distribusi kesalahan normal dengan rata-rata sama dengan nol, dan variabel nonstokastik (Hasan, 1999). Metode kuadrat terkecil merupakan metode yang meminimumkan jumlah kuadrat sisa (selisih antara data yang sebenarnya dengan data dugaan dari model regresi yang terbentuk, yang dinyatakan sebagai berikut (Sembiring, 1995):

�� − �� =∑��=1��2 1.1

Pencilan (Outlier) adalah data yang tidak mengikuti pola umum (Sembiring, 1995, hal. 72). Jika dalam data amatan ditemukan suatu pencilan, maka alternatif penolakan begitu saja bukanlah prosedur yang bijaksana. Ada kalanya pencilan memberikan informasi yang tidak bisa diberikan oleh titik data lainnya (Drafer dan Smith, 1992). Menurut Soemartini (2007), pencilan dapat dideteksi menggunakan beberapa metode yakni metode Grafis, Boxplot, Internal studenzation (residu yang distudentkan), berdasarkan nilai Leverage, DfFITS, Cook’s Distance, dan DfBETA(s). Metode yang akan dipakai penulis untuk mendeteksi pencilan yaitu metode Scatterplot dan metode berdasarkan nilai DfFITS.

(19)

pencilan dan memberikan hasil terhadap adanya pencilan (Chen, 2002). Metode regresi robust yang diketahui tahan terhadap pencilan terus berkembang dan banyak digunakan dalam meneliti berbagai permalasahan, seperti: pengoptimalan kekuatan torque pada lampu TL yaitu menggunakan metode penduga parameter LTS, dengan alasan terdapat pencilan pada data kekuatan torque (Akbar dan Maftukhah, 2007) dan penelitian pada estimasi parameter produksi jagung di Indonesia tahun 2010 dengan metode penduga-S (Sahari R. J., 2012 ).

1.5 Tujuan Penelitian

Tujuan penelitian ini adalah untuk membandingkan regresi robust metode penduga least trimmed squares (LTS) dan penduga-S dalam melakukan pendugaan parameter model regresi sehingga didapatkan pendugaan yang terbaik berdasarkan rataan kuadrat sisa (mean square error).

1.6 Kontribusi Penelitian

Manfaat yang diperoleh dari penelitian ini adalah sebagai bahan referensi dalam hal pendugaan parameter model regresi yang memiliki pencilan.

1.7 Metodologi Penelitian

Adapun metodologi penelitian dalam tulisan ini adalah sebagai berikut: 1. Membangkitkan data dengan program R.

2. Melakukan pendugaan parameter regresi dengan metode kuadrat terkecil. 3. Melakukan pendeteksian pencilan pada data amatan dengan metode

scatterplot dan berdasarkan nilai DfFITS.

(20)

5. Mengolah data menggunakan bantuan program Macro MINITAB.

(21)

BAB 2

LANDASAN TEORI

2.1 Regresi Linier

Analisis regresi digunakan untuk mengetahui hubungan antara variabel terikat (Y) dengan satu atau lebih variabel bebas (X). Menurut Hair et al (2009) regresi linear sederhana dapat efektif dengan ukuran sampel sebanyak 20 observasi. Menurut

Nawari (2010), model regresi linier untuk satu variabel bebas yaitu model regresi

linier sederhana, dinyatakan dalam persamaan berikut:

�� =�0+�1��+ �� 2.1

Keterangan: i = 1, 2, ..., �

Yi = variabel terikat Xi = variabel bebas �0, �1 = parameter regresi

�� = sisaan/galat

Nilai �₀ dan �₁ adalah parameter regresi yang tidak diketahui nilainya dan akan dicari nilai estimasinya.

Model penduga regresi linier sederhana untuk persamaan 2.1 adalah sebagai berikut:

�� =�̂0+�̂1�� 2.2

Keterangan:

(22)

2.2 Metode Kuadrat Terkecil

Metode kuadrat terkecil merupakan salah satu penduga parameter (nilai �̂₀,�̂₁) model regresi linier sederhana. Menurut Sembiring (1995), metode kuadrat terkecil merupakan metode yang meminimumkan jumlah kuadrat sisa (selisih antara data yang sebenarnya dengan data dugaan dari model regresi yang terbentuk). Dari persamaan regresi linier sederhana 2.1, nilai residu (sisaan) ke-i pada model yaitu:

�� =�_� − ��_� 2.3

�� =�� −( �̂0+�̂1��) 2.4

Prinsip dasar metode kuadrat terkecil adalah meminimumkan jumlah kuadrat sisaan yang dinyatakan sebagai berikut:

Minimum ∑�_�₌₁�_�2 2.5

∑��=1 ��2 = ∑ �� − ��

2

� �=1

= ∑ ��_��₌₁ _� −( �̂₀+�̂₁�� )�2

∑��=1 ��2 = ∑ �� − �̂0− �̂1�� 2

�

�=1 2.6

Keterangan:

�� = data sebenarnya �� = data dugaan

�̂0,�̂1 = penduga parameter

��2 = sisaan kuadrat

Andaikan ∑�_�₌₁�_�2 dinotasikan dengan �, � merupakan fungsi dari nilai �̂₀ dan �̂₁ sehingga nilai-nilai � dapat ditentukan dengan menurunkan persamaan (2.6) terhadap �̂₀ dan �̂₁ kemudian menyamakan tiap turunannya dengan nol, diperolehlah nilai sebagai berikut:

� =∑�_�₌₁�2= ∑ ��_�₌₁ _�− �̂₀− �̂₁�_��2

(23)

��

Dari persamaan 2.7 maka akan dicari nilai �̂₀ sebagai berikut: ∑��=1�� =��̂0+ �̂1∑�_�=1��

�̂0 =

∑��=1��− �̂1∑��=1��

�

�̂0 = �� − �̂1�� 2.9

Selanjutnya, dari persamaan 2.8, akan dicari nilai �̂₁ sebagai berikut: ∑��=1�� = �̂0∑_��=1��+�̂1∑�_�=1�_�2

maka diperolehlah �̂₁yaitu:

�̂1 =

2.3 Rataan Kuadrat Sisa (Mean Square Error)

(24)

semakin baik modelnya. Ukuran ini memperhitungkan banyaknya parameter dalam model melalui pembagian dengan derajat kebebasannya. Untuk menentukan rataan kuadrat sisa dinyatakan dalam rumus sebagai berikut:

�2 ₌��

�−� =

�� −��

�−� 2.11

Keterangan:

JKS = Jumlah Kuadrat Sisa

JKT = Jumlah Kuadrat Total = ∑(�_� − ��)2

JKR = Jumlah Kuadrat Regresi = ∑(��_� − ��)2

� = Banyaknya sampel � = Banyaknya parameter �� = Data sebenarnya �� = Data dugaan

�� = Rataan data sebenarnya

2.4 Pencilan

2.4.1 Pengertian Pencilan

Menurut Sembiring (1995), secara umum pencilan ialah data yang tidak mengikuti pola umum model.

2.4.2 Dampak Pencilan

Menurut Soemartini (2007), keberadaan data pencilan akan mengganggu dalam proses analisis data dan harus dihindari dalam banyak hal. Salah satu penyebab tidak terpenuhi asumsi kenormalan galat adalah pencilan (Gujarati, 1991). Dalam kaitannya dengan analisis regresi, pencilan dapat menyebabkan hal-hal berikut: 1. Residual yang besar dari model yang terbentuk

(25)

2.4.3 Pendeteksian Pencilan

Menurut Soemartini (2007) beberapa metode dan nilai yang dapat digunakan untuk mendeteksi ada atau tidak adanya pencilan ialah sebagai berikut:

1. Metode Grafik

Metode grafik merupakan salah satu cara pendeteksian pencilan yang mudah dipahami karena menampilkan data secara grafis (gambar) tanpa melibatkan perhitungan yang rumit. Namun, kelemahan metode ini yaitu yang menentukan data tersebut sebagai pencilan atau tidak tergantung pada kebijakan (judgement) peneliti, karena metode ini hanya mengandalkan visualisasi gambar. Pendeteksian pencilan dengan metode grafik di antaranya ialah:

a. Diagram Pencar (Scatter Plot)

Metode ini dilakukan dengan cara memplot data dengan observasi ke-� (� = 1, 2, …, �). Selain itu, setelah diperoleh model regresi maka dapat dilakukan dengan cara memplot antara residual (�) dengan nilai prediksi Y (��). Jika terdapat satu atau beberapa data yang terletak jauh dari pola kumpulan data keseluruhan maka hal ini mengindikasikan adanya pencilan.

b. Boxplot

(26)

Gambar 2.1 Skema Identifikasi Data Pencilan dengan IQR atau Box Plot

2. Leverage Values, DFFITS, Cook’s Distance, dan DfBETA(s)

Cara mendeteksi pencilan dapat juga dengan menentukan nilai Leverage, DFFITS, Cook’s Distance, dan DfBETA(s). Definisi dari masing-masing nilai tersebut ialah sebagai berikut:

a. Leverage Values; menampilkan nilai leverage (pengaruh)terpusat.

b. DFFITS atau Standardized DfFIT; menampilkan nilai perubahan dalam harga yang diprediksi bilamana case tertentu dikeluarkan dan sudah distandarkan.

c. Cook’s Distance; menampilkan nilai jarak Cook.

(27)

Ketentuan dalam pendeteksian pencilan dengan nilai-nilai tersebut adalah:

Gambar 2.2 Kriteria Pengambilan Keputusan Adanya Pencilan

atau Tidak

Keterangan:

n = jumlah observasi (sampel). p = jumlah parameter.

2.5 Regresi Robust

Menurut Drafer dan Smith (1981), penolakan begitu saja suatu pencilan bukanlah prosedur yang bijaksana, adakalanya pencilan memberikan informasi yang tidak bisa diberikan oleh titik data lainnya. Metode kuadrat terkecil (MKT) merupakan metode yang baik untuk menduga � pada model regresi linier. Tetapi jika dalam penelitian diketahui terdapat pengamatan yang merupakan pencilan, maka penggunaan MKT akan menghasilkan kesimpulan yang tidak sempurna. Sebagai alternatif digunakan regresi robust.

Secara umum robust memiliki arti kekar. Regresi robust merupakan alat yang penting untuk menganalisis data yang terkontaminasi oleh pencilan dan memberikan hasil yang lebih fleksibel. Regresi robust tetap menggunakan seluruh data, tetapi dengan memberikan bobot yang kecil untuk data pencilan(Soemartini, 2007: 12). Regresi robust digunakan untuk mendeteksi pencilan dan memberikan hasil terhadap adanya pencilan (Chen, 2002).

(28)

2.5.1 Regresi Robust Penduga-S

Penduga-S (Scale) pertama kali diperkenalkan oleh Rousseeuw dan Yohai (1984) di mana metode ini merupakan keluarga high breakdown point yaitu ukuran umum proporsi dari data pencilan yang dapat ditangani sebelum pengamatan tersebut mempengaruhi model prediksi. Disebut penduga-S karena mengestimasi berdasarkan skala. Skala yang digunakan adalah simpangan baku sisaan.

Pendugaan koefisien regresi pada model regresi linier dengan MKT dilandasi pada peubah �� = �_� − ��_� pada persamaan:

∑�_�₌₁�� = 0 2.12

Bentuk yang lebih umum dari pendugaan parameter pada model regresi adalah pemecahan terhadap:

∑�_�₌₁�(��)�� = 0 2.13

Di mana

�� = _�� 2.14

Dengan S didefinisikan sebagai:

�� =��|��|, �= 1, 2, . . . ,� 2.15 Di mana �_� adalah sisaan yang diperoleh dari MKT.

Penyelesaian koefisien regresi pada persamaan 2.13 disebut dengan penduga-M dan dapat diselesaikan dengan MKT terboboti berikut:

β * = (X’WX)-1

X’WY

di mana W (matriks diagonal ��) = diagonal utama [�₁,�2, … ,��], ��

merupakan pembobot pengamatan ke-� (Myers, 1990).

Jika �� =�(��)

�� maka persamaan 2.13 menjadi:

(29)

Tahapan iterasi dalam penaksiran koefisien regresi (Winahju, 2010) adalah:

1. Dihitung penaksir β, dinotasikan b menggunakan least square, sehingga

didapatkan yˆ_i_,₀ dan εi,0 = yi −yˆi,0, (i = 1, 2, ... n) yang diperlakukan sebagai

6. Selanjutnya langkah 2 sampai dengan 5 diulang sampai didapatkan

∑

=

Persamaan 2.15 menunjukkan bahwa penduga-M hanya menggunakan median pada pembentukan nilai pembobot. Kelemahan median adalah kurangnya pertimbangan pada pola sebaran data dan bukan merupakan fungsi dari keseluruhan data. Rousseeuw dan Yohai (1984) memperkenalkan penduga-S yang merupakan pengembangan dari penduga-M. Penduga-S menggunakan simpangan baku sisaan untuk mengatasi kelemahan dari median. Menurut Salibian dan Yohai (2006) penduga-S (�̂_�) dinyatakan dalam bentuk rumus sebagai berikut:

�̂� = min∑��=1� �_��_��

atau

�̂� = min∑��=1� ��−�_�_�� 2.17

(30)

��

�� =∑��=1��

��

��= 0 2.18

� disebut fungsi pengaruh yang merupakan turunan dari �, sedangkan �_� didefinisikan sebagai:

Di mana �_�� adalah sisaan yang diperoleh melalui penduga-M. Persamaan 2.18 dapat diselesaikan melalui MKT terboboti secara iterasi yang disebut Iteratively Reweighted Least Squares (Iterasi kuadrat terkecil terboboti kembali). Sisaan awal yang digunakan pada penduga-S adalah sisaan yang diperoleh dari penduga-M. Selanjutnya dikatakan bahwa Iterasi kuadrat terkecil terboboti kembali merupakan proses pendugaan melalui metode kuadrat terkecil terboboti dilanjutkan dengan menghitung sisaan dan pembobot �(�_�) yang baru dan dilakukan pendugaan secara berulang-ulang sampai konvergen. Kekonvergen tercapai jika perubahan jumlah mutlak sisaan, ∑�_�=1|�_�:�| dari iterasi terakhir ke

iterasi berikutnya kurang dari 0,01 (Salibian dan Yohai, 2006).

Fungsi � pada persamaan 2.17 disebut fungsi kriteria � disarankan memakai fungsi obyektif berikut (Tukey, 1977, dalam Chen, 2002):

�(u_i) =�

(31)

bobot yang besar. Secara ringkas, fungsi obyektif dan pembobot dari estimator Least Square, Huber, dan Tukey Bisquare dapat dilihat pada Tabel 2.1.

Tabel 2.1 Fungsi Objektif, Fungsi Influence dan Fungsi Pembobot untuk

Least Square, Huber, dan Tukey Bisquare

Metode Least

Sumber: Fox (2002), Montgomery (1992)

Langkah-langkah menentukan regresi robust penduga-S (Salibian dan Yohai, 2006) adalah sebagai berikut:

a. Didapatkan vektor penduga awal �₁,�2, … ,�� dari model regresi dengan

MKT didapatkan galat �_�0.

b. Dari sisaan awal dihitung �� sesuai persamaan (2.15) untuk mendapatkan �� berdasarkan persamaan (2.14).

c. Menghitung nilai �_� sesuai persamaan (2.21).

d. Dengan menggunakan MKT terboboti didapatkan penduga kuadrat terkecil terboboti:

β * = (X’WX)-1 X’WY

e. Menjadikan sisaan langkah (d) sebagai sisaan awal pada langkah (b), sehingga didapatkan nilai �_� dan pembobot �_� yang baru.

(32)

g. Dari sisaan yang diperoleh pada langkah (f), dihitung robust �_� sesuai persamaan(2.19) untuk mendapatkan nilai �� sesuai persamaan (2.14).

h. Menghitung nilai �_� sesuai persamaan (2.21).

i. Digunakan MKT terboboti untuk mendapatkan penduga kuadrat terkecil terboboti:

β * = (X’WX)-1 X’WY

j. Menjadikan sisaan yang diperoleh pada langkah (i) sebagai sisaan pada langkah (g), sehingga didapatkan nilai �_� dan pembobot �_� yang baru.

k. Iterasi ulang sampai didapatkan kekonvergenan sehingga diperoleh �0�,�1�, … ,�� yang merupakan penduga-S.

2.5.2 Regresi Robust Penduga Least Trimmed Squares (LTS)

Least Trimmed Squares (LTS) merupakan metode penduga regresi robust yang menggunakan konsep pengepasan metode kuadrat terkecil (ordinary least squares) untuk meminimumkan jumlah kuadrat sisaan (Akbar dan Maftukhah, 2007). Menurut Rousseeuw dan Leroy (1987), penduga LTS (�̂) dinyatakan dalam bentuk rumus sebagai berikut:

�̂�� = min∑ℎ_�=1(�2)_�:� 2.22

Keterangan:

(�2)_1:_� ≤ (�2)_2:_� ≤ … ≤ (�2)_�_:_� = sisaan kuadrat yang diurutkan ℎ= �

2+

�+1 2 =

�+�+1 2

n = banyaknya sampel p = banyaknya parameter

(33)

BAB 3

PEMBAHASAN

3.1 Data

Data yang akan digunakan dalam bab ini yaitu 4 model data simulasi yang mengandung permasalahan pencilan di berbagai letak (ujung bawah, tengah bawah, ujung atas, tengah atas) pada garis regresi dengan bantuan software R, sintaxnya dapat dilihat di lampiran 1. Prosedur pembangkitan data simulasi adalah sebagai berikut:

1. Tentukan parameter �₀ dan �₁. Dalam kasus ini �₀ = 0 dan �₁ = 1. 2. Bangkitkan nilai �_� acak normal dengan nilai tengah 10 dan ragam 1. 3. Bangkitkan sisaan � acak normal dengan nilai tengah 0 dan ragam 1. 4. Tentukan nilai �= �� +�.

5. Tentukan nilai � dan � yang akan dijadikan data pencilan, dalam hal ini penulis mensimulasi data ke-5 setiap kelompok data sebagai pencilan.

6. Data dideteksi dengan metode scatterplot dan DfFITS.

7. Menentukan model regresi robust penduga-Least Trimmed Square dan penduga-S dengan bantuan R dan program Macro MINITAB.

8. Membandingkan model regresi robust penduga-Least Trimmed Square dan penduga-S berdasarkan nilai rataan kuadrat sisa.

9. Ulangi langkah 2-8 sebanyak 20 kali. 10. Membuat kesimpulan.

(34)

(35)

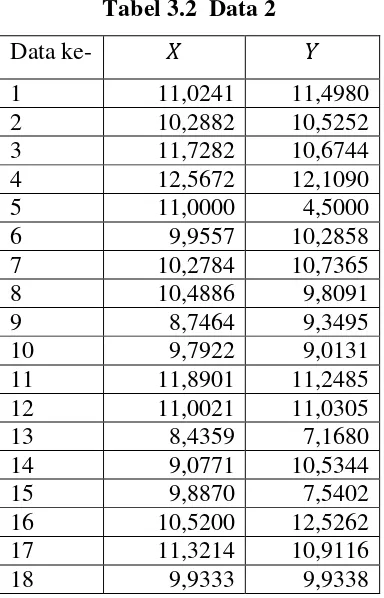
Data ke- � �

19 10,9497 10,1612

20 8,5925 7,3656

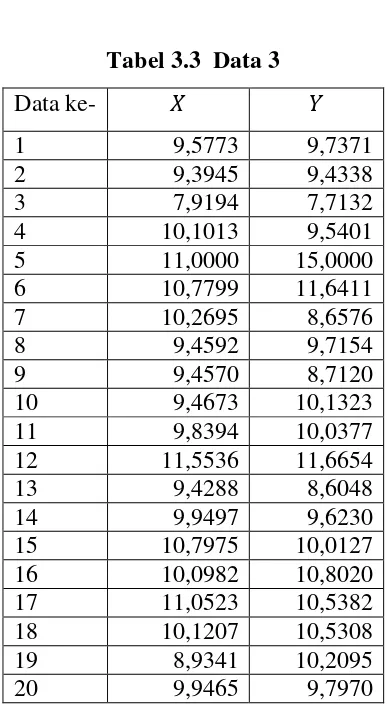
Tabel 3.3 Data 3

Data ke- � �

1 9,5773 9,7371

2 9,3945 9,4338

3 7,9194 7,7132

4 10,1013 9,5401

5 11,0000 15,0000

6 10,7799 11,6411

7 10,2695 8,6576

8 9,4592 9,7154

9 9,4570 8,7120

10 9,4673 10,1323

11 9,8394 10,0377

12 11,5536 11,6654

13 9,4288 8,6048

14 9,9497 9,6230

15 10,7975 10,0127

16 10,0982 10,8020

17 11,0523 10,5382

18 10,1207 10,5308

19 8,9341 10,2095

20 9,9465 9,7970

Tabel 3.4 Data 4

Data ke- � �

1 9,5036 9,5427

2 8,9949 9,0709

3 9,7543 9,6939

4 10,4547 11,0912

5 9,0000 15,0000

6 11,8226 12,5695

7 10,1489 10,0318

8 9,0099 9,1426

9 10,4718 9,6921

10 8,3023 6,9711

(36)

Data ke- � �

12 9,6586 9,1162

13 9,0581 8,7251

14 9,4222 8,6212

15 9,9249 12,0854

16 9,0239 10,8013

17 10,5082 9,6814

18 11,0018 11,2574

19 8,4898 7,6267

20 8,8304 8,7640

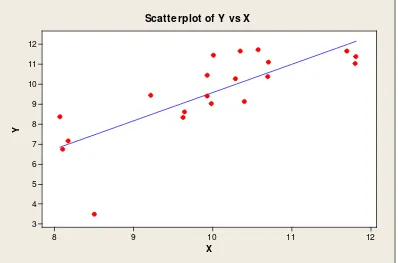
3.2 Pendeteksian Pencilan/Outlier

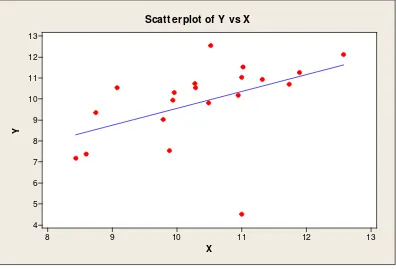
Pendeteksian pencilan data dilakukan menggunakan metode Scatterplot dan dengan menentukan nilai |DFFITS|. Gambar dan tabel berikut merupakan hasil output dengan bantuan software MINITAB 16:

12 11

10 9

8 12

11

10

9

8

7

6

5

4

3

X

Y

Scatterplot of Y vs X

(37)

13 12

11 10

9 8

13

12

11

10

9

8

7

6

5

4

X

Y

Gambar 3.2 Scatterplot Data 2

12 11

10 9

8 15

14

13

12

11

10

9

8

7

X

Y

(38)

12

Gambar 3.4 Scatterplot Data 4

Gambar 3.1, Gambar 3.2, Gambar 3.3 dan Gambar 3.4 merupakan hasil scatter plot yang diperoleh dan dapat dilihat secara grafis bahwa semua gambar mengandung pencilan.

Tabel 3.5 Nilai DfFITS dan |DfFITS|

Data ke-

Data 1 Data 2 Data 3 Data 4

(39)

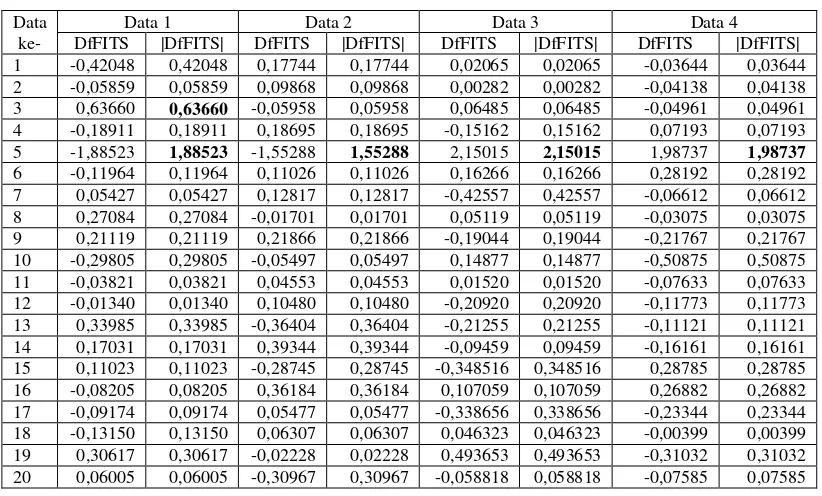
Berdasarkan kriteria dalam pendeteksian pencilan metode DfFITSbahwa yang merupakan pencilan adalah data yang memiliki nilai |DfFITS| lebih besar

dari 2�_�� = 2�2

20= 0,632456. Dari Tabel 3.2 menunjukkan adanya pencilan pada

data ke-3 dan ke-5 (pada data 1), data ke-5 (pada data 2), data ke-5 (pada data 3), data ke-5 (pada data 4).

3.3 Metode Kuadrat Terkecil

Prinsip dasar metode kuadrat terkecil adalah untuk meminimumkan jumlah kuadrat sisaan dari model regresi yang terbentuk yaitu:

�� ∑�_�₌₁�_�2

Model regresi yang akan dibentuk yaitu regresi linier sederhana dengan persamaan sebagai berikut:

�� =�0+�1�1� + �� ; i = 1, 2, ...,N

Dengan model penduga regresinya adalah: �� = �̂0+�̂1�1�

Tabel 3.6, Tabel 3.7, Tabel 3.8, dan Tabel 3.9 merupakan hasil perkalian antara variabel bebas dan variabel terikat untuk masing-masing data yaitu data 1, data 2, data 3, dan data 4. Dari hasil perhitungan yang diperoleh pada masing-masing tabel akan dihitung nilai penduga paramater �̂₀ dan �̂₁ untuk model penduga dengan metode kuadrat terkecil berdasarkan rumus pada (2.9) dan (2.10) yaitu:

�̂0 = �� − �̂1��

dan

�̂1 =

∑��=1�� − ∑ ��∑ �� =1

� �=1

� �−1_�[∑�_�₌₁�_�]2₊∑ �

(40)

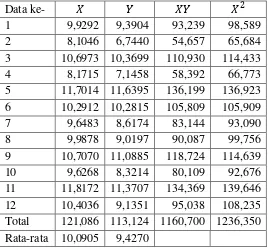
Tabel 3.6 Perkalian Variabel Bebasdan Variabel Terikat untuk Data 1

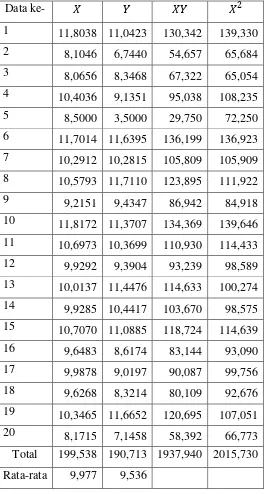
Data ke- � � �� 2

1 _{11,8038 11,0423} _130,342 _139,330 2 _8,1046 _6,7440 _54,657 _65,684 3 _8,0656 _8,3468 _67,322 _65,054 4 _10,4036 _9,1351 _95,038 _108,235 5 _8,5000 _3,5000 _29,750 _72,250 6 _{11,7014 11,6395} _136,199 _136,923 7 _{10,2912 10,2815} _105,809 _105,909 8 _{10,5793 11,7110} _123,895 _111,922 9 _9,2151 _9,4347 _86,942 _84,918 10 _{11,8172 11,3707} _134,369 _139,646 11 _{10,6973 10,3699} _110,930 _114,433 12 _9,9292 _9,3904 _93,239 _98,589 13 _{10,0137 11,4476} _114,633 _100,274 14 _{9,9285 10,4417} _103,670 _98,575 15 _{10,7070 11,0885} _118,724 _114,639 16 _9,6483 _8,6174 _83,144 _93,090 17 _9,9878 _9,0197 _90,087 _99,756 18 _9,6268 _8,3214 _80,109 _92,676 19 _{10,3465 11,6652} _120,695 _107,051 20 _8,1715 _7,1458 _58,392 _66,773 Total 199,538 190,713 1937,940 2015,730 Rata-rata 9,977 9,536

Perhitungan �̂₀ dan �̂₁ sebagai berikut:

�̂1 =

1937,940− �190,713₂₀�199,538�

−₂₀1 (199,538)2_{+ 2015,730}

�̂1 =

1937,940−1902,724

(41)

�̂1 =

35,216 24,959

�̂1= 1,41

Substitusikan nilai �̂₁ sehingga: �̂0 = 9,536−1,41(9,977)

�̂0= −4,55

Jadi, diperolehlah model penduga (penaksir) untuk persamaan regresi linier sederhana dengan metode kuadrat terkecil yaitu:

�� =�̂0+�̂1�1�

��= −4,55 + 1,41�.

Penduga model metode kuadrat terkecil dapat diperoleh dari tampilan MINITAB 16 yang dapat dilihat di lampiran 2, yakni:

Data 1: ��=−4,55 + 1,41� Data 2: ��= 1,5 + 0,81�

Data 3: ��=− 1,97 + 1,21�

Data 4: ��= 0,46 + 0,98�

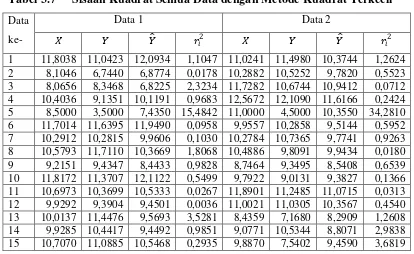
Tabel 3.7 Sisaan Kuadrat Semua Data dengan Metode Kuadrat Terkecil

Data

ke-

Data 1 Data 2

� � �� _�2 _� _� _�� _�

�2

1 11,8038 11,0423 12,0934 1,1047 11,0241 11,4980 10,3744 1,2624

2 8,1046 6,7440 6,8774 0,0178 10,2882 10,5252 9,7820 0,5523

3 8,0656 8,3468 6,8225 2,3234 11,7282 10,6744 10,9412 0,0712

4 10,4036 9,1351 10,1191 0,9683 12,5672 12,1090 11,6166 0,2424

5 8,5000 3,5000 7,4350 15,4842 11,0000 4,5000 10,3550 34,2810

6 11,7014 11,6395 11,9490 0,0958 9,9557 10,2858 9,5144 0,5952

7 10,2912 10,2815 9,9606 0,1030 10,2784 10,7365 9,7741 0,9263

8 10,5793 11,7110 10,3669 1,8068 10,4886 9,8091 9,9434 0,0180

9 9,2151 9,4347 8,4433 0,9828 8,7464 9,3495 8,5408 0,6539

10 11,8172 11,3707 12,1122 0,5499 9,7922 9,0131 9,3827 0,1366

11 10,6973 10,3699 10,5333 0,0267 11,8901 11,2485 11,0715 0,0313

12 9,9292 9,3904 9,4501 0,0036 11,0021 11,0305 10,3567 0,4540

13 10,0137 11,4476 9,5693 3,5281 8,4359 7,1680 8,2909 1,2608

14 9,9285 10,4417 9,4492 0,9851 9,0771 10,5344 8,8071 2,9838

(42)

Data

Metode regresi robust merupakan metode yang digunakan untuk mengatasi permasalahan pencilan dan dikembangkan dengan tujuan untuk mendapatkan sifat robust (kuat) yang mampu mengenali dan mengatasi adanya pencilan. Metode penduga ini adalah metode pendugaan parameter regresi robust dengan menggunakan konsep pengepasan MKT untuk meminimumkan jumlah kuadrat

(43)

Nilai sisaan kuadrat

∑

akan diurutkan dari terkecil hingga terbesar

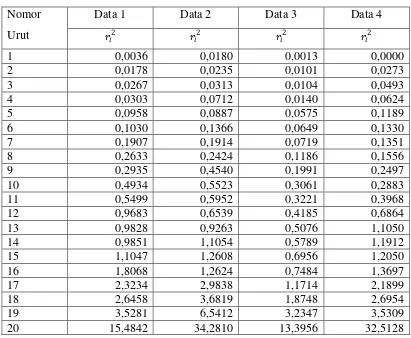
menjadi sebanyak h untuk mendapatkan model penduga dengan metode Least Trimmed Squares. Nilai h dapat dicari dengan rumus ℎ= ��

sehingga dengan jumlah n =20 maka diperolehlah nilai ℎ =20+2+1

2 = 11,5 ≈12.

Tabel 3.8 Sisaaan Kuadrat yang Diurutkan

Tabel 3.9 Data yang Terbentuk dari Sisaan Kuadrat Sudah Diurutkan

(44)

Data

(45)

Tabel 3.10 Perkalian Variabel untuk Data 1 dengan Penduga-LTS

Data ke- � � �� 2

1 9,9292 9,3904 93,239 98,589 2 8,1046 6,7440 54,657 65,684 3 10,6973 10,3699 110,930 114,433 4 8,1715 7,1458 58,392 66,773 5 11,7014 11,6395 136,199 136,923 6 10,2912 10,2815 105,809 105,909 7 9,6483 8,6174 83,144 93,090 8 9,9878 9,0197 90,087 99,756 9 10,7070 11,0885 118,724 114,639 10 9,6268 8,3214 80,109 92,676 11 11,8172 11,3707 134,369 139,646 12 10,4036 9,1351 95,038 108,235 Total 121,086 113,124 1160,700 1236,350 Rata-rata 10,0905 9,4270

Perhitungan nilai �̂₀ dan �̂₁ sebagai berikut:

�̂1 =

1160,700−113,124₁₂�121,086

−₁₂1 (121,086)2_{+ 1236,350}

�̂1 =

1160,700−1141,478

−1221,818 + 1236,350

�̂1 =

19,222 14,532

�̂1 = 1,32

dan

�̂0 = 9,4270−1,32(10,0905)

�̂0 = −3,92

Jadi, diperolehlah model penduga Least Trimmed Squares dengan metode kuadrat terkecilyaitu:

�� =�̂0+�̂1�1�

(46)

Selanjutnya data dengan nilai sisaan kuadrat yang telah diurutkan sebanyak h=12, diperoleh penduga dengan metode kuadrat terkecil melalui tampilan MINITAB 16 (Lampiran 3):

Data 1: ��=−3,92 + 1,32� Data 2: ��= 2,91 + 0,701�

Data 3: ��=− 1,25 + 1,15�

Data 4: ��=−2,63 + 1,27�

3.4.1 Rataan Kuadrat Sisa (Mean Square Error) untuk Penduga-LTS

Setelah diperoleh model untuk penduga-LTS, akan dihitung nilai rataan kuadrat sisa (Mean Square Error) dengan menggunakan rumus berikut:

�2 ₌ ��

� − �

=�� − ��

� − �

Untuk mendapatkan nilai rata-rata kuadrat sisa, akan dihitung nilai jumlah kuadrat regresi dan jumlah kuadrat total dengan hasil perhitungan berikut:

Tabel 3.11 Nilai Jumlah Kuadrat Regresi dan Jumlah Kuadrat Total

Menggunakan Penduga-LTS untuk Data 1

Data

ke- � � �� − ��

2

(�_� − ��)2

1 _11,8038 _11,0423 _11,6610 _4,51718 _2,2700

2 _8,1046 _6,7440 _6,7780 _7,60460 _7,7932

3 _8,0656 _8,3468 _6,7266 _7,89086 _1,4135

4 _10,4036 _9,1351 _9,8128 _0,07678 _0,1605

5 _8,5000 _3,5000 _7,3000 _4,99818 _36,4292

6 _11,7014 _11,6395 _11,5258 _3,96084 _4,4262

(47)

Data

ke- � � �� − ��

2

(�_� − ��)2

8 _10,5793 _11,7110 _10,0447 _0,25914 _4,7322

9 _9,2151 _9,4347 _8,2440 _1,66850 _0,0102

10 _11,8172 _11,3707 _11,6787 _4,59255 _3,3672

11 _10,6973 _10,3699 _10,2005 _0,44201 _0,6960

12 _9,9292 _9,3904 _9,1865 _0,12191 _0,0211

13 _10,0137 _11,4476 _9,2981 _0,05645 _3,6556

14 _9,9285 _10,4417 _9,1856 _0,12255 _0,8208

15 _10,7070 _11,0885 _10,2132 _0,45904 _2,4114

16 _9,6483 _8,6174 _8,8158 _0,51826 _0,8431

17 _9,9878 _9,0197 _9,2639 _0,07385 _0,2662

18 _9,6268 _8,3214 _8,7874 _0,55985 _1,4744

19 _10,3465 _11,6652 _9,7374 _0,04071 _4,5350

20 _8,1715 _7,1458 _6,8664 _7,12504 _5,7116

Jumlah _45,1049 _81,5936

Dari hasil perhitungan pada Tabel 3.11, maka nilai rata-rata kuadrat sisa adalah:

�2 ₌ 81,5936−45,1049 20−2

=36,4887 18

= 2,0272

Jadi, nilai rataan kuadrat sisa data 1 adalah 2,0272.

Data

ke- � � �� − ��

2

(�_� − ��)2

1 _11,0241 _11,4980 _10,6379 _0,62703 _2,7289

2 _10,2882 _10,5252 _10,1220 _0,07617 _0,4612

(48)

Data

ke- � � �� − ��

2

(�_� − ��)2

4 _12,5672 _12,1090 _11,7196 _3,51039 _5,1210

5 _11,0000 _4,5000 _10,6210 _0,60058 _28,5800

6 _9,9557 _10,2858 _9,8890 _0,00184 _0,1934

7 _10,2784 _10,7365 _10,1151 _0,07242 _0,7930

8 _10,4886 _9,8091 _10,2625 _0,17348 _0,0014

9 _8,7464 _9,3495 _9,0412 _0,64772 _0,2466

10 _9,7922 _9,0131 _9,7743 _0,00514 _0,6937

11 _11,8901 _11,2485 _11,2449 _1,95695 _1,9670

12 _11,0021 _11,0305 _10,6225 _0,60288 _1,4029

13 _8,4359 _7,1680 _8,8236 _1,04545 _7,1717

14 _9,0771 _10,5344 _9,2731 _0,32830 _0,4739

15 _9,8870 _7,5402 _9,8408 _0,00003 _5,3169

16 _10,5200 _12,5262 _10,2845 _0,19230 _7,1833

17 _11,3214 _10,9116 _10,8463 _1,00057 _1,1355

18 _9,9333 _9,9338 _9,8732 _0,00074 _0,0077

19 _10,9497 _10,1612 _10,5858 _0,54721 _0,0993

20 _8,5925 _7,3656 _8,9334 _0,83298 _6,1525

Jumlah _13,8746 _70,4161

�2 ₌ 70,4161−13,8746 20−2

=56,5415 18

= 3,1412

(49)

Data

ke- � � �� − ��

2

(�_� − ��)2

1 _9,5773 _9,7371 _9,7639 _0,11646 _0,1355

2 _9,3945 _9,4338 _9,5537 _0,30419 _0,4508

3 _7,9194 _7,7132 _7,8574 _5,05272 _5,7217

4 _10,1013 _9,5401 _10,3665 _0,06830 _0,3193

5 _11,0000 _15,0000 _11,4000 _1,67654 _23,9592

6 _10,7799 _11,6411 _11,1468 _1,08502 _2,3591

7 _10,2695 _8,6576 _10,5600 _0,20681 _2,0955

8 _9,4592 _9,7154 _9,6281 _0,22764 _0,1519

9 _9,4570 _8,7120 _9,6255 _0,23010 _1,9409

10 _9,4673 _10,1323 _9,6374 _0,21886 _0,0007

11 _9,8394 _10,0377 _10,0653 _0,00159 _0,0046

12 _11,5536 _11,6654 _12,0366 _3,73037 _2,4343

13 _9,4288 _8,6048 _9,5931 _0,26223 _2,2511

14 _9,9497 _9,6230 _10,1922 _0,00757 _0,2325

15 _10,7975 _10,0127 _11,1672 _1,12777 _0,0086

16 _10,0982 _10,8020 _10,3629 _0,06640 _0,4855

17 _11,0523 _10,5382 _11,4602 _1,83595 _0,1875

18 _10,1207 _10,5308 _10,3888 _0,08042 _0,1811

19 _8,9341 _10,2095 _9,0242 _1,16847 _0,0109

20 _9,9465 _9,7970 _10,1884 _0,00693 _0,0950

Jumlah _17,4743 _43,0256

�2 ₌ 43,0256−17,4743 20−2

=25,5513 18

(50)

Data

ke- � � �� − ��

2

(�_� − ��)2

1 _9,5036 _9,5427 _9,4396 _0,25300 _0,1599

2 _8,9949 _9,0709 _8,7935 _1,32042 _0,7599

3 _9,7543 _9,6939 _9,7580 _0,03408 _0,0618

4 _10,4547 _11,0912 _10,6474 _0,49675 _1,3192

5 _9,0000 _15,0000 _8,8000 _1,30554 _25,5773

6 _11,8226 _12,5695 _12,3847 _5,96374 _6,9007

7 _10,1489 _10,0318 _10,2591 _0,10014 _0,0079

8 _9,0099 _9,1426 _8,8126 _1,27698 _0,6401

9 _10,4718 _9,6921 _10,6692 _0,52801 _0,0627

10 _8,3023 _6,9711 _7,9139 _4,11546 _8,8298

11 _9,6177 _9,3676 _9,5845 _0,12822 _0,3306

12 _9,6586 _9,1162 _9,6364 _0,09377 _0,6829

13 _9,0581 _8,7251 _8,8737 _1,14249 _1,4823

14 _9,4222 _8,6212 _9,3362 _0,36772 _1,7461

15 _9,9249 _12,0854 _9,9747 _0,00103 _4,5914

16 _9,0239 _10,8013 _8,8303 _1,23711 _0,7374

17 _10,5082 _9,6814 _10,7154 _0,59727 _0,0682

18 _11,0018 _11,2574 _11,3423 _1,95913 _1,7287

19 _8,4898 _7,6267 _8,1521 _3,20590 _5,3635

20 _8,8304 _8,7640 _8,5846 _1,84407 _1,3892

Jumlah _25,9708 _62,4396

(51)

=36,4688 18

= 2,0260

3.5 Regresi Robust Penduga-S

Regresi robust penduga-S dapat diselesaikan melalui MKT terboboti secara iterasi yang disebut Iteratively Reweighted Least Squares (Iterasi kuadrat terkecil terboboti kembali) dengan sisaan awal yang diperoleh dari regresi robust penduga-M.

Proses perhitungan penduga koefisien regresi penduga-M dan pengolahan data 1 yang terdapat pada Tabel 3.1 dapat dilakukan dengan mengikuti prosedur sebagai berikut:

1. Menghitung koefisien regresi menggunakan metode kuadrat terkecil, didapatkan nilai b dan ε�_,0.

2. Menghitung nilai ��₀= 1,5 (median |ε�_,0|) sehingga didapatkan nilai �_�∗_,0 dan |�_�∗_,0|.

3. Menentukan nilai ψ(εi*) dan pembobot wi,0 sesuai dengan fungsi Huber.

Hasil perhitungan terdapat pada Tabel 3.15.

Prosedur berikutnya yaitu:

4. Melakukan perhitungan bRobust ke-1 sebagai penaksir weighted least square

dengan pembobot wi,0, diperolehlah koefisien bRobust ke 1 , ε�,1, ��1 = 1,5

(median |ε_�_,1|), �_�∗_,0, ψ(εi*) dan pembobot wi,1, serta nilai ∑ ��=1 ,1�.

(52)

Tabel 3.15 Hasil Perhitungan Koefisien Regresi Iterasi ke-1

� ε_�,0 |ε�,0| ��∗,0 |��∗,0 | ��,0=

ψ(�_�∗_,0)

�_�∗,0

-4,54687 1,05104 1,05104 0,97049 0,97049 1,0000 1,41151 0,13339 0,13339 0,12317 0,12317 1,0000 -1,52426 1,52426 -1,40745 1,40745 0,7105 0,98401 0,98401 0,90860 0,90860 1,0000 3,93500 3,93500 3,63344 3,63344 0,2752 0,30945 0,30945 0,28574 0,28574 1,0000 -0,32091 0,32091 -0,29632 0,29632 1,0000 -1,34416 1,34416 -1,24115 1,24115 0,8057 -0,99138 0,99138 -0,91541 0,91541 1,0000 0,74158 0,74158 0,68474 0,68474 1,0000 0,16336 0,16336 0,15084 0,15084 1,0000 0,05976 0,05976 0,05518 0,05518 1,0000 -1,87833 1,87833 -1,73438 1,73438 0,5766 -0,99251 0,99251 -0,91644 0,91644 1,0912 -0,54172 0,54172 -0,50020 0,50020 1,0000 0,43667 0,43667 0,40320 0,40320 1,0000 0,51310 0,51310 0,47378 0,47378 1,0000 0,70242 0,70242 0,64859 0,64859 1,0000 -1,62659 1,62659 -1,50193 1,50193 0,6658 -0,17395 0,17395 -0,16062 0,16062 1,0000

� ε�,1 |ε�,1| �_�∗,1 |��∗,1 | ��,1=

ψ(�_�∗_,1)

�_�∗,1

(53)

� ε_�,1 |ε�,1| ��∗,1 |��∗,1 | ��,1=

ψ(�_�∗_,1)

�_�∗,1

-0,30224 0,30224 -0,27181 0,27181 1,0000 -1,32506 1,32506 -1,19162 1,19162 0,8392 -0,97434 0,97434 -0,87622 0,87622 1,0000 0,76255 0,76255 0,68576 0,68576 1,0000 0,18264 0,18264 0,16425 0,16425 1,0000 0,07789 0,07789 0,07004 0,07004 1,0000 -1,86008 1,86008 -1,67277 1,67277 0,5978 -0,97438 0,97438 -0,87626 0,87626 1,0000 -0,52242 0,52242 -0,46981 0,46981 1,0000 0,45437 0,45437 0,40861 0,40861 1,0000 0,53131 0,53131 0,47781 0,47781 1,0000 0,72009 0,72009 0,64757 0,64757 1,0000 -1,60783 1,60783 -1,44592 1,44592 0,6916 -0,15848 0,15848 -0,14252 0,14252 1,0000

Selanjutnya, pembobot wi,1 digunakan untuk menghitung koefisien regresi

yang baru yaitu bRobust ke 2. Perhitungan ini dilanjutkan sampai didapatkan nilai

∑ ��_�=1 ,�� yang konvergen. Selain perhitungan dengan prosedur, pendugaan

koefisien regresi dengan penduga-M dapat juga dihitung menggunakan bantuan program macro MINITAB di Lampiran 4 untuk mendapatkan estimasi parameter regresi. Selanjutnya, hasil output dari program dapat dilihat di Lampiran 5. Sementara itu, perhitungan penaksir koefisien regresi untuk data 2, data 3 dan data 4 juga dilakukan dilakukan dengan prosedur yang sama dengan data 1.

Regresi Robust penduga-M diperoleh melalui MKT terboboti secara iterasi dengan bantuan MACRO MINITAB 16 dapat dilihat di lampiran 5 yakni:

Tabel 3.17 Nilai Koefisien Regresi Penduga-M

Koefisien Regresi

Data 1 Data 2 Data 3 Data 4 Iterai ke-7 Iterasi ke-15 Iterasi ke-12 Iterasi ke-10 �0 -2,31699 0,41707 -0,15310 -2,72275

�1 1,19616 0,93058 1,01610 1,27240

(54)

Berdasarkan nilai pada Tabel 3.26, maka diperoleh model regresi robust

Tabel 3.18 Sisaan dari Persamaan Penduga-M

(55)

Data ke-

Data 3 Data 4

� � ��

14 9,9497 9,6230 9,9568 0,33381 9,4222 8,6212 9,2657 0,64448

15 10,7975 10,0127 10,8183 0,80560 9,9249 12,0854 9,9053 -2,18003 16 10,0982 10,8020 10,1076 -0,69436 9,0239 10,8013 8,7589 -2,04241 17 11,0523 10,5382 11,0772 0,53894 10,5082 9,6814 10,6475 0,96611 18 10,1207 10,5308 10,1305 -0,40028 11,0018 11,2574 11,2755 0,01808 19 8,9341 10,2095 8,9249 -1,28464 8,4898 7,6267 8,0794 0,45269

20 9,9465 9,7970 9,9535 0,15646 8,8304 8,7640 8,5127 -0,25124

Proses perhitungan penduga koefisien regresi robust penduga-S dan pengolahan data 1 yang terdapat pada Tabel 3.1 setelah didapatkan penduga-M adalah sebagai berikut:

a. Dari sisaan yang diperoleh pada penduga-M, dihitung robust �� sesuai persamaan (2.19) untuk mendapatkan nilai �_� sesuai persamaan(2.14).

b. Menghitung nilai �� sesuai persamaan (2.21).

c. Digunakan MKT terboboti untuk mendapatkan penduga kuadrat terkecil terboboti:

β * = (X’WX)-1 X’WY

d. Menjadikan sisaan yang diperoleh pada langkah (c) sebagai sisaan pada langkah (a), sehingga didapatkan nilai �_� dan pembobot �� yang baru.

Hasil perhitungan terdapat pada Tabel 3.19.

Iterasi ulang sampai didapatkan kekonvergenan sehingga diperoleh �₀�,�1�, … ,��

yang merupakan penduga-S.

�� = 1,31884; � = 1,547

� ε_�,0 ��∗,0 |��∗,0 | ��,0

(56)

� ε�,0 ��∗,0 |��∗,0 | ��,0

0,04024 0,03051 0,03051 0,9992 -0,28857 -0,21881 0,21881 0,9604 -1,37344 -1,04140 1,04140 0,2990 -0,72893 -0,55271 0,55271 0,7610 0,44760 0,33939 0,33939 0,9061 0,10885 0,08253 0,08253 0,9943 0,16952 0,12854 0,12854 0,9862 -1,78665 -1,35472 1,35472 0,0544 -0,88260 -0,66923 0,66923 0,6607 -0,59829 -0,45365 0,45365 0,8354 0,60648 0,45986 0,45986 0,8311 0,61031 0,46277 0,46277 0,8290 0,87683 0,66485 0,66485 0,6647 -1,60608 -1,21780 1,21780 0,1446 0,31167 0,23632 0,23632 0,9539

�� = 1,33121;� = 1,547

� ε�,1 �_�∗,1 |��∗,1 | ��,1

(57)

� ε�,1 ��∗,1 |��∗,1 | ��,1

-1,85996 -1,39720 1,39720 0,0340 -0,95150 -0,71477 0,71477 0,6186 -0,70747 -0,53145 0,53145 0,7779 0,55208 0,41472 0,41472 0,8614 0,53834 0,40440 0,40440 0,8680 0,82354 0,61864 0,61864 0,7057 -1,69662 -1,27450 1,27450 0,1032 0,33369 0,25067 0,25067 0,9482

Selanjutnya, pembobot ��, 1 digunakan untuk menghitung koefisien regresi yang baru yaitu �Robust ke-2. Perhitungan ini dilanjutkan sampai didapatkan

nilai ∑ ��_�₌₁ _,_�� yang konvergen. Selain perhitungan dengan prosedur, pendugaan koefisien regresi dengan penduga-S dapat juga dihitung menggunakan bantuan R di Lampiran 6 untuk mendapatkan estimasi parameter regresi. Sementara itu, perhitungan penduga koefisien regresi untuk data 2, data 3, data 4 juga dilakukan dilakukan dengan prosedur yang sama dengan data 1.

Berdasarkan hasil output yang dihasilkan untuk masing-masing data menggunakan MINITAB 16 dan R, diperolehlah regresi robust penduga-S yakni nilai ∑�_�₌₁|��_:_�| yang konvergen pada masing-masing data yaitu sebagai berikut:

Tabel 3.21 Nilai Koefisien Regresi Penduga-S

Koefisien Regresi

Data 1 Data 2 Data 3 Data 4 Iterasi ke-3 Iterasi ke-2 Iterasi ke-4 Iterasi ke-5 �0 -1,75707 0,46289 0,11834 -3,35955

�1 1,12792 0,93006 0,98561 1,32403

∑�_�=1|�_�:�| 18,1323 20,8661 14,4742 17,4313

Berdasarkan nilai pada Tabel 3.19, maka diperoleh model regresi robust penduga-S sebagai berikut:

(58)

Data 2: ��_� = 0,4628948 + 0,93006�

Data 3: ��_� = 0,11834 + 0,98561�

Data 4: ��_� = −3,35955 + 1,32403�

3.5.1 Rataan Kuadrat Sisa (Mean Square Error) untuk Penduga-S

Setelah diperoleh model untuk penduga-S, akan dihitung nilai rataan kuadrat sisa (Mean Square Error) dengan menggunakan rumus berikut:

�2 = ��

� − �

=�� −��

�−�

Untuk mendapatkan nilai rata-rata kuadrat sisa, akan dihitung nilai jumlah kuadrat regresi dan jumlah kuadrat total dengan hasil perhitungan berikut:

Tabel 3.22 Nilai Jumlah Kuadrat Regresi dan Jumlah Kuadrat Total

Menggunakan Penduga-S untuk Data 1

Data

ke- � � �� − ��

2

(�_� − ��)2

1 _11,8038 _11,0423 _11,5567 _4,08459 _2,2700

2 _8,1046 _6,7440 _7,3842 _4,62864 _7,7932

3 _8,0656 _8,3468 _7,3403 _4,81964 _1,4135

4 _10,4036 _9,1351 _9,9774 _0,19511 _0,1605

5 _8,5000 _3,5000 _7,8303 _2,90839 _36,4292

6 _11,7014 _11,6395 _11,4412 _3,63104 _4,4262

7 _10,2912 _10,2815 _9,8506 _0,09917 _0,5563

8 _10,5793 _11,7110 _10,1756 _0,40950 _4,7322

9 _9,2151 _9,4347 _8,6369 _0,80785 _0,0102

10 _11,8172 _11,3707 _11,5718 _4,14581 _3,3672

(59)

Data

ke- � � �� − ��

2

(�_� − ��)2

12 _9,9292 _9,3904 _9,4423 _0,00872 _0,0211

13 _10,0137 _11,4476 _9,5376 _0,00000 _3,6556

14 _9,9285 _10,4417 _9,4415 _0,00887 _0,8208

15 _10,7070 _11,0885 _10,3195 _0,61446 _2,4114

16 _9,6483 _8,6174 _9,1255 _0,16827 _0,8431

17 _9,9878 _9,0197 _9,5084 _0,00074 _0,2662

18 _9,6268 _8,3214 _9,1012 _0,18871 _1,4744

19 _10,3465 _11,6652 _9,9130 _0,14240 _4,5350

20 _8,1715 _7,1458 _7,4597 _4,30944 _5,7116

Jumlah _31,7689 _81,5936

�2 ₌ 81,5936−31,7689 20−2

=49,8247 18

= 2,7680

Data

ke- � � �� − ��

2

(�_� − ��)2

1 _11,0241 _11,4980 _10,7159 _0,75673 _2,7289

2 _10,2882 _10,5252 _10,0315 _0,03440 _0,4612

3 _11,7282 _10,6744 _11,3708 _2,32499 _0,6862

4 _12,5672 _12,1090 _12,1511 _5,31358 _5,1210

5 _11,0000 _4,5000 _10,6935 _0,71826 _28,5800

6 _9,9557 _10,2858 _9,7223 _0,01531 _0,1934

(60)

Data

ke- � � �� − ��

2

(�_� − ��)2

8 _10,4886 _9,8091 _10,2179 _0,13832 _0,0014

9 _8,7464 _9,3495 _8,5975 _1,55871 _0,2466

10 _9,7922 _9,0131 _9,5702 _0,07610 _0,6937

11 _11,8901 _11,2485 _11,5213 _2,80669 _1,9670

12 _11,0021 _11,0305 _10,6955 _0,72160 _1,4029

13 _8,4359 _7,1680 _8,3088 _2,36320 _7,1717

14 _9,0771 _10,5344 _8,9051 _0,88528 _0,4739

15 _9,8870 _7,5402 _9,6584 _0,03522 _5,3169

16 _10,5200 _12,5262 _10,2471 _0,16089 _7,1833

17 _11,3214 _10,9116 _10,9925 _1,31433 _1,1355

18 _9,9333 _9,9338 _9,7014 _0,02091 _0,0077

19 _10,9497 _10,1612 _10,6468 _0,64121 _0,0993

20 _8,5925 _7,3656 _8,4544 _1,93655 _6,1525

Jumlah _21,8533 _70,4161

�2 ₌ 70,4161−21,8533 20−2

=48,5628 18

= 2,6979

Tabel 3.24 Nilai Jumlah Kuadrat Regresi dan Jumlah Kuadrat Total

Data

ke- � � �� − ��

2

(�_� − ��)2

1 _9,5773 _9,7371 _9,5579 _0,29957 _0,1355

2 _9,3945 _9,4338 _9,3776 _0,52932 _0,4508

(61)

Data

ke- � � �� − ��

2

(�_� − ��)2

4 _10,1013 _9,5401 _10,0743 _0,00095 _0,3193

5 _11,0000 _15,0000 _10,9601 _0,73081 _23,9592

6 _10,7799 _11,6411 _10,7431 _0,40691 _2,3591

7 _10,2695 _8,6576 _10,2401 _0,01820 _2,0955

8 _9,4592 _9,7154 _9,4414 _0,44058 _0,1519

9 _9,4570 _8,7120 _9,4392 _0,44351 _1,9409

10 _9,4673 _10,1323 _9,4494 _0,43007 _0,0007

11 _9,8394 _10,0377 _9,8162 _0,08352 _0,0046

12 _11,5536 _11,6654 _11,5057 _1,96133 _2,4343

13 _9,4288 _8,6048 _9,4115 _0,48126 _2,2511

14 _9,9497 _9,6230 _9,9249 _0,03250 _0,2325

15 _10,7975 _10,0127 _10,7605 _0,42943 _0,0086

16 _10,0982 _10,8020 _10,0712 _0,00116 _0,4855

17 _11,0523 _10,5382 _11,0116 _0,82162 _0,1875

18 _10,1207 _10,5308 _10,0934 _0,00014 _0,1811

19 _8,9341 _10,2095 _8,9239 _1,39544 _0,0109

20 _9,9465 _9,7970 _9,9217 _0,03368 _0,0950

Jumlah _13,2983 _43,0256

�2 ₌ 43,0256−13,2983 20−2

=29,7273 18

= 1,6515