MODEL PENJADWALAN GURU MENGGUNAKAN
GRAPH COLORING DENGAN ALGORITMA
BEE COLONY
TESIS
Oleh
SETIAWAN TANADI 117021027/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MODELPENJADWALAN GURU MENGGUNAKAN
GRAPH COLORING DENGAN ALGORITMA
BEE COLONY
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
SETIAWAN TANADI
117021027/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
Judul Tesis : MODELPENJADWALAN GURU MENGGUNAKAN GRAPH COLORING DENGAN ALGORITMA
BEE COLONY Nama Mahasiswa : Setiawan Tanadi Nomor Pokok : 117021027
Program Studi : Magister Matematika
Menyetujui, Komisi Pembimbing
(Prof. Dr. Opim Salim S, M.Sc ) (Dr. Marwan Ramli, M.Si )
Ketua Anggota
Ketua Program Studi Dekan
(Prof. Dr. Herman Mawengkang ) (Dr. Sutarman, M.Sc )
Telah diuji pada
Tanggal : 3 Juni 2013
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Opim Salim S, M.Sc Anggota : 1. Dr. Marwan Ramli, M.Si
PERNYATAAN
MODEL PENJADWALAN GURU MENGGUNAKAN GRAPH COLORING DENGAN ALGORITMA BEE COLONY
TESIS
Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing dituliskan sumbernya
Medan, 3 Juni 2014 Penulis,
ABSTRAK
Penjadwalan merupakan salah satu masalah periodik yang rumit dan sering menga-lami kesulitan khususnya disetiap sekolah dan universitas yang terdapat diseluruh dunia. Banyak faktor yang mempengaruhi penyusunan penjadwalan. Salah satu diantaranya adalah pengalokasian mata pelajaran dengan guru dan ruangan kelas sering mengalami benturan dengan jadwal mata pelajaran, guru dan ruangan kelas yang lain dalam satu periode jadwal sekolah. Oleh karena itu, penelitian ini akan memfokuskan pada masalah bagaimana memodelkan penjadwalan menggunakan teknik pewarnaan graph dengan algoritma bee colonydimana vertex merepresen-tasikanmata pelajaran yang akan dijadwalkan, edge merepresentasikan pasangan jam mengajaryang bisa menimbulkan konflik dan warna pada vertex merepresen-tasikan periode waktu kapan pelajaran tersebut dijadwalkan. Jika terdapat dua vertexvdanwyang terhubung oleh sebuah edge vw maka kedua vertex harus diwar-nai dengan warna yang berbeda. Jumlah minimum warna yang dibutuhkan untuk mewarnai sebuah graph disebut angkakromatik dari G atau dinotasikan dengan X(G). Sebuah graph dengan pewarnaan vertex yang tepat akan mewarnai sepasang vertex yang terhubung oleh edge dengan warna yang berbeda. Pasangan vertex yang tidak terhubung oleh edge bisa menggunakan dua warna yang sama atau berbeda. Salah satu algoritma metaheuristik yaitu bee colony digunakan dalam tesis ini untuk fungsi pewarnaan graph sehingga menghasilkan suatu model pen-jadwalan guru yang dapat digunakan untuk mengatur jadwal secara optimal agar proses belajar mengajar dapat berlangsung dengan lancar.
ABSTRACT
Scheduling is a one of the most complicated periodically problem that often meet difficulties especially at schools and universitiesall around the world. Many factors may influence the scheduling management. One of them is allocation among the teachers, lessons and classrooms with other teachers, lessons and classrooms in one periodic of time. Therefore, this research will focus on how to create a schedu-lings model by usingcoloring graph technique and algorithm of bee colony, which the vertex represents lesson that is needed to be scheduled, edge represents a pairing in teachings time which may have aconflict and color in the vertex represents aperiodic of time, whenever the lessons are scheduled. If there are 2 vertex v and w which is connected by an edge vw, so these two vertexs must be colored with different color. The sum of the minimum color which is needed for coloring a graph named cromatic number of G or notated as X(G). A graph with the exact coloring vertex will colora pair of vertex which is connected by an edge with different color. Pairing vertex which is not connected by the edge can use two same colors or different ones. One of the metaheuristic algorithm is bee colony which used to have the function of co-loring graph so that the model can create an optimum result of teachers scheduling in order to proceed a better process in teaching.
KATA PENGANTAR
Puji syukur penulis mengucapkan kepada Tuhan Yang Maha Esa yang telah melimpahkan rahmat, hidayah, dan karunia-Nya, sehingga penulis dapatmenyele-saikan tesis dengan judul: MODEL PENJADWALAN GURU
MENGGU-NAKAN GRAPH COLORING DENGAN ALGORITMA BEE COLONY.
Tesis ini merupakan salah satu syarat untuk menyelesaikan studi pada Program Stu-di Magister Matematika FMIPA Universitas Sumatera Utara.Pada kesempatan ini, penulis menyampaikan ucapan terima kasih dan penghargaan yang sebesar-besarnya kepada:
Prof. Dr. dr. Syahril Pasaribu, DTMH, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara.
Dr. Sutarman, M.Sc selaku Dekan FMIPA Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Studi Ma-gister Matematika di Sekolah Pascasarjana Universitas Sumatera Utara.
Prof. Dr. HermanMawengkangselaku Ketua Program Studi Magister Matem-atika FMIPA Universitas Sumatera Utara dan selaku pembanding tesis.
Prof. Dr. Saib Suwilo, M.Scselaku Sekretaris Program Studi Magister Matem-atika FMIPA Universitas Sumatera Utara.
Prof. Dr. Opim Salim S, M.Sc selaku pembimbing utama yang dengan sabar memberikan bimbingan dan arahan yang telah banyak memberikan bantuan dalam penulisan tesis ini.
Dr. Marwan Ramli, M.Si selaku pembimbing kedua yang telah banyak mem-berikan bimbingan dan motivasi dalam menyelesaikan penulisan tesis ini.
Dr. Erna Budhiarti selaku Tim Pembanding Tesis.
Saudari Misiani, S.Si selaku Staf Administrasi Program Studi Magister Matem-atika Universitas Sumatera Utara yang telah banyak memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.
Seluruh rekan-rekan Mahasiswa angkatan 2011-2013 pada Program Studi Ma-gister Matematika Universitas Sumatera Utara yang telah memberikan bantuan moril dan dorongan kepada penulis.
Secara khusus penulis menyampaikan terimakasih dan sayang yang mendalam kepada orang tua penulis, Ayah Ng Tiam Meng dan ibu Lie Sioe Hing, serta kepada seluruh keluarga yang senantiasa memberikan dukungan dan mendoakan keberhasilan penulis dalam menyelesaikan pendidikan ini.
Kepada seluruh pihak yang tidak dapat penulis sebutkan satu persatu, penulis berterima kasih atas semua bantuan yang diberikan, semoga Tuhan membalaskan segala kebaikan yang telah diberikan, amin.
Penulis menyadari bahwa tesis ini masih jauh dari sempurna, untuk itu penulis mengharapkan kritik saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya baik perkem-bangan ilmu pengetahuan.
Medan, Penulis,
RIWAYAT HIDUP
DAFTAR ISI
Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Rumusan Masalah 2
1.3 Tujuan Penelitian 2
1.4 Manfaat Penelitian 3
BAB 2 TINJAUAN PUSTAKA 4
2.1 Model Penjadwalan 5
2.2 Graph 5
2.2.1 Teori Graph 5
2.2.2 Graph berbobot 8
2.2.3 Representasi Graph 8
2.2.4 Lintasan terpendek (shortest path) 10
2.2.5 Pewarnaan graph 11
2.2.6 Bilangan kromatik 12
2.3.1 Penjadwalan dengan metode graph 14
2.4 Masalah Pewarnaan Graph dalam Penjadwalan 14
2.4.1 Multicoloring 14
2.4.2 Precoloring extension 15
2.4.3 List coloring 15
2.4.4 Minimum sum coloring 15
2.5 Algoritma Bee Colony 15
BAB 3 METODOLOGI PENELITIAN 19
3.1 Teknik Pewarnaan Graph 19
3.2 Pengumpulan Data 20
3.3 Konstruksi Graph Konflik Pelajaran 20
3.4 Pewarnaan Graph Konflik Pelajaran 22
BAB 4 MODEL PENJADWALAN GURU 25
BAB 5 KESIMPULAN 31
5.1 Kesimpulan 31
DAFTAR GAMBAR
Nomor Judul Halaman
2.1 Graph tak berarah 7
2.2 Graph berarah 7
2.3 Graph berbobot 8
2.4 Graph matriks ketetanggaan 9
2.5 Graph Matriks Bersisian 9
3.1 Mata pelajaran mi dan mj dijadwalkan pada slot waktu yang
berbeda 21
3.2 Mata pelajaran mi dan mj di pasangkan pada slot waktu yang
sama 22
3.3 Mata pelajaran mi dan mj di pasang pada ruangan kelas yang
berbeda dan slot waktu yang berbeda 22
3.4 Mata pelajaran mi dan mj di pasang pada ruangan kelas yang
sama dan slot waktu yang berbeda 23
3.5 Mata pelajaran mi dan mj tidak berpotensi menimbulkan konflik,
di pasang pada ruangan kelas yang berbeda dan slot waktu yang
berbeda 23
3.6 Mata pelajaran mi dan mj tidak berpotensi menimbulkan konflik,
di pasang pada ruangan kelas yang berbeda dan slot waktu yang
sama 24
3.7 Mata pelajaran mi dan mj tidak berpotensi menimbulkan konflik,
di pasang pada ruangan kelas yang sama dan slot waktu yang
ABSTRAK
Penjadwalan merupakan salah satu masalah periodik yang rumit dan sering menga-lami kesulitan khususnya disetiap sekolah dan universitas yang terdapat diseluruh dunia. Banyak faktor yang mempengaruhi penyusunan penjadwalan. Salah satu diantaranya adalah pengalokasian mata pelajaran dengan guru dan ruangan kelas sering mengalami benturan dengan jadwal mata pelajaran, guru dan ruangan kelas yang lain dalam satu periode jadwal sekolah. Oleh karena itu, penelitian ini akan memfokuskan pada masalah bagaimana memodelkan penjadwalan menggunakan teknik pewarnaan graph dengan algoritma bee colonydimana vertex merepresen-tasikanmata pelajaran yang akan dijadwalkan, edge merepresentasikan pasangan jam mengajaryang bisa menimbulkan konflik dan warna pada vertex merepresen-tasikan periode waktu kapan pelajaran tersebut dijadwalkan. Jika terdapat dua vertexvdanwyang terhubung oleh sebuah edge vw maka kedua vertex harus diwar-nai dengan warna yang berbeda. Jumlah minimum warna yang dibutuhkan untuk mewarnai sebuah graph disebut angkakromatik dari G atau dinotasikan dengan X(G). Sebuah graph dengan pewarnaan vertex yang tepat akan mewarnai sepasang vertex yang terhubung oleh edge dengan warna yang berbeda. Pasangan vertex yang tidak terhubung oleh edge bisa menggunakan dua warna yang sama atau berbeda. Salah satu algoritma metaheuristik yaitu bee colony digunakan dalam tesis ini untuk fungsi pewarnaan graph sehingga menghasilkan suatu model pen-jadwalan guru yang dapat digunakan untuk mengatur jadwal secara optimal agar proses belajar mengajar dapat berlangsung dengan lancar.
ABSTRACT
Scheduling is a one of the most complicated periodically problem that often meet difficulties especially at schools and universitiesall around the world. Many factors may influence the scheduling management. One of them is allocation among the teachers, lessons and classrooms with other teachers, lessons and classrooms in one periodic of time. Therefore, this research will focus on how to create a schedu-lings model by usingcoloring graph technique and algorithm of bee colony, which the vertex represents lesson that is needed to be scheduled, edge represents a pairing in teachings time which may have aconflict and color in the vertex represents aperiodic of time, whenever the lessons are scheduled. If there are 2 vertex v and w which is connected by an edge vw, so these two vertexs must be colored with different color. The sum of the minimum color which is needed for coloring a graph named cromatic number of G or notated as X(G). A graph with the exact coloring vertex will colora pair of vertex which is connected by an edge with different color. Pairing vertex which is not connected by the edge can use two same colors or different ones. One of the metaheuristic algorithm is bee colony which used to have the function of co-loring graph so that the model can create an optimum result of teachers scheduling in order to proceed a better process in teaching.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Penjadwalan merupakan proses untuk menyusun suatu jadwal atau urutan proses yang diperlukan dalam sebuah persoalan. Penjadwalan juga merupakan pengalokasian sumber daya baik alam maupun manusia dalam rentang waktu ter-tentu untuk menyelesaikan sekumpulan tugas. Di samping itu penjadwalan juga penting dalam merancang dan mengatur suatu sistem yang terdiri dari sejumlah kegiatan dengan keterbatasan sumber daya. Perubahan metode atau kurikulum pendidikan yang dinamis dan interaktif berdampak pada modelmodel penyusunan jadwal. Perubahan ini mengakibatkan masalah penjadwalan dalam institusi pen-didikan merupakan masalah optimisasi yang ditemukan pada situasi nyata, (Ariani dan Fahriza, 2004).
Persoalan penjadwalan bukan hanya berhubungan dengan penjadwalan kelas dalam sekolah atau perkuliahan melainkan juga dalam ruang lingkup yang tidak jauh berbeda seperti penjadwalan ujian maupun penjadwalan karyawan, baik dalam suatu perusahaan ataupun dalam sebuah rumah sakit. Dalam penjadwalan kuliah, akan dibahas tentang pembagian jadwal untuk tiap mahasiswa pada kuliah tertentu sekaligus dosen pengajarnya, dalam penjadwalan pelajaran sekolah akan dibahas tentang pembagian jadwal pelajaran untuk masing masing kelas yang ada beserta guru yang mengampu pelajaran tersebut, dalam penjadwalan ujian akan dibahas tentang pengaturan dosen atau guru yang mengawas saat ujian dan mahasiswa atau murid yang menempati ruang ujian yang ada, sedangkan pada penjadwalan karyawan, dilakukan pengaturan karyawan yang akan bekerja pada waktu tertentu di bagian tertentu, (Ariani dan Fahriza, 2004).
mela-2
kukan hal ini dan memungkinkan terjadinya pelanggaran constraintakibat human error. Pelanggaran constraintdalam penjadwalan menjadikan jadwal yang tersusun menjadi tidak valid dan harus direkonstruksi ulang. Jika kejadian seperti ini selalu berulang pada saat menghadapi tahun ajaran baru, maka sepatutnya permasala-han ini mendapat prioritas untuk dicari solusinya demi peningkatan mutu sistem akademik di sekolah.
Di perguruan tinggi maupun sekolahsekolah, penjadwalan merupakan salah satu hal penting dalam proses belajar mengajar, karena semua kegiatan guru dan siswa bergantung pada jadwal yang ada, sehingga harus disusun dengan benar dan diperbaiki pada awal tahun akademik, sehingga nantinya tidak mengganggu aktivitas belajar mengajar antara guru/dosen dan siswa/mahasiswa.
Selama ini penjadwalan roster guru di sekolah SMP swasta Sutomo 1 Medan masih dilakukan secara manual, sehingga pada saat menyusun roster tersebut agar para guru bisa mengajar di kelas masingmasing dengan baik dan lancar, diperlukan waktu dan pengaturan yang cukup rumit. Oleh karena itu dalam tesis ini, penulis akan menggunakan teknik pewarnaan graph dengan algoritma bee colony untuk menyusun model penjadwalan kelas termasuk di dalamnya penjadwalan praktikum,
yakni praktikum Biologi, Fisika dan Bahasa Inggris. Hal ini disebabkan jadwal praktikum merupakan salah satu faktor penting yang perlu dijadwalkan karena termasuk dalam kurikulum pendidikan sekolah.
1.2 Rumusan Masalah
Penjadwalan guru adalah hal yang kompleks dan NP Hard karena banyak con-straint yang harus dipenuhi. Oleh karena itu diperlukan suatu model penjadwalan yang dapat menggambarkan semua constraintyang harus dipenuhi.
1.3 Tujuan Penelitian
3
1.4 Manfaat Penelitian
BAB 2
TINJAUAN PUSTAKA
Pada umumnya beragam model penjadwalan telah dikembangkan seperti pro-gram matematis dengan berbagai teknik diantaranya Wardoyo (2003) menggunakan logika Fuzzy, yakni suatu cara untuk memetakan suatu ruang masukkan ke dalam suatu ruang keluaran, Betrianis dan Aryawan (2003) menggunakan algoritma Tabu Search, yang mana merupakan salah satu metode pemecahan permasalahan opti-masi kombinatorial yang tergabung ke dalam local search methods, Ronny et al. (2005) menggunakan algoritma Branch and Bound untuk mencari solusi optimal pada masalah optimisasi kombinatorial seperti masalah penjadwalan.
Salah satu penelitian untuk penyelesaian penjadwalan dilakukan oleh Redl dan Anton (2004). Yang bersangkutan menawarkan proses pemasangan kelas di-lakukan bersamaan dengan proses pencarian slot waktu itu sendiri. Teknik ini dapat menghemat waktu yang harus dilakukan. Dalam hal ini, Redl dan Anton (2004) memanfaatkan teknik pewarnaan graphyang diselesaikan dengan menggunakan al-goritma sekuensial dan alal-goritma greedy. Algoritma sekuensial merupakan suatu algoritma runtun dimana teknik pengerjaannya harus dilakukan secara berurutan mulai dari baris pertama sampai dengan baris terakhir tanpa ada loncatan atau perulangan sedangkan algoritma greedyadalah suatu algoritma yang dalam meme-cahkan suatu masalah selalu mengambil pilihan yang terbaik dan dapat diperoleh pada saat itu tanpa memperhatikan lagi konsekuensi di depan (”take what you can get now ”).
Penelitian lain tentang penjadwalan dilakukan pula oleh Komang (2008) de-ngan menggunakan algoritma metaheuristik kombinasi genetika dede-ngantabu search. Penelitian tersebut melakukan perbandingan hasil yang diperoleh saat menggu-nakan algoritma genetika dengan algoritma kombinasi genetika dan tabu search.
penjad-5
Search kemudian dievaluasi sehingga menghasilkan solusi yang layak.
Menurut Rachmawatiet al. (2011) banyak faktor yang harus dipertimbangkan untuk memperoleh solusi yang optimal dan seringkali tidak dapat memuaskan kare-na tidak semua kebutuhan terpenuhi. Oleh karekare-na itu, perlu ditetapkan suatu batasan dalam penyusunan jadwal yang mutlak harus dipenuhi (hard constraint) dan tidak harus dipenuhi (soft constraint), akan tetapi tetap menjadi acuan dalam proses pembuatan jadwal. Sebuah jadwal dikatakan layak, apabila solusi tersebut memenuhi semua ketentuanhard constrainttanpa ada pelanggaran. Sementara so-lusi jadwal dikatakan optimal apabila jumlah pelanggaran terhadap soft constraint minimum.
2.1 Model Penjadwalan
Permasalahan penjadwalan dapat dimodelkan dan diselesaikan dengan teknik pewarnaan graph. Masalah pewarnaan graph dikenal dengan Optimisasi Kombi-natorial. Rachmawati et al. (2011), menyatakan selain untuk penjadwalan, pe-warnaan graph juga dapat digunakan dalam aplikasi pemasangan frekuensi pada jaringan selular, pemasangan kru karyawan dan sebagainya. Pada model konven-sional pewarnaan graph untuk penjadwalan, vertex merepresentasikan mata pela-jaran yang akan dijadwalkan, edge merepresentasikan pasangan jam mengajar yang bisa menimbulkan konflik (tidak bisa dijadwalkan pada waktu yang sama), dan war-na pada vertex merepresentasikan periode waktu pelajaran tersebut dijadwalkan. Jika terdapat dua vertexvdanwyang terhubung oleh sebuah edgevwmaka kedua vertex harus diwarnai dengan warna yang berbeda. Jumlah minimum warna yang dibutuhkan untuk mewarnai sebuah graph disebut angka kromatik dari G atau dinotasikan dengan X(G).
2.2 Graph
2.2.1 Teori Graph
6
jembatan Konigsberg. Dari permasalahan itu, akhirnya Euler mengembangkan be-berapa konsep mengenai teori graph. Materi -materi yang terdapat dalam teori graph itu sendiri adalah ilmu yang mempelajari mengenai logika dari persoalan yang berhubungan dengan himpunan dan relasi binary. (Hariyanto, 2003).
Graph merupakan salah satu model matematika yang kompleks dan cukup sulit, akan tetapi bisa juga menjadi solusi yang sangat bagus untuk masalah ter-tentu. Oleh sebab itu, representasi dari suatu graph bergantung dari sifat data dan operasi yang dilakukan terhadap data dari sebuah kasus tertentu. Dalam ke-hidupan sehari-hari banyak sekali persoalan yang diimplementasikan dengan graph. Bidang-bidang yang menggunakan penerapan graph antara lain switching network, coding theory, electric analysis, operation research, aljabar, computer science dan kimia. (Deo, 1974).
Keunikan teori graph adalah kesederhanaan pokok bahasan yang dipelajarinya karena dapat disajikan dengan titik (simpul atau vertex) dan garis (sisi atau edge). Meskipun pokok bahasan dari topik-topik teori graph sangat sederhana tetapi isi di dalamnya belum tentu sesederhana itu. Kerumitan demi kerumitan masalah selalu ada dan bahkan sampai saat ini masih ada masalah yang belum terpecahkan. Teori
graph telah banyak memberikan masukan kepada ilmu baru salah satunya adalah pewarnaan graph. Graph juga digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Banyak persoalan pada dunia nyata yang sebenarnya merupakan representasi visual dari graph. Contoh salah satu representasi visual dari graph adalah peta. Banyak hal yang dapat digali dari representasi visual dari graph. (Jusuf, 2009).
Menurut Munir (2003), graph adalah struktur diskrit yang terdiri dari simpul (vertex) dan sisi (edge) atau secara matematis Graph G didefenisikan sebagai pa-sangan himpunan (V, E) yang manaV adalah himpunan tidak kosong dari simpul-simpul (verticles atau node) : {v1, v2, . . . vn} dan E adalah himpunan sisi (edges
atau arcs) yang menghubungkan sepasang simpul : {e1, e2, . . . en} atau dapat
7
Berdasarkan orientasi arah pada sisi, secara umum graph dibedakan atas dua jenis, yaitu sebagai berikut:
1. Graph tak berarah.
Graph tak berarah adalah graph yang sisinya tidak mempunyai orientasi arah. Pada graph tak berarah, urutan pasangan simpul yang dihubungkan oleh sisi tidak diperhatikan. Jadi, (vj, vk) = (vk, vj) adalah sisi yang sama.
Gambar 2.1 Graph tak berarah
2. Graph berarah.
Graph berarah adalah graph yang sisinya diberikan orientasi arah. Pada umumnya, sisi yang berarah disebut dengan busur (arc). Pada graph be-rarah, (vj, vk) dan (vk, vj) menyatakan 2 buah busur yang berbeda, atau dengan kata lain (vj, vk) 6= (vk, vj). Untuk busur (vj, vk), simpul vj dina-makan simpul asal (initial vertex) dan simpulvk dinamakan simpul terminal (terminal vertex).
8
2.2.2 Graph berbobot
Graph berbobot adalah graph yang setiap sisinya diberikan sebuah harga (bobot). Bobot pada setiap sisi dapat menyatakan jarak antara dua buah kota, biaya perjalanan, waktu tempuh, ongkos produksi dan sebagainya.
Gambar 2.3 Graph berbobot
2.2.3 Representasi Graph
Menurut Munir (2003), agar graph dapat diproses dalam program komputer, graph harus direpresentasikan ke dalam memori. Terdapat beberapa representasi untuk graph, antara lain matriks ketetanggaan, matriks bersisian dan senarai kete-tanggaan.
2.2.3.1 Matriks ketetanggaan (Adjacency Matrix)
Misalkan G = (V, E) graph sederhana dimana |V|= n, n >1 Maka, matriks ketetanggaan A dari Gadalah matriks n×n dimana A= [aij],[aij] menjadi 1 bila
simpul i dan j bertetangga [aij] menjadi 0 bila simpul i dan j tidak bertetangga.
Jumlah elemen matriks bertetanggaan untuk graph dengan n simpul adalah n2.
9
Pada graph berbobot, dimanaaij menyatakan bobot tiap sisi yang menghubungkan
simpul i dengan simpul j. Bila tidak ada sisi dari simpul i ke simpul j atau dari simpul j ke simpul i, maka, aij diberi nilai tak berhingga.
Gambar 2.4 Graph matriks ketetanggaan
Bentuk matriks ketetanggaan dari graph pada gambar 2.4 adalah :
1 2 3 4
2.2.3.2 Matriks bersisian (incidency matrix)
Matriks bersisian menyatakan kebersisian simpul dengan sisi. Misalkan G = (V, E) adalah graph dengan n simpul dan m sisi, maka matriks kebersisian A dari
G adalah matriks berukuran m×n dimana A = [aij],[aij] menjadi 1 bila simpul i
dan sisi j bersisian [aij] menjadi 0 bila simpul i dan sisij tidak bersisian
10
Bentuk matriks bersisian dari graph pada gambar 2.5 adalah :
e1 e2 e3 e4
2.2.3.3 Senarai ketetanggaan (adjacency list)
Matriks ketetanggaan memiliki kelemahan apabila graph memiliki jumlah sisi yang relatif sedikit sehingga graph sebagian besar berisi bilangan 0. Hal ini meru-pakan pemborosan terhadap memori, karena banyak menyimpan bilangan 0 yang seharusnya tidak perlu disimpan. Untuk kepentingan efisiensi ruang, maka tiap baris matriks tersebut digantikan senarai yang hanya berisikan vertex-vertex dalam adjacency set Vx dari setiap vertexx4.
2.2.4 Lintasan terpendek (shortest path)
Lintasan terpendek merupakan lintasan paling minimum yang ditempuh dari suatu tempat untuk mencapai tempat tujuan tertentu. Graph yang digunakan merupakan graph berbobot, yaitu graph yang setiap edgenya memiliki nilai. Nilai pada sisi graph dapat berupa jarak, waktu, biaya, ataupun yang lainnya.
Ada beberapa macam persoalan lintasan terpendek, antara lain adalah sebagai berikut:
1. Lintasan terpendek antara dua buah simpul tertentu.
2. Lintasan terpendek antara semua pasangan simpul.
3. Lintasan terpendek dari simpul tertentu ke semua simpul yang lain.
11
2.2.5 Pewarnaan graph
Dalam pewarnaan graph jumlah warna minimum yang dapat digunakan untuk mewarnai graph dinyatakan dengan bilangan kromatik yang disimbolkan dengan
χ(G). Graph yang memiliki bilangan kromatik 1 adalah graph kosong yaitu graph yang hanya terdiri dari sebuah simpul. Sementara suatu graph dikatakan planar jika tidak ada dua buah titik yang saling berpotongan yaitu graph yang dapat digambarkan pada bidang datar tanpa ada sisi yang menyilang diatas sisi lainnya dimana jumlah warna yang digunakan hanya 4 warna. (Kubale, 2004).
Sebuah kasus khusus yang terkenal dari ”m colorability decision problem” yaitu masalah 4 warna dari suatu graph planar. Masalah ini disertai pernyataan sebagai berikut : berikan beberapa wilayah yang dapat menimbulkan daerah-daerah yang diwarnai sedemikian rupa sehingga daerah - daerah yang berdampingan tidak memiliki warna yang sama, akan tetapi hanya empat buah warna yang dipakai. (Rosen, 1999).
Masalah pewarnaan seperti itu dapat berubah menjadi sangat berguna kare-na wilayah tersebut dapat dengan mudah diubah bentuknya menjadi sebuah graph. Masing-masing daerah dari wilayah itu menjadi sebuah simpul dan jika dua buah daerah berdampingan maka ke dua buah simpulnya berhubungan, kemudian hu-bungkan dengan sebuah sisi.
Teori pewarnaan graph banyak diimplementasikan pada berbagai kasus, salah satu diantaranya adalahscheduling (penjadwalan), yaitu mengefektifkan waktu un-tuk banyak keperluan dan jumlah resource yang terbatas. Dalam penjadwalan, setiap pekerjaan dinyatakan sebagai simpul dan sisi menggambarkan bahwa kedua job yang terhubung oleh sisi tersebut berjalan secara bersamaan (konflik). Tujuan dari penerapan graph adalah agar mengetahuijobyang konflik (tidak bertetangga).
12
Dalam proses pewarnaan, graph alternatif mengunakan prosedur yang sama dengan graph konvensional, tetapi dengan satu pengecualian bahwa hanya satu ruang saja yang diberikan warna. Seperti dalam graph konvensional setiap warna dalam graph konflik yang telah melewati proses pewarnaan melambangkan slot waktu yang berbeda. Dalam graph konflik alternatif, sebuah vertexvirnyang telah
diwarnai mengimplikasikan bahwa mata pelajaran mi telah dipasang pada ruangan
rn dan dijadwalkan pada sebuah slot waktu tertentu.
Oleh karena itu ada dua hal yang perlu diperhatikan dalam memodelkan sis-tem penjadwalan, yaitu:
1. Graph mungkin dapat memiliki suatu struktur khusus sehingga memudahkan dalam pewarnaan.
2. Jika tidak dapat menemukan solusi optimum, maka dapat digunakan metode aproksimasi yang tidak memberikan solusi optimum tetapi setidaknya mem-berikan performansi yang lebih baik.
2.2.6 Bilangan kromatik
Bilangan Kromatik GraphG(χ(G)) adalah jumlah warna minimum yang da-pat digunakan untuk mewarnai simpul (verteks/ V). Penyelesaian kasus penjad-walan pada hakikatnya adalah berupaya untuk mengalokasikan sejumlah aktivitas yang mengandung constraint atau batasan ke dalam timeslot (matriks ruang dan waktu). Jumlah timeslot yang tersedia juga memiliki batasan baik berupa jum-lah ruang, maupun waktu penggunaannya. Oleh karena itu, penjadwalan yang baik haruslah dapat menyesuaikan sejumlah keterbatasan resource atau sumber daya yang ada agar seluruh aktivitas dapat tetap terlaksana tanpa melanggar con-straintnya. Pewarnaan graph untuk mengakomodasi hal tersebut dilakukan dengan bilangan kromatik.
2.3 Graph Konflik (Shift Ganda)
13
untuk penjadwalan mata pelajaran tersebut. Misalkan terdapat sebuah himpunan terdiri dari n mata pelajaran {m1, m2, . . . , mn} yang akan dijadwalkan dan
ter-dapat sebuah himpunan yang terdiri dari p ruangan kelas {k1, k2, . . . , kp} sebagai
pasangan dari {m1, m2, . . . , mn}. Apabila darip ruangan kelas itu terdapat subset
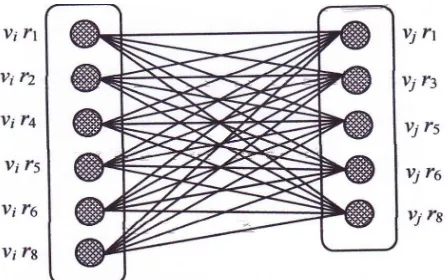
{r1, r2, r4, r5, r6, r8}yakni suatu ruangan dimana setiap mata pelajaran hanya bisa
dipasangkan berdasarkan beberapa faktor (misalnya kapasitas ruangan, tipe ruan-gan yang diminta guru). Jadi, untuk setiap mata pelajaran dalam graph konflik dengan lima vertex dapat digambarkan sebagai {vir1, vir2, vir4, vir5, vir6, vir8},
di-mana tiap vertex merepresentasikan satu kemungkinan pemasangan ruangan kelas untuk setiap mata pelajaran yang ada. Pada keadaan sebenarnya hanya akan terda-pat satu ruangan kelas misalnyarn yang akan dipergunakan untuk satu mata
pela-jaran mi, yang mana akan direpresentasikan oleh vertexvirn. Apabila terdapat dua
mata pelajaran yang dapat menimbulkan konflik sepertimi danmj, maka di antara
kedua vertex itu harus ditambahkan sebuah edge. Edge yang ditambahkan kemudi-an akkemudi-an menjadi sebuah subgraph bipartie ykemudi-ang terdiri dari sekumpulkemudi-an vertex ykemudi-ang berhubungan dengan mata pelajaran mi dan mj. Sebagai contoh, jika mata
pela-jaran mi dan mj terdiri dari kumpulan vertex {vir1, vir2, vir4, vir5, vir6, vir8} dan
{vjr1, vjr3, vjr5, vjr6, vjr8}, maka vertex vir1, vir2, vir4, vir5, vir6 dan vir8 menjadi
himpunan bagian pertama sedangkan vertex vjr1, vjr3, vjr5, vjr6 dan vjr8 menjadi
himpuan bagian kedua.
Dengan kata lain jika mata pelajaran mi dan mj tidak menimbulkan
kon-flik maka mi dan mj bebas untuk dipasangkan dalam slot waktu yang sama, oleh
karena itu, dalam pewarnaan graph penjadwalan konvensional mungkin tidak per-lu menambahkan edge di antara vertex vi dan vj. Pada graph konflik alternatif
tetap ditambahkan edge di antara dua kumpulan vertex yang memiliki ruangan yang sama virn danvjrn. Jika mata pelajaranmi danmj yang memiliki
14
2.3.1 Penjadwalan dengan metode graph
Ada tiga macam pewarnaan graph, yaitu :
1. Pewarnaan simpul (vertex colouring), merupakan pemberian warna atau label pada setiap simpul sehingga tidak ada 2 simpul bertetangga yang memiliki warna sama.
2. Pewarnaan sisi (edge coloring), merupakan pemberian warna pada setiap sisi pada graph sehingga sisi-sisi yang berhubungan tidak memiliki warna yang sama.
3. Pewarnaan wilayah (region colouring), merupakan pemberian warna pada se-tiap wilayah pada graph sehingga tidak ada wilayah yang bersebelahan yang memiliki warna yang sama.
Penulis dapat memberikan sembarang warna pada simpul-simpul asalkan berbe-da dengan simpul tetangganya. Dalam persoalan pewarnaan graph tiberbe-dak hanya sekedar mewarnai simpul-simpul dengan warna berbeda dari warna simpul tetang-ganya saja, namun juga menginginkan jumlah macam warna yang digunakan sesedik-it mungkin.
2.4 Masalah Pewarnaan Graph dalam Penjadwalan
Berikut ini adalah masalah - masalah konflik dalam pewarnaan graph pada sistem penjadwalan :
2.4.1 Multicoloring
Dalam multicoloring setiap simpul v memiliki demand x(v) sehingga harus sebanyak x(v) warna diberikan pada setiap simpul v dan setiap tetangga memiliki warna yang berbeda. Multicoloring dapat diterapkan dalam penjadwalan job yang membutuhkan waktu yang berbeda. Ada dua jenismulticoloring yaitu:
15
2. Preemptive, pada varian inijobdapat diinterupsi karena set warna tidak bersi-fat kontinu.
2.4.2 Precoloring extension
Dalam penjadwalan, jadwal tidak dapat dikontrol secara penuh. Ada saat ketika terdapat suatujob yang sudah memiliki waktu kerja yang tertentu (pengam-bilan slot waktu telah diputuskan sebelumnya dan tidak dapat diubah atau disebut juga precoloring).
2.4.3 List coloring
Dalam list coloring setiap simpul v memiliki sejumlah/set warna yang dapat diberikan. Dan tujuan dari list coloring adalah untuk mencari warna yang tepat dari himpunan warna yang tersedia. Model ini dapat diterapkan jika suatu job hanya dapat dikerjakan oleh suatu orang/suatu mesin tertentu saja tetapi terdapat beberapa opsi waktu sampai orang/mesin tersebut tersedia.
2.4.4 Minimum sum coloring
Tujuan lain dalam penjadwalan adalah meminimalkan waktu total yang dibu-tuhkan dalam pengerjaan job dalam jadwal. Minimum sum coloring mewarnai graph sehingga jumlah warna yang diberikan pada seluruh job bernilai minimum.
2.5 Algoritma Bee Colony
al-16
goritma metaheuristik yaitu algoritma bee colony dimana lebah pengumpul mani-san/lebah pekerja mengambil peranan sebagai mata pelajaran (vertex) dan sumber makanan/solusi mengambil peranan sebagai ruangan kelas.
Ada dua jenis lebah yang berperan dalam algoritma ini yakni lebah pramuka dan lebah pekerja.
1. Lebah pramuka : lebah yang melakukan pencarian awal dan di dalam wilayah pencarian, mereka menggunakan deduksi sendiri.
2. Lebah pekerja : lebah yang menemukan hasil yang lebih baik dibandingkan dengan lebah lainnya. Hanya lebah - lebah ini yang akan melakukan tarian kibasan (waggle dance).
17
bunganya senilai dengan kerja keras yang akan dilakukan berikutnya. Jika iya, ma-ka ia melakuma-kan tarian getarnya agar dipahami maksudnya oleh lebah-lebah lain. Lama tarian ini memperlihatkan seberapa besar keuntungan yang mungkin dapat diperoleh dari sumber bunga ini.
Menurut Wonget al. (2009), model yang diperbolehkan untuk mengeksplorasi dan mencari jalan tur sampai selesai. Sebelum meninggalkan sarang, lebah akan mengamati tarian yang dilakukan oleh lebah lainnya. Kemudian lebah akan diset dengan pengetahuan yang didapatkan dari tarian. Set pergerakan, yaitu ”preffered path ” yang dinotasikan dengan , maka akan berfungsi sebagai panduan dalam proses mencari makanan. berisi tur lengkap yang telah dieksplorasi sebelumnya oleh lebah yang akan pergi ke tempat tujuan.
Selama proses pencarian makanan, lebah akan melakukan perjalanan dari satu tempat ke tempat lain sampai mencapai tujuan. Aturan ini terdiri dari dua faktor yakni arc fitness dan jarak. Arc fitness dihitung untuk semua path yang mungkin untuk tempat - tempat yang bisa dikunjungi. Arc fitness yang lebih tinggi ditu-gaskan untuk tepi yang merupakan pilihan jalur. Dengan melakukan ini, lebah cenderung memilih tempat berdasarkan jalan pilihan. Di sisi lain, dibawah
pen-garuh jarak heuristik lebih cenderung memilih tempat berikutnya yang terdekat dengan tempat saat ini.
18
Langkah-langkah penyesuaian algoritma lebah sebagai berikut:
a. Forage
Tahapan ini akan diberikan pada setiap lebah yang akan mengunjungi sumber makanan, aturan ini diberlakukan ketika lebah dihadapkan pada beberapa pilihan vertex.
b. Waggle dance
Saat lebah hendak melakukan pencarian makanan sekembalinya ke sarang dari eksplorasi nektar, lebah akan mencoba dengan probabilitas puntuk me-nunjukkan waggle dance dalam dance floor. Jika seekor lebah menari, tarian lebah akan berlangsung selama beberapa durasi. Jika lebah memilih untuk mengikuti tarian yang terpilih, dia akan menggunakanpathyang diambil oleh lebah yang menunjukkan tarian untuk memandu sebagai pemimpin bunga yang ada. Path disebut sebagai lintasan yang paling disukai. Path untuk lebah merupakan rangkaian penunjuk dari sumber (sarang) ke tujuan (nek-tar). Tarian akan dilakukan oleh seekor lebah ke lebah yang lainnya selama dia mengikuti aturan bahwa lebah yang membangun path lebih pendek atau lebih cepat dari percobaan sebelumnya yang diijinkan untuk melakukan tar-ian. Dengan kata lain, tidak semua lebah diijinkan untuk melakukan waggle dance. Tetapi hanya lebah yang berhasil mendapatkan solusi yang lebih baik dari solusi terbaik yang dimiliki saat ini yang boleh melakukanwaggle dance.
c. Neighbourhood Search
BAB 3
METODOLOGI PENELITIAN
Perancangan struktur penyelesaian masalah dilakukan dengan pendeskripsian masalah dan batasan-batasan dalam formula teknik pewarnaan graph untuk pen-jadwalan dan merancang teknik pencarian solusi dengan algoritma bee colony.
Adapun tahap pemodelan dalam penelitian ini adalah sebagai berikut :
1. Menjelaskan dengan singkat tentang teknik pewarnaan graph
2. Mengumpulkan data-data sekolah
3. Mengkonstruksi graph konflik pelajaran
4. Mewarnai graph konflik pelajaran
5. Memodelkan penjadwalan guru menggunakan teknik pewarnaan graph de-ngan algoritma bee colony
6. Menyimpulkan hasil penelitian
3.1 Teknik Pewarnaan Graph
20
3.2 Pengumpulan Data
Pada tahap ini, data yang perlukan adalah jumlah semua guru, jumlah ruan-gan kelas, jumlah mata pelajaran, nama pelajaran serta hari efektif yang diperlukan untuk memulai suatu pelajaran. Pengumpulan data dilakukan pada sekolah SMP Swasta Sutomo 1 Medan, khususnya kelas IX (sembilan) SMP pada tahun ajaran 2012/2013.
3.3 Konstruksi Graph Konflik Pelajaran
Langkah-langkah untuk mengkonstruksi graph konflik suatu pelajaran adalah merepresentasikan sebuah mata pelajaran dengan sekumpulan vertex, dimana se-tiap vertex pada sebuah kumpulan merepresentasikan ruangan kelas yang mungkin untuk memulai suatu pelajaran disekolah.
Pada sekolah SMP Swasta Sutomo 1 Medan khususnya kelas IX - SMP ter-dapat sebuah himpunan yang terdiri dari 15 mata pelajaran {m1, m2, . . . , m15}
yang akan dijadwalkan dan terdapat sebuah himpunan yang terdiri dari 8 ruan-gan kelas {k1, k2, . . . , k8} sebagai pasangan dari {m1, m2, . . . , m15}. Apabila dari
8 ruangan kelas itu terdapat subset {r1, r2, r4, r5, r6, r8} yakni suatu ruangan
di-mana setiap mata pelajaran hanya bisa dipasangkan berdasarkan beberapa faktor (misalnya kapasitas ruangan, tipe ruangan yang diminta guru). Jadi, untuk setiap mata pelajaran dalam graf konflik dengan lima vertex dapat digambarkan sebagai {vir1, vir2, vir4, vir5, vir6, vir8}, dimana tiap vertex merepresentasikan satu
kemu-ngkinan pemasangan ruangan kelas untuk setiap mata pelajaran yang ada. Pada keadaan sebenarnya hanya akan terdapat satu ruangan kelas misalnyarnyang akan
dipergunakan untuk satu mata pelajaran mi, yang mana akan direpresentasikan
oleh vertex virn. Apabila terdapat dua mata pelajaran yang dapat menimbulkan
konflik seperti mi dan mj, maka di antara kedua vertex itu harus ditambahkan
sebuah edge.
Sebagai contoh, jika mata pelajaran mi dan mj terdiri dari kumpulan vertex
{vir1, vir2, vir4, vir5, vir6, vir8}dan{vjr1, vjr3, vjr5, vjr6, vjr8}, maka vertexvir1, vir2,
vir4, vir5, vir6 danvir8 menjadi himpunan bagian pertama sedangkan vertexvjr1, vj
21
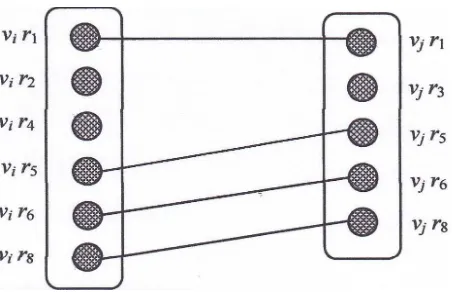
keadaan ini dapat diperlihatkan pada gambar 3.1.
Gambar 3.1 Mata pelajaranmi danmj dijadwalkan pada slot waktu yang berbeda
Pada gambar 3.1 terlihat bahwa di antara dua kumpulan vertex yang memi-liki ruangan kelas yang sama virn dan vjrn selalu ditambahkan edge meskipun
mata pelajaran mi dan mj tidak menimbulkan konflik sehingga mi dan mj bebas
untuk dipasangkan dalam slot waktu yang sama, jika mata pelajaran mi dan mj
memiliki kemungkinan pemasangan t ruangan kelas yang sama, maka sebanyak t
edge pula yang harus ditambahkan ke sekumpulan vertex untuk mata pelajaran
mi dan mj. Sebagai contoh, jika mata pelajaran mi dan mj terdiri dari kumpulan
vertex {vir1, vir2, vir4, vir5, vir6, vir8} dan {vjr1, vjr3, vjr5, vjr6, vjr8}, maka harus
ditambahkan edge di antara vir1 danvjr1, vir5 danvjr5, vir6dan vjr6, vir8 dan vjr8,
sehingga jika mata pelajaran mi dan mj dijadwalkan pada slot waktu yang sama
22
Gambar 3.2 Mata pelajaran mi dan mj di pasangkan pada slot waktu yang sama
3.4 Pewarnaan Graph Konflik Pelajaran
Sebuah graph dengan pewarnaan vertex yang tepat akan mewarnai sepasang vertex yang terhubung oleh edge dengan warna yang berbeda. Pasangan vertex yang tidak terhubung oleh edge bisa menggunakan dua warna yang sama atau berbeda. Dalam proses pewarnaan, hanya satu vertex dalam sebuah kumpulan yang akan diwarnai, dengan kata lain setiap mata pelajaran yang dipasang dengan salah satu ruangan kelas saja yang diberikan warna. Dalam graph konflik, sebuah vertex virn yang telah diwarnai mengimplikasikan bahwa mata pelajaran mi telah
dipasangkan pada ruangan kelas rn dan dijadwalkan pada sebuah slot waktu
ter-tentu seperti yang diperlihatkan pada gambar 3.3 berikut :
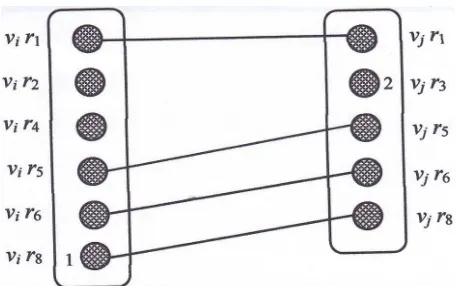
Gambar 3.3 Mata pelajaranmi danmjdi pasang pada ruangan kelas yang berbeda
dan slot waktu yang berbeda
Gambar 3.3 memperlihatkan bahwa mata pelajaran mi dan mj harus
23
vertex vjr8 diwarnai dengan warna 2, mengimplikasikan bahwa mata pelajaran mi
danmjdijadwalkan pada slot waktu yang berbeda dan ruangan kelas yang berbeda.
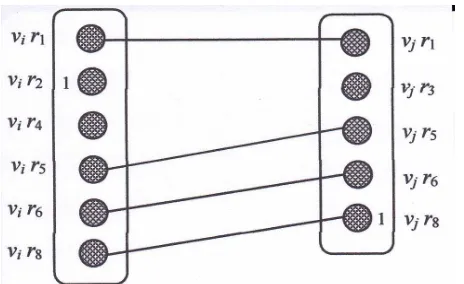
Gambar 3.4 Mata pelajaran mi dan mj di pasang pada ruangan kelas yang sama
dan slot waktu yang berbeda
Gambar 3.4 memperlihatkan bahwa mata pelajaran mi dan mj harus
dijad-walkan pada waktu yang berbeda. Vertexvir6 diwarnai dengan warna 1 dan vertex
vjr6 diwarnai dengan warna 2, mengimplikasikan bahwa mata pelajaranmi dan mj
dijadwalkan pada slot waktu yang berbeda tetapi dengan ruangan kelas yang sama yaitu r6.
Gambar 3.5 Mata pelajaran mi dan mj tidak berpotensi menimbulkan konflik, di
pasang pada ruangan kelas yang berbeda dan slot waktu yang berbeda
Gambar 3.5 memperlihatkan bahwa mata pelajaranmi dan mj tidak
menim-bulkan konflik, sehingga bisa dijadwalkan pada slot waktu yang sama atau berbe-da.Vertexvir8diwarnai dengan warna 1 dan vertexvjr3diwarnai dengan 2,
mengim-plikasikan bahwa mata pelajaran mi dan mj dijadwalkan pada slot waktu yang
24
Gambar 3.6 Mata pelajaran mi dan mj tidak berpotensi menimbulkan konflik, di
pasang pada ruangan kelas yang berbeda dan slot waktu yang sama
Gambar 3.6 memperlihatkan bahwa mata pelajaranmi dan mj tidak
menim-bulkan konflik, sehingga bisa dijadwalkan pada slot waktu yang sama atau berbe-da.Vertexvir2diwarnai dengan warna 1 dan vertexvjr8diwarnai dengan 1,
mengim-plikasikan bahwa mata pelajaranmidanmj dijadwalkan pada slot waktu yang sama
menggunakan ruangan kelas yang berbeda.
Gambar 3.7 Mata pelajaran mi dan mj tidak berpotensi menimbulkan konflik, di
pasang pada ruangan kelas yang sama dan slot waktu yang berbeda
Gambar 3.7 memperlihatkan bahwa mata pelajaranmi dan mj tidak
menim-bulkan konflik, sehingga bisa dijadwalkan pada slot waktu yang sama atau berbe-da.Vertexvir5diwarnai dengan warna 1 dan vertexvjr5diwarnai dengan 2,
mengim-plikasikan bahwa mata pelajaran mi dan mj dijadwalkan pada slot waktu yang
BAB 4
MODEL PENJADWALAN GURU
Pembuatan jadwal adalah sebuah masalah periodik yang sering dihadapi oleh sekolah dan universitas serta perusahaan manufaktur lainnya yang terdapat di selu-ruh dunia. Pada tesis ini, peneliti akan membahas tentang masalah penjadwalan guru khususnya di sekolah SMP Swasta Sutomo 1 Medan untuk tingkatan kelas IX - SMP. Dengan banyaknya faktor yang mempengaruhi penyusunan suatu jad-wal seperti jumlah ruangan kelas, daya tampung ruangan kelas dan slot waktu yang terbatas menjadikan penyusunan jadwal sekolah menjadi sangat rumit. Dasar permasalahan penyusunan jadwal guru di sekolah adalah bagaimana menempatkan setiap mata pelajaran pada masing-masing ruangan kelas yang tersedia dengan jum-lah slot waktu yang sangat terbatas sehingga guru dan murid bisa melangsungkan proses belajar mengajar dengan lancar dan tepat waktu. Pada umumnya sebuah jadwal akan muncul terlebih dahulu sebelum siswa memilih ruangan kelas yang akan diikuti, sehingga siswa-lah yang cenderung menyesuaikan diri dengan jadwal yang telah disusun. Di samping itu juga terdapat beberapa ketentuan khusus yang harus dipenuhi dalam membangun sebuah jadwal yang optimal, yakni :
1. Dua atau lebih mata pelajaran yang diampu oleh guru yang sama tidak bisa dijadwalkan pada slot waktu yang sama.
2. Dua atau lebih mata pelajaran yang membutuhkan ruangan yang sama tidak bisa dijadwalkan pada slot waktu sama.
Ketentuan lain yang bersifat tambahan merupakan ketentuan yang tidak wa-jib dipenuhi untuk membangun sebuah jadwal yang layak namun akan lebih diter-ima oleh siswa jika dapat dipenuhi. Beberapa contoh dari ketentuan tambahan ini adalah :
26
2. Beberapa guru mungkin ingin memilih ruangan kelas tertentu saja seperti ruangan untuk multimedia dll.
3. Meminimalisasikan penggunaan ruangan kelas dalam membangun sebuah pen-jadwalan.
Berikut ini diberikan langkah-langkah yang harus ditempuh dalam menyusun model penjadwalan guru dengan algoritma bee colony:
1. Forage
(a) Menemukan solusi awal
Merupakan suatu langkah awal dimana total jumlah guru yang men-gajar adalah sama dengan jumlah ruangan kelas yang tersedia/Verteks (N). Masingmasing guru yang mengajar dialokasikan ke dalam ruangan kelas yang tersedia secara random, kemudian ruangan kelas itu dipil-ih dari beberapa kemungkinan lalu diwarnai. Prosedur ini dilakukan secara berulang sampai seluruh ruangan kelas selesai diwarnai. Pada tahap akhir dari fase ini, solusi awal yang dihasilkan dapat dirumuskan dengan persamaan probabilitas di bawah ini:
P viS =
PviS = Probabilitas dari ruangan kelas (Vi) yang telah dipasangkan
dengan guru (S)
ws = Himpunan ruangan kelas yang telah dipilih oleh guru(S)
N = Jumlah ruangan kelas yang tersedia
(b) (b) Mengevaluasi nilai fitness dari solusi awal
Untuk mengevaluasi kualitas dari masingmasing solusi yang ditemukan, maka perlu dipertimbangkan nilai fitness dari masingmasing solusi yang dapat dihitung dengan rumus di bawah ini:
27
Dimana :
k(S) = Jumlah warna yang telah digunakan untuk guru yang telah terpilih
fit(S) = Nilai fitness dari sebuah solusi yang telah diperoleh guru dimana guru yang mengajar adalah sejumlah guru yang terpilih dan dianggap telah memiliki solusi terbaik. Jumlah guru yang mengajar = kapasitas ruangan yang tersedia.
2. Waggle dance
Setelah diperoleh solusi awal dengan terpilihnya beberapa guru, langkah berikut-nya adalah memastikan bahwa guruguru tersebut telah dipasangkan secara
tepat terhadap masingmasing ruangan kelas yang tersedia. Untuk itu diper-lukan suatu rumusan yang dapat dipakai untuk menghitung nilai dari mas-ingmasing ruangan kelas, yakni :
τ Vi =
τ Vi = Jumlah informasi yang terdapat pada masingmasing ruangan
kelas vi.
vi = Banyaknya ruangan kelas yang akan diwarnai.
s = Guru yang ditempatkan ke ruangan kelas yang telah diwarnai.
φ = Nilai parameter fitness yang digunakan ebee = Jumlah guru
CS(Vi) = Warna dari ruangan kelasVi yang dihasilkan oleh guru
28
3. Neighbourhood Search / Pencarian Lingkungan.
Definisi 1 : Jika deg (Va) =mdan vertex adjacent dariVaadalahV1, V2,· · ·Vm
maka:
Hdeg(Va) =deg(v1) +deg(v2) +· · ·+deg(vm) (4.4)
Definisi 2 : Jika himpunan kelas dari solusi yang dihasilkan oleh guru telah memiliki warna yang sama, misalkan T adalah {V1, V2, V3,· · ·VDT}, maka:
DT adalah jumlah kelas yang diwarnai oleh warna T
QST adalah kumpulan kelas yang memiliki warna yang sama
Definisi 3 : Jika seluruh ruangan kelas yang memiliki warna sama akan di-warnai oleh T, sehingga :
λST =
DT X
i=1
τ Vi (4.6)
λST adalah total kumpulan kelas yang memiliki informasi sama yang diwarnai oleh T.
τ Vi adalah jumlah informasi yang terdapat pada masingmasing ruangan vi.
Definisi 4 : Jika N adalah jumlah ruangan kelas danK(s) adalah angka dari warna yang digunakan oleh guru untuk mewarnai graph, maka:
Fs=
N
K(S) (4.7)
Pada tahapNeighbourhood Search, masingmasing data guru akan ditempatkan ke ruangan kelas sebagai solusi sementara yang diasumsikan sebagai XiS(i∈
{1,2,· · · , k}). Jika d = max(XiS), maka warna i akan diseleksi:
Fase 1 : Jikai > 1, Di−1 > Fs, i1∈bsmaka semua ruangan kelas yang memiliki warna i1 pada solusi dari guru akan diwarnai oleh fungsi pewarnaan vertex dan i1 akan ditambahkan ke himpunan bs. Himpunan bs dikelompokkan ke warna
yang digunakan dalam pencarian lingkungan oleh guru.
Fase 2 : Jikai < K(s), Di+1 > Fs, i+ 16∈bs maka semua ruangan kelas yang memiliki
29
Fase 3 : Jika 1 6∈bs maka semua ruangan kelas yang memiliki warna i akan diwarnai
oleh fungsi pewarnaan vertex dan iakan ditambahkan pada himpunan bs.
Fase 4 : Warna berikutnya akan dihitung dengan fungsi probabilitas di bawah ini:
PSi =
Psi = Probabilitas dari warna yang terpilih pada solusi.
K(s) = Jumlah warna yang dipakai dalam pewarnaan graph
bs = Warna yang digunakan untuk pencarian lingkungan oleh guru
α danβ = Dua peubah/integer positif
Q = Berasal dari perumusan definisi 2
λ = Berasal dari perumusan definisi 3
Setelah membahasi, kembali ke fase 1 dan ulangi lagi dari fase 1 s.d 4 sampai diperoleh semua ruangan kelas dari pewarnaan graph dan juga solusi ling-kungan dari solusi utama. Setelah melalui semua tahap, maka akan dilakukan suatu perbandingan antara fitness dari solusi pencarian lingkungan dengan fitness dari solusi utama. Jika fitness dari pencarian lingkungan lebih baik atau sama dengan fitness dari solusi utama, maka nilai dari solusi utama akan dieliminasi dari kumpulan guru dan solusi lingkungan akan dipertimbangkan sebagai solusi utama oleh guru.
Berikut ini didefinisikan notasi dalam model penjadwalan guru di sekolah SMP swasta Sutomo 1 Medan:
PARAMETER
i = Mata pelajaran, yakni sejumlah tugas yang dibebankan kepada masingmasing guru pada ruangan kelas Vi dan pada satuan
waktu tertentu.
S = Guru yang ditempatkan ke ruangan kelas yang telah diwarnai.
bs = Jumlah guru.
Cis = Ruangan kelas yang telah diwarnai
30
1 jika guru tepat ditugaskan pada mata pelajaran i dan pada ruangan kelasVi
0jika tidak tepat
Model matematika untuk masalah penjadwalan guru di sekolah SMP swasta Sutomo 1 Medan dapat dijelaskan di bawah ini:
min
Model (4.9) merepresentasikan bahwa jadwal guru di sekolah SMP swasta Sutomo 1 Medan disusun dengan meminimalkan jumlah ruangan kelas yang bisa dipasangkan secara tepat pada mata pelajaran i dan guru S. Ini berarti jumlah guru harus disesuaikan dengan jumlah ruangan kelas yang telah diwarnai sehingga dalam slot waktu yang sama tidak akan terdapat guru yang mengampu dua mata pelajaran sekaligus.
Untuk semua guru dari 1 sampai m, kendala yang terdapat pada persamaan (4.10) dapat dipenuhi apabila jumlah ruangan kelas pada mata pelajaran i lebih sedikit atau sama dengan jumlah guru yang tersedia. Hal ini dilakukan untuk mengantisipasi apabila terdapat guru yang berhalangan hadir dalam melaksanakan tugas mengajarnya, maka guru yang lain dapat dengan segera menggantikannya sehingga proses belajar mengajar tidak terganggu.
Untuk semua mata pelajaran dari 1 sampai n, kendala yang terdapat
BAB 5
KESIMPULAN
5.1 Kesimpulan
DAFTAR PUSTAKA
Agustina, Ira (2005), ”Penjadwalan Pelajaran SMU Negeri Mojoagung dengan Al-goritma Swarm”. Tugas Akhir ITS, Surabaya.
Ariani, D dan Arna Fahriza (2004), ”Optimasi Penjadwalan Mata Kuliah Di Jurusan Teknik Informatika PENS dengan Menggunakan Algoritma Particle Swarm Optimization (PSO)”.
Betrianis dan Aryawan, P.T. (2003), ” Penerapan algoritma Tabu search dalam penjadwalan job shop”, Makara, Teknologi, Vol. 7, No. 3.
Butt, Norman. (2009). ”Bee Colonies Applied To Multiprocessor Schedulin.”. Bor-lange Sweeden: Dalarna University.
Carlos, L, Flores, J.J dan Calderon, F. (2008), ”Solving a school Timetabling Prob-lem Using a Bee Algorithm ”, MICAI.
Deo, Narsingh. (1974). ”Graph Theory With Application To Engineering And Com-puter Science. Prentice hall ”.
Faraji, M dan Javadi, S. (2011), ” Proposing a New Algorithm Based on Bees Be-haviour for solving Graph Coloring ”. International Journal Contemps. Math. Sciences, Vol. 6, no. 1, 41 - 49.
Hariyanto, Bambang. (2003). ” Struktur Data”, Bandung.
Jusuf, Heni (2009). ” Pewarnaan Graph Pada Simpul Untuk Mendeteksi Konflik Pen-jadwalan Kuliah”, Seminar Nasional Aplikasi Teknologi Informasi, Yogyakarta.
Karaboga, D. Ozturk, C. (2010). ” Fuzzy Clustering with Artificial Bee Colony Al-gorithm”, Scientific Research and Essays Vol. 5(14): hal. 1899-1902.
Komang, S. (2008), ”Kombinasi Algoritma Genetika dan Tabu Search dalam Pem-buatan Tabel Jadwal Mata Kuliah”, Institut Teknologi Sepuluh November , Surabaya.
Kubale, Marek. (2004). ” Graph Coloring ” , AMS Bookstore.
Munir, Rinaldi (2003). ” Teori Graf dalam Matematika Diskrit”.
Nismah. (2006). ” Evaluasi Perilaku Antara Lebah Pekerja Apis Cerana Ja-vana FABR Untuk Menginformasikan Sumber Makanan”. Indonesia: Institut Teknologi Bandung.
Rachmawati, H, Purnama, I.K.E dan Purnomo, M.H. (2011), ”Analisis Penyelesaian Masalah Penjadwalan Mata Kuliah menggunakan Teknik Pewarnaan Graph Dengan Algoritma Koloni Lebah”, SNPs- XI.
Redl dan Anton, T. (2004), ”A Study of University Timetabling that Blends Graph Coloring with the Satisfaction of Various Essential and Preferential Condi-tions”, Tesis, Rice University.
ma-33
Rosen, Kenneth, H. (1999). ” Discrete And Combinatorial Matematics”, 495-557. CRC Press.
Seeley. (1995). ”A Decision of Making in Nest-Site Selection by Honey Bees”.
Talbi. (2009). ” A Heuristic To Manage”. Operation Research, Vol 36, 3013-3018.
Wardoyo, Alamsyah, R. (2003), ”Optimalisasi Penjadwalan Multi Constraint meng-gunakan Logika Fuzzy ”, Tesis, Universitas Gajah Mada, Yogyakarta.