METODE BRANCH AND BOUND UNTUK
MENYELESAIKAN PROGRAM STOKASTIK
INTEGER DENGAN ADANYA RESIKO
TESIS
Oleh
ADIL H. PANGARIBUAN
087021052/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2010
METODE BRANCH AND BOUND UNTUK
MENYELESAIKAN PROGRAM STOKASTIK
INTEGER DENGAN ADANYA RESIKO
TESIS
Diajukan Sebagai Salah Satu Syarat
Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
ADIL H. PANGARIBUAN
087021052/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2010
Judul Tesis : METODE BRANCH AND BOUND UNTUK MENYELESAIKAN PROGRAM STOKASTIK INTEGER DENGAN ADANYA RESIKO
Nama Mahasiswa : Adil H. Pangaribuan Nomor Pokok : 087021052
Program Studi : Matematika
Menyetujui,
Komisi Pembimbing
(Prof. Dr. Herman Mawengkang) (Dr. Saib Suwilo, MSc)
Ketua Anggota
Ketua Program Studi, Dekan,
(Prof. Dr. Herman Mawengkang) (Prof. Dr. Eddy Marlianto, M.Sc)
Tanggal lulus: 18 Mei 2010
Telah diuji pada
Tanggal 18 Mei 2010
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Herman Mawengkang Anggota : 1. Dr. Saib Suwilo, MSc
2. Dr. Sutarman, M.Sc. 3. Dra. Mardiningsih, M.Si.
ABSTRAK
Tesis ini bertujuan melakukan pengembangan pada metode branch-and-bound, yaitu dalam rangka menyelesaikan permasalahan multistage stochastic integer programs with risk dalam hubungannya dengan permasalahan wait-and-see yang dapat dipi-sahkan kedalam kasus seperti resiko netral. Model-model yang termasuk dalam kelas ini penyelesaiannya akan disajikan sebagai suatu kombinasi dari algoritma branch-and-bound dengan relaksasi non-anticipativity dan kendala percabang (constraint branching) sepanjang subspaces non-anticipativity.
Kata kunci : Pemograman Stokastik Bilangan Bulat, Model Multi-Tahap, Model Mean-Risk, Optimasi Program Cacah Campuran.
ABSTRACT
This thesis is addressed to develop branch-and-bound methods, that is to solve multi-stage stochastic integer programs with risk objectives which is related to wait-and-see problems which could be separated like risk neutral. All model classified to this is over-come by presenting a combination between branch-and-bound algorithm and relaxation of non-anticipativity and constraint branching along non-anticipativity subspaces.
Keywords : Stochastic Integer Programming, Multistage Models, Mean-Risk Models, Mixed-Integer Optimization
ii
KATA PENGANTAR
Puji Tuhan dan syukur kehadirat-Nya penulis panjatkan, karena berkat dan kasih karunia-Nya sehingga saya dapat menyelesaikan perkuliahan tepat waktu dan me-nyelesaikan tugas akhir ini, yang berupa tesis dengan judul ”METODE BRANCH AND BOUND UNTUK MENYELESAIKAN PROGRAM STOKASTIK INTEGER DENGAN ADANYA RESIKO”.
Pada kesempatan ini, penulis menyampaikan ucapan terima kasih dan penghar-gaan yang sebesar-besarnya kepada:
Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) se-laku Rektor Universitas Sumatera Utara.
Bapak Prof. Dr. Eddy Marlianto, M.Sc selaku Dekan FMIPA Universitas Su-matera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti perkuliahan pada Program Studi Magister Matematika.
Bapak Prof. Dr. Herman Mawengkang selaku Ketua Program Studi Magister Matematika pada Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Su-matera Utara dan juga selaku Ketua Komisi pembimbing tesis ini, yang telah dengan penuh kesabaran memotivasi dan membimbing penulis hingga selesainya tesis ini de-ngan baik.
Bapak Dr. Saib Suwilo, MScselaku Sekretaris Program Studi Magister Matema-tika pada Fakultas MatemaMatema-tika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara dan juga selaku anggota pembimbing tesis, yang telah banyak memberikan saran dan masukan, juga motivasi belajar selama masa perkuliahan.
Bapak Dr. Sutarman, M.Sc dan Ibu Dra. Mardiningsih, M.Si selaku pem-banding dan penguji atas segala saran dan petunjuk yang diberikan.
Gubernur Sumatera Utara yang telah memberi bantuan Beasiswa pendidikan kepada penulis melalui BAPEDASU.
Bapak Prof. Dr. Drs. Iryanto, M.si;Prof. Dr. Opim Salim, MIkom. PhD ;
Drs. Marwan Harahap, M.Eng;Dr. Tulus, M.Si;Drs. Open Darnius, M.Sc
;Drs. Marihat Situmorang,M.Kom;Drs. S.Arriswoyo,M.Sc;Drs. Sawalud-din,M.IT sebagai staf pengajar yang telah memberikan ilmunya kepada penulis se-lama perkuliahan.
Rekan mahasiswa angkatan 2007-2008 atas kerjasama dan kebersamaan yang in-dah selama perkuliahan dan rekan guru SMA Negeri 4 Medan yang turut memberi
motivasi. Juga kepada adinda tercinta Sri Wahyuni Sirait.SE yang banyak
mem-beri semangat dan inspirasi kepada penulis sebelum dan semasa perkuliahan.
Secara khusus penulis menyampaikan terimakasih dan sayang yang mendalam
kepada orang tua penulisAyahanda Drs. JT. PangaribuandanIbunda T. br
Na-pitupulu (alm), abang, adik-adik, ipar dan semua keponakan saya yang senantiasa memberikan dukungan dan mendoakan keberhasilan penulis dalam menyelesaikan pendidikan ini.
Kepada seluruh pihak yang tidak dapat penulis sebutkan satu persatu, penulis berterimakasih atas semua bantuan yang diberikan, semoga Tuhan Yang Maha Kuasa membalaskan segala kebaikan yang telah diberikan, Amin.
Penulis menyadari tesis ini masih jauh dari sempurna, namunpun demikian penulis berharapan semoga tesis ini bermanfaat bagi pembaca dan pihak-pihak yang memer-lukannya. Sekian dan terimakasih.
Medan, 18 Mei 2010
Penulis,
Adil H. Pangaribuan
iv
RIWAYAT HIDUP
A. DATA PRIBADI
Nama : Adil H. Pangaribuan
Tempat/tanggal lahir : Jakarta/10 Pebruari 1967
Jenis kelamin : Laki-laki
Agama : Kristen Protestan
Alamat Rumah : Jl. Helvetia Raya No.65 Medan 20124
Nama Orang Tua : Drs.JT.Pangaribuan (Ayah)
: (Alm) T. br. Napitupulu (Ibu)
B. Riwayat Pendidikan
1973-1979 : SD Bethel Jakarta
1979-1982 : SMP Bethel Jakarta, SMP Nasrani Medan
1982-1985 : SMA Negeri 11 Medan
1985-1988 : FMIPA Program D-3 Matematika USU Medan
1993-1996 : FPMIPA Program Pendidikan Matematika IKIP Medan
2008-2010 : Program Pascasarjana Magister Matematika USU Medan
C. Pengalaman Kerja
1989-1991 : Guru PNS pada SMU Negeri Ranai Kab. Kep.RIAU
1991-Sekarang : Guru PNS pada SMU Negeri 4 Medan
DAFTAR SIMBOL
Scenario tree representation
τ = number of stages
G = set of scenario groups.
Gt = set of scenario groups in staget, fort= 1, . . . , τ
Z = Benefit at end of period H
The Algorithm
L = Daftar subproblem
i = Nomor iterasi; also used to indicate the subproblem selected
Pi = Subset corresponding to iteration i
αi = Batas atas yang diperoleh pada iterasi ke i
βi = Batas bawah pada subproblem ke i
Xi = Penyelesaian layak untuk nilai subproblem ke i
U = Batas atas pada nilai optimal global
L = Batas bawah pada nilai optimal global
X∗
= Kandidat optimum global
Probabilitas dan Ukurannya
Ω = ruang kejadian
ω = elemen dari Ω, kejadian
P = ukuran probabilitas pada Ω
(Ω, ω,P) = ruang probabilitas
ξ = variabel acak pada (Ω, ω,P) dengan realisasi didalam R
E = nilai ekspektasi
R = ukuran resiko umum
Fungsi Biaya Acak
x = variabel keputusan dalamRn
ξ = parameter acak dalamRl
QE = fungsi nilai ekspektasi yang dipetakan dari dariRn keR
QR = fungsi resiko umum yang dipetakan dari Rn keR
(ξt) T
t=1 = proses stokastik data diskrit
vi
DAFTAR ISI
Halaman
ABSTRAK i
ABSTRACT ii
KATA PENGANTAR iii
RIWAYAT HIDUP v
DAFTAR SIMBOL vi
DAFTAR ISI vii
DAFTAR TABEL ix
DAFTAR GAMBAR x
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Tujuan Penelitian 3
1.4 Kontribusi Penelitian 3
1.5 Metode Penelitian 3
BAB 2 TINJAUAN PUSTAKA 5
BAB 3 LANDASAN TEORI 7
3.1 Program Stokastik 7
3.2 Program Stokastik Dua-Tahap (two-stage models) 8
3.2.1 Program Stokastik Cacah Campuran 9
3.3 Program Stokastik Multi Tahap (Multistage Stochastic Program) 10
3.3.1 Model Ekspektasi 10
3.3.2 Pemahaman Resiko dan Ukuran Resiko (Risk Measures) 11
3.4 Separable Wait-And-See Problems 15
BAB 4 PEMBAHASAN 19
4.1 Metode Branch And Bound 19
4.2 Pengembangan Metode Branch And Bound 21
4.2.1 Algoritma 21
4.2.2 Pengembangan Algoritma 23
4.3 Komputasi 26
BAB 5 KESIMPULAN DAN SARAN 28
5.1 Kesimpulan 28
5.2 Saran 28
DAFTAR PUSTAKA 29
LAMPIRAN 1 30
LAMPIRAN 2 31
LAMPIRAN 3 34
viii
DAFTAR TABEL
Nomor Judul Halaman
5.1 Computational results for multiknapsack problems 30
DAFTAR GAMBAR
Nomor Judul Halaman
4.1 Scenario tree ; multistage 20
4.2 The enumeration tree 20
4.3 Tree of subproblems and results of LP relaxations 21
x
ABSTRAK
Tesis ini bertujuan melakukan pengembangan pada metode branch-and-bound, yaitu dalam rangka menyelesaikan permasalahan multistage stochastic integer programs with risk dalam hubungannya dengan permasalahan wait-and-see yang dapat dipi-sahkan kedalam kasus seperti resiko netral. Model-model yang termasuk dalam kelas ini penyelesaiannya akan disajikan sebagai suatu kombinasi dari algoritma branch-and-bound dengan relaksasi non-anticipativity dan kendala percabang (constraint branching) sepanjang subspaces non-anticipativity.
Kata kunci : Pemograman Stokastik Bilangan Bulat, Model Multi-Tahap, Model Mean-Risk, Optimasi Program Cacah Campuran.
ABSTRACT
This thesis is addressed to develop branch-and-bound methods, that is to solve multi-stage stochastic integer programs with risk objectives which is related to wait-and-see problems which could be separated like risk neutral. All model classified to this is over-come by presenting a combination between branch-and-bound algorithm and relaxation of non-anticipativity and constraint branching along non-anticipativity subspaces.
Keywords : Stochastic Integer Programming, Multistage Models, Mean-Risk Models, Mixed-Integer Optimization
ii
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Dalam setiap pengambilan keputusan para pengambil keputusan akan selalu berha-dapan dengan lingkungan dimana salah satu karakteristik yang paling menyulitkan
adalah adanya ketidakpastian/ketidakmenentuan (uncertainty). Pemograman
sto-kastik merupakan model optimalisasi masalah (optimazion problem) yang melibatkan
ketidakpastian dalam lingkungan data yang tidak lengkap dari suatu waktu ke waktu yang berikutnya. Sebagai contoh, jika banjir melanda, model pemograman stokastik akan bekerja menggunakan berbagai skenario banjir; kemampuan mensuplai sumber daya ke berbagai lokasi terpisah, serta biaya tetap dan variabel yang terkait dengan penyebaran berbagai sumber daya pengelolaan banjir untuk mengelola beragam tin-dakan resiko. Resiko merupakan suatu kondisi tidak pasti dengan peluang kejadian tertentu yang jika terjadi akan menimbulkan konsekuensi tidak menguntungkan.
Dengan menggunakan probabilitas untuk faktor-faktor yang mempengaruhi hasil-nya, model akan menggambarkan bagaimana sumber daya yang terbatas dapat me-menuhi kebutuhan atau kekurangan di waktu mendatang. Dengan demikian, resiko dan manfaat dari berbagai kemungkinan dapat ditelusuri. Pemograman stokastik menawarkan kekuatan dan fleksibilitas pemodelan yang lebih besar, tetapi membu-tuhkan waktu pemrosesan berbiaya tinggi. Namun demikian, pemograman stokastik mengalami kemajuan berkat pengembangan algoritma yang lebih efisien dan prosesor komputer yang lebih cepat. Artinya, masa depan tidak diprediksi dengan peramalan, tetapi keputusan yang diambil mendukung berbagai skenario yang mungkin.
Dalam model optimasi stokastik, parameter tertentu adalah variabel stokastik yang mempunyai beberapa distribusi peluang yang kontiniu atau diskrit (Birge, et al., 1997). Model ini mengandung unsur acak atau distribusi peluang dimana
be-berapa data yang termuat pada fungsi tujuan (objective function) ataupun kendala
(constraints) mengandung ketidakpastian yang dicirikan oleh distribusi peluang pada parameter dan keputusan yang akan dioptimalkan tersebut tidak harus mengantisipasi (non-anticipativity) hasil berikutnya (future information).
Berbagai jenis program stokastik, satu diantaranya adalah yang berkenaan
de-ngan resiko (risk aversion). Risk aversion telah mendapat perhatian dalam
pemogra-man stokastik. Bagaipemogra-mana menggabungkan faktor risiko ke dalam program stokastik,
2
telah menjadi hal yang menarik. Alat analisa yang digunakan dalam kasus resiko dan ketidakpastian adalah probabilitas. Fungsi tujuan pada pemograman linier tidak lagi
didasarkan hanya pada nilai harapan semata (expected value), tetapi telah disertakan
suatu ukuran yang pantas untuk mengekspresikan risiko kedalamnya. Risiko diukur dengan ekspektasi deviasi dari varibel acak yang cocok terhadap rata-rata atau dari target yang ditentukan.
Dalam pemograman dinamik (dynamic programming), suatu permasalahan yang
kompleks dan berskala besar dipecah-pecah/diuraikan menjadi beberapa bagian
ke-cil (dekomposisi/decomposability) untuk kemudian dioptimalisasi (Carøe et.al 1999).
Model ketidakpastian dengan objek acak dapat menyebabkan persoalan program
sto-kastik menjadi disversi, yang sering dikenal sebagai model dua-tahap (two-stage
mod-els). Program stokastik multi-tahap (Multistage stochastic programs) dinamikanya
lebih kompleks dan memerlukan perlakuan non-anticipativity yang lebih terperinci,
dimana ketidakpastian juga dilenyapkan secara bertahap dengan tingkat keputusan yang tidak harus mengantisipasi informasi yang akan datang. Two-and-multistage risk neutralstochastic programs berubah menjadi masalah pengoptimuman dari struk-tur blok berskala besar jika yang mendasarinya adalah distribusi probabilitas diskrit.
Hubungannya dengan risk-aversion adalah membahas tentang berbagai pemilihan
ukuran resiko yang memiliki dampak cukup berarti untuk dipertimbangkan, misalnya
deviasi, model mean-risk, koheren dan konveks, polyhedral risk measure, dan
Multi-period CV aR risk measure .
Program linier cacah campuran (mixed-integer linear programs) yang berskala
besar, telah membawa program stokastik ke model wait-and-see, yakni: kendala
re-laxing non-anticipativity, fully-decouples dimana model ini dimasukkan ke masing-masing subproblem untuk setiap skenario dari sebaran probabilitas diskrit. Untuk
ukuran yang lainnya, relaxing non-anticipativity tidak cukup untuk sampai di
ske-nario tunggal subproblem. Dalam kasus multistage, ada suatu sistim yang utuh dari
identitas-identitas yang sesuai untuk setiap langkah yang menghubungkan
subset-subset dari skenario. Hal ini membuat masing-masing heuristik permasalahan
men-jadi jauh lebih kompleks/rumit. Dengan mengidentifikasi ukuran resiko multiperiod
lalu menggabungkannya ke multistage linear mixed-integer stochastic programs
ma-ka ama-kan melibatma-kan modelwait-and-see, sehingga diharap dapat dikembangkan suatu
model penyelesaian bagi masalah-masalah multistage linear mixed-integer stochastic programs yang menyertakan resiko. Hal-hal ini memberikan dasar bagi suatu
pengem-banganalgoritma branch-and-bound yang melibatkanrelaxation of non-anticipativity.
3
1.2 Perumusan Masalah
Resiko (risk aversion) telah menjadi bidang penelitian aktif pada stochastic integer
programming. Dan metode branch-and-bound yang berupa pohon pencarian telah umum digunakan dalam menyelesaikan masalah-masalah yang melibatkan pemogra-man linier bilangan bulat. Untuk problem stokastik dengan jumlah skenario yang besar dirasa perlu adanya suatu metode penyelesaian yang lebih efisien. Selanjut-nya, berdasarkan latarbelakang di atas, maka rumusan masalah dalam penelitian ini adalah bagaimana mengembangkan metode branch and bound tersebut sehingga da-pat menangani persoalan program linier yang stokastik khususnya yang menyertakan resiko pada fungsi objektifnya.
1.3 Tujuan Penelitian
Tujuan dari penelitian ini adalah melakukan pengembangan pada metode and-bound. Pengembangan dilakukan dengan memperbaharui kembali algoritma branch-and-bound yang umum, sehingga diharap dapat menyelesaikan masalah-masalah yang
berhubungan dengan program stokastik linier cacah campuran multi-tahap (
multi-stage linear mixed-integer stochastic programs) yang menyertakan resiko pada fungsi objektifnya.
1.4 Kontribusi Penelitian
Penelitian ini diharapkan dapat memberikan sumbangan teoritis dalam bidang ma-tematika secara umum, khususnya mama-tematika terapan sehingga berguna bagi para mahasiswa/peneliti dalam memahami hal-hal yang berkaitan dengan metode branch and bound untuk menyelesaikan program stokastik integer.
1.5 Metode Penelitian
Metodologi penelitian yang dilakukan adalah bersifat literatur yaitu berupa penje-lasan dan uraian. Informasi dikumpulkan dari berbagai referensi: buku dan jurnal-jurnal ilmiah internasional yang berhubungan dengan judul tersebut.
Adapun langkah-langkah yang dilakukan adalah sebagai berikut:
1. Mengkaji berbagai literatur terkait, untuk menguraikan hal-hal:
(a) Program Stokastik Integer (stochastic integer programming).
(b) Program Stokastik dua-tahap (two-stage models).
4
2. Menguraikan inti dari penelitian ini, yaitu melakukan pengembangan metode branch-and-bound dalam menangani persoalan stokastik integer yang menyer-takan resiko pada fungsi objektifnya dengan langkah-langkah:
(a) Mengkaji multistage stochastic integer programs yang meliputi:
i. Model Ekspektasi
ii. Ukuran Resiko:
a. One-Period Polyhedral b. Expected Excess
c. Conditional Value-at-Risk (CV aR)
d. Multiperiod Polyhedral
e. Multiperiod CV aR
(b) Mengkaji Wait-and-See problem.
(c) Menyajikan Algoritma Branch And Bound yang dimaksud.
3. Bagian akhir adalah menetapkan kesimpulan dan saran-saran.
BAB 2
TINJAUAN PUSTAKA
Problema-problema yang disebabkan oleh ketidakpastian didalam data disajikan
de-ngan stokastik, yakni stokastik programming atau optimasi pada kondisi
ketidakpas-tian. Semakin besar ketidakpastian akan tingkah-laku suatu sistem, semakin penting pula penerapan model stokastiknya. Didalam model optimasi stokastik, parameter tertentu adalah variabel stokastik yang mempunyai beberapa distribusi peluang yang kontiniu atau diskrit (Birge dan Louveaux, 1997 ; Kall dan Wallace,1994). Belakangan
ini hal risk aversion mendapat perhatian lebih pada pemograman stokastik.
Peng-ukuran resiko yang berhubungan dengan ketidakpastian investasi telah menjadi topik
utama dalam matematika finansial untuk beberapa dekade ini. Fungsi tujuan (
ob-jective function) kini tidak lagi didasarkan hanya pada nilai harapan/expectation
se-mata tetapi juga tinjauan resiko/risk measure yaitu suatu nilai/ukuran yang pantas
untuk mengekspresikan risiko tersebut. Markert dan Schultz (2005) telah
menun-jukkan ektensi dari ekspektasi tradisional berdasarkan program integer stokastik ke
model mean-risk. Risiko diukur dengan ekspektasi deviasi dari varibel acak yang
co-cok terhadap rata-rata atau dari target yang ditentukan. Ukuran deviasi termasuk ukuran resiko yang mencerminkan dispersi dari objek acak dan juga model mean-risk yang diperluas dari hasil model berdasarkan sifat-sifat struktur seperti kontinuitas, turunan (diferensial) dan konveksitas dari kestabilannya.
Sifat-sifat struktural dari hasil program stokastik dan algoritma untuk dekom-posisi masalah juga diperlihatkan. Eichhorn dan Romisch (2000) telah menunjukkan
program stokastik multi-tahap dengan ukuran resiko polihedral pada fungsi
objek-tifnya serta sifat-sifat kestabilannya berdasarkan struktur dekomposisi.
Hasil kestabilan yang didapat untuk program stokastik multi-tahap dengan eks-pektasi, dibawa kedalam kasus objektifitas resiko polihedral. Ukuran resiko polyhe-dral didefnisikan sebagai nilai optimal dari program stokastik linier yang pasti dimana
argumen dari ukuran resiko berdasarkan ruas kanan (right hand side) dari kendala
di-namik. Representasi dual untuk ukuran resiko polihedral diturunkan dan digunakan
untuk menghasilkan kriteria konveksitas dan koherensi. Pengukuran risiko lainnya
adalahmultiperiod yang akan digabungkan ke dalam program stokastik multi-tahap,
membentuk model wait-and-see. Selanjutnya pembahasan komprehensif dari order
stokastik termasuk dominan stokastik digunakan pada konsep dominan stokastik un-tuk mendisain algoritma pada masalah optimisasi stokastik spesial telah diperlihatkan
6
oleh Artzner et al. (1999, 2003) yang merupakan konsep aksiomatik dari ukuran resiko koheren dan konveks secara luas.
Pengembangan algoritma yang efisien dan mampu menyelesaikan problem de-ngan jumlah skenario besar merupakan salah satu tantade-ngan dalam program sto-kastik. Teori penyelesaian program-program stokastik dua-tahap dengan algoritma yang membatasi nilai yang progresif telah disajikan oleh Rockafellar and Wets (1998).
Teknik optimalisasi ganda (Dualitas Lagrangean), mendasari algoritma yang
diperke-nalkan oleh Caroe dan Schultz (1999) dengan mengajukan teknik heuristics untuk
dipakai dalam algoritma branch and bound. Lulli dan Sen mengusulkan algorit-ma branch and price untuk menyelesaikan tahap-ganda dengan struktur tertentu.
Alonso-Ayuso, et al., mengajukan skema koordinasibranch and fix untuk
menyelesai-kan pure integer stokastik. Mereka menyelesaikan metode branch and bound untuk setiap problem skenario dengan merealisasikan kendala dan antisipatinitas melalui prosedure yang dirancang untuk mengkoordinasikan kendala pencarian branch and bound, sehingga kendala dan antisipatinitasnya dipenuhi.
BAB 3
LANDASAN TEORI
3.1 Program Stokastik
Persoalan keputusan dapat dimodelkan dengan menggunakan program matemati-ka yang bertujuan untuk menentumatemati-kan nilai optimal. Program stomatemati-kastik merupamatemati-kan bagian dari program matematika, dimana beberapa data yang termuat pada fungsi tujuan (fungsi objektif) atau kendala mengandung ketidakpastian yang dicirikan de-ngan distribusi peluang pada parameternya. Program stokastik dapat berupa linier, cacah, cacah campuran, ataupun non linear, dengan menyertakan elemen stokastik pada data.
Secara formal proses stokastik dinyatakan dengan X = {X(t) ; t∈T} yang
didefinisikan sebagai barisan variabel acak, yang mana untuk setiap t dati T
mem-punyai variabel acak X(t) dengan t disebut indeks atau parameter ”waktu”.
Se-mua kemungkinan nilai yang terdapat pada variabel acak disebut ruang status (state
space). Persoalan seperti pertambahan biaya marginal atau penurunan perolehan marginal dari sebuah proses produksi atau proses penjualan atau proses investasi dan lain sebagainya, merupakan persoalan program matematika yang secara umum dapat dimodelkan sebagai:
MinZ =g0(x)
dengan kendala gi(x) ≤ 0, i= 1,2,3, . . . , m x∈X ⊂ Rn
dimana diketahui X adalah himpunan real yang non-negative
dan x adalah variabel keputusan
gi : Rn→R, i= 0,1,2, . . . , m
Model proses pengambilan keputusan terhadap suatu persoalan stokastik, dimana yang diperlukan adalah membuat sebuah keputusan sekarang dan meminimumkan biaya rata-rata harapan (ekspektasi) sebagai konsekwensi dari keputusan yang telah
diambil, dikenal sebagai model rekursif (recourse).
Program linier acak dari tipe ini adalah:
inf x∈X,y(ω)∈R+m
{c x+q(ω)y(ω) :T(ω)x +W(ω)y(ω) =h (ω)} (3.1)
8
Parameter acak ξ := (q, T, W, h) : Ω → Rm×Rs×n×Rs×m×Rs adalah terdefinisi
pada ruang probabilitas (Ω,P, A) dan himpunanX ⊂ x∈Rn+ : A x=b ,
mengan-dung semua kendala deterministik pada variabelx. Model recourse dibentuk dengan
menambahkan ukuran fungsi objektif, yang dinyatakan dengan model seperti berikut:
inf x∈X
{c(ω)x+ Φ (x, ξ(ω))} (3.2)
dimana , Φ (x, ξ(ω)) = inf
x∈Rn
+
{qy : T (ω)x + W y=h(ω)} (3.3)
asalkan Φ : Rn × Rs×n ×Rs → ×R dapat diukur dan Z := {c x+ Φ (x, ξ(ω))
: x∈X} dianggap sebagai rumpun variabel-variabel acak. Sekarang setiap fungsi
R : Z → R berupa nilai ekspektasi, dan merupakan ukuran resiko atau jumlah
bobot keduanya (expectation dan risk) yang dapat digunakan sebagai ukuran fungsi
objektifnya.
3.2 Program Stokastik Dua-Tahap (two-stage models)
Konsep dari recourse telah banyak diaplikasikan pada program stokastik linier, pro-gram integer dan program non linier. Persamaan kendala pada (3.1) dapat dipedo-mani dengan menambah variabel-variabel slack yang tepat, dan model yang
ditun-jukkan sebagai model dengan dua-tahap (two-stage models). Untuk program stokastik
linier dua-tahap mempunyai formulasi standar:
M in cTx + Eω∈Ω [Q(x, ω)] dimana: x∈X, (3.4)
dengan: Q(x, ω) = Min f(ω)T
y (3.5)
dimana: D(ω)y ≥ h(ω) +T(ω)x,
y ∈Y,
dimanaX ⊆Rn1,c∈Rn1 dan Y ⊆Rn2 adalah himpunan Polyhedral. c∈Rn1 dan ω
sebuah variabel acak dari ruang probabilitas (ω, F, P) dengan Ω ⊆Rk , f : Ω→Rn2
, h : Ω→ Rm2, D : Ω → Rm2×n2 dan T : Ω→ Rm2×n1. Problema pada persamaan
(3.4) dengan variabelxmerupakan tahap pertama yang diperlukan untuk ditentukan
terlebih dahulu guna merealisasikan parameter ketidakpastian ω ∈Ω pada problema
persamaan (3.5) dimanay merupakan variabel tahap kedua.
9
Sebagai ilustrasi, bentuk persoalan two-stage stochastic integer program (pure
integer), misalnya seperti berikut:
Min: −1.5x1−4x2 +E[Q(x1, x2, ω1, ω2)]
s.t: x1, x2 ∈[0,5] ∩Z,
dengan: Q(x1, x2, ω1, ω2) = min {−16y1−19y2−23y3−28y4}
s.t: 2y1+ 3y2+ 4y3+ 5y4 ≤ω1− 1
3x1−
2 3x2
6y1+y2+ 3y3+ 2y4 ≤ω2− 2
3x1−
1 3x2
y1, y2, y3, y4 ∈ {0,1},
3.2.1 Program Stokastik Cacah Campuran
Pada program Stokastik integer campuran, beberapa variabel tertentu dibatasi pa-da bilangan integer, sepa-dangkan yang lanya tipa-dak. Dalam problema stokastik
in-teger campuran ini, dilakukan bertahap atau rekursif dengan minimal dua-tahap.
Pendekatan penyelesaian dari masalah program stokastik dua-tahap (recourse)adalah
dengan variabel-variabel tahap pertama yang diskrit yakni:
X ={x∈Zn1 A x=b, 0≤x}
dan variabel-variabel tahap kedua yang kontiniu atau diskrit yaitu:
y∈Y =
y∈Rn
+ beberapa yi boleh integer (3.6)
Selanjutnya diidentifikasi parameter acak dari program stokastik integer campuran berikut:
Min ncTx+qTy : T x+W y=Z(ω) , x∈X, y ∈Zm
+ ×Rm t +
o
(3.7)
Bersamaan dengan informasi dari kendala yang ada bahwa dalam tahap pertama
xharus dipilih terlebih dahulu untuk meninjau Z(ω), selanjutnya pada tahap kedua
y yang dipilih dan kondisi ini sering menjadi acuan agar pemilihan y ini tidak
men-dahului pemilihan nilai x. Berikutnya diasumsikan bahwa vektor-vektor dan matriks
pada persamaan (3.7) memiliki ukuran yang dapat dipenuhi, dimana W memiliki
masukkan bilangan rasional, dan x ⊆ Rm adalah sebuah polyhedron tak nol, yang
boleh jadi meliputi integer yang dibutuhkan untuk nilai komponen-komponen darix.
10
3.3 Program Stokastik Multi Tahap (Multistage Stochastic Program) 3.3.1 Model Ekspektasi
Pertimbangkan urutan yang terbatas dari proses pengambilan keputusan di bawah
ketidakpastian dimana keputusan χt∈Rnt untuk setiap t ∈ {1, ..., T} hanya berlaku
menurut informasi yang tersedia sampai pada waktut saja. Informasi terjadi sebagai
satu proses data discrete time stochastic ξ = (ξt)
T
t=1 pada beberapa ruang
proba-bilitas (Ω,F,P) dengan nilai dari XT
t=1Rmt. Dengan menguraikan Ft = σ(ξ1, ..., ξt)
,t =1, ...,T, menurut aljabar zigma dapat dihasilkan vektor acak (ξ1, ..., ξt).
Ke-mudian diasumsikan bahwa ξ1 adalah deterministik, yaitu F1 = {Ø,Ω}, dan bahwa
Fr = F, jelaslah bahwa Ft ⊆ Ft+1 untuk semua t =1, ...,T −1 Non-anticipativity.
Dengan menggunakan conditional expectations, kemudian dapat diekspresikan
seba-gai: Ht(χt) :=χt−E[χt|Ft] = 0.
Diperlukan bahwa χ= (χt)
T
t=1 harus memenuhi kendala-kendala:
χt ∈ Xt,
Himpunan tertutupXtyangconvex hulls adalah berbentuk polyhedra, ini adalah
kelompok pertama dari model sederhana yang menentukan kendala. Secara khusus,
ini mencakup persyaratan untuk keutuhan komponen dariχ. Kelompok kedua adalah
model non-anticipativity. Kelompok ketiga dan keempat selanjutnya adalah pasangan
kendala (coupling constraints) dan kendala-kendala dinamis (dynamic constraints)
yang menghubungkan setiap langkah berturut-turut.
Koefisien biaya bt(.), ruas kanan dt(.), ht(.), dan matriks At,τ(.), Bt(.) seharusnya
memiliki dimensi yang sesuai dan bergantung pada persamaan linierξt, untuk semua
t dan τ yang bersesuaian.
Variabel-variabel keputusan χt dipahami sebagai fungsi keanggotaan (members
of function) dari ruang Lp(Ω,F,P; Rnt), p∈[1,∞], t∈ {1, ..., T}. Kendala-kendala
dari kelompok yang pertama, ketiga dan keempat dipahami sebagai yang terpenting
dalam penerapanP. Kelompok kendala yang kedua menentukanfunctional conditions,
yang dalam kenyataannya fungsi keanggotaan dalam subspace linier cocok terhadap
×T
t=1 Lp(Ω,F, P; Rnt). Yang mana X(ξ) menunjukkan suatu himpunan yang layak
11
untuk semua χ ∈ ×T
t=1 Lp(Ω,F,P; Rnt). Selanjutnya, pembahasan dititikberatkan
pada isu algoritmik dalam hubungannya dengan finite discrete ξ. Oleh karena itu,
untukp=∞asumsi berikut dapat dipahami. Untuk setiap daerah feasibleχ∈ X (ξ)
mempengaruhi variabel-variabel biaya-acak (random cost variables):
zt := t X τ=1
bτ(ξτ) T
χτ, t= 1, . . . , T (3.8)
yang mana z1 adalah deterministik karena ξ1 juga deterministik.
Variabel-variabel acak ini, mewakili akumulasi biaya dari waktu ke waktu, yang dapat ditinjau dari sudut pandang yang berbeda: dalam kasus hanya permasalahan biaya
akhir, berarti zT adalah obyek yang penting. Jika pemantauan intermediate cost
adalah sebuah isu, maka seluruh vektor (z1, . . . ,zT) harus disertakan kedalam
per-hitungan. Kemungkinan lain adalah dengan mempertimbangkan kenaikan dari pada
biaya-biaya yang terakumulasi, yang mana perbedaan-perbedaan zτ+1−zτ, τ = 1,
. . . , T −1 menjadi bersesuaian. Hal ini mencerminkan pandangan-pandangan yang berbeda dari suatu perbedaan yang utama antara permasalahan multi-tahap dan
dua-tahap. Untuk selanjutnya, yang hanya menjadi perhatian dari random cost
ob-ject adalah zT = z2 .
Apapun pandangan yang diambil, dalam menyelesaikan programmultistage
stoc-hastic tersebut, yaitu dengan mencari sebuah χ ∈ X (ξ) yang ’terbaik’ untuk
men-emukan anggota keluarga vektor acak {(z1, . . . ,zT) : χ ∈ X(ξ) yang ’terbaik’ atau
suatu keluarga terkait yang berasal dari salah satu pandangan-pandangan di atas. Spesifikasi yang ’terbaik’ kemudian tercapai dengan membandingkan vektor-acak
de-ngan bantuan parameter statistik. Padarisk neutral multistage stochastic programs,
parameter yang relevan adalahexpectation yang diterapkan terhadap seluruh
akumu-lasi biaya zT, yang dinyatakan dalam model ekspektasi:
min {E [zT] : χ∈ X(ξ)} (3.9)
3.3.2 Pemahaman Resiko dan Ukuran Resiko (Risk Measures)
Sebagian besar masalah di dunia nyata dalam riset operasi melibatkan data yang tidak pasti. Jadi, mencari keputusan yang optimal untuk memilih sebuah yang ”terbaik” dari variabel acak. Kemudian muncul pertanyaan, kriteria apa yang akan digunakan untuk penseleksian tersebut. Untuk menggabungkan risiko ke dalam program
stokas-tik multi-tahap, parameter -parameter statisstokas-tik yang disebut risk-measures
diterap-kan ke variabel-variabel acakz1,. . .,zT modelexpectation dari sub-bagian 3.3.1 diatas.
Pada suatu program multistage stochastic, hasil dari sebuah vektor biaya-acak
mem-pengaruhi pemilihan hasil pada fungsi tujuan dalam dua-tahap dengan mengambil
12
sebahagian dari nilai variabel acak. Konsep dari ukuran resiko polyhedral (
polyhedral-risk) yang diperkenalkan oleh Eichhorn and Romisch, (2005) terbukti sangat fleksibel
yang merupakan aspek penting dari pemodelan multiperiod dan dalam menurunkan
struktur hasilnya.
Program stokastik dengan resiko pada fungsi tujuan (polyhedral risk-objectives)
akan membentuk suatu kelas yang substansial pada algorithma branch and bound.
Suatu ukuran risikoρdipahami sebagai suatu fungsi dari beberapa rangkaian variabel
acak yang bernilai real ke bilangan real (pengukuran risiko one-periode) atau
seba-gai fungsi dari beberapa himpunan vektor acak ke bilangan real (pengukuran risiko multiperiod).
Definisi 1 : (Ukuran Resiko One-Period Polyhedral)
Suatu ukuran risiko ρ pada Lp(Ω,F,P) dengan beberapa ρ ∈ [1,∞] disebut sebagai
polyhedral jika terdapat k1, k2 ∈ N, c1, w1 ∈ Rk1 , c2, w2 ∈ Rk2 , sebuah polyhedral
yang tidak kosong Y1 ⊆ Rk1 , dan sebuah kerucut polyhedral Y2 ⊆ Rk1 untuk setiap z ∈ Lp(Ω,F,P)
ρ(z) = inf
cT1y1 +E
cT2y2
:y1 ∈Y1, y2 ∈Lp(Ω,F,P), y2 ∈Y2, wT
1y1+wT2y2 =−z (3.10)
Dalam penyajian penelitian ini, yang diterapkan adalah pengaturan minimisasi.
Pada definisi 1 dapat mengakomodasi pengaturanmean-risk dimana risiko z diukur
dengan sejumlah E[z] dan beberapa ρ (z) yang memenuhi pada persamaan (3.10).
Memang, denganµ∈[0,1] jumlah bobot ˆρ:=µρ+(1−µ)Esesuai dengan persamaan
(3.10) ketika pengaturan ˆc1 := µc1−(1−µ)w1 , ˆc2 :=µc2−(1−µ)w2 , ˆw:= w1
, ˆw2 := w2
Suatu polyhedral risk measure dapat dilihat sebagai suatu nilai yang optimal
pada suatu program stokastik dua-tahap dengan ruas kanan yang random. Istilah ’polyhedral’ didorong oleh fakta bahwa untuk ♯Ω yang berhingga (finite), ρ adalah
suatu fungsi polyhedral pada R♯Ω .
Definisi 1 meliputi tindakan pengukuran resiko sebagaimana yang ditunjukkan pada contoh-contoh berikut:
Contoh 1 (Expected excess)
13
Contoh 2 ( Conditional Value-at-Risk/CV aR )
Dengan beberapa probability α ∈]0,1[ dan α− conditional value-at-risk (α−CV aR)
Hal ini sesuai dengan persamaan (3.10) dengan pengaturan: k1 := 1, k2 := 2, c1 :=
1, c2 := (1/(1−α),0) , w1 :=−1, w2 := (−1,1) , Y1 :=R, Y2 :=R2
+.
Secara khusus, skenario dekomposisi dapat diakomodasi untuk menghasilkan
penyelesaian yang lebih berarti darimean-risk problems.
Ukuran lain bagi ’resiko’ yang telah dipelajari dalam konteks dua-tahap program
integer stokastik adalah probabilitasP[z> η] melampaui targetη∈Ryang diberikan.
Meskipun tidak ada perwakilan dari ukuran resikopolyhedral yang dikenal sebagai
ak-ses probabilitas, skenario dekomposisi masih dapat diak-sesuaikan. SemideviationSD(z)
:=E[(z−E(z))+] adalah sebuah contoh untuk sebuah risk measure (ukuran resiko)
di-mana skenario dekomposisi tidak dapat diakomodasi secara langsung, karena setelah
relaksasi non-anticipativity beberapa pasangan skenario masih tetap dalam model
dua-tahap. Batas bawah merupakan fungsi yang diharapkan dengan target yang dipi-lih secara tepat, juga memungkinkan penggunaan skenario dekomposisi dalam sebuah
cara pendekatan (approximative). Transisi ke pengukuran resiko multiperiod
polyhe-dral dicapai melalui persamaan (3.10) dari sebuah two-stage ke sebuah multi-stage
stochastic program:
Definisi 2 : (multiperiod polyhedra)
Suatu ukuran bagi resiko multiperiod ρ pada ×T
14
Beberapa spesifikasi dari persamaan (3.11) yang dibahas, mengarah ke ukuran resiko multiperiod dengan kompleksitas yang berbeda. Antara lain, terlihat bahwa
peng-aturan yang cukup banyak termasuk filtrasi/penyaringan {Ft}Tt=1, contohnya yaitu
arus informasi dari waktu ke waktu, dimasukkan ke dalam definisi ukuran resiko. Berikut ini disajikan contoh yang relatif sederhana.
Contoh 3 (Multiperiod CV aR )
Dengan bobot γ2, ..., γT yang tidak negatif (non-negative weights) dan tingkat
keper-cayaan (confidence levels)α2, ..., αT ∈]0,1[dengan menjumlahkan setiap CV aRdalam
langkah-langkah:
e1 sebagai penanda kanonik vektor basis yang ke t dalam RT.
Object biaya acak yang diberi oleh persamaan (3.8), dan ukuran resiko multiperiod
seperti pada definisi 2 menjadi:
15
Ukuran resiko polyhedral yang diberi oleh suatu program stokastik multi-tahap
denganexpectation objective ini menyarankan untuk menganggap model program
sto-kastik multi-tahap berbasis expectation sebagai berikut:
min
Model-model tersebut membentuk proposisi berikut:
Proposisi 1 :
Meminimalkan persamaan (3.14)terhadap xadalah ekuivalen dengan meminimalkan persamaan (3.15) yang berkenaan dengan semua pasangan (x, y) dalam arti: Nilai-nilai optimal dari kedua masalah, saling bersesuaian dan(x∗
, y∗
)adalah sebuah solusi untuk persamaan (3.15) jika x∗
solusi bagi persamaan (3.14) dan y∗
adalah solusi untuk masalah minimisasi yang didefinisikan sebagai:
ρ
3.4 Separable Wait-And-See Problems
Masalah optimisasi yang muncul ketika menetaskannon-anticipativity dari suatu
pro-gram stochastic, biasa disebut wait-and-see problems.
Selanjutnya, terdapat masalah wait and see yaitu:
Z
yang berhubungan dengan ekspektasi matematika yang tanggap terhadap distribusi peluang pada nilai optimal. Pada prakteknya sering menggantikan parameter acak
A(ω) dan b(ω) dengan nilai ekspektasi:
Jelas, hasil dari masalah deterministiknya adalah: inf
x∈X⊂Rn
{c x, :A x ≥b}yang
meru-pakan bagian terbesar dari informasi yang diberikan oleh ukuran probabilitas P dan
akan dimanfaatkan untuk skala yang lebih besar atau situasi kompleks dimana model lain tak dapat diaplikasikan.
16
Lemma 1 : Relaxation non-anticipativas dalam multistage stochastic program pada persamaan (3.15) berhubungan dengan suatu masalah wait-and-see dimana ω ∈ Ω adalah yang dapat dipisahkan.
Bukti 1 : Tanpa non-anticipativity tidak ada kendala pada persamaan (3.15) yang mengandung komponen kendala dari ξ(.) dengan argumen ω, ω′
. Hal ini memung-kinkan pertukaran antara integration and minimization, dan problem wait-and-see dipahami sebagai berikut:
Karenanya minimisasi tersebut dapat dilakukan secara terpisah untuk masing-masing
ω∈Ω. Terbukti.
Keterpisahan pada hasil di atas telah dikenal dalam pengaturan terdahulu yang
berbasis expectation pada program stokastik multi-tahap, sehingga kenyataan
bah-wa masalah-masalah dengan multiperiod polyhedral risk objective adalah merupakan
representasi dari problems expectation Proposisi 1). Pertimbangkan hal berikut ini sebagai pengembangan multiperiod dari semideviation.
SDmp(z) =
T X
t=2
γtSD(zt), dengan γt≥0, t= 2, ..., T (3.17)
Untuk melihat bahwa di sini keterpisahan yang diinginkan selalu gagal, maka diberikan
γ2 =· · ·=γT−1 = 0 , γT = 1 dan pertimbangkan masalah:
min{SD(zT) : x ∈ X(ξ)}
Dengan sebuah variabel baru θT ∈ R (dan mengingat bahwa FT = F mencakup
non-anticipativas) sehingga masalah di atas setara dengan:
min{E[θT] : x ∈ X(ξ), θT ≥0, θT ≥zT −E[zT]}
Kendala θT ≥zT −E[zT] menghasilkan sejumlah pasanganω ∈Ω yang berbeda, dan
pasangan ini tetap merupakanrelaxation of non-anticipativity.
17
Masalah keterpisahanω, dalam penelitian ini akan ditekankan pada batas bawah.
Jadi, sebuah pemisahan batas bawah pada fungsi objektif yang mempunyai resiko, akan mungkin dilakukan. Lema yang berikut mengidentifikasi batas seperti itu untuk persamaan (3.13).
Lemma 2 : Jika ηt≤E[zt], t= 2, . . . , T, maka 0≤Eηt[zt]−E[zt] +ηt≤SD(zt), t= 2, . . . , T. Pertidaksamaan pertama berlaku jika dan hanya jika P[ηt>zt]>0.
Bukti 2 : Tanpa pembatasan ηt itu menyatakan bahwa max{zt, ηt} ≥ zt , dan
karenanya max {zt−ηt,0} +ηt ≥ zt . Akibatnya expectations menghasilkan
per-tidaksamaan yang pertama. Dengan ηt ≤ E[zt] diperoleh suatu max {zt, ηt} ≤ max {zt,E[zt]}. Oleh karena itu, max{zt−ηt,0}+ηt ≤ max {zt−E[zt],0} +E[zt] ,
dan pertidaksamaan kedua diverifikasi lagi dengan mengambil nilai expectations. Per-tidaksamaan pertama berlaku jika dan hanya jika 0<E[max{ηt−zt,0}] , yaitu jika
dan hanya jika P[ηt>zt]>0.
Expected excess adalah sebuah ukuran risiko polyhedral. Jadi batas bawah,
me-mang, tidak dapat dipisahkan dalam ω. Lemma ini juga mengatakan bahwa batas
tersebut lebih baik setelah hasil zt jauh di bawah target ηt dengan probabilitas yang
positif. Juga zt tergantung pada x, perhatikan pada persamaan (3.8). Sebuah
per-masalahanwait-and-seedapat memperbesarfeasible setyang mungkin, hal ini
menye-diakan suatu pilihan yang mungkin dariηt untuk semua x yang sesuai.
ηtws :=E[min {zt : x∈ X (ξ), with non-anticipativity dropped}], t= 2, . . . , T.
Kesimpulan bagian ini merupakan pengembangan multiperiod dari one-period excess
probability.
Tidak ada perwakilan dari ukuran resiko polyhedral yang dikenal dalam kasus ini,
tetapi tujuan pemisahan dari relaksasi wait-and-see masih berlaku.
Contoh 4 : Pertimbangkan pengembangan multiperiod dari EPη(z) :=P[z> η]
EPmp(z) :=
T X
t=2
γtEPηt(zt) , (3.18)
dengan faktor bobot γt≥0 dan level target ηt∈R, t= 2, . . . , T.
Untuk permasalahan:
min {EPmp(z) : x∈ X(ξ)}
18
diasumsikan bahwa semua himpunan{zt: x∈ X(ξ)}, t= 2, . . . , T adalah batas atas P. Maka terdapat konstan M > 0 sedemikian rupa, sehingga masalahnya ekuivalen
dengan:
min
( E
" T X
t=2 γtut
#
: x∈ X (ξ),
zt−ηt≤ M ut, ut ∈ {0,1} , H(ut) = 0, t= 2, ..., T }. (3.19)
Penguraiannon-anticipativity di atas menciptakan keterpisahan di ω.
BAB 4
PEMBAHASAN
4.1 Metode Branch And Bound
Algoritma Branch and Bound merupakan metode pencarian di dalam ruang solusi secara sistematis. Ruang solusi diorganisasikan ke dalam pohon ruang status.
Al-goritma dimulai dengan pengisian sebuah nilai ke akar (root) dari pohon
pencari-an tersebut. Kemudipencari-an permasalahpencari-an diuraikpencari-an kedalam subregion-subregion yang
mungkin akan mengarah ke solusi. Inilah yang disebut dengan cabang (branching).
Branching dilakukan dengan memasang sebuah pending node ke pending node lain
yang lebih rendah levelnya. Bobot juga dihitung pada setiap proses dan ditulis di
simpul pohon. Prosedur ini akan dilakukan berulang-ulang secararekursif untuk
se-tiap subregion dan sese-tiap subregion yang dihasilkan akan membentuk sebuah struktur pohon yang disebut sebagai pohon pencarian atau pohon branch-and-bound di mana simpul-simpulnya membangun subregion-subregion.
Selain branching, algoritma ini juga melakukan apa yang disebut dengan
bound-ing yang merupakan cara untuk mencari batas atas dan batas bawah untuk solusi
optimal pada subregion yang mengarah ke solusi. Jika sebuah simpul diketahui meru-pakan solusi yang tidak mungkin bagi persoalan yang dihadapai, simpul tersebut diisi
dengan nilai tak terbatas (infinity). Algoritma berhenti ketika: sudah tidak mungkin
lagi untuk membentuk simpul baru di pohon atau hasil terakhir yang ditemukan merupakan hasil yang lebih rendah (minimum) dari isi simpul yang telah ada pada level yang lebih rendah .
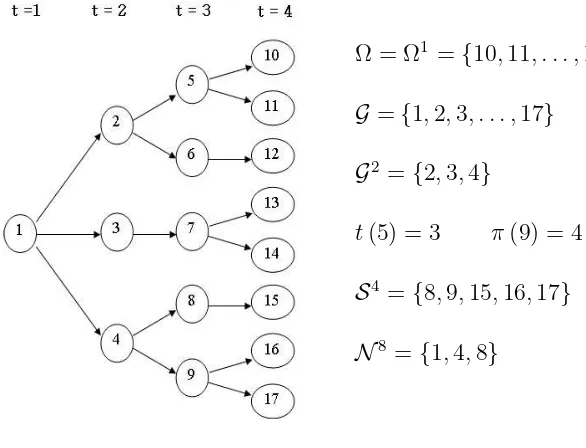
Ilustrasi berikut menampilkan pohon skenario dari mulistage dengan parameter
stokastik:
20
Ω = Ω1 ={10,11, . . . ,17} Ω2 ={10,11,12}
G ={1,2,3, . . . ,17} G2 ={2,3,4}
t(5) = 3 π(9) = 4
S4 ={8,9,15,16,17}
N8 ={1,4,8}
Gambar 4.1 Scenario tree ; multistage
Berikut ini contoh sederhana penerapan metode branch-and-bound pada
per-soalanInteger Programming.
Contoh 5 (program linier cacah campuran)
Maksimumkan:Z = 5X1+ 8X2
dengan kendala : X1+ X2 ≤6
5X1+ 9X2 ≤45
Penyelesaian:
Maksimum Z = 40 untuk X1 = 0 dan X2 = 5 ,
(detail penyelesaian dengan Maple ver.12: pada Lampiran 2.)
Gambar 4.2 The enumeration tree
21
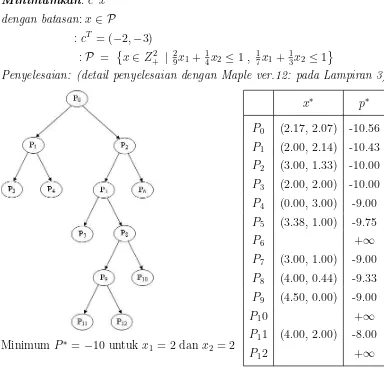
Contoh 6 ( Integer Linear Programming Relaxation )
Minimumkan:cTx
Penyelesaian: (detail penyelesaian dengan Maple ver.12: pada Lampiran 3)
x∗
p∗
P0 (2.17, 2.07) -10.56
P1 (2.00, 2.14) -10.43
P2 (3.00, 1.33) -10.00
P3 (2.00, 2.00) -10.00
P4 (0.00, 3.00) -9.00
Gambar 4.3 Tree of subproblems and results of LP relaxations
4.2 Pengembangan Metode Branch And Bound
4.2.1 Algoritma
Formulasi dua-tahap dapat digunakan untuk problema multi-tahap yang
dipasang-kan dengan model ketidakpastian sebagai sebuah proses filtrasi. Perlakuan numerik
pada program stokastik multi-tahap biasanya membutuhkan distribusi probabilitas diskret. Peralihan kedistribusi probabilitas diskrit ini dapat dibenarkan oleh stabili-tas hasil untuk program stokastik dengan distribusi-distribusi yang random. Berikut-nya Ω = {ω1, ..., ωS} , πs := P({ωs}), ξs := ξ(ωs) , s = 1, ..., S. Program stokastik
multi-tahap dari rumusan pada bagian 3.3 dan 3.4 merupakan masalah optimasi berdimensi tak berhingga yang kemudian menjadi dimensi berhingga. Selanjutnya
dengan aljabar zigma, F menjadi himpunan kuasa 2Ω dari Ω. Untuk setiap
subalge-bra Ft dengan t = 1, ..., T terdapat suatu keluarga εt ⊆ 2Ω yang membentuk sebuah
22
partisi Ω dan menggenerate Ft. Karena Ft ⊆ Ft+1 setiap unsur εt adalah gabungan
elemen dalamεt+1. Banyaknya unsur-unsur diεtbertepatan dengan banyaknya unsur
yang berbeda (ξ1
τ) t
τ=1 , ...., ξτS t
τ=1 yang merupakan perwujudan dari ξ untuk saat t.
Hubungan antara unsur-unsurξtdanξt+1 untukt= 1, ..., T−1 dapat dinyatakan oleh
sebuah pohon (tree), yang disebut pohon skenario (scenario tree). Simpul (node) dari
pohon ini terjadi dalam lapisan (layers) untuk t = 1, ..., T yang mana setiap simpul
berkorespondensi dengan unsur dariξt pada beberapat ∈ {1, ..., T}. Arcs hanya ada
antara simpul-simpul di dalam lapisan-lapisan yang bersebelahan. Setiap node
di-dalamξt terhubung dengan semua node didalamξt+1 yang gabungannya membentuk
ξt. Skenario ξs = (ξτs) T
τ=1 , s = 1, ..., S sesuai dengan maximal paths dalam pohon
skenario tersebut.
Dalam pohon skenario ini,non-anticipativity dari keputusan (×s)S
s=1= (×(ωs)) S s=1
mengatakan bahwa komponen xs dan xs′
harus mencapai nilai-nilai yang sama
sepa-njang korespondensi pathsξs dan ξs′
bersamaan. Lebih tepatnya, di belakang notasi
Ht(xt) = 0, t = 1, ..., T yang diperkenalkan pada bagian 3.3, kini terdapat sistem
Berikutnya merumuskan program-program integer stokastik multi-tahap. Di
samping model tradisional pada persamaan (3.9) perhatikan ekspektasi dari model di persamaan (3.15) dan persamaan (3.19) sebagai yang ekuivalen dengan model-model resiko pada fungsi tujuan.
Semua spesifikasi model stokastik multi-tahap ini dapat diperoleh sebagai berikut:
23
dan keterpisahan yang dibahas pada bagian 3.4, dimana model ini equivalent dengan:
S
Algoritma ini didasarkan pada pemahaman persamaan (4.1) sebagai sebuah masalah non-convex global minimization yang ditangani oleh branch-and-bound. Himpunan
yang layak akan dipartisi menggunakan subspaces non-anticipativity. Unsur-unsur
partisi, dari pengembangan tipe persamaan (4.2) akan menyediakan batas bawah (lower bounds) untuk nilai-nilai objektif yang optimal. Batas atas (upper bounds)
diperoleh dari solusi persamaan (4.2) yang memenuhirelaxed non-anticipativity, atau
heuristics yang sesuai.
Asumsikan bahwa persamaan (4.1) dibatasi seperti di bawah ini. Sehingga skema dasar dari algoritma menjadi sebagai berikut:
Langkah 0: (Initialization)
P:={persamaan (4.2)} - daftarkan permasalahan;
GU B := +∞- Sebuah batas atas global untuk nilai yang optimal;
IN C := kosong - Saat ini merupakan suatu solusi yang terbaik;
0< ε - Suatu parameter toleransi untuk penghentian (stop);
δ > 0 - Suatu parameter toleransi untuk percabangan (branching) ;
LB(persamaan (4.2)) := kosong - Sebuah batas bawah untuk anggota P.
Langkah 1: (Termination/Penghentian)
Jika P= Ø atau (GU B−minp∈PLB(P))/(1 +|minp∈PLB(P)|)< ε,
maka STOP; IN C sudah optimal.
Langkah 2: (Seleksi masalah dan solusinya)
Pilih P ∈ P dan hapus ini dariP . SolusinyaP.
Langkah 3: (Pruning by infeasibility)
Jika daerah layak P masih kosong, maka ulangi ke langkah 1.
Jika tidak, set ϕ(P) ke nilai optimal
dan x(P) menjadi solusi optimal dari P.
24
Langkah 4: (Pruning by inferiority)
Jika ϕ(P)≥GU B, maka kembali ke langkah 1.
Langkah 5: (Pruning by optimality)
Jika x(P) memenuhi relaxed non-anticipativity,
maka hapus dari Pseluruh problem P denganLB(P)≥ϕ(P) .
Jika ϕ(P)< GU B, maka atur GU B :=ϕ(P) dan IN C :=x(P). Kembali ke langkah 1.
Langkah 6: (Feasibility heuristic)
Terapkan suatu permulaan heuristic keluar darix(P) untuk memperoleh suatu
feasible point x¯(P) untuk persamaan (4.1).
Jika nilai fungsi objektif ¯ϕ(P) yang terakhir memenuhi pada ¯ϕ(P) < GU B,
maka atur GU B := ¯ϕ(P) dan IN C := ¯x(P).
Langkah 7: (Branching/Pencabangan)
Pilih suatu komponen ×(P)st,(i) dari ×(P) yang melanggarnon-anticipativas.
Berikan Gt untuk menandakan elemen (yang unik) dari εt (untuk dikaitkan
de-ngan suatu simpul di dalam layer t dari pohon skenario) yang mengkaitkan
path/jalur yang sesuai dengans melalui Gt.
1. Jika ×(P)st,(i) adalah variabel bilangan cacah, buatkan dua subproblem
baru P1 dan P2 untuk ditambahkan keP, pada setiap s′
dalam jalur/path
pohon skenario yang dilewati Gt, dengan batasan-batasan:
×s′
2. Jika ×(P)st,(i) adalah variabel diskrit kontiniu, buatkan dua subproblem
baru P1 dan P2 untuk ditambahkan keP, pada setiap s′
dalam jalur/path
pohon skenario yang dilewati Gt, dengan batasan-batasan:
×s′
Kembali ke langkah 1.
Algorithma ini mempunyai dua fitur utama yaitu: pada langkah 2 solusi masalah tercapai menurut skenario tersebut, dan pada langkah 7 percabangan dilaksanakan di kelompok variabel yang dibanding dengan masing-masing variabel.
Inisialisasi pada Langkah 0, non-anticipativity merupakan pengembangan dari
persamaan (4.2), yang mana oleh persamaan (4.3) ada sejumlah koleksi masalah
25
single-scenario untuk s = 1, . . . , S. Algoritma hanya bekerja pada single-scenario. Hal tersebut diperbarui pada Langkah 7 dimana non-anticipativity disusun kembali langkah demi langkah. Keterpisahan dari rumus pada persamaan (4.3) kemudian dipertahankan sejak adanya masalah baru dari langkah 7 yang tidak tepat mengarah kepasangan skenario. Modifikasi problem pada langkah 7 biasanya hanya melibatkan himpunan bagian dari skenario. Oleh karena itu, masalah - masalah pada single-scenario yang tidak diubah dalam langkah 7 menanggung potensi untuk digunakan
ulang pada langkah 2 ketika menyelesaikan masalah berikutnya dari P. Langkah 7
dapat dilihat sebagai kendala percabangan pada kondisi non - anticipativity. Ketika
percabangan berupa variabel kontinu, toleransi δ digunakan untuk menghindari
per-baikan yang tak ada habisnya. Pengecekan non-anticipativity di awali dari langkah 7
yang mana komponen dengan jarak kurang dari δ dianggap tepat. Dengan toleransi
δ, penghentian terbatas dari algoritma terjadi jika untuk himpunan yang layak pada
persamaan (4.1) dibatasi. Dalam perhitungan praktis contohnya masalah dimensi, biasanya akan dibutuhkan untuk memaksa penghentian algoritma dengan membatasi waktu eksekusi atau kuantitas yang relevan lainnya.
Untuk heuristik pada Langkah 6, pengguna dapat menentukan urutan prioritas
dari variabel, atau mengikuti tahapan t = 1, ..., T. Ternyata dalam hal ini
bergu-na untuk menentukan peringkat model variabel-variabel yang disebabkan oleh
peng-ukuran resiko, sepertiηt pada Contoh 3 (Multiperiod CVaR), dengan prioritas
teren-dah. Proses heuristik kemudian memperbaiki bagian dari variabel-variabel menurut urutan/prioritasnya dan memecahkan permasalahan dengan mengurangi sisa variabel yang tidak tetap. Langkah 6 sendiri adalah opsional, dan pemilihan dapat diulangi
beberapa kali dalam satuloop dikeseluruhan algoritma.
Urutan prioritas dari Langkah 6 juga digunakan untuk pemilihan komponen
×s
t,(i) dalam Langkah 7. Konsepnya, pemilihan komponen ini memiliki beberapa
ke-samaan dengan pemilihan variabel percabangan (branching variable) seperti pada
pe-mograman linier tradisional (LP) yang mendasari branch-and-bound untuk program-program integer. Yakni, pada akhir sebuah variabel melanggar integritas yang dipilih.
Di sini, sebuah variabel melanggarnon-anticipativity mengambil tempat.
Pemilihan-nya kemudian mengikuti aturan prioritas. Sebagai alternatif, meniru ’aturan variabel pecahan yang paling kecil’ juga seperti pada pemograman integer, dan memilih se-buah variabel yang paling antisipatif (kebanyakan variable anticipative), yaitu satu dengan dispersi maksimum ke seluruh skenario (dengan menentukan beberapa uku-ran dispersi). Dalam perumusan dari Langkah 7 di atas, uku-range variabel dibagi atas ×(P)st,(i), s= 1, . . . , S.
26
4.3 Komputasi
Sebagai contoh perhitungan, dilampirkankan tabel hasil penelitian sebelumnya yang
dilakukan oleh Thomas Heinze (March 2007), dalam bukunya dengan judulA
branch-and-bound method for multistage stochastic integer programs with risk objectives pada halaman 291. Tabel 1 (Lampiran 1) ini merupakan sebahagian laporan dari hasil
algoritma tersebut untuk model multiknapsack multi-tahap, terhadap model yang
dibuat untuk menghasilkan tes akademis secara instan. Perhitungan-perhitungan untuk model ini dilaksanakan pada komputer Sun Ultra Sparc III dengan processor 1.2 GHz dan 32 GB RAM.
Model-model tersebut dapat diringkas sebagai berikut:
Diketahui sebuah proses data stokastikdt(ξt) , t= 2, . . . , T yang merupakan vektor
-vektor anggaran (budget vectors), keputusan-keputusan multiknapsack, xt∈Z
n1
t−1 adalah sebuah matriks yang berisi bilangan non-negatif, dan 1 adalah
sebuah vektor dari semua vektor satuan, dan M sebuah angka positif cukup besar.
Sehingga keputusan multiknapsackxt−1pada waktut−1 yang diikuti oleh perwujudan
anggaran pada waktu t dan kerugian yt, yang mana masing-masing komponennya
adalah 1 jika anggaran yang sesuai terlewati.
Lalu terdapat batasan-batasan pasangan keputusan multiknapsack pada saat:
t−1
X τ=0
A2t,τxt−τ ≤ ht, t= 1, . . . , T −1.
Batasan-batasan itu diselesaikan oleh non-anticipativas:
H1(x1) = 0 , Ht(xt, yt) = 0 , t= 2, . . . , T −1, HT (yT) = 0
di mana klaim terakhir tentu saja kosong.
Tujuannya adalah pemaksimalanutilitas dengan kontribusi b1T
t xt, t = 1, . . . , T −1
oleh multiknapsack dan−b1T
t yt , t= 2, . . . , T, oleh kompensasi keputusan-keputusan
(dengan b1
t, b2t positif). Sebagai ukuran multiperiod risk digunakan bobot (weighted
sums) dari expectation dan multiperiod CVaR pada persamaan (3.12). Bobot bagi
expectation selalu 1, dan multiperiod CV aRdengan bobot β non-negatif.
Kolom 1 sampai 5 dari Tabel 1 (Lampiran 1) masing-masing menunjukkan
di-mensi dan faktor bobot the weight factors. Kolom 6 menunjukkan gap (GU B−
minP∈PLB(P)
/ 1 +|minP∈PLB(P)|
yang dicapai dengan algoritma setelah 2
27
jam waktu perhitungan (dalam persen). Entri ’0.1%’ menunjukkan bahwagap
menu-run di bawah nilai ini, yang berakhir sebelum 2 jam. Kolom 7 menampilkangaps yang
diperoleh setelah 2 jam dari waktu komputasi. Entri ’−’ menandai contoh di mana
ke-senjangan/gap tidak jatuh di bawah 1000% dalam waktu 2 jam. Kolom 8 melaporkan
(savings problemsversion bb-tree) problem single-scenario dengan menghindari solusi
MILPs (mixed-integer linear programs stochastic) yang identik berulang.
Persentase mencerminkan hasil bagi dari banyaknya permasalahan single-scenario yang sebenarnya terpecahkan dengan maksimum yang mungkin secara teoritis, yaitu
produk dari banyaknya skenario dan banyaknya pengulangan (loops) yang melalui
Langkah 2 pada algoritma tersebut. Kolom 9 (version bb-tree) menampilkan gap
ketika penyelesaian melalui langkah 2 pada setiap perulangan untuk masing-masing permasalahan pada single-scenario yang baru, lalu kembali lagi ke langkah awal.
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Penggunaan metode branch and bound yang standar adalah gagal dalam menye-lesaikan persoalan stokastik integer yang menyertakan resiko pada fungsi tujuan-nya. Untuk itu dilakukan pengembangan terhadap metode tersebut melalui
algo-ritmanya yaitu dengan memasukkankan pendekatan dekomposisi (decomposition
ap-proach) yang telah menyediakan solusi yang layak (feasible solutions) bagi optimali-tas penyelesaian persoalan program stokastik linier cacah campuran multi-tahap yang menyertakan resiko di fungsi objektifnya. Algoritma tersebut juga menghindari
peru-langan solusi permasalahansingle-scenario yang identik, dan menunjukkan
kecende-rungan bahwasolusi subproblems sering terbatas pada persentase yang cukup rendah
dari kasus-kasus yang secara teoritis dimungkinkan.
5.2 Saran
Disarankan agar algoritma branch and bound terus dikembangkan. Terutama untuk program komputer, sebab dirasa sangat diperlukan dalam menangani permasalah multistage stochastic integer programs yang berskala besar dan melibatkan banyak variabel keputusan maupun fungsi kendala, sementara algoritma tersebut tetap saja menghitung kemungkinan solusi dengan variabel bilangan bertipe real walaupun pada akhirnya kemungkinan solusi ini tidak dipertimbangkan. Hal ini telah menyebabkan waktu yang dibutuhkan untuk komputasi menjadi bertambah lama dan hampir tidak memungkinkan dipandang dari sudut ketersediaan waktu untuk diselesaikan secara manual.
28
DAFTAR PUSTAKA
A. Alonso-Ayuso, L.F. Escudero, and M.T. Ortuno, BFC. 2003. , A branch-and-fix coordination algorithmic framework for solving some types of stochastic pure
and mixed 0-1 programs.Eur. J.Oper. Res. 151: 503-519.
A. Eichhorn and W. Romisch. 2005. Polyhedral risk measures in stochastic
program-ming.SIAM J.Opt. 16: 69-95.
A. Markert and R. Schultz. 2005. On deviation measures in stochastic integer
pro-gramming.Oper. Res.Lett. 33: 441-449.
C.C. Carøe and R. Schultz. 1999. Dual decomposition in stochastic integer
program-ming.Oper. Res.Lett. 24: 37-45.
G. Lulli and S. Sen. 2004. A branch-and-price algorithm for multistage stochastic
in-teger programming with application to stochastic batch-sizing problems.Manag.
Sci.50: 786-796.
J.R. Birge and F. Louveaux. 1997. Introduction to Stochastic Programming. Springer,
New York.
M.P. Nowak and W. Romisch. 2000. Stochastic Lagrangian relaxation applied to power
scheduling in a hydro-thermal system under uncertainty.Annal. Oper. Res.Lett.
100: 251-272.
P. Kall and S.W. Wallace. 1994. Stochastic Programming, Wiley, Chichester.
P. Artzner, F. Delbaen, J.-M. Eber, et al. 1999. Coherent measures of risk. Math.
Financ. 9: 203-228.
R.T. Rockafellar and R.J-B. Wets. 1998. Variational Analysis. Springer, Berlin.
R. Schultz and S. Tiedemann. 2006. Conditional value-at-risk in stochastic programs
with mixed-integer recourse.Math. Program. 105: 365-386.
S. Kuhn and R. Schultz. 2006. Risk neutral and risk averse power optimization in
electricity networks with dispersed generation. Department of Mathematics, Uni-versity of Duisburg-Essen.
T. Heinze and R.Schultz. 2007. A branch-and-bound method for multistage stochastic
integer programs with risk objectives.Optimization. 57: 276-293.
LAMPIRAN 1
T S Cont/Int/Bin Const. β Tree CPLEX S.problems S.gap Hash
0/21/1080 1083 0 0.1% 468.7% 1.142% 0.1% 0.1%
3 48 56/21/1080 1137 0.5 0.1% – 0.025% 122.9% 0.1%
56/21/1080 1137 1 0.1% – 0.005% 962.1% 0.1%
56/21/1080 1137 2 0.1% – 0.002% – 0.1%
0/9/2000 2003 0 0.1% 271.1% 68.604% 0.1% 0.1%
3 96 102/9/2000 2103 0.5 0.1% 520.1% 21.433% 0.1% 0.1%
102/9/2000 2103 1 0.1% 359.7% 21.602% 55.4% 0.1%
102/9/2000 2103 2 0.1% – 10.073 – 0.1%
0/33/1160 1163 0 0.1% 344.7% 1.210% – 0.1%
4 48 61/33/1160 1221 0.5 0.1% 430.5% 0.502% – 0.1%
61/33/1160 1221 1 0.1% 377.1% 0.114% – 0.1%
61/33/1160 1221 2 1.3% – 0.036% – 21.7%
0/33/2120 2123 0 0.1% 567.6% 2.876% – 0.1%
4 96 109/33/2120 2229 0.5 0.1% – 2.434% 50.3% 0.1%
109/33/2120 2229 1 0.1% – 0.439% 53.8% 0.1%
109/33/2120 2229 2 2.3% – 0.029% 60.8% 55.3%
0/45/2200 1243 0 0.1% 300.5% 0.093% 511.1% 0.1%
5 48 66/45/1240 1305 0.5 0.1% 443.2% 0.060% 617.5% 0.1%
66/45/1240 1305 1 0.1% 521.8% 0.033% 716.1% 1.7%
66/45/1240 1305 2 99.1% – 0.008% 818.3% 71.1%
0/45/2200 2203 0 0.1% 589.3% 0.145% 656.8% 0.1%
5 96 114/45/2200 2313 0.5 0.2% – 0.263% 750.6% 0.2%
114/45/2200 2313 1 2.1% – 0.091% 823.2% 4.9%
114/45/2200 2313 2 15.1% 904.5% 0.024% – 23.1%
0/93/1560 1563 0 19.8% 570.3% 0.006% 394.4% 77.3%
6 48 83/93/1560 1641 0.5 29.6% – 0.002% 454.1% 33.9%
83/93/1560 1641 1 33.5% – 0.009% 462.2% 34.6%
83/93/1560 1641 2 33.2% – 0.024% 620.8% 51.7%
0/93/2520 2523 0 10.1% 406.9% 0.005% 918.2% 41.9%
6 96 131/93/2520 2649 0.5 19.5% 561.4% 0.004% – 35.6%
131/93/2520 2649 1 35.4% 476.7% 0.006% 615.4% 42.3%
131/93/2520 2649 2 46.1% – 0.002% – 60.5%
0/189/2200 2203 0 0.1% 211.8% 0.167% 896.6% 0.1%
Tabel 5.1 Computational results for multiknapsack problems
30
LAMPIRAN 2
OPTIMAL SOLUTION OF THE LP-RELAXATION with BRANCH AND BOUND
Maksimalkan profit : 5 X1 + 8 X2 dengan kendala : X1 + X2 ≤ 6
5 X1 + 9 X2 ≤ 45 dan X1, X2 ≥ 0
with Optimization
ImportMPS,Interactive,LPSolve,LSSolve,Maximize,Minimize,NLPSolve,QPSolve
kendalad x1Cx2%6, 5 x1C9 x2%45,x1R 0,x2R 0 kendala:= 0%x1, 0%x2,x1Cx2%6, 5x1C9x2%45
Typesetting:-RuleAssistant ; fungsiTujuand 5 x1C8$x2
fungsi
Tujuan:= 5x1C8x2
LPSolve fungsiTujuan,kendala,maximize
41.250000000000, x1= 2.24999999999999956,x2= 3.75000000000000000
atau :
dengan Metode Branch & Bound
LPSolve fungsiTujuan,kendala,maximize,assume = nonnegative, integer , depthlimit = 50
40, x1= 0,x2= 5
evalf LPSolve fungsiTujuan,kendala,maximize , 4
32
O O
O O
(11) (11) O
O
(10) (10) (9) (9)
X1 X2
X1
Subdividing the feasible region S1 :
evalf LPSolve fungsi
Tujuan, x1Cx2%6, 5 x1C9 x2%45,x1R0,x2%3 ,maximize , 4
39., x1= 3.,x2= 3.
x1= 3 danx2= 3 sudah bulat, maka STOP
S2 :
evalf LPSolve fungsi
Tujuan, x1Cx2%6, 5 x1C9 x2%45,x1R0,x2R4 ,maximize , 4
41., x1= 1.800,x2= 4.
x1= 1.800 padaS2sebagaipecahanterbesar,
makaakanbercabangkeS3untukx1%1 dan S4untukx1R2
X1
S3 :
evalf LPSolve fungsi
Tujuan, x1Cx2%6, 5 x1C9 x2%45,x1%1,x2R4 ,maximize , 4