KAJ I AN TENTANG PENDEK ATAN DISTRIBUSI BINOMI AL OLEH DISTRIBUSI NORM AL
SKRIPSI
MUSTAFA KEM AL R AMBE 090823073
DEPARTEMEN M ATEM ATIK A
FAKULTAS MATEMATIK A DAN I LMU PENGETAH UAN ALAM UNIVER SITAS SUMATER A UTAR A
KAJ I AN TENTANGN PENDEK ATAN DI STRIBUSI BINOMI AL OLEH DISTRIBUSI NORM AL
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MUSTAFA KEM AL R AMBE 090823073
DEPARTEMEN M ATEM ATIK A
FAKULTAS MATEMATIK A DAN I LMU PENGETAH UAN ALAM UNIVER SITAS SUMATER A UTAR A
PERSETUJUAN
JUDUL : KAJIAN TENTANG PENDEKATAN DISTRIBUSI BINOMIAL OLEH DISTRIBUSI NORMAL
KATEGORI : SKRIPSI
NAMA : MUSTAFA KEMAL RAMBE
NIM : 090823073
PROGRAM STUDI : SARJANA (S-1) MATEMATIKA
DEPARTEMEN : MATEMATIKA
FAKULTAS : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di : Medan, Agustus 2012
Komisi pembimbing :
Pembimbing 2 : Pembimbing 1 :
Drs. Ujian Sinulingga, M.Si Drs. Pengarapen Bangun, M.Si Nip. 19560303 198403 1 004 Nip. 19560815 198503 1 005
Diketahui/ Disetujui oleh
Departemen Matematika FMIPA USU Ketua
Prof. Dr. Tulus, M.Si
PENGHARGAAN
Puji syukur penulis panjatkan kepada Allah SWT dengan limpahan dan karunia-Nya sehingga skripsi ini dapat diselesaikan.
ABSTRAK
Proses Bernoulli adalah suatu proses yang berlangsung n kali dan tiap eksperimen berlangsung dalam cara dan kondisi yang sama. Untuk setiap eksperimen hanya ada 2 (dua) kejadian yang mungkin yang mana kejadian itu saling asing dan juga independent satu sama lain, yang biasa dinotasikan dengan kejadian sukses dan gagal. Jika nilai n cukup besar, proses Bernoulli akan mendekati distribusi normal , dengan menggunakan rumus :
�=� − �
� =
� − �� ����
DAFTAR ISI
Halaman
Persetujuan i
Pernyataan ii
Penghargaan iii
Abstrak iv
Abstrac v
Daftar Isi vi
Daftar Tabel vii
Daftar Gambar viii
BAB 1 PENDAHULUAN
1.1Latar Belakang 1
1.2Permasalahan 2
1.3Tinjauan Pustaka 2
1.4Tujuan Penelitian 4
1.5Manfaat Penelitian 4
1.6Metode Penelitian 4
BAB 2 LANDASAN TEORI
2.1 Probabilitas 6
2.2 Opereasi-operasi dalam Kejadian 9
2.2.1 Gabungan (Union) 9
2.2.2 Irisan (Intersection) 9
2.2.3 Komplemen (Complement) 10
2.2.4 Selisih 10
2.2.5 Kejadian Majemuk 11
2.3 Probablitas Bersyarat 12
2.4 Titik Sampel 13
2.4.1 Kombinasi (Combination) 13
2.4.2 Permutasi (Permutation) 14
2.5 Distribusi Probabilitas Diskrit 15
2.5.1 Distribusi Seragam 15
2.5.2 Distribusi Binomial 16
2.5.3 Nilai Harapan Distribusi Binomial 17
2.5.4 Variansi Distribusi Binomial 18
2.6.1 Nilai Harapan Variabel acak Normal 19 2.6.2 Variansi Variabel Acak Normal 21 2.6.3 Distribusi Normal Standard 23 2.6.4 Sifat-sifat Normal Standard 23 2.7 Menghampiri Distribusi Binomial dengan Distribusi Normal 26
BAB 3 PEMBAHASAN
3.1 Pendekatan Distribusi Binomial denngan menggunakan
Distribusi Normal 27
3.2 Sifat Distribusi Binomial 28
3.3 Teorema-teorema Pendukung 30
3.3.1 Teorema Limit Pusat (Central Limit Theorem) 30 3.3.2 Teorema Dde Moivre-Laplace 32 3.4 Teknik Perhitungan Pendekatan Distribusi Binomial oleh
Distribusi Normal 32
3.5 Contoh Kasus 384
3.6 Simpangan Akibat Pendekaatan 36
BAB 4 KESIMPULAN DAN SARAN
4.1 Kesimpulan 38
4.2 Saran3
DAFTAR PUSTAKA
DAFTAR GAMBAR
Halaman
Gambar 2.1 Gabungan 9
Gambar 2.2 Irisan 10
Gambar 2.3 Komplemen 10
Gambar 2.4 Selisih 11
Gambar 2.5 Distribusi Seragam 16
Gambar 2.6 Kurva Normal 18
DAFTAR TABEL
Halaman
Tabel 2.1 Percobaan Dan Hasil 7
ABSTRAK
Proses Bernoulli adalah suatu proses yang berlangsung n kali dan tiap eksperimen berlangsung dalam cara dan kondisi yang sama. Untuk setiap eksperimen hanya ada 2 (dua) kejadian yang mungkin yang mana kejadian itu saling asing dan juga independent satu sama lain, yang biasa dinotasikan dengan kejadian sukses dan gagal. Jika nilai n cukup besar, proses Bernoulli akan mendekati distribusi normal , dengan menggunakan rumus :
�=� − �
� =
� − �� ����
BAB 1
PENDAHULUAN
1.1Latar Belakang
Dalam probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal) yang saling bebas, dimana setiap hasil percobaan memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut adalah dalam uji signifikansi statistik.
Distribusi ini seringkali digunakan untuk memodelkan jumlah keberhasilan pada jumlah sampel n dari jumlah populasi N. Apabila sampel tidak saling bebas (yakni pengambilan sampel tanpa pengembalian), distribusi yang dihasilkan adalah binomial merupakan pendekatan yang baik dan banyak digunakan.
Distribusi normal, disebut pula distribusi Gauss adalah yang paling banyak digunakan dalam berbagai analisis baku adalah distribusi normal yang memiliki nol dansatu. Distribusi ini juga dijuluki kurva lonceng (bell curve) karena grafik mirip dengan bentuk lonceng. Distribusi Normal memodelkan
fenomena kuantitatif pa
dan fenomena seperti jumlahdapat dihitung melalui pendekatan dengan mengikuti distribusi normal. Distribusi normal banyak digunakan dalam berbagai
bidang akan mendekati normal,
juga banyak digunakan dalam berbagai distribusi dalams tatistika, dan kebanyakan mengasumsikan normalitas suatu data. Oleh karena itu saya memilih judul ini, yakni Kajian Tentang Pendekatan Distribusi Binomial Oleh Distribusi Normal.
1.2 Permasalahan
Masalah yang dihadapi dalam penelitian ini adalah bagaimana kajian pendekatan distribusi binomial oleh distribusi normal, dan sejauh mana simpangan yang ditimbulkan akibat dari dilakukannya pendekatan oleh distribusi normal, jika dibandingkan dengan hasil perhitungan dari distribusi aslinya (distribusi binomial).
1.3Tinjauan Pustaka
• DistribusiBinomial
Sebuah eksperimen yang hanya menghasilkan dua peristiwa A dan B, dengan P(A) = p = peluang terjadinya peristiwa A. jika pada tiap eksperimen itu p= P(A) tetap harganya, maka percobaan yang berulang-ulang dari eksperimen itu dinamakan percobaan Bernoulli. Jika kita lakukan percobaan Bernoulli sebanyak N kali secara independen, X diantaranya p = P(A) untuk tiap percobaan, jadi 1-p = q, maka peluang terjadinya peristiwa A sebanyak X = x kali diantara N dihitung oleh :
�
(
�
) =
�
(
�
=
�
) = (
��)
�
�(1
− �
)
�−�Dengan x = 0,1,2,…,N 0 < p < 1 Koefisien binom :
�
��
�
=
�!
�!(�−�)!
Satu diantara variable acak kontinu adalah Distribusi Normal ataus ering pula disebut distribusi Gauss. Distribusi ini merupakan salah satu yang paling penting dan paling banyak digunakan. Jika variable acak kontinu X mempunyai fungsi densitas pada X = x dengan persamaan :
�
(
�
) =
1
�√
2
�
�
−1/2(�−�� )²
Dengan :
� = nilai konstan yang bila ditulis hingga 4 desimal �=3.1416
� = bilangan konstan, bila ditulis hingga 4 desimal �=2,7183
� = parameter, ternyata merupakan rata-rata untuk distribusi
� = parameter, merpakan simpangan baku untuk distribusi
Dan nilai x mempunyai batas -∞<x<∞, maka dikatakan bahwa variable acak X berdistribusi normal. Variable acak diskrit X menentukan distribusi peluang apabila untuk nilai-nilai �1,�2,…�� terdapat peluang p (�� =��) sehingga :
�p(��) = 1
�
�=1
p(x) disebut fungsi peluang untuk variable acak X pada harga X = x. untuk menentukan peluang harga X antara a dan b, yakni P(a < X < b) digunakan rumus :
�
1
�√
2
�
�
−1/2(�−�� )²
�
� ��
Untuk penggunaan praktis, untunglah rumus-rumus diatas tak perlu dirisaukan, karena sebuah daftar telah disusun untuk keperluan dimaksud. Daftar itu ialah daftar distribusi normal standar atau normal baku yang diberikan dalam lampiran Daftar F. Distribusi normal standar adalah distribusi normal dengan rata-rata � = 0 dan simpangan baku� =1. Fungsi densitasnya berbentuk :
�(�) =
1
√
2
�
�
untuk z dalam daerah -∞ <z< ∞, dengan demikian kita memperoleh rumus distribusi normal baku yang sudah ditransformasikan seperti berikut :
�=� − �
�
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah untuk mengetahui proses pendekatan distribusi binomial oleh distribusi normal.
1.5Manfaat Penelitian
Suatu percobaan sering terdiri atas beberapa usaha, tiap usaha dengan dua kemungkinan hasil yang dapat diberi nama sukses dan gagal. Bila percobaan dilakukan n kali dengan n ∞maka akan sedikit sulit menghitungnya dengan distribusi binomial, bentuk distribusi normal akan membantu dalam analisis yang lebih lanjut.
1.6 Metode Penelitian
Metode yang digunakan dalam penelitian ini adalah :
- Dengan melakukan studi literatur terlebih dahulu mengenai pendekatan Distribusi Binomial dengan menggunakan Distribusi Normal.
- Memaparkan sifat Distribusi Biomial dalam kajian pendekatan Distribusi Binomial dengan menggunakan Distribusi Normal.
- Membuat contoh kasus dalam kajian pendekatan Distribusi Binomial dengan menggunakan Distribusi Normal.
BAB 2
LANDASAN TEORI
2.1 Probabilitas
Probabilitas adalah suatu nilai untuk mengukur tingkat kemungkinan terjadinya suatu peristiwa (event) akan terjadi di masa mendatang yang hasilnya tidak pasti (uncertain event). Probabilitas dinyatakan antara 0 (nol) sampai 1 (satu) atau dalam persentase.
Probabilitas 0 menunjukkan peristiwa yang tidak mungkin terjadi, sedangkan probabilitas 1 menunjukkan peristiwa yang pasti terjadi. P(A) = 0,99 artinya probabilitas bahwa kejadian A akan terjadi sebesar 99 % dan probabilitas A tidak terjadi adalah sebesar 1%.
Ada tiga hal penting dalam rangka membicarakan probabilitas, yaitu percobaan (experiment), ruang sampel (sample space) dan kejadian (event).
Percobaan (experiment) adalah pengamatan terhadap beberapa aktivitas atau proses yang memungkinkan timbulnya paling sedikit 2 (dua) peristiwa tanpa memperhatikan peristiwa mana yang akan terjadi.
Contoh :
Ruang sampel (sample space) atau semesta (universe) merupakan himpunan dari semua hasil (outcome) yang mungkin dari suatu percobaan (experiment). Jadi ruang sampel adalah seluruh kemungkinan peristiwa yang akan terjadi akibat adanya suatu percobaan atau kegiatan.
Dari kegiatan diatas dapat diperoleh hasil sebagai berikut : Tabel 2.1 Percobaan dan Hasil
PERCOBAAN RUANG SAMPEL
Melempar Mata Uang (gambar, angka) Perdagangan Saham (menjual, membeli) Perubahan Angka (inflasi, deflasi) Pertandingan Sepak Bola (menang, kalah, seri)
Kejadian (event) adalah kumpulan dari satu atau lebih hasil yang terjadi pada sebuah percobaan atau kegiatan. Kejadian menunjukkan hasil yang terjadi dari suatu percobaan. Dalam setiap percobaan atau kegiatan hanya ada satu hasil. Pada kegiatan jual beli saham, kalau tidak membeli berarti menjual. Pada perubahan harga terjadi inflasi atau deflasi. Dua peristiwa tersebut tidak dapat terjadi bersamaan. Pada pertandingan sepak bola juga hanya terjadi satu peristiwa, apakah klub sepak bola tersebut menang, kalah atau seri. Tidak mungkin dalam suatu pertandingan sepak bola, misalnya Persipura dan PSM, hasilnya adalah Persipura menang juga kalah. Peristiwa yang mungkin adalah Persipura menang, Persipura kalah, atau seri. Urutan antara percobaan, ruang sampel dan peristiwa yaitu:
Tabel 2.2 Urutan Percobaan, Hasil dan Peristiwa
Percobaan/ Kegiatan Pertandingan sepak bola antara PSMS VS PSM di Stadion Teladan, Medan, 7 Februari 2010
Ruang Sampel PSMS Menang
PSMS Kalah
Nilai probabilitas dapat dihitung berdasarkan nilai hasil observasi (sifatnya subyektif) tau berdasarkan pertimbangan pembuat keputusan atau tenaga ahli dalam bidangnya secara subyektif.
Besarnya nilai kemungkinan bagi munculnya suatu kejadian adalah selalu diantara 0 (nol) dan 1 (satu). Pernyataan ini dapat ditulis sebagai 0 ≤ P(A) ≤ 1, dimana P(A) menyatakan nilai kemungkinan bagi munculnya kejadian A. Jika suatu percobaan dapat menghasilkan N macam hasil yang berkemungkinan sama (equally likely) dan jika tepat terdapat sebanyak n hasil yang berkaitan dengan kejadian A, maka probabilitas kejadian A adalah :
�(�) =� N
Contoh:
Didalam kegiatan pengendalian mutu produk, ada 100 buah barang yang diperiksa, ternyata ada 12 buah barang yang cacat atau rusak. Kalau kebetulan diambil secara acak satu saja, berapa probabilitasnya bahwa barang yang diambil adalah barang yang rusak.
Dari soal diketahui bahwa: N = 100 buah barang
n = 12 buah barang yang rusak A = barang yang diambil secara acak
Jadi, probabilitas memperoleh barang yang rusak adalah :
�(�) =� N
�(�) = 12
100 = 0.12
Jika n=0, berarti tidak ada barang yang rusak. P(A)= N0 =0, kejadian ini disebut impossible event (tidak mungkin terjadi) tetapi jika N=100 berarti semua barang rusak P(A)= 100
2.2 Operasi-Operasi Dalam Kejadian
Ada beberapa operasi-operasi dalam kejadian yaitu: gabungan (union), irisan (intersection), komplemen (complement), selisih dan kejadian majemuk.
2.2.1 Gabungan (Union)
Gabungan dua kejadian A dan B, dinyatakan dengan A∪B, merupakan kejadian yang mengandung semua elemen yang termasuk A atau B atau keduanya.
A∪ B = {x : x ∈ A atau x ∈ B}
Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan A ∪ B.
Gambar 2.1 Gabungan
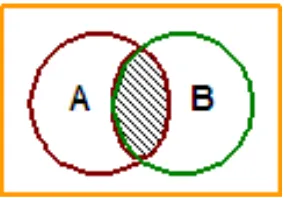
2.2.2 Irisan (Intersection)
Irisan dua kejadian A dan B, dinyatakan dengan A ∩ B, merupakan kejadian yang elemen-elemennya merupakan anggota dari A dan B.
A∩ B = {x : x∈ A dan x∈ B }
Gambar 2.2 Irisan
2.2.3 Komplemen (Complament)
Komplemen dari kejadian A, dinyatakan dengan Ac, adalah kejadian dari elemen-elemen yang merupakan anggota semesta tetapi bukan anggota A.
Ac = {x : x∈S, x∉ A}
Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan Ac.
Gambar 2.3 Komplemen
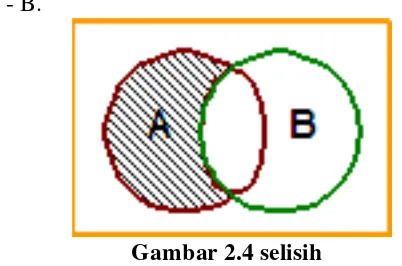
2.2.4 Selisih
Selisih kejadian B dari kejadian A dinyatakan dengan A – B adalah kejadian dari elemen-elemen yang merupakan anggota dari A tetapi bukan anggota dari B.
Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan A - B.
Gambar 2.4 selisih
2.2.5 Kejadian Majemuk
1. Bila A dan B mutually exclusive (kejadian yang terpisah), maka : P(A∪ B) = P(A) + P(B)
2. Bila A dan B dua kejadian sembarang, maka : P(A∪ B) = P(A) + P(B) − P(A∩ B)
3. Bila K kejadian yaitu �1,�2,....��,...��yang mutually exclusive dan membentuk kejadian A, maka :
P(A)=P(�1 ∪ �2 ∪ �� ∪ ��)
�(�) =�P(��)
�
�=1
P(A) = 1
4. Bila A dan B independent (bebas), maka :
P(A∩ B) = P(A)P(B)
P(A∩ B) = P(A)P(B | A)
P(A∩ B) = P(B)P(A | B), dimana P(A) ≠ 0, P(B) ≠ 0.
2.3 Probabilitas Bersyarat
Peluang terjadinya suatu kejadian A bila diketahui bahwa kejadian B telah terjadi disebut peluang bersyarat dan dinyatakan dengan P(A|B).
P(A|B) =P(A∩B) P(B)
Sama halnya dengan peluang terjadinya suatu kejadian B bila diketaui bahwa kejadian A telah terjadi dan dinyatakan dengan P(B|A).
P(B|A) =P(A∩B) P(A)
Dengan mengkombinasikan kedua persamaan maka diperoleh :
P(A|B) = P(A∩B)P(A|B)P(A)
P(A|B) =P(A∩B)
P(B) =
P(A|B)P(A) P(B)
P(A|B) =P(A∩B) P(B) Contoh:
Dari 900 nama, terdapat 500 orang pria dengan status 460 orang bekerja, sedangkan 40 orang lagi tidak bekerja, dan 400 orang wanita dengan status 140 orang bekerja sedangkan 260 orang lagi tidak bekerja. Berapa probabilitas terpilihnya pria dengan status telah bekerja?
A = pria terpilih
P(B) = 600
900 = 2/3
P(B∩A) = 460
900 = 23/45
�(� | �) = 23/45
2/3 = 23/30
Dari perhitungan diatas maka diperoleh kemungkinan bahwa nama yang terpilih adalah pria dengan status bekerja adalah sebesar 0,77 atau 77%.
2.4 TITIK SAMPEL
Titik sampel (sample point) merupakan tiap anggota atau elemen dari ruang sampel. Jika suatu operasi dapat dilakukan dengan �1 cara, dan bila untuk setiap cara ini operasi kedua dapat dilakukan dengan �2 cara, dan bila untuk setiap cara ini operasi ketiga dapat dilakukan dengan �3 cara, dst, maka deretan k operasi dapat dilakukan dengan �1,�2, … ,�� cara.
Contoh:
Tiga buah koin (uang logam) dilemparkan sekali. Banyaknya titik sampel dalam ruang sampel ?
Koin I dapat menghasilkan 2 hasil yang mungkin, muka (M) atau belakang (B) Koin II dapat menghasilkan 2 hasil yang mungkin, M atau B
Koin III dapat menghasilkan 2 hasil yang mungkin, M atau B Jumlah titik sampel yang dihasilkan = (2) (2) (2) = 8
2.4.1 Kombinasi (Combbination)
memilih r obyek dari sejumlah n obyek tanpa memperhatikan urutannya. Kombinasi merupakan sekatan dengan dua sel, sel pertama berisi r obyek yang dipilih dan (n – r) obyek sisanya. Jumlah kombinasi dari n obyek yang berlainan jika diambil sebanyak r.
��� =�!(� − ��! )!
Contoh:
Suatu kelas terdiri atas 4 pria dan 3 wanita Banyaknya panitia yang dibentuk yang beranggotakan 2 pria dan 1 wanita?
Banyaknya cara memilih 2 dari 4 pria = �24= 4!
2!(4−2)! = 6 Banyaknya cara memilih 1 dari 3 wanita = �13 = 3!
1!(3−1)! = 3 Banyaknya panitia yang dapat dibentuk = (6) (3) = 18
2.4.2 Permutasi (Permutation)
Permutasi merupakan susunan dari suatu himpunan obyek yang dapat dibentuk yang memperhatikan urutan. Banyaknya permutasi n obyek berlainan adalah n! Banyaknya permutasi n obyek berlainan bila diambil r sekaligus ��� =� �!
!(�−�)!. Banyaknya permutasi n benda berlainan yang disusun melingkar adalah (n – 1)!.
Banyaknya permutasi yang berlainan dari n obyek bila �1 adalah jumlah obyek jenis pertama, �2 adalah jumlah obyek jenis kedua, ..., �� jumlah obyek ke-k adalah:
�!
�1!�2! …��! .
Banyaknya cara menyekat n obyek dalam r sel bila masing-masing berisi �1 obyek pada sel pertama, �2 obyek pada sel kedua, dan seterusnya adalah :
�!
2.5 Distribusi Probabilitas Diskrit
Penyajian distribusi probabilitas dalam bentuk grafis, tabel atau melalui rumusan tidak masalah, yang ingin dilukiskan adalah perilaku (kelakuan) perubah acak tersebut. Sering di menjumpai, pengamatan yang dihasilkan melalui percobaan statistik yang berbeda mempunyai bentuk kelakuan umum yang sama.
Oleh karena itu perubah acak diskrit yang berkenaan dengan percobaan tersebut dapat dilukiskan dengan distribusi probabilitas yang sama, dan dapat dinyatakan dengan rumus yang sama.
Dalam banyak praktek yang sering di jumpai, hanya memerlukan beberapa distribusi probabilitas yang penting untuk menyatakan banyak perubah acak diskrit.
2.5.1 Distribusi Seragam
Distribusi probabilitas yang paling sederhana adalah yang semua perubah acaknya mempunyai probabilitas yang sama. Distribusi ini disebut distribusi probabilitas seragam diskrit.
Jika perubah acak X mendapat nilai �1,�2, … ,�� dengan probabilitas yang sama , maka distribusi probabilitas diskrit diberikan oleh:
�(�;�) = 1� , untuk x = �1,�2, … ,��
1/k
X1 X2 X3 Xk
Gambar 2.5 Distribusi Seragam
Rata-rata dan varians dari distribusi seragam diskrit adalah :
� =∑��=���� �2 =∑ (��−�) 2
� �=1
�
Contoh:
Sebuah dadu seimbang dilemparkan satu kali, maka tiap unsur dalam ruang sampel S={1, 2,3 4, 5, 6}. Muncul dengan probabilitas 1/6. Jadi jika X menyatakan mata dadu yang muncul, maka X terdistribusi peluang seragam (uniform) yakni f(x;6)=1/6, untuk x = 1, 2, 3, 4, 5, 6
2.5.2 Distribusi Binomial
Suatu percobaan yang terdiri atas beberapa usaha, tiap-tiap usaha, memberikan hasil yang dapat dikelompokan menjadi 2-kategori yaitu sukses atau gagal, dan tiap-tiap ulangan percobaan bebas satu sama lainnya. Probabilitas kesuksesan tidak berubah dari percobaan satu ke percobaan lainnya. Proses ini disebut proses Bernoulli. Jadi proses Bernoulli harus memenuhi persyaratan berikut:
1. Percobaan terdiri atas n-eksperimen yang berulang
2. Tiap-tiap eksperimen memberikan hasil yang dapat dikelompokan menjadi 2- kategori, sukses atau gagal
3. Peluang kesuksesan dinyatakan dengan p, tidak berubah dari satu eksperimen ke eksperimen berikutnya.
Jadi proses Bernoulli adalah suatu proses dengan ciri-ciri eksperimen berlangsung n kali dan tiap eksperimen berlangsung dalam cara dan kondisi yang sama. Untuk setiap eksperimen hanya ada 2 (dua) kejadian yang mungkin terjadi, dimana 2 (dua) kejadian tersebut adalah saling asing dan juga independent satu sama lain. Biasanya 2 (dua) kejadian tersebut dinotasikan sebagai kejadian sukses dan kejadian gagal. Probabilitas sukses dilambangkan dengan p, sedangkan probabilitas gagal dilambangkan dengan q, dan p + q =1. Dari proses tersebut, yang di definisikan sebagai variabel adalah munculnya kejadian sukses, yang dilambangkan dengan x. Untuk distribusi Binomial semacam itu, bisa dihitung probabilitas x sukses akan muncul dalam n percobaan tersebut dengan rumus :
�(�)=�(�,�;�)=���)����−� = �!
�!(� − �)! ����−�
Dengan:
x = munculnya sukses yang ingin di hitung n = jumlah eksperimen
p = probabilitas sukses dalam tiap eksperimen q = probabilitas gagal dalam tiap eksperimen = 1 – p n-x = jumlah gagal dalam n eksperimen
Distribusi binomial mempunyai nilai rata-rata µ = np dan nilai simpangan baku � =����.
2.5.3 Nilai Harapan Distribusi Binomial
Untuk mencari rata-rata (µ) digunakan Rumus :
�(�) =�� (�+�)�−1 = ��(1)�−1 =��
2.5.4 Variansi Distribusi Binomial
���(�)=�[�2] – (�[�])2
�[�]2 = n(n−1)p2�qn−2+(n−2)pqn−3+⋯+ pn−2�+ np = n(n−1)p2(q + p)n−2+ np
= n(n−1)pn+ np
Jadi,
Var (�)= �[�2] – (�[�])2
= n(n−1)p2+ np− �2�2 = np(1-p)
= npq
Jadi, varian dari distribusi binomial adalah npq.
2.6 DISTRIBUSI NORMAL
Distribusi probailitas kontinyu yang terpenting di bidang statistik adalah distribusi Normal. Grafiknya disebut kurva normal, berbentuk lonceng. Distribusi ini ditemukan Karl Friedrich Gauss (1777-1855) yang juga disebut distribusi Gauss. Perubah acak X yang bentuknya seperti lonceng disebut perubah acak normal dengan persamaan matematik distribusi probabilitas yang bergantung paramerter µ (mean) dan σ (simpangan baku). Dinyatakan n(x,µ ,σ )
04
03
02
01
0
-4 -2 a 0 b 2 4
Fungsi padat perubah acak normal X, dengan rata-rata µ dan simpangan baku σ dinyatakan sebagai :
�(�;�;�) 1
√2���−�12��
�−� � �
2
, untuk − ∞< � <∞
Dengan :
µ = mean
σ = simpangan baku π = 3,14159... e = 2,71828...
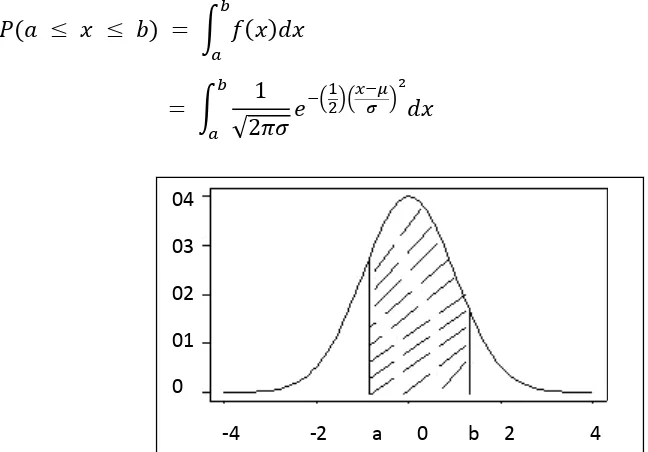
Luas daerah kurva normal antara x = a dan x = b dinyatakan sebagai berikut:
�(� ≤ � ≤ �) = � �(�)��
�
�
= � 1
√2���−�12��
�−� � �
2
��
�
�
Gambar 2.7 Luas Derah P(a < x < b) = Luas Daerah Diarsir
2.6.1 Nilai Harapan Variabel acak Normal
E(X) = � ��(�)��
∞
= � � 1
�√2��
−1/2(�−�� �)2
��
∞
−∞
= � 1
�√2�� � ��
−1/2(�−�� �)2
�� ∞ −∞ �= � − �� � ; ��+�� =� ; �� = 1 ��� ; �� =��� = 1
�√2�� (��+
∞
−∞ ��)�
−12�2
���
= 1
√2�� (��+
∞
−∞ ��)�
−12�2
��
= �
√2�� �
∞
−∞ � −12�2
��+ ��
√2�� �−12�
2
��
∞
−∞
untuk, �
√2�=
�
√2�(� ��−12�
2 ��+ 0 −∞ � �� −12�2 ��) ∞ 0
�= 1 2�
2 ;�� = ��� ; �� =��
�
= �
√2��� �
−���+ 0 −∞ � � −��� ∞ 0 �
untuk,� �
∞ 0 � −12�2 �� =� � ∞ 0 � −��� � =� �−� ∞
0 �� = [�
−�] 0 ∞
dimana, lim
�→∞�−� = 0 ; maka � �−��� ∞
0 = 0
Akibatnya, �
√2�� �
∞
−∞ � −12�2
��= �
√2�(0 + 0) = 0
untuk, ��
√2�� �−12�
2
��=
∞
−∞
��
√2�(� �−12�
2
��+� �−12�2��)
∞
−∞ ∞
−∞
�= 1 2�
2→ �= √2�
�� = ��� → ��= ��
�
= ��
√2�� �
= ��
√2�( 1
√2� �−12�
−���+ 1
√2� �−12�
−���) ∞ 0 0 −∞ = ��
√2��
√2�
2 +
√2�
2 �=��
Sehingga : E[X] = �
√2�� �
∞
−∞ �
−12�2��+ ��
√2�� �−12�
2
��
∞
−∞
E[X] = 0 + �� =��
2.6.2 Variansi Variabel Acak Normal
Var (�)= �[�2] – (�[�])2
�[�2] = ��2 1
�√2��
−1/2(�−���)2�� ∞
−∞
= 1
�√2� � �
2�−1/2(�−���)2�� ∞
−∞
�= �−�� �→ ��+�� =�
��= 1
��� → �� =���
= 1
�√2� �(��+��)
2�−12�2��� ∞
−∞
= 1
√2� �(��
2+ 2���
�+��)2�−12�2�� ∞
−∞
= 1
√2� � ��
2�−12�2��+ ∞
−∞
1
√2� �2����
∞
−∞
�−12�2��+ 1
√2� � ��
2�−12�2�� ∞
−∞
= �
2
√2� � �
2�−12�2��+ ∞
−∞
2����
√2� � �
∞
−∞
�−12�2��+ � �−12�2��
∞
= �
2
√2� � �
2�−12�2��+ 0 + ∞
−∞
��2
√2�(√2�)
= �
2
√2� � �
2�−12�2��+ ∞
−∞
��2
untuk, �
2
√2� � �
2�−12�2��= ∞
−∞
�2
√2�� � �
2�−12�2��+ ∞
−∞
� �2�−12�2�� ∞
−∞
�
�=1 2�
2
→ �=�2�
�� = ��� → �� =��
� = �� �2�
�2 √2� ��
2�−12� 2
��=
∞
−∞
�2
√2�� �2��
−� ��
�2�+�2��
−� ∞ 0 0 −∞ ��
�2��
= �
2
√2�� � 2
�2�
0
−∞
�12�−���+� 2
�2�
∞
0
�12�−����
= �
2
√2��√2 1 2ᴦ �
1
2�+√2 1 2ᴦ �
1 2��
= �
2
√2��
√2�
2 +
√2� 2 � =�2
Sehingga : E[X2] =�2+��2 Maka :
2.6.3 Distribusi Normal Standar
Keluarga distribusi normal memiliki jumlah yang banyak sekali, akibat pengaruh rata-rata dan simpangan baku. Akan tetapi, untuk mencari probabilitas suatu interval dari variabel random kontinu dapat di permudah dengan menggunakan bantuan distribusi normal standard.
Distribusi normal standard adalah distribusi normal yang memiliki rata-rata (μ)= 0 dan simpangan baku (σ ) = 1. Bentuk fungsinya adalah :
�(�) = 1
√2��−12�
2
Untuk mengubah distribusi normal umum menjadi distribusi normal standard di gunakan nilai Z (standard units). Bentuk rumusnya adalah:
�=� − �
�
Dengan :
Z = Skor Z atau nilai normal baku
X = Nilai dari suatu pengamatan atau pengukuran µ = nilai rata-rata hitung suatu distribusi
σ = standar deviasi suatu distribusi
Nilai Z (standard units) adalah angka atau indeks yang menyatakan penyimpangan suatu nilai variabel random (X) dari rata-rata (µ ) dihitung dalam satuan simpangan baku (σ ).
2.6.4 Sifat-sifat Normal Standar
1) Grafiknya selalu ada di atas sumbu datar x 2) Bentuknya simetrik terhadap x = µ
3) Mempunyai satu modus, jadi kurva unimodal, tercapai pada x = µ
4) Grafiknya mendekati (berasimtutkan) sumbu datar x di mulai dari x = µ + 3σ ke kanan dan x = µ − 3σ ke kiri
5) Luas daerah grafik selalu sama dengan satu unit persegi.
Untuk tiap pasang µ dan σ , sifat-sifat di atas selalu di penuhi, hanya bentuk kurvanya saja yang berlainan. Jika σ makin besar, kurvanya makin rendah (platikurtik) dan untuk σ makin kecil, kurvanya makin tinggi (leptokurtik).
Gambar 2.8 Distribusi Kurva Normal dengan μ Sama dan σ Berbeda
Gambar 2.9 Distribusi Kurva Normal dengan μ Berbeda dan σ Sama
Pada Gambar 2.9 menunjukkan bentuk distribusi probabilitas dan kurva normal dengan μ berbeda dan σ sama, mempunyai jarak antara kurva yang berbeda, namun bentuk kurva tetap sama. Hal demikian bisa terjadi karena kemampuan antar populasi berbeda, namun setiap populasi mempunyai keragaman yang hampir sama.
Gambar 2.10 Distribusi Kurva Normal dengan µ dan σ Berbeda
2.7 Menghampiri Distribusi Binomial Dengan Distribusi Normal
Sebagaimana distribusi poisson sebagai penghampir distribusi binomial, maka distribusi binomial dapat juga dihampiri dengan distribusi normal. Penghampiran ini atas dasar teori asimtotik, yaitu dengan memisalkan banyak pengamatan � → ∞ dan p tetap. Atas dasar pemisalan ini maka :
�(�) =�(� =�) = �!
�! (� − �)!�
�(1− �)�−�
Pendekatan distribusi normal ini dapat di gunakan untuk pendekatan distribusi binomial, dengan memenuhi beberapa syarat, yaitu :
a. Jumlah pengamatan relatif besar (n ≥ 30), dan nilai dari np ≥ 5 dan n(1-p) ≥ 5, dimana n = jumlah data dan p adalah probabilitas sukses.
b. Memenuhi syarat binomial yaitu mempunyai peristiwa hanya 2 (dua), antara percobaan bersifat independent, probabilitas sukses dan gagal sama untuk semua percobaan dan data merupakan hasil perhitungan.
c. Rumus nilai normal untuk mendekati binomial adalah : �=�−��
√���
BAB 3
PEMBAHASAN
3.1 Pendekatan distribusi binomial dengan mengunakan Distribusi Normal
Dalam melakukan proses pengendalian kualitas, penting untuk melakukan pendekatan suatu distribusi probabilitas dengan distribusi probabilitas yang lain. Proses pendekatan akan berguna pada saat nilai tabel dari suatu distribusi tak ada. Dengan pendekatan distribusi yang lain akan didapatkan nilainya dengan tabel. Selain itu pendekatan distribusi dilakukan jika penggunaan distribusi aslinya tidak praktis.
Meskipun distribusi Poisson dapat di gunakan untuk mendekati distribusi binomial, terutama dalam kasus-kasus dimana n sangat besar, sedangkan p sangat kecil. Sebagai penggantinya kita dapat menggunakan distribusi normal untuk mendekati distribusi binomial apabila n bertambah besar. Umumnya jika µ = np > 5 , kita akan dapat menggunakan distribusi normal.
Dengan melakukan proses standarisasi peta kendali p berarti dilakukan pendekatan distribusi Binomial yang merupakan distribusi asli probabilitas cacat dengan menggunakan distribusi Normal.
Karena distribusi Binomial merupakan distribusi yang diskrit, dan distribusi Normal merupakan distribusi yang kontinu, maka perlu ditambahkan faktor koreksi kontinuitas (continuity correction), yaitu sebesar 0.5. Jika n bernilai besar, maka pendekatan
Beberapa hal yang perlu dilakukan adalah dengan mengubah atau membakukan distribusi normal dalam bentuk distribusi normal standard yang dikenal dengan nilai Z atau skor Z. Rumus nilai Z adalah :
�=� − � �
Dengan :
Z = Skor Z atau nilai normal standar
X = Nilai dari suatu pengamatan atau pengukuran
µ = nilai rata-rata hitung suatu distribusi σ = standar deviasi suatu distribusi.
Untuk mengubah pendekatan dari binomial ke normal menurut Lind (2002) diperlukan faktor koreksi, selain syarat binomial terpenuhi yaitu : hanya terdapat dua peristiwa, peristiwa tersebut bersifat independent, besar probabilitas sukses dan gagal sama setiap percobaan dan data merupakan hasil penghitungan.
Apabila sudah memenuhi syarat binomial, maka kita menggunakan faktor koreksi yang besarnya 0,05. Faktor koreksi ini diperlukan untuk mentransformasi dari binomial menuju normal yang merupakan variabel acak kontinu.
3.2 Sifat Distribusi Binomial
Suatu percobaan yang terdiri atas beberapa usaha, tiap-tiap usaha, memberikan hasil yang dapat dikelompokan menjadi 2-kategori yaitu sukses atau gagal, dan tiap-tiap ulangan percobaan bebas satu sama lainnya. Probabilitas kesuksesan tidak berubah dari percobaan satu ke percobaan lainnya. Proses ini disebut proses Bernoulli. Jadi proses Bernoulli harus memenuhi persyaratan berikut:
2. Tiap-tiap eksperimen memberikan hasil yang dapat dikelompokan menjadi 2 kategori, sukses atau gagal
3.Peluang kesuksesan dinyatakan dengan p, tidak berubah dari satu eksperimen ke eksperimen berikutnya.
4. Tiap eksperimen bebas dengan eksperimen lainnya.
Banyaknya X yang sukses dalam n- eksperimen Bernoulli disebut “peubah acak binomial”, dan distribusi dari peubah acak ini disebut “distribusi Binomial”. Jika p menyatakan probabilitas kesuksesan dalam suatu eksperimen, maka distribusi peubah acak X ini dinyatakan dengan b(x;n,p). Karena nilainya bergantung pada banyaknya eksperimen (n).
Probabilitas x kesuksesan dan n-x kegagalan dalam urutan tertentu. Tiap kesuksesan dengan probabilitas p dan tiap kegagalan dengan probabilitas q=1-p. Banyaknya cara untuk memisahkan n-hasil menjadi dua kelompok, sehingga x hasil ada pada kelompok pertama dan sisanya n-x pada kelompok kedua, jumlah ini dinyatakan sebagai ���� Karena pembagian tersebut saling terpisah (bebas) maka probabilitasnya adalah ��������−�.
Suatu usaha bernoulli dapat menghasilkan kesuksesan dengan probabilitas p dan kegagalan dengan probabilitas q=1-p, maka distribusi probabilitas peubah acak binomial X yaitu banyaknya kesuksesan dalam n- eksperimen bebas adalah :
�(�) =�(�;�;�) =��
������−� =�������−� �������= 1,2,3, …�
Adapun sifat-sifat dari distribusi binomial ini adalah:
1. Nilai rata-rata (µ ) dari distribusi binomial yaitu banyaknya eksperimen dikalikan dengan banyaknya sukses atau dengan kata lain µ = E (X) = np. 2. Nilai dari varians (�2) untuk distribusi binomial adalah banyaknya eksperimen
dikalikan dengan banyaknya sukses dan banyaknya gagal atau dengan kata lain
�2 = E (X − µ)2 = npq.
3.3 Teorema-teorema Pendukung
Dalam proses untuk mendekatkan distribusi binomial dengan menggunakan distribusi normal, maka diperlukan teorema-teorema pendukung yang terkait.
3.3.1 Teorema Limit Pusat ( Central Limit Theorem )
Teorema limit pusat menyatakan bahwa nilai tengah suatu sampel yang terdiri dari n buah nilai variabel random yang menyebar secara tidak normal, akan tetapi menyebar secara identik (dengan perkataan lain �1,�2, … ,�� memiliki fungsi kepadatan yang sama) serta bebas terhadap sesamanya, penyebarannya akan mendekati sebaran normal dengan pertambahan besarnya nilai n, jadi juga dengan bertambahnya ukuran sampel.
Jika �1,�2, … ,�� adalah n variabel random independent dengan distribusi yang identik dan memiliki mean µ dan varians �2. Jumlahnya dinyatakan sebagai berikut: X = �1+�2+⋯+��.
Karena mean dari jumlah adalah jumlah semua mean dan varian dari jumlah adalah jumlah semua varian, untuk variabel random independent, maka :
E (X) = nµ ; Var (X) = n�2
Untuk setiap variabel random, mengurangi mean dan membaginya dengan standart deviasi akan menghasilkan variabel random dengan mean 0 dan varian 1. maka variabel random :
�=� − �(�) ����(�)=
�� − �� √��2
Kemudian dengan membagi pembilang dan penyebutnya dengan n, maka:
Dengan:
��=�1+�2+⋯ ��
� =
X
� ,�����ℎ��������� − ������.
Central Limit Theorem, jika �1+�2+⋯ �� adalah n variabel random independent dengan distribusi yang identik, dengan mean µ dan varian �2. Dilambangkan dengan X dan �� adalah jumlah dari rata-rata dari variabel random ini. Sejalan dengan bertambahnya n, distribusi :
�=� − �� √��2 =
�� − � � √�
�������������������������������.
Dengan bantuan Central Limit Theorem ini, dalam prakteknya untuk masalah jumlah dan rata-rata variabel random, distribusi normal akan memberikan perkiraan yang cukup tepat mengenai distribusi yang sebenarnya.
Apapun distribusi dari sekelompok variabel random, selama variannya bersifat finit, jumlah atau rata-rata dari sejumlah besar variabel tersebut akan berupa variabel random dengan distribusi mendekati normal. Namun rata-rata variabel random dengan distribusi seragam yang independent dalam jumlah cukup besar, akan memiliki distribusi mendekati normal pula.
Bila nilai n makin besar, maka akan mendekati normal standard. Bentuk fungsi densitas probabilitas untuk n variabel random independent dari distribusi Chi-squere dengan derajat kebebasan 1. Validitas Central Limit Theorem tidak terbatas hanya untuk jumlah variabel random kontinu, juga bisa berlaku untuk variabel random diskrit.
Misalkan �1,�2, … ,�� suatu barisan variabel random, Sn menyatakan banyaknya sukses dalam suatu eksperimen binomial dengan n kali percobaan, masing-masing dengan probabilitas sukses p, 0<p<1. Misalkan Zn, n = 1, 2, ... barisan variabel random dengan:
�
�=
�
�− ��
����
,
Dan misalkan z suatu tetapan. Maka, bila n menuju ke takberhingga, P(Zn > z) mendekati luas pada distribusi normal standard di sebelah kanan z.
Atau dengan pernyataan lain teorema De Moivre-Laplace menyatakan bahwa : Jika Sn banyaknya sukses dalam n percobaan Bernoulli dan p adalah probabilitas sukses dan
�
�=
�
�− ��
����
,
���� ∶
�
��(
�
) =
�
(
�
�>
�
)
→ � �
−� 22 �
−∞
��
,
������
� → ∞
.
Teorema De Moivre-Laplace merupakan suatu bentuk dari teorema limit pusat yang cukup umum. Teorema ini membicarakan limit distribusi jumlah variabel random, dan limit distribusinya biasanya normal. Pentingnya teorema ini ialah bahwa dengan menggunakannya, dapat di hitung pendekatan peluang untuk jumlah variabel random dengan menggunakan distribusi normal tanpa perlu tahu distribusi jumlah variabel random dengan tepat.
3.4 Teknik Perhitungan Pendekatan Distribusi Binomial oleh Distribusi Normal
Oleh karena distribusi binomial adalah distribusi untuk variabel random diskrit yang mana probabilitasnya berupa ordinat. Sedangkan distribusi normal merupakan distribusi untuk variabel random kontinu yang mana probabilitasnya berupa area (luasan), maka perlu diadakan penyesuaian (perubahan) dari ordinat menjadi luas. (panjang dikalikan lebar). Penyesuaian ini dilakukan sebagai berikut :
panjang dan lebarnya diambil 1 unit. Jadi seolah-olah dibentuk persegi panjang berpusat pada x, dengan panjang setinggi nilai ordinat dan lebarnya adalah 1 unit (panjang interval x – 0,5 sampai dengan x + 0,5), sehingga didapatkan probabilitas yang asli (probabilitas diskrit = ordinat) sama dengan luas persegi panjang tersebut.
Dengan memperhatikan proses pendekatan dari distribusi binomial ke distribusi normal yang telah dibahas di atas, maka perhitungan pendekatan distribusi binomial oleh distribusi normal dapat dilakukan dengan cara sebagai berikut :
Jika X ~ B(n,p), maka untuk keperluan penghitungan P(X=x) dengan menggunakan distribusi normal adalah sebagai berikut:
P(X = x) = P (x – 0,5 < X < x + 0,5)
=
�
(
� −
0,5)
− ��
����
<
� − ��
����
<
(
�
+ 0,5)
− ��
����
�
=
� �
(
� −
0,5)
− ��
����
<
�
<
(
�
+ 0,5)
− ��
����
�
Dengan Z ~ N(0,1).
�
(
� ≥ �
) =
� �� ≥
(
� −
0,5)
− ��
����
�
�
(
� ≤ �
) =
� �� ≥
(
�
+ 0,5)
− ��
����
�
�
(
�
1<
�
<
�
2) =
�
(
�
1−
0,5 <
�
<
�
2+ 0,5)
=
� �
(
�
1−
0,5)
− ��
����
<
� − ��
����
<
(
�
2+ 0,5)
− ��
����
�
=
� �
(
�
1−
0,5)
− ��
����
<
�
<
(
�
2+ 0,5)
− ��
3.5 Contoh Kasus
[image:44.595.111.516.200.376.2]Dari data kelahiran bayi menurut jenis kelamin, selama bulan Januari – Juni diperoleh data seperti tabel di bawah ini:
Tabel 3.1 Tabel Kelahiran Bayi Menurut Jenis Kelamin
Bulan Laki-laki Perempuan Jumlah
Januari 36 orang 40 orang 76 orang
Februari 45 orang 37 orang 82 orang
Maret 41 orang 43 orang 84 orang
April 29 orang 41 orang 70 orang
Mei 44 orang 47 orang 91 orang
Juni 34 orang 33 orang 67 orang
Jumlah 229 orang 241 orang 470 orang
Dari data jenis kelamin bayi yang lahir diatas, dapat di peroleh hasil sebagai berikut : Banyak bayi lahir = 470 orang, yang terdiri dari :
Jenis kelamin laki-laki = 229 orang Jenis kelamin perempuan = 241 orang
Maka dapat dihitung misalnya :
a. Probabilitas proporsi kelahiran bayi laki-laki > 0,5 b. Probabilitas proporsi kelahiran bayi laki-laki < 0,5 c. Probabilitas proporsi kelahiran bayi laki-laki = 0,5
d. Probabilitas proporsi kelahiran bayi laki-laki antara 0,4 dan 0,5
Penyelesaian :
Misalkan X adalah variabel random yang menyatakan banyaknya bayi laki-laki yang lahir.
n = 468 orang, p = peluang kelahiran bayi laki-laki = 229
470= 0,4872,
a. Probabilitas kelahiran bayi laki-laki = 0,5 berarti :
X = (0,5) . (470) = 235, Sehingga :
Probabilitas proporsi kelahiran bayi laki-laki > 0,5 adalah : P(X > 235) = P(Z >(� −0,5)− ��
���� )
= P(Z >(235−0,5)−229
10,8361 )
= P(Z >0,50) = 0,5−0,1915 = 0,3085
Jadi probabilitas banyaknya bayi laki-laki lebih dari 235 orang adalah 0,3085
a. Probabilitas proporsi kelahiran bayi laki-laki < 0,5
P(X > 235) = P(Z <(�+ 0,5)− ��
���� )
= P(Z <(235+0,5)−229
10,8361 )
= P(Z <0,59) = 0,5 + 0,2224 = 0,7224
Jadi, probabilitas banyaknya bayi laki-laki kurang dari 235 adalah 0,7224
b. Probabilitas proporsi kelahiran bayi laki-laki = 0,5
�
(
�
= 235) =
� �
(
� −
0,5)
− ��
����
<
�
<
(
�
+ 0,5)
− ��
����
�
=
� �
(235
−
0,5)
−
229
10,8361
<
�
<
=
�
(0,50 <
�
< 0,59)
= 0,2224
−
0,1915
= 0,0309
Jadi, probabilitas banyaknya bayi laki-laki sama dengan 234 adalah 0,0274
c. Probabilitas kelahiran bayi laki-laki = 0,4 berarti :
X = (0,4) . (470) = 188, sehingga :
Probabilitas proporsi kelahiran bayi laki-laki antara 0,4 dan 0,5 adalah :
�
(188 <
�
< 235) =
� �
(
� −
0,5)
− ��
����
<
�
<
(
�
+ 0,5)
− ��
����
�
=
� �
(188
−
0,5)
−
229
10,8361
<
�
<
(235 + 0,5)
−
229
10,8361
�
=
�
(
−
3,82 <
�
< 0,59)
= 0,4999 + 0,2224
= 0,7223
BAB 3
PEMBAHASAN
3.1 Pendekatan distribusi binomial dengan mengunakan Distribusi Normal
Dalam melakukan proses pengendalian kualitas, penting untuk melakukan pendekatan suatu distribusi probabilitas dengan distribusi probabilitas yang lain. Proses pendekatan akan berguna pada saat nilai tabel dari suatu distribusi tak ada. Dengan pendekatan distribusi yang lain akan didapatkan nilainya dengan tabel. Selain itu pendekatan distribusi dilakukan jika penggunaan distribusi aslinya tidak praktis.
Meskipun distribusi Poisson dapat di gunakan untuk mendekati distribusi binomial, terutama dalam kasus-kasus dimana n sangat besar, sedangkan p sangat kecil. Sebagai penggantinya kita dapat menggunakan distribusi normal untuk mendekati distribusi binomial apabila n bertambah besar. Umumnya jika µ = np > 5 , kita akan dapat menggunakan distribusi normal.
Karena distribusi Binomial merupakan distribusi yang diskrit, dan distribusi Normal merupakan distribusi yang kontinu, maka perlu ditambahkan faktor koreksi kontinuitas (continuity correction), yaitu sebesar 0.5. Jika n bernilai besar, maka pendekatan
distribusi Binomial dengan distribusi Normal dapat dilakukan dengan µ = np dan σ = ����.
Beberapa hal yang perlu dilakukan adalah dengan mengubah atau membakukan distribusi normal dalam bentuk distribusi normal standard yang dikenal dengan nilai Z atau skor Z. Rumus nilai Z adalah :
�=� − � �
Dengan :
Z = Skor Z atau nilai normal standar
X = Nilai dari suatu pengamatan atau pengukuran
µ = nilai rata-rata hitung suatu distribusi σ = standar deviasi suatu distribusi.
Untuk mengubah pendekatan dari binomial ke normal menurut Lind (2002) diperlukan faktor koreksi, selain syarat binomial terpenuhi yaitu : hanya terdapat dua peristiwa, peristiwa tersebut bersifat independent, besar probabilitas sukses dan gagal sama setiap percobaan dan data merupakan hasil penghitungan.
Apabila sudah memenuhi syarat binomial, maka kita menggunakan faktor koreksi yang besarnya 0,05. Faktor koreksi ini diperlukan untuk mentransformasi dari binomial menuju normal yang merupakan variabel acak kontinu.
3.2 Sifat Distribusi Binomial
satu ke percobaan lainnya. Proses ini disebut proses Bernoulli. Jadi proses Bernoulli harus memenuhi persyaratan berikut:
1. Percobaan terdiri atas n-eksperimen yang berulang
2. Tiap-tiap eksperimen memberikan hasil yang dapat dikelompokan menjadi 2 kategori, sukses atau gagal
3.Peluang kesuksesan dinyatakan dengan p, tidak berubah dari satu eksperimen ke eksperimen berikutnya.
4. Tiap eksperimen bebas dengan eksperimen lainnya.
Banyaknya X yang sukses dalam n- eksperimen Bernoulli disebut “peubah acak binomial”, dan distribusi dari peubah acak ini disebut “distribusi Binomial”. Jika p menyatakan probabilitas kesuksesan dalam suatu eksperimen, maka distribusi peubah acak X ini dinyatakan dengan b(x;n,p). Karena nilainya bergantung pada banyaknya eksperimen (n).
Probabilitas x kesuksesan dan n-x kegagalan dalam urutan tertentu. Tiap kesuksesan dengan probabilitas p dan tiap kegagalan dengan probabilitas q=1-p. Banyaknya cara untuk memisahkan n-hasil menjadi dua kelompok, sehingga x hasil ada pada kelompok pertama dan sisanya n-x pada kelompok kedua, jumlah ini dinyatakan sebagai ���� Karena pembagian tersebut saling terpisah (bebas) maka probabilitasnya adalah ��������−�.
Suatu usaha bernoulli dapat menghasilkan kesuksesan dengan probabilitas p dan kegagalan dengan probabilitas q=1-p, maka distribusi probabilitas peubah acak binomial X yaitu banyaknya kesuksesan dalam n- eksperimen bebas adalah :
�(�) =�(�;�;�) =��
������−� =�������−� �������= 1,2,3, …�
Adapun sifat-sifat dari distribusi binomial ini adalah:
2. Nilai dari varians (�2) untuk distribusi binomial adalah banyaknya eksperimen dikalikan dengan banyaknya sukses dan banyaknya gagal atau dengan kata lain
�2 = E (X − µ)2 = npq.
3. Nilai dari Simpangan baku (σ ) untuk distribusi binomial adalah akar dari varians atau dengan kata lain σ = ���� .
3.3 Teorema-teorema Pendukung
Dalam proses untuk mendekatkan distribusi binomial dengan menggunakan distribusi normal, maka diperlukan teorema-teorema pendukung yang terkait.
3.3.1 Teorema Limit Pusat ( Central Limit Theorem )
Teorema limit pusat menyatakan bahwa nilai tengah suatu sampel yang terdiri dari n buah nilai variabel random yang menyebar secara tidak normal, akan tetapi menyebar secara identik (dengan perkataan lain �1,�2, … ,�� memiliki fungsi kepadatan yang sama) serta bebas terhadap sesamanya, penyebarannya akan mendekati sebaran normal dengan pertambahan besarnya nilai n, jadi juga dengan bertambahnya ukuran sampel.
Jika �1,�2, … ,�� adalah n variabel random independent dengan distribusi yang identik dan memiliki mean µ dan varians �2. Jumlahnya dinyatakan sebagai berikut: X = �1+�2+⋯+��.
Karena mean dari jumlah adalah jumlah semua mean dan varian dari jumlah adalah jumlah semua varian, untuk variabel random independent, maka :
E (X) = nµ ; Var (X) = n�2
�=� − �(�) ����(�)=
�� − �� √��2
Kemudian dengan membagi pembilang dan penyebutnya dengan n, maka:
�= � − �� �/√�
Dengan:
��=�1+�2+⋯ ��
� =
X
� ,�����ℎ��������� − ������.
Central Limit Theorem, jika �1+�2+⋯ �� adalah n variabel random independent dengan distribusi yang identik, dengan mean µ dan varian �2. Dilambangkan dengan X dan �� adalah jumlah dari rata-rata dari variabel random ini. Sejalan dengan bertambahnya n, distribusi :
�=� − �� √��2 =
�� − � � √�
�������������������������������.
Dengan bantuan Central Limit Theorem ini, dalam prakteknya untuk masalah jumlah dan rata-rata variabel random, distribusi normal akan memberikan perkiraan yang cukup tepat mengenai distribusi yang sebenarnya.
Apapun distribusi dari sekelompok variabel random, selama variannya bersifat finit, jumlah atau rata-rata dari sejumlah besar variabel tersebut akan berupa variabel random dengan distribusi mendekati normal. Namun rata-rata variabel random dengan distribusi seragam yang independent dalam jumlah cukup besar, akan memiliki distribusi mendekati normal pula.
3.3.2 Teorema De Moivre-Laplace
Misalkan �1,�2, … ,�� suatu barisan variabel random, Sn menyatakan banyaknya sukses dalam suatu eksperimen binomial dengan n kali percobaan, masing-masing dengan probabilitas sukses p, 0<p<1. Misalkan Zn, n = 1, 2, ... barisan variabel random dengan:
�
�=
�
�− ��
����
,
Dan misalkan z suatu tetapan. Maka, bila n menuju ke takberhingga, P(Zn > z) mendekati luas pada distribusi normal standard di sebelah kanan z.
Atau dengan pernyataan lain teorema De Moivre-Laplace menyatakan bahwa : Jika Sn banyaknya sukses dalam n percobaan Bernoulli dan p adalah probabilitas sukses dan
�
�=
�
�− ��
����
,
���� ∶
�
��(
�
) =
�
(
�
�>
�
)
→ � �
−� 22 �
−∞
��
,
������
� → ∞
.
Teorema De Moivre-Laplace merupakan suatu bentuk dari teorema limit pusat yang cukup umum. Teorema ini membicarakan limit distribusi jumlah variabel random, dan limit distribusinya biasanya normal. Pentingnya teorema ini ialah bahwa dengan menggunakannya, dapat di hitung pendekatan peluang untuk jumlah variabel random dengan menggunakan distribusi normal tanpa perlu tahu distribusi jumlah variabel random dengan tepat.
Oleh karena distribusi binomial adalah distribusi untuk variabel random diskrit yang mana probabilitasnya berupa ordinat. Sedangkan distribusi normal merupakan distribusi untuk variabel random kontinu yang mana probabilitasnya berupa area (luasan), maka perlu diadakan penyesuaian (perubahan) dari ordinat menjadi luas. (panjang dikalikan lebar). Penyesuaian ini dilakukan sebagai berikut :
Misalkan X berdistribusi B(n,p), maka P(X=x) merupakan ordinat pada absis x. Tinggi ordinat sebagai nilai probabilitas dalam distribusi binomial, diambil sebagai panjang dan lebarnya diambil 1 unit. Jadi seolah-olah dibentuk persegi panjang berpusat pada x, dengan panjang setinggi nilai ordinat dan lebarnya adalah 1 unit (panjang interval x – 0,5 sampai dengan x + 0,5), sehingga didapatkan probabilitas yang asli (probabilitas diskrit = ordinat) sama dengan luas persegi panjang tersebut.
Dengan memperhatikan proses pendekatan dari distribusi binomial ke distribusi normal yang telah dibahas di atas, maka perhitungan pendekatan distribusi binomial oleh distribusi normal dapat dilakukan dengan cara sebagai berikut :
Jika X ~ B(n,p), maka untuk keperluan penghitungan P(X=x) dengan menggunakan distribusi normal adalah sebagai berikut:
P(X = x) = P (x – 0,5 < X < x + 0,5)
=
�
(
� −
0,5)
− ��
����
<
� − ��
����
<
(
�
+ 0,5)
− ��
����
�
=
� �
(
� −
0,5)
− ��
����
<
�
<
(
�
+ 0,5)
− ��
����
�
Dengan Z ~ N(0,1).
�
(
� ≥ �
) =
� �� ≥
(
� −
0,5)
− ��
����
�
�
(
� ≤ �
) =
� �� ≥
(
�
+ 0,5)
− ��
�
(
�
1<
�
<
�
2) =
�
(
�
1−
0,5 <
�
<
�
2+ 0,5)
=
� �
(
�
1−
0,5)
− ��
����
<
� − ��
����
<
(
�
2+ 0,5)
− ��
����
�
=
� �
(
�
1−
0,5)
− ��
����
<
�
<
(
�
2+ 0,5)
− ��
����
�
3.5 Contoh Kasus
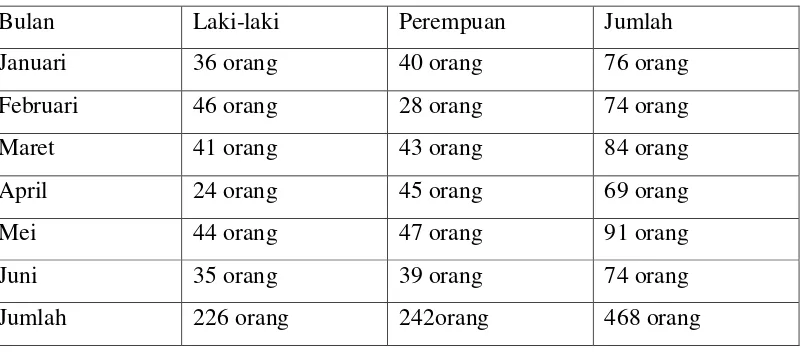
[image:54.595.114.516.381.557.2]Dari data kelahiran bayi menurut jenis kelamin, selama bulan Januari – Juni diperoleh data seperti tabel di bawah ini:
Tabel 3.1 Tabel Kelahiran Bayi Menurut Jenis Kelamin
Bulan Laki-laki Perempuan Jumlah
Januari 36 orang 40 orang 76 orang
Februari 46 orang 28 orang 74 orang
Maret 41 orang 43 orang 84 orang
April 24 orang 45 orang 69 orang
Mei 44 orang 47 orang 91 orang
Juni 35 orang 39 orang 74 orang
Jumlah 226 orang 242orang 468 orang
Dari data jenis kelamin bayi yang lahir diatas, dapat di peroleh hasil sebagai berikut : Banyak bayi lahir = 468 orang, yang terdiri dari :
Jenis kelamin laki-laki = 226 orang Jenis kelamin perempuan = 242 orang
Maka dapat dihitung misalnya :
b. Probabilitas proporsi kelahiran bayi laki-laki > 0,5 b. Probabilitas proporsi kelahiran bayi laki-laki < 0,5 c. Probabilitas proporsi kelahiran bayi laki-laki = 0,5
Penyelesaian :
Misalkan X adalah variabel random yang menyatakan banyaknya bayi laki-laki yang lahir.
n = 468 orang, p = peluang kelahiran bayi laki-laki = 226
468= 0,4829,
q = 1- 0,4829 = 0,5171 σ = ����= 10,8103
b. Probabilitas kelahiran bayi laki-laki = 0,5 berarti :
X = (0,5) . (468) = 234, Sehingga :
Probabilitas proporsi kelahiran bayi laki-laki > 0,5 adalah : P(X > 234) = P(Z >(� −0,5)− ��
���� )
= P(Z >(234−0,5)−226
10,8103 )
= P(Z >0,69) = 0,5−0,2549 = 0,2451
Jadi probabilitas banyaknya bayi laki-laki lebih dari 234 orang adalah 0,2451
d. Probabilitas proporsi kelahiran bayi laki-laki < 0,5
P(X < 234) = P(Z <(�+ 0,5)− ��
���� )
= P(Z <(234+0,5)−226
10,8103 )
= P(Z <0,78) = 0,5 + 0,2823 = 0,7823
e. Probabilitas proporsi kelahiran bayi laki-laki = 0,5
�
(
�
= 234) =
� �
(
� −
0,5)
− ��
����
<
�
<
(
�
+ 0,5)
− ��
����
�
=
� �
(234
−
0,5)
−
226
10,8103
<
�
<
(234 + 0,5)
−
226
10,8103
�
=
�
(0,69 <
�
< 0,78)
= 0,2823
−
0,2549
= 0,0274
Jadi, probabilitas banyaknya bayi laki-laki sama dengan 234 adalah 0,0274
f. Probabilitas kelahiran bayi laki-laki = 0,4 berarti :
X = (0,4) . (468) = 187, sehingga :
Probabilitas proporsi kelahiran bayi laki-laki antara 0,4 dan 0,5 adalah :
�
(187 <
�
< 234) =
� �
(
� −
0,5)
− ��
����
<
�
<
(
�
+ 0,5)
− ��
����
�
=
� �
(187
−
0,5)
− ��
10,8103
<
�
<
(234 + 0,5)
−
226
10,8103
�
=
�
(
−
3,65 <
�
< 0,69)
= 0,4999 + 0,2549
= 0,7548
Jadi, probabbilitas banyaknya bayi laki-laki antara 187 dan 234 adalah 0,7548.
Untuk melihat besarnya simpangan yang terjadi akibat pendekatan, akan diperlihatkan hasil perhitungan simpangan yang terjadi untuk setiap variabel random X (banyaknya sukses) dalam distribusi binomial dengan parameter n dan p, untuk pendekatan suku tunggal binomial maupun pendekatan binomial kumulatif. Dalam perhitungan ini digunakan program microsoft excel.
Tabel Distribusi Binomial (Terlampir) di peroleh dengan jalan menjalankan program untuk setiap parameter n dan p yang telah diketahui secara berulang-ulang.
Untuk probabilitas proporsi kelahiran bayi laki-laki > 0,5 dengan menggunakan distribusi binomial adalah sebesar 0,2437. Sedangkan dengan pendekatan distribusi normal diperoleh 0,2451. Itu berarti simpangan yang terjadi adalah sebesar 0,2451 – 0,2437 = 0,0014.
Untuk probabilitas proporsi kelahiran bayi laki-laki < 0,5 dengan menggunakan distribusi binomial adalah sebesar 0,7842. Sedangkan dengan pendekatan distribusi normal diperoleh 0,7823. Itu berarti simpangan yang terjadi adalah sebesar 0,7842 – 0,7823 = 0,0019.
Untuk probabilitas proporsi kelahiran bayi laki-laki = 0,5 dengan menggunakan distribusi binomial adalah sebesar 0,0280. Sedangkan dengan pendekatan distribusi normal diperoleh 0,0274. Itu berarti simpangan yang terjadi adalah sebesar 0,0280 – 0,0274 = 0,0006.
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Dari uraian bab-bab sebelumnya, maka dapatlah dibuat kesimpulan sebagai berikut : 1. Distribusi binomial dapat didekati oleh distribusi normal dengan parameter n
dan p.
2. Pendekatan distribusi binomial oleh distribusi normal kurang baik dilakukan untuk kondisi p yang berjarak jauh terhadap 0,5 dan n yang kecil.
2.2Saran
Saran yang dianggap perlu untuk dikemukakan sehubungan dengan kesimpulan, yaitu: 1. Dalam menentukan ukuran sampel yang akan digunakan dalam pendekatan
DAFTAR PUSTAKA
Adiningsih, Sri. 1993. Statistik. Yogyakarta: BPFE. Dixon, Wilfrid. J. 1991. Pengantar Analisis Statistik
Yogyakarta: UGM PRESS
Hakim, Abdul. 2002. Statistik Induktif untuk Ekonomi dan Bisnis. Yogyakarta: Ekonisia.
Sudjana, 2005. Metode Statistika Bandung: Tarsito
Walpole. Ronald E. 1993. Pengantar Statistika Jakarta: PT. Gramedia Pustaka Utama
Walpole, Ronald. E. 1995. Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuwan
Bandung: ITB